反比例函数常见几何模型
反比例函数19种模型

反比例函数19种模型反比例函数是数学中常见的函数类型之一,用来表示两个变量之间的反比关系。
以下是反比例函数的一些常见模型:1.直线模型:y = k/x,其中k为常数。
2.比例关系模型:y = (kx)/(ax + b),其中k、a、b为常数。
3.反比例关系模型:y = (k/x) + a,其中k、a为常数。
4.工作时间模型:y = k/t,其中k为常数,t表示时间。
5.人口密度模型:y = k/A,其中k为常数,A表示面积。
6.速度和时间模型:y = k/t,其中k为常数,t表示时间。
7.飞行时间和飞行距离模型:y = k/(x^2),其中k为常数,x表示距离。
8.投资收益模型:y = k/(x+a),其中k和a为常数,x表示投资金额。
9.流量与管道直径模型:y = k/(x^2),其中k为常数,x表示管道直径。
10.压力和体积模型:y = k/x,其中k为常数,x表示体积。
11.购买力和价格模型:y = k/x,其中k为常数,x表示价格。
12.照明强度和距离模型:y = k/(x^2),其中k为常数,x表示距离。
13.土地价格和面积模型:y = k/A,其中k为常数,A表示面积。
14.音量和距离模型:y = k/(x^2),其中k为常数,x表示距离。
15.饼干消耗和人数模型:y = k/n,其中k为常数,n表示人数。
16.温度和容器大小模型:y = k/V,其中k为常数,V表示容器大小。
17.实验结果和样本数量模型:y = k/n,其中k为常数,n表示样本数量。
18.电阻和电流模型:y = k/I,其中k为常数,I表示电流。
19.体积和浓度模型:y = k/C,其中k为常数,C表示浓度。
这些模型仅是反比例函数在不同应用领域中的一些示例。
实际上,反比例函数可以描述的反比关系很多,取决于具体应用的背景和需求。
对于不同的问题和场景,可以选择适合的反比例模型来建模和分析。
反比例函数常见几何模型(最新整理)

反比例函数常见模型一、知识点回顾例1:如图的锐角顶点是直线y=x+m 与双曲线y=在第一象限的交点,且ABC Rt ∆xm,(1)求m 的值 (2)求的面积3=∆AOB S ABC ∆分别过,,作y 轴平行1A 2A 3A ,作x 轴的平行线,2B 3B 影部分的面积之和为上,且AB ∥x 轴,C 、D 在x 轴上,任意不重合的两点,直线AB 交轴于Mx 轴于F 点,x BF ⊥DF例2:如图,一次函数y ax b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①;②相似于DEF CEF S S ∆∆=AOB ∆图1图2模型三:如图,已知反比例函数(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,ky x=交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则.S S =两点,)的中点E ,交AB 于点D ,若梯形 D. xy 6=题3 题4题5如图,A,B 是函数的图像上关于原点对称的任意xy 2=两点,BC//x 轴,AC//y 轴,的面积记为S ,则S (ABC ∆A.S=2 B.S=4 C.2<S<4 AB=AC=2,直角顶点A 在直线y=x 分别平行于x 轴,y 轴,若双曲线y=kx(1≤k<4B 1、如图,点A 在双曲线上,点B 在双曲线上,且AB ∥x 轴,C 、D 在x 轴上,1y x =3y x=若四边形ABCD 为矩形,则它的面积为 .、如图,双曲线经过四边形的顶点A 、C ,∠ABC =90°,OC )0(2x xy =轴正半轴的夹角,AB ∥轴,将△x交轴于,若,则的解析式是 .y C 1AOB S ∆=2y 课后习练一、填空题42、反比例函数y=kx的图像上有一点k=_______;点P 到原点的距离3、已知双曲线xy=1与直线4、反比例函数y=k的图像经过点 D .22到原点的距离为3)A.0个B.2个C.4个D.无数个。
反比例函数常见几何模型归纳(七大模型)(解析版)-初中数学
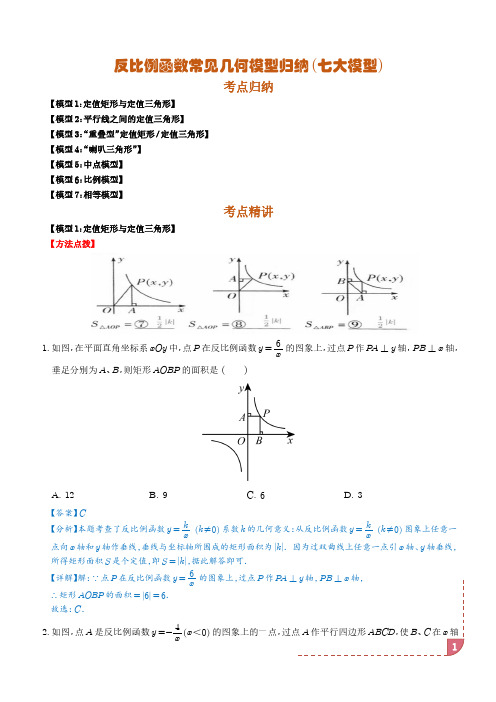
反比例函数常见几何模型归纳(七大模型)考点归纳【模型1:定值矩形与定值三角形】【模型2:平行线之间的定值三角形】【模型3:“重叠型”定值矩形/定值三角形】【模型4:“喇叭三角形”】【模型5:中点模型】【模型6:比例模型】【模型7:相等模型】考点精讲【模型1:定值矩形与定值三角形】【方法点拨】1.如图,在平面直角坐标系xOy 中,点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,垂足分别为A 、B ,则矩形AOBP 的面积是()A.12B.9C.6D.3【答案】C【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .因为过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积S 是个定值,即S =k ,据此解答即可.【详解】解:∵点P 在反比例函数y =6x的图象上,过点P 作P A ⊥y 轴,PB ⊥x 轴,∴矩形AOBP 的面积=6 =6.故选:C .2.如图,点A 是反比例函数y =-4x <0 的图象上的一点,过点A 作平行四边形ABCD ,使B 、C 在x 轴上,点D 在y 轴上,则平行四边形ABCD 的面积为()A.2B.4C.6D.8【答案】B【分析】本题考查了反比例函数y =k x k ≠0 系数k 的几何意义:从反比例函数y =kxk ≠0 图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为k .作AH ⊥OB 于H ,根据平行四边形的性质得AD ∥OB ,则S 平行四边形ABCD =S 矩形AHOD ,再根据反比例函数y =kxk ≠0 系数k 的几何意义得到S 矩形AHOD =-4 =4,所以有S 平行四边形ABCD =4.【详解】解:作AH ⊥OB 于H ,如图,∵四边形ABCD 是平行四边形,∴AD ∥OB ,∴S 平行四边形ABCD =S 矩形AHOD ,∵点A 是反比例函数y =-4xx <0 的图象上的一点,∴S 矩形AHOD =-4 =4,∴S 平行四边形ABCD =4.故选:B .3.如图,A 、B 是反比例函数y =kx(k ≠0)的图象上两点,点C 、D 、E 、F 分别在坐标轴上,若正方形OCAD 的面积为6,则矩形OEBF 的面积为.【答案】6【分析】本题主要考查反比例函数中比例系数k 的几何意义和函数图象的对称性,难易程度适中,是中考较常见的考查点.根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的四边形的面积S 的关系即S =k ,进行解答即可.【详解】解:∵S 正方形OCAD =OD ⋅OC =x A ⋅y A =k =6,∴S 长方形OCAD =OE ⋅OF =x B ⋅y B =k =6.故答案为:6.4.如图是反比例函数y =-4x在第二象限内的图象,则图中矩形BCOA 的面积为.【答案】4【分析】根据矩形的面积公式S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,再根据反比例函数的性质解答即可.本题考查了矩形的面积公式,反比例函数的性质,熟练运用反比例函数的性质是解题的关键.【详解】解:设点B a ,b ,∵四边形BCOA 是矩形,∴AB =a ,BC =b ,∴S 矩形BCOA =AB ⋅BC =a ⋅b =ab ,∵点B 在反比例函数y =-4x在图象上,∴a ⋅b =-4,∴a ⋅b =4,∴S 矩形BCOA =ab =4;故答案为4.【模型2:平行线之间的定值三角形】【方法点拨】5.如图,是反比例函数y =5x 和y =-9x在x 轴上方的图象,x 轴的平行线AB 分别与这两个函数图象相交于点A ,B ,则△AOB 的面积是()A.7B.14C.18D.28【答案】A【分析】本题考查了反比例函数k 的几何意义,利用反比例函数的比例系数的几何意义直接写出答案即可.【详解】解:∵x 轴的平行线AB 分别与这两个函数图象相交于点A .B ,∴AB ⊥y 轴,∵点A 、B 在反比例函数y =5x 和y =-9x 的x 轴上方的图象上,∴S △AOB =S △COB +S △AOC =12(5+9)=7,故选:A .6.已知反比例函数y =-6x x <0 与y =2xx >0 的图象如图所示,过y 轴正半轴上的任意一点P 作x 轴的平行线,分别与这两个函数的图象交于M ,N 两点.若点A 是x 轴上的任意一点,连接MA ,NA ,则S △AMN 等于.【答案】4【分析】本题考查了反比例函数k 的几何意义,连接MO ,NO ,根据MN ∥x 轴可得,S △AMN =S △OMN ,进而即可求解.【详解】解:如图所示,连接MO ,NO ,∵MN ∥x 轴∴S △AMN =S △OMN =S △POM +S △PON =-62+22=4故答案为:4.7.如图,在函数y =2x x >0 的图象上任取一点A ,过点A 作y 轴的垂线交函数y =-8xx <0 的图象于点B ,连接OA 、OB ,则△AOB 的面积是.【答案】5【分析】根据反比例函数系数k 的几何意义进行计算即可.理解反比例函数系数k 的几何意义是正确解答的关键.【详解】解:如图,∵点A 在函数y =2xx >0 的图象上,∴S △AOC =12×2=1,又∵点B 在反比例函数y =-8xx <0 的图象上,∴S △BOC =12×8=4,∴S △AOB =S △AOC +S △BOC =1+4=5,故答案为:5.8.如图,B 、C 两点分别在函数y =5x (x >0)和y =-1x(x <0)的图象上,线段BC ⊥y 轴,点A 在x 轴上,则△ABC 的面积为.【答案】3【分析】设B m ,n ,则mn =5,结合BC ⊥y 轴,得到C -1n ,n ,计算BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为1BC ·y B =1m +1×n 计算即可.本题考查了反比例函数的性质,平行线间距离处处相等,熟练掌握反比例函数的性质是解题的关键.【详解】设B m ,n ,根据题意,得mn =5,∵BC ⊥y 轴,∴C -1n ,n ,∴BC =m --1n =m +1n,根据平行线间的距离处处相等,得到△ABC 的面积为12BC ·y B =12m +1n ×n =12mn +1 =3,故答案为:3.【模型3:“重叠型”定值矩形/定值三角形】【方法点拨】9.如图,点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,且AB ∥x 轴,点C .D 在x 轴上,若四边形ABCD 为长方形,则它的面积为.【答案】2【分析】此题考查了反比例函数的系数k 的几何意义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.首先延长BA 交y 轴于点E ,易得四边形ADOE 与四边形BCOE 是矩形,又由点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,即可得S 矩形ADOE =1,S 矩形BCOE =3,继而求得答案.【详解】解:延长BA 交y 轴于点E ,∵四边形ABCD 为矩形,且AB ∥x 轴,点C 、D 在x 轴上,∴AE ⊥y 轴,∴四边形ADOE 与四边形BCOE 是矩形,∵点A 在反比例函数y =1x 的图像上,点B 在反比例函数y =3x的图像上,∴S 矩形ADOE =1,S 矩形BCOE =3,∴S 矩形ABCD =S 矩形BCOE -S 矩形ADOE =3-1=2.故答案为:2.10.如图,点A 、B 分别是反比例函数y =3xx >0 的图象上两点,分别过点A 、B 向坐标轴作垂线,四边形ACEG 的面积记作S 1,四边形BFDG 的面积记作S 2,则S 1S 2(填>、<或=).【答案】=【分析】本题考查了反比例系数k 的几何意义,在反比例函数y =kx图像中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值k ,在反比例函数的图像上任意一点作坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12k ,且保持不变.根据反比例函数解析式中k 的几何意义可知S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,得出S 1=3-m ,S 2=3-m ,即可得出答案.【详解】解:∵A ,B 两点在反比例函数y =3xx >0 的图像上,∴S 矩形ACOD =S 矩形BEOF =3,设S 矩形DOEG =m ,∴S 1=3-m ,S 2=3-m ,∴S 1=S 2.故答案为:=.11.如图,平行于x 轴的直线l 与函数y =6x (x >0)和y =2x(x >0)的图象分别相交于A ,B 两点,分别连接AO 、BO ,则△ABO 的面积为.【答案】2【分析】本题考查反比例函数图象上点的坐标特征,k 的几何意义,设l 交y 轴于点M ,根据反比例函数k 的几何意义,得出S △ABO =S △AOM -S △BOM =2,即可求解.【详解】解:如图,设l 交y 轴于点M ,∵S △AOM =3,S △BOM =1,则S △ABO =S △AOM -S △BOM =2,故答案为:2.12.如图,点A 在双曲线y =1x 上,点B 在双曲线y =3x上,且AB ∥x 轴,则△ABO 的面积是.【答案】1【分析】本题主要考查了反比例函数比例系数的几何意义,延长BA 交y 轴于C ,则AB ⊥y 轴,根据反比例函数比例系数的几何意义可得S △AOC =12,S △BOC =32,则S △AOB =S △BOC -S △AOC =1.【详解】解:如图所示,延长BA 交y 轴于C ,∵AB ∥x 轴,∴AB ⊥y 轴,∵点A 在双曲线y =1x 上,点B 在双曲线y =3x上,∴S △AOC =12,S △BOC =32,∴S △AOB =S △BOC -S △AOC =1,故答案为:1.【模型4:“喇叭三角形”】【方法点拨】13.如图,点A ,B ,在反比例函数y =4x的图象上,连接OA ,OB ,分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,图中两块阴影部分面积分别为S 1、S 2;若S 1=1,则AMBN=.【答案】2【分析】本题考查的是反比例函数系数k 的几何意义,熟知在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积为12|k |是解答此题的关键.利用k 的几何意义求出△OAM 、△OBN 的面积,然后求出△OCM 的面积,利用相似三角形的性质得到S △OCM S △OBN =OM ON 2即可求解.【详解】解:设OB 交AM 于点C ,∵分别过点A ,B 作x 轴的垂线,垂足分别为M ,N ,∴S △OAM =S △OBN =2,∴S △OCM =S △OAM -S 1=2-1=1,又∵AM ∥BN ,∴△OCM ∽△OBN ,∴S △OCM S △OBN =OM ON2=12,∴OM ON=22,又∵OM ⋅AM =ON ⋅BN ,∴AM BN =ON OM =2.故答案为:214.如图是一个反比例函数(x >0)的图象,点A (2,4)在图象上,AC ⊥x 轴于C ,当点A 运动到图象上的点B (4,2)处,BD ⊥x 轴于D ,△AOC 与△BOD 重叠部分的面积为()A.1B.2C.34D.13【答案】A【解答】解:如图所示:∵点A (2,4),点B (4,2),AC ⊥x 轴于C ,BD ⊥x 轴于D ,∴点C 的坐标为(2,0),点D 的坐标为(4,0),AC ∥BD ,∴△OCE ∽△ODB ,∴OC OD =CE DB ,即24=CE 2解得CE =1,∴S △OCE OC ⋅CE 2=2×12=1,即△AOC 与△BOD 重叠部分的面积为1.故选:A .15.如图,过反比例函数y =9x(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得()A.S 1>S 2B.S 1=S 2C.S 1<S 2D.大小关系不能确定【答案】B 【解答】解:由于A 、B 均在反比例函数y =9x 的图象上,且AC ⊥x 轴,BD ⊥x 轴,则S 1=92;S 2=92.故S 1=S 2.故选:B .16.如图,在第一象限内,点P (2,3),M (a ,2)是双曲线y =k x (k ≠0)上的两点,P A ⊥x 轴于点A ,MB ⊥x 轴于点B ,P A 与OM 交于点C ,则△OAC 的面积为()A.32B.43C.2D.83【答案】B 【解答】解:把P (2,3),M (a ,2)代入y =k x得k =2×3=2a ,解得k =6,a =3,设直线OM 的解析式为y =mx ,把M (3,2)代入得3m =2,解得m =23,所以直线OM 的解析式为y =23x ,当x =2时,y =23×2=43,所以C 点坐标为(2,43),所以△OAC 的面积=12×2×43=43.故选:B .【方法点拨】条件:A /B 两点分别位y =k x上不同两点,延长AB 交x 轴与点F ,B 位AF 的中点结论:①▲ACF ~▲BDF ,且相似比为BF AF =12。
反比例函数常见几何模型(完整资料).doc

【最新整理,下载后即可编辑】反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=k x(k≠0).其解析式有三种表示方法:①xk y = (0≠k );②1-=kx y (0≠k );③k xy =2.反比例函数y=k x(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=k x 中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=k x图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-. (5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=m 在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x=上,点B 在双曲线3y x=上,且AB∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB交x 轴于M 点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数kyx=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEFS S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE≌△CDF ;④A CB D =其中正确的结论是 .(把你认为正确结论的序号都填上)y xDC A BOFEDFABDF MN xy O例3:一次函数y ax b=+的图象分别与x轴、y轴交于点,M N,与反比例函数kyx=的图象相交于点,A B.过点A分别作AC x⊥轴,AE y⊥轴,垂足分别为,C E;过点B分别作BF x⊥轴,BD y⊥轴,垂足分别为F D,,AC与BD交于点K,连接CD.(1)若点A B,在反比例函数kyx=的图象的同一分支上,如图1,试证明:①AEDK CFBKS S=四边形四边形;②AN BM=.(2)若点A B,分别在反比例函数kyx=的图象的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论.模型三:如图,已知反比例函数kyx=(k≠0,x>0)上任意两点P、C,过P做PA⊥x轴,交x轴于点A,过C做CD⊥x轴,交x轴于点D,则OPC PADCS S∆=梯形.图1 图2例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)k y k x=>交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)k y k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)k y x x=>的图象与AC 边交于点E ,则CEaCFb=.例7:两个反比例函数k y x=和1y x=在第一象限内的图象如图所示,点P 在k y x=的图象上,PC ⊥x 轴于点C ,交1y x=的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在k y x=的图象上运动时,以下结论: ①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发xBFC EAOy生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )A. B. C. D2、如图,点A 在双曲线xy 6=上,且OA=4,过点A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC于B,则ABC ∆的周长为( )A.72B.5C.74D.223、如图,双曲线xk y =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( )A.xy 1= B.xy 2=C.xy 3=D.x y 6=题 3 题 4 题54、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,则S ( )A.S=2B.S=4C.2<S<4D.S>45、如图所示,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,若双曲线y=k x(k≠0)与△ABC 有交点,则k 的取值范围是( )A .1<k<2B .1≤k≤3C .1≤k≤4 D.1≤k<4二、填空题1、如图,点A 在双曲线1y x=上,点B 在双曲线3y x=上,且AB∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .2、如图,双曲线)0(2 x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 . 3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′.(1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 .4、如图,已知双曲线(0)k y k x=<经过直角三角形OAB 斜边OA 的DBAyxOC中点D,且与直角边AB相交于点C.若点A的坐标为(6-,4),则△AOC的面积为.5、双曲线1y、2y在第一象限的图像如图,14yx=,过1y上的任意一点A,作x轴的平行线交2y于B,交y轴于C,若1AOBS∆=,则2y的解析式是.课后习练一、填空题1、如图,直线y=kx(k>0)与双曲线y=4x交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1的值等于_______.2、反比例函数y=kx的图像上有一点P(a,b),且a,b是方程t2-4t-2=0的两个根,则k=_______;点P到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b无交点,则b的取值范围是______.4、反比例函数y=kx的图像经过点P(a,b),其中a,b是一元学习靠自觉,进步靠努力,每天比别人多付出一点点,将来比别人收获多许多!!! 【最新整理,下载后即可编辑】 二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______.5、如图,已知双曲线)0k (xk y > 经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图6、如图,已知点A 是一次函数y=x 的图像与反比例函数y=2x 的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( )A .2B .22C .2D .22 7、已知P 为函数y=2x 的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( ) A .0个 B .2个C .4个D .无数个AB CD E y x O。
反比例函数十大模型

反比例函数十大模型反比例函数是一种常见的数学函数,它可以用来描述两个变量之间的反比例关系。
它的表达式为:y=k/x,其中k为常数,x为自变量,y为因变量。
反比例函数的特点是:当x增大时,y减小;当x减小时,y增大。
反比例函数是一种数学模型,它表示两个变量之间呈规律性反比关系的函数。
反比例函数的一般形式为 y=k/x,其中 x 和 y 是两个变量,k 是常数。
在这个模型中,当 x 的值变大时,y 的值会变小;当 x 的值变小时,y 的值会变大。
下面列举出十种常见的反比例函数模型:1.空气阻力模型:在一些物理运动的过程中,物体的运动受到空气的阻力影响,空气阻力与物体的速度呈规律性反比关系,可以用反比例函数来描述。
例如:F=kv^2,其中F 是空气阻力,v 是物体的速度,k 是常数。
2.电视天线模型:电视天线的收视质量与天线的高度呈规律性反比关系,可以用反比例函数来描述。
例如:Q=k/h,其中 Q 是电视天线的收视质量,h 是天线的高度,k 是常数。
3.热传导模型:在热传导过程中,热传导速度与热导率之间呈规律性反比关系,可以用反比例函数来描述。
例如:q=k/δ,其中 q 是热流密度,δ是热导率,k 是常数。
4.声音传播模型:声音在空气中的传播速度与温度之间呈规律性反比关系,可以用反比例函数来描述。
例如:v=k/T,其中 v 是声音的传播速度,T 是温度,k 是常数。
5.水流流速模型:水流的流速与水流的流量之间呈规律性反比关系,可以用反比例函数来描述。
例如:v=k/q,其中 v 是水流的流速,q 是水流的流量,k 是常数。
6.车辆油耗模型:车辆的油耗与车辆的速度之间呈规律性反比关系,可以用反比例函数来描述。
例如:F=k/v,其中 F 是车辆的油耗,v 是车辆的速度,k 是常数。
7.转角灵敏度模型:机器人的转角灵敏度与机器人的转速之间呈规律性反比关系,可以用反比例函数来描述。
例如:θ=k/ω,其中θ是机器人的转角灵敏度,ω是机器人的转速,k 是常数。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kxk≠0).其解析式有三种表示方法:①xk y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=kx图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练模型一:如图,点A 为反比例函数xky =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M 点,交y轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D=其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数k y x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD . (1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.图1图2模型三:如图,已知反比例函数ky x=(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则OPC PADC S S ∆=梯形.例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点,且点A 的横坐标为4.(1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)ky x x =>的图象与AC 边交于点E ,则CE a CF b=.例7:两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形P AOB 的面积不会发生变化;③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).xBFC EAOy课堂练习一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )A. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,则ABC ∆的周长为( )A.72B.5C.74D.22 3、如图,双曲线xky =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( )A.x y 1=B. x y 2=C. xy 3= D. xy 6=题3 题4 题5 4、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,则S ( )A.S=2B.S=4C.2<S<4D.S>45、如图所示,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,A y其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,若双曲线y=k x(k≠0)与△ABC 有交点,则k 的取值范围是( )A .1<k<2B .1≤k≤3C .1≤k≤4D .1≤k<4二、填空题1、如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .2、如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 .3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 .4、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .- 11 - 课后习练 一、填空题 1、如图,直线y=kx (k>0)与双曲线y=4x交于A (x 1,y 1),B (x 2,y 2)两点,则2x 1y 2-7x 2y 1的值等于_______.2、反比例函数y=k x的图像上有一点P (a ,b ),且a ,b 是方程t 2-4t -2=0的两个根,则k=_______;点P 到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b 无交点,则b 的取值范围是______.4、反比例函数y=k x的图像经过点P (a ,b ),其中a ,b 是一元二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______. 5、如图,已知双曲线)0k (x k y >经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图6、如图,已知点A 是一次函数y=x 的图像与反比例函数y=2x的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( )A .2B .22 C .2 D .22 7、已知P 为函数y=2x的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( ) A .0个 B .2个 C .4个 D .无数个A B CDE y x O。
6反比例函数九种基本模型

反比例函数九种基本模型
一、2个矩形模型
模型特点:曲线切坐标矩形 模型特点:曲线截坐标矩形
结论:k S OABC =矩形 结论:(1)DE ∥AC (2)2)(OB
OF CB CE AB AD == 二、3个等线段模型
模型特点:经过原点双交曲 模型特点:与双曲线单支 模型特点:与双曲线双交直线 线的直线 相交直线
结论:OA =OB 结论:AB =CD 结论:AB =CD 三、4类三角形模型
(1)一点在线,两点在轴,一边或两边垂直于轴 结论:k S 2
1=∆
(2)两点在线,原点对称,一边垂直于轴 结论:k S =∆
(3)两点在线,原点对称,两边垂直于轴 (4)两点在线,一点在心
结论:k S 2=∆ 结论:ACDB OAB S S 梯形=∆。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kxk≠0).其解析式有三种表示方法:①xk y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=kx图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =ANDFAB DF MNxy O例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD .(1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.y x DC A B O F E图1图2模型三:如图,已知反比例函数ky x=(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则OPC PADC S S ∆=梯形.例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F点的反比例函数(0)ky x x =>的图象与AC 边交于点E,则CEa CF b=.例7:两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x=的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形P AOB 的面积不会发生变化;③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )xB FC E A O yA. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,则ABC ∆的周长为( ) A.72 C.74 D.22 3、如图,双曲线xky =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( ) A.x y 1=B. x y 2=C. x y 3=D. xy 6=题 3 题 4 题54、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC ABC∆k x 1y x =3y x=DB AyxO C2、如图,双曲线)0(2φx xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 .3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 .4、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .课后习练一、填空题1、如图,直线y=kx (k>0)与双曲线y=4x交于A (x 1,y 1),B (x 2,y 2)两点,则2x 1y 2-7x 2y 1的值等于_______.2、反比例函数y=kx的图像上有一点P (a ,b ),且a ,b 是方程t 2-4t -2=0的两个根,则k=_______;点P 到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b 无交点,则b 的取值范围是______.4、反比例函数y=kx的图像经过点P (a ,b ),其中a ,b 是一元二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______. 5、如图,已知双曲线)0k (xky >经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图 像与反比例函数y=2x的图6、如图,已知点A 是一次函数y=x 的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( ) A .2 B .22C .2D .227、已知P 为函数y=2x的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( ) A .0个 B .2个 C .4个 D .无数个AB CD E yx O。
反比例函数:11类模型梳理

反⽐例函数:11类模型梳理⼀、反⽐例函数的基本性质1、反⽐例函数图象是由两条曲线组成的双曲线,双曲线向坐标轴⽆限延伸,但不能与坐标轴相交;2、k的正负性,决定双曲线⼤致位置及y随x的变化情况;3、双曲线上的点是关于中⼼对称的,双曲线也是轴对称图形,对称轴是直线y=x及y=-x.4、反⽐例函数y=k/x中| k |的⼏何意义是:| k |等于双曲线上任意⼀点作x轴、y轴的垂线的矩形的⾯积。
⼆、反⽐例函数的基本模型模型⼀、对称性结论:∵正⽐例、反⽐例函数的图象都是关于原点成中⼼对称图形,∴①OA=OB,OC=OD;②四边形ACBD是平⾏四边形;模型⼆:双曲矩形结论:1、不论P在双曲线上何处,2、当OA在x轴上平移时,同理:当OB在y轴上平移时,等底同⾼可证,证明略模型三:双曲三⾓形结论:1、不论P在双曲线上何处,2、不论O'在y轴上何处,同底等⾼可证,证明略模型四:等分⾯积结论:3、若Q为AB中点,则P也必为BC中点。
由2可得,证明略模型五:三⾓转梯形结论:模型六:斜向平⾏线结论:过双曲线上任意两点P、Q分别作PC⊥y轴于C,QA⊥x轴于A,连结AC,则PQ∥AC模型七:等长线段结论:过双曲线上任意两点P、Q作直线PQ分别交x轴、y轴于点M、N,则PN=QM模型⼋:等⾓1——平四型结论:P、Q在双曲线上,A、B分别在y轴和x轴上,若四边形ABQP为平⾏四边形,则∠1=∠2,∠3=∠4证明:过P作DE⊥y轴于E过Q作DC⊥x轴于C交DE于D,延长PQ交x轴、y轴于M、N由模型七得∵ABQP为平⾏四边形∴PQ∥AB,AP∥BQ,PQ=AB,AP=BQ∴∠2=∠6=∠EPA∵∠PEA=∠BCQ=90°∴△PEA≌△BCQ(AAS)∴PE=BC=a,∵OM=a+b,OC=b,∴CM=OM-OC=a∴BC=CM∴△QCB≌△QCM,∴∠2=∠5,⼜∵∠1=∠5,∴∠1=∠2同理可证∠3=∠4模型九:等⾓2——对称型结论:正⽐例函数图象与双曲线交于Q、R两点,则∠1=∠2,∠3=∠4证明:作P点关于点O对称点S,连SR,SP,SQ易证四边形PQSQ为平⾏四边形由模型⼋可知∠2=∠5,⼜∵PR∥QS,∴∠5=∠1,∴∠1=∠2∵∠2+∠4=90°,∠3+∠1=90°∴∠3=∠4模型⼗:等腰黄⾦⽐结论:P、Q都在双曲线上,OP=PQ,OP⊥PQ,证明:过P作BC⊥y轴于C,过Q作BA⊥x轴于A交BC于B ∵P(a,b)∴PC=a,OC=b∵OP=PQ,OP⊥PQ,∴∠CPO +∠COP= 90°,∠CPO+∠BPQ=90°∴∠COP=∠BPQ∵∠OCP=∠PBQ,∴△OCP≌△PBQ∴PC=BQ=a,OC=PB=b∴B(a+b,b-a),Q(a+b,b-a)连AC,由模型六可知,PQ∥AC模型⼗⼀:平⾏黄⾦⽐结论:P在双曲线上,过P作PA⊥x轴于A,过A作AQ∥OP交双曲线于Q.证明:过P作BC⊥y轴于C,过Q作BD⊥x轴于D,交BC于B由AQ∥OP易证△OAP≌△ADQ怎么样?11类反⽐例模型都掌握了么?除此,今天⾼分君给⼤家带了《反⽐例函数培优40讲》课程。
反比例函数6个模型

反比例函数6个模型反比例函数是数学中常见的一种函数关系,表示两个变量之间的关系,其中一个变量的值与另一个变量的值成反比。
在实际生活中,有很多与反比例函数相关的问题,如速度与时间、密度与体积等。
下面将介绍6个反比例函数的模型及其应用。
一、速度与时间模型速度与时间成反比例函数的模型可以表示为v=k/t,其中v表示速度,t表示时间,k为比例常数。
在实际应用中,比如汽车行驶,行驶的速度与所用的时间成反比。
这个模型在物理学和工程学中非常常见。
二、密度与体积模型密度与体积成反比例函数的模型可以表示为d=k/V,其中d表示密度,V表示体积,k为比例常数。
例如,气体的密度与其体积成反比,当气体的体积增大时,密度相应减小。
三、电阻与电流模型电阻与电流成反比例函数的模型可以表示为R=k/I,其中R表示电阻,I表示电流,k为比例常数。
这个模型在电路中非常重要,它描述了电阻对电流的阻碍作用。
四、人口增长与资源消耗模型人口增长与资源消耗成反比例函数的模型可以表示为P=k/R,其中P表示人口数量,R表示资源消耗,k为比例常数。
这个模型可以用来研究人口爆炸对资源的需求与消耗关系。
五、物体质量与重力加速度模型物体质量与重力加速度成反比例函数的模型可以表示为m=k/g,其中m表示物体质量,g表示重力加速度,k为比例常数。
这个模型可用于计算物体在不同重力场中的质量。
六、电压与电流模型电压与电流成反比例函数的模型可以表示为V=k/I,其中V表示电压,I表示电流,k为比例常数。
这个模型在电路分析中广泛使用,它描述了电阻对电流和电压的影响。
总结起来,反比例函数具有多种模型,分别应用于速度与时间关系、密度与体积关系、电阻与电流关系、人口增长与资源消耗关系、物体质量与重力加速度关系以及电压与电流关系。
这些模型在不同领域有着广泛的应用,帮助我们理解和解决实际问题。
(完整)反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kx(k≠0).其解析式有三种表示方法:①x k y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质 (1)当k 〉0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小. (2)当k 〈0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=k x图像上一点(a,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A为反比例函数xky =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x 8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M 点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是 .(把你认为正确结论的序号都填上)y DA B ODFAB DF MN xy O例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD . (1)若点A B ,在反比例函数k y x=的图象的同一分支上,如图1,试证明:①AEDK CFBK S S =四边形四边形;②AN BM =.(2)若点A B ,分别在反比例函数k y x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.模型三:如图,已知反比例函数k y x=(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则OPC PADC S S ∆=梯形.图1图2例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.比例函数例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反是______.2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积两点,且点例6:如图1,已知直线12y x =与双曲线(0)k y k x =>交于A 、BA 的横坐标为4.(1)求k的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)k y k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)ky x x=>的图象与AC 边交于点E ,则CE aCF b=。
反比例函数常见几何模型

反比例函数常见几何模型反比例函数是一种特殊的函数类型,它描述了一种比例关系,其中一个变量的变化与另一个变量的变化成反比。
它在数学上的一般形式为y=k/x,其中k是一个常数,x和y是变量。
在几何学中,反比例函数常见于许多不同的模型中。
以下是一些常见的几何模型,这些模型可以用反比例函数来描述。
1.电阻和电流:欧姆定律描述了电阻和电流之间的关系,即电流与电阻成反比。
根据欧姆定律,电流I在电阻R中的关系为I=V/R,其中V是电压。
这个关系可以使用反比例函数来描述。
2.凸透镜的放大力:凸透镜的放大力与物体离透镜的距离成反比。
放大力是指通过透镜放大影像的能力。
根据物理学的知识,放大力F与物体离透镜的距离s的关系为F=k/s,其中k是一个常数。
这个关系可以使用反比例函数来表示。
3.时间和速度:根据物理学中的速度定义,速度v等于物体所走的距离d除以所花费的时间t。
因此,速度与时间成反比。
速度v和时间t之间的关系可以表示为v=k/t,其中k是一个常数。
这个关系可以使用反比例函数来描述。
4.管道流量和管道直径:在液体或气体流体力学中,管道的直径和流量之间成反比。
根据伯努利原理,如果管道的截面积减小,则液体或气体的速度增加,从而使流量增加。
因此,管道的直径和流量之间的关系可以用反比例函数表示。
5.球体的表面积和半径:球体的表面积与其半径成反比。
根据数学知识,球体的表面积S与其半径r之间的关系为S=4πr^2、从这个方程可以看出,当半径增加时,表面积会减小。
因此,球体的表面积和半径之间可以用反比例函数描述。
6.声波的衰减:声波在传播过程中会经历衰减,衰减的程度与传播距离成反比。
声波的衰减率与传播距离之间的关系可以用反比例函数来描述。
以上是反比例函数在几何模型中的一些常见应用。
这些模型在科学研究和实际应用中都具有重要的意义。
通过理解和运用反比例函数,我们可以更好地了解和解释这些几何模型。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kx(k≠0).其解析式有三种表示方法:①xky =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=k x图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =ANDFA B DF MNxyO例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD .(1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.y x DC A B OFE图 1图2模型三:如图,已知反比例函数ky x =(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则OPC PADC S S ∆=梯形.例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)k y k x =>交于A 、B 两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(0)ky x x=>的图象与AC 边交于点E ,则CE a CF b =.例7:两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在k y x=的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )xB FC E A OyA. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,则ABC ∆的周长为( )A.72B.5C.74D.22 3、如图,双曲线xky =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( ) A.x y 1=B. x y 2=C. x y 3=D. xy 6=题 3 题 4 题54、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,则S ( )A.S=2B.S=4C.2<S<4D.S>45、如图所示,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,若双曲线y=kx(k≠0)与△ABC 有交点,则k 的取值范围是( )A .1<k<2B .1≤k≤3C .1≤k≤4 D.1≤k<4二、填空题DB AyxO C1、如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为.2、如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 .3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是.4、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B ,交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .课后习练一、填空题1、如图,直线y=kx (k>0)与双曲线y=4x交于A (x 1,y 1),B (x 2,y 2)两点,则2x 1y 2-7x 2y 1的值等于_______.2、反比例函数y=k x的图像上有一点P (a ,b ),且a ,b 是方程t 2-4t -2=0的两个根,则k=_______;点P 到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b 无交点,则b 的取值范围是______.4、反比例函数y=k x的图像经过点P (a ,b ),其中a ,b 是一元二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______.5、如图,已知双曲线)0k (xk y >=经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图与反比例函数y=2x的图像6、如图,已知点A 是一次函数y=x 的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( ) A .2 B .22C .2D .22 7、已知P 为函数y=2x的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( ) ABCD EyxOA.0个 B.2个 C.4个 D.无数个。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kxk≠0).其解析式有三种表示方法:①xk y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=kx图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =AN例2:如图,一次函数y a x b =+的图象与x y 轴交于A ,B 两点,与反比例函数k y x=的图象相交于C ,D 两点,分别过C D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D=其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x =的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD . (1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明:①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗?试证明你的结论.模型三:如图,已知反比例函数ky x=(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴y xDCA B O F E图1图2 DF A B D F M Nxy O于点D ,则OPC PADC S S ∆=梯形.例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______. 例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)ky k x=>交于A 、B两点,且点A 的横坐标为4. (1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F点的反比例函数(0)ky x x =>的图象与AC 边交于点E ,则CE a CF b =.例7:两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x=的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形P AOB 的面积不会发生变化;③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上). 课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )A. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,则ABC ∆的周长为( )A.72B.5C.74D.22 3、如图,双曲线xky =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( ) A.x y 1=B. x y 2=C. x y 3=D. xy 6= 题3 题4 题5 4、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC//x 轴,AC//y 轴,ABC ∆的面积记为S ,则S ( )A.S=2B.S=4C.2<S<4D.S>45、如图所示,等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y=x 上,其中A 点的横坐标为1,且两条直角边AB ,AC 分别平行于x 轴,y 轴,若双曲线y=kx(k≠0)与△ABC 有交点,则k 的取值范围是( )A .1<k<2B .1≤k≤3C .1≤k≤4D .1≤k<4 二、填空题1、如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 . 2、如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 .3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = k x,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 . 4、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .课后习练一、填空题1、如图,直线y=kx(k>0)与双曲线y=4x交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1的值等于_______.2、反比例函数y=kx的图像上有一点P(a,b),且a,b是方程t2-4t-2=0的两个根,则k=_______;点P到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b无交点,则b的取值范围是______.4、反比例函数y=kx的图像经过点P(a,b),其中a,b是一元二次方程x2+kx+4=0的两个根,那么点P的坐标是_______.5、如图,已知双曲线)0k(xky>经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=___.第5题图第6题图6、如图,已知点A是一次函数y=x的图像与反比例函数y=2x的图像在第一象限内的交点,点B在x轴的负半轴上,且OA=OB,那么△AOB的面积为()A.2 B.22C.2D.227、已知P为函数y=2x的图像上一点,且P到原点的距离为3,则符合条件的P点数为()A.0个B.2个C.4个D.无数个ABCDEyxO。
反比例函数常见几何模型

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线,故也称双曲线y=kx(k≠0).其解析式有三种表示方法:①xk y =(0≠k );②1-=kx y (0≠k );③k xy = 2.反比例函数y=kx(k≠0)的性质(1)当k>0时⇔函数图像的两个分支分别在第一,三象限内⇔在每一象限内,y 随x 的增大而减小.(2)当k<0时⇔函数图像的两个分支分别在第二,四象限内⇔在每一象限内,y 随x 的增大而增大.(3)在反比例函数y=kx中,其解析式变形为xy=k ,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).(4)若双曲线y=k x图像上一点(a ,b )满足a ,b 是方程Z 2-4Z -2=0的两根,求双曲线的解析式.由根与系数关系得ab=-2,又ab=k ,∴k=-2,故双曲线的解析式是y=2x-.(5)由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴,y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.二、新知讲解与例题训练 模型一:如图,点A 为反比例函数xk y =图象上的任意一点,且AB 垂直于x 轴,则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点,且3=∆AOB S ,(1)求m 的值 (2)求ABC ∆的面积变式题1、如图所示,点1A ,2A ,3A 在x 轴上,且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线,与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二:如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点,直线AB 交x 轴于M 点,交y 轴于N 点,再过A 、B 两点分别作y AD ⊥轴于D 点,x BF ⊥轴于F 点,再连结DF 两点,则有:AB DF ||且BM =ANDFAB DF MNxy O例2:如图,一次函数y a x b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆;③△DCE ≌△CDF ;④A C B D =其中正确的结论是 .(把你认为正确结论的序号都填上)例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ,与反比例函数ky x=的图象相交于点,A B .过点A 分别作AC x ⊥轴,AE y ⊥轴,垂足分别为,C E ;过点B 分别作BF x ⊥轴,BD y ⊥轴,垂足分别为F D ,,AC 与BD 交于点K ,连接CD .(1)若点A B ,在反比例函数ky x=的图象的同一分支上,如图1,试证明: ①AEDK CFBK S S =四边形四边形;②AN BM =. (2)若点A B ,分别在反比例函数ky x=的图象的不同分支上,如图2,则AN 与BM 还相等吗试证明你的结论.y xDCA B O FE 图1图1图2模型三:如图,已知反比例函数ky x=(k ≠0,x>0)上任意两点P 、C ,过P 做PA ⊥x 轴,交x 轴于点A ,过C 做CD ⊥x 轴,交x 轴于点D ,则OPC PADC S S ∆=梯形.例4:如图,在直角坐标系中,一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4,1)两点,则△AOB 的面积是______.例5:如图,在直角坐标系中,一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A (1,4)、B (3,m )两点,则△AOB 的面积是______.例6:如图1,已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点,且点A 的横坐标为4.(1)求k 的值;(2)如图2,过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点(点C 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐标.模型四:在矩形AOBC 中,OB =a ,OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F点的反比例函数(0)ky x x =>的图象与AC 边交于点E,则CEa CF b=.例7:两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 _________(把你认为正确结论的序号都填上).课堂练习: 一、选择题1、已知m<0,则函数mx y =1与xmy -=2的图像如图,大致是( )xB FC E A O yA. B. C. D 2、如图,点A 在双曲线xy 6=上,且OA=4,过点 A 作AC ⊥x 轴,垂足为c ,OA 的垂直平分线交OC 于B,则ABC ∆的周长为( ) A.72 C.74 D.22 3、如图,双曲线xky =(k>0)经过矩形OABC 的边BC 的中点E ,交AB 于点D ,若梯形ODBC 的面积为3,则双曲线的解析式为( )A.x y 1=B. x y 2=C. x y 3=D. xy 6=题 3 题 4 题54、如图,A,B 是函数xy 2=的图像上关于原点对称的任意两点,BC ABC∆k x 1y x =3y x=DB AyxO C2、如图,双曲线)0(2x xy =经过四边形OABC 的顶点A 、C ,∠ABC =90°,OC 平分OA 与x 轴正半轴的夹角,AB ∥x 轴,将△ABC 沿AC 翻折后得到△AB 'C ,B '点落在OA 上,则四边形OABC 的面积是 .3、如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOB =60°,点A 在第一象限,过点A 的双曲线为y = kx,在x 轴上取一点P ,过点P 作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′.(1)当点O ′与点A 重合时,点P 的坐标是 .(2)设P (t ,0),当O ′B ′与双曲线有交点时,t 的取值范围是 .4、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图,14y x=, 过1y 上的任意一点A ,作x 轴的平行线交2y 于B , 交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .课后习练一、填空题1、如图,直线y=kx (k>0)与双曲线y=4x交于A (x 1,y 1),B (x 2,y 2)两点,则2x 1y 2-7x 2y 1的值等于_______.2、反比例函数y=k x的图像上有一点P (a ,b ),且a ,b 是方程t 2-4t -2=0的两个根,则k=_______;点P 到原点的距离OP=_______.3、已知双曲线xy=1与直线y=-x+b 无交点,则b 的取值范围是______.4、反比例函数y=k x的图像经过点P (a ,b ),其中a ,b 是一元二次方程x 2+kx+4=0的两个根,那么点P 的坐标是_______.5、如图,已知双曲线)0k (xky >经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC 的面积为3,则k =___.第5题图 第6题图 的图像与反比例函数y=2x6、如图,已知点A 是一次函数y=x 的图像在第一象限内的交点,点B 在x 轴的负半轴上,且OA=OB ,那么△AOB 的面积为( ) A .2 B .22C .2D .227、已知P 为函数y=2x的图像上一点,且P 到原点的距离为3,则符合条件的P 点数为( )A .0个B .2个C .4个D .无数个ABCDE yxO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数常见模型邑⅛E-、知识点回顾k1..反比例函数的图像是双曲线,故也称双曲线y=—(k≠0.其解析式有三种表示方法:X① y =k ( k≠0);② y=kx' ( k≠0);③ xy = kXk2.反比例函数y=—( k≠0的性质X(1)当k>0时=函数图像的两个分支分别在第一,三象限内U 在每一象限内,y随X 的增大而减小.(2)当k<0时二函数图像的两个分支分别在第二,四象限内= 在每一象限内,y随X 的增大而增大.k(3)在反比例函数y=k中,其解析式变形为Xy=k ,故要求k的值(也就是求其图像上X一点横坐标与纵坐标之积).(4)若双曲线y=-图像上一点(a,b)满足a,b是方程Z2- 4Z —2=0的两根,求双X曲线的解析式.由根与系数关系得ab= 2 ,又ab=k,∙∙ k= 2,故双曲线的解析式是y= .X(5)由于反比例函数中自变量X和函数y的值都不能为零,所以图像和X轴,y轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势.】、新知讲解与例题训练模型一:如图,点A为反比例函数V则有SOAB -Ikl学习靠自觉,进步靠努力,每天比别人mS AOB = 3 , (1)求m 的值多付出一点点,将来比别人收获多许多-一L -*例1 :如图RtLABC的锐角顶点是直线y=x+m与双曲线^y=—Jta-「—,j变式题1、如图所示,点A1, A2, A3在X轴上,且O A = AA2= A2 A3,分别过A∣, A2, A3作y轴平行8线,与反比例函数y= — (χ>0)的图像交于点B1, B2,B3 ,分别过点B1,B2, B3作X轴的平行X线,分别与y轴交于点C1,C2, C3,连结OB i ,OB2,OB3 ,那么图中阴影部分的面积之和为1y 上,点B在双曲线X若四边形ABCD为矩形,则它的面积为2、如图,点A在双曲线模型二:, k如图:点A、B是双曲线y = —(k=0)任意不重合的两点,X点,交y轴于N点,再过A、B两点分别作AD — y轴于D点,BF — X轴于F例2:如图,一次函数y =ax ∙b 的图象与数∙^k 的的图象相交于七,D 两点,分另过C ,D 两点作y 轴,X 轴的垂X*■为E,F ,连接CF,DE .有下列四个结论:①SpJ=S^EF ;②山AoB 相似于A FoE ;③厶DCE ◎△ CDF ;④AC =BD 其中正确的结论是 ____________________ .(把你认例3: 一次函数y =ax b 的图象分别与X 轴、y 轴交于点M ,N ,与反比例函数k 、,y=-的图象相交于点 代B .过点A 分别作AC _ X 轴,AE _ y 轴,垂足分别为 XC,E ;过点B 分别作BF _x 轴,BD _ y 轴,垂足分别为F , D, AC 与BD 交于 点K ,连接CD .—(1)若点A B 在反比例函数y=r 的图象的同一分支上,如图1,试证明:X ①S 四边形AEDK =S 四边形CFBK:②AN= BM .(2)若点A, B 分别在反比例函数y的图象的不同分支上,如图2,则AN 与XBM 还相等吗?试证明你的结论./轴父于A , B 两点,与反比厂线^足为正确结论的序号都填上)交X 轴于点A ,过C 做CD 丄X 轴,交X 轴于点D ,则S∙0pc = S 弟形PADC .例4:如图,在直角坐标系中,一次函数 y=k ιx+b 的图象与反比例函数y=∙k2的X图象交于A(1,4)、B(4, 1)两点,则△AOB 的面积是 _______ .例5:如图,在直角坐标系中,一次函数 y=k 1χ∙b 的图象与反比例函数y=蜃的图象交于A ( 1,4)、B (3, m )两点,则△AOB 的X面积是 ______ .1k例6:如图1,已知直线y =1X 与双曲线y =°(k 0)交于A 、B 两2 X点,且点A 的横坐标为4.(1)求k 的值;(2)如图2,过原点O 的另一条直线I 交双曲线y=k (k 0)于C 、D 两点(点XC 在第一象限且在点A 的左边),当四边形ACBD 的面积为24时,求点C 的坐 标.出一点点,将来比另从收获多许多如图,已知反比例函数y =t" 7k ≠0^x>0)上任意两点P 、C ,过P 做PA ⊥X 轴,X ■模型四:在矩形AoBC 中,0B=a , OA=b ,分别以OB, OA 所在直线为X 轴和y 轴,建 立如图所示的平面直角坐标系.F 是BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数y =Λ(χ .0)的图象与AC 边交于点E ,则^a .XCF b例7:两个反比例函数y=兰和y=1在第一象限内的图象如图所示,点P 在y 」XXX 的图象上,PC ⊥ X 轴于点C ,交y=1的图象于点A ,PD 丄y 轴于点D ,交y J XX的图象于点B ,当点P 在y=k 的图象上运动时,以下结论:X①△ODB与△OCA 的面积相等;②四边形 FAOB 的面积不会发生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点•其中一定正 确的是 ______________________ (把你认为正确结论的序号都填上)•课堂练习: 一、选择题Xm的图像如图,大致是(A. B. 62、如图,点A 在双曲线y 上,且OA=4,过点XA 作AC _X 轴,垂足为c , OA 的垂直平分线交 于B,则AABC 的周长为()OCC. A. 2 7 B.5 C. 4. 7D. 223、如图,双曲线ODBC 的面积为 1A. y =3, k (k>0)经过矩形 OABCX则双曲线的解析式为( 2D. 6 y =- X4、如图, A,B 是函数意两点, S ()A.S=2BC//X 轴,AC∕∕y 轴,. ABC 的面积记为 S ,则 °】B.S=4C.2<S<4D.S>4D的边BC 的中点E ,交AB 于点D ,若梯形题 5B. y =)C. y = ?2 的图像上关于原点对称的任XC5、如图所示,等腰直角三角形ABC位于第一象限,AB=AC=2 ,直角顶点A在直线y=x上,k 其中A点的横坐标为1 ,且两条直角边AB ,AC分别平行于X轴,y轴,若双曲线y=—(k≠0)X 与厶ABC有交点,贝U k的取值范围是( )A. 1<k<2 B . 1 ≤ k≤3C. 1≤k≤4 D. 1 ≤k<4、填空题学习靠自觉,进步靠努力,每天比别人 出一点点,将来比另从收获多许多1、如图,点A 在双曲线y . 上,点B在双曲线y=二上,且AB// X 轴,C若四边形TABCD 为矩形,则它的面积^,直线l 为对称轴,线段 OB 经轴对称变换后的像是 O' B' •(1) _______________________________________________ 当点O 与点A 重合时,点P 的坐标是 _____________________________________________________•(2) ____________________________________________________________ 设P( t , 0),当O B'与双曲线有交点时,t 的取值范围是 _____________________________________ . ______k 4、如图,已知双曲线 y (k :::0)经过直角三角形 OAB 斜边OA 的中点D ,且与直角边 AB X相交于点C .若点A 的坐标为(-6 , 4),则厶AOC 的面积为 —•45、双曲线y ι、y 在第一象限的图像如图, y 1= X过y 1上的任意一点 A ,作X 轴的平行线交 y 于B ,2、如图,双曲线y 2 (X - 0)经过四边形 X AB// X 轴,将△ ABC 沿 AC 翻折后得到OABC 勺顶点A 、 C,∠ ABC= 90°, OC 平分 OA 与 X 轴正半轴的夹角, 边形OABG 的面积是3、如图,将一块直角三角板OAB 放在平面直角坐标系中, k 在第一象限,过点 A 的双曲线为y = X ,在X 轴上取一点P, X AB C, B /点落在OA 上,则四 B (2,0),∠ AOB= 60° ,点 A过点P 作直线OA 勺垂线l ,以 第17题图 D CE学习靠自觉,进步靠努力,每天比别人出一点点,将来比另从收获多许多41、如图,直线y=kx (k>0)与双曲线y=-交于A (x1. y1),B (x?,y2)两点,贝U 2x1y?X—7χ2y1的值等于2、反比例函数k=k 2y=—的图像上有一点P (a,b),且a,b是方程t2—4t—2=0的两个根,则XP到原点的距离OP= ________ .3、已知双曲线xy=1与直线y= —x+ '. b无交点,则b的取值范围是4、反比例函数根,那么点ky=—的图像经过点P (a,b),其中a,b是一元二次方程x2+kx+4=0的两个XP的坐标是________ .k5、如图,已知双曲线y (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相X交于点C.若△ OBC的面积为3,则k = ___.么厶AOB的面积为()第6题图2像与反比例函数y= 的图X负半轴上,且OA=OB,那7、2已知P为函数y= 的图像上一点,X且P到原点的距离为-3 ,则符合条件的P点数为(、填空题,则y的解析式是课.交y轴于C ,若学习靠自觉,进步靠努力,每7⅛ J • 0个。
