正弦余弦公式总结
三角形正弦余弦公式大全

三角形正弦余弦公式大全三角形是几何学中的一个重要概念,对于它的研究和应用有着广泛的需求。
在三角形的研究中,正弦和余弦公式是常用的工具,用于计算和解决各种三角形相关问题。
本文将详细介绍三角形正弦余弦公式并提供一些实例进行说明。
一、正弦公式在一个三角形ABC中,假设角A、B、C的对边分别为a、b、c,那么正弦公式可以表示为:sinA/a = sinB/b = sinC/c其中,sinA、sinB、sinC表示角A、B、C的正弦值,a、b、c表示对应边的长度。
正弦公式的应用非常广泛,可以用于求解三角形的各种边长和角度。
下面通过几个实例来说明正弦公式的具体应用。
实例1:已知一个三角形的两边长度分别为2厘米和3厘米,夹角为45度,求第三边的长度。
解:根据正弦公式有 sin45°/2 = sinC/c,即 sinC = (2/3)sin45°。
根据sin45°的值可以求得sinC的值,进而可以求得第三边的长度c。
实例2:已知一个三角形的两边长度分别为6厘米和8厘米,夹角为60度,求第三边的长度。
解:根据正弦公式有 sin60°/6 = sinC/8,即 sinC = (8/6)sin60°。
根据sin60°的值可以求得sinC的值,进而可以求得第三边的长度c。
二、余弦公式在一个三角形ABC中,假设角A、B、C的对边分别为a、b、c,那么余弦公式可以表示为:c² = a² + b² - 2abcosCa² = b² + c² - 2bccosAb² = a² + c² - 2accosB其中,cosA、cosB、cosC表示角A、B、C的余弦值。
余弦公式也是用于解决各种三角形问题的重要工具,可以通过已知的边长和角度来求解其他未知的边长和角度。
下面通过几个实例来说明余弦公式的具体应用。
高中数学正弦余弦公式大全

正弦定理和余弦定理一:基础知识理解1 .正弦定理分类内容定理===2 R ( R 是△ ABC 外接圆的半径 )变形公式① a = 2 R sin _ A , b = 2 R sin _ B , c = 2 R sin _ C ,② sin A ∶ sin B ∶ sin C =a ∶ b ∶ c ,③ sin A =,sin B =,sin C =解决的问题① 已知两角和任一边,求其他两边和另一角,② 已知两边和其中一边的对角,求另一边的对角2 .余弦定理分类内容定理在△ ABC 中,有 a 2 = b 2 + c 2 -2 bc cos _ A ;b 2 = a 2 +c 2 -2 ac cos _ B ; c 2 = a 2 + b 2 -2 ab cos _ C 变形公式cos A =;cos B =;cos C =解决的问题① 已知三边,求各角;② 已知两边和它们的夹角,求第三边和其他两个角3 .三角形中常用的面积公式( 1 ) S = ah ( h 表示边 a 上的高 );( 2 ) S = bc sin A = ac sin B = ab sin C ;( 3 ) S = r ( a + b + c )( r 为三角形的内切圆半径 ).二:基础知识应用演练1 .( 2012·广东高考 ) 在△ ABC 中,若∠ A = 60°,∠ B = 45°, BC = 3 ,则 AC =()A . 4B . 22 .在△ ABC 中, a =, b = 1 , c = 2 ,则 A 等于 ()A . 30°B . 45°C . 60°D . 75°3 .( 教材习题改编 ) 在△ ABC 中,若 a = 18 , b = 24 , A = 45°,则此三角形有 ()A .无解B .两解C .一解D .解的个数不确定4 .( 2012·陕西高考 ) 在△ ABC 中,角 A , B , C 所对边的长分别为 a , b , c .若 a = 2 , B =, c = 2 ,则 b = ________.5 .△ ABC 中, B = 120°, AC = 7 , AB = 5 ,则△ ABC 的面积为________ .解析:1 选B 由正弦定理得:=,即=,所以 AC = × =2 .2 选C ∵ cos A ===,又∵ 0°< A <180°,∴ A =60°.3 选B ∵ =,∴ sin B = sin A = sin 45°,∴ sinB = .又∵ a < b ,∴ B 有两个.4 由余弦定理得 b 2 = a 2 + c 2 -2 ac cos B =4+12-2×2×2 × =4,所以 b =2.答案:25、解析:设 BC = x ,由余弦定理得49=25+ x 2 -10 x cos 120°,整理得 x 2+5 x -24=0,即 x =3.因此 S △ ABC = AB × BC ×sin B = ×3×5× = . 答案:小结: ( 1 ) 在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ ABC 中,A > B ⇔ a > b ⇔ sin A >sin B .( 2 ) 在△ ABC 中,已知 a 、 b 和 A 时,解的情况如下:A 为锐角 A 为钝角或直角图形关系式 a = b sin A b sin A < a < b a ≥ b a > b解的个数一解两解一解一解三、典型题型精讲(1)利用正弦、余弦定理解三角形[例1] ( 2012·浙江高考 ) 在△ ABC 中,内角 A , B , C 的对边分别为 a , b ,c ,且 b sin A = a cos B .( 1 ) 求角 B 的大小; ( 2 ) 若 b = 3 , sin C = 2sin A ,求 a , c 的值.解析: ( 1 ) 由 b sin A = a cos B 及正弦定理=,得sinB = cos B ,所以tan B =,所以 B = .(2) 由 sin C =2sin A 及=,得 c = 2 a . 由 b =3 及余弦定理 b 2 = a 2 + c 2 -2 ac cos B ,得 9= a 2 + c 2 - ac . 所以 a =, c =2 .思考一下:在本例 ( 2 ) 的条件下,试求角 A 的大小.方法小结:1 .应熟练掌握正、余弦定理及其变形.解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.2 .已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.试题变式演练 1 .△ ABC 的三个内角 A , B , C 所对的边分别为 a , b , c , a sin A sin B + b cos 2 A = a .( 1 ) 求;( 2 ) 若 c 2 = b 2 + a 2 ,求 B .解: ( 1 ) 由正弦定理得,sin 2 A sin B +sin B cos 2 A = sin A ,即 sin B ( sin 2 A +cos 2 A ) = sin A .故 sin B = sin A ,所以= .( 2 ) 由余弦定理和 c 2 = b 2 + a 2 ,得 cos B = .由 (1) 知 b 2 = 2 a 2 ,故 c 2 =(2+ ) a 2 . 可得 cos 2 B =,又 cos B >0,故 cos B =,所以 B =45°.(2)利用正弦、余弦定理判定三角形的形状[例2] 在△ ABC 中 a , b , c 分别为内角 A , B , C 的对边,且2 a sin A =( 2 b + c ) sin B +( 2 c + b ) sin C .( 1 ) 求 A 的大小;( 2 ) 若sin B + sin C = 1 ,试判断△ ABC 的形状.[ 解析 ] ( 1 ) 由已知,根据正弦定理得 2 a 2 = ( 2 b + c ) · b + ( 2 c + b ) c ,即a 2 = b 2 + c 2 + bc .由余弦定理得 a 2 = b 2 + c 2 -2 bc cos A ,故 cos A =-,∵ 0< A <180°,∴ A =120°.(2) 由 (1) 得 sin 2 A =sin 2 B +sin 2 C +sin B sin C =又 sin B +sin C =1,解得 sin B =sin C = .∵ 0°< B <60°,0°< C <60°,故 B = C ,∴△ ABC 是等腰的钝角三角形.方法小结:依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法:( 1 ) 利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;( 2 ) 利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用 A + B + C =π这个结论.[注意] 在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.试题变式演练 ( 2012·安徽名校模拟 ) 已知△ ABC 的三个内角 A , B , C 所对的边分别为 a , b , c ,向量 m =( 4 ,- 1 ), n =,且m · n = .( 1 ) 求角 A 的大小;( 2 ) 若 b + c = 2 a = 2 ,试判断△ ABC 的形状.解:( 1 ) ∵ m = ( 4,-1 ) , n =,∴ m · n =4cos 2 -cos 2 A =4·- ( 2cos 2 A -1 ) =-2cos 2 A +2cos A +3.又∵ m · n =,∴ -2cos 2 A +2cos A +3=,解得 cos A =. ∵ 0< A < π ,∴ A = .(2) 在△ ABC 中, a 2 = b 2 + c 2 -2 bc cos A ,且 a =,∴ ( ) 2 =b 2 +c 2 -2 bc ·= b 2 + c 2 -bc . ①又∵ b + c =2 ,∴ b =2 - c ,代入① 式整理得 c 2 - 2 c +3=0,解得 c =,∴ b =,于是 a = b = c =,即△ ABC 为等边三角形.(3)与三角形面积有关的问题[例3] ( 2012·新课标全国卷 ) 已知 a , b , c 分别为△ ABC 三个内角 A , B ,C 的对边, a cos C + a sin C - b - c = 0.( 1 ) 求 A ;( 2 ) 若 a = 2 ,△ ABC 的面积为,求 b , c .[ 解 ] ( 1 ) 由 a cos C + a sin C - b - c =0及正弦定理得sin A cos C + sin A sin C -sin B -sin C =0.因为 B =π- A - C ,所以 sin A sin C -cos A sin C -sin C =0.由于sin C ≠0,所以sin = . 又0< A <π,故 A = .( 2 ) △ ABC 的面积 S = bc sin A =,故 bc =4.而 a 2 = b 2 + c 2 -2 bc cos A ,故 b 2 + c 2 =8. 解得 b = c =2.方法小结:1 .正弦定理和余弦定理并不是孤立的.解题时要根据具体题目合理选用,有时还需要交替使用.2 .在解决三角形问题中,面积公式 S = ab sin C = bc sin A = ac sin B 最常用,因为公式中既有边也有角,容易和正弦定理、余弦定理结合应用.试题变式演练 ( 2012·江西重点中学联考 ) 在△ ABC 中, cos 2 A = cos 2 A -cos A .( 1 ) 求角 A 的大小;( 2 ) 若 a = 3 , sin B = 2sin C ,求 S △ ABC .解: ( 1 ) 由已知得 ( 2cos 2 A -1 ) =cos 2 A -cos A ,则cos A = .因为0< A <π,所以 A = .( 2 ) 由=,可得==2,即 b = 2 c .所以cos A ===,解得 c =, b =2 ,所以 S △ ABC = bc sin A = ×2 × × = .课后强化与提高练习(基础篇-必会题)1 .在△ ABC 中, a 、 b 分别是角 A 、 B 所对的边,条件“ a < b ”是使“cosA >cosB ”成立的 ()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2 .( 2012·泉州模拟 ) 在△ ABC 中, a , b , c 分别是角 A , B , C 所对的边.若 A =, b = 1 ,△ ABC 的面积为,则 a 的值为 ()A . 1B . 23 .( 2013·“江南十校”联考 ) 在△ ABC 中,角 A , B , C 所对的边分别为 a , b ,c ,已知 a = 2 , c = 2 , 1 +=,则 C =()A . 30°B . 45°C . 45°或135°D . 60°4 .( 2012·陕西高考 ) 在△ ABC 中,角 A , B , C 所对边的长分别为 a , b , c ,若 a 2 + b 2 = 2 c 2 ,则cos C 的最小值为 ()D .-5 .( 2012·上海高考 ) 在△ ABC 中,若sin 2 A + sin 2 B <sin 2 C ,则△ ABC 的形状是 ()A .锐角三角形B .直角三角形C .钝角三角形D .不能确定6 .在△ ABC 中,角 A 、 B 、 C 所对的边分别是 a 、 b 、 c .若 b = 2 a sin B ,则角 A 的大小为________ .解析:由正弦定理得sin B =2sin A sin B ,∵ sin B ≠0,7 .在△ ABC 中,若 a = 3 , b =, A =,则 C 的大小为________ .8 .( 2012·北京西城期末 ) 在△ ABC 中,三个内角 A , B , C 的对边分别为 a ,b ,c .若 b = 2 , B =, sin C =,则 c = ________ ; a = ________.9 .( 2012·北京高考 ) 在△ ABC 中,若 a = 2 , b + c = 7 , cos B =-,则 b = ________.10 .△ ABC 的内角 A , B , C 的对边分别为 a , b , c , a sin A + c sin C -a sin C =b sin B .( 1 ) 求 B ;( 2 ) 若 A = 75°, b = 2 ,求 a , c .11 .( 2013·北京朝阳统考 ) 在锐角三角形 ABC 中, a , b , c 分别为内角 A , B ,C 所对的边,且满足 a - 2 b sin A = 0.( 1 ) 求角 B 的大小;( 2 ) 若 a + c = 5 ,且 a > c , b =,求 ·的值.12 .( 2012·山东高考 ) 在△ ABC 中,内角 A , B , C 所对的边分别为 a , b ,c ,已知sin B ( tan A + tan C )= tan A tan C .( 1 ) 求证: a , b , c 成等比数列;( 2 ) 若 a = 1 , c = 2 ,求△ ABC 的面积 S .课后强化与提高练习(提高篇-选做题)1 .( 2012·湖北高考 ) 设△ ABC 的内角 A , B , C 所对的边分别为 a , b , c .若三边的长为连续的三个正整数,且 A > B > C , 3 b = 20 a cos A ,则sin A ∶ sin B ∶ sin C 为 ()A .4 ∶ 3 ∶ 2B .5 ∶ 6 ∶ 7C .5 ∶ 4 ∶ 3D .6 ∶ 5 ∶ 42 .( 2012·长春调研 ) 在△ ABC 中,角 A , B , C 的对边分别为 a , b , c ,已知4sin 2 - cos 2 C =,且 a + b = 5 , c =,则△ ABC 的面积为________ .3 .在△ ABC 中,角 A , B , C 的对边分别为 a , b , c ,且满足 ( 2 b - c ) cos A - a cos C = 0.( 1 ) 求角 A 的大小;( 2 ) 若 a =, S △ ABC =,试判断△ ABC 的形状,并说明理由.选做题1 .已知 a , b , c 分别是△ ABC 的三个内角 A , B , C 所对的边.若 a = 1 ,b =, A + C = 2 B ,则sin C = ________.2 .在△ ABC 中, a = 2 b cos C ,则这个三角形一定是 ()A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形3 .在△ ABC 中,角 A , B , C 所对的边分别为 a , b , c ,已知cos 2 C =- .( 1 ) 求sin C 的值;( 2 ) 当 a = 2 , 2sin A = sin C 时,求 b 及 c 的长.4 .设△ ABC 的内角 A , B , C 所对的边长分别为 a , b , c ,且cos B =, b = 2.( 1 ) 当 A = 30°时,求 a 的值;( 2 ) 当△ ABC 的面积为3时,求 a + c 的值.课后强化与提高练习(基础篇-必会题)解析1 解析:选C a < b ⇔ A < B ⇔ cos A >cos B .2 解析:选D 由已知得 bc sin A = ×1× c ×sin =,解得 c = 2 ,则由余弦定理可得 a 2 = 4 + 1 - 2×2×1×cos =3 ⇒ a = .3 解析:选B 由1 +=和正弦定理得 cos A sin B +sin A cos B=2sin C cos A ,即 sin C =2sin C cos A ,所以 cos A =,则 A =60°. 由正弦定理得=,则 sin C =,又 c < a ,则 C <60°,故 C =45°.4 解析:选 C 由余弦定理得 a 2 + b 2 - c 2 =2 ab cos C ,又 c 2 =( a 2 + b 2 ),得 2 ab cos C = ( a 2 + b 2 ),即 cos C =≥ = .6 解析:选 C 由正弦定理得 a 2 + b 2 < c 2 ,所以 cos C =<0,所以 C 是钝角,故△ ABC 是钝角三角形.∴ sin A =,∴ A =30°或 A =150°. 答案:30°或 150°7 解析:由正弦定理可知 sin B ===,所以 B =或 ( 舍去 ),所以 C =π - A - B =π --= . 答案:8 解析:根据正弦定理得=,则 c ==2 ,再由余弦定理得 b 2 = a 2 + c 2 -2 ac cos B ,即 a 2 - 4 a -12=0,( a +2)( a -6)=0,解得 a =6 或 a =-2( 舍去 ).答案:2 69 解析:根据余弦定理代入 b 2 =4+(7- b ) 2 -2×2×(7- b )× ,解得b =4. 答案:410 解:(1) 由正弦定理得 a 2 + c 2 - ac = b 2 . 由余弦定理得 b 2 = a 2 +c 2 -2 ac cos B .故cos B =,因此 B =45°.(2)sin A =sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°= .故 a = b × ==1+, c = b × =2×= .1 1 解:(1) 因为 a -2 b sin A =0,所以 sin A -2sin B sin A =0,因为sin A ≠0,所以 sin B = . 又 B 为锐角,所以 B = .( 2 ) 由 ( 1 ) 可知, B = .因为 b = .根据余弦定理,得7= a 2 + c 2 -2 ac cos ,整理,得 ( a + c ) 2 - 3 ac =7.由已知 a + c =5,得 ac =6.又 a > c ,故 a =3, c =2.于是cos A ===,所以 ·=| |·| |cos A = cb cos A=2× × =1.12 解: ( 1 ) 证明:在△ ABC 中,由于sin B ( tan A +tan C ) =tan A tan C ,所以sin B = ·,因此sin B ( sin A cos C +cos A sin C ) =sin A sin C ,所以 sin B sin( A + C )=sin A sin C .又 A + B + C =π ,所以 sin( A + C )=sin B ,因此 sin 2 B =sin A sin C .由正弦定理得 b 2 = ac ,即 a , b , c 成等比数列.( 2 ) 因为 a =1, c =2,所以 b =,由余弦定理得cos B ===,因为0< B <π,所以sin B ==,故△ ABC 的面积 S = ac sin B = ×1×2× = .课后强化与提高练习(提高篇-选做题)解析1 解析:选D 由题意可得 a > b > c ,且为连续正整数,设 c = n , b = n +1,a = n +2 ( n >1,且n ∈ N * ) ,则由余弦定理可得3 ( n +1 ) =20 ( n +2 ) ·,化简得7 n 2 -13 n -60=0,n ∈ N * ,解得 n =4,由正弦定理可得sin A ∶ sin B ∶ sin C =a ∶ b ∶ c =6 ∶ 5 ∶ 4.2 解析:因为4sin 2 -cos 2 C =,所以2[1-cos( A + B )]-2cos 2 C +1=,2+2cos C -2cos 2 C +1=,cos 2 C -cos C +=0,解得cos C = .根据余弦定理有cos C ==,ab = a 2 + b 2 -7 , 3 ab = a 2 + b 2 +2 ab -7= ( a + b ) 2 -7=25-7=18,ab =6,所以△ ABC 的面积 S △ ABC = ab sin C = ×6× =.答案:3 解: ( 1 ) 法一:由 ( 2 b - c ) cos A - a cos C =0及正弦定理,得(2sin B -sin C )cos A -sin A cos C =0,∴ 2sin B cos A -sin( A + C )=0,sin B (2cos A -1)=0. ∵ 0< B < π ,∴ sin B ≠0,∴ cos A =. ∵ 0< A < π ,∴ A= .法二:由 (2 b - c )cos A - a cos C =0,及余弦定理,得 (2 b - c )·- a ·=0,整理,得 b 2 + c 2 - a 2 = bc ,∴ cos A ==,∵ 0<A < π ,∴ A = .(2) ∵ S △ ABC = bc sin A =,即 bc sin =,∴ bc =3,①∵ a 2 = b 2 + c 2 -2 bc cos A , a =, A =,∴ b 2 + c 2 =6,② 由①② 得 b = c =,∴△ ABC 为等边三角形.选择题解析1 解析:在△ ABC 中, A + C =2 B ,∴ B =60°. 又∵ sin A ==,∴ A =30°或 150°( 舍 ),∴ C =90°,∴ sin C =1.答案:12 解析:选A 法一: ( 化边为角 ) 由正弦定理知:sin A =2sin B cos C ,又 A =π -( B + C ),∴ sin A =sin( B + C )=2sin B cos C .∴ sin B cos C +cos B sin C =2sin B cos C ,∴ sin B cos C -cos B sin C =0,∴ sin ( B - C ) =0.又∵ B 、 C 为三角形内角,∴ B = C .法二: ( 化角为边 ) 由余弦定理知cos C =,∴ a =2 b ·=,∴ a 2 = a 2 + b 2 - c 2 ,∴ b 2 = c 2 ,∴ b = c .3 解: ( 1 ) 因为cos 2 C =1-2sin 2 C =-,且0< C <π,所以sin C = .( 2 ) 当 a =2 , 2sin A =sin C 时,由正弦定理=,得 c =4.由cos 2 C =2cos 2 C -1=-,及0< C <π得cos C =± .由余弦定理 c 2 = a 2 + b 2 -2 ab cos C ,得 b 2 ± b -12=0,解得 b =或2 ,所以或4 解: ( 1 ) 因为cos B =,所以sin B = .由正弦定理=,可得=,所以 a = .( 2 ) 因为△ ABC 的面积 S = ac ·sin B ,sin B =,所以 ac =3, ac =10.由余弦定理得 b 2 = a 2 + c 2 -2 ac cos B ,得4= a 2 + c 2 - ac = a 2 + c 2 -16,即 a 2 + c 2 =20.所以 ( a + c ) 2 - 2 ac =20, ( a + c ) 2 =40.所以 a + c =2 .。
正弦定理和余弦定理总结

cot A/2 sinA/ 1 cosA 1 cosA /sinA.
sin2 1 cos2 2 2
cos2 1 cos2 2 2
正弦定理
• • • • • 正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。 即a/sinA=b/sinB=c/sinC=2R (2R是此三角形外接圆的半径的两倍) 方法一 证明:在锐角△ABC中,设BC=a,AC=b,AB=c 作CH⊥AB垂足为点H
余弦定理
• 两式相加
a2 b2 accos bccos abcos abcos
• 整理得:
a2 b2 c2 2abcos
a2 b2 2ab cos c2
tan(3π/2-α)= cotα
cos(3π/2-α)= -sinα
cot(3π/2-α)= tanα
诱导公式记背诀窍:奇变偶不变,符号看象限
以上k∈Z
两角和公式
• sin(α+β)=sinαcosβ+cosαsinβ
• sin(α-β)=sinαcosβ –cosαsinβ • cos(α+β)=cosαcosβ-sinαsinβ • cos(α-β)=cosαcosβ+sinαsinβ
三角函数
锐角三角函数公式
正弦:sin 的对边 的斜边 余弦:cos 的邻边 的斜边
正切:tan 的对边 的邻边
余切:cot 的邻边 的对边
简单的三角函数
• 定义
cot 1 tan
csc 1 sin
1 sec cos
• • • • •
CH=a· sinB CH=b· sinA
正弦余弦公式总结

1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(2π-a)=cos(a)cos(2π-a)=sin(a)sin(2π+a)=cos(a)cos(2π+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)tgA=tanA=sinAcosA2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)tan(b)] tan(a-b)=[tan(a)-tan(b)]/[1+tan(a)tan(b)] 3.和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)4.积化和差公式(上面公式反过来就得到了)sin(a)sin(b)=-1/2* [cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2* [cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2* [sin(a+b)+sin(a-b)]cos(a)sin(b)=1/2* [sin(a+b)-sin(a-b)]5.二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a)6.半角公式2sin2(a/2)=1-cos(a)2cos2(a/2)=1+cos(a)tan(a/2)=[1-cos(a)]/sin(a)=sina/[1+cos(a)]tan2(a/2)= [1-cos(a)]/[1+cos(a)]7.万能公式sin(a)=2tan(a/2)/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=2tan(a/2)/[1-tan2(a/2)]8.其它公式(推导出来的)a*sin(a)+b*cos(a)=sin(a+c) 其中tan(c)=b/a a*sin(a)-b*cos(a)=cos(a-c) 其中tan(c)=a/b1+sin(a)=(sin(a/2)+cos(a/2))21-sin(a)=(sin(a/2)-cos(a/2))2三、正弦定理:a/sinA=b/sinB=c/sinC=2R其中R是三角形外接圆半径正弦定理可以解决下列三角问题:①已知两角和任一边,求其它两边和一角。
正弦定理和余弦定理公式大全

正余弦定理指正弦定理和余弦定理,是揭示 三角形 边角关系的重要定理,直接运用它 可解决三角形的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方 便、灵活。
正弦定理
概述
a/sinA=b/sinB=c/sinC=2R 正弦定理 [1] (Sine theorem)
(1 )已知三角形的两角与一边, 解三角形
(2 )已知三角形的两边和其中一边所对的角, 解三角形
(3 )运用 a : b :c=sinA : sinB : sinC 解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的
正弦 。 [1]
Байду номын сангаас
证明
步骤 1 在锐角 △ABC 中,设 BC=a , AC=b , AB=c 。作 CH ⊥ AB 垂足为点 H
CH=a·sinB CH=b·sinA ∴a·sinB=b ·sinA 得到
a/sinA=b/sinB 同理,在 △ABC 中,
余弦
b/sinB=c/sinC 步骤 2. 证明 a/sinA=b/sinB=c/sinC=2R : 如图, 任意三角形 ABC, 作 ABC 的 外接圆 O. 作直径 BD 交⊙ O 于 D.
高中数学知识点总结正弦定理与余弦定理

高中数学知识点总结正弦定理与余弦定理正弦定理与余弦定理是高中数学中的重要知识点,用于求解不规则三角形的边长和角度。
本文将对这两个定理进行详细总结与讲解。
一、正弦定理1.1 定义正弦定理是指在任意三角形中,三条边与其对应的角的正弦值之间的关系。
设三角形的三边分别为a、b、c,对应的角度为A、B、C,则正弦定理的表达式为:a/sinA = b/sinB = c/sinC1.2 推导我们通过利用三角形的面积公式S=1/2 * a * b * sinC,并将其转换为对角线的形式,可以得到正弦定理的推导过程。
1.3 应用正弦定理可以用于求解不规则三角形的边长和角度。
当我们已知三条边或者两条边和夹角时,可以利用正弦定理求解未知的边长或者角度。
二、余弦定理2.1 定义余弦定理是指在任意三角形中,三条边和它们对应的角之间的关系。
设三角形的三边分别为a、b、c,对应的角度为A、B、C,则余弦定理的表达式为:c^2 = a^2 + b^2 - 2ab * cosC2.2 推导我们可以通过利用向量的几何关系,将余弦定理的表达式推导出来。
这个过程较为繁琐,这里就不做详细讲解。
2.3 应用余弦定理可以用于求解不规则三角形的边长和角度。
当我们已知三条边或者两条边和夹角时,可以利用余弦定理求解未知的边长或者角度。
三、正弦定理与余弦定理的比较3.1 适用范围正弦定理适用于任意三角形,而余弦定理只适用于任意三角形,不能用于直角三角形。
3.2 计算难度正弦定理的计算相对简单,只需要记住一个公式,而余弦定理的计算稍复杂,需要使用开方和乘法等运算。
3.3 精度误差由于余弦定理中涉及到平方运算,可能会带来一定的误差,而正弦定理中没有涉及到平方运算,计算结果更加准确。
3.4 应用场景正弦定理在计算不规则三角形的边长和角度时较为常用,尤其适用于已知两边和夹角的情况。
而余弦定理在计算不规则三角形的边长和角度时同样常用,特别适用于已知三边的情况。
余弦定理公式大全

正弦、余弦定理 解斜三角形建构知识结构1.三角形基本公式:(1)内角和定理:A+B+C=180°,sin(A+B)=sinC, cos(A+B)= -cosC,cos2C =sin 2B A +, sin 2C =cos 2B A + (2)面积公式:S=21absinC=21bcsinA=21casinBS= pr =))()((c p b p a p p --- (其中p=2cb a ++, r 为内切圆半径)(3)射影定理:a = b cos C + c cos B ;b = a cos C + c cos A ;c = a cos B + b cos A 2.正弦定理:2sin sin sin a b cR A B C===外 证明:由三角形面积111sin sin sin 222S ab C bc A ac B ===得sin sin sin a b c A B C==画出三角形的外接圆及直径易得:2sin sin sin a b cR A B C===3.余弦定理:a 2=b 2+c 2-2bccosA , 222cos 2b c aA bc+-=;证明:如图ΔABC 中,sin ,cos ,cos CH b A AH b A BH c b A ===-22222222sin (cos )2cos a CH BH b A c b A b c bc A=+=+-=+-当A 、B 是钝角时,类似可证。
正弦、余弦定理可用向量方法证明。
要掌握正弦定理、余弦定理及其变形,结合三角公式,能解有关三角形中的问题. 4.利用正弦定理,可以解决以下两类问题:(1)已知两角和任一边,求其他两边和一角; (2)已知两边和其中一边的对角,求另一边的对角;有三种情况:bsinA<a<b 时有两解;a=bsinA 或a=b 时有 解;a<bsinA 时无解。
5.利用余弦定理,可以解决以下两类问题:(1)已知三边,求三角;(2)已知两边和它们的夹角,求第三边和其他两角。
最新正弦余弦公式总结

1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(2π-a)=cos(a)cos(2π-a)=sin(a)sin(2π+a)=cos(a)cos(2π+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)tgA=tanA=sinAcosA2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)tan(b)] tan(a-b)=[tan(a)-tan(b)]/[1+tan(a)tan(b)] 3.和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)4.积化和差公式(上面公式反过来就得到了)sin(a)sin(b)=-1/2* [cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2* [cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2* [sin(a+b)+sin(a-b)]cos(a)sin(b)=1/2* [sin(a+b)-sin(a-b)]5.二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a)6.半角公式2sin2(a/2)=1-cos(a)2cos2(a/2)=1+cos(a)tan(a/2)=[1-cos(a)]/sin(a)=sina/[1+cos(a)]tan2(a/2)= [1-cos(a)]/[1+cos(a)]7.万能公式sin(a)=2tan(a/2)/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=2tan(a/2)/[1-tan2(a/2)]8.其它公式(推导出来的)a*sin(a)+b*cos(a)=sin(a+c) 其中tan(c)=b/aa*sin(a)-b*cos(a)=cos(a-c) 其中tan(c)=a/b1+sin(a)=(sin(a/2)+cos(a/2))21-sin(a)=(sin(a/2)-cos(a/2))2三、正弦定理:a/sinA=b/sinB=c/sinC=2R其中R是三角形外接圆半径正弦定理可以解决下列三角问题:①已知两角和任一边,求其它两边和一角。
正弦定理余弦定理知识点
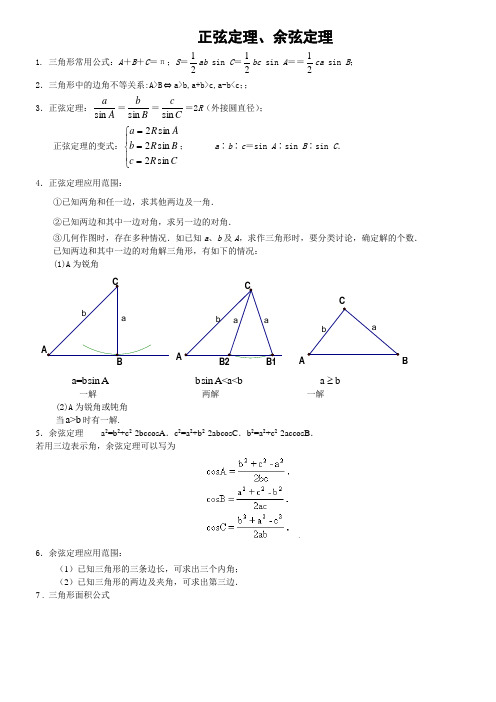
正弦定理、余弦定理1. 三角形常用公式:A +B +C =π;S =21ab sin C =21bc sin A ==21ca sin B ; 2.三角形中的边角不等关系:A>B ⇔a>b,a+b>c,a-b<c ;; 3.正弦定理:A a sin =B b sin =Ccsin =2R (外接圆直径); 正弦定理的变式:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2; a ∶b ∶c =sin A ∶sin B ∶sin C .4.正弦定理应用范围:①已知两角和任一边,求其他两边及一角. ②已知两边和其中一边对角,求另一边的对角.③几何作图时,存在多种情况.如已知a 、b 及A ,求作三角形时,要分类讨论,确定解的个数. 已知两边和其中一边的对角解三角形,有如下的情况: (1)A 为锐角babaabaB1BACACA BCB2a=bsin A bsin A<a<b a b ≥ 一解 两解 一解(2)A 为锐角或钝角 当a>b 时有一解.5.余弦定理 a 2=b 2+c 2-2bccosA .c 2=a 2+b 2-2abcosC .b 2=a 2+c 2-2accosB . 若用三边表示角,余弦定理可以写为、6.余弦定理应用范围:(1)已知三角形的三条边长,可求出三个内角; (2)已知三角形的两边及夹角,可求出第三边. 7 . 三角形面积公式课堂互动知识点1 运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状. 【答案】解法1:由扩充的正弦定理:代入已知式 2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 , sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bca cb b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a = 即△ABC 为等腰三角形. 巩固练习1.在∆ABC 中,若2222sin sin 2cos cos b C c B b B C +=,试判断三角形的形状.2.在ABC ∆中,已知a 2tanB=b 2tanA,试判断这个三角形的形状. 3.已知ABC ∆中,有cos 2cos sin cos 2cos sin A C BA B C+=+,判断三角形形状.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理:①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角. 例题2 在△ABC 中,已知3=a ,2=b ,B=45︒ 求A 、C 及c .【分析】在解斜三角形应用过程中,注意要灵活地选择正弦定和余弦定理,解得其它的边和角【答案】解法1:由正弦定理得:23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BC b c 当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2:设c =x 由余弦定理 B ac c a b cos 2222-+=将已知条件代入,整理:0162=+-x x 解之:226±=x 当226+=c 时2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 从而A=60︒ ,C=75︒ 当226-=c 时同理可求得:A=120︒ C=15︒. 巩固练习1.已知在ABC ∆中,,6,45=︒=∠BC AB A 在ABC ∆中,213,2tan tan +=-=c b bb c B A3.在ABC ∆中,已知A 、B 、C 成等差数列,且sin 求三边a 、b 、c .4.在ABC ∆中,已知B C A 2=+,tan tan ⋅C A 又知顶点C 的对边C 上的高等于34知识点3 例题3 已知A 、B 、C 为锐角,tanA=1,tanB=2 角的范围确定角.本题应先求出A+B 和C 式求出A+B+C .【答案】 A B C 、、为锐角 ∴<0°A tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++ =所以A+B+C=πsin sin sin sin cos 22222ααββα-++-221336-+=(cos cos sin sin )αβαβ --=-25936cos()αβ∴-=cos()αβ5972巩固练习1.在∆ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,设a+c=2b,A-C=3π,求sinB 的值. 2.在∆ABC 中,a ,b ,c 分别是∠∠∠A B C ,,的对边长,已知a ,b ,c 成等比数列,且a c ac bc 22-=-,求∠A 的大小及b Bcsin 的值. 3.在ABC ∆中,若4,5==b a且3231)cos(=-B A ,求这个三角形的面积. 例题4 在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c,证明:C B A cb a sin )sin(222-=-.【分析】在用三角式的恒等变形证明三角形中的三角等式时,其解题的一般规律是:二项化积、倍角公式,提取公因式,再化积.遇有三角式的平方项,则利用半角公式降次. 【答案】证法一:由正弦定理得C A B C B A c b a 2222222sin 22cos 2cos sin sin sin -=-=-=C A B A B 2sin 2)sin()sin(2-+-=CB AC 2sin )sin(sin -=C B A sin )sin(-.证法二:由余弦定理得a 2=b 2+c 2-2bccosA,则222c b a -=22cos 2cA bc c -=1-c b 2∙cosA,又由正弦定理得c b =C Bsin sin ,∴222c b a -=1-C B sin sin 2∙cosA=C A B C sin cos sin 2sin -=C A B B A sin cos sin 2)sin(-+=C A B B A sin cos sin cos sin -=C B A sin )sin(-. 证法三:C B A sin )sin(-=CAB B A sin cos sin cos sin -. 由正弦定理得cbC B c a C A ==sin sin ,sin sin ,∴CB A sin )sin(-=cAb B a cos cos -,又由余弦定理得CB A sin )sin(-=cbc a c b b ac b c a a 22222222-+⋅--+⋅=22222222)()(c a c b b c a -+--+=222c b a -.巩固练习1.已知锐角三角形ABC 中,3sin()5A B +=,1sin()5A B -=. (1)求证tan 2tan A B =;(2)设3AB =,求AB 边上的高.【考题再现】1.(04年全国Ⅲ)在ABC ∆中,3AB =,BC =4AC =,则边AC 上的高(A (B (C )32(D )2.(05年湖南卷)已知在△ABC 中,sinA (sinB +cosB )-sinC =0,sinB +cos2C =0,求角A 、B 、C 的大小.3.( 春季北京)在△ABC 中,sin A +cos A =22,AC =2,AB =3,求tan A 的值和△ABC 的面积. 4. (05年江苏卷)ABC ∆中,3A π=,3BC =,则ABC ∆的周长为(A )33B π⎛⎫++ ⎪⎝⎭ (B )36B π⎛⎫++ ⎪⎝⎭ (C )6sin 33B π⎛⎫++ ⎪⎝⎭ (D )6sin 36B π⎛⎫++ ⎪⎝⎭5.(06年湖北卷)若ABC ∆的内角A 满足2sin 23A =,则sin cos A A +=A.3 B .3- C .53 D .53- 6. ( 安徽卷)如果111A B C ∆的三个内角的余弦值分别等于222A B C ∆的三个内角的正弦值,则( )A .111ABC ∆和222A B C ∆都是锐角三角形 B .111A B C ∆和222A B C ∆都是钝角三角形 C .111A B C ∆是钝角三角形,222A B C ∆是锐角三角形D .111A B C ∆是锐角三角形,222A B C ∆是钝角三角形【模拟训练】1.( 北京市朝阳区二模题)在∆ABC 中,cos2cos2B A >是A B >的() (A ) 充分而不必要条件 (B )必要而不充分条件(C )充要条件 (D )既不充分也不必要条件2.(04年南京市二模题)在∆ABC 中,A ,B ,C 为三角形的三个内角,且A B C <<,4sin 5B =4cos(2)5A C +=-,求cos2A 的值3.(04年华南师大附中)在∆ABC 中,,,a b c 分别为角,,A B C 的对边,且274sin cos 222B C A +-= (1)求A ∠的度数 (2)若a =3b c +=,求b 和c 的值4.(05年南通市基地学校联考) 在∆ABC 中,边AB为最长边,且sin sin A B ⋅=,则cos cos A B ⋅的最大值是5.(06年湖北八校第二次联考)已知关于x 的方程22cos cos 2sin02Cx x A B -⋅+=的两根之和等于两根之积的一半,则ABC ∆一定是(A )直角三角形(B )钝角三角形(C )等腰三角形(D )等边三角形.6.(06年黄岗市荆州市高三年级模拟)已知ABC ∆的三个内角为A 、B 、C 所对的三边为a 、b 、c ,若ABC ∆的面积为222()S a b c =--,则tan2A=__________. 教考链接在证明三角形问题或者三角恒等式时,要注意正弦定理、余弦定理的适用题型与所证结论的联系,并注意特殊正、余弦关系的应用,比如互补角的正弦值相等,互补角的余弦值互为相反数等;另外,在三角恒等式的证明或者三角形形状的判断,关键是正、余弦定理的边角互换.运用正、余弦定理求解三角形的有关问题,要非常熟悉了三角函数公式及三角形的有关性质,如三角函数的定义、勾股定理、正弦定理、余弦定理是常用的工具,同时注意三角形面积公式ah S 21=,C ab S sin 21=,还要注意三角形内角和π=++C B A 的制约关系,此外,要对常见解题方法与解题技巧的总结,这样才能不断提高三角形问题的求解能力.参考答案课堂互动例题1 巩固练习1.【答案】[解法1]:由正弦定理2sin sin sin a b cR A B C===,R 为∆ABC 外接圆的半径,将原式化为22228sin sin 8sin sin cos cos R B C R B C B C =,sin sin 0B C ≠,sin sin cos cos B C B C ∴=. 即cos()0B C +=,90B C ∴+=,90A =. 故∆ABC 为直角三角形[解法2]:将已知等式变为2222(1cos )(1cos )2cos cos b C c B b B C -+-=,由余弦定理可得22222222222222a b c a c b b c b c ab ac ⎛⎫⎛⎫+-+-+-⋅-⋅ ⎪ ⎪⎝⎭⎝⎭222222222a c b a b c bc ac ab+-+-=⋅⋅,即22b c +22222222()()4a b c a c b a⎡⎤+-++-⎣⎦= 也即222b c a +=,故∆ABC 为直角三角形.2.【答案】解法1:由已知得A A bB B a cos sin cos sin 22=,由正弦定理得AAB B B A cos sin sin cos sin sin 22=,∵sinAsinB ≠0,∴sinAcosA=sinBcosB,即sin2A=sin2B,∴2A=2B 或2A=1800-2B,即A=B 或A+B=900.∴ABC ∆是等腰三角形或直角三角形.解法2: 由已知得A A bB B a cos sin cos sin 22=,由正弦定理得A a b b a cos cosB 22=,即Aba cos cosB =,又由余弦定理得bcac b b a 22ac b -c a 222222-+=+,整理得(a 2-b 2)(a 2+b 2-c 2)=0,∴a=b,或a 2+b 2=c 2, ∴ABC ∆是等腰三角形或直角三角形. 3.解:由已知得例题2 巩固练习1.【答案】解法1:由正弦定理,得2345sin 26sin =︒=C 因3226sin =⨯=⋅A AB 6,2==AB BC 由623<<,则有二解,即︒=∠60C 或︒=∠120C︒=︒-︒-︒=∠754560180B 或︒=︒-︒-︒=∠1545120180B故13sin sin +=⇒⋅=AC B ABC AC 或13-=AC ,︒=∠︒=∠15,120B C ︒=∠︒=∠75,60B C 解法2:令AC=b ,则由余弦定理222245cos 62)6(=︒-+b b 1302322±=⇒=+-b b b又C b b cos 222)6(222⋅-+=︒=∠±=⇒60,21cos C C 或︒=∠120C ︒=︒+︒-︒=∠⇒75)6045(180B 或︒=︒+︒-︒=∠15)12045(180B . 2【答案】由已知有bc B A 21tan tan =+,化简并利用正弦定理:B C B A B A B A sin sin 2sin cos sin cos cos sin =+ BCB A B A sin sin 2sin cos )sin(=+0cos sin 2sin =-A C C由0sin ≠,故︒=⇒=6021cos A A 由213+=cb,可设k c k b 2,)13(=+=,由余弦定理,得 k a k k k a 6)13(24)13(22222=⇒+-++=由正弦定理Cc A a sin sin =得 226232sin sin =⋅==kk a A c C 由b c <则C 是锐角,故︒=--︒=︒=75180,45C A B C3.【答案】由已知,得2C A B +=,又由︒=++180C B A ︒=⇒60B 故4160cos sin sin 2=︒=C A ①又由B c a S ABC sin 2134⋅⋅==∆164334=⇒=⇒ac ac ② 故64)sin ()sin (sin sin 22===C c A a C A ac 8sin sin ==⇒Cc A a由3460sin 8sin 8sin sin =︒⋅=⋅==B AB a b 则21260cos cos 222=-+=︒=ac b c a B即964848)(3)(222=+=+⇒=-+c a ac b c a 64=+⇒c a ③ 把③与②联立,得)26(2),26(2-=+=c a 或)26(2),26(2+=-=c a4.【答案】由已知B C A 2=+,及︒=+︒=⇒︒=++120,60180C A B C B A由CA C A C A tan tan 1tan tan )tan(-+=+及32tan tan ,3)tan(+=⋅-=+C A C A得33tan tan +=+C A ,以C A tan ,tan 为一元二次方程032)33(2=+++-x x 的两个根,解方程,得⎩⎨⎧+==32tan 1tan C A 或⎩⎨⎧=+=1tan 32tan C A ⎩⎨⎧︒=︒=⇒7545C A 或⎩⎨⎧︒=︒=4575C A 若︒=︒=75,45C A ,则860sin 34=︒=a ,6445sin 34=︒=b ,)13(445sin 75sin 8sin sin +=︒︒==A C a c若︒=︒=45,75C A ,则︒=60sin 34a ︒==75sin 34,8b )13(64-=)623(4-=)13(8sin sin -==B C b c 例题3 巩固练习1.【答案】由正弦定理和已知条件a+c=2b,得sinA+sinC=2sinB.由和差化积公式,得2sin 2C A +cos 2C A -=2sinB. 由A+B+C=π得sin 2C A +=cos 2B .又A-C=3π,得2cos 23B =sinB.∴2cos 23B=2sin 2B cos 2B ,∵0<2B <2π,∴cos 2B ≠0,∴sin2B =43.∴cos 2B =2sin 12B -=413,∴sinB=2sin 2B cos 2B =2∙43∙413=839. 2.【答案】(I ) a b c ,,成等比数列 ∴=b ac 2又a c ac bc 22-=- ∴+-=b c a bc 222 在∆ABC 中,由余弦定理得cos A b c a bc bc bc =+-==2222212∴∠=︒A 60 (II )在∆ABC 中,由正弦定理得sin sin B b Aa= ∴=︒=︒=b B c b ca sin sin sin 2606032. 3.【答案】解法1:由余弦定理得c c bc a c b A 892cos 2222-=-+= cc ac b c a B 1092cos 2222+=-+= 由正弦定理得:B A B A sin 45sin sin 4sin 5=⇒= 3231)cos 1(4510989222=-++⋅-⇒B c c c c 3231])109(1[4580812224=+-+-c c c c 63632318016282222=⇒=⇒=-⇒c c cc 故1694893689cos 2=-=-=c c A7165sin =A 4715sin 21=⋅⋅=∆A c b S ABC解法2:如图,作B A CAD -=∠,AD 交BC 于D ,令x CD = 则由5=a 知,x AD x BD -=-=5,5,在CAD ∆中由余弦定理3231)5(84)5()cos(222=--+-=-x x x B A化简得199=⇒=x x ,在CAD ∆中由正弦定理)sin(4)sin(sin )sin(sin B A B A CD ADC B A CD C AD -=-⋅=⇒-=783)(cos 142=--=B A 74158735421sin 21=⨯⨯⨯=⋅⋅=∆C BC AC S ABC例题4 巩固练习1.【答案】(1)证明:因为3sin()5A B +=,1sin()5A B -=, 所以3sin cos cos sin 51sin cos cos sin 5A B A B A B A B ⎧+=⎪⎪⎨⎪-=⎪⎩,2sin cos 51cos sin 5A B A B ⎧=⎪⎪⇒⎨⎪=⎪⎩,tan 2tan A B ⇒=.所以tan 2tan A B =(2)因为2A B ππ<+<,3sin()5A B +=, 所以3tan()4A B +=-,即tan tan 31tan tan 4A B A B +=--, 将tan 2tan A B =代入上式并整理得 22tan 4tan 10B B --=.解得tan B =tan B =tan 2tan 2A B ==. 设AB 边上的高为CD.则tan tan CD CD AB AD DB A B =+=+=AB=3,得CD= 2AB边上的高等于2考题再现1.【答案】由余弦定理,得1cos 2A =,60A ︒=,所以AC边上的高sin 2BD AB A =⋅=选B.2.【答案】解法1: 由0sin )cos (sin sin =-+C B B A 得.0)sin(cos sin sin sin =+-+B A B A B A所以.0sin cos cos sin cos sin sin sin =--+B A B A B A B A 即.0)cos (sin sin =-A A B因为),,0(π∈B 所以0sin ≠B ,从而.sin cos A A = 由),,0(π∈A 知.4π=A 从而π43=+C B . 由.0)43(2cos sin 02cos sin =-+=+B B C B π得 即.0cos sin 2sin .02sin sin =-=-B B B B B 亦即由此得.125,3,21cos ππ===C B B 所以,4π=A .125,3ππ==C B 解法2: 由).223sin(2cos sin 02cos sin C C B C B -=-==+π得由B <0、π<c ,所以.22223ππ-=-=C B C B 或即.22232ππ=-=+B C C B 或由0sin )cos (sin sin =-+C B B A 得 .0)sin(cos sin sin sin =+-+B A B A B A 所以.0sin cos cos sin cos sin sin sin =--+B A B A B A B A 即.0)cos (sin sin =-A A B 因为0sin ≠B ,所以.sin cos A A =由.4),,0(ππ=∈A A 知从而π43=+C B ,知B+2C=23π不合要求.再由π212=-B C ,得.125,3ππ==C B 所以,4π=A .125,3ππ==C B .3.【答案】解法1:∵sin A +cos A =2cos (A -45°)=22,∴cos (A -45°)=21. 又0°<A <180°,∴A -45°=60°,A =105°. ∴tan A =tan (45°+60°)=3131-+=-2-3.∴sin A =sin105°=sin (45°+60°)=sin45°cos60°+cos45°sin60°=462+. ∴S △ABC =21AC ·AB sin A =21·2·3·462+=43(2+6).4.【答案】在ABC ∆内,由正弦定理得3sin sin sin sin 3AC AB BC B C A π====∴(),3AC B AB C A B B ππ⎛⎫===-+=+⎡⎤ ⎪⎣⎦⎝⎭ ∴周长为AB AC BC ++sin sin 33B B π⎤⎛⎫=+++ ⎪⎥⎝⎭⎦3sin 32B B ⎫=+⎪⎪⎭6sin 36B π⎛⎫=++ ⎪⎝⎭ 5.【答案】由sin2A =2sinAcosA >0,可知A 这锐角,所以sinA +cosA >0,又25(sin cos )1sin 23A A A +=+=,故选A.6.【答案】111A B C ∆的三个内角的余弦值均大于0,则111A B C ∆是锐角三角形,若222A B C ∆是锐角三角形,由211211211sin cos sin()2sin cos sin()2sin cos sin()2A A A B B B C C C πππ⎧==-⎪⎪⎪==-⎨⎪⎪==-⎪⎩,得212121222A A B B C C πππ⎧=-⎪⎪⎪=-⎨⎪⎪=-⎪⎩,那么,2222A B C π++=,所以222A B C ∆是钝角三角形.故选D .模拟训练1.【答案】2222cos 2cos 212sin 12sin sin sin B A B A B A >⇔->-⇔<⇔sin sin A B A B >⇔> 2.【答案】∵A B C <<,A B C π++=,∴0,022B AC ππ<<<+<,由4sin 5B =得3cos 5B =,∴4sin()5A C +=,()3cos 5A C +=- 又由4cos(2)5A C +=-得3sin(2)5A C += ∴()33447sin sin 2()555525A A C A C ⎛⎫⎛⎫=+--=⨯---⨯=⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭2527cos 212sin 625A A =-=. 3.【答案】由题意得[]2721cos()2cos 12B C A -+-+= ()2721cos 2cos 12A θ+-+= ∴1cos 2A = 03A π<<2221cos 22b c a A bc +-==()223b c a bc +-=将3a b c =+=代入得2,bc =由3b c +=及2bc =,得1,2b c ==或2,1b c ==.4.【答案】因为cos cos sin sin cos()1A B A B A B ⋅+⋅=-≤,易得cos cos A B ⋅的最大值为24+. 5.【答案】由题意可知:211cos cos cos 2sin 222C CA B -=⋅⋅=,从而2cos cos 1cos()1cos cos sin sin A B A B A B A B =++=+-cos cos sin sin 1A B A B +=,cos()1A B -=又因为A B ππ-<-<所以0A B -=,所以ABC ∆一定是等腰三角形选C6.【答案】1sin 2S bc A =,222()S a b c =--,2222cos a b c bc A =+-, ∴1sin 22cos 2bc A bc bc A =-,∴22sin 11cos 2tan 4sin 22sin cos 22A A A A A A -===。
正弦定理和余弦定理公式

正弦定理和余弦定理公式设任意三角形△ABC,角A、B、C的对边分别记作a、b、c,则可得到正弦定理、余弦定理的公式及其推论如下。
正弦定理:在一个三角形中,各边和它所对的角的正弦的比相等。
一、正弦定理公式a/sinA=b/sinB=c/sinC=2R。
【注1】其中“R”为三角形△ABC外接圆半径。
下同。
【注2】正弦定理适用于所有三角形。
初中数学中,三角形内角的正弦值等于“对比斜”仅适用于直角三角形。
二、正弦定理推论公式1、(1)a=2RsinA;(2)b=2RsinB;(3)c=2RsinC。
2、(1)a:b=sinA:sinB;(2)a:c=sinA:sinC;(3)b:c=sinB:sinC;(4)a:b:c=sinA:sinB:sinC。
【注】多用于“边”、“角”间的互化。
三角板的边角关系也满足正、余弦定理3、由“a/sinA=b/sinB=c/sinC=2R”可得:(1)(a+b)/(sinA+sinB)=2R;(2)(a+c)/(sinA+sinC)=2R;(3)(b+c)/(sinB+sinC)=2R;(4)(a+b+c)/(sinA+sinB+sinC)=2R。
4、三角形ABC中,常用到的几个等价不等式。
(1)“a>b”、“A>B”、“sinA>sinB”,三者间两两等价。
(2)“a+b>c”等价于“sinA+sinB>sinC”。
(3)“a+c>b”等价于“sinA+sinC>sinB”。
(4)“b+c>a”等价于“sinB+sinC>sinA”。
5、三角形△ABC的面积S=(abc)/4R。
其中“R”为三角形△ABC的外接圆半径。
部分三角函数公式余弦定理公式及其推论余弦定理:三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
一、余弦定理公式(1)a^2=b^2+c^2-2bccosA;(2)b^2=a^2+c^2-2accosB;(3)c^2=a^2+b^2-2abcosC。
正弦余弦正切公式大全

正弦余弦正切公式大全正弦公式:正弦函数是指在直角三角形中,对于任意角度θ,对边与斜边的比值。
正弦函数使用sin(θ)表示,其中θ为角度。
正弦公式可以表示为:sin(θ) = 对边/斜边余弦公式:余弦函数是指在直角三角形中,对于任意角度θ,邻边与斜边的比值。
余弦函数使用cos(θ)表示,其中θ为角度。
余弦公式可以表示为:cos(θ) = 邻边/斜边正切公式:正切函数是指在直角三角形中,对于任意角度θ,对边与邻边的比值。
正切函数使用tan(θ)表示,其中θ为角度。
正切公式可以表示为:tan(θ) = 对边/邻边在直角三角形中,还有两个重要的三角函数:余切函数和正割函数。
余切公式:余切函数是指在直角三角形中,对于任意角度θ,邻边与对边的比值。
余切函数使用cot(θ)表示,其中θ为角度。
余切公式可以表示为:cot(θ) = 邻边/对边正割公式:正割函数是指在直角三角形中,对于任意角度θ,斜边与邻边的比值。
正割函数使用sec(θ)表示,其中θ为角度。
正割公式可以表示为:sec(θ) = 斜边/邻边除了以上基本的三角函数公式,还有一些重要的三角函数恒等式:1.和差公式:sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B)cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)tan(A ± B) = (tan(A) ± tan(B))/(1 ∓ tan(A)tan(B))2.二倍角公式:sin(2A) = 2sin(A)cos(A)cos(2A) = cos^2(A) - sin^2(A)tan(2A) = 2tan(A)/(1 - tan^2(A))3.三倍角公式:sin(3A) = 3sin(A) - 4sin^3(A)cos(3A) = 4cos^3(A) -3cos(A)tan(3A) = (3tan(A) - tan^3(A))/(1 - 3tan^2(A))4.万能公式:sin^2(A) + cos^2(A) = 11 + tan^2(A) = sec^2(A)1 + cot^2(A) = csc^2(A)这些公式在解决三角函数的运算、证明、及物理模型等问题中起到非常关键的作用。
三角形的正弦余弦和正切的计算

三角形的正弦余弦和正切的计算三角函数是数学中重要的基础概念之一,用于解决与三角形相关的计算问题。
其中,正弦、余弦和正切是三角函数中最常用的三个函数。
在本文中,我们将介绍如何计算三角形的正弦、余弦和正切值。
一、正弦的计算正弦函数(sin)表示一个角的对边与斜边之比。
在计算三角形的正弦时,我们可以使用以下公式:sin A = 对边 / 斜边其中,A代表角度,对边是指与这个角相对的边,斜边则是三角形的斜边。
二、余弦的计算余弦函数(cos)表示一个角的邻边与斜边之比。
计算三角形的余弦时,我们可以使用以下公式:cos A = 邻边 / 斜边同样,A代表角度,邻边是指与这个角相邻的边。
三、正切的计算正切函数(tan)表示一个角的对边与邻边之比。
计算三角形的正切时,我们可以使用以下公式:tan A = 对边 / 邻边同样地,A代表角度,对边是指与这个角相对的边,邻边是指与这个角相邻的边。
在实际问题中,我们通常已知三角形的某些边长或角度,然后根据需要计算其他边长或角度的值。
下面通过几个实例来具体说明。
例一:已知一个直角三角形,其中一个角为30度,斜边长度为10,求其他两边的长度。
根据正弦和余弦的定义,可以得出正弦30度等于所求边长x除以斜边长度10,即sin 30度 = x / 10。
解方程可得x ≈ 5。
同样地,余弦30度等于所求边长y除以斜边长度10,即cos 30度 = y / 10。
解方程可得y ≈ 8.66。
因此,在这个直角三角形中,除了斜边长为10,另外两边的长度分别约为5和8.66。
例二:已知一个等边三角形,其中一个角为60度,边长为5,求其他两个角的正弦、余弦和正切值。
在等边三角形中,三个角的大小相等,所以我们要计算的三个角的正弦、余弦和正切值都相等。
根据定义,sin 60度 = 对边 / 斜边,cos 60度 = 邻边 / 斜边,tan 60度 = 对边 / 邻边。
因为等边三角形中各边长度相等,所以对边和邻边的长度也相等,斜边的长度为5。
三角形正玄余玄正切定理公式

三角形正玄余玄正切定理公式
三角形的正弦、余弦和正切定理公式如下:
1. 正弦定理:在任意三角形ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R,直径为D。
则有:
a/sinA=b/sinB=c/sinC=2r=D(r为外接圆半径,D为直径)。
2. 余弦定理:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
对于边长为a、b、c而相应角为A、B、C的三角形则有:
a²=b²+c²-2bc·cosA;
b²=a²+c²-2ac·cosB;
c²=a²+b²-2ab·cosC。
也可表示为:
cosC=(a²+b²-c²)/2ab;
cosB=(a²+c²-b²)/2ac;
cosA=(c²+b²-a²)/2bc。
3. 正切定理:在三角形中,任意两条边的和除以第一条边减第二条边的差所得的商,等于这两条边对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。
对于边长为a,b和c而相应角为A,B
和C的三角形,有:
(a-b)/(a+b)=[tan(A-B)/2]/[tan(A+B)/2];
(b-c)/(b+c)=[tan(B-C)/2]/[tan(B+C)/2];
(c-a)/(c+a)=[tan(C-A)/2]/[tan(C+A)/2]。
以上信息仅供参考,如果您还有疑问,建议咨询数学领域专业人士或查阅数学书籍。
(完整版)正弦定理、余弦定理知识点

正弦定理、余弦定理讲师:王光明【基础知识点】1. 三角形常用公式:A +B +C =π;S =ab sin C =bc sin A ==ca sin B ;2121212.三角形中的边角不等关系: A>B a>b,a+b>c,a-b<c ;;⇔3.【正弦定理】:===2R (外接圆直径);A a sin B b sin Ccsin 正弦定理的变式:; a ∶b ∶c =sin A ∶sin B ∶sin C .⎪⎩⎪⎨⎧===C R c B R b AR a sin 2sin 2sin 24.正弦定理应用范围: ①已知两角和任一边,求其他两边及一角. ②已知两边和其中一边对角,求另一边的对角.③几何作图时,存在多种情况.如已知a 、b 及A ,求作三角形时,要分类讨论,确定解的个数.已知两边和其中一边的对角解三角形,有如下的情况:(1)A 为锐角AABa=bsin A bsin A<a<b a b ≥ 一解 两解 一解(2)A 为锐角或钝角当时有一解.a>b 5.【余弦定理】 a 2=b 2+c 2-2bccosA .c 2=a 2+b 2-2abcosC .b 2=a 2+c 2-2accosB .若用三边表示角,余弦定理可以写为、6.余弦定理应用范围:(1)已知三角形的三条边长,可求出三个内角;(2)已知三角形的两边及夹角,可求出第三边.【习题知识点】知识点1 运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状.【解析】解法1:由扩充的正弦定理:代入已知式2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 , sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bc a c b b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a =即△ABC 为等腰三角形.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理: ①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角.例题2 在△ABC 中,已知,,B=45︒ 求A 、C 及c .3=a 2=b 【分析】在解斜三角形应用过程中,注意要灵活地选择正弦定和余弦定理,解得其它的边和角【解析】解法1:由正弦定理得:23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BCb c当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2:设c =x 由余弦定理将已知条件代入,整理:解之:B ac c a b cos 2222-+=0162=+-x x 226±=x 当时 从而A=60︒ ,C=75︒226+=c 2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 当时同理可求得:A=120︒ C=15︒.226-=c 知识点3 解决与三角形在关的证明、计算问题例题3 已知A 、B 、C 为锐角,tanA=1,tanB=2,tanC=3,求A+B+C 的值. 【分析】本题是要求角,要求角先要求出这个角的某一个三角函数值,再根据角的范围确定角.本题应先求出A+B 和C 的正切值,再一次运用两角和的正切公式求出A+B+C .【解析】 A B C 、、为锐角∴<++<0270°°A B C 又,,由公式可得tan tan A B ==12tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++=++-+⋅tan()tan tan()tan A B C A B C 1 =-+--⨯33133() =0所以A+B+C=π知识点4 求三角形的面积例题4 △ABC 中,D 在边BC 上,且BD =2,DC =1,∠B =60o ,∠ADC =150o ,求AC 的长及△ABC 的面积.【解析】在△ABC 中,∠BAD =150o -60o =90o ,∴AD =2sin60o =3.A在△ACD 中,AD 2=(3)2+12-2×3×1×cos150o =7,∴AC =7. ∴AB =2cos60o =1.S △ABC =21×1×3×sin60o =343.知识点4 解决实际为题例题4 如图,海中有一小岛,周围3.8海里内有暗礁。
正弦余弦公式总结

1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(2π-a)=cos(a)cos(2π-a)=sin(a)sin(2π+a)=cos(a)cos(2π+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)tgA=tanA=sinAcosA2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)tan(b)] tan(a-b)=[tan(a)-tan(b)]/[1+tan(a)tan(b)] 3.和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)4.积化和差公式(上面公式反过来就得到了)sin(a)sin(b)=-1/2* [cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2* [cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2* [sin(a+b)+sin(a-b)]cos(a)sin(b)=1/2* [sin(a+b)-sin(a-b)]5.二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a)6.半角公式2sin2(a/2)=1-cos(a)2cos2(a/2)=1+cos(a)tan(a/2)=[1-cos(a)]/sin(a)=sina/[1+cos(a)]tan2(a/2)= [1-cos(a)]/[1+cos(a)]7.万能公式sin(a)=2tan(a/2)/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=2tan(a/2)/[1-tan2(a/2)]8.其它公式(推导出来的)a*sin(a)+b*cos(a)=√a2+b2sin(a+c) 其中tan(c)=b/aa*sin(a)-b*cos(a)=√a2+b2cos(a-c) 其中tan(c)=a/b 1+sin(a)=(sin(a/2)+cos(a/2))21-sin(a)=(sin(a/2)-cos(a/2))2三、正弦定理:a/sinA=b/sinB=c/sinC=2R其中R是三角形外接圆半径正弦定理可以解决下列三角问题:①已知两角和任一边,求其它两边和一角。
正弦公式cos公式大全

正弦公式cos公式大全
正弦公式和余弦公式是三角函数中的重要公式,它们在解决三角形和周期性现象中起着重要作用。
下面我将从多个角度详细介绍正弦公式和余弦公式。
首先,我们来看正弦公式。
在直角三角形中,正弦公式可以表示为,sin(A) = a/c,sin(B) = b/c,其中A和B分别为三角形的两个锐角,a和b分别为A和B对应的对边,c为斜边。
在任意三角形中,正弦公式可以表示为,a/sin(A) = b/sin(B) = c/sin(C),其中A、B、C为三角形的三个内角,a、b、c为相应的边长。
接下来是余弦公式。
在直角三角形中,余弦公式可以表示为,cos(A) = b/c,cos(B) = a/c,其中A和B分别为三角形的两个锐角,a和b分别为A和B对应的对边,c为斜边。
在任意三角形中,余弦公式可以表示为,c^2 = a^2 + b^2 2abcos(C),a^2 = b^2 + c^2 2bccos(A),b^2 = a^2 + c^2 2accos(B),其中A、B、C为三角形的三个内角,a、b、c为相应的边长。
除了在三角形中的应用,正弦公式和余弦公式还可以用于描述周期性现象中的波动规律。
在物理学和工程学中,正弦函数和余弦
函数经常用于描述振动、波动、交流电流等周期性现象,它们的周期、频率、相位等特性都可以通过正弦公式和余弦公式来描述和分析。
总的来说,正弦公式和余弦公式是数学中重要的公式,它们不仅在三角形的计算中有着重要的应用,还在描述周期性现象中起着关键作用。
希望以上内容能够对你有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦余弦公式总结 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
1.诱导公式
sin(-a)=-sin(a)
cos(-a)=cos(a)
sin(2π-a)=cos(a)
cos(2π-a)=sin(a)
sin(2π+a)=cos(a)
cos(2π+a)=-sin(a)
sin(π-a)=sin(a)
cos(π-a)=-cos(a)
sin(π+a)=-sin(a)
cos(π+a)=-cos(a)
tgA=tanA=sinAcosA
2.两角和与差的三角函数
sin(a+b)=sin(a)cos(b)+cos(α)sin(b)
cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
sin(a-b)=sin(a)cos(b)-cos(a)sin(b)
cos(a-b)=cos(a)cos(b)+sin(a)sin(b)
tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)tan(b)] tan(a-b)=[tan(a)-tan(b)]/[1+tan(a)tan(b)] 3.和差化积公式
sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)sin(b)=2cos((a+b)/2)sin((a-b)/2)
cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)
cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)
4.积化和差公式 (上面公式反过来就得到了)
sin(a)sin(b)=-1/2* [cos(a+b)-cos(a-b)]
cos(a)cos(b)=1/2* [cos(a+b)+cos(a-b)]
sin(a)cos(b)=1/2* [sin(a+b)+sin(a-b)]
cos(a)sin(b)=1/2* [sin(a+b)-sin(a-b)]
5.二倍角公式
sin(2a)=2sin(a)cos(a)
cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a)
6.半角公式
2sin2(a/2)=1-cos(a)
2cos2(a/2)=1+cos(a)
tan(a/2)=[1-cos(a)]/sin(a)=sina/[1+cos(a)]
tan2(a/2)= [1-cos(a)]/[1+cos(a)]
7.万能公式
sin(a)=2tan(a/2)/[1+tan2(a/2)]
cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]
tan(a)=2tan(a/2)/[1-tan2(a/2)]
8.其它公式(推导出来的)
a*sin(a)+b*cos(a)=2+b2其中 tan(c)=b/a a*sin(a)-b*cos(a)= √a2+b2cos(a-c) 其中 tan(c)=a/b
1+sin(a)=(sin(a/2)+cos(a/2))2
1-sin(a)=(sin(a/2)-cos(a/2))2
三、正弦定理:
a/sinA=b/sinB=c/sinC=2R
其中R是三角形外接圆半径
正弦定理可以解决下列三角问题:
①已知两角和任一边,求其它两边和一角。
②已知两边和其中一边的对角,求另一边的对角。
⑵公式的变形:a:b:c=sinA:sinB:sinC
a=k*sinA, b=k*sinB, c=k*sinC
四、余弦定理:
a2=b2+c2-2bccosA
b2=a2+c2-2accosB
c2=a2+b2-2abcosC。
