控制系统校正的根轨迹方法

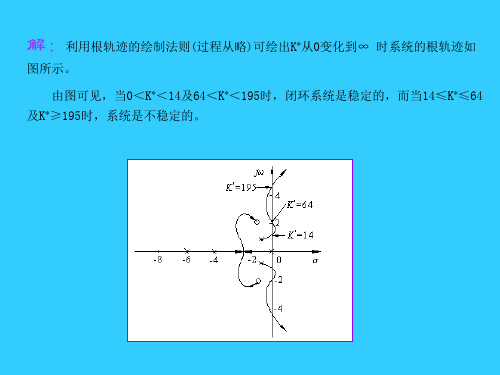
控制系统校正的根轨迹方法

用根轨迹法进行校正的基础，是通过在系统开环传递函数中增加零点和极点以改变根轨迹的形状，从而使系统根轨迹在S 平面上通过希望的闭环极点。根轨迹法校正的特征是基于闭环系统具有一对主导闭环极点，当然，零点和附加的极点会影响响应特性。

应用根轨迹进行校正，实质上是通过采用校正装置改变根轨迹的，从而将一对主导闭环极点配置到期望的位置上。

在开环传递函数中增加极点，可以使根轨迹向右方移动，从而降低系统的相对稳定性，增大系统调节时间。等同于积分控制，相当于给系统增加了位于原点的极点，因此降低了系统的稳定性。

在开环传递函数中增加零点，可以使根轨迹向左方移动，从而提高系统的相对稳定性，减小系统调节时间。等同于微分控制，相当于给系统前向通道中增加了零点，因此增加了系统的超调量，并且加快了瞬态响应。 根轨迹超前校正计算步骤如下。 (1)作原系统根轨迹图；

(2)根据动态性能指标，确定主导极点i s 在S 平面上的正确位置； 如果主导极点位于原系统根轨迹的左边，可确定采用微分校正，使原系统根轨迹左移，过主导极点。

(3)在新的主导极点上，由幅角条件计算所需补偿的相角差φ； 计算公式为：

i

s s

=?±=(s)][G arg -180o ? (1)

此相角差φ表明原根轨迹不过主导极点。为了使得根轨迹能够通过该点，必须校正装置，使补偿后的系统满足幅角条件。 (4)根据相角差φ，确定微分校正装置的零极点位置； 微分校正装置的传递函数为：

1

1

++=sTp sTz Kc

Gc (2)

例题：已知系统开环传递函数： 试设计超前校正环节，使其校正后系统的静态速度误差系数Kv ≤4.6，闭环主导极点满足阻尼比ζ=0.2，自然振荡角频率ωn=12.0rad/s ，并绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。

解： 由6.4)(*)(0*lim 0

==→s Gc s G s Kv s 得kc=2

计算串联超前校正环节的matlab 程序如下： 主函数: close; num=2.3;

den=conv([1,0],conv([0.2,1],[0.15,1])); G=tf(num,den) %校正前系统开环传函 zata=0.2;wn=12.0; %要求参数 [num,den]=ord2(wn,zata); %追加系统动态特性 s=roots(den); s1=s(1);

kc=2; %增益kc Gc=cqjz_root(G,s1,kc)

GGc=G*Gc*kc %校正后系统开环传函 Gy_close=feedback(G,1) %校正前系统闭环传函 Gx_close=feedback(GGc,1) %校正后系统闭环传函 figure(1);

step(Gx_close,'b',3.5); %校正后单位阶跃响应 hold on

step(Gy_close,'r',3.5); %校正前单位阶跃响应 grid;

gtext('校正前的'); gtext('校正后的'); figure(2);

0 2.3

s(1+0.2s)(1+0.15s)

G =

impulse(Gx_close,'b',3.5); %校正后单位冲激响应 hold on

impulse(Gy_close,'r',3.5); %校正前单位冲激响应 grid;

gtext('校正前的'); gtext('校正后的'); figure(3);

rlocus(G,GGc); %根轨迹图 grid;

gtext('校正前的'); gtext('校正后的');

为使校正后系统的根轨迹能经过期望闭环主导极点，其闭环特征方程跟必须满足幅值和相角条件，即πθj j e e M Tp s Tz s Kc

s G S Gc 11

1

)(0)(0

011=++=-，式中，M 0是校正

前系统在1s 处的幅值，θ0是对应的相角。

令1

11θj e M s -=，代入得)1(111

1

101+=

+---P j j c j z j T e

M e

M K e T e M θθπ

θ

解得0sin )sin(sin 101001θθθθM M K M K T c C Z --=

；0

sin )

sin(sin 11010θθθθM M K T c p ++-=

从而计算串联超前环节参数子函数为: function Gc=cqjz_root(G,s1,kc) numG=G.num{1};, DenG=G.den{1}; ngv=polyval(numG,s1); dgv=polyval(denGs1); g=ngv/dgv;

theta_0=angle(g); %相角θ0 theta_1=angle(s1); %相角θ1 M1=abs(g); %幅值M1 M0=abs(s1); %幅值M0

Tz=(sin(theta_1)-kc*M0*sin(theta_0-theta_1))/(kc*M0*M1*sin(theta_0)); Tp=-(kc*M0*sin(theta_1)+ sin(theta_0-theta_1))/(M1*sin(theta_0);

Gc=tf([Tz,1],[Tp,1]);

运行结果：

校正前系统开环传递函数：

Transfer function:

2.3

-----------------------

0.03 s^3 + 0.35 s^2 + s

超前校正传递函数：

Transfer function:

1.016 s + 1

------------

0.0404 s + 1

校正后系统开环传递函数：

Transfer function:

4.672 s + 4.6

-------------------------------------------

0.001212 s^4 + 0.04414 s^3 + 0.3904 s^2 + s

校正前系统闭环传递函数：

Transfer function:

2.3

-----------------------------

0.03 s^3 + 0.35 s^2 + s + 2.3

校正后系统闭环传递函数：

Transfer function:

4.672 s + 4.6

------------------------------------------------------- 0.001212 s^4 + 0.04414 s^3 + 0.3904 s^2 + 5.672 s + 4.6 得到以下图形：

图1-系统校正前后的单位冲激响应图

-4

-2

2

4

6

8

Impulse Response

Time (sec)

A m p l i t u d e

图2-系统校正前后的单位阶跃响应

图3-系统校正前后的根轨迹曲线

00.51 1.5

2 2.5

3 3.5

0.2

0.4

0.6

0.8

1

1.2

1.4

Step Response

Time (sec)

A m p l i t u d e

-70

-60

-50

-40

-30

-20

-10

10

20

-50-40

-30-20-10

01020

304050

Root Locus

Real Axis

I m a g i n a r y A x i s

根据系统校正前后的单位阶跃响应可以得到校正前超调量σ1=17.3%，校正后超调量 σ2=31.7%，如图4

图4-超调量

根据系统校正前后的单位阶跃响应可以得到校正前调节时间=2.92s ，校正后调节时

间 =2.3s ，如图5

图5-调节时间

Step Response

Time (sec)

A m p l i t u d e

00.51 1.5

2 2.5

3 3.5

0.2

0.4

0.6

0.8

1

1.2

1.4

校正前的

校正后的

System: Gx_close P eak amplitude: 1.32Overshoot (%): 31.7At time (sec): 0.301

System: Gy_close P eak amplitude: 1.17Overshoot (%): 17.3At time (sec): 1.33

Step Response

Time (sec)

A m p l i t u d e

校正前的

校正后的

System: Gx_close Settling Time (sec): 2.3

System: Gy_close

Settling Time (sec): 2.92

根据系统校正前后的单位阶跃响应可以得到校正前上升时间=0.58s ，校正后上升时

间 =0.123s ，如图6

图6-上升时间

由上可知，虽然系统的超调量增大了，但系统的上升时间和调节时间都缩短了，系统的性能有所提高。

由系统的根轨迹可以得到校正后的根轨迹左移，从而提高了系统的相对稳定性，缩短了系统的调节时间。

图7-校正前结构图

Step Response

Time (sec)

A m p l i t u d e

00.51 1.5

2 2.5

3 3.5

0.2

0.4

0.6

0.8

1

1.2

1.4

校正前的

校正后的

System: Gx_close Rise Time (sec): 0.123

System: Gy_close Rise Time (sec): 0.58

2.3

0.03s +0.35s +s

32T rans fer Fcn

Step

Scope

图8-校正后结构图

系统单位阶跃响应对比

图9-系统校正前后单位阶跃响应

1.016s+10.0404s+1Transfer Fcn1

2.3

0.03s +0.35s +s

32Transfer Fcn

Step

Scope