平面直角坐标变换
平面直角坐标系规律

平面直角坐标系规律
在平面直角坐标系中,规律主要体现在点的坐标表示、距离
计算、直线方程和图形变换等方面。
1.坐标表示:
平面直角坐标系中,每个点都可以用一个有序对(x,y)表示,
其中x表示点在x轴上的投影长度,y表示点在y轴上的投影
长度。
根据坐标的正负,可以判断点在哪个象限。
2.距离计算:
两点之间的距离可以通过勾股定理计算,即
$d=\sqrt{(x_2x_1)^2+(y_2y_1)^2}$。
这个公式可以用来
计算两点之间的直线距离。
3.直线方程:
在平面直角坐标系中,直线可以用一般式、斜截式、点斜式
和截距式等多种形式表示。
例如,一般式表示为Ax+By+C=0,其中A、B、C为常数;斜截式表示为y=kx+b,其中k为斜率,b为y轴截距;点斜式表示为yy_1=k(xx_1),其中(x_1,y_1)
为直线上一点的坐标;截距式表示为x/a+y/b=1,其中a、b
为x和y轴的截距。
4.图形变换:
平面直角坐标系中,常见的图形变换包括平移、旋转、缩放和对称等。
平移是通过给坐标加上一个平移向量实现,旋转是通过坐标旋转变换矩阵实现,缩放是通过给坐标乘上一个缩放因子实现,对称是通过以某一直线或点为中心实现。
总结一下,平面直角坐标系中的规律主要体现在坐标表示、距离计算、直线方程和图形变换等方面。
这些规律在几何学、图像处理、物理学等领域中都有广泛应用。
平面直角坐标系点的坐标移动规律

平面直角坐标系点的坐标移动规律平面直角坐标系中的点的坐标移动规律在平面直角坐标系中,点的坐标移动规律是描述点在平面上移动的方式和规则。
点的坐标由x轴和y轴上的数值组成,通过改变这些数值,我们可以改变点在平面上的位置。
点的坐标移动可以有多种方式,下面我们将介绍一些常见的移动规律。
1. 平移:平移是指点在平面上沿着某个方向移动一定的距离。
平移可以分为水平平移和垂直平移两种。
水平平移是指点在x轴方向上移动,垂直平移是指点在y轴方向上移动。
在平移过程中,点的x 轴和y轴坐标同时改变,但是它们的差值保持不变。
2. 旋转:旋转是指点围绕某个固定点旋转一定的角度。
旋转可以分为顺时针旋转和逆时针旋转两种。
顺时针旋转是指点沿着一个圆周顺时针方向旋转,逆时针旋转是指点沿着一个圆周逆时针方向旋转。
在旋转过程中,点的坐标随着旋转角度的变化而改变。
3. 缩放:缩放是指改变点到固定点的距离。
缩放可以分为放大和缩小两种。
放大是指点到固定点的距离变大,缩小是指点到固定点的距离变小。
在缩放过程中,点的x轴和y轴坐标同时改变,但是它们的比例保持不变。
4. 对称:对称是指点关于某条直线或某个点对称。
关于直线对称是指点在直线两侧对称,关于点对称是指点关于一个点对称。
在对称过程中,点的x轴和y轴坐标同时改变,但是它们的符号改变。
这些移动规律可以单独应用,也可以同时应用。
通过组合使用这些规律,我们可以描述点在平面上的任意移动方式。
在实际应用中,点的坐标移动规律被广泛应用于几何学、物理学、计算机图形学等领域。
在几何学中,点的坐标移动规律可以用来描述线段、角度、面积等几何概念。
在物理学中,点的坐标移动规律可以用来描述物体的运动轨迹和变形过程。
在计算机图形学中,点的坐标移动规律可以用来生成图像和动画效果。
点的坐标移动规律是描述点在平面上移动的方式和规则。
通过改变点的x轴和y轴坐标,我们可以改变点在平面上的位置。
这些移动规律可以单独应用,也可以同时应用,通过组合使用这些规律,我们可以描述点在平面上的任意移动方式。
平面直角坐标系下的图形变换

平面直角坐标系下的图形变换王建华图形变换是近几年来中考热点,除了选择题、解答题外,创新探索题往往以“图形变换”为载体,将试题设计成探索性问题、开放性问题综合考察学生的逻辑推理能力,一般难度较大。
在平面直角坐标系中,探索图形坐标的的变化和平移、对称、旋转和伸缩间的关系,是中考考查平面直角坐标系的命题热点和趋势,这类试题设计灵活平移: 上下平移横坐标不变,纵坐标改变左右平移横坐标改变,纵坐标不变对称: 关于x轴对称横坐标不变,纵坐标改变关于y轴对称横坐标不变,纵坐标不变关于中心对称横坐标、纵坐标都互为相反数旋转:改变图形的位置,不改变图形的大小和形状旋转角旋转半径弧长公式L=nπR/180一、平移例1,如图1,已知△ABC的位置,画出将ABC向右平移5个单位长度后所得的ABC,并写出三角形各顶点的坐标,平移后与平移前对应点的坐标有什么变化?解析:△ABC的三个顶点的坐标是:A(-2,5)、B(-4,3)、C(-1,2).向右平移5个单位长度后,得到的△A′B′C′对应的顶点的坐标是:A′(3,5,、B′(1,3)、C′(4,2).比较对应顶点的坐标可以得到:沿x轴向右平移之后,三个顶点的纵坐标都没有变化,而横坐标都增加了5个单位长度.友情提示:如果将△ABC沿y轴向下平移5个单位,三角形各顶点的横坐标都不变,而纵坐标都减少5个单位.(请你画画看).例2. 如图,要把线段AB平移,使得点A到达点A'(4,2),点B到达点B',那么点B'的坐标是_______。
析解:由图可知点A移动到A/可以认为先向右平移4个单位,再向上平移1个单位,∴)3,3(B经过相同的平移后可得)4,7(/B反思:①根据平移的坐标变化规律:★左右平移时:向左平移h个单位),(),(bhaba-→向右平移h个单位),(),(bhaba+→★上下平移时:向上平移h个单位),(),(hbaba+→向下平移h个单位),(),(hbaba-→二、旋转例3.如图2,已知△ABC,画出△ABC关于坐标原点0旋转180°后所得△A′B′C′,并写出三角形各顶点的坐标,旋转后与旋转前对应点的坐标有什么变化?解析:△ABC三个顶点的坐标分别是:A(-2,4),B(-4,2),C(-1,1).△A′B′C′三个顶点的坐标分别是:图2图1B/图2图1A′(2,-4),B′(4,-2),C′(1,-1).比较对应点的坐标可以发现:将△ABC沿坐标原点旋转180°后,各顶点的坐标分别是原三角形各顶点坐标的相反数.例3如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O 对称,….对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标.分析:本题是一道和对称有关的探索题,是在中心对称和点的坐标知识基础上的拓宽题,由于是规律循环的对称,所以解决问题的关键是找出循环规律.如图,标出P1到P7各点,可以发现点P7和点P1重合,继续下去可以发现点P8和点P2循环,所以6个点循环一次,这样可以求出各点的坐标.解:如图P2(1,-1),P7(1,1),因为100除以6余4,所以点P100和点P4的坐标相同,所以P100的坐标为(1,-3).三、对称例4.如图3,已知△ABC,画出△ABC关于x轴对称的△A′B′C′,并写出各顶点的坐标.关于x轴对称的两个三角形对应顶点的坐标有什么关系?解析:△ABC三个顶点的坐标分别是:A(1,4),B(3,1),C(-2,2).△A′B′C′三个顶点的坐标分别是:A′(1,-4),B′(3,-1),C′(-2,-2).观察各对应顶点的坐标可以发现:关于x轴对称两个三角形的对应顶点的横坐标不变,纵坐标互为相反数.友情提示:关于y轴对成的两个图形,对称点的纵坐标不变,横坐标互为相反数.在直角坐标系中,ABC△的三个顶点的位置如图3所示.(1)请画出ABC△关于y轴对称的A B C'''△(其中A B C''',,分别是A B C,,的对应点,不写画法);(2)直接写出A B C''',,三点的坐标:(_____)(_____)(_____)A B C''',,.析解:如图4,根据关于y轴对称的点的纵坐标不变,横坐标为原横坐标的相反数,即横坐标乘以1-,故可得(2)(23)A',,(31)B',,(12)C'--,反思:★关于x轴对称的点的横坐标不变,纵坐标为原纵坐标的相反数,即纵坐标乘以1-★关于y轴对称的点的纵坐标不变,横坐标为原横坐标的相反数,即横坐标乘以1-★关于原点成中心对称的点的,横坐标为原横坐标的相反数,纵坐标为原纵坐标的相反数,即横坐标、纵坐标同乘以1-四、位似例4 如图4,已知△ABC,画出△ABC以坐标原点0为位似中心的位似△A′B′C′,使△A′B′C′在第三象限,与△ABC 的位似比为21,写出三角形各顶点的坐标,位似变换后对应顶点发生什么变化?解析:△ABC三个顶点的坐标分别是:A(2,2),B(6,4),C(4,6).△A′B′C′三个顶点的坐标分别是:A′(-1,-1),B′(-3,-2),C′(-2,-3).图31 2 xO1-1ABCy1 2 xO1-1ABCA'B'C'y图3 图4C B AA 2C 2A 1B 1C 1O观图形可知,△A ′B ′C ′各顶点的坐标分别是△ABC对应各顶点坐标21的相反数.友情提示: △ABC 以坐标原点0为位似中心的位似△A ′B ′C ′,当△A ′B ′C ′与△ABC 的位似比为21,且△A ′B ′C ′在第一象限时, △A ′B ′C ′各顶点的坐标分别是△ABC 各顶点坐标的21.课前练习:在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC 的三个顶点都在格点上(每个小方格的顶点叫格点). ⑴画出△ABC 向下平移4个单位后的△A 1B 1C 1;⑵画出△ABC 绕点O 顺时针旋转90°后的△A 2B 2C 2,并求出A 旋转到A 2所经过的路线长.解:⑴画出△A 1B 1C 1;⑵画出△A 2B 2C 2, ,连接OA 1、OA 2,OA=2223+=13点A 旋转到A 2,所经过的路线长为:ι=9013131802ππ⋅=点评:图形的变换可以转化为点的问题,即找到顶点变换后的对应点,再顺次连接这些点即可得到图形.旋转变换要明确旋转中心、旋转方向、旋转半径、旋转角度;平移变换要明确平移的方向和距离;作一个图形关于某点的中心对称图形要明确对应点的连线经过对称中心,且对应点到对称中心的距离相等;作一个图形关于某一条直线的的对称图形,要明确对应点的连线被对称轴平分,且对应点到对称轴的距离相等。
空间大地坐标系及平面直角坐标系转换公式

§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。
人们为了描述空间位置,采用了多种方法,从而也产生了不同的坐标系,如直角坐标系、极坐标系等。
在测量中常用的坐标系有以下几种:一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心,Z 轴指向参考椭球的北极,X 轴指向起始子午面与赤道的交点,Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示:图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。
空间大地坐标系可用图2-4来表示:图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换,将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上,这种变换又称为投影变换。
投影变换的方法有很多,如横轴墨卡托投影、UTM 投影、兰勃特投影等。
在我XX 用的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例,只是投影的个别参数不同而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲,是一种横轴椭圆柱正切投影。
如图左侧所示,设想有一个椭圆柱面横套在椭球外面,并与某一子午线相切〔此子午线称为中央子午线或轴子午线〕,椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。
高斯投影满足以下两个条件:1、 它是正形投影;2、 中央子午线投影后应为x 轴,且长度保持不变。
将中央子午线东西各一定经差〔一般为6度或3度〕X 围内的地区投影到椭圆柱面上,再将此柱面沿某一棱线展开,便构成了高斯平面直角坐标系,如以下图2-5右侧所示。
平面直角坐标系坐标变化

平面直角坐标系中的变换彳----------- 必标系屮的对称平而l'i角坐标系屮的变换坐标系中的平移\------------ 怡标系屮的面枳和规律问题编写思路:本讲求而积时主要让学生掌握将点坐标转化为线段长度的过程•让学生亲自动手在坐标系中画出某个点关于横轴、纵轴以及原点的对应点,并且让他们自己总结两个对称点的横.纵坐标关系。
二:(1)对于点的平移:让学生亲自动手将某个点进行上、下、左、右平移,并且自己总结点的坐标变化规律。
对于任意的平移,可以将貝理解先上下平移、后左右平移的组合。
(2)对于图形的平移:让学生充分认识本质就是图形上的每个点都进行同一过程的平移,即对应点之间的平移过程完全一样。
从而将图形的平移转化成为点的平移。
并让学生体会平移前后的两个图形完全一样。
三、简单的数形结合:求三角形而积问题。
让学生充分掌握割补法求三角形而积,并理解为何要用割补法。
让学生熟练掌握并体会坐标与线段长的讣算关系。
四.找规律问题:老师可带着学生探索常见找规律问题的思路和方法.点P(-b)关于X轴的对称点是叫,-巧,即横坐标不变,纵坐标互为相反数.点P(a,b)关于y轴的对称点是P©,b),即纵坐标不变,横坐标互为相反数.点P(a.b)关于坐标原点的对称点是P'(—d),即横坐标互为相反数,纵坐标也互为相反数.【引例】在平而直角坐标系中,卩(-4 5)关于X 轴的对称点的坐标是 __________ 坐标是 ________ ,关于原点的对称点是 ___________【例1】(1)点P(3, -5)关于x 轴对称的点的坐标为()⑵点"-2, 1)关于y 轴对称的点的坐标为()⑶ 在平而直角坐标系中,点P(2, -3)关于原点对称点P 的坐标是 _____________ ⑷ 点P(2, 3)关于直线x = 3的对称点为 ________ ,关于直线y = 5的对称点为 ________ ⑸已知点P(“ + l,加-1)关于x 轴的对称点在第一彖限,求d 的取值范围.【例2】如图,在平而直角坐标系中,直线/是第一、三象限的角平分线.实验与探究:(1) 由图观察易知A(2, 0)关于直线/的对称点/V 的坐标为(0,2),请在图中分别标明3(5,3), C(-2,5)关于直线/的对称点X 、C'的位置,并写岀它们的坐标: B' __________ ,C ____________ ;归纳与发现:(2) 结合图形观察以上三组点的坐标,你会发现:坐标平而内任一点关于第一、三象限的角平分线/的对称点P 的坐标为 ______________ (不必证明): ⑶点A(a , b)在直线/的下方,则d, 〃的大小关系为 ________________ :若在直线/的上方,则 __________ ・h + d\丁 >・(选讲),关于y 轴的对称点的A. (—3, —5)B. (5, 3)C. (一3, 5) D ・(3, 5)B. (2,1)C. (2, -1)D. (-2, 1)点P(a ,b)和点Q(c , d)的中点是M(1)点平移:①将点(x, y)向右(或向左)平移4个单位可得对应点(x + a t y)或(x-“, y).②将点(x, y)向上(或向下)平移〃个单位可得对应点(x,>'+/?)或(x, y-h).⑵图形平移:①把一个图形%个点的横坐标都加上(或减去)一个正数d ,相应的新图形就是把原图形向右(或向左)平移Q个单位.②如果把图形各个点的纵坐标都加上(或减去)一个正数d ,相应的新图形就是把原图形向上(或向下)平移a个单位.注意:平移只改变图形的位置,图形的大小和形状不发生变化.【弓I例】点M(-3, -5)向上平移7个单位得到点M,的坐标为:再向左平移3个单位得到【例3】(1)平而直角坐标系中,将P(-2,l)向右平移4个单位,向下平移3个单位,得到P __________ ,□平而直角坐标系中,线段虫妨'是由线段佔经过平移得到的,点A(-1,-4)的对应点为人(1, -1),那么此过程是先向________ 平移____ 个单位再向______ 平移 _____ 个单位得到的,则点B (1, 1)的对应点$坐标为______________ .⑶将点P(m-2,” + 1)沿求轴负方向平移3个单位,得到P^i-rn, 2),则点P坐标是_____________⑷ 平而直角坐标系中,线段A'B'是由线段初经过平移得到的,点A(-2, 1)的对应点为A f (3. 4),点B 的对应点为B'(4,0),则点B 的坐标为()A ・(9,3) B. (一 1,一3) C ・(3, — 3) D. (一3, —1)【例4】二如下左图,在平面直角坐标系中,右边的图案是由左边的图案经过平移得到的,左边图案 中左.右眼睛的坐标分别是(-4, 2), (-2, 2),右边图案中左眼的坐标是(3, 4),则右边 图案中右眼的坐标是 _____________________ .-如下右图是由若干个边长为1的小正方形组成的网格,请在图中作岀将“蘑菇”ABCDE 绕A点逆时针旋转奸 再向右平移2个单位的图形(其中C 、D 为所在小正方形边的中点).二如图,把图1中的04经过平移得到00(如图2),如果图1中04上一点P 的坐标为伽皿),那么平移后在图2中的对应点P 的坐标为 __________ ・大图形的总而积减去周用小三角形的面积.一般方法有割补法和等积变换法.找规律的题目一左要先找/7 = 1、2、3几个图形规律,再推广到“的情况.从简单情形入手,从中发现规律,猜想、推测.归纳出结论,这是创造性思维的特点.i/\ V1例题精讲A ・v图1 图2在平面直角坐标系或网格中求而积,一般将难以求解的图形分割成易求解的图形的面积,可以用F二兀一 - —【引例】如图,直角坐标系中,△ABC的顶点都在网格点上,英中点A坐k标为(2,-1),则△4BC 的而积为 _____________ 平方单位.二如上右图,AABC,将△ABC 向右平移3个单位长度,然后再向上平移2个单位长度,可 以得到△ ・ ① 画出平移后的△人妨6 :② 写出△ AB.C,三个顶点的坐标:(在图中标岀)③ 已知点P 在x 轴上,以B“ P 为顶点的三角形面积为4,求P 点的坐标.【探究1】如图所示,4(1,4),B(4,3),(7(5,0),求图形如C 的面积.【例5】□直角坐标系中,已知人(-1,0)、5(3, 0)两点,点C 在y 轴上,△ABC 的而积是4,则点C 的坐标是 ___________ ■0如右图,已知直角坐标系中A(-1,4)、B(0,2),平移线段初,使点B 移到点C(3,0),此时点A 记作点D ,贝IJ 四边形ABCD 的 而积是 ___________ .【例6】□如下左图,在平而直角坐标系中,四边形ABCD 各顶点的坐标分别为A(0,0), 8(9,0), C(7,5),D(2, 7)・求四边形ABCD 的而积.「41「J 1_1 T 丿r k —厂」I 厂 11- T 4—n T klrLIr典题精练L LIL」I- T -I- +• -1 ~J_L J•V A【探究2】如下图所示,A(-3,5), B(4,3),求图形OAB的而积.【教师备选】方法三、转化法:平行线,一边转到轴上【探究4】如图所示,求三角形AOB的而积.解析:过点A做0B的平行线,交y轴于点C,连接BC由一次函数知识可求出直线OB:y=-x t设直线AC:y=-x+b -2 - 2 求得y=l x+2 ,得C(0,2)由等积变换可知S厶AOB = S^Bg. ―― x 2x 4=4解析:过点A作BC的平行线交y轴于点D,连接DC利用一次函数求得BC:y=2x+2 ,设直线AD:y=2x+b 求得尸2x+7, D(0,7) 由等积变换可知S沁=S沁弓x 1 x 5=|【变式】已知,在平而直角坐标系中,A「B两点分别在才轴、y轴的正半轴上,且OB = OA = 3. ⑴直接写出点A、B的坐标:⑵若点C(-2, 2),求△BOC的面积;⑶点P是与〉,轴平行的直线上一点,且点P的横坐标为1.若的面积是6,求点P的坐标.【例7】□任平而直角坐标系中,横坐标、纵坐标都为整数的点称为整点,图中的正方形的四个顶点都在格点上,观察图中每一个正方形四条边上的整点的个数,请你猜测由里向外第10个正方形四条边上的整点个数共有_______ 个.□如图,在平而直角坐标系中,第1次将MAB变换成△ OA.B.,第二次将变换成第3次将MAB 变换成△0比尽・已知A(l, 3), 4(2, 3), 4(4, 3), A(8, 3), B(2, 0), $(4, 0) , BJ8, 0),耳(16, 0)观察每次变化前后的三角形,找岀规律,按此变化规律再将△OA&3变换成△ O儿则点比的坐标是 _____ ,点厲的坐标是 _____ ,点人的坐标是_______ ,点乞的坐标是 ___________ ・【例8】一个粒子在第一象限内及x轴、y轴上运动,在第lmin内它从原点运动到(1, 0),而后接着按如图所示方式在与X轴、轴平行的方向上来回运动,且每分钟移动1个单位长度,那么,在2013min后,求这个粒子所处的位置坐标・【变式】将正整数按如图所示的规律在平而直角坐标系中进行排列,每个正整数对应一个整点坐标(X, y)9且x, y均为整数.如数5对应的坐标为(-1,1),则数_________________ 对应的坐标是(-2,3),数2012对应的坐标是__________________【拓展】数1950对应的坐标是______________ ・【教师备选】【备选1】类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1 个单位,用实数加法表示为3 + (-2) = 1.若坐标平而上的点作如下平移:沿*轴方向平移的数屋为d (向右为正,向左为负,平移冋 个单位),沿y 轴方向平移的数量为方(向上为正,向下为负,平移问个单位),则把有序 数对{“,b}叫做这一平移的“平移量”;“平移量” {a, b}与“平移量” {c, d}的加法运算 法则为{“,b} + {c, d} = {a+c, b + d}. 解决问题:(1) 计算:{3, 1} + {1, 2};(2) 动点P 从坐标原点O 出发,先按照"平移量”{3, 1}平移到A,再按照"平移量”{1, 2} 平移到若先把动点P 按照“平移量” {1, 2}平移到C,再按照“平移量” {3, 1}平 移,最后的位置还是点B 吗?在图1中画出四边形OABC.(3) 如图2, 一艘船从码头O 出发,先航行到湖心岛码头P (2,3),再从码头P 航行到码头0(5, 5),最后回到出发点O,请用“平移量”加法算式表示它的航行过程.37 36 35 34 3332 31 30 297 16 15 1413 12 11 18 19 61 2 2() 78 ,10 27 2122 23 2425 26图1【备选2】观察下列有规律的点的坐标:儿(1, 1), 4(2, -4), 4(3, 4),人(4, 一2),人(5, 7),肩6, -寸,4(7, 10), 4(8, —1)依此规律,人|的坐标为______________ ,州2的坐标为 ______________________________【备选3】一个动点P在平而直角坐标系中作折线运动,第一次从原点运动到(b 1)>然后按图中箭头所示方向运动,每次移动三角形的一边长•即(1, 1)-* (2, 0) - (3, 2) - (4, 0)-(5, 1)—........... ,按这样的运动规律,经过第17次运动后,动点P的坐标是___________ ,经过第2011次运动后,动点P的坐标是 __________ .【备选4】如图,在长方形网格中,每个小长方形的长为2,宽为1, B 两点在网格格点上,若点C也在网格格点上,以A、3、C为顶点的三角形面积为2,则满足条件的点C个数是( )A. 5B. 4B AD・2【备选5】在平而直角坐标系中,已知八(2・-2),任y轴上确左点P.使8"为等腰三角形,则符合条件的点P共有( )A. 2个B. 3个C. 4个D. 5个题型一坐标系中的对称巩固练习【练习1】□在平面直角坐标系中,点A(2,5)与点B关于y轴对称,则点B的坐标是( )A. (—5,—2)B. (一2, —5)C. (一2,5)D. (2, —5)□已知点P(x, y), n),如果x +加=0, y + 〃= 0 ,那么点P, Q ( )A・关于原点对称 B.关于x轴对称C・关于y轴对称D・关于过点(0,0), (1,1)的直线对称□已知:lx-ll+(.y + 2『=0,则(x, y)关于原点对称的点为_________________ .□已知点P(" + 3b,3)与点0(-5,“ + 2b)关于x轴对称,贝比= ______________ , b = _________ .题型二坐标系中的平移巩固练习【练习2】⑴线段CD是由线段初平移得到的,点A(-l, 5)的对应点是C(4, 2),则点B(4, -1)的对应点D的坐标为__________ ・⑵在平面直角坐标系中有一个已知点A ,现在x轴向下平移3个单位,y轴向左平移2个单位,单位长度不变,得到新的坐标系,在新的坐标系下点A的坐标为(-1,2),在旧的坐标系下,点A的坐标为_______ ・【练习3】如图,在平而直角坐标系中,若每一个方格的边长代表一个单位.□线段DC是线段经过怎样的平移得到的?□若C点的坐标是(4, 1), A点的坐标是(-1,-2),你能写岀B、D两点的坐标吗?□求平行四边形ABCD的而积.题型三坐标系中的面积和规律问题巩固练习【练习4】□已知A(0,—2), B(5,0), C(4,3),求△ABC的而积.□已知:A(4,0), 3(1-斗0), 0(1, 3), ZVWC 的而积=6,1)A B求代数式2A-2-5X + X2+4X-3X2 -2 的值.【练习5】如图,长为1,宽为2的长方形ABCQ以右下角的顶点为中心顺时针旋转90°,此时A点的坐标为________ :依次旋转2009次,则顶点A的坐标为___________ ・。
平面直角坐标系中的位似变换
2
标是( D )
y
A
A' A''
B''
A.(3,2) C.(12,8)
O
x
B'
B
B.(12,8)或(-12,8) D.(3,2)或(-3,-2)
(2)、在平面直角坐标系中,四边形OBCD与四边形OEFG位似,位似
中心是原点O,已知C与F是对应点,且C、F的坐标分别是C(3,7)F
(9,21),那么四边形OBCD与四边形OEFG的相似比是 1:3 ,
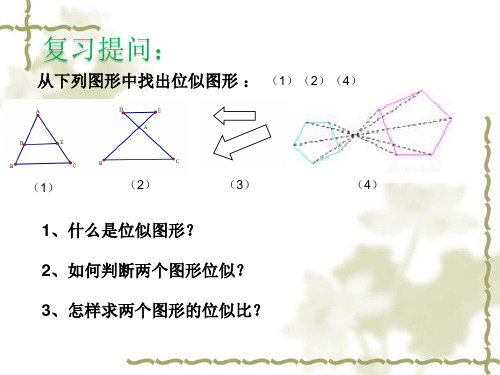
复习提问:
从下列图形中找出位似图形 : (1)(2)(4)
(1)
(2)
(3)
1、什么是位似图形? 2、如何判断两个图形位似? 3、怎样求两个图形的位似比?
(4)
学习目标
重点:能熟练在坐标系中根据坐标的变化规律做出位似图形 难点:理解位似图形的坐标变换规律.
问题探究
探究一:
如图,在平面直角坐标系中,△OAB三个顶点的坐标分别为
坐标 都
C
乘以
-
1 2
,画出所得到的图形,你发
现了什么?
x
探究点拨:当图中各点的 横、纵坐标缩小一定的倍 数k,依次连接各点所得到 新图形与原图形 位似 , 位似中心是 坐标原点,位似 比是 |k| 。
定理 在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘 同一个数k(k≠0),所对应的图形与原图形 位似 ,位似中心是 坐标原点 , 它们的位似比为 |k| .
D、 (m , n ) 22
课堂小结
定理
平面直角坐标系 中的位似变化
在平面直角坐标系中,将一个多边形每个顶点的横 坐标、纵坐标都乘同一个数k(k≠0),所对应的图形 与原图形位似,位似中心是坐标原点,它们的相似 比位|k|.
坐标系的转换

对于坐标系之间的转换,目前我们国家有以下几种:1、大地坐标(BLH)对平面直角坐标(XYZ);2、北京54全国80及WGS84坐标系的相互转换;3、任意两空间坐标系的转换。
坐标转换就是转换参数。
常用的方法有三参数法、四参数法和七参数法。
以下对上述三种情况作转换基本原理描述如下:1、大地坐标(BLH)对平面直角坐标(XYZ)常规的转换应先确定转换参数,即椭球参数、分带标准(3度,6度)和中央子午线的经度。
椭球参数就是指平面直角坐标系采用什么样的椭球基准,对应有不同的长短轴及扁率。
一般的工程中3度带应用较为广泛。
对于中央子午线的确定的一般方法是:平面直角坐标系中Y坐标的前两位*3,即可得到对应的中央子午线的经度。
如x=3888888m,y=388888666m,则中央子午线的经度=38*3=114度。
另外一些工程采用自身特殊的分带标准,则对应的参数确定不在上述之列。
确定参数之后,可以用软件进行转换,以下提供坐标转换的程序下载。
2、北京54全国80及WGS84坐标系的相互转换这三个坐标系统是当前国内较为常用的,它们均采用不同的椭球基准。
其中北京54坐标系,属三心坐标系,大地原点在苏联的普而科沃,长轴6378245m,短轴6356863,扁率1/298.3;西安80坐标系,属三心坐标系,大地原点在陕西省径阳县永乐镇,长轴6378140m,短轴6356755,扁率1/298.25722101;WGS84坐标系,长轴6378137.000m,短轴6356752.314,扁率1/298.257223563。
由于采用的椭球基准不一样,并且由于投影的局限性,使的全国各地并不存在一至的转换参数。
对于这种转换由于量较大,有条件的话,一般都采用GPS联测已知点,应用GPS软件自动完成坐标的转换。
当然若条件不许可,且有足够的重合点,也可以进行人工解算。
详细方法见第三类。
3、任意两空间坐标系的转换由于测量坐标系和施工坐标系采用不同的标准,要进行精确转换,必须知道至少3个重合点(即为在两坐标系中坐标均为已知的点。
平面直角坐标系中的位似变换

8),O(0, 0),C′ (10, 0); A"(-8,-8),O(0,0), C″ (-10, 0).
归纳
知1-导
在平面直角坐标系中,如果位似变换是以原点 为位似中心,相似比为k,那么位似图形对应点的坐 标的比等于k或-k.即若原图形的某一顶点坐标为(x0, y0),则其位 似 图 形 对 应 顶 点 的 坐 标 为 ( k x 0, k y 0) 或 (-kx0,-ky0).
知1-练
3 如图,线段CD的两个端点的坐标分别为C(1,2), D(2,0),以原点为位似中心,将线段CD放大得 到线段AB,若点B的坐标为(5,0),则点A的坐标 为( B ) A.(2,5) B.(2.5,5) C.(3,5) D.(3,6)
知1-练
4 (中考•东营)如图,在平面直角坐标系中,已知点 A(-3,6),B(-9,-3),以原点O为位似中心, 相似比为 1 , 把△ABO缩小,则点A的对应点A′的
事实上,幻灯机工作的实质是将图片中的图形放大. 本节知识将对上述问题作系统的讲解.
知1-导
知识点 1 平面直角坐标系中的位似变换
问题
如图(1),在直角坐标系中,有两点A(6,3),B(6,
0).以原点O为位似中心,相似 比为 1 ,把线段AB缩小.观察
3 对应点之间坐标的变化,你有
什么发现?
如图(2),△AOC三个顶点的
3
坐标是( D ) A.(-1,2) B.(-9,18) C.(-9,18)或(9,-18) D.(-1,2)或(1,-2)
知1-练
5 【中考·烟台】如图,在平面直角坐标系中,正方 形ABCD与正方形BEFG是以原点O为位似中心的 位似图形,且相似比为 1 , 点A,B,E在x轴上,
两个平面直角坐标系转换公式

两个平面直角坐标系之间的转换公式包括以下三种情况:
1. 单纯移轴:设Oxy,O'x'y'是两个直角坐标系,坐标轴有相同的方向,O'在Oxy中的坐标为(x0,y0)。
用(x,y),(x',y')分别代表点M 在坐标系Oxy,O'x'y'中的坐标。
在移轴下,坐标转换公式是x=x'+x0,y=y'+y0。
2. 单纯转轴:设新旧坐标系有相同的坐标原点O,由Ox到Ox'的角度为t,坐标转换公式是x=x'cost-y'sint,y=x'sint+y'cost。
3. 一般的坐标转换公式:设Oxy,O'x'y'是两个坐标系,O'在Oxy 中的坐标为(x0,y0),由x轴到x'轴的角度为t,坐标转换公式是x=x'cost-y'sint+x0,y=x'sint+y'cost+y0。
以上是通过新坐标来表示旧坐标,同样可以通过旧坐标来表示新坐标。
平面直角坐标系及伸缩变换

=4.动圆 M 与圆 O1 内切,又与圆 O2 外切,建立适当的坐标系,
求动圆圆心 M 的轨迹方程,并说明轨迹是何种曲线.
解: 如图所示,以 O1O2 的中点 O 为原点,O1O2 所在直线为
x 轴建立平面直角坐标系.
y
由由|O|O1O1O2|=2|=4,4,得得OO11((- -22, ,00)),、OO2(22(,20,0))..
A1(- a,0),A2(a,0)
ec (e1) a
y b x a
A1(0,-a),A2(0,a)
ec (e1) a
y a x b
图形 ly
OF x
标准方程
y2=2px (p>0)
焦点坐标 准线方程
( p ,0 ) x p
2
2
二 抛
物
yl
FO
y2=-2px x (p>0)
( p ,0) 2
lll和和和lll的的的距距距离离离的的的最最最小小小值值值为为为|1|122||1±5±52441|±5.2|.45|.4 | .
O
x
∴∴∴点点点QQQ与与与ll的l的的最最最小小小值值值为为为88558555..5.
题 型 三 定义法求轨迹方程
【例 3】已知两个定圆 O1和 O2,它们的半径分别是 1 和 2,且|O1O2|
所以有 x02
4
把①代入②,
y02
得
4
1.
(2x)2
②
(2y)2 1,
4
整理, 得 x24y21.
MP
O
x
所以点M的轨迹方程是 x24y21.
课堂小结
平面直角坐标系建系时,根据几何特点选 择适当的直角坐标系。
平面直角坐标系变化规律

平面直角坐标系变化规律一、平面直角坐标系中的平移变化规律1. 点的平移- 在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x + a,y)(或(x - a,y));- 将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y + b)(或(x,y - b))。
- 例如:点A(2,3)向右平移3个单位长度,得到点A'(2 + 3,3)=(5,3);点A(2,3)向下平移2个单位长度,得到点A''(2,3 - 2)=(2,1)。
2. 图形的平移- 图形的平移实际上就是图形上各个点的平移。
例如,三角形ABC三个顶点A(x_1,y_1)、B(x_2,y_2)、C(x_3,y_3),将三角形ABC向右平移a个单位长度,再向上平移b个单位长度,则A点变为A'(x_1 + a,y_1 + b),B点变为B'(x_2+a,y_2 + b),C点变为C'(x_3 + a,y_3 + b),新的三角形A'B'C'就是原三角形ABC平移后的图形。
二、平面直角坐标系中的对称变化规律1. 关于x轴对称- 点(x,y)关于x轴对称的点的坐标为(x,-y)。
- 例如:点P(3,4)关于x轴对称的点P'(3,-4)。
- 对于图形来说,图形关于x轴对称,就是图形上所有点关于x轴对称后得到的新图形。
如三角形ABC关于x轴对称,A(x_1,y_1)变为A''(x_1,-y_1),B(x_2,y_2)变为B''(x_2,-y_2),C(x_3,y_3)变为C''(x_3,-y_3),新的三角形A''B''C''就是三角形ABC关于x轴对称后的图形。
2. 关于y轴对称- 点(x,y)关于y轴对称的点的坐标为( - x,y)。
二次曲线的方程化简与分类

x y
A2 x A1x
B2 y C2 z
A22 B22 B1 y C1z
A2 A22 B22
cos ,
A12B2B12 A22 B22
sin ,
(﹡)
A1 A12 B12
sin ,
B1 A12 B12
cos
.
(*)的符号选取要使得第一式右端 x 的系数与第二式
与二次曲线的中心重合,则在新坐标系下二次曲线的新方程 中一次项消失.
张 之 正 解析几何
6
Mathematical Scien20c2e1/C8o/2l9lege
2.二次曲线方程的化简与分类
2. 转轴:
数学科学学院
x xcos ysin
y
x sin
y
cos
转轴变换规律:
1°二次项系数一般要改变.
定理2 通过适当选取坐标系,二次曲线的方程 总可以写成下面九种标准方程的一种形式:
[1] x2 y2 1 (椭 圆) a2 b2
张 之 正 解析几何
12
Mathematical Scien20c2e1/C8o/2l9lege
2.二次曲线方程的化简与分类
数学科学学院
[2]
x2 a2
y2 b2
1 (虚 椭 圆)
a12 0 .为此,取 ,使得
a12 a22 a11sin cos a12 cos2 sin2 0 ,
即 a22 a11 sin 2 2a12 cos 2 0 ,
cot 2 a11 a22
∴
2a12
张 之 正 解析几何
8
Mathematical Scien20c2e1/C8o/2l9lege
§5.6 二次曲线的方程化简与分类
平面直角坐标变换

§6 平面直角坐标变换一 平移坐标变换定义:若二平面直角坐标系{O ;i ,j}和{O ′;i ′,j ′}满足i=i ′,j=j ′,则坐标系{O ′;i ′,j ′}可看成是由{O ;i ,j }经过平移得到的,称由坐标系{O ;i ,j}到坐标系{O ′;i ′,j ′}的变换为平移坐标变换。
平移变换公式设平面上一点M 在新系{O ′;i ′,j ′}与旧系{O ;i ,j}下的坐标分别为 (x ′,y ′),(x,y ),而O ′在旧系下的坐标为(a,b ),则 xi+yj= OP = O O +P O '=ai+bj+x ′i ′+y ′j ′=ai+bj+x ′i+y ′j=(a+x ′)i+(b+y ′)j∴⎩⎨⎧+'=+'=b y y a x x ——平移坐标变换公式 二 旋转坐标变换:定义:若二坐标系{O ;i ,j}和{O ′;i ′,j ′}满足O ≡O ′,另∠(i ,j ′)=θ 则坐标系{O ′;i ′,j ′}可看成是由坐标系{O ;i ,j}绕O 旋转θ角得到的,称由{O ;i ,j}到{O ′;i ′,j ′}的变换为旋转坐标变换。
旋转变换公式由于∠(i ,i ′)=0,∴∠(i ,j ′)=2π+θ ∴i ′=cos θi+sin θj ,j ′=cos (2π+θ)i+sin (2π+θ)j=-sin θi+cos θj ∴xi+yj=OP =P O '=x ′i ′+y ′j ′=x ′(cos θi+sin θj )+y ′(-sin θi+cosθj )=(x ′cos θ-y ′sin θ)i+(x ′sin θ+y ′cos θ)j即⎩⎨⎧'+'='-'=θθθθcos sin sin cos y x y y x x用x,y 表示x ′,y ′,有⎩⎨⎧+-='+='θθθθcos sin sin cos y x y y x x 三 一般坐标变换:称由坐标系{O ;i ,j}得坐标系{O ′;i ′,j ′}的变换为一般坐标变换。
空间大地坐标系与平面直角坐标系转换公式

§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。
人们为了描述空间位置,采用了多种方法,从而也产生了不同的坐标系,如直角坐标系、极坐标系等。
在测量中常用的坐标系有以下几种:一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心,Z 轴指向参考椭球的北极,X 轴指向起始子午面与赤道的交点,Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示:图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。
空间大地坐标系可用图2-4来表示:图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换,将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上,这种变换又称为投影变换。
投影变换的方法有很多,如横轴墨卡托投影、UTM 投影、兰勃特投影等。
在我国采用的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例,只是投影的个别参数不同而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲,是一种横轴椭圆柱正切投影。
如图左侧所示,设想有一个椭圆柱面横套在椭球外面,并与某一子午线相切(此子午线称为中央子午线或轴子午线),椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。
高斯投影满足以下两个条件:1、 它是正形投影;2、 中央子午线投影后应为x 轴,且长度保持不变。
将中央子午线东西各一定经差(一般为6度或3度)范围内的地区投影到椭圆柱面上,再将此柱面沿某一棱线展开,便构成了高斯平面直角坐标系,如下图2-5右侧所示。
平面直角坐标系中的伸缩变换

x y
' '
x y
( 0) ( 0)
的作用下,点P(x,y)对应 P' (x', y') 称 为平面直角坐
标系中的伸缩变换。
注 : (1)λ>0,μ>0
(2)把图形看成点的运动轨迹,平面图形的伸缩 变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同 一直角坐标系下进行伸缩变换。
坐标伸长变换
8
6
4 2
- 10
-5 -2 -4
5
10
-6
-8
设P( x, y)是平面直角坐标系中的任意一点,保持
横坐标x不变,将纵坐标y伸长为原来的3倍,得到
点P '
(
x'
,
y'
),那么{
x' x y' 3 y
(2)
我们把(2)式叫做平面直角坐标系中的一个坐标
伸长变换。
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写 出其坐标变换
平面直角坐标系的伸缩变换
定义:设点P( x, y)是平面直角坐标系中的
任意一点,在变换
φ:{ yx
λ μ
x( y(
λ μ
0) 0)
的作用下,点P( x, y)对到应点P( x, y),称 为
平面直角坐标系中的坐 标伸缩变换简称伸缩变 换
定义:设P(x,y)是平面直角坐标系中任意一点,在变
换
:
压缩变换。
(2)怎样由正弦曲线y sin x得到曲线y 3sin x?
如图,在正弦曲线 y sin x上任取一点P( x, y), 保持横坐标x不变,将纵坐标 y伸长原来的3倍, 那么正弦曲线y sin x就变成曲线y 3sin x
平面直角坐标系中的变换

第4讲 平面直角坐标系中的变换已知点P (a ,b ),则点P 到x 轴的距离为 ; 点P 到y 轴的距离为 . 若点P (a ,b )在第一、三象限的角平分线上,则 ,即横、纵坐标 ; 若点P (a ,b )在第二、四象限的角平分线上,则 ,即横、纵坐标 .【例1】基础过关(1)点A (3,-1)在第______象限,点B (-1,-3)在第______象限,点C (3, 1)在第______象限,点A (-3,1)在第______象限.(2)若点P (a ,b )在第二象限,则点(-b ,a )在第______象限.(3)如果点P 在轴上,则____,此时P 的坐标为_____ ;当____时,点P 在横轴上,此时P 点坐标为 ______ ;(4)点P(x ,y),若xy=0,则点P 在____________上.(5)已知点P (-x+1,2x-7)在第三象限的角平分线上,则x=______.(6)已知点P (2x ,x+3)在第二象限坐标轴夹角平分线上,则点Q (-x+2,2x+3)的坐标为 .(7)如果点A (2,m ),点B (n-6) 且AB//y 轴,则_______.(8)点P 在第四象限,且到x 轴的距离为2,到y 轴的距离为5,则点P 的坐标为_______.(9)点P (-a 2-2,b 2+1)到x 轴的距离为______,到y 轴的距离为______.【例2】基础过关(1)如果a -b <0,且ab <0,那么点(a ,b)在( )A 、第一象限B 、第二象限C 、第三象限,D 、第四象限.()5,2a a +-y a =a =(),1a a -板块一 平面直角坐标系的基础知识(2)如果<0,那么点P (x ,y )在( )A 、第二象限B 、第四象限C 、第四象限或第二象限D 、第一象限或第三象限(3)点(x ,1-x )不可能在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限(4)已知点P (2x-10,3-x )在第三象限,则x 的取值范围是( )A 、53<<xB 、3≤x ≤5C 、5>x 或3<xD 、x ≥5或x ≤3 点P (m ,n)关于x 轴的对称点为 ,即横坐标不变,纵坐标互为相反数;点P (m ,n)关于y 轴的对称点为 ,即纵坐标不变,横坐标互为相反数;点P (m ,n)关于原点的对称点为 ,即横、纵坐标都互为相反数;点P (m ,n)关于点Q (a ,b )的对称点是 .【例3】基础过关(1)点P (3,-5)关于x 轴对称的点的坐标为( )A .(-3,-5)B .(5,3)C .(-3,5)D .(3,5)(2)点P (-2,1)关于y 轴对称的点的坐标为( )A . (-2,-1)B .(2,1)C .(2,-1)D .(-2,1)(3) 在平面直接坐标系中,P (-4,5)关于x 轴对称点的坐标是 ,关于y 轴的对称点的坐标是 ,关于原点的对称点是 .(4)点P (2,3)关于直线x =3的对称点为 ,关于直线y =5的对称点为 .(5)点(-2,3)关于点(1,2)对称的点是 .(6)已知点P (a +1,2a-1)关于x 轴的对称点在第一象限,求a 的取值范围.xy 板块二 坐标系中的对称【例4】对称的应用如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.(1)观察与探究:由图观察已知A(2,0)关于直线l的对称点A’的坐标为(0,2),请在图中分别标明B(5,3),C(-2,5)关于直线l的对称点B’、C’的位置,并写出它们的坐标:B’,C’;(2)归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P (a,b)关于第一、三象限的角平分线l的对称点P’的坐标为(不必证明);(3)运用与拓展:点A(a,b)在直线l的下方,则a,b的大小关系为;若在直线l的上方,则.板块三坐标系中的平移将点(x,y)向右平移a个单位长度,得到的对应点的坐标是:____________;将点(x,y)向左平移a个单位长度,得到的对应点的坐标是:____________;将点(x,y)向上平移b个单位长度,得到的对应点的坐标是:____________;将点(x,y)向下平移b个单位长度,得到的对应点的坐标是:.将一个图形各个点的横坐标加上(或减去)一个正数a,相应的新图形将向(或向)平移个单位长度;将一个图形各个点的纵坐标加上(或减去)一个正数a,相应的新图形将向(或向)平移个单位长度;平移只改变图形的,图形的和不发生改变.平行于x轴(或横轴)的直线上的点的相同;平行于y轴(或纵轴)的直线上的点的相同.【例5】基础过关(1)点M(-3,-5)向上平移7个单位得到点M1的坐标为;再向左平移3个单位得到点M2的坐标为.(2)在平面直角坐标系中,若将点p(x,y)向右平移a个长度单位得到点的坐标是,若向下平移b个长度单位,得到的点的坐标是.(3)平面直角坐标系中,线段A1B1是由线段AB经过平移得到的,点A(-1,-4)的对应点为A1(1,-1),点B(1,1)的对应点B1为.(4)将点P(m-2,n+1)沿x轴负方向平移3个单位,得到P1(1-m,2),则点P坐标是.【例6】平移的应用(1)如图1,在平面直角坐标系中,右边的图案是由左边的图案经过平移得到的,左边图案中左、右眼睛坐标分别是(-4,2)(-2,2),右边图案中左眼的坐标是(3,4),则右边图案中右眼的坐标是.(2)如图2是由若干个边长为1的小正方形组成的网格,请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90°再向右平移2个单位的图形(其中C、D为所在小正方形边的中点).图1 图2 图3 图4 板块四坐标系中的面积与规律问题【例7】面积问题(1)如图3,直角坐标系中,△ABC的顶点都在网格点上,其中点A的坐标为(2,-1),则△ABC的面积为平方单位.(2)如图4,已知直角坐标系中A(-1,4)、B(0,2),平移线段AB,使点B移到点C (3,0),此时点A记作点D,则四边形ABCD的面积是.(3)已知:如图,在平面直角坐标系中,四边形ABCD各项点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).求四边形ABCD的面积.【例8】找规律问题(1)如图5,在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,图中的正方形的四个顶点都在格点上,观察图中每一个正方形四条边上的整点的个数,请你猜测由里向外第10个正方形四条边上的整点个数共有个.(清华附中期中)(2)如图6,在平面直角坐标系中,第1次将△OAB 变换成△OA 1B 1,第二次将三角形OAB 变换成OA 2B 2,第三次将△OAB 变换成△OA 3B 3.已知A (1,3),A 1(2,3),A 2(4,3),A 3(8,3),B (2,0),B 1(4,0),B 2(8,0),B 3(16,0).观察每次变化前后的三角形,找出规律,按此变化规律再将△OA 3B 3变换成△OA 4B 4,则点A 4的坐标是 ,则点B 4的坐标是 ,则点A n 的坐标是 ,则点B n 的坐标是 .(北京十二中期中)(3)如图,一个粒子在第一象限内及x 轴、y 轴上运动,在第1min 内它从原点运动到(1,0),而后接着按如图所示方式在与x 轴、y 轴平行的方向上来回运动,且每分钟移动1个单位长度,那么,在1989min 后,求这个粒子所处的位置坐标.【巩固练习】1.已知点A ()4,x y -,点()1,2B y x -关于x 轴对称,求x y 的值.2.如图,将边长为1的正方形OAPB 沿x 轴正方向边连续翻转2006次,点P 依次落在点1232006,,P P P P 的位置,则2006P 的横坐标2006x =______,2006P 的纵坐标2006y =______.3.在平面直角坐标系中,等腰三角形ABC 的顶点A 的坐标为(2,2).(1)若底边BC 在x 轴上,设点B 、C 坐标分别为(m ,0)、(n ,0),你认为m 、n 应满足怎样的条件?答:____________. (2)若底边BC 两端点分别在x 轴、y 轴上,设点B 、C 的坐标分别为(m ,0)、(0,n ),你认为m 、n 应满足怎样的条件?答:____________.课后作业1.(1)在平面直角坐标系中,点A(2,5)与点B关于y轴对称,则点B的坐标是()A.(-5,-2)B.(-2,-5)C.(-2,5)D.(-2,-5)(2)已知点P(x,y),Q(m,n),如果x+m=0,y+n=0那么点P,Q()A.关于原点对称B.关于x轴对称C.关于y轴对称D.关于过点(0,0)(1,1)的直线对称(3)已知:|x-1|+(y+2)²=0,则(x,y)关于原点对称的点为.(4)已知点P(a+3b,3)与点Q(-5,a+2b)关于x轴对称,则a=b= 2.(1)将点P(-4,3)先向右平移2个单位,再向上平移1个单位后,则得到点P’的坐标为.(2)点A向左平移3个单位,再向下平移1个单位到点(-1,3),则点A的坐标为.(3)在平面直角坐标系中有一个已知点A,现在x轴向下平移3个单位,y轴向左平移2个单位,单位长度不变,得到新的坐标系,在新的坐标系下点A的坐标系下点A的坐标为(-1,2),在旧的坐标系下点A的坐标为.(4)在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比()A.向右平移了3个单位B.向左平移了3个单位C.向上平移了3个单位D.向下平移了3个单位(5)已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.3.如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).(1)求出△ABC的面积.(2)在图中画出△ABC向右平移3个单位,再向下平移2个单位的图形△A1B1C1.(3)写出点A1,B1,C1的坐标.4.如图,在平面直角坐标系中,若每一个方格的边长代表一个单位.(1)线段DC是线段AB经过怎样的平移得到的?(2)若C点的坐标是(4,1),A点的坐标是(-1,-2),你能写出B、D两点的坐标吗?(3)求平行四边形ABCD的面积.5.如图,长为1,宽为2的长方形ABCD以右下角的顶点为中心顺时针旋转90°,此时A 点的坐标为;依次旋转2009次,则顶点A的坐标为.。
空间大地坐标系与平面直角坐标系转换公式

§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。
人们为了描述空间位置,采用了多种方法,从而也产生了不同的坐标系,如直角坐标系、极坐标系等。
在测量中常用的坐标系有以下几种:一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心,Z 轴指向参考椭球的北极,X 轴指向起始子午面与赤道的交点,Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。
某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。
空间直角坐标系可用图2-3来表示:图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。
空间大地坐标系可用图2-4来表示:图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换,将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上,这种变换又称为投影变换。
投影变换的方法有很多,如横轴墨卡托投影、UTM 投影、兰勃特投影等。
在我国采用的是高斯-克吕格投影也称为高斯投影。
UTM 投影和高斯投影都是横轴墨卡托投影的特例,只是投影的个别参数不同而已。
高斯投影是一种横轴、椭圆柱面、等角投影。
从几何意义上讲,是一种横轴椭圆柱正切投影。
如图左侧所示,设想有一个椭圆柱面横套在椭球外面,并与某一子午线相切(此子午线称为中央子午线或轴子午线),椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。
高斯投影满足以下两个条件:1、 它是正形投影;2、 中央子午线投影后应为x 轴,且长度保持不变。
将中央子午线东西各一定经差(一般为6度或3度)范围内的地区投影到椭圆柱面上,再将此柱面沿某一棱线展开,便构成了高斯平面直角坐标系,如下图2-5右侧所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5.7 平面直角坐标变换为了考虑同一图形在不同的坐标系下的方程之间的关系,我们首先需要建立同一个点在不同的坐标系下的坐标之间的关系,这就是坐标变换的问题,因为我们研究的图形是点的轨迹.我们仅考虑平面直角坐标变换.设在平面上给出了由两个标架 {O ;i , j } 和 {O';i', j' } 所决定的右手直角坐标系,这里i 和j 以及i' 和j' 是两组坐标基向量,它们是平面上的两个标准正交基,我们依次称这两个坐标系为旧坐标系和新坐标系.由于坐标系的位置完全由原点和坐标基向量所决定,所以新坐标系与旧坐标系之间的关系,就由O' 在 {O ;i , j } 中的坐标以及i' 和j' 在 {O ;i , j } 中的分量所决定.任一直角坐标变换总可以分解成移轴(也叫坐标平移)和转轴(也叫坐标旋转)两个步骤.1.移轴如果两个标架 {O ;i , j } 和 {O';i , j' } 的原点O 与O' 不同,O' 在{O ;i , j }中的坐标为 (x 0,y 0),但两标架的坐标基向量相同,即有i' = i , j' = j那么标架 {O';i', j'} 可以看成是由标架 {O ;i , j } 将原点平移到O'点而得来的(图5.7.1).这种坐标变换叫做移轴(坐标平移).设P 是平面内任意一点,它对标架 {O ;i , j } 和 {O';i', j'} 的坐标分别为 (x ,y ) 与(y x '',),则有P O O O OP '+'=但 j i y x OP +=,j i y x P O '+'=',j i 00y x O O +='于是有j i j i )()(00y y x x y x +'++'=+故 {x ,y } = {x 0,y 0} + {x',y' }根据向量相等的定义得移轴公式为 图5.7.1⎩⎨⎧+'=+'=00y y y x x x (5.7-1)从中解出x' 和y',就得逆变换公式为⎩⎨⎧-='-='00y y y x x x(5.7-2)2.转轴若两个标架 {O ;i , j } 和 {O';i', j'} 的原点相同,即O = O',但坐标基向量不同,且有∠(i ,i' ) = α,则标架 {O';i',j'} 可以看成是由标架 {O ;i ,j } 绕O 点旋转α 角而得来的(图5.7.2).这种由标架 {O ;i ,j } 到标架 {O';i',j'}的坐标变换叫做转轴(坐标旋转).下面推导转轴公式.设P 是平面内任意一点,它对 {O ;i , j } 和 {O';i', j'} 的坐标分别为 (x ,y ) 与 (y x '',),即有j i j i ''+''='+=y x P O y x OP因为∠(i ,i' ) = α,新旧坐标基本向量之间有关系ααsin cos j i i +='图5.7.2ααααcos sin 2πsin 2πcos j i j i j +-=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+='于是有ji j i j i )cos sin ()sin cos ()cos sin ()sin cos (ααααααααy x y x y x P O '+'+'-'=+-'++'='因为O 和O'是同一点,P O OP '=,故可直接得到转轴公式:⎩⎨⎧'+'='-'=ααααcos sin sin cos y x y y x x(5.7-3)从(5.7-3)中解出x' 和y ',就得到用旧坐标表示新坐标的逆变换公式: ⎩⎨⎧+-='+='ααααcos sin sin cos y x y y x x(5.7-4)式中的α 为坐标轴的旋转角.(5.7-4)式也可看成是由标架 {O ;i',j'} 绕O 旋转- α 角变到 {O ;i ,j } 的转轴公式.* 根据线性代数的理论,(5.7-3)可写为⎥⎦⎤⎢⎣⎡''=⎥⎦⎤⎢⎣⎡y x y x Q ,这里的坐标变换的矩阵⎥⎦⎤⎢⎣⎡-=ααααcos sin sin cos Q 是一个正交矩阵,因而其逆矩阵T 1Q Q =-,逆变换公式可以直接由⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''y x y x T Q 写出.3.一般坐标变换公式在一般情况下,由旧坐标系O -xy 变成新坐标系O'-x'y',总可以分两步来完成.即先移轴使坐标原点与新坐标系的原点O' 重合,变成坐标系O'-y x '''',然后再由辅助坐标系O'-x"y" 转轴而成新坐标系O'-x'y'(图5.7.3).设平面上任一点P 的旧坐标与新坐标分别为 (x ,y ) 与 (x',y' ),而在辅助坐标系O'-x"y" 中的坐标为 (x",y" ),那么由(5.7-1)与(5.7-4)分别得⎩⎨⎧+''=+''=00x y y x x x 与 ⎩⎨⎧'+'='''-'=''ααααcos sin sin cos y x y y x x由上两式得一般坐标变换公式为图5.7.3⎩⎨⎧+'+'=+'-'=00cos sin sin cos y y x y x y x x αααα (5.7-5)由(5.7-5)解出x',y' 便得逆变换公式⎩⎨⎧+--+-='+-+=')cos sin (cos sin )sin cos (sin cos 0000ααααααααy x y x y y x y x x(5.7-6)平面直角坐标变换公式(5.7-5)是由新坐标系原点的坐标 (x 0, y 0) 与坐标轴的旋转角 α 决定的.4.由给定的新坐标轴确定的坐标变换确定坐标变换公式,除了坐标平移和旋转外,还可以有其它方法.假定已给出了新坐标系的两坐标轴在旧坐标系中的方程,并规定了一个轴的正方向,就可以确定又一种坐标变换公式.设在直角坐标系xOy 里给定了两条相互垂直的直线 l 1:0111=++C y B x A , l 2:0222=++C y B x A其中02121=+B B A A .如果取直线l 1为新坐标系中的横轴O'x',而直线l 2为纵轴O'y',并设平面上任意点M 的旧坐标与新坐标分别是(x ,y )与(x',y').因为 | x' | 是点M (x ,y )到O'y' 轴的距离,也就是M 点到l 2的距离(图5.7.4),所以有图5.7.42222222||B A C y B x A x +++=' 同理可得2121111||BA C yB x A y +++='于是在去掉绝对值符号以后,便得到一个坐标变换公式⎪⎪⎩⎪⎪⎨⎧+++±='+++±='21211112222222B A C y B x A y B A C y B x A x (5.7-7)为了使新坐标系仍然是右手坐标系,可将(5.7-7)式与公式(5.7-4)比较来决定(5.7-7)中的符号.因ααsin ,cos 2222222222=+±=+±B A B B A A ααcos ,sin 2121121211=+±-=+±BA B BA A因此(5.7-7)中的第一式右端的x 的系数应与第二式的右端的y 的系数相等,所以(5.7-7)的符号选取要使得这两项的系数是同号的.这种坐标变换的方法常用来在求得一般中心二次曲线的主直径的情况下,用两条主直径作为新坐标轴,把二次曲线的方程化为标准方程.以上给出的坐标变换的公式(5.7-5)、(5.7-6)和(5.7-7)实质上都是一样的.* 5.坐标变换下代数曲线及其次数的不变性在直角坐标系下,如果我们所讨论的平面曲线的方程能写成F (x ,y ) = 0的形式,其中F (x ,y ) 是关于x 和y 的多项式,那么这种方程就叫做代数方程,它所表示的平面曲线叫做代数曲线.不是代数曲线的曲线叫做超越曲线.代数方程的次数叫做代数曲线的次数.由于上面给出的几个坐标变换公式都是一次式(线性的),而任何代数方程经过一次式的变换之后必然还是代数方程,任何超越方程经过一次式的变换之后也必然还是超越方程.因此有命题5.7.1 曲线的代数性和超越性在线性坐标变换下保持不变.另一方面,代数方程的次数在一次式的变换之下也是保持不变的,因此还有 命题5.7.2 代数曲线的次数在线性坐标变换下保持不变.例1 已知新坐标系的x' 轴与y' 轴的方程分别为3x - 4y + 6=0与4x + 3y - 17=0,求坐标变换公式,并求点A (0,1)关于新坐标系的坐标.解 由题意,设M (x ,y ) 是旧坐标系下任一点,其新坐标为 ( x', y' ),则有⎪⎪⎩⎪⎪⎨⎧+-±='-+±='564351734y x y y x x 根据上面的符号选取法则得变换公式为⎪⎪⎩⎪⎪⎨⎧+--='-+='564351734y x y y x x 或 ⎪⎪⎩⎪⎪⎨⎧+-='-+-='564351734y x y y x x 若选第一个坐标变换公式,则点A (0,1) 关于新坐标系的坐标是(- 14/5,- 2/5);若选第二个,则点A (0,1) 关于新坐标系的坐标是(14/5,2/5).注 若用前一公式,绝非将坐标原点平移到⎪⎭⎫ ⎝⎛±±56,517,而是移到了点 (2,3).2和3是由(5.7-6)确定的⎩⎨⎧=+-=+64317340000y x y x 的解.因53sin =a >0,旋转角为小于π的正角;若用后一公式,也非将坐标原点平移到点⎪⎭⎫ ⎝⎛56,517.由于取了53sin -=a <0,所以旋转角为绝对值小于 π 的负角.。
