三视图代码
AutoCAD教程:设置视图solview和设置图形soldraw命令将三维实体转为三视图
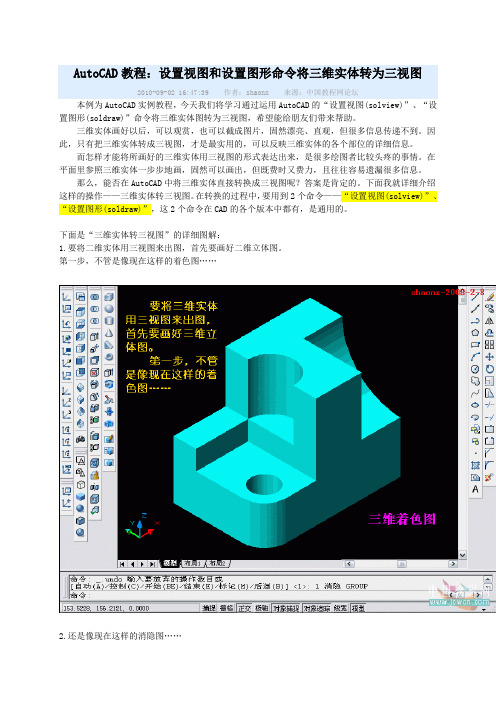
AutoCAD教程:设置视图和设置图形命令将三维实体转为三视图2010-09-02 16:47:39 作者:shaonx 来源:中国教程网论坛本例为AutoCAD实例教程,今天我们将学习通过运用AutoCAD的“设置视图(solview)”、“设置图形(so ldraw)”命令将三维实体图转为三视图,希望能给朋友们带来帮助。
三维实体画好以后,可以观赏,也可以截成图片,固然漂亮、直观,但很多信息传递不到。
因此,只有把三维实体转成三视图,才是最实用的,可以反映三维实体的各个部位的详细信息。
而怎样才能将所画好的三维实体用三视图的形式表达出来,是很多绘图者比较头疼的事情。
在平面里参照三维实体一步步地画,固然可以画出,但既费时又费力,且往往容易遗漏很多信息。
那么,能否在AutoCAD中将三维实体直接转换成三视图呢?答案是肯定的。
下面我就详细介绍这样的操作——三维实体转三视图。
在转换的过程中,要用到2个命令——“设置视图(solview)”、“设置图形(soldraw)”,这2个命令在CAD的各个版本中都有,是通用的。
下面是“三维实体转三视图”的详细图解:1.要将二维实体用三视图来出图,首先要画好二维立体图。
第一步,不管是像现在这样的着色图……2.还是像现在这样的消隐图……3.都要转换到“二维线框”模式,原因是要显示所有线条,包括因阻挡但实际存在的线条,以备以后有用。
4.在正式转三视图之前,先把出图的纸张格式定好,包括纸张横式/竖式,是否黑白打印……5.打印设备设置6.打印布局设置7.点击“设置视图”命令,或在命令行中输入solview,这个命令在布局里创建每个视图放置可见线和隐藏经线的图层(设置视图命令)8.界面自动转到而已窗口,删除自动生成的布局。
方法:点击外围的框线,实线变虚,Delete就删除了,点击Esc键,退出刚才的命令。
9.界面变成了完全的空白,再点击“设置视图”按钮,这回是正式开始设置视图了。
工程制图中的三个面角度的字母

工程制图中的三个面角度的字母
正面投影、水平投影、侧面投影分别称为正视图、俯视图、侧视图;在建筑工程制图中则分别称为正立面图(简称正面图)、平面图、左侧立面图(简称侧面图)。
物体的三面投影图总称为三视图或三面图。
一般不太复杂的形体,用其三面图就能将它表达清楚。
正投影面,大写字母表示V(vertical垂直面)
水平投影面,大写字母表示H(horizontal水平面)
侧(宽)面投影图,大写字母W表示(width宽度)
在三个投影图之间还有“三等”关系:
正立面图的长与平面图的长相等
正立面图的高与侧立面图的高相等
平面图的宽与侧立面图的宽相等
“三等”的关系是绘制和阅读正投影图必须遵循的投影规律,在通常情况下,三个视图的位置不应随意移动。
根据轴测图绘制三视图图例(精华版)

实用文档
50
51
标准文案
实用文档
52
标准文案
实用文档
53 54
55
标准文案
实用文档
56
57
标准文案
实用文档
58
59
标准文案
实用文档
60
61
标准文案
实用文档
62
标准文案
实用文档
63
64
标准文案
实用文档
65
66
标准文案
实用文档
67
68
标准文案
69 70
实用文档
71
标准文案
实用文档
198
O 12
20 10
55 12
R10 70
R12 10 30
199
标准文案
实用文档
200
标准文案
实用文档
95
96
标准文案
实用文档
97
98
标准文案
实用文档
99
100
标准文案
实用文档
101
102
标准文案
实用文档
103
104
标准文案
实用文档
105
106
标准文案
实用文档
107
108
标准文案
实用文档
109
110
标准文案
实用文档
111
112
标准文案
实用文档
113 114 115
116
标准文案
72
73
标准文案
实用文档
74
75
标准文案
实用文档
76
77
标准文案
CAD命令、特殊符号代码大全

常用命令:A——ARC——圆弧 B——BLOCK——块定义C——CIRCLE——圆 D——DIMSTYLE——标注样式E/DEL键——ERASE——删除 F——FILIET——倒圆角H——BHATCH——填充 L——LINE——直线M/S——MOVE——移动 O——OFFSET——偏移P——PAN——实时平移(图标为小手) X——EXPLODE——分解PO——POINT——点 XL——XLINE——射线ML——MLINE——多线 PL——PLINE——多段线POL——POLYGON——正多边形 REC——RECTANGLE——矩形DO——DONUT——圆环 EL——ELLIPSE——椭圆CO——COPY——复制 MI——MIRROR——镜像AR——ARRAY——阵列 RO——ROTATE——旋转TR——TRIM——修剪 EX——EXTEND——延伸CHA——CHAMFER——倒角 F——FILIET——倒圆角BR——BREAK——打断尺寸标注:DLI——DIMLINEAR——直线标注 DAL——DIMALIGNED——对齐标注DRA——DIMRADIUS——半径标注 DDI——DIMDIAMETER——直径标注DAN——DIMANGULAR——角度标注 DCE——DIMCENTER——中心标注DOR——DIMORDINATE——点标注 TOL——TOLERANCE——标注形位公差LE——QLEADER——快速引出标注 DBA——DIMBASELINE——基线标注DCO——DIMCONTINUE——连续标注 DED——DIMEDIT——编辑标注DOV——DIMOVERRIDE——替换标注系统变量常用CTRL快捷键:【CTRL】+1—PROPERTIES—修改特性【CTRL】+2—ADCENTER—设计中心【CTRL】+O——OPEN——打开文件【CTRL】+N/M——NEW——新建文件【CTRL】+P——PRINT——打印文件【CTRL】+S——SAVE——保存文件【CTRL】+Z——UNDO——放弃【CTRL】+X——CUTCLIP——剪切【CTRL】+C——COPYCLIP——复制【CTRL】+V——PASTECLIP——粘贴【CTRL】+B——SNAP——栅格捕捉【CTRL】+F——OSNAP——对象捕捉【CTRL】+G——GRID——栅格【CTRL】+L——ORTHO——正交【CTRL】+W——对象追踪【CTRL】+U ——极轴常用功能键:【F1】——HELP——帮助【F3】——OSNAP——对象捕捉【F7】——GRIP——栅格【F8】——ORTHO——正交A常见的快捷命令:(一)字母类1、对象特性【MA】——MATCHPROP(属性匹配)【ST】——STYLE(文字样式)【COL】——COLOR(设置颜色)【LA】——LAYER(图层操作)【LT】——LINETYPE(线形)【 LTS】——LTSCALE(线形比例)【LW】——LWEIGHT (线宽)【UN】——UNITS(图形单位)【ATT】——ATTDEF(属性定义)【ATE】——ATTEDIT(编辑属性)【AL】—ALIGN(对齐)【EXP】—EXPORT(输出其它格式文件)【LI】——LIST(显示图形数据信息)【IMP】——IMPORT(输入文件)【ADC】—ADCENTER(设计中心Ctrl+2)【EXIT】——QUIT(退出)【 CH / MO】—PROPERTIES(修改特性Ctrl+1) 【OP,PR】——OPTIONS 【BO】——BOUNDARY(边界创建,包括创建闭合多段线和面域)2、(自定义CAD设置)【PRINT】——PLOT(打印)【PU】——PURGE(清除垃圾)【R】——REDRAW(重新生成)【 REN】——RENAME(重命名)【SN】——SNAP(捕捉栅格)【DS】——DSETTINGS(设置极轴追踪)【OS】——OSNAP(设置捕捉模式)【PRE】——PREVIEW(打印预览)【TO】——TOOLBAR(工具栏)【V】——VIEW(命名视图)【AA】——AREA(面积)【DI】——DIST(距离)3、绘图命令【PO】——POINT(点)【L】——LINE(直线)【XL】——XLINE(射线)【PL】——PLINE(多段线)【ML】——MLINE(多线)【SPL】——SPLINE(样条曲线)【POL】——POLYGON(正多边形)【REC】——RECTANGLE(矩形)【C】——CIRCLE(圆) 【A】——ARC(圆弧) 【DO】——DONUT(圆环)【EL】——ELLIPSE(椭圆)【REG】——REGION(面域)【MT】——MTEXT(多行文本)【T】——MTEXT(多行文本)【B】——BLOCK(块定义)【I】——INSERT(插入块)【W】——WBLOCK(定义块文件)【DIV】——DIVIDE(等分)【H】——BHATCH(填充)4、修改命令【CO】——COPY(复制)【MI】——MIRROR(镜像)【AR】——ARRAY(阵列)【O】——OFFSET(偏移)【RO】——ROTATE(旋转)【M】——MOVE(移动)【E】——DEL键——ERASE(删除)【X】——EXPLODE(分解)【TR】——TRIM(修剪)【EX】——EXTEND(延伸)【S】——STRETCH(拉伸)【LEN】——LENGTHEN(直线拉长)【SC】——SCALE(比例缩放)【BR】——BREAK(打断)【CHA】——CHAMFER(倒角) 【F】——FILLET(倒圆角)【PE】——PEDIT(多段线编辑)【ED】——DDEDIT(修改文本)【Find】——查找替换【Find】——查找替换5、视窗缩放【P】——PAN(平移)【Z】+空格+空格——实时缩放【Z】——局部放大【Z+P】——返回上一视图【Z+E】——显示全图6、尺寸标注【DLI】——DIMLINEAR(直线标注)【DAL】,——DIMALIGNED(对齐标注)【DRA】——DIMRADIUS(半径标注)【DDI】——DIMDIAMETER(直径标注)【DAN】——DIMANGULAR(角度标注)【DCE】——DIMCENTER(中心标注)【DOR】—DIMORDINATE(点标注)【TOL】—TOLERANCE(标注形位公差)【LE】—QLEADER(快速引出标注)【DBA】—DIMBASELINE(基线标注)【DCO】—DIMCONTINUE(连续标注)【D】—DIMSTYLE(标注样式)【DOV】—DIMOVERRIDE(替换标注系统变量【DED】—DIMEDIT(编辑标注)(二)常用CTRL快捷键【CTRL+1】——PROPERTIES(修改特性) 【CTRL+2 】——ADCENTER(设计中心)【CTRL+O】——OPEN(打开文件)【CTRL+N、M】——NEW(新建文件)【CTRL+P】 *PRINT(打印文件)【CTRL+S 】——SAVE(保存文件)【CTRL+Z】——UNDO(放弃)【CTRL+X 】——CUTCLIP(剪切)【CTRL+C】——COPYCLIP(复制)【CTRL+V】——PASTECLIP(粘贴)【CTRL+B】——SNAP(栅格捕捉)【CTRL+F】——OSNAP(对象捕捉)【CTRL+G】——GRID(栅格)【CTRL+L】——ORTHO(正交)【CTRL+W】——(对象追踪)【CTRL+U】——(极轴)(三)常用功能键【F1】——HELP(帮助)【F2】——(文本窗口)【F3】——OSNAP(对象捕捉)【F7】——GRIP(栅格)【F8】——ORTHO(正交)输入方式详见下表:七个命令让你成为CAD高手一、绘制基本图形对象1、几个基本常用的命令1.1 鼠标操作通常情况下左键代表选择功能,右键代表确定“回车”功能。
三视图(计图)
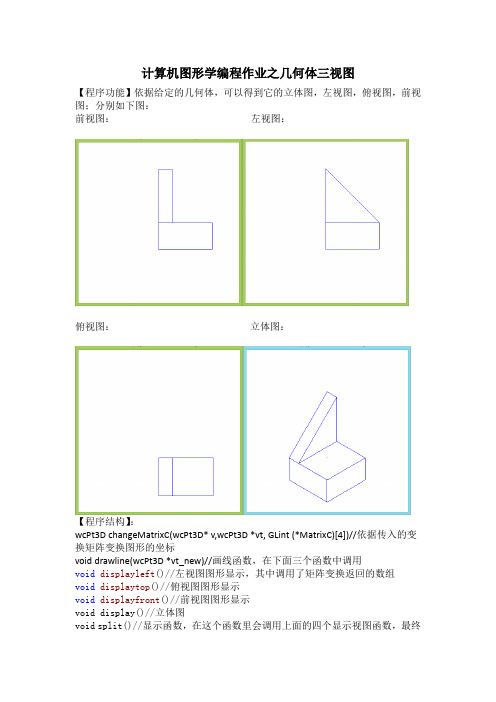
计算机图形学编程作业之几何体三视图【程序功能】依据给定的几何体,可以得到它的立体图,左视图,俯视图,前视图;分别如下图:前视图:左视图:俯视图:立体图:【程序结构】:wcPt3D changeMatrixC(wcPt3D* v,wcPt3D *vt,GLint (*MatrixC)[4])//依据传入的变换矩阵变换图形的坐标void drawline(wcPt3D *vt_new)//画线函数,在下面三个函数中调用void displayleft()//左视图图形显示,其中调用了矩阵变换返回的数组void displaytop()//俯视图图形显示void displayfront()//前视图图形显示void display()//立体图void split()//显示函数,在这个函数里会调用上面的四个显示视图函数,最终在main函数里调用split(),进行图像在窗口的输出显示;main()函数里调用split();【核心算法】:1.构造类表示三维坐标系下的点2.class wcPt3D{public:GLfloatx,y,z,h;};为顶点建立顶点表:wcPt3Dvt[VER_NUM]={…};3.定义各个视图的变换矩阵以及显示函数4.首先把立体图显示的算法罗列在这里:void display()//立体图{glClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0,0.0,1.0);//设置线型为绿色glLoadIdentity();gluLookAt (20,20,20, 0, 0, 0, 0, 20, 0);static constGLintnum[13][2]={1,2,2,3,3,4,4,5,5,6,6,7,7,9,9,10,4,10,8,9,2,5,1,6,7,8};//边表的两端顶点序号for(inti=0;i<13;i++){glBegin(GL_LINES);glVertex3f(vt[num[i][0]].x,vt[num[i][0]].y,vt[num[i][0]].z);//画线glVertex3f(vt[num[i][1]].x,vt[num[i][1]].y,vt[num[i][1]].z);glEnd();}glutWireCube (1.0);//以立方体模式观察模型glFlush();//强制刷新缓冲,保证绘图命令将被执行,而不是存储在缓冲区中等待其他的OpenGL命令。
三视图绘制示例

三视图绘制示例1、设置绘图环境,关闭“栅格”、“捕捉”、“正交”、“DYN”功能。
2、选中“对象捕捉”,单击鼠标右键,在弹出的快捷菜单中的“设置”选项里勾选“启用对象捕捉”、“启用对象捕捉追踪”、“端点”、“中点”、“交点”、“切点”、“延伸”点等选项。
单击“极轴追踪”选项,极轴角设为90度,点选“仅正交追踪”,单击“确定”按钮。
3、开启“对象捕捉”、“极轴”、“对象追踪”功能,调出“对象捕捉”工具栏。
4、切换到中心线层,用“构造线”命令绘制两正交辅助线作为长基准和宽基准;用“直线”命令绘制垂直中心线交水平辅助线于O点。
5、切换到粗实线层,绘制底座主视图:单击“直线”按钮→单击“捕捉自”按钮/单击鼠标左键得O点→极轴向右导向,输入12/确定,得A点→极轴向上导向→输入2/确定,得B 点→极轴向左导向,输入24/确定,得C点→极轴向下导向,捕捉与水平极轴相交点,单击得D点→单击“捕捉自”按钮,极轴向右导向,到O点单击→极轴向左导向,输入18/确定,得E点→极轴向上导向,输入5/确定,得F点→极轴向右导向,输入36/确定,得G点→极轴向下导向→捕捉到水平极轴交点,单击得H点→与A点闭合,完成底座主视图的绘制。
6、绘制底座俯视图:单击“直线”按钮→捕捉E点,极轴向下导向到M点,单击鼠标左键→极轴向右导向,捕捉H点,极轴交到K点,单击鼠标左键→极轴向下导向,输入24/确定,得N点→极轴向左导向,捕捉M点,极轴交到W点→与M点闭合。
7、确定键槽两半圆圆心:切换到中心线层,单击“直线”按钮→单击“临时追踪点”按钮,捕捉W点→极轴向右导向,输入13/确定→极轴向上导向,输入10/确定,得1点→极轴向右导向,输入10/确定,得2点,则点1和点2即为键槽两半圆圆心。
8、切换到粗实线层绘制键槽:单击“圆”按钮→单击点1,输入半径3/确定→重复“圆”命令→单击点2,输入半径3/确定,→单击“直线”按钮,连接两圆切点→单击“修剪”按钮,剪去多余线段。
识图及三视图

柱
多样形反映该形体的特征。
体
2、锥(台)体三视图与锥(台)体三视图的识读
图例
说明
圆锥体的三视图有一个反映锥体底面
圆
实形的投影和两个外轮廓为相同等腰三角
锥
形的投影,三角形的顶点是一个点(锥顶)
体
的投影。
棱锥体的三视图有一个反映锥体底面
棱
的投影和两个外轮廓为三角形的投影,三
锥
角形的顶点是一个点(锥顶)的投影,三
第一部分 机械识图
第1章 第2章 第3章 第4章
识图的基本知识 图样基本表示法 零件图 装配图的识读
第1章 识图的基本知识
1.1 机械图样 1.2 识图的基本知识 1.3 斜度和锥度 1.4 投影规律 1.5 基本体三视图识读 1.6 组合体三视图识读
1.1 机械图样
图样:工程技术上根据投影方法并遵照国家标准的规定绘 制成的用于工程施工或产品制造等用途的图叫做工程图样, 简称图样。 机械制造业所使用的图样称为机械图样, 图样是工程技术人员借以表达和交流技术思想不可缺少的 工程语言。
构成组合体的最小单元且不需要再分解的物体形状,叫做基本体。
1、柱体三视图与柱体三视图的识读 图例
说明
圆
圆柱体的三视图是由一个圆和两个
柱
矩形。
体
圆的投影反映该形体的特征。
棱
棱柱体的三视图是由一个正多边形
柱
和两个矩形。
体
多边形的投影反映该形体的特征。
一
一般柱体的三视图都是由一个
般
多样形和两个矩形来表述。
与锥高之比。如果是圆
锥 度
锥台则是上、下底圆直 径之差与锥台高度之比,
写成1:n的形式。
AutoCAD三视图教程:图形设置显示控制

第五章 图形设置及显示控制
2.使用向导(Wizard)创建图形文件 使用向导( 使用向导 ) Step 2 “Units(单位)”设置
在Wizard(向导)中可通过两种途径进行设置,即上图中所示的“Quick Setup(快速设 置)”和“Advanced Setup(高级设置)”。 为了解图形设置的主要 过程,选择“Advanced Setup(高级设置)”, 这时将切换到AutoCAD 2002系统窗口,并弹出 (Advanced Setup)对 话框。
第五章 图形设置及显示控制
1.使用样板(Template)创建图形文件 使用样板( 使用样板 ) 在上一章中已经了解了使用样板创建文件的过程。下面介绍样 板的概念与作用。样板文件(Template Files)是一种包含有特定 图形设置的图形文件(扩展名为“DWT”),通常在样板文件中的设 置包括: (1) 单位类型和精度 (2) 图形界限 (3) 捕捉、栅格和正交设置 (4) 图层组织 (5) 标题栏、边框和徽标 (6) 标注和文字样式 (7) 线型和线宽
注意:由于AutoCAD中的界限检查只是针对输入点, 注意:由于AutoCAD中的界限检查只是针对输入点,因此 AutoCAD中的界限检查只是针对输入点 在打开界限检查后, 在打开界限检查后,创建图形对象仍有可能导致图形对 象的某部分绘制在图形界限之外。例如绘制圆时, 象的某部分绘制在图形界限之外。例如绘制圆时,在图形 界限内部指定圆心点后,如果半径很大, 界限内部指定圆心点后,如果半径很大,则有可能部分圆 弧将绘制在图形界限之外。 弧将绘制在图形界限之外。
第五章 图形设置及显示控制
2.使用向导(Wizard)创建图形文件 使用向导( 使用向导 )
在该对话框中将进行5个步骤的设置,首先对“Units(单位)”设置, AutoCAD提供了5种测量单位,见下表 类 型 说 明 Decimal 小数制,公制格式的小数形式,如15.5000 Engineering 工程制,英制格式的小数形式,如1'-3.5000" Architecture 建筑制,英制格式的分数形式,如1'-3 1/2" Fractional 分数制,公制格式的分数形式,如15 1/2 Scientific 科学制,科学格式,如1.5500E+01 用户可根据实际情况选择其中一种,并可相应地在“Precision(精度)” 下拉列表框中指定单位的显示精度。 用户所选择的精度只是用于数值显示,而不是数值计算。AutoCAD系统 注意 用户所选择的精度只是用于数值显示,而不是数值计算。AutoCAD系统 内部始终使用最高精度进行计算
图形学三视图、正轴测投影c#代码
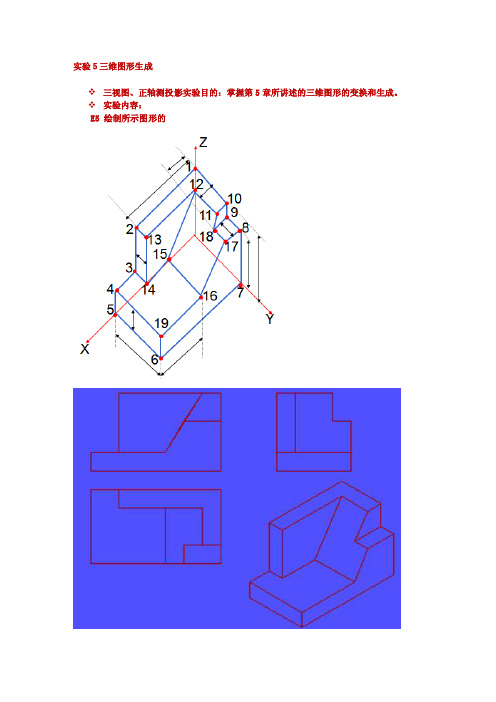
实验5三维图形生成三视图、正轴测投影实验目的:掌握第5章所讲述的三维图形的变换和生成。
实验内容:E5 绘制所示图形的Form1.csusing System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Text;using System.Windows.Forms;namespace E5{//!!说明:主视图有两点连线不对,应该是坐标连线的问题,但连线太多所以没找到是哪两点连错。
public partial class Form1 : Form{int x0 = 150;int z0 = -150;double c = Math.Cos(Math.PI / 2);double s = Math.Sin(Math.PI / 2);double c1 = Math.Cos(Math.PI / 4);double s1 = Math.Sin(Math.PI / 4);Matrix[] p3d = new Matrix[20];//三维顶点Matrix[] p3dv = new Matrix[20];//主视图顶点Matrix[] p3dw = new Matrix[20];//侧视图顶点Matrix[] p3dh = new Matrix[20];//俯视图顶点Matrix[] p3dc = new Matrix[20];//正轴侧顶点/* double[,] p = new double[17,4]{{0,0,42,1},{55,0,42,1},{55,0,10,1},{70,0,10,1},{70,0,0,1},{70,40,0,1},{0,40,0,1},{0,40,27,1},{0,30,27,1},{0,30,42,1},{10,30,42,1},{10,10,42,1},{55,10,42,1},{55,10,10,1},{30,10,10,1},{30,40,10,1},{20,40,27,1},{20,30,27,1},{70,40,10,1}}; */void Getp3d(ref Matrix[] p3d)//三维顶点赋值{for(int i=0;i<19;i++){p3d[i]=new Matrix(1,4);//三维顶点}p3d[0].Data = new double[1, 4] { {0,0,42,1} };p3d[1].Data = new double[1, 4] { { 55, 0, 42, 1 } }; p3d[2].Data = new double[1, 4] { { 55, 0, 10, 1 } }; p3d[3].Data = new double[1, 4] { { 70, 0, 10, 1 } }; p3d[4].Data = new double[1, 4] { { 70, 0, 0, 1 } };p3d[5].Data = new double[1, 4] { { 70, 40, 0, 1 } }; p3d[6].Data = new double[1, 4] { { 0, 40, 0, 1 } };p3d[7].Data = new double[1, 4] { { 0, 40, 27, 1 } }; p3d[8].Data = new double[1, 4] { { 0, 30, 27, 1 } }; p3d[9].Data = new double[1, 4] { { 0, 30, 42, 1 } }; p3d[10].Data = new double[1, 4] { { 10, 30, 42, 1 } }; p3d[11].Data = new double[1, 4] { { 10, 10, 42, 1 } }; p3d[12].Data = new double[1, 4] { { 55, 10, 42, 1 } }; p3d[13].Data = new double[1, 4] { { 55, 10, 10, 1 } }; p3d[14].Data = new double[1, 4] { { 30, 10, 10, 1 } }; p3d[15].Data = new double[1, 4] { { 30, 40, 10, 1 } }; p3d[16].Data = new double[1, 4] { { 20, 40, 27, 1 } }; p3d[17].Data = new double[1, 4] { { 20, 30, 27, 1 } }; p3d[18].Data = new double[1, 4] { { 70, 40, 10, 1 } };}public Form1(){InitializeComponent();}private void Form1_Paint(object sender, PaintEventArgs e){Getp3d(ref p3d);//主视图矩阵Matrix Tv = new Matrix(4);Tv.Data = new double[4,4]{{1 , 0 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};//侧视图Matrix Tw1 = new Matrix(4); Tw1.Data = new double[4, 4] {{0 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};Matrix Tw2 = new Matrix(4); Tw2.Data = new double[4, 4] {{c , s , 0 , 0},{-s , c , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , 0 , 1}};Matrix Tw3 = new Matrix(4); Tw3.Data = new double[4, 4] {{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{x0 , 0 , 0 , 1}};//俯视图//俯视图的投影变换Matrix Th1 = new Matrix(4); Th1.Data = new double[4, 4] {{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 0 , 1}};//使H面绕X轴负向旋转90°Matrix Th2 = new Matrix(4);Th2.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , c , -s , 0},{0 , s , c , 0},{0 , 0 , 0 , 1}};//使H面沿Z轴负向平移一段距离z0Matrix Th3 = new Matrix(4);Th3.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , 1 , 0 , 0},{0 , 0 , 1 , 0},{0 , 0 , -z0,1}};//正轴侧// 先绕Z轴正向旋转α角//再绕X轴反向旋转β角//将三维形体向XOZ平面(V面)作正投影得到正轴测投影的投影变换矩阵Matrix Tc1 = new Matrix(4);Tc1.Data = new double[4, 4]{{c1 , s1 , 0 , 0},{-s1 , c1 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 0 , 1}};Matrix Tc2 = new Matrix(4);Tc2.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , c1 , -s1 , 0},{0 , s1 , c1 , 0},{0 , 0 , 0 , 1}};Matrix Tc3 = new Matrix(4);Tc3.Data = new double[4, 4]{{1 , 0 , 0 , 0},{0 , 0 , 0 , 0},{0 , 0 , 1 , 0},{150 , 0 , 150 , 1}};//矩阵变换for(int i=0;i<19;i++){p3dv[i] = new Matrix(1, 4);//p3dv[i] = p3d[i] * Tv;p3dw[i] = new Matrix(1, 4);//p3dw[i] = p3d[i] * Tw1 * Tw2 * Tw3;p3dh[i] = new Matrix(1, 4);//p3dh[i] = p3d[i] * Th1 * Th2 * Th3;p3dc[i] = new Matrix(1, 4);//p3dc[i] = p3d[i] * Tc1 * Tc2 * Tc3;}Graphics g=e.Graphics;Pen mypen = new Pen(Color.Yellow, 1.0f);//主视图Point[] pp3d=new Point[19];for (int i = 0; i < 18; i++){//矩阵变换为二维坐标pp3d[i].X=Convert.ToInt16( p3dv[i].Data[0,0]); pp3d[i].Y =Convert.ToInt16( p3dv[i].Data[0,2]); }g.DrawLines(mypen, pp3d);// g.DrawLine(mypen, pp3d[0], pp3d[9]);// g.DrawLine(mypen, pp3d[1], pp3d[12]);// g.DrawLine(mypen, pp3d[2], pp3d[13]);// g.DrawLine(mypen, pp3d[3], pp3d[18]);g.DrawLine(mypen, pp3d[7], pp3d[16]);// g.DrawLine(mypen, pp3d[8], pp3d[17]);g.DrawLine(mypen, pp3d[10], pp3d[17]);// g.DrawLine(mypen, pp3d[11], pp3d[14]);// g.DrawLine(mypen, pp3d[15], pp3d[18]);//侧视图Point[] pp3d1 = new Point[18];for (int i = 0; i < 18; i++){pp3d1[i].X = Convert.ToInt16(p3dw[i].Data[0, 0]); pp3d1[i].Y = Convert.ToInt16(p3dw[i].Data[0, 2]); }g.DrawLines(mypen, pp3d1);// pp3d1[19] = pp3d1[0];g.DrawLine(mypen, pp3d1[0], pp3d1[9]);g.DrawLine(mypen, pp3d1[1], pp3d1[12]);g.DrawLine(mypen, pp3d1[2], pp3d1[13]);// g.DrawLine(mypen, pp3d1[3], pp3d1[18]);g.DrawLine(mypen, pp3d1[7], pp3d1[16]);g.DrawLine(mypen, pp3d1[8], pp3d1[17]);g.DrawLine(mypen, pp3d1[10], pp3d1[17]);g.DrawLine(mypen, pp3d1[11], pp3d1[14]);// g.DrawLine(mypen, pp3d1[15], pp3d1[18]);//俯视图Point[] pp3d2 = new Point[18];for (int i = 0; i < 18; i++){pp3d2[i].X = Convert.ToInt16(p3dh[i].Data[0, 0]); pp3d2[i].Y = Convert.ToInt16(p3dh[i].Data[0, 2]); }g.DrawLines(mypen, pp3d2);g.DrawLine(mypen, pp3d2[0], pp3d2[9]);g.DrawLine(mypen, pp3d2[1], pp3d2[12]);g.DrawLine(mypen, pp3d2[2], pp3d2[13]);// g.DrawLine(mypen, pp3d2[3], pp3d2[18]);g.DrawLine(mypen, pp3d2[7], pp3d2[16]);g.DrawLine(mypen, pp3d2[8], pp3d2[17]);g.DrawLine(mypen, pp3d2[10], pp3d2[17]);g.DrawLine(mypen, pp3d2[11], pp3d2[14]);// g.DrawLine(mypen, pp3d2[15], pp3d2[18]);//正轴侧Point[] pp3d3 = new Point[18];for (int i = 0; i < 18; i++){pp3d3[i].X = Convert.ToInt16(p3dc[i].Data[0, 0]); pp3d3[i].Y = Convert.ToInt16(p3dc[i].Data[0, 2]); }//pp3d3[19] = pp3d3[0];g.DrawLines(mypen, pp3d3);g.DrawLine(mypen, pp3d3[0], pp3d3[9]);g.DrawLine(mypen, pp3d3[1], pp3d3[12]);g.DrawLine(mypen, pp3d3[2], pp3d3[13]);// g.DrawLine(mypen, pp3d[3], pp3d[18]);g.DrawLine(mypen, pp3d3[7], pp3d3[16]);g.DrawLine(mypen, pp3d3[8], pp3d3[17]);g.DrawLine(mypen, pp3d3[10], pp3d3[17]);g.DrawLine(mypen, pp3d3[11], pp3d3[14]);// g.DrawLine(mypen, pp3d[15], pp3d[18]);}}}Matrix.csusing System;using System.Collections.Generic;using System.Text;namespace E5{class Matrix{public double[,] Data;public Matrix(){ }public Matrix(int size){this.Data = new double[size, size];}public Matrix(int rows, int cols){this.Data = new double[rows, cols];}public Matrix(double[,] data){Data = data;}public static Matrix operator *(Matrix M1, Matrix M2){int r1 = M1.Data.GetLength(0); int r2 = M2.Data.GetLength(0);int c1 = M1.Data.GetLength(1); int c2 = M2.Data.GetLength(1);// try// {if (c1 != r2){throw new System.Exception("Matrix dimensions donot agree ");}// }double[,] res = new double[r1, c2];for (int i = 0; i < r1; i++){for (int j = 0; j < c2; j++){for (int k = 0; k < r2; k++){res[i, j] = res[i, j] + (M1.Data[i, k] * M2.Data[k, j]); }}}return new Matrix(res);}}}。
实验3 图形编辑操作(三视图的绘制)

实验3 图形编辑操作(三视图的画法)一、目的和要求1.学习三视图的绘制方法和技巧2.练习相关图形的位置布置以及辅助线的使用技术3.绘制三视图必须保证“三等”关系,即:主、俯视图长对正,主、左视图高平齐,左、俯视图宽相等。
在长度和高度上比较容易保证,在宽度方向上,通过作辅助线或画辅助圆的方式来保证。
二、上机准备1.复习参照线XLINE、圆CIRCLE、导圆角FILLET、直线LINE等绘图命令的使用方法;2.复习修剪TRIM、删除ERASE、复制COPY、打断BREAK和偏移OFFSET等编辑命令的使用方法;3.复习图层LAYER、图形界限LIMITS等命令的功能及操作方法;4.复习对象捕捉方式设定和使用方法三、上机操作1、环境设置⑴设置图形界限按照该图所标注的尺寸,设置成A3(420×297)大小的界限即可。
⑵设置对象捕捉模式通过“草图设置”对话框设置捕捉模式为“交点”、“端点”、“垂足”。
如下图所示2、图层设置该图形包含了粗实线、虚线、点划线以及标注线,所以按照下图设置图层。
3、粗略布局用射线命令画出各视图可作为基准的关键线,把粗实线层置为当前图层。
4、用偏移命令(OFFSET)将基准线进行偏移,画出各视图的大致轮廓,画出如下图所示。
过程是:对1线:往上偏移15往上偏移75对2线:往左偏移35 对3线:往下偏移25往右偏移35 往下偏移60往左偏移60 往下偏移70往右偏移60对4线:往右偏移25往右偏移60往右偏移704、修剪(T rim)线条,使轮廓更加清晰注意:修剪过程还是要讲究一点技巧的,掌握得好的话,一次命令就能完成任务,否则,可能要重复几次命令,甚至要动用删除等命令才能达到图示效果。
选择剪切边时可用窗口法全部选定,选择要修剪的线时则只能老老实实一条一条选,但顺序最好是从外往里一圈一圈来剪。
修剪后如下图所示5、把中心线置为点划线图层,接下来的画图还是把粗实线层置为当前图层。
图形学读取立方体、兔子、八字三维模型代码及截图(内容参考)

#include <stdlib.h>#include <GL/glut.h>#include <stdio.h>#include <iostream>#include <string>#include <fstream>#include <sstream>#include<cmath>using namespace std;int v_num = 0; //记录点的数量int f_num = 0; //记录面的数量int vn_num = 0;//记录法向量的数量int vt_num = 0;GLfloat **vArr; //存放点的二维数组int **fvArr; //存放面顶点的二维数组int **fnArr;//存放面法向量的二维数组int **ftArr;GLfloat **vtArr;GLfloat **vnArr;//存放法向量的二维数组string s1, s2, s3, s4;GLfloat f2, f3, f4;void getLineNum(string addrstr) //获取点和面的数量{ifstream infile(addrstr.c_str()); //打开指定文件string sline;//每一行int i = 0, j = 0;while (getline(infile, sline)) //从指定文件逐行读取{if (sline[0] == 'v'){if (sline[1] == 'n'){vn_num++;}else if(sline[1] == 't'){vt_num++;}else{v_num++;}}if (sline[0] == 'f'){f_num++;}}}int readfile(string addrstr) //将文件内容读到数组中去{//getLineNum(addrstr);//new二维数组vArr = new GLfloat*[v_num];for (int i = 0; i<v_num; i++){vArr[i] = new GLfloat[3];}vnArr = new GLfloat*[vn_num]; for (int i = 0; i<vn_num; i++) {vnArr[i] = new GLfloat[3]; }vtArr = new GLfloat*[vt_num]; for (int i = 0; i<vt_num; i++) {vtArr[i] = new GLfloat[2]; }fvArr = new int*[f_num]; fnArr = new int*[f_num];ftArr = new int*[f_num];for (int i = 0; i<f_num; i++) {fvArr[i] = new int[3];fnArr[i] = new int[3];ftArr[i] = new int[2];}ifstream infile(addrstr.c_str());。
三视图的画法,各种符号的含义

三视图的画法,各种符号的含义能够正确反映物体长、宽、高尺寸的正投影工程图(主视图,俯视图,左视图三个基本视图)为三视图,这是工程界一种对物体几何形状约定俗成的抽象表达方式。
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
飞机三视图将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为视图。
一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状,从物体的左面向右面投射所得的视图称左视图(侧视图)——能反映物体的左面形状,还有其它三个视图不是很常用。
三视图就是主视图(正视图)、俯视图、左视图(侧视图)的总称。
特点一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
投影规则规则主俯长对正、主左高平齐、俯左宽相等即:主视图和俯视图的长要相等主视图和左视图的高要相等左视图和俯视图的宽要相等。
物体的投影在许多情况下,只用一个投影不加任何注解,是不能完整清晰地表达和确定形体的形状和结构的。
如图所示,三个形体在同一个方向的投影完全相同,但三个形体的空间结构却不相同。
可见只用一个方向的投影来表达形体形状是不行的。
一般必须将形体向几个方向投影,才能完整清晰地表达出形体的形状和结构。
一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
三投影面体系投影体系我们设立三个互相垂直的平面,叫做三投影面。
这三个平面将空间分为八个部分,每一部分叫做一个分角,分别称为Ⅰ 分角、Ⅱ 分角 (Ⅷ)分角,如图所示。
我们把这个体系叫三投影面体系,世界上有些国家规定将形体放在第一分角内进行投影。
三视图的画法,各种符号的含义

三视图的画法,各种符号的含义三视图的画法,各种符号的含义能够正确反映物体长、宽、高尺寸的正投影工程图(主视图,俯视图,左视图三个基本视图)为三视图,这是工程界一种对物体几何形状约定俗成的抽象表达方式。
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
飞机三视图将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为视图。
一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状,从物体的左面向右面投射所得的视图称左视图(侧视图)——能反映物体的左面形状,还有其它三个视图不是很常用。
三视图就是主视图(正视图)、俯视图、左视图(侧视图)的总称。
特点一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
投影规则规则主俯长对正、主左高平齐、俯左宽相等即:of thiourea, and diluted to 100mL and mix. 31.5 trivalent arsenic (As3+) standard liquid weigh accurately arsenic trioxide 0.1320g, plus 100g/L 1mL and a small amount of potassium hydroxide sub-boilingdistilled water dissolve into 100mL the bottle volume. This standard solution contains trivalent arsenic (As3+) 1mg/mL. Water level when using diluted to standard concentration for arsenic trivalent (As3+) 1 μg. Refrigerator use 7 days. 32 glass apparatus 15% nitrate soaked before using 24h. 32.1 atomic fluorescence spectrometer. 32.2, thermostatic water bath. 33 33.1 sample analysis steps deal with the body: learn from crushing 80 mesh sieve-like 2.50g (sample weight according to the content of the sample, as appropriate, increase or decrease) in 25mL graduated test tube. Add hydrochloric acid (1+1) solution 20mL, mixing, or 5.00g weigh fresh sample (sample should be homogenized into) in 25mL scale in a test tube, add 5mL hydrochloric acid and hydrochloric acid (1+1) solution diluted to scales, mixing。
三视图的画法各种符号的含义

三视图的画法,各种符号的含义能够正确反映物体长、宽、高尺寸的正投影工程图(主视图,俯视图,左视图三个基本视图)为三视图,这是工程界一种对物体几何形状约定俗成的抽象表达方式。
三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形。
飞机三视图将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为视图。
一个物体有六个视图:从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状,从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状,从物体的左面向右面投射所得的视图称左视图(侧视图)——能反映物体的左面形状,还有其它三个视图不是很常用。
三视图就是主视图(正视图)、俯视图、左视图(侧视图)的总称。
特点一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
投影规则规则主俯长对正、主左高平齐、俯左宽相等即:主视图和俯视图的长要相等主视图和左视图的高要相等左视图和俯视图的宽要相等。
物体的投影在许多情况下,只用一个投影不加任何注解,是不能完整清晰地表达和确定形体的形状和结构的。
如图所示,三个形体在同一个方向的投影完全相同,但三个形体的空间结构却不相同。
可见只用一个方向的投影来表达形体形状是不行的。
一般必须将形体向几个方向投影,才能完整清晰地表达出形体的形状和结构。
一个视图只能反映物体的一个方位的形状,不能完整反映物体的结构形状。
三视图是从三个不同方向对同一个物体进行投射的结果,另外还有如剖面图、半剖面图等做为辅助,基本能完整的表达物体的结构。
视图命令,快速绘制三视图

如何快速绘制三视图摘要:在制造行业中,很多企业的在绘图的过程中都需要绘制三视图,当我们绘制好一个三维模型的时候,然后在对齐进行三视图的绘制,其实也可以通过CAD中快速的自动生成三视图,这样可以大大的节约我们的时间,减去手动的绘制三视图的步骤,今天我们来讲解如何快速的绘制三视图。
在制造行业中,很多企业的在绘图的过程中都需要绘制三视图,当我们绘制好一个三维模型的时候,然后在对齐进行三视图的绘制,其实也可以通过CAD 中快速的自动生成三视图,这样可以大大的节约我们的时间,减去手动的绘制三视图的步骤,今天我们来讲解如何快速的绘制三视图。
首先,选择布局,我们建立3个视口,通过快捷键CO复制命令,分别建立第二个和第三个视口,然后绘制一个三维模型,例如我们现在绘制好一个茶壶。
如图1:图1我们建立好视口之后,我们三个视口的视角分别设置为主视图、左视图、俯视图。
通过双击视口,选择视图---三维视图---主视图、左视图、俯视图。
如图2:图2当我们创建好视口视觉之后,然后我们把三个视口的比例都设置为一样的,如图3,这样能够是我们的三视图比例对称。
图3这样我们的三视图就已经绘制完毕了,这样的方法比我们手动绘制的三视图在时间上大大的提高了,节约了不少的时间。
通过自动生成,三视图会更加精准,快速,如图4:图4以上就是我们三维视图的创建过程,在浩辰机械中,还有一些视图功能。
浩辰机械---辅助工具---创建视图。
该功能内包含了显示图、转交投影、剖视图、局部放大、孔轴投影几个功能,这个几个功能也能够提高我们的工作效率。
如图5:图5在接下来的CAD教程中,我们还会陆续介绍更多的相关知识,欢迎继续关注。
浩辰机械2012标准版 /cad_56_80.html。
计算机图形学光照与三维图形源代码

viewer[1]+= 1.0;
}
if(key == 'z') {
viewer[2]-= 1.0; }
if(key == 'Z') {
viewer[2]+= 1.0;
}
glutPostRedisplay ();
}
void mouse(int button,int state,int x,int y)
glutMouseFunc(mouse);
glutKeyboardFunc(Keyboard);
glutMainLoop();
return 0;
}
计算机图形学光照与三维图形源代码图形光照代码源程序三维图形光照代码源代码三维立体原代码图形学
#include <glut.h>
#include <math.h>
#include<stdio.h>
static int spin=0;
float a=0.0;
float b=1.0;
float m=0.0,n=0.0;
glEnable(GL_LIGHT0);
}
if (key == '2'){
a+=0.1;
}
if(key =='3'){
b-=0.1;
}
if(key == 'x') {
viewer[0]-= 1.0;
}
if(key == 'X'){
viewer[0]+= 1.0;
}
if(key == 'y'){
计算机图形学用C++绘制简易三视图
line(490, 100, 490, 250);
line(370, 250, 490, 250);
circle(160, 360, 60);
getch();
closegraph();
}
注:运行这段程序时电脑上安装的C++应该装有一个EasyX的插件,此插件为C++提供了一个名为graphics.h的头文件。
输入程序截图如下:
运行程序,得到如下图的圆柱体三视图结果:
绘制三视图计算机图形学计算机图形学pdf实时计算机图形学计算机图形学就业计算机图形学书籍计算机图形学视频交互式计算机图形学计算机图形学数学计算机图形学教材
计算机图形学用C++绘制圆柱体三视图
姓名:学号:班级:
我编写的程序如下:
#include <graphics.h>
#include <conio.h>
voidபைடு நூலகம்main()
{
initgraph(640, 480);
line(100, 100, 220, 100);
line(100, 100, 100, 250);
line(220, 100, 220, 250);
line(100, 250, 220, 250);
line(370, 100, 490, 100);
图形学读取立方体、兔子、八字三维模型代码及截图

#include <stdlib.h>#include <GL/glut.h>#include <stdio.h>#include <iostream>#include <string>#include <fstream>#include <sstream>#include<cmath>using namespace std;int v_num = 0; //记录点的数量int f_num = 0; //记录面的数量int vn_num = 0;//记录法向量的数量int vt_num = 0;GLfloat **vArr; //存放点的二维数组int **fvArr; //存放面顶点的二维数组int **fnArr;//存放面法向量的二维数组int **ftArr;GLfloat **vtArr;GLfloat **vnArr;//存放法向量的二维数组string s1, s2, s3, s4;GLfloat f2, f3, f4;void getLineNum(string addrstr) //获取点和面的数量{ifstream infile(addrstr.c_str()); //打开指定文件string sline;//每一行int i = 0, j = 0;while (getline(infile, sline)) //从指定文件逐行读取{if (sline[0] == 'v'){if (sline[1] == 'n'){vn_num++;}else if(sline[1] == 't'){vt_num++;}else{v_num++;}}if (sline[0] == 'f'){f_num++;}}}int readfile(string addrstr) //将文件内容读到数组中去{//getLineNum(addrstr);//new二维数组vArr = new GLfloat*[v_num];for (int i = 0; i<v_num; i++){vArr[i] = new GLfloat[3];}vnArr = new GLfloat*[vn_num];for (int i = 0; i<vn_num; i++){vnArr[i] = new GLfloat[3];}vtArr = new GLfloat*[vt_num];for (int i = 0; i<vt_num; i++){vtArr[i] = new GLfloat[2];}fvArr = new int*[f_num];fnArr = new int*[f_num];ftArr = new int*[f_num];for (int i = 0; i<f_num; i++){fvArr[i] = new int[3];fnArr[i] = new int[3];ftArr[i] = new int[2];}ifstream infile(addrstr.c_str()); string sline;//每一行int ii = 0, jj = 0, kk = 0, mm = 0;while (getline(infile, sline)){if (sline[0] == 'v'){if (sline[1] == 'n')//vn{istringstream sin(sline);sin >> s1 >> f2 >> f3 >> f4;vnArr[ii][0] = f2;vnArr[ii][1] = f3;vnArr[ii][2] = f4;ii++;}else if (sline[1] == 't'){istringstream sin(sline);sin >> s1 >> f2 >> f3 ;cout << f2 << f3;vtArr[mm][0] = f2;vtArr[mm][1] = f3;// vtArr[mm][2] = f4;mm++;}else//v{istringstream sin(sline);sin >> s1 >> f2 >> f3 >> f4;vArr[jj][0] = f2;vArr[jj][1] = f3;vArr[jj][2] = f4;jj++;}}if (sline[0] == 'f') //存储面{istringstream in(sline);GLfloat a;in >> s1;//去掉fint i, k;for (i = 0; i < 3; i++){in >> s1;cout << s1 << endl;//取出第一个顶点和法线索引a = 0;//int len = sizeof(s1);int len = s1.length();cout << len;for (int m = 0; m <len; m++){if (s1[m] != '/'){a = a * 10 + (s1[m] - 48);fvArr[kk][i] = a;}else{m++;if (m <=3){if (s1[m] != '/'){a = a * 10 + (s1[m] - 48);ftArr[kk][i] = a;}else{m++;a = a * 10 + (s1[m] - 48);fnArr[kk][i] = a;}}else{// m++;a = a * 10 + (s1[m] - 48);fnArr[kk][i] = a;}}}//for (k = 0; s1[k] != '/'; k++)// {//a = a * 10 + (s1[k] - 48);// }// fvArr[kk][i] = a;// a = 0;//for (k = k + 2; s1[k]; k++)// {// a = a * 10 + (s1[k] - 48);// }// fnArr[kk][i] = a;}kk++;}}return 0;}void init(void){getLineNum("Eight.obj");readfile("Eight.obj");GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat mat_shininess[] = { 50.0 };//材料的镜面指数,其值越大越精细GLfloat light_position[] = { 1.0, 1.0f, 1.0, 0.0 };GLfloat white_light[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat lmodel_ambient[] = { 0.1, 0.1, 0.1, 1.0 };glClearColor(0.0, 0.0, 0.0, 0.0);glShadeModel(GL_SMOOTH);glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);glLightfv(GL_LIGHT0, GL_POSITION, light_position);//光源位置glLightfv(GL_LIGHT0, GL_DIFFUSE, white_light);//漫反射光源glLightfv(GL_LIGHT0, GL_SPECULAR, white_light);//镜面反射光源glLightModelfv(GL_LIGHT_MODEL_AMBIENT,lmodel_ambient);//环境光源glEnable(GL_LIGHTING);//启动光照glEnable(GL_LIGHT0);//启用0度光源glEnable(GL_DEPTH_TEST);//启动深度测试/*glShadeModel(GL_SMOOTH); // Enable Smooth ShadingglClearColor(0.0f, 0.0f, 0.0f, 0.5f); // 黑色背景glClearDepth(1.0f); // 深度缓冲区设置glEnable(GL_DEPTH_TEST); // 允许深度测试glDepthFunc(GL_LEQUAL); // 定义深度测试类型glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST); // Really Nice Perspective Calculation*/}void display(void){glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);//gluLookAt(-2.0, -2.0, -2.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0); //设置观察的位置glTranslatef(1.0, -0.0, -8.0);glScalef(0.1, 0.1, 0.1);for (int i = 0; i<f_num; i++){glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);glBegin(GL_TRIANGLES);if (vn_num == 0){//glNormal3f(vnArr[fnArr[i][0] - 1][0], vnArr[fnArr[i][0] - 1][1], vnArr[fnArr[i][0] - 1][2]);glVertex3f(vArr[fvArr[i][0] - 1][0], vArr[fvArr[i][0] - 1][1], vArr[fvArr[i][0] - 1][2]);//glNormal3f(vnArr[fnArr[i][1] - 1][0], vnArr[fnArr[i][1] - 1][1], vnArr[fnArr[i][1] - 1][2]);glVertex3f(vArr[fvArr[i][1] - 1][0], vArr[fvArr[i][1] - 1][1], vArr[fvArr[i][1] - 1][2]);//glNormal3f(vnArr[fnArr[i][2] - 1][0], vnArr[fnArr[i][2] - 1][1], vnArr[fnArr[i][2] - 1][2]);glVertex3f(vArr[fvArr[i][2] - 1][0], vArr[fvArr[i][2] - 1][1], vArr[fvArr[i][2] - 1][2]);}else{glTexCoord2f(vtArr[ftArr[i][0] - 1][0], vtArr[ftArr[i][0] - 1][1]);// glNormal3f(vnArr[fnArr[i][0] - 1][0], vnArr[fnArr[i][0] - 1][1], vnArr[fnArr[i][0] - 1][2]);glVertex3f(vArr[fvArr[i][0] - 1][0], vArr[fvArr[i][0] - 1][1], vArr[fvArr[i][0] - 1][2]);glTexCoord2f(vtArr[ftArr[i][1] - 1][0], vtArr[ftArr[i][1] - 1][1]);// glNormal3f(vnArr[fnArr[i][1] - 1][0], vnArr[fnArr[i][1] - 1][1], vnArr[fnArr[i][1] - 1][2]);glVertex3f(vArr[fvArr[i][1] - 1][0], vArr[fvArr[i][1] - 1][1], vArr[fvArr[i][1] - 1][2]);glTexCoord2f(vtArr[ftArr[i][2] - 1][0], vtArr[ftArr[i][2] - 1][1]);// glNormal3f(vnArr[fnArr[i][2] - 1][0], vnArr[fnArr[i][2] - 1][1], vnArr[fnArr[i][2] - 1][2]);glVertex3f(vArr[fvArr[i][2] - 1][0], vArr[fvArr[i][2] - 1][1], vArr[fvArr[i][2] - 1][2]);}glEnd();}glFlush();//强制绘图}void reshape(int w, int h){glViewport(0, 0, (GLsizei)w, (GLsizei)h); //视口设置glMatrixMode(GL_PROJECTION);glLoadIdentity();if (w <= h)//描绘了两种不同情况下的平行修剪空间glOrtho(-1.5, 1.5, -1.5 * (GLfloat)h / (GLfloat)w, 1.5 * (GLfloat)h / (GLfloat)w, -10.0, 10.0);elseglOrtho(-1.5*(GLfloat)w / (GLfloat)h, 1.5*(GLfloat)w / (GLfloat)h, -1.5, 1.5, -10.0, 10.0);glMatrixMode(GL_MODELVIEW);glLoadIdentity();}int main(int argc, char **argv){glutInit(&argc, argv);//对GLUT进行初始化glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);//设置显示方式,单缓冲、RGB颜色glutInitWindowSize(500, 500);glutInitWindowPosition(100, 100);//glutCreateWindow(argv[0]);glutCreateWindow("Test");init();glutDisplayFunc(display);glutReshapeFunc(reshape);glutMainLoop();return 0;}◆cube.obj文件没有运用光照时输出的模型:①点:②边:③面:运用光照时输出的模型:①通过顶点法向量画出:②通过面的法向量画出:③画出面的法向量移动某个顶点:◆bunny.obj文件没有运用光照时输出的模型:①点:②边:③面:运用光照时输出的模型:①通过顶点法向量画出:②通过面的法向量画出:③画出面的法向量:◆Eight.obj文件没有运用光照时输出的模型:①点:②边:③面:运用光照时输出的模型:①通过顶点法向量画出:②通过面的法向量画出:③画出面的法向量:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
void OnDraw(DefPoint TempPoint[])
{
glBegin(GL_LINES);
for (int i = 0; i<FaceNum; i++)
{
int size = Face[i].size();
for (int j = 0; j<size; j++)
glVertex2d(TempPoint[3].x, TempPoint[3].y);
glVertex2d(TempPoint[1].x, TempPoint[1].y);
glVertex2d(TempPoint[2].x, TempPoint[2].y);
glVertex2d(TempPoint[1].x, TempPoint[1].y);
OnDraw(XOYPoint);
glColor3f(0.0f, 0.0f, 1.0f);
OnDraw(YOZPoint);
glColor3f(1.0f, 0.0f, 0.0f);
OnDraw_O(YOYPoint);
glutSwapBuffers();
}
void GetThPmidView()
{
NewPoint[i].x /= NewPoint[i].tag,
NewPoint[i].y /= NewPoint[i].tag,
NewPoint[i].z /= NewPoint[i].tag,
NewPoint[i].tag = 1;
}
}
}
tz*Tran[2][0] + ttag*Tran[3][0];
NewPoint[i].y = tx*Tran[0][1] + ty*Tran[1][1] +
tz*Tran[2][1] + ttag*Tran[3][1];
NewPoint[i].z = tx*Tran[0][2] + ty*Tran[1][2] +
YOZPoint[MaxNum],YOYPoint[MaxNum];
void ThPmidInit()
{
PointNum = 4;
Point[0].x = 400, Point[0].y = 0, Point[0].z = 0, Point[0].tag = 1;
Point[1].x = 400, Point[1].y = 200, Point[1].z = 0, Point[1].tag = 1;
#include "stdafx.h"
#include "stdlib.h"
#include <GL\glut.h>
#include <vector>
#include <iostream>
using namespace std;
const int MaxNum = 200;vector<int>Face[10];
glutInitWindowSize(1000, 600);
glutInitWindowPosition(150, 100);
glutCreateWindow("三视图");
glutDisplayFunc(Display);
glutReshapeFunc(ReShape);
Initial();
void ReShape(int w, int h)
{
winWidth = w; winHeight = h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(0.0, winWidth, 0.0, winHeight);
glVertex2d(0, winHeight / 2);
glVertex2d(winWidth, winHeight / 2);
glEnd();
glColor3f(1.0f, 0.0f, 0.0f);
OnDraw(XOZPoint);
glColor3f(0.0f, 1.0f, 0.0f);
glVertex2d(TempPoint[1].x, TempPoint[1].y);
glVertex2d(TempPoint[0].x, TempPoint[0].y);
glVertex2d(TempPoint[2].x, TempPoint[2].y);
glVertex2d(TempPoint[0].x, TempPoint[0].y);
glClearColor(1.0f,1.0f, 1.0f, 1.0f);
ThPmidInit();
GetThPmidView();
}
int main(int argc, char* argv[])
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
Face[0].push_back(0); Face[0].push_back(1); Face[0].push_back(2);
Face[1].push_back(0); Face[1].push_back(1); Face[1].push_back(3);
Face[2].push_back(0); Face[2].push_back(2); Face[2].push_back(3);
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f, 0.0f, 0.0f);
glBegin(GL_LINES);
glVertex2d(winWidth / 2, 0);
glVertex2d(winWidth / 2, winHeight);
int winWidth = 1000, winHeight = 600;
int PointNum = 4, FaceNum = 4;
double Matrix[4][4] = { { 1, 0, 0, 0 }, { 0, 1, 0, 0 },
{ 0, 0, 1, 0 }, { 500, 300, 300, 1 } };
{
TransForm(XOZPoint, Point, XOZ);
TransForm(XOYPoint, Point, XOY);
TransForm(YOZPoint, Point, YOZ);
TransForm(YOYPoint, Point, YOY);
TransForm(XOZPoint, XOZPoint, Matrix);
{
double tx = OldPoint[i].x, ty = OldPoint[i].y,
tz = OldPoint[i].z, ttag = OldPoint[i].tag;
NewPoint[i].x = tx*Tran[0][0] + ty*Tran[1][0] +
}
}
glEnd();
}
void OnDraw_O(DefPoint TempPoint[])
{
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_LINES);
glVertex2d(TempPoint[0].x, TempPoint[0].y);
{ 0, 0, 0, 1 / DD }, { LL, MM, 0, 1 + NN / DD } };
struct DefPoint
{
double x, y, z, tag;
}Point[MaxNum], TPoint[MaxNum], XOZPoint[MaxNum], XOYPoint[MaxNum],
glutMainLoop();
return 0;
}
Point[2].x = 0, Point[2].y = 200, Point[2].z = 0, Point[2].tag = 1;
Point[3].x = 200, Point[3].y = 200, Point[3].z = 200, Point[3].tag = 1;
FaceNum = 4;
Face[3].push_back(1); Face[3].push_back(2); Face[3].push_back(3);
}
void TransForm(DefPoint NewPoint[], DefPoint OldPoint[], doubl 0; i<PointNum; i++)
TransForm(XOYPoint, XOYPoint, Matrix);
TransForm(YOZPoint, YOZPoint, Matrix);
TransForm(YOYPoint, YOYPoint, Matrix);
}
void Initial()
{
for (int i = 0; i<10; i++)Face[i].clear();
tz*Tran[2][2] + ttag*Tran[3][2];
NewPoint[i].tag = tx*Tran[0][3] + ty*Tran[1][3] +
tz*Tran[2][3] + ttag*Tran[3][3];
