一维对流方程在三种差分格式下的解
基于一维对流方程差分格式的哲学思考

基于一维对流方程差分格式的哲学思考【摘要】水力学中对流扩散方程都具有通用微分方程的形式,如N-S方程组中的运动方程等。
通用微分方程通常用数值方法进行求解。
对流项的离散格式对差分方程的稳定性有着重要影响。
一维对流方程是研究对流项特性的模化方程。
对于初值问题,对流项差分格式为一阶精度时,差分方程是有条件稳定的;而对流项差分格式为二阶精度时,差分方程却是不稳定的。
从物理实质上,后者与实际情况也是不符的。
由此可见,局部高精度并不能保证整体的高精度,甚至会导致整体稳定性的破坏。
这表明,做事都要从实际出发,个人利益往往要服从集体利益。
【关键词】哲学;水力学;对流方程;差分格式0 引言同类事物的共同本质及其所表现出来的共同现象,即共性。
由于不同学科的复杂程度或发展的快慢不同,研究成果所达到的水平也不同。
复杂程度是学科研究内容本身所固有的,学科发展的快慢受社会需求的影响。
[1-2]人文科学相对于自然科学是复杂的。
就此而言,人文科学相对于自然科学研究水平相对较低,是必然的也是客观的。
所以,基于同类事物的共性,人文科学可以借鉴自然科学的研究成果。
水力学是自然科学的一个分支。
数值方法是目前水力学常用的研究手段之一。
基于一维对流方程差分格式等进行一些哲学思考是有益的。
1 通用微分方程及一维对流方程[3]1.1 通用微分方程通用微分方程的形式可写为:■+■=■Γ■■+S■(1)上式为张量式。
式中Φ为通用变量,Γ■是扩散系数,S■为源项。
方程各项依次为时变项、对流项、扩散项和源项。
对应于特定意义的Φ,Γ■和S■具有特定的形式。
该通用微分方程可以转化为连续方程、运动方程、雷诺方程、浓度输运方程或热输运方程等。
1.2 一维对流方程运动方程是水力学通用微分方程中最常见的形式。
张量式为:■+■=■ρv■-■+ρfi(2)对于不可压缩流体ρ为常数,并且忽略扩散项和源项(含压强梯度项和质量力项),则上式可简化为:■+■=0(3)一维问题的形式为:■+u■=0(4)对流项线性化之后的形式为:■+α■=0(5)式中α是不为零的常数。
计算程序_计算流体力学_对流方程_有限差分法_Lax格式_迎风格式_FTCS格式

% 一维对流方程迎风格式、Lax格式、FTCS格式差分法计算% 潭花林清华大学航天航空学院% FTCS格式对于一维对流方程不稳定,最好不用clcclear all% 1.参数定义dx=1;x1=-18;x2=18;x=x1:dx:x2;L1=length(x);% dt=0.5*dx; % 收敛dt=2*dx; % 不收敛t1=0;t2=t1+80*dt;t=t1:dt:t2;L2=length(t);alpha=1;lambda=alpha*dt/dx;geshi=1; % 迎风格式% geshi=2; % Lax格式% geshi=3; % FTCS格式% 2.显式求解zeta=zeros(L1,L2);for kk=1:3geshi=kk;for ii=1:L1if x(ii)>0zeta(ii,1)=1;elseif x(ii)==0zeta(ii,1)=1/2;elseif x(ii)<0zeta(ii,1)=0;endendendendif geshi==1for ii=2:L1for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda*(zeta(ii,jj)-z eta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);endzeta1=zeta;else if geshi==2for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=(zeta(ii+1,jj)+zeta(ii-1,jj))/2-. ..lambda/2*(zeta(ii+1,jj)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta2=zeta;else if geshi==3for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda/2*(zeta(ii+1,j j)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta3=zeta;endendendend% 3.绘图% 3.1 t=0figure(1)n=1;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=0时刻的计算结果') %%% 标题axis([-18,18,-0.2,1.2])% 3.2 t=10figure(2)n=(10-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=10s时刻的计算结果') %%% 标题% 3.3 t=20figure(3)n=(20-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') %%% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=20s时刻的计算结果') %%% 标题% 3.4 t=40figure(4)n=(40-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=40s时刻的计算结果') %%% 标题。
22192839_一维对流弥散方程的显式差分法求解及其收敛性分析

(7) (8)
犮狀+1 犻
-犮犻狀
Δ狋
α犔 =
[犞犻+
1 2
(犮犻狀+1
-犮犻狀)-犞犻- (Δ狓)2
1 2
(犮犻狀
-犮犻狀-1)]-犞犻犮犻狀
-犞犻-1犮犻狀-1 Δ狓
(1≤犻<犖)
(9)
当犻=犖
时 ,认 为犮狀犖+1=β犮狀犖
,犞犖+
1 2
=犞犖
,其 中β 为 边 界 衰 减 因 子 ,其 值 介 于 [0,1]之 间 ,反 映 浓 度 在 边
2 研究方法
2.1 一 维 对 流 弥 散 方 程 以一维对流弥散方程为研究对象,不计 源 汇 项,且 孔 隙 率狀 为 常 数,在 稳 定 渗 流 场 中,若 求 解 对 流 弥
散方程得出溶质浓度变化引起的水密度变化可以忽略,则 水流 方程 和溶 质迁 移方 程可以 独立 求解。由 水
流方程的解得出研究区域及时段的速度分量,然后把速度作 为 输入 代入 对流 弥散 方程。这 种“去耦”法计 算效率高 。 [8]
有限差分法是一种古典的数值计算方法。随着数值计算 方法 的研 究和 发展,差 分法 已经 被广 泛 应 用 在地下水渗流问题和浓度扩散问题中。其基本思想是:用渗流 区内 有限 个离 散点 的集 合代 替连 续的渗 流 区,在这些离散点上用差商近似地代 替 微 商,将 微 分 方 程 及 其 定 解 条 件 化 为 以 未 知 函 数 在 离 散 点 上 的 近 似值为未知量的代数方程(称为差 分 方 程),然 后 求 解 差 分 方 程,从 而 得 到 微 分 方 程 的 解 在 离 散 点 上 的 近 似值。有限差分法难免会产生截断误差、舍入误差和测量 误 差,如 果在 某个 节点 某个 时阶 处出现 误 差 后, 会对下一步的迭代求解过程产生影 响,是 误 差 逐 渐 变 小 还 是 被 无 限 放 大,需 要 讨 论 差 分 法 的 收 敛 性 和 稳 定 性 。 [34]
求解一维对流方程的高精度紧致差分格式___

应用数学MATHEMATICA APPLICATA2019,32(3):635-642求解一维对流方程的高精度紧致差分格式侯波,葛永斌(宁夏大学数学统计学院,宁夏银川750021)摘要:本文提出数值求解一维对流方程的一种两层隐式紧致差分格式,采用泰勒级数展开法以及对截断误差余项中的三阶导数进行修正的方法对时间和空间导数进行离散.格式的截断误差为O(τ4+τ2h2+h4),即该格式在时间和空间上均可达到四阶精度.利用von Neumann方法分析得到该格式是无条件稳定的.通过数值实验验证了本文格式的精确性和稳定性.关键词:对流方程;高精度;紧致格式;无条件稳定;有限差分法中图分类号:O241.82AMS(2000)主题分类:65M06;65M12文献标识码:A文章编号:1001-9847(2019)03-0635-081.引言对流方程在生物数学、能源开发、空气动力学等许多领域都具有十分广泛的应用,因此求解该类方程具有非常重要的理论价值和实际意义.然而,由于实际问题通常十分复杂,往往难以求得精确解,因此研究其精确稳定的数值解法是十分必要的.针对对流方程国内外很多学者提出了很多的数值方法.如张天德和孙传灼[1]针对一维对流方程采用待定系数法,得到了两层四点格式和四阶六点格式,并且是无条件稳定的,该方法适用于在点数确定的前提下,得到精度高的差分格式;于志玲和朱少红[2]针对一维问题建立了中间层为两个节点的三层显格式,其截断误差为O(τ2+h2);曾文平[3]针对一维对流方程推导出了一种两层半显式格式,其截断误差为O(τ2+h2),该格式是无条件稳定的.姚朝辉等人[5]将二阶的迎风格式和中心差分格式进行加权得到了WSUC格式,该格式是无条件稳定的;但该格式时间方向和空间方向仅有二阶精度.汤寒松等人[6]通过立方插值拟质点方法(CIP方法),给出了一些保单调的CIP格式;Erdogan[9]针对一维的对流方程推导出了一种指数拟合的差分格式,其截断误差为O(τ2+h2);Bourchtein[10]构造了对流方程的三层五点中心型蛙跳格式,该格式的截断误差为O(τ4+h4);即该格式时间和空间均具有四阶精度,但是该格式是三层的,空间方向需要五个点,并且是条件稳定的;Kim[11]构造了多层无耗散的迎风蛙跳格式,即时间和空间分别具有二阶、四阶、六阶精度,但格式为三层甚至是四层的,并且六阶格式空间方向最多需要五个点,给靠近边界的内点的计算带来困难.综上所述,文献中已经有的数值计算方法大多为低阶精度的,而高精度方法涉及多个时间层,需要一个或多个时间启动步,或者空间方向的网格节点多于三个,这都给计算造成困难或不便.为此本文将构造一种紧致格式,这里紧致格式的定义为对时间导数项的离散采用不超过∗收稿日期:2018-08-10基金项目:国家自然科学基金(11772165,11361045),宁夏自然科学基金重点项目(2018AAC02003),宁夏自治区重点研发项目(2018BEE03007)作者简介:侯波,男,汉族,河南人,研究方向:偏微分方程数值解法.通讯作者:葛永斌.636应用数学2019三个时间层,而对空间导数项的离散采用不超过三个网格点,时间和空间即可以达到高阶精度(三阶及三阶以上)的格式.本文拟构造的格式时间方向仅用到两个时间层上的函数值,在每个时间层上仅涉及到三个空间网格点,格式时间和空间具有整体的四阶精度.该格式的优点是无须启动步的计算,并且在对靠近边界点的计算时,不会用到计算域以外的网格节点.此外该格式为无条件稳定的,可以采用比较大的时间步长进行计算.最后通过数值实验验证本文格式的精确性和稳定性.2.差分格式的建立考虑如下一维对流方程:∂u ∂t +a∂u∂x=f,b≤x≤c,t≥0,(2.1)给定初始条件为:u(x,0)=φ(x),b≤x≤c,(2.2)给定周期性边界条件为:u(b,t)=u(c,t),t≥0,(2.3)其中,u(x,t)为未知函数,f为非齐次项,a为对流项系数,φ(x)为已知函数.将求解区域[b,c]等距剖分为N个子区间:b=x0,x1,···,x N−1,x N=c,并且定义h=c−bN,时间也采用等距剖分,步长用τ表示.在本文中,我们利用u ni ,u n+1i,u n+12i分别表示u在(x i,t n),(x i,t n+1)和(x i,t n+12)点处的函数值.假设方程(2.1)在点(x i,t n+12)成立,简写表示为:(∂u ∂t )n+12i+a(∂u∂x)n+12i=f n+12i.(2.4)将u n+1i 和u ni在点(x i,t n+12)处做泰勒级数展开,可得:u n+1i=u n+12i+τ2(∂u∂t)n+12i+(τ2)22!(∂2u∂t2)n+12i+(τ2)33!(∂3u∂t3)n+12i+O(τ4),(2.5)u ni=u n+12i−τ2(∂u∂t)n+12i+(τ2)22!(∂2u∂t2)n+12i−(τ2)33!(∂3u∂t3)n+12i+O(τ4).(2.6)(2.5)-(2.6)可得:(∂u∂t)n+12i=δt u n+12i−τ224(∂3u∂t3)n+12i+O(τ4),(2.7)其中,δt u n+12i =u n+1i−u n iτ.同理可得:(∂u∂x)n+12i=δx u n+12i−h26(∂3u∂x3)n+12i+O(h4),(2.8)其中,δx u n+12i =un+12i+1−u n+12i−12h.将(2.7)和(2.8)代入(2.4)整理可得:δt u n+12i −τ224(∂3u∂t3)n+12i+aδx u n+12i−ah26(∂3u∂x3)n+12i=f n+12i+O(τ4+h4).(2.9)为了使该格式在时间方向和空间方向上均达到四阶精度,须对(2.9)式中的∂3u∂t3和∂3u∂x3项进行二阶的离散,同时为了保证本文格式的紧致性,即空间方向不超过三个网格点,我们对(2.1)式进行如下变形:∂u ∂t =−a∂u∂x+f,∂2u∂t2=a2∂2u∂x2−a∂f∂x+∂f∂t,第3期侯波等:求解一维对流方程的高精度紧致差分格式637∂3u ∂t 3=a 2∂3u ∂x 2∂t −a ∂2f ∂x∂t +∂2f ∂t 2,∂3u ∂x 3=−1a ∂3u ∂x 2∂t +1a ∂2f ∂x 2.(2.10)将上述∂3u ∂t 3和∂3u∂x 3的表达式(2.10)代入(2.9)并整理可得:δt u n +12i+aδx u n +12i +124(4h 2−a 2τ2)(∂3u ∂x 2∂t)n +12i −τ224(∂2f ∂t 2)n +12i −h 26(∂2f ∂x 2)n +12i +aτ224(∂2f ∂x∂t)n +12i =f n +12i +O (τ4+h 4).(2.11)如果对上式中的δx u n +12i 项采用时间方向算术平均,即δx u n +12i =δx u n +1i+u n i 2,则会导致格式时间退化为二阶精度,为此利用(2.5)+(2.6)可得:u n +12i =12(u n +1i +u n i )−τ28(∂2u ∂t2)n +12i +O (τ4).(2.12)从而可得:δx u n +12i =12δx (u n +1i +u n i )−τ28δx (∂2u ∂t2)n +12i +O (τ4).(2.13)将(2.13)代入(2.11)得:δt u n +12i +a 2δx (u n +1i +u n i )−aτ28δx (∂2u ∂t 2)n +12i +124(4h 2−a 2τ2)(∂3u ∂x 2∂t )n +12i −τ224(∂2f ∂t 2)n +12i −h 26(∂2f ∂x 2)n +12i +aτ224(∂2f ∂x∂t)n +12i =f n +12i +O (τ4+h 4).(2.14)由于δx (∂2u ∂t 2)n +12i =(∂3u ∂x∂t 2)n +12i+O (h 2),所以可得:δt u n +12i +a 2δx (u n +1i +u n i )−aτ28(∂3u ∂x∂t 2)n +12i +124(4h 2−a 2τ2)(∂3u ∂x 2∂t)n +12i −τ224(∂2f ∂t 2)n +12i −h 26(∂2f ∂x 2)n +12i +aτ224(∂2f ∂x∂t)n +12i =f n +12i +O (τ4+τ2h 2+h 4).又因为∂3u ∂x∂t 2=−a ∂3u∂x 2∂t +∂2f ∂x∂t ,所以有:δt u n +12i +a 2δx (u n +1i +u n i )−aτ28(−a ∂3u ∂x 2∂t +∂2f ∂x∂t )n +12i +124(4h 2−a 2τ2)(∂3u ∂x 2∂t )n +12i −τ224(∂2f ∂t 2)n +12i −h 26(∂2f ∂x 2)n +12i +aτ224(∂2f ∂x∂t)n +12i =f n +12i +O (τ4+τ2h 2+h 4),即,δt u n +12i +a 2δx (u n +1i +u n i )+(a 2τ212+h 26)(∂3u ∂x 2∂t )n +12i −τ224(∂2f ∂t 2)n +12i −h 26(∂2f ∂x 2)n +12i −aτ212(∂2f ∂x∂t )n +12i =f n +12i +O (τ4+τ2h 2+h 4).由于(∂3u ∂x 2∂t )n +12i=δ2x (∂u ∂t )n +12i +O (h 2),所以有:u n +1i −u n i τ+a 4h(u n +1i +1−u n +1i −1+u ni +1−u n i −1)+(h 26+a 2τ212)δ2x u n +1i −u n i τ−τ224(f n +1i −2f n +12i +f n −1i (τ2)2)−h 212[(∂2f ∂x 2)n +1i +(∂2f ∂x 2)n −1i ]−aτ12[(∂f ∂x )n +1i −(∂f ∂x)n −1i ]=f n +12i +O (τ4+τ2h 2+h 4),其中,δ2xu i =u i +1−2u i +u i −1h 2,舍去O (τ4+τ2h 2+h 4),等式两边同时乘以τ,并令λ=τ/h ,整理可得:u n +1i +aλ4(u n +1i +1−u n +1i −1)+(16+a 2λ212)(u n +1i +1−2u n +1i +u n +1i −1)638应用数学2019=u n i−aλ4(u n i +1−u n i −1)+(16+a 2λ212)(u n i +1−2u n i +u ni −1)+τ6(f n +1i −2f n +12i +f n i )+τ12(f n +1i +1−2f n +1i +f n +1i −1+f n i +1−2f n i +f n i −1)+aτλ24(f n +1i +1−f n +1i −1−f n i +1+f ni −1)+τf n +12i,即,(23−a 2λ26)u n +1i +(16+aλ4+a 2λ212)u n +1i +1+(16−aλ4+a 2λ212)u n +1i −1=(23−a 2λ26)u n i +(16−aλ4+a 2λ212)u n i +1+(16+aλ4+a 2λ212)u n i −1+(τ12+aλτ24)f n +1i +1(τ12−aλτ24)f n +1i −1+(τ12−aλτ24)f n i +1+(τ12+aλτ24)f n i −1+2τ3f n +12i .(2.15)由推导过程可知,该格式的截断误差为O (τ4+τ2h 2+h 4),即格式(2.15)在时间和空间上均可达到四阶精度.我们注意到,格式为两层格式,并且格式每层仅用到三个网格点,形成的代数方程组系数矩阵为循环三对角矩阵,可采用追赶法进行求解[8],同时由于要求未知时间层上(第n +1层)中间点的系数不能等于0,即23−a 2λ26=0,因此aλ=2.3.稳定性分析下面采用von Neumann 方法分析本文所推导的差分格式(2.15)的稳定性.对于(2.15)式,舍掉非齐次项f ,即假设f 项精确成立,令u n i =ηn e Iσx i,其中,η为振幅,σ为波数,I =√−1为虚数单位,有(23−a 2λ26)ηn +1e Iσx i +(16+aλ4+a 2λ212)ηn +1e Iσx i +1+(16−aλ4+a 2λ212)ηn +1e Iσx i −1=(23−a 2λ26)ηn e Iσx i +(16−aλ4+a 2λ212)ηn e Iσx i +1+(16+aλ4+a 2λ212)ηn e Iσx i −1.(3.1)两边同时约掉e Iσx i ,并整理可得:(23−a 2λ26)ηn +1+(16+a 2λ212)ηn +1(e Iσh +e −Iσh )+aλ4ηn +1(e Iσh −e −Iσh )=(23−a 2λ26)ηn+(16+a 2λ212)ηn (e Iσh +e −Iσh )−aλ4ηn +1(e Iσh −e −Iσh ).(3.2)利用Euler 公式,即e Iσh =cos σh +I sin σh,e −Iσh =cos σh −I sin σh ,可得:(23−a 2λ26)ηn +1+[(13+a 2λ26)cos σh ]ηn +1+(aλI 2sin σh )ηn +1=(23−a 2λ26)ηn +[(13+a 2λ26)cos σh ]ηn −(aλI 2sin σh )ηn .(3.3)对上式进行化简整理有[(23−a 2λ26)+(13+a 2λ26)cos σh +aλI sin σh 2]ηn +1=[(23−a 2λ26)+(13+a 2λ26)cos σh −aλI sin σh 2]ηn .(3.4)从而可得格式(2.15)的误差放大因子为:G =ηn +1ηn =(23−a 2λ26)+(13+a 2λ26)cos σh −aλI sin σh2(23−a 2λ26)+(13+a 2λ26)cos σh +aλI sin σh2.(3.5)由von Numann 稳定性定理可知当|G |≤1时,格式是稳定的,由(3.5)可得|G |=1,因此,格式(2.15)是无条件稳定的.4.数值实验第3期侯波等:求解一维对流方程的高精度紧致差分格式639为了验证本文格式(2.15)的精确性和稳定性,现考虑以下三个具有精确解的初边值问题.分别采用Crank-Nicolson(C-N)格式,文[7]中格式和本文格式(2.15)进行计算;其中,最大绝对误差及收敛阶的定义为:L∞=maxi |u n i−u(x i,t n)|,Rate=log[L∞(h1)/L∞(h2)]log(h1/h2)L∞(h1)和L∞(h2)为空间网格步长分别为h1和h2时的最大绝对误差.问题1[7]:∂u ∂t +∂u∂x=0,0≤x≤2,t>0,u(x,0)=sin(πx),0≤x≤2,u(0,t)=u(2,t),t>0,该问题的精确解为:u(x,t)=sin[π(x−t)].表1问题1当λ=τ/h=0.5,t=1时刻的最大绝对误差及收敛阶h推进步数(n)C-N格式文[7]本文格式L∞误差Rate L∞误差Rate L∞误差Rate 1/510 2.217(-1) 4.865(-2) 1.993(-3)1/1020 5.752(-2) 1.95 1.263(-2) 1.95 1.208(-4) 4.041/2040 1.450(-2) 1.99 3.199(-3) 1.987.490(-6) 4.011/4080 3.631(-3) 2.008.038(-4) 1.99 4.672(-7) 4.001/801609.082(-4) 2.00 2.014(-4) 2.00 2.919(-8) 4.001/160320 2.271(-4) 2.00 5.041(-5) 2.00 1.824(-9) 4.00表2问题1当τ=λh,t=2时刻的最大绝对误差hτλC-N格式文献[7]本文格式1/160.050000000.8 5.290(-2) 1.292(-2) 1.574(-5) 0.10000000 1.69.013(-2) 5.095(-2) 3.198(-3) 0.20000000 3.2 2.307(-1) 1.941(-1) 6.055(-2) 0.40000000 6.4 6.874(-1) 6.597(-1) 1.746(-2)1/320.025000000.8 1.330(-2) 3.230(-3)9.814(-7) 0.20000000 6.4 2.041(-1) 1.950(-1) 1.575(-3) 0.4000000012.8 6.668(-1) 6.601(-1) 1.916(-2)图1问题1当N=32,τ=0.03125,t=0.2时刻的数值解与精确解640应用数学2019表1给出了针对问题1三种格式在不同空间步长h下,当λ=τ/h=0.5,t=1时的最大绝对误差和收敛阶.我们发现C-N格式在时间和空间上都为二阶精度,由于文[7]格式时间具有二阶精度,空间具有四阶精度,因此当取τ=O(h)时,格式空间仅有二阶精度,而本文格式时间和空间均为四阶精度.图1给出N=32,τ=0.03125,t=0.2数值解与精确解对比图,可以看出数值解与精确解吻合的很好.表2给出了当h=1/16和h=1/32时,τ=λh,t=2时刻对问题1采用三种格式计算的最大绝对误差.可以看出网格比λ最大取到12.8,计算仍然是稳定的,因此本文格式是无条件稳定的.并且本文格式在所有参数下,其计算结果比C-N格式和文[7]格式计算结果更加精确.问题2[7]:∂u ∂t +∂u∂x=0,0≤x≤2,t>0,u(x,0)=e cos(πx),0≤x≤2,u(0,t)=u(2,t),t>0,该问题的精确解为:u(x,t)=e cos[π(x−t)].表3问题2当λ=τ/h=0.5,t=1时刻的最大绝对误差及收敛阶h推进步数(n)C-N格式文[7]本文格式L∞误差Rate L∞误差Rate L∞误差Rate 1/510 6.754(-1) 1.428(-1) 5.567(-2)1/1020 2.310(-1) 1.55 3.099(-2) 2.20 3.041(-3) 4.191/2040 6.027(-2) 1.94 6.825(-3) 2.18 1.904(-4) 4.001/4080 1.492(-2) 2.01 1.658(-3) 2.04 1.165(-5) 4.031/80160 3.705(-3) 2.01 4.115(-4) 2.017.252(-7) 4.011/1603209.250(-4) 2.00 1.028(-4) 2.00 4.527(-8) 4.00表4问题2当τ=λh,t=2时刻的最大绝对误差hτλC-N格式文[7]本文格式1/160.050000000.8 2.171(-1) 5.372(-2) 3.897(-4) 0.10000000 1.6 3.450(-1) 2.056(-1)7.795(-3) 0.20000000 3.2 6.810(-1) 6.111(-1) 3.416(-1) 0.40000000 6.4 1.220 1.198 2.017(-1)1/320.025000000.8 5.575(-2) 1.325(-2) 2.449(-5) 0.20000000 6.4 6.302(-1) 6.109(-1) 2.350(-2) 0.4000000012.8 1.204 1.199 2.201(-1)表3和表4给出了针对问题2利用本文格式和C-N格式以及文[7]格式的计算结果.表3考察了格式的精度,表4验证了格式的稳定性.可以看出本文格式在时间和空间上均可达到四阶精度,并且是无条件稳定的.问题3∂u ∂t +a∂u∂x=f,0≤x≤2,t>0,u(x,0)=cos(πx),0≤x≤2,u(0,t)=u(2,t),t>0,f=π(1−a)sin[π(x−t)],该问题的精确解为:u(x,t)=cos[π(x−t)].第3期侯波等:求解一维对流方程的高精度紧致差分格式641表5问题3当λ=τ/h=0.5,a=0.5,t=1时刻的最大绝对误差及收敛阶h推进步数(n)C-N格式本文格式L∞误差Rate L∞误差Rate1/510 1.124(-1) 4.244(-4)1/1020 3.520(-2) 1.67 2.744(-5) 3.951/20409.957(-3) 1.82 1.739(-6) 3.981/4080 2.551(-3) 1.96 1.134(-7) 3.941/80160 6.413(-4) 1.99 1.351(-8) 3.07问题3为非齐次问题,由于文[7]的方程模型为齐次方程,不能计算非齐次问题,因此该问题我们采用本文格式和C-N进行计算和比较,表5给出了两种格式在不同空间步长h下,当t=1时的最大绝对误差和收敛阶.可以看出当λ=τ/h=0.5,a=0.5时,C-N格式在时间和空间上都为二阶精度,而本文格式时间和空间均为四阶精度.5.结论本文针对一维对流方程提出了一种两层隐式高精度紧致差分格式,时间和空间均采用泰勒级数展开法以及截断误差余项修正法进行处理,格式截断误差为O(τ4+τ2h2+h4),即该格式在时间和空间上均可达到四阶精度.并通过von Neumann方法分析得到该格式为无条件稳定的.最后通过三个数值算例验证了格式的精确性和稳定性.通过上述研究,我们可以得出如下结论:1.文献(如[10-11])中的高精度格式往往是时间多层格式,需要另外构造启动步的计算格式,如果采用低精度格式启动,必然会影响以后时间层的计算精度.而本文格式仅为两层格式,无须启动步的计算,时间即可达到四阶精度.2.文献(如[1,10-11])中的高精度格式空间方向上往往超过三个网格节点,导致靠近边界的内点计算困难,需要采用特殊处理,而本文格式仅用到三个网格节点,可以有效避免这一问题.3.尽管本文格式要求aλ=2,这是本文格式的一个缺陷,但是由于本文格式是无条件稳定的,从理论上讲可以采用任意网格比,因此可以很容易避开aλ=2的条件限制,使得这一缺陷并不太影响格式的使用.4.由于本文方法推导过程中涉及到∂2u∂t2,∂3u∂t3,∂3u∂x3的计算,需要用原方程进行多次求导并进行反复代入计算,在考虑对流项为变系数问题时,将涉及到a(x,t)关于x和t的二阶导数,由于我们考虑在时间半点处,即(x i,t n+12)处的函数值,即要用到(∂2a∂t2)n+12i,如果采用中心差分,则时间仅具有二阶精度,因此本文方法不适用于变系数问题.5.本文方法可直接推广到二维和三维问题中去,我们将另文报道.参考文献:[1]张天德,孙传灼.对流方程的差分格式[J].计算物理,1995,12(2):191-195.[2]于志玲,朱少红.关于对流方程一类三层显格式[J].南开大学学报(自然科学版),1998,31(3):27-30.[3]曾文平.解对流方程的加耗散项的差分格式[J].应用数学,2001,14(S1):154-158.[4]陆金甫,关治.偏微分方程数值解法[M].北京:北京大学出版社,1987.[5]姚朝晖,张锡文,任玉新等.一种低耗散、无伪振荡的实用差分格式[J].水动力学研究与进展(A辑),2001,16(02):195-199.[6]汤寒松,张德良,李椿萱.对流方程保单调CIP格式[J].水动力学研究与进展(A辑),1997(02):181-187.[7]赵飞,蔡志权,葛永斌.一维非定常对流扩散方程的有理型高阶紧致差分公式[J].江西师范大学学报(自然科学版),2014,38(4):413-418.642应用数学2019[8]李青,王能超.解循环三对角线性方程组的追赶法[J].小型微型计算机系统,2002(23):1393-1395.[9]ERDOGAN U.Improved upwind discretization of the advection equation[J].Numer.Meth.PartDiffer.Equ.,2014,30:773-787.[10]BOURCHTEIN A,BOURCHTEIN L.Explicitfinite schemes with extended stability for advectionequations[J]put.Appl.Math.,2012,236:3591-3604.[11]KIM C.Accurate multi-level schemes for advection[J].Int.J.Numer.Methods Fluids.,2003,41:471-494.A High-Order Compact Difference Scheme for Solving the1DConvection EquationHOU Bo,GE Yongbin(School of Mathematics and Statistics,Ningxia University,Yinchuan750021,China)Abstract:In this paper,a two-level implicit compact difference scheme for solving the one-dimensional convection equation is proposed.Taylor series expansion and correction for the third derivative in the truncation error remainder of the central difference scheme are used for the discretization of time and space.The local truncation error of the scheme is O(τ4+τ2h2+h4),i.e.,it has the fourth-order accuracy in both time and space.The unconditional stability is obtained by the von Neumann method. The accuracy and the stability of the present scheme are validated by some numerical experiments.Key words:Convection equation;High accuracy;Compact difference scheme;Unconditional sta-bility;Finite difference method。
一维对流方程在三种差分格式下的解

(x, 0) 1 x -1 x 0 这里初始时刻的方程为 (x, 0) x 1 0 x 1 ,即为三角波,其中传播速度为 1,我们 (x, 0) 0 x 1 或 x 1
可以写如下 Fortran90 程序:
!主程序,根据输入选择差分格式,输入1为A格式,2为B格式,3为C格式 !其中输入DX_DT为差分比值,根据输入的比值划分时间网格,其中空间网格为0.05,区间为-8到8 !在A格式中,根据依赖区域,不能计算的左右上三角强行赋值为0 !在B格式中,根据依赖区域右上三角赋值为0 !在C格式中,根据依赖区域左上三角赋值为0 !最后输出为csv格式表格,其中第一列为时间,第二列为空间,第三列为波形数值 !画图时,需要选定同一时间点的二三两列,即可画图 PROGRAM MAIN IMPLICIT NONE !声明差分比值 REAL:: DX_DT !声明差分类型 INTEGER::TYPE_ABC WRITE(*,*)'请输入Dx/Dt,0.5,1或2' READ(*,*)DX_DT WRITE(*,*)'请选择差分格式,A格式输入1,B格式输入2,C格式输入3' READ(*,*)TYPE_ABC !判断类型调用不同的子程序 IF(TYPE_ABC==1) THEN CALL FORMAT_A(DX_DT) ELSE IF(TYPE_ABC==2) THEN CALL FORMAT_B(DX_DT) ELSE IF(TYPE_ABC==3) THEN CALL FORMAT_C(DX_DT) END IF WRITE(*,*)'请在目录下查看结果' PAUSE STOP END
x =1 数值的 t
x =1 为例进行 A,B,C 三种格式的计算结果说明。 t A 格式,根据所的结果,我们绘制不同时刻的波形图像,选取时刻为初始时刻,第 35 个 时间区间时刻(3.5s) ,和最后的 80 区间时刻(8s) ,图像如下:
第五章对流扩散问题(一维稳态对流扩散问题)
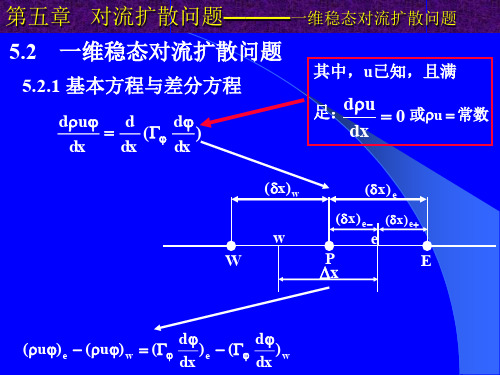
第五章 对流扩散问题———一维稳态对流扩散问题
对控制方程在P点的控制容积积分后,得到如下方程
(u ) e (u ) w ( d d ) e ( )e dx dx
第五章 对流扩散问题———一维稳态对流扩散问题
所以,当 F 2D,即意味着两节点对其间变量分布 的影响特性是受扩散控制的,当 F 2D时,即意味 着两节点对其间变量分布的影响特性是受对流控 制的。对于前者,两节点之间的变量分布偏离线 性分布,但尚不显著,而对于后者两节点之间的 变量分布则严重偏离线性分布。
P<<-1
P=-1
P=0
P=1 P>>1
0
0 L/2 L
第五章 对流扩散问题———一维稳态对流扩散问题
说明
由图很容易看出,只有在贝克列数为零的极限条 件下,即对纯扩散问题或导热问题,变量在任意 两点之间的变化才是线性的。即在没有流动的情 况下,我们假定变量在任意两个节点之间的线性 分布才是可以接受的。 当贝克列数不为零时,即存在对流过程时,变量 在任意两点之间的变化是偏离线性的。贝克列数 的绝对值越大,这种偏离越严重。所以我们在用 控制容积法推导差分方程时,假定任意两个节点 之间变量呈线性变化显然是有问题的。
e P e E
如果 Fe 0 如果 Fe
0
同样
w W
w P
如果 Fw 0
如果 Fw 0
为了能写出差分方程,我们定义一个新的算子,如下:
A, B AMAX( A, B)
(参考资料)一维对流扩散方程的数值解法
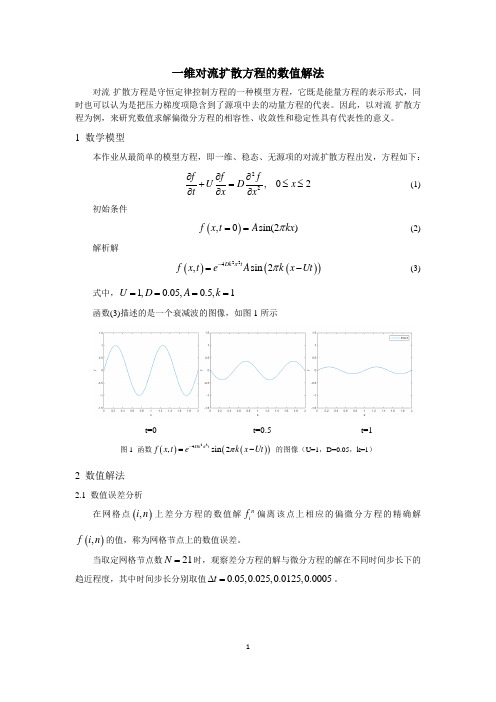
一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程,它既是能量方程的表示形式,同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。
因此,以对流-扩散方程为例,来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。
1 数学模型本作业从最简单的模型方程,即一维、稳态、无源项的对流扩散方程出发,方程如下: 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中,1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像,如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像(U=1,D=0.05,k=1)2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值,称为网格节点上的数值误差。
当取定网格节点数21N =时,观察差分方程的解与微分方程的解在不同时间步长下的趋近程度,其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。
(a )21,0.05N t =∆= (b )21,0.025N t =∆=(c )21,0.0125N t =∆= (d )201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出,数值误差与步长的大小有关。
在满足稳定性条件的前提下,数值误差随着时间步长的减小而减小,同时,图(d )表示增大网格的分辨率也有助于减小网格误差。
为了对数值误差有一个定量的认识,接下来取定时间步长为0.0005t ∆=,分别算出11,21,41,61,81,101,121,161N =时,指标E =1所示。
一维热传导方程的差分格式

一维热传导方程的差分格式一维热传导方程的差分格式《微分方程数值解》学生姓名1:许慧卿学号: 20214329 学生姓名2:向裕学号: 20214327 学生姓名3:邱文林学号: 20214349 学生姓名4:高俊学号: 20214305 学生姓名5:赵禹恒学号: 20214359 学生姓名6:刘志刚学号: 20214346 学院:理学院专业: 14级信息与计算科学指导教师:陈红斌2021年6 月25日《一维热传导方程的差分格式》论文一、《微分方程数值解》课程论文的格式 1)引言:介绍研究问题的意义和现状 2)格式:给出数值格式3)截断误差:给出数值格式的截断误差 4)数值例子:按所给数值格式给出数值例子 5)参考文献:论文所涉及的文献和教材二、《微分方程数值解》课程论文的评分标准 1)文献综述:10分;2)课题研究方案可行性:10分; 3)数值格式:20分;4)数值格式的算法、流程图:10分; 5)数值格式的程序:10分;6)论文撰写的条理性和完整性:10分; 7)论文工作量的大小及课题的难度:10分; 8)课程设计态度:10分; 9)独立性和创新性:10分。
一维热传导方程的差分格式考虑如下一维非齐次热传导方程Dirichlet 初边值问题=a 2+f (x , t ), cu (x ,0) =ϕ(x ), c ≤x ≤d , (1.2)u (c , t ) =α(t ), u (d , t ) =β(t ), 0的有限差分方法, 其中a 为正常数, f (x , t ), ϕ(x ), α(t ),β(t ) 为已知常数, ϕ(c ) =α(0),ϕ(d ) =β(0). 称(1.2)为初值条件, (1.3)为边值条件.本文将给出(1.1) (1.3)的向前Euler 格式, 向后Euler 格式和Crank -Nicolson 格式, 并给出其截断误差和数值例子. 经对比发现, Crank -Nicolson 格式误差最小, 向前Euler 格式次之, 向后Euler 格式误差最大.2 差分格式的建立2.1 向前Euler 格式将区间[c , d ]作M 等分, 将[0, T ]作N 等分, 并记 h =(d -c ) /M , τ=T /N ,x j =c +jh , 0≤j ≤M , t k =k τ, 0≤k ≤N . 分别称h 和τ为空间步长和时间步长. 用x =x j , 0≤j ≤M , t =t k , 0≤k ≤N将Ω分割成矩形网格. 记Ωh =x j |0≤j ≤M , Ωτ={t k |0≤k ≤N }, Ωhτ=Ωh ⨯Ωτ. 称x j , t k 为结点.定义Ωh τ上的网格函数Ω=U j |0≤j ≤M ,0≤k ≤N , 其中U j =u x j , t k .在结点x j , t k 处考虑方程(1.1),有∂u (x j , t k )=a∂2u (x j , t k )+f (x j , t k ), 1≤j ≤M -1, 1≤k ≤N -1. (2.1)将u (x j , t k +1)以结点(x j , t k )为中心关于t 运用泰勒级数展开, 有u (x u ''(x j , t k )τ2j , t k +1)=u (x j , t k )+u '(x j , t k )τ++o (τ2).u (x 2j , t k +1)-u (x j , t k )=∂u (x j , t k )τ∂u (x j , t k )τ∂t +2∂t+o (τ). (2.2) 再将(x j -1, t k ), (x j +1, t k )分别以结点(x j , t k )为中心关于x 运用泰勒级数展开, 有u (x j , t k ()-h )j -1, t k )=u (x j , t k )+u '(x j , t k )(-h )j , t k )(-h )+u ''(x 2!u '''(x 3u (4)(x j , t k )(-h )+o (h 4) , (x u (x u ''(x j , t k )h 2u '''(x j , t k )h 3u j +1, t k )=j , t k )+u '(x j , t k )h +u (4)(x j , t k )h 4+o (h 4).由上述两式可得u (x j -1, t k )-2u (x j , t k )+u (x j +1, t k )∂2u (x j , t k h 2=)∂x 2+h 2∂4(x j , t k )12∂x+o (h 2) . (2.3) 将(2.2), (2.3)两式代入(2.1)中, 得u (x j , t k +1)-u (x j , t k )k )+u (x j +1, t k )u (x j -1, t k )-2u (x j , t h+f (x j , t k )+R k j . (2.4)2其中R k ah ∂4u (x j , t k)τ2∂2(x j , t k )j=-12∂x 4+2∂t 2+o (τ+h 2) 为方程(2.1)的截断误差. 舍去截断误差, 用u kj 代替u (x j , t k ), 得到如下差分方程u k +1-u k j ju k k kj -1-2u j +u j +1+f k j , 1≤j ≤M -1, 0≤k ≤N -1. 结合初边值条件, 可得如下差分格式+1u k -u k j ju k j -1-2u j +u j +1+f j k , 1≤j ≤M -1, 1≤k ≤N -1, (2.6)u 0j =ϕ(x j ), 0≤j ≤M , (2.7)k k u 0=α(t j ), u M =β(t k ), 1≤k ≤N . (2.8)2.2 向后Euler 差分格式在结点x j , t k +1处考虑方程(1.1), 有∂u (x j , t k +1)∂t∂2u (x j , t k +1)∂x 2+f (x j , t k +1), 1≤j ≤M -1, 1≤k ≤N . (2.9)将u x j , t k 以x j , t k +1为中心关于t 运用泰勒级数展开, 有u (x j , t k )=u (x j , t k +1)+u '(x j , t k +1)(-τ) +u ''(x j , t k +1)(-τ) 2+o (τ2).u (x j , t k +1)-u (x j , t k )∂u (x j , t k +1)τ∂2u (x j , t k +1)=-+o (τ). (2.10) 2再将u x j -1, t k +1, u x j +1, t k +1分别以x j , t k +1为中心关于x 运用泰勒级数展开, 有u (x j -1, t k +1)=u (x j , t k +1)+u '(x j , t k +1)(-h )+u ''(x j , t k +1)(-h )u '''(x j , t k +1()-h )u (4)(x j , t k +1)(-h )+o (h 4), u ''(x j , t k +1)h 22! +o (h 4).u '''(x j , t k +1)h 3u (x j +1, t k +1)=u (x j , t k +1)+u '(x j , t k +1)h +u (4)(x j , t k +1)h 4由上述两式可得u (x j -1, t k +1)-2u (x j , t k +1)+u (x j +1, t k +1)∂2u (x j , t k +1)h 2∂4(x j , t k +1)=++o (h 2) . (2.11) 224h ∂x 12∂x将(2.10), (2.11)两式代入(2.9)中, 得+f (x j , t k +1)+R k j . (2.12)τ∂(x i , t k +1)ah 2∂u (x i , t k +1)+o (τ+h 2) 为方程(2.9)的截断误差.舍去截断误差, 用u j 代替u x j , t k , 得到如下差分方程+1u k -u k j j+1k +1+1u k +u k j -1-2u j j +1+f j k +1, 1≤j ≤M -1, 1≤k ≤N . (2.13)结合初边值条件, 可得如下差分格式u k -u k j j+1k +1+1u k +u k j -1-2u j j +1+f j k +1, 1≤j ≤M -1, 1≤k ≤N , (2.14)u 0j =ϕ(x j ), 0≤j ≤M , (2.15)k k u 0=α(t k ), u M =β(t k ), 1≤k ≤N . (2.16)2.3 Crank -Nicolson 差分格式在结点x j , t k +1/2处考虑方程(1.1), 有∂u (x j , t k +1/2)∂t∂2u (x j , t k +1/2)∂x+f (x j , t k +1/2), 1≤j ≤M -1, 0≤k ≤N -1. (2.17)将u x j , t k +1, u x j , t k 以x j , t k +1/2为中心关于t 运用泰勒级数展开, 有u ''(x j , t k +1/2)⎛τ⎛2u (x j , t k +1)=u (x j , t k +1/2)+u '(x j , t k +1/2)+ ⎛22! ⎛2⎛u '''(x j , t k +1/2)⎛τ⎛3+ ⎛+o (τ).τ⎛u ''(x j , t k +1/2)⎛τ⎛⎛u (x j , t k )=u (x j , t k +1/2)+u '(x j , t k +1/2) -⎛+ -⎛22! ⎛⎛⎛2⎛u '''(x j , t k +1/2)⎛τ⎛3+ -⎛+o (τ).将上述两式整理得=++o (τ3). (2.18) 3∂t 24∂t再将u x j -1, t k , u x j +1, t k 分别以x j , t k 为中心关于x 运用泰勒级数展开, 有u (x j -1, t k )=u (x j , t k )+u '(x j , t k )(-h )+u ''(x j , t k )(-h )u '''(x j , t k () -h )u (4)(x j , t k )(-h )4! u ''(x j , t k )h 2+o (h 4) , u '''(x j , t k )h 3u (4)(x j , t k )h 4u (x j +1, t k )=u (x j , t k )+u '(x j , t k )h ++o (h 4).u (x j -1, t k )-2u (x j , t k )+u (x j +1, t k )∂2u (x j , t k )h 2∂4(xj , t k )2=++o (h ). (2.19) 224h ∂x 12∂x同理, 将u x j -1, t k +1, u x j +1, t k +1分别以x j , t k +1为中心关于x 泰勒级数展开, 整理得u (x j -1, t k +1)-2u (x j , t k +1)+u (x j +1, t k +1)∂2u (x j , t k +1)h 2∂4(x j , t k +1)=++o (h 2). (2.20) 224h ∂x 12∂x此时,分别将u x j , t k +1, u x j , t k 以u x j , t k +1/2为中心关于t 泰勒级数展开,有∂2u (x j , t k +1)∂2u (x j , t k +1/2)∂3u (x j , t k +1/2)τ1∂4u (x j , t k +1/2)⎛τ⎛2=+++o τ, () ⎛22222∂x ∂x ∂x ∂t 22! ∂x ∂t ⎛2⎛∂2u (x j , t k )∂2u (x j , t k +1/2)∂3u (x j , t k +1/2)⎛τ⎛=+ -⎛ 222∂x ∂x ∂x ∂t ⎛2⎛1∂u (x j , t k +1/2)⎛τ⎛2+ -⎛+o (τ). 222! ∂x ∂t ⎛2⎛利用上述两式得∂2u (x j , t k +1/2)∂x 21⎛∂u (x j , t k +1)∂u (x j , t k )⎛1⎛∂u (x j , t k +1/2)⎛τ⎛⎛2⎛ ⎛= +-+o τ. () ⎛2222⎛ ⎛2∂x ∂x 2∂x ∂t ⎛2⎛⎛⎛⎛⎛利用(2.19), (2.20)两式, 整理有∂2u (x j , t k +1)∂x∂2u (x j , t k )∂xu (x j -1, t k )-2u (x j , t k )+u (x j +1, t k )u (x j -1, t k +1)-2u (x j , t k +1)+u (x j +1, t k +1)h 2∂(x j , t k ) -h 2∂(x j , t k +1)2-+o h . (2.22) ()412∂x结合(2.21),(2.22)两式, 整理得∂2u (x j , t k +1/2)∂xu (x j -1, t k )-2u (x j , t k )+u (x j +1, t k )u (x j -1, t k +1)-2u (x j , t k +1)+u (x j +1, t k +1)1⎛∂u (x j , t k +1/2)⎛τ⎛⎛- ⎛⎛⎛2 ∂x 2∂t 22⎛⎛⎛⎛⎛1⎛h 2∂(x j , t k )h 2∂(x j , t k +1)2- ++o (h )⎛. (2.23) 44⎛212∂x 12∂x ⎛⎛将(2.18), (2.23)式代入(2.17)得u (x j , t k +1)-u (x j , t k )u (x j -1, t k )-2u (x j , t k )+u (x j +1, t k )u (x j -1, t k +1)-2u (x j , t k +1)+u (x j +1, t k +1)+f (x j , t k )+R k j . (2.24)⎛h 2∂4(x j , t k )h 2∂4(x j , t k +1)∂4u (x j , t k +1/2)⎛τ⎛2⎛τ2∂3u (x j , t k +1/2)a⎛+R k ++ j =- ⎛44223⎛2 12∂x 12∂x ∂x ∂t 224∂t ⎛⎛⎛⎛+o (τ3+h 2) 为方程(2.17)的截断误差.舍去截断误差, 用u j 代替u (x j , t k ) , 可得如下差分方程u k -u k j ju k j -1-2u j +u j +1+1k +1+1u k +u k j -1-2u j j +1+f j k +1/2,1≤j ≤M -1, 0≤k ≤N -1. (2.24)结合初边值条件, 可得如下差分格式u k -u k j ju k j -1-2u j +u j +1+1k +1+1u k +u k j -1-2u j j +1+f j k +1/2,1≤j ≤M -1, 0≤k ≤N -1, (2.25)u 0j =ϕ(x j ), 0≤j ≤M , (2.26)k k u 0=α(t k ), u M =β(t k ), 1≤k ≤N . (2.27)3 差分格式的求解3.1 向前Euler 格式记r =a τ, 称r 为步长比. 差分格式(2.6) (2.8)中(2.6)可改写为u k +1j =r ⋅u k ) u k k kj -1+(1-2r j +r ⋅u j +1+τ⋅f j ,1≤j ≤M -1 , 0≤k ≤N -1 .将(3.1)写成如下形式U k +1=A ⋅U k +τ⋅F k +r ⋅F 1 .U k +1=⎛u k +1, u k +1, , u k +1⎛TU k =⎛u k , u k k⎛12M -1⎛, ⎛12, , u M -1⎛, F k =⎛f k , f k , , f k⎛T F =⎛u k , 0, k ⎛T⎛12M -1⎛, 1⎛00, , 0, u M ⎛(M -1)*1, ⎛ 1-2r r ⎛r 1-2r r ⎛A = ⎛⎛r 1-2r ⎛⎛(M -1)*(M -1)3.2 向后Euler 格式记r =a τ, 称r 为步长比. 差分格式(2.14) (2.16)中(2.14)可改写为-u k j =r ⋅u k +1k +1k +1k +1j -1-(1+2r ) u j +r ⋅u j +1+τ⋅f j1≤j ≤M -1 , 1≤k ≤N .将(3.2)写成如下形式A ⋅U k +1=-U k -τ⋅F k +1-r ⋅F 1 .k +1k +1k +1k k k k⎛⎛⎛U k +1=⎛u , u , , u U =u , u , , u , 12M -112M -1⎛, ⎛⎛⎛ k +1k +1k +1k +1k +1⎛⎛⎛F k +1=⎛f , f , , f F =u , 0, 0, , 0, u , 12M -110M ⎛⎛⎛⎛T T (M -1)*1r ⎛-(1+2r ) ⎛r -(1+2r ) r ⎛⎛A = . rr -(1+2r ) ⎛⎛⎛(M -1)*(M -1)3.3 Crank -Nicolson 格式记r =a τ, 称r 为步长比. 差分格式(2.25) (2.27)中(2.25)可改写为+1k +1k +1k k k k +1/2, -[r /2⋅u k -(1+r ) u +r /2⋅u ]=r /2⋅u +(1-r ) u +r /2⋅u +τ⋅f j -1j j +1j -1j j +1j将(3.3)写成如下形式1≤j ≤M -1 , 0≤k ≤N -1 .. -A 2⋅U k +1=A 1⋅U k +τ⋅F k +1/2+r (F 1+F 2)k +1k +1k +1k k k k⎛⎛⎛U k +1=⎛u , u , , u U =u , u , , u , 12M -112M -1⎛, ⎛⎛⎛k k k +1k +1F 1=⎛⎛u 0, 0, 0, , 0, u M ⎛⎛(M -1)*1, F 2=⎛⎛u 0, 0, 0, , 0, u M ⎛⎛(M -1)*1,k +1/2k +1/2⎛=⎛, f 2k +1/2, , f M -1⎛, ⎛f 1⎛1-r r /2⎛⎛r /21-r r /2 ⎛⎛A 1= , r /2r /21-r ⎛⎛⎛(M -1)*(M -1)r /2⎛-(1+r ) ⎛ ⎛r /2-(1+r ) r /2 ⎛⎛A 2= . r /2r /2-(1+r ) ⎛⎛⎛(M -1)*(M -1)在本文中, 将应用向前Euler 格式(2.6) (2.8), 向后Euler 格式(2.14) (2.16)和Crank -Nicolson 格式(2.25) (2.27)分别来求解如下算例.算例现有如下定解问题∂u ∂2u x +2t=2+e , 0u (x ,0) =e x , 0≤x ≤1,u (0,t ) =e 2t , u (1,t ) =e 1+2t , 0上述定解问题的精确解为u (x , t ) =e 4.1 向前Euler 格式在表4.1.1中给出了取步长h =1/10和τ=1/200(步长比r =1/2) 时计算得到的部分数值结果. 表4.1.2给出了取步长h =1/10和τ=1/100(步长比r =1) 时计算得到的部分数值结果, 随着计算层数的增加, 误差越来越大, 数值结果是发散的. 经步长比r 的多次取值发现, 当r ≤1/2时, 其数值结果是收敛的, 当r >1/2时, 其数值结果是发散的. 表4.1.3给出了r =1/2时, 取不同步长, 数值解的最大误差E ∞(h , τ) =max |u (x j , t k ) -u j k |.1≤j ≤M -11≤k ≤N从表4.1.3可以看出当空间步长缩小到原来的1/2, 时间步长缩小到原来的1/4时, 最大误差约缩小到原来的1/4.图4.1.1给出了t =1时的数值解曲线(h =1/10,τ=1/200) 与精确解曲线. 图4.1.2给出了t =1时不同步长数值解的误差曲线图(r =1/2) , 由图4.1.2可知, 当步长比r 保持不变, 随着时间与空间方向上的加密, 误差越来越小. 图4.1.3给出了不同步长的误差曲面图.表4.1.1 算例在部分结点处数值解、精确解和绝对误差(h =1/10,τ=1/200)(x , t )(0.5,0.1)数值解 1.802810精确解 1.803988|精确解-数值解|1.178e-360 80 100 120 140 160 180 200(0.5,0.3) (0.5,0.4) (0.5,0.5) (0.5,0.6) (0.5,0.7) (0.5,0.8) (0.5,0.9) (0.5,1.0)2.6886513.2838564.010886 4.8988975.983523 7.308290 8.926366 10.9026872.6912343.2870814.014850 4.9037495.989452 7.315534 8.935213 10.9134942.583e-33.225e-3 3.965e-34.852e-35.929e-3 7.243e-3 8.847e-3 1.081e-3表4.1.2 算例在部分结点处数值解、精确解和绝对误差(h =1/10,τ=1/100)1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17(x , t )(0.5,0.01) (0.5,0.02) (0.5,0.03) (0.5,0.04) (0.5,0.05) (0.5,0.06)(0.5,0.07) (0.5,0.08) (0.5,0.09) (0.5,0.10) (0.5,0.11) (0.5,0.12) (0.5,0.13) (0.5,0.14) (0.5,0.15) (0.5,0.16) (0.5,0.17)数值解 1.521674 1.552123 1.583184 1.614870 1.647386 1.679785 1.716057 1.741446 1.807089 1,744143 2.092546 1.164923 4.148393 -4.709415 21.998093 -57.422399 178.294623精确解 1.521962 1.552707 1.584074 1.616074 1.648721 1.682028 1.7160071.750673 1.786038 1.822119 1.858928 1.896481 1.934792 1.9738782.0137532.054433 2.095936|精确解-数值解|2.879e-4 5.845e-4 8.901e-4 1.205e-3 1.336e-3 2.242e-3 5.051e-5 9.227e-3 2.105e-2 7.798e-2 2.336e-1 7.316e-1 2.213e+0 6.684e+0 1.998e+1 5.948e+11.762e+2表4.1.3 算例取不同步长时数值解的最大误差(r =1/2)1/10 1/20 1/40 1/801/200 1/800 1/3200 1/12800E ∞(h , τ)1.178e-22.973e-3 7.431e-4 1.858e-4E ∞(2h ,4τ) /E ∞(h , τ)* 3.964 4.000 4.000图4.1.1 算例取t =1时的数值解曲线(h =1/10,τ=1/200) 与精确解曲线图4.1.2 算例取t =1时不同步长数值解的误差曲线(r =1/2)图4.1.3 算例取不同步长数值解的误差曲面(r =1/2)4.2 向后Euler 格式在表4.2.1和表4.2.2中分别给出了h =1/10,τ=1/200(步长比r =1/2) 和h =1/10, τ=1/100(步长比r =1) 时计算得到的部分数值结果, 发现两表的数值结果都是收敛的, 经步长比r 的多次取值发现, 无论r 取任何值, 其数值结果都是收敛的. 表4.2.3 给出了r =1/2时, 取不同步长, 数值解的最大误差E ∞(h , τ) =max |u (x j , t k ) -u j k |.1≤j ≤M -11≤k ≤N从表4.2.3可以看出当空间步长缩小到原来的1/2, 时间步长缩小到原来的1/4时, 最大误差缩小到原来的1/4. 表4.2.4给出了r =1时的类似结论.图4.2.1给出了t =1时的数值解曲线(h =1/10,τ=1/200) 与精确解曲线. 图4.2.2给出了t =1时, 取不同步长数值解的误差曲线图(r =1/2) , 由图4.2.2可知, 当步长比r 保持不变, 随着时间与空间方向上的加密, 误差越来越小. 图4.2.3和图4.2.4分别当给出了步长比r =1/2和r =1下不同步长的误差曲面图.表4.2.1 算例在部分结点处数值解、精确解和绝对误差(h =1/10,τ=1/200)20 40 60 80 100 120 140 160 180 200(x , t )(0.5,0.1) (0.5,0.2) (0.5,0.3) (0.5,0.4) (0.5,0.5) (0.5,0.6) (0.5,0.7) (0.5,0.8) (0.5,0.9) (0.5,1.0)数值解 1.805343 2.205674 2.694258 3.290867 4.019509 4.909453 5.9964257.324052 10.926203 10.926203精确解 1.803988 2.203396 2.691234 3.287081 4.014850 4.903749 5.989452 7.315534 8.935213 10.913494|精确解-数值解|1.355e-32.278e-33.023e-3 3.785e-34.659e-35.704e-36.973e-3 8.518e-3 1.041e-2 1.271e-2表4.2.2 算例在部分结点处数值解、精确解和绝对误差(h =1/10,τ=1/100)10 20 30 40 50 60 70 80 90 100(x , t )(0.5,0.1) (0.5,0.2) (0.5,0.3) (0.5,0.4) (0.5,0.5) (0.5,0.6) (0.5,0.7) (0.5,0.8) (0.5,0.9) (0.5,1.0)数值解 1.788500 2.185742 2.670171 3.261551 3.983745 4.865788 5.943098 7.258921 8.866068 10.829041精确解 1.786038 2.181472 2.664456 3.254374 3.974902 4.854956 5.929856 7.242743 8.846306 10.804903|精确解-数值解|2.461e-3 4.269e-3 5.715e-3 7.177e-3 8.843e-3 1.083e-2 1.324e-2 1.618e-2 1.976e-2 2.414e-2表4.2.3 算例取不同步长时数值解的最大误差(r =1/2)1/10 1/20 1/40 1/801/200 1/800 1/3200 1/12800E ∞(h , τ)1.386e-2 3.509e-3 8.779e-42.195e-4E ∞(2h ,4τ) /E ∞(h , τ)* 3.950 3.997 3.999表4.2.4 算例取不同步长时数值解的最大误差(r =1)1/10 1/20 1/401/100 1/400 1/1600E ∞(h , τ)2.659e-2 6.744e-3 1.688e-3E ∞(2h ,4τ) /E ∞(h , τ)* 3.943 3.9551/6400 4.222e-4 3.999图4.2.1 算例取t =1时的数值解曲线(h =1/10,τ=1/200) 与精确解曲线图4.2.2 算例取t =1 时不同步长数值解的误差曲线(r =1/2)图 4.2.3 算例取不同步长数值解的误差曲面(r =图 4.2.4 算例取不同步长数值解的误差曲面(r =1)4.3 Crank -Nicolson 格式在表4.3.1中给出了取步长h =1/10,τ=1/10时计算得到的部分数值结果, 表4.3.2给出了取步长h =1/100,τ=1/100时计算得到的部分数值结果, 发现两表的数值结果都是收敛的, 经步长比r 的多次取值发现, 无论r 取任何值, 其数值结果都是收敛的. 表4.3.3给出了取不同步长时, 所得数值解的最大误差E ∞(h , τ) =max |u (x j , t k ) -u j k |.1≤j ≤M -11≤k ≤N从表可以看出当空间步长缩小到原来的1/2, 时间步长缩小到原来的1/2时, 最大误差缩小到原来的1/4.图4.3.1给出了t =1时的数值解曲线(h =1/10,τ=1/10)与精确解曲线. 图4.3.2给出了t =1时, 取不同步长数值解的误差曲线图, 由图4.3.2可知, 当步长比r 保持不变, 随着时间与空间方向上的加密, 误差越来越小. 图4.3.3给出了取不同步长时所得数值解的误差曲面图. 图4.3.4给出了向前Euler , 向后Euler 和Crank -Nicolson 三种方法数值解的误差对比图(h =1/10,τ=1/200) , 由图4.3.4分析可得, 当时间方向t 与空间方向x 都取相同步长时, Crank -Nicolson 方法误差最小, 精度最高, 向前Euler 方法次之,向后Euler 方法所得误差最大, 精度最低.表4.3.1 算例在部分结点处数值解、精确解和绝对误差(h =1/10,τ=1/10)1 2 3 4 5 6 7 8 9 10(x , t )(0.5,0.1) (0.5,0.2) (0.5,0.3) (0.5,0.4) (0.5,0.5) (0.5,0.6) (0.5,0.7) (0.5,0.8) (0.5,0.9) (0.5,1.0)数值解 1.823114 2.227196 2.720414 3.322776 4.058460 4.957021 6.054520 7.395008 9.032284 11.032056精确解 1.822119 2.225541 2.718282 3.320217 4.055200 4.953032 6.049647 7.389056 9.025013 11.023176|精确解-数值解|9.949e-4 1.656e-3 2.132e-3 2.659e-3 3.260e-3 3.988e-3 4.873e-3 5.952e-3 7.271e-3 8.880e-3表4.3.2 算例在部分结点处数值解、精确解和绝对误差(h =1/100,τ=1/100)10 20 30 40 50 60 70 80 90 100(x , t )(0.5,0.1) (0.5,0.2) (0.5,0.3) (0.5,0.4) (0.5,0.5) (0.5,0.6) (0.5,0.7) (0.5,0.8) (0.5,0.9) (0.5,1.0)数值解 1.993726 2.435147 2.974297 3.632815 4.437131 5.919524 6.619421 8.084979 9.875016 12.061372精确解 1.993715 2.435130 2.974297 3.632786 4.437096 5.419481 6.619369 8.084915 9.874938 12.061276|精确解-数值解|1.081e-5 1.749e-52.296e-5 2.864e-53.521e-54.308e-55.266e-56.433e-57.857e-5 9.597e-5表4.3.3 算例取不同步长时数值解得最大误差1/10 1/20 1/40 1/80 1/160 1/320 1/6401/10 1/20 1/40 1/80 1/160 1/320 1/640E ∞(h , τ)9.588e-3 2.429e-3 6.078e-4 1.520e-4 3.799e-5 9.499e-6 2.375e-6E ∞(2h ,2τ) /E ∞(h , τ)* 3.9457 3.9961 3.9990 3.9998 3.9999 4.0000图4.3.1 算例取t =1时数值解曲线(h =1/10,τ=1/10)与精确解曲线图4.3.2 算例取t 1时不同步长数值解的误差曲线图4.3.3 算例取不同步长数值解的误差曲面图4.3.4 算例取t =1时三种方法数值解的误差对比曲线(h =1/10,τ=1/200)在本文中, 给出了向前Euler , 向后Euler 和Crank -Nicolson 三种差分格式, 分别对抛物型方程进行求解, 其中向前Euler 格式是条件稳定的, 后两者是无条件稳定的. 经对比发现, Crank -Nicolson 格式的精度最高, 误差最小, 向前Euler 格式次之, 向后Euler 格式精度最低, 误差最大.[1] 孙志忠. 偏微分方程数值解法[M]. 第二版. 北京: 科学出版社, 2021.[2] 李荣华. 偏微分方程数值解法[M]. 第二版. 北京: 高等教育出版社, 2021.[3] 刘卫国. MATLAB程序设计教程[M]. 第二版. 北京: 中国水利水电出版社, 2021.◆ 程序流程图1 向前Euler 法2 向后Euler 法3 Crank Nicolson 法(向前Euler 法)建立函数文件ForwardEuler.m ,如下:% 求解一维非齐次热传导方程 ut-uxx=e^(x+2t), 0% u(x,0)=e^x, 0% u(0,t)=e^(2t), u(1,t)=e^(1+2t), 0% 该问题的定解为 u(x,t)=e^(x+2t).% 其中取a=1, h1表示时间t 方向上的步长, h2表示空间x 方向上的步长.function [uxy,u,eps]=ForwardEuler(h1,h2,M,N,T)% 求解一维非齐次热传导方程 ut-uxx=f(x,t),(a>0)% 其中M,N 分别为x 与t 方向上的网格数。
一维定常对流扩散反应方程的高精度紧致差分格式

一维定常对流扩散反应方程的高精度紧致差分格式祁应楠;武莉莉【摘要】针对一维定常对流扩散反应方程,提出了一种四阶精度的有理型紧致差分格式,其局部截断误差为O(h4);然后通过Richardson外推技术和算子插值法将本文格式的精度提高到六阶.因为格式仅涉及到3个网格基架点,所以对于Dirichlet 边值问题,由差分格式可得三对角线性方程组,可采用追赶法进行求解.最后通过数值算例验证了本文方法的精确性和可靠性.【期刊名称】《华中师范大学学报(自然科学版)》【年(卷),期】2017(051)001【总页数】6页(P1-6)【关键词】对流扩散反应方程;高阶紧致格式;Richardson外推;有限差分法【作者】祁应楠;武莉莉【作者单位】宁夏师范学院数学与计算机科学学院,宁夏固原756000;宁夏师范学院数学与计算机科学学院,宁夏固原756000【正文语种】中文【中图分类】O241.8对流扩散反应问题是流体力学、传热学、传质学等学科以及环境、化工等应用领域中经常遇到的典型问题之一,由于问题的准确解往往很难获得,所以人们经常采用数值方法来寻求问题的近似解.目前,所流行的近似计算方法包括有限差分法、有限元法和边界元法等.其中有限差分方法是一种常用的数值计算方法.目前,国内外已经有许多有关该问题高阶紧致差分格式的研究报道.如:魏剑英[1]针对一维对流扩散方程,提出了一种指数型高阶紧致差分格式.王彩华[2]利用泰勒展开公式和数项级数收敛性给出了一线性对流扩散问题的一类高精度紧致差分格式.田芳和田振夫[3]基于非均匀网格上函数的泰勒级数展开,构造了非均匀网格上的高精度紧致差分格式.Sun和Zhang[4]构造了定常对流扩散反应方程的多项式型四阶紧致差分格式,并用Richardson外推法[5]和算子插值技术将格式的精度提高到了六阶.Tian和Dai [6]构造对流扩散问题的指数型格式,其空间具有四阶精度.文献[7]研究了非定常对流扩散方程的有理型高阶紧致差分格式并得到了很好的计算效果.杨志峰等[8]构造了含源项非定常对流扩散问题的紧致四阶格式.文献[9-11]研究了利用样条插值的方法来构造高精度紧致差分格式.文献[12]通过消除对流项,并利用Pade格式,构造了一维非定常对流扩散反应方程无条件稳定的四阶紧致差分格式.文献[13]针对非定常对流扩散方程,对空间采用三点紧致差分格式,并对时间采用单对角隐式Runge-Kutta方法进行离散,得到了截断误差为O(τ4+h4)的无条件稳定的隐格式.文献[14]通过简单的分裂算法及增加特殊网格点的方法,对时间的处理采用C-N格式与向后欧拉结合的技巧,推导出求解高维非定常对流扩散反应方程的隐式差分格式.本文针对一维定常对流扩散反应方程,基于截断误差余项修正思想,并结合原方程本身,推导得到了求解该方程的一种四阶精度的有理型紧致差分格式.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后给出了数值算例. 本文讨论的方程模型为两点边值问题:其中,边界条件为:u(0)=q0,u(L)=qL.这里,a,p(x),b(x)分别为扩散、对流和反应项系数.且a>0,p(x)和b(x)均为关于空间变量x的光滑函数.首先将定义域[0,L]离散为:0=x0<x1<x2<…<xN=L,记为网格数,空间步长定义为.为了方便书写,用ui表示表示,依此类推.将式(1)改写为:由此定义空间一阶和二阶导数的中心差分算子为:将式(1)利用中心差分代替,并利用关于u的一阶数和二阶导数的定义,可得:).如果略去i和i项,及高阶截断误差项O(h4),即可得到二阶中心差分格式.为了得到高精度的差分格式,将式(5)中的三阶和四阶导数项进行处理,为此对式(2)两边同时关于x求一阶导和二阶导数可得:.将式(6)代入式(7)消去xi化简可得:.将式(6)和式(8)代入式(5)可得:fi+O(h4).将式(3)和式(4)代入式(9),略去高阶项后化简整理可得:其中式(10)即为多项式型四阶紧致(FOC)差分格式,此格式色散误差和耗散误差较大.为了能精确数值求解此类方程,我们推导一种有理型的四阶紧致差分格式.将式(2)代入式(6)可得:.在式(15)中令,则式(15)可简化为:将式(2)和式(15)代入式(7),整理可得:.令则式(17)可化简为:将式(16)和式(18)代入式(5),整理可得:其中,.接着,将式(19)中的一阶导数用中心差分代替加×(5),利用式(3)和(4)对u的一阶和二阶导数进行离散,整理可得:).将式(15)和式(17)代入式(20)加×(5),同样利用u的一阶和二阶导数进行离散,整理可得:).令则式(21)可化简为:(γ4f+γ5fx+γ6fxx)i+O(h4).然后,略去式(22)中i和i项,并将式(3)和式(4)代入式(22),化简整理可得有理型的高阶紧致差分格式:,其中,.此格式的高阶截断误差为O(h4),即此格式具有四阶精度.本文格式之所以称之为有理型格式,是因为其差分算子的系数为有理型函数,记为RHOC.从推导过程可以看出,FOC格式只是其中的一种特殊情况,有理型格式的推导更具有广泛性.结合原方程可得到具有不同性质的高精度格式,对于不同性质的问题可选用与之相适应的格式进行求解,此类格式均为三个网格基架点,只发生系数的变化.下面使用Richardson外推方法[5]将本文的四阶格式RHOC提高到六阶精度.◆………… ◆——◆0 1 2 ……N/2◆—●—◆…… ◆—●—◆0 1 2 3 4……N-1 N首先,用格式(23)分别在粗网格和细网格上计算一遍可得粗网格和细网格具有四阶精度的近似解.然后利用Richardson外推公式:可得到在粗网格具有六阶精度的解,其中和分别为粗网格和细网格上的解,即通过Richardson外推公式(24)可将细网格上偶数点(菱形点)的精度提高到六阶.为了使细网格上奇数点(圆点)的精度也达到六阶,使用算子插值法.由式(23)可得:).由于细网格上偶数点(菱形点)已经算出,因此只须采用式(26)计算奇数点(圆点),即可得如下算子插值公式:.通过式(26)利用细网格上具有六阶精度的偶数点来计算奇数点,从而可使得细网格上点的精度均为六阶,整个过程我们将其记为RRHOC,其算法步骤如下:1) 在粗网格上用格式(23)计算一遍,可得;2) 在细网格上用格式(23)计算一遍,可得;3) 通过外推式(24)将细网格上偶数点(菱形点)的精度计算至六阶,4) 通过式(26)将细网格上奇数点(圆点)的精度计算至六阶.为了验证本文格式的精确性和可靠性,分别采用RHOC格式和RRHOC格式对以下两个有精确解的问题进行数值实验,并与中心差分格式、多项式型四阶紧致格式(FOC) [4]和六阶格式(REC) [4]的计算结果进行比较.其中,L∞范数误差和收敛阶(Rate)的定义如下:L∞范数误差,其中,Ui表示点xi处的精确解,ui表示点xi处的数值解,L∞(uh1)和L∞(uh2)分别表示网格步长为h1和h2时对应的L∞范数误差.问题1:该问题的精确解为:u(x)=ex.取:a=1,b(x)=x2+1,f(x)=x2ex.问题2:该问题的精确解为:u(x)=e-4πsin(x).取:a=1,p(x)=1,b(x)=1,f(x)=e-4π(cos x+2sin x).对于问题1和问题2,表1和表3列出了取不同步长h时,采用中心差分格式、FOC格式[4]与本文RHOC格式计算的L∞范数误差和Rate(收敛阶).不难得到,本文所提的四阶精度的有理型格式(RHOC)格式比多项式型格式(FOC) 和中心差分格式均具有更高的准确度.而且,当网格数不断增加时,RHOC格式的L∞范数误差比中心差分格式小四个数量级不等,比同是四阶的FOC格式计算结果更精确.表2和表4列出了取不同网格步长h时,REC格式[4]与本文RHOC格式的最大绝对误差和收敛阶,从表中可以看出经过外推和算子插值之后的REC格式和本文RHOC格式均有六阶精度,但是本文RHOC格式的计算误差明显优于REC格式[4].本文基于中心差分格式的截断误差余项修正,并利用原方程本身,提出了数值求解一维两点边值问题的一种紧致的高精度差分方法,由理论推导可知所提格式为四阶精度.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后,采用本文两种方法计算了两个数值算例,并与传统的中心差分格式以及文献[4]中的FOC格式和REC格式进行了对比,充分体现了本文方法的精确性和有效性. 【相关文献】[1] 魏剑英. 定常对流扩散反应方程的指数型高阶差分格式[J].宁夏大学学报(自然科学版), 2012,33(2):140-143.[2] 王彩华. 一维对流扩散方程的一类新型高精度紧致差分格式[J].水动力学研究与进展, 2004,19(5):655-663.[3] 田芳,田振夫. 定常对流扩散反应方程非均匀网格上的高精度紧致差分格式[J].宁夏师范学院学报(自然科学版), 2009, 26(2):219-225.[4] SUN H, ZHANG J. A High order finite difference discretization strategy based on extrapolation for convection diffusion equations[J].Numer Methods Partial Differential Eq,2004, 20(1):18-32[5] CHENEY W, KINCARD D. Numerical Mathematics and Computing[M]. 4th Ed. CA:Brooks/Cole Publishing,Pacific Grove,CA. 1999.[6] TIAN Z F, DAI S Q. High-order compact exponential finite difference methods for convection-diffusion type problems[J]. J Comput Phys, 2007, 220:952-974.[7] 赵飞,蔡志权,葛永斌. 一维非定常对流扩散方程的有理型高阶紧致差分格式[J].江西师范大学学报(自然科学版), 2014, 38(4):413-418.[8] 杨志峰,陈国谦. 含源项非定常对流扩散问题紧致四阶差分格式[J].科学通报, 1993,38(2):113-116.[9] LANG F G, XU X P. Quintic B-spline collocation method for second order mixed boundary value problem[J]. Computer Physics Communications. 2012, 183:913-921.[10] GOH J, MAJID A A, ISMAIL A I M. A quartic B-spline for second-order singular boundary value problems[J]. Computers and Mathematics with Applications. 2012,64:115-120.[11] 林建国,许维德,陶尧森.含源项非定常非线性对流扩散方程的三次样条四阶差分格式[J].水动力学研究与进展(A辑), 1994, 9(2):599-602.[12] 杨录峰,李春光.一种求解对流扩散反应方程的高阶紧致差分格式[J]. 宁夏大学学报(自然科学版), 2013, 34(2): 101-104.[13] PIAO X, CHOI H J, KIM S D, et al. A fast singly diagonally implicit Runge-Kutta method for solving 1D unsteady convection-diffusion equations[J]. Numercal Methods for Partial Differential Equations,2013(30):788-812.[14] ADEM K. Finite difference approximations of multidimensional unsteady convection-diffusion-reaction equations[J]. Journal of Computational Physics, 2015, 285:331-349.。
一维热传导方程的差分法

一维热传导方程的差分法【摘要】本文主要介绍了一维热传导方程的差分法,通过离散化处理将连续的热传导方程转化为离散的计算形式,包括显式差分法、隐式差分法和Crank-Nicolson方法。
这些方法在计算热传导过程中具有重要的应用意义。
在稳定性分析部分,讨论了各种差分方法的稳定性条件,以保证数值计算的准确性和稳定性。
结论部分总结了各种方法的优缺点,并展望了未来在热传导领域的研究方向和实际应用前景。
一维热传导方程的差分法为热传导问题的数值模拟提供了重要的数值计算手段,为工程技术和科学研究提供了有力的支持。
【关键词】一维热传导方程、差分法、离散化处理、显式差分法、隐式差分法、Crank-Nicolson方法、稳定性分析、热传导、热传导方程、数值模拟、数值计算、实际应用、稳定性、研究意义、展望未来、总结。
1. 引言1.1 背景介绍一维热传导方程是描述热传导过程的数学模型,通过该方程可以研究材料内部温度分布随时间的变化规律。
在实际工程和科学研究中,热传导方程具有广泛的应用,包括材料热处理、地热能利用、气候变化模拟等领域。
背景介绍:热传导方程最初由法拉第提出,是研究热传导现象最基本的方程之一。
热传导方程的一维形式可以表示为:\frac{\partial u(x,t)}{\partial t} = \alpha \frac{\partial^2u(x,t)}{\partial x^2}u(x,t)表示位置x处在时间t时的温度分布,\alpha为热传导系数。
通过求解这个偏微分方程,可以得到材料内部温度分布对时间的变化情况。
在本文中,我们将使用差分法对一维热传导方程进行数值求解。
差分法是一种常用的数值计算方法,在离散化处理方程后,将时间和空间离散化处理,然后利用差分格式来逼近偏微分方程的解。
通过显式差分法、隐式差分法和Crank-Nicolson方法的分析,我们将探讨这些方法在解决一维热传导方程中的应用和稳定性分析。
一维对流方程在A、B、C三种差分格式

一、上机目的用数值方法计算一维对流方程在A 、B、C三种差分格式下的解。
x∆取为0.05. xt∆∆取值为0.5,1,2。
并作相关讨论。
二、实验原理1x1x0)(x,1x10)(x,x1-x10)(x,t8x8-,0>-<=≤≤+-=≤≤+=>≤≤=∂∂+∂∂或ζζζζζxxt三、上机要求:1.学会对MS-FORTRAN的基本操作。
2.用Fortran编写程序计算一维对流方程在A、B、C三种格式下的解。
3.讨论各种格式下不同的tx∆∆值的差分格式解的特点。
四、实验程序以A格式为例,对微分方程进行离散化,得出 A 格式的差分解的表达式:B、C格式同理可以写出。
由此编写如下的Fortran程序。
注:除了循环时间层的计算公式略有不同外,三个程序没有区别,因此这里只用一个主程序,并根据!空间节点321,dx=0.05 输出依次为(时间,空间,数值)program mainimplicit nonereal dx_dt !定义的值integer abc,r_t,i,j,k !定义变量,abc为格式类型,r_t为时间网格数,其余为循环变量real,allocatable::s(:,:) !定义存储矩阵swrite(*,*) "输入dx_dt=0.5,1,2"read(*,*) dx_dtwrite(*,*) "选择格式,A,B,C分别输入1,2或3"read(*,*) abc!根据格式选择生成相应的文件if(abc==1) thenopen(unit=8,file='out_a.csv')elseif(abc==2) thenopen(unit=8,file='out_b.csv')elseif(abc==3) thenopen(unit=8,file='out_c.csv')endifr_t=160/dx_dt !计算时间网格总数allocate(s(r_t+1,321)) !分配存储矩阵的空间!第一层赋初值do i=1,140,1s(1,i)=0write(8,*)"1",",",i,",",s(1,i)end dodo i=141,161,1s(1,i)=1+0.05*(i-161)write(8,*)"1",",",i,",",s(1,i)end dodo i=162,181,1s(1,i)=1-0.05*(i-161)write(8,*)"1",",",i,",",s(1,i)end dodo i=182,321,1s(1,i)=0write(8,*)"1",",",i,",",s(1,i)end do!循环时间层,根据格式的选择来判断执行哪一部分if(abc==1) thendo i=2,r_t,1do j=i,322-i,1s(i,j)=s(i-1,j)-(s(i-1,j+1)-s(i-1,j-1))/(dx_dt*2)write(8,*)i,',',j,',',s(i,j)end dodo k=1,i-1,1 !余下部分赋值0,下同s(i,k)=0write(8,*)i,',',k,',',s(i,k)end dodo k=322-i,321,1s(i,k)=0write(8,*)i,',',k,',',s(i,k)end doend doelseif(abc==2) thendo i=2,r_t+1,1do j=1,322-i,1s(i,j)=s(i-1,j)-(s(i-1,j+1)-s(i-1,j))/dx_dtwrite(8,*)i,',',j,',',s(i,j)end dodo k=322-i,321,1s(i,k)=0write(8,*)i,',',k,',',s(i,k)end doend doelseif(abc==3) thendo i=2,r_t+1,1do j=i,321,1s(i,j)=s(i-1,j)-(s(i-1,j)-s(i-1,j-1))/dx_dtwrite(8,*)i,',',j,',',s(i,j)end dodo k=1,i-1,1s(i,k)=0write(8,*)i,',',k,',',s(i,k)end doend doendif!完成提示write(*,*)'数据已输出至源目录'pausestopend program五、实验结果及分析程序运行后在对应目录下生成csv表格文件,根据输入的的值不同生成对应的网格并计算各节点数值。
对流扩散方程有限差分方式

对流扩散方程有限差分方式求解对流扩散方程的差分格式有很多种,在本节中将介绍以下3种有限差分格式:中心差分格式、Samarskii 格式、Crank-Nicolson 型隐式差分格式。
3.1 中心差分格式时刻导数用向前差商、空间导数用中心差商来逼近,那么就取得了(1)式的中心差分格式]6[21111122h u u u vhu u au u nj n j n j nj n j n jn j -+-+++-=-+-τ(3)假设令 haτλ=,2h vτμ=,那么(3)式可改写为)2()(2111111nj n j n j n j n j n j n j u u u u u u u -+-+++-+--=μλ (4)从上式咱们看到,在新的时刻层1+n 上只包括了一个未知量1+n j u ,它能够由时刻层n 上的值n j u 1-,n j u ,n j u 1+直接计算出来。
因此,中心差分格式是求解对流扩散方程的显示格式。
假定),(t x u 是定解问题的充分滑腻的解,将1+n j u ,n j u 1+,nj u 1-别离在),(n j t x 处进行Taylor 展开:)(),(),(211ττO t u t x u t x u unjn j n j n j+⎥⎦⎤⎢⎣⎡∂∂+==++)(2),(),(322211h O x u h x u h t x u t x u u nj nj n j n j n j +⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂+==++ )(2),(),(322211h O x u h x u h t x u t x u u njnj n j n j n j +⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂-==--代入(4)式,有 21111122),(hu u u vhu u au u t x T nj n j n j nj n j n jn j n j -+-+++---+-=τ)()()(2222h O v x u v h O a x u a O t u nj nj nj ⋅-⎥⎦⎤⎢⎣⎡∂∂-⋅+⎥⎦⎤⎢⎣⎡∂∂++⎥⎦⎤⎢⎣⎡∂∂=τ )()()(222h O v a O x u v x u a t u njnj nj ⋅-++⎥⎦⎤⎢⎣⎡∂∂-⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂=τ )(2h O +=τ显然,当0→τ,0→h 时,0),(→n j t x T ,即中心差分格式与定解问题是相容的。
数值传热学习题答案权威版

数值传热学习题答案权威版习题4-2⼀维稳态导热问题的控制⽅程:022=+??S xTλ依据本题给定条件,对节点2节点3采⽤第三类边界条件具有⼆阶精度的差分格式,最后得到各节点的离散⽅程:节点1: 1001=T 节点2: 1505105321-=+-T T T 节点3:75432=+-T T 求解结果:852=T ,403=T对整个控制容积作能量平衡,有:02150)4020(15)(3=?+-?=?+-=?+x S T T h x S q f f B即:计算区域总体守恒要求满⾜习题4-5在4-2习题中,如果25.03)(10f T T h -?=,则各节点离散⽅程如下:节点1: 1001=T节点2: 1505105321-=+-T T T节点3:25.03325.032)20(4015])20(21[-?+=-?++-T T T T对于节点3中的相关项作局部线性化处理,然后迭代计算;求解结果:818.822=T ,635.353=T (迭代精度为10-4)迭代计算的Matlab 程序如下: x=30; x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b; x1=x; x=t(3,1); endtcal=t习题4-12的Matlab程序%代数⽅程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数A=cos(x);%TDMA的主对⾓元素B=sin(x);%TDMA的下对⾓线元素C=cos(x)+exp(x); %TDMA的上对⾓线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif ncoematrix(n,n+1)=-1*C(1,n);endend%计算D⽮量D=(coematrix*T')';%由已知的A、B、C、D⽤TDMA⽅法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图⽐较给定T值和计算T值plot(Tcal,'r*')hold on结果⽐较如下,由⽐较可知两者值⾮常切合(在⼩数点后8位之后才有区别):习题4-14充分发展区的温度控制⽅程如下:)(1rTr r r x T uc p =??λρ对于三种⽆量纲定义w b w T T T T --=Θ、∞∞--=ΘT T T T w 、ww T T T T --=Θ∞进⾏分析如下1)由wb wT T T T --=Θ得:w w b T T T T +Θ-=)(由T 可得:x T x T x T T T x T w b w w b ??Θ-+??Θ=?+Θ-?=??)1(])[(rT r T T r T T T r T w w b w w b ??Θ-+?Θ?-=?+Θ-?=??)1()(])[( 由b T 与r ⽆关、Θ与x ⽆关以及x T ??、rT的表达式可知,除了w T 均匀的情况外,该⽆量纲温度定义在⼀般情况下是不能⽤分离变量法的; 2)由∞∞--=ΘT T T T w 得: ∞∞+Θ-=T T T T w )(由T 可得:xT x T T T x T w w ??Θ=?+Θ-?=??∞∞])[(rx T ??、rT的表达式可知,在常见的四种边界条件中除了轴向及周向均匀热流const q w =的情况外,有0=??rT w,则该⽆量纲温度定义是可以⽤分离变量法的; 3)由wwT T T T --=Θ∞得: w w T T T T +Θ-=∞)(由T 可得:xT x T T T x T w w w ??Θ-=?+Θ-?=??∞)1(])[(rT r T T r T T T r T w w w w ??Θ-+?Θ-=+Θ-?=??∞∞)1()(])[( 同2)分析可知,除了轴向及周向均匀热流const q w =温度定义是可以⽤分离变量法的;习题4-181)采⽤柱坐标分析,写出统⼀的稳态柱坐标形式动量⽅程:S r r r r r r x x w r v r r r u x +++=??+??+??)(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ x 、r 和θ分别是圆柱坐标的3个坐标轴,u 、v 和w 分别是其对应的速度分量,其中x 是管内的流动⽅向;对于管内的层流充分发展有:0=v 、0=w ,0=??xu;并且x ⽅向的源项:x pS ??-=r ⽅向的源项:r pS ??-=r S 1由以上分析可得到圆柱坐标下的动量⽅程: x ⽅向:0)(1)(1=??-+x pu r r r u r r r θλθλ r ⽅向:0=??r pθ⽅向:0=??θp边界条件: R r =,0=u0=r ,0=??r u ;对称线上,0=??θu不考虑液体的轴向导热,并简化分析可以得到充分发展的能量⽅程为:)(1)(1θλθλρ+=??Tr r r T r r r x T uc p 边界条件: R r =,w q r T =??λ;0=r ,0=??rTπθ/0=,0=??-θλT2)定义⽆量纲流速:dxdp R uU 2-=λ并定义⽆量纲半径:R r /=η;将⽆量纲流速和⽆量纲半径代⼊x ⽅向的动量⽅程得:0))1((1))1((122=??-?-+?-xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得:ηθηηηηηU U 边界条件:1=η,0=U0=η,0=??ηU;对称线上,0=??θU 定义⽆量纲温度:λ/0R q T T b -=Θ其中,0q 是折算到管壁表⾯上的平均热流密度,即:Rq q wπ=0;由⽆量纲温度定义可得:b T Rq T +Θ=λ将T 表达式和⽆量纲半径η代⼊能量⽅程得:)(1)(100θληλθηηλληηηρ?Θ+?Θ=??R q R R R R q R R R x T uc b p 化简得:)1(1)(10θηθηηηηηρ?Θ+?Θ=??x T u c q R b p (1)由热平衡条件关系可以得:mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T u c 020221221)(===??=??ππρρρ将上式代⼊式(1)可得:)1(1)(12θηθηηηηη?Θ+?Θ=m U U 边界条件:0=η,0=?Θ?η;1=η,R q q w πη10==?Θ?0=?Θ?θ;πθ=,0=?Θθ单值条件:由定义可知:0/0=-=ΘλR q T T b b b 且: ??Θ=ΘAAb U d AU d A 即得单值性条件:0=Θ??AA UdAUdA3)由阻⼒系数f 及Re 定义有:228)(2/Re ??? ??=-=D D U D u u dx dp D f e m e m me νρ且:m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5-21.⼀维稳态⽆源项的对流-扩散⽅程如下所⽰:xx u 22??Γ=??φφρ(取常物性)边界条件如下:L L x x φφφφ====,;,00上述⽅程的精确解如下:11)/(00--=--?PeL x Pe L e e φφφφΓ=/uL Pe ρ 2.将L 分成20等份,所以有:=P Pe 201 2 3 4 5 6 ………… …………… 17 18 19 20 21 对于中⼼差分、⼀阶迎风、混合格式和QUICK 格式分别分析如下: 1)中⼼)5.01()5.01(11-?+?++-=i i i P P φφφ 20,2 =i2)⼀阶迎风中间节点: ?-?++++=P P i i i 2)1(11φφφ 20,2 =i3)混合格式当1=?P 时,中间节点:2)5.01()5.01(11-?+?++-=i i i P P φφφ20,2 =i当10,5=?P 时,中间节点: 1-=i i φφ 20,2 =i 4) QUICK 格式*12111)35(8122121---++++++=+--??-??+?i i i i i i i P P P P P φφφφφφφ 2≠i *1111)336(8122121--++++++=+-?-??+?i i i i i i P P P P P φφφφφφ 2=i数值计算结果与精确解的计算程序如下:%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solution y=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')%grid Pe numbertt=[1 5 10];%dimensionless lengthm=20;%mdim is the number of inner nodemdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculationy0=1;yL=2;%cal exact solutionfor n=1:size(tt,2)t=m*tt(1,n);if t==0yval1(n,:)=eval(y1);elseyval1(n,:)=eval(y);endend%extra treatment because max number in MATLAB is 10^308 if max(isnan(yval1(:)))yval1=yval1';yval1=yval1(:);indexf=find(isnan(yval1));for n=1:size(indexf,1)if rem(indexf(n,1),size(X,2))==0yval1(indexf(n),1)=yL;elseyval1(indexf(n),1)=y0;endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';endd=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt); title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt); title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt); title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1, nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt (1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt (1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL); elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5 com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn))); endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------ function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------ function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));精确解与数值解的对⽐图,其中边界条件给定10=φ,2=L φ。
对流方程差分格式稳定性判定

对流方程差分格式稳定性判定李五明【摘要】The paper decided the stability of different difference schemes of the one dimension convection equation using Fourier stability analysis. The fundamental idea of Fourier stability analysis is to extend periodically the error of solution for the linear differential equation and express it using Fourier series, then check the enlargement and decay of every component of the Fourier series. According to Fourier series for each component change over time, we judged the stability of difference schemes by the magnification factor. Using the method, the paper decided the stability of different difference schemes for the given equation.%用傅里叶稳定性分析法判断一维对流方程不同差分格式的稳定性.傅里叶稳定性分析法的基本思想是:对于线性微分方程,将解的误差做周期延拓并用傅里叶级数表示出来,然后考察每一个傅里叶级数分量的增大和衰减情况;根据傅里叶级数每一个分量随时间的变化情况,由放大因子判断差分格式的稳定性.用该方法对给定方程不同差分格式的稳定性进行了判断.【期刊名称】《河南理工大学学报(自然科学版)》【年(卷),期】2012(031)003【总页数】4页(P369-372)【关键词】对流方程;差分格式;稳定性【作者】李五明【作者单位】河南理工大学数学与信息科学学院,河南焦作454000【正文语种】中文【中图分类】O175.210 引言用有限差分法数值求解偏微分方程是计算数学中的一个重要课题.在有限差分法中,差商代替了微商,差分方程代替了微分方程.然而,并不是任何情况下,差分方程都可以逼近原微分方程.因为,方程形式的逼近是一回事,方程解的逼近又是一回事.因此,在基本理论上必须解决数值计算中可能出现的诸如稳定性、精度等问题.采用有限差分法求解由偏微分方程所描述的具体问题时,在确定差分离散格式是否可用之前必须解决3个问题:当差分网格的时间与空间步长都趋近于零时,差分方程是否充分逼近原微分方程;差分格式的真解是否充分逼近原微分方程的精确解;差分格式的近似解与真解之间的误差是否有界.这3个问题在有限差分理论中分别称为相容性、收敛性和稳定性.差分格式的相容、收敛和稳定并不是孤立的,而是互有联系.根据LAX等价定理,若线性微分方程的初值问题适定、差分格式相容,则稳定性是收敛性的必要和充分条件.因此,常常通过判定一个差分格式的稳定性来判定其收敛性.因为,直接证明一个差分格式的收敛性是比较困难的,但对稳定性的证明却容易得多,且现有的方法也比较有效.本文介绍其中最常用的一种分析差分格式稳定性的方法:傅里叶稳定性分析法.傅里叶稳定性分析法的基本思想是将解的误差做周期延拓并用傅里叶级数表示出来,然后考察每一个傅里叶级数分量的增大和衰减情况.如果每一个分量的强度(或振幅)是随时间的推移而增大的,则所讨论的差分格式是不稳定的;反之,若每一个分量的振幅是随时间的推移而衰减或保持不变的,则格式是稳定的.为了进行这种分析,可以把某一分量的表达式代入到误差传播方程中,以得出相邻两时间层该分量的振幅比(通常称为放大因子).稳定性的条件要求放大因子的绝对值(或模)小于或等于1.当放大因子等于1时,称为中性稳定.在这种情况下,任何时刻引进的误差都不会衰减或放大.本文主要针对一维对流方程,利用傅里叶稳定性分析方法讨论其不同差分格式的稳定性.1 傅里叶稳定性分析法针对一个具体的方程来考察傅里叶稳定性分析法,然后再将该方法推广到其他差分格式.一维对流方程的初值问题如下:,(1)问题的定解域为x-t的上平面(图1),分别引入平行于x轴和平行于t轴的两族直线,把求解域划分为矩形网格.网格线的交点称为节点,x方向上网格线之间的距离Δx称为空间步长,t方向上网格线之间的距离Δx称为时间步长.这样,两族网格可记为x=xi=iΔx,(i=0,±1,±2,…),t=tn=nΔt,(n=0,1,2,…).网格划定后,就可针对其中的任一节点,如图1中的节点(xi,tn).将函数u在该点记为,tn)=u(iΔx,nΔt).(2)方程(1)的FTCS(Forward Time Central Space)格式为α.(3)将式(3)改写为易于递推计算的差分格式,有,式中:λ为网格比.相应于上式的误差传播方程为,(4)式中:ε为各节点上的误差.如果对ε在正负方向上作周期延拓,即把ε看作是以某一定值为周期的周期函数,则εn,εn+1可以展开为以下的傅里叶级数[5-6]:.于是,,(5),(6)式中:将式(5)和(6)代入式(4)得.(7)式(7)相当于将零展开成傅里叶级数,式中{ }内相当于傅里叶系数,它对于所有的k都等于零,即,(8)令,(9)则式(8)成为(不失一般性,支掉式中的下标记号k)Cn+1=GCn,(10)表示误差从第n层传播到第n+1层时,以傅里叶级数表示的每一误差分量的振幅放大或衰减了G倍.所以,称G为放大因子.傅里叶稳定性分析法就集中在对G 的分析上,如果|G|>1,则误差的振幅随n的增大而增大,差分格式不稳定;如果|G|≤1,则误差的振幅随n的增大而减小或不变,差分格式稳定.应用欧拉公式e±iz=cos z±isin z,将式(9)改写为G=1-iαλsin kΔx,得|G|2=1+α2λ2sin2kΔx.当sin2kΔx≠0时,选取网格比λ总有|G|>1.因此,差分格式(3)是不稳定的.从上例的分析注意到,以傅里叶稳定性分析法判断差分格式稳定性时,是从误差传播方程出发,将计算节点的误差延拓为傅里叶级数,并通过分析式(7)中傅里叶级数任一系数来确定放大因子G,进而确定差分格式的稳定性.对于齐次线性微分方程,由于误差传播方程与其相应的差分方程形式相同,在傅里叶稳定性分析中,只要令,(11)并将它们代入相应的差分格式中,同样可以得到与上例相同的放大因子G的表达式.为方便起见,在以后的傅里叶稳定性分析讨论中将采用式(11)的方式.2 应用举例例1 试讨论一维对流方程(1)的FTCS隐式差分格式的稳定性.解:方程(1)的FTCS隐式差分格式为α,(12)或写为,λ,将式(11)代入上式,有Cn+1eik(xi-Δx)]=Cneikxi,约去公因子eikxi后,得,即,由此得放大因子为,即≤1,所以,式(12)是无条件稳定的.例2 试讨论一维对流方程(1)的格式的稳定性.解:方程(1)的格式为,(13)或,λ,将式(11)代入上式,有,约掉公因子eikxi,得,由此得放大因子为,有|G|2=1.所以,差分格式(13)是无条件稳定的.3 结论(1)本文利用傅里叶稳定性分析法仅讨论一维对流方程不同差分格式稳定性的判断,实际上,该方法对二维对流方程、一(二)维扩散方程、一维对流-扩散方程也是适用的.(2)本文没有给出一维对流方程迎风格式稳定性的判定,主要是因为需要考虑CFL(Courant-Friedrichs-Lewy)条件,并且要对α的正负进行讨论.限于篇幅,略去.(3)傅里叶稳定性分析法只适用于线性微分方程,对于非线性方程差分格式稳定性的判定,目前还没有严格的一般性理论处理.通常的做法是,从非线性方程对应的线性化模型得出的稳定性判定准则出发,对非线性方程差分格式的稳定性进行大致估计,然后在实际计算中采用试算方法将其扩展到非线性问题中去.参考文献:[1] 张国强,吴家鸣.流体力学[M].北京:机械工业出版社,2005.[2] 顾丽珍.求解对流扩散方程的一些高阶差分格式[J].清华大学学报:自然科学版,1996,36(2):9-14.[3] 管秋琴.一类对流扩散方程组的差分格式与稳定性[J].上海电力学院学报,2009,25(2):192-195.[4] 余德浩,汤华中.微分方程数值解法[M].北京:科学出版社,2003.[5] 范德辉,陈辉,王秀凤,等.对流扩散方程差分格式稳定性分析[J].暨南大学学报:自然科学与医学版,2006,27(1):24-29.[6] 阴继翔,李国君,李卫华,等.对流扩散方程不同格式的数值稳定性分析[J].太原理工大学学报:自然科学版,2004,35(2):121-124,133.[7] 马荣,石建省,张翼龙,等.对流-弥散方程显式差分法稳定性分析方法的初探[J].水资源与水工程学报,2010,21(1):132-134.[8] 陆金甫,关治.偏微分方程数值解解法[M].北京:清华大学出版社,2004.[9] 王静,王艳.RICCATI方程有理展开法及其在非线性反应扩散方程中的应用[J].河南理工大学学报:自然科学版,2010,29(5):689-694.[10] 王同科,马明书.二维对流扩散方程的二阶精度特征差分格式[J].工程数学学报,2004,21(5):727-731.。
有限差分求解1维流体方程

有限差分求解1维流体方程全文共四篇示例,供读者参考第一篇示例:有限差分法是求解偏微分方程的一种常用数值方法,它将连续的微分方程离散化为有限个点上的代数方程组,通过对这些代数方程进行求解得到数值解。
在流体力学中,有限差分法被广泛应用于求解流体方程,其中涉及了流体的运动和力学性质。
本文将着重介绍有限差分法求解一维流体方程的方法和步骤。
一维流体方程是描述流体在一维空间中运动的数学模型,通常可以描述为一维流体方程组。
有限差分法的基本思想是将一维流体方程中的时间和空间进行离散化,将连续的一维空间划分为有限个网格点,时间也进行离散化为有限个时间步长,通过有限差分近似代替微分算子,并在每个网格点上建立代数方程组,最终通过求解这些代数方程组得到数值解。
具体来说,有限差分法求解一维流体方程的步骤如下:1. 确定求解区域和边界条件:首先需要确定求解区域的大小和边界条件,包括流体的初始状态和边界条件。
这些信息将决定了求解的范围和边界条件的设定。
2. 离散化:将一维空间和时间进行离散化,将空间和时间分别划分为有限个网格点和时间步长。
这一步是有限差分法的核心思想,通过离散化将连续的微分方程转化为离散的代数方程。
3. 近似微分算子:在每个网格点上近似代替微分算子,例如将一维流体方程中的导数项用差分近似代替,通常采用中心差分、前向差分或后向差分等方式。
通过这种方式可以将微分方程转化为代数方程。
4. 建立代数方程组:在每个网格点上建立代数方程组,将近似的微分算子代入原始方程中,然后利用相邻网格点之间的关系建立代数方程,得到形如Ax=b的线性方程组。
5. 求解线性方程组:通过求解线性方程组得到数值解,这可以采用各种求解线性方程组的方法,如直接法、迭代法或者共轭梯度法等。
6. 可视化和分析:最后通过对数值解进行可视化和分析,可以得到流体在一维空间中的运动情况和物理性质,例如流速、压强等。
第二篇示例:有限差分法是一种常用的数值计算方法,常用于求解偏微分方程。
计算程序_计算流体力学_对流方程_有限差分法_Lax格式_迎风格式_FTCS格式

% 一维对流方程迎风格式、Lax格式、FTCS格式差分法计算% 潭花林清华大学航天航空学院% FTCS格式对于一维对流方程不稳定,最好不用clcclear all% 1.参数定义dx=1;x1=-18;x2=18;x=x1:dx:x2;L1=length(x);% dt=0.5*dx; % 收敛dt=2*dx; % 不收敛t1=0;t2=t1+80*dt;t=t1:dt:t2;L2=length(t);alpha=1;lambda=alpha*dt/dx;geshi=1; % 迎风格式% geshi=2; % Lax格式% geshi=3; % FTCS格式% 2.显式求解zeta=zeros(L1,L2);for kk=1:3geshi=kk;for ii=1:L1if x(ii)>0zeta(ii,1)=1;elseif x(ii)==0zeta(ii,1)=1/2;elseif x(ii)<0zeta(ii,1)=0;endendendendif geshi==1for ii=2:L1for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda*(zeta(ii,jj)-z eta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);endzeta1=zeta;else if geshi==2for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=(zeta(ii+1,jj)+zeta(ii-1,jj))/2-. ..lambda/2*(zeta(ii+1,jj)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta2=zeta;else if geshi==3for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda/2*(zeta(ii+1,j j)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta3=zeta;endendendend% 3.绘图% 3.1 t=0figure(1)n=1;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=0时刻的计算结果') %%% 标题axis([-18,18,-0.2,1.2])% 3.2 t=10figure(2)n=(10-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=10s时刻的计算结果') %%% 标题% 3.3 t=20figure(3)n=(20-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') %%% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=20s时刻的计算结果') %%% 标题% 3.4 t=40figure(4)n=(40-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=40s时刻的计算结果') %%% 标题聚乙烯(PE)简介1.1聚乙烯化学名称:聚乙烯英文名称:polyethylene,简称PE结构式:聚乙烯是乙烯经聚合制得的一种热塑性树脂,也包括乙烯与少量α-烯烃的共聚物。
计算程序_计算流体力学_对流方程_有限差分法_Lax格式_迎风格式_FTCS格式

% 一维对流方程迎风格式、Lax格式、FTCS格式差分法计算% 潭花林清华大学航天航空学院% FTCS格式对于一维对流方程不稳定,最好不用clcclear all% 1.参数定义dx=1;x1=-18;x2=18;x=x1:dx:x2;L1=length(x);% dt=0.5*dx; % 收敛dt=2*dx; % 不收敛t1=0;t2=t1+80*dt;t=t1:dt:t2;L2=length(t);alpha=1;lambda=alpha*dt/dx;geshi=1; % 迎风格式% geshi=2; % Lax格式% geshi=3; % FTCS格式% 2.显式求解zeta=zeros(L1,L2);for kk=1:3geshi=kk;for ii=1:L1if x(ii)>0zeta(ii,1)=1;elseif x(ii)==0zeta(ii,1)=1/2;elseif x(ii)<0zeta(ii,1)=0;endendendendif geshi==1for ii=2:L1for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda*(zeta(ii,jj)-z eta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);endzeta1=zeta;else if geshi==2for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=(zeta(ii+1,jj)+zeta(ii-1,jj))/2-. ..lambda/2*(zeta(ii+1,jj)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta2=zeta;else if geshi==3for ii=2:(L1-1)for jj=1:(L2-1)zeta(ii,jj+1)=zeta(ii,jj)-lambda/2*(zeta(ii+1,j j)-zeta(ii-1,jj));endzeta(1,jj+1)=zeta(2,jj+1);zeta(L1,jj+1)=zeta(L1,jj)-lambda*(zeta(L1,jj)-z eta(L1-1,jj));endzeta3=zeta;endendendend% 3.绘图% 3.1 t=0figure(1)n=1;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=0时刻的计算结果') %%% 标题axis([-18,18,-0.2,1.2])% 3.2 t=10figure(2)n=(10-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=10s时刻的计算结果') %%% 标题% 3.3 t=20figure(3)n=(20-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') %%% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=20s时刻的计算结果') %%% 标题% 3.4 t=40figure(4)n=(40-t(1))/dt;plot(x,zeta1(1:L1,n),'-k',x,zeta2(1:L1,n),'-.k' ,x,zeta3(1:L1,n),'--k')% 作图% axis equal %%% 是否要求x、y坐标间距相等% grid on %%% 是否要求画网格xlabel('x/m'),ylabel('t/s') % %% x,y轴表示的变量含义%text(1,2,'f(x)') %%% 图中文字标识legend('迎风格式','Lax格式','FTCS格式') %%% 不同曲线的线型区分title('t=40s时刻的计算结果') %%% 标题聚乙烯(PE)简介1.1聚乙烯化学名称:聚乙烯英文名称:polyethylene,简称PE结构式:聚乙烯是乙烯经聚合制得的一种热塑性树脂,也包括乙烯与少量α-烯烃的共聚物。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Page 3 of 12
中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验二
对流方程差分格式下的解
《计算流体力学试验》课程实验报告纸
院系:工学院
SUBROUTINE FORMAT_A(DX_DT) IMPLICIT NONE !I,J,K为循环变量,REC_T为时间网格总数 INTEGER::I,J,K,REC_T !输入dx/dt的比值 REAL::DX_DT !声明动态矩阵,用于存储计算结果 REAL,ALLOCATABLE::M(:,:) !打开通道号8,输出OUTPUT_C.CSV OPEN(UNIT=8,FILE='OUTPUT_A.CSV') !计算时间T的网格,节点数为网格数加1 REC_T=160/DX_DT !确定M大小,开始在网格第一层赋初值,其中循环不能从负数开始,X网格右移 ALLOCATE(M(REC_T+1,321)) DO I=1,140,1 M(1,I)=0 WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=141,161,1 M(1,I)=1+0.05*(I-161) WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=162,181,1 M(1,I)=1-0.05*(I-161) WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=182,321,1 M(1,I)=0 WRITE(8,*)'1',',',I,',',M(1,I) END DO !时间上从第二层开始循环,逐步积分,注意,时间层循环上限为Rec_T DO I=2,REC_T,1 !计算三角网格部分数值,循环部分从I到322-I DO J=I,322-I,1 M(I,J)=M(I-1,J)-(M(I-1,J+1)-M(I-1,J-1))/(2*DX_DT) WRITE(8,*)I,',',J,',',M(I,J)
Page 6 of 12
中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验二
对流方程差分格式下的解
《计算流体力学试验》课程实验报告纸
院系:工学院 姓名:刘广 学号:11309018 日期:2014 年 03 月 31 号
REC_T=160/DX_DT !确定M大小,开始在网格第一层赋初值,其中循环不能从负数开始,X网格右移 ALLOCATE(M(REC_T+1,321)) DO I=1,140,1 M(1,I)=0 WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=141,161,1 M(1,I)=1+0.05*(I-161) WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=162,181,1 M(1,I)=1-0.05*(I-161) WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=182,321,1 M(1,I)=0 WRITE(8,*)'1',',',I,',',M(1,I) END DO !时间上从第二层开始循环,逐步积分 DO I=2,REC_T+1,1 !计算三角网格部分数值,循环部分从I到321 DO J=I,321,1 M(I,J)=M(I-1,J)-(M(I-1,J)-M(I-1,J-1))/DX_DT WRITE(8,*)I,',',J,',',M(I,J) END DO !左上三角强行赋值为0 DO K=1,I-1,1 M(I,K)=0 WRITE(8,*)I,',',K,',',M(I,K) END DO END DO RETURN END SUBROUTINE
姓名:刘广
学号:11309018
日期:2014 年 03 月 31 号
ห้องสมุดไป่ตู้
Page 5 of 12
中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验二
对流方程差分格式下的解
《计算流体力学试验》课程实验报告纸
院系:工学院 姓名:刘广 学号:11309018 日期:2014 年 03 月 31 号
(x, 0) 1 x -1 x 0 这里初始时刻的方程为 (x, 0) x 1 0 x 1 ,即为三角波,其中传播速度为 1,我们 (x, 0) 0 x 1 或 x 1
可以写如下 Fortran90 程序:
!主程序,根据输入选择差分格式,输入1为A格式,2为B格式,3为C格式 !其中输入DX_DT为差分比值,根据输入的比值划分时间网格,其中空间网格为0.05,区间为-8到8 !在A格式中,根据依赖区域,不能计算的左右上三角强行赋值为0 !在B格式中,根据依赖区域右上三角赋值为0 !在C格式中,根据依赖区域左上三角赋值为0 !最后输出为csv格式表格,其中第一列为时间,第二列为空间,第三列为波形数值 !画图时,需要选定同一时间点的二三两列,即可画图 PROGRAM MAIN IMPLICIT NONE !声明差分比值 REAL:: DX_DT !声明差分类型 INTEGER::TYPE_ABC WRITE(*,*)'请输入Dx/Dt,0.5,1或2' READ(*,*)DX_DT WRITE(*,*)'请选择差分格式,A格式输入1,B格式输入2,C格式输入3' READ(*,*)TYPE_ABC !判断类型调用不同的子程序 IF(TYPE_ABC==1) THEN CALL FORMAT_A(DX_DT) ELSE IF(TYPE_ABC==2) THEN CALL FORMAT_B(DX_DT) ELSE IF(TYPE_ABC==3) THEN CALL FORMAT_C(DX_DT) END IF WRITE(*,*)'请在目录下查看结果' PAUSE STOP END
Page 7 of 12
中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验二
对流方程差分格式下的解
《计算流体力学试验》课程实验报告纸
院系:工学院 姓名:刘广 学号:11309018 日期:2014 年 03 月 31 号
其中对于程序说明在程序注释中已经说明的很清楚,这里不再赘述。 四:实验结果 最终程序执行完毕之后会在目录下生成对应的输出文档,根据用户输入的 大小生成对应的网格,然后计算出所有网格节点的数值。 五:实验结果分析
t n ( in 1 i 1 ) 2x
Page 2 of 12
中山大学工学院、理论与应用力学刘广编制
实验编号及题目:实验二
对流方程差分格式下的解
《计算流体力学试验》课程实验报告纸
院系:工学院 姓名:刘广 学号:11309018 日期:2014 年 03 月 31 号
DO I=162,181,1 M(1,I)=1-0.05*(I-161) WRITE(8,*)'1',',',I,',',M(1,I) END DO DO I=182,321,1 M(1,I)=0 WRITE(8,*)'1',',',I,',',M(1,I) END DO !时间上从第二层开始循环,逐步积分 DO I=2,REC_T+1,1 !计算三角网格部分数值,循环部分从1到322-I DO J=1,322-I,1 M(I,J)=M(I-1,J)-(M(I-1,J+1)-M(I-1,J))/DX_DT WRITE(8,*)I,',',J,',',M(I,J) END DO !右上三角强行赋值为0 DO K=322-I,321,1 M(I,K)=0 WRITE(8,*)I,',',K,',',M(I,K) END DO END DO RETURN END SUBROUTINE SUBROUTINE FORMAT_C(DX_DT) !I,J,K为循环变量,REC_T为时间网格总数 INTEGER::I,J,K,REC_T !输入dx/dt的比值 REAL::DX_DT !声明动态矩阵,用于存储计算结果 REAL,ALLOCATABLE::M(:,:) !打开通道号8,输出OUTPUT_C.CSV OPEN(UNIT=8,FILE='OUTPUT_C.CSV') !计算时间T的网格,节点数为网格数加1
二:实验仪器与设备: ① 装有 Fortran 的计算机 三、实验原理 1台
0, - 8 x 8 t 0 t x (x, 0) 1 x -1 x 0 (x, 0) x 1 0 x 1
(x, 0) 0
x 1 或 x 1
1.40E+00 1.20E+00 1.00E+00 8.00E-01 6.00E-01 4.00E-01 2.00E-01 0.00E+00 -2.00E-01 0 -4.00E-01 -6.00E-01
1 15 29 43 57 71 85 99 113 127 141 155 169 183 197 211 225 239 253 267 281 295 309
学会对 MS-FORTRAN 的基本操作。 用 Fortran 编写程序计算一维对流方程在 A、B、C 三 种格式下的解。讨论各种格式下不同的 三:实验步骤: 首先 A 格式,我们对微分方程进行离散化,得出 A 格式的差分解的表达式,为
