MATLAB数理统计程序
高校统计学专业数理统计建模算法Matlab实现代码详解

高校统计学专业数理统计建模算法Matlab实现代码详解统计学专业是现代社会中非常重要的学科之一,因为它帮助我们理解和解释各种数据,从而为决策提供依据。
在统计学领域中,数理统计建模是一种重要的方法,它利用数学模型来描述和预测数据的行为。
而Matlab作为一种强大的科学计算软件,可以有效地实现数理统计建模算法。
本文将详细介绍高校统计学专业数理统计建模算法在Matlab中的实现代码。
首先,我们将介绍几种常见的数理统计建模算法,并展示它们在Matlab中的具体代码实现。
随后,我们将详细解释这些代码的原理和使用方法,以便读者能够更好地理解和运用这些算法。
1. 线性回归线性回归是数理统计建模中最基本的算法之一。
它通过拟合一个线性模型来预测连续变量的值。
在Matlab中,可以使用“fitlm”函数实现线性回归。
以下是代码示例:```matlabdata = readtable('data.csv'); % 读取数据集model = fitlm(data, 'Y ~ X1 + X2'); % 构建线性回归模型summary(model); % 打印模型摘要信息```2. 逻辑回归逻辑回归是一种常用的分类算法,它用于预测二元变量的概率。
在Matlab中,可以使用“fitglm”函数实现逻辑回归。
以下是代码示例:```matlabdata = readtable('data.csv'); % 读取数据集model = fitglm(data, 'Y ~ X1 + X2', 'Distribution', 'binomial'); % 构建逻辑回归模型summary(model); % 打印模型摘要信息```3. 决策树决策树是一种常用的分类和回归算法,它通过构建一个树状模型来预测变量的取值。
在Matlab中,可以使用“fitctree”函数实现决策树。
概率论和数理统计的Matlab 实现

expcdf 函数 功能:计算累加指数分布函数。 语法:P = expcdf(X,MU) 描述:expcdf(X,MU) 计算参数为 MU 的数据 X 的累加指数分布函数。指数 MU 必须为
正。 累加指数分布函数的计算公式为:
概率论和数理统计的 Matlab 实现
1概 述
自然界和社会上会发生各种各样的现象,其中有的现象在一定条件下是一定要发生的, 有的则表现出一定的随机性,但总体上又有一定的规律可循。一般称前者为确定性事件, 后者为不确定性事件(或称随机事件)。概率论和数理统计就是研究和揭示不确定事件统计 规律性的一门数学学科。
f (x |l) =
lx x!
e-l
I (0,1,K )
(x)
y=
f (x | b) =
x b2
çæ - x 2 ÷ö
eçè 2b2 ÷ø
y
=
f
(x
| v)
=
Gçæ è
v
+ 2
1
÷ö ø
Gçæ è
v 2
÷ö ø
1
1
vp
ççèæ1 +
v +1
x2 v
÷÷øö
2
y=
f (x | N) =
1 N
I (1,..., N ) ( x)
y
=f(x|r,p)
=
ççèæ
r
+
x x
+
1÷÷øö
p
x
q
x
I
(
0,1,...)
(
x)
其中, q = 1 - p
(完整版)Matlab概率论与数理统计

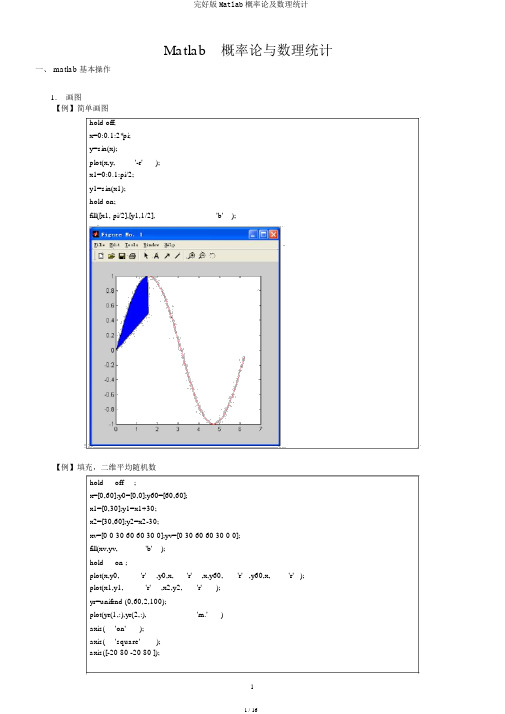
Matlab 概率论与数理统计、matlab 基本操作 1. 画图【例01.01】简单画图hold off; x=0:0.1:2*pi; y=sin (x);plot(x,y, '-r'); x1=0:0.1:pi/2; y1=s in( x1); hold on;fill([x1, pi/2],[y1,1/2],'b');【例01.02】填充,二维均匀随机数hold off ;x=[0,60];y0=[0,0];y60=[60,60]; x1=[0,30];y1=x1+30; x2=[30,60];y2=x2-30;plot(x,y0, 'r' ,y0,x, plot(x1,y1, 'r' ,x2,y2, yr=u nifrnd (0,60,2,100);plot(yr(1,:),yr(2,:), axis( 'on'); axis( 'square' ); axis([-20 80 -20 80 ]);xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0]; fill(xv,yv, 'b');hold on ;'r' ,x,y60, 'r' ,y60,x,'r')'r');'m.')2. 排列组合kC=nchoosek(n,k) : CC n ,例 nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2):从 n1 至U n2 的连乘【例01.03】至少有两个人生日相同的概率365 364|||(365 rs 1)rs365365 364 365 rs 1 365 365365rs=[20,25,30,35,40,45,50]; %每班的人数p1= on es(1,le ngth(rs)); p2=on es(1,le ngth(rs));%用连乘公式计算for i=1:le ngth(rs) p1(i)=prod(365-rs(i)+1:365)/365A rs(i); end%用公式计算(改进) for i=1:le ngth(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365); end ; end%用公式计算(取对数) for i=1:le ngth(rs)p1(i)=exp(sum(log(365-rs(i)+1:365))-rs(i)*log(365)); end公式计算P 1n!C NN nN!1 (N n)!1N nN (N 1) (N n 1)、随机数的生成3. 均匀分布随机数rand(m,n);产生m行n列的(0,1)均匀分布的随机数rand(n);产生n行n列的(0,1)均匀分布的随机数【练习】生成(a,b)上的均匀分布4. 正态分布随机数randn(m,n); 产生m行n列的标准正态分布的随机数【练习】生成N(nu,sigma42)上的正态分布5. 其它分布随机数三、一维随机变量的概率分布1. 离散型随机变量的分布率(1) 0-1分布(2) 均匀分布_ k k n k(3) 二项分布:binopdf(x,n,p),若X ~ B(n, p),则P{X k} C n p (1 p),x=0:9 ;n=9;p=0.3;y= bin opdf(x ,n, p);plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]当n较大时二项分布近似为正态分布x=0:100; n=100;p=0.3;y= bin opdf(x ,n, p);plot(x,y,'b-',x,y,'r*')ke⑷泊松分布:piosspdf(x, lambda),若X ~ (),贝U P{ X k}k!x=0:9; lambda = 3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081,0.0027]k 1⑸几何分布:geopdf (x, p),贝U P{X k} p(1 p)x=0:9;p=0.3y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ] x=0:10;N=20;M=8; n=4;y= hygepdf(x,N,M, n); plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2. 概率密度函数(1)均匀分布:unifpdf(x,a,b) , f (x)其它a=0;b=1;x=a:0.1:b; y= uni fpdf (x,a,b);1 2 厂(x )2 ■厂ex=-10:0.1:12;mu=1;sigma=4;y= no rmpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); % 产生 10000 个正态分布的随机数 d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;%以a 为横轴,求出10000个正态分布的随机数的频率(6)超几何分布:hygepdf(x,N,M,n),则 P{Xk}C k nM CNC N(2)正态分布:normpdf(x,mu,sigma) , f (x)plot(x,y,'b-',a,b,'r.')1 _x⑶指数分布:exppdf(x,mu), f (x)其它x=0:0.1:10;mu=1/2;■ t京■I_ey= exppdf(x,mu); plot(x,y,'b-',x,y,'r*')1n i F⑷2分布:chi2pdf(x,n) , f (x; n) 2n ^( n 2) % e x 0hold onx=0:0.1:30;n=4;y= chi2pdf(x, n);plot(x,y,'b');%blue n=6;y= chi2pdf(x, n);plot(x,y,'r');%red n=8;y=chi2pdf(x ,n );plot(x,y,'c');%cya n n=10;y= chi2pdf(x, n);plot(x,y,'k');%black lege nd(' n=4', 'n=6', 'n=8', 'n=10');n 1((n 1) 2) x2 2⑸t 分布:tpdf(x,n) , f (x; n) ------------------ 1 -J n (n. 2) nhold onx=-10:0.1:10;n=2;y= tpdf(x, n);plot(x,y,'b');%bluen=6;y= tpdf(x, n);plot(x,y,'r');%redn=10;y= tpdf(x ,n );plot(x,y,'c');%cya nn=20;y= tpdf(x, n);plot(x,y,'k');%black lege nd(' n=2', 'n=6', 'n=10', 'n=20');((m山m 门2n2) 2)小2% 2 1 5 % 2(n2 2) n2n2x 0(6) F 分布:fpdf(x,n1,n2) , f (x; n「n2) (E 2)0 x 0hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x, n1, n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x, n1, n2);plot(x,y,'r');%red n1=10; n2=6;y= fpdf(x, n1, n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x, n1,n 2);plot(x,y,'k');%black legend(' n仁2; n2=6', ' n1= 6; n2=10', ' n仁10;n2=6', ' n仁10; n2=10');3.分布函数F(x) P{X x}【例03.01】求正态分布的累积概率值设X ~ N(3,22),求 P{2 X 5}, P{ 4 X 10}, P{ X 2}, P{X 3},14.逆分布函数,临界值y F(x) P{X x} , x F (y) , x称之为临界值【例03.02】求标准正态分布的累积概率值y=0:0.01:1;x=normin v(y,0,1);【例03.03】求2(9)分布的累积概率值hold offy=[0.025,0.975];x=ch i2in v(y,9);n=9;x0=0:0.1:30;y0=chi2pdf(x0, n); plot(x0,y0, 'r'); x1=0:0.1:x(1);y1=chi2pdf(x1, n);x2=x(2):0.1:30;y2=chi2pdf(x2 ,n);hold onfill([x1, x(1)],[y1,0], 'b');fill([x(2),x2],[0,y2], 'b');【练习1.1】二项分布、泊松分布、正态分布(1)对n 10, p 0.2二项分布,画出b(n,p)的分布律点和折线;(2)对np,画出泊松分布()的分布律点和折线;(3)对np, 2叩(1 p),画出正态分布N( , 2)的密度函数曲线;(4)调整n, p,观察折线与曲线的变化趋势。
MATLAB数理统计分析

1. 3 MATLAB的开发环境
1.3.1 MATLAB桌面平台
桌面平台是各桌面组件的展示平台,默认设置情况下 的桌面平台包括4个窗口,即命令窗口(Command Window)、命令历史窗口(Command History)、当前目录 窗口(Current Directory)和工作空间窗口(Workspace)。此 外,MATLAB还有编译窗口、图形窗口和帮助窗口等其他 种类的窗口。
subplot(3,1,1) capaplot(data,[-inf,xalpha1]);axis([-3,3,0,0.45]) subplot(3,1,2) capaplot(data,[xalpha2,inf]);axis([-3,3,0,0.45]) subplot(3,1,3) capaplot(data,[-inf,xalpha3]);axis([-3,3,0,0.45]) hold on capaplot(data,[xalpha4,inf]);axis([-3,3,0,0.45]) hold off
hold off text(-0.5,yy(6)+0.005,'\fontsize{14}95.44%') text(-0.5,yy(5)+0.005,'\fontsize{14}68.26%') text(-0.5,yy(7)+0.005,'\fontsize{14}99.74%') text(-3.2,-0.03,'\fontsize{10}μ-3σ') text(-2.2,-0.03,'\fontsize{10}μ-2σ') text(-1.2,-0.03,'\fontsize{10}μ-σ') text(-0.05,-0.03,'\fontsize{10}μ') text(0.8,-0.03,'\fontsize{10}μ+σ') text(1.8,-0.03,'\fontsize{10}μ+2σ') text(2.8,-0.03,'\fontsize{10}μ+3σ')
数理统计的MATLAB求解

2019/3/2
8
3.1 随机变量及其分布
p2=binopdf(x,100,0.5);plot(x,p2,'*r');title('概率分布图')
2019/3/2
9
3.1 随机变量及其分布
例3.2设X~N(2,0.25) (1) 求概率P{1<X<2.5}; (2)绘制分布函数图象和分布密度图象; (3)画出区间[1.5,1.9]上的分布密度曲线下方区域。 程序:(1)p=normcdf(2.5,2,0.5)- normcdf(1,2,0.5) p = 0.8186 (2) x=0:0.1:4;px=normpdf(x,2,0.5); fx= normcdf(x,2,0.5); plot(x,px,'+b');hold on; plot(x,fx,'*r');legend('正态分布函数','正态分布密度'); (3) specs=[1.5,1.9]; pp=normspec(specs,2,0.5)
2019/3/2
10
3.1 随机变量及其分布
0.8 0.7
Probability Between Limits is 0.26209
0.6
0.5
Density
0.4
0.3
0.2
0.1
0
0
0.5
1
1.5
2 Critical Value
2.5
3
3.5
4
2019/3/2
11
3.2 随机变量函数的分布
2019/3/2
2
常见分布的随机数产生
2019/3/2
使用Matlab进行统计分析和假设检验的步骤

使用Matlab进行统计分析和假设检验的步骤统计分析在科学研究和实际应用中起着重要的作用,可以帮助我们理解和解释数据背后的信息。
而Matlab作为一种强大的数据处理和分析软件,不仅可以进行常见的统计分析,还能进行假设检验。
本文将介绍使用Matlab进行统计分析和假设检验的步骤,具体内容如下:1. 数据准备和导入首先,我们需要准备待分析的数据,并将其导入到Matlab中。
可以使用Matlab提供的函数来读取数据文件,例如`csvread`或`xlsread`函数。
确保数据被正确导入,并查看数据的整体情况和结构。
2. 描述性统计在进行进一步的统计分析之前,我们需要对数据进行描述性统计,以了解数据的基本特征。
Matlab提供了一些常用的描述性统计函数,例如`mean`、`std`和`var`等,可以帮助计算均值、标准差和方差等统计量。
此外,还可以绘制直方图、箱线图和散点图等图形,以便更好地理解数据的分布和关系。
3. 参数估计和假设检验接下来,我们可以使用Matlab进行参数估计和假设检验,以验证对数据的猜测和假设。
参数估计可以通过最大似然估计或贝叶斯估计来实现,并使用Matlab 提供的相应函数进行计算。
在假设检验方面,Matlab还提供了一些常用的函数,例如`ttest`、`anova`和`chi2test`等,可以用于检验两个或多个总体间的均值差异、方差差异或相关性等。
在使用这些函数进行假设检验时,需要指定显著性水平(通常是0.05),以决定是否拒绝原假设。
4. 非参数统计分析除了参数估计和假设检验外,Matlab还支持非参数统计分析方法。
非参数方法不依赖于总体分布的具体形式,因此更加灵活和广泛适用。
在Matlab中,可以使用`ranksum`、`kstest`和`signrank`等函数来进行非参数假设检验,例如Wilcoxon秩和检验和Kolmogorov-Smirnov检验等。
5. 数据可视化最后,在完成统计分析和假设检验后,我们可以使用Matlab提供的数据可视化工具来展示分析结果。
利用Matlab进行数据分析与统计方法详解

利用Matlab进行数据分析与统计方法详解数据分析和统计方法在现代科学、工程和商业领域中是非常重要的工具。
而Matlab作为一种强大的计算软件和编程语言,提供了丰富的功能和工具,可以帮助我们进行数据分析和统计。
一、Matlab数据分析工具介绍Matlab提供了许多数据分析工具,包括数据可视化、数据处理、统计分析等。
其中,数据可视化是数据分析中重要的一环,可以用于展示数据的分布、趋势和关系。
Matlab中的绘图函数可以绘制各种类型的图形,如折线图、散点图、柱状图等。
我们可以利用这些图形来直观地理解数据并发现潜在的模式。
二、常用的数据处理方法在进行数据分析之前,我们通常需要对数据进行预处理,以去除噪声、填补缺失值和标准化数据等。
Matlab提供了丰富的函数和工具来处理这些问题。
例如,可以使用滤波函数对信号进行平滑处理,使用插值函数填补缺失值,并使用标准化函数将数据转化为标准分布。
三、基本的统计分析方法在进行统计分析时,我们常常需要计算各种统计量,如均值、方差、标准差等。
Matlab提供了一系列统计函数,如mean、var和std等,可以轻松计算这些统计量。
此外,Matlab还提供了假设检验、方差分析、回归分析等高级统计方法的函数,方便我们进行进一步的研究。
四、数据挖掘和机器学习方法数据挖掘和机器学习是数据分析的前沿领域,能够从大量的数据中发现隐藏的模式和规律。
Matlab作为一种强大的计算工具,提供了丰富的数据挖掘和机器学习函数。
例如,可以利用聚类分析函数对数据进行聚类,使用分类函数进行分类,还可以使用神经网络函数构建和训练神经网络模型。
五、案例分析:利用Matlab进行股票市场分析为了更好地理解Matlab在数据分析和统计方法中的应用,我们以股票市场分析为例进行讲解。
股票市场是一个涉及大量数据和复杂关系的系统,利用Matlab可以对其进行深入分析。
首先,我们可以利用Matlab的数据导入和处理函数,将股票市场的历史数据导入到Matlab中,并对数据进行预处理,如去除异常值和填补缺失值。
数理统计方法的Matlab实现(6.5版)

数理统计的Matlab实现
[H,SIG,CI]=ttest2 (x, y, ,tail) 对两个正态总 体的均值作检验 若tail=0, 表示 H 1 : 1 2 若tail=1, 表示 H 1 : 1 2 若tail=-1,表示 H 1 : 1 2 结论:H=0,表示接受原假设 H 0 : 1 2 H=1,表示拒绝原假设 H 0 : 1 2 SIG为犯错误的概率,CI为均值差的置信区间。
因素A 因素B B1 B2 B3
A1 95 93 85 86 72 76 A2 A3 A4
97 96 87 89 90 91 89 90 84 87 92 90 75 73 85 86 88 89
AB2=[95 93 97 96 87 89 90 91;85 86 89 90 84 87 92 90;72 76 75 73 85 86 88 89 ] anova2(AB2',2)
数理统计的Matlab实现
例2自动包装机包装出的产品服从正态分 布 N (0.5 , 0.0152 ) ,从中抽取出9个样品,它们的 重量是 0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512 问包装机的工作是否正常? ( =0.05) x=[0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512]; [H,SIG]=ztest(x, 0.5, 0.015, 0.05,0)
数理统计的Matlab实现
其中 y:y的 n 1 数据向量 x:x的数据 n m 矩阵 b: b0 , b1 ,, bm 的估计值 bint:b的置信区间 r:残差 rint :r的置信区间 stats:第一个值是回归方程的置信度,第二值是F统 计量的值,第三值小说明所建的回归方程有意义。
Matlab在数理统计中的运用

Matlab在数理统计中的运用摘要:概率论与数理统计是现代数学的重要分支,近年来随着计算机的普及,概率论在经济,管理,金融,保险,生物,医学等方面都发挥着越来越大的作用。
使得概率统计成为今天各类各专业大学生最重要的数学必修课之一。
然而,传统的概率统计教学过于偏重理论的阐述、公式的推导、繁琐的初等运算;同时,缺乏与计算机的结合,给学生的学习带来很多困难。
本文介绍概率统计中的主要问题在Matlab中的实现,让我们从繁琐的计算中解放出来,把更多的时间和精力用于基本概念和基本理论的思考和方法的创新,从而提高教师的教学效率和学生的学习效率。
关键词:区间估计,matlab,概率统计一、常用概率密度的计算Matlab中计算某种概率分布在指定点的概率密度的函数,都以代表特定概率分布的字母开头,以pdf (probability density function)结尾,例如:unidpdf(X, N):计算1到N上的离散均匀分布在X每一点处的概率密度;poisspdf(X, Lambda):计算参数为Lambda的泊松分布在X每一点处的概率密度;exppdf(X, mu):计算参数为mu的指数分布在X每一点处的概率密度;normpdf(X, mu, sigma):计算参数为mu, sigma的正态分布在X每一点处的概率密度。
其他如连续均匀分布、二项分布、超几何分布等也都有相应的计算概率密度的函数。
除计算概率密度的函数外,Matlab中还有计算累积概率密度、逆概率分布函数及产生服从某分布的随机数的函数,分别以cdf,inv和rnd结尾。
下面我们来用一个具体的例子说明一下:例1:计算正态分布N(0,1)的随机变量X在点0.6578的密度函数值。
解:>> pdf('norm',0.6578,0,1)ans =0.3213例2:自由度为8的卡方分布,在点2.18处的密度函数值。
解:>> pdf('chi2',2.18,8)ans = 0.0363二、随机变量数字特征的计算(一)数学期望与方差对离散型随机变量,可利用Matlab矩阵运算计算出其数学期望和方差;而对于连续型随机变量,则可以利用Matlab符号运行计算。
概率论与数理统计的MATLAB实现讲稿

第9章 概率论与数理统计的MATLAB 实现MATLAB 总包提供了一些进行数据统计分析的函数,但不完整。
利用MATLAB 统计工具箱,可以进行基本概率和数理统计分析,以及进行比较复杂的多元统计分析。
本章主要针对大学本科的概率统计课程介绍工具箱的部分功能。
9.1 随机变量及其分布利用统计工具箱提供的函数,可以比较方便地计算随机变量的分布律(概率密度函数)和分布函数。
9.1.1 离散型随机变量及其分布律如果随机变量全部可能取到的不相同的值是有限个或可列个无限多个,则称为离散型随机变量。
MATLAB 提供的计算常见离散型随机变量分布律的函数及调用格式: 函数调用格式(对应的分布) 分布律y=binopdf(x,n,p)(二项分布) )()1(),|(),,1,0(x I p p x n p n x f n xn x --⎪⎪⎭⎫ ⎝⎛=y=geopdf(x,p)(几何分布) xp p p x f )1()|(-= ),1,0( =xy=hygepdf(x,M,K,n)(超几何分布) ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=n M x n K M x K n K M x f ),,|(y=poisspdf(x,lambda)(泊松分布) λλλ-=e x x f x !)|(),1,0( =x y=unidpdf(x,n)(离散均匀分布) NN x f 1)|(=9.1.2 连续型随机变量及其概率密度对于随机变量X 的分布函数)(x F ,如果存在非负函数)(x f ,使对于任意实数x 有⎰∞-=x dt t f x F )()(则称X 为连续型随机变量,其中函数)(x f 称为X 的概率密度函数。
MA TLAB 提供的计算常见连续型随机变量分布概率密度函数的函数及调用格式:函数调用格式(对应的分布) 概率密度函数y=betapdf(x,a,b)(β分布) )10()1(),(1),|(11<<-=--x x x b a B b a x f b ay=chi2pdf(x,v)(卡方分布) )2(2)|(2212v exv x f v x v Γ=--)0(≥xy=exppdf(x,mu)(指数分布) μμμxe xf -=1)|()0(≥xy=fpdf(x,v1,v2)(F 分布) 2211222121212121111)2()2()2(),|(v v v v v x v x vv v v v v v v x f +-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛ΓΓ+Γ= y=gampdf(x,a,b)(伽马分布) b xa a e x ab b a x f --Γ=1)(1),|()0(≥xy=normpdf(x,mu,sigma)(正态分布) 22)(21),|(σμπσσμ--=x ex fy=lognpdf(x,mu,sigma)(对数正态分布) 22)(ln 21),|(σμπσσμ--=x ex x fy=raylpdf(x,b)(瑞利分布) 222)|(b x e b x b x f -=y=tpdf(x,v)(学生氏t 分布) 2121)2()21()|(+-⎪⎪⎭⎫ ⎝⎛+Γ+Γ=v v x v v v v x f πy=unifpdf(x,a,b)(连续均匀分布) )(1),|(],[x I ab b a x f b a -=y=weibpdf(x,a,b)(威布尔分布) )(),|(),0(1x I eabx b a x f bax b ∞--= 比如,用normpdf 函数计算正态概率密度函数值。
MATLAB教程第八章 概率和数理统计

t0 t0
某人到此办事,若等待时间超过15分钟,他就离 去。设此人一个月要去该处10次,试求: (1)恰好有两次有两次离去的概率; (4)离去的次数占多数的概率。
解:首先求任一次离去的概率,
解: p1=Hygepdf(1,500,50,10) p1 = 0.3913 p2=Hygepdf(0,500,50,10)+Hygepdf(1,500,50,10) p2 = 0.7365 p3=1-Hygepdf(0,500,50,10) p3 = 0.6548
例5:计算指数密度函数值
解: y=exppdf(5,1:5) y= 0.0067 0.0410 0.0630 0.0716 0.0736 y=exppdf(1:5,1:5) y= 0.3679 0.1839 0.1226 0.0920 0.0736
分布
例1 :某单位有内线电话300部,假设任意一时刻每部电话打外线电
话的概率为0.01,求在某一时刻恰有4部电话打外线的概率。在某一时 刻打外线电话的最可能部数是多少?
解:设X表示某一时刻该单位打外线电话的电话部数, 则X的统计规律可用二项分布来描述,X~B(300,0.01)。 记A=“某一时刻恰有4部电话打外线”,则所求概率为 p=p(A)=p(X=4)。 p=binopdf(4,300,0.01) p = 0.1689 计算某一时刻打外线电话的最可能部数 y=binopdf([0:300],300,0.01); [pp,m]=max(y) pp = 0.2252 m= 4
概率与分位数的关系 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 2.1171 2.5 p=0.9
matlab在数理统计中的应用1

matlab在数理统计中的应用1一、直方图与经验分布函数图的绘制hist(A,n) ——对矩阵A按列作统计频数直方图, n为条形图的条数hist(A,x0) ——对矩阵A按列作以向量x0为划分区间中点的频数直方图ni=hist(A,n) 或ni=hist(A,x0) ——对矩阵A按列得各划分区间内的统计频数注意: 当A为向量时, 上述所有命令直接作用在向量上, 而不是列优先.bar(x,y) ——绘制分别以x和y为横纵坐标的二维条形图cdfplot(x) ——绘制样本x的经验分布函数图[Fn,x0]=ecdf(x) ——得到样本x的经验分布函数值Fn, 当x中有m个不同的数(记为向量x0) 时, 则Fn的个数为m+1个例如:>> x = [6 4 5 3 6 8 6 7 3 4];>> [Fn,x0]=ecdf(x)Fn = 0 0.2000 0.4000 0.5000 0.8000 0.9000 1.0000x0 = 3 3 4 5 6 7 8>>cdfplot(x)【例1-1】在齿轮加工中, 齿轮的径向综合误差是个随机变量, 今对200件同样的齿轮进行测量, 测得的数值(mm) 如下, 求作的频率密度直方图, 并作出的经验分布函数图形.16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 2420 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 2118 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 2813 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 1314 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 1619 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 2819 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 1818 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 3308 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 2417 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18·编写函数文件example1_6_1.m:function [ni,frequency]=example1_6_1(Y,k)%Y为试验数据%k为分组参数n=length(Y);m=min(Y);M=max(Y);%(1)下面作频率密度直方图delta=(M-m)/k;x=m:delta:M;ni=hist(Y,x);frequency=ni/n;density=frequency/delta;bar(x,density) %作频率密度直方图pause%(2)下面作经验分布函数图·编写命令文件example1_6_2.m:F=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 24....20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21....18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28....13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13....14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16....19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28....19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18....18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33....08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24....17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18];[ni,frequency]=example1_6_1(F,9)·运行命令文件example1_6_2.m:>> example1_6_2ni = 5 16 21 34 44 25 23 22 4 6frequency = 0.0250 0.0800 0.1050 0.1700 0.2200 0.1250 0.1150 0.1100 0.0200 0.0300图1-1(a) 图1-1(b)二、常见的概率分布表1.1概率分布分类表三、MATLAB为常见分布提供的五类函数1) 概率密度函数(pdf);2) (累积)分布函数(cdf);3) 逆(累积)分布函数(icdf);4) 随机数发生器(random);5) 均值和方差(stat).1、概率密度函数注意: Y=normpdf (X, MU, SIGMA)的SIGMA是指标准差, 而非.【例1-2】绘制标准正态分布的概率密度图.y=normpdf(x,0,1);plot(x,y)title('N(0,1)的概率密度曲线图')图1-22、累积分布函数表1.3累积分布函数(cdf)常见的概率分布(matlab作图)一、常见的概率分布表1.1概率分布分类表二、MATLAB为常见分布提供的五类函数1) 概率密度函数(pdf);2) (累积)分布函数(cdf);3) 逆(累积)分布函数(icdf);4) 随机数发生器(random);5) 均值和方差(stat).1、概率密度函数表1.2概率密度函数(pdf)注意【例1-2】绘制标准正态分布的概率密度图.x=-4:0.1:4;y=normpdf(x,0,1);title('N(0,1)的概率密度曲线图')图1-22、累积分布函数表1.3累积分布函数(cdf)【例1-3】求服从标准正态分布的随机变量落在区间[-2, 2]上的概率.>> P=normcdf ([-2, 2])ans = 0.0228 0.9772>>P(2)-P(1)ans = 0.95453、逆累积分布函数(用于求分位点)【例1-4】(书P22例1.13) 求下列分位数:(i) ; (ii) ; (iii) ; (iv) .>> u_alpha=norminv(0.9,0,1)u_alpha = 1.2816>> t_alpha=tinv(0.25,4)t_alpha = -0.7407>> F_alpha=finv(0.1,14,10)F_alpha = 0.4772>> X2_alpha=chi2inv(0.025,50)X2_alpha = 32.35744、随机数发生函数表1.5随机数发生函数(random)5、均值和方差表1.6常见分布的均值和方差函数(stat)注意:三、常用的统计量表1.7常用统计量说明:(1) y=var(X) ——计算X中数据的方差. .y=var(X, 1) —— , 得到样本的二阶中心矩(转动惯量).(2) C=cov(X) ——返回一个协方差矩阵, 其中输入矩阵X的每列元素代表着一个随机变量的观测值. 如果X为n×m 的矩阵, 则C为m×m的矩阵.(3) var(X)=diag(cov(X)), std(X)=sqrt(diag(cov(X))).参数估计(matlab)参数估计包含两种常用方式: 点估计和区间估计.Matlab统计工具箱给出了常用概率分布中参数的点估计(采用最大似然估计法) 与区间估计, 另外还提供了部分分布的对数似然函数的计算功能.由于点估计中的矩估计法的实质是求与未知参数相应的样本的各阶矩,统计工具箱提供了常用的求矩函数(见第一章), 读者可根据需要选择合适的矩函数进行点估计.表2.1统计工具箱中的参数估计函数(fit / like)说明: 调用格式只罗列了其中的一种. 需另外说明的是:(1) unifit和normfit的格式与其它函数均不同, 此二者要求左边的输出变量必须将参数或分别列出.(2) binofit (x,n,alpha)根据试验成功的次数x和总的试验次数n, 对中的p进行最大似然估计, 同时返回置信度为100(1-alpha)%的置信区间pci.【例2-1】(书P692.3) 使用一测量仪器对同一值进行了12次独立测量, 其结果为(单位: mm) 232.50, 232.48, 232.15, 232.52, 232.53, 232.30, 232.48, 232.05, 232.45, 232.60, 232.47, 232.30 试用矩法估计测量的真值和方差(设仪器无系统误差).·编写命令文件exercise2_3.m:%P66_2.3 mu与sigma^2的矩估计x=[232.50, 232.48, 232.15, 232.52, 232.53, 232.30,...232.48, 232.05, 232.45, 232.60, 232.47, 232.30];mu_ju=mean(x)sigma2_ju=var(x,1)·运行命令文件exercise2_3.m:>> exercise2_3mu_ju = 232.4025sigma2_ju = 0.0255【例2-2】(书P692.22) 随机地从一批零件中抽取16个, 测得长度(单位: cm) 为:2.14, 2.10, 2.13, 2.15, 2.13, 2.12, 2.13, 2.10, 2.15, 2.12, 2.14, 2.10, 2.13, 2.11, 2.14, 2.11设零件长度的分布为正态的, 试求总体均值的90%的置信区间:(1)若(cm); (2) 若未知.(1)·编写函数文件zestimate.m:%P69_2.22(1)sigma已知时mu的区间估计function muci=zestimate(x,sigma,alpha)n=length(x);xhat=mean(x);u_alpha=norminv(1-alpha/2,0,1);delta1=sigma/sqrt(n)*u_alpha;muci=[xhat-delta1,xhat+delta1];·调用函数文件zestimate.m:>> x=[2.14, 2.10, 2.13, 2.15, 2.13, 2.12, 2.13, 2.10, 2.15, 2.12, 2.14, 2.10, 2.13, 2.11, 2.14, 2.11];>>sigma=0.01;>>alpha=0.1;>>muci=zestimate(x,sigma,alpha)muci = 2.1209 2.1291(2)·编写命令文件exercise2_22_2.m:%P69_2.22(1)sigma未知时mu的区间估计x=[2.14, 2.10, 2.13, 2.15, 2.13, 2.12, 2.13, 2.10, 2.15, 2.12, 2.14, 2.10, 2.13, 2.11, 2.14, 2.11];alpha=0.1;[muhat,sigmahat,muci,sigmaci]= normfit(x,alpha);muci·运行命令文件exercise2_22_2.m:>> exercise2_22_2muci = 2.1175 2.1325【例2-3】(书P66例2.31) 对一批产品, 欲通过抽样检查其合格率. 若产品不合格率在5%以下, 则该批产品可出厂. 检验时要求结果具有0.95的置信水平. 今抽取产品100件, 发现不合格品有4件, 问这批产品能否出厂?>> [phat,pci]=binofit(4,100,0.05)phat = 0.0400pci = 0.0110 0.0993由于置信区间的上限超出了规定指标(不合格率在5%以下), 因此不能出厂.假设检验1假设检验分为两种: 参数假设检验与分布假设检验.一、正态总体的参数假设检验表3.1的说明:对一个正态总体, 抽取样本;对两个正态总体, , 且X与Y独立,分别抽取样本与.表3.1正态总体的参数假设检验二、非参数假设检验表3.2非参数假设检验三、统计工具箱中的假设检验表3.3统计工具箱中的假设检验(test / rank)1、jbtest, lillietest与kstest的比较:(1) jbtest与lillietest均是检验样本是否来自正态分布, 而kstest可检验样本来自任意指定的分布;(2) jbtest是利用偏度峰度来检验, 适用于大样本; 而对于小样本, 则用lillietest来检验;(3) lillietest与kstest的检验原理均是用x的经验分布函数与一个有相同均值与方差的正态分布的分布函数进行比较, 不同的是lisllietest中正态分布的参数是由x估计得来, 而kstest中正态分布的参数是事先指定的.2、kstest2对应于斯米尔诺夫检验.3、命令说明:(1) [h,sig,ci,zval] = ztest(x,mu0,sigma,alpha,tail) 对已知方差的单个总体均值进行Z检验. 进行显著性水平为的Z假设检验, 以检验标准差为的正态分布样本的均值与的关系. 并可通过指定tail的值来控制备择假设的类型. tail 的取值及表示意义如下:tail=0 备择假设为 (缺省值);tail=1备择假设为;tail= -1备择假设为. (原假设则为)·输出变量含义:h——如果h=0, 则接受; 如果h=1, 则拒绝而接受备择假设;sig——Z的观察值在下较大或统计意义上较大的概率值;ci——方差未知时均值的的置信区间.zval——Z统计量的观测值.·单边检验对应单侧区间估计.(2) [h,sig,ci,tval] = ttest(x,mu0,alpha,tail) 格式调用中无“tval”这个输出变量, 但可加上此项.tval——包含两个结果: tstat表示t统计量的值; df表示t分布的自由度.(3) [h,p,jbstat,cv] = jbtest(x,alpha) 对“单个总体服从正态分布(未指定均值和方差)”假设进行显著水平为的Jarque-Bera检验. 此检验基于x的偏度与峰度. 对于真实的正态分布, 样本偏度应接近于0, 样本峰度应接近于3. Jarque-Bera检验通过统计量来判定样本偏度和峰度是否与它们的期望值显著不同.·输出变量含义:h——如果h=0, 则接受“ : 认为x来自正态总体”; 如果h=1, 则接受备择假设“ : 认为x不是来自正态总体”; p——检验的概率p-值;jbstat——检验统计量的值;cv——判断是否拒绝原假设的关键值.(4) [h,p,ksstat,cv] = kstest(x,cdf,alpha,tail) 对“x的总体服从由两列矩阵cdf指定的分布G”假设进行显著水平为的Kolmogorov-Smirnov检验. 矩阵cdf的第一列包含可能的x值, 第二列包含相应的理论累积分布函数值G(x0). 在可能的情况下, 应定义cdf使每一列包含x中的值. 如果cdf=[ ], kstest( )将使用标准正态分布.(5) [h,p,ksstat] = kstest2(x,cdf,alpha,tail) 对“两个样本来自同一连续分布”假设进行显著水平为的Kolmogorov-Smirnov检验. 对于大容量的样本来说, p-值将很精确, 一般来说, 当样本容量N1和N2满足时, p-值即可认为是精确的.(6) normplot(x) 绘出x中数据的正态检验概率图. 如果x是一个矩阵, 则对每一列绘出一条线. 图中样本数据用符号…+‟来表示, 叠加在数据上的实线是数据的第一个与第三个四分位点之间的连线(为样本顺序统计量的鲁棒线性拟合). 这条线延伸到样本数据的两端, 以便估计数据的线性度. 如果数据是来自一个正态分布, 则…+‟线近似地在一直线上. 一般地, 中间的点离直线位置的偏差不能过大, 两头的点的偏差可以允许大一些. 当中间的点离直线位置偏差太大时, 就认为x来自其它分布.(7) qqplot(x,y) 绘出两样本的分位数-分位数图. 图中样本数据用符号…+‟来表示, 叠加在数据上的实线是各分布的第一个与第三个四分位点之间的连线(为两个样本顺序统计量的鲁棒线性拟合). 这条线延伸到样本数据的两端以便估计数据的线性度. 如果两个样本来源于同一个分布, 则…+‟线近似地在一直线上.qqplot(x) 绘出样本x的分位数-正态分布的理论分位数图. 如x为正态分布, 则…+‟线近似地在一直线上.【例3-1】(例3.4) 一台包装机装洗衣粉, 额定标准重量为500g, 根据以往经验, 包装机的实际装袋重量服从正态分布, 其中g, 为检验包装机工作是否正常, 随机抽取9袋, 称得洗衣粉净重数据如下(单位: g):497 506 518 524 488 517 510 515 516若取显著性水平, 问这包装机工作是否正常?>> x=[497,506,518,524,488,517,510,515,516];>> [h,sig,ci,zval]=ztest(x,500,15,0.01,0)h = 0 %接受sig = 0.0432 % 为真条件下P( )的值ci = 497.2320 522.9903 % 未知时的置信水平为0.95的双侧置信区间zval = 2.0222 %Z统计量的值.所以认为包装机工作正常.【例3-2】(例3.5) 某部门对当前市场的价格情况进行调查. 以鸡蛋为例, 所抽查的全省20个集市上, 售价分别为(单位: 元/500克)3.05, 3.31, 3.34, 3.82, 3.30, 3.16, 3.84, 3.10, 3.90, 3.18,3.88, 3.22, 3.28, 3.34, 3.62, 3.28, 3.30, 3.22, 3.54, 3.30.已知往年的平均售价一直稳定在3.25元/500克左右, 在显著性水平下, 能否认为全省当前的鸡蛋售价明显高于往年?>> x=[3.05,3.31,3.34,3.82,3.30,3.16,3.84,3.10,3.90,3.18,...3.88,3.22,3.28,3.34,3.62,3.28,3.30,3.22,3.54,3.30];>> [h,sig,ci,tval]=ttest(x,3.25,0.025,1)h = 1sig = 0.0114ci = 3.2731 Inftval = tstat: 2.4763 df: 19所以认为全省当前的鸡蛋售价明显高于往年.假设检验2【例3-3】(例3.6) 某工厂生产某种电器材料. 要检验原来使用的材料与一种新研制的材料的疲劳寿命有无显著性差异, 各取若干样品, 做疲劳寿命试验, 所得数据如下(单位: 小时) :原材料: 40, 110, 150, 65, 90, 210, 270,新材料: 60, 150, 220, 310, 350, 250, 450, 110, 175.一般认为, 材料的疲劳寿命服从对数正态分布, 并可以假定原材料疲劳寿命的对数与新材料疲劳寿命的对数有相同的方差, 即可设, . 在显著性水平下, 能否认为两种材料的疲劳寿命没有显著性差异?>> x=[40,110,150,65,90,210,270];>> y=[60,150,220,310,350,250,450,110,175];>> [h,sig,ci,tval]=ttest2(log(x),log(y),0.05,0)h = 0sig = 0.1001ci = -1.2655 0.1244tval = tstat: -1.7609 df: 14所以认为两种材料的疲劳寿命没有显著差异.【例3-4】(例3.18) 对一台设备进行寿命试验, 记录10次无故障工作时间, 并从小到大排列得420, 500, 920, 1380, 1510, 1650, 1760, 2100,2300, 2350问此设备的无故障工作时间X的分布是否服从的指数分布( )?>> x=[420, 500, 920, 1380, 1510, 1650, 1760, 2100,2300, 2350];>> [h,p,ksstat,cv]=kstest(x,[x',expcdf(x',1500)],0.05,0)h = 0p = 0.2700ksstat = 0.3015cv = 0.4093所以认为此设备的无故障工作时间X服从的指数分布.【例3-5】(例3.20) 在20天内, 从维尼纶正常生产时生产报表上看到的维尼纶纤度(表示纤维粗细程度的一个量) 的情况, 有如下100个数据:1.36, 1.49, 1.43, 1.41, 1.37, 1.40, 1.32, 1.42, 1.47, 1.391.41, 1.36, 1.40, 1.34, 1.42, 1.42, 1.45, 1.35, 1.42, 1.391.44, 1.42, 1.39, 1.42, 1.42, 1.30, 1.34, 1.42, 1.37, 1.361.37, 1.34, 1.37, 1.37, 1.44, 1.45, 1.32, 1.48, 1.40, 1.451.39, 1.46, 1.39, 1.53, 1.36, 1.48, 1.40, 1.39, 1.38, 1.401.36, 1.45, 1.50, 1.43, 1.38, 1.43, 1.41, 1.48, 1.39, 1.451.37, 1.37, 1.39, 1.45, 1.31, 1.41, 1.44, 1.44, 1.42, 1.471.35, 1.36, 1.39, 1.40, 1.38, 1.35, 1.42, 1.43, 1.42, 1.421.42, 1.40, 1.41, 1.37, 1.46, 1.36, 1.37, 1.27, 1.37, 1.381.42, 1.34, 1.43, 1.42, 1.41, 1.41, 1.44, 1.48, 1.55, 1.37要求在显著性水平下检验假设其中F(x)为纤度的分布函数, 为标准正态分布函数.>> x=[1.36, 1.49, 1.43, 1.41, 1.37, 1.40, 1.32, 1.42, 1.47, 1.39...1.41, 1.36, 1.40, 1.34, 1.42, 1.42, 1.45, 1.35, 1.42, 1.39...1.44, 1.42, 1.39, 1.42, 1.42, 1.30, 1.34, 1.42, 1.37, 1.36...1.37, 1.34, 1.37, 1.37, 1.44, 1.45, 1.32, 1.48, 1.40, 1.45...1.39, 1.46, 1.39, 1.53, 1.36, 1.48, 1.40, 1.39, 1.38, 1.40...1.36, 1.45, 1.50, 1.43, 1.38, 1.43, 1.41, 1.48, 1.39, 1.45...1.37, 1.37, 1.39, 1.45, 1.31, 1.41, 1.44, 1.44, 1.42, 1.47...1.35, 1.36, 1.39, 1.40, 1.38, 1.35, 1.42, 1.43, 1.42, 1.42...1.42, 1.40, 1.41, 1.37, 1.46, 1.36, 1.37, 1.27, 1.37, 1.38...1.42, 1.34, 1.43, 1.42, 1.41, 1.41, 1.44, 1.48, 1.55, 1.37];%法一(偏度峰度检验)>> [h,p,jbstat,cv]= jbtest(x,0.01)h = 0p = 0.4432jbstat = 1.6276cv = 9.2103%法二(Lilliefors检验)>> [h,p,lstat,cv]= lillietest(x,0.01)h = 0p = 0.0467lstat = 0.0904cv = 0.1103所以不论是偏度峰度检验, 还是Lilliefors检验, 均认为维尼纶纤度服从正态分布.【例3-6】(例3.23) 抽查用克矽平治疗的矽肺患者10名, 得他们治疗前后血红蛋白的差(g%)如下: 2.7, -1.2, -1.0, 0, 0.7, 2.0, 3.7, -0.6, 0.8, -0.3试检验治疗前后血红蛋白的差是否服从正态分布( ).>> x=[2.7,-1.2,-1.0,0,0.7,.0,.7,-0.6,.8,-0.3];>> [h,p,lstat,cv]= lillietest(x,0.05) %本题采用的是Lilliefors检验, 而非书上的W检验.h = 0p = NaNlstat = 0.1915cv = 0.2580所以认为治疗前后血红蛋白的差服从正态分布.【例3-7】(例3.25) 以下是两个地区所种小麦的蛋白质含量检验数据:地区1: 12.6, 13.4, 11.9, 12.8, 13.0地区2: 13.1, 13.4, 12.8, 13.5, 13.3, 12.7, 12.4问两地区小麦的蛋白质含量有无显著性差异( )?>> x=[12.6,13.4,11.9,12.8,13.0];>> y=[13.1,13.4,12.8,13.5,13.3,12.7,12.4];>> [p,h,stats] = ranksum(x,y,0.05) %秩和检验p = 0.4066h = 0stats = ranksum: 27>> h=kstest2(x,y,0.05) %斯米尔乐夫检验h = 0所以不论是秩和检验还是斯米尔乐夫检验, 均认为两地区小麦的蛋白质含量无显著差异.【例(注: 这批数据实际上是来自参数为100的指数分布)·编写命令文件addexample3_1.m:%几种正态分布检验方法的比较x=[0.05,4.29,5.22,6.10,6.93,6.96,11.11,11.78,14.18,16.12...16.53,19.43,26.15,26.59,28.06,35.40,39.64,40.63,51.43,56.79...57.62,64.99,69.63,78.73,98.07,98.11,98.84,114.16,123.62,124.20...125.12,133.10,138.15,145.12,155.12,156.41,161.02,203.27,203.30,210.44...14.51,228.69,234.95,251.246,260.79,272.85,276.26,300.59,301.50,306.54];normplot(x)pauseqqplot(x)[h_jbtest,p,jbstat,cv]=jbtest(x,0.05) %偏度峰度检验[h_lillitest,p,lstat,cv]= lillietest(x,0.05)%Lillifors检验·运行命令文件addexample3_1.m:>> addexample3_1h_jbtest = 0p = 0.0742jbstat = 5.2014cv = 5.9915h_lillitest = 1p = 0.0288lstat = 0.1416cv = 0.1253所以由正态概率纸、qq图、偏度峰度检验及Lilliefors检验均认为这批数据不是来自正态分布.回归分析1一、线性回归模型线性模型是指因变量与一个或多个自变量之间的关系可由式(6.1)形式表示:(4.1) 其中,y——表示n×1的因变量观测值向量;X——表示n×(p+1)的由自变量决定的设计矩阵;——表示(p+1)×1的参数向量;——表示n×1的随机干扰向量, 相互独立且通常具有正态分布.二、回归分析中研究的主要问题:1) 确定因变量y与自变量间的定量关系表达式. 这种表达式称为回归方程.2) 对求得的回归方程的可信度进行检验.3) 判断自变量对y有无影响.4) 利用所求得的回归方程进行预测和控制.Matlab的统计工具箱提供了几种常用的回归分析方法.三、分析函数(1) [b,bint,r,rint,stats] = regress(y,X,alpha) 通过求解线性模型(4.1), 返回y关于X的最小二乘估计. 其中y——表示n×1的观测向量;X——表示n×(p+1)的设计矩阵;b——表示的估计;bint——表示的置信水平为的估计区间, 是(p+1)×2的矩阵;r——表示残差, 是n×1的矩阵;rint——表示残差的置信水平为的估计区间, 是n×2的矩阵;stats——包含回归中的(复) 相关系数的平方R2统计量和F统计量以及概率p.(2) Malab提供了多项式拟合(polyfit)、多项式评估(polyval)等函数.p=polyfit(x,y,n) 在最小二乘意义下, 将向量x,y进行n次多项式拟合, 并返回多项式的系数p.y_fit=polyval(p,x) 返回给定系数p的多项式在x处的预测值y_fit.★p的第一个元素为的系数, 最后一个元素为常数项, 这与regress命令中的输出b的顺序刚好相反.【例4-1】(书P例4.1-4.4) 为研究温度对某个化学过程的生产量的影响, 收集到如下数据(规范化形式):(1)利用最小二乘法求y对x的回归方程, 作拟合曲线图与观测数据的散点图;(2)在正态分布下利用F检验法检验回归方程效果是否显著( );(3)求出回归系数的置信区间( );(4)取, 求的预测值与置信水平为的预测区间·编写命令文件example4_1.m:%书P138-159例4.1-4.4alpha=0.05;x=[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]';n=length(x);X=[ones(n,1),x];y=[1, 5, 4, 7, 10, 8, 9, 13, 14, 13, 18]';plot(x,y,'b.')hold on[b,bint,r,rint,stats] = regress(y,X,alpha); %利用最小二乘法进行线性回归beta_hat=b %第(1)小题y_hat=X*beta_hat;plot(x,y_hat,'r')legend('散点图','回归直线')hold offF_equation=stats(2:3) %第(2)小题beta_ci=bint %第(3)小题x0=3; %第(4)小题,y0的点估计y0_hat=[1,x0]*beta_hatQe=r'*r; %第(4)小题,y0的区间估计sigma_hat=sqrt(Qe/(n-2));t_alpha=tinv(1-alpha/2,n-2);Lxx=(x-mean(x))'*(x-mean(x));delta=sigma_hat*t_alpha*sqrt(1+1/n+(x0-mean(x))^2/Lxx);y0_ci=[y0_hat-delta,y0_hat+delta]·运行命令文件example4_1.m:>> example4_1回归分析2beta_hat = 9.2727 1.4364F_equation = 96.1798 0.0000beta_ci = 8.2250 10.32041.1050 1.7677y0_hat = 13.5818y0_ci = 9.8188 17.3449所以, 有:(1)回归方程为, 回归直线与观测数据散点图见图4-1;(2)F检验法表明在显著性水平拒绝原假设, 说明回归方程显著;(3) 的置信区间为[8.225, 10.3204], 的置信区间为[1.1050, 1.7677];(4)当, , 的置信水平为的预测区间为[9.8188, 17.3449].【例4-2】(例4.5-4.7) 在平炉炼钢中, 由于矿石与炉气的氧化作用, 铁水的总含碳量在不断降低, 一炉钢在冶炼初期总的去碳量y与所加的两种矿石的量及熔化时间有关. 经实测某号平炉的49组数据如下表4-6所列:设y与之间有线性关系(1)求y与的回归方程;(2)检验回归方程和回归系数的显著性. 如有不显著的变量, 请剔除之并求剔除不显著的变量之后的回归方程( );(3)在不剔除不显著变量的前提下, 求回归系数的置信区间( );(4)在不剔除不显著变量的前提下, 若取, 求的置信水平为95%的预测区间.·编写命令文件example4_5.m:%A为观测数据阵, 共49行4列, 此处省略.x=A(:,1:3);[n,p]=size(x);X=[ones(n,1),x];Y=A(:,4);alpha_1=0.01;p0=p; %用于记录删除某个自变量后剩余的自变量个数for i=1:p[b,bint,r,rint,stats]=regress(Y,X,alpha_1); %第(1)小题--多元线性回归beta_hat=b %beta的LS估计F_equation=stats(2:3) %第(2)小题:回归方程的显著性检验Qe=r'*r; %回归系数的显著性检验C=inv(X'*X);Cii=diag(C);F_coeff=(beta_hat(2:p0+1).^2./Cii(2:p0+1))./(Qe/(n-p0-1))F0=Finv(1-alpha_1,1,n-p0-1)Hi=F_coeff>F0 %Hi=0,接受原假设H0i=0k=find(Hi~=0) %剔除不显著变量再次建立回归方程并进行显著性检验if length(k)<p0p0=length(k);x=x(:,k);X=[ones(n,1),x];elsebreakendendx=A(:,1:3); %第(3)小题[n,p]=size(x);X=[ones(n,1),x];alpha_3=0.05;[b,bint,r,rint,stats]=regress(Y,X,alpha_3);beta_ci=bint(2:p+1);x0=[5,10,50]; %第(4)小题y0_hat=[1,x0]*b;Qe=r'*r;sigma=sqrt(Qe/(n-p-1));t_alpha=tinv(1-alpha_3/2,n-p-1);y0_ci=[y0_hat-sigma*t_alpha,y0_hat+sigma*t_alpha]·运行命令文件example4_5.m:>> example4_5beta_hat = 0.6952 0.1606 0.1076 0.0359 %(1)小题F_equation = 7.7011 0.0003 %(2)小题F_coeff = 7.0935 8.2716 11.5683F0 = 7.2339Hi = 0 1 1k = 2 3beta_hat = 2.5150 0.0233 0.0364F_equation = 7.0686 0.0021F_coeff = 1.2050 10.4884F0 = 7.2200Hi = 0 1k = 2beta_hat = 2.6475 0.0393F_equation = 12.8760 0.0008F_coeff = 12.8760F0 = 7.2068Hi = 1k = 1beta_ci = 0.0392 0.2821 %(3)小题0.0322 0.18290.0147 0.0572y0_ci = 2.7359 6.0069 %(4)小题所以, 有:(1)回归方程为;(2)F检验法表明在显著性水平拒绝原假设, 说明回归方程显著;第一次线性回归得回归方程为: , 经F检验知不显著;剔除进行第二次线性回归, 得回归方程为: , 经F检验知不显著;剔除进行第三次线性回归, 得回归方程为: , 经F检验知显著, 故最终的线性回归为.(3) 的置信区间为[0.0392, 0.2821], 的置信区间为[0.0322, 0.1829], 的置信区间为[0.0147, 0.0572];(4)当, 的置信水平为的预测区间为[2.7359, 6.0069].回归分析3【例4-3】(书P194例4.10) 某种半成品在生产过程中的废品率y(%)与它所含的某种化学成分x(0.01%)有关, 现将试验所得的16组数据记录如下:求y对x·编写命令文件example4_10.m:%书P194例4.10x=[34,36,37,38,39,39,39,40,40,41,42,43,43,45,47,48];y=[1.30,1.00,0.73,0.90,0.81,0.70,0.60,0.50,0.44,0.56,0.30,0.42,0.35,0.40,0.41,0.60];plot(x,y,'r*')hold onp=polyfit(x,y,2)y_fit=polyval(p,x); y的拟合值Qe=(y-y_fit)*(y-y_fit)' %残差平方和plot(x,y_fit,'k')hold off·运行命令文件example4_10.m:>> example4_10p = 0.0092 -0.8097 18.2642Qe = 0.1304回归分析4出钢时所用的盛钢水的钢包, 由于钢水对耐火材料的浸蚀, 容积不断增大. 我们希望找出使用次数x与增大的容积y 之间的关系. 试验数据列于下表4-7. 首先利用双曲线、倒指数曲线与对数曲线进行非线性回归并利用F检验法进行显著性检验, 然后作出散点图与拟合曲线图, 最后在显著性的模型中比较哪个模型为优. ( )·编写命令文件example4_8.m:%书P190例4.8x=2:16;y=[6.42, 8.20, 9.58, 9.50, 9.70, 10.00, 9.93, 9.99, 10.49, 10.59, 10.60, 10.80, 10.60, 10.90, 10.76];plot(x,y,'kO')hold onn=length(x);y1=1./y; %(1)双曲线拟合x1=1./x;p1=polyfit(x1,y1,1);ab=[p1(2),p1(1)]y1_fit=polyval(p1,x1);U1=(y1_fit-mean(y))*(y1_fit-mean(y))'; %方程的显著性检验Qe1=(y1-y1_fit)*(y1-y1_fit)';F1=U1/Qe1/(n-2);F0=Finv(1-0.01,1,n-2);if F1>F0h=1elseh=0endy_fit=1./y1_fit;Qe=(y-y_fit)*(y-y_fit)' %残差平方和plot(x,y_fit,'r')y2=log(y); %(2)倒指数曲线拟合x2=1./x;p2=polyfit(x2,y2,1);ab=[exp(p2(2)),p2(1)]y2_fit=polyval(p2,x2);U2=(y2_fit-mean(y))*(y2_fit-mean(y))'; %方程的显著性检验Qe2=(y2-y2_fit)*(y2-y2_fit)';F2=U2/Qe2/(n-2);F0=Finv(1-0.01,1,n-2);if F2>F0h=1elseh=0endy_fit=exp(y2_fit);Qe=(y-y_fit)*(y-y_fit)' %残差平方和plot(x,y_fit,'b-.')y3=y; %(3)对数曲线拟合x3=log(x);p3=polyfit(x3,y3,1);ab=[p3(2),p3(1)]y3_fit=polyval(p3,x3);U3=(y3_fit-mean(y))*(y3_fit-mean(y))'; %方程的显著性检验Qe3=(y3-y3_fit)*(y3-y3_fit)';F3=U3/Qe3/(n-2);F0=Finv(1-0.01,1,n-2);if F3>F0h=1elseh=0endy_fit=y3_fit;Qe=(y-y_fit)*(y-y_fit)' %残差平方和plot(x,y_fit,'m:')hold offlegend('散点图','1/y=a+b/x拟合','y=a*e^(b/x)拟合','y=a+b*lnx拟合')·运行命令文件example4_8.m:>> example4_8ab = 0.0823 0.1312 %第(1)模型的结果h = 1Qe = 1.4396ab = 11.6789 -1.1107 %第(2)模型的结果h = 1Qe = 0.8913ab = 6.2389 1.7761 %第(3)模型的结果h = 0Qe = 2.5592所以, 有:(1)双曲线回归方程为, 此方程显著 ;倒指数曲线回归方程为, 此方程也显著 ;对数曲线回归方程为, 此方程不显著.(2)在显著型模型中, 倒指数模型由于残差平方和最小, 所以比双曲线模型更优.方差分析1单因素方差与双因素方差分析均假定X中的数据具有以下特征: 独立、正态、方差齐性.表5.1方差分析部分分析函数(1) [p,table,stats] = anova1(X) 进行均衡的单因素方差分析(如果数据缺失, 用NaN补齐). 检验数据X (m×n矩阵)中各列的均值是否相等, X的每一列(一个水平) 表示独立样本, 每个样本包含m个相互独立的观察值. 默认返回两幅图表, 第一幅为标准anova表, 第二幅为X各列数据的盒形(box) 图. 如果盒形图的中心线差别很大, 则对应的F 值很大, 相应的概率p-值就小.p——零假设( : 各样本具有相同的均值)的概率值. 如果p-值接近零则应对零假设置疑, 表明至少有一个样本的均值与其它样本的均值显著不同;table——以单元数组的形式返回anova表;stats——利用stats可接下来进行多重比较检验. 用户可以将stats结构作为输入利用multcompare函数进行这种检验.(2) [p,table,stats] = anova2(X,reps,'displayopt') 进行均衡的双因素方差分析(对于不均衡设计, 使用函数anovan). 检验数据X中各列或各行的均值是否相等. 不同列中的数据表示因素A引起的变化情况, 不同行中的数据表示因素B 引起的变化. 如果对于因素A和B的每一种水平组合都有超过一个的观察值(这种情况又称重复试验双因素方差分析), 则输入reps表示每个单元(cell) (对应一个水平组合) 中观察值的个数, 它必须为常数.X数据的结构格式为一矩阵. 比如下面这个矩阵, 其中列因素A有两个水平, 行因素B有三个水平, 每个水平对有两个观察值(reps=2). 下标分别表示行、列和每个水平对中的观察值.当reps=1 (缺省值) 时, anova2返回的向量p中包含如下两个零假设的概率值:: 因素A各样本(即X中所有的列样本) 均来自相同的总体, 或指因素A的不同水平对试验结果具有相同的影响); : 因素B各样本(即X中所有的行样本) 均来自相同的总体;当reps>1时, anova2返回的向量p还包含下面这个零假设的概率值:: 因素A与B之间无交互作用.(3) c = multcompare(stats,alpha,'displayopt') 均值或其它估计量的多重比较. 利用上面命令输出中的stats结构中的信息进行多重比较检验, 返回成对比较的结果矩阵c. c包含5列矩阵. 矩阵的每一行代表一次检验, 每一对均值比较对应一行. 行中的第一、二个数据表示比较组的编号, 第四个数据表示正在被比较的均值差的估计值, 第三、五个数据表示正在被比较的均值差的置信区间. 如果置信区间中包含0, 则说明在alpha的显著水平上差异不是显著的. 此命令结果也显示一个表示检验的交互式图形. 图中每组的均值用一个符号和符号周围的区间表示. 如果两个均值的区间不交叠, 说明它们显著不同; 如果两个区间交叠, 则说明它们不是显著不同的. 可以用鼠标选中任何一组, 图中其它任何与之显著不同的组将会高亮度显示.【例5-1】(书P209例5.3) 对六种不同的农药在相同的条件下分别进行杀虫试验, 试验结果见下表. 问杀虫率是否因·编写命令文件example5_3.m:%书P209例5.3X=[87,90,56,55,92,75;85,88,62,48,99,72;80,87,NaN,NaN,95,81;NaN,94,NaN,NaN,91,NaN];n=length(find(X>0));r=6;[p,table,stats] = anova1(X);F0=Finv(1-0.01,r-1,n-r)pausec = multcompare(stats,0.01)21 / 21。
matlab--算法大全--第10章_数据的统计描述和分析

废品分类),学校全体学生的身高。
总体中的每一个基本单位称为个体,个体的特征用一个变量(如 x )来表示,如一
件产品是合格品记 x = 0 ,是废品记 x = 1 ;一个身高 170(cm)的学生记 x = 170 。
从总体中随机产生的若干个个体的集合称为样本,或子样,如n 件产品,100 名学
生的身高,或者一根轴直径的 10 次测量。实际上这就是从总体中随机取得的一批数据,
load data.txt
这样在内存中建立了一个变量 data,它是一个包含有 20 ×10 个数据的矩阵。
为了得到我们需要的 100 个身高和体重各为一列的矩阵,应做如下的改变: high=data(:,1:2:9);high=high(:) weight=data(:,2:2:10);weight=weight(:)
不妨记作 x1, x2 ,L, xn , n 称为样本容量。
简单地说,统计的任务是由样本推断总体。
1.2 频数表和直方图
一组数据(样本)往往是杂乱无章的,做出它的频数表和直方图,可以看作是对这
组数据的一个初步整理和直观描述。
将数据的取值范围划分为若干个区间,然后统计这组数据在每个区间中出现的次
数,称为频数,由此得到一个频数表。以数据的取值为横坐标,频数为纵坐标,画出一
你可能注意到标准差 s 的定义(2)中,对 n 个 (xi − x) 的平方求和,却被 (n −1) 除, 这是出于无偏估计的要求。若需要改为被 n 除,Matlab 可用 std(x,1)和 var(x,1)来实现。
(iii)中心矩、表示分布形状的统计量—偏度和峰度
随机变量 x 的 r 阶中心矩为 E( x − Ex)r 。
标准差 s 定义为
MATLAB软件教程 (6)

统计结果最后写到 一个纯文本文件 pinshu.txt中。
概率分布
离散型随机变量: 离散均匀分布 二项分布 泊松分布 几何分布 超几何分布 负二项分布
连续型随机变量: 连续均匀分布
指数分布
正态分布
对数正态分布
χ2分布 非中心χ2分布 t分布 非中心t分布 F分布 非中心F分布
β分布 γ分布 Rayleigh分布 Weibull分布
MATLAB数理统计
引言
• 数理统计研究的对象是受随机因素影响的数据 • 数据样本少则几个,多则成千上万,人们希望能用
少数几个包含其最多相关信息的数值来体现数据样 本总体的规律。 • 面对一批数据如何进行描述与分析,需要掌握参数 估计和假设检验这两个数理统计的最基本方法。 • 我们将用MATLAB 的统计工具箱(Statistics Toolbox) 来实现数据的统计描述和分析。
为了检验字符串是否只包含a、g、
i=i+1;
c、t四个字符
end
f
he=[sum(f(:,1)) sum(f(:,2)) sum(f(:,3)) sum(f(:,4))...
sum(f(:,5)) sum(f(:,6))] fid2=fopen('pinshu.txt','w'); fprintf(fid2,'%8d %8d %8d %8d %8d %8d\n',f'); fclose(fid1);fclose(fid2);
>> phat=mle('normal',data)
phat =
0.5669 0.2835
>>data=[1,2,3,4,5,6,7,8,9,10];
【生物数学】MATLAB数理统计方法与实例

之间用英文逗号或空格分开,两行之间用英文分号分开。字 符串必须用英文单引号引起来,字符串中含有单引号时必须 成对输入,例如:
x=[1 2,3; 5,7 9]
msg1= 'You are right!'
msg2 = 'You''re right!'
2. sig-值为0.8668, 远超过0.5, 不能拒绝零假设 3. 95%的置信区间为[113.4, 116.9], 它完全包括115, 且精度很
高. .
2. 总体方差sigma2未知时,总体均值的t-检验
[h,sig,ci] = ttest(x,m,alpha,tail) 检验数据 x 的关于均值的某一假设是否成立,其 中alpha 为显著性水平,究竟检验什么假设取决于 tail 的取值: tail = 0,检验假设“x 的均值等于 m ” tail = 1,检验假设“x 的均值大于 m ” tail =-1,检验假设“x 的均值小于 m ” tail的缺省值为 0, alpha的缺省值为 0.05.
回一个空数组x=[]。 x=a:h:b 返回间隔矢量x=[a,a+h,a+2h,…,a+mh],这里
m=fix((b-a)/h)为(b-a)/h向零取整。当h=0,或h>0且a>b,或 h<0且a<b时,返回空数组x=[]。h=1为缺省值。
2. 使用函数y=linspace(a,b,n)产生以a,b为端点具有n个等间隔点 的行向量y。
3.8334 5.0288 6.1191 此命令产生了2×3的正态分布随机数矩阵,各数分别服从 N(1,0.12), N(2,22), N(3, 32), N(4,0.12), N(5, 22),N(6, 32).
第9章概率论与数理统计的MATLAB实现讲稿

第9章概率论与数理统计的MATLAB实现讲稿第9章概率论与数理统计的MATLAB 实现MA TLAB 总包提供了一些进行数据统计分析的函数,但不完整。
利用MA TLAB 统计工具箱,可以进行基本概率和数理统计分析,以及进行比较复杂的多元统计分析。
本章主要针对大学本科的概率统计课程介绍工具箱的部分功能。
9.1 随机变量及其分布利用统计工具箱提供的函数,可以比较方便地计算随机变量的分布律(概率密度函数)和分布函数。
9.1.1 离散型随机变量及其分布律如果随机变量全部可能取到的不相同的值是有限个或可列个无限多个,则称为离散型随机变量。
MA TLAB 提供的计算常见离散型随机变量分布律的函数及调用格式:函数调用格式(对应的分布) 分布律y=binopdf(x,n,p)(二项分布) )()1(),|(),,1,0(x I p p x n p n x f n x n x --?= y=geopdf(x,p)(几何分布) x p p p x f )1()|(-= ),1,0( =xy=hygepdf(x,M,K,n)(超几何分布)--???? ??=n M x n K M x K n K M x f ),,|(y=poisspdf(x,lambda)(泊松分布) λλλ-=e x x f x !)|(),1,0( =x y=unidpdf(x,n)(离散均匀分布) NN x f 1)|(= 9.1.2 连续型随机变量及其概率密度对于随机变量X 的分布函数)(x F ,如果存在非负函数)(x f ,使对于任意实数x 有∞-=x dt t f x F )()(则称X 为连续型随机变量,其中函数)(x f 称为X 的概率密度函数。
MA TLAB 提供的计算常见连续型随机变量分布概率密度函数的函数及调用格式:函数调用格式(对应的分布) 概率密度函数y=betapdf(x,a,b)(β分布) )10()1(),(1),|(11<<-=--x x x b a B b a x f b ay=chi2pdf(x,v)(卡方分布) )2(2)|(2212v exv x f v x v Γ=--)0(≥xy=exppdf(x,mu)(指数分布) μμμxex f -=1)|()0(≥xy=fpdf(x,v1,v2)(F 分布) 2211222121212121111)2()2()2(),|(v v v v v x v x vv v v v v v v x f +-?+???? ??ΓΓ+Γ= y=gampdf(x,a,b)(伽马分布) b xa a e x ab b a x f --Γ=1)(1),|()0(≥xy=normpdf(x,mu,sigma)(正态分布) 222)(21),|(σμπσσμ--=x ex fy=lognpdf(x,mu,sigma)(对数正态分布) 222)(ln 21),|(σμπσσμ--=x ex x fy=raylpdf(x,b)(瑞利分布) 2222)|(b x e b x b x f -=y=tpdf(x,v)(学生氏t 分布) 2121)2()21()|(+-???? ?+Γ+Γ=v v x v v v v x f πy=unifpdf(x,a,b)(连续均匀分布) )(1),|(],[x I ab b a x f b a -=y=weibpdf(x,a,b)(威布尔分布) )(),|(),0(1x I eabx b a x f bax b ∞--= 比如,用normpdf 函数计算正态概率密度函数值。
应用数理统计matlab使用入门

MATLAB基础知识一、MATLAB软件简介1967年美国Mathwork公司推出了、基于矩阵运算的“Matrix Laboratory”(缩写为MATLAB) 的交互式软件包. MATLAB既是一种直观、高效的计算机语言, 同时又是一个科学计算平台. 它为数据分析和数据可视化、算法和应用程序开发提供了最核心的数学和高级图形工具. 根据它提供的500多个数学和工程函数, 工程技术人员和科学工作者可以在它的集成环境中交互或编程以完成各自的计算. MATLA-B一般用于线性代数、概率统计、图像处理、样条分析、信号处理、小波分析、振动理论、神经网络、自动控制、系统识别、算法优化和财政金融等各个方面.不过, MATLAB作为一种新的计算机语言, 要想运用自如, 充分发挥它的威力, 也需要系统的学习. 但由于使用MATLAB编程运算与人进行科学计算的思路和表达方式完全一致, 所以不像学习其他高级语言如Basic、Fortan和C语言等那样难于掌握. 下面的内容均是基于MATLAB7.5版本.1、MATLAB的主要功能(1) 数值计算功能(Numeric)(2) 符号计算功能(Symblic)(3) 图形和可视化功能(Graphic)(4) MATLAB的活笔记本功能(Notebook)(5) 可视化建模和仿真功能(Simulink)2、MATLAB的工作环境MATLAB的工作环境主要包括:·【Command Window】命令窗口;·【File Editor】文本编辑窗口;·【Figure Window】图形窗口.图0-1MATLAB 6.x的命令窗、文本编辑窗、图形窗、菜单栏和工具栏MATLAB 7.5还包含几个辅助视窗, 组成其“桌面系统”. 它们分别为:·【Workspace】工作台窗口;·【Command History】指令历史纪录窗口;·【Current Directory】当前目录选择窗口.图0-2MATLAB 7.5的桌面系统和命令窗口3、MATLAB的工作原理(1) 语言结构:MATLAB语言= 窗口命令+ M文件(2) 窗口命令:在MATLAB命令窗口中输入的MATLAB语句, 并直接执行它们完成相应的运算、绘图等.(3) M文件:在MATLAB文本编辑窗口中用MATLAB语句编写的磁盘文件, 扩展名为“.M”.二、MATLAB入门1、数学运算符及特殊字符数组的算术运算符: + - .* ./ .\ .^矩阵的算术运算符: + - * / \ ^关系运算符: < <= > >= = = ∽=逻辑运算符: & 与; | 或; ~ 非三种运算的顺序依次为: 算术运算、关系运算、逻辑运算.pi 数学常数, 即3.1415926535897....2 eps 系统的浮点(Floating-ponit) 精确度. 在PC机上, 它等于52Inf 正无穷大, 定义为1 0ans 计算结果的默认变量名NaN 不定值, 由Inf/Inf或0/0等运算产生2、基本库函数(1) 常用三角函数:sin, cos, tan, cot, sec, csc, asin, acos, atan, acot, asec, acsc等(2) 常用基本函数:sqrt(x)—开平方abs(x)—取绝对值exp(x)—以e为底的指数log(x)—自然对数log10(x)—以10为底的对数log2(x)—以2为底的对数sum(x)—求和prod(x)-求积max(x)—最大值min(x)—最小值fix(x)—对称取整sign(x)—符号函数length(x)—矩阵行数与列数中的最大值size(x)—矩阵的行数与列数注意: (1) 由于MATLAB是基于矩阵的运算,所以上面的x均表示矩阵, 数可看作是1×1的矩阵.(2) 对非向量型矩阵, 如不作特殊说明, 都是列优先.3、命令行的编写随时输入指令并按回车键, 即时给出结果;在指令最后不用任何符号并按回车键, 将显示最后结果;在指令最后用“; ”并按回车键, 将只计算但不显示最后结果.同时输入几条指令时, 用“, ”或“; ”隔开.【例0-1】数学运算符、特殊字符与基本库函数的应用>>3*(-5), 2/5, [1 2 3].*[2 4 5], [1 2 3]./[2 4 5], [2,4,5].^2ans = -15ans = 0.4000ans = 2 8 15ans = 0.5000 0.5000 0.6000ans = 4 16 25>> sin(pi/4), log(exp(1))ans = 0.7071ans = 14、变量与表达式在MATLAB中, 把由下标表示次序的标量的集合称为矩阵或数组. MATLAB是基于矩阵运算的, 因此其基本数据结构只有一个: 矩阵. 一个数也是矩阵, 只不过它是1行×1列的矩阵. MATLAB中的变量可用来存放数据, 也可用来存放向量或矩阵, 并进行各种运算.变量命名的规则为:·变量名、函数名是要区分大小写字母的;·第一个字符必须是英文字母;·字符间不可留空格;·最多只能有31个字符(只能有英文字母、数字和下连字符) .表达式由变量名、运算符和函数名等组成. 如x/sin(x), 其中x为变量名, /为运算符, sin为函数名.MATLAB语句有两种最常见形式: 1) 表达式; 2) 赋值语句: 变量= 表达式.【例0-2】赋值语句的使用>> x=1; y=x/sin(x)y = 1.1884>> x=[pi/6,pi/4,pi/3,pi/2]; sin(x)ans =0.5000 0.7071 0.8660 1.0000>> x=0:0.1:2*pi; y=sin(x); plot(x,y)图0-3y=sin(x)的曲线图5、M文件的建立、编写、保存与调用(1) 进入文本编辑窗口的方式: 在菜单栏“File”下直接点击“新建…”进入文本编辑窗口.(2) M文件的分类与格式:①命令文件: 由一系列MATLAB语句组成, 运行时将自动执行一系列命令直至给出最后结果, 而不交互地等待键盘输入. 命令文件定义的变量为全局变量, 存放于内存.②函数文件: 第一行必须包含“function”, 主要功能是建立一个函数. 函数文件定义的变量为局部变量.function 因变量名= 函数名(自变量名)注意: 函数文件要求函数名和文件名相同, 且函数名、文件名与变量名的命名规则一样.(3) 退出文本编辑窗口: 录入完毕, 存盘退出文本编辑窗口则可.【例0-3】已知1232,3,1x x x =-==, 而2112112122233,y z z z x y z z z x x =+⎧=⎧⎨⎨=-=+⎩⎩, 试求12,y y 的值.·在文本编辑窗口中编写命令文件f0_3.m:x1=-2;x2=3;x3=1; z1=3*x1^2; z2=x2+x3; y1=z1+z2 y2=z1-z2·在命令窗口中运行命令文件f0_3.m:>> f0_3y1 = 16 y2 = 8【例0-4】求()f x =分别在0,5,10x x x ===处的函数值. ·在文本编辑窗口中编写函数文件f0_4.m:function y=f0_4(x)y=log10(sqrt((x-5).^2+(x-100).^2)); ·在命令窗口中调用函数文件f0_4.m:>>x=[0,5,10]; y=f0_4(x);y = 2.0005 1.9777 1.95496、MATLAB 的在线帮助 (1) 从菜单栏上的“help ”进入 (2) 其它命令窗口帮助clc——清除显示屏上的内容clear —— 清除内存变量和函数what —— 列出当前目录下的M 、MAT 、MEX 文件 who——列出当前工作空间 (Workspace) 的变量名7、路径的设置在保存M 文件时, MATLAB 的默认位置是C:\MATLAB6p5\work. 如果用户将编写的M 文件保存在E:\experiment 目录下, 则从MATLAB 窗口的“File ”菜单中单击子菜单“Save As …”, 选择E:\experiment, 再输入本M 文件的文件名, 按“保存”键返回则可.第一章 数理统计的基本概念一、直方图与经验分布函数图的绘制hist(A,n) ——对矩阵A 按列作统计频数直方图, n 为条形图的条数ni=hist(A,n)—— 对矩阵A 按列得各划分区间内的统计频数注意: 当A 为向量时, 上述所有命令直接作用在向量上, 而不是列优先.[Fn,x0]=ecdf(x) —— 得到样本x 的经验分布函数值Fn, 当x 中有m 个不同的数 (记为向量x0) 时, 则Fn 的个数为m+1个ecdfhist(Fn,x0, m) —— 绘制数据x 的频率(密度)直方图, 其中Fn 与x0是由ecdf 函数得到的样本x 的经验分布函数值Fn 与分段点x0, m 为条形的个数, m 的默认值为10cdfplot(x) —— 绘制样本x 的经验分布函数图例如:>> x = [6 4 5 3 6 8 6 7 3 4]; >> [Fn,x0]=ecdf(x)Fn = 0 0.2000 0.4000 0.5000 0.8000 0.9000 1.0000 x0 = 3 3 4 5 67 8>> cdfplot(x)图1-1 经验分布函数图【例1】在齿轮加工中, 齿轮的径向综合误差i F ''∆是个随机变量, 今对200件同样的齿轮进行测量, 测得i F ''∆的数值 (mm) 如下, 求作i F ''∆的频率密度直方图, 并作出i F ''∆的经验分布函数图形.16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 24 20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 2118 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 2813 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 1314 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 1619 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 2819 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 1818 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 3308 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 2417 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18 ·编写命令文件example1_6.m:F=[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22 24....20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21....18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28....13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13....14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16....19 28 19 12 14 19 28 28 28 13 21 28 19 11 15 18 24 18 16 28....19 15 13 22 14 16 24 20 28 18 18 28 14 13 28 29 24 28 14 18....18 18 08 21 16 24 32 16 28 19 15 18 18 10 12 16 26 18 19 33....08 11 18 27 23 11 22 22 13 28 14 22 18 26 18 16 32 27 25 24....17 17 28 33 16 20 28 32 19 23 18 28 15 24 28 29 16 17 19 18];%(1)下面作频数直方图figure(1)hist(F,8)title('频数直方图');xlabel('齿轮的径向综合误差(mm)');%(2)下面作频率(密度)直方图[Fn,x0]=ecdf(F);figure(2)ecdfhist(Fn,x0,8);title('频率(密度)直方图');xlabel('齿轮的径向综合误差(mm)');%(3)下面作经验分布函数图figure(3)cdfplot(F)title('经验分布函数图');xlabel('齿轮的径向综合误差(mm)');·运行命令文件example1_6.m:>> example1_6图1-2二、常见的概率分布表1-1 常用概率分布及代码频数直方图齿轮的径向综合误差(mm)频率(密度)直方图齿轮的径向综合误差(mm)齿轮的径向综合误差(mm)F (x )经验分布函数图三、MATLAB 为常见分布提供的五类函数1) 概率密度函数(分布名+pdf) 2) (累积)分布函数(分布名+cdf) 3) 逆(累积)分布函数(分布名+inv) 4) 随机数发生器(分布名+rnd) 5) 均值和方差(分布名+stat) 1、概率密度函数表1-2 概率密度函数(pdf)注意: Y=normpdf (X, mu, sigma)的sigma 是指标准差σ, 而非2σ. 【例2】 绘制标准正态分布(0,1)N 的概率密度图.x=-4:0.1:4; y=normpdf(x,0,1); plot(x,y)title('N(0,1)的概率密度曲线图')图1-3 标准正态分布的概率密度图2、累积分布函数表1-3 累积分布函数(cdf)【例3】求服从标准正态分布的随机变量落在区间[-2, 2]上的概率.>> P=normcdf (2,0,1)-normcdf(-2,0,1)ans = 0.95453、逆累积分布函数 (用于求分位点)表1-4 逆累积分布函数(inv)【例4】 求下列分位数: (i) 0.9u ;(ii) 0.25(4)t ;(iii) 0.1(14,10)F ;(iv) 20.025(50)χ.>> u_alpha=norminv(0.9,0,1)u_alpha = 1.2816 >> t_alpha=tinv(0.25,4)t_alpha = -0.7407 >> F_alpha=finv(0.1,14,10)F_alpha = 0.4772 >> X2_alpha=chi2inv(0.025,50)X2_alpha = 32.35744、随机数发生函数表1-5 随机数发生函数(rnd)5、均值和方差表1-6 常见分布的均值和方差函数(stat)注意: (1) MATLAB 中的指数分布的概率密度函数是1,0()0,0xue xf x u x -⎧>⎪=⎨⎪≤⎩.(2) 如果省略调用格式左边的[M, V], 则只计算出均值.四、常用的统计量表1-7 常用统计量说明:(1) y=var(X) ——计算X 中数据的方差, 其中211var()()1ni i X x x n ==--∑. y=var(X, 1) ——211var(,1)()n i i X x x n ==-∑, 得到样本的二阶中心矩 (转动惯量).(2) C =cov(X) ——返回一个协方差矩阵, 其中输入矩阵X 的每列元素代表着一个随机变量的观测值. 如果X 为n ×m 的矩阵, 则C 为m ×m 的矩阵.(3) var(X)=diag(cov(X)), std(X)=sqrt(diag(cov(X))).。
完整版Matlab概率论及数理统计
Matlab概率论与数理统计一、 matlab 基本操作1.画图【例】简单画图hold off;x=0:0.1:2*pi;y=sin(x);plot(x,y,'-r');x1=0:0.1:pi/2;y1=sin(x1);hold on;fill([x1, pi/2],[y1,1/2],'b' );【例】填充,二维平均随机数hold off;x=[0,60];y0=[0,0];y60=[60,60];x1=[0,30];y1=x1+30;x2=[30,60];y2=x2-30;xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0];fill(xv,yv,'b');hold on ;plot(x,y0,'r',y0,x,'r',x,y60,'r' ,y60,x,'r' );plot(x1,y1,'r',x2,y2,'r');yr=unifrnd (0,60,2,100);plot(yr(1,:),yr(2,:),'m.')axis('on');axis('square');2.排列组合C=nchoosek(n,k) :C C n k,例 nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2) :从 n1 到 n2 的连乘【例】最少有两个人寿辰相同的概率n!C N nN !( N n)!N(N1)(N n1)公式计算 p 111N nN n N n365 364 (365rs1)365364365rs 1 1365rs1365365365rs=[20,25,30,35,40,45,50];%每班的人数p1=ones(1,length(rs));p2=ones(1,length(rs));%用连乘公式计算for i=1:length(rs)p1(i)=prod(365-rs(i)+1:365)/365^rs(i);end%用公式计算(改进)for i=1:length(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365);end ;endp1(i)=exp(sum(log(365-rs(i)+1:365))-rs(i)*log(365));endp_r1=1-p1;p_r2=1-p2;Rs =[20253035404550 ]P_r=[0.4114 0.5687 0.7063 0.8144 0.8912 0.9410 0.9704]二、随机数的生成3.平均分布随机数rand(m,n); 产生 m 行 n 列的 (0,1) 平均分布的随机数rand(n); 产生 n 行 n 列的 (0,1)平均分布的随机数【练习】生成(a,b)上的平均分布4.正态分布随机数randn(m,n); 产生 m 行 n 列的标准正态分布的随机数【练习】生成N(nu,sigma.^2) 上的正态分布5.其他分布随机数函数名调用形式注释Unidrnd unid rnd (N,m,n)平均分布(失散)随机数binornd bino rnd (N,P,m,n)参数为 N, p的二项分布随机数Poissrnd poiss rnd (Lambda,m,n)参数为 Lambda的泊松分布随机数geornd geornd (P,m,n)参数为 p 的几何分布随机数hygernd hygernd (M,K,N,m,n)参数为 M, K, N 的超几何分布随机数Normrnd normrnd (MU,SIGMA,m,n)参数为 MU, SIGMA的正态分布随机数,SIGMA是标准差Unifrnd unif rnd ( A,B,m,n)[A,B] 上平均分布 ( 连续 ) 随机数Exprnd exprnd (MU,m,n)参数为 MU的指数分布随机数chi2rnd chi2 rnd(N,m,n)自由度为 N 的卡方分布随机数Trnd t rnd(N,m,n)自由度为 N 的 t分布随机数Frnd f rnd(N1, N2,m,n)第一自由度为N1, 第二自由度为 N2 的 F 分布随机数gamrnd gamrnd(A, B,m,n)参数为 A, B的分布随机数betarnd betarnd(A, B,m,n)参数为 A, B的分布随机数lognrnd lognrnd(MU, SIGMA,m,n)参数为 MU, SIGMA的对数正态分布随机数nbinrnd nbinrnd(R, P,m,n)参数为 R,P 的负二项式分布随机数ncfrnd ncfrnd(N1, N2, delta,m,n)参数为 N1, N2, delta 的非中心 F 分布随机数nctrnd nctrnd(N, delta,m,n)参数为 N,delta的非中心 t 分布随机数ncx2rnd ncx2rnd(N, delta,m,n)参数为 N,delta的非中心卡方分布随机数raylrnd raylrnd(B,m,n)参数为 B 的瑞利分布随机数weibrnd weibrnd(A, B,m,n)参数为 A, B的韦伯分布随机数三、一维随机变量的概率分布1.失散型随机变量的分布率(1)0-1 分布(2)平均分布(3) 二项分布: binopdf(x,n,p) ,若X ~ B(n, p),则P{ X k} C n k p k (1p) n k,x=0:9;n=9;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]‘当 n 较大时二项分布近似为正态分布x=0:100;n=100;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')(4) 泊松分布: piosspdf(x, lambda) ,若X ~k e ( ) ,则 P{ X k}k !x=0:9; lambda = 3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081, 0.0027 ](5) 几何分布: geopdf (x, p),则P{ X k} p(1p) k 1y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ]C M k C N n k Mx=0:10;N=20;M=8;n=4;y= hygepdf(x,N,M,n);plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2.概率密度函数1a x b(1)平均分布: unifpdf(x,a,b) ,f ( x)b a0其他a=0;b=1;x=a:0.1:b;y= unifpdf (x,a,b);112(2)正态分布: normpdf(x,mu,sigma) ,f ( x)e2 2 ( x)2x=-10:0.1:12;mu=1;sigma=4;y= normpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); %产生 10000 个正态分布的随机数d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;% 以 a 为横轴,求出 10000 个正态分布的随机数的频率plot(x,y,'b-',a,b,'r.')(3) 指数分布: exppdf(x,mu) ,f (x)1 e1xa x by= exppdf(x,mu); plot(x,y,'b-',x,y,'r*')1n1(4)2分布: chi2pdf(x,n) , f (x; n)2n 2x2( n 2)hold on x=0:0.1:30;n=4;y= chi2pdf(x,n);plot(x,y,'b');%blue n=6;y= chi2pdf(x,n);plot(x,y,'r');%redn=8;y= chi2pdf(x,n);plot(x,y,'c');%cyan n=10;y= chi2pdf(x,n);plot(x,y,'k');%black legend('n=4', 'n=6', 'n=8', 'n=10');(( n 1) 2) x 2(5) t 分布: tpdf(x,n) , f (x; n)(n 2)1nnhold on x=-10:0.1:10;n=2;y= tpdf(x,n);plot(x,y,'b');%blue e 2n 1 2x 0x 0n=20;y= tpdf(x,n);plot(x,y,'k');%black legend('n=2', 'n=6', 'n=10', 'n=20');n1n1 2n1n222(6) F 分布: fpdf(x,n1,n2) ,f ( x; n1, n2)(( n1n2 ) 2) n1x 21n1x x 0 (n1 2)(n2 2) n2n20x 0hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x,n1,n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x,n1,n2);plot(x,y,'r');%redn1=10; n2=6;y= fpdf(x,n1,n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x,n1,n2);plot(x,y,'k');%blacklegend(' n1=2; n2=6', ' n1=6; n2=10', ' n1=10; n2=6', ' n1=10; n2=10');3.分布函数 F (x) P{ X x}【例】求正态分布的累积概率值设 X ~ N(3,22),求P{2X 5},P{ 4 X 10},P{ X 2}, P{X3} ,4.逆分布函数,临界值y F (x) P{ X x} , x F 1 ( y) , x 称之为临界值【例】求标准正态分布的累积概率值y=0:0.01:1;x=norminv(y,0,1);【例】求2 (9) 分布的累积概率值hold offy=[0.025,0.975];x=chi2inv(y,9);n=9;x0=0:0.1:30;y0=chi2pdf(x0,n);plot(x0,y0,'r');x1=0:0.1:x(1);y1=chi2pdf(x1,n);x2=x(2):0.1:30;y2=chi2pdf(x2,n);hold onfill([x1, x(1)],[y1,0],'b');fill([x(2),x2],[0,y2],'b');5. 数字特色函数名调用形式注释sort sort(x),sort(A)排序 ,x 是向量, A 是矩阵,按各列排序sortrows sortrows(A) A 是矩阵,按各行排序mean mean(x)向量 x 的样本均值var var(x)向量 x 的样本方差std std(x)向量 x 的样本标准差median median(x)向量 x 的样本中位数geomean geomean(x)向量 x 的样本几何平均值harmmean harmmean(x)向量 x 的样本调停平均值skewness skewness(x)向量 x 的样本偏度max max(x)向量 x 的最大值min min(x)向量 x 的最小值cov cov(x), cov(x,y)向量 x 的方差,向量x,y 的协方差矩阵corrcoef corrcoef(x,y)向量 x,y 的相关系数矩阵【练习】二项分布、泊松分布、正态分布( 1)对n10, p 0.2 二项分布,画出 b(n, p) 的分布律点和折线;( 2)对np ,画出泊松分布( ) 的分布律点和折线;( 3)对np,2np(1 p) ,画出正态分布N ( , 2 )的密度函数曲线;( 4)调整 n, p ,观察折线与曲线的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态总体均值、方差的参数估计与置信区间估计P316 例6.5.1 置信区间估计clear;Y=[14.85 13.01 13.50 14.93 16.97 13.80 17.95 13.37 16.29 12.38]; X=normrnd(15,2,10,1) % 随机产生数[muhat,sigmahat,muci,sigmaci]=normfit(X,0.1) % 正态拟合[muhat,sigmahat,muci,sigmaci]=normfit(Y,0.1) % 正态拟合X =15.257316.312912.664414.078814.475112.573712.361116.862415.022513.7097muhat =14.3318sigmahat =1.5595muci =13.427815.2358sigmaci =1.13742.5657muhat =14.7050sigmahat =1.8432muci =13.636515.7735sigmaci =1.34433.0324P320例6.5.5 置信区间估计clear;Y=[4.68 4.85 4.32 4.85 4.61 5.02 5.20 4.60 4.58 4.72 4.38 4.70]; [muhat,sigmahat,muci,sigmaci]=normfit(Y,0.05)muhat =4.7092sigmahat =0.2480muci =4.55164.8667sigmaci =0.17570.4211P321 例6.5.6 置信区间估计clear;Y=[45.3 45.4 45.1 45.3 45.5 45.7 45.4 45.3 45.6]; [muhat,sigmahat,muci,sigmaci]=normfit(Y,0.05) muhat =45.4000sigmahat =0.1803muci =45.261445.5386sigmaci =0.12180.3454单正态总体均值的假设检验方差sigma已知时P338 例7.2.1%[h,p,ci,zval]=ztest(X,mu,sigma,alpha,tail,dim)clear all;X=[ 8.05 8.15 8.2 8.1 8.25];[h,p,ci,zval]=ztest(X,8,0.2,0.05)h =p =0.0935ci =7.9747 8.3253zval =1.6771注:p为观察值的概率ci为置信区间;zval统计量值若h=0: 表示在显著性水平alpha下,不能否定原假设;若h=1: 表示在显著性水平alpha下,否定原假设;若tail=0:表示双边假设检验;若tail=1:表示单边假设检验(mu>mu0);若tail=0:表示单边假设检验(mu<mu0);dim表示根据指定的维数进行检验%[h,p,ci,zval]=ztest(X,mu,sigma,alpha)% X=normrnd(mu,sigma,N,M); 随机产生均值为mu,标准差为sigma的M行N例随机数;clear all;X=normrnd(100,5,100,1);mu=mean(X)sigmal=5;[h,p,ci,zval]=ztest(X,100,5,0.05)mu =99.8810h =p =0.8119ci =98.9011100.8610zval =-0.2379单正态总体均值的假设检验方差sigma未知时P338 例7.2.2%[h,p,ci,tstat]=ttest(X,mu0,alpha,tail,dim)clear all;X=[ 239.7 239.6 239 240 239.2];[h,p,ci,tstat]=ttest(X,240,0.05)h =1p =0.0491ci =239.0033 239.9967tstat =tstat: -2.7951df: 4sd: 0.4000注:p为观察值的概率ci为置信区间;tstat统计量值若h=0: 表示在显著性水平alpha下,不能否定原假设;若h=1: 表示在显著性水平alpha下,否定原假设;df为自由度;sd为样本标准背离若tail=0:表示双边假设检验;若tail=1:表示单边假设检验(mu>mu0);若tail=0:表示单边假设检验(mu<mu0);dim表示根据指定的维数进行检验单正态总体方差的假设检验总体均值未知时%[h,p,varci,stats]=vartest(x,var0,alpha,tail)clear all;X=[49.4 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9];[h,p,varci,stats]=vartest(X,1.5,0.05,0)h =p =0.8383varci =0.6970 5.6072stats =chisqstat: 8.1481df: 8注:p为观察值的概率varci为方差的置信区间;stats 为卡方统计量的观测值若h=0: 表示在显著性水平alpha下,不能否定原假设;若h=1: 表示在显著性水平alpha下,否定原假设;df为自由度;若tail=0:表示双边假设检验;若tail=1:表示单边假设检验(mu>mu0);若tail=0:表示单边假设检验(mu<mu0);两正态总体均值差的假设检验方差未知但相等情形% h=ttest2(x,y,alpha,tail,vartype,dim)%样本X与Y在给定检验水平alpha下,进行双边(tail为0)或单边>(tail为+1)或单边<(tail为-1)且vartype('equal' or 'unequal')指定方差是否相等的假设检验P342例7.2.3clear all;X=[76.43 76.21 73.58 69.69 65.29 70.83 82.75 72.34];Y=[73.66 64.27 69.34 71.37 69.77 68.12 67.27 68.7];[h,sig,ci]=ttest2(X,Y,0.05,1,'equal')h =1sig =0.0290ci =0.6357 Inf注:h=1: 表明在alpha=0.05条件下,应拒绝原假设,即认为镍合金硬度有显著提高。
sig =0.0290:表明两个总体均值相等的概率;ci:表示均值差的置信区间两正态总体方差比的假设检验总体均值未知但时%[h,p,varci.stats]=vartest2(X,Y,alpha,tail)P345 例7.2.5clear all;X=[16.2 16.4 15.8 15.5 16.7 15.6 15.8];Y=[15.9 16.0 16.4 16.1 16.5 15.8 15.7 15.0];[h,p,varci,stats]=vartest2(X,Y,0.05,0)h =p =0.9232varci =0.1775 5.1754stats =fstat: 0.9087df1: 6df2: 7注:p为观察值的概率varci为方差的置信区间;stats 为卡方统计量的观测值fstat为F统计量的观测值;df1 df2分别为F分布的第一、第二自由度;若h=0: 表示在显著性水平alpha下,不能否定原假设,认为二台机床加工的精度一致。
若tail=0:表示双边假设检验;若tail=1:表示单边假设检验(mu>mu0);若tail=0:表示单边假设检验(mu<mu0);clear all;X=[20.1 20.0 19.3 20.6 20.2 19.9 20.0 19.9 19.1 19.9];Y=[18.6 19.1 20.0 20.0 20.0 19.7 19.9 19.6 20.2];[h,p,varci,stats]=vartest2(X,Y,0.05,0)h =p =0.5798varci =0.1567 2.8001stats =fstat: 0.6826df1: 9df2: 8Chi_Square(卡方)拟合优度检验检验样本是否服从指定的分布。
调用格式:1. h=chi2gof(X)检验样本X是否样本是否服从正态分布(原假设为样本服从正态分布)。
输出参数h为0(在显著性水平0.05下接受原假设,认为X服从正态分布)或1(在显著性水平0.05下拒绝原假设,认为X不服从正态分布)2.[h,p]=chi2gof(X)返回检验P值: 当P值小于或等于显著性水平alpha时,拒绝原假设,否则接受原假设。
3.[h,p,stats]=chi2gof(X)返回一个结构体变量stats,它包含字段:chi2stat: 卡方统计量;df: 自由度;edges: 合并后各区间的边界向量;O:落入每个小区间内观测的个数,即实际频数;E:每个小区间对应的理论频数4.[h,p,stats]=chi2gof(X,name1,vall,name2,val2,….)通过可选的成对出现的参数名与参数值来控制初始分组、原假设中的分布、显著性水平等。
等等其它调用格式,参见有关Matlab统计资料P357 例7.4.2clear all;bins=0:11;%总体分成的区间总类obsCounts=[57 203 383 525 532 408 273 139 45 27 10 6];%对应区间上样本观测值个数n=sum(obsCounts);%总的观测样本数据lambdaHat=sum(bins.*obsCounts) / n; %参数的MLE估计值expCounts = n * poisspdf(bins,lambdaHat);% 理论频数[h,p,st] = chi2gof(bins,'ctrs',bins,'frequency',obsCounts, ...'expected',expCounts,'nparams',1) %'frequency'指定观测值中出现的频数, 'expected'指定各区间的理论频数,'nparams'指定分布中待估参数的个数h =p =0.1692st =chi2stat: 12.8577df: 9edges: [-0.5000 0.5000 1.5000 2.5000 3.5000 4.5000 5.5000 6.5000 7.5000 8.5000 9.5000 11.5000]O: [57 203 383 525 532 408 273 139 45 27 16]E: [54.4187 210.5802 407.4339 525.5397 508.4113 393.4729 253.7659 140.2829 67.8554 29.1751 15.2612]注:h=0(p值>0.05)接受原假设: Poisson分布;P356 例7.4.1clear all;close;bins=1:6;%总体分成的区间总类obsCounts=[2 6 6 3 3 0];%对应区间上样本观测值个数n=sum(obsCounts);%总的观测样本数据expCounts=[n*0.1 n*0.2 n*0.3 n*0.2 n*0.1 n*0.1];%对应区间上的理论频数[h,p,st] = chi2gof(bins,'ctrs',bins,'frequency',obsCounts,'expected',expCounts,'nparams',0) %'nparams'指定分布中待估参数的个数h =p =0.5580st =chi2stat: 1.1667df: 2edges: [0.5000 2.5000 3.5000 6.5000]O: [8 6 6]E: [6 6 8]注:h=0(p值>0.05)接受原假设分布;clear all;bins=1:6;%总体分成的区间总类obsCounts=[2 6 6 3 3 0];%对应区间上样本观测值个数n=sum(obsCounts);%总的观测样本数据expCounts=[n*0.1 n*0.2 n*0.3 n*0.2 n*0.1 n*0.1];%对应区间上的理论频数[h,p,st]=chi2gof(bins,'ctrs',bins,'frequency',obsCounts,'expected',expCo unts,'frequency',obsCounts,'expected',expCounts,'frequency',obsCounts,'e xpected',expCounts,'frequency',obsCounts,'expected',expCounts,'frequency ',obsCounts,'expected',expCounts,'frequency',obsCounts,'expected',expCou nts) %'nparams'指定分布中待估参数的个数注:h=0(p 值>0.05) 接受原假设分布;例2 丢掷骰子100次,分别出现的点数为13次 14次 20次 17次 15次 21次 1点 2点 3点 4点 5点 6 点检验这粒骰子是否均匀?解:0H :均匀,即P {1点朝上}=……=P {6点朝上}=61 根据观测值:5667.166100>==i np 1.11)106(200.3)(216122=--<=-=-=∑αχχi i i i np np n⇒ 接受0H ,认为总体服从均匀分布,这粒骰子是均匀的.bins=1:6;%总体分成的区间总类obsCounts=[13 14 20 17 15 21];%对应区间上样本观测值个数n=sum(obsCounts);%总的观测样本数据 lambdaHat=1/6; %参数的MLE 估计值expCounts=[n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat];% 理论频数,即均为100/6[h,p,st]=chi2gof(bins,'ctrs',bins,'frequency',obsCounts,'expected',expCo unts,'nparams',0) %'nparams'指定分布中待估参数的个数h = 0 p =0.6692 st =chi2stat: 3.2000 df: 5edges: [0.5000 1.5000 2.5000 3.5000 4.5000 5.5000 6.5000] O: [13 14 20 17 15 21]E: [16.6667 16.6667 16.6667 16.6667 16.6667 16.6667]说明:h=0(p 值>0.05)故接受原假设,认为总体服从均匀分布,这粒骰子是均匀的.例3 某工厂近5年发升63次事故,按星期几分类如下星期 一 二 三 四 五 六 次数 9 10 11 8 13 12问事故发生与否与星期几有关?解 0H :61)6()1(=====X P XP 5.106163=⨯==i x p n np X 1 2 3 4 5 6i n 9 10 11 8 13 12 i np 10.5 10.5 10.5 10.5 10.5 10.507.1167.1ˆ)ˆ(295.021122==≤=-=--=∑χχχ k ki i i i p n p n n接受0H 认为事故发生与星期几无关.bins=1:6;%总体分成的区间总类obsCounts=[ 9 10 11 8 13 12];%对应区间上样本观测值个数 n=sum(obsCounts);%总的观测样本数据 lambdaHat=1/6; %参数的MLE 估计值expCounts=[n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat n*lambdaHat];% 理论频数,即均为63/6[h,p,st]=chi2gof(bins,'ctrs',bins,'frequency',obsCounts,'expected',expCo unts,'nparams',0) %'nparams'指定分布中待估参数的个数h = 0 p =0.8931 st =chi2stat: 1.6667 df: 5edges: [0.5000 1.5000 2.5000 3.5000 4.5000 5.5000 6.5000] O: [9 10 11 8 13 12]E: [10.5000 10.5000 10.5000 10.5000 10.5000 10.5000]说明:h=0(p 值>0.05)故接受原假设,认为事故发生与星期几无关.Klomogorov-Smirnov 检验Klomogorov-Smirnov 检验是检验任意已知分布函数的一种有效的假设检验算法。
