MATLAB数理统计分析
MATLAB中的统计指标计算与分析技术

MATLAB中的统计指标计算与分析技术1. 引言统计指标是用于描述和衡量数据集中分布特征的数值,对于数据分析和处理有着重要的作用。
而MATLAB作为一种强大的科学计算软件,提供了丰富的统计函数与工具,可以方便地进行统计指标的计算与分析。
本文将详细介绍MATLAB中常用的统计指标计算与分析技术,包括均值、中位数、方差、标准差等指标的计算方法,以及数据分布的可视化分析等内容。
2. 均值与中位数计算均值和中位数是常用的描述数据集中趋势的指标。
在MATLAB中,计算均值使用mean()函数,计算中位数使用median()函数。
这两个函数的使用方法非常简单,只需要输入数据集即可。
例如,对于一个包含100个数据点的数据集,可以使用以下代码计算均值和中位数:```matlabdata = randn(1, 100); % 生成一个包含100个随机数据点的数据集mean_value = mean(data); % 计算均值median_value = median(data); % 计算中位数```通过这样的计算,我们可以获得数据集的中心趋势信息,帮助我们进一步分析和理解数据。
3. 方差与标准差计算方差和标准差是度量数据集分散程度的重要指标。
方差表示数据点与均值之间的差异程度,标准差则是方差的平方根。
在MATLAB中,分别可以使用var()和std()函数来计算方差和标准差。
同样地,我们只需要输入数据集作为输入参数即可。
下面是一个例子:```matlabdata = randn(1, 100); % 生成一个包含100个随机数据点的数据集variance = var(data); % 计算方差standard_deviation = std(data); % 计算标准差```方差和标准差的计算结果可以用来描述数据集的分散情况,提供了对数据集变异程度的度量。
4. 数据分布可视化除了计算常见的统计指标,MATLAB还提供了各种数据分布可视化的函数,例如直方图、箱线图等。
MATLAB数理统计分析

1. 3 MATLAB的开发环境
1.3.1 MATLAB桌面平台
桌面平台是各桌面组件的展示平台,默认设置情况下 的桌面平台包括4个窗口,即命令窗口(Command Window)、命令历史窗口(Command History)、当前目录 窗口(Current Directory)和工作空间窗口(Workspace)。此 外,MATLAB还有编译窗口、图形窗口和帮助窗口等其他 种类的窗口。
subplot(3,1,1) capaplot(data,[-inf,xalpha1]);axis([-3,3,0,0.45]) subplot(3,1,2) capaplot(data,[xalpha2,inf]);axis([-3,3,0,0.45]) subplot(3,1,3) capaplot(data,[-inf,xalpha3]);axis([-3,3,0,0.45]) hold on capaplot(data,[xalpha4,inf]);axis([-3,3,0,0.45]) hold off
hold off text(-0.5,yy(6)+0.005,'\fontsize{14}95.44%') text(-0.5,yy(5)+0.005,'\fontsize{14}68.26%') text(-0.5,yy(7)+0.005,'\fontsize{14}99.74%') text(-3.2,-0.03,'\fontsize{10}μ-3σ') text(-2.2,-0.03,'\fontsize{10}μ-2σ') text(-1.2,-0.03,'\fontsize{10}μ-σ') text(-0.05,-0.03,'\fontsize{10}μ') text(0.8,-0.03,'\fontsize{10}μ+σ') text(1.8,-0.03,'\fontsize{10}μ+2σ') text(2.8,-0.03,'\fontsize{10}μ+3σ')
matlab中数据的统计描述和分析

matlab中数据的统计描述和分析MATLAB是一种基于计算机语言的数学软件包,它提供了处理各种数学和工程问题的工具,并在数据统计描述和分析方面发挥了重要作用。
在本文中,我们将探讨MATLAB中数据的统计描述和分析方法。
1. 数据的导入与预处理数据的导入是数据分析的第一步,MATLAB支持各种数据格式的导入,包括CSV,XLS,MAT等文件类型。
在导入数据后,预处理成为必要的步骤。
预处理的目的是删除异常值和不一致的数据点,以确保数据的准确性。
MATLAB提供了各种功能,例如删除重复值和缺失值、转换数据类型、缩放数据、标准化数据、去除噪声等,有助于准确性。
2. 数据的可视化数据的可视化是了解数据中存在的模式和趋势的重要方法,MATLAB提供了许多可视化工具,包括条形图、折线图、散点图、热力图等,以及专门用于可视化统计数据的Anova、Boxplot等工具。
3. 统计描述统计描述提供了对数据的整体理解的方法。
MATLAB提供了许多统计描述的函数,如mean(平均数)、median(中位数)、min(最小值)、max(最大值)、range(极差)、var(方差)、std(标准差)、skewness(偏度)、kurtosis(峰度)、cov(协方差)和corrcoef(相关系数)等函数可以用于计算数据的统计描述信息。
例如,假设我们有一个高斯分布的数据集,可以使用MATLAB的“randn”函数生成一个具有100项的随机高斯数据集。
data = randn(100,1);现在,使用MATLAB的“mean”和“std”函数可以计算出这些数据的统计描述信息。
平均数和标准差告诉我们有关数据的“中心”位置和分散程度的一些信息。
sigma = std(data)4. 假设检验假设检验是判断所提出的关于总体参数的假设是否显著的一种统计分析方法。
假设检验包括参数检验和非参数检验两类。
MATLAB中包含了各种假设检验的函数,例如单样本t检验、双样本t检验、方差分析、卡方检验、K-S检验等。
利用MATLAB进行统计分析

利用MATLAB进行统计分析使用 MATLAB 进行统计分析引言统计分析是一种常用的数据分析方法,可以帮助我们理解数据背后的趋势和规律。
MATLAB 提供了一套强大的统计工具箱,可以帮助用户进行数据的统计计算、可视化和建模分析。
本文将介绍如何利用 MATLAB 进行统计分析,并以实例展示其应用。
一、数据导入和预处理在开始统计分析之前,首先需要导入数据并进行预处理。
MATLAB 提供了多种导入数据的方式,可以根据实际情况选择合适的方法。
例如,可以使用`readtable` 函数导入Excel 表格数据,或使用`csvread` 函数导入CSV 格式的数据。
导入数据后,我们需要对数据进行预处理,以确保数据的质量和准确性。
预处理包括数据清洗、缺失值处理、异常值处理等步骤。
MATLAB 提供了丰富的函数和工具,可以帮助用户进行数据预处理。
例如,可以使用 `fillmissing` 函数填充缺失值,使用 `isoutlier` 函数识别并处理异常值。
二、描述统计分析描述统计分析是对数据的基本特征进行概括和总结的方法,可以帮助我们了解数据的分布、中心趋势和变异程度。
MATLAB 提供了多种描述统计分析的函数,可以方便地计算数据的均值、标准差、方差、分位数等指标。
例如,可以使用 `mean` 函数计算数据的均值,使用 `std` 函数计算数据的标准差,使用 `median` 函数计算数据的中位数。
此外,MATLAB 还提供了 `histogram`函数和 `boxplot` 函数,可以绘制数据的直方图和箱线图,从而更直观地展现数据的分布特征。
三、假设检验假设检验是统计分析中常用的推断方法,用于检验关于总体参数的假设。
MATLAB 提供了多种假设检验的函数,可以帮助用户进行单样本检验、双样本检验、方差分析等分析。
例如,可以使用 `ttest` 函数进行单样本 t 检验,用于检验一个总体均值是否等于某个给定值。
可以使用 `anova1` 函数进行单因素方差分析,用于比较不同组之间的均值差异是否显著。
matlab中数据的统计描述与分析

第十章数据的统计描述和分析数理统计研究的对象是受随机因素阻碍的数据,以下数理统计就简称统计,统计是以概率论为根底的一门应用学科.数据样本少那么几个, 多那么成千上万,人们希望能用少数几个包括其最多相关信息的数值来表现数据样本整体的规律.描述性统计确实是搜集、整理、加工和分析统计数据,使之系统化、层次化,以显示出数据资料的趋势、特点和数量关系.它是统计推断的根底,有效性较强,在统计工作中常常利用.面对一批数据如何进行描述与分析,需要把握参数估量和假设查验这两个数理统计的最大体方式.咱们将用Matlab的统计工具箱〔Statistics Toolbox〕来实现数据的统计描述和分析.§ 1统计的大体概念整体和样本整体是人们研究对象的全部,又称母体,如工厂一天生产的全数产品〔按合格品及废品分类〕,学校全部学生的身高.整体中的每一个大体单位称为个体,个体的特点用一个变量〔如x〕来表示,如一件产品是合格品记x 0,是废品记x 1; 一个身高170 〔cm〕的学生记x 170.从整体中随机产生的假设干个个体的集合称为样本,或子样,如n件产品,100名学生的身高,或一根轴直径的10次测量.事实上这确实是从整体中随机取得的一批数据,不妨记作x1,x2, , x n, n称为样本容量.简单地说,统计的任务是由样本推断整体.频数表和直方图一组数据〔样本〕往往是杂乱无章的,作出它的频数表和直方图,能够看做是对这组数据的一个初步整理和直观描述.将数据的取值范围划分为假设干个区间,然后统计这组数据在每一个区间中显现的次数,称为频数,由此取得一个频数表.以数据的取值为横坐标,频数为纵坐标,画出一个阶梯形的图,称为直方图,或频数散布图.假设样本容量不大,能够手工作出频数表和直方图,当样本容量较大时那么能够借助Matlab如此的软件了.让咱们以下面的例子为例,介绍频数表和直方图的作法.例1学生的身高和体重学校随机抽取100名学生,测量他们的身高和体重,所得数据如表(i )数据输入数据输入通常有两种方式,一种是在交互环境中直接输入,假设是在统计中数据量比较大,如此作不太方便;另一种方法是先把数据写入一个纯文本数据文件中,格式如例1的表格,有20行、10歹U,数据列之间用空格键或Tab键分割,该数据文件存放在matlab\work 子目录下,在Matlab顶用load命令读入数据,具体作法是:load如此在内存中成立了一个变量data,它是一个包括有20 10个数据的矩阵.为了取得咱们需要的100个身高和体重各为一列的矩阵,应做如下的改变:high=data(:,1:2:9);high=high(:)weight=data(:,2:2:10);weight=weight(:)(ii )作频数表及直方图用hist命令实现,其用法是:[N,X] = hist(Y,M)数组(行、列都可) Y的频数表.它将区间[min(Y),max(Y)] 等分为M份(缺省时M设定为10), N返回M个小区间白频数,X返回M个小区间的中点.hist(Y,M)数组Y的直方图.关于例1的数据,编写程序如下:load ;high=data(:,1:2:9);high=high(:);weight=data(:,2:2:10);weight=weight(:);[n1,x1]=hist(high)%不面语句与hist命令等价%n1=[length(find(high<),…% length(find(high>=&high<),…% length(find(high>=&high<),…% length(find(high>=&high<),…% length(find(high>=&high<),…% length(find(high>=&high<),…% length(find(high>=&high<),…% length(find(high>=&high<180)),…% length(find(high>=180&high<),…% length(find(high>=)][n2,x2]=hist(weight)subplot(1,2,1)hist(high) subplot(1,2,2) hist(weight)计算结果略,直方图如以下列图所示:从直方图上能够看出,身高的散布大致呈中间高、两头低的钟形;而体重那么看不出什么规律.要想从数值上给出更确切的描述,需要进一步研究反映数据特点的所谓“统计量〞.直方图所展现的身高的散布形状可看做正态散布,固然也能够用这组数据对散布作假设查验.例2 统计以下五行字符串中字符a、g、c、t显现的频数解把上述五行复制到一个纯文本数据文件中,放在matlab\work子目录下,编写如下程序:clcfid1=fopen( '' ,'r');i=1;while (~feof(fid1))data=fgetl(fid1);a=length(find(data==97));b=length(find(data==99));c=length(find(data==103));d=length(find(data==116));e=length(find(data>=97&data<=122));f(i,:)=[a b c d e a+b+c+d];i=i+1;endfhe=[sum(f(:,1)) sum(f(:,2)) sum(f(:,3)) sum(f(:,4))sum(f(:,5)) sum(f(:,6))]fid2=fopen( " , 'w');fprintf(fid2,'%8d %8d %8d %8d %8d %8d\n' 力;fclose(fid1);fclose(fid2);咱们把统计结果最后写到一个纯文本文件中,在程序中多引进了几个变量,是为了查验字符串是不是只包括a、g、c、t四个字符.统计量假设有一个容量为n的样本(即一组数据),记作x (x1,x2, ,x n),需要对它进行必然的加工,才能提出有效的信息,用作对整体(散布)参数的估量和查验.统计量确实是加工出来的、反映样本数量特点的函数,它不含任何未知量.下面咱们介绍几种经常使用的统计量.(i )表示位置的统计量一算术平均值和中位数算术平均值(简称均值)描述数据取值的平均位置,记作x ,_ 1 nx —x in i 1中位数是将数据由小到大排序后位于中间位置的那个数值.Matlab中mean(x)返回x的均值,median(x)返回中位数.标准差s概念为12 x)2它是各个数据与均值偏离程度的气宇,这种偏离不妨称为变异. (1)(ii )表示变异程度的统计量一标准差、方差和极差(2)方差是标准差的平方s 2.极差是x (x 1 ,x 2,,x n )的最大值与最小值之差.Matlab 中std(x)返回x 的标准差,var(x)返回方差,range(x)返回极差.你可能注意到标准差 s 的概念(2)中,对n 个(x i x)的平方求和,却被(n 1)除, 这是出于无偏估量的要求.假设需要改成被n 除,Matlab 可用std(x,1)和var(x,1)来 实现.(iii )中央矩、表示散布形状的统计量一偏度和峰度随机变量x 的r 阶中央矩为E(x Ex)「.随机变量x 的偏度和峰度指的是 x 的标准化变量(x Ex)/V Dx 的三阶中央矩和 四阶中央矩:__3E x E(x)~、3/2-D(x)__4E x E(x) D(x) 2侧的多;1 0称为左偏态,情形相反;而1接近0那么能够为散布是对称的.峰度是散布形状的另一种气宇,正态散布的峰度为 3,假设2比3大得多,表示散 布有繁重的尾巴,说明样本中含有较多远离均值的数据,因此峰度能够用作衡量偏离正 态散布的尺度之一.Matlab 中moment(x,order) 返回x 的order 阶中央矩,order 为中央矩的阶数. skewness(x)返回x 的偏度,kurtosis(x) 返回峰度.在以上用Matlab 计算各个统计量的命令中,假设x 为矩阵,那么作用于 x 的列, 返回一个行向量.对例1给出的学生身高和体重,用 Matlab 计算这些统计量,程序如下: clc load ;high=data(:,1:2:9);high=high(:);x E(x) .D(x) x E(x) ,D(x)偏度反映散布的对称性, 0称为右偏态,现在数据位于均值右边的比位于左weight=data(:,2:2:10);weight=weight(:);shuju=[high weight];jun_zhi=mean([high weight])zhong_wei_shu=median(shuju)biao_zhun_cha=std(shuju)ji_cha=range(shuju)pian_du=skewness(shuju)feng_du=kurtosis(shuju)统计量中最重要、最经常使用的是均值和标准差,由于样本是随机变量,它们作为样本的函数自然也是随机变量,当用它们去推断整体时,有多大的靠得住性就与统计量的概率散布有关,因此咱们需要明白几个重要散布的简单性质.统计中几个重要的概率散布散布函数、密度函数和分位数随机变量的特性完全由它的(概率)散布函数或(概率)密度函数来描述.设有随机变量X ,其散布函数概念为X x的概率,即F (x) P{ X x}.假设X是持续型随机变量,那么其密度函数p(x)与F(x)的关系为xF (x)p(x)dx.分位数是下面经常使用的一个概念,其概念为:关于01,使某散布函数F(x) 的x,成为那个散布的分位数,记作x.咱们前面画过的直方图是频数散布图,频数除以样本容量n,称为频率,n充分大时频率是概率的近似,因此直方图能够看做密度函数图形的(离散化)近似.统计中几个重要的概率散布(i )正态散布正态散布随机变量X的密度函数曲线呈中间高两边低、对称的钟形,期望(均值)22、EX ,方差DX 2,记作X ~ N( , 2), 称均方差或标准差,当0,1时称为标准正态散布,记作X ~ N(0,1).正态散布完全由均值和方差2决定,它的偏度为0,峰度为3.正态散布能够说是最多见的(持续型)概率散布, 成批生产时零件的尺寸,射击中弹着点的位置,仪器反复量测的结果,自然界中一种生物的数量特点等,多数情形下都服从正态散布,这不仅是观看和体会的总结,而且有着深刻的理论依据,即在大量彼此独立的、作用差不多大的随机因素阻碍下形成的随机变量,其极限散布为正态散布.鉴于正态散布的随机变量在实际生活中如此地常见,记住下面3个数字是有效的:68%勺数值落在距均值左右1个标准差的范围内,即P{ X } 0.68;95%勺数值落在距均值左右2个标准差的范围内,即P{ 2 X 2 } 0.95;%勺数值落在距均值左右3个标准差的范围内,即P{ 3 X 3 } 0.997.(ii )2散布(Chi square)假设X i,X2, ,X n为彼此独立的、服从标准正态散布N (0,1)的随机变量,那么它们n的平方和YX:服从2散布,记作Y〜2(n) , n称自由度,它的期望EY n ,i 1方差DY 2n.(iii ) t散布X假设X〜N (0,1) , Y〜2(n),且彼此独立,那么T ~^= 服从t散布,记作.Y/nT ~ t(n) , n称自由度.t散布又称学生氏(Student)散布.t散布的密度函数曲线和N (0,1)曲线形状相似.理论上n 时,T ~t(n)N(0,1),实际被骗n 30时它与N(0,1)就相差无几了.(iv ) F散布X/n 假设X〜2(n.,Y〜2(电),且彼此独立,那么F 1服从F散布,记作Y/n2F〜F(n1,n2),⑺〜奥)称自由度.Matlab 统计工具箱(Toolbox\Stats)中的概率散布Matlab统计工具箱中有20种概率散布,那个地址只对上面所述4种散布列出命令的字符:norm 正态散布;chi2 2散布;t t散布F散布工具箱对每一种散布都提供5类函数,其命令的字符是:pdf概率密度;cdf 散布函数;inv散布函数的反函数;stat均值与方差;rnd 随机数生成当需要一种散布的某一类函数时,将以上所列的散布命令字符与函数命令字符接起来,并输入自变量(能够是标量、数组或矩阵)和参数就好了,如:p=normpdf(x,mu,sigma) 均值mu标准差sigma的正态散布在x的密度函数(mu=0, sigma=1 时可缺省).p=tcdf(x,n) t散布(自由度n)在x的散布函数.x=chi2inv(p,n) 2散布(自由度n)使散布函数F(x)=p的x(即p分位数).[m,v]=fstat(n1,n2) F散布(自由度n1,n2)的均值m和方差v.几个散布的密度函数图形就能够够用这些命令作出,如:x=-6::6;y=normpdf(x);z=normpdf(x,0,2);plot(x,y,x,z),gtext( 'N(0,1), ),gtext( 'N(0,2A2),)散布函数的反函数的意义从下例看出:x=chi2inv,10)x =假设是反过来计算,那么P=chi2cdf,10)P =正态整体统计量的散布用样本来推断整体,需要明白样本统计量的散布,而样本又是一组与整体同散布的随机变量,因此样本统计量的散布依托于整体的散布.当整体服从一样的散布时,求某个样本统计量的散布是很困难的,只有在整体服从正态散布时,一些重要的样本统计量(均值、标准差)的散布才有便于利用的结果.另一方面,现实生活中需要进行统计推断的整体,多数能够以为服从(或近似服从)正态散布,因此统计中人们在正态整体的假定下研究统计量的散布,是必要的与合理的.设整体X - N( , 2), x1,x2, ,x n为一容量n的样本,其均值x和标准差s由式〔1〕、〔2〕确信,那么用 X 和S 构造的下面几个散布在统计中是超级有效的.样本确信的均值X, y 和标准差S 1,S 2,那么要反复用到这些散布.§ 2参数估量般是X ~ N 〔 , 2〕,估量参数的散布,如,2.参数估量分点估量和区间估量两种.点估量点估量是用样本统计量确信整体参数的一个数值.评判估量好坏的标准有无偏性、 最小方差性、有效性等,估量的方式有矩法、极大似然法等.最经常使用的是对整体均值和2方差〔或标准差〕作点估量.让咱们临时抛 开评判标准,当从一个样本依照式〔1〕、〔2〕算出样本均值X 和方差S 2后,对 和2〔或 〕一个自然、合理的点估量显然是〔在字母上加人表示它的估量值〕? x, ?2 s 2, ? s(9)区间估量点估量尽管给出了待估参数的一个数值,却没有告知咱们那个估量值的精度和可信2-,、 X X - N (,——)或一 n ——〜N(0,1)/、n(3)(n 1)S 222(n 1).X―^~t(n S / . n1)(5)设有两个整体 X~N 〔 1,;〕和Y~N 〔 2,2、2〕,及由容量别离为n 1,rb 的两个其中S 2关于〔7〕 (X121) (y / n 1——2) ~ N (0,1) ;/口2(X 1) (y 2)2 ,2 ,,,S /n 1 S /n 2~t(n 1 n 2 2)(6)22〔n 1 1内〔出1底 n in 2 2S ;/ S |/2B~F(n 1 1,叫 1)2(8)式,假定2,但它们未知,于是用S 代替.在下面的统计推断中咱们利用样本对整体进行统计推断的一类问题是参数估量, 即假定整体的散布,程度.一样地,整体的待估参数记作(如,2),由样本算出的的估量量记作 ,人们常希望给出一个区间[?,?],使以必然的概率落在此区间内.假设有P{?2} 1,01(10)那么[?, ?2]称为的置信区间,?,2别离称为置信下限和置信上限,i 称为置信概率或置信水平,称为显著性水平.给出的置信水平为i 的置信区间[?,?],称为的区间估量.置信区间越小, 估量的精度越高;置信水平越大,估量的可信程度越高.可是这两个指标显然是矛盾的, 一般是在必然的置信水平下使置信区间尽可能小.通俗地说,区间估量给出了点估量的误差范围.参数估量的Matlab实现Matlab统计工具箱中,有专门计算整体均值、标准差的点估量和区间估量的函数.关于正态整体,命令是[mu,sigma,muci,sigmaci]=normfit(x,alpha)其中x为样本(数组或矩阵),alpha为显著性水平(alpha缺省时设定为),返回整体均值和标准差的点估量mu和sigma ,及整体均值和标准差的区间估量muci 和sigmaci.当x为矩阵时返回行向量.Matlab统计工具箱中还提供了一些具有特定散布整体的区间估量的命令,如expfit , poissfit , gamfit ,你能够从这些字头猜出它们用于哪个散布,具体用法参见帮助系统.§ 3假设查验统计推断的另一类重要问题是假设查验问题.在整体的散布函数完全未知或只知其形式但不知其参数的情形,为了推断整体的某些性质,提出某些关于整体的假设.例如, 提出整体服从泊松散布的假设,又如关于正态整体提出数学期望等于0的假设等.假设查验确实是依照样本对所提出的假设做出判定:是同意仍是拒绝.这确实是所谓的假设查验问题.单个整体N〔 , 2〕均值的查验原假设〔或零假设〕为:H0:备选假设有三种可能:111:0,111:0,111:0.2…….,关于的查验〔u查验〕在Matlab中u查验法由函数ztest来实现,命令为[h,p,ci]=ztest〔x,mu,sigma,alpha,tail〕其中输入参数x是样本,mu是H0中的0, sigma是整体标准差,alpha是显著性水平〔alpha缺省时设定为〕,tail是对备选假设H^^选择:H1为0时用tail=0〔可缺省〕;也为0时用tail=1 ; H1为0时用tail=-1.输出参数h=0表示同意H0, h=1表示拒绝H0, p表示在假设H O下样本均值显现的概率,p越小H O越值得疑心,ci是0的置信区间.例3某车间用一台包装机包装糖果.包得的袋装糖重是一个随机变量,它服从正态散布.当机械正常时,其均值为千克,标准差为千克.某日开工后为查验包装机是不是正常,随机地抽取它所包装的糖9袋,称得净重为〔千克〕:问机械是不是正常解整体 ,x〜N〔 ,0.0152〕, 未知.于是提出假设H O :O 0.5和H1 :0.5.Matlab实现如下:x=[...];[h,p,ci]=ztest〔x,,求得h=1, p=,说明在的水平下,可拒绝原假设,即以为此日包装机工作不正常.2未知,关于的查验〔t查验〕在Matlab中t查验法由函数ttest来实现,命令为[h,p,ci]=ttest〔x,mu,alpha,tail〕例4某种电子元件的寿命x〔以小时计〕服从正态散布,,2均未知.现得16只元件的寿命如下159 280 101 212 224 379 179 264222 362 168 250 149 260 485 170问是不是有理由以为元件的平均寿命大于225(小时)?解按题意需查验H0:0225, H1 :225,取0.05.Matlab实现如下:x=[159 280 101 212 224 379 179 264...222 362 168 250 149 260 485 170];[h,p,ci]=ttest(x,225,,1)求得h=0, p=,说明在显著水平为的情形下,不能拒绝原假设,以为元件的平均寿命不大于225小时.两个正态整体均彳1差的查验〔t查验〕还能够用t查验法查验具有相同方差的2个正态整体均值差的假设.在Matlab中由函数ttest2 实现,命令为:[h,p,ci]=ttest2〔x,y,alpha,tail〕与上面的ttest相较,不同处只在于输入的是两个样本x,y 〔长度不必然相同〕,而不是一个样本和它的整体均值;tail的用法与ttest相似,可参看帮助系统.例5在平炉上进行一项实验以确信改变操作方式的建议是不是会增加钢的得率,实验是在同一平炉上进行的.每炼一炉钢时除操作方式外,其它条件都可能做到相同.先用标准方式炼一炉,然后用建议的新方式炼一炉,以后互换进行,各炼了10炉,其得率别离为10标准方式2新方式设这两个样本彼此独立且别离来自正态整体N〔1, 2〕和N〔2, 2〕, 1, 2, 2均未知,问建议的新方式可否提升得率〔取0.05.〕解〔i 〕需要查验假设20, H I:I 20.(ii)Matlab 实现];y=[]; [h,p,ci]=ttest2(x,y,,-1)求得h=1,p= x 10-4.说明在0.05的显著水平下,能够拒绝原假设,即以为建议的新操作方式较原方式优.散布拟合查验在实际问题中,有时不能预知整体服从什么类型的散布,这时就需要依照样本来查验关于散布的假设.下面介绍2查验法和专用于查验散布是不是为正态的“偏峰、峰度查验法〞. 2 ・. ■查验法H .:整体x 的散布函数为F(x),H i :整体x 的散布函数不是 F(x).在用下述2查验法查验假设 H o 时,假设在假设 H o 下F (x)的形式,但其参数值未知,这时需要先用极大似然估量法估量参数,然后作查验.2 .查验法的大体思想如下:将随机实验可能结果的全部分为k 个互不相容的事k件 AAA,...' (A k ,AA j ,i j,i,j 1,2,,k).于是在假设 H o 下,1 1咱们能够计算p i P(A)(或i ?(A)), i 1,2,...,k .在n 次实验中,事件A 显现的频率f i /n 与p i (色)往往有不同,但一样来讲,假设H o 为真,且实验的次数又甚多时 那么这种不同不该该专门大.基于这种方式,皮尔逊利用0k (f. np. )2 o k (f. n? )22 -J ―匕或 2—i ― i 1 np i i 1 n ?j作为查验假设H 0的统计量.并证实了以下定理.定理 假设n 充分大,那么当H .为真时(不管H .中的散布属什么散布 ),统计量(11)老是近似地服从自由度为 k r 1的2散布,其中r 是被估量的参数的个数.于是,假设在假设H 0下算彳导(11)有2222(k r 1),在显著性水平下拒绝H 0,不然就同意.注意:在利用2查验法时,要求样本容量n 不小于50,和每一个nR 都不小于5,x=[(11)而且np i最好是在5以上.不然应适本地归并A ,以知足那个要求.例6下面列出了84个伊特拉斯坎(Etruscan )人男子的头颅的最大宽度(mm, 试查验这些数据是不是来自正态整体(取0.1).141148132138154142150146155158150140147148144150149145149158143141144144126140144142141140145135147146141136140146142137148154137139143140131143141149148135148152143144141143147146150132142142143153149146149138142149142137134144146147140142140137152145解编写Matlab程序如下:clcx=[141 148 132 138 154 142 150 146 155 158...150 140147148144150149145149158...143 141144144126140144142141140...145 135147146141136140146142137...148 154137139143140131143141149...148 135148152143144141143147146...150 132142142143153149146149138...142 149142137134144146147140142...140 137152145];min(x),max(x) %求数据中的最小数和最大数hist(x,8) %画直方图fi=[length(find(x<135)), ...length(find(x>=135&x<138)),length(find(x>=138&x<142)),length(find(x>=142&x<146)),length(find(x>=146&x<150)),length(find(x>=150&x<154)),mu=mean(x),sigma=std(x) %均值和标准差fendian=[135,138,142,146,150,154] %区间的分点p0=normcdf(fendian,mu,sigma) %分点处散布函数的值求得皮尔逊统计量 chisum=, 京(7 2 1)H 0,即以为数据来自正态散布整体.偏度、峰度查验(留作习题 1)其它非参数查验Matlab 还提供了一些非参数方式.Wilcoxon 秩和查验在Matlab 中,秩和查验由函数ranksum 实现.命令为:[p,h]=ranksum(x,y,alpha)其中x, y 可为不等长向量,alpha 为给定的显著水平,它必需为.和1之间的数量.p 返回 产生两独立样本的整体是不是相同的显著性概率,h 返回假设查验的结果.假设是 x 和y 的整体不同不显著,那么 h 为零;假设是x 和y 的整体不同显著,那么 h 为1.假设是p 接近于零, 那么可对原假设质疑.例7某商店为了确信向公司 A 或公司B 购置某种产品,将 A, B 公司以往各次进 货的次品率进行比拟,数据如下所示,设两样本独立.问两公司的商品的质量有无显著 不同.设两公司的商品的次品的密度最多只差一个平移,取0.05.A :B :length(find(x>=154))] %各区间上显现的频数p1=diff(p0) p=[p0(1),p1,1-p0(6)]chi=(fi-84*p).A 2./(84*p)chisum=sum(chi)x_a=chi2inv,4) %chi2% % % 散布的分位数中间各区间的概率 所有区间的概率 皮尔逊统计量的值 2.1(4) 7.7794,故在水平下同意解别离以A、B记公司A、B的商品次品率整体的均值.所需查验的假设是H0 : A B,H1: A B -Matlab实现如下:a=[];b=[];[p,h]=ranksum(a,b)求得p=, h=0,说明两样本整体均值相等的概率为,并非很接近于零,且h=0说明能够同意原假设,即以为两个公司的商品的质量无明显不同.中位数查验在假设查验中还有一种查3^方式为中位数查验,在一样的教学中不必然介绍,但在实际中也是被普遍应用到的.在Matlab中提供了这种查验的函数.函数的利用方式简单, 下面只给出函数介绍.signrank 函数signrank Wilcoxon符号秩查验[p,h]=signrank(x,y,alpha)其中p给出两个配对样本x和y的中位数相等的假设的显著性概率.向量x, y的长度必需相同,alpha为给出的显著性水平, 取值为0和1之间的数.h返回假设查验的结果. 假设是这两个样本的中位数之差几乎为0,那么h=0;假设有显著不同,那么h=1osigntest 函数signtest符号查验[p,h]= signtest(x,y,alpha)其中p给出两个配对样本x和y的中位数相等的假设的显著性概率.x和y假设为向量,二者的长度必需相同;y亦可为标量,在此情形下,计算x的中位数与常数y之间的不同. alpha和h同上.习题十1.试用偏度、峰度查验法查验例6中的数据是不是来自正态整体(取0.1).2. 下面列出的是某工厂随机选取的20只部件的装配时刻(分):,,,,,,,,,,,,,,,,,,,.设装配时刻的整体服从正态散布,是不是能够以为装配时刻的均值显著地大于10 (取0.05) ?3.下表别离给出两个文学家马克・吐温(Mark Twain)的八篇小品文及斯诺特格拉斯(Snodgrass)的10篇小品文中由3个字母组成的词的比例.马克・吐温斯诺特格拉斯设两组数据别离来自正态整体,且两整体方差相等. 两样本彼此独立,问两个作家所写的小品文中包括由3个字母组成的词的比例是不是有显著的不同(取0.05) ?。
Matlab中常用的统计分析方法与函数

Matlab中常用的统计分析方法与函数统计分析是一种通过数理统计方法对数据进行分析和处理的方式,是研究各类现象的规律性和变异性的重要手段。
在实际应用中,Matlab作为一种功能强大的数学软件,提供了许多常用的统计分析方法与函数,能够方便地进行数据处理和分析。
本文将介绍一些Matlab中常用的统计分析方法与函数,帮助读者更好地运用这些功能。
一、数据可视化分析数据可视化是统计分析的重要环节,可以直观地展示数据的分布和趋势,有助于我们对数据的理解和分析。
在Matlab中,有许多函数可以帮助我们进行数据可视化分析,如plot函数可以绘制一维数据的曲线图;scatter函数可以绘制二维数据的散点图;histogram函数可以绘制数据的直方图等等。
通过这些函数,我们可以直观地看到数据的分布情况,从而对数据进行更深入的分析。
二、数据处理与统计分析在数据处理和统计分析方面,Matlab也提供了丰富的函数和方法。
对于数据处理,Matlab中有一系列的函数可以帮助我们进行数据的读取和写入,数据的清洗和筛选等操作。
通过这些函数,我们可以方便地对各种格式的数据进行处理,提高数据的质量和准确性。
在统计分析方面,Matlab提供了许多统计量的计算函数,如mean函数可以计算数据的均值;median函数可以计算数据的中位数;std函数可以计算数据的标准差等等。
此外,Matlab还支持假设检验、方差分析、回归分析等常用的统计方法,通过调用相应的函数可以实现这些分析。
三、概率分布及随机数生成概率分布是描述随机变量取值的概率特征的数学函数,是统计分析中常用的工具之一。
在Matlab中,有许多函数可以用来模拟各种常见的概率分布,如正态分布、均匀分布、指数分布等。
通过这些函数,我们可以生成服从指定概率分布的随机数,以进行模拟实验和概率计算。
此外,Matlab还提供了一些函数来计算概率密度函数、累积分布函数以及分布的随机数等。
四、回归分析回归分析是一种用于研究两个或多个变量之间关系的统计方法,广泛应用于各个领域。
数理统计方法的Matlab实现(6.5版)

数理统计的Matlab实现
[H,SIG,CI]=ttest2 (x, y, ,tail) 对两个正态总 体的均值作检验 若tail=0, 表示 H 1 : 1 2 若tail=1, 表示 H 1 : 1 2 若tail=-1,表示 H 1 : 1 2 结论:H=0,表示接受原假设 H 0 : 1 2 H=1,表示拒绝原假设 H 0 : 1 2 SIG为犯错误的概率,CI为均值差的置信区间。
因素A 因素B B1 B2 B3
A1 95 93 85 86 72 76 A2 A3 A4
97 96 87 89 90 91 89 90 84 87 92 90 75 73 85 86 88 89
AB2=[95 93 97 96 87 89 90 91;85 86 89 90 84 87 92 90;72 76 75 73 85 86 88 89 ] anova2(AB2',2)
数理统计的Matlab实现
例2自动包装机包装出的产品服从正态分 布 N (0.5 , 0.0152 ) ,从中抽取出9个样品,它们的 重量是 0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512 问包装机的工作是否正常? ( =0.05) x=[0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512]; [H,SIG]=ztest(x, 0.5, 0.015, 0.05,0)
数理统计的Matlab实现
其中 y:y的 n 1 数据向量 x:x的数据 n m 矩阵 b: b0 , b1 ,, bm 的估计值 bint:b的置信区间 r:残差 rint :r的置信区间 stats:第一个值是回归方程的置信度,第二值是F统 计量的值,第三值小说明所建的回归方程有意义。
使用Matlab进行统计分析的基本步骤

使用Matlab进行统计分析的基本步骤统计分析是指通过对收集到的数据进行整理、描述、分析和解释,从而揭示数据背后的规律和关联性。
Matlab是一种强大的数值计算和科学工程软件,广泛应用于各个领域的数据分析和建模。
本文将介绍使用Matlab进行统计分析的基本步骤。
一、数据准备和导入进行任何统计分析之前,首先需要准备和导入数据。
数据可以来自于实验、调查、采样等方式收集得到。
在Matlab中,可以通过各种途径导入数据,如文本文件、Excel文件、数据库等。
在导入数据之前,需要确保数据格式正确、无误,并进行必要的清洗和预处理。
二、数据的描述统计描述统计是对数据进行描述和分析的过程。
通过描述统计,可以获得数据的中心趋势、离散程度、分布特征等信息。
在Matlab中,可以使用一系列函数进行描述统计分析。
例如,mean函数可以计算数据的均值,std函数可以计算标准差,median函数可以计算中位数,hist函数可以绘制直方图等。
三、数据的可视化分析数据可视化是将数据以图形或图表的形式展示出来,以便更直观地理解数据之间的关系和趋势。
Matlab提供了强大的绘图功能,可以绘制散点图、柱状图、折线图等多种图形。
通过调用相应的绘图函数,可以将数据可视化展示出来,并进行进一步的分析和解读。
四、假设检验与推断统计假设检验与推断统计是统计学中重要的分析方法,用于对总体参数、分布或数据之间的关系进行推断。
在Matlab中,可以使用ttest函数进行单样本或双样本的假设检验,使用anova 函数进行方差分析,使用corrcov函数计算相关系数矩阵等。
这些函数可以帮助我们进行假设检验和推断统计,以得出对总体或样本的推断性结论。
五、回归分析和建模回归分析是研究变量之间相互依赖关系的一种统计方法,常用于预测、数据建模和因果推断。
在Matlab中,可以通过调用regress函数实现线性回归分析,使用fitlm函数进行多元线性回归分析,使用glm函数进行广义线性模型分析等。
Matlab中常用的统计分析方法

Matlab中常用的统计分析方法统计分析是一项对数据进行收集、整理、分析和解释的过程,它对于研究和决策具有重要意义。
在各个领域中,Matlab作为一种强大的数据分析工具,为我们提供了许多常用的统计分析方法。
本文将介绍一些常见的统计分析方法,并讨论它们在Matlab中的应用。
一、描述性统计分析描述性统计分析是对数据进行描述和总结的一种方法。
它通过计算数据的均值、中位数、标准差、最大值、最小值等指标来揭示数据的集中趋势和离散程度。
在Matlab中,我们可以利用函数mean()、median()、std()、max()、min()等来进行描述性统计分析。
例如,我们可以使用mean()函数计算数据的均值:```matlabdata = [1, 2, 3, 4, 5];mean_value = mean(data);```二、假设检验假设检验是用来评估两个或多个数据集之间是否存在显著差异的方法。
在Matlab中,我们可以利用ttest2()函数来进行双样本t检验,利用anova1()函数来进行单因素方差分析。
双样本t检验常用于比较两个样本平均值是否有显著差异。
例如,我们想比较两组学生的成绩是否存在差异,可以使用ttest2()函数:```matlabgroup1 = [80, 85, 90, 95, 100];group2 = [70, 75, 80, 85, 90];[p, h] = ttest2(group1, group2); % p值表示差异的显著性```单因素方差分析用于比较多个样本平均值是否有显著差异。
例如,我们想比较三个不同条件下的实验结果是否有差异,可以使用anova1()函数:```matlabdata = [80, 85, 90; 70, 75, 80; 90, 95, 100];p = anova1(data); % p值表示差异的显著性```三、相关性分析相关性分析用于评估两个或多个变量之间的关联程度。
如何利用Matlab进行统计分析

如何利用Matlab进行统计分析利用Matlab进行统计分析概述:Matlab是一种功能强大的数值分析和科学计算工具,广泛应用于统计分析领域。
本文将介绍如何利用Matlab进行统计分析,包括数据预处理、描述性统计分析、假设检验和回归分析等内容。
通过学习和运用Matlab的统计工具箱,可以更高效、准确地进行统计分析。
数据预处理:在进行统计分析之前,首先需要对数据进行预处理。
Matlab提供了多种数据导入和处理的函数,可轻松处理各种格式的数据文件。
例如,可以使用"readtable"函数读取Excel文件,使用"csvread"函数读取CSV文件。
同时,Matlab还提供了数据清洗的功能,例如删除空值、异常值或重复值等。
数据预处理的目的是减少数据集中的噪音和错误,以获得高质量的统计结果。
描述性统计分析:描述性统计分析是统计学中最基础的方法,用于对数据集的各个属性进行描述和总结。
Matlab提供了丰富的描述性统计函数,可用于计算数据的均值、中位数、标准差、方差等基本统计量。
通过这些函数,我们可以对数据的分布、偏态和峰度等特征进行直观的描述和分析。
假设检验:假设检验是统计分析中常用的方法,用于对样本数据与总体假设之间的差异进行验证。
Matlab提供了多种假设检验函数,包括单样本t检验、双样本t检验、方差分析等。
用户可以根据实际需求选择相应的假设检验方法,并通过统计结果得出结论。
通过假设检验,我们可以验证某种观察结果是否显著,从而对研究问题提供可靠的解释和支持。
回归分析:回归分析是统计学中常用的方法,用于研究变量之间的相关性和预测。
Matlab 提供了多种回归分析函数,包括线性回归、多项式回归、逻辑回归等。
通过这些函数,可以拟合数据并得出回归模型,进一步进行预测和模型评估。
回归分析在经济学、社会学、市场研究等领域具有重要应用,能帮助我们深入理解和预测变量之间的关系。
MATLAB中的统计分析方法介绍

MATLAB中的统计分析方法介绍引言:统计分析是一种重要的数据分析技术,它可以帮助我们从数据中获取有用的信息和洞察力。
作为一种强大的数值计算工具,MATLAB提供了丰富的统计分析函数和工具箱,本文将介绍一些MATLAB中常用的统计分析方法。
一、描述统计分析方法描述统计分析是对数据进行整体性的概括和描述,通常包括中心趋势和离散度两方面的指标。
在MATLAB中,我们可以使用mean、median、mode、std等函数计算这些指标。
例如,使用mean函数可以计算数据的平均值:```matlabdata = [1, 2, 3, 4, 5];avg = mean(data);disp(avg);```除了计算单个变量的描述统计量外,我们还可以使用corrcov函数计算协方差矩阵和相关系数矩阵,从而评估数据之间的相关性。
二、概率分布和假设检验概率分布是统计分析中最基本的工具之一,它描述了随机变量的取值概率。
MATLAB提供了多种概率分布函数,例如正态分布、指数分布、泊松分布等。
我们可以使用这些函数生成服从特定概率分布的随机数,并进行各种假设检验。
例如,我们可以使用normrnd函数生成服从正态分布的随机数,并使用normfit 函数计算正态分布的参数。
另外,我们还可以使用chi2gof函数对数据进行卡方检验,用ttest函数对均值进行假设检验等。
三、回归分析和方差分析回归分析和方差分析是一类广泛应用于数据建模和预测的统计分析方法。
MATLAB提供了regress函数和anova函数用于执行这两类分析。
在回归分析中,我们可以使用regress函数根据给定的自变量和因变量数据拟合出一个线性回归模型,并可视化模型结果。
此外,我们还可以使用polyfit函数进行多项式回归分析,或使用fitlm函数进行更复杂的线性回归分析。
对于方差分析,我们可以使用anova1函数进行单因素方差分析,进行不同样本之间的差异性比较。
MATLAB的统计分析

MATLAB的统计分析MATLAB是一种强大的计算机软件,用于数值分析、统计分析和数据可视化等多个领域。
它提供了丰富的工具和函数,可以帮助用户进行各种统计分析任务,如描述统计、假设检验、回归分析和聚类分析等。
在本文中,我们将详细介绍MATLAB在统计分析方面的功能和应用。
首先,MATLAB提供了一系列用于描述统计的函数。
通过这些函数,用户可以计算一些样本或数据集的基本统计指标,如平均值、中位数、标准差、方差和百分位数等。
例如,可以使用mean函数计算数据集的平均值,使用std函数计算标准差。
此外,MATLAB还提供了一些用于绘制统计图表的函数。
通过这些函数,可以可视化数据的分布、趋势和关系等。
例如,使用histogram函数可以生成直方图,使用scatter函数可以生成散点图,使用boxplot函数可以生成箱线图。
除了描述统计,MATLAB还提供了一些假设检验的函数,用于检验样本或数据集的参数。
这些函数可以帮助用户进行t检验、方差分析、卡方检验和置信区间估计等。
例如,使用ttest函数可以进行单样本t检验,使用anova1函数可以进行单因素方差分析。
此外,MATLAB还提供了一些回归分析的函数,用于建立和评估回归模型。
这些函数可以帮助用户进行线性回归、多项式回归和非线性回归等。
例如,使用polyfit函数可以进行多项式回归分析,使用regress函数可以进行线性回归分析。
最后,MATLAB还提供了一些聚类分析的函数,用于将数据集划分为不同的类别。
这些函数可以帮助用户进行k均值聚类、层次聚类和谱聚类等。
例如,使用kmeans函数可以进行k均值聚类分析,使用pdist函数和linkage函数可以进行层次聚类分析。
除了以上提到的功能和应用,MATLAB还具有其他许多统计分析方面的功能。
例如,它提供了一些非参数统计方法的函数,如核密度估计、秩和检验和傅立叶分析等。
此外,MATLAB还支持大数据的统计分析,提供了一些用于处理大数据的函数,如分布式计算和并行计算等。
Matlab中常用的统计分析方法介绍

Matlab中常用的统计分析方法介绍统计分析是一种通过对数据的收集、整理、分析和解释,来推测并描述数据所呈现出的规律和规律性的方法。
作为一种重要的数据处理工具,Matlab提供了许多功能强大的统计分析方法,以帮助研究人员对数据进行深入的研究和解读。
在本文中,我们将介绍一些常用的统计分析方法,并对其原理和应用进行简要概述。
一、描述统计分析方法1. 均值与方差:均值是对样本数据的集中趋势进行度量的指标,可以通过Matlab的mean函数计算得到。
方差则是数据的离散程度度量,可以通过Matlab的var函数计算。
均值和方差是描述一个数据集的基本统计指标,可以帮助我们快速了解数据的分布情况。
2. 频数分布:频数分布可以将数据按照一定的区间划分,并统计每个区间中数据的数量。
Matlab提供了hist函数可以直接绘制频数直方图,进而帮助我们了解数据的分布情况和集中区间。
3. 分位数:分位数是将数据按大小顺序排列后分成若干部分的值。
常见的分位数有四分位数、百分位数等。
Matlab的quantile函数可以帮助我们计算任意分位数,从而得到数据分布的具体信息。
二、假设检验分析方法1. 单样本t检验:单样本t检验是一种用于判断样本均值与总体均值之间是否存在显著差异的方法。
在Matlab中,可以使用ttest函数进行单样本t检验。
通过设置显著性水平和计算得到的t值,我们可以对样本数据是否足够代表总体数据进行判断。
2. 独立样本t检验:独立样本t检验是一种用于比较两组独立样本均值是否存在显著差异的方法。
在Matlab中,可以使用ttest2函数进行独立样本t检验。
通过设置显著性水平和计算得到的t值,我们可以得出两组样本均值是否存在显著差异的结论。
3. 方差分析:方差分析是一种用于比较多组样本均值之间是否存在显著差异的方法。
在Matlab中,可以使用anova1或anova2函数进行方差分析。
通过计算得到的F值和p值,我们可以判断样本组间的差异是否显著。
如何在Matlab中进行统计分析

如何在Matlab中进行统计分析在Matlab中进行统计分析一、介绍Matlab是一种功能强大的数值计算和编程环境,广泛应用于各个领域的科学研究和工程实践中。
统计分析是Matlab中非常重要且常见的任务之一,可以帮助研究者从数据中提取有用的信息和结论。
本文将介绍如何在Matlab中进行统计分析的基本方法和技巧,帮助读者更好地利用这一工具进行数据分析。
二、数据导入和预处理在进行统计分析之前,首先需要将数据导入到Matlab中,然后进行必要的数据预处理。
Matlab提供了多种导入数据的方法,例如使用csvread()函数导入CSV 格式的数据文件,使用xlsread()函数导入Excel格式的数据文件等。
在导入数据之后,需要对数据进行清洗和预处理,包括处理缺失值、异常值和重复值等。
Matlab 提供了丰富的函数和工具箱,如missing处理函数、四分位数函数和独热编码函数等,可用于处理和预处理数据。
三、描述统计分析描述统计分析是统计学中最基本和常见的一种分析方法,用于对数据的基本特征进行概括和描述。
Matlab中提供了一些函数来计算和呈现数据的描述统计量,如平均值、中位数、标准差、方差和分位数等。
使用这些函数和工具,可以对数据的中心趋势、离散程度、分布形状和异常值等进行描述和分析,以便更好地理解数据。
四、假设检验假设检验是统计分析中用来验证假设的一种方法,常用于判断两组数据是否存在显著差异。
在Matlab中,可以使用t检验、方差分析、卡方检验等函数进行假设检验。
通过设置正确的参数和显著性水平,可以得出检验结果和结论,从而判断两组数据是否具有显著性差异。
此外,Matlab还提供了统计图表工具,如直方图、箱线图和散点图等,可以帮助更直观地呈现和分析数据。
五、相关性分析相关性分析是统计学中用于判断两个或多个变量之间关系的一种方法,常用于研究因果关系、相关度和相互依赖等。
在Matlab中,可以使用相关系数函数(如Pearson相关系数、Spearman相关系数和Kendall相关系数)来计算和研究变量之间的相关性。
第九讲MATLAB基本统计分析

fpdf
均匀分布
unifpdf
伽马分布
gampdf
Weibull分布
weibpdf
几何分布
geopdf
非中心F分布
ncfpdf
超几何分布
hygepdf
非中心T分布
nctpdf
对数正态分布
lognpdf
非中心卡方布
ncx2pdf
如果将上述命令中的后缀pdf分别改为cdf,inv,rnd,stat 就得到相应 的随机变量的分布函数、分位数、随机数的生成以及均值与方差.
例1 已知 X ~ N(2,0.52 ) 试求:P{X 3}, P{1 X 2} 解:normcdf(3,2,0.5)= 0.9772;
normcdf(2,2,0.5)- normcdf(1,2,0.5)= 0.4772
2. 做出密度函数曲线、求分位数
已知X的均值和标准差及概率p=P{X<x},求x的命令为:
N 600,196.6292
正态分布的检验: 1.大样本
h=jbtest(x), h=0,接受正态分布,h=1拒绝正态分布 2.小样本
h=lillietest(x),
h=0,接受正态分布,h=1拒绝正态分布
作业: 1.根据下表计算七项指标的均值、方差、偏度与峰度
全国 北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东 湖南
1.数据的下、上截断点
计算上、下截断点的公式如下:
Q1 1.5R , Q3 1.5R
其中,R为四分位极差,Q1 ,Q3 分别称为下四分位数与 上四分位数 .
对于0≤p<1,和样本容量为n的样本 X1, X2 ,..., Xn其 次序统计量记为: X(1) , X(2) , ..., X(n) 于是计算样本的P分位数的公式为:
【生物数学】MATLAB数理统计方法与实例

之间用英文逗号或空格分开,两行之间用英文分号分开。字 符串必须用英文单引号引起来,字符串中含有单引号时必须 成对输入,例如:
x=[1 2,3; 5,7 9]
msg1= 'You are right!'
msg2 = 'You''re right!'
2. sig-值为0.8668, 远超过0.5, 不能拒绝零假设 3. 95%的置信区间为[113.4, 116.9], 它完全包括115, 且精度很
高. .
2. 总体方差sigma2未知时,总体均值的t-检验
[h,sig,ci] = ttest(x,m,alpha,tail) 检验数据 x 的关于均值的某一假设是否成立,其 中alpha 为显著性水平,究竟检验什么假设取决于 tail 的取值: tail = 0,检验假设“x 的均值等于 m ” tail = 1,检验假设“x 的均值大于 m ” tail =-1,检验假设“x 的均值小于 m ” tail的缺省值为 0, alpha的缺省值为 0.05.
回一个空数组x=[]。 x=a:h:b 返回间隔矢量x=[a,a+h,a+2h,…,a+mh],这里
m=fix((b-a)/h)为(b-a)/h向零取整。当h=0,或h>0且a>b,或 h<0且a<b时,返回空数组x=[]。h=1为缺省值。
2. 使用函数y=linspace(a,b,n)产生以a,b为端点具有n个等间隔点 的行向量y。
3.8334 5.0288 6.1191 此命令产生了2×3的正态分布随机数矩阵,各数分别服从 N(1,0.12), N(2,22), N(3, 32), N(4,0.12), N(5, 22),N(6, 32).
完整版Matlab概率论及数理统计
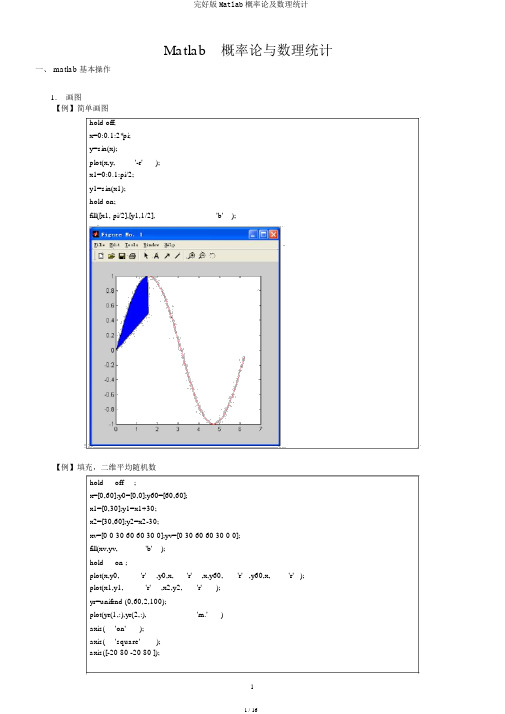
Matlab概率论与数理统计一、 matlab 基本操作1.画图【例】简单画图hold off;x=0:0.1:2*pi;y=sin(x);plot(x,y,'-r');x1=0:0.1:pi/2;y1=sin(x1);hold on;fill([x1, pi/2],[y1,1/2],'b' );【例】填充,二维平均随机数hold off;x=[0,60];y0=[0,0];y60=[60,60];x1=[0,30];y1=x1+30;x2=[30,60];y2=x2-30;xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0];fill(xv,yv,'b');hold on ;plot(x,y0,'r',y0,x,'r',x,y60,'r' ,y60,x,'r' );plot(x1,y1,'r',x2,y2,'r');yr=unifrnd (0,60,2,100);plot(yr(1,:),yr(2,:),'m.')axis('on');axis('square');2.排列组合C=nchoosek(n,k) :C C n k,例 nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2) :从 n1 到 n2 的连乘【例】最少有两个人寿辰相同的概率n!C N nN !( N n)!N(N1)(N n1)公式计算 p 111N nN n N n365 364 (365rs1)365364365rs 1 1365rs1365365365rs=[20,25,30,35,40,45,50];%每班的人数p1=ones(1,length(rs));p2=ones(1,length(rs));%用连乘公式计算for i=1:length(rs)p1(i)=prod(365-rs(i)+1:365)/365^rs(i);end%用公式计算(改进)for i=1:length(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365);end ;endp1(i)=exp(sum(log(365-rs(i)+1:365))-rs(i)*log(365));endp_r1=1-p1;p_r2=1-p2;Rs =[20253035404550 ]P_r=[0.4114 0.5687 0.7063 0.8144 0.8912 0.9410 0.9704]二、随机数的生成3.平均分布随机数rand(m,n); 产生 m 行 n 列的 (0,1) 平均分布的随机数rand(n); 产生 n 行 n 列的 (0,1)平均分布的随机数【练习】生成(a,b)上的平均分布4.正态分布随机数randn(m,n); 产生 m 行 n 列的标准正态分布的随机数【练习】生成N(nu,sigma.^2) 上的正态分布5.其他分布随机数函数名调用形式注释Unidrnd unid rnd (N,m,n)平均分布(失散)随机数binornd bino rnd (N,P,m,n)参数为 N, p的二项分布随机数Poissrnd poiss rnd (Lambda,m,n)参数为 Lambda的泊松分布随机数geornd geornd (P,m,n)参数为 p 的几何分布随机数hygernd hygernd (M,K,N,m,n)参数为 M, K, N 的超几何分布随机数Normrnd normrnd (MU,SIGMA,m,n)参数为 MU, SIGMA的正态分布随机数,SIGMA是标准差Unifrnd unif rnd ( A,B,m,n)[A,B] 上平均分布 ( 连续 ) 随机数Exprnd exprnd (MU,m,n)参数为 MU的指数分布随机数chi2rnd chi2 rnd(N,m,n)自由度为 N 的卡方分布随机数Trnd t rnd(N,m,n)自由度为 N 的 t分布随机数Frnd f rnd(N1, N2,m,n)第一自由度为N1, 第二自由度为 N2 的 F 分布随机数gamrnd gamrnd(A, B,m,n)参数为 A, B的分布随机数betarnd betarnd(A, B,m,n)参数为 A, B的分布随机数lognrnd lognrnd(MU, SIGMA,m,n)参数为 MU, SIGMA的对数正态分布随机数nbinrnd nbinrnd(R, P,m,n)参数为 R,P 的负二项式分布随机数ncfrnd ncfrnd(N1, N2, delta,m,n)参数为 N1, N2, delta 的非中心 F 分布随机数nctrnd nctrnd(N, delta,m,n)参数为 N,delta的非中心 t 分布随机数ncx2rnd ncx2rnd(N, delta,m,n)参数为 N,delta的非中心卡方分布随机数raylrnd raylrnd(B,m,n)参数为 B 的瑞利分布随机数weibrnd weibrnd(A, B,m,n)参数为 A, B的韦伯分布随机数三、一维随机变量的概率分布1.失散型随机变量的分布率(1)0-1 分布(2)平均分布(3) 二项分布: binopdf(x,n,p) ,若X ~ B(n, p),则P{ X k} C n k p k (1p) n k,x=0:9;n=9;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]‘当 n 较大时二项分布近似为正态分布x=0:100;n=100;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')(4) 泊松分布: piosspdf(x, lambda) ,若X ~k e ( ) ,则 P{ X k}k !x=0:9; lambda = 3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081, 0.0027 ](5) 几何分布: geopdf (x, p),则P{ X k} p(1p) k 1y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ]C M k C N n k Mx=0:10;N=20;M=8;n=4;y= hygepdf(x,N,M,n);plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2.概率密度函数1a x b(1)平均分布: unifpdf(x,a,b) ,f ( x)b a0其他a=0;b=1;x=a:0.1:b;y= unifpdf (x,a,b);112(2)正态分布: normpdf(x,mu,sigma) ,f ( x)e2 2 ( x)2x=-10:0.1:12;mu=1;sigma=4;y= normpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); %产生 10000 个正态分布的随机数d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;% 以 a 为横轴,求出 10000 个正态分布的随机数的频率plot(x,y,'b-',a,b,'r.')(3) 指数分布: exppdf(x,mu) ,f (x)1 e1xa x by= exppdf(x,mu); plot(x,y,'b-',x,y,'r*')1n1(4)2分布: chi2pdf(x,n) , f (x; n)2n 2x2( n 2)hold on x=0:0.1:30;n=4;y= chi2pdf(x,n);plot(x,y,'b');%blue n=6;y= chi2pdf(x,n);plot(x,y,'r');%redn=8;y= chi2pdf(x,n);plot(x,y,'c');%cyan n=10;y= chi2pdf(x,n);plot(x,y,'k');%black legend('n=4', 'n=6', 'n=8', 'n=10');(( n 1) 2) x 2(5) t 分布: tpdf(x,n) , f (x; n)(n 2)1nnhold on x=-10:0.1:10;n=2;y= tpdf(x,n);plot(x,y,'b');%blue e 2n 1 2x 0x 0n=20;y= tpdf(x,n);plot(x,y,'k');%black legend('n=2', 'n=6', 'n=10', 'n=20');n1n1 2n1n222(6) F 分布: fpdf(x,n1,n2) ,f ( x; n1, n2)(( n1n2 ) 2) n1x 21n1x x 0 (n1 2)(n2 2) n2n20x 0hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x,n1,n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x,n1,n2);plot(x,y,'r');%redn1=10; n2=6;y= fpdf(x,n1,n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x,n1,n2);plot(x,y,'k');%blacklegend(' n1=2; n2=6', ' n1=6; n2=10', ' n1=10; n2=6', ' n1=10; n2=10');3.分布函数 F (x) P{ X x}【例】求正态分布的累积概率值设 X ~ N(3,22),求P{2X 5},P{ 4 X 10},P{ X 2}, P{X3} ,4.逆分布函数,临界值y F (x) P{ X x} , x F 1 ( y) , x 称之为临界值【例】求标准正态分布的累积概率值y=0:0.01:1;x=norminv(y,0,1);【例】求2 (9) 分布的累积概率值hold offy=[0.025,0.975];x=chi2inv(y,9);n=9;x0=0:0.1:30;y0=chi2pdf(x0,n);plot(x0,y0,'r');x1=0:0.1:x(1);y1=chi2pdf(x1,n);x2=x(2):0.1:30;y2=chi2pdf(x2,n);hold onfill([x1, x(1)],[y1,0],'b');fill([x(2),x2],[0,y2],'b');5. 数字特色函数名调用形式注释sort sort(x),sort(A)排序 ,x 是向量, A 是矩阵,按各列排序sortrows sortrows(A) A 是矩阵,按各行排序mean mean(x)向量 x 的样本均值var var(x)向量 x 的样本方差std std(x)向量 x 的样本标准差median median(x)向量 x 的样本中位数geomean geomean(x)向量 x 的样本几何平均值harmmean harmmean(x)向量 x 的样本调停平均值skewness skewness(x)向量 x 的样本偏度max max(x)向量 x 的最大值min min(x)向量 x 的最小值cov cov(x), cov(x,y)向量 x 的方差,向量x,y 的协方差矩阵corrcoef corrcoef(x,y)向量 x,y 的相关系数矩阵【练习】二项分布、泊松分布、正态分布( 1)对n10, p 0.2 二项分布,画出 b(n, p) 的分布律点和折线;( 2)对np ,画出泊松分布( ) 的分布律点和折线;( 3)对np,2np(1 p) ,画出正态分布N ( , 2 )的密度函数曲线;( 4)调整 n, p ,观察折线与曲线的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-2 朝鲜半岛的数字高程模型
图1-3 经过光照处理的三维图
MATLAB主要功能如下: (1)MATLAB。MATLAB是Math Works公司所有产品的数值 分析和图形基础环境,它将二维和三维图形、MATLAB语 言能力集成到一个单一的、易学易用的环境之中。 (2)MATLAB Toolbox。工具箱是一系列专用的MATLAB函 数库,以解决特定领域的问题,它是开放的、可扩展的, 也就是说用户可以查看其中的算法或开发自己的算法。 (3)MATLAB Compiler。编译器可以将MATLAB语言编写的 M-文件自动转换成C或C++文件,支持用户进行独立应用 开发。 (4)Simulink。Simulink是结合了框图界面和交互仿真能力 的非线性动态系统仿真工具,它以MATLAB的核心数学、 图形和语言为基础。
(5)Stateflow。Stateflow与Simulink框图模型相结合,描 述复杂事件驱动系统的逻辑行为,驱动系统在不同的模式 之间进行切换。 (6)Real-Time Workshop。直接从Simulink框图自动生成C 代码,整个代码的生成可以根据需要进行完全定制。 (7)Simulink Blockset。专门为特定领域设计的Simulink功 能块的集合,用户也可以利用已有的块或自动编写的C和 MATLAB程序建立自己的块。
由图可以看出尽管正态变量的取值范围是(∞,+∞),但它的值落在(μ-3σ, μ+3σ)内几乎是肯 定的事。
2.2 统计分析的基本工具
2.2.1 数据集中度的度量
1.样本均值
函数名称:mean 调用格式:m=mean(X)
2.样本中值
函数名称:median 调用格式:m=median(X)
3.几何平均
2. α分位数的定义、求上侧、下侧、双侧α分 位数
介绍程序中几个关键的MATLAB函数: (1)计算标准正态分布的0.05分位点。如上侧α/2分位点 的计算指令是: xalpha=norminv(0.975,0,1) 下面几个数值是标准正态分布的0.05分位点: 下侧分位点:-1.6449; 上侧分位点: 1.6449; 双侧分位点:-1.9600,1.9600。 (2)生成样本数据。如生成300个标准正态分布随机数的计 算指令是: data=normrnd(0,1,300,1)
1. 3 MATLAB的开发环境
1.3.1 MATLAB桌面平台
桌面平台是各桌面组件的展示平台,默认设置情况下 的桌面平台包括4个窗口,即命令窗口(Command Window)、命令历史窗口(Command History)、当前目录 窗口(Current Directory)和工作空间窗口(Workspace)。此 外,MATLAB还有编译窗口、图形窗口和帮助窗口等其他 种类的窗口。
1.3.2. 运行方式
MATLAB提供了两种运行方式,即命令行方式和M文 件方式。
1.3.3. MATLAB帮助系统 1.3.4. 工具箱
第二章 统计分析的基本概念、工具及推理基础
2.1 变量与数据的基本概念
2.1.1 变量及其概率分布
1. 绘制正态分布的密度函数、分布函数 程序如下:
clear mu=2.5; sigma=0.6; x=(mu-4*sigma):0.005:(mu+4*sigma); y=normpdf(x,mu,sigma); f=normcdf(x,mu,sigma); plot(x,y,'-g',x,f,':b') legend('pdf','cdf',-1)
hold off text(-0.5,yy(6)+0.005,'\fontsize{14}95.44%') text(-0.5,yy(5)+0.005,'\fontsize{14}68.26%') text(-0.5,yy(7)+0.005,'\fontsize{14}99.74%') text(-3.2,-0.03,'\fontsize{10}μ-3σ') text(-2.2,-0.03,'\fontsize{10}μ-2σ') text(-1.2,-0.03,'\fontsize{10}μ-σ') text(-0.05,-0.03,'\fontsize{10}μ') text(0.8,-0.03,'\fontsize{10}μ+σ') text(1.8,-0.03,'\fontsize{10}μ+2σ') text(2.8,-0.03,'\fontsize{10}μ+3σ')
(3)绘制工序能力图(绘制由分位点控制的密度曲线下的 面积图,用阴影表示,并计算样本数据落入控制区域的概 率,显示在标题位置上)。计算指令是: capaplot(data,[xalpha,inf]) 程序如下: %alpha分位点示意图(alpha=0.05) clear clf data=normrnd(0,1,300,1); xalpha1=norminv(0.05,0,1); xalpha2=norminv(0.95,0,1); xalpha3=norminv(0.025,0,1); xalpha4=norminv(0.975,0,1);
1.1.2 MATLAB的语言特点
MATLAB命令和数学中的符号、公式非常接近,可读 性强,容易掌握。MATLAB语言除了具有强大数值计算和 图形功能以外,还提供了应用于许多领域的工具箱。它与 其他语言的接口能够保证其与各种强大的计算机软件相结 合,可扩展性很强。MATLAB目前为止可以在各种类型的 计算机上运行,程序也可以直接移植到其他机型上使用。 可以说MATLAB是和机器类型及操作系统基本无关的软件。 MATLAB语言具有较高的运算精度,矩阵类运算可以达到 10-15数量级的精度,符合一般科学与工程运算的要求。
subplot(1,2,1) plot(x,y1,'-g',x,y2,'-b') xlabel('\fontsize{12}mu1<mu2,sigma1=sigma2') legend('mu1','mu2') subplot(1,2,2) plot(x,y3,'-g',x,y4,'-b') xlabel('\fontsize{12}mu1=mu2,sigma1<sigma2') legend('sigma1','sigma2')
1. 2 MATLAB的功能
MATLAB产品族被广泛地应用于信号图 像处理、控制系统设计、通信、系统仿真、 虚拟现实等诸多领域。它的一大特性是有 众多面向具体应用的工具箱和仿真块,包 含了完整的函数集用来对信号和图像处理、 控制系统设计、神经网络等特殊应用进行 分析和设计。
图1-1 世界正则矩阵地图
表2-1线型和颜色控制符
线形
- 实线 : 虚线 -. 点划线 -- 间断线
点标记
.点 o 小圆圈 x 叉子符 + 加号 * 星号 s 方格 d 菱形 ^ 朝上三角 v 朝下三角 > 朝右三角 < 朝左三角 p 五角星 h 六角星
颜色
y黄 m 棕色 c 青色 r 红色 g 绿色 b 蓝色 w 白色 k 黑色
第三章 统计估计
3.1 变量分布形态的估计
3. 正态分布参数μ和σ对变量X取值规律的约 束—3σ原则
clear,clf X=linspace(-5,5,100); Y=normpdf(X,0,1); yy=normpdf([-3,-2,-1,0,1,2,3],0,1); plot(X,Y,'k-',[0,0],[0,yy(4)],'c-.') hold on plot([-2,-2],[0,yy(2)],'m:',[2,2],[0,yy(6)],'m:',[-2,0.5],[yy(6),yy(6)],'m:',[0.5,2],[yy(6),yy(6)],'m:') plot([-1,-1],[0,yy(3)],'g:',[1,1],[0,yy(5)],'g:',[-1,0.5],[yy(5),yy(5)],'g:',[0.5,1],[yy(5),yy(5)],'g:') plot([-3,-3],[0,yy(1)],'b:',[3,3],[0,yy(7)],'b:',[-3,0.5],[yy(7),yy(7)],'b:',[0.5,3],[yy(7),yy(7)],'b:')
2.2.3 数据分布特征的度量
1.样本的经验分位数
函数名称:prctile 调用格式:y= prctile(X,p)
2.样本峰度
函数名称:kurtosis 调用格式:y= kurtosis(X)
3.样本偏度
函数名称:skewness 调用格式:y= skewness(X)
2.2.4 两组数据线性相依程度的度量
函数名称:geomean 调用格式:m=geomean(X)
4.调和平均
函数名称:harmmean 调用格式:m=harmmean(X)
2.2.2 数据差异性的度量
1.样本方差
函数名称:var 调用格式:y=var(X)
2.样本标准差
函数名称:std 调用格式:y=std(X)
3.样本极差
函数名称:range 调用格式:y=range(X)
2. 正态分布参数μ和σ对密度曲线的影响 程序如下: clear mu1=2.5; mu2=3; sigma1=0.5; sigma2=0.6; x=(mu2-4*sigma2):0.01:(mu2+4*sigma2); y1=normpdf(x,mu1,sigma1); y2=normpdf(x,mu2,sigma1); y3=normpdf(x,mu1,sigma1); y4=normpdf(x,mu1,sigma2);
