传热学典型例题讲解共41页
传热学例题

例4-1某平壁厚度为0.37m,内表面温度t1为1650℃,外表面温度t2为300℃,平壁材料导热系数(式中t的单位为℃,λ的单位为W/(m·℃))。
若将导热系数分别按常量(取平均导热系数)和变量计算时,试求平壁的温度分布关系式和导热热通量。
解:(1)导热系数按常量计算平壁的平均温度为:平壁材料的平均导热系数为:由式可求得导热热通量为:设壁厚x处的温度为t,则由式可得:故上式即为平壁的温度分布关系式,表示平壁距离x和等温表面的温度呈直线关系。
(2)导热系数按变量计算由式得:或积分得(a)当时,,代入式a,可得:整理上式得:解得:上式即为当λ随t呈线性变化时单层平壁的温度分布关系式,此时温度分布为曲线。
计算结果表明,将导热系数按常量或变量计算时,所得的导热通量是相同的;而温度分布则不同,前者为直线,后者为曲线。
例4-2燃烧炉的平壁由三种材料构成。
最内层为耐火砖,厚度为150mm,中间层为绝热转,厚度为290mm,最外层为普通砖,厚度为228mm。
已知炉内、外壁表面分别为1016℃和34℃,试求耐火砖和绝热砖间以及绝热砖和普通砖间界面的温度。
假设各层接触良好。
解:在求解本题时,需知道各层材料的导热系数λ,但λ值与各层的平均温度有关,即又需知道各层间的界面温度,而界面温度正是题目所待求的。
此时需采用试算法,先假设各层平均温度(或界面温度),由手册或附录查得该温度下材料的导热系数(若知道材料的导热系数与温度的函数关系式,则可由该式计算得到λ值),再利用导热速率方程式计算各层间接触界面的温度。
若计算结果与所设的温度不符,则要重新试算。
一般经5几次试算后,可得合理的估算值。
下面列出经几次试算后的结果。
耐火砖绝热砖普通砖设t2耐火砖和绝热砖间界面温度,t3绝热砖和普通砖间界面温度。
,由式可知:再由式得:所以所以各层的温度差和热阻的数值如本列附表所示。
由表可见,各层的热阻愈大,温度差也愈大。
导热中温度差和热阻是成正比的。
传热学第一章习题详解

第一章思考题1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是:在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传播,辐射换热时不仅有能量的转移还伴有能量形式的转换。
2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答:① 傅立叶定律:dx dt q λ-=,其中,q -热流密度;λ-导热系数;dx dt -沿x 方向的温度变化率,“-”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式:)(f w t t h q -=,其中,q -热流密度;h -表面传热系数;w t -固体表面温度;f t -流体的温度。
③ 斯忒藩-玻耳兹曼定律:4T q σ=,其中,q -热流密度;σ-斯忒藩-玻耳兹曼常数;T -辐射物体的热力学温度。
3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?答:① 导热系数的单位是:W/(m.K);② 表面传热系数的单位是:W/(m 2.K);③ 传热系数的单位是:W/(m 2.K)。
这三个参数中,只有导热系数是物性参数,其它均与过程有关。
4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工程技术中经常遇到的一种典型热量传递过程。
5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。
传热学课堂例题分解

绪论:思考题:(课本)6.冬夏室内温度相同,穿衣不同人对冷暖的感觉主要取决于散热量的大小。
(1)冬季和夏季的最大区别是室外温度的不同。
(2)因此在室内温度相同的情况下,冬季和夏季墙壁内表面温度不同,夏季高而冬季低。
因此人体在冬季通过与墙壁的辐射换热的散热量比夏季要大得多。
(3)因此冬季要穿厚一些的绒衣,增大导热热阻,来减少散热。
9.暖水瓶热水——内层内侧:对流换热内层内侧——内层外侧:导热内层外侧——外层内侧:热辐射外层内侧——外层外侧:导热外层外侧——空气:对流换热保温措施:a .夹层抽真空,消除对流换热;b.夹层内两侧镀银,减少辐射换热。
第二章补充题:例1:用一平底壶烧开水,壶底与水接触面的温度为111ºC,通过壶底的热流密度为424002W m,如在壶底结一层水垢厚3mm,/1/W m C λ=⋅︒,此时水垢层与水接触面上的温度和通过的热流密度均不变,计算:(1) 水垢层与壶底接触面上的温度;(2) 单位面积上的导热热阻。
解(1)2321231242400/,111,3310,1/31042400111238.21w w w w w q w m t C mm m w m Ct t q t q t C δλδλδλ--==︒==⨯=⋅︒-=⨯=⋅+=⨯+=︒(2)32310/m k w δλ-=⨯⋅分析:水垢层热阻比金属层热阻大得多。
换热器中要及时清除水垢。
(铝的导热系数:237/W m K λ=⋅,32310/m K W δλ-=⨯⋅, δ=0.711m,即相当于0.711m 厚的铝的热阻。
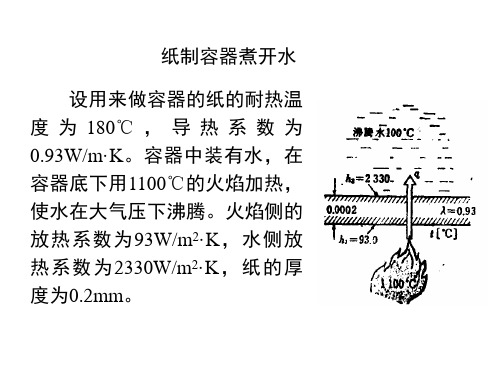
)例2:野外工作者常用纸制容器烧水,设厚为0.2mm 的纸的0.9/()W m K λ=⋅,水侧沸腾换热22400/h W m K =⋅,容器用1100ºC的火焰加热,火焰与纸面的295/h Wm K =⋅,若纸的耐火温度为200ºC ,证明:该纸制容器能耐火。
证明:12111211111157.2f f f w w t t t t q h h h t Cδλ--==++=︒ 思考:从耐火角度考虑,纸厚好还是薄好?例3:人对冷热的感觉以皮肤表面的热损失作为衡量依据。
传热学典型习题详解1

绪论部分一、基本概念主要包括导热、对流换热、辐射换热的特点及热传递方式辨析。
1、冬天,经过在白天太阳底下晒过的棉被,晚上盖起来感到很暖和,并且经过拍打以后,效果更加明显。
试解释原因。
答:棉被经过晾晒以后,可使棉花的空隙里进人更多的空气。
而空气在狭小的棉絮空间里的热量传递方式主要是导热,由于空气的导热系数较小(20℃,1.01325×105Pa时,空气导热系数为0.0259W/(m·K),具有良好的保温性能。
而经过拍打的棉被可以让更多的空气进入,因而效果更明显。
2、夏季在维持20℃的室内工作,穿单衣感到舒适,而冬季在保持22℃的室内工作时,却必须穿绒衣才觉得舒服。
试从传热的观点分析原因。
答:首先,冬季和夏季的最大区别是室外温度的不同。
夏季室外温度比室内气温高,因此通过墙壁的热量传递方向是出室外传向室内。
而冬季室外气温比室内低,通过墙壁的热量传递方向是由室内传向室外。
因此冬季和夏季墙壁内表面温度不同,夏季高而冬季低。
因此,尽管冬季室内温度(22℃)比夏季略高(20℃),但人体在冬季通过辐射与墙壁的散热比夏季高很多。
根据上题人体对冷感的感受主要是散热量的原理,在冬季散热量大,因此要穿厚一些的绒衣。
3、试分析室内暖气片的散热过程,各环节有哪些热量传递方式?以暖气片管内走热水为例。
答:有以下换热环节及热传递方式(1)由热水到暖气片管到内壁,热传递方式是对流换热(强制对流);(2)由暖气片管道内壁至外壁,热传递方式为导热;(3)由暖气片外壁至室内环境和空气,热传递方式有辐射换热和对流换热。
4、冬季晴朗的夜晚,测得室外空气温度t高于0℃,有人却发现地面上结有—层簿冰,试解释原因(若不考虑水表面的蒸发)。
解:如图所示。
假定地面温度为了Te ,太空温度为Tsky,设过程已达稳态,空气与地面的表面传热系数为h,地球表面近似看成温度为Tc 的黑体,太空可看成温度为Tsky的黑体。
则由热平衡:,由于Ta >0℃,而Tsky<0℃,因此,地球表面温度Te有可能低于0℃,即有可能结冰。
传热学例题讲解(习题附答案)

240s
3-2 工程上常用非稳态导热的方法测得燃气轮 机表面的传热系数,一种方法是:把边长为 6mm的铜质立方体埋入机片,使立方体只有一 面与高温燃气接触,立方体与叶片间加有一薄 层高温粘结剂。因粘结剂的热扩散率较小,叶 片与立方体之间可近似视为绝热,设初温为 38℃他铜块与538℃的高温燃气接触3.7s后,温 度升为232℃。求叶片表面的传热系数。 铜:
一温度为21℃,横截面积为50mm×100mm的矩 形长杆放入温度为593℃的热处理炉中消除热应力, 宽100mm的一面置于炉子底面上,长杆表面与高 2 温流体的表面传热系数为114 W /(m ,根据 .K ) 工艺要求,要加热到580℃以上才能消除应力,试 说明1h后,能否满足工艺要求?
35W /(m .K ) a 0.037m / h
380W / m.K 3 8940kg / m cp 385J / kg.K
解:
6 6 6mm
3
A 166.7 V
306 ln ln 0.491 500 0
已知:0 t0 t f ℃ 538 306℃ 0 -500 38 -500℃
3
m 0.98 0.38 m 0
m 0.38 0.98 0.372 0 o m
t t f (t0 t f ) 0.372 t t f (t0 t f ) 0.372
70 (200 70) 0.372
cp 430J / kg.K
分析:
8W / m.K
100 0.0037 Bi 0.044 0.1 8 hR
可以用集总参数法。
已知:
传热学习题 演示文稿
代入边界条件: x=0处,t=100℃; x=10mm = 0.01m处,t =60℃; x=20mm = 0.02m处,t =40℃
b 2 0 (100 100 ) c2 2 b 2 0 (60 60 ) c1 0.01 c2 2 b 2 0 (40 40 ) c1 0.02 c2 2
总 结
1.通过平壁的导热(λ= const)
t 2 t1 t x t1
t2 t1 q t f 1 t f 2 q 1 1
t t w 1 w2 t t t2 t1 w1 w2 Φ t t1 ln( r r1 ) q ln( r2 r1 ) r ln(r2 r1 ) ln( r2 r1 )
稳态传热
无能量累积
3 hAt h A( x dx) A( x) (t t ) hdA( x)(t t )
A( x ) A( x ) A( x dx ) A( x ) A( x ) dx A( x ) dx dA( x ) x x
t1 t2 ql 465 ln(r2 r1 ) 2
2(t1 t 2 ) Inr2 / r1 465 2 3.14 0.088625 350 0.41912 465
r2 r1 1.52 r1 r1
34.6mm 35mm
dA( x ) d dt h ( t t ) ( A ( ) )0 c x dx dx dx
例 2 :一厚度为 50mm的无限大平壁,其稳态温度分
布为: t a bx 2 ℃式中a=200℃,b=-2000℃/m2。 若平壁材料导热系数为45W/m.℃,试求:(1)平壁两
传热学题及解析-05-09

为 30mm,面积为 0.02m2,则该材料的导热系数为:
(A)5.0W/(m·K)
(B)0.5W/(m·K)
(C)0.05W/(m·K)
(D)1.0W/(m·K)
解析:根据一维平壁稳态导热公式
Φ = λ A tw1 − tw2 ,得出 λ = Φδ = 1× 0.03 = 0.05 W/(m·K)
解析:无内热源,长物性一维非稳态导热的微分方程为
∂t
=
a
∂2t
,对时间域采用显式格式写出差分方程:
t k +1
i
−
tik
=
a
tk
i −1
+
tk
i +1
−
2tik
∂τ ∂x
Δτ
Δx2
( ) ( ) 整理为 tik+1 = Fo
tk
i −1
+
tk
i +1
+ 1− 2Fo
tik ,
由此可知显式差分格式的稳定性条件 1− 2Fo ≥ 0 ,则 FC) t1
+ t2
+ t3
− 3t4
+
2qw Δx λ
=
0
(D) t1
+
2t2
+
t3
−
4t4
+
qw Δx λ
=
0
解析:列节点 4 的热平衡方程
λ
t2 − t4 Δx
Δy + λ
t1 − t4 Δy
Δx 2
+λ
t3 − t4 Δy
Δx 2
+ qwΔy
=0
Δx
(整理)传热学典型习题详解1.

绪论部分一、基本概念主要包括导热、对流换热、辐射换热的特点及热传递方式辨析。
1、冬天,经过在白天太阳底下晒过的棉被,晚上盖起来感到很暖和,并且经过拍打以后,效果更加明显。
试解释原因。
答:棉被经过晾晒以后,可使棉花的空隙里进人更多的空气。
而空气在狭小的棉絮空间里的热量传递方式主要是导热,由于空气的导热系数较小(20℃,1.01325×105Pa时,空气导热系数为0.0259W/(m·K),具有良好的保温性能。
而经过拍打的棉被可以让更多的空气进入,因而效果更明显。
2、夏季在维持20℃的室内工作,穿单衣感到舒适,而冬季在保持22℃的室内工作时,却必须穿绒衣才觉得舒服。
试从传热的观点分析原因。
答:首先,冬季和夏季的最大区别是室外温度的不同。
夏季室外温度比室内气温高,因此通过墙壁的热量传递方向是出室外传向室内。
而冬季室外气温比室内低,通过墙壁的热量传递方向是由室内传向室外。
因此冬季和夏季墙壁内表面温度不同,夏季高而冬季低。
因此,尽管冬季室内温度(22℃)比夏季略高(20℃),但人体在冬季通过辐射与墙壁的散热比夏季高很多。
根据上题人体对冷感的感受主要是散热量的原理,在冬季散热量大,因此要穿厚一些的绒衣。
3、试分析室内暖气片的散热过程,各环节有哪些热量传递方式?以暖气片管内走热水为例。
答:有以下换热环节及热传递方式(1)由热水到暖气片管到内壁,热传递方式是对流换热(强制对流);(2)由暖气片管道内壁至外壁,热传递方式为导热;(3)由暖气片外壁至室内环境和空气,热传递方式有辐射换热和对流换热。
4、冬季晴朗的夜晚,测得室外空气温度t高于0℃,有人却发现地面上结有—层簿冰,试解释原因(若不考虑水表面的蒸发)。
解:如图所示。
假定地面温度为了Te ,太空温度为Tsky,设过程已达稳态,空气与地面的表面传热系数为h,地球表面近似看成温度为Tc 的黑体,太空可看成温度为Tsky的黑体。
则由热平衡:,由于Ta >0℃,而Tsky<0℃,因此,地球表面温度Te有可能低于0℃,即有可能结冰。
传热学例题

例4-1某平壁厚度为0.37m,内表面温度t1为1650℃,外表面温度t2为300℃,平壁材料导热系数(式中t的单位为℃,λ的单位为W/(m·℃))。
若将导热系数分别按常量(取平均导热系数)和变量计算时,试求平壁的温度分布关系式和导热热通量。
解:(1)导热系数按常量计算平壁的平均温度为:平壁材料的平均导热系数为:由式可求得导热热通量为:设壁厚x处的温度为t,则由式可得:故上式即为平壁的温度分布关系式,表示平壁距离x和等温表面的温度呈直线关系。
(2)导热系数按变量计算由式得:或积分得(a)当时,,代入式a,可得:整理上式得:解得:上式即为当λ随t呈线性变化时单层平壁的温度分布关系式,此时温度分布为曲线。
计算结果表明,将导热系数按常量或变量计算时,所得的导热通量是相同的;而温度分布则不同,前者为直线,后者为曲线。
例4-2燃烧炉的平壁由三种材料构成。
最内层为耐火砖,厚度为150mm,中间层为绝热转,厚度为290mm,最外层为普通砖,厚度为228mm。
已知炉内、外壁表面分别为1016℃和34℃,试求耐火砖和绝热砖间以及绝热砖和普通砖间界面的温度。
假设各层接触良好。
解:在求解本题时,需知道各层材料的导热系数λ,但λ值与各层的平均温度有关,即又需知道各层间的界面温度,而界面温度正是题目所待求的。
此时需采用试算法,先假设各层平均温度(或界面温度),由手册或附录查得该温度下材料的导热系数(若知道材料的导热系数与温度的函数关系式,则可由该式计算得到λ值),再利用导热速率方程式计算各层间接触界面的温度。
若计算结果与所设的温度不符,则要重新试算。
一般经5几次试算后,可得合理的估算值。
下面列出经几次试算后的结果。
耐火砖绝热砖普通砖设t2耐火砖和绝热砖间界面温度,t3绝热砖和普通砖间界面温度。
,由式可知:再由式得:所以所以各层的温度差和热阻的数值如本列附表所示。
由表可见,各层的热阻愈大,温度差也愈大。
导热中温度差和热阻是成正比的。
传热学重点章节典型例题

第一章1-1 对于附图所示的两种水平夹层,试分析冷、热表面间热量交换的方式有何不同?如果要通过实验来测定夹层中流体的导热系数,应采用哪一种布置?解:( a )中热量交换的方式主要有热传导和热辐射。
( b )热量交换的方式主要有热传导,自然对流和热辐射。
所以如果要通过实验来测定夹层中流体的导热系数,应采用( a )布置。
1-7 一炉子的炉墙厚 13cm ,总面积为 20m 2 ,平均导热系数为 1.04w/m · k ,内外壁温分别是 520 ℃及 50 ℃。
试计算通过炉墙的热损失。
如果所燃用的煤的发热量是 2.09 × 10 4 kJ/kg ,问每天因热损失要用掉多少千克煤?解:根据傅利叶公式每天用煤1-9 在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度 t w = 69 ℃,空气温度 t f = 20 ℃,管子外径 d= 14mm ,加热段长 80mm ,输入加热段的功率 8.5w ,如果全部热量通过对流换热传给空气,试问此时的对流换热表面传热系数多大?解:根据牛顿冷却公式1-14 宇宙空间可近似的看作 0K 的真空空间。
一航天器在太空中飞行,其外表面平均温度为250K ,表面发射率为 0.7 ,试计算航天器单位表面上的换热量?解:航天器单位表面上的换热量1-27 附图所示的空腔由两个平行黑体表面组成,孔腔内抽成真空,且空腔的厚度远小于其高度与宽度。
其余已知条件如图。
表面 2 是厚δ = 0.1m 的平板的一侧面,其另一侧表面 3 被高温流体加热,平板的平均导热系数λ =17.5w/m ? K ,试问在稳态工况下表面 3 的 t w3 温度为多少?解:表面 1 到表面 2 的辐射换热量 = 表面 2 到表面 3 的导热量第二章2-4 一烘箱的炉门由两种保温材料 A 和 B 做成,且δ A =2 δ B ( 见附图 ) 。
已知λ A =0.1 w/m ? K ,λ B =0.06 w/m ? K 。
热工基础习题集-传热学部分解析

热⼯基础习题集-传热学部分解析第⼀章1-1试列举⽣活中热传导、对流传热核辐射传热的事例。
1-2 冬天,上午晒被⼦,晚上睡觉为什么还感到暖和?答:被⼦散热可是为⽆限⼤平⾯导热。
晒被⼦使被⼦变得蓬松,含有更多的空⽓,⽽空⽓热导率较⼩,使被⼦的表现电导率变⼩。
另外,被⼦晒后厚度增加。
总之,被⼦晒后,其导热热阻δ/λA变⼤,⼈体热量不易向外散失,睡在被⼦⾥感到暖和(被⼦蓄热不必考虑:①被⼦蓄热不多;②上午晒被⼦,晚上蓄热早已散光)。
1-3通过实验测定夹层中流体的热导率时,应采⽤图1-6种哪个装置?为什么?答:左边⼀种。
这种装置热⾯在上,冷⾯在下,使流体对流传热减少到零,由这种装置测得的热导率不受对流传热的影响。
如果采⽤右边⼀种装置,由于对流传热的影响⽽测得的热导率偏⼤。
1-4在思考题1-3中,流体为空⽓时热导率可⽤式(1-1)计算,式中Δt为热、冷⾯的温度差,δ为空⽓夹层的厚度,Φ为通过空⽓夹层的热流量,A为空⽓夹层的导热⾯积。
实践证明,Δt 不能太⼤,否则测得的热导率⽐真实热导率⼤。
试分析其原因。
答:热⾯和冷⾯的传热热流量Φ=Φc+Φd+Φr=λΔtA/δ。
由思考题1-3可见,左边⼀种装置虽然减少了对流传热的影响,但如Δt 较⼤,辐射传热量Φr对测量⽓体热导率的影响却不能忽略,会影响热导率λ测定的准确性。
这时,热传导率实质上是以导热和辐射传热两种⽅式传递热量形式的表现热导率λe。
显然,λe>λ(其中λ为⽓体的真实热导率)。
由于辐射传热量Φr正⽐于热⾯和冷⾯温度的四次⽅之差(T14-T24),只有在热⾯和冷⾯温度之差(t1-t2)较⼩时,辐射传热的影响才可忽略,Φ≈Φd=λΔtA/δ。
1-5从传热的⾓度出发,采暖散热器和冷风机应放在什么⾼度最合适?答:采暖器和冷风机主要通过对流传热的⽅式使周围空⽓变热和变冷,使⼈⽣活在合适的温度范围中,空⽓对流实在密度差的推动下流动,如采暖器放得太⾼,房间⾥上部空⽓被加热,但⽆法产⽣⾃然对流使下部空⽓也变热,这样⼈仍然⽣活在冷空⽓中。
传热学典型习题详解

传热学典型习题详解绪论部分一、基本概念主要包括导热、对流换热、辐射换热的特点及热传递方式辨析。
1、冬天,经过在白天太阳底下晒过的棉被,晚上盖起来感到很暖和,并且经过拍打以后,效果更加明显。
试解释原因。
答:棉被经过晾晒以后,可使棉花的空隙里进人更多的空气。
而空气在狭小的棉絮空间里的热量传递方式主要是导热,由于空气的导热系数较小(20℃,1.01325×105Pa 时,空气导热系数为0.0259W/(m ·K),具有良好的保温性能。
而经过拍打的棉被可以让更多的空气进入,因而效果更明显。
2、夏季在维持20℃的室内工作,穿单衣感到舒适,而冬季在保持22℃的室内工作时,却必须穿绒衣才觉得舒服。
试从传热的观点分析原因。
答:首先,冬季和夏季的最大区别是室外温度的不同。
夏季室外温度比室内气温高,因此通过墙壁的热量传递方向是出室外传向室内。
而冬季室外气温比室内低,通过墙壁的热量传递方向是由室内传向室外。
因此冬季和夏季墙壁内表面温度不同,夏季高而冬季低。
因此,尽管冬季室内温度(22℃)比夏季略高(20℃),但人体在冬季通过辐射与墙壁的散热比夏季高很多。
根据上题人体对冷感的感受主要是散热量的原理,在冬季散热量大,因此要穿厚一些的绒衣。
3、试分析室内暖气片的散热过程,各环节有哪些热量传递方式?以暖气片管内走热水为例。
答:有以下换热环节及热传递方式(1)由热水到暖气片管到内壁,热传递方式是对流换热(强制对流); (2)由暖气片管道内壁至外壁,热传递方式为导热;(3)由暖气片外壁至室内环境和空气,热传递方式有辐射换热和对流换热。
4、冬季晴朗的夜晚,测得室外空气温度t 高于0℃,有人却发现地面上结有—层簿冰,试解释原因(若不考虑水表面的蒸发)。
解:如图所示。
假定地面温度为了T e ,太空温度为T sky ,设过程已达稳态,空气与地面的表面传热系数为h ,地球表面近似看成温度为T c 的黑体,太空可看成温度为T sky 的黑体。
传热学典型例题讲解课件

新型传热材料的研发
总结词
新型传热材料的研发是传热学领域的重要研 究方向,旨在开发具有优异性能的传热材料, 以满足不断发展的能源和环境需求。
详细描述
新型传热材料主要包括金属基复合材料、陶 瓷基复合材料、高分子复合材料等。这些材 料具有高效传热、耐高温、抗氧化、抗腐蚀 等优异性能,可广泛应用于航空航天、汽车、
工业传热
总结词
工业传热涉及广泛的领域,如化工、制药、食品加工等,传热学在工业传热中解决了许多实际的生产 问题。
详细描述
工业传热主要关注反应过程中的热量传递与控制、蒸发和结晶过程以及热力设备的优化设计等。通过 高效的传热技术,可以提高生产效率和产品质量,降低能耗和生产成本。
05 传热学实验与模拟
实验设备与操作
传热的基本方式
导热
通过物体内部的微观粒子运动传 递热量的方式,如金属的热传导。
对流
由于流体运动而引起的热量传递方 式,如空调制冷时冷气在房间内的 流动。
辐射
以电磁波的形式传递热量的方式, 如太阳光照射地球的热量传递。
传热学的发展历程
古代的传热应用
如火炉、熔炼炉等。
工业革命时期的传热研究
随着蒸汽机、内燃机等工业设备的出现,人们开始深入研究热量传 递的规律。
实验设备
介绍实验所需的设备,如热流计、 温度传感器、加热器等,并说明 其作用和工作原理。
实验操作
详细描述实验操作步骤,包括设 备安装、调试、实验运行等,确 保实验的准确性和可靠性。
实验数据处理与分析
数据处理
介绍实验数据的处理方法,如数据采集、 整理、转换等,确保数据的准确性和可 靠性。
VS
数据分析
导热问题的求解方法
采用有限差分法、有限元法和 有限体积法等数值方法求解导
传热学典型习题详解2

传热学典型习题详解2单相流体对流换热及准则关联式部分⼀、基本概念主要包括管内强制对流换热基本特点;外部流动强制对流换热基本特点;⾃然对流换热基本特点;对流换热影响因素及其强化措施。
1、对皆内强制对流换热,为何采⽤短管和弯管可以强化流体的换热答:采⽤短管,主要是利⽤流体在管内换热处于⼊⼝段温度边界层较薄,因⽽换热强的特点,即所谓的“⼊⼝效应”,从⽽强化换热。
⽽对于弯管,流体流经弯管时,由于离⼼⼒作⽤,在横截⾯上产⽣⼆次环流,增加了扰动,从⽽强化了换热。
2、其他条件相同时,同⼀根管⼦横向冲刷与纵向冲刷相⽐,哪个的表⾯传热系数⼤,为什么¥答:横向冲刷时表⾯传热系数⼤。
因为纵向冲刷时相当于外掠平板的流动,热边界层较厚,⽽横向冲刷时热边界层薄且存在由于边界层分离⽽产⽣的旋涡,增加了流体的扰动,因⽽换热强。
3、在进⾏外掠圆柱体的层流强制对流换热实验研究时,为了测量平均表⾯传热系数,需要布置测量外壁温度的热电偶。
试问热电偶应布置在圆柱体周向⽅向何处答:横掠圆管局部表⾯传热系数如图。
在0-1800内表⾯传热系数的平均值hm 与该曲线有两个交点,其所对应的周向⾓分别为φ1,φ2。
布置热电偶时,应布置在φ1,φ2所对应的圆周上。
由于对称性,在圆柱的下半周还有两个点以布置。
4、在地球表⾯某实验室内设计的⾃然对流换热实验,到太空中是否仍然有效,为什么答:该实验到太空中⽆法得到地⾯上的实验结果。
因为⾃然对流是由流体内部的温度差从⽽引起密度差并在重⼒的作⽤下引起的。
在太空中实验装置格处于失重状态,因⽽⽆法形成⾃然对流,所以⽆法得到顶期的实验结果。
5、管束的顺排和叉排是如何影响换热的`答:这是个相当复杂的问题,可简答如下:叉排时,流体在管间交替收缩和扩张的弯曲通道中流动,⽽顺排时则流道相对⽐较平直,并且当流速和纵向管间距s 2较⼩时,易在管的尾部形成滞流区.因此,⼀般地说,叉排时流体扰动较好,换热⽐顺排强.或:顺排时,第⼀排管⼦正⾯受到来流的冲击,故φ=0处换热最为激烈,从第⼆排起所受到的冲击变弱,管列间的流体受到管壁的⼲扰较⼩,流动较为稳定。
传热学例题(docX页)

例4-1某平壁厚度为0.37m,内表面温度t1为1650℃,外表面温度t2为300℃,平壁材料导热系数(式中t的单位为℃,λ的单位为W/(m·℃))。
若将导热系数分别按常量(取平均导热系数)和变量计算时,试求平壁的温度分布关系式和导热热通量。
解:(1)导热系数按常量计算平壁的平均温度为:平壁材料的平均导热系数为:由式可求得导热热通量为:设壁厚x处的温度为t,则由式可得:故上式即为平壁的温度分布关系式,表示平壁距离x和等温表面的温度呈直线关系。
(2)导热系数按变量计算由式得:或积分得(a)当时,,代入式a,可得:整理上式得:解得:上式即为当λ随t呈线性变化时单层平壁的温度分布关系式,此时温度分布为曲线。
计算结果表明,将导热系数按常量或变量计算时,所得的导热通量是相同的;而温度分布则不同,前者为直线,后者为曲线。
例4-2燃烧炉的平壁由三种材料构成。
最内层为耐火砖,厚度为150mm,中间层为绝热转,厚度为290mm,最外层为普通砖,厚度为228mm。
已知炉内、外壁表面分别为1016℃和34℃,试求耐火砖和绝热砖间以及绝热砖和普通砖间界面的温度。
假设各层接触良好。
解:在求解本题时,需知道各层材料的导热系数λ,但λ值与各层的平均温度有关,即又需知道各层间的界面温度,而界面温度正是题目所待求的。
此时需采用试算法,先假设各层平均温度(或界面温度),由手册或附录查得该温度下材料的导热系数(若知道材料的导热系数与温度的函数关系式,则可由该式计算得到λ值),再利用导热速率方程式计算各层间接触界面的温度。
若计算结果与所设的温度不符,则要重新试算。
一般经5几次试算后,可得合理的估算值。
下面列出经几次试算后的结果。
耐火砖绝热砖普通砖设t2耐火砖和绝热砖间界面温度,t3绝热砖和普通砖间界面温度。
,由式可知:再由式得:所以所以各层的温度差和热阻的数值如本列附表所示。
由表可见,各层的热阻愈大,温度差也愈大。
导热中温度差和热阻是成正比的。
《传热学》习题课(对流换热部分)解析

Pr 4.31 40 37.5 5.42 4.31 4.587
40 30
61.8 40 37.5 63.5 61.8 62.225102
40 30 0.62225W / mK
第五章 对流换热—习题
传热学 课件
传热学 课件
5-2.对于油、空气及液态金属。分别有Pr>>1、
Pr≈1、Pr<<1。试就外掠等温平板的层流边界层
流动,画出三种流体边界层中速度分布与温度分布
的大致图像(要能显示出δ与δt的相对大小) 解: 20℃的液态金属水银:ν=11.4×10-8m2/s,
Pr=2.72×10-2
5.07410 3
t 1 ( x)
510 3
0
0
0
2
4
6
8
10
0
x
10
4.64 x
u
t
4.52
Pr
1 3
x
u
4.52
Pr
1 3
4.64
第五章 对流换热—习题
传热学 课件
解:20℃的14#润滑油:ν=410.9×10-6m2/s,Pr=4846
0.1 0.094
0.08
2(x) 0.06 t2(x) 0.04
0.02
H
第五章 对流换热—习题
速度和温度分布
积分简化能量方程可得:
t f3xy f4x
代入上下面的温度边界条件得:
t
tw2
tw1 tw2 H
y
传热学 课件
第五章 对流换热—习题
传热学 课件
5-14 实验测得一置于水中的平板某点的切应 力为1.5Pa,如果水温与平板温度分别为15℃ 与60℃,试计算当地的局部热流密度。
