流体力学标准化作业答案第三章之欧阳数创编
流体力学课后习题详解(第三、四章)

第三章 流体运动学3-1解:质点的运动速度1031014,1024,1011034=-=-==-=w v u 质点的轨迹方程1031,52,103000twt z z t vt y y t ut x x +=+=+=+=+=+=3-2 解:2/12/12/3222/12/12/3220375.0232501.02501.00375.0232501.02501.00t t t dt d dt y d a t t t dt d dt x d a a y x z =⨯⨯=⎪⎭⎫⎝⎛⨯===⨯⨯=⎪⎭⎫⎝⎛⨯===由501.01t x +=和10=Ax ,得19.1501.011001.015252=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=A x t故206.00146.0146.00,146.0,014619.150375.0222222/1=++=++=====⨯=zyxz x y x a a a a a a a a3-3解:当t=1s 时,点A (1,2)处的流速()()sm s m yt xt v s m s m y xt u /1/1211/5/2211222-=⨯-⨯=-==⨯+⨯=+=流速偏导数112221121,1,/12,1,/1-----=-=∂∂==∂∂==∂∂=∂∂==∂∂==∂∂s t yvs t x v s m t t v s yu s t x u s m x t u点A(1,2)处的加速度分量()[]()()[]222/11151/3/21151s m y v v x v u t v Dt Dv a s m s m yuv x u u t u Dt Du a y x -⨯-+⨯+=∂∂+∂∂+∂∂===⨯-+⨯+=∂∂+∂∂+∂∂==3-4解:(1)迹线微分方程为dt udy dt u dx ==, 将u,t 代入,得()tdtdy dt y dx =-=1利用初始条件y(t=0)=0,积分该式,得221t y =将该式代入到式(a ),得dx=(1-t 2/2)dt.利用初始条件x(t=0)=0,积分得361t t x -=联立(c )和(d )两式消去t,得过(0,0)点的迹线方程023492223=-+-x y y y (2)流线微分方程为=.将u,v 代入,得()tdx dy y tdyy dx =-=-11或将t 视为参数,积分得C xt y y +=-221 据条件x(t=1)=0和y(t=1)=0,得C=0.故流线方程为xt y y =-221 3-5 答:()(),满足满足002,0001=+-=∂∂+∂∂+∂∂++=∂∂+∂∂+∂∂k k zw y v x u zw y v x u()()()(),满足,满足000040223222222=++=∂∂+∂∂+∂∂=+-++=∂∂+∂∂+∂∂zw yv xu yxxyyxxyzw yv xu()()()()()()处满足,其他处不满足仅在,不满足,满足,满足满足,满足0,41049000018001760000522==∂∂+∂∂=∂∂+∂∂=++=∂∂++∂∂=++-=∂∂++∂∂=++=∂∂+∂∂+∂∂y y yv x u yv x u u r r u r u rk r k u r r u r u zw yv xu r r r rθθθθ3-6 解:max 02042020max 20320max 20200max 2020214222111000u r r r r u dr r r r r u rdrdr r u r udA r V r rAr =⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-==⎰⎰⎰⎰⎰πππππ3-7 证:设微元体abcd 中心的速度为u r ,u θ。
流体力学第三章

第三章习题简答3-1 已知流体流动的速度分布为22y x u x -= ,xy u y 2-=,求通过1,1==y x 的一条流线。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 dy y x xydx )(222-=-两边积分可得C y y x yx +-=-3322即0623=+-C y x y将x=1,y=1代入上式,可得C=5,则 流线方程为05623=+-y x y(与课本后的答案不一样,课本为02323=+-y x y 。
课本答案应该是错的)3-3 已知流体的速度分布为⎭⎬⎫==-=-=tx x u ty y u y x 00εωεω(ω>0,0ε>0)试求流线方程,并画流线图。
解:由流线微分方程yx u dyu dx =得dy u dx u x y =则有 tydy txdx 00εε-=两边积分可得C y x +-=22流线方程为C y x =+223-5 以平均速度s m v /5.1=流入直径为D=2cm 的排孔管中的液体,全部经8个直径d=1mm 的排孔流出,假定每孔出流速度依次降低2%,试求第一孔与第八孔的出流速度各为多少?题3-5图解:由题意得:v 2=v 1(1-2%),v 3=v 1(1-2%)2,…,v 8=v 1(1-2%)7 根据质量守恒定律可得282322212832144444d v d v d v d v D v Q Q Q Q Q πππππ⋅+⋅⋅⋅+⋅+⋅+⋅=⋅+⋅⋅⋅+++=sm d vD v v d v v v v d D v /4.80)98.01(001.002.002.05.1)98.01()98.01(98.01)98.01(4)(448228221812832122=-⨯⨯⨯=--⋅=∴--⋅=+⋅⋅⋅+++⋅=⋅πππ则 v 8=v 1(1-2%)7=80.4×(1-2%)7=69.8m/s(与课本后的答案不一样,课本为8.04 m/s 和6.98m/s 。
流体力学课后题题解(第3章)
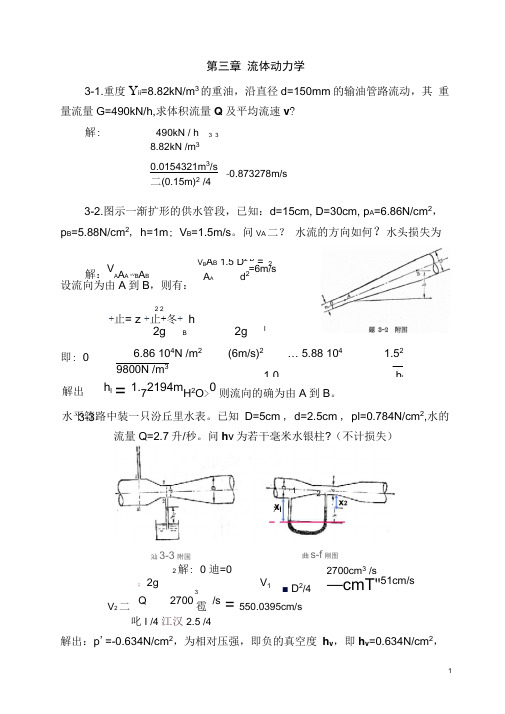
第三章 流体动力学3-1.重度Y ii =8.82kN/m 3的重油,沿直径d=150mm 的输油管路流动,其 重量流量G=490kN/h,求体积流量Q 及平均流速v ?3 3解:490kN / h8.82kN /m 30.0154321m 3/s二(0.15m)2/4-0.873278m/s3-2.图示一渐扩形的供水管段,已知:d=15cm, D=30cm, p A =6.86N/cm 2, p B =5.88N/cm 2, h=1m ; V B =1.5m/s 。
问V A 二? 水流的方向如何?水头损失为V B A B 1.5 D 2 B = 2=6m/sA A d 2设流向为由A 到B ,则有:解:VA A A =VB A B 2 2+止= z +止+冬+ h2g B2gl即: 0 6.86 104N /m 2 (6m/s)2… 5.88 104 1.52― 1.0h l9800N /m 3解出h l=1.72194mH 2O >0则流向的确为由A 到B 。
3-3汕3-3附国2解: 0 迪=0; 2g3V 2 二Q 2700雹/s= 550.0395cm/s叱I /4 江汉2.5 /4V 1■ D 2/42700cm 3 /s—cmT"51cm/s解出:p '=-0.634N/cm 2,为相对压强,即负的真空度 h v ,即h v =0.634N/cm 2,x i曲s-f 刚图水平管路中装一只汾丘里水表。
已知 D=5cm , d=2.5cm , pl=0.784N/cm 2,水的流量Q=2.7升/秒。
问h v 为若干毫米水银柱?(不计损失)二55.556m3/h 二0.0154321m3/ s而1N/cm2=75.061mmHg,故h v=47.588 mmHg。
3-4水银压差计连接在水平放置的汾丘里流量计上。
今测得其中水银面高差h=80mm。
已知D=10cm, d=5cm,汾丘里流量计的流量系数卩=0.98 问水通过流量计的实际流量为若干?解:0 . P . v! = 0 . p .遵P1- P2 _ v2 _ V:w 2g _w 2g w 「2g而p i w(X i D/2) = p2 M h wX d/2)即P i w(h X2 d/2) = p2 M h w(X2 d /2)贝U P i - P2 = h( M -w) —---- -- - h(— - 1) = 100.8mw w2 2 2二v2 -v1 = 2g 汉100.8cm = 197568(cm/s)V1A1 = V2 A?故v2 = 197568(:m/S)二210739.2 ; V2 二459.06cm/ s-(D)4贝U Q =J v2A^ 0.98 459.06cm/s 二52/^ 8833.415cm3/ s= 8.83 升/s3-5某选矿厂的一台碎矿机,每小时可以处理矿石352.8kN。
流体力学第三章课后习题答案

流体力学第三章课后习题答案流体力学第三章课后习题答案流体力学是研究流体运动和流体力学性质的学科。
在学习流体力学的过程中,课后习题是巩固知识和提高理解能力的重要环节。
本文将为大家提供流体力学第三章的课后习题答案,帮助读者更好地掌握流体力学的相关知识。
1. 一个液体的密度为1000 kg/m³,重力加速度为9.8 m/s²,求其比重。
解答:比重定义为物体的密度与水的密度之比。
水的密度为1000 kg/m³,所以比重为1。
因此,该液体的比重也为1。
2. 一个物体在液体中的浮力与物体的重力相等,求物体在液体中的浸没深度。
解答:根据阿基米德原理,物体在液体中的浮力等于物体所排除液体的重量。
浮力的大小等于液体的密度乘以物体的体积乘以重力加速度。
物体的重力等于物体的质量乘以重力加速度。
根据题目条件,浮力等于重力,所以液体的密度乘以物体的体积等于物体的质量。
浸没深度可以通过浸没体积与物体的底面积之比来计算。
3. 一个圆柱形容器中盛有液体,容器的高度为10 cm,直径为5 cm,液体的密度为800 kg/m³,求液体的压强。
解答:液体的压强等于液体的密度乘以重力加速度乘以液体的深度。
容器的高度为10 cm,所以液体的深度为10 cm。
重力加速度为9.8 m/s²,所以液体的压强为800 kg/m³乘以9.8 m/s²乘以0.1 m,即784 Pa。
4. 一个水龙头的出水口半径为2 cm,水流速度为10 m/s,求水龙头出水口附近的压强。
解答:根据质量守恒定律,水流速度越大,压强越小。
根据伯努利定律,水流速度越大,压强越小。
因此,水龙头出水口附近的压强较小。
5. 在一个垂直于水平面的圆柱形容器中,盛有密度为900 kg/m³的液体。
容器的半径为10 cm,液体的高度为20 cm。
求液体对容器底部的压力。
解答:液体对容器底部的压力等于液体的密度乘以重力加速度乘以液体的高度。
流体力学课后习题答案 第3章习题

0
0
x
2 Q2 Q1 2 Q
1
Q1
45°
2
Q2
1
2
Q Q1 Q2
Q2 Q1
2Q 2
Q1
1
2 2
0.172
Q2 1 2
2
Q
0 1
Q1
1
0
45°
y
x
2
Q2
2
解:
VA
Q AA
3.18m/s
Q VB AB 5.66m/s
列A和B面伯努利方程:
pgA
VA2 2g
pBg
VB2 2g
A
1.8m
以2-2为基准面,列1-1和2-2面
d
伯努利方程:
1
1
z1
V12 2g
V22 2g
V 12.364m/s 2 2
6.0m
2
G F Q V3 V2
F
3d
1.8m
3
F G Q V2 V3 2.32KN
1
4m
1
2
3
d2
B
V2
2
pM 1
2gz1
8.745m/s
4m
d1
4m
4m
2
A
3
所以:(1)Q V2 A2 0.154m3/s (2)VA Q / A1 19.677m/s
(3)管中压强最低点的位置及其负压值 M
分析:压强最低点应是位置最 高或速度最高点,只有可能是 1 2点3点
解:以2-2为基准面,列3-3和2 -2面伯努利方程:
z3
pMg3
V32 2g
pMg2
V2 2 2g
工程流体力学第三章部分习题答案

概念题
伯努利方程的适用条件
伯努利方程适用于不可压缩、无粘性、无热传导的理想流体在重力场作稳定流动时,流体的动能、势能和内能相互转化的守 恒定律。
概念题
流体阻力的类型
流体阻力包括摩擦阻力和形状阻力。摩擦阻力是由于流体内 部摩擦而产生的阻力,形状阻力是由于流体流经物体时,因 流体速度变化而产生的阻力。
工程流体力学第三章部 分习题答案
contents
目录
• 习题一:基础概念理解 • 习题二:流体运动分析 • 习题三:流体压力和阻力 • 习题四:流体的无损检测技术
习题一:基础概念理
01
解
概念题
理解概念 题目:解释流线、迹线、流管、流束、流量等基本概念。
概念题
流线
表示某一瞬时流场中流体质点的 运动轨迹线,流线上各点的方向 与流速方向一致。
概念题
流体阻力的影响因素
流体阻力的影响因素包括流体的性质、 流速、物体的形状和大小、流道表面 的粗糙度等。
计算题
流体静压力的计算
根据流体静压力的定义,流体静压力的大小可以用流体深 度和当地的重力加速度计算得出。如果已知流体的密度和 重力加速度,也可以用流体质量和重力加速度计算得出。
计算题
伯努利方程的应用
计算题
题目
计算流体通过某一管道的流量。
答案
根据流量公式,流体通过某一管道的流量Q可以表示为Q = A × v,其中A为管 道截面积,v为流体在管道中的平均流速。如果已知管道截面积A和流速v,可以 直接计算出流量Q。
03
习题三:流体压力和
阻力
概念题
流体静压力的概念
流体静压力是指流体在静止状态下,由于重力作用在单位面积上的力,其大小与深度有关,深度越大 ,压力越大。
流体力学习题及答案-第三章

第三章 流体运动学3-1粘性流体平面定常流动中是否存在流函数? 答:对于粘性流体定常平面流动,连续方程为:()()0=∂∂+∂∂yv x u ρρ; 存在函数:v t y x P ρ-=),,(和()u t y x Q ρ=,,,并且满足条件:()()yP x Q ∂∂=∂∂。
因此,存在流函数,且为:()()()dy u dx v Qdy Pdx t y x ρρψ+-=+=⎰⎰,,。
3-2轴对称流动中流函数是否满足拉普拉斯方程?答:如果流体为不可压缩流体,流动为无旋流动,那么流函数为调和函数,满足拉普拉斯方程。
3-3 就下面两种平面不可压缩流场的速度分布分别求加速度。
(1)22222 ,2yx ym v y x x m u +⋅=+⋅=ππ (2)()()()222222222 ,yxKtxyv yxx y Kt u +-=+-=,其中m ,K 为常数。
答:(1)流场的加速度表达式为:yv v x v u t v a y u v x u u t u a x ∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=y ,。
由速度分布,可以计算得到:0 ,0=∂∂=∂∂tvt u ,因此: ()222222y x x y m x u +-⋅=∂∂π,()22222y x xy m y u +-⋅=∂∂π;()22222y x xy m x v +-⋅=∂∂π,()222222y x y x m y v +-⋅=∂∂π。
代入到加速度表达式中:()()()22222222222222222222220y x x m y x xym y x y m y x x y m y x x m a x +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ()()()22222222222222222222220y x y m y x y x m y x y m y x xym y x x m a y +⋅⎪⎭⎫⎝⎛-=+-⋅⋅+⋅++-⋅⋅+⋅+=πππππ(2)由速度分布函数可以得到:()()()322222222 ,y x Kxyt v y x x y K t u +-=∂∂+-=∂∂ ()()3222232y x y x Ktx x u +-⋅=∂∂,()()3222232y x y x Kty y u +-⋅=∂∂; ()()3222232y x x y Kty x v +-⋅-=∂∂,()()3222232yx y x Ktx y v +-⋅-=∂∂。
流体力学课后习题及答案-第3章

3-1 用欧拉法表示流体质点的加速度 a等于:u u tu d u u c t u b t r a)()( ;))(( ;)( ;d d )(22∇⋅+∂∂∇⋅∂∂3-5 无旋流动限于:(a) 流线是直线的流动; (b) 迹线是直线的流动; (c) 微团无旋转的流动; (d) 恒定流动。
3-8 已知流速场 31 32xy u y u xy u z y x =-==,,试求: (1)点(1,2,3)的加速度; (2)是几元流动; (3)是恒定流还是非恒定流。
解: (1) 先求加速度各分量43223102310xy xy y y xy z u u y u u x u u t u a x z x y x x x x =+⋅-⋅+=∂∂+∂∂+∂∂+∂∂=523310))(31(00y y y z u u yu u xu u tu a yzy yy xy y =+--++=∂∂+∂∂+∂∂+∂∂=332320310xy x y y xy z u u y u u x u u t u a z z z y z x z z =+⋅-⋅+=∂∂+∂∂+∂∂+∂∂=将x =1,y =2, z =3代入以上各式得2m/s 33.5=x a 2m/s 67.10=y a 2m/s 33.5=z a2222m/s 06.13=++=z y x a a a a (2)是三元流动; (3)是恒定流。
3-14 已知不可压缩流体平面流动,在 y 方向的速度分量为y x y u y 222+-=。
试求速度在x 方向的分量 u x 。
解: 由不可压缩流体平面流动的连续性微分方程得22--=∂∂-=∂∂y yu x u y x )(22 y f x xy u x +--=⇒3-15 如图在送风道的璧上有一面积为0.4m 2的风口,试求风口出流的平均速度解: 风口出流流量为/s m 5.15.243=-=Q风口过流断面面积为2m 2.030sin 4.0== A风口出流的平均速度为m/s 5.7==AQv 3-18 已知流动速度场为 32 32 32y x u x z u z y u z y x +=+=+=,,试求旋转角速度和角变形速度。
流体力学标准化作业答案第三章

流体力学标准化作业(三)——流体动力学本次作业知识点总结1、描述流体运动得两种方法(1)拉格朗日法;(2)欧拉法。
2、流体流动得加速度、质点导数流场得速度分布与空间坐标与时间有关,即流体质点得加速度等于速度对时间得变化率,即投影式为或在欧拉法中质点得加速度由两部分组成, 为固定空间点,由时间变化引起得加速度,称为当地加速度或时变加速度,由流场得不恒定性引起。
为同一时刻,由流场得空间位置变化引起得加速度,称为迁移加速度或位变加速度,由流场得不均匀性引起。
欧拉法描述流体运动,质点得物理量不论矢量还就是标量,对时间得变化率称为该物理量得质点导数或随体导数。
例如不可压缩流体,密度得随体导数3、流体流动得分类(1)恒定流与非恒定流(2)一维、二维与三维流动(3)均匀流与非均匀流4、流体流动得基本概念(1)流线与迹线流线微分方程迹线微分方程(2)流管、流束与总流(3)过流断面、流量及断面平均流速体积流量质量流量断面平均流速(4)渐变流与急变流5、连续性方程(1)不可压缩流体连续性微分方程(2)元流得连续性方程(3)总流得连续性方程6、运动微分方程(1)理想流体得运动微分方程(欧拉运动微分方程)矢量表示式(2)粘性流体运动微分方程(N-S方程)矢量表示式7、理想流体得伯努利方(1)理想流体元流得伯努利方程(2)理想流体总流得伯努利方程8、实际流体得伯努利方程(1)实际流体元流得伯努利方程(2)实际流体总流得伯努利方程10、恒定总流得动量方程投影分量形式标准化作业(5)——流体运动学选择题1、用欧拉法表示流体质点得加速度等于()。
A、B、C、D、2、水在一条管道中流动,若两截面得管径比,则速度比为( )。
A、3B、1/3C、9D、1/93、通过一个曲面上得体积流量与曲面上得( )有关。
A、法向速度B、切向速度C、密度分布D、压强4、连续性方程表示控制体得( )守恒。
A、能量B、动量C、流量D、质量5、在( )流动中,流线与迹线重合。
(完整版)流体力学第三章课后习题答案

(完整版)流体⼒学第三章课后习题答案⼀元流体动⼒学基础1.直径为150mm 的给⽔管道,输⽔量为h kN /7.980,试求断⾯平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=?→//A Qv ρ=得:s m v /57.1=2.断⾯为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出⼝处断⾯收缩为150mm ×400mm,求该断⾯的平均流速解:由流量公式vA Q = 得:A Q v =由连续性⽅程知2211A v A v = 得:s m v /5.122=3.⽔从⽔箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流⼊⼤⽓中. 当出⼝流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解:(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性⽅程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输⽔量为h kg /294210的给⽔管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代⼊得343.0=d ∽m 275.0 ∵直径是mm 50的倍数,所以取m d 3.0= 代⼊vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3/h,,流速不超过20 m/s 。
试设计直径,根据所定直径求流速。
直径规定为50 mm 的倍数。
解:vA Q = 将s m v /20≤代⼊得:mm d 5.420≥ 取mm d 450= 代⼊vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断⾯上,⽤下法选定五个点,以测局部风速。
工程流体力学教学工程流体力学习题+答案(部分)之欧阳学创编

闻建龙主编的《工程流体力学》习题参考答案第一章绪论1-1 物质是按什么原则分为固体和液体两大类的?解:从物质受力和运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。
如空气、水等。
而在同等条件下,固体则产生有限的变形。
因此,可以说:流体不管是液体还是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。
与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。
1-2 何谓连续介质假设?引入连续介质模型的目的是什么?在解决流动问题时,应用连续介质模型的条件是什么?解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。
流体连续性假设是流体力学中第一个根本性假设,将真实流体看成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可看成时间和空间位置的连续函数,使我们有可能用数学分析来讨论和解决流体力学问题。
在一些特定情况下,连续介质假设是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm )内的流动。
1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水和C 020时密度为3856m kg的原油时,移动平板所需的力各为多大?题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水: 233/410416101m N u =⨯⨯=⋅=--δμτ 油: 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ 1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律是直线。
流体力学第三章习题答案培训讲学

流体力学第三章习题答案第三章习题答案选择题(单选题)3.1 用欧拉法表示流体质点的加速度a r等于:(d )(a )22d r dtr ;(b )u t ∂∂r ;(c )()u u ⋅∇r r ;(d )u t ∂∂r+()u u ⋅∇rr 。
3.2 恒定流是:(b )(a )流动随时间按一定规律变化;(b )各空间点上的流动参数不随时间变化;(c )各过流断面的速度分布相同;(d )迁移加速度为零。
3.3 一维流动限于:(c )(a )流线是直线;(b )速度分布按直线变化;(c )流动参数是一个空间坐标和时间变量的函数;(d )流动参数不随时间变化的流动。
3.4 均匀流是:(b )(a )当地加速度为零;(b )迁移加速度为零;(c )向心加速度为零;(d )合加速度为零。
3.5 无旋流动限于:(c )(a )流线是直线的流动;(b )迹线是直线的流动;(c )微团无旋转的流动;(d )恒定流动。
3.6 变直径管,直径1d =320mm, 2d =160mm,流速1v =1.5m/s 。
2v 为:(c )(a )3m/s ;(b )4m/s ;(c )6m/s ;(d )9m/s 。
2.23 已知速度场x u =2t +2x +2y ,y u =t -y +z ,z u =t +x -z 。
试求点(2,2,1)在t =3时的加速度。
解: x x x x x x y z u u u ua u u u t x y z∂∂∂∂=+++∂∂∂∂ ()()2222220t x y t y z =+++⋅+-+⋅+26422t x y z =++++()2321t x y z =++++ y y y y y xyzu u u u a u u u t x y z ∂∂∂∂=+++∂∂∂∂()()101t y z t x z =+--+++-⋅12x y z =++-z z z z z x y z u u u ua u u u t x y z∂∂∂∂=+++∂∂∂∂ ()()12220t x y t x z =++++-+-12t x y z =++++()()3,2,2,12332221134x a =⨯⨯+⨯+++=(m/s 2) ()3,2,2,112223y a =++-=(m/s 2) ()3,2,2,11324111z a =++++=(m/s 2)35.86a ===(m/s 2)答:点(2,2,1)在t =3时的加速度35.86a =m/s 2。
【尚择优选】流体力学标准化作业答案第三章

流体力学标准化作业(三)——流体动力学本次作业知识点总结1.描述流体运动的两种方法 (1)拉格朗日法;(2)欧拉法。
2.流体流动的加速度、质点导数流场的速度分布与空间坐标(,,)x y z 和时间t 有关,即(,,,)u u x y z t =流体质点的加速度等于速度对时间的变化率,即Du u u dx u dy u dz a Dt t x dt y dt z dt ∂∂∂∂==+++∂∂∂∂投影式为x x x x x x y z y y y y y x y z z z z z z x y z u u u u a u u u t x y z u u u u a u u u t x y z u u u ua u u u t x y z ∂∂∂∂⎧=+++⎪∂∂∂∂⎪∂∂∂∂⎪=+++⎨∂∂∂∂⎪⎪∂∂∂∂=+++⎪∂∂∂∂⎩或()du ua u u dt t∂==+⋅∇∂ 在欧拉法中质点的加速度du dt 由两部分组成,u t∂∂为固定空间点,由时间变化引起的加速度,称为当地加速度或时变加速度,由流场的不恒定性引起。
()u u ⋅∇为同一时刻,由流场的空间位置变化引起的加速度,称为迁移加速度或位变加速度,由流场的不均匀性引起。
欧拉法描述流体运动,质点的物理量不论矢量还是标量,对时间的变化率称为该物理量的质点导数或随体导数。
例如不可压缩流体,密度的随体导数D D u t tρρρ∂=+⋅∇∂() 3.流体流动的分类(1)恒定流和非恒定流 (2)一维、二维和三维流动(3)均匀流和非均匀流 4.流体流动的基本概念 (1)流线和迹线流线微分方程x y zdx dy dz u u u == 迹线微分方程x y zdx dy dz dt u u u === (2)流管、流束与总流(3)过流断面、流量及断面平均流速体积流量3(/)AQ udAm s =⎰ 质量流量(/)m AQ udAkg s ρ=⎰断面平均流速AudA Qv AA==⎰(4)渐变流与急变流5.连续性方程(1)不可压缩流体连续性微分方程0y x zu u u x y z ∂∂∂++=∂∂∂ (2)元流的连续性方程121122dQ dQ u dA u dA =⎧⎨=⎩ (3)总流的连续性方程1122u dA u dA =6.运动微分方程(1)理想流体的运动微分方程(欧拉运动微分方程)111xx x x x y z yy y y x y z zz z z x y z u u u u p X u u u x t x y zu u u u p Y u u u x t x y z u u u u p Z u u u x t x y z ρρρ∂∂∂∂∂⎫-=+++⎪∂∂∂∂∂⎪∂∂∂∂⎪∂-=+++⎬∂∂∂∂∂⎪⎪∂∂∂∂∂-=+++⎪∂∂∂∂∂⎭矢量表示式1()uf p u u tρ∂+∇=+⋅∇∂(2)粘性流体运动微分方程(N-S 方程)222111x x x x x x y z y y y y y x y z z z z z z x y z u u u u pX u u u u x t x y zu u u u pY u u u u x t x y z u u u u pZ u u u u x t x y z νρνρνρ∂∂∂∂∂⎫-+∇=+++⎪∂∂∂∂∂⎪∂∂∂∂⎪∂-+∇=+++⎬∂∂∂∂∂⎪⎪∂∂∂∂∂-+∇=+++⎪∂∂∂∂∂⎭矢量表示式21()uf p u u u tνρ∂+∇+∇=+⋅∇∂ 7.理想流体的伯努利方(1)理想流体元流的伯努利方程22p u z C g gρ++= (2)理想流体总流的伯努利方程221112221222p v p v z z g g g g ααρρ++=++8.实际流体的伯努利方程(1)实际流体元流的伯努利方程2211221222w p u p u z z h g g g g ρρ++=+++(2)实际流体总流的伯努利方程2211122212w 22p v p v z z h g g g g ααρρ++=+++10.恒定总流的动量方程()2211F Q vv ρββ=-∑投影分量形式()()()221122112211xx x y y y z z z F Q v v F Q v v FQ v v ρββρββρββ⎫=-⎪⎪=-⎬⎪=-⎪⎭∑∑∑标准化作业(5)——流体运动学选择题1.用欧拉法表示流体质点的加速度a 等于( )。
流体力学标准化作业答案第三章之欧阳德创编

流体力学标准化作业(三)——流体动力学本次作业知识点总结 1 •描述流体运动的两种方法(1) 拉格朗日法;(2)欧拉法。
2流体流动的加速度、质点导数流场的速度分布与空间坐标(X*⑵和时间f 有 关,即 流体质点的加速度等于速度对时间的变化率, 即 投影式为du du z —=—+ («• V )Mdu在欧拉法中质点的加速度〃由两部分组成,彳 为固定空间点,由时间变化引起的加速度,称为当 地加速度或时变加速度,由流场的不恒定性引起。
(,刃帀为同一时刻,由流场的空间位置变化引起的加 速度,称为迁移加速度或位变加速度,由流场的不 均匀性引起。
欧拉法描述流体运动,质点的物理量不论矢 量还是标量,对时间的变化率称为该物理量的质点 导数或随体导数。
例如不可压缩流体,密度的随体欧阳德创编创作:欧阳德导数3 •流体流动的分类(1)恒定流和非恒定流(2)—维、二维和三维流动(3)均匀流和非均匀流4 •流体流动的基本概念(1)流线和迹线流线微分方程迹线微分方程(2)流管、流束与总流(3)过流断面、流量及断面平均流速体积流量。
叮曲质量流量“订严人伙g/y)一」严人断面平均流速人人(4)渐变流与急变流5.连续性方程(1)不可压缩流体连续性微分方程(2)元流的连续性方程(3)总流的连续性方程6.运动微分方程(1)理想流体的运动微分方程(欧拉运动微分方程)矢量表示式(2)粘性流体运动微分方程(N-S方程)y + lvp + i^2z7 = —+ («V)w 矢量表示式P dt 7 •理想流体的伯努利方(1)理想流体元流的伯努利方程欧阳德创编欧阳德创编2021.03.07 欧阳德创编2021.03.07(2)理想流体总流的伯努利方程8 •实际流体的伯努利方程(1)实际流体元流的伯努利方程(2)实际流体总流的伯努利方程10垣定总流的动量方程投影分量形式标准化作业(5)——流体运动学选择题1 •用欧拉法表示流体质点的加速度"等于()o/厂dv dv . z n A\ vA.drB. dtC.(V,A),VD.厉°2.水在一条管道中流动,若两截面的管径比必2 =3,则速度比”化为()。
水力学(闻德荪)习题答案第三章之欧阳学文创编

选择题(单选题)3.1欧阳歌谷(2021.02.01)3.2 用欧拉法表示流体质点的加速度a 等于:(d )(a )22d rdt;(b )u t ∂∂;(c )()u u ⋅∇;(d )ut∂∂+()u u ⋅∇。
3.3恒定流是:(b )(a )流动随时间按一定规律变化;(b )各空间点上的流动参数不随时间变化;(c )各过流断面的速度分布相同;(d )迁移加速度为零。
3.4一维流动限于:(c ) (a )流线是直线;(b )速度分布按直线变化;(c )流动参数是一个空间坐标和时间变量的函数;(d )流动参数不随时间变化的流动。
3.5均匀流是:(b )(a )当地加速度为零;(b )迁移加速度为零;(c )向心加速度为零;(d )合加速度为零。
3.6无旋流动限于:(c )(a )流线是直线的流动;(b )迹线是直线的流动;(c )微团无旋转的流动;(d )恒定流动。
3.7变直径管,直径1d =320mm,2d =160mm,流速1v =1.5m/s 。
2v 为:(c )(a )3m/s ;(b )4m/s ;(c )6m/s ;(d )9m/s 。
3.7已知速度场x u =2t +2x +2y ,y u =t -y +z ,z u =t +x -z 。
试求点(2,2,1)在t =3时的加速度。
解: x x x x x x y z u u u ua u u u t x y z∂∂∂∂=+++∂∂∂∂ ()()3,2,2,12332221134x a =⨯⨯+⨯+++=(m/s2) ()3,2,2,112223y a =++-=(m/s2) ()3,2,2,11324111z a =++++=(m/s2)35.86a ===(m/s2)答:点(2,2,1)在t =3时的加速度35.86a =m/s2。
3.8已知速度场x u =2xy ,y u =–331y ,z u =xy 。
试求:(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流。
流体力学标准化作业答案第三章

流体力学标准化作业答案第三章案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
流体力学-流体第三章作业答案

作业答案:3.1什么是流线?流线有什么特性?答:流线:流场中的瞬时光滑曲线,曲线上各点的切线方向与该点的瞬时速度方向一致。
流线特性:1 )定常流动中流线不随时间变化,而且流体质点的轨迹与流线重合。
2)实际流场中除驻点或奇点外,流线不能相交,不能突然转折。
3.2理想流体微小流束伯努利方程各项的意义是什么?导出条件是什么?基准面为什么要取水平面?答:(1)方程形式:z p v2c2g物理意义:z----单位(重力流体具有的)位能;p-g -----单位压能;v22g----单位动能。
几何意义:z----位置水头;p—g ---压强水头;- 流速水头。
(2)导出条件:1)质量力只有重力;2)定常流;3)沿流线;4)不可压缩流体(或C )。
(3)因为基准面是在重力场中衡量位置势能大小的,因此要以水平面为基准。
3.3总流伯努利方程是什么形式?导出条件及应用条件是什么?2 2答:形式:Z i 卫也Z2 卫2—hwg 2g g 2g导出条件及应用条件:1)质量力只有重力;2)定常流动;3)断面必须是均匀流断面或缓变流断面;4)不可压缩流体。
3.5题略答:当阀门A开度一定,各管段是稳定流;阀门A逐渐关闭的过程中,各点运动参数随时间发生变化,管中流动为非稳定流动。
3.8题略解:坐标取在叶片上,则流动为定常流取水平向右为X轴正向,以射流及叶片围成的流体为研究对象,列X方向动量方程:3.38题略解:列空气初始状态 1与接有测压装置处的过流断面2 2_P 1 V^P 2 V 2 2的伯努利方程,不计损失,g 2g g 2g式中,在所建坐标系下的初速度,也即射流的相对速度:V ix V u ,相对流量:q Vr\ Uq V由伯努利方程,可知射流从叶片流出的相对速度大小 V 2 V 1x V u则 V2xV2cos (V u)cos流体所受外力F XR x把各项代入式( 1),有R xVu r V q V [(V u)cos (V u)]即Rx —U%[(V u)cos (V u)](V u)2/ q VV (1 cos )所以,叶片所受力F 1 R x(V u)2“ q V (1 cos ),方向向右V可知,在有射流冲】 击力的情况下,当u 增大时,F 减小。
流体力学作业2答案之欧阳歌谷创编

作业2答案(第3章、第4章)欧阳歌谷(2021.02.01)第3章一、选择题1、流体运动的连续性方程是根据(C)原理导出的。
A、动量守恒B、质量守恒C、能量守恒D、力的平衡2、流线和迹线重合的条件为( C )A、恒定流B、非恒定流C、非恒定均匀流二、判断题1、以每个流体质点运动规律为研究对象的方法称为拉格朗日法。
(正确)2、恒定流一定是均匀流。
(错误)3、涡流是指流体质点在运动中不绕自身轴旋转的流动。
(正确)4、无旋流就是无涡流。
(正确)5、非均匀流一定是非恒定流。
(错误)三、简答题1、述流体运动的两种方法是什么?简述其内容。
答:研究流体运动有两种不同的观点,因而形成两种不同的方法:一种方法是从分析流体各个质点的运动着手,即跟踪流体质点的方法来研究整个流体的运动,称之为拉格朗日法;另一种方法则是从分析流体所占据的空间中各固定点处的流体的运动着手,即设立观察站的方法来研究流体在整个空间里的运动,称其为欧拉法2. 流体微团体运动分为哪几种形式?答:①平移②线变形③角变形④旋转变形。
3. 写出恒定平面势流中流函数、势函数与流速的关系。
(改为:写出恒定平面势流中流函数具有的性质,流函数与流速势的关系。
)答:流函数具有的性质(1)流函数相等的点组成的线即流线,或曰,同一流线上个点的流函数为常数。
(2)两流线间的函数值之差为为单宽流量。
(3)平面势流的流函数为一个调和函数。
答:流函数与流速势的关系(1)流函数与势函数为调和函数。
(2)等势线与等流函数线正交。
4.什么是过流断面和断面平均流速?为什么要引入断面平均流速?答:与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
5.如图所示,水流通过由两段等截面及一段变截面组成的管道,试问:(1)当阀门开度一定,上游水位保持不变,各段管中,是恒定流还是非恒定流?是均匀流还是非均匀流?(2)当阀门开度一定,上游水位随时间下降,这时管中是恒定流还是非恒定流?(3)恒定流情况下,当判别第II 段管中是渐变流还是急变流时,与该段管长有无关系?答:(1)是恒定流。
水力学课后答案之欧阳文创编

交谈中请勿轻信汇款、中奖信息、陌生电话,勿使用外挂软件。
弟弟17:52:55弟弟17:53:39弟弟17:54:01弟弟17:54:26弟弟17:54:45弟弟17:55:00弟弟17:55:13弟弟17:55:26弟弟17:55:42弟弟17:55:57弟弟17:56:17弟弟17:56:32弟弟17:56:48弟弟17:57:06弟弟17:57:22弟弟17:57:37弟弟17:57:52弟弟17:58:06弟弟17:58:18弟弟17:58:38时间:2021.03.12 创作:欧阳文交谈中请勿轻信汇款、中奖信息、陌生电话,勿使用外挂软件。
弟弟18:03:18弟弟18:03:39弟弟18:03:57弟弟18:04:11弟弟18:04:27弟弟18:04:56弟弟18:05:11弟弟18:05:22弟弟18:05:34弟弟18:05:44弟弟18:05:57弟弟18:06:07弟弟18:06:21弟弟18:06:33弟弟18:06:48弟弟18:07:00弟弟18:07:14弟弟18:07:25弟弟18:07:35弟弟18:07:49弟弟18:08:00弟弟18:08:09弟弟18:08:23弟弟18:08:36弟弟18:08:48弟弟18:08:58弟弟18:09:11弟弟18:09:20弟弟18:09:32弟弟18:09:41弟弟18:09:53弟弟18:10:06弟弟18:10:19弟弟18:10:30弟弟18:10:41交谈中请勿轻信汇款、中奖信息、陌生电话,勿使用外挂软件。
弟弟18:12:37弟弟18:12:53弟弟18:13:03弟弟18:13:15弟弟18:13:30弟弟18:13:45弟弟18:13:56弟弟18:14:11弟弟18:14:25弟弟18:14:36。
流体力学作业2答案之欧阳家百创编

作业2答案(第3章、第4章)欧阳家百(2021.03.07)第3章一、选择题1、流体运动的连续性方程是根据(C)原理导出的。
A、动量守恒B、质量守恒C、能量守恒D、力的平衡2、流线和迹线重合的条件为( C )A、恒定流B、非恒定流C、非恒定均匀流二、判断题1、以每个流体质点运动规律为研究对象的方法称为拉格朗日法。
(正确)2、恒定流一定是均匀流。
(错误)3、涡流是指流体质点在运动中不绕自身轴旋转的流动。
(正确)4、无旋流就是无涡流。
(正确)5、非均匀流一定是非恒定流。
(错误)三、简答题1、述流体运动的两种方法是什么?简述其内容。
答:研究流体运动有两种不同的观点,因而形成两种不同的方法:一种方法是从分析流体各个质点的运动着手,即跟踪流体质点的方法来研究整个流体的运动,称之为拉格朗日法;另一种方法则是从分析流体所占据的空间中各固定点处的流体的运动着手,即设立观察站的方法来研究流体在整个空间里的运动,称其为欧拉法2. 流体微团体运动分为哪几种形式?答:①平移②线变形③角变形④旋转变形。
3. 写出恒定平面势流中流函数、势函数与流速的关系。
(改为:写出恒定平面势流中流函数具有的性质,流函数与流速势的关系。
)答:流函数具有的性质(1)流函数相等的点组成的线即流线,或曰,同一流线上个点的流函数为常数。
(2)两流线间的函数值之差为为单宽流量。
(3)平面势流的流函数为一个调和函数。
答:流函数与流速势的关系(1)流函数与势函数为调和函数。
(2)等势线与等流函数线正交。
4.什么是过流断面和断面平均流速?为什么要引入断面平均流速?答:与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
5.如图所示,水流通过由两段等截面及一段变截面组成的管道,试问:(1)当阀门开度一定,上游水位保持不变,各段管中,是恒定流还是非恒定流?是均匀流还是非均匀流?(2)当阀门开度一定,上游水位随时间下降,这时管中是恒定流还是非恒定流?(3)恒定流情况下,当判别第II 段管中是渐变流还是急变流时,与该段管长有无关系?答:(1)是恒定流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流体力学标准化作业(三)——流体动力学本次作业知识点总结1.描述流体运动的两种方法(1)拉格朗日法;(2)欧拉法。
2.流体流动的加速度、质点导数 流场的速度分布与空间坐标(,,)x y z 和时间t有关,即流体质点的加速度等于速度对时间的变化率,即投影式为或 ()du u a u u dt t ∂==+⋅∇∂在欧拉法中质点的加速度dudt 由两部分组成,ut ∂∂为固定空间点,由时间变化引起的加速度,称为当地加速度或时变加速度,由流场的不恒定性引起。
()u u ⋅∇为同一时刻,由流场的空间位置变化引起的加速度,称为迁移加速度或位变加速度,由流场的不均匀性引起。
欧拉法描述流体运动,质点的物理量不论矢量还是标量,对时间的变化率称为该物理量的质点导数或随体导数。
例如不可压缩流体,密度的随体导数3.流体流动的分类(1)恒定流和非恒定流(2)一维、二维和三维流动(3)均匀流和非均匀流4.流体流动的基本概念(1)流线和迹线流线微分方程迹线微分方程(2)流管、流束与总流(3)过流断面、流量及断面平均流速体积流量3(/)A Q udA m s =⎰ 质量流量(/)m A Q udA kg s ρ=⎰ 断面平均流速A udAQ v A A ==⎰(4)渐变流与急变流5. 连续性方程(1)不可压缩流体连续性微分方程(2)元流的连续性方程(3)总流的连续性方程6. 运动微分方程(1)理想流体的运动微分方程(欧拉运动微分方程)矢量表示式(2)粘性流体运动微分方程(N-S 方程) 矢量表示式21()u f p u u u t νρ∂+∇+∇=+⋅∇∂7.理想流体的伯努利方(1)理想流体元流的伯努利方程(2)理想流体总流的伯努利方程8.实际流体的伯努利方程(1)实际流体元流的伯努利方程(2)实际流体总流的伯努利方程10.恒定总流的动量方程投影分量形式标准化作业(5)——流体运动学选择题1. 用欧拉法表示流体质点的加速度a 等于( )。
A. 22d r dt B. v t ∂∂ C. ()v v ⋅∆⋅ D. ()v v v t ∂+⋅∆⋅∂2. 水在一条管道中流动,若两截面的管径比321=d d ,则速度比12v v 为 ( )。
A. 3B. 1/3C. 9D. 1/93. 通过一个曲面上的体积流量与曲面上的( )有关。
A. 法向速度B. 切向速度C. 密度分布D. 压强4. 连续性方程表示控制体的( )守恒。
A. 能量B. 动量C. 流量D. 质量5. 在( )流动中,流线和迹线重合。
A .不可压缩B .无黏C .恒定D .非恒定6. 一维流动中,“截面积大处速度小,截面积小处速度大”成立的必要条件是()。
A.理想流体B.黏性流体C.可压缩流体D.不可压缩流体7.当陨星在天空中下坠时,其划过的白线是( ) 。
A.流线B.迹线C.等势线D.等流函数线8. 欧拉法()描述流体质点的运动。
A.直接B.间接C.不能D.只在恒定时能。
9. 流体微团的运动与刚体运动相比,多了一项()运动。
A.平移B.旋转C.变形D.加速10.均匀流是()。
A. 当地加速度为零B. 迁移加速度为零C. 向心加速度为零D. 合加速度为零11.一元流动限于()。
A. 流线是直线B.速度分布按直线变化C.运动参数是一个空间坐标和时间变量的函数D .运动参数不随时间变化的流动。
12.已知不可压缩流体的流速场为0)(),(===z y x u x f u z y f u ,,,则该流动为( )。
A.一元流B.二元流C.三元流D.均匀流13.恒定流是( )。
A.流动随时间按一定规律变化B.各过流断面的速度分布相同C.各空间点上的运动要素不随时间变化D. 迁移加速度为零15.根据图1所示三通管流,可得( )。
A.321V V V q q q =+B.321V V V q q q =-C.321V V V q q q +=D.0321=++V V V q q q二、填空题1.流线一般不能相交,且只能是一条曲线。
2.体积流量V q 与质量流量m q 的关系是。
3.渐变流断面上各点的测压管水头g p z ρ+近似等于。
4. 在研究工程流体力学时主要采 。
5. 用欧拉法表示流体的质点加速度由和两部分组成。
三、判断题1.根据流动的分类,三元流是指0,0,0≠≠≠z y x u u u的流动。
( )2.恒定流的迁移加速度等于零,而均匀流的当地加速度等于零。
( )3.若流动的合加速度不等于零,则该流动必为非恒定流。
( )4. 恒定流是指运动要素不随时间和空间变化的流动。
( )5.均匀流是指过流断面上各点流速均匀相等的流动。
( )6.急变流是指流线近似为平行直线的流动。
( )7.渐变流是指流速分布沿程不变的流动。
( )8.拉格朗日法是以流场中每一流体质点作为研究对象。
( )9.驻点上流线是相交的,这是因为驻点速度为无穷大的缘故。
( )10.过水断面都是平面。
( )四、计算题1、已知流场中的速度分布为u yz t =+,v xz t =-,xy ω=。
(1)试问此流动是否恒定?(2)求流体质点在通过场中(1,1,1)点时的加速度。
2. 一流动的速度场为22(1)(2)v x t i y t j =+++,试确定在1t =时,通过(2,1)点的迹线方程和流线方程。
3. 不可压缩流体,下面的运动能否出现(是否满足连续性条件)?(1)22322(2)x y u x y u x x y y =+=--;(2)22x y u xt y u xt yt =+=-;(3)22223412222x y z u y xz u yz x yz u x z x y =+=-+=-;; 4. 已知速度场2x u xy =,313y u y =-,z u xy =,试求(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流。
标准化作业(6)——伯努利方程一、选择题1. 应用总流的伯努利方程时,两过水断面之间( )。
A.必须都是急变流B.必须都是缓变流C.不能出现急变流D.可以出现急变流2. 伯努利方程中g v g p z 22αρ++表示( )。
A.单位重量流体具有的机械能B.单位质量流体具有的机械能C.单位体积流体具有的机械能D.通过过流断面流体的总机械能3. 皮托管用于测量( )。
A.点速度B.压强C.密度D.流量4. 如图1所示,输油管路中安装有一文丘里流量计,已知水银压差计中水银柱高差为p h ,则=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+g p z g p z ρρ1122-( )。
A.p h ρρ水银B.p h ⎪⎪⎭⎫ ⎝⎛-ρρ水银1 C.p h ⎪⎪⎭⎫ ⎝⎛-1ρρ水银 D.p h ⎪⎪⎭⎫ ⎝⎛+ρρ水银1 5. 文丘里用于测量( )。
A.点速度B.压强C.密度D.流量6. 关于水流流向的正确说法是( )。
A.水一定是从高处往低处流B.水一定是从流速大处往流速小处流C.水一定是从机械能大处往机械能小处流D.水一定是从测压管水头高处往测压管水头低处流7. 伯努利方程中g v g p z 22αρ++表示( )。
A .单位重量流体具有的机械能;B .单位质量流体具有的机械能;C .单位体积流体具有的机械能;D .通过过流断面流体的总机械能。
8. 水平放置的渐扩管,如忽略水头损失,断面形心点的压强,有以下关系( )。
A.12p p >B.12p p =C.12p p <D.不定9.图2所示文丘里管,已知管道直径m m 1001=d ,喉道直径m m 502=d ,文丘里流量计系数94.0=μ,水银压差计读数cm 25=p h ,则通过管道的水流量=V q ( )3m /s 。
A.0.030B.0.025C.0.020D.0.0110. 图3所示等径长直管流中,M-M 为过流断面,N-N 为水平面,则有( )。
A.21p p =B.43p p =图1C.g p z g p z ρρ2211+=+ D.g p z g p z ρρ4433+=+ 图2 图3二、填空题1. 只要比较总流中两个渐变流过流断面上单位重量流体的____________大小,就能判断出流动方向。
2. 水管内径=150mm d ,在1小时内排水310m ,则管内流量Q =______,断面平均流速v =_____。
3.列伯努利方程式时,过水断面必须取在_________。
4.黏性流体总水头线沿程的变化是。
5.安装在风道内的毕托管的测速管和测压管间的压差为O m m H 1002,若毕托管的流速系数为0.99,风道内空气的密度为31.12kg/m ,则风道内的风速为m/s 。
三、判断题1. 由于黏性是流体的固有属性,因此,不管是理想流体还是实际流体,其机械能总是沿程减小的。
( )2.在流量Q 一定条件下,流速水头g v 22与管径d成正比。
( ) 3. 渐变流过水断面上动水压强的分布规律可近图4似地看作与静水压强分布规律相同。
( )4.实际流体总水头线是沿程下降的,而测压管水头线在一定条件下会沿程升。
( )5.位置高度与测压管高度之和,称为测压管水头。
( )6.测压管水头线沿流体的流动方向是时升时降。
( )7.虹吸管最高处的压强大于大气压。
( )四、计算题1. 水流过一段转弯变径管,如图5所示,已知小管径1200mm d =,截面压力170kPa p =,大管径2400mm d =400mm ,压力240kPa p =,流速21m/s v =。
两截面中心高度差1m z =,求管中流量及水流方向。
52.利用皮托管原理,测量水管中的点流速u ,如图6所示。
如读值60mm h ∆=,求该点流速。
图63. 高压水箱的出水管如图3-4所示,出水管的直径=0.1m D ,当阀门关闭时,压力表的读数为424.910N/m ⨯,当阀门打开时压力表的读数为421.9610N/m ⨯。
不考虑水头损失时,试求出水流量。
若水头损失为2.5m 时,求出水流量。
图74. 如图8所示,两个紧靠的水箱逐级放水,放水孔的截面积分别为1A 与2A ,试问:1h 与2h 成什么关系时流动处于恒定状态?这时须在左边水箱补充多大流量?85.离心式通风机如图9,用管道A 从大气中吸取空气,在直径=0.2m D 处接一玻璃管,其下端插入水槽中,水沿此管上升=0.25m H ,空气密度为31.23kg/m ρ=。
求每秒钟管道A 所吸取的空气量。
96. 如10图所式。
设一虹吸管2m a =,=6m h ,=15m d 。
试求:(1)管内的流量;(2)管内最高点S 的压强;(3)若h 不变,点S 继续升高(即a 增大,而上端管口始终浸入水内),问使吸虹管内的水不能连续流动的值a 为多大?10标准化作业(7)——动量方程一、选择题1. 恒定总流的连续性方程、伯努利方程、动量方程中的流速为( )。
