最新初三数学寒假培优提高班讲义——圆(1)

合集下载

初三九年级上册_圆的概念和性质辅导讲义(学生版)

初三九年级上册_圆的概念和性质辅导讲义知识图谱圆的相关概念知识精讲知识精讲一．圆的相关概念1.圆的概念（1）描述性定义:在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，其中固定端点O叫做圆心，OA叫做半径；（2）集合性定义:平面内到定点的距离等于定长的点的集合叫做圆，定点叫做圆心，定长叫做半径；（3）圆的表示方法:用符号表示圆，定义中以O为圆心，OA为半径的圆记作“O”，读作“圆O”；（4）同圆、同心圆、等圆：①圆心相同且半径相等的圆叫同圆；②圆心相同，半径不相等的两个圆叫做同心圆；③能够重合的两个圆叫做等圆．2.弦与弧的相关概念：（1）弦：连结圆上任意两点的线段叫做弦；（2）直径：经过圆心的弦叫做圆的直径，直径等于半径的2倍；（3）弦心距：从圆心到弦的距离叫做弦心距；（4）弧：圆上任意两点间的部分叫做圆弧，简称弧．以A B、为端点的圆弧记作 AB，读作弧AB；（5）等弧：在同圆或等圆中，能够互相重合的弧叫做等弧；（6）半圆：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆；（7）优弧、劣弧：大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧；（8）弓形：由弦及其所对的弧组成的图形叫做弓形．3.圆心角与圆周角（1）圆心角:顶点在圆心的角叫做圆心角；①将整个圆分为360等份，每一份的弧对应1︒的圆心角，我们也称这样的弧为1︒的弧；②圆心角的度数和它所对的弧的度数相等；（2）圆周角:顶点在圆上，并且两边都和圆相交的角叫做圆周角．三点剖析一．考点：圆的相关概念二．重难点：1.圆的两种定义的理解；2.弦心距、优弧、圆周角等陌生概念的理解与记忆．三．易错点：1.圆是一条封闭曲线并不包含所围成图形内部部分；2.弓形只是由弧和弦所构成不包含半径；3.同圆、等圆、同心圆的联系与区别．圆的相关概念例题例题1、判断：（1）直径是弦，弦是直径（）（2）半圆是圆弧（）（3）长度相等的弧是等弧（）（4）能够重合的弧是等弧（）（5）圆弧分为优弧和劣弧（）（6）优弧一定大于劣弧（）（7）半径相等的圆是等圆（）例题2、设想有一根铁丝套在地球的赤道上，刚好拉紧后，又放长了15米，并使得铁丝均匀地离开地面．则下面说法中比较合理的是（）A.你只能塞过一张纸 B.你只能塞过一只书包C.你能钻过铁丝 D.你能直起身体走过铁丝随练随练1、下列说法中，结论错误的是（）A.直径相等的两个圆是等圆B.长度相等的两条弧是等弧C.圆中最长的弦是直径D.一条弦把圆分成两条弧，这两条弧可能是等弧随练2、过圆上一点可以做出圆的最长弦的条数是（）A.1条 B.2条 C.3条D.无数条随练3、如图，O 的直径AB 与弦CD 的延长线交于点E ，若DE OB =，74AOC ∠=︒，则E ∠=．垂径定理知识精讲一．垂径定理1.定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．2.推论1：（1）平分弦（非直径）的直径，垂直于弦，并且平分弦所对的两条弧．（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．推论2：圆的两条平行弦所夹的弧相等．应用垂径定理与推论进行计算时，往往要构造如右图所示的直角三角形，根据垂径定理与勾股定理有：222()2ar d =+，根据此公式，在a ，r ，d 三个量中知道任何两个量就可以求出第三个量．补充说明：做题过程中，定理与推论1（1）可以直接使用，而推论1（2）、（3）需证明后再使用．三点剖析一．考点：垂径定理二．重难点：利用垂径定理求圆的半径、弦长和弦心距．三．易错点：对垂径定理的理解不够，不会正确添加辅助线运用直角三角形进行解题垂径定理例题例题1、在直径为200cm 的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm ，则油的最大深度为（）A.40cmB.60cmC.80cmD.100cm例题2、如图，“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何．”用几何语言可表述为：CD 为O 的直径，弦AB CD ⊥于E ，1CE =寸，10AB =寸，则直径CD 的长为（）A.12.5寸B.13寸C.25寸D.26寸例题3、如图是一个隧道的横截面，它的形状是以点O 为圆心的圆的一部分．如果M 是O 中弦CD 的中点，EM 经过圆心O 交O 于点E ，并且4CD =，6EM =，求O 的半径．例题4、如图是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB 宽为8cm ，水面最深地方的高度为2cm ，则该输水管的半径为（）A.3cmB.4cmC.5cmD.6cm例题5、⊙O 的半径为10，两平行弦AC ，BD 的长分别为12，16，则两弦间的距离是（）A.2B.14C.6或8D.2或14随练随练1、如图，⊙O 的弦AB 垂直半径OC 于点D ，∠CBA=30°，OC=3cm ，则弦AB 的长为（）A.9cmB.3cmC.cmD.cm随练2、如图，ABC ∆内接于O ，D 为线段AB 的中点，延长OD 交O 于点E ，连接AE ，BE ，则下列五个结论AB DE AE BE OD DE AEO C ⊥==∠=∠①，②，③，④， 12AE AEB=⑤，正确结论的是随练3、如图，当圆形桥孔中的水面宽度AB 为8米时，弧ACB 恰为半圆．当水面上涨1米时，桥孔中的水面宽度A B ''为（）15米 B.215米 C.217米 D.不能计算随练4、如图，在梯形ABCD 中，AB DC ∥，AB BC ⊥，2cm AB =，4cm CD =．以BC 上一点O 为圆心的圆经过A 、D 两点，且90AOD ∠=︒，则圆心O 到弦AD 的距离是多少？弧，弦，圆心角之间的关系知一推二知识精讲一．圆心角、弧、弦之间的关系1.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弧也相等．若AOB A OB ''∠=∠，则 AB A B ''=，AB A B ''=，AM A M ''=．2.推论：同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量分别相等．二．应用1.在解答圆的问题时，若遇弧相等常转化为它们所对的圆心角相等或弦相等来解答；2.有弦的中点时常作弦心距，利用垂径定理及圆心角、弧、弦、弦心距之间的关系来证题；另外，证明两弦相等也常作弦心距；3.在计算弧的度数时，或有等弧的条件时，或证等弧时，常作弧所对的圆心角；4.有弧的中点或证弧的中点时，常有以下几种引辅助线的方法：（1）连过弧中点的半径；（2）连等弧对的弦；（3）作等弧所对的圆心角三点剖析一．考点：弧、弦、圆心角、弦心距的关系二．重难点：弧、弦、圆心角、弦心距的关系三．易错点：1.两条弧存在倍数关系，但所对应的弦并不是存在相同的倍数关系；2.判断题中，注意题中前提条件，必须是在等圆或同圆中．弧，弦，圆心角之间的关系知一推二例题例题1、下列说法中正确的是（）①圆心角是顶点在圆心的角；②两个圆心角相等，它们所对的弦相等；③两条弦相等，圆心到这两弦的距离相等；④在等圆中，圆心角不变，所对的弦也不变．A.①③ B.②④ C.①④ D.②③例题2、如图，以ABC ∆的边BC 为直径的O 分别交AB AC 、于点D E 、，连结OD OE 、，若65A ∠=︒，则DOE ∠=．例题3、如图，AB 、CD 为⊙O 的直径， AC CE=，（1）试说明BD CE =；（2）若连结BE ，问BE 与CD 平行吗？请说明理由．随练随练1、如图所示，点D 是弦AB 的中点，点C 在⊙O 上，CD 经过圆心O ，则下列结论中不一定正确的是（）A.CD ⊥ABB.∠OAD=2∠CBDC.∠AOD=2∠BCDD.弧AC=弧BC随练2、如图，A ，B ，C ，D 均为⊙O 上的点，且AB CD =，则下列说法不正确的是（）A.AOB COD ∠=∠B.AOC BOD ∠=∠C.AC BD =D.OC CD=随练3、如图，⊙O 是△ABC 的外接圆，∠AOB=70°，AB=AC ，则∠ABC=___________．拓展拓展1、如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）A.45（）cm B.9cm C.45 D.62cm拓展2、下列说法正确的有（）①在同圆或等圆中能够完全重合的弧叫等弧；②在同一平面内，圆是到定点距离等于定长的点的集合；③度数相等的弧叫做等弧；④优弧大于劣弧；⑤直角三角形的外心是其斜边中点．A.①②③④⑤B.①②⑤C.①②③⑤D.②④⑤拓展3、如图，⊙O的直径为10cm，弦AB=8cm，P是弦AB上的一个动点，则OP的长度范围为____cm≤OP≤____cm．拓展4、如图，已知四边形ABCD是边长为4的正方形，以AB为直径向正方形内作半圆，P为半圆上一动点（不与A、B重合），当PA=时，△PAD为等腰三角形．拓展5、在⊙O中，AB是⊙O的直径，AB=8cm，^^^AC CD BD==，M是AB上一动点，CM+DM的最小值是__________．拓展6、如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，能完全覆盖这个平面图形的圆面的最小半径是mm．拓展7、在⊙O 中，点C 是劣弧AB 的中点，则线段AB 和线段AC 的大小为（）A.2AB AC =B.2AB AC >C.2AB AC< D.无法确定拓展8、如图，在⊙O 中，∠AOB 的度数为m ，C 是弧ACB 上一点，D 、E 是弧AB 上不同的两点（不与A 、B 两点重合），则D E ∠+∠的度数为（）A.mB.1802m︒-C.902m ︒+D.2m 拓展9、如图，在半径为2的⊙O 中，弦AB=2，⊙O 上存在点C ，使得弦AC=22BOC=______________°．拓展10、如图9A 、B 是⊙O 上的两点，∠AOB ＝120°，C 是弧 AB 的中点，求证四边形OACB 是菱形．图9。

初三数学圆的讲点讲义-新课教材

24.1.1 圆24.1.2 垂直于弦的直径 24.1.3 弧、弦、圆心角 24.1.4 圆周角》（1） 24.1.4 圆周角》（2）24.2.1 点和圆的位置关系24.2.2 直线和圆的位置关系（1）24.2.2 直线和圆的位置关系（2） 24.2.2 直线和圆的位置关系（3） 24.2.2 直线和圆的位置关系（4） 24.2.3 圆和圆的位置关系 24.3 正多边形和圆 24.4 弧长与扇形面积24.4 弧长和扇形面积（2）第24章圆复习课（一）导学案第24章圆复习课（二）导学案第24章圆复习课（三）导学案第24章圆复习课（四）导学案圆新课讲义24.1.1 《圆》学习目标1．了解圆的两种定义，理解弧、弦、半圆、直径等有关概念. 2．了解圆是圆周而非圆面，理解等圆、等弧的概念. 学习重点：了解圆的两种定义，理解弦、弧等相关概念学习难点：理解等圆、等弧的概念。

学习过程一．自主学习1．为什么车轮要做成圆形的？ 2．你是怎样画圆的？根据画圆的不同方法，你能描述一下形成圆的过程吗？二．探索新知1．圆的两种定义：动态：在一个平面内，线段OA 绕着它旋转一周，形成的图形叫做圆。

静态：圆心为O 、半径为r 的圆可以看作是 . 例如：半径是3cm 的圆可以看作 .确定一个圆有两个要素，一是______，二是______，_____确定圆的位置，_____确定圆的大小.__________相等的圆叫等圆，___________相同的圆叫同心圆. 2．圆中相关概念如图1：_____________叫做圆心，__________叫做半径，以O 为圆心的圆记做_____.① 连接圆上任意两点的线段叫做；过圆心的弦叫做；圆中最长的弦是_____； ② 圆上任意两点之间的部分叫做______，弧AB 记做______；圆的任意一条直径的两个端点把圆分成两条弧，每一条弧叫做______；比半圆长的弧叫做_____，比半圆短的弧叫做____.③ 能够重合的圆叫做_________；能够重合的弧叫做_____________. 三。

九年级圆的知识点讲义

九年级圆的知识点讲义1. 什么是圆？圆是平面上所有到一个固定点距离都相等的点的集合。

这个固定点称为圆心，到圆心的距离称为半径。

2. 圆的基本要素圆的基本要素包括圆心、半径、直径、弧和弦。

- 圆心：圆的中心点，用字母O表示。

- 半径：从圆心到圆上任意一点的距离，用字母r表示。

- 直径：穿过圆心的线段，并且两个端点都在圆上，直径的长度是半径的两倍，用字母d表示。

- 弧：圆上两点间的一段弯曲部分。

- 弦：圆上任意两点间直线段。

3. 圆的性质（1）半径相等性质：圆上任意两点之间的半径都相等。

（2）直径长为两倍性质：圆的直径长等于其半径的两倍，即d=2r。

（3）弧长和弧度性质：圆的弧长与圆心角的度数成正比，弧长等于圆周率π乘以半径的长度，用公式l = πr表示。

（4）圆周率π：π是一个无理数，大约等于3.14，用来计算圆的周长和面积。

4. 圆的坐标系表示圆可以在平面直角坐标系中表示为一个方程。

以圆心坐标为（h，k），半径为r的圆表示为：(x - h)² + (y - k)² = r²5. 圆的相关公式和定理（1）周长计算公式：圆的周长等于直径乘以π，或等于2倍半径乘以π，用公式C = πd或C = 2πr表示。

（2）面积计算公式：圆的面积等于半径的平方乘以π，用公式A = πr²表示。

（3）相交弧的性质：当两个圆相交时，它们的相交弧的度数之和等于360度。

（4）切线和半径垂直定理：切线和半径之间的夹角是直角。

6. 圆的应用圆在生活和科学中有广泛的应用，例如建筑结构中的圆形拱门、运动学中的圆周运动、天文学中的星体运动轨迹等等。

以上就是九年级圆的知识点讲义。

希望这份讲义能够帮助你更好地理解和掌握圆的相关知识。

初中九年级数学圆的讲义

初中九年级数学圆的讲义圆一、基本概念与性质在平面内把线段OP绕着端点O旋转一周，端点P所形成的图形叫做圆。

其中，点O叫做圆心，线段OP叫做半径。

以点O为圆心的圆，记作⊙O ，读作圆O 。

点和圆的位置关系：如果⊙O的半径是r，点P到圆心O的距离为d，则d>r时，点P在__________d=r时，点P在__________d<r时，点p在__________< p="">圆是中心对称图形，圆心是它的对称中心。

圆是轴对称图形，过圆心的任意一条直线都是它的对称轴。

弦与弧连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径，是圆最长的弦。

圆上任意两点间的部分叫圆弧，简称弧，符号：以C、D为端点的弧，记作，读作圆的任意一条直径的两个端点把圆分成两条弧，每条弧都叫做半圆，大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧。

顶点在圆心的角叫做圆心角，顶点在圆上且两边与圆相交的角叫做圆周角。

圆心相同，半径不相等的两个圆叫做同心圆，能够互相重合的两个圆叫做等圆，能够互相重合的弧叫做等弧。

同圆或等圆的半径相等。

圆心角、弧、弦之间的关系：1.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

2.推论：在同圆或等圆中，若两条弧相等，那么它们所对的圆心角和弦都相等。

在同圆或等圆中，若两条弦相等，则它们所对的圆心角和弧都相等。

3.圆心角的度数与它所对的弧的度数相等。

圆心角与圆周角的关系：1.同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

2.推论：半圆（或直径）所对的圆周角是直角，90°圆周角所对的弦是直径。

垂径定理：1.垂直弦的直径平分弦，并且平分弦所对的两条弧。

2.推论：平分弦（非直径）的直径垂直于弦，并且平分弦所对的弧确定圆的条件：1.经过一点A作圆2.经过A、B两点作圆3.经过A、B、C三点作圆——a)当三点位于一条直线时b)当三点不在一条直线上时4.结论：不在同一条直线上的三点确定一个圆三角形的三个顶点确定一个圆。

九年级数学寒假班培优精品讲义

个性化教学辅导教案学生姓名年级九年级学科数学上课时间2017年月日教师姓名课题圆的有关概念教学目标1．理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等孤的概念．2．探索并掌握垂径定理及其推论．3．探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论．4．知道三角形的外心，并能画任意三角形的外接圆．教学过程教师活动学生活动1．圆的基本概念：在同一平面内，线段OA绕它固定的一个端点_______形成的图形叫做圆，_______叫做圆心，_______叫做半径．圆上任意两点间的_______叫做圆弧；在同圆或等圆中，能够_______的弧叫做等弧．2．圆的有关性质：(1)对称性：圆是中心对称图形，_______是它的对称中心；圆也是轴对称图形，_______都是它的对称轴．(2)圆心角、弧、弦之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别_______．(3)垂径定理：垂直于弦的直径_______弦，并且平分弦所对的两条弧．推论：平分弦（不是直径）的直径________于弦，且平分这条弦所对的两条弧．3．圆心角和圆周角：(1)圆心角：顶点在_______的角叫做圆心角；圆心角的度数_______它所对的弧的度数．圆周角：顶点在圆上，两边都与圆_______的角叫做圆周角．1．如图，CD是⊙A．AE＝BE2．如图，在⊙O中，弦AB∥CD．若∠ABC＝40°，则∠BOD的度数为( ) A．20°B．40° C．50° D．80°3．如图，⊙C过原点，且与两坐标轴分别交于点A、B，点A的坐标为(0，3)，M 是第三象限内弧OB BMO＝120°，则⊙C的半径长为( )取线，上一点，OD⊥AC，教学目标：1、理解圆、弧、弦、圆心角、圆周角的概念，了解等圆、等孤的概念．2、探索并掌握垂径定理及其推论．3、探索圆周角与圆心角及其所对弧的关系，了解并证明圆周角定理及其推论．4、知道三角形的外心，并能画任意三角形的外接圆．目标分解：【掌握圆的有关概念和计算】①知道圆由圆心与半径确定，了解圆的对称性．②通过图形直观识别圆的弦、弧、圆心角等基本元素．③利用圆的对称性探索弧、弦、圆心角之间的关系，并会进行简单计算和说理．④探索并了解圆周角与圆心角的关系、直径所对圆周角的特征．⑤掌握垂径定理及其推论，并能进行计算和说理．⑥了解三角形外心、三角形外接圆和圆内接三角形的概念．⑦掌握圆内接四边形的性质知识点梳理：1.圆的有关概念和性质(1) 圆的有关概念①圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆，其中定点为圆心，定长为半径．②弧：圆上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧．③弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径．（2）圆的有关性质①圆是轴对称图形；其对称轴是任意一条过圆心的直线；圆是中心对称图形，对称中心为圆心．②垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧．③弧、弦、圆心角的关系：在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．推论：在同圆或等圆中，同弧或等弧所对的圆周角相等；直径所对的圆周角是直角；90”的圆周角所对的弦是直径．④三角形的内心和外心ⓐ：确定圆的条件：不在同一直线上的三个点确定一个圆．ⓑ：三角形的外心：三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆，外接圆的圆心就是三角形三边的垂直平分线的交点，叫做三角形的外心．ⓒ：三角形的内心：和三角形的三边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心2.与圆有关的角（1）圆心角：顶点在圆心的角叫圆心角。

(完整版)初三数学圆的经典讲义

圆目录圆的定义及相关概念垂经定理及其推论圆周角与圆心角圆心角、弧、弦、弦心距关系定理圆内接四边形会用切线, 能证切线切线长定理三角形的内切圆了解弦切角与圆幂定理（选学）圆与圆的位置关系圆的有关计算一．圆的定义及相关概念【考点速览】考点1：圆的对称性：圆既是轴对称图形又是中心对称图形。

经过圆心的每一条直线都是它的对称轴。

圆心是它的对称中心。

考点2：确定圆的条件；圆心和半径①圆心确定圆的位置，半径确定圆的大小；②不在同一条直线上的三点确定一个圆；考点3：弦：连结圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。

直径是圆中最大的弦。

弦心距：圆心到弦的距离叫做弦心距。

弧：圆上任意两点间的部分叫做弧。

弧分为半圆，优弧、劣弧三种。

（请务必注意区分等弧，等弦，等圆的概念）弓形：弦与它所对应的弧所构成的封闭图形。

弓高：弓形中弦的中点与弧的中点的连线段。

（请务必注意在圆中一条弦将圆分割为两个弓形，对应两个弓高）固定的已经不能再固定的方法：求弦心距，弦长，弓高，半径时通常要做弦心距，并连接圆心和弦的一个端点，得到直角三角形。

如下图：考点4：三角形的外接圆：锐角三角形的外心在，直角三角形的外心在 ,钝角三角形的外心在。

考点5点和圆的位置关系设圆的半径为r ，点到圆心的距离为d ，则点与圆的位置关系有三种。

①点在圆外⇔d ＞r ；②点在圆上⇔d=r ；③点在圆内⇔ d ＜r ；【典型例题】例1 在⊿ABC 中，∠ACB =90°,AC =2,BC =4，CM 是AB 边上的中线，以点C 为圆心，以5为半径作圆，试确定A,B,M 三点分别与⊙C 有怎样的位置关系，并说明你的理由。

例2．已知，如图，CD 是直径，︒=∠84EOD ，AE 交⊙O 于B ，且AB=OC ，求∠A 的度数。

M A B C DOEBC例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ，最大为8cm ，则这圆的半径是_________cm 。

上海九年级数学上册复习寒假班讲义-圆与圆,圆与正多边形(学生版)

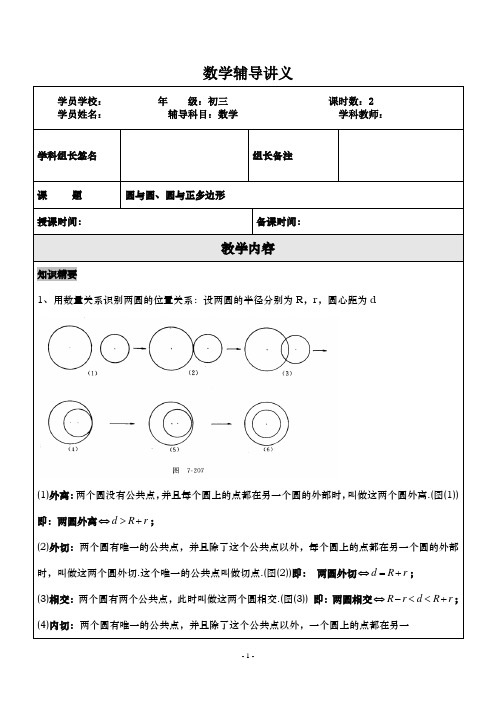
数学辅导讲义学员学校：年级：初三课时数：2学员姓名：辅导科目：数学学科教师：学科组长签名组长备注课题圆与圆、圆与正多边形授课时间：备课时间：教学内容知识精要1、用数量关系识别两圆的位置关系：设两圆的半径分别为R，r，圆心距为d(1)外离：两个圆没有公共点，并且每个圆上的点都在另一个圆的外部时，叫做这两个圆外离.(图(1)) 即：两圆外离d R r⇔>+；(2)外切：两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部时，叫做这两个圆外切.这个唯一的公共点叫做切点.(图(2))即：两圆外切d R r⇔=+；(3)相交：两个圆有两个公共点，此时叫做这两个圆相交.(图(3)) 即：两圆相交R r d R r⇔-<<+；(4)内切：两个圆有唯一的公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部时，叫做这两个圆内切.这个唯一的公共点叫做切点.(图(4))即：两圆内切d R r ⇔=-； (5)内含：两个圆没有公共点，并且一个圆上的点都在另一个圆的内部时，叫做这两个圆内含(图(5)).两圆同心是两圆内含的一个特例.(图(6)) 即：两圆内含0d R r ⇔≤<-。

2、按公共点的个数分类可分为三类①相离 ②相切 ③相交圆与圆的位置关系两圆位置关系外离外切相交内切内含（包括同心）公共点d 与,R r 的关系外公切线内公切线3、相交、相切两圆的性质定理相切两圆的性质定理：（1）两圆相切连心线必过切点。

（2）两圆外（内）公切线长相等。

相交两圆的性质定理：两圆相交，连心线垂直平分公共弦。

（一）正多边形的概念 1.各边相等、各角也相等的多边形叫做正多边形。

有n 条边的正多边形(n 是正整数，且错误！未找到引用源。

)就称作正n 边形. 当n 为奇数时，正n 边形不是中心对称图形；当n 为偶数时，正n 边形是中心对称图形，对称中心是它的两条对称轴的交点。

九年级圆全章辅导讲义

九年级圆全章辅导讲义学生：科目：第单元第节第课时教师：ABCD=12×15×12×12 =45cm 2知识概括、方法总结与易错点分析 1、点与圆的位置关系 2、直线与圆的位置关系 3、圆与圆的位置关系 4、内心外心的理解针对性练习一、选择题1、如图，是北京奥运会自行车比赛项目标志，则图中两轮所在圆的位置关系是【】A ．内含B ．相交C ．相切D ．外离2．已知两圆的半径分别为6和8，圆心距为7，则两圆的位置关系是 ( ) A ．外离 B ．外切 C ．相交 D ．内切3．若1O 的半径为3cm ，2O 的半径为4cm ，且圆心距121cm O O =，则1O 与2O 的位置关系是（） A ．外离 B ．内切 C ．相交 D ．内含4． ⊙O 的半径为5，圆心O 到直线l 的距离为3，则直线l 与⊙O 的位置关系是（）A ．相交B ．相切C ．相离D ．无法确定5．如图，⊙O 的半径为2，点A 的坐标为（2，32），直线AB 为⊙O 的切线，B 为切点．则B 点的坐标为A ．⎪⎪⎭⎫ ⎝⎛-5823, B ．()13,- C ．⎪⎭⎫⎝⎛-5954, D ．()31,-7. 以正方形ABCD 的BC 边为直径作半圆O ，过点D 作直线切半圆于点F ，交AB 边于点E ，则ΔADE 和直角梯形EBCD 周长之比为( )A. 3:4 B. 4:5 C. 5:6 D.6:78．如图，正方形ABCD 中，E 是BC 边上一点，以E 为圆心、EC 为半径的半圆与以A 为圆心，AB 为半径的圆弧外切，则sin EAB ∠的值为（） A ．43B ．34 C ．45D ．359．如图1，从圆O 外一点P 引圆O 的两条切线PA PB ，，切点分别为A B ，．如果60APB ∠=，8PA =，那么弦AB 的长是（）A ．4 B ．8C ．43D ．8310．如图，PA PB ，分别是O 的切线，A B ，为切点，AC 是O 的直径，已知35BAC ∠=，P ∠的度数为（）A ．35B ．45C ．60D ．70（第8题） x yO1 1BAPB AO第9第10题图ABCO P（第11题A B C EFD O11、如图，直线AB 与半径为2的⊙O 相切于点C ，D 是⊙O 上一点，且∠EDC ＝30°，弦EF ∥AB ，则EF 的长度为（） A ．2 B ．23 C ．3 D ．2212．已知⊙O 1和⊙O 2相切，两圆的圆心距为9cm ，⊙1O 的半径为4cm ，则⊙O 2的半径为（） A ．5cm B ．13cm C ．9 cm 或13cm D ．5cm 或13cm 二、填空题1．如图，已知O 是ABC △的内切圆，且50BAC ∠=°，则BOC ∠为度．2．如图①，1O ，2O ，3O ，4O 为四个等圆的圆心，A ，B ，C ，D 为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点是；如图②，1O ，2O ，3O ，4O ，5O 为五个等圆的圆心，A ，B ，C ，D ，E 为切点，请你在图中画出一条直线，将这五个圆．．．分成面积相等的两部分，并说明这条直线经过的两个点是．3．如图，在△ABC 中，AB =2，AC =2，以A 为圆心，1为半径的圆与边BC 相切，则BAC ∠的度数是．4．如图，轮椅车的大小两车轮（在同一平面上）与地面的触点A B ，间距离为80cm ，两车轮的直径分别为136cm ，16cm ，则此两车轮的圆心相距 cm ．5. 如图，奥运五环标志里，包含了圆与圆的位置关系中的外离．．和． 6．如图，从O 外一点P 引O 的两条切线PA PB ，，切点分别是A B ，，若8cm PA =，C 是AB 上的一个动点（点C 与A B ，两点不重合），过点C 作O 的切线，分别交PA PB ，于点D E ，，则PED △的周长是． 7．如图，AB 是O 的直径，AM 为弦，30MAB ∠=，过M 点的O 的切线交AB延长线于点N ．若12cm ON =，则O 的半径为 cm ．8.分别以梯形ABCD 的上底AD 、下底BC 的长为直径作⊙1O 、⊙2O ，若两圆的圆心距等于这个梯形的中位线长，则这两个圆的位置关系是____________. 三、解答题1．如图，已知⊙O 是△ABC 的外接圆，AB 为直径，若PA ⊥AB ，PO 过AC 的中点M ，求证：PC 是⊙O 的切线．BCA O （第1题）1o 2o 3o 4oCB D A 第（2）题图① 第（2）题图② 1o 2o 3o4o5oA BCEDABC第3题图（第4题图）A B OA DPE B C（第6题图）AOBNMABO C PMPA2.如图所示，AB 是O 的直径，AD 是弦，DBC A ∠=∠，OC BD ⊥于点E ．（1）求证：BC 是O 的切线；（2）若1210BD EC ==，，求AD 的长．3.如图，ABC △内接于O ，AB 为O 的直径，2BAC B ∠=∠，6AC =，过点A 作O 的切线与OC 的延长线交于点P ，求PA 的长．4.如图所示，ABC △是直角三角形，90ABC ∠=，以AB 为直径的O 交AC 于点E ，点D 是BC 边的中点，连结DE ．（1）求证：DE 与O 相切；（2）若O 的半径为3，3DE =，求AE ．5.（08山东潍坊20题）如图，AC 是圆O 的直径，10AC =厘米，PA PB ，是圆O 的切线，A B ，为切点．过A 作AD BP ⊥，交BP 于D 点，连结AB BC ，．（1）求证ABC ADB △∽△；（2）若切线AP 的长为12厘米，求弦AB 的长．6.已知：如图，ABC △中，AB AC =，以AB 为直径的O 交BC 于点P ，PD AC ⊥于点D ．（1）求证：PD 是O 的切线；（2）若1202CAB AB ∠==，，求BC 的值．7、为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得PA=5cm ，求铁环的半径.BCPO AB DCEAOA PDBCO CPBO A D8.如图，在Rt ABC △中，90C ∠=，BE 平分ABC ∠交AC 于点E ，点D 在AB 边上且DE BE ⊥．（1）判断直线AC 与DBE △外接圆的位置关系，并说明理由；（2）若662AD AE ==，，求BC 的长．9、已知：如图，在△ABC 中，AB =AC ，以BC 为直径的半圆O 与边AB 相交于点D ，切线DE ⊥AC ，垂足为点E ．求证：（1）△ABC 是等边三角形；（2）CE AE 31=．．10.如图10，AB 为O 的直径，D 为弦BE 的中点，连接OD 并延长交O 于点F ，与过B 点的切线相交于点C ．若点E 为弧AF 的中点，连接AE ．求证：ABE OCB △≌△．11.已知：如图，在Rt ABC △中，90C ∠=，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC AB ，分别交于点D E ，，且CBD A ∠=∠．（1）判断直线BD 与O 的位置关系，并证明你的结论；（2）若:8:5AD AO =，2BC =，求BD 的长．12.如图14，直线AB 经过O 上的点C ，并且OA OB =，CA CB =，O 交直线OB 于E D ，，连接EC CD ，．（1）求证：直线AB 是O 的切线；（2）试猜想BC BD BE ，，三者之间的等量关系，并加以证明；（3）若1tan 2CED ∠=，O 的半径为3，求OA 的长．13.如图，⊙O 是△ABC 的外接圆，且AB =AC ，点D 在弧BC 上运动，过点D 作DE ∥BC ，DE 交AB 的延长线于点E ，ADBOCE图ODBCF E ADCOABEC（第8题）BDAE连结AD 、BD ．（1）求证：∠ADB =∠E ；（3分）（2）当点D 运动到什么位置时，DE 是⊙O 的切线？请说明理由．（3）当AB =5，BC =6时，求⊙O 的半径．（4分）14.如图，BD 是⊙O 的直径，AB 与⊙O 相切于点B ，过点D 作OA 的平行线交⊙O 于点C ，AC 与BD 的延长线相交于点E ．(1) 试探究A E 与⊙O 的位置关系，并说明理由；(2) 已知EC ＝a ，ED ＝b ，AB ＝c ，请你思考后，选用以上适当的数据，设计出计算⊙O 的半径r 的一种方案： ①你选用的已知数是；②写出求解过程（结果用字母表示）．15、如图，AB 是⊙O 的直径，∠BAC=30°，M 是OA 上一点，过M 作AB 的垂线交AC 于点N ，交BC 的延长线于点E ，直线CF 交EN 于点F ，且∠ECF=∠E. （1）证明CF 是⊙O 的切线；（2）设⊙O 的半径为1，且AC=CE ，求MO 的长.巩固作业1. 已知：AB 交圆O 于C 、D ，且AC ＝BD.你认为OA ＝OB 吗？为什么？2. 如图所示，是一个直径为650mm 的圆柱形输油管的横截面，若油面宽AB=600mm ，求油面的最大深度。

圆培优讲义

《圆》培优讲义（一）一、圆的基本概念例：思考：车轮为什么是圆的？否则：试想，如果车轮是方的或者是椭圆的，坐车的人会有什么感觉？例：如图：AB、CB 为⊙O的两条弦，试说出图中的所有弧。

COBA例：判断对错1、长度相等的两条弧是等弧。

2、一条弦把圆分成两条弧，这两条弧不可能是等弧。

3、两个半圆是等弧。

4、半径相等的弧是等弧。

5、半径相等的两个半圆是等弧。

6、分别在两个等圆上的两条弧是等弧。

例：下列说法错误的是A、直径相等的两个圆是等圆。

B、圆中最大的弦是通过圆心的弦。

C、同圆中，优弧和劣弧的和等于一个整圆。

D、直径是圆中最长的弦。

例：AB 为圆O 的直径，点C 在圆O 上，OD//BC。

求证：OD 是AC 的垂直平分线ADOC B例：圆O 的半径为5，弦AB//CD，且AB=6，CD=8，求以两平行弦为底的梯形的面积。

对应练习：1. 设AB＝3 厘米，画图说明具有下列性质的点的集合是怎样的图形：（1）和点 A 的距离等于2 厘米的点的集合；（2）和点 B 的距离等于2 厘米的点的集合；（3）和点 A、B 的距离都等于2 厘米的点的集合；（4）和点 A、B 的距离都小于2 厘米的点的集合B2. 在下面的矩形中，如果 OA、OB、OC、OD 的中点分别为E、F、G、H。

求证：E、F、G、H4 个点在同一个圆上。

二、圆的轴对称性例 1. 如图，已知在⊙O中，弦AB 的长为8 厘米，圆心O 到AB 的距离为3 厘米，求⊙O的半径。

EAO变式 1：如上图，若以 O 为圆心再画一个圆交弦 AB 于C，D，则AC 与BD 间可能存在什么关系?A C E D BO （1）A C D BO（2）变式 2：如下图，若将 AB 向下平移，当移到过圆心时，结论 AC＝BD 还成立吗?变式 4：如图，设 AO ＝BO ，求证 AC ＝BD 。

变式 5：如图，设 OC ＝OD ，求证 AC ＝BD 。

结论：得出解决这类题的关键在于利用垂径定理，由圆心 O 引弦 AB 的垂线。

{教育管理}初三数学辅导班学习讲义圆

{教育管理}初三数学辅导班学习讲义圆（1）当d=14 厘米时，因为 d R+r，则⊙O1和⊙O2位置关系是：（2）当d=2厘米时，因为d R－r，则⊙O1和⊙O2位置关系是：（3）当d=15 厘米时，因为，则⊙O1和⊙O2位置关系是：（4）当d=7 厘米时，因为，则⊙O1和⊙O2位置关系是：（5）当d=1 厘米时，因为，则⊙O1和⊙O2位置关系是：6、切线性质：例4：（1）如图，PA 是⊙O的切线，点A 是切点，则∠PAO=度（2）如图，PA、PB 是⊙O的切线，点 A、B 是切点，则= ，∠=∠；7、圆中的有关计算（1）弧长的计算公式：例 5：若扇形的圆心角为60°，半径为 3，则这个扇形的弧长是多少？解：因为扇形的弧长=所以== (答案保留π)（2）扇形的面积：例 6：①若扇形的圆心角为60°，半径为 3，则这个扇形的面积为多少？解：因为扇形的面积 S=所以 S== (答案保留π)②若扇形的弧长为12πcm，半径为 6㎝，则这个扇形的面积是多少？解：因为扇形的面积S=所以 S= =（3）圆锥：例 7：圆锥的母线长为 5cm，半径为 4cm，则圆锥的侧面积是多少？解：∵圆锥的侧面展开图是形，展开图的弧长等于∴圆锥的侧面积=8、三角形的外接圆的圆心——三角形的外心——三角形的交点；三角形的内切圆的圆心——三角形的内心——三角形的交点；例 8：画出下列三角形的外心或内心（1）画三角形 ABC 的内切圆，（2）画出三角形 DEF 的外接圆，并标出它的内心；并标出它的外心 D二、练习：（一）填空题1、如图，弦 AB 分圆为 1：3 两段，则的度数的度数等于度；∠AOB＝度，∠ACB2、如图，已知 A 、B 、C 为⊙O 上三点，若、、的度数之比为 1∶2∶3，则∠AOB＝，∠AOC＝，∠ACB＝，3、如图 1－3－2，在⊙O 中，弦 AB=1.8cm ，圆周角∠ACB=30○，则⊙O 的半径等于=cm ．4、⊙O 的半径为 5，圆心 O 到弦 A B 的距离 O D=3，则 AD=，AB 的长为；5、如图，已知⊙O 的半径 OA=13㎝，弦 AB ＝24㎝，则 OD=㎝。

(完整word版)初三数学圆的讲义

圆一．圆的定义及相关概念考点1：圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

考点2：确定圆的条件：圆心和半径①圆心确定圆的位置，半径确定圆的大小；②不在同一条直线上的三点确定一个圆。

考点2：（圆的性质）圆的对称性：圆既是轴对称图形又是中心对称图形。

经过圆心的每一条直线都是它的对称轴。

圆心是它的对称中心。

考点3：弦：连结圆上任意两点的线段叫弦。

经过圆心的弦叫做直径。

直径是圆中最大的弦。

弦心距：圆心到弦的距离叫做弦心距。

弧：圆上任意两点间的部分叫做弧。

弧分为半圆，优弧、劣弧三种。

（请务必注意区分等弧，等弦，等圆的概念）弓形：弦与它所对应的弧所构成的封闭图形。

弓高：弓形中弦的中点与弧的中点的连线段。

（请务必注意在圆中一条弦将圆分割为两个弓形，对应两个弓高）考点4：三角形的外接圆：锐角三角形的外心在，直角三角形的外心在 ,钝角三角形的外心在。

考点5点和圆的位置关系设圆的半径为r，点到圆心的距离为d，则点与圆的位置关系有三种。

①点在圆外⇔d＞r；②点在圆上⇔d=r；③点在圆内⇔ d＜r；【典型例题】例1 在⊿ABC 中，∠ACB =90°,AC =2,BC =4，CM 是AB 边上的中线，以点C 为圆心，以5为半径作圆，试确定A,B,M 三点分别与⊙C 有怎样的位置关系，并说明你的理由。

例2．已知，如图，CD 是直径，︒=∠84EOD ，AE 交⊙O 于B ，且AB=OC ，求∠A 的度数。

例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ，最大为8cm ，则这圆的半径是_________cm 。

例4 在半径为5cm 的圆中，弦AB ∥CD ，AB=6cm ，CD=8cm ，则AB 和CD 的距离是多少？例5 如图,⊙O 的直径AB 和弦CD 相交于点E ，已知AE=6cm ，EB=2cm,ο30=∠CEA ，求CD 的长．例6.已知：⊙O 的半径0A=1，弦AB 、AC 的长分别为3,2，求BAC ∠的度数．AB DCO· E二．垂径定理及其推论考点1垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论1：①平分弦（不是直径）的直径重直于弦，并且平分弦所对的两条弧．②弦的垂直平分线经过圆心，并且平分弦所对的两条弧．③平分弦所对的一条弧的直径,垂直平分弦，并且平分弦所对的另一条弧．推论2．圆的两条平行弦所夹的弧相等．垂径定理及推论1中的三条可概括为：①经过圆心；②垂直于弦；③平分弦(不是直径)；④平分弦所对的优弧；⑤平分弦所对的劣弧．以上五点已知其中的任意两点，都可以推得其它两点固定的已经不能再固定的方法：求弦心距，弦长，弓高，半径时通常要做弦心距，并连接圆心和弦的一个端点，得到直角三角形。

初三数学寒假讲义第3讲.圆教师版

1考试内容考试要求层次ABC 圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆；能利用圆的有关概念解决简单问题圆的性质知道圆的对称性，了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题，能用垂径定理解决有关问题能运用圆的性质解决有关问题圆周角了解圆周角与圆心角的关系；知道直径所对的圆周角是直角会求圆周角的度数，能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题弧长会计算弧长能利用弧长解决有关问题扇形会计算扇形面积能利用扇形面积解决有关问题圆锥的侧面积和全面积会求圆锥的侧面积和全面积能解决与圆锥有关的简单实际问题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系；了解切线的概念，理解切线与过切点的半径之间的关系；会过圆上一点画圆的切线，了解切线长的概念能判定一条直线是否为圆的切线；能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题本讲结构中考大纲剖析3中考第一轮复习圆2一、垂径定理1. 定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．2. 推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.二、弧、弦、圆心角定理1. 定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．2. 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量分别相等．三、圆周角定理定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论1：在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等．推论2：半圆（或直径）所对的圆周角是直角，90︒的圆周角所对的弦是直径．四、与圆相关的位置关系1.点和圆的位置关系：设O ⊙的半径为r ，点P 到圆心O 的距离为d ，则有：点在圆外⇔d r >；点在圆上⇔d r =；点在圆内⇔d r <.2.直线和圆的位置关系：设O ⊙的半径为r ，圆心O 到直线l 的距离为d ，则有： d r >⇔直线l 与O ⊙相离；d r =⇔直线l 与O ⊙相切；d r <⇔直线l 与O ⊙相交切线的性质：定理：圆的切线垂直于过切点的半径．推论1：经过圆心且垂直于切线的直线必经过切点．推论2：经过切点且垂直于切线的直线必经过圆心．切线的判定：定义：和圆只有一个公共点的直线是圆的切线；距离：和圆心距离等于半径的直线是圆的切线；定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．3.圆和圆的位置关系：设12O O 、⊙⊙的半径分别为r R 、（其中R r >），两圆圆心距为d ，则有：d R r >+⇔两圆外离；d R r =+⇔两圆外切；R r d R r -<<+⇔两圆相交； d R r =-⇔两圆内切；0d R r <-⇔≤两圆内含.五、圆中的相关计算公式设O ⊙的半径为R ，n ︒圆心角所对弧长为l ，1. 弧长公式：π180n Rl =2. 扇形面积公式：21π3602n S R lR ==扇形3. 圆柱体表面积公式：22π2πS R Rh =+4. 圆锥体表面积公式：2ππS R Rl =+（l 为母线）六、圆中常见辅助线作法知识导航3连半径，得等腰三角形作相等圆周角作2倍角关系作直径所对圆周角，得垂直知弦长或求弦长作弦心距，用勾股证切线，连半径，证垂直；知切线，连半径，得垂直七、圆中常见倒角模型【编写思路】本讲包括以下知识点：圆的基本性质，包括垂径定理、弦弧圆周角定理、圆周角定理及其推论等的综合运用；点圆、线圆、圆圆位置关系；圆中弧的长度、扇形弓形面积、阴影面积等的求法.知识点较多，容量较大.其中针对中考中“圆”的两问题中的难点——第二问圆中的相似问题进行探究，旨在锻炼学生解决此类问题的方法和速度.【例1】（1）如图，OC 是⊙O 的半径，AB 是弦，且OC ⊥AB ，点P 在⊙O上，∠APC=26°,则∠BOC=_________. （2013贵州遵义）（2）如图，⊙O 的半径OD ⊥弦AB 于点C ，连结AO 并延长交⊙O 于点E ，连结EC ．若AB ＝8，CD ＝2，则EC 的长为（）A.215B.8C.210D.213 （2013浙江嘉兴）（3）现有直径为2的半圆O 和一块等腰直角三角板① 将三角板如图1放置，锐角顶点P 在圆上，斜边经过点B ，一条直角边交圆于点Q ，则BQ 的长为_____；② 将三角板如图2放置，锐角顶点P 在圆上，斜边经过点B ，一条直角边的延长线交圆于Q ，则BQ 的长为______ . （2013大兴期末）夯实基础模块一圆的基本性质QP OBAQPO BA BA OEC BAO4图1 图2【解析】（1）52°；（2）A.（3）①2，连结OQ ，290QOB P ∠=∠=︒ ②2.连结AQ ，45A P ∠=∠=︒.【例2】如图，点P 是等边三角形ABC 外接圆⊙O 上的点，在以下判断中，不正确．．．的是（） A 、当弦PB 最长时， △APC 是等腰三角形. B 、当△APC 是等腰三角形时，PO ⊥AC .C 、当PO ⊥AC 时，∠ACP =30°.D 、当∠ACP =30°，△PBC 是直角三角形. (2013安徽中考)【解析】C ，当点P 与点B 重合时不成立；【例3】 ⑴ 如图，在平面直角坐标系中，P ⊙与x 轴相切于原点O ，平行于y 轴、的直线交P ⊙于M N ，两点．若点M 的坐标是()21-，，则点N 的坐标是 _____________．（浙江绍兴中考）（2）已知，如图，四边形ABCD 内接于O ⊙，AB 为O ⊙的直径，MN 切O ⊙于C ，38BCM ∠=︒，则ADC ∠的度数为___________．（3）如图，Rt ABC △的内切圆O ⊙与两直角边AB 、AC 分别相切于点D 、E ，过劣弧DE （不包括端点D 、E ）上任意一点P 作O ⊙的切线MN 与AB 、 BC 分别交于点M 、N ，若O ⊙的半径为r ，则Rt MBN △的周长为（） A .r B.1.5r C.2r D.2.5r夯实基础模块二与圆有关的位置关系能力提升xyNM POO ND BA OPCBE OP N M DCB A5（4）在同一平面上，已知1O ⊙和2O ⊙的直径分别为6cm 和8cm ，请在不同条件下写出1O ⊙和2O ⊙的位置关系：当12O O =7cm ，两圆__________；当12O O =5cm ，两圆__________；当12O O =8cm ，两圆__________. 【解析】（1）（2，-4）过点P 作MN 的垂线，先求出半径为2.5；（2）128°，连结OC ；（3）C ，切线长定理；（4）外切；相交；外离.【例4】 1. 如图，在ABC △中，AB AC =，以AB 为直径的O ⊙分别交AC 、BC 于点D 、E ，点F 在AC 的延长线上，且12CBF CAB ∠=∠．⑴ 求证：直线BF 是O ⊙的切线；⑵ 若5AB =，5sin 5CBF ∠=，求BC 和BF 的长．（2011北京）（【解析】⑴ 证明：连结AE .∵AB 是O 的直径，∴90AEB ∠=︒. ∴1290∠+∠=︒.∵AB AC =， ∴112CAB ∠=∠.∵12CBF CAB ∠=∠， ∴1CBF ∠=∠.∴290CBF ∠+∠=︒.即90ABF ∠=︒.∵AB 是O 的直径， ∴直线BF 是O 的切线． ⑵ 解：过点C 作CG AB ⊥于点G ．∵5sin 15CBF CBF ∠=∠=∠，，∴5sin 15∠=． ∵905AEB AB ∠=︒=，，∴sin 15BE AB =⋅∠=.∵90AB AC AEB =∠=︒，，∴225BC BE ==.由Rt ABE △中，由勾股定理得222 5.AE AB BE =-=∴255sin 2cos 255∠=∠=，. 在Rt CBG △中，可求得42GC GB ==，.∴3AG =.∵GC BF ∥，∴AGC ABF △∽△.∴GC AGBF AB =. ∴203GC AB BF AG ⋅==. 所以CD =83. 另：如图，也可以过点C 作CG BF ⊥，构造“A”字图用相似.2. 如图AB 是O 的直径，PA ，PC 与O 分别相切于点A ，C ，PC 交AB 的延长线于点D ，DE PO ⊥交PO 的延长线于点E .能力提升OEFCDA 12G A DCFE O AO BCD EPOFEDCA6（1）求证：EPD EDO ∠=∠；（2）若6PC =，3tan 4PDA ∠=，求OE 的长. （2013北京）【解析】（1）∵PA 、PC 与O 分别相切于点A 、C∴APO EPD ∠=∠且PA AO ⊥即90PAO ∠=︒ ∵AOP EOD ∠=∠，90PAO E ∠=∠=︒ ∴APO EDO ∠=∠ 即EPD EDO ∠=∠ （2）连结OC ，∴6PA PC ==∵3tan 4PDA ∠= ∴在Rt PAD △中8AD =，10PD =∴4CD = ∵3tan 4PDA ∠=∴在Rt OCD △中，3OC OA ==，5OD = ∵EPD EDO ∠=∠∴OED △∽DEP △ ∴10251PD DE OD OE === 在Rt OED △中，2225OE DE +=，∴OE本讲探究主题：圆中的相似【探究1】如图，⊙O 是△ABC 是的外接圆，BC 为⊙O 直径，作∠CAD =∠B ，且点D 在BC 的延长线上．若sin ∠CAD=4，⊙O 的半径为8，求CD 长．【解析】过点C 作CE ⊥AD 于点E .∵∠CAD =∠B , ∴sinB =sin ∠CAD. ∵⊙O 的半径为8，∴BC=16. ∴AC =sin BC B ⋅=. ∴在Rt △ACE 中，CE=sin AC CAD ⋅∠=2. ∵CE ⊥AD , ∴∠CED =∠OAD =90°. ∴CE ∥OA . ∴△CED ∽△OAD . ∴CD CEOD OA =. 设CD =x ，则OD =x +8.即288x x =+. 解得x =83.【探究2】如图，AB 是O ⊙的直径，点C 在O ⊙上，CAB ∠的平分线交O ⊙于点D ，连接BC 交AD 于点F .若108AB AD ==，，求CF 的长.【解析】连结BD ．∵AB 是O ⊙的直径，∴90ADB ∠=°．∴ .622=-=AD AB BDBABB7∵ BAD CAD CBD ADB BDF ∠=∠=∠∠=∠，． ∴ .DAB DBF △∽△∴AD BD BD FD =，即866FD =，得92FD =． ∴ 97822AF AD FD =-=-=．可证FAC FBD △∽△∴ .CF AFFD BF = ∴ 2110CF =【探究3】已知：如图，AB 是O ⊙的直径，C 是O ⊙上一点，OD BC⊥于点D ，过点B 作O ⊙的切线，交OD 的延长线于点E ，连结BE ．连结AD 并延长交BE 于点F ，若9OB =，2sin 3ABC ∠=，求BF 的长．【解析】过点D 作DM AB ⊥于点M ，则DM ∥FB .在Rt ODB ∆中， 2909sin 3sin 6.ODB OB ABC OD OB ABC ∠==∠=∴=⋅∠=，，，由勾股定理得BD == 在Rt DMB ∆中，同理得sin 5.DM BD ABC BM =⋅∠===O 是AB 的中点， 18.13.AB AM AB BM ∴=∴=-= DM ∥FB ，..AMD ABF MD AMBF ABMD AB BF AM ∴∴=⋅∴==△∽△【探究4】如图，AB 是⊙O 的直径，点C 在⊙O 上，CE ⊥ AB 于E ,CD 平分∠ECB , 交过点B 的射线于D , 交AB 于F , 且BC=BD .若AE =9, CE =12, 求BF 的长.【解析】连接AC ，∵ AB 是⊙O 直径， ∴ 90ACB ∠=. ∵CE AB ⊥, 可得 2CE AE EB =⋅.∴ .162==AECE EB在Rt △CEB 中，∠CEB =90︒, 由勾股定理得20.BC∴ 20BD BC ==.∵ 1D ∠=∠, ∠EFC =∠BFD ,ABFEBAABEF8∴ △EFC ∽△BFD. ∴ BFEFBD EC =. ∴121620BFBF-=. ∴ BF =10.【点评】圆中的相似常见有以下模型：（老师根据自己的教学可以总结出更多更好的！）【例5】（1）如图，如果从半径为9cm 的圆形纸片剪去13圆的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为（）A ．6cmB ．35cmC ．8cmD ．53cm（通州一模）（2）如图所示，已知大正方形的边长为10厘米，小正方形的边长为7厘米，则阴影部分面积为（）A ．132π平方厘米B ．312π平方厘米C ．25π平方厘米D ．无法计算（3）如图，在边长为1的等边△ABC 中，若将两条含120︒圆心角的AOB 、BOC 及边AC 所围成的阴影部分的面积记为S ，则S 与△ABC 面积的比是．【解析】（1）B ；（2）C ，作出两条对角线，用平行线等积变换将面积转成扇形面积；（3）13或1:3，连结AO 、BO 、CO .能力提升夯实基础模块三有关圆的计算9【例6】（1）已知每个网格中小正方形的边长都是1，图中的阴影图案是由三段以格点为圆心，半径分别为1和2的圆弧围成．则阴影部分的面积是．（2）如图，正方形ABCD 的边1AB =，BD 和AC 都是以1为半径的圆弧，则无阴影部分的两部分的面积之差是（）A.12π-B.14π- C.13π- D.16π- （湖北罗田中考）【解析】（1）π-2，连对角线，转化为弓形面积；（2）A ，面积差=两个扇形面积和-正方形面积；【思维拓展训练】提高班训练1. 如图，C 为O 直径AB 上一动点，过点C 的直线交O 于D 、E 两点，且45ACD ∠=︒，DF AB ⊥于点F ，EG AB ⊥于点G ．当点C 在AB 上运动时，设AF x =，DE y =，下列图象中，能表示y 与x 的函数关系的图象大致是（）（2009北京中考）【解析】A.直径是圆中最长的弦.训练2. 如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 的延长线交于点P ，∠COB =2∠PCB . （1）求证：PC 是⊙O 的切线；（2）点M 是弧AB 的中点，CM 交AB 于点N ，若MN · MC =8，求⊙O 的直径. （2013西城一模）【解析】（1）证明：∵OA =OC ， ∴∠A =∠ACO . ∴∠COB =2∠ACO .又∵∠COB =2∠PCB ，∴∠ACO =∠PCB .D CBA NO P CBA10∵AB 是⊙O 的直径，∴∠ACO +∠OCB =90° . ∴∠PCB +∠OCB =90°，即OC ⊥CP .∵OC 是⊙O 的半径， ∴PC 是⊙O 的切线. （2）解：连接MA 、MB .∵点M 是弧AB 的中点，∴∠ACM =∠BAM .∵∠AMC =∠AMN ，∴△AMC ∽△NMA . ∴AM MC NM MA=. ∴2AM MC MN =⋅. ∵MC MN ⋅=8， ∴22AM =.∵AB 是⊙O 的直径，点M 是弧AB 的中点， ∴∠AMB =90°，AM =BM=22. ∴224AB AM BM =+=.训练3. 阅读下列材料，然后解答问题．经过正四边形（即正方形）各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．如图，正方形ABCD 内接于⊙O ，⊙O 的面积为S 1，正方形ABCD 的面积为S 2．以圆心O 为顶点作∠MON ，使∠MON ＝90°．将∠MON 绕点O 旋转，OM 、ON 分别与⊙O 交于点E 、F ，分别与正方形ABCD 的边交于点G 、H ．设由OE 、OF 、EF ⌒及正方形ABCD 的边围成的图形（阴影部分）的面积为S ．⑴当OM 经过点A 时（如图①），则S 、S 1、S 2之间的关系为：（用含S 1、S 2的代数式表示）；⑵当OM ⊥AB 于G 时（如图②），则⑴中的结论仍然成立吗？请说明理由； ⑶当∠MON 旋转到任意位置时（如图③），则⑴中的结论仍然成立吗？请说明理由．（湖南邵阳中考）【解析】（1）根据图形的对称性，得214S S S =-（2）结论仍成立，∵扇形OEF 的面积仍是圆面积的1/4∴四边形OGBH 的面积仍是正方形的面积的1/4 （3）作OP ⊥AB ，OQ ⊥BC ，可以证明△OPG ≌△OQH ．结合（2）中的结论即可证明A BCDDDC C ABABOO O M M NM NG HG H (E ) (F ) E FEF图①图②图③模块一圆的基本性质课后演练【演练1】如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为（）A.2cmB.3cmC.23cmD.25cm（连云港中考）【解析】C.【演练2】 ⑴如下左图，点O 为优弧ACB 所在圆的圆心，108AOC ∠=︒，点D 在AB 的延长线上，BD BC =，则D ∠=____________.（河北中考） ⑵ 如下右图，ABC △是⊙O 的内接三角形，点D 是BC 的中点，已知∠AOB =98°，∠COB =120°．则 ∠ABD 的度数是．（舟山中考）ODCBA【解析】（1）27°；（2）101°.模块二与圆有关的位置关系课后演练【演练3】（1）如图，已知⊙O 是以坐标原点O 为圆心，1为半径的圆，∠AOB ＝45°，点P 在x 轴上运动，若过点P 且与OA 平行的直线与 ⊙O 有公共点，设P (x ，0)，则x 的取值范围是．（2）如图，1O ⊙、2O ⊙内切于点A ，其半径分别是8和4，将2O ⊙沿直线12O O 平移至两圆相外切时，则点2O 移动的长度是（） A ．4 B ．8 C ．16 D ．8 或16（茂名中考）【解析】（1）22x -≤≤ 且0x ≠；（2）D ，左右平移均可.【演练4】已知：如图，AB 是⊙O 的直径，AC 是⊙O 的弦，M 为AB 上一点，过点M 作DM ⊥AB ，交弦AC 于点E ，交⊙O 于点F ，且DC ＝DE ．ABCDO实战演练OBAO 2O 1AOE M FDC BA12（1）求证：DC 是⊙O 的切线；（2）如果DM ＝15，CE ＝10，5cos 13AEM ∠=，求⊙O 半径的长．（2013门头沟一模）【解析】如图，过点D 作DG ⊥AC 于点G ，连结BC ．∵DC ＝DE ，CE ＝10，∴EG ＝12CE ＝5． ∵cos ∠DEG ＝cos ∠AEM ＝EG DE ＝513，∴DE ＝13．∴DG ＝22DE EG -＝12． ∵DM ＝15，∴EM ＝DM -DE ＝2． ∵∠AME ＝∠DGE ＝90°，∠AEM ＝∠DEG ， ∴△AEM ∽△DEG ． ∴AM EM AE =DG EG DE =．∴212513AM AE==． ∴245AM =，265AE =． ∴AC AE EC =+=765．∵AB 为⊙O 的直径，∴∠ACB ＝90°． ∴cos A ＝AM AC AE AB=．∴24715AB = ∴⊙O 的半径长为1247230AB =．模块三有关圆的计算课后演练【演练5】如图，AB 为半圆的直径，点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 和PB 为直径作半圆，则图中阴影部分的面积S 与时间t 之间的函数图象大致为A ．B ．C ．D ．GABCD F ME O图2【解析】D13第十八种品格：坚持冰冻三尺非一日之寒晋代的大文学家陶渊明隐居田园后，某一天，有一个读书的少年前来拜访他，向他请教求知之道。

九年级数学寒假辅导讲义第07讲圆(原卷版)

第7讲圆中考分析解读圆的主要内容包括基本定理：垂径定理、弦弧圆心角定理、圆周角定理，切线定理：切线判定定理、切线性质定理、切线长定理，其中圆的角度计算、边长计算等基础题难度较小，圆经常与三角形、四边形综合考查，难度偏大，考查形式以解答题为主. 圆在中考中分值约为10~15分.模块一圆中基本概念及计算一、知识导图二、知识清单1、圆的有关概念（1）圆上各点到圆心的距离相等；到定点的距离等于定长的点都在同一个圆上．（2）在同圆或等圆中，能够互相重合的弧叫做等弧．（3）圆是轴对称图形，每一条经过圆心的直线都是它的对称轴；圆也是中心对称图形，对称中心是圆心．2、垂径定理（1）垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．，如图，CD是O的直径，AB为弦，若CD AB垂足为E ，则：AE BE =，AD BD =，AC BC =．（2）垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．如图，CD 是O 的直径，AB 为弦，若AE BE =，则：CD AB ⊥，AD BD =，AC BC =．3、垂径定理的应用半径、弦的一半、弦的弦心距，这三条线段可以围成直角三角形，满足勾股定理．通常，半径、弦长、弦心距，弓高，这四个条件“知二推二”. 4、圆周角定理及推论（1）圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．（2）圆周角定理的推论① 同弧或等弧所对的圆周角相等．② 半圆（或直径）所对的圆周角是直角，90︒的圆周角所对的弦是直径． ③ 圆内接四边形的对角互补．基础演练一、选择题1．（2020•朝阳区一模）如图，直线12//l l ，点A 在直线1l 上，以点A 为圆心，适当长度为半径画弧，分别交直线1l ，2l 于B ，C 两点，以点C 为圆心，CB 长为半径画弧，与前弧交于点D （不与点B 重合），连接AC ，AD ，BC ，CD ，其中AD 交2l 于点E ．若40ECA ∠=︒，则下列结论错误的是( )A．70=D．CE AE=∠=︒C．CE CD∠=︒B．80ABCBAD2．（2020•泰安）如图，ABC∆是O的内接三角形，AB BCBAC∠=︒，AD是直径，=，30AD=，则AC的长为()8A．4B．C D．3．（2020•鞍山）如图，O是ABC∠的度数=，则A∆的外接圆，半径为2cm，若2BC cm为()A．30︒B．25︒C．15︒D．10︒4．（2020•广州）往直径为52cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽=，则水的最大深度为()48AB cmA．8cm B．10cm C．16cm D．20cm二、填空题5．（2020•聊城）如图，在O中，四边形OABC为菱形，点D在AmC上，则ADC∠的度数是．6．（2010•镇江）如图，AB为O的直径，弦CD ABCD=，那AB=，8⊥于点E．如果10么OE的长为．7．（2020•顺义区二模）如图，在每个小正方形的边长为1cm的网格中，画出了一个过格点A，B的圆，通过测量、计算，求得该圆的周长是cm．（结果保留一位小数）8．（2020•北京二模）如图，边长为1的小正方形网格中，点A，B，C，D，E均在格点上，半径为2的A与BC交于点F，则tan DEF∠=．9．（2020•石景山区一模）《九章算术》是中国传统数学重要的著作之一，奠定了中国传统数学的基本框架．其中卷九中记载了一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”其意思是：如图，AB为O的直径，弦CD AB⊥于点E，1BE=寸，1=寸）根据题意，该圆CD=尺，那么直径AB的长为多少寸？（注:1尺10的直径为寸．10．（2020•宁夏）我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小．用锯去锯这木材，锯口深1ED=寸，锯道长AB=尺(1尺101=寸）．问这根圆形木材的直径是寸．能力提升一、选择题1．（2020•丰台区一模）在O中按如下步骤作图：（1）作O的直径AD；（2）以点D为圆心，DO长为半径画弧，交O于B，C两点；（3）连接DB，DC，AB，AC，BC．根据以上作图过程及所作图形，下列四个结论中错误的是()A．90ABD∠=︒B．BAD CBD∠=∠C．AD BC⊥D．2AC CD= 2．（2020•牡丹区三模）已知O．如图，（1）作O的直径AB；（2）以点A为圆心，AO长为半径画弧，交O于C，D两点；（3）连接CD交AB于点E，连接AC，BC．根据以上作图过程及所作图形，有下面三个推断：①CE DE=；②3BE AE=；③2BC CE=．所有正确推断的序号是．3．（2020•西山区模拟）如图，O的直径AB垂直于弦CD，垂足为E，4CD=，1tan2C=，则AB的长为()A．2.5B．4C．5D．10 4．（2020•十堰）如图，点A，B，C，D在O上，OA BC⊥，垂足为E．若30ADC∠=︒，1AE=，则(BC=)A．2B．4C D．5．（2020•武汉）如图，在半径为3的O中，AB是直径，AC是弦，D是AC的中点，AC 与BD交于点E．若E是BD的中点，则AC的长是()A B．C．D．6．（2020•泰州二模）如图，点A，B，C，D在O上，弦AD的延长线与弦BC的延长线相交于点E．用①AB是O的直径，②CB CE=中的两个作为题设，余下的=，③AB AE一个作为结论组成一个命题，则组成真命题的个数为()A．0B．1C．2D．3 7．（2020•河北）有一题目：“已知：点O为ABC∠．”嘉嘉的∠=︒，求ABOC∆的外心，130解答为：画ABC∠=∠=︒，得∆以及它的外接圆O，连接OB，OC．如图，由2130BOC A∠还应有另一个不同的值．”下列判断正确的∠=︒．而淇淇说：“嘉嘉考虑的不周全，AA65是()A．淇淇说的对，且A∠的另一个值是115︒B．淇淇说的不对，A∠就得65︒C．嘉嘉求的结果不对，A∠应得50︒D．两人都不对，A∠应有3个不同值8．（2020•福建）如图，四边形ABCD内接于O，AB CD∠=︒，BDC=，A为BD中点，60则ADB∠等于()A．40︒B．50︒C．60︒D．70︒9．（2020•陕西）如图，ABCA∠=︒．E是边BC的中点，连接OE并延长，∆内接于O，50交O于点D，连接BD，则D∠的大小为()A．55︒B．65︒C．60︒D．75︒二、填空题10．（2020•遵义）如图，O是ABC⊥于点D，延长AD∠=︒，AD BC∆的外接圆，45BAC交O于点E，若4BD=，1CD=，则DE的长是．11．（2020•房山区一模）如图，AC是O的弦，6AC=，点B是O上的一个动点，且∠=︒，若点M、N分别是AC、BC的中点，则MN的最大值是．60ABC三、解答题12．（2020•大连）四边形ABCD内接于O，AB是O的直径，AD CD=．（1）如图1，求证2ABC ACD∠=∠；（2）过点D作O的切线，交BC延长线于点P（如图2)．若5tan12CAB∠=，1BC=，求PD的长．模块二点与圆、直线与圆的位置关系一、知识导图二、知识清单1、点与圆的位置关系设O的半径为r，圆心O到直线l的距离为d，则：2、直线与圆的位置关系（1）切线的性质与判定①切线的性质定理：圆的切线垂直于过切点的半径．几何语言：AB是O切线，C为切点∴OC AB⊥②切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．几何语言：OC AB⊥，AB经过半径外端∴AB是O切线3、切线长定理过圆外一点引圆的两条切线，它们的切线长相等，这一点与圆心的连线平分两条切线的夹角．基础演练一、选择题1．（2020•重庆）如图，AB是O的切线，A为切点，连接OA，OB，若20B∠=︒，则AOB∠的度数为()A．40︒B．50︒C．60︒D．70︒2．（2020•重庆）如图，AB是O的切线，A为切点，连接OA，OB．若35B∠=︒，则AOB∠的度数为()A．65︒B．55︒C．45︒D．35︒3．（2020•海淀区一模）如图，AB与O相切于点B，AO的延长线交O于点C，连结BC，若12OC OA=，则C∠等于()A ．15︒B ．30︒C ．45︒D ．60︒二、解答题4．（2020•天津）在O 中，弦CD 与直径AB 相交于点P ，63ABC ∠=︒．（Ⅰ）如图①，若100APC ∠=︒，求BAD ∠和CDB ∠的大小；（Ⅱ）如图②，若CD AB ⊥，过点D 作O 的切线，与AB 的延长线相交于点E ，求E ∠的大小．5．（2020•顺义区一模）如图，在ABCD 中，45B ∠=︒，点C 恰好在以AB 为直径的O 上．（1）求证：CD 是O 的切线；（2）连接BD ，若8AB =，求BD 的长．6．（2020•遵义）如图，AB是O的直径，点C是O上一点，CAB∠的平分线AD交BC 于点D，过点D作//DE BC交AC的延长线于点E．（1）求证：DE是O的切线；（2）过点D作DF ABBF=，求BD的长度．⊥于点F，连接BD．若1OF=，27．（2020•聊城）如图，在ABC∆的边AB为直径作O，交AC于∆中，AB BC=，以ABC点D，过点D作DE BC⊥，垂足为点E．（1）试证明DE是O的切线；（2）若O的半径为5，AC=DE的长．能力提升一、选择题1．（2020•泰安）如图，PA是O的切线，点A为切点，OP交O于点B，10P∠=︒，点∠等于()C在O上，//OC AB．则BACA．20︒B．25︒C．30︒D．50︒2．（2020•哈尔滨）如图，AB为O的切线，点A为切点，OB交O于点C，点D在O 上，连接AD、CD，OA，若35ADC∠的度数为()∠=︒，则ABOA．25︒B．20︒C．30︒D．35︒二、填空题3．（2019O与边长为8的等边三角形ABC的两边AB、BC都相切，连接OC，则tan OCB∠=．4．（2020•滨州）如图，O是正方形ABCD的内切圆，切点分别为E、F、G、H，ED 与O相交于点M，则sin MFG∠的值为．三、解答题5．（2020•北京）如图，AB为O的直径，C为BA延长线上一点，CD是O的切线，D 为切点，OF AD⊥于点E，交CD于点F．（1）求证：ADC AOF∠=∠；（2）若1sin3C=，8BD=，求EF的长．6．（2020•新疆）如图，在O中，AB为O的直径，C为O上一点，P是BC的中点，过点P作AC的垂线，交AC的延长线于点D，连接OP．（1）求证：DP是O的切线；（2）若5AC=，5sin13APC∠=，求AP的长．7．（2020•广东）如图1，在四边形ABCD中，//∠=︒，AB是O的直径，DABAD BC，90∠．CO平分BCD（1）求证：直线CD与O相切；（2）如图2，记（1）中的切点为E，P为优弧AE上一点，1AD=，2∠BC=．求tan APE 的值．模块三圆中的计算一、知识导图二、知识清单圆中的有关计算 1、扇形的弧长与面积扇形弧长公式：π180n Rl =扇形面积公式：2π1==3602n R S lR 常见的求图形周长、面积的几种常用方法： ①公式法；②割补法；③等积变换法. 2、圆锥①侧面展开图弧长与底面圆周长相等；②侧面展开图面积：2ππ360n R S rR ==侧（R 为圆锥的母线） ③母线、高、底面半径的关系：222R h r =+基础演练一、选择题1．（2020•山西）中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花．图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到12AC BD cm ==，C ，D 两点之间的距离为4cm ，圆心角为60︒，则图中摆盘的面积是( )A ．280cm πB ．240cm πC ．224cm πD ．22cm π2．（2020•宁夏）如图，等腰直角三角形ABC 中，90C ∠=︒，AC =C 为圆心画弧与斜边AB 相切于点D ，交AC 于点E ，交BC 于点F ，则图中阴影部分的面积是( )A ．14π-B ．14π- C ．24π-D ．14π+3．（2020•日照）如图，AB 是O 的直径，CD 为O 的弦，AB CD ⊥于点E ，若CD =，9AE =，则阴影部分的面积为( )A ．6πB ．12π-C ．3πD ．4．（2020•聊城）如图，AB 是O 的直径，弦CD AB ⊥，垂足为点M ，连接OC ，DB ．如果//OC DB ，OC =( )A ．πB ．2πC ．3πD ．4π能力提升一、选择题1．（2020•丰台区二模）如图，点A ，B 是O 上的定点，点P 为优弧AB 上的动点（不与点A ，B 重合），在点P 运动的过程中，以下结论正确的是( )A ．APB ∠的大小改变B ．点P 到弦AB 所在直线的距离存在最大值C ．线段PA 与PB 的长度之和不变D ．图中阴影部分的面积不变2．（2020•遂宁）如图，在Rt ABC ∆中，90C ∠=︒，AC BC =，点O 在AB 上，经过点A 的O 与BC 相切于点D ，交AB 于点E ，若CD =( )A ．42π-B ．22π-C ．2π-D ．14π-3．（2020•聊城）如图，有一块半径为1m ，圆心角为90︒的扇形铁皮，要把它做成一个圆锥形容器（接缝忽略不计），那么这个圆锥形容器的高为( )A ．14mB ．34mC D 4．（2020•云南）如图，正方形ABCD 的边长为4，以点A 为圆心，AD 为半径，画圆弧DE 得到扇形DAE （阴影部分，点E 在对角线AC 上）．若扇形DAE 正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是( )A B ．1C D ．125．（2020•乐山）在ABC ∆中，已知90ABC ∠=︒，30BAC ∠=︒，1BC =．如图所示，将ABC ∆绕点A 按逆时针方向旋转90︒后得到△AB C ''．则图中阴影部分面积为( )A ．4πB C D 6．（2020•淄博）如图，放置在直线l 上的扇形OAB ．由图①滚动（无滑动）到图②，再由图②滚动到图③．若半径2OA =，45AOB ∠=︒，则点O 所经过的运动路径的长是( )A ．22π+B ．3πC ．52πD ．522π+二、填空题7．（2020•广东）如图，从一块半径为1m的圆形铁皮上剪出一个圆周角为120︒的扇形ABC，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为m．8．（2020•新疆）如图，O的半径是2，扇形BAC的圆心角为60︒．若将扇形BAC剪下围成一个圆锥，则此圆锥的底面圆的半径为．9．（2020•重庆）如图，在菱形ABCD中，对角线AC，BD交于点O，120∠=︒，AB=ABC以点O为圆心，OB长为半径画弧，分别与菱形的边相交，则图中阴影部分的面积π为．（结果保留)10．（2020•泰安）如图，点O是半圆圆心，BE是半圆的直径，点A，D在半圆上，且//AD BO，AB=，过点D作DC BE⊥于点C，则阴影部分的面积是．∠=︒，860ABO11．（2020•十堰）如图，圆心角为90︒的扇形ACB内，以BC为直径作半圆，连接AB．若π-，则AC=．阴影部分的面积为(1)三、解答题12．（2020•江西）已知MPN∠的两边分别与O相切于点A，B，O的半径为r．（1）如图1，点C在点A，B之间的优弧上，80∠的度数；∠=︒，求ACBMPN（2）如图2，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，APB∠的度数应为多少？请说明理由；（3）若PC交O于点D，求第（2）问中对应的阴影部分的周长（用含r的式子表示）．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初三数学寒假培优提高班讲义（1）————圆（1）
1、如图，⊙O 的半径是10cm ，弦AB 的长是12cm ，OC 是⊙O 的半径且OC AB ，垂足为D ，CD =__________cm.
2、Rt △ABC ，∠A=90
°，AB=6，AC=8，以A 为圆心，AB 为半径的圆交BC 于D ，求弦BD 的长。

3、在半径为5cm 的圆内，有两条平行弦长分别为6cm,8cm,则这两条平行弦之间的距离是多少？
4、矩形ABCD 中，AB =5，BC =12
，如果分别以A
、C 为圆心的两圆相切，点D 在圆C 内，点B 在圆C 外，那么圆A 的半径r 的取值范围是
5、已知半径分别是17cm 和10cm ，⊙O 1与⊙O 2相交于A 、B 两点，如果公共弦AB 的长是16cm ，求圆心距0102的长.
图5-2
图5-1
6、（2005年上海中考）已知：如图6，圆O 是△ABC 的外接圆，圆心O 在这个三角形的高CD 上，E 、F 分别是边AC 和BC 的中点，求证：四边形CEDF 是菱形.
7、（2006年上海中考）本市新建的滴水湖是圆形人工湖．为测量该湖的半径，小杰和小丽沿湖边选取A ，B ，C 三根木柱，使得A ，B 之间的距离与A ，C 之间的距离相等，并测得BC 长为240米，A 到BC 的距离为5米，如图5所示．请你帮他们求出滴水湖的半径．
8、（2008年上海中考）“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上，导致其中部分图形和数据看不清楚（如图7所示）．已知图纸上的图形是某建筑物横断面的示意图，它是以圆O 的半径OC 所在的直线为对称轴的轴对称图形，A 是OD 与圆O 的交点．
（1）请你帮助小王在图8中把图形补画完整；
（2）由于图纸中圆O 的半径r 的值已看不清楚，根据上述信息（图纸中1:0.75i 是坡面CE 的坡度），求r 的值．
E F D B A O C 图7
O
C A 图8
9、（2004年上海中考）在△ ABC 中, ∠ BAC=90°,AB=AC=2 2 ,圆A 的半径为1,如图5所示,若点O 在BC 边上运动(与点B 、C 不重合),设BO=x,△AOC 的面积为y,（1）求y 关于x 的函数解析式,并写出函数的定义域;
（2）以点O 为圆心,BO 长为半径作圆O,求当圆O 与圆A 相切时,△AOC 的面积.
压轴题练习
1、（2008年上海中考）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．
（1）设BE x =，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．
B
A
D M
E
C
图13
B
A D C
备用图
B C O
2.已知：在△ABC 中，AB =AC ，∠B =30º，BC =6，点D 在边BC 上，点E 在线段DC 上，DE =3，△DEF 是等边三角形，边DF 、EF 与边BA 、CA 分别相交于点M 、N ．（1）求证：△BDM ∽△CEN ；
（2）当点M 、N 分别在边BA 、CA 上时,设BD =x ，△ABC 与△DEF 重叠部分的面积为y ，
求y 关于x 的函数解析式，并写出定义域．
（3）是否存在点D ，使以M 为圆心, BM 为半径的圆与直线EF 相切, 如果存在，请求出x
的值；如不存在，请说明理由．
做好国有粮食企业廉政风险防控工作的思考
A
B
F D
E
M
N
C
近期，在开展党的群众路线教育实践活动中，我们带着拟定的专题“如何推进国有粮食企业廉政风险防控工作”，深入基层调研走访，着力查找问题的主要表现，分析产生问题的原因，探求解决问题的办法。

调研组认为：只有坚持不懈地抓好教育培训，落实防控制度，创新防控手段，上下协同纠风，规范权力运行，强化督查指导，才能把廉政风险防控工作向粮食系统和粮食流通环节延伸并收到成效。

一、国有粮食企业廉政风险的主要表现
国有粮食企业围绕“权、钱、粮”和“购、销、储”活动，其廉政风险主要表现在如下几个环节上：
1.政策性粮食购销环节。

在粮食收购阶段，易发生压级压价，多除皮或有意压秤；对收购的质量、标准把关不严，入库粮食水分、杂质超标，造成库存短少、质量下降，埋下粮食库存安全隐患。

在粮食储存阶段，易发生违规擅自动用政策性粮食，虚报瞒报库存，弄虚作假，套取国家财政补贴。

在粮食轮换阶段，易发生在价格和数量上作文章，低价入库、高价报账；粮食出库时，违规加收出库费用，掺杂使假，赚取不正当收益；有的不经粮食批发市场公开招标，暗箱操作，谋取私利；有的甚至搞“转圈粮”，套取国家财政补贴等问题。

2.资产处置和租赁环节。