第二次信号与系统作业
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
201403学期信号与系统作业二答案

201403学期信号与系统作业二答案第1题已知某系统的系统函数H(s), 唯一决定该系统冲激响应h(t)函数形式的是( )。
A、H(s)的零点B、H(s)的极点C、系统的激励D、激励与H(s)的极点答案:B第2题下列 ( )不是LTI系统的性质。
A、线性B、时不变性C、非因果性D、稳定性答案:C第3题信号的时宽与信号的频宽之间呈( )。
A、正比关系B、反比关系C、平方关系D、没有关系答案:B第4题时域是实偶函数,其傅氏变换一定是( )。
A、实偶函数B、纯虚函数C、任意复函数D、任意实函数答案:A第5题信号〔ε(t)-ε(t-2)〕的拉氏变换的收敛域为 ( )。
A、Re[s]>0B、Re[s]>2C、全S平面D、不存在答案:C第6题已知某连续时间系统的系统函数H(s)=1/(s+1),该系统属于什么类型( )。
A、高通滤波器B、低通滤波器C、带通滤波器D、带阻滤波器答案:B第7题线性系统具有()。
A、分解特性B、零状态线性C、零输入线性D、ABC答案:D第8题零输入响应是( )。
A、全部自由响应B、部分自由响应C、部分零状态响应D、全响应与强迫响应之差答案:B第9题在工程上,从抽样信号恢复原始信号时需要通过的滤波器( )。
A、高通滤波器B、低通滤波器C、带通滤波器D、带阻滤波器答案:B第10题理想低通滤波器一定是( )。
A、稳定的物理可实现系统B、稳定的物理不可实现系统C、不稳定的物理可实现系统D、不稳定的物理不可实现系统答案:B判断题第11题 H (s)的零点和极点中仅极点决定了h (t) 的函数形式。
()正确错误答案:正确第12题系统的系统函数为 H(s),若同时存在频响函数H(jω),则该系统必须满足条件稳定系统。
()正确错误答案:正确第13题对于信号f(t)=sin2Πt的最小采样频率是2Hz。
()正确错误答案:正确()第14题如果一个系统的幅频响应是常数,那么这个系统就称为全通系统。
信号与系统 于敏慧(第二版)第二周作业答案

y0(t)
1
t
0
2
4
(6) x(t) = dx0 (t) , h(t) = dh0 (t) 。
dt
dt
x(t) * h(t) = dx0 (t) * dh0 (t) = d 2 y0 (t)
dt dt
dt 2
x(t) ∗ h(t) = 0.5δ(t) − 0.5δ(t − 2)
2.10 求 y[n] = x1[n]* x2[n]* x3[n] 。 其 中 x1[n] = (0.5)n u[n] , x2[n] = u[n + 3] 和
(2)利用(1)的结果,求系统的逆系统的单位样值(脉冲)响应。
(3)利用(2)的结果,结合卷积性质,求一信号 x[n],使之满足
x[n]* h[n] = 2n (u[n] − u[n − 4])
解:(1) h[n] − Ah[n −1] = δ [n],其中 h[n] = (1 )n u[n] , 2
(通项: an = a1q n−1 )
n
∑ 此题: a1 = 1, q = 2 ; x[n]* h[n] = 2nu[n]*u[n] = ( 2k )u[n] = (2n+1 −1)u[n] k =0
2.6 计算图 2-45(b)与(c)所示信号 x(n)与 h(n)的卷积和,注意:N=4。 解:(b)利用脉冲信号δ(n)的卷积性质以及卷积的延时性质计算:
k =−∞
+ 3] =
u[n + 3] 0.5k
k =0
;
= 2(1 − 0.5n+4 )u[n + 3]
(2) x1[n]* x2[n]* x3[n] = 2(1 − 0.5n+4 )u[n + 3]* (δ [n] − δ [n −1]) ; = 2(1 − 0.5n+4 )u[n + 3] − 2(1 − 0.5n+3 )u[n + 2]
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
17秋北航《信号与系统》在线作业二满分答案

北航《信号与系统》在线作业二
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1. 连续周期信号的傅氏变换是 ________。
A. 连续的
B. 周期性的
C. 离散的
D. 与单周期的相同
满分:3 分
正确答案:C
2. 某系统的系统函数为 H ( s ),若同时存在频响函数 H ( j ω),则该系统必须满足条件 ________。
A. 时不变系统
B. 因果系统
C. 稳定系统
D. 线性系统
满分:3 分
正确答案:A
3. 欲使信号通过系统后只产生相位变化,则该系统一定是 ________。
A. 高通滤波网络
B. 带通滤波网络
C. 全通网络
D. 最小相移网络
满分:3 分
正确答案:C
4. 已知某连续时间系统的系统函数H(s)= 1/(s+1),该系统属于什么类型 ________。
A. 高通滤波器
B. 低通滤波器
C. 带通滤波器
D. 带阻滤波器
满分:3 分
正确答案:B
5. 当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为 ________。
A. 无穷大
B. 不为零的常数
C. 0。
2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t), 0 , f(0 )且 4 ;已知 f(t)f(2t) 的波形如图所示,试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立,
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
(a)y(t) dx(t) dt
时不变、线性、因果、 稳定
( b) y(t)co3t)sx((t) 时变、线性、因果、稳 定
(c)y(t) 2t x()d
(d)y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
(3)4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
( 4)(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
(5)t (t2)(t2)dt4t (t2)d t4u(t2)
2015年苏州大学信号与系统课程第2次过程化试卷答案

苏州大学 信号与系统 课程 第2次过程化考试参考答案 共 页一、 简算、填空与作图(每题4分,共40分)1、已知−→−F t f )()(j ωF ,则()(25)()F y t f t Y j ω=+−−→= 。
521()22j j ωF e ω 2、已知频谱)]()([)(00ωωδωωδπω-++=j F ,则原时间信号=)(t f 。
0cos()t ω3、3、已知周期信号()f t 前四分之一周期的波形如图所示,且()f t 是t 的偶函数,其傅里叶级数只有奇次谐波,画出整个周期内()f t 信号的波形。
4、计算222)(ta at f +=的傅里叶变换()F j ω= 。
2a eωπ-5、图中所示电路的频率响应)(ωj H = 。
RR j Lω+6、理想低通滤波器在物理上是否可以实现? ,说明理由: 。
不能实现,因为违背了因果律7、画出图中)(t f 的偶分量波形。
8、简述周期信号频谱的特点: 。
离散性、谐波性、收敛性9、已知系统的幅频特性1)(=ωj H ,信号通过该系统是否会失真? ,理由是 。
不一定失真,该系统相频特性未知,若相频特性是经过原点的直线则不会失真,否则失真。
10、已知理想高通滤波器的系统函数()()00()0 0 j tj Ke H j H j e ωϕωωωωωωω--⎧>⎪==⎨<⎪⎩,则该系统的冲激响应()h t = 。
00000000sin[()]()()[()]()K t t K K t t K t t S t t t t ωωδδαωππ---=----二、 (10分)计算如图所示波形信号)(t f 的频谱函数)(ωj F 。
解: ()()2()()f t t t t ετεετ=+-+- (2分)()'()2()()f t t t t δτδδτ=+-+- (3分)()22cos()24sin()2j j j F j e e ωτωτωτωωωτ-=-+=-=- (3分)()24sin ()2j F j ωτωω=或2cos()2j ωτω-或22()2j S ωττα (2分)三、 (10分)已知1()f t 的频谱函数为121F (),()()j f t f t ω与波形有如图所示的关系,试用1()f t 的频谱函数表示2()f t 的频谱函数)(F 2ωj 。
《信号与系统(第2版》【附录+习题答案】

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
福师(2021-2022)《信号与系统》在线作业二(3)-辅导资料(答案)

福师[2021-2022]《信号与系统》在线作业二
注:本科目作业有多套随机试卷,请核实是否与您的试卷顺序相一致!!!
一、单选题(共25题,50分)
1、函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的初值等于( )。
[A]1
[B]0
[C]6
[D]2
提示:认真复习课本知识302,并完成以上题目
[正确答案是]:[A]
2、单位序列响应h(n)=δ(n-5)的系统是( )系统。
[A]因果及稳定
[B]非因果及稳定
[C]因果及非稳定
[D]非因果及非稳定
提示:认真复习课本知识302,并完成以上题目
[正确答案是]:[A]
3、一个矩形脉冲信号,当脉冲幅度提高一倍,脉冲宽度扩大一倍,则其频带宽度较原来频带宽度()。
[A]缩小一倍
[B]扩大一倍
[C]不变
[D]不能确定
提示:认真复习课本知识302,并完成以上题目
[正确答案是]:[A]
4、在一个周期内绝对可积是周期信号频谱存在的( )条件。
[A]充分
[B]必要
[C]充要
[D]以上答案都不正确
提示:认真复习课本知识302,并完成以上题目
[正确答案是]:[B]
5、函数f(s)=1/s+1/(s+1)逆变换的初值等于( )。
[A]0
[B]1
[C]2
[D]3
提示:认真复习课本知识302,并完成以上题目。
信号与系统第二版课后答案

信号与系统第二版课后答案《信号与系统》(第二版)课后习题解析燕庆明主编高等教育出版社目录第1章习题解析 2 第2章习题解析 5 第3章习题解析15 第4章习题解析22 第5章习题解析30 第6章习题解析40 第7章习题解析48 第8章习题解析54第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?c d题1-1图解 a 、 c 、 d 为连续信号; b 为离散信号; d 为周期信号;其余为非周期信号; a 、 b 、 c 为有始(因果)信号。
1-2 给定题1-2图示信号f t ,试画出下列信号的波形。
[提示:f 2t 表示将f t 波形压缩,f 表示将f t 波形展宽。
]a 2 f t 2b f 2tc fd f t +1题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R、L、C元件可以看成以电流为输入,电压为响应的简单线性系统SR、SL、SC,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解各系统响应与输入的关系可分别表示为;;1-4 如题1-4图示系统由加法器、积分器和放大量为a的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x t ,由于且故有即1-5 已知某系统的输入 f t 与输出y t 的关系为y t | f t |,试判定该系统是否为线性时不变系统?解设T为系统的运算子,则可以表示为:不失一般性,设f t f1 t + f2 t ,则;故有显然即不满足可加性,故为非线性时不变系统。
1-6 判断下列方程所表示的系统的性质。
1 23 4解 1 线性; 2 线性时不变; 3 线性时变; 4 非线性时不变。
1-7 试证明方程所描述的系统为线性系统。
式中a为常量。
证明不失一般性,设输入有两个分量,且则有相加得即可见即满足可加性,齐次性是显然的。
福师《信号与系统》在线作业二【参考答案】

福师《信号与系统》在线作业二-0006
试卷总分:100 得分:100
一、单选题 (共 25 道试题,共 50 分)
1.在变换域中解差分方程时,首先要对差分方程两端进行( )。
A.拉普拉斯变换
B.傅立叶变换
C.以上答案都不正确
D.Z变换
答案:D
2.信号f(t)与δ(t)的卷积等于( )。
A.δ(t)
B.f(t)δ(t)
C.f(t)
D.0
答案:C
3.在一个周期内绝对可积是周期信号频谱存在的( )条件。
A.必要
B.充要
C.充分
D.以上答案都不正确
答案:A
4.零输入响应是( )。
A.部分零状态响应
B.部分自由响应
C.全部自由响应
D.全响应与强迫响应之差
答案:B
5.信号f(t)=[A+sin(200πt)]cos(2000πt)的归一化功率等于( )。
A.以上答案都不正确
B.A*A/2+1/4
C.A*A/2
D.1/4
答案:B
6.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的终值等于( )。
A.6
B.2
C.1
D.0
答案:D。
信号与系统第二版课后习题解答(3-4)

Chap 33.1 A continuous-time periodic signal x(t) is real value and has a fundamental period T=8. The nonzero Fourier series coefficients for x(t) arej a a a a 4,2*3311====--.Express x(t) in the form)cos()(0k k k k t A t x φω+=∑∞=Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑3.2 A discrete-time periodic signal x[n] is real valued and has afundamental period N=5.The nonzero Fourier series coefficients for x[n] are10=a ,4/2πj e a --=,4/2πj e a =,3/*442πj ea a ==- Express x[n] in the form)sin(][10k k k k n A A n x φω++=∑∞=Solution:for, 10=a , 4/2πj ea --=, 4/2πj ea =, 3/42πj ea --=,3/42πj e a =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=nj j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++=)358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n n3.3 For the continuous-time periodic signal)35sin(4)32cos(2)(t t t x ππ++=Determine the fundamental frequency 0ω and the Fourier series coefficients k a such thattjk k kea t x 0)(ω∑∞-∞==.Solution: forthe period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6, i.e. 3/6/20ππ==w )35sin(4)32cos(2)(t t t x ππ++=)5sin(4)2cos(21200t t ωω++=0000225512()2()2j t j t j t j t e e j e e ωωωω--=++--then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Let 1()x t be a continuous-time periodic signal with fundamental frequency 1ω and Fourier coefficients k a . Given that211()(1)(1)x t x t x t =-+-How is the fundamental frequency 2ω of 2()x t related to? Also, find a relationship between the Fourier series coefficients k b of 2()x t and the coefficients k a You may use the properties listed in Table 3.1. Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x ,that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw t k TT b x t e dt x t x t e dt T --==-+-⎰⎰ 111111(1)(1)jkw t jkw t TTx t e dt x t e dt T T --=-+-⎰⎰111)(jkw k k jkw k jkw k e a a e a e a -----+=+=3.8 Suppose given the following information about a signal x(t): 1. x(t) is real and odd.2. x(t) is periodic with period T=2 and has Fourier coefficients k a .3. 0=k a for 1||>k .4 1|)(|21202=⎰dt t x .Specify two different signals that satisfy these conditions. Solution:0()j kt k k x t a e ω∞=-∞=∑while: )(t x is real and odd, then k a is purely imaginary and odd ,00=a , k k a a --=,.2=T , then 02/2ωππ==and 0=k a for 1>k so0()j kt k k x t a e ω∞=-∞=∑00011j t j t a a e a e ωω--=++)sin(2)(11t a e ea t j tj πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x ∴ j a 2/21±=∴ )sin(2)(t t x π±=3.13 Consider a continuous-time LTI system whose frequency response is⎰∞∞--==ωωωω)4sin()()(dt e t h j H t jIf the input to this system is a periodic signal⎩⎨⎧<≤-<≤=84,140,1)(t t t x With period T=8,determine the corresponding system output y(t). Solution:Fundamental period 8T =.02/8/4ωππ==0()j kt k k x t a e ω∞=-∞=∑∴ 00()()jk t k k y t a H jk e ωω∞=-∞=∑0004, 0sin(4)()0, 0k k H jk k k ωωω=⎧==⎨≠⎩ ∴ 000()()4jkw t k k y t a H jk e a ω∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=⎰⎰⎰另:x(t)为实奇信号,则a k 为纯虚奇函数,也可以得到a 0为0。
奥本海姆《信号与系统(第二版)》习题参考答案
2.23
解: x (t ) =
k = −∞
∑ δ (t − kT ) , y(t ) = x(t ) * h(t ) = x(t ) *
+∞
k = −∞
∑ δ (t − kT ) =
+∞
k = −∞
∑ x(t − kT )
+∞
(根据: x (t ) * δ (t − t 0 ) = x (t − t 0 ) ) 故: (a) T=4,则 y(t)为 x(t)以周期 4 做周期拓延;
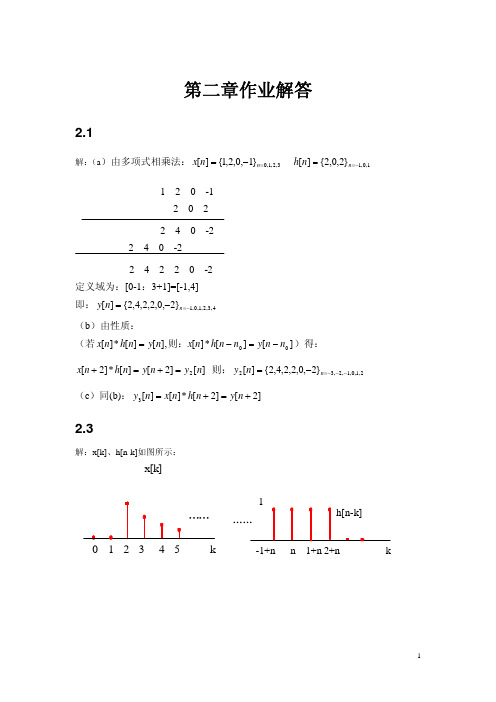
第二章作业解答
2.1
解: (a)由多项式相乘法: x[n] = {1,2,0,−1}n =0,1, 2,3
h[n] = {2,0,2}n = −1, 0,1
1 2 0 -1 2 0 2 2 4 0 -2 2 4 0 -2 2 4 2 2 0 -2
定义域为:[0-1:3+1]=[-1,4] 即: y[n] = {2,4,2,2,0,−2}n = −1, 0,1, 2,3, 4 (b)由性质: (若 x[n] * h[n] = y[n], 则:x[n] * h[n − n0 ] = y[n − n0 ] )得:
1 τ
τ
t
(1) α ≠
β
0 t<0 ⎧ ⎪ y (t ) = x(t ) * h(t ) = ⎨ t − aτ − β ( t −τ ) e e dτ t>0 ⎪ ⎩∫0 t<0 ⎧0 = ⎨ − β t − (α − β ) t − 1] t > 0 ⎩e [e t<0 ⎧0 ⎪ −αt − βt = ⎨ e −e t>0 ⎪[ α − β ] ⎩ e −αt − e − βt =( )u (t ) β −α
复旦 汪源源 信号与通信系统 第二次习题课(课堂PPT)

➢ 分析:
抽样信号:经抽样得到的信号,不是信号本身,也不 是δT(t)
奈奎斯特频率
带通信号抽样频率
➢ 答案:
g(t) 10 cos(120 t) cos(200 t)
➢ (1) G() 10 ( ( 120 ) ( 120 )) ( ( 200 ) ( 200 ))
V
➢ 答案:波形
(1) BASK f (1 r) (2 2r)MHz
(2) 100MHz与104MHz:
BFSK f1 f2 BASK (6 2r)MHz
100MHz与120MHz:
BFSK f1 f2 BASK (22 2r)MHz
20
4-3
➢ 答案:P205
(1)
f2 fs
6π/Tb
Tb
Tb
h(kTs
)
3 Tb
Sa(
3kπ 2
)
k为奇数时 h(kTs) ≠ 0,因此不满足。
(c) TS 1 / fS Tb / 2
H
()
1
4π/Tb 0
, ,
<4π/Tb
else
2
h(t)
2 Tb
2πt
Sa(
Tb
)
h(kTs
)
2 Tb
Sa(kπ)2
满足。
14
3-25
➢ 答案:
解码后量化误差 -6ΔV1
100001 1001 10 0001 1101 1000
9
3-14
➢ 分析:
✓ (1) 抽样定理,注意题目要求“相同速率抽样”
✓
(2)
时分多路信号所需最小带宽:FC
1 2
NF,S
P133公式(3-2-15),注意同步信号
西安交通大学_信号与系统A课后习题(第3、4章)

6
7
8
9
10
t
(c)
1
《第二次课后作业》 28 对下图所示的离散时间周期信号 x[n] 求傅里叶级数系数, 并画出每一组系数 ak 的模和相位。
x[n] … -12 -6 1 … 0 6 12 n
(b)
x[n] 2 … -12 -6 1 … 0 -1 6 12 n
(c) 11 现对一信号 x[n] 给出如下信息: 1. x[n] 是实、偶信号。 3. a11 = 5 2. x[n] 有周期 N = 10 和傅里叶系数 ak 。 4.
《第二次课后作业》 11 已知下列关系:
y (t ) = x(t ) ∗ h(t )
和
g (t ) = x(3t ) ∗ h(3t )
并已知 x(t ) 的傅里叶变换是 X ( jω ) , h(t ) 的傅里叶变换是 H ( jω ) ,利用傅里叶变换性质证明
g (t ) 为 g (t ) = Ay ( Bt )
x(t ) = t , 0 < t < 1
3
画出 x(t ) 并求出它的傅里叶级数系数。 45 设 x(t ) 是一个实周期信号,其正弦-余弦形式的傅里叶级数表示为
x(t ) = a0 + 2∑ [ Bk cos kω0t − Ck sin kω0t ]
k =1
∞
(a) 求 x(t ) 的偶部和奇部的指数形式的傅里叶级数表示;也就是利用上式的系数求下面 两式中的 α k 和 β k ,
h (t ) = e
−4 t
z[n] = x[n] y[ n]
对下列各输入情况下,求输出 y (t ) 的傅里叶级数表示: (b) x(t ) = ∑ n =−∞ (−1) n δ (t − n)
信号作业及解答(C1-C2)

Signals and SystemChap11.6 Determine whether or not each of the following signals is periodic:(a): (/4)1()2()j t x t e u t π+= (b): 2[][][]x n u n u n =+-(c): 3[]{[4][14]}k x n n k n k δδ∞=-∞=----∑Solution:(a).No 【周期信号无始无终,单边肯定不周期】Because 12cos()2sin(),0()440,0t j t t x t t ππ⎧+++>⎪=⎨⎪<⎩when t<0, )(1t x =0.(b).No 【注意n =0】Because 21,0[]2,01,0n n n n x >⎧⎪==⎨⎪<⎩(c).Y es 【画图、归纳】Because∑∞-∞=--+--+=+k k m n k m n m n x ]}414[]44[{]4[3δδ∑∞-∞=------=k m k n m k n )]}(41[)](4[{δδ{[4][14]}k n k n k δδ∞=-∞=----∑N=4.1.9 Determine whether or not each of the following signals is periodic, If a signal is periodic , specify its fundamental period:(a): 101()j tx t je =(b): (1)2()j t x t e -+=(c): 73[]j n x n e π=(d): 3(1/2)/54[]3j n x n e π+= (e): 3/5(1/2)5[]3j n x n e += Solution:(a). T=π/5Because 0w =10, T=2π/10=π/5.(b). Not periodic.Because jt t e e t x --=)(2, while t e -is not periodic,)(2t x is not periodic.(c). N=2Because 0w =7π, N=(2π/0w )*m, and m=7.(d). N=10Because n j j e e n x )5/3(10/343)(ππ=, that is 0w =3π/5,N=(2π/0w )*m, and m=3. (e). Not periodic.Because 0w =3/5, N=(2π/0w )*m=10πm/3 , it ’s not arational number.1.14 consider a periodic signal 1,01()2,12t x t t ≤≤⎧=⎨-<<⎩with periodT=2. The derivative of this signal is related to the “impulse train ”()(2)k g t t k δ∞=-∞=-∑, with period T=2. It can be shown that1122()()()dx t A g t t A g t t dt=-+-. Determine the values of 1A , 1t ,2A , 2t .Solution:A1=3, t1=0, A2=-3, t2=1 or -1x(t) isdtt dx )(isBecause∑∞-∞=-=k k t t g )2()(δ,dtt dx )(=3g(t)-3g(t-1) ordtt dx )(=3g(t)-3g(t+1)1.15.Consider a system S with input x[n] and output y[n].This system is obtained through a series interconnection of a system S 1 followed by a system S2. The input-output relationships for S 1 and S 2 are S 1: ],1[4][2][111-+=n x n x n y S 2: ]3[21]2[][222-+-=n x n x n yWhere ][1n x and ][2n x denote input signals.(a) Determine the input-output relationship for system S.(b)Does the input-output relationship of system S change if the order in which S 1 and S 2 are connected in series is reversed(ie., if S 2 follows S 1)? Solution:(a)]3[21]2[][222-+-=n x n x n y]3[21]2[11-+-=n y n y]}4[4]3[2{21]}3[4]2[2{1111-+-+-+-=n x n x n x n x]4[2]3[5]2[2111-+-+-=n x n x n xThen, ]4[2]3[5]2[2][-+-+-=n x n x n x n y【可以考虑先求取单位脉冲响应,再做卷积】 (b).No. because it ’s linear.1.16.Consider a discrete-time system with input x[n] and output y[n].The input-output relationship for this system is]2[][][-=n x n x n y(a) Is the system memoryless?(b) Determine the output of the system when the input is ][n A δ, where A is any real or complex number. (c) Is the system invertible?Solution:(a). No.For example, when n=0, y[0]=x[0]x[-2]. So the system is memory . (b). y[n]=0.When the input is ][n A δ, ]2[][][2-=n n A n y δδ, so y[n]=0. (c). No.For example, when x[n]=0, y[n]=0; when x[n]=][n A δ, y[n]=0. So the system is not invertible.1.17.Consider a continuous-time system with input x(t) and output y(t) related by ))(sin()(t x t y =, (a) Is this system causal? (b) Is this system linear? Solution: (a). No.For example, )0()(x y =-π. So it ’s not causal.【得到什么启示?】 (b). Y es.Because : ))(sin()(11t x t y = , (sin()(22tx t y =))(sin())(sin()()(2121t bx t ax t by t ay +=+1.21.A continous-time signal ()x t is shown in Figure P1.21. Sketch and label carefully each of the following signals:(a): (1)x t - (b): (2)x t - (c): (21)x t + (d): (4/2)x t - (e): [()()]()x t x t u t +-(f): ()[(3/2)(3/2)]x t t t δδ+-- Solution: (a).(b).(c).(d).【自己动手,做做e 、f 题】1.22. A discrete-time signal ()x t is shown in Figure P1.22. Sketch and label carefully each of the following signals: (a): [4]x n - (b): [3]x n - (c): [3]x n(d): [31]x n + (e): [][3]x n u n -(f): [2][2]x n n δ--(g): 11[](1)[]22nx n x n +-(h): 2[(1)]x n -Solution:(a).(b).(e).(f)δ]2n[-(g)(h) 【做做看】1.25.Determine whether or not each of the following continuous-time signals is periodic. If the signal is periodic, determine its fundamental period.(a): ()3cos(4)3x t t π=+ (b): (1)()j t x t e π-=(c): 2()[cos(2)]3x t t π=-(d): (){cos(4)()}x t t u t ενπ=(e): (){sin(4)()}x t t u t ενπ= (f): (2)()t n n x t e∞--=-∞=∑Solution:(a). Periodic. T=π/2.Solution: T=2π/4=π/2. (b). Periodic. T=2. Solution: T=2π/π=2.(c). Periodic. T=π/2.【括号内周期,平方后仍然周期,或者做三角变换】(d). Periodic. T=0.5. Solution: )}()4{cos()(t u t E t x v π= )}())(4cos()()4{cos(21t u t t u t --+=ππ )}()(){4cos(21t u t u t -+=π)4cos(21t π=So, T=2π/4π=0.5【值得商榷】(e)、(f)非周期信号。
信号与系统西安邮电习题答案

信号与系统西安邮电习题答案第一次1.1画出下列各个信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)解:正弦信号周期(2)解:,正弦信号周期(3)解:,正弦信号周期(4)(5)1.2画出下列各信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)(2)(3)解:(4)(5)1.3写出下图所示各波形的表达式(1)解:(2)解:1.4写出下图所示各序列的闭合形式的表示式(a)解:(b)解:(课堂已讲)1.5判别下列各序列是否为周期性的,如果是,确定其周期(1)解:周期序列(2)解:,,m取3,;,,;故(3)解:,,故非周期;,,;故非周期 1.6已知信号的波形如下图所示,画出下列各函数的波形(1)(2)(3)1.7已知序列的图形如图所示,画出下列各序列的图形(1)(2)1.8信号的波形图如下所示,试画出和的波形解:由图可知:,则当时,;当时,当时,(课堂已讲)1.9已知信号的波形如图所示,分别画出和的波形解:第二次1.10计算下列各题,(1)解:(2)解:(3)解:(4)解:(5)解:(6)解:(7)解:(8)解:(课堂已讲)1.11设系统的初始状态为,激励为,各系统的全响应与激励和初始状态的关系如下,试分析各系统是否是线性的。
第二次信号与系统作业

第二次信号与系统作业信号与系统下半年作业1一、判断题:1.拉普拉斯变换满足线性性。
√2.拉普拉斯变换是连续时间系统进行分析的一种方法。
√3.冲击信号的拉氏变换结果是一个常数。
√4.单位阶跃响应的拉氏变换称为传递函数。
×二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为全通系统。
2.单位冲击信号的拉氏变换结果是( 1 ) 。
3.单位阶跃信号的拉氏变换结果是(1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s因子用 j代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:⎰∞-=0)()(dte tf s F st .7、双边拉普拉斯变换(LT)的定义式是:⎰∞∞--=dte tf s F st )()(.三、计算题1. 求出以下传递函数的原函数 1) F (s )=1/s 解:)()(t u t f = 2) F(s)=11+s 解:f (t)=)(t u et- 3) F(s)= )1(12-ss 解:F(s)= )1(12-s s =)1)(1(1+-s s s =15.0-+s 15.0++s -s 1 f (t)=+-)(5.0t u e t -)(5.0t u e t )(t u2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
L[)](t δ=⎰+∞∞--dtet st)(δ=1L[u (t)]= ⎰+∞∞--dtet u st)(=⎰+∞-0dtest=s1 3、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s ,试求)0(f =?答案:0lim )(lim )(lim )0(2==⋅==∞→∞→→s ss F s t f f s s t5、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 答案:由终值定理02.0)100010()10)(2(lim )(lim )(2=++++==∞→→s s s s s s s sF f s s5、求)()(3t u t t f =的拉氏变换答案:46)]([s t f L =(Re(s) > 0)一、 判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
信号与系统作业答案

硕士研究生信号与系统选修综合课作业题一、试证明:二阶测量系统当阻尼率ζ为0.7时,输入信号在0~0.58ωn 的频率范围内,其幅频特性A(ω)的变化不超过5%。
答:二阶系统的幅频特性为:()[]()2222411)(n n w ww ww A ζ+-=当阻尼率ζ为0.7时,输入信号在0~0.58ωn 的频率范围内,其幅频特性A(ω)的变化范围为1~0.9535.即A(ω)的最大变化率为4.65%,小于5%,命题得证。
二、一个加速度传感器的幅度-频率特性如图所示,现在需要测量一个频率范围在3kHz 内的加速度信号。
(1)完成下面的系统框图,并简述其工作原理。
(2)系统要不失真测量这个信号应满足什么条件(时域和频域条件)?为使信 号完整,ADC 的采样频率至少应该是多少kHz ,为什么?(3)设被测加速度信号的范围是0-5g ,如果采用8位的理想ADC ,利用单一量程时,系统可分辨出最小加速度信号是多少g?答:(1) 系统框图如上图。
通过加速度传感器采集加速度信号的变化,转化成电信号,然后经过放大和滤波电路得到需要的频率范围在3kHz 内的加速度信号,然后输入到采样保持电路进行电压保持,再将此加速度信号输入模数转换电路,最终输出对应的数字量。
(2)系统不失真测量信号应满足:设系统的输出y(t)与输入x(t)时域条件:y(t)=A 0x(t-t 0)8 f(kHz)10 A传感器放大滤波采样保持ADC数字量输出频域条件:Y(w)=A 0e -jwt0X(w),即H(jw)=Ke -jwt0 ,幅度特性是常数K,相位特性是斜率为-t 0的直线。
为使信号完整,根据抽样定理,ADC 的最低采样频率应该是6kHz 。
(3)系统可分辨的最小加速度信号=5/(28-1)=5/255=0.0196g 三、计算题1、已知描述系统的微分方程和初始状态如下,求其完全响应,零输入响应,零状态响应,暂态响应和稳态响应。
)()(3)(4)(22t x t y t y dtd t y dtd =++1)0(=-y 1)0('=-y )()(t u t x =答:(1)求系统的完全响应: 求齐次解:系统的特征方程: 0342=++αα()()031=++αα特征根: 3,121-=-=αα故有齐次解:t t h e A e A t y 321)(--+=求特解:由于)()(t u t x =,即0≥t 时,1)(=t x ,所以令特解B t y p =)(,代入原微分方程有,31=B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统下半年作业1一、判断题:1.拉普拉斯变换满足线性性。
√2.拉普拉斯变换是连续时间系统进行分析的一种方法。
√ 3.冲击信号的拉氏变换结果是一个常数。
√ 4.单位阶跃响应的拉氏变换称为传递函数。
× 二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用ωj 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:⎰∞-=0)()(dt e t f s F st . 7、双边拉普拉斯变换(LT)的定义式是:⎰∞∞--=dt e t f s F st )()(.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:)()(t u t f = 2)F(s)=11+s 解:f (t)=)(t u e t-3)F(s)=)1(12-s s解:F(s)=)1(12-s s =)1)(1(1+-s s s =15.0-+s 15.0++s -s1f (t)= +-)(5.0t u et-)(5.0t u e t )(t u2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
L [)](t δ=⎰+∞∞--dt e t st )(δ=1L [u (t)]=⎰+∞∞--dt e t u st)(=⎰+∞-0dt e st=s 1 3、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s ,试求)0(f =? 答案:0lim)(lim )(lim )0(2==⋅==∞→∞→→s ss F s t f f s s t5、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =?答案:由终值定理02.0)100010()10)(2(lim )(lim )(2=++++==∞→→s s s s s ss sF f s s5、求)()(3t u t t f =的拉氏变换 答案:46)]([s t f L =(Re(s) > 0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
√ (2)时不变系统的响应与激励施加的时刻有关。
× (3)nx(n)的Z 变换结果是-zX(z)。
× (4)单位阶跃序列的Z 变换结果是常数 ×二、填空题1.对于理想的低通滤波器,所有高于截止频率的频率分量都将 不能 通过系统,而低于截止频率的频率分量都将 能够 的通过系统。
2.称X(n)与X (z )是一对 ZT 变换对 。
3离散时间系统是指输入、输出都是 序列 的系统。
4.在没有激励的情况下,系统的响应称为 零输入响应 。
5.离散系统的传递函数定义式是: H (z )=Y(z) / X(z) 。
6。
系统的零状态响应等于激励与 其单位冲激响应之间的卷积 。
信号与系统下半年作业21、 已知序列()f k 的()F z 如下,求初值(0)f , (1)f 及终值()f ∞。
221(1) (), 11(1)()2(2) (), 2(2)(1)z z F z z z z z F z z z z ++=>-+=>-- 解21(1) (0)lim 11(1)()2z z z f z z →∞++==-+33()322(1)lim [()(0)]lim12(1)()2z z z z f z F z f z z →∞→∞+=-==-+2111()lim(1)()lim 212z z z z f z F z z →→++∞=-==+2(2) (0)lim 1(2)(1)z z f z z →∞==--(32)(1)lim [()(0)]lim3(2)(1)z z z z f z F z f z z →∞→∞-=-==--()2F z z >因为的收敛域,不满足应用终值定理的条件,故终值不存在。
2、试用z 变换的性质求下列序列的z 变换()F z 。
(1) 1()[1(1)]()2k f k U k =--(2) ()()(6)f k U k U k =--(3)()(1)()kf k k U k =- (4) ()(1)()f k k k U k =+(5)()cos()2f k kU k π=(6) 1()()cos()()22k f k k U k π=解(1)211()21211z z z F z z z z =⨯-⨯=-+-(2)56()111z z z z F z z z z z ---=-=--- (3)2d ()[]d 1(1)z zF z zz z z -=-=++(4) ()()()f k k kU k kU k =⨯+222323d ()[]d (1)(1)(1) (1)(1)(1)z z F z zz z z z z z z z z z =-+--+=+=---故(5) 221()[]()2j kj k f k e e U k ππ-=+故22221()[]21jjz z z F z z z ez eππ=+=+-+(6) 由尺度变换性质得12222124()41()1zz F z zz ==++3、求下列各像函数)(s F 的原函数)(t f 。
(1) ()()()()()4231++++=s s s s s s F (2) ()()()126516222++++=s s s s s F(3) ()2399222++++=s s s s s F (4) ()()s s s s s F 2323++= (5) ()8666223++++=s s s s s s F (6) ()()2211+=s s s F(7) ()()()41221+-+=--s e s F s (8) ()()se s s F --=11 (9) ()21⎥⎦⎤⎢⎣⎡-=-s e s F s 解:(1)42)(321++++=s K s K s K s F83)4)(2()3)(1(01=⨯++++==s s s s s s s K41)2()4)(2()3)(1(22=+++++=-=s s s s s s s K83)4()4)(2()3)(1(43=+++++=-=s s s s s s s K48324183)(++++=s s s s F )()834183()(42*t U e e t f t t -++=(2)1245152393425121232)(321+++-++=+++++=s s s s K s K s K s F )()45152934512()(1232t U e e e t f tt t ---+-=(3)21122)2)(1(532)(++++=++++=s s s s s s F)()2()(2)(2t U e e t t f tt --++=δ (4)24111)2)(1(23123)(22+-++=+++-=++=s s s s s s s s s F )()4()()(2t U e e t t f tt ---+=δ(5)4422)(+-+++=s s s s F)()42()()(42t U e e t t f tt ---+'=δ(6)s s s s s s K s K s K s K s K s F 3113)2(2)1(11)1()1()(2232222113212311-+++++++=+++++++=)()3()()321()()33221()(22t U t t U e t t t U t e te e t t f t t t t -+++=-+++=---- (7)因22)1(222)1(2212)1(2)(+-⨯++-=--s e s s F s又因有42)(2sin 2+↔s t tU故由时移性有 se s t U t -+↔--42)1()1(2sin 2又由复频移性有)1(24)1(2)1()1(2sin --+-↔--s t es t U t e故 )1()1(2sin 21)(2sin )(--+=t U t e t tU e t f t t(8)s e s s F --⨯=111)( 故∑∑∞=∞=-=-*=0)()()()(n k K t U K t t U t f δ, N K ∈(9)s e e s F ss ---⨯-=121)( 因有 )1(1)1()(s e s t U t U --↔--故[][])2()2()1()1(2)()1()()1()()(--+---=--*--=t U t t U t t tU t U t U t U t U t f 4、已知系统函数)(ϖj H 如图所示,激励)(t f 的波形如图所示。
求系统的响应)(t y ,并画出)(t y 的频谱图。
解:)(sin 2ϖπG tt⇔ )]1000()1000([1000cos -++⇔ωδωδπt)1000(21)1000(21)]1000()1000([)(21)(221-++=-++*=ωωωδωδπωπωG G G j F又:t t f t s t f t y 1000cos )()()()(1== 所以:=-++*=)]1000()1000([)(21)(1ωδωδπωπωj F j Y)2000(41)(21)2000(41222-+++ωωωG G G所以:)(21)()()(21ϖϖϖϖG j H j Y j Y ==所以:)(21)(t Sa t y π=5、图题所示系统,)(ϖj H 的图形如图 (b)所示,)(t f 的波形如图(c)所示。
求响应)(t y 的频谱)(ϖj Y ,并画出)(ϖj Y 的图形。
解: )()(t Sa t f c cϖπϖ= 所以:)()(2ϖϖϖc G j F =)()()()()(2ωωωωωωc G j H j H j F j Y ==)(ϖj Y 的图形如图 (d)所示。
6、 求信号)100()(t Sa t f =的频宽(只计正频率部分);若对)(t f 进行均匀冲激抽样,求奈奎斯特频率N f 与奈奎斯特周期N T 。
解: )(t f 的图形如图(a)所示。
)(100)100()(2ϖπG t Sa t f ⇔=,其频谱图如图(b)所示。
