信号与系统课程作业
信号与系统作业作业答案

信号与系统作业作业答案Document serial number【UU89WT-UU98YT-UU8CB-UUUT-第二章 作业答案2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。
(1))()(2)(2)(3)(t e t e t y t y t y +'=+'+''2)0(=-y ,1)0(-='-y解:根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ 所以,零输入响应可设为:0)(221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧-=--='=+=--3112)0(2)0(212121C C C C y C C y 所以,03)(2≥-=--t e e t y tt zi(2))(2)()(6)(5)(t e t e t y t y t y -'=+'+''1)0()0(=='--y y 。
解:根据微分方程,可知特征方程为:0)3)(2(0652=++⇒=++λλλλ所以,其特征根为: 3,221-=-=λλ 所以,零输入响应可设为:0)(3221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧-==⇒⎩⎨⎧=--='=+=--34132)0(1)0(212121C C C C y C C y 所以,034)(32≥-=--t e e t y tt zi2–2 某LTI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+''已知1)0(=-y ,2)0(='-y ,试求:(1) 系统的零输入响应)(t y zi ;(2) 输入)()(t t e ε=时,系统的零状态响应)(t y zs 和全响应)(t y 。
信号与系统仿真作业

nGDOU-B—11—112广东海洋大学学生实验报告书(学生用表)课程名称课程号学院(系)信息学院专业班级学生姓名学号实验地点04002 实验日期实验一连时间信号的MATLAB表示和连续时间LTI系统的时域分析一、实验目的1.掌握MA TLAB产生常用连续时间信号的编程方法,并熟悉常用连续时间信号的波形和特性;2.运用MATLAB符号求解连续系统的零输入响应和零状态响应;3.运用MATLAB数值求解连续系统的零状态响应;4.运用MATLAB求解连续系统的冲激响应和阶跃响应;5.运用MATLAB卷积积分法求解系统的零状态响应。
二、实验原理1. 连续信号MATLAB实现原理从严格意义上讲,MA TLAB数值计算的方法并不能处理连续时间信号.然而,可用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能够被MATLAB处理,并且能较好地近似表示连续信号.MATLAB提供了大量生成基本信号的函数.比如常用的指数信号、正余弦信号等都是MATLAB的内部函数。
为了表示连续时间信号,需定义某一时间或自变量的范围和取样时间间隔,然后调用该函数计算这些点的函数值,最后画出其波形图.三、实验内容1.实例分析与验证根据以上典型信号的MA TLAB函数,分析与验证下列典型信号MA TLAB程序,并实现各信号波形图的显示,连续信号的图形显示使用连续二维图函数plot().(1)正弦信号:用MA TLAB命令产生正弦信号2sin(2/4)ππ+,并会出时间0≤t≤3的波形图。
程序如下:K=2;w=2*pi ;phi=pi/4;t=0:0.01:3;ft=K*sin (w*t+phi );plot(t,ft ),grid on ;axis ([0,3,-2。
2,2.2])title (’正弦信号’)(2) 抽样信号:用MA TLAB 中的sinc(t)函数命令产生抽样信号Sa(t),并会出时间为66t ππ-≤≤的波形图。
信号与系统作业任务作业任务1(第二章)答案解析

第二章作业答案2 - 已知描述某LTI 连续系统的微分方程和系统的初始状态如下, 此系统的零输入响应(1)y (t) 3y(t) 2y(t) 2e(t) e(t)y(0 ) 2,y(0 ) 1解:y (0 ) y(0 ) 1。
解:23 2 0( 1)( 2) 0所以, 其特征根为:i2, 21所以, 零输入响应可设为:y zi (t)C 1e 2tC 2e ty(° ) C i C 22C 1 1又因为y (0 ) 2C iC 21C 2 3所以,y zi (t) 3e t e 2tt根据微分方程, 可知 特征方程为:t 0试求(2)y (t) 5y (t) 6y(t) e(t) 2e(t)根据微分方程,可知特征方程为:(2)( 3) 0所以,其特征根为:i 2 , 2 3所以,零输入响应可设为:y zi(t) C1e 2t C2e 3t t 0”y(0 ) C i C2 1 C1 4又因为y (0 ) 2C i 3C2 1 C2 3所以,y zi (t) 4e 2t 3e 3t t 0某LTI连续系统的微分方程为y (t) 3y(t) 2y(t) e (t)3e(t) 已知y(0 ) 1,y(0 ) 2,试求:(1)系统的零输入响应y zi(t);(2)输入e(t) (t)时,系统的零状态响应y zs(t)和全响应y(t)解:(1 )根据微分方程,可知特征方程为:2 3 2 0 ( 1)( 2) 0所以,其特征根为: 1 2, 2 1所以,零输入响应可设为:y zi (t) C1e 2t C2e t t 0y(0 ) C i C 2 1 y (0 ) 2C i C 2 2所以,yd)4e ' 3e 2t t 0C i 3C 2 4(2) 可设零状态响应为:y zs (t) C xi e 2t C x2e t p其中p 为特解,由激励信号和系统方程确定。
因为e(t) (t)所以,p 为常数,根据系统方程可知,p 于是,零状态响应可设为为:y zs (t)C xi e” C x2e t 3 232。
信号与系统第一章作业

10 级《信号与系统》 第一章作业 物理与电子工程学院 电子系 专业班级班 学号 姓名 题号一 二 三 四 五 六 七 八 九 十 总分 评卷人 分数20 20 10 50 100 评分 承江红一、单项选择题(每小题2分,共20分)1、已知 f(t),为求 f(32t),应按下列哪种运算求得正确结果?答案:_____A. f(2t)左移 3个单位B. f(2t)右移 3 个单位C. f(2t)左移 3/2个单位D. f(2t)右移 3/2 个单位2、下列说法正确的是:__________________A.线性时不变系统一定具备叠加性与均匀性;B.线性时不变系统一定是无记忆系统;C.线性时不变系统一定是稳定系统;D.线性时不变系统一定是可逆系统;3、下列函数式中哪一个是连续时间信号的表示?答案:_____________A.e at sin w tB.cos(n p )C.(0.5) nD. Sin(n w 0)4、下列各式为描述连续时间系统的微分方程,已知系统的激励为 e(t),响应为 r(t)。
其中______ 方程描述的系统是线性时不变系统。
A. ) ( ) 4 5 sin( ( t e t t r + = )B. ) ( ) ( 3 ) ( 2 t e t r dtt dr t = + C. ) 2 ( ) ( t e t r = D. ) ( ) ( 3 ( 2 ) ( 3 ) ( 2 2 2 2 t e dtt e d t r dt t dr dt t r d + = + + ) 5、下列各式为描述离散时间系统的差分方程,已知系统的激励为 y(n),响应为 x(n)。
其中______ 方程描述的系统是线性、时不变、无记忆的系统。
A. )( 3 ) ( n x n y = B. ) 3 cos( ) ( 2 ) ( n n x n y = C. ) ( ( 2 n x n y = ) D. )( ) 1 ( 4 ) ( n x n y n y = - + 6、信号x(n), n=0,1,2,3,…是能量有限的意思是 ( )a) x (n )有限;b) |x (n )|有界;c) ( ) 2 0 n x n ¥= <¥ å ; d) ( ) 0 1 Nn x n N = <¥ å 。
第二次信号与系统作业答案

下半年信号与系统作业1一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确 3.冲击信号的拉氏变换结果是一个常数。
正确 4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用j ω 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:.7、双边拉普拉斯变换(LT)的定义式是:.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:f (t)=u(t) 2)F(s)=11+s 解:f (t)=e -tu(t)3)F(s)=)1(12-s s解:F(S)=)1(12-s s =)1)(1(1+-s s s =)1(5.0-s +)1(5.0+s -s1F(t)=0.5e-tu(t)+ 0.5e -t u(t)-U(t)2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
解:L[δ(t)]= ⎰+∞∞-δ(t) e -st dt=1L[u(t)]= ⎰+∞∞-u(t) e -stdt=⎰+∞∞- e -st dt=s13、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s,试求)0(f =? )0(f =lim 0→t )(t f =lim ∞→s S ·F(s)=lim∞→s 2ss =0 4、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 由终值定理)(∞f =lim 0→s SF(s)=lim→s s)100010()10)(2(2++++s s s s s =0.025、求)()(3t u t t f =的拉氏变换答:L[)(t f ]=46s(Re(s)>0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
信号与系统作业作业1(第二章)答案

信号与系统作业作业1(第二章)答案1第二章 作业答案2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。
(1))()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ,1)0(-='-y解:根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为:1,221-=-=λλ所以,零输入响应可设为:0)(221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧-=--='=+=--3112)0(2)0(212121C C C C y C C y所以,03)(2≥-=--t e e t ytt zi(2))(2)()(6)(5)(t e t e t y t y t y -'=+'+'' 1)0()0(=='--y y 。
解:根据微分方程,可知特征方程为:0)3)(2(0652=++⇒=++λλλλ所以,其特征根为:3,221-=-=λλ2所以,零输入响应可设为:0)(3221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧-==⇒⎩⎨⎧=--='=+=--34132)0(1)0(212121C C C C y C C y所以,034)(32≥-=--t e e t ytt zi2–2 某LTI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ,2)0(='-y ,试求: (1) 系统的零输入响应)(t y zi ;(2) 输入)()(t t e ε=时,系统的零状态响应)(t y zs 和全响应)(t y 。
解:(1)根据微分方程,可知特征方程为: 0)2)(1(0232=++⇒=++λλλλ所以,其特征根为:1,221-=-=λλ所以,零输入响应可设为:0)(221≥+=--t e C e C t y tt zi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧=--='=+=--4322)0(1)0(212121C C C C y C C y所以,034)(2≥-=--t e e t yt t zi(2) 可设零状态响应为:0)(221>++=--t p e C e C t y tx tx zs其中p 为特解,由激励信号和系统方程确定。
信号与系统北邮第一次作业

信号与系统北邮第一次作业
今天是我在北邮的第一天,老师给我们布置了信号与系统的第一次作业,我一听就愣住了,心里嘀咕:这是什么呀?好难听起来哦!我赶紧回到宿舍,打开书本,“哎呀,怎么这么多公式呀?!”我一看一堆复杂的东西,头都大了。
我把书扔到一边,皱着小眉头开始想:“嗯,不能放弃呀,做作业可不能怕困难!”我翻来翻去,把那堆公式看了一遍又一遍,脑袋嗡嗡的,像是被蜂蜜罐撞了一下,乱成一团。
哎呀,不行,得静下心来!
突然,耳朵里好像听见老师在说:“信号就是一段时间内的变化!”我脑袋一下清晰了点,心想:“哦,原来就是那些看上去像波浪一样的东西嘛!”
我仔细琢磨琢磨,忽然好像明白了一些。
小手在作业本上划来划去,呐呐地念:“这是不是这样做呀?”做着做着,觉得还挺有意思的。
作业终于做完啦,心里高兴得不行,嘻嘻,虽然有点难,但我觉得自己一点点进步了呢!
—— 1 —1 —。
信号与系统第4章作业解答

s5 sr (0 ) 3r (0 ) r (0 ) 4 3 2 Rzi ( s) 2 s 3s 2 s 3s 2 s 1 s 2
rzi (t ) 4e t 3e 2t
(t 0)
10
2 6 求激励信号和起始状态 为以下二种情况下系统 的完全响应, 并指出其零输入响应、 零状态响应、 自 由响应、 强迫响应各分量 . (2) e(t ) e 3t u (t ), r (0 ) 1, r (0 ) 2.
4
4 5 分别求下列函数的逆变换的初值和终值
s3 (2) ( s 1) 2 ( s 2)
s3 f (0 ) lim sF ( s) lim s 0 2 s s ( s 1) ( s 2)
s3 f () lim sF ( s) lim s 0 2 s 0 s 0 ( s 1) ( s 2)
(1) r (t ) rzi (t ) rzs (t )
d g (t ) g (t ) (t ) 2e t u (t ) dt
2 s 1 sG ( s ) G ( s ) 1 s 1 s 1 1 G(s) g (t ) e t u (t ) s 1
f (t ) (t 2et tet e t e2t )u(t )
7
4 4 求下列函数的拉普拉斯逆变换
e s (19) 4s( s 2 1)
1 A Bs C 2 2 s( s 1) s s 1
A B 0 C 0 A 1
( s 3) E ( s ) e(0 ) Rzs ( s ) s 2 3s 2
1 (2) E ( s ) e( 0 ) 0 s3
[信号与系统作业解答]第二章
![[信号与系统作业解答]第二章](https://img.taocdn.com/s3/m/90bd92d5240c844769eaeeda.png)
特征方程为 2 3 2 0 ,特征根为 1
1和 2
2。
所以rzi(t) C1e t C2e 2t, t 0
将 rzi(0 ) r (0 ) 2 和rzi(0 ) r(0 ) 1代入可求得
g(t) 1 e 12t cos 3 t 2
1 e 12t sin 3 t u(t)
3
2
由于系统的冲激响应h(t) h(t) e 12t cos 3 t
2
d g(t) ,所以系统的冲激响应为 dt
1 e 12t sin 3 t u(t)
3
2
3)系统的冲激响应满足方程
d dt
h(t)
2h(t)
(t) 3 (t)
电容两端电压不会发生跳变,vc(0 ) vc(0 ) 10V ,所以i(0 ) 0 ;
因此,电阻两端无电压,电感两端电压变成 10V,所以i (0 ) 10 。
(2)换路后系统的微分方程为
i (t) i (t) i(t) e (t) e(t) 20u(t)
t 0 时间内描述系统的微分方程为
i (t) i (t) i(t) 20 (t)
e(t) (1) 0 (2)
整理得:
2vo(t) 5vo(t) 5vo(t) 3vo(t) 2e (t)
2-4 已知系统相应的齐次方程及其对应的 0+状态条件,求系统的零输入响应。
1)
d2 dt 2
r(t)
2
d dt
r(t
)
2r(t)
0 ,给定r(0 )
1 ,r (0 )
2
[信号与系统作业解答]第一章
![[信号与系统作业解答]第一章](https://img.taocdn.com/s3/m/9bc4ece8f8c75fbfc77db2da.png)
1-3、分别求下列各周期信号的周期 T 1) cos(10 t ) cos(30 t) ; 2) e j 10 t ; 4)
(1)n[u(t nT ) u(t nT T )]
n 0
n
(1) [u(t nT ) u(t nT T )]
图(b)表达式为:
f ( t ) u( t ) u( t 1) 2[u( t 1) u( t 2)] 3u( t 2) ; u( t ) u( t 1) u( t 2)
图(c)表达式为: f ( t ) sin
t [u( t ) u( t T )] ; T
C1e1 (t ) C2e2 (t ) sin[C1e1 (t ) C2e2 (t )]u(t ) C1r1 (t ) C2r2 (t )
由于
所以系统是非线性的。
e( t ) r (t ) sin[e( t )]u(t )
而
e(t t0 ) sin[e(t t0 )]u(t ) r (t t0 ) sin[e(t t0 )]u(t t0 )
5)由于 e1 (t ) r1 (t ) e1 (2t ) , e2 (t ) r2 (t ) e2 (2t ) , 而
C1e1 (t ) C2e2 (t ) C1e1 (2t ) C2e2 (2t ) C1r1 (t ) C2r2 (t )
由于
所以系统是线性的。
C1e1 ( t ) C 2e2 ( t ) C1e1 (t ) C 2e2 (t ) C1r1 (t ) C 2r2 (t )
由于
2
所以系统是非线性的。
北交《信号与系统》在线作业二【满分答案】

北交《信号与系统》在线作业二-0005---------------------------单选题1.在工程上,从抽样信号恢复原始信号时需要通过的滤波器是()。
A.高通滤波器B.低通滤波器C.带通滤波器D.带阻滤波器正确答案:B2.当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为()。
A.无穷大B.不为零的常数C. 0D.随输入信号而定正确答案:C3.信号的时宽与信号的频宽之间呈()。
A.正比关系B.反比关系C.平方关系D.没有关系正确答案:B4.离散时间单位延迟器D的单位序列响应为()。
A. δ(k)B.δ(k+1)C.δ(k-1)D. 1正确答案:C5.信号f(t)=3cos(4t+π/3)的周期是()。
A. 2πB. πC. π/2D. π/4正确答案:C6.线性系统具有()。
A.分解特性B.零状态线性C.零输入线性D.以上全对正确答案:D7.零输入响应是()。
A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差正确答案:B8.Sa[π(t-4)]δ(t-4)等于()。
A.δ(t-4)B.sinπ(t-4)C. 1D. 0正确答案:A9.欲使信号通过系统后只产生相位变化,则该系统一定是()。
A.高通滤波网络B.带通滤波网络C.全通网络D.最小相移网络正确答案:C10.设系统零状态响应与激励的关系是:yzs(t)=|f(t)|,则以下表述不对的是()。
A.系统是线性的B.系统是时不变的C.系统是因果的D.系统是稳定的正确答案:A---------------------------判断题1.若一个连续LTI系统是因果系统,它一定是一个稳定系统。
A. 错误B. 正确正确答案:A2.稳定系统的H(s)极点一定在s平面的左半平面。
A. 错误B. 正确正确答案:A3.一个因果的稳定系统的系统函数所有的零、极点必须都在s平面的左半平面内。
A. 错误B. 正确正确答案:A4.对连续周期信号取样所得的离散时间序列也是周期信号。
信号与系统 高等教育出版社 第一章作业解答

(6) r(t) = e (t)
2
ae1 (t ) + be2 (t ) ⇒ [ae1 (t ) + be2 (t )]2 ar1 (t ) + br2 (t ) = ae (t ) + be (t )
2 1 2 2
非线性
e(t ) ⇒ e(t − t0 ) ⇒ e (t − t0 )
2
e(t ) ⇒ e (t ) ⇒ e (t − t0 )
2 2
时不变
该系统为非线性、时不变、因果系统 该系统为非线性、时不变、
4
1-20 判断下列系统是否为线性的、时不变的、 判断下列系统是否为线性的、时不变的、 因果的? 因果的? 5t (8) r(t) = ∫ e(τ )dτ
−∞
ae1 (t ) + be2 (t ) ⇒ ∫ [ae1 (τ ) + be2 (τ )]dτ
2
1-20 判断下列系统是否为线性的、时不变的、 判断下列系统是否为线性的、时不变的、 因果的? 因果的?
(4) r(t) = e(1−t)
ae1 (t ) + be2 (t ) ⇒ ae1 (1 − t ) + be2 (1 − t ) ar1 (t ) + br2 (t ) = ae1 (1 − t ) + be2 (1 − t )
d δ (t ) = u (t ) dt
d e2 (t ) = e1 (t ) dt
d r2 (t ) = r1 (t ) dt
d −αt −αt −αt r2 (t ) = [e u (t )] = −αe u (t ) + e δ (t ) dt −αt = δ (t ) − αe u (t )
西南大学21春[1073]《信号与系统》作业答案
![西南大学21春[1073]《信号与系统》作业答案](https://img.taocdn.com/s3/m/d03a7839d15abe23492f4d9e.png)
1073 20211单项选择题1、设是信号的傅里叶变换,的波形如图所示,则等于()。
1.4pi2.2pi3.6pi4.02、完整表示对理想滤波器的逼近,可以采用()1.误差容限图2.阻带最小衰减3.对模拟与数字滤波器要区别对待4.通带内最大误差3、冲激函数的单边(下限规定为从0-时刻开始)拉氏变换为1.js2.03.s4.14、下列滤波器中,通带最平坦的是()1.巴特沃思2.贝塞尔滤波器3.椭圆滤波器4.切比雪夫5、等于()1. F. 12.03.e^-54.e^-16、()1.f(-1)2.f(1)3.04.f(0)7、已知信号x(t)的傅里叶变换为,则信号y(t)的频谱为()。
1.R(w)cos(w)2.R(w)/23.R(w/2)4.R(w)8、关于抽样,下列说法错误的是()1. E. 理想的冲激采样可表示零阶保持抽样,二者的频谱变化是一致的。
2.时域抽样,频域会产生周期延拓3.频域抽样,时域会产生周期延拓4.由时域抽样可知,序列的频谱是周期连续的频谱9、已知,则等于()1.2pi2.03.1/24.110、周期信号的波形如图所示,则其傅里叶级数中含有()。
1.正弦分量与余弦分量2.直流分量与正弦分量3.奇次谐波分量4.直流分量与余弦分量11、从S域到Z域的映射中,为保证映射前后滤波器的稳定性不变,则应满足()1.s域左半平面映射到z域的单位圆内,虚轴到单位圆外2.s域左半平面映射到z域的单位圆外,虚轴到单位圆内3.s域左半平面映射到z域的单位圆外部,虚轴到单位圆4.s域左半平面映射到z域的单位圆内,虚轴到单位圆12、关于傅里叶变换,时域做虚指数加权,频域()1.左移2.尺度3.右移4.平移13、已知二端口网络如下图所示,则该系统为()。
1.带阻2.带通3.低通4.高通判断题14、抽样函数可简写为Sa(t)=sin(t)/t,是偶对称的函数。
1. A.√2. B.×15、连续信号的移位、翻转、尺度等运算,都是针对独立变量t而言。
福师《信号与系统》在线作业二满分答案

福师《信号与系统》在线作业二试卷总分:100 测试时间:--一、单选题(共25 道试题,共50 分。
)1. 在变换域中解差分方程时,首先要对差分方程两端进行( )。
A. 傅立叶变换B. 拉普拉斯变换C. Z变换D. 以上答案都不正确满分:2 分2. 激励为x(n)时,响应y(n)=x(n)sin(2πn/7+π/6)的系统是( )系统。
A. 线性且时不变B. 非线性且时不变C. 线性且时变D. 非线性且时变满分:2 分3. 某系统的系统函数为H(z)=z/[(z-0.5)*(z-2)],若该系统是稳定系统,则其收敛区为( )。
A. |z|<0.5B. |z|>2C. 0.5<|z|<2D. 以上答案都不对满分:2 分4. 单位序列响应h(n)是指离散系统的激励为( ) 时,系统的零状态响应。
A. 单位序列B. E指数序列C. 对数序列D. 以上答案都不正确满分:2 分5. f(t)的频宽是200Hz,那么f(-2t-6)的奈奎斯特频率为( )。
A. 400HzB. 200HzC. 800HzD. 100Hz满分:2 分6. 信号f(t)=Asin(500πt)cos(2000πt)的归一化功率等于( )。
A. A*A/2B. A*A/4C. 1/4D. 以上答案都不正确满分:2 分7. 离散信号f(n)是指()。
A. n的取值是连续的,而f(n)的取值是任意的信号B. n的取值是离散的,而f(n)的取值是任意的信号C. n的取值是连续的,而f(n)的取值是连续的信号D. n的取值是连续的,而f(n)的取值是离散的信号满分:2 分8. 函数f(s)=1/s+1/(s+1)逆变换的初值等于( )。
A. 0B. 1C. 2D. 3满分:2 分9. 信号f(t)=Sa(100t)+Sa(50t)的奈奎斯特间隔等于( )。
A. 100/πB. π/100C. 100D. 1/100满分:2 分10. 信号f(t)=Acos(2000πt)+Bsin(200πt)的归一化功率等于( )。
信号与系统课后答案(PDF)
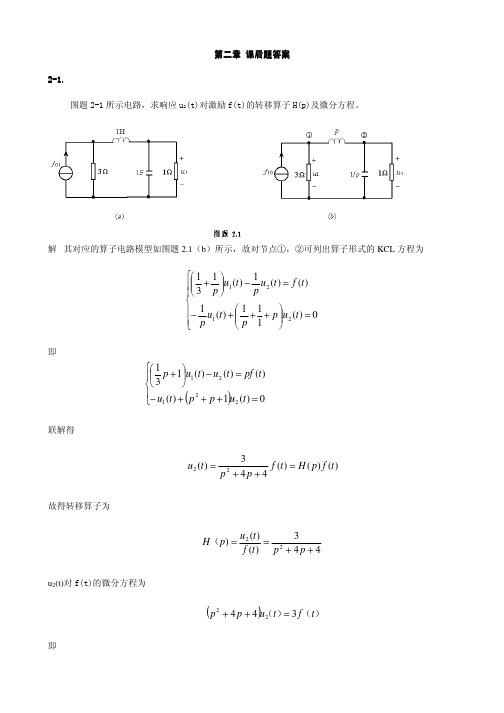
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
[信号与系统作业解答]第三章
![[信号与系统作业解答]第三章](https://img.taocdn.com/s3/m/4cd40f1ca8114431b90dd8da.png)
3-4 求下图所示周期三角信号的傅里叶级数(三角形式)。
解:从图中可知,周期信号的在[ T / 2,T / 2] 的表达式为
f (t)
2E T
t,
0
t
T /2
2E T
t
T /2 t 0
周期为T ,基频 0
2 T。
1)三角形式的傅里叶级数
f (t) a0
[an cos(n 0t) bn sin(n 0t)]
解:
f (t)cos( 0t)
F1( )
1 2
[F(
0) F(
0 )]
f (t)e j 0t F2( ) F(
0)
f (t)cos( 1t)
F3( )
1 2
[F(
1) F(
1)]
3-39 确定下列信号的最低抽样率与奈奎斯特间隔。
(1) Sa(100t )
(3)Sa(100t) Sa(50t)
解:(1)因为Sa(100t) 50G200( ) ,最高频率为 m 100 rad / s ,所以最低抽样
所以
F [fo(t)] 1 [F( ) 2
1 2F
[f (t)
F *( )]
f *( t)] j Im[F( )]
(2)因为 fr (t)
1 2
[f
(t)
f *(t)] ,
所以
F [fr (t)]
1 2F
[f (t)
f *(t)]
1 [F( ) F *( 2
)]
同样的, fi (t)
1 [f (t) 2j
1因为20010050sa最高频率为100所以最低抽样频率为2002又因为另一个分量1005025sa最高频率为100所以最低抽样频率为200341系统如图所示求最大抽样间隔max100020003000300030001000200010001000300010003000波形如下图所示可知的最高频率为3000要进行无失真的恢复则最低抽样频率为min6000对应的最大抽样间隔为maxmin波形如下图所示其中
秋北交信号与系统在线作业一

秋北交《信号与系统》在线作业一北交《信号与系统》在线作业一一、单选题(共10 道试题,共30 分。
)1. 卷积δ(t)*f(t)*δ(t)的结果为()。
A. δ(t)B. δ(2t)C. f(t)D. f(2t)正确答案:2. 线性系统具有()。
A. 分解特性B. 零状态线性C. 零输入线性D. 以上全对正确答案:3. 时域是实偶函数,其傅氏变换一定是()。
A. 实偶函数B. 纯虚函数C. 任意复函数D. 任意实函数正确答案:4. 对于某连续因果系统,系统函数H(s)=(s-2)/(s+2),下面说法不对的是()。
A. 这是一个一阶系统B. 这是一个稳定系统C. 这是一个最小相位系统D. 这是一个全通系统正确答案:5. 信号〔ε(t)-ε(t-2)〕的拉氏变换的收敛域为()。
A. Re[s]>0B. Re[s]>2C. 全S平面D. 不存在正确答案:6. ε(k)*ε(k-1)=()。
A. (k+1)ε(k)B. kε(k-1)C. (k-1)ε(k)D. (k-1)ε(k-1)正确答案:7. 理想低通滤波器是()。
A. 因果系统B. 物理可实现系统C. 非因果系统D. 响应不超前于激励发生的系统正确答案:8. 连续时间信号f(t)的拉氏变换的收敛域是()。
A. 带状B. 环状C. 与σ无关D. 与ω变量有关正确答案:9. 1/jω具有()。
A. 微分特性B. 积分特性C. 延时特性D. 因果特性正确答案:10. 设系统零状态响应与激励的关系是:yzs(t)=|f(t)|,则以下表述不对的是()。
A. 系统是线性的B. 系统是时不变的C. 系统是因果的D. 系统是稳定的正确答案:北交《信号与系统》在线作业一二、判断题(共10 道试题,共30 分。
)1. 一个系统的零状态响应就等于它的自由响应。
A. 错误B. 正确正确答案:2. 稳定系统的H(s)极点一定在s平面的左半平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、题目 1. 已知信号f(t)=sin(20πt)+sin(80πt),用如图所示的采样频率为fs=100Hz,大小为1的信号对其进行采样,使用MATLAB编程,
(1) 绘制采样后的信号时域上的波形图; (2) 对采样后的信号进行频谱分析,画出其幅度谱; (3) 要从采样信号中恢复出原始信号f(t),在MATLAB中设计滤波器,画出滤波后的幅度谱; (4) 将信号f(t)加载到载波信号s(t)=cos(500πt)上,画出调制后信号的波形图和幅度谱。
二、原理 1、信号的采样 “取样”就是利用从连续时间信号f(t)中“抽取”一系列离散样本值的过程。这样得到的离散信号称为取样信号。采样信号f(t)可以看成连续信号f(t)和取样脉冲序列s(t)的乘积。其中取样脉冲序列s(t)也称为开关函数。如果其各脉冲间隔时间相同,均为Ts,就称为均匀取样。Ts称为取样周期,fs=1/Ts称为取样频率或取样率,ωs=2πfs=2π/Ts称为取样角频率。
如果f(t)↔F(jω),s(t)↔S(jω),则由频域卷积定理,得取样信号fs(t)的频谱函数为
本题的取样脉冲序列s(t)是周期为Ts=0.01s的冲激函数序列δTs,也就是冲激取样。而冲激序列δTs(这里T=Ts,Ω=2π/Ts=ωs)的频谱函数也是周期冲激序列,即 2、采样定理 所谓模拟信号的数字处理方法就是将待处理模拟信号经过采样、量化和编码形成数字信号,再利用数字信号处理技术对采样得到的数字信号进行处理。
一个频带限制在(0,fc)Hz的模拟信号m(t),若以采样频率fs≥2fc对模拟信号m(t)进行采样,得到最终的采样值,则可无混叠失真地恢复原始模拟信号m(t)。
其中,无混叠失真地恢复原始模拟信号m(t)是指被恢复信号与原始模拟信号在频谱上无混叠失真,并不是说被恢复信号与原始信号在时域上完全一样。由于采样和恢复器件的精度限制以及量化误差等存在,两者实际是存在一定误差或失真的。奈奎斯特频率:通常把最低允许的采样频率fs=2fc称为奈奎斯特频率。
3、信号的重构 设信号f(t)被采样后形成的采样信号为fs(t),信号的重构是指由fs(t)经过插处理后,恢复出原来的信号f(t)的过程。因此又称为信号恢复。
在采样频率ωs≥2ωm的条件下,采样信号的频谱Fs(jω)是以ωs为周期的谱线。选择一个理想低通滤
波器,使其频率特性H(jω)满足: ccjH,, 0Ts)( 式中的ωc称为滤波器的截止频率,满足ωm≤ωc≤ωs/2。将采样信号通过该理想低通滤波器,输出信号的频谱将与原信号的频谱相同。因此,经过理想滤波器还原得到的信号即为原信号本身。
通过以上分析,得到如下的时域采样定理:一个带宽为ωm的带限信号f(t),可唯一地由它的均匀取样信号fs(nTs)确定,其中,取样间隔Ts许取样频率fs=2fm就是奈奎斯特频率。
使用matlab的sinc(x)的函数,sinc(x) 代表的是 sin(pix)/(pix) 。 4、调制信号 调制信号是原始信息变换而来的低频信号。调制本身是一个电信号变换的过程。调制信号去改变载波信号的某些特征值(如振幅、频率、相位等),导致载波信号的这个特征值发生有规律的变化,这个规律是调制信号本身的规律所决定的。
载波是被调制以传输信号的波形,一般为正弦波。一般要求正弦载波的频率远高于调制信号的带宽,否则会发生混叠,使传输信号失真。我们一般需要发送的数据的频率是低频的,如果按照本身的数据的频率来传输,不利于接收和同步。使用载波传输,我们可以将数据的信号加载到载波的信号上,接收方按照载波的频率来接收数据信号,有意义的信号波的波幅与无意义的信号的波幅是不同的,将这些信号提取出来就是我们需要的数据信号。
二. 源程序(附源程序说明) fy='sin(20*pi*t)+sin(80*pi*t)'; %原信号 %第一问:对信号采样 fs=100;%采样频率 Ts = 1/fs;%采样周期 tp=0.1; t1 = -tp:Ts:tp;%采样时间序列 f1 = [fs*k2/m2,fs*k1/m1];%设置采样信号的频率数组 t = t1; fz = eval(fy);%获取采样序列 %画采样序列波形 figure subplot(111),stem(t,fz,'.'); title('采样信号时域图') xlabel('t(s)'),ylabel('y(t)') line([min(t),max(t)],[0,0]); grid on %第二问:画采样信号频谱 FZ = fz*exp(-1j*(1:length(fz))'*w);%采样信号的离散时间傅里叶变换 subplot(111),plot(f1,abs(FZ),'m'); title('采样信号幅度谱谱') xlabel('f(Hz)'),ylabel('FZ') grid on
%第三问:信号的恢复及频谱函数 T = 1/fs;%采样周期 dt = T/10; %时间间隔,在每个抽样点前面插入9个值 tp = 0.1;%时间围赋值 t = -tp:dt:tp; %时间围 n = -tp/T:tp/T;%计算在重构的时间区间之有多少个采样周期 TMN = ones(length(n),1)*t-n'*T*ones(1,length(t));%生成TMN矩阵 fh = fz*sinc(fs*TMN);%由采样信号恢复原信号 k1 = 0:999; k2 = -999:-1; m1 = length(k1);m2 = length(k2); w = [-2*pi*k2/m2,2*pi*k1/m1];%频率变量 FH = fh*exp(-1j*(1:length(fh))'*w);%恢复后的信号的离散时间傅里叶变换 figure %画滤波后的频谱 f = [10*fs*k2/m2,10*fs*k1/m1];%频率围 subplot(111),plot(f,abs(FH),'g') title('滤波后信号的幅度谱'); xlabel('f(Hz)'),ylabel('FH'); axis([-100 100 0 max(abs(FH))+2]); grid on %第四问:调制 T = 1/fs; dt = T/10; tp = 0.1; t = -tp:dt:tp; n = -tp/T:tp/T; k1 = 0:999; k2 = -999:-1; m1 = length(k1);m2 = length(k2); ft = [10*fs*k2/m2,10*fs*k1/m1];%频率围 yc=cos(500*pi*t);%载波信号 fc= eval(fy); y=fc.*yc;%调制后的信号 FY = y*exp(-1j*(1:length(y))'*w);%已调信号的离散时间傅里叶变换 %画调制后信号波形 figure subplot(211),stem(t,y,'.'); title('已调信号') xlabel('t(s)'),ylabel('y(t)') line([min(t),max(t)],[0,0]); grid on %画调制后信号频谱 subplot(212),plot(ft,abs(FY),'m'); title('已调信号幅度谱') xlabel('f(y)'),ylabel('FY') grid on 四、运行结果与分析 1、第一问
分析:采样信号在时域的表示为无穷多冲激函数的线性组合,其权值为原始信号在对应采样时刻的定义值。 2、第二问 分析:采样信号fs(t)的频谱就是将原始信号f(t)的频谱在频率轴上以采样角频率ωs为周期进行周期延拓后的结果(幅度为原频谱的1/Ts)。由取样信号fs(t)的频谱可以看出,如果ωs>2ωm(即fs>2fm或Ts<1/2fm),那么各相邻频移后的频谱不会发生重叠。
3、第三问 分析:采样信号在一定条件下可以恢复为原来的信号,只需用带宽为Ws/2的理想低通滤波器将各次谐波调制频谱滤去,保留不失真的基带频谱,从而不失真地还原出原来的信号。 4、第四问 分析:按照载波的频率来接收数据信号,有意义的信号波的波幅与无意义的信号的波幅是不同的,提取出来的这些信号就是我们需要的数据信号。
一、题目 2.离散的时间系统差分方程为: 0.863y(k)-0.49y(k-1)+0.124 y(k-2)=1.328f(k)+0.572 f(k-1)+0.98 f(k-2) 初始状态为y(-1)=-3.02,y(-2)=1.35,激励信号f(k)=cos(0.25πk+0.46π)U(k) (1) 利用MATLAB画出系统单位序列响应h(k)的波形图; (2) 分别画出系统的零状态响应和全响应的波形图。 二、原理 1、求系统单位序列响应h(k),可调用函数:impz 功能:求解数字系统的冲激响应。 调用格式: [h,t]=impz(b,a); %求解数字系统的冲激响应 h,取样点数为缺省值。
