高中数学联赛平面几何定理
数学奥赛平面几何

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理:1、梅涅劳斯定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
2、塞瓦定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
3、托勒密定理:四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理:设P 是ABC ∆外接圆上任一点,过P 向ABC ∆的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
5、斯德瓦特定理:设P 是ABC ∆的边BC 边上的任一点,则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理:设ABC ∆和C B A '''∆中有一个角相等或互补(不妨设A=A ')则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理:设ABC ∆和C B A '''∆中有一个边相等,则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明:1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点,且AM:AC=CN:CE=k,如果BMN 三点共线,试求k 。
(IMO23,1982)2、在四边形ABCD 中,ABD ∆、BCD ∆、ABC ∆的面积之比为3:4:1,点M 、N 分别 是AC 、CD 上的点,且AM:AC=CN:CD, 并且BMN 三点共线,求证:M 、N 分别是AC 、 CD 的中点。
高中数学联赛平面几何常用定理

(高中)平面几何常用基本定理1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边及另一边在这边上的射影乘积的两倍.2. 射影定理(欧几里得定理)3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=.4. 垂线定理:2222BD BC AD AC CD AB -=-⇔⊥. 高线长:C b B c A abc c p b p a p p a h a sin sin sin ))()((2===---=. 5. 角平分线定理:三角形一个角的平分线分对边所成的两条线段及这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则ACAB DC BD =;(外角平分线定理). 角平分线长:2cos 2)(2A c b bc a p bcp c b t a +=-+=(其中p 为周长一半). 6. 张角定理:AB DAC AC BAD AD BAC ∠+∠=∠sin sin sin .7. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2·DC +AC 2·BD -AD 2·BC =BC ·DC ·BD .8. 圆周角定理:同弧所对的圆周角相等,等于圆心角的一半.(圆外角如何转化?)9. 弦切角定理:弦切角等于夹弧所对的圆周角.10.圆幂定理:(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:)11.布拉美古塔(Brahmagupta)定理:在圆内接四边形ABCD中,AC ⊥BD,自对角线的交点P向一边作垂线,其延长线必平分对边.12.点到圆的幂:设P为⊙O所在平面上任意一点,PO=d,⊙O的半径为r,则d2-r2就是点P对于⊙O的幂.过P任作一直线及⊙O交于点A、B,则PA·PB= |d2-r2|.“到两圆等幂的点的轨迹是及此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点.13.托勒密(Ptolemy)定理:圆内接四边形对角线之积等于两组对边乘积之和,即AC·BD=AB·CD+AD·BC,(逆命题成立) .(广义托勒密定理)AB·CD+AD·BC≥AC·BD.14.蝴蝶定理:AB是⊙O的弦,M是其中点,弦CD、EF经过点M,CF、DE交AB于P、Q,求证:MP=QM.15.费马点:定理1等边三角形外接圆上一点,到该三角形较近两顶点距离之和等于到另一顶点的距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距离.定理2三角形每一内角都小于120°时,在三角形内必存在一点,它对三条边所张的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一内角不小于120°时,此角的顶点即为费马点.16.拿破仑三角形:在任意△ABC的外侧,分别作等边△ABD、△BCE、△CAF,则AE、AB、CD三线共点,并且AE=BF=CD,这个命题称为拿破仑定理.以△ABC的三条边分别向外作等边△ABD、△BCE、△CAF,它们的外接圆⊙C1 、⊙A1 、⊙B1的圆心构成的△——外拿破仑的三角形,⊙C1 、⊙A1 、⊙B1三圆共点,外拿破仑三角形是一个等边三角形;△ABC的三条边分别向△ABC的内侧作等边△ABD、△BCE、△CAF,它们的外接圆⊙C2 、⊙A2 、⊙B2的圆心构成的△——内拿破仑三角形,⊙C2 、⊙A2 、⊙B2三圆共点,内拿破仑三角形也是一个等边三角形.这两个拿破仑三角形还具有相同的中心.17.九点圆(Ninepointround或欧拉圆或费尔巴赫圆):三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心及各顶点连线的中点,这九个点在同一个圆上,九点圆具有许多有趣的性质,例如:(1)三角形的九点圆的半径是三角形的外接圆半径之半;18.(2)九点圆的圆心在欧拉线上,且恰为垂心及外心连线的中点;(3)三角形的九点圆及三角形的内切圆,三个旁切圆均相切〔费尔巴哈定理〕.19.欧拉(Euler)线:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上.20.欧拉(Euler)公式:设三角形的外接圆半径为R,内切圆半径为r,外心及内心的距离为d,则d2=R2-2Rr.21.锐角三角形的外接圆半径及内切圆半径的和等于外心到各边距离的和.22. 重心:三角形的三条中线交于一点,并且各中线被这个点分成2:1的两部分;)3,3(C B A C B A y y y x x x G ++++ 23. 重心性质:(1)设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ;24.(2)设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31; 25. (3)设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===AB KH CA FP BC DE AB KH CA FP BC DE ; 26.(4)设G 为△ABC 的重心,则 27.③22222223PG GC GB GA PC PB PA +++=++(P 为△ABC 内任意一点); 28. ④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;29. ⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).30. 垂心:三角形的三条高线的交点;)cos cos cos cos cos cos ,cos cos cos cos cos cos (C c B b A a y C c y B b y A a C c B b A a x C c x B b x A a H C B A C B A ++++++++31. 垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍;32.(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上; 33. (3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;34. (4)设O ,H 分别为△ABC 的外心和垂心,则HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,.35. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等;36. 内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然;37. (2)设I 为△ABC 的内心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,2190;38. (3)三角形一内角平分线及其外接圆的交点到另两顶点的距离及到内心的距离相等;反之,若A ∠平分线交△ABC 外接圆于点K ,I 为线段AK 上的点且满足KI=KB ,则I 为△ABC 的内心;39. (4)设I 为△ABC 的内心,,,,c AB b AC a BC ===A ∠平分线交BC 于D ,交△ABC 外接圆于点K ,则a c b KD IK KI AK ID AI +===; 40. (5)设I 为△ABC 的内心,,,,c AB b AC a BC ===I 在AB AC BC ,,上的射影分别为F E D ,,,内切圆半径为r ,令)(21c b a p ++=,则①pr S ABC =∆;②c p CD CE b p BF BD a p AF AE -==-==-==;;;③CI BI AI p abcr ⋅⋅⋅=.41. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;42.外心性质:(1)外心到三角形各顶点距离相等; 43. (2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360;44. (3)∆=S abcR 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆及外接圆半径之和.45. 旁心:一内角平分线及两外角平分线交点——旁切圆圆心;设△ABC的三边,,,c AB b AC a BC ===令)(21c b a p ++=,分别及AB AC BC ,,外侧相切的旁切圆圆心记为C B A I I I ,,,其半径分别记为C B A r r r ,,.旁心性质:(1),21,2190A C BI C BI A C BI C B A ∠=∠=∠∠-︒=∠(对于顶角B ,C 也有类似的式子);(2))(21C A I I I C B A ∠+∠=∠; (3)设A AI 的连线交△ABC 的外接圆于D ,则DC DB DI A ==(对于C B CI BI ,有同样的结论);(4)△ABC 是△I A I B I C 的垂足三角形,且△I A I B I C 的外接圆半径'R 等于△ABC 的直径为2R .46. 三角形面积公式:C B A R R abc C ab ah S a ABC sin sin sin 24sin 21212====∆)cot cot (cot 4222C B A c b a ++++= ))()((c p b p a p p pr ---==,其中a h 表示BC 边上的高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++=. 47.三角形中内切圆,旁切圆和外接圆半径的相互关系: 48. 梅涅劳斯(Menelaus )定理:设△ABC 的三边BC 、CA 、AB 或其延长线和一条不经过它们任一顶点的直线的交点分别为P 、Q 、R 则有 1=⋅⋅RBAR QA CQ PC BP .(逆定理也成立) 49. 梅涅劳斯定理的应用定理1:设△ABC 的∠A 的外角平分线交边CA 于Q ,∠C 的平分线交边AB 于R ,∠B 的平分线交边CA 于Q ,则P 、Q 、R 三点共线.50. 梅涅劳斯定理的应用定理2:过任意△ABC 的三个顶点A 、B 、C 作它的外接圆的切线,分别和BC 、CA 、AB 的延长线交于点P 、Q 、R ,则P 、Q 、R 三点共线.51. 塞瓦(Ceva )定理:设X 、Y 、Z 分别为△ABC 的边BC 、CA 、AB 上的一点,则AX 、BY 、CZ 所在直线交于一点的充要条件是AZ ZB ·BX XC ·CY YA =1. 52. 塞瓦定理的应用定理:设平行于△ABC 的边BC 的直线及两边AB 、AC 的交点分别是D 、E ,又设BE 和CD 交于S ,则AS 一定过边BC 的中点M . 53.塞瓦定理的逆定理:(略) 54. 塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点,三角形的三条高线交于一点,三角形的三条角分线交于一点.55. 塞瓦定理的逆定理的应用定理2:设△ABC 的内切圆和边BC 、CA 、AB 分别相切于点R 、S 、T ,则AR 、BS 、CT 交于一点.56.西摩松(Simson)定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线Simson line).57.西摩松定理的逆定理:(略)58.关于西摩松线的定理1:△ABC的外接圆的两个端点P、Q关于该三角形的西摩松线互相垂直,其交点在九点圆上.59.关于西摩松线的定理2(安宁定理):在一个圆周上有4点,以其中任三点作三角形,再作其余一点的关于该三角形的西摩松线,这些西摩松线交于一点.60.史坦纳定理:设△ABC的垂心为H,其外接圆的任意点P,这时关于△ABC 的点P的西摩松线通过线段PH的中心.61.史坦纳定理的应用定理:△ABC的外接圆上的一点P的关于边BC、CA、AB的对称点和△ABC的垂心H同在一条(及西摩松线平行的)直线上.这条直线被叫做点P关于△ABC的镜象线.62.牛顿定理1:四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点,三点共线.这条直线叫做这个四边形的牛顿线.63.牛顿定理2:圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线.64.笛沙格定理1:平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线.65.笛沙格定理2:相异平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线.66.波朗杰、腾下定理:设△ABC的外接圆上的三点为P、Q、R,则P、Q、R关于△ABC交于一点的充要条件是:弧AP+弧BQ+弧CR=0(mod2 ) .67.波朗杰、腾下定理推论1:设P、Q、R为△ABC的外接圆上的三点,若P、Q、R关于△ABC的西摩松线交于一点,则A、B、C三点关于△PQR 的的西摩松线交于及前相同的一点.68.波朗杰、腾下定理推论2:在推论1中,三条西摩松线的交点是A、B、C、P、Q、R六点任取三点所作的三角形的垂心和其余三点所作的三角形的垂心的连线段的中点.69.波朗杰、腾下定理推论3:考查△ABC的外接圆上的一点P的关于△ABC 的西摩松线,如设QR为垂直于这条西摩松线该外接圆的弦,则三点P、Q、R的关于△ABC的西摩松线交于一点.70.波朗杰、腾下定理推论4:从△ABC的顶点向边BC、CA、AB引垂线,设垂足分别是D、E、F,且设边BC、CA、AB的中点分别是L、M、N,则D、E、F、L、M、N六点在同一个圆上,这时L、M、N点关于关于△ABC 的西摩松线交于一点.71.卡诺定理:通过△ABC的外接圆的一点P,引及△ABC的三边BC、CA、AB分别成同向的等角的直线PD、PE、PF,及三边的交点分别是D、E、F,则D、E、F三点共线.72.奥倍尔定理:通过△ABC的三个顶点引互相平行的三条直线,设它们及△ABC的外接圆的交点分别是L、M、N,在△ABC的外接圆上取一点P,则PL、PM、PN及△ABC的三边BC、CA、AB或其延长线的交点分别是D、E、F,则D、E、F三点共线.73.清宫定理:设P、Q为△ABC的外接圆的异于A、B、C的两点,P点的关于三边BC、CA、AB的对称点分别是U、V、W,这时,QU、QV、QW和边BC、CA、AB或其延长线的交点分别是D、E、F,则D、E、F 三点共线.74.他拿定理:设P、Q为关于△ABC的外接圆的一对反点,点P的关于三边BC、CA、AB的对称点分别是U、V、W,这时,如果QU、QV、QW 和边BC、CA、AB或其延长线的交点分别是D、E、F,则D、E、F三点共线.(反点:P、Q分别为圆O的半径OC和其延长线的两点,如果OC2=OQ×OP则称P、Q两点关于圆O互为反点)75.朗古来定理:在同一圆周上有A1、B1、C1、D1四点,以其中任三点作三角形,在圆周取一点P,作P点的关于这4个三角形的西摩松线,再从P向这4条西摩松线引垂线,则四个垂足在同一条直线上.76.从三角形各边的中点,向这条边所对的顶点处的外接圆的切线引垂线,这些垂线交于该三角形的九点圆的圆心.77.一个圆周上有n个点,从其中任意n-1个点的重心,向该圆周的在其余一点处的切线所引的垂线都交于一点.78.康托尔定理1:一个圆周上有n个点,从其中任意n-2个点的重心向余下两点的连线所引的垂线共点.79.康托尔定理2:一个圆周上有A、B、C、D四点及M、N两点,则M 和N点关于四个三角形△BCD、△CDA、△DAB、△ABC中的每一个的两条西摩松线的交点在同一直线上.这条直线叫做M、N两点关于四边形ABCD 的康托尔线.80.康托尔定理3:一个圆周上有A、B、C、D四点及M、N、L三点,则M、N两点的关于四边形ABCD的康托尔线、L、N两点的关于四边形ABCD 的康托尔线、M、L两点的关于四边形ABCD的康托尔线交于一点.这个点叫做M、N、L三点关于四边形ABCD的康托尔点.81.康托尔定理4:一个圆周上有A、B、C、D、E五点及M、N、L三点,则M、N、L三点关于四边形BCDE、CDEA、DEAB、EABC中的每一个康托尔点在一条直线上.这条直线叫做M、N、L三点关于五边形A、B、C、D、E的康托尔线.82.费尔巴赫定理:三角形的九点圆及内切圆和旁切圆相切.83.莫利定理:将三角形的三个内角三等分,靠近某边的两条三分角线相得到一个交点,则这样的三个交点可以构成一个正三角形.这个三角形常被称作莫利正三角形.84.布利安松定理:连结外切于圆的六边形ABCDEF相对的顶点A和D、B和E、C和F,则这三线共点.85.帕斯卡(Paskal)定理:圆内接六边形ABCDEF相对的边AB和DE、BC和EF、CD和FA的(或延长线的)交点共线.86. 阿波罗尼斯(Apollonius )定理:到两定点A 、B 的距离之比为定比m :n (值不为1)的点P ,位于将线段AB 分成m :n 的内分点C 和外分点D 为直径两端点的定圆周上.这个圆称为阿波罗尼斯圆.87. 库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆.88. 密格尔(Miquel )点:若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点,构成四个三角形,它们是△ABF 、△AED 、△BCE 、△DCF ,则这四个三角形的外接圆共点,这个点称为密格尔点.89. 葛尔刚(Gergonne )点:△ABC 的内切圆分别切边AB 、BC 、CA 于点D 、E 、F ,则AE 、BF 、CD 三线共点,这个点称为葛尔刚点.90. 欧拉关于垂足三角形的面积公式:O 是三角形的外心,M 是三角形中的任意一点,过M 向三边作垂线,三个垂足形成的三角形的面积,其公式:222ABC D 4||R d R S S EF -=∆∆. 斯特瓦尔特定理斯特瓦尔特(stewart)定理设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB^2·DC+AC^2·BD -AD^2·BC=BC·DC·BD。
赣县中学高中数学竞赛平面几何第9九讲托定理勒密
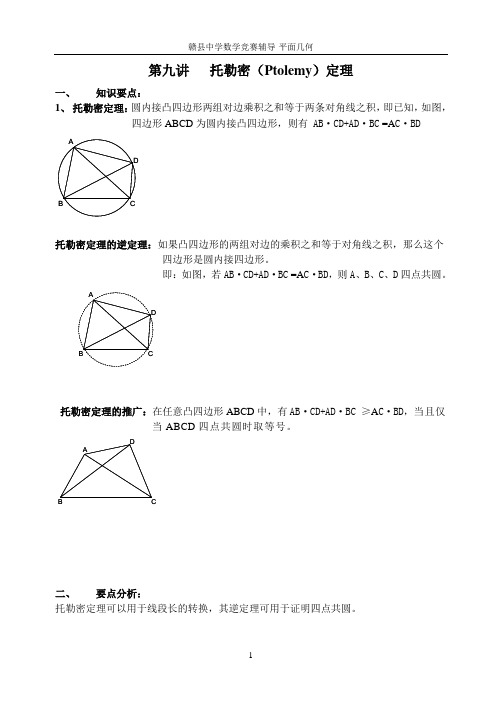
第九讲托勒密(Ptolemy)定理一、知识要点:1、托勒密定理:圆内接凸四边形两组对边乘积之和等于两条对角线之积,即已知,如图,四边形ABCD为圆内接凸四边形,则有 AB·CD+AD·BC =A C·BD ADB C托勒密定理的逆定理:如果凸四边形的两组对边的乘积之和等于对角线之积,那么这个四边形是圆内接四边形。
即:如图,若AB·CD+AD·BC =A C·BD,则A、B、C、D四点共圆。
ADB C托勒密定理的推广:在任意凸四边形ABCD中,有AB·CD+AD·BC ≥A C·BD,当且仅当ABCD四点共圆时取等号。
DAB C二、要点分析:托勒密定理可以用于线段长的转换,其逆定理可用于证明四点共圆。
三、 例题讲解:例1、设ABCD 为圆内接正方形,P 为弧DC 上的一点,求证:PA(PA+PC)=PB(PB+PD) PD CA B例2、如图,设P 、Q 为平行四边形ABCD 的边AB 、AD 上的两点,APQ ∆的外接圆交对角线AC 于R ,求证:A P ·AB+AQ ·AD=AR ·RCDA B CQP R例3、已知ABC ∆中,C B ∠=∠2,求证:AC 2=AB 2+AB ·BCAB C例4、如图所示,已知两同心圆O,四边形ABCD 内接于内圆,AB 、BC 、CD 、DA 的延长线交外圆于A 1、B 1、C 1、D 1,若外圆的半径是内圆的半径的2倍,求证:四边形A 1B 1C 1D 1的周长≥四边形ABCD 的周长的2倍,并确定等号成立的条件。
D 1例5、已知ABC ∆中,AB>AC,A ∠的一个外角平分线交ABC ∆的外接圆于点E,过E 作EF ⊥AB,垂足为F (如图),求证:2AF=AB-ACABC EF第九讲 托勒密(Ptolemy )定理练习1、 如图,已知圆内接正五边形ABCDE,若P 为弧AB 上一点,求证:PA+PD+PB=PE+PC AB C D EP2、 ABCD 为圆内接四边形,DC=BC ,对角线DB 与AC 交于E,若CE :EA=1:3,AB+AD=m,求BD 的长。
数学名师叶中豪整理高中数学竞赛平面几何讲义(完整版)

完全四边形与Miquel点
垂足三角形与等角共轭
反演与配极,调和四边形
射影几何
复数法及重心坐标方法
例题和习题
1.四边形ABCD中,AB=BC,DE⊥AB,CD⊥BC,EF⊥BC,且。求证: 2EF=DE+DC。(10081902.gsp)
2.已知相交两圆O和O'交于A、B两点,且O'恰在圆O上,P为圆O的AO'B弧 段上任意一点。∠APB的平分线交圆O'于Q点。求证:PQ2=PA×PB。 (10092401-1. gsp)
(09022301.gsp)
31.已知半圆圆心为O,直径为AB,一直线交半圆于C、D,交AB延长线于 P,设M是△AOC与△BOD外接圆除O点外的另一交点。求证: OM⊥MP。(10091001.gsp)
32.凸四边形ABCD内接于圆O,两组对边所在直线分别交于点E、F,对角 线AC、BD交于G,作GH⊥EF于H,圆O的弦MN经过G点。求证:GH 与圆O交点恰是△HMN的内心。(10092103-2.gsp)
实用标准文档高中平面几何学习要点几何问题的转化ptolemy定理及应用几何变换及相似理论位似及其应用完全四边形与miquel垂足三角形与等角共轭反演与配极调和四边形射影几何复数法及重心坐标方法例题和习题1
高中平面几何
学习要点
几何问题的转化
叶中豪圆幂与根轴Biblioteka P’tolemy定理及应用
几何变换及相似理论
位似及其应用
53.已知:AD是高,O、H是外心和垂心,过D作OD垂线,交AC 于E。求证:∠DHE=∠C。(09022202.gsp)
54.△ABC中,AD为边BC上的中线,E、F、G分别为AB、AC、AD上
赣县中学高中数学竞赛平面几何第5五讲梅捏劳斯定理
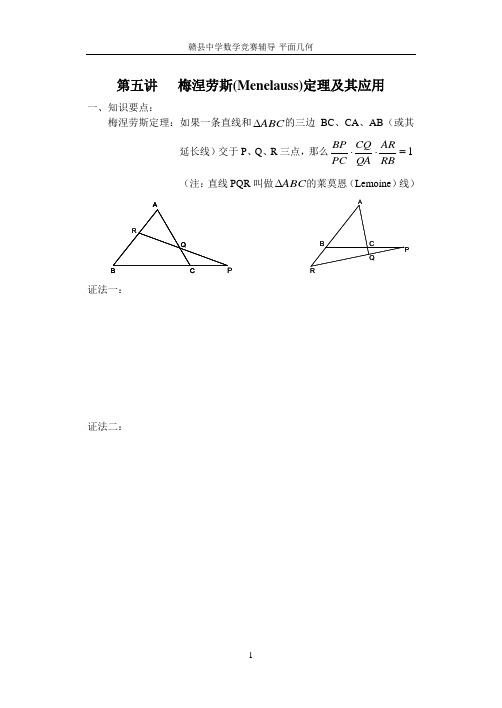
第五讲 梅涅劳斯(Menelauss)定理及其应用一、知识要点:梅涅劳斯定理:如果一条直线和ABC ∆的三边BC 、CA 、AB (或其延长线)交于P 、Q 、R 三点,那么1=⋅⋅RBAR QA CQ PC BP (注:直线PQR 叫做ABC ∆的莱莫恩(Lemoine )线) RP A B C Q AB CPQ R 证法一:证法二:2、梅涅劳斯定理逆定理:设P 、Q 、R 分别是ABC ∆的三边BC 、CA 、AC上或它们延长线上三点,若有1=⋅⋅RBAR QA CQ PC BP ,则P 、Q 、R 三点在同一直线上 RP A B C Q AB CPQ R 证明:二、要点分析:梅涅劳斯定理及其逆定理在几何证明中有着广泛的应用,而且往往使证明过程异常简捷,思路流畅,难度趋易。
在应用梅涅劳斯定理时要抓住“哪条直线截哪个三角形”,其逆定理常应用于证明三点共线问题。
三、例题讲解例1、设AD 为ABC ∆的边BC 上的中线,直线CF 交AD 于E,交AB 于F,求证:FBAF ED AE 2= AB C D EF例2、已知D 、F 分别是ABC ∆的边AB 、AC 上的点,且AD:DB=CF:FA=2:3,连DF 交BC 边的延长线于E ,那么EF:FD=________AB C E FD例3、设ABC ∆的A ∠的外角平分线与BC 的延长线交于P,B ∠的平分线与AC 交于Q,C ∠的平分线和AB 交于R,求证:P 、Q 、R 三点共线 AB C R QP例4、在ABC ∆中,M 是BC 的中点,BC 的中垂线分别交AC 于P,交BA的延长线于Q,且PM=PQ,求证:)sin(3sin C B A -= AB C M PQ例5、设AM 是ABC ∆的边BC 上的中线,任作一直线分别交AB 、AC 、AM 于P 、Q 、N,求证:NANM QA QC PA PB 2=+ AC B M QNP第五讲 梅涅劳斯定理(Menelauss)及其应用练习1、 在ABC ∆的两边AB 、AC 上分别取点Q 、R,满足AQ:QB=2:1,AR:RC=1:2,连接QR 交CB 延长线于P,则_____=PBPC AB C P Q R2、 如图:在平行四边形ABCD ,DC=12,CE=4,CB=10,则CF=_______ A B C DO E F3、 如图,在ABC ∆中,D 在BC 边上且使23=DC BD ,E 在AD 上,使65=ED AE ,BE 交AC 于F,则______=EF BE AB C D EF4、 设D 、E 分别在ABC ∆的边AC 和AB 上,BD 与CE 交于F,AE=EB,32=DC AD ,40=∆ABCS ,求AEFD S AC B E DF5、如图,过ABC ∆的三个顶点A 、B 、C 作它的外接圆的切线,分别和BC 、CA 、AB 的延长线交于P 、Q 、R,求证:P 、Q 、R 三点共线P。
高中数学的归纳平面几何基本定理与证明总结

高中数学的归纳平面几何基本定理与证明总结在高中数学中,平面几何是一个非常重要的分支,它研究了平面内各种图形之间的关系和性质。
而在学习平面几何时,归纳法是一个常用的证明方法。
本文将对高中数学中的归纳平面几何基本定理与证明进行总结。
一、线段中点定理线段中点定理是平面几何中的基本定理之一,它指出:在一条线段的中点上,可以作一条平行于这条线段的直线。
换句话说,如果在线段AB的中点M上作一条直线l,那么l与AB平行。
证明:连接AM、BM。
由于M是线段AB的中点,所以AM=BM,且由中点连线定理可知,AM∥BM。
根据平行线的性质可知,l∥AB。
二、角平分线定理角平分线定理是另一个重要的平面几何定理,它指出:一条角的平分线将这个角分成两个相等的小角。
证明:设∠AOB为一锐角,其中OC是∠AOB的平分线。
要证明∠AOC=∠BOC,我们可以利用三角形AOB和COA的相似性来进行证明。
由于OC是∠AOB的平分线,所以∠AOC=∠BOC。
又因为∠AOB是个锐角,所以∠COA也是个锐角,故∆COA和∆AOB是相似三角形。
根据相似三角形的性质可知,AO/CO=BO/CO,即AO=BO。
因此,∠AOC=∠BOC。
三、垂直平分线定理垂直平分线定理也是平面几何中的重要定理,它指出:一条线段的垂直平分线上所有点到线段的两个端点的距离相等。
证明:设线段AB上的垂直平分线为l,垂直平分线上的一点为M。
要证明AM=BM,我们可以利用三角形AMO和BMO的全等性来进行证明。
由于l是线段AB的垂直平分线,所以AM=BM,且∠AMO=∠BMO=90°。
又因为OM是l的一部分,所以MO=MO,自反性成立。
故∆AMO和∆BMO是全等三角形。
根据全等三角形的定义,可知AM=BM。
四、角的外角定理角的外角定理指出:一个三角形的外角等于它的两个不相邻内角的和。
证明:设三角形ABC的三个内角分别为∠A、∠B和∠C,对于∠A,其外角为∠D。
我们可以利用∆ABC和∆ACD的相似性来进行证明。
高中数学联赛常用定理

常用定理1、费马点(I)基本概念定义:在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
(II)证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠PA1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)PA+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结PD,则△PDB 为等边三角形,所以∠BPD=60度又∠BPA=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故PA+PB+PC=AA1。
(3)PA+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、CM,将△BMC以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1<A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
平面四边形费马点平面四边形中费马点证明相对于三角型中较为简易,也较容易研究。
(1)在凸四边形ABCD中,费马点为两对角线AC、BD交点P。
费马点(2)在凹四边形ABCD中,费马点为凹顶点D(P)。
经过上述的推导,我们即得出了三角形中费马点的找法:当三角形有一个内角大于或等于一百二十度的时候,费马点就是这个内角的顶点;如果三个内角都在120度以内,那么,费马点就是使得费马点与三角形三顶点的连线两两夹角为120度的点。
最新高中数学竞赛平面几何定理证明大全

Gerrald 加油坚持住Gerrald 加油坚持住Gerrald 加油坚持住莫利定理:将任意三角形的各角三等分,则每两个角的相邻三等分线的交点构成一个正三角形。
設△ABC中的∠B,∠C的两条三等分角线分別交于P, D两个点(图1),按照莫利定理,D是莫莱三角形的一個頂点,当然D就是△BPC的內心,因為BD, CD正好是∠CBP, ∠BCP 的角平分线。
莫利三角形的另两个頂点E, F应该分別落在CP和BP上,因此我们产生了一个念头,如果能夠在CP, BP上找到E, F这两个点,使△DEF是个正三角形,再证AE、AF正好是∠BAC的三等分线就行了为此,先把DP连起來,在CP, BP上分別取两点E, F使∠EDP=∠FDP=30°,于是就得到一个三角形△DEF。
为什么它是一个正三角形呢?因为D是△BPC的內心,所以DP是∠BPC的角平分线,即∠DPE=∠DPF,由作图知∠EDP=∠FDP =30°,在△DPE和△DPF中,DP是公共边,而夹此边的两角又是对应相等的,所以△DPE≌△DPF。
于是DE=DF,即△DEF是个等腰三角形,它的腰是DE和DF,而它的頂角又是60°,所以它当然是个正三角形。
接下來,我们的目标就是希望能证明△DEF真的是莫利三角形,亦即AE, AF 的确会三等分∠BAC。
如图2所示,在AB, AC上各取一点G,H,使得BG=BD, CH=CD,把G、 F、E、H各点依次连起來,根据△BFD≌△BFG,△CED≌△CEH,我们就得到GF=FD =FE=ED=EH。
下面,如果能夠证明G,F,E,H,A五点共圆,則定理的证明就完成了,因为∠GAF,∠FAE,∠EAH这三个圆周角所对的弦GF, FE, EH都等長,因而这三个圆周角也就都相等了。
为了证明G,H,E,F,A共圓,必须证明∠FGE=∠FHE=∠A/3。
看图2,首先我们注意到△GFE是个等腰三角形,∠GFE是它的顶角,如果这个角能求出來,其底角∠FGE也就能求出来了。
高中数学竞赛常用定理

高中数学竞赛常用定理在高中数学竞赛中,掌握一些常用的数学定理和公式是至关重要的。
这些定理和公式可以帮助学生在比赛中更快、更准确地解决问题,提高竞赛成绩。
下面我们就来介绍一些高中数学竞赛中常用的定理和公式。
1. 三角函数的基本关系:- 正弦定理:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sinC}=2R$,其中$a$、$b$、$c$分别为三角形$ABC$的三边长度,$A$、$B$、$C$为对应的内角,$R$为三角形$ABC$的外接圆半径。
- 余弦定理:$a^2=b^2+c^2-2bc\cos A$,$b^2=a^2+c^2-2ac\cos B$,$c^2=a^2+b^2-2ab\cos C$。
- 正弦函数和余弦函数的关系:$\sin(a \pm b)=\sin a \cos b \pm \cosa \sin b$,$\cos(a \pm b)=\cos a \cosb \mp \sin a \sin b$。
2. 相似三角形的性质:- 相似三角形的对应角相等,对应边成比例。
- 直角三角形中,正弦、余弦、正切函数的关系:$\sinA=\frac{a}{c}$,$\cos A=\frac{b}{c}$,$\tan A=\frac{a}{b}$。
3. 平面几何中的重要定理:- 圆的性质:圆内角的和为$180^\circ$,圆周角等于其对应圆心角的一半。
- 相交弦定理:相交弦乘积相等,即$AB \times CD=BC \timesDA$。
- 切线和半径的关系:切线和半径垂直,切线与半径的交点与圆心连线构成直角三角形。
- 内切圆和外切圆的性质:内切圆的切点和三角形的顶点共线,外切圆的切点和三角形的对边中点共线。
4. 数列和级数中的常用公式:- 等差数列前$n$项和公式:$S_n=\frac{n}{2}(a_1+a_n)$。
- 等比数列前$n$项和公式:$S_n=\frac{a_1(1-q^n)}{1-q}$。
2022年全国高中数学联赛几何专题(平面几何解析几何)

2022年全国高中数学联赛几何专题(平面几何解析几何)数学竞赛中的平面几何一、引言1.国际数学竞赛中出现的几何问题,包括平面几何与立体几何,但以平面几何为主体.国际数学竞赛中的平面几何题数量较多、难度适中、方法多样(综合几何法、代数计算法、几何变换法等),从内容上看可以分成三个层次:第一层次,中学几何问题.这是与中学教材结合比较紧密的常规几何题,虽然也有轨迹与作图,但主要是以全等法、相似法为基础的证明题,重点是与圆有关的命题,因为圆的命题知识容量大、变化余地大、综合性也强,是编拟竞赛试题的优质素材.第二层次,中学几何的拓展.第三层次,组合几何——几何与组合的交叉.这是用组合数学的成果来解决几何学中的问题,主要研究几何图形的拓扑性质和有限制条件的欧几里得性质.所涉及的类型包括计数、分类、构造、覆盖、递推关系以及相邻、相交、包含等拓扑性质.这类问题在第六届IMO(1964)就出现了,但近30年,无论内容、形式和难度都上了新的台阶,成为一类极有竞赛味、也极具挑战性的新颖题目.组合几何的异军突起是数学竞赛的三大热点之一.2.在中国的数学竞赛大纲中,对平面几何内容除了教材内容外有如下的补充.初中竞赛大纲:四种命题及其关系;三角形的不等关系;同一个三角形中的边角不等关系,不同三角形中的边角不等关系;面积及等积变换;三角形的心(内心、外心、垂心、重心)及其性质.高中竞赛大纲:几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理;三角形中的几个特殊点:旁心、费马点,欧拉线;几何不等式;几何极值问题;几何中的变换:对称、平移、旋转;圆的幂和根轴;面积方法,复数方法,向量方法,解析几何方法.二、基本内容全等三角形的判别与性质,相似三角形的判别与性质,等腰三角形的判别与性质,“三线八角”基本图形,中位线定理,平行线截割定理,圆中角(圆心角、圆周角、弦切角)定理等大家都已经非常熟悉,此外,竞赛中还经常用到以下基本内容.定义1点集的直径是指两个端点都属于这个集合且长度达到最大值的线段(一个点集可能有多条直径,也可能没有直径).定义2如果对点集A中的任意两点,以这两点为端点的线段包含在A 里,则集合A称为是凸的.定义3设M1,M2,,Mn是多边形,如果MM1M2Mn并且当ij时,Mi与Mj 没有公共的内点,则称多边形M剖分为多边形M1,M2,,Mn.定义4如果凸边形N的所有顶点都在凸多边形M的边上,则称多边形N内接于多边性M.定理1两点之间直线距离最短.推论三角形的两边之和大于第三边,两边之差小于第三边.定理2三角形的内角之等于180.凸n边形(n3)的n个内角和等于(n2)外角和为180180;(每一个顶点处只计算一个外角).702022年全国高中数学联赛集训暨2022年中国数学奥林匹克赛前训练材料--内部使用证明如图1,过C作CE//AB,则有ECAA,(两直线平行,内错角相等)得ABCACB(结合律)ECBB(等量代换)180.(两直线平行,同旁内角互补图1推论三角形的一个外角等于两个不相邻内角之和.定理3三角形中大边对大角、小边对小角.证明(1)如图2,在ABC中,已知ABAC,可在AB上截取ADAC,则在等腰ACD中有12.(等腰三角形的性质定理)又在BCD中,2B,(外角定理)更有C12B.(传递性)说明由上面的证明知ABACBC,ABACBC,ABACBC,这样的分断式命题,其逆命题必定成立.证明如下:图2(2)反之,在ABC中,若CB,这时AB,AC有且只有三种关系ABAC,ABAC,ABAC.若ABAC,由上证得CB,与已知CB矛盾.若ABAC,由等腰三角形性质定理得CB,与已知CB矛盾.所以ABAC.定理4在ABC与A1B1C1中,若ABA1B1,ACAC11,则AA1BCB1C1.定理5凸四边形ABCD内接于圆的充分必要条件是:ABCCDA180(或BADDCB180).证明当四边形ABCD内接于圆时,由圆周角定理有ABCCDA1111ADCABCADCABC180.2222同理可证BADDCB180.反之,当ABCCDA180时,首先过不共线的三点A,B,C作O,若点D不在O上,则有两种可能:(1)D在O的外部(如图3(1)).记AD与O相交于S,连CS,在CDS中有ASCCDA.又由上证,有ABCASC180,得180ABCCDAABCASC180,矛盾.712022年全国高中数学联赛集训暨2022年中国数学奥林匹克赛前训练材料--内部使用图3(2)D在O的内部(如图3(2)).记AD的延长线与O相交于S,连CS,在CDS中有ASCCDA.又由上证,有ABCASC180,得180ABCCDAABCASC180,矛盾.定理6凸四边形ABCD外切于圆的充分必要条件是ABCDBCAD.证明当凸四边形ABCD外切于圆时,设各边的切点分别为P,Q,R,S (如图4),根据圆外一点到圆的两切线长相等,有APAS,PBBQ,CRQC,DRDS.相加APPBCRDRASBQQCDS,得ABCDBCAD.图4反之,若ABCDBCAD,我们引B,C的平分线,因为BC360,所以,两条角平分线必定相交于四边形内部一点,记为N,则N到三边AB,BC,CD的距离相等,可以以N为圆心作N与AB,BC,CD同时相切,这时AD与N的关系有且只有三种可能:相离、相切、相交.(1)若AD与N相离(如图5(1)).过A作切线与CD相交于D,在ADD中,有//DDADAD.①//但由上证,有ABCDBCAD,又由已知,有ABCDBCAD相减得CDCDADAD,////DD/ADAD/,与①矛盾.图5722022年全国高中数学联赛集训暨2022年中国数学奥林匹克赛前训练材料--内部使用(2)若AD与N相交(如图5(2)).过A作切线与CD的延长线相交于D,在ADD中,有①//DDADAD.//但由上证,有ABCDBCAD,//又由已知,有ABCDBCAD相减得CDCDADAD,//即DDADAD,与①矛盾.综上得AD与N的相切,即凸四边形ABCD外切于圆.定理7(相交弦定理)圆内的两条相交弦,被交点分成的两条线段长的积相等.定理8(切割线定理)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.定义5从一点A作O的割线交O于B,C,则点A到两交点B,C的线段长度之积ABAC称为点A对O的羃.对于两个已知圆有等羃的点的轨迹,称为两圆的根轴(或等羃轴).定理9若两圆相交,其根轴在两圆公共弦所在的直线上;若两圆相切,其根轴在过两圆切点的公切线上;若两圆相离,则两圆的四条公切线的中点在根轴上.定理10(三角形面积公式)在ABC中,记a,b,c为三边长,p//1(abc)为半周长,R是2外接圆半径,r为内切圆半径,ha是边BC上的高,ra是与边BC及AB,AC的延长线相切的旁切圆的半径,则ABC的面积S为:(1)S111ahabhbchc;222111(2)SabinCacinBbcinA;222(3)Sp(pa)(pb)(pc);(4)Sabc2R2inAinBinC;4R(5)Srp;1ra(bca);21(7)SR2(in2Ain2Bin2C).2定理11在RtABC中,有(6)S(1)abc,(勾股定理的逆定理也成立)(2)r2221c(abc),R.22732022年全国高中数学联赛集训暨2022年中国数学奥林匹克赛前训练材料--内部使用定理12(角平分线定理)设AD是ABC中A的平分线,则.ABBD.ACDC此定理有10多种证法,下面是有辅助线与无辅助线的两种代表性证法.证明1(相似法)如图6,延长BA到E,使AEAC,连CE,则BAD1A(已知)21AECACE(外角定理)2AEC,(等腰三角形的两个底角相等)有AD//CE,BDABAB得.(平行线截割定理)图6DCAEAC11ABADinABCSABD2AB2证明2(面积法).DCSACD1ACADin1AAC22定理13(正弦定理、余弦定理)在ABC中,有(1)abcoBccoC,bacoAccoC,cacoAbcoB.abC2R;(2)inAinBinC222(3)abc2bccoA,b2a2c22accoB,c2a2b22abcoC.(4)inAinBinC2inBinCcoA.222abC2R;inAinBinC证明1(1)当ABC为直角三角形时,命题显然成立.(2)当ABC为锐角三角形时,如图7(1),作ABC外接圆O,则圆心O在ABC的内部,(2)连BO交O于D,连结DC.因为BD是O的直径,所以BCD90,在直角BCD中有aabc2R,但AD,故得2R.同理可证2R,2R.inDinAinBinCabC2R.得inAinBinC(1)(2)图7(3)当ABC为钝角三角形时,记A为钝角,则圆心O在ABC的外部,过A作直径,仿上证74。
高中数学联赛常用定理

常用定理1、费马点(I)基本概念定义:在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
(II)证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠P A1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)P A+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结△PD,则PDB为等边三角形,所以∠BPD=60度又∠BP A=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故P A+PB+PC=AA1。
(3)P A+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、△CM,将BMC以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1<A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
平面四边形费马点平面四边形中费马点证明相对于三角型中较为简易,也较容易研究。
(1)在凸四边形ABCD中,费马点为两对角线AC、BD交点P。
费马点(2)在凹四边形ABCD中,费马点为凹顶点D(P)。
经过上述的推导,我们即得出了三角形中费马点的找法:当三角形有一个内角大于或等于一百二十度的时候,费马点就是这个内角的顶点;如果三个内角都在120度以内,那么,费马点就是使得费马点与三角形三顶点的连线两两夹角为120度的点。
个人精心高中数学联赛竞赛平面几何四大定理及考纲

个人精心高中数学联赛竞赛平面几何四大定理及考纲Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#1、数学竞赛考纲二试1、平面几何基本要求:掌握高中数学竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理:梅涅劳斯定理、、、。
几个重要的极值:到三角形三顶点距离之和最小的点--。
到三角形三顶点距离的平方和最小的点--。
三角形内到三边距离之积最大的点--重心。
几何不等式。
简单的。
了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大。
在周长一定的的集合中,圆的面积最大。
在面积一定的n边形的集合中,正n边形的周长最小。
在面积一定的简单闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
方法、方法。
平面、及应用。
2、代数在一试大纲的基础上另外要求的内容:周期函数与周期,带的函数的图像。
,三角形的一些简单的恒等式,三角不等式。
,一阶、二阶递归,法。
函数,求n次迭代,简单的函数方程。
n个变元的平均不等式,,及应用。
复数的指数形式,欧拉公式,,单位根,单位根的应用。
圆排列,有重复的排列与组合,简单的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简单的初等数论问题,除初中大纲中所包括的内容外,还应包括,,欧几里得除法,非负最小完全剩余类,,,,,格点及其性质。
3、立体几何多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4、平面解析几何直线的式,直线的,直线束及其应用。
二元一次不等式表示的区域。
三角形的。
圆锥曲线的切线和法线。
圆的幂和根轴。
5、其它。
集合的划分。
覆盖。
西姆松线的存在性及性质()。
及其逆定理。
一、平面几何1. 梅涅劳斯定理(Menelaus)定理(简称梅氏定理)是由数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
高中数学竞赛平面几何中的几个重要定理

. 证明:运用面积比可得. 根据等比定理有
, 所以.同理可得,. 三式相乘得. 注:在运用三角形的面积比时,要把握住两个三角形是“等高”还 是“等底”,这样就可以产生出“边之比”.
又因为Q/PF =PQ/F/,即Q/PF =MQ/F/.所以有
MDF/ =MQ/F/.
这说明Q/、D、F/、M四点共圆,即得MF/Q/ =Q/DM.
因为MF/Q/ =MFP,所以MFP =Q/DM.而MFP =EDM,所以EDM =Q/DM.
这说明点Q与点Q/重合,即得PM = MQ.
此定理还可用解析法来证明: 想法:设法证明直线DE和CF在x轴上的截距互为相反数. 证:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标
பைடு நூலகம்
上.则由,得,这说明A、B、C、D四点共圆.
证法2(构造转移法)
延长DA到A/,延长DB到B/,使A、B、B/、A/四点共圆.延长DC到
C/,使得B、C、C/、B/四点共圆.(如果能证明A/、B/、C/共线,则命
题获证)
那么,据圆幂定理知A、C、C/、A/四点也 Image
共圆.
因此,,.
可得 .
另一方面,,即.
3.梅涅劳斯定理及其证明
G
定理:一条直线与ABC的三边AB、BC、CA所在直线分别交于点D、 E、F,且D、E、F均不是ABC的顶点,则有
.
证明:如图,过点C作AB的平行线,交EF于点G.
高中数学竞赛 平面几何的几个重要定理——塞瓦定理

塞瓦定理:1:=⋅⋅∆RBAR QA CQ PC BPCR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点,则、、的分别是、、设,111BCM ABP BMP ABM ACP CMP ACM ABM AP BQ CR M S S S S BP CQ AR PC S S S QA S RB BP CQ AR PC QA RBBP CQ AR AP BQ PC QA RBBP CQ AR AR PC QA R B ∆∆∆∆∆∆∆∆=====⋅⋅⋅⋅=⋅⋅=拻‘证:先证必要性:设、、相交于点,则:同理:以上三式相乘,得:再证充分性:若,设与相交于由塞瓦定理有:,于是:AR R B RB AB R R AP BQ CR ‘’=段上,所以必与重合,故、、交于一点;:证明:三角形的中线例1111111111111111111,,1ABC AA BB CC C B AC B A AC BA CB AC C B BA AC CB B A ABC ∆⋅⋅====⋅⋅=∴∆证明:记的中线,,,我们只须证明而显然有:即成立,交于一点;】证明:三角形的角平【练习1】证明:锐角三角形的【练习22ABC C AB L L AC BC M N AN BM P CP AB∆∠⊥例:在锐角中,角的平分线交于于,从作边和的垂线,垂足分别是和,设和的交点是,证明: 111CK AB CK BM AN P CK BM AN AM CN BKMC CNMC NB AKAM BK AM ALAML AKC AK NB AK ACBK BC AL BCBNL BKC NB BL AC BL⊥⋅⋅==⋅=∆≅∆⇒=∴∆≅∆⇒=⋅=证:作下证、、三线共点,且为点,要证、、三线共点,依塞瓦定理即要证:又即要证明:即要证1AL BC AC BLCK BM AN P CP AB⋅=∴∴⊥依三角形的角平分线定理可知:、、三线共点,且为点3.AD ABC D BC P AD BP CP AC AB E F EDA FDA∆∠∠例设是的高,且在边上,若是上任一点,、分别与、交于和,则=A AD DE DF M N EDA FDA ∠=∠证:过作的垂线,与、的延长线分别交于、。
高中数学竞赛基础平面几何知识点总结

高中数学竞赛平面几何知识点基础1、相似三角形的判定及性质相似三角形的判定:(1)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似;(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为:两边对应成比例且夹角相等,两个三角形相似.);(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(简叙为:三边对应成比例,两个三角形相似.);(4)如果两个三角形的两个角分别对应相等(或三个角分别对应相等),则有两个三角形相似(简叙为两角对应相等,两个三角形相似.).直角三角形相似的判定定理:(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似;(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.常见模型:相似三角形的性质:(1)相似三角形对应角相等(2)相似三角形对应边的比值相等,都等于相似比(3)相似三角形对应边上的高、角平分线、中线的比值都等于相似比(4)相似三角形的周长比等于相似比(5)相似三角形的面积比等于相似比的平方2、内、外角平分线定理及其逆定理内角平分线定理及其逆定理:三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例。
如图所示,若AM平分∠BAC,则该命题有逆定理:如果三角形一边上的某个点与这条边所成的两条线段与这条边的对角的两边对应成比例,那么该点与对角顶点的连线是三角形的一条角平分线外角平分线定理:三角形任一外角平分线外分对边成两线段,这两条线段和夹相应的内角的两边成比例。
如图所示,AD平分△ABC的外角∠CAE,则其逆定理也成立:若D是△ABC的BC边延长线上的一点,且满足则AD是∠A的外角的平分线内外角平分线定理相结合:如图所示,AD平分∠BAC,AE平分∠BAC的外角∠CAE,则3、射影定理在Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,则有射影定理如下:BD2=AD·CDAB2=AC·ADBC2=CD·AC对于一般三角形:在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,则有a=bcosC+ccosB b=ccosA+acosC c=acosB+bcosA4、旋转相似当一对相似三角形有公共定点且其边不重合时,则会产生另一对相似三角形,寻找方法:连接对应点,找对应点连线和一组对应边所成的三角形,可以得到一组角相等和一组对应边成比例,如图中若△ABC∽△AED,则△ACD∽△ABE5、张角定理在△ABC中D为BC边上一点,则sin∠BAD/AC+sin∠CAD/AB=sin∠BAC/AD6、圆内有关角度的定理圆周角定理及其推论:(1)圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半(2)同弧所对的圆周角相等(3)直径所对的圆周角是直角,直角所对的弦是直径(4)圆内接四边形对角互补(5)圆内接四边形的外角等于其内对角弦切角定理:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
高中数学竞赛 平面几何的几个重要定理——托勒密定理

托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).即:ABCD AB CD AD BC AC BD ⋅+⋅≥⋅定理:在四边形中,有:ABCD 并且当且仅当四边形内接于圆时,等式成立;()ABCD E BAE CAD ABE ACDAB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC ADBC ED AD BC AC ED AC ADAB CD AD BC AC BE ED AB CD AD BC AC BD E BD A B C ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅证:在四边形内取点,使,则:和相似又且和相似且等号当且仅当在上时成立,即当且仅当、、、一、直接应用托勒密定理例1 如图2,P 是正△ABC 外接圆的劣弧上任一点(不与B 、C 重合), 求证:PA=PB +PC .分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,∵AB=BC=AC . ∴PA=PB+PC .二、完善图形 借助托勒密定理例2 证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2 证明:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.由托勒密定理,有 AC ·BD=AB ·CD +AD ·BC . ①又∵ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD . ②把②代人①,得AC 2=AB 2+BC 2.例3 如图,在△ABC 中,∠A 的平分 线交外接∠圆于D ,连结BD ,求证:AD ·BC=BD(AB +AC).证明:连结CD ,依托勒密定理,有AD ·BC =AB ·CD +AC ·BD .∵∠1=∠2,∴ BD=CD .故 AD ·BC=AB ·BD +AC ·BD=BD(AB +AC).三、构造图形 借助托勒密定理例4 若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.证明:如图作直径AB=1的圆,在AB 两边任作Rt △ACB 和Rt △ADB ,使AC =a,BC=b,BD =x ,AD =y .由勾股定理知a 、b 、x 、y 是满足题设条件的.据托勒密定理,有AC ·BD +BC ·AD=AB ·CD .∵CD ≤AB =1,∴ax +by ≤1.四、巧变原式 妙构图形,借助托勒密定理例5 已知a 、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .分析:将a 2=b(b +c)变形为a ·a=b ·b +bc ,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b ,两对角线为a ,一底边为c .证明:如图 ,作△ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D ,连结BD 、DC 、DA .∵AD=BC ,ACD BDC =∴∠ABD=∠BAC .又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.依托勒密定理,有BC ·AD=AB ·CD +BD ·AC . ①而已知a 2=b(b +c),即a ·a=b ·c +b 2. ②∴∠BAC=2∠ABC .五、巧变形 妙引线 借肋托勒密定理例6 在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,分析:将结论变形为AC ·BC +AB ·BC=AB ·AC ,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图,作△ABC 的外接圆,作弦BD=BC ,边结AD 、CD .在圆内接四边形ADBC 中,由托勒密定理,有AC ·BD +BC ·AD=AB ·CD易证AB=AD ,CD=AC ,∴AC ·BC +BC ·AB=AB ·AC ,1.已知△ABC 中,∠B=2∠C 。
2023年赣县中学高中数学竞赛平面几何角平分线定理
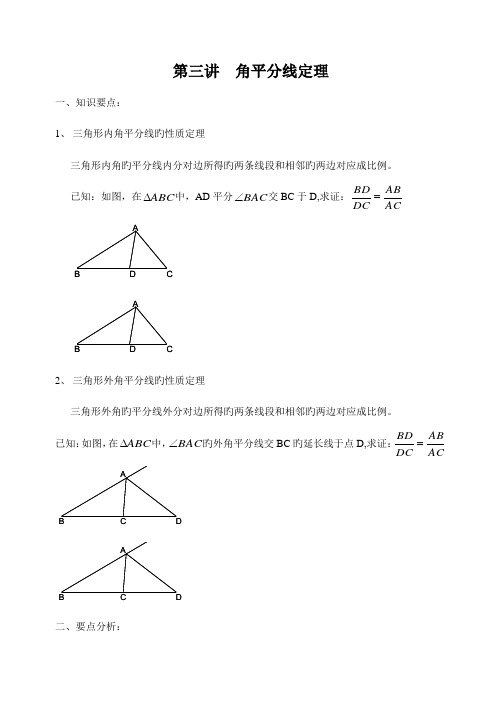
第三讲 角平分线定理一、知识要点:1、 三角形内角平分线旳性质定理三角形内角旳平分线内分对边所得旳两条线段和相邻旳两边对应成比例。
已知:如图,在ABC ∆中,AD 平分BAC ∠交BC 于D,求证:ACAB DC BD = A B C DA B C D2、 三角形外角平分线旳性质定理三角形外角旳平分线外分对边所得旳两条线段和相邻旳两边对应成比例。
已知:如图,在ABC ∆中,BAC ∠旳外角平分线交BC 旳延长线于点D,求证:ACAB DC BD = A B D CA B D C二、要点分析:1、 对于波及与角平分线有关旳计算,常由角平分线性质定理列出比例式进行计算;2、 对于有关角平分线旳证明题,常由角平分线性质定理列出比例式进行代换,到达证明旳目旳;三、例题讲解:题型一:计算题例1、 在ABC ∆中,90=∠C ,CD 是C ∠旳平分线,且CA=3,CB=4,求CD 旳长。
CA B D例2、 如图:若PA=PB,ACB APB ∠=∠2,AC 与PB 相交于点D,且PB=4,PD=3,求DC AD ⋅旳值。
PA B C D题型二:证明题 例3、 如图:I 是ABC ∆三个内角平分线旳交点,AI 交对边于D,求证:BCAC AB ID AI +=AB C D I例4、如图:Rt ABC ∆中, 90=∠ACB ,CD ⊥AB 于D,AF 平分CAB ∠交CD 于E,交CB于F,且EG ∥AB 交CB 于G,求证: CF=GB A B CD FEG例5:如图:在ABC ∆中,AD 平分BAC ∠,C E ⊥AD 交AB 于G,AM 是BC 边旳中线,交CG 于F,求证:AC ∥DF AB C D E GF例6、如图:在ABC ∆中,A 、B 、C 旳对边分别是c b a 、、,且c b a >>,AS 、'AS 为A ∠旳平分线与外角平分线,'BT 、BT 为B ∠旳平分线与外角平分线,'C U CU 、为B ∠旳平分线与外角平分线,求证:'''111TT UU SS =+ S AS ’B C角平分线定理练习1、 在直角三角形中,90=∠C ,AD 平分A ∠,且BD :DC=2:1,则=∠B ________.2、 在Rt ABC ∆中, 90=∠C ,CD 是斜边AB 上旳高,CE 是C ∠旳平分线,若32=EB AE ,则DBAD 旳值为_________. 3、 已知:AD 是Rt ABC ∆斜边BC 上旳高,ABC ∠旳平分线交AD 于M,DAC ∠旳平分线交CD 于N,求证:M N ∥ACBC AD MN4、 已知AD 是等腰ABC ∆底边BC 上旳高,BM 及BN 是B ∠旳三等分线,分别交AD 于M 、N,连接CN 并延长交AB 于E,求证:MNAM EB AE = ABC D E MN5、 如图:在ABC ∆中,AB=AC,BC 边上旳高AD=5,M 为AD 上一点,MD=1,且BAC BMC ∠=∠3,试求ABC ∆旳周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①鸡爪定理:设△ABC的内心为I,∠A内的旁心为J,AI的延长线交三角形外接圆
于K,则KI=KJ=KB=KC。
由内心和旁心的定义可知∠IBC=∠ABC/2,∠JBC=(180°-∠ABC)/2
∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ
同理,∠ICJ=90°
∵∠IBJ+∠ICJ=180°
∴IBJC四点共圆,且IJ为圆的直径
∵AK平分∠BAC
∴KB=KC(相等的圆周角所对的弦相等)
又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB
∴KB=KI
∵IBJC四点共圆且KB=KI=KC
∴点K是四边形IBJC的外接圆的圆心(只有圆心满足与圆周上超过三个以上的点的距离相等)
∴KB=KI=KJ=KC
鸡爪定理逆定理:设△ABC中∠BAC的平分线交△ABC的外接圆于K。
在AK及延长线上截取KI=KB=KJ,其中I在△ABC的内部,J在△ABC的外部。
则I是△ABC的内心,J是△ABC的旁心。
证明:利用同一法可轻松证明该定理的逆定理。
取△ABC的内心I'和旁心J’,根据定理有KB=KC=KI'=KJ'
又∵KB=KI=KJ
∴I和I'重合,J和J’重合
即I和J分别是内心和旁心。
②蝴蝶定理:设S为圆内弦AB的中点,过S作弦EF和CD。
设CF和DE各相交AB于点M和N,则S是MN的
中点。
过O作OL⊥ED,OT⊥CF,垂足为L、T,
连接ON,OM,OS,SL,ST,易明△ESD∽△CSF
证法1:霍纳证法
∴ES/CS=ED/FC
根据垂径定理得:LD=ED/2,FT=FC/2
∴ES/CS=EL/CT
又∵∠E=∠C
∴△ESL∽△CST
∴∠SLN=∠STM
∵S是AB的中点所以OS⊥AB
∴∠OSN=∠OLN=90°
∴O,S,N,L四点共圆,(一中同长)
同理,O,T,M,S四点共圆
∴∠STM=∠SOM,∠SLN=∠SON
∴∠SON=∠SOM
∵OS⊥AB
∴MS=NS
③西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线。
(此线常称为西姆松线)。
西姆松定理的逆定理为:若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上。
证明一:△ABC外接圆上有点P,且PE⊥AC于E,PF⊥BC于F,PD⊥AB于D,分别连FE、FD、BP、CP.
易证P、B、D、F和P、F、C、E分别共圆,(四点共圆)
在PBDF圆内,∠DBP+∠DFP=180度,在ABPC圆内∠ABP+∠ACP =180度,
∴∠DFP=∠ACP ①,在PFCE圆内∠PFE=∠PCE②
而∠ACP+∠PCE=180°③∴∠DFP+∠PFE=180°④,即D、F、E共线。
反之,当D、F、E共线时,由④→②→③→①可见A、B、P、C共圆。
④九点圆:三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共圆。
作图如下:△ABC的BC边垂足为D,BC边中点为L,
AC边垂足为E,AC边中点为M,AB边垂足为F,AB边中点为N,
垂心为H,AH,BH,CH中点分别为P,Q,R
(思路:以PL为直径,其它任意某点,去证P某L为90°)
证明:(由中位线)PM∥CH,LM∥AB,又CH⊥AB∴PM⊥LM,又PD⊥
LD
∴PMDL共圆。
(由中位线)PR∥AC,LR∥BH,BH⊥AC,所以PR⊥LR
∴PMRDL五点共圆。
PE为Rt△AHE斜边中线
∴∠PEA=∠PAE
同理∠LEC=∠LCE所以∠PEL=180°—∠ADC
∴∠LEP等于90°
∴PEMRDL六点共圆,PL为直径,同理PFNQL五点共圆,PL为直径
∴PEMRDLQNF九点共圆,PL为直径,PL中点(设为V)就是圆心
下证九点圆的圆心在垂心与外心连线的中点
O为外心,OL平行等于AH一半(小定理)所以OL平行等于PH
OLPH为平行四边形,V是PL中点,就是OH中点。
⑤托勒密定理:圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ACD,连接DE.
则△ABE∽△ACD
所以BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,
所以△ABC∽△AED.
BC/ED=AC/AD,即ED·AC=BC·AD (2)
(1)+(2),得
AC(BE+ED)=AB·CD+AD·BC
又因为BE+ED≥BD
(仅在四边形ABCD是某圆的内接四边形时,等号成立,即"托勒密定理")
⑥三弦定理:圆上一点A,引出三条弦AB(左)、AC(右)、及中间弦AD,BC与AD交于P,则:
ABsin∠CAP +ACsin∠BAP= ADsin∠BAC。
证明如下;连BD、CD, 由圆的相交弦定理→△ABP∽△CDP→AB/CD=AP/CP→AB·CP=CD·AP→
AB·CP-CD·AP=0→同理→AC·BP-BD·AP=0, 所以有AB(AB·CP-CD·AP)=0, AC(AC·BP-BD·AP)=0,两式相加→AB·AB·CP + AC·AC·BP=AB·CD·AP +AC·BD·AP=AP(AB·CD+AC·BD)=AP·BC·AD⑴(托氏定理)。
由AC外分∠BAP, 由《分角定理》→(sin∠CAP/ sin∠BAC)=(CP/BC) ·(AB/AP), →
(ABsin∠CAP/ sin∠BAC)=(CP/BC) ·(AB·AB/AP)⑵, 同理有, 由AB外分∠CAP, 由《分角定理》→
(ACsin∠BAP/ sin∠BAC)=(BP/BC) ·(AC·AC/AP)⑶, 由⑵+⑶→
(ABsin∠CAP+ ACsin∠BAP) / sin∠BAC=( AB·AB·CP+ AC·AC·BP)/BC·AP,由⑴→
( AB·AB·CP+ AC·AC·BP)/BC·AP=AD, 所以(ABsin∠CAP+ ACsin∠BAP) / sin∠BAC=AD,
所以,ABsin∠CAP+ ACsin∠BAP= ADsin∠BAC。
证毕。
