高中奥林匹克竞赛数学平面几何100题——珍藏版
平面几何100题及答案(前80题)
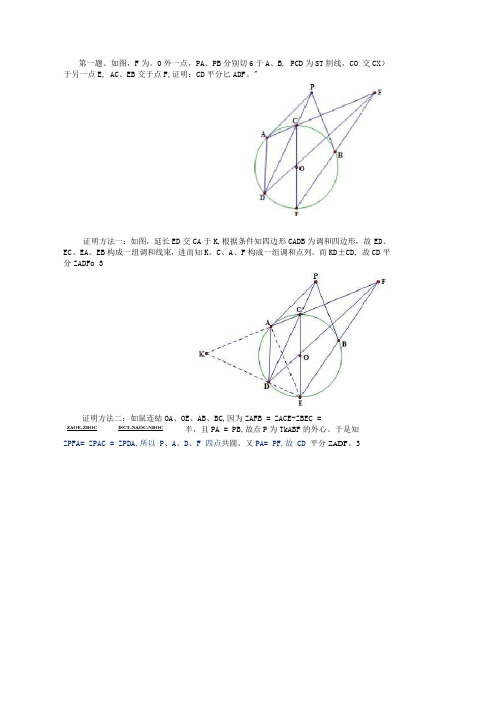
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
数学奥林匹克竞赛训练题:几何部分(2)平面几何计算

数学奥林匹克竞赛训练题:几何部分(2)平面几何计算C2-001 设P是正方形ABCD内的一点,满足PA∶PB∶PC=1∶2∶3,求∠APB.【题说】1979年内蒙古区赛二试题4.【解】作点Q,使CQ=PA,BQ=PB.再连PQ,显然△APB≌△BQC,故∠APB=∠BQC∠ABP=∠CBQ因而△PBQ是等腰直角三角形.且PQ2=PB2=8PA2,因此PC2=9PA2=PQ2+CQ2于是△CPQ是直角三角形,故∠APB=∠BQC=∠CQP+∠PQ BC2-002设N是正九边形,O为其外接圆圆心,PQ和QR是N的两个邻边.A为PQ的中点,B为垂直于QR的半径的中点.试求AO与AB的夹角.【题说】1992年澳大利亚数学奥林匹克题1.【解】设C为垂直于QR的半径与外接圆的交点,则△POC为等边三角形,从而PB⊥OC;又因PA ⊥OA,所以A、B、O、P四点共圆.故∠OAB=∠OPB=30°.C2-003 如图,在等腰△ABC中.AC=BC,∠ACB=40°.在三角形的外部取一点M,使∠MAB=20°,∠MBA=40°,求∠MCB.【题说】1992年友谊杯国际数学竞赛八年级题3.【解】不妨设AC=BC=1,则由余弦定理知AB=2sin20°.再由正C2-004 锐角△ABC的外心为O.线段OA,BC的中点分别为M、N.∠ABC=4∠OMN,∠ACB =6∠OMN.求∠OMN.【题说】1995年日本数学奥林匹克预选赛题3.【解】如图,设∠OMN=θ,则∠ABC=4θ,∠ACB=6θ,∠BAC=180°-10θ,∠NOC=∠BOC /2=∠BAC=180°-10θ,∠MOC=2∠ABC=8θ.从而∠MON=8θ+(180°-10θ)=180°-2θ∠ONM=180°-(∠MON+∠OMN)=θ-∠OMN所以∠OMN为等腰三角形.从而ON=OM=OA/2=OC/2.故∠NOC=60°=180°-10θ,θ=12°.C2-005 一直线与正六边形ABCDEF相交,截出一个△AKN,其中AK+AN=AB.试求∠KAN+∠KBN+∠KCN+∠KDN+∠KEN+∠KFN等于多少度?【题说】第五十八届(1995年)莫斯科数学奥林匹克八年级题6.【解】不妨设点N位于边AB上.点K位于边AF上,由于AK+AN=AB.故FK=AN.分别在边BC、CD、DE、EF上取点P、R、S、T.使得FK=AN=BP=CR=DS=ET(见图).于是∠KBN=∠TAK∠KCN=∠SAT∠KDN=∠RAS∠KEN=∠PAR∠KFN=∠NAP所以∠KAN+∠KBN+∠KCN+∠KDN+∠KEN+∠KFN=∠KAN+∠TAK+∠SAT+∠RAS+∠PAR+∠NAP=∠KAN+∠KAN=2×120°=240°C2-006 锐角△ABC的高AA1、BB1和CC1的中点分别是A2、B2和C2,求∠B2A1C2、∠C2B1A2与∠A2C1B2之和.【题说】第二十一届(1995年)全俄数学奥林匹克九年级题6.【解】设M是AB边的中点.线段MA2和MB2分别是△AA1B和△AB1B的中位线,由此得∠A2MB2=∠ACB设H为△ABC的垂心,则∠HC1M=∠HA2M=∠HB2M=90°,所以M、A2、H、B2、C1都在以HM为直径的圆上,所以∠A2C1B2=∠A2MB2=∠ACB同理∠B2A1C2=∠BAC,∠C2B1A2=∠CBA所以所求的三个角之和等于△ABC三内角之和,即180°.C2-007 设△ABC是一个等腰三角形,其中AB=AC.假如∠B平分线交AC于D,且BC=BD+AD.求∠A度数.【题说】第二十八届(1996年)加拿大数学奥林匹克题4.【解】在BC上取BE=BD.则EC=AD.由分角线定理,有又∠C公用,故△ABC∽△EDC.设∠ABD=∠CBD=α,则∠CDE=∠DCE=2α∠BDE=∠BED=4α从而9α=180°,α=20°∠A=∠CED=5α=100°C2-009 作三边长为a、b、c的三角形ABC的内切圆.又作三条分别平行于这三角形各边的圆的切线.这三条切线从三角形ABC中截得三个新的三角形,再在每个新的三角形中作内切圆,计算这四个圆的面积和.【题说】第六届(1964年)国际数学奥林匹克题3.本题由南斯拉夫提供.【解】考虑一个截得的三角形;比如△APQ.(如图)因△APQ∽△ABC,所以其中r a为△APQ的内切圆半径.因此,所求面积和为(Δ,s分别为△ABC的面积与半周长)C2-010 凸四边形ABCD的边AD和BC延长相交于E.设H和G分别是BD和AC的中点.求△EHG的面积对四边形ABCD面积的比.【题说】第十届(1978年)加拿大数学奥林匹克题4.【解】连AH、CH,有S△EGH=S△ECH-S△GCH-S△EGC因此S△EHG∶S ABCD=1∶4.C2-011A、B、C三点共线并且B在A与C之间,在AC的同一侧分别以AB、BC、AC为直径作半圆,前两个半圆的外公切线的切点分别为U、V,而过点B的公切线与第三个【题说】1980年五国国际数学竞赛题2.本题由卢森堡提供.【解】设EA、EC分别交前两个半圆于U'、V',则四边形EU'BV'是矩形,∠V'U'B=∠EBU'=∠EAB,∠U'V'B=∠ECB,U'V'是两个半圆的公切线,U'即U,V'即V.C2-012 一金工车间的切割工具呈有缺口的圆形,如图所示,圆B点到圆心的距离(以厘米为单位)的平方.【题说】第一届(1983年)美国数学邀请赛题4.OB2=OA2+AB2-2×OA×AB×cos∠OAB=26C2-013 如图,在△ABC内选取一点P,过P作三条分别平行于各边的直线,这样所得到的三个三角形t1、t2、t3的面积,分别是4、9、49.求△ABC的面积,【题说】第二届(1984年)美国数学邀请赛题3.【解】t1,t2,t3的对应边的比:即BH∶AG∶GH=2∶3∶7所以AB∶GH=12∶7S△ABC∶S△PGH=122∶72S△ABC=144C2-014 如图所示,将△ABC的三个顶点与同一个内点连接起来,所得三条连线把△ABC分成6个小三角形,其中4个小三角形的面积已在图上标出.试求△ABC面积.【题说】第三届(1885年)美国数学邀请赛题6.【解】设S△CDP=x,S△AEP=y,则有由(1)、(2)解得x=70,y=56,故S△ABC=315.C2-015 一个梯形被两条对角线分成四个三角形,若用A、B分别表示以梯形上、下底为底边且有公共顶点的两个三角形的面积,求此梯形的面积.【题说】1988年新加坡数学奥林匹克(A组)题8.原题为选择题.【解】如图所示,过三角形A、B的公共顶点引高,分别记为x、y,记另两个三角形的面积为C、D.容易证得:所以梯形的面积=A+B+C+DC2-016 △ABC是面积为1的直角三角形.A'、B'、C'分别是A、B、C关于各自对边的反射(对称)点.求△A'B'C'的面积.【题说】第二十一届(1989年)加拿大数学奥林匹克题2.【解】如图,设C'C交AB于D,延长交A'B'于D',则易知C'D'⊥A'B',AB=A'B'.C'D'=3CD,故C2-017 D、E为△ABC边AB、AC上的点,BE、CD交于P.△ADE、△BPD、△CEP的面积分别是5、8、3,求△ABC的面积.【题说】1994年日本数学奥林匹克预选赛题5.【解】如图,设△PDE、△PBC的面积分别为x、y,则(5+x+3)∶(8+y)=AD∶DB=5∶(x+8)即x2+16x+24=5y (1)又8∶y=DP∶PC=x∶3,即xy=24 (2)由(1)、(2)解得x=2,y=12.从而△ABC的面积为30.C2-018 凸五边形ABCDE中,BE分别交AC、AD于S、R,BD分别交CA、CE于T、P,AD交CE于Q.且△ASR、△BTS、△CPT、△DQP、△ERQ的面积均为1.(1)求五边形PQRST的面积;(2)求五边形ABCDE的面积.【题说】1995年日本数学奥林匹克题3.【解】(1)设五边形PQRST的面积为x.由S△BST=S△ASR得S△BTR=S△ATR,从而BA∥TR.所以同理可得BC∥AD,CD∥BE,DE∥AC,EA∥BD.由AE∥BD得即整理得x2=5(2)由AC∥DE得C2-019 设A'、B'、C'、D'、E',F'分别是六边形ABCDEF的六边AB、BC、CD、DE、EF、FA的中点.试利用△ABC'、△BCD'、△CDE'、△DEF'、△EFA'、△FAB'的面积表示六边形ABCDEF的面积.【题说】1996年城市数学联赛高年级高水平题3.【解】A′是AB的中点,故2S△EFA′=S△EFA+S△EFB同理可得2S△FAB′=S△FAB+S△FAC2S△ABC′=S△ABC+S△ABD2S△BCD′=S△BCD+S△BCE2S△CDE′=S△CDE+S△CDF2S△DEF′=S△DEF+S△DEA另一方面S ABCDE=S△EFA+S△DEA+S△ABD+S△BCD=S△FAB+S△EFB+S△BCE+S△CDE=S△ABC+S△FAC+S△CDF+S△DEFC2-020在一个边长为1的正六边形内部有一点P,已知P到某两【题说】1963年北京市赛高二二试题3.C2-021侦察机沿以A为圆心、半径为10公里的圆周飞行,速度为每小时1000公里.某时刻从A 点发射一枚与飞机具有相同速度的火箭,无论何时火箭总在连结圆心与飞机的直线上,问火箭发射后,什么时间可以追上飞机?【题说】1965年全俄数学奥林匹克十年级题5.【解】设火箭发射时,飞机在Q点,半径AB⊥AQ(如图),以AB为直径作半圆.对半圆上任一点R,延长AR交⊙A于P,连RB,C2-022 给定三个单位圆,两两相切,求切于所有三个圆的圆的半径.【题说】第四届(1972年)加拿大数学奥林匹克题1.【解】设三单位圆心为A、B、C.则△ABC为边长为2的正C2-023 一个矩形桌子长和宽如图所示.一小球从P撞击到Q,反射到R,又从R反射到S,从S反射回原处P,入射角与反射角相等(例如∠PQA=∠RQB等等).试求小球所走的路径的长.【题说】1979年广东省赛二试题4.【解】易知四边形PQRS是平行四边形.由△QBR≌△SDP及△PDS≌△RCS,得因而小球所走路径长为[别解] 利用轴对称可发现所以2(PQ+QR)=34.C2-024设AD为△ABC的高线,求一切△ABC使AB+AC=2cm,【题说】1979年英国数学奥林匹克题1.【解】设x=BD,y=DC,且z=AD,诸线段均指有向线段,使得x+y>0且z>0,则x2+z2≥(2x+z)2/5当且仅当x=2z时,等号成立.当且仅当y=2z时,等号成立.由(3)与(4)得由(1)与(2),(5)中等号成立,因此x=y=2z,故适合这问题的唯一的三角形的边为:C2-025AC、CE是正六边形ABCDEF的两条对角线,点M、N分别内分AC、CE使AM:AC=CN:CE=r.如果B、M、N三点共线,试求r的值.【题说】第二十三届(1982年)国际数学奥林匹克题5.【解】连结BD、ND,将△MBC绕外接圆的圆心O逆时针旋转120°,则重合于△NDE,故知∠BND=120°.以BD为一边向N点另一侧作等边三角形BDG,则N、B、G、D四点共圆且C为此圆的圆心.从而CN=CB.【别解】因B、M、N共线,由梅涅劳斯定理得其中X是AC与BE的交点.设正六边形的边长是1.则C2-026在一个面积为1的正方形中构作一个如下的小正方形:将单位正方形的每条边作n等分,然后将每个顶点和它相对的顶点最接近的分点连接起来.如果小正方形(图中阴影部分)的面积恰为1/1985,求n的值.【题说】第三届(1985年)美国数学邀请赛题4.【解】作EF⊥HB,则Rt△BEF∽Rt△EDA从而即整理得2n2-2n+1=1985或2(n-32)(n+31)=0.解得n=32(负根舍弃)C2-027 如图,AOB是半圆的直径,AC=BC,E为BC中点,一l,求[10l],其中[x]表示不超过x的最大整数.【题说】1986年北京市赛高一题2(7).【解】由已知条件知O、E、F三点共线,且EF为小圈直径.连AE交小圆于K,连FK,易证△EKF∽△ACE.所以EK∶AC=EF∶AE故34.1<10l<34.2 即[10l]=34.C2-028如图所示,S1和S2是直角三角形ABC的两个内接正方形,若S1的面积为441,S2的面积为440,求AC+CB的值.【题说】第五届(1987年)美国数学邀请赛题15.【解】令T1、T2、T′1、T′2、T3表示图c、d中直角三角形面积,S△ABC=S.则S=T′1+T′2+T3+440又设h、h1分别△ABC及T3斜边上高,则而ch=ab=2S于是(a+b)2=a2+b2+2ab所以a+b=21×22=462.【别解】设S1、S2的边长分别为a、b,∠B=θ.则所以a2(1+2sinθcosθ)=b2(sin2θcos2θ+2sinθcosθ+1)记t=sinθcosθ,将a2=441,b2=440代入上式并整理得440t2-2t-1=0AC+BC=(a+a tgθ)+(a+a ctgθ)=462C2-029令P是△ABC的一个内点,延长AP、BP、CP与对边相交,如图,a、b、c、d表示各相应线段的长.已知a+b+c=43,d=3,求abc=?【题说】第六届(1988年)美国数学邀请赛题12.利用三角形面积比.【解】三式相加,得整理后,得2d3+(a+b+c)d2-abc=0由是知abc=2×33+43×33=441C2-030设圆内两弦AB,CD交于圆内一点E.在直线段EB的内部取一点M,然后过点D、E、M 作圆,再过E作此圆的切线分别交【题说】第三十一届(1990年)国际数学奥林匹克题1.本题由印度提供.【解】如图所示,连DA、DM及DB.显然有∠CEF=∠DEG=∠EMD;∠ECF=∠MAD于是△CEF ∽△AMD,从而CE·MD=AM·EF.另一方面,又有∠ECG=∠MBD,于是∠CGE=∠CEF-∠ECG=∠EMD-∠MBD=∠BDM故△CGE∽△BDM,从而GE·MB=CE·MD于是GE·MB=AM·EF,故C2-031十二只完全相同的圆盘放置在半径为1的圆周上,使得这十二只圆盘覆盖这圆周,但没有两只圆盘重叠,所以这十二只圆盘的每一个与它两旁的两只圆盘相切.圆盘的排列如图所示.这十二只圆盘的被任一素数的平方整除.求a+b+c.【题说】第九届(1991年)美国数学邀请赛题11.【解】设小圆半径为r,大圆半径R=1.a+b+c=84+48+3=135C2-032梯形ABCD的边AB=92,BC=50,CD=19,AD=70,且AB∥CD.一圆的圆心P在AB上,且与BC和AD相切,设AP=m/n,其中m和n是互素的正整数,求m+n.【题说】第十届(199年)美国数学邀请赛题9.【解】延长AD和BC交于点Q.因为点P到AQ和BQ之距离C2-033 在正△ABC的边BC、CA、AB上有内分点D、E、F将边分成3∶(n-6)(n>6).线段AD、BE、CF相交所成的三角形面积是正三角形面积的4/49时,求n的值.【题说】1992年日本数学奥林匹克预选赛题6.【解】如图,由梅内劳斯定理知于是所以整理得5n2-64n+192=0即(5n-24)(n-8)=0由于n>6,所以所求的值为8.C2-034图中ABCD为正方形,U、V分别为边AB、CD内部的点.确定使四边形PUQV面积为最大时,U、V的所有可能情况.【题说】第二十四届(1992年)加拿大数学奥林匹克题3.【解】不妨设BU≥CV.显然,△VQC∽△BQU,所以QU≥QC并且V到QC的距离≤B到UQ的距离.在QU上取E,使QE=QC,则S△BUE≥S△VUE,S△VQC=S△VQE又由BU∥CV易知S△BQC=S△QUV,所以S△UBQ+S△VQC=S△BUE+S△BQE+S△VQE≥S△VUE+S△BQC+S△VQE=2S△UQV从而同理相加得当且仅当BU=CV时等号成立.因此,在BU=CV时,四边形PUQV面积最大.C2-035直线l1与l2分别切圆周于点A和点B.在直线l1与l2上分别取1993个点A1,A2,…,A1993与B1,B2,…,B1993,使AA i=(i+1)BB i(i=1,2,…,1993),并且A i B i的延长线与AB的延长线相交于点M i(i=1,2,…,1993).试问:【题说】1993年第十六届哈尔滨市高中数学竞赛二试题1.【解】过点B i作AA i的平行线交AB于点B i′,显然△B i B i′B是等腰三角形,从而BB i=B i′B i,AA i=(i+1)B i′B i,又由B i′B i∥AA i知C2-036 设D是锐角三角形ABC内部的一个点,使得∠ADB=∠ACB+90°并有AC·BD=AD·BC(2)求证△ACD的外接圆和△BCD的外接圆在C点的切线互相垂直.【题说】第三十四届(1993年)国际数学奥林匹克题2.【解】(1)如图a,以BC为边向△ABC外作△CBE∽△CAD,∠DBC+∠CAD=∠ADB-∠ACB=90°.所以△DBE是等腰直角三角形,(2)证明:如图b,设CK是△ACD的外接圆的切线,CL是△BCD的外接圆的切线.则∠LCK=∠LCD+∠KCD=∠CBD+∠CAD=90°即CL⊥CK.C2-037 一个三角形的3条边长及一条高是4个相继的正整数,且这条高将三角形分成的两个直角三角形的边长均为整数.求这三角形的三边长,并证明这是唯一的.【题说】第二十五届(1993)加拿大数学奥林匹克题1.【解】设△ABC中三边及高AD为正整数n,n+1,n+2,n+3.不妨设AB>AC,则AB>AC>AD,故AD=n或n+1.(1)若AD=n+1,则AB=n+3,AC=n+2,BC=n.从而都不是整数.因此满足要求的三角形不存在.①若BC=n+1,则AC=n+2,AB=n+3.这时②若BC=n+2,则AC=n+1,AB=n,这时AC=13,BC=14,AB=15综上所述,满足要求的三角形ABC,只有一解,其边长分别为13、14、15.C2-038在△ABC中,CH为高,R、S分别为△ACH和△BCH的内切圆与CH的切点.若AB=1995,AC=1994,BC=1993,则RS【题说】第十一届(1993年)美国数学邀请赛题15.【解】1997.如图,令△ABC的三边BC、AC、AB分别为a、b、c,CH= h,AH= x,BH= y,两内切圆的半径分别为r1、r2.于是,RS=|RH-SH| =|r1-r2|.又因x2-y2=b2-a2将(2)代入(1),得所以m+n=332+665=997.C2-039设AB为圆的直径.点P不在直线AB上.直线PA、PB分别交圆于U、V.设PU=sPA,PV=tPB,s、t为非负实数.用s、t表出cos∠APB.【题说】第二十六届(1994年)加拿大数学奥林匹克题4.【解】若P在圆外(如图a、b、c),则若P在圆上(如图d),则若P在圆内(如图e),则同理所以C2-040如图,PQ=10,以PQ为直径的圆与一个以20为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外【题说】第十二届(1994年)美国数学邀请赛题2.【解】如图,设大圆圆心为O,则直线PQ过O,设这直线交AB于R,AB=x,那么RO=RQ-OQ=x-10,由勾股定理m+n=8+304=312C2-041在Rt△ABC中,∠C为直角,CD为AB边上的高,D质的正整数,求m+ n.【题说】第十二届(1994年)美国数学邀请赛题10.【解】如图,我们用a、b、c分别表示BC、AC、AB的长度.设p=29,则BD= p3.熟知有a2=p3c因为p是素数,所以,存在自然数x,使a= p2x,c= px2,从而b2=c2-a2=p2x4-p4x2=p2x2(x2-p2)从而,存在正整数y,使x2-p2=y2,故p2=x2-y2=(x-y)(x+ y)因为p是素数,且x-y<x+y,则有x-y=1和x+ y= p2,即因此,m+n=450.C2-042 半径为3和6的两圆互相外切,并内切于一半径为9的圆.半径为9的圆有一条弦是另两圆的公切线.求这弦的长度的平方.【题说】第十三届(1995年)美国数学邀请赛题4.【解】如图,设三圆圆心分别为O1、O、O2,它们在已知弦BC上的射影分别为A1、A、A2.由相切关系易知O1、O、O2共线,并且OO1=9-6=3OO2=9-3=6又易知O1A1、O2A2是两圆的半径,所以O1A1=6,O2A2=3.由定比分点公式BC2=4(OB2-OA2)=4(92-52)=4×4×14=152-1=224C2-043△ABC为等腰三角形,AB=AC,且高AM=11.设在AM上有一点D,使得AD=10,∠BDC=3∠BAC,△ABC的周长可写成【题说】第十三届(1995年)美国数学邀请赛题9.【解】设∠BAM=α,则∠BDM=3α.设tanα=x,由倍角公式易得a+b=11+605=616C2-044在一个半径为42的圆中,两条长为78的弦相交,交点与圆心的距离为18.两条弦将圆的内部分成四个区域,其中两个区域由两条长度不相等的线段围成.这两个区域中任一个的面积能唯一地表成m求m+n+d.【题说】第十三届(1995年)美国数学邀请赛题14.【解】如图,两弦AB,CD长均为78,所以它们关于过交点P的直径EF对称.设圆心为O,AB中点为M,则∠OMA=90°,OM=m+n+d=294+81+3=378C2-046 在已知圆内求作内接等腰三角形,使这个等腰三角形的底与其底上的高的和为极大.【题说】1956年上海市赛决赛题5.【解】如图,任作一圆内接等腰三角形ABC,并作高D,延长AD至E,使DE=BC,则AE为底与底上的高的和.连结EC,由DC∶DE=1∶2知EC的方向确定.在与EC平行的各直线中,能使AE最大,且与圆有公共点时应为圆的切线.因此,作与EC平行的切线切圆于H.连AH并在圆上取I使AI=AH,则△AIH即为所求.C2-047由密度均匀的金属细丝绷成一个三角形框架,求这个三角形框架重心的位置.【题说】1962年成都市赛高三二试题3.【解】边BC、CA、AB的重心即各自的中点D、E、F.问题化为在D、E、F处分别放有质量a、b、c,求D、E、F的重心.P是E、F的重心.从而D、E、F的重心在DP上.同理这重心在∠DEF的平分线上.因此D、E、F 的重心即△DEF的内心G.G也是金属框架的中心.C2-048正n边形(n>5)的最长对角线与最短对角线的差等于边长,求n.【题说】第二届(1968年)全苏数学奥林匹克九年级题1.【解】设a n是边,D n和d n是最长的和最短的对角线.当n=6和n=7时,由三角形两边之差小于第三边,即得D n-d n<a n.当n=8时(如图a),从最短对角线BD的端点向最长的对角线AE作垂线BK和DL.∠ABK=90°-∠BAK=22.5°<30°.所以,AB= a8>2AK=D8-d8.当n=9时(如图b),同理有∠ABK=30°,所以AB= a9=2AK=D9-d9.当n>9时,考虑半径为1的圆的内接正n边形.显然,D n≥D9,d n<d9,a n<a9.因此,D n-d n>D9-d9=a9>an.综上所述,n=9.C2-049一个战士想要查遍一个正三角形(包括边)区域内或边界上有无地雷,他的探测器的有效度等于正三角形高的一半.这个战士从三角形的一个顶点开始探测.问他循怎样的探测路线才能使查遍整个区域的路程最短.【题说】第十五届(1973年)国际数学奥林匹克题4.本题由南斯拉夫提供.【解】设战士从顶点A出发探测正三角形区域ABC,△ABC的高为2d.以B为圆心,d为半径作圆与AB、BC分别交于M、N;C为圆心,d为半径作圆与AC,BC分别交于P、Q.路不短于AD′+D′E′≥AD′+D′E″≥AD+DE,后一个不等式是由于AD+DC≤AD′+D′C.同时由于D与AC的距离为d,可见战士沿路线ADE就可以完成搜索任务,因此ADE就是最短路径.还有C2-050已知两个半径分别为R和r的圆,作出一些不同的梯形ABCD,使得每个圆与梯形的两条腰及一条底边相切.求出腰AB可取的最小长度.【题说】第八届(1974年)全苏数学奥林匹克九年级题2.【解】当⊙O1(R)与⊙O2(r)外离或外切或相交时,才有符合题意的梯形存在.不妨设两圆外切于T点,梯形ABCD的一腰AB分别切⊙O1与⊙O2于E与F,如图,过T点作这两圆的公切线交EF于P点,延长梯形的两腰交于O点.则△O1PE∽△PO2F及△BO1E∽△O2AF,于是,PE·PF= Rr及BE·AF =Rr.所以,梯形的腰长还要R<3r这一附加条件,这样,就不难画出符合题意的梯形ABCD.C2-051E是某圆直径AC上的定点.经过点E,求作弦BD,使四边形ABCD的面积为最大.【题说】第十四届(1980年)全苏数学奥林匹克九、十年级题2.【解】设O为圆心,R为圆的半径,OE= a,则S OED∶S ACD=a∶2RS OEB∶S ABC=a∶2R所以应与直径AC垂直.C2-052已知△ABC的面积为1,设A1、B1和C1分别是边BC、CA和AB的中点,如果K、L和M 分别位于线段AB1、CA1和BC1上,那么△A1B1C1和△KLM的公共部分的最小面积是多少?【题说】第八届(1974年)全苏数学奥林匹克十年级题6.【解】设△A1B1C1的三边与△KLM的三边的交点为D、D1、E、E1、F、F1,如图所示,且它们的公共部分的面于是A1D1≤D1D,因此,S△A1D1F≤S△D1DF同理,S△B1E1D≤S△E1EDS△C1F1E≤S△F1FE所以S△A1B1C1-S≤S△D1DF+S△E1ED+S F1FE=S-S△DEF≤SC2-053在一个面积为32cm2的平面凸四边形中,两条对边和一条对角线的长度之和为16cm,试确定另一条对角线的所有可能长度.【题说】第十八届(1976年)国际数学奥林匹克题1.本题由捷克斯洛伐克提供.【解】设凸四边形ABCD(图a)的面积为32cm2.AB+BD+CD=16cm于是32=S△ABD+S△BCD故式中应取等号,从而AB+CD=DB=8,则AB⊥DB,CD⊥DB(图b).因此,C2-054设三角形三边长为3、4、5,P为这三角形内一点,求P到这三角形三边距离乘积的最大值.【题说】1979年陕西省赛二试题7.【解】如图,设BC=3,CA=4,AB=5.点P到AB、BC、CA的距离分别为x、y、z,因5x+3y+4z=125x·3y·4z=64为最大.故xyz的最大值为16/15.C2-055在已知锐角△ABC中作内接正方形,试求其面积最大者.【题说】1979年云南省赛二试题7.【解】如图,内接正方形MNPQ有两个顶点在BC上.边长为x a,面积为S a,则其中a= BC,h a= AH.设△ABC中,c≥b≥a,熟知a+ h a≥b+ h b≥c+ h a所以在锐角△ABC三边上的三个内接正方形中,最小边上的内接正方形的面积最大.C2-056已知两个等腰直角三角形,将一个的三个顶点分别放在另一个三角形的三条边上,问这两个三角形的面积之比最小值是多少?【题说】第十三届(1979年)全苏数学奥林匹克八、九年级题1.较小三角形的直角顶点位置有两种情况:(1)当放在较大三角形的斜边上时,(如图a)两个三角形直角边的比小于1/2,它们的面积之比不小于1/4.(2)当放在较大三角形的直角边上时(如图b),x2+y2=a2,且C2-057 已知边长为4的正三角形ABC,D、E、F分别是BC、QS,P点在△RQS内及其边上移动,P点到△ABC三边的距离分别记作x、y、z.1.求证:当P点在△RQS的顶点位置时,乘积xyz有极小值.2.求上述乘积的极小值.【题说】1982年全国联赛题4.【解】如图a,第一步,先固定x,考虑yz最小值.即过P作直线l∥BC,当P在l上变化时,yz何时最小?第二步,证两个引理:引理1:z+y+z=定值,这个定值就是△ABC的高.端点处取得最小值.这两个引理很容易证明.由此不难得到结论:如果P′、P″为l上两点,那么当P在区间[P′,P″]上变动时,xyz在端点P′或P″处取得最小值.第三步,扩大P点的变化区域:根据上面所述,当P点在l上变动时,xyz的值在P′或P″处为最小,这里P′、P″是l与△RQS 的边界的交点.但△RQS的边不与△ABC的边平行,因而在P移到△RQS的边界后,不能搬用上述方法再将P′或P″调整为△RQS的顶点.但是我们可以把P′点变化区域由△PQR扩大为图b所示的六边形RR′QQ′SS′,其中RR′∥Q′S∥CA,R′Q∥SS′∥BC,QQ′∥RS′∥AB,也就是说:R′与R关于∠ABC的平分线为对称.S′与R关于∠ACB的平分线为对称,等等.过P作平行于BC的直线l,将P调整为l与六边形RR′QQ′SS′的边界的交点P′(或P″),再将P′调整为顶点R或S′,每一次调整都使xyz的值减小.由于对称,xyz在六个顶点R、R′、Q、Q′、S、S′处的值显然相等,因而命题成立.2.由题易知,△ABE≌△BCF≌△CAD,从而△AER≌△BFQ≌△CDS,△RQS是正三角形.由1,我们只考虑S点x,y,z的取值.求得C2-058 在正方形ABCD的边AB、BC上分别取点P、Q,连接DP、DQ、PQ,分别记△DPQ、△DAP、△DQC和△PBQ的面值?【题说】第二届(1987年)东北三省数学邀请赛题5.【解】不妨设正方形边长为1.如图建立坐标系.设P(0,b)与Q(a,0),于是,C2-059 边长为5的菱形,它的一条对角线的长不大于6,另一条不小于6,求这个菱形两条对角线长度之和的最大值.【题说】1987年全国联赛一试题1(2).原题为选择题.【解】设菱形的两条对角线长分别为x及y,则由已知考虑平行直线族x+y=c.当直线过点(8,6)时,得x+y的最大值14.C2-060在边长为10的正三角形ABC中,以如图所示的方式内接两个正方形(甲、乙两个正方形有一边相重迭,都有一边落在BC上,甲有一顶点在AB上,乙有一顶点在AC上).求这样内接的两个正方形面积和的最小值.【题说】1988年北京市赛高一题3.【解】设甲、乙两正方形的边长分别为x、y,易知BC边上的四条线段之和为:记甲、乙两正方形面积之和为S,则有C2-051E是某圆直径AC上的定点.经过点E,求作弦BD,使四边形ABCD的面积为最大.【题说】第十四届(1980年)全苏数学奥林匹克九、十年级题2.【解】设O为圆心,R为圆的半径,OE= a,则S OED∶S ACD=a∶2RS OEB∶S ABC=a∶2R所以应与直径AC垂直.C2-052已知△ABC的面积为1,设A1、B1和C1分别是边BC、CA和AB的中点,如果K、L和M分别位于线段AB1、CA1和BC1上,那么△A1B1C1和△KLM的公共部分的最小面积是多少?【题说】第八届(1974年)全苏数学奥林匹克十年级题6.【解】设△A1B1C1的三边与△KLM的三边的交点为D、D1、E、E1、F、F1,如图所示,且它们的公共部分的面于是A1D1≤D1D,因此,S△A1D1F≤S△D1DF同理,S△B1E1D≤S△E1EDS△C1F1E≤S△F1FE所以S△A1B1C1-S≤S△D1DF+S△E1ED+S F1FE=S-S△DEF≤SC2-053在一个面积为32cm2的平面凸四边形中,两条对边和一条对角线的长度之和为16cm,试确定另一条对角线的所有可能长度.【题说】第十八届(1976年)国际数学奥林匹克题1.本题由捷克斯洛伐克提供.【解】设凸四边形ABCD(图a)的面积为32cm2.AB+BD+CD=16cm于是32=S△ABD+S△BCD故式中应取等号,从而AB+CD=DB=8,则AB⊥DB,CD⊥DB(图b).因此,C2-054设三角形三边长为3、4、5,P为这三角形内一点,求P到这三角形三边距离乘积的最大值.【题说】1979年陕西省赛二试题7.【解】如图,设BC=3,CA=4,AB=5.点P到AB、BC、CA的距离分别为x、y、z,因5x+3y+4z=125x·3y·4z=64为最大.故xyz的最大值为16/15.C2-055在已知锐角△ABC中作内接正方形,试求其面积最大者.【题说】1979年云南省赛二试题7.【解】如图,内接正方形MNPQ有两个顶点在BC上.边长为x a,面积为S a,则其中a= BC,h a= AH.设△ABC中,c≥b≥a,熟知a+ h a≥b+ h b≥c+ h a所以在锐角△ABC三边上的三个内接正方形中,最小边上的内接正方形的面积最大.C2-056已知两个等腰直角三角形,将一个的三个顶点分别放在另一个三角形的三条边上,问这两个三角形的面积之比最小值是多少?【题说】第十三届(1979年)全苏数学奥林匹克八、九年级题1.较小三角形的直角顶点位置有两种情况:(1)当放在较大三角形的斜边上时,(如图a)两个三角形直角边的比小于1/2,它们的面积之比不小于1/4.(2)当放在较大三角形的直角边上时(如图b),x2+y2=a2,且C2-057 已知边长为4的正三角形ABC,D、E、F分别是BC、QS,P点在△RQS内及其边上移动,P点到△ABC三边的距离分别记作x、y、z.1.求证:当P点在△RQS的顶点位置时,乘积xyz有极小值.2.求上述乘积的极小值.【题说】1982年全国联赛题4.【解】如图a,第一步,先固定x,考虑yz最小值.即过P作直线l∥BC,当P在l上变化时,yz何时最小?第二步,证两个引理:引理1:z+y+z=定值,这个定值就是△ABC的高.端点处取得最小值.这两个引理很容易证明.由此不难得到结论:如果P′、P″为l上两点,那么当P在区间[P′,P″]上变动时,xyz在端点P′或P″处取得最小值.第三步,扩大P点的变化区域:根据上面所述,当P点在l上变动时,xyz的值在P′或P″处为最小,这里P′、P″是l与△RQS 的边界的交点.但△RQS的边不与△ABC的边平行,因而在P移到△RQS的边界后,不能搬用上述方法再将P′或P″调整为△RQS的顶点.但是我们可以把P′点变化区域由△PQR扩大为图b所示的六边形RR′QQ′SS′,其中RR′∥Q′S∥CA,R′Q∥SS′∥BC,QQ′∥RS′∥AB,也就是说:R′与R关于∠ABC的平分线为对称.S′与R关于∠ACB的平分线为对称,等等.过P作平行于BC的直线l,将P调整为l与六边形RR′QQ′SS′的边界的交点P′(或P″),再将P′调整为顶点R或S′,每一次调整都使xyz的值减小.由于对称,xyz在六个顶点R、R′、Q、Q′、S、S′处的值显然相等,因而命题成立.2.由题易知,△ABE≌△BCF≌△CAD,从而△AER≌△BFQ≌△CDS,△RQS是正三角形.由1,我们只考虑S点x,y,z的取值.求得C2-058 在正方形ABCD的边AB、BC上分别取点P、Q,连接DP、DQ、PQ,分别记△DPQ、△DAP、△DQC和△PBQ的面值?【题说】第二届(1987年)东北三省数学邀请赛题5.【解】不妨设正方形边长为1.如图建立坐标系.设P(0,b)与Q(a,0),于是,C2-059 边长为5的菱形,它的一条对角线的长不大于6,另一条不小于6,求这个菱形两条对角线长度之和的最大值.【题说】1987年全国联赛一试题1(2).原题为选择题.【解】设菱形的两条对角线长分别为x及y,则由已知考虑平行直线族x+y=c.当直线过点(8,6)时,得x+y的最大值14.C2-060在边长为10的正三角形ABC中,以如图所示的方式内接两个正方形(甲、乙两个正方形有一边相重迭,都有一边落在BC上,甲有一顶点在AB上,乙有一顶点在AC上).求这样内接的两个正方形面积和的最小值.【题说】1988年北京市赛高一题3.【解】设甲、乙两正方形的边长分别为x、y,易知BC边上的四条线段之和为:。
高中奥赛试题汇编及答案

高中奥赛试题汇编及答案一、数学奥赛试题1. 题目:证明对于任意正整数 \( n \),\( 1^2 + 1 + 2^2 + 2 + \ldots + n^2 + n = \frac{n(n + 1)(2n + 1)}{6} \)。
答案:我们可以使用数学归纳法来证明这个等式。
首先验证 \( n = 1 \) 时等式成立。
然后假设对于 \( n = k \) 时等式成立,即:\[ 1^2 + 1 + 2^2 + 2 + \ldots + k^2 + k = \frac{k(k + 1)(2k + 1)}{6} \]我们需要证明对于 \( n = k + 1 \) 时等式也成立:\[ 1^2 + 1 + 2^2 + 2 + \ldots + k^2 + k + (k + 1)^2 + (k + 1) \]\[ = \frac{k(k + 1)(2k + 1)}{6} + (k + 1)^2 + (k + 1) \]\[ = \frac{k(k + 1)(2k + 1) + 6(k + 1)^2 + 6(k + 1)}{6} \]\[ = \frac{(k + 1)[(2k + 1)k + 6(k + 1) + 6]}{6} \]\[ = \frac{(k + 1)(2k^2 + 7k + 6)}{6} \]\[ = \frac{(k + 1)(k + 3)(2k + 3)}{6} \]这样我们就证明了对于 \( n = k + 1 \) 时等式也成立。
因此,根据数学归纳法,等式对所有正整数 \( n \) 成立。
二、物理奥赛试题1. 题目:一个质量为 \( m \) 的物体从静止开始自由下落,忽略空气阻力。
求物体下落 \( t \) 秒后的速度和位移。
答案:根据自由落体运动的公式,物体下落 \( t \) 秒后的速度\( v \) 为:\[ v = gt \]其中 \( g \) 是重力加速度,通常取 \( 9.8 \, \text{m/s}^2 \)。
全国高中数学联赛二试平面几何赛题精选

历年全国高中数学联赛二试几何题汇总1 (类似九点圆)如图,在锐角∆ABC 中,AB<AC ,AD 是边BC 上的高,P 是线段AD 内一点。
过P 作PE ⊥AC ,垂足为E ,作PF ⊥AB ,垂足为F 。
1O 、2O 分别是∆BDF 、∆CDE 的外心。
求证:1O 、2O 、E 、F 四点共圆的充要条件为P 是∆ABC 的垂心。
证明:连BP 、CP 、1O 2O 、E 2O 、EF 、F 1O 。
因为PD ⊥BC ,PF ⊥AB ,则B 、D 、P 、F 四点共圆,且BP 为该圆的直径。
又因为1O 是∆BDF 的外心,故1O 在BP 上且是BP 的中点。
同理可证,C 、D 、P 、E 四点共圆,且2O 是CP 的中点。
于是,1O 2O 平行于BC ,则∠P 2O 1O =∠PCB 。
因为AF*AB = AP*AD = AE*AC ,所以B 、C 、E 、F 四点共圆。
充分性:设P 是∆ABC 的垂心,由于PE ⊥AC ,PF ⊥AB ,所以,B 、1O 、P 、E 四点共线,C 、2O 、P 、F 四点共线,∠F 2O 1O =∠FCB =∠FEB = ∠FE 1O ,故1O 、2O 、E 、F 四点共圆 必要性:设1O 、2O 、E 、F 四点共圆,则∠1O 2O E + ∠EF 1O = π注意到∠P 2O 1O =∠PCB=∠ACB - ∠ACP ,又因为2O 是直角∆CEP 的斜边中点,也就是∆CEP 的外心,所以∠P 2O E=2∠ACP 。
ABDCEFP1O 2O因为1O 是直角∆BFP 的斜边中点,也就是∆BFP 的外心,从而∠PF 1O =2π - ∠BF 1O = 2π- ∠ABP 因为B 、C 、E 、F 四点共圆,所以∠AFE =∠ACB ,∠PFE =2π- ∠ACB 于是,由∠1O 2O E + ∠EF 1O = π得: (∠ACB - ∠ACP+ 2∠ACP )+ (2π - ∠ABP +2π- ∠ACB) = π , 即∠ABP =∠ACP 。
高考数学平面解析几何专项训练(100题-含答案)

高考数学平面解析几何专项训练(100题-含答案)1.在平面直角坐标系xOy 中,已知点12(1,0),(1,0)F F -,点M 满足12MF MF +=记点M 的轨迹为曲线C .(1)求曲线C 的方程;(2)点T 在直线2x =上,过T 的两条直线分别交C 于,A B 两点和,P Q 两点,且||||||||TA TB TP TQ ⋅=⋅,求直线AB 的斜率与直线PQ 的斜率之和.【答案】(1)2212x y +=(2)0【解析】【分析】(1)根据122MF MF +=,利用椭圆的定义求解;(2)设()2,T m ,直线AB 的参数方程为()2cos ,sin x t y m t θθθ=+⎧⎨=+⎩为参数,与椭圆方程联立,利用参数的几何意义求解.(1)解:因为122MF MF +=,所以点M 的轨迹是以12(1,0),(1,0)F F -为焦点的椭圆,则21,1a c b ===,所以椭圆的方程是2212x y +=;(2)设()2,T m ,直线AB 的参数方程为()2cos ,sin x t y m t θθθ=+⎧⎨=+⎩为参数,与椭圆方程联立()()2222cos 2sin 4cos 4sin 420t m t m θθθθ+++++=,由参数的几何意义知:12,TA t TB t ==,则22122224242cos 2sin 2cos m m t t θθθ++⋅=-=-+-,设直线PQ 的参数方程为:()2cos ,sin x y m λαλλα=+⎧⎨=+⎩为参数,则12,TP TQ λλ==,则22122224242cos 2sin 2cos m m λλααα++⋅=-=-+-,由题意得:222242422cos 2cos m m θα++-=---,即22cos cos θα=,因为αθ≠,所以cos cos θα=-,因为0,0θπαπ<<<<,所以θαπ+=,所以直线AB 的斜率tan θ与直线PQ 的斜率tan α之和为0.2.设n S 是数列{}n a 的前n 项和,13a =,点(),N n S n n n *⎛⎫∈ ⎪⎝⎭在斜率为1的直线上.(1)求数列{}n a 的通项公式;(2)求数列12n n a +⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)21n a n =+(2)152522n n n T ++=-【解析】【分析】(1)根据斜率公式可得出()222n S n n n =+≥,可知13S =满足()222n S n n n =+≥,可得出22n S n n =+,再利用11,1,2n n n S n a S S n -=⎧=⎨-≥⎩可求得数列{}n a 的通项公式;(2)求得1212n n n c ++=,利用错位相减法可求得n T .(1)解:由13a =,点,n S n n ⎛⎫ ⎪⎝⎭在斜率为1的直线上,知1111n S S n n -=-,即()222n S n n n =+≥.当1n =时,113S a ==也符合上式,故22n S n n =+.当2n ≥时,()()221212121n n n a S S n n n n n -⎡⎤=-=+--+-=+⎣⎦;13a =也满足上式,故21n a n =+.(2)解:112122n n n n a n c +++==.则2341357212222n n n T ++=++++ ,所以,3412135212122222n n n n n T ++-+=++++ ,上式-下式得1232211113111213214212422224212n n n n n n n T -++⎛⎫- ⎪++⎛⎫⎝⎭=++++-=+- ⎝⎭- 252542n n ++=-,因此,152522n n n T ++=-.3.椭圆2222:1(0)x y C a b a b +=>>的离心率为3,且过点(3,1).(1)求椭圆C 的方程;(2)A ,B ,P 三点在椭圆C 上,O 为原点,设直线,OA OB 的斜率分别是12,k k ,且1213k k ⋅=-,若OP OA OB λμ=+,证明:221λμ+=.【答案】(1)221124x y +=(2)证明见解析【解析】【分析】(1)由条件可得c a22911a b +=,222c b a +=,解出即可;(2)设()()()112200,,,,,A x y B x y P x y ,由条件可得012012x x x y y y λμλμ=+⎧⎨=+⎩,12123x x y y =-,然后将01212x x x y y y λμλμ=+⎧⎨=+⎩代入椭圆方程可得2222221122121221124124124x y x y x x y y λμλμ⎛⎫⎛⎫⎛⎫+++++= ⎪ ⎪⎝⎭⎝⎭⎝⎭,然后可得答案.(1)因为ca=22911a b +=,222c b a +=所以可解得2a b ⎧=⎪⎨=⎪⎩所以椭圆C 的方程221124x y +=.(2)设()()()112200,,,,,A x y B x y P x yOP OA OB λμ=+ ,012012x x x y y y λμλμ=+⎧∴⎨=+⎩()()222212120011124124x x y y x y λμλμ+++=∴+= 即2222221122121221124124124x y x y x x y y λμλμ⎛⎫⎛⎫⎛⎫+++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222112211124124x y x y +=+= ,,即22121221124x x y y λμλμ⎛⎫+++= ⎪⎝⎭又1212121133y y k k x x ⋅=-∴=- ,即12123x x y y =-,221λμ∴+=4.已知椭圆()2222:10x y C a b a b+=>>,A 、B 分别为椭圆C 的右顶点、上顶点,F 为椭圆C的右焦点,椭圆C 的离心率为12,ABF 的面积为32.(1)求椭圆C 的标准方程;(2)点P 为椭圆C 上的动点(不是顶点),点P 与点M ,N 分别关于原点、y 轴对称,连接MN 与x 轴交于点E ,并延长PE 交椭圆C 于点Q ,则直线MP 的斜率与直线MQ 的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.【答案】(1)22143x y +=(2)是定值,定值为32-【解析】【分析】(1)根据椭圆的离心率可得到a,b,c 的关系,再结合ABF 的面积可得到()a c b -=,由此解得a,b ,可得答案.(2)设直线方程,并联立椭圆方程,得到根与系数的关系式,结合直线MP 的斜率与直线MQ 的斜率之积,代入化简可得答案.(1)由题意得12c a =,则2a c =,b =.ABF 的面积为()1322a cb -=,则()a c b -将2a c =,b =代入上式,得1c =,则2a =,b =,故椭圆C 的标准方程为22143x y +=.(2)由题意可知直线PQ 的斜率一定存在,设直线PQ 的方程为y kx m =+,设()11,P x y ,()22,Q x y ,则()11,M x y --,()11,N x y -,()1,0E x -,联立方程22143x y y kx m ⎧+=⎪⎨⎪=+⎩,得()2223484120k x kmx m +++-=,∴122834kmx x k +=-+,∴()12122286223434km m y y k x x m k m k k ⎛⎫+=++=-+= ⎪++⎝⎭,∴21212263348434MQmy y k k km x x kk ++===-+-+,112PEPQ y k k k x ===,∵11112222MP PE y yk k k x x ====,∴33242MP MQ k k k k ⋅=-⨯=-∴MP MQ k k ⋅为定值32-.【点睛】本题考查了椭圆方程的求法以及直线和椭圆的位置关系,综合考查了学生分析问题,解决问题以及计算方面的能力和综合素养,解答的关键是理清解决问题的思路,并能正确地进行计算.5.已知圆M 过点()1,0,且与直线1x =-相切.(1)求圆心M 的轨迹C 的方程;(2)过点()2,0P 作直线l 交轨迹C 于A 、B 两点,点A 关于x 轴的对称点为A '.问A B '是否经过定点,若经过定点,求出定点坐标;若不经过,请说明理由.【答案】(1)24y x =(2)()2,0-【解析】【分析】(1)根据抛物线的定义计算可得;(2)设直线l 的方程为2x ty =+,()11,A x y 、()22,B x y ,则()11,A x y '-,联立直线与抛物线方程,消元、列出韦达定理,再表示出直线A B '的方程,将12y y +、12y y 代入整理即可得解;(1)解:由题意知动点M 的轨迹C 是以(0,0)O 为顶点,()1,0为焦点,1x =-为准线的抛物线,所以动圆圆心M 的轨迹方程为:24y x =;(2)解:设直线l 的方程为2x ty =+,()11,A x y 、()22,B x y 不妨令21y y >,则()11,A x y '-,联立直线l 与抛物线方程得224x ty y x =+⎧⎨=⎩消去x 得2480y ty --=,则124y y t +=、128y y =-,则直线A B '的方程为()()211121y y y y x x x x +--=--,即()()21212121x x y x y y y x y x -+=+-,则()()()()2121212122ty ty y ty y y y x y ty -++=+-+,()()()2121211222t y y y y y x ty y y y -=+--+,即()()21211222y y y x ty y y y =+--+,所以()42824y tx t t ⋅=-⨯--⨯,即()2y t x =+,令200x y +=⎧⎨=⎩解得20x y =-⎧⎨=⎩,所以直线A B '恒过定点()2,0-;6.已知1F ,2F 是椭圆C :()222104x yb b+=>的左、右焦点,过1F 的直线与C 交于A ,B两点,且22::3:4:5AF AB BF =.(1)求C 的离心率;(2)设M ,N 分别为C 的左、右顶点,点P 在C 上(P 不与M ,N 重合),证明:MPN MAN ∠≤∠.【答案】(2)见解析【解析】【分析】(1)由题意设223,4,5AF m AB m BF m ===,由勾股定理的逆定理可得290BAF ∠=︒,再根据椭圆的定义可求出m 的值,从而可求出12,AF AF 的值,则可得点A 是椭圆短轴的一个端点,进而可求出离心率,(2)由椭圆的对称性,不妨设00(,)P x y,0y ∈,,PMN PNM αβ=∠=∠,则可得0000tan ,tan 22y y x x αβ==+-,然后求出tan tan αβ+,tan tan αβ,再利用正切的两角和公式可得02tan()y αβ+=,由正切函数可求出αβ+的最小值,从而可求出()MPN παβ∠=-+的最大值,进而可证得结论(1)由()222104x y b b+=>,得24a =,得2a =,由题意设223,4,5AF m AB m BF m ===,则22222AF AB BF +=,所以290BAF ∠=︒,因为223451248AF AB BF m m m m a ++=++===,所以23m =,所以22AF =,所以122422AF a AF =-=-=,所以12AF F △为等腰直角三角形,所以点A 是椭圆短轴的一个端点,所以b c =,因为222224b c b a +===,得b c =所以椭圆的离心率为2c e a ==(2)由(1)可得椭圆方程为22142x y +=,则(2,0),(2,0)M N -,因为点A是椭圆短轴的一个端点,所以不妨设A ,由椭圆的对称性,不妨设00(,)P x y,0y ∈,,PMN PNM αβ=∠=∠,则0000tan ,tan 22y y x x αβ==+-,2200142x y +=,所以2200002200001tan tan 22422y y y y x x x y αβ⋅=⋅===+--,00002200000442tan tan 2242y y y y x x x y y αβ+=+===+--,所以0tan tan 4tan()1tan tan y αβαβαβ++==-,所以当0y =tan()αβ+取得最小值由(1)可知290BAF ∠=︒,所以()0,2παβ⎛⎫+∈ ⎪⎝⎭,所以当tan()αβ+取得最小值时,αβ+取得最小值,即点P 与点A 重合时,αβ+取得最小值,此时()MPN παβ∠=-+取得最大,所以MPN MAN∠≤∠7.已知椭圆()2222:10x y C a b a b+=>>的长轴长为,且过点)P(1)求C 的方程:(2)设直线()0y kx m m =+>交y 轴于点M ,交C 于不同两点A ,B ,点N 与M 关于原点对称,BO AN ⊥,Q 为垂足.问:是否存在定点M ,使得·NQ NA 为定值?【答案】(1)221102x y +=(2)存在【解析】【分析】(1)利用待定系数法求方程;(2)联立方程组,结合韦达定理可得直线恒过定点,进而求解.(1)依题意知2a =a =所以C 的方程可化为222110x y b+=,将点)P代入C 得251110b +=,解得22b =,所以椭圆方程为221102x y +=;(2)设点()11,A x y ,()22,B x y ,联立221102x y y kx m ⎧+=⎪⎨⎪=+⎩得,()22215105100k x kmx m +++-=,()()()222104155100km k m ∆=-+->,解得22210m k <+,1221015km x x k -+=+,212251015m x x k -=+,注意到Q ,N ,A 三点共线,NQ NA NQ NA ⋅=⋅,又()NQ NA NB BQ NA NB NA ⋅=+⋅=⋅()()()()1212121222x x y m y m x x kx m kx m =+++=+++()()()()222222212122215102012441515k m k mkx xmk x x mm kk+-=++++=-+++()222221510510415k m m m k--+-=++当()2215105510m m --=-,解得1m =±,因为0m >,所以1m =,此时1NQ NA ⋅=-,满足0∆>,故存在定点()0,1M ,使得1NQ NA ⋅=-等于定值1.【点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.8.已知椭圆C :22221(0)x y a b a b +=>>,4a M b ⎛⎫ ⎪⎝⎭为焦点是22y x =的抛物线上一点,H 为直线y a =-上任一点,A ,B 分别为椭圆C 的上,下顶点,且A ,B ,H 三点的连线可以构成三角形.(1)求椭圆C 的方程;(2)直线HA ,HB 与椭圆C 的另一交点分别交于点D ,E ,求证:直线DE 过定点.【答案】(1)2214x y +=(2)证明见解析【解析】【分析】(1)由椭圆的离心率求出,a c 的关系式,再由,4a M b ⎛⎫⎪⎝⎭为抛物线22=y x 上的点,结合222a b c =+,即可求出椭圆C 的方程.(2)设点()(),20H m m -≠,求得HA ,HB 的方程,与椭圆联立求得,D E 坐标,写出直线DE 的方程,即可求出DE 恒过的定点.(1)由题意知,222224c aa b a b c⎧=⎪⎪⎪=⨯⎨⎪=+⎪⎪⎩,解得21a b c ⎧=⎪=⎨⎪=⎩,∴椭圆C 的方程为2214x y +=.(2)设点()(),20H m m -≠,易知()0,1A ,()0,1B -,∴直线HA 的方程为31y x m =-+,直线HB 的方程为11y x m=--.联立223114y x m x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,得22362410x x m m ⎛⎫+-= ⎪⎝⎭,∴22436D m x m =+,223636D m y m -=+,同理可得284E m x m -=+,2244E m y m -=+,∴直线DE 的斜率为21216m k m-=,∴直线DE 的方程为222241284164m m m y x m m m --⎛⎫-=+ ⎪++⎝⎭,即2121162m y x m -=-,∴直线DE 过定点10,2⎛⎫- ⎪⎝⎭.9.已知点(1,2)M -在抛物线2:2(0)E y px p =>上.(1)求抛物线E 的方程;(2)直线12,l l 都过点12(2,0),,l l 的斜率之积为1-,且12,l l 分别与抛物线E 相交于点A ,C 和点B ,D ,设M 是AC 的中点,N 是BD 的中点,求证:直线MN 恒过定点.【答案】(1)24y x =(2)证明见解析【解析】【分析】(1)将点坐标代入求解抛物线方程;(2)设出直线方程,表达出,M N 的坐标,求出直线MN 的斜率,利用直线斜率之积为-1,求出直线MN 恒过的定点,从而证明出结论.(1)∵点(1,2)M -在抛物线2:2E y px =上,∴2(2)2p -=,∴解得:2p =,∴抛物线E 的方程为:24y x =.(2)由12,l l 分别与E 相交于点A ,C 和点B ,D ,且由条件知:两直线的斜率存在且不为零.∴设1122:2,:2l x m y l x m y =+=+由214,2y x x m y ⎧=⎨=+⎩得:21480y m y --=设()()1122,,,A x y C x y ,则1214y y m +=,∴12M y m =,又2122M x m =+,即()21122,2M m m +同理可得:()22222,2N m m +∴()()212212212212222MN m m k m m m m -==++-+,∴()211121:222MN y m x m m m -=--+即MN :()1212121y x m m m m =--⎡⎤⎣⎦+,∵12,l l 的斜率之积为1-,∴12111m m ⋅=-,即121m m =-,∴121:(4)MN y x m m =-+,即直线MN 过定点(4,0).10.已知抛物线()20x ay a =>,过点0,2a M ⎛⎫ ⎪⎝⎭作两条互相垂直的直线12,l l ,设12,l l 分别与抛物线相交于,A B 及,C D 两点,当A 点的横坐标为2时,抛物线在点A 处的切线斜率为1.(1)求抛物线的方程;(2)设线段,AB CD 的中点分别为,E F ,O 为坐标原点,求证直线EF 过定点.【答案】(1)24x y =;(2)证明见解析.【解析】【分析】(1)结合导数知识,利用切线斜率构造方程可得a ,由此可得抛物线方程;(2)将直线AB 方程代入抛物线方程中,结合韦达定理可确定中点坐标,同理可得CD中点坐标,利用直线方程两点式可得直线EF 方程,化简可知其过定点()0,4.(1)由2x ay =得:21y ax =,则2y x a '=,241x y a=∴==',解得:4a =,∴抛物线方程为:24x y =;(2)由题意知:直线12,l l 的斜率都存在且都不为零,由(1)知:()0,2M ,设直线:2AB y kx =+,代入24x y =得:2480x kx --=,设()11,A x y ,()22,B x y ,则124x x k +=,128x x =-,()21212444y y k x x k ∴+=++=+,AB ∴中点()22,22E k k +;12l l ⊥ ,1:2CD y x k ∴=-+,同理可得:CD 中点222,2F k k ⎛⎫-+ ⎪⎝⎭;EF ∴的方程为:()()222222222222k k y k x k k k ⎛⎫+-+ ⎪⎝⎭-+=-+,化简整理得:14y k x k ⎛⎫=-+ ⎪⎝⎭,则当0x =时,4y =,∴直线EF 恒过定点()0,4.【点睛】思路点睛:本题考查直线与抛物线综合应用中的直线过定点问题的求解,求解此类问题的基本思路如下:①假设直线方程,与抛物线方程联立,整理为关于x 或y 的一元二次方程的形式;②利用0∆>求得变量的取值范围,得到韦达定理的形式;③利用韦达定理表示出已知中的等量关系,代入韦达定理可整理得到变量间的关系,从而化简直线方程;④根据直线过定点的求解方法可求得结果.11.在直角坐标系xOy 中,曲线:C 221x y +=经过伸缩变换x xy '='=⎧⎪⎨⎪⎩后的曲线为1C ,以x 轴正半轴为级轴,建立极坐标系.曲线2C的极坐标方程为sin 4πρθ⎛⎫+= ⎪⎝⎭(1)写出1C 的普通方程和2C 的直角坐标方程;(2)若1C 上的一点P 到2C 的距离的最大,求距离的最大值及P 点的坐标.【答案】(1)1C :2213y x +=,2C :40x y +-=;(2)max d =,1322P ⎛⎫-- ⎪⎝⎭,.【解析】【分析】()1直接利用转换关系,把参数方程,直角坐标方程和极坐标方程之间进行转换;()2利用三角函数关系式的变换和点到直线的距离公式的应用求出结果.(1)解:由伸缩变换x xy '='=⎧⎪⎨⎪⎩得,代入曲线:C 221x y +=得:1C 的普通方程为2213y x +=,由极坐标方程sin 4πρθ⎛⎫+= ⎪⎝⎭sin y ρθ=,cos x ρθ=可得:2C 的直角坐标方程为40x y +-=.(2)解:直线2C 的普通方程为40x y +-=,设1C上的为点()cos P θθ,到2C 的距离为d =当且仅当()223k k Z πθπ=-+∈时,取得max d =,又因为1cos 23y 2x θθ⎧==-⎪⎪⎨⎪==-⎪⎩,即点P 的坐标为1322⎛⎫-- ⎪⎝⎭.12.已知椭圆C :2222+x y a b=1(a >b >0)经过点A (0,1),且右焦点为F (1,0).(1)求C 的标准方程;(2)过点(0,12)的直线l 与椭圆C 交于两个不同的点P .Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N .证明:以MN 为直径的圆过y 轴上的定点.【答案】(1)2212x y +=(2)证明见解析【解析】【分析】(1)由已知得,c b ,再求得a ,即得椭圆方程;(2)由题意直线l 斜率存在,可设直线1:2l y kx =+,设()()1122,,,P x y Q x y ,直线方程代入椭圆方程应用韦达定理得1212,x x x x +,由直线,AP AQ 方程求出,M N 坐标,求出以MN 为直径的圆的方程,然后代入1212,x x x x +求得圆方程的常数项,从而可得y 的定点坐标.(1)由题意可得1,1c b ==从而22a =.所以椭圆的标准方程为2212x y +=.(2)证明:由题意直线l 斜率存在,可设直线1:2l y kx =+,设()()1122,,,P x y Q x y ,将直线l 代入椭圆方程得()2242430k x kx ++-=,所以12122243,,4242k x x x x k k --+==++,直线AP 的方程为1111y y x x -=+,直线AQ 的方程为2211y y x x -=+.可得1212,0,,011x x M N y y ⎛⎫⎛⎫--⎪ ⎪--⎝⎭⎝⎭,以MN 为直径的圆方程为,21212011x x x x y y y ⎛⎫⎛⎫+++= ⎪⎪--⎝⎭⎝⎭,即()()221212121201111x x x x x y x y y y y ⎛⎫++++= ⎪----⎝⎭.①因为()()()1212122121212124111142122x x x x x x y y k x x k x x kx kx ==---++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭22212612842k k k -==--+++.所以在①中令0x =,得26y =,即以MN 为直径的圆过y轴上的定点(0,,13.已知抛物线C :()220y px p =>,过点()2,0R 作x 轴的垂线交抛物线C 于G ,H 两点,且OG OH ⊥(O 为坐标原点).(1)求p ;(2)过()2,1Q 任意作一条不与x 轴垂直的直线交抛物线C 于A ,B 两点,直线AR 交抛物线C 于不同于点A 的另一点M ,直线BR 交抛物线C 于不同于点B 的另一点N .求证:直线MN 过定点.【答案】(1)1p =(2)证明见解析【解析】【分析】(1)由题意知2RG OR ==,不妨设()2,2G ,代入抛物线方程中可求出p 的值,(2)设211,2y A y ⎛⎫ ⎪⎝⎭,222,2y B y ⎛⎫ ⎪⎝⎭,233,2y M y ⎛⎫ ⎪⎝⎭,244,2y N y ⎛⎫⎪⎝⎭,则可表示出直线AB ,AM ,BN 的方程,再由直线AB 过()2,1Q 及直线AM ,BN 过()2,0R 可得()121240y y y y -++=,13244y y y y ==-,再表示出直线MN 的方程,结合前面的式子化简可得结论(1)由题意知,2RG OR ==.不妨设()2,2G ,代入抛物线C 的方程,得44p =解得1p =.(2)由(1)知,抛物线C 的方程为22y x =.设211,2y A y ⎛⎫ ⎪⎝⎭,222,2y B y ⎛⎫ ⎪⎝⎭,233,2y M y ⎛⎫ ⎪⎝⎭,244,2y N y ⎛⎫ ⎪⎝⎭,则直线AB 的斜率为12221212222AB y y k y y y y -==+-.所以直线AB 的方程为2111222y y x y y y ⎛⎫=-+ ⎪+⎝⎭,即()121220x y y y y y -++=.同理直线AM ,BN ,MN 的方程分别为()131320x y y y y y -++=,()242420x y y y y y -++=,()343420x y y y y y -++=,由直线AB 过()2,1Q 及直线AM ,BN 过()2,0R 可得()121240y y y y -++=,13244y y y y ==-.又直线MN 的方程为()343420x y y y y y -++=,即1212441620x y y y y y ⎛⎫+++= ⎪⎝⎭.所以直线MN 的方程为()1212280y y x y y y +++=.把()121240y y y y -++=代入()1212280y y x y y y +++=,得()12122480y y x y y y +++=,()122)880(y y x y y +++=,所以由20x y +=,880y +=可得2x =,1y =-.所以直线MN 过定点()2,1-.14.已知抛物线C :y 2=4x 的焦点为F ,过点F 的直线l 与抛物线C 交于P ,A 两点,且PF λFA = .(1)若λ=4,求直线l 的方程;(2)设点E (a ,0),直线PE 与抛物线C 的另一个交点为B ,且PE EB μ=.若λ=4μ,求a的值.【答案】(1)4340x y --=或4340x y +-=(2)4【解析】【分析】(1)由4PF FA =得014y y =-,设直线l :1x my =+,与抛物线C :24y x =联立,结合韦达定理,即得解;(2)由PF λFA = 得01y y λ=-,结合014y y =-,可得204y λ=,再由PE EB μ= 得02y y μ=-,设直线PB :x ny a =+,与抛物线C :24y x =联立由韦达定理可得024y y a =-,故204y aμ=,又4λμ=,代入运算即得解(1)易知焦点F (1,0),设P (0x ,0y ),A (1x ,1y )由4PF FA =得014y y =-设直线l :1x my =+,与抛物线C :24y x =联立得2440y my --=,其中216160m ∆=+>,所以014y y =-由①②可得0141y y =⎧⎨=-⎩或0141y y =-⎧⎨=⎩又014y y m +=,所以34m =或34m =-所以直线l 的方程为314x y =+或314x y =-+.化简得4340x y --=或4340x y +-=(2)由PF λFA =得01y y λ=-又014y y =-可得204y λ=设点B (2x ,2y ),由PE EB μ= 得02y y μ=-设直线PB :x ny a =+,与抛物线C :24y x =联立得2440y ny a --=.所以216()0n a ∆=+>,024y y a=-故204y aμ=又4λμ=,所以2200444y y a=⋅,考虑到点P 异于原点,所以00y ≠,解得4a =此时2216()16(4)0n a n ∆=+=+>所以a 的值为415.平面直角坐标系xOy 中,双曲线22:136x y C -=的右焦点为F ,T 为直线:1l x =上一点,过F 作TF 的垂线分别交C 的左、右支于P 、Q 两点,交l 于点A .(1)证明:直线OT 平分线段PQ ;(2)若3PA QF =,求2TF 的值.【答案】(1)证明见解析(2)12+【解析】【分析】(1)设直线PQ 的方程为3x ty =+,设点()11,P x y 、()22,Q x y ,将直线PQ 的方程与双曲线的方程联立,列出韦达定理,求出线段PQ 的中点N 的坐标,计算得出ON OT k k =,证明出O 、T 、N 三点共线,即可证得结论成立;(2)由3PA QF =得3PA QF = ,可得出1238x x -+=,变形可得出()()12212184384x x x x x x ⎧++=⎪⎨+-=⎪⎩,两式相乘结合韦达定理可求得2t 的值,再利用两点间的距离公式可求得2TF 的值.(1)解:依题意,3F x ==,即()3,0F ,设()1,2T t ,则直线PQ 的方程为3x ty =+,由22326x ty x y =+⎧⎨-=⎩得()222112120t y ty -++=,设()11,P x y 、()22,Q x y ,则()222210Δ14448210t t t ⎧-≠⎪⎨=-->⎪⎩,故212t ≠,由韦达定理可得1221221t y y t +=--,1221221y y t =-,所以()121226621x x t y y t +=++=--,又直线PQ 分别交C 的左、右支于P 、Q 两点,所以()()()22121212122963339021t x x ty ty t y y t y y t +=++=+++=-<-,故212t >所以PQ 中点为2236,2121t N t t ⎛⎫-- ⎪--⎝⎭,所以2ON OT k t k ==,故O 、T 、N 三点共线,即直线OT 平分线段PQ .(2)解:依题意,由3PA QF =得3PA QF =,则()12133x x -=-,即1238x x -+=,所以()12284x x x ++=,①,()121384x x x +-=,②①×②得()()21212123166416x x x x x x +++-=,所以()22222366963166416212121t t t t+⨯-⨯-=-⨯---,解得28374t +=,或28374t -=(舍去),此时,224412t TF =+=+【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()11,x y 、()22,x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,必要时计算∆;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.16.已知抛物线2:4E y x =,F 为其焦点,O 为原点,A ,B 是E 上位于x 轴两侧的不同两点,且5OA OB ⋅=.(1)求证:直线AB 恒过一定点;(2)在x 轴上求一定点C ,使F 到直线AC 和BC 的距离相等;(3)在(2)的条件下,当F 为ABC 的内心时,求ABC 重心的横坐标.【答案】(1)证明见解析(2)见解析(3)173【解析】【分析】(1)设直线AB 的方程为x my n =+,211(,)4y A y ,222(,)4y B y ,联立24x my n y x =+⎧⎨=⎩,消x 得:2440y my n --=,124y y m +=,124y y n =-,结合向量的数量积,转化求解直线AB 的方程,推出结果.(2)在x 轴上求一定点C ,使F 到直线AC 和BC 的距离相等即CF 平分ACB ∠,即直线AC 与直线BC 关于x 轴对称,根据斜率和为零,从而可得结果;(3)设11(,)A x y ,22(,)B x y ,直线AB 与x 轴交于N ,由题意可得32AC CF AN NF ==,坐标化,结合点在抛物线上可得点的坐标,从而得到结果.(1)设直线AB 的方程为x my n =+,211(,)4y A y ,222(,)4y B y ,联立24x my n y x=+⎧⎨=⎩,消x 得:2440y my n --=,则124y y m +=,124y y n =-,由5OA OB ⋅= 得:21212()516y y y y +=,所以:1220y y =-或124y y =(舍去),即4205n n -=-⇒=,所以直线AB 的方程为5x my =+,所以直线AB 过定点(5,0)P .(2)由(1)知,直线AB 过定点(5,0)P 可设直线AB 的方程为5x my =+,此时124y y m +=,1220y y =-,设x 轴上定点C 坐标为(,0)t ,要使F 到直线AC 和BC 的距离相等,则CF 平分ACB ∠,即直线AC 与直线BC 关于x 轴对称,故0AC BC k k +=,即21210y yx t x t+=--,∴()()21120y x t y x t -+-=,∴()()1212250my y t y y +-+=,∴()40450m m t -+-=对任意m 恒成立,∴510t -=,5t =-,故在x 轴上有一定点C (5,0)-,使F 到直线AC 和BC 的距离相等;(3)设11(,)A x y ,22(,)B x y ,直线AB 与x 轴交于N ,∵F 为ABC 的内心,∴32AC CF AN NF ==,32=,即2211126250x y x +-+=,又2114y x =,∴21122250x x -+=,同理22222250x x -+=,∴12,x x 是方程222250x x -+=的两个根,∴1222x x +=,∴三角形重心的横坐标为1251733x x +-=.17.已知椭圆C 的两个顶点分别为()2,0A -,()2,0B ,焦点在x (1)求椭圆C 的方程;(2)若直线()()10y k x k =-≠与x 轴交于点P ,与椭圆C 交于M ,N 两点,线段MN 的垂直平分线与x 轴交于Q ,求MN PQ的取值范围.【答案】(1)2214x y +=;(2)(4,【解析】【分析】(1)由顶点和离心率直接求,,a b c 即可;(2)先联立直线和椭圆方程,借助弦长公式表示出弦长MN ,再求出垂直平分线和Q 坐标,表示出PQ ,最后分离常数求取值范围即可.(1)由题意知2222,a c a a b c =⎧⎪⎪=⎨⎪=+⎪⎩可得1,2a b ==,故椭圆C 的方程为2214x y +=.(2)由()22114y k x x y ⎧=-⎪⎨+=⎪⎩,可得()2222418440k x k x k +-+-=,设()()1122,,,M x y N x y ,则22121222844,4141k k x x x x k k -+=⋅=++,()121222241k y y k x x k -+=+-=+,线段MN 的中点为2224,4141k k k k ⎛⎫- ⎪++⎝⎭,线段MN 的垂直平分线方程为22214()4141k k y x k k k --=--++,令0y =,得22341kx k =+,所以223,041k Q k ⎛⎫ ⎪+⎝⎭,又(1,0)P ,则22223114141k k PQ k k +=-=++,又12MN x x =-=所以2241141MN k k PQk +==++220,1331k k ≠∴<-<+ ,故MN PQ的取值范围为(4,.【点睛】(1)关键在于建立,,a b c 的关系式求解;(2)关键在于联立直线和椭圆方程,依次求出垂直平分线和弦长MN 、PQ ,转化成关于k 的代数式求范围即可.18.定义平面曲线的法线如下:经过平面曲线C 上一点M ,且与曲线C 在点M 处的切线垂直的直线称为曲线C 在点M 处的法线.设点()()000,0M x y y >为抛物线2:2(0)C y px p =>上一点.(1)求抛物线C 在点M 处的切线的方程(结果不含0x );(2)求抛物线C 在点M 处的法线被抛物线C 截得的弦长||AB 的最小值,并求此时点M 的坐标.【答案】(1)002y py x y =+(2);()p 【解析】【分析】(1)先化简求导确定切线斜率,再按照在点处的切线方程进行求解;(2)先联立法线和抛物线方程,借助弦长公式表示弦长,最后换元构造函数,求导确定最小值.(1)因为点()()000,0M x y y >在抛物线上方,所以由2:2(0)C y px p =>得y =py y'=,所以在点M 处的切线斜率0y y pk y y ='==,所求切线方程为000()py y x x y -=-,又202y x p=,故切线方程为2000()2y p y y x y p -=-,即002y p y x y =+.(2)点M 处的法线方程为2000()2y y y y x p p-=--,即220022y p p x y y p +=-+.联立抛物线2:2(0)C y px p =>,可得()2232000220y y p y y p y +-+=,可知0∆>,设()()1122,,,A x y B x y ,()2221212002,2p y y y y y p y +=-⋅=-+,所以322212202()y p AB y y y +⋅-=.令200t y =>,则3222()(0)t p AB t t +=>,令3222()()(0)t p f t t t +=>,1312222222223()()()(2)2()2t p t t p t p t p f t t t +⋅-++⋅-'=⨯=,所以()f t 在()20,2p 单调递减,在()22,p +∞单调递增,所以()2min ()2f t f p ==,即min AB =,此时点M的坐标为()p .【点睛】(1)关键在于化简出0y >时的抛物线方程,借助求导确定切线斜率;(2)写出法线方程,联立抛物线求弦长是通用解法,关键在于换元构造函数之后,借助导数求出最小值.19.已知点()11,0F -,()21,0F ,M 为圆22:4O x y +=上的动点,延长1F M 至N ,使得1MN MF =,1F N 的垂直平分线与2F N 交于点P ,记P 的轨迹为Γ.(1)求Γ的方程;(2)过2F 的直线l 与Γ交于,A B 两点,纵坐标不为0的点E 在直线4x =上,线段OE 分别与线段AB ,Γ交于,C D 两点,且2OD OC OE =⋅,证明:AC BC =.【答案】(1)22143x y +=;(2)证明见解析.【解析】【分析】(1)由线段垂直平分线和三角形中位线性质可证得12124PF PF F F +=>,可知P 点轨迹为椭圆,由此可得轨迹方程;(2)由已知可知24D C x x =;当l 斜率不存在时显然不成立;当l 斜率存在时,设l 方程,将其与椭圆方程联立,结合韦达定理可得AB 中点横坐标;设():0OE y k x k ''=≠,与直线l 和椭圆方程联立可求得34k k'=-,由此可整理得到C x ,与AB 中点横坐标相同,由此可得结论.(1)连接1,MO PF,PM 是1NF 的垂直平分线,1PF PN ∴=,1222PF PF PN PF NF ∴+=+=;,M O 分别为112,NF F F 中点,224NF MO ∴==,12124PF PF F F ∴+=>,P ∴点轨迹是以12,F F 为焦点,长轴长为4的椭圆,即2a =,1c =,23b ∴=,P ∴点轨迹Γ的方程为:22143x y +=;(2)2OD OC OE =⋅ ,即OD OE OC OD =,D EC Dx x x x ∴=,由题意知:0C x >,4E x =,24D C x x ∴=,①当直线l 斜率不存在时,即:1l x =,此时1C x =,2D x <,此时24D C x x =不成立;②当直线l 斜率存在时,设():1l y k x =-,()11,A x y ,()22,B x y ,由()221431x y y k x ⎧+=⎪⎨⎪=-⎩得:()22223484120k x k x k +-+-=,2122212283441234k x x k k x x k ⎧+=⎪⎪+∴⎨-⎪=⎪+⎩,AB ∴中点的横坐标为21224234x x k k +=+;设直线OE 的方程为:()0y k x k ''=≠,由()1y k x y k x ='=⎧⎨-⎩得:kx k k ='-,即C k x k k ='-;由22143y k xx y =⎧='⎪⎨+⎪⎩得:221234x k ='+,即221234D x k ='+;由24D C x x =得:212434k k k k =''+-,整理可得:34k k '=-,2122434324C x x kk x k k k+∴===++,C ∴为线段AB 的中点,AC BC ∴=.【点睛】关键点点睛:本题考查定义法求解轨迹方程、直线与椭圆综合应用问题;本题证明C 为AB 中点的关键是能够通过已知等式得到,C D 两点横坐标之间满足的等量关系,进而表示出AB 中点横坐标和C 点横坐标,证明二者相等即可.20.已知椭圆()2222:10x y E a b a b +=>>的左、右焦点分别为1F ,2F,离心率2e =,P为椭圆上一动点,12PF F △面积的最大值为2.(1)求椭圆E 的方程;(2)若C ,D 分别是椭圆E 长轴的左、右端点,动点M 满足MD CD ⊥,连结CM 交椭圆于点N ,O 为坐标原点.证明:OM ON ⋅为定值;(3)平面内到两定点距离之比是常数()1λλ≠的点的轨迹是圆.椭圆E 的短轴上端点为A ,点Q 在圆228x y +=上,求22QA QP PF +-的最小值.【答案】(1)22142x y +=;(2)见解析;4.【解析】【分析】(1)结合离心率和12PF F △面积的最大值列出关于,,a b c 的方程,解方程即可;(2)设直线CM 方程,写出点M 坐标,联立椭圆方程,求点N 坐标,通过向量数量积计算即可;(3)设点R 坐标,借助点Q 在圆228x y +=上,将2QA 转化成RA ,再借助椭圆定义将2PF 转化成14PF -,最后通过1,,R P F 三点共线求出最小值.(1)当P 为短轴端点时,12PF F △的面积最大,2bc =,222222,c a bc a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得2,a b c ===,故椭圆E 的方程为22142x y +=.(2)由(1)知,()2,0,(2,0)C D -,设直线():2CM y k x =+,11(,)N x y ,,(2,4)MD CD M k ⊥∴ ,联立221,42(2)x y y k x ⎧+=⎪⎨⎪=+⎩整理得()22222218840k x k x k +++-=,由21284221k x k --=+得2122421k x k -=+,1124(2)21ky k x k =+=+,222244(,)2121k k N k k -∴++,2222442442121k kOM ON k k k -⋅=⨯⨯++ ,故OM ON ⋅为定值4.(3)由题意(A ,设()(0,),,R m Q x y ,使2QA QR =,()()22222,4QR x y m QAx y +-==+,整理得222282833m m x y y --++=,又点Q 在圆228x y +=上,20,883m =∴⎨-⎪=⎪⎩解得m =,(0,R 由椭圆定义得124PF PF =-,2112(4)4QA QP PF QR QP PF QR QP PF +-=+--∴=++-,当1,,R P F三点共线时,(10,,(R F 22QA QP PF +-∴4.【点睛】(1)关键在于建立,,a b c 的方程;(2)关键在于设出直线方程,联立得出点N 坐标;(3)关键在于利用题目中给出的圆的定义将2QA 转化成RA ,再结合椭圆定义,将问题简化成共线问题.21.已知椭圆C :22221(0)x y a b a b+=>>的长轴长为4,点31,2⎛⎫ ⎪⎝⎭在椭圆C 上.(1)求椭圆C 的标准方程;(2)已知O 为坐标原点,P 为椭圆C 上的一个动点,过点E0)作OP 的平行线交椭圆C 于M ,N 两点,问:是否存在实数t (t >0),使得||,||,||EM t OP EN 构成等比数列?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)22143x y +=(2)存在,12t =【解析】【分析】(1)由题意可得2a =,再将点31,2⎛⎫ ⎪⎝⎭代入椭圆方程中可求出2b ,从而可求得椭圆的方程,(2)①当OP 的斜率存在时,设直线OP 的方程为y kx =,将直线方程代入椭圆方程中可求出22,x y ,则可得2OP ,设直线MN的方程为()()1122(,,,y k x M x y N x y =,将直线方程代入椭圆方程消去y ,利用根与系数的关系,再利用两点间的距离公式表示出||,||EM EN ,再计算||||EM EN 与2OP 比较可求出t 的值,②当OP 的斜率不存在时,可得||OP =MN的方程为x ||||EM EN 的值,进而可求出t (1)由题意可得24a =,所以2a =.因为点(1,32)在椭圆C 上,所以221914a b +=,解得23b =.所以椭圆C 的标准方程为22143x y +=.(2)①当OP 的斜率存在时,设直线OP 的方程为y kx =.联立方程,得22143y kxx y =⎧⎪⎨+=⎪⎩解得221234x k =+,2221234k y k =+.解得()2222221211212||343434k k OP k k k+=+=+++,设直线MN的方程为()()1122(,,,y k x M x y N x y =-.联立方程,得(22143y k x x y ⎧=-⎪⎨⎪+=⎩化简,得()22223412120k x x k +=+-=.因为点E0)在椭圆内部,所0∆>,221213221212,3434k x x x x k k-+=⋅=++,所以1||EM x =-.同理可得2||EN x =所以()(())22121212||||113EM EN kx xk x x x x ⋅=+=+⋅++()()22222223112122413343434k k kk k k k +-=+⋅-+=+++,假设存在实数(0)t t >),使得||,||,||EM t OP EN 构成等比数列,则22||||||EM EN t OP ⋅=.所以()()22222311213434k k tk k ++=⋅++.解得214t=.四为1t >,所以12t =,②当OP 的斜率不存在时,||OP =MN 的方程为x =x =22143x y +=,得234y =.所以||||2EM EN ==,当||,||,||EM t OP EN 构成等比数列时,22||||||EM EN t OP ⋅=,即2334t =.因为0t >,所以12t =.综上所述,存在实数12t =,使得||,||,||EM t OP EN 构成等比数列.22.在平面直角坐标系xOy 中,曲线C 的参数方程为x y αααα⎧=-⎪⎨=+⎪⎩(α为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.直线l 的极坐标方程为()cos sin 3m m ρθθ++=l 与曲线C 交于A ,B 两点.(1)求曲线C 的普通方程和直线l 的直角坐标方程;(2)过A ,B 分别作l 的垂线与x 轴交于C ,D 两点,若AB =CD .【答案】(1)2212x y +=,30mx y m ++=;(2)4.【解析】【分析】(1)消参法求曲线C 的普通方程,公式法求直线l 的直角坐标方程.(2)由(1)所得普通方程,结合圆中弦长、半径、弦心距的几何关系求圆心到直线l 的距离,再利用点线距离公式列方程求参数m ,即可得直线的倾斜角大小,由AB 、CD 的关系求CD 即可.(1)由题意,消去参数α,得曲线C 的普通方程为2212x y +=.将cos x ρθ=,sin y ρθ=代入()cos sin 3m m ρθθ++得直线l的直角坐标方程为30mx y m ++=.(2)设圆心到直线l:30mx y m ++=的距离为d,则AB =3d =.3=,解得3m =-.所以直线l的方程为60x +=,则直线l 的倾斜角为30θ=︒.所以4cos30AB CD ==︒.23.在平面直角坐标系xOy中,已知直线340x y ++=与圆1C :222x y r +=相切,另外,椭圆2C :()222210x y a b a b +=>>的离心率为32,过左焦点1F 作x 轴的垂线交椭圆于C ,D 两点.且1CD =.(1)求圆1C 的方程与椭圆2C 的方程;(2)经过圆1C 上一点P 作椭圆2C 的两条切线,切点分别记为A ,B ,直线PA ,PB 分别与圆1C 相交于M ,N 两点(异于点P ),求△OAB 的面积的取值范围.【答案】(1)225x y +=,2214x y +=;(2)4,15⎡⎤⎢⎥⎣⎦.【解析】【分析】(1)由直线与圆的相切关系及点线距离公式求参数r ,即可得圆1C 的方程,根据椭圆离心率、22b CD a=及椭圆参数关系求出a 、b 、c ,即可得椭圆2C 的方程.(2)设()11,A x y 、()22,B x y 、()00,P x y ,讨论直线PA ,PB 斜率存在性,则直线PA 为()111y k x x y =-+、直线PB 为()222y k x x y =-+,联立椭圆方程并结合所得一元二次方程0∆=求1k 、2k ,进而得直线PA 为1114x x y y +=、直线PB 为2214x xy y +=,结合P 在直线PA ,PB 上有AB 为0014x xy y +=,联立椭圆方程,应用韦达定理、弦长公式、点线距离公式,结合三角形面积公式得0OAB S = .(1)由题设,圆1C :222x y r +=的圆心为()0,0,因为直线340x y ++=与圆1C相切,则r ==所以圆1C 的方程为225x y +=,因为椭圆2Cc e a ==c =,由221b CD a==,则22a b =,又222a b c =+,所以22324a a a =+,解得2a =,1b =,所以椭圆2C 的方程为2214x y +=.综上,圆1C 为225x y +=,椭圆2C 为2214x y +=.(2)设点()11,A x y ,()22,B x y ,()00,P x y .当直线PA ,PB 斜率存在时,设直线PA ,PB 的斜率分别为1k ,2k ,则直线PA 为()111y k x x y =-+,直线PB 为()222y k x x y =-+.由()11122440y k x x y x y ⎧=-+⎨+-=⎩,消去y 得:()()()22211111111148440k x k y k x x y k x ++-+--=.所以()()()2222111111116441444k y k x k y k x ⎡⎤∆=--+--⎣⎦.令0∆=,整理得()2221111114210x k x y k y -++-=,则11111122111444x y x y x k x y y --=-==-,所以直线PA 为()11114x y x x y y -=-+,化简得:22111144x x y y y x +=+,即1114x x y y +=.经验证,当直线PA 斜率不存在时,直线PA 为2x =或2x =-也满足1114x xy y +=.同理,可得直线PB 为2214x xy y +=.因为()00,P x y 在直线PA ,PB 上,所以101014x x y y +=,202014x xy y +=.综上,直线AB 为0014x xy y +=.由00221444x xy y x y ⎧+=⎪⎨⎪+=⎩,消去y 得:()22200035816160y x x x y +-+-=.所以01220835x x x y +=+,21220161635y x x y -=+.所以12AB x =-=)20203135y y +==+.又O 到直线AB的距离d ==所以)20200311235OABy S y +=⋅+ t =,[]1,4t ∈,则24444OAB t S t t t∆==++,又[]44,5t t+∈,所以△OAB 的面积的取值范围为4,15⎡⎤⎢⎥⎣⎦.【点睛】关键点点睛:第二问,设点及直线PA ,PB 的方程,联立椭圆结合相切关系求参数关系,进而确定PA ,PB 的方程,由P 在直线PA ,PB 上求直线AB 的方程,再联立椭圆并应用韦达定理、弦长公式、点线距离公式求三角形面积的范围.24.已知点A ,B 是抛物线x 2=2py (p 为常数且p >0)上不同于坐标原点O 的两个点,且0OA OB ⋅= .(1)求证:直线AB 过定点;(2)过点A 、B 分别作抛物线的切线,两切线相交于点M ,记 OMA 、 OAB 、 OMB 的面积分别为S 1、S 2、S 3;是否存在定值λ使得22s =λS 1S 3?若存在,求出λ值;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,4λ=【解析】【分析】(1)设11(,)A x y ,22(,)B x y ,设直线AB 方程为y kx t =+,代入抛物线方程中,消去y ,。
高中奥林匹克竞赛数学平面几何100题——珍藏版

高中数学联赛难度几何题100道第一题:学习证明角平分 (4)第二题:学习证明四点共圆 (5)第三题:学习证明角的倍数关系 (6)第四题:证明线与圆相切 (7)第五题:证明垂直 (8)第六题:证明线段相等 (9)第七题:证明线段为比例中项 (10)第八题:证明垂直 (11)第九题:证明线段相等 (12)第十题:证明角平分 (13)第十一题:证明垂直 (14)第十二题:证明线段相等 (15)第十三题:证明角相等 (16)第十四题:证明中点 (17)第十五题:证明线段的二次等式 (18)第十六题:证明角平分 (19)第十七题:证明中点 (20)第十八题:证明角相等 (21)第十九题:证明中点 (22)第二十题:证明线段相等 (23)第二十一题:证明垂直 (24)第二十二题:证明角相等 (25)第二十三题:证明四点共圆 (26)第二十四题:证明两圆相切 (27)第二十五题:证明线段相等 (28)第二十六题:证明四条线段相等 (29)第二十七题:证明线段比例等式 (30)第二十八题:证明角的倍数关系 (31)第二十九题:证明三线共点 (32)第三十题:证明平行 (33)第三十一题:证明线段相等 (34)第三十二题:证明四点共圆 (35)第三十三题:证明三角形相似 (36)第三十四题:证明角相等 (37)第三十五题:证明内心 (38)第三十六题:证明角平分 (39)第三十七题:证明垂直 (40)第三十八题:证明面积等式 (41)第三十九题:证明角平分 (42)第四十题:证明角相等 (43)第四十二题:证明中点 (45)第四十三题:证明角相等 (46)第四十四题:证明垂直 (47)第四十五题:证明角相等 (48)第四十六题:证明垂直 (49)第四十七题:证明四点共圆 (50)第四十八题:证明四点共圆 (51)第四十九题:证明四点共圆 (52)第五十题:证明角平分 (53)第五十一题:证明线段相等 (54)第五十二题:证明两圆外切 (55)第五十三题:证明垂直 (56)第五十四题:证明垂直 (57)第五十五题:证明垂直 (58)第五十六题:证明垂直 (59)第五十七题:证中点 (60)第五十八题:证明角相等 (61)第五十九题:证明角相等 (62)第六十题:证明四点共圆 (63)第六十一题:证明四点共圆 (64)第六十二题:证明四点共圆 (65)第六十三题:证明角相等 (66)第六十四题:证明角的倍数关系 (67)第六十五题:证明中点 (68)第六十六题:伪旁切圆 (69)第六十七题:证明垂直 (70)第六十八题:证明平行 (71)第六十九题:证明圆心在某线上 (72)第七十题:证明三线共点 (73)第七十一题:证明垂直 (74)第七十二题:证明垂直 (75)第七十三题:证明中点 (76)第七十四题:证明垂直 (77)第七十五题:证明垂直 (78)第七十六题:证明三线共点 (79)第七十七题:证明平行 (80)第七十八题:证明平行 (81)第七十九题:证明三线共点、证明垂直 (82)第八十题:证明三点共线(牛顿定理) (83)第八十一题:证明角平分 (84)第八十二题:证明角相等 (85)第八十三题:证明三点共线 (86)第八十四题:证明四圆共点 (87)第八十六题:证明线段相等 (89)第八十七题:证明角相等 (90)第八十八题:证明线段相等 (91)第八十九题:证明线段相等 (92)第九十题:证明线段相等 (93)第九十一题:证明中点 (94)第九十二题:证明四点共圆 (95)第九十三题:证明西姆松定理及逆定理 (96)第九十四题:证明线段的和差关系等式 (97)第九十五题:证明角相等 (98)第九十六题:证明托勒密定理及逆定理 (99)第九十七题:证明线段的和差关系等式 (100)第九十八题:证明角相等 (101)第九十九题:证明四点共圆 (102)第一百题:证明两三角形共内心 (103)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
【高中数学竞赛专题大全】 竞赛专题9 平面几何(50题竞赛真题强化训练)解析版+原卷版

【高中数学竞赛专题大全】 竞赛专题9 平面几何 (50题竞赛真题强化训练)一、填空题1.(2018·天津·高三竞赛)凸六边形ABCDEF 的6条边长相等,内角A 、B 、C 分别为134°、106°、134°.则内角E 是___________(用度数作答). 【答案】134° 【解析】 【详解】不妨设边长为1,设AC 、DF 的中点分别为M 、N ,且A 在DF 上的射影为K ,则37BAM ∠=︒,97MAF ∠=︒,83AFK ∠=︒,即cos83FK =︒,cos37KN AM ==︒.又设EFN x ∠=,则cos FN x =,利用FN FK KN =+, 我们有cos cos83cos372cos60cos23cos23x =︒+︒=︒︒=︒,因此23x =︒,即等腰△DEF 的底角为23°,可见其顶角E 为134°. 故答案为134°2.(2020·江苏·高三竞赛)在平面直角坐标系xOy 中,直线y kx =与圆C :()()2227365x y -+-=交于A ,B ,则OA OB ⋅=__________.【答案】2020 【解析】 【详解】解析:222020OA OB OC R ⋅=-=. 故答案为:2020.3.(2021·全国·高三竞赛)在ABC 中,ABC ∠所对的旁切圆与边AC 相切于点D ,ACB ∠所对的旁切圆与边AB 相切于点E .若||1,||2AB AC ==,则ADE 面积的最大值为_______.【解析】 【详解】设边BC 、CA 、AB 的长度分别为a 、b 、c ,则11||(),||()22AD a b c AE a c b =+-=+-,故1||||sin 2ADESAD AE A =⋅⋅ 221()sin 8a b c A ⎡⎤=--⋅⎣⎦ 22211sin 282a b c A bc bc ⎛⎫--=⋅+⋅⋅ ⎪⎝⎭2311(1cos )sin 42sin 2cos sin 2sin cos 8222222A A A A A A A =-⋅=⋅⋅=⋅⋅ 故()2222622sin sin sin 2224sin cos 427cos 223332ADEA A A A SAA==⨯⨯⨯⨯⨯, 42222sin sin sin 222+++cos 273332427464A A A A ⎛⎫ ⎪⎪≤⨯⨯= ⎪ ⎪⎪ ⎪⎝⎭, 故338ADES≤(等号在23A π=时取到).故答案为:338. 4.(2021·浙江·高三竞赛)在ABC 中,AB AC BC >>,在M ,N 为AB 上两点,且AN AC =,BM BC =,点P 为ABC 的内心.若75MPN ∠=°,则ACB =∠______.【答案】105 【解析】 【分析】 【详解】证明:连接P A 、PB 、PC 及PM 、PN . 由已知易证△APC ≌△APN ,△BPC ≌△BPM . 从而PC =PN ,PC =PM ,即PM =PN =PC . 故P 为△CMN 的外心,此时有∠MPN =2∠MCN .而∠ACN =90°12-∠A ,∠BCM =90°12-∠B , 故∠ACN +∠BCM =180°12-(∠A +∠B ), 即∠MCN +∠ACB =180°12-(∠A +∠B ), 则∠MCN =∠MCN +∠ACB -∠ACB =(180°-∠ACB )12-(∠A +∠B ) =()12A B ∠∠+-(∠A +∠B ) =12(∠A +∠B ). 故∠MPN =2∠MCN =∠A +∠B =180°-∠C 所以∠C =180°-∠MPN =180°75-︒=105°.故答案为:105°.5.(2021·全国·高三竞赛)设三个不同的正整数a b c 、、成等差数列,且以555a b c 、、为三边长可以构成一个三角形,则a 的最小可能值为________. 【答案】10 【解析】 【分析】 【详解】设,a b k c b k =-=+为正整数,由于以555 a b c 、、为三边长可以构成一个三角形, 则55554235()()10202b k b b k b b k b k k -+>+⇔>++, 所以5410,10b b k b k >>,于是9a b k k =->,即有9110a k ≥+≥. 故答案为:10.6.(2019·贵州·高三竞赛)如图,在△ABC 中,AB =30,AC =20,S △ABC =210,D 、E 分别为边AB 、AC 的中点,∠BAC 的平分线分别与DE 、BC 交于点F 、G ,则四边形BGFD 的面积为________.【答案】1892【解析】 【详解】如图,在△ABC 中,由AG 平分∠BAC 知23CG AC BG AB ==,故35ABG ABCS BG S BC ==.又S △ABC =210,则3321012655ABGABCSS ==⨯=. 由D 、E 分别为边AB 、AC 的中点知12DE BC ,所以△ADF ∽△ABG . 由14ADF ABGS S=,得到632ADFS =,故BGFD S 四边形6318912622=-=. 故答案为:1892. 7.(2018·山东·高三竞赛)若直线65280x y --=交椭圆22221x y a b +=(0a b >>,且2a 、b 为整数)于点A 、C .设()0,B b 为椭圆的上顶点,而ABC 的重心为椭圆的右焦点2F ,则椭圆的方程为______. 【答案】2212016x y += 【解析】 【详解】设()11,A x y ,()22,C x y ,由题意ABC 的重心为椭圆的右焦点2F ,整理得213x x c +=,21y y b +=-. 由()11,A x y ,()22,C x y 在直线65280x y --=上,得到212165y y x x -=-.由()11,A x y ,()22,C x y 在椭圆()222210x y a b a b +=>>上,得到2211221x y a b +=,2222221x y a b+=. 两式相减并整理得()()()()2212122121635y y y y b b a x x x x c +---==⋅+-, 整理得225a bc =. ①因为()11,A x y ,()22,C x y 在直线65280x y --=上, 所以有1165280x y --=,2265280x y --=.将123x x c +=,12y y b +=-代入得()635560c b ⨯---=, 整理得18556c b +=. ②联立①②,且注意到a 、b 为整数,解得2c =,4b =,220a =.故所求的椭圆方程为2212016x y +=.8.(2018·河北·高三竞赛)在△ABC 中,3AC =,sin sin (k 2)C k A =≥,则△ABC 的面积最大值为_____. 【答案】3 【解析】 【详解】由正弦定理将sin sin C k A =变形为c ka =,其中,c AB a BC ==.以线段AC 所在直线为x 轴,以AC 的中点O 为坐标原点建立平面直角坐标系,则33,0,,022A C ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,(),B x y ,由c ka ==两边平方整理得()()()()22222291133104k x k y k x k -+--++-= 因为2k ,所以上述方程可化为为()2222339014k x y x k ++-+=-由此可知点B 的轨迹是以()()2231,021k k ⎛⎫+ ⎪ ⎪-⎝⎭为圆心,以231k r k =-为半径的圆.所以当点B 在圆上运动时,点B 到x 轴的最大距离为半径231kr k =-,所以ABC 的面积()21391321212k S k k k k =⨯⨯=⨯--在2k 上单调递减,所以max 9131222S =⨯=-. 9.(2021·全国·高三竞赛)已知直角梯形ABCD 中,//AB CD ,对角线AC 、BD 相交于O ,90DAB ∠=︒,P 、Q 分别是腰AD 、BC 上的点,且,BPA DPC AQB DQC ∠=∠∠=∠,若23AB CD =,则OPOQ=_________. 【答案】1 【解析】 【分析】 【详解】如图所示,记P 为过O 点在AD 上的垂线的垂足,Q 为过P 点在BC 上的垂线的垂足,下证P 、Q 即为所求. 对P 点,在DP DO CDAP OB AB==,所以有CDP BAP ∽,从而CPD BPA ∠=∠. 对Q ,PQ BC ⊥,所以P 、Q 、C 、D ,P 、Q 、B 、A 均四点共圆, 所以有DQC CPD BPA AQB ∠=∠=∠=∠.设AD 、BC 交于T ,K 为TP 的中点.不妨设5AD =, 则10,2DT DP ==,3,12,6,4,6AP TP KP KD TK =====, 从而23DK DO KT OB ==,所以//OK BT ,所以OK PQ ⊥. 由KP KQ =,所以OP OQ =,从而有1OPOQ=.故答案为:1.10.(2019·山东·高三竞赛)△ABC 中,16,9AB BC CA ===.在△ABC 外部,到点B 、C 的距离小于6的点组成的集合,所覆盖平面区域的面积是______ .【答案】54π【解析】 【详解】分别以点B 、C 为圆心,6为半径作圆,交于三角形外一点D ,连结BD 、CD ; 有5353cos ,cos 7272A BDC =∠=-,故A 、B 、D 、C 四点共圆,所以∠ABD +∠ACD =π. 又易知AB 与圆C 相离,故所求的面积为2个圆的面积去掉半个圆的面积再加上△BCD 的面积等于54π+故答案为:54π 二、解答题11.(2021·全国·高三竞赛)已知ABC 满足60A ∠=︒,E 、F 分别为AB AC 、延长线上的点,且,BE CF BC ACE ==的外接圆与EF 交于不同于E 的点K .证明:点K 在BAC ∠的角平分线上.【答案】证明见解析 【解析】 【详解】设BF 与CE 相交于点T .连结BK 、CK .由BCE BEC ABC ∠+∠=∠,及BC BE =,得12BCE ABC ∠=∠, 类似可得12CBF ACB ∠=∠,故 1()602CTF BCE CBF ABC ACB ∠=∠+∠=∠+∠=︒,因此,A 、B 、T 、C 四点共圆.进而,,180180EBF ACE AKE ABF EBF AKE AKF ∠=∠=∠∠=︒-∠=︒-∠=∠, 所以A 、B 、K 、F 四点共圆.由,EBK CFK BEK FCK ∠=∠∠=∠,及BE FC =,得KBE KFC ≌. 于是KC KE =.因此,KC KE =,即AK 是BAC ∠的角平分线.12.(2021·全国·高三竞赛)如图,在平行四边形ABCD 中,1A 、1C 分别是边AB BC 、上的点,线段1AC 、1CA 交于点P ,1AA P 和1CC P △的外接圆的第二个交点Q 位于ACD △的内部.证明:PDA QBA ∠=∠.【答案】证明见解析 【解析】 【详解】对完全四边形11BC CPAA 用密克定理,知Q 、1A 、B 、C 四点共圆,所以1QCB AAQ APQ ∠=∠=∠. 又因为1PAQ PAQ CBQ ∠=∠=∠,所以PAQ CBQ ∽. 因此AP BC ADPQ QC QC==, 结合1PAD PC B PQC ∠=∠=∠知PAD PQC ∽. 因此PDA PCQ ABQ ∠=∠=∠.13.(2021·全国·高三竞赛)如图,设O 、H 分别为ABC 的外心与垂心,M 、N 分别为BH 、CH 的中点.BB '是ABC 的外接圆的一条直径,如果HONM 是一个圆的内接四边形,证明:12B N AC '=.【答案】证明见解析 【解析】 【分析】如图,设F 为AC 的中点,连接,,,,,,,AH AB B C AO FN OF OM OH '',可证F 、A 、O 、H 四点共圆,从而可证明四边形B FNC '为等腰梯形,故可证12B N AC '=. 【详解】如图,连接,,,AH AB B C AO '',则,AH BC B C BC '⊥⊥,故//AH B C ',同理//AB HC ',故四边形AHCB '为平行四边形设F 为AC 的中点,故B '、F 、H 共线,且F 为B H '的中点, 连接,FN OF ,结合N 为CH 的中点可知,//FN B C '.连接,OM OH ,则//OM B H ',故FHO HOM HNM HCB ππ∠=∠=-∠=-∠, 另一方面,容易得到2FAO ABC HCB π∠=-∠=∠,故FHO FAO π∠+∠=,从而F 、A 、O 、H 四点共圆,从而可知FB C FHA FOA ABC AB C NCB π∠=∠=∠=∠=-=∠'∠'', 从而四边形B FNC '为等腰梯形,进而12B N CF AC ='=,证毕. 【点睛】思路点睛:竞赛中的平面几何,大多数与四点共圆相关,因此需要结合三角形中各类角的性质进行大小关系的转化.14.(2021·全国·高三竞赛)如图,已知锐角ABC 的外接圆为Γ,过B 、C 分别作圆Γ的切线交于点P ,P 在直线BC 、AC 、AB 上的投影分别为D 、E 、F ,DEF 的外接圆与BC 交于点N (不同于点D ),A 在BC 上的投影为M .求证:BN CM =.【答案】证明见解析 【解析】 【分析】 【详解】连结AP 、EF 、DE 、FN .因为,PD BC PF AB ⊥⊥,所以DPF ABC ∠=∠.因为PB 、PC 与O 相切,所以BAC BCP CBP ∠=∠=∠.因此180180PCE ACB PCB ACB BAC ABC DPF ∠=︒-∠-∠=︒-∠-∠=∠=∠. 又因为,PD BC PE AC ⊥⊥,所以PCE PDE ∠=∠. 所以PF //DE ,因此PFE DEF ∠=∠.又因为F 、E 、D 、N 四点共圆,所以BNF DEF ∠=∠. 又因为P 、E 、A 、F 四点共圆,所以BNF PFE PAC ∠=∠=∠. 又因为PCE ABC ∠=∠,所以ACP MBF ∠=∠, 故BFN CPA ∽,所以BN ACBF CP=, 因此cos cos BF BFBN AC AC AC PBF AC ACB CM CP BP=⋅=⋅=⋅∠=⋅∠=. 15.(2021·全国·高三竞赛)如图,已知等腰三角形ABC 中,AB AC =,M 为BC 的中点.D 为线段BM 上一点,E 、F 分别为AC AB 、上的点,且四边形AEDF 为平行四边形.BO 交DE 于点P ,CO 的延长线交DF 的延长线于点Q ,ABC 的外接圆O 交ADM △的外接圆于A 、K 两点.求证:K 、Q 、P 、O 四点共圆. 【答案】证明见解析 【解析】 【分析】 【详解】因为,,OB OA AE FD BF OBA OAB EAO ===∠=∠=∠, 所以OAE OBF △≌△,所以BFO AEO ∠=∠, 所以A 、E 、F 、O 四点共圆,记该圆为ω.又OPE OBA OAE ∠=∠=∠,故有P 在圆ω上,同理Q 也在ω上.ADM △的外接圆圆心N 为AD 的中点,即EF 的中点.又OE OF =,故有ON EF ⊥,所以O 、N 与ω的圆心共线. 所以三圆关于直线ON 对称,故K 也在ω上. 所以K 、Q 、P 、O 四点共圆.16.(2021·全国·高三竞赛)如图,AE 、AF 为圆的两切线,ABC 为圆的一条割线,EF 为切点连线,D 为过C 、B 关于圆的切线的交点,证明:D 、E 、F 共线.【答案】证明见解析. 【解析】 【分析】 【详解】 法一:共圆证法. 作圆心O ,连结AOEF M =,连结MB 、OC .由于DC 、DB 为圆O 的切线,故O 、C 、D 、B 四点共圆. 对Rt AOF 用射影定理2AM AO AF ⇒⋅=.又2AF AB AC AM AO AB AC =⋅⇒⋅=⋅,即M 、O 、C 、B 四点共圆.⇒O 、C 、D 、B 、M 五点共圆,故D 、C 、M 、B 四点共圆.AMB OCB OBC OMC MF ⇒∠=∠=∠=∠⇒平分CMB ∠.又CD BD MF =⇒过D ,即D 、E 、F 共线. 法二:塞瓦定理. 对F 及CDB △用塞瓦定理,sin sin sin 1sin sin sin BDF FCD CBFCDF BCF FBD ∠∠∠⨯⨯=∠∠∠.对E 及CBD 用塞瓦定理,sin sin sin 1sin sin sin BDE DCE EBCCDE ECB EBD∠∠∠⨯⨯=∠∠∠.由于2sin sin ,sin sin BDF FBD FCD CBF BCF FBD CDF CBF ∠∠⎛⎫∠=∠∠=∠⇒= ⎪∠∠⎝⎭.由于2sin sin 180,180sin sin BDE EBC DCE EBC EBD ECB CDE ECB ∠∠⎛⎫∠=︒-∠∠=︒-∠⇒= ⎪∠∠⎝⎭.sin sin sin sin FBD EBC CF CECBF ECB BF BE∠∠=⇔=∠∠.由,CF AC AC CEABF AFC ABE AEC BF AF AE BE⇒===∽∽. 从而D 、E 、F 共线.17.(2021·全国·高三竞赛)如图,在Rt ABC 中,90ACB ∠=︒,G 为重心,P 为射线AG 上一点,满足CPA CAB ∠=∠,Q 为射线BG 上一点,满足CQB ABC ∠=∠,证明:AQG 、BPG 的外接圆的另一个交点在AB 上.【答案】证明见解析. 【解析】 【分析】 【详解】如图,延长CG 与AB 交于点J ,则J 为AB 的中点,故CPA CAB ACG ∠=∠=∠. 从而2ACG APC AG AP AC ⇒⋅=∽. 同理,2BG BQ BC ⋅=.设BPG 的外接圆圆M 与AB 的另一个交点为K , 由圆幂定理知:2AK AB AG AP AC ⋅=⋅=, 所以CK AB ⊥,于是2BK BA BC BG BQ ⋅==⋅.因此A 、K 、G 、Q 四点共圆,所以AQG 、BPG 的外接圆的另一个交点在AB 上. 18.(2021·全国·高三竞赛)如图,设圆内接四边形ABCD 的对角线AC 与BD 交于点P ,并且DA 与CB 交于Q .若PQ AC ⊥,且E 是AB 的中点.求证:PE BC ⊥.【答案】证明见解析 【解析】 【分析】 【详解】过B 作//BF PE 交AC 于F ,连结FQ .则有AP PF =,于是PQ 是AF 的中垂线,故,QA QF = 180180QFA QAF DAC DBC QBP ∠=∠=︒-∠=︒-∠=∠.因此Q 、P 、F 、B 共圆,再由QP PF ⊥,得BF BQ ⊥. 而//BF PE ,故PE BQ ⊥,即PE BC ⊥.19.(2021·全国·高三竞赛)如图,在ABC 中,BC 最短,D 、E 分别在AB AC 、上满足BD CE BC ==,设I 是ABC 内心,O 是ADE 外心,求证:OI BC ⊥.【答案】证明见解析 【解析】 【分析】 【详解】设ABC 的外接圆P ,M 、N 、Q 分别是弧AB AC BC 、、的中点. 如图连结线段,则由BC CE =得MB ME =. 又MA MB =,所以MA ME =,于是MO AE ⊥. 又PN AC ⊥,所以//MO PN .同理//NO PM , 再由PM PN =,即知四边形OMPN 是菱形, 所以MN OP ⊥,并且2sin2AOP PM QB QI =⋅==.另一方面,由鸡爪定理又有MN AI ⊥,所以//OP QI 且OP QI =, 即四边形OPQI 是平行四边形,所以//OI PQ ,所以OI BC ⊥.20.(2021·全国·高三竞赛)如图,锐角ABC 中,D 为边BC 中点,ABD △内切圆与边AB 切一点,E ACD 的内切圆与边AC 切于点F ,若四边形EDFG 为平行四边形,求证:G 在BAC ∠的平分线上.【答案】证明见解析. 【解析】【分析】 【详解】设ABD △的内切圆分别与BD AD 、切H I 于、两点;ACD △的内切圆分别与DC AD 、切于J K 、两点.作平行四边形AGFM ,连结DM ,交AC 于点L ,则FAG AFM ∠=∠, 且,AM GF ED AM GF ED ==∥∥, 所以AEDM 是平行四边形,所以AE DM ∥.又AG MF ∥,所以EAG DMF ∠=∠,所以要证明EAG FAG FML AFM LF LM ∠=∠⇔∠=∠⇔=. 因为D 是BC 的中点,AE DM ∥,所以L 是AC 的中点,且12DL AB =. 因此:2222LM DM DL AE AB =-=-AE EB AI BH =-=-AI BD HD =-+AI BD DK KI =-++.222222LF AF AL AK AL AK AC =-=-=- AK FC AI IK CF AI IK CJ =-=+-=+- AI IK CD DJ AI IK BD DK =+-+=+-+,所以LM LF =,所以AG 是BAC ∠的平分线.21.(2021·全国·高三竞赛)如图,已知圆O 是ABC 的外接圆,切线、BP CP 交于点P ,D 是BC 的中点,K 、L 分别在线段AB AC 、上,且满足KD LD ⊥,连结KP LP 、,求证:2BPC KPL ∠=∠.【答案】证明见解析. 【解析】 【分析】 【详解】如图,过P 作,PM AB PN AC ⊥⊥,垂足分别为M 、N .首先,由题意知PD BC ⊥,则B 、M 、P 、D 共圆,C 、N 、P 、D 共圆, 而90KMD BPD CPD LND A ∠=∠=∠=∠=-︒,则90MKD KDM A ∠+∠=︒+, 而90MKD NLD A ∠+∠=︒+,故NLD KDM ∠=∠,即KDM DLN ∽, 因此KM DNMD NL=. 又因为PMD PBD PCD PND ∠=∠=∠=∠,()18018090MPN A MKD KDM ︒∠=︒-=-∠+∠-︒ 36090LDN KDM MDN =-︒-∠-∠=∠︒.故四边形MPND 为平行四边形,即得KM PM KM PNPN NL MP NL=⇔=, 结合直角,故Rt KMP Rt PNL ∽,即90KPM LPN ∠+∠=︒, 则()901809090KPL MPN A A ∠=∠-︒=︒=︒-︒--. 而1802BPC A ∠=︒-,故2BPC KPL ∠=∠.22.(2021·全国·高三竞赛)点P 为椭圆22221(0)x y a b a b+=>>外一点,过P 作椭圆两条切线PA 、PB ,切点分别为A 、B ,连结AB ,点M 、N 分别为PA 、AB 中点,连结MN 并延长交椭圆于点C ,连结PC 交椭圆于另一点D ,连结ND 并延长交PB 于Q ,证明:Q 为PB 的中点. 【答案】证明见解析. 【解析】 【分析】 【详解】PC 与AB 交于点K .首先证明:P 、D 、K 、C 为调和点列,即||||||||PD KD PC KC =. 设()00,P x y ,则直线AB 方程为00221x x y ya b+=. 设P 、D 、K '、C 为调和点列,且||||K DPD PC K Cλ='='. 设()()()112233,,,,,A x y B x y K x y ',则12123121203,,11,.11x x x x x x y y y y y y λλλλλλλλ⎧-+⎧==⎪⎪⎪⎪-+⎨⎨-+⎪⎪==⎪⎪-+⎩⎩ 故()()()()1212121203032222211x x x x y y y y x x y y a b a b λλλλλ-+-+⎡⎤+=+⎢⎥-⎣⎦22222112222222111x y x y ab a b λλ⎡⎤⎛⎫=+-+=⎢⎥ ⎪-⎝⎭⎣⎦,所以K '在直线AB 上,即K '与K 重合,结论成立. 下面证明原题:由梅涅劳斯定理可知1CN MA PKNM AP KC⋅⋅=, 又由12AM AP =,可知2CN CK NM PK=, ① 由直线上托勒密定理可知,CD KP CK PD CP DK ⋅=⋅+⋅,由P 、D 、K 、C 四点调和可知,CK PD CP DK ⋅=⋅,故2CD KP CK PD ⋅=⋅,即2CD CKPD KP= ② 结合①、②可知,CN CD NM PD=.故//ND PM . 又N 为AB 的中点,所以Q 为PB 的中点.23.(2021·全国·高三竞赛)如图,在锐角ABC 中,AB AC >,D 、E 分别是AB 、AC 的中点,ADE 的外接圆与BCE 的外接圆交于点P (异于E ),ADE 的外接圆与BCD △的外接圆交于点Q (异于D ),证明:AP AQ =.【答案】证明见解析 【解析】 【分析】 【详解】连结BP 、DE 、QC 、PE 、DQ 、PD ,由于D 、E 分别是边AB 、AC 的中点可知//DE BC ,则180APD AED DAE ADE DAE DBC ∠=︒-∠=∠+∠=∠+∠180180DQE DQC EQC =︒-∠+︒-∠=∠,180BPD BPE DPE ACB DAE ∠=∠-∠=-∠-∠︒ ABC ADE APE AQE =∠=∠=∠=∠,APB APD BPD EQC EQA AQC ∠=∠+∠=∠+∠=∠,且:1sin sin 21sin sin 2PBD PADAP PB PD BPD AP AP SBPD BP BP SAPD BP PA PD APD ⎛⎫⋅⋅⋅∠ ⎪⋅∠⎝⎭===⋅∠⎛⎫⋅⋅⋅∠ ⎪⎝⎭1sin sin 21sin sin 2AQE CQECQ AQ AE AQE CQ S AQE CQCQE AQ SAQAQ CQ QE CQE ⎛⎫⋅⋅⋅∠ ⎪⋅∠⎝⎭====∠⋅⎛⎫⋅⋅⋅∠ ⎪⎝⎭, 所以APB CQA ∽,所以:AQP ADP PBD BPD QAE AQE QEC APQ ∠=∠=∠+∠=∠+∠=∠=∠,所以AP AQ =.24.(2019·江西·高三竞赛)如图所示,BE 、CF 分别是锐角三角形△ABC 的两条高,以AB 为直径的圆与直线CF 相交于点M 、N ,以AC 为直径的圆与直线BE 相交于点P 、Q .证明:M 、N 、P 、Q 四点共圆.【答案】见解析 【解析】 【详解】如图,设△ABC 的垂心为H ,则()()MH HN MF HF NF HF ⋅=-+ ()()MF HF MF HF =-+22MF HF =-()22AF FB AH AF =⋅--2AF AB AH =⋅- ①同理有2PH HQ AE AC AH ⋅=⋅-, ②因B 、C 、E 、F 四点共圆,知 AF AB AE AC ⋅=⋅ ③ 故由①、②、③式得MH HN PH HQ ⋅=⋅. 所以M 、N 、P 、Q 四点共圆.25.(2019·山东·高三竞赛)已知:正方形ABCD 的边长为1点M 是边AD 的中点以M 为圆心AD 为直径作圆,点E 在线段AB 上,且直线CE 与圆相切.求△CBE 的面积. 【答案】38【解析】 【详解】设直线CE 与圆Γ相切于点N ,连结ME 、MN 、MC .在Rt △MNC 和Rt △MDC 中,MC =MN ,m =MC ,所以△MNC ≌△MDC ,故∠NMC =∠DMC . 同理∠EMN =∠AME .所以∠EMC =90°. 故MN 是Rt △EMC 斜边上的高,所以EN MNNM NC =,故14EN =. 所以13,44AE BE ==.因此△CBE 的面积等于38.26.(2018·江西·高三竞赛)如图,ABC 的内心为I ,D 、E 、F 分别是边BC 、CA 、AB 的中点,证明:直线DI 平分DEF 的周长.【答案】见解析 【解析】 【详解】如图①,不妨设AB AC ≥,ABC 的内切圆切BC 、CA 、AB 于T 、1K 、2K .图①过T 作内切圆的直径TK ,过K 作I 的切线分别交AC 、AB 于M 、N ,则NM BC . 由于I 是AMN 的旁切圆,12AK AK =,因1MK MK =,2NK NK =, 所以有AM MK AN NK +=+.延长AK 交BC 于G ,则BG CT =,因此DT DG =, 故DI 是TGK 的中位线,所以DP AG ,因四边形BDEF 为平行四边形,所以DEP ∽ABG ,相似比为12DE AB =. 同理,DEP ∽ACG ,相似比为12DF AC =. 又注意AMK ∽ACG ,ANK ∽ABG ,相似比均为AKAG, 既然有AM MK AN NK +=+,所以AC CG AB BG +=+, 因此,DF FP DE EP +=+,即所证结论成立. 附注 在几何题中用到三角形内切圆的一个基本性质. 如图②,在ABC 中,内切圆I 切BC 于D ,设DH 是I 的直径,若AH 交BC 于M ,则BM CD =. 证明:过H 作EF BC ,点E 、F 分别在AB 、AC 上.设I 的半径为r ,HF x =,CD y =,EH z =,BM t =,MD d =,连结BI 、CI 、EI 、FI ,由于CI 、FI 分别平分一对互补角BCF ∠、EFC ∠, 所以90CIF ∠=︒,且CDI ∽IHF ,则y rr x=,2xy r =. 同理BDI ∽IHE ,则t d rr z +=,()2z t d r +=, 所以()xy z t d =+,则x t dz y+=. ①又由EF BC ,得x AH z y d AM t ==+,所以x y d z t +=, ② 根据①②式得,t d y dy t ++=,所以22t td y yd +=+,即()()0y t y t d -++=, 由此得,0y t -=,即t y =,也就是BM CD =.(同时也有CM BD =.)27.(2018·福建·高三竞赛)如图,在锐角ABC 中,E 、E 是边BC 上的点,ABC 、ABD △、ADC 的外心分别为O 、P 、Q .证明:(1)APQ ∽ABC ;(2)若EO PQ ⊥,则QO PE ⊥. 【答案】(1)见解析(2)见解析 【解析】 【详解】(1)如图,连结PD 、QD .因为P 、Q 分别为ABD 、ADC 的外心,所以PQ 为线段AD 的垂直平分线. 所以12APQ APD ABD ABC ∠=∠=∠=∠,12AQP AQD ACD ACB ∠=∠=∠=∠.故APQ ∽ABC .(2)如图,连结OA 、OB 、OP 、PB 、QC .延长OQ 与AC 相交于点F . 由O 、P 、Q 分别为ABC 、ABD 、ADC 的外心, 知OP 、OQ 、PQ 分别是线段AB 、AC 、AD 的垂直平分线. 所以()22APB APD BPD ABD BAD ADC AQC ∠=∠+∠=∠+∠=∠=∠. 又OBP OAP ∠=∠,1122AQF AQC APB APO ∠=∠=∠=∠.所以A 、P 、O 、Q 四点共圆,OAP OQP ∠=∠.又EO PQ ⊥,DQ PQ ⊥,所以EO DA ,12OEC ADC APB BPO ∠=∠=∠=∠.所以P 、B 、E 、O 四点共圆,OEP OBP ∠=∠. 设EO 、QO 的延长线分别与PQ 、PE 相交于M 、N ,则OEP OBP OAP OQP ∠=∠=∠=∠.故M 、N 、E 、Q 四点共圆. 又EO PQ ⊥,所以90QNE QME ∠=∠=︒.故QO PE ⊥.28.(2019·全国·高三竞赛)在ABC ∆中,设∠C=90°,CD AB ⊥,垂足为D ,P 、Q 分别为ADC ∆、BDC ∆的内心,PQ 与CD 交于点K ,记ABC ∆的面积为S.证明:22111CK CD S-=. 【答案】见解析 【解析】 【详解】如图,延长PQ ,分别与AC 、BC 交于点M 、N ,联结DP 、DQ 、CP. 分别过M 、N 作CD 的平行线与BC 、AC 的延长线交于点F 、E. 易知,Rt ADC Rt CDB ∆~∆.又P 、Q 分别为ADC ∆、BDC ∆的内心, 故AC DPRt ACB Rt PDQ QPD BAC BC DQ=⇒∆~∆⇒∠=∠ A D P M ⇒、、、四点共圆45CMN ADP CM CN ⇒∠=∠=︒⇒=.易证Rt CPM Rt CPD ∆≅∆. 于是,CM=CD=CN.由∠FMC=∠ACD ,CM=DC Rt FCM Rt ADC MF AC ⇒∆≅∆⇒=. 类似地,NE=BC. 根据三平行线定理得222111111121CK MF NE AC BC CK AC AC BC BC=+=+⇒=++⋅. 再由直角三角形恒等式得222111CD AC BC =+,12S AC BC=⋅. 故22111CK CD S-=.29.(2018·全国·高三竞赛)如图,1O 与2O 的半径相等,交于X 、Y 两点. ABC ∆内接于1O ,且其垂心H 在2O 上,点Z 使得四边形CXZY 为平行四边形.证明:AB 、XY 、HZ三线共点.【答案】见解析 【解析】 【详解】如图,设1O 、2O 的半径为R ,XY 的中点为M. 则点Z 与C 关于M 对称,点1O 与2O 关于M 对称. 因此,点Z 在2O 上.记ABH ∆的外接圆为3O ,其半径为1R .则()12sin 2sin 2sin AB AB ABR R AHB ACB ACBπ====∠-∠∠.接下来证明:Z 为2O 与3O 的交点(异于H ).由1O 、2O 、3O 的半径均为R ,知四边形12XO YO 、四边形31AO BO 均为菱形. 记AB 中点为N ,则N 也为13O O 的中点. 注意到,H 与1O 分别为ABC ∆的垂心与外心. 故1132CH O N OO ==,即13CO HO =. 因为,XZ CY =.所以,22O Z O X XZ =+ 113YO CY CO HO =+==. 又H 为2O 、3O 的一个交点,则Z 为两圆另一交点. 于是,AB 、XY 、HZ 恰为1O 、2O 、3O 两两的公共弦. 由根轴定理知AB 、XY 、HZ 三线共点.30.(2021·全国·高三竞赛)如图,以AB 为直径的圆上有C 、D 两点,AC 、BD 两点的中点为E 、F ,直线EF 与直线AD 、BC 分别交于G 、H ,求证:以FG 为直径的圆和以EH 为直径的圆有一交点在CD 上.【答案】证明见解析 【解析】 【详解】取D 关于AB 的对称点D ,延长D C '与BA 交于I 点,则IAC ID B IDB '.因为AC 、BD 两点的中点为E 、F ,所以IAE IDF ,而IACID B ',故ICB IEF IAD ,所以IBC IFE IDA ∠=∠=∠,所以I 、D 、G 、F 四点共圆.又ICB IEF ∠=∠,所以IEH ICH ∠=∠,所以I 、E 、C 、H 四点共圆,注意到90HDA GDF ∠=∠=︒, 故EH 、FG 为直径的圆过I .取I 关于HE 的对称点I ',则EH 、FG 为直径的圆交于I 、I ', 则I '、H 、I 、E 、C 五点共圆,所以I CH ICH BCD BCD ∠=∠==∠'∠'. 所以I '在CD 上,即以FG 为直径的圆和以EH 为直径的圆有一交点在CD 上.31.(2021·全国·高三竞赛)如图所示,在等腰ABC 中,AB AC =,设点D 是边AC 上一点,点E 是线段BD 的中点,延长AE 与底边BC 交于点F ,证明:若BF EF =,求证:2AE AB AD =⋅.【答案】证明见解析 【解析】 【详解】证法1:设ABD △的外接圆为Γ,其中弧BD 的中点为N , 如图1,连结BN ,DN ,AN 与BD 交于点M .易见AN 平分BAC ∠,从而AN BC ⊥.又由于ABM AND ∠=∠,故ABM AND ∽,进而得到 AM AN AB AD ⋅=⋅.另一方面,由垂径定理可知NE BD ⊥.因此909090()ANE EMN AMD ABM BAM ∠=︒-∠=-∠=︒-∠+∠()90BAM ABD ABC ABD EBF =︒-∠-∠=∠-∠=∠. 注意到AEM BEF EBF ∠=∠=∠,故ANE AEM ∠=∠. 这说明ANE AEM ∽,从而得到2AE AM AN AB AD =⋅=⋅.证法2:设BCE 的外接圆为Ω,圆心为O ;如图2,连结OB OC 、OE OF 、、;连结OA 与线段BC BD 、分别交于点N 、G ,取边AB 的中点M ,连结MN CE FG 、、.由条件及OB OE =可知,OF 垂直平分BE ,即OF BG ⊥. 同理BF OG ⊥,因此F 是OBG △的垂心,从而FG OB ⊥.另一方面,E 是BD 的中点,而MN 是ABC 的中位线,因此M 、E 、N 三点共线, 由塞瓦定理,我们有1AG NF BMGN FB MA⋅⋅=, 注意到BM MA =,因此AG BFGN FN=,从而//FG AB . 综上可知AB OB ⊥,因此Ω与边AB 相切于点B . 再由对称性,Ω必然与边AC 相切于点C ,因此 ACE CBE BEF AED ∠=∠=∠=∠,从而ACE AED ∽.故2AE AC AD AB AD =⋅=⋅.32.(2021·全国·高三竞赛)如图,在锐角ABC 中,已知点D 、E 、F 分别是点A 、B 、C 在边BC 、CA 、AB 上的投影,AEF 、BDF 的内心分别为1I 、2I ,1ACI 、2BCI 的外心分别为1O 、2O ,证明:1212//I I O O .【答案】证明见解析 【解析】 【详解】设,,CAB A ABC B BCA C ∠=∠=∠=,1AI 、2BI 的延长线交于点I . 由1AI 、2BI 分别为CAB ∠、ABC ∠的角平分线知I 为ABC 的内心.因为点E 、F 均在以BC 为直径的圆上,所以,AEF ABC AFE ACB ∠=∠∠=∠, 则AEF ABC ∽,相似比cos AEA AB=. 又因为1I 、I 分别为AEF 、ABC 的内心,所以1cos I A IA A =. 故211(1cos )2sin2A II IA I A IA A IA =-=-=,同理,222sin 2B II IB =.在ABI △中,由正弦定理知sinsin 22A BIA IB =,则 22122sin 2sin 22A B II IA IA IB II IB ⎛⎫⎛⎫⋅===⋅ ⎪ ⎪⎝⎭⎝⎭,故A 、B 、2I 、1I 四点共圆,且I 关于1O 、2O 等幂.于是,CI 是1O 与2O 的根轴.故12CI O O ⊥.设CI 与12I I 交于点Q ,则1112II Q I IQ II I ACI CAI ∠+∠=∠+∠+∠ 2ABI ACI CAI =∠+∠+∠90222B C A=++=︒. 因此12CI I I ⊥,从而1212//I I O O .33.(2021·全国·高三竞赛)如图,AB 是O 的一条弦,AB 的垂直平分线交O 于M N 、两点,交AB 于点D .P 为O 内一点,DMP 外接圆交PN 于点,E ABE 的外接圆交MP 于点F ,且点M P E F 、、、在直线AB 同侧.证明:EF PN ⊥.【答案】证明见解析 【解析】 【详解】延长MF 交O 于点G ,直线NG 交AB 于点H .因为90MDH MGH ∠=∠=︒,所以M D G H 、、、四点共圆. 又M D E P 、、、四点共圆,所以NG NH ND NM NE NP ⋅=⋅=⋅.于是P E G H 、、、四点共圆,所以90HEP ∠=︒.设HE 交MP 于点F ',则90HEN HGF ∠=∠'=︒,所以E N G F '、、、四点共圆. 又A B G N 、、、四点共圆,于是···HE HF HN NG HA HB '==, 所以A B F E '、、、四点共圆,于是F F =',故90FEP ∠=︒,即EF PN ⊥.34.(2021·全国·高三竞赛)如图,锐角ABC 的外接圆为Γ,D 是A 在BC 上的射影,假设AD BC =,点M 为DC 中点,ADC ∠的角平分线与AC 交于点N ,Γ上一点P 满足//BP AC .直线DN 与AM 交于点F ,直线PF 与圆Γ再交于点Q .直线AC 与PNQ 的外接圆再交于点E .证明:90DQE ∠=︒.【答案】证明见解析. 【解析】 【详解】先证明//QC AB .事实上设Q '在Γ上异于C ,//Q C PB '只要证Q '、F 、P 共线. 易知AP AQ BC AD ==='.设A 关于M 的对称点为,A AA ''另交Γ于T ,则 ,CTM ABM CTD ABA MTD MBA '⇒'∽∽∽.因为BC AD A C ==',故45A BC '∠=︒即45MTD FDA ∠=︒=∠, 因此222AF AT AD AP AQ '⋅===, 知Q '、F 、P 三点共线,故Q '、Q 重合. 再证A 、N 、D 、P 共圆,事实上由119090()22APD DAP CAP CAD ∠=︒-∠=︒-∠-∠()190901352C C C =︒-∠-︒+∠=︒-∠ CND =∠,即得.因此结合AP AD =知,NA 是DNP ∠的外角平分线,故设D 关于AC 的对称点为D ,则D 、N 、P 共线.设PQ 与AC 交于点K ,则22AK AC AP AD ⋅==, 故,,DD AC PQ '共点K .因为90AD C ADC ∠=∠='︒,故A 、D 、C 、D 共圆. 故KQ KP KC KA KD KD D ⋅=⋅=⋅⇒''、Q 、D 、P 共圆, 从而QEN QPN QDK ∠=∠=∠,于是Q 、K 、D 、E 共圆, 所以90EQD EKD ∠=∠=︒.35.(2021·浙江·高三竞赛)如图,O 是ABC 的外接圆,D 是弧BC (不含A )上一点,S 为弧BAC 的中点.P 为线段SD 上一点,过P 作DB 的平行线交AB 于点E ,过P 作DC 的平行线交AC 于点F ,过O 作SD 的平行线交弧BDC 于点T .已知O 上的点Q 满足QAP ∠被AT 平分.证明:QE QF =.【答案】证明见解析 【解析】 【分析】 【详解】设M 是弧BDC 的中点,OT ,SD 分别与BC 交于点K ,L .由πAEP AFP ABD ACD ∠+∠=∠+∠=知A ,E ,P ,F 共圆.由ASP ACD AFP ∠=∠=∠知S ,A ,P ,F 共圆,即S ,A ,E ,P ,F 五点共圆. 注意SEF SAF SBC ∠=∠=∠,同理πSFE SAE SCB ∠=-∠=∠可知SEF 与SBC △相似.因此SE SB SF SC=,即SE SF =. π22TAC TOC TKC KCO DLC A ⎛⎫∠=∠=∠-∠=∠--∠ ⎪⎝⎭πππ222A DBC BDS A DSC A -⎛⎫⎛⎫⎛⎫∠+∠--∠=∠+--∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭12DSC A =∠+∠由AT 平分QAP ∠可知:11222QAC TAC PAC DSC A PSF A FSC ∠=∠-∠=∠+∠-∠=∠+∠因此1122QSF QSC FSC QAC FSC A ESF ∠=∠-∠=∠-∠=∠=∠.即QS 是ESF ∠的平分线,结合SE SF =可知SQ 是EF 的垂直平分线,故QE QF =. 36.(2021·全国·高三竞赛)在锐角ABC 中,D 为边BC 上一定点,P 为AD 边上一动点,直线CP 交AB 于点Q ,DQ 交BP 于点X .BCX 、CAX 、ABX 的三个外接圆分别交DQ 于X 外的另三点1Y 、2Y 、3Y ,过1Y 、2Y 、3Y 分别作DQ 垂线1l 、2l 、3l ,证明:1l 、2l 、3l 均过定点.【答案】证明见解析. 【解析】 【分析】 【详解】连结AX 并延长交BC 于E .对ABD △和点X ,由赛瓦定理得1BE DP AQED PA QB⋅⋅=. 对ABD △和截线CPQ ,由梅涅劳斯定理得1BC DP AQCD PA QB⋅⋅=. 结合两式有BE BCED CD=,所以E 为定点,延长BC 至1B 使得1CB CB =,这样有11,BE B C BD B DED CD ED CD==. 所以11XD DY BD CD B D ED ⋅=⋅=⋅,进而X 、E 、1Y 、1B 四点共圆.所以11DY B DEX DEA ∠=∠=∠为定角.又D 、1B 为定点,所以1Y 在过D 的定圆上运动,取该圆上D 的对径点1D (直径的另外一个端点),则1D 为定点,且1D 在直线1l 上.又2CY D CAX CAE ∠=∠=∠为定角,C 、D 为定点,所以2Y 在过D 的定圆上运动,取该圆上D 的对径点2D ,则2D 为定点,且2D 在直线2l 上,又33BY D BY X BAX BAE ∠=∠=∠=∠为定角,B 、D 为定点,所以3Y 在过D 的定圆上运动,取该圆上D 的对径点3D ,则3D 为定点,且3D 在直线3l 上. 命题得证.37.(2021·全国·高三竞赛)在ABC 中,点P 、Q 、R 分别位于边BC 、CA 、AB 上,A ω、B ω、C ω分别是AQR 、BRP △、CPQ 的外接圆,线段AP 与A ω、B ω、C ω分别相交于点X 、Y 、Z .证明:YX BPXZ PC=.【答案】证明见解析. 【解析】 【分析】 【详解】设圆A ω与B ω交于异于点R 的点N (三角形密克点),则P 、N 、Q 、C 共圆. 设直线AP 与直线RN 交于点K ,直线AP 与直线QN 交于点M ,设,NPX NRY NXA BRK αβ∠=∠=∠=∠=, 由于sin sin sin sin sin sin MNP MNXMP SNP MNP CMX S NX MNX PAQβα⋅∠===⋅∠∠,sin sin sin sin sin sin KRY ARKKY SRY KRY PAB AK SRA ARK B αβ∠∠===∠.我们有sin sin sin sin sin sin KY MP PAB C AB PAB BP AK MX B PAQ AC PAQ CP⋅∠⋅⋅∠===⋅⋅∠⋅∠.另一方面由PK KY KN KR AK KX ⋅=⋅=⋅得()AP KY AK KP KY AK KY AK XK AK XY ⋅=+=⋅+⋅=⋅.同理由MZ MP MN MQ MX MA ⋅=⋅=⋅得: ()MP XZ MP XM MZ MP XM MP MZ ⋅=⋅+=⋅+⋅MP XM MA XM MX AP =⋅+⋅=⋅因此XY KY MP XZ AK MX =,由此得到YX BPXZ PC=. 38.(2021·全国·高三竞赛)点O 是ABC 的外接圆圆心,含点A 的BC 的中点为S ,点T 在不包含点A 的BC 上.点M 在圆O 上且//SM OT .点P 在线段SM 上.过点P 作MB 的平行线交AB 于点F ,过点P 作MC 的平行线交AC 于点E .点Q 在圆O 上,使得AT 是PAQ ∠的角平分线.证明:QE QF =.【答案】证明见解析 【解析】 【分析】 【详解】因为,FP BM EP CM ∥∥,所以sin sin sin sin FB PMB PMC ECPM FBM ECM PM∠∠===∠∠,即FB EC =. 又SB SC =,且SBF SCE ∠=∠,故SBF SCE ≌,所以SF SE =.于是,要证QE QF =,只需证SQ EF ⊥.又由SBF SCE ≌知,SFA SEA ∠=∠,故S A F E 、、、四点共圆. 而180AFP AEP ABM ACE ∠+∠=∠+∠=︒,故A F P E 、、、四点共圆. 从而S A F P E 、、、、五点共圆.则:180ESQ SEF ESP PSQ SAF ∠+∠=∠+∠+︒-∠1902EAP MAQ BAC =∠+∠+︒-∠1902EAP MAT TAQ BAC =∠+∠+∠+︒-∠1902EAT MAT BAC =∠+∠+︒-∠190902CAT JAT BAC =∠+∠+-∠=︒︒.其中,S T 、关于QO 对径点分别为J K 、. 则JT KS TM ==,即SQ EF ⊥.故QE QF =. 证毕.39.(2021·全国·高三竞赛)如图,在ABC 中,A B C ∠≥∠≥∠,且AD 为BC 边上的高,BE 为AC 边上的中线,CF 为C ∠的平分线,AD 与CF BE 、分别交于P R 、两点,BE 与CF 交于Q 点,令PQR ABCS x S=.求证:16x <,且16是最好的界(即可以无限接近于16).【答案】证明见解析.【解析】 【分析】 【详解】由A B C ∠≥∠≥∠,知B C ∠∠、均为锐角,可知D 在边BC 上,且BD CD ≤. 连结AQ 并延长交BC 于S .由CF 平分C ∠,得AF ACFB BC=, 又A B ∠≥∠,从而知1AC BC ≤,得1AFFB ≤. 由塞瓦定理得1BS CE AF SC EA FB ⋅⋅=,可知1BS FB SC AF=≥,得BS SC ≥, 所以如图S 在BC 的中点的右边,而D 在BC 的中点左边,综上可得D 在线段BS 上.由D 在BS 上,知Q 在ADC 内,连DE 交CP 于O 点,由CP 平分C ∠,有,PD CD OD CDAP AC OE CE ==. 将1,2AC CD CE AC >=代入上式可得21,2PD OD CDAP OE AC<=<, 所以12,23PD OD AD DE <<,故13OPD ADES PD OD S AD DE ⋅=<⋅. 由AE EC =,可知16OPD ACDSS<. 又,OPDPQR ACDABC SSSS≥≤知16PQR OPD OPD ABCABCACDS S S x SSS=≤≤<. 若令1AC BC ==,则AF BF =,而AE CE =,得Q 为ABC 的重心, 16BFQ ABCS S=,16BFQ BFPR BFPR ABC ABCS S S x S S -==-. 令0C ∠→,则0ABD ABCSS→,知0BFPRABC S S →,故16x →,且x 可无限接近16. 40.(2021·全国·高三竞赛)设ABC 的内心为点I ,内切圆分别切BC CA AB 、、于D E F 、、.直线DF 与EI 交于点N .连结并延长BN ,交AC 于点M .求证:M 是AC 中点.【答案】证明见解析【解析】【分析】【详解】过N 作AC 平行线,分别交AB BC 、于P Q 、,连结ID IF IP IQ 、、、.由IN AC ⊥得IN PQ ⊥,又IF AB ⊥,因此F P N I 、、、四点共圆.因此IFN IPN ∠=∠,同理IDN IQN ∠-∠.又由ID IF =知IDN IFN ∠=∠,从而IPN IQN ∠=∠,即IP IQ =.再由IN PQ ⊥可得PN QN =.再由PQ AC ∥得PN BN QN AM BM CM==,因此,AM CM M =是AC 中点. 41.(2021·全国·高三竞赛)已知O 上依次四点A 、B 、C 、D ,射线AB DC 、交于点P .射线AD BC 、交于点Q ,弦AC BD 、交于点R ,点M 为线段PQ 的中点.过点O 作MR 的垂线,分别PQ MR 、于点U 、V .过点U 作O 的切线UK ,与O 切于点K .证明:(1)P 、Q 、V 、O 四点共圆;(2)K 、M 、R 三点共线.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】【详解】 首先证明一个引理:引理:已知O 上依次四点E 、F 、G 、H ,直线EF GH 、交于点X ,直线EH FG 、交于点Y ,直线EG 、FH 交于点Z ,则点O 为XYZ 的垂心.引理的证明:注意到X 、Y 、Z 分别是直线YZ ZX XY 、、关于O 的极点,从而OX YZ ⊥,,OY ZX OZ XY ⊥⊥,即O 是XYZ 的垂心. 回到原题,由引理知O 是PQR 的垂心.设OP QR ⊥于点0P ,OQ RP ⊥于点0,Q OR PQ ⊥于点0R ,直线00P Q 与PQ 交于点0U , 则P 、0P 、0Q 、Q 四点共圆,且圆心为M .由引理知M 为0OU R 的垂心,则0MR OU ⊥.由题意,MR OU ⊥知U 与0U 重合,从而V 、O 、0P 、R 、0Q 五点均在以OR 为直径的圆上. 故00UV UO UQ UP UQ UP P ⋅=⋅=⋅⇒、Q 、V 、O 四点共圆.由090RVU RR U ∠=∠=︒知U 、V 、R 、0R 四点共圆,推出002OV OU OR OR OP OP r ⋅⋅===⋅,其中r 为O 的半径,最后一步是由配极原理得到.在直线MR 上取点0K ,满足20VK VO VU =⋅.则090OK U ∠=︒,且220OK OU OV r ⋅==,即0UK 为O 的切线,故K 与0K 重合,K 、M 、R 三点共线.42.(2020·全国·高三竞赛)如图,在等腰ABC 中,AB BC =,I 为内心,M 为BI 的中点,P 为边AC 上一点,满足3AP PC =,PI 延长线上一点H 满足MH PH ⊥,Q 为ABC 的外接圆上劣弧AB 的中点.证明:BH QH ⊥.【答案】证明见解析.【解析】【分析】取AC 的中点N ,结合已知条件证得//QM CN ,再由三角形边之间的比例关系证得三角形相似,可得四点共圆,即得证.【详解】证明:取AC 的中点N .连接QB 、QM ,由3AP PC =,可知P 为NC 的中点.易知B ,I ,N 共线,90INC ∠=︒.由I 为ABC 的内心,可知CI 经过点Q ,且QIB IBC ICB ABI ACQ ABI ABQ QBI ∠=∠+∠=∠+∠=∠+∠=∠,又M 为BI 的中点,所以QM BI ⊥.进而//QM CN .。
高中数学联赛真题分类平面解析几何C辑(原卷版)

备战2021年高中数学联赛之历年真题汇编(1981-2020)专题17平面解析几何C 辑历年联赛真题汇编1.【2020高中数学联赛A 卷(第01试)】在平面直角坐标系中,点A ,B ,C 在双曲线xy =1上,满足△ABC 为等腰直角三角形.求△ABC 的面积的最小值.2.【2020高中数学联赛B 卷(第01试)】在椭圆Γ中,A 为长轴的一个端点,B 为短轴的一个端点, F 1,F 2为两个焦点.若AF 1⃗⃗⃗⃗⃗⃗⃗ ⋅AF 2⃗⃗⃗⃗⃗⃗⃗ +BF 1⃗⃗⃗⃗⃗⃗⃗ ⋅BF 2⃗⃗⃗⃗⃗⃗⃗ =0,求tan∠ABF 1⋅tan∠ABF 2的值.3.【2019高中数学联赛A 卷(第01试)】在平面直角坐标系xOy 中,圆Ω与抛物线Γ:y 2=4x 恰有一个公共点,且圆Ω与x 轴相切于Γ的焦点F .求圆Ω的半径.4.【2019高中数学联赛B 卷(第01试)】在椭圆中,F 为一个焦点,A 、B 为两个顶点若|F A |=3,|FB|=2,求AB 的所有可能值.5.【2018高中数学联赛B 卷(第01试)】如图所示,在平面直角坐标系xOy 中,A 、B 与C 、D 分别是椭圆Γ:x 2a2+y 2b 2=1(a >b >0)的左、右顶点与上、下顶点.设P ,Q 是Γ上且位于第一象限的两点,满足OQ ∥AP ,M是线段AP 的中点,射线OM 与椭圆交于点R .证明:线段OQ ,OR ,BC 能构成一个直角三角形.6.【2017高中数学联赛B 卷(第01试)】在平面直角坐标系xOy 中,曲线C 1:y 2=4x ,曲线C 2:(x −4)2+y 2=8.经过C 1上一点P 作一条倾斜角为45°的直线l ,与C 2交于两个不同的点Q 、R ,求|PQ|⋅|PR|的取值范围.7.【2015高中数学联赛(第01试)】在平面直角坐标系xOy 中,F 1,F 2分别是椭圆x 22+y 2=1的左、右焦点.设不经过焦点F 1的直线l 与椭圆交于两个不同的点A ,B ,焦点F 1到直线l 的距离为d .如果直线AF 1,l ,BF 1的斜率依次成等差数列,求d的取值范围8.【2014高中数学联赛(第01试)】平面直角坐标系xOy中,P是不在x轴上的一个动点,满足条件:过P可作抛物线y2=4x的两条切线,两切点连线l与PO垂直.设直线l与直线PO,x轴的交点分别为Q,R.(1)证明R是一个定点;(2)求|PQ||QR|的最小值.9.【2013高中数学联赛(第01试)】在平面直角坐标系xOy中,椭圆的方程为x2a2+y2b2=1(a>b>0),A1,A2分别为椭圆的左、右顶点,F1,F2分别为椭圆的左、右焦点,P为椭圆上不同于A1和A2的任意一点.若平面中两个点Q,R满足QA1⊥PA1,QA2⊥PA2,RF1⊥PF1,RF2⊥PF2,试确定线段QR的长度与b的大小关系,并给出证明.10.【2012高中数学联赛(第01试)】在平面直角坐标系xOy中,菱形ABCD的边长为4,且|OB|=|OD|=6.(1)求证:|OA|⋅|OC|为定值;(2)当点A在半圆M:(x-2)2+y2=4(2≤x≤4)上运动时,求点C的轨迹.11.【2011高中数学联赛(第01试)】作斜率为13的直线l与椭圆C:x236+y24=1交于AB两点(如图所示),且P(3√2,√2)在直线l的左上方.(1)证明:△P AB的内切圆的圆心在一条定直线上;(2)若∠APB=60°,求△P AB的面积.12.【2010高中数学联赛(第01试)】已知抛物线y2=6x上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+ x2=4.线段AB的垂直平分线与x轴交于点C,求△ABC面积的最大值.13.【2009高中数学联赛(第01试)】设直线l:y=kx+m(其中k,m为整数)与椭圆x216+y212=1交于不同两点A,B,与双曲线x24−y212=1交于不同两点C,D,问是否存在直线l使得向量AC⃗⃗⃗⃗⃗ +BD⃗⃗⃗⃗⃗⃗ =0,若存在,指出这样的直线有多少条?若不存在,请说明理由.14.【2008高中数学联赛(第01试)】如图,P是抛物线y2=2x上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.15.【2007高中数学联赛(第01试)】已知过点(0,1)的直线l与曲线C:y=x+1x(x>0)交于两个不同点M和N.求曲线C在点M,N处的切线的交点轨迹.16.【2006高中数学联赛(第01试)】给定整数n≥2,设M0(x0,y0)是抛物线y2=nx-1与直线y=x的一个交点.试证明对于任意正整数m,必存在整数k≥2,使(x0m,y0m)为抛物线y2=kx-1与直线y=x的一个交点.17.【2005高中数学联赛(第01试)】过抛物线y=x2上的一点A(1,1)作抛物线的切线,分别交x轴于D,交y轴于B.点C在抛物线上,点E在线段AC上,满足AEEC =λ1;点F在线段BC上,满足BFFC=λ2,且λ1+λ2=1,线段CD与EF交于点P.当点C在抛物线上移动时,求点P的轨迹方程.18.【2004高中数学联赛(第01试)】在平面直角坐标系xOy中,给定三点A(0,43),B(−1,0),C(1,0),点P到直线BC的距离是该点到直线AB,AC距离的等比中项.(1)求点P的轨迹方程;(2)若直线l经过△ABC的内心(设D),且与点P的轨迹恰好有3个公共点,求l的斜率k的取值范围. 19.【2002高中数学联赛(第01试)】已知点A(0,2)和抛物线y2=x+4上两点B,C使得AB⊥BC,求点C的纵坐标的取值范围.20.【2001高中数学联赛(第01试)】设曲线C1:x2a2+y2=1(a为正的常数)与C2:y2=2(x+m)在x轴上方有一个公共点P.(1)求实数m的取值范围(用a表示);(2)O为原点,若C与x轴的负半轴交于点A,当0<a<12时,试求△OAP的面积的最大值(用a表示).21.【2000高中数学联赛(第01试)】已知C0:x2+y2=1和C1:x2a2+y2b2=1(a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C0外切,与C1内接的平行四边形?并证明你的结论22.【1999高中数学联赛(第01试)】给定A(-2,2),已知B是椭圆x225+y216=1上的动点,F是左焦点,当|AB|+53|BF|取最小值时,求B的坐标.23.【1998高中数学联赛(第01试)】已知抛物线y2=2px及定点A(a,b),B(-a,0)(ab≠0,b2≠2pa),M是抛物线上的点,设直线AM,BM与抛物线的另一交点分别为M1,M2.求证:当点M在抛物线上变动时(只要M1,M2存在且M1≠M2),直线M1M2恒过一个定点,并求出这个定点的坐标.24.【1993高中数学联赛(第01试)】设0<a<b,过两定点A(a,0)和B(b,0)分别引直线l和m,使之与抛物线y2=x有四个不同的交点,当这四点共圆时,求这种直线l与m的交点P的轨迹.25.【1991高中数学联赛(第01试)】设O为抛物线的顶点,F为焦点,且PQ为过F的弦,已知OF=a,PQ= b,求△OPQ的面积.优质模拟题强化训练1.易知椭圆E:x2a2+y2b2=1(a>b>0),其短轴为4,离心率为e1.双曲线x2m−y2n=1(m>0,n>0)的渐近线为y=±x,离心率为e2,且e1⋅e2=1.(1)求椭圆E的方程;(2)设椭圆E的右焦点为F,过点G(4,0)斜率不为0的直线交椭圆E于M、N两点设直线FM和FN的斜率为k1,k2,试判断k1+k2是否为定值,若是定值,求出该定值;若不是定值,请说明理由.2.如图,椭圆C1:x24+y2=1,抛物线C2:x2=2py(p>0),设C1,C2相交于A、B两点,O为坐标原点.(1)若△ABO的外心在椭圆上,求实数p的值;(2)若△ABO的外接圆经过点N(0,132),求实数p的值.3.如图所示,设k>0且k≠1,直线l:y=kx+1与l1:y=k1x+1关于直线y=x+1对称,直线l与l1分别交椭圆E:x24+y2=1于点A、M和A、N.(1)求k⋅k1的值;(2)求证:对任意的实数k,直线MN恒过定点.4.已知椭圆C:x2a2+y2b2=1(a>b>0)的左右焦点分别为F1、F2,右顶点为A,P为椭圆C上任意一点.已知PF1⃗⃗⃗⃗⃗⃗⃗ ⋅PF2⃗⃗⃗⃗⃗⃗⃗ 的最大值为3,最小值为2.(1)求椭圆C的方程;(2)若直线l:y=kx+m与椭圆C相交于M、N两点(M、N不是左右顶点),且以MN为直径的圆过点A.求证:直线l过定点,并求出该定点的坐标.5.已知椭圆C:x2a2+y2b2=1过点M(0,2),且右焦点为F(2,0).(1)求椭圆C的方程;(2)过点F 的直线l 与椭圆C 交于A,B 两点,交y 轴于点P .若PA =mAF,PB =nBF ,求证:m +n 为定值; (3)在(2)的条件下,若点P 不在椭圆C 的内部,点Q 是点P 关于原点O 的对称点,试求三角形QAB 面积的最小值. 6..已知点F 是椭圆x 21+a 2+y 2=1(a >0)右焦点,点M(m,0)、N(0,n)分别是x 轴、y 上的动点,且满足MN ⃗⃗⃗⃗⃗⃗⃗ ⋅NF ⃗⃗⃗⃗⃗ =0,若点P 满足OM ⃗⃗⃗⃗⃗⃗ =2ON ⃗⃗⃗⃗⃗⃗ +PO ⃗⃗⃗⃗⃗ . (1)求P 点的轨迹C 的方程;(2)设过点F 任作一直线与点P 的轨迹C 交于A 、B 两点,直线OA 、OB 与直线x =−a 分别交于点S 、T (其中O 为坐标原点),试判断是否为定值?若是,求出这个定值;若不是,请说明理由.7.设O 是坐标原点,双曲线C :x 2a2−y 2b 2=1上动点M 处的切线,交C 的两条渐近线于A 、B 两点.⑴求证:△AOB 的面积S 是定值; ⑵求△AOB 的外心P 的轨迹方程.8.已知离心率为12的椭圆的左焦点F 1为抛物线y 2=4px(p >0)的准线与x 轴的交点,右焦点F 2也为抛物线的焦点,椭圆与抛物线在x 轴上方的交点为P ,延长PF 1,与该抛物线交于点Q ,M 为抛物线上一个动点,且M 在点P 与Q 之间运动.若ΔPF 1F 2的边长恰为三个连续的正整数,求ΔMPQ 面积的最大值. 9.如图,已知⊙G:(x −2)2+y 2=r 2是椭圆x 216+y 2=1的内接△ABC 的内切圆,其中,A 为椭圆的左顶点.(1)求⊙G 的半径r ;(2)过点M (0,1)作⊙G 的两条切线与椭圆交于E 、F 两点,证明:直线EF 与⊙G 相切.10.已知双曲线x2−y2=2的左、右焦分别为点F1、F2,过定点P(2,3)作双曲线x2−y2=2的切线,切点分别为A、B,且点A的横坐标小于点B的横坐标。
高中奥林匹克竞赛数学平面几何100题——珍藏版

高中数学联赛难度几何题100道第一题:学习证明角平分 (4)第二题:学习证明四点共圆 (5)第三题:学习证明角的倍数关系 (6)第四题:证明线与圆相切 (7)第五题:证明垂直 (8)第六题:证明线段相等 (9)第七题:证明线段为比例中项 (10)第八题:证明垂直 (11)第九题:证明线段相等 (12)第十题:证明角平分 (13)第十一题:证明垂直 (14)第十二题:证明线段相等 (15)第十三题:证明角相等 (16)第十四题:证明中点 (17)第十五题:证明线段的二次等式 (18)第十六题:证明角平分 (19)第十七题:证明中点 (20)第十八题:证明角相等 (21)第十九题:证明中点 (22)第二十题:证明线段相等 (23)第二十一题:证明垂直 (24)第二十二题:证明角相等 (25)第二十三题:证明四点共圆 (26)第二十四题:证明两圆相切 (27)第二十五题:证明线段相等 (28)第二十六题:证明四条线段相等 (29)第二十七题:证明线段比例等式 (30)第二十八题:证明角的倍数关系 (31)第二十九题:证明三线共点 (32)第三十题:证明平行 (33)第三十一题:证明线段相等 (34)第三十二题:证明四点共圆 (35)第三十三题:证明三角形相似 (36)第三十四题:证明角相等 (37)第三十五题:证明内心 (38)第三十六题:证明角平分 (39)第三十七题:证明垂直 (40)第三十八题:证明面积等式 (41)第三十九题:证明角平分 (42)第四十题:证明角相等 (43)第四十二题:证明中点 (45)第四十三题:证明角相等 (46)第四十四题:证明垂直 (47)第四十五题:证明角相等 (48)第四十六题:证明垂直 (49)第四十七题:证明四点共圆 (50)第四十八题:证明四点共圆 (51)第四十九题:证明四点共圆 (52)第五十题:证明角平分 (53)第五十一题:证明线段相等 (54)第五十二题:证明两圆外切 (55)第五十三题:证明垂直 (56)第五十四题:证明垂直 (57)第五十五题:证明垂直 (58)第五十六题:证明垂直 (59)第五十七题:证中点 (60)第五十八题:证明角相等 (61)第五十九题:证明角相等 (62)第六十题:证明四点共圆 (63)第六十一题:证明四点共圆 (64)第六十二题:证明四点共圆 (65)第六十三题:证明角相等 (66)第六十四题:证明角的倍数关系 (67)第六十五题:证明中点 (68)第六十六题:伪旁切圆 (69)第六十七题:证明垂直 (70)第六十八题:证明平行 (71)第六十九题:证明圆心在某线上 (72)第七十题:证明三线共点 (73)第七十一题:证明垂直 (74)第七十二题:证明垂直 (75)第七十三题:证明中点 (76)第七十四题:证明垂直 (77)第七十五题:证明垂直 (78)第七十六题:证明三线共点 (79)第七十七题:证明平行 (80)第七十八题:证明平行 (81)第七十九题:证明三线共点、证明垂直 (82)第八十题:证明三点共线(牛顿定理) (83)第八十一题:证明角平分 (84)第八十二题:证明角相等 (85)第八十三题:证明三点共线 (86)第八十四题:证明四圆共点 (87)第八十六题:证明线段相等 (89)第八十七题:证明角相等 (90)第八十八题:证明线段相等 (91)第八十九题:证明线段相等 (92)第九十题:证明线段相等 (93)第九十一题:证明中点 (94)第九十二题:证明四点共圆 (95)第九十三题:证明西姆松定理及逆定理 (96)第九十四题:证明线段的和差关系等式 (97)第九十五题:证明角相等 (98)第九十六题:证明托勒密定理及逆定理 (99)第九十七题:证明线段的和差关系等式 (100)第九十八题:证明角相等 (101)第九十九题:证明四点共圆 (102)第一百题:证明两三角形共内心 (103)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
【精品】数学奥林匹克竞赛高中训练题集【共36份】

奥林匹克数学竞赛高中训练题集
目 录
数学奥林匹克高中训练题(01) ........................................................................................................................... 1 数学奥林匹克高中训练题(02) ........................................................................................................................... 3 数学奥林匹克高中训练题(03) .............................................................................................. 4 数学奥林匹克高中训练题(04) ........................................................................................................................... 6 数学奥林匹克高中训练题(05) ...................................................................................................
高中数学竞赛题之平面几何

第一讲 注意添加平行线证题在同一平面内,不相交的两条直线叫平行线.平行线是初中平面几何最基本的,也是非常重要的图形.在证明某些平面几何问题时,若能依据证题的需要,添加恰当的平行线,则能使证明顺畅、简洁. 添加平行线证题,一般有如下四种情况. 1 为了改变角的位置大家知道,两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.利用这些性质,常可通过添加平行线,将某些角的位置改变,以满足求解的需要. 例1 设P 、Q 为线段BC 上两点,且BP =CQ ,A 为BC 外一动点(如图1).当点A 运动到使 ∠BAP =∠CAQ 时,△ABC 是什么三角形?试证明你的结论. 答: 当点A 运动到使∠BAP =∠CAQ 时,△ABC 为等腰三角形. 证明:如图1,分别过点P 、B 作AC 、AQ 的平行线得交点D .连结DA .在△DBP =∠AQC 中,显然 ∠DBP =∠AQC ,∠DPB =∠C .由BP =CQ ,可知 △DBP ≌△AQC . 有DP =AC ,∠BDP =∠QAC . 于是,DA ∥BP ,∠BAP =∠BDP .则A 、D 、B 、P 四点共圆,且四边形ADBP 为等腰梯形.故AB =DP . 所以AB =AC .这里,通过作平行线,将∠QAC “平推”到∠BDP 的位置.由于A 、D 、B 、P 四点共圆,使证明很顺畅. 例2 如图2,四边形ABCD 为平行四边形,∠BAF =∠BCE .求证:∠EBA =∠ADE . 证明:如图2,分别过点A 、B 作ED 、EC 的平行线,得交点P ,连PE .由AB CD ,易知△PBA ≌△ECD .有PA =ED ,PB =EC . 显然,四边形PBCE 、PADE 均为平行四边形.有 ∠BCE =∠BPE ,∠APE =∠ADE .由∠BAF =∠BCE ,可知 ∠BAF =∠BPE .有P 、B 、A 、E 四点共圆. 于是,∠EBA =∠APE . 所以,∠EBA =∠ADE .这里,通过添加平行线,使已知与未知中的四个角通过P 、B 、A 、E 四点共圆,紧密联系起来.∠APE 成为∠EBA 与∠ADE 相等的媒介,证法很巧妙. 2 欲“送”线段到当处利用“平行线间距离相等”、“夹在平行线间的平行线段相等”这两条,常可通过添加平行线,将某些线段“送”到恰当位置,以证题.例3 在△ABC 中,BD 、CE 为角平分线,P 为ED 上任意一点.过P 分别作AC 、AB 、BC 的垂线,M 、N 、Q 为垂足.求证:PM +PN =PQ .证明:如图3,过点P 作AB 的平行线交BD 于F ,过点F 作BC 的平行线分别交PQ 、AC 于K 、G ,连PG . 由BD 平行∠ABC ,可知点F 到AB 、BC 两边距离相等.有KQ =PN .显然,PD EP =FD EF =GDCG,可知PG ∥EC .由CE 平分∠BCA ,知GP 平分∠FGA .有PK =PM .于是, PM +PN =PK +KQ =PQ .这里,通过添加平行线,将PQ “掐开”成两段,证得PM =PK ,就有PM +PN =PQ .证法非常简捷. 3 为了线段比的转化由于“平行于三角形一边的直线截其它两边,所得对应线段成比例”,在一些问题中,可以通过添加平行线,实现某些线段比的良性转化.这在平面几何证题中是会经常遇到的.例4 设M 1、M 2是△ABC 的BC 边上的点,且BM 1=CM 2.任作一直线分别交AB 、AC 、AM 1、AM 2于P 、Q 、N 1、N 2.试证:AP AB+AQ AC =11AN AM +22AN AM . ∥=A DB Q C图1PED G A B F C图2AN EBQK G CDMF P 图3证明:如图4,若PQ ∥BC ,易证结论成立. 若PQ 与BC 不平行,设PQ 交直线BC 于D .过点A 作PQ 的平行线交直线BC 于E .由BM 1=CM 2,可知BE +CE =M 1E +M 2E ,易知 AP AB =DE BE ,AQ AC =DECE ,11AN AM =DE E M 1,22AN AM =DE E M 2. 则AP AB +AQ AC =DE CE BE +=DE E M E M 21+=11AN AM +22AN AM .所以,AP AB+AQ AC =11AN AM +22AN AM . 这里,仅仅添加了一条平行线,将求证式中的四个线段比“通分”,使公分母为DE ,于是问题迎刃而解.例5 AD 是△ABC 的高线,K 为AD 上一点,BK 交AC 于E ,CK 交AB 于F .求证:∠FDA =∠EDA . 证明:如图5,过点A 作BC 的平行线,分别交直线DE 、DF 、BE 、CF 于Q 、P 、N 、M .显然,AN BD =KA KD =AMDC. 有BD ·AM =DC ·AN . (1)由BD AP =FB AF =BC AM ,有 AP =BC AM BD ·. (2) 由DCAQ =EC AE =BC AN ,有 AQ =BC AN DC ·. (3)对比(1)、(2)、(3)有 AP =AQ .显然AD 为PQ 的中垂线,故AD 平分∠PDQ . 所以,∠FDA =∠EDA .这里,原题并未涉及线段比,添加BC 的平行线,就有大量的比例式产生,恰当地运用这些比例式,就使AP 与AQ 的相等关系显现出来.4 为了线段相等的传递当题目给出或求证某点为线段中点时,应注意到平行线等分线段定理,用平行线将线段相等的关系传递开去.例6 在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN =90°.如果BM 2+CN 2=DM 2+DN 2,求证:AD 2=41(AB 2+AC 2). 证明:如图6,过点B 作AC 的平行线交ND 延长线于E .连ME .由BD =DC ,可知ED =DN .有 △BED ≌△CND . 于是,BE =NC .显然,MD 为EN 的中垂线.有 EM =MN .由BM 2+BE 2=BM 2+NC 2=MD 2+DN 2=MN 2=EM 2,可知△BEM 为直角三角形,∠MBE =90°. 有 ∠ABC +∠ACB =∠ABC +∠EBC =90°. 于是,∠BAC =90°.所以,AD 2=221⎪⎭⎫⎝⎛BC =41(AB 2+AC 2).这里,添加AC 的平行线,将BC 的以D 为中点的性质传递给EN ,使解题找到出路.例7 如图7,AB 为半圆直径,D 为AB 上一点,分别在半圆上取点E 、F ,使EA =DA ,FB =DB .过D 作AB 的垂线,交半圆于C .求证:CD 平分EF .证明:如图7,分别过点E 、F 作AB 的垂线,G 、H 为垂足,连FA 、EB .易知 DB 2=FB 2=AB ·HB ,APEDM 2M 1BQN 1N 2图4图5MP A Q NFBD CEK图6ANC DEB MA GD O H BFCE 图7AD =AE =AG ·AB .二式相减,得 DB 2-AD 2=AB ·(HB -AG ),或 (DB -AD )·AB =AB ·(HB -AG ).于是,DB -AD =HB -AG ,或 DB -HB =AD -AG . 就是DH =GD . 显然,EG ∥CD ∥FH . 故CD 平分EF .这里,为证明CD 平分EF ,想到可先证CD 平分GH .为此添加CD 的两条平行线EG 、FH ,从而得到G 、H 两点.证明很精彩.经过一点的若干直线称为一组直线束.一组直线束在一条直线上截得的线段相等,在该直线的平行直线上截得的线段也相等.如图8,三直线AB 、AN 、AC 构成一组直线束,DE 是与BC 平行的直线.于是,有BN DM =AN AM =NC ME ,即 BN DM =NCME 或ME DM =NC BN .此式表明,DM =ME 的充要条件是 BN =NC .利用平行线的这一性质,解决某些线段相等的问题会很漂亮.例8 如图9,ABCD 为四边形,两组对边延长后得交点E 、F ,对角线BD ∥EF ,AC 的延长线交EF 于G .求证:EG =GF .证明:如图9,过C 作EF 的平行线分别交AE 、AF 于M 、N .由BD ∥EF ,可知MN ∥BD .易知S △BEF =S △DEF . 有S △BEC =S △ⅡKG - *5ⅡDFC .可得MC =CN .所以,EG =GF .例9 如图10,⊙O 是△ABC 的边BC 外的旁切圆,D 、E 、F 分别为⊙O 与BC 、CA 、AB 的切点.若OD 与EF 相交于K ,求证:AK 平分BC . 证明:如图10,过点K 作BC 的行平线分别交直线AB 、AC 于Q 、P 两点,连OP 、OQ 、 OE 、OF . 由OD ⊥BC ,可知OK ⊥PQ .由OF ⊥AB ,可知O 、K 、F 、Q 四点共圆,有 ∠FOQ =∠FKQ .由OE ⊥AC ,可知O 、K 、P 、E 四点共圆.有 ∠EOP =∠EKP .显然,∠FKQ =∠EKP ,可知 ∠FOQ =∠EOP .由OF =OE ,可知 Rt △OFQ ≌Rt △OEP . 则OQ =OP . 于是,OK 为PQ 的中垂线,故 QK =KP . 所以,AK 平分BC .综上,我们介绍了平行线在平面几何问题中的应用.同学们在实践中应注意适时添加平行线,让平行线在平面几何证题中发挥应有的作用.练习题1. 四边形ABCD 中,AB =CD ,M 、N 分别为AD 、BC 的中点,延长BA 交直线NM 于E ,延长CD 交直线NM 于F .求证:∠BEN =∠CFN .(提示:设P 为AC 的中点,易证PM =PN .)2. 设P 为△ABC 边BC 上一点,且PC =2PB .已知∠ABC =45°,∠APC =60°.求∠ACB . (提示:过点C 作PA 的平行线交BA 延长线于点D .易证△ACD ∽△PBA .答:75°)3. 六边开ABCDEF 的各角相等,FA =AB =BC ,∠EBD =60°,S △EBD =60cm 2.求六边形ABCDEF 的面积.(提示:设EF 、DC 分别交直线AB 于P 、Q ,过点E 作DC 的平行线交AB 于点M .所求面积与EMQD 面积相等.答:120cm 2)4. AD 为Rt △ABC 的斜边BC 上的高,P 是AD 的中点,连BP 并延长交AC 于E .已知AC :AB =k .求AE :EC .图8A DB N CE M图9AB M E NDC GO 图10(提示:过点A 作BC 的平行线交BE 延长线于点F .设BC =1,有AD =k ,DC =k 2.答:21k) 5. AB 为半圆直径,C 为半圆上一点,CD ⊥AB 于D ,E 为DB 上一点,过D 作CE 的垂线交CB 于F .求证:DE AD =FBCF. (提示:过点F 作AB 的平行线交CE 于点H .H 为△CDF 的垂心.)6. 在△ABC 中,∠A :∠B :∠C =4:2:1,∠A 、∠B 、∠C 的对边分别为a 、b 、c .求证:a 1+b 1=c1. (提示:在BC 上取一点D ,使AD =AB .分别过点B 、C 作AD 的平行线交直线CA 、BA 于点E 、F .) 7. 分别以△ABC 的边AC 和BC 为一边在△ABC 外作正方形ACDE 和CBFG ,点P 是EF 的中点.求证:P 点到边AB 的距离是AB 的一半.8. △ABC 的内切圆分别切BC 、CA 、AB 于点D 、E 、F ,过点F 作BC 的平行线分别交直线DA 、DE 于点H 、G .求证:FH =HG .(提示:过点A 作BC 的平行线分别交直线DE 、DF 于点M 、N .)9. AD 为⊙O 的直径,PD 为⊙O 的切线,PCB 为⊙O 的割线,PO 分别交AB 、AC 于点M 、N .求证:OM =ON . (提示:过点C 作PM 的平行线分别交AB 、AD 于点E 、F .过O 作BP 的垂线,G 为垂足.AB ∥GF .)第二讲 巧添辅助 妙解竞赛题在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路. 1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化.1.1 作出三角形的外接圆例1 如图1,在△ABC 中,AB =AC ,D 是底边BC 上一点,E 是线段AD 上一点且∠BED =2∠CED =∠A .求证:BD =2CD .分析:关键是寻求∠BED =2∠CED 与结论的联系.容易想到作∠BED 的平分线,但因BE ≠ED ,故不能直接证出BD =2CD .若延长AD 交△ABC 的外接圆于F , 则可得EB =EF ,从而获取. 证明:如图1,延长AD 与△ABC 的外接圆相交于点F ,连结CF 与BF ,则∠BFA =∠BCA =∠ABC =∠AFC ,即∠BFD =∠CFD .故BF :CF =BD :DC .又∠BEF =∠BAC ,∠BFE =∠BCA ,从而∠FBE =∠ABC =∠ACB =∠BFE . 故EB =EF .作∠BEF 的平分线交BF 于G ,则BG =GF . 因∠GEF =21∠BEF =∠CEF ,∠GFE =∠CFE ,故△FEG ≌△FEC .从而GF =FC . 于是,BF =2CF .故BD =2CD . 1.2 利用四点共圆例2 凸四边形ABCD 中,∠ABC =60°,∠BAD =∠BCD =90°, AB =2,CD =1, 对角线AC 、BD 交于点O ,如图2.则sin ∠AOB =____.分析:由∠BAD =∠BCD =90°可知A 、B 、C 、D四点共圆,欲求sin ∠AOB ,联想到托勒密定理,只须求出BC 、AD 即可.解:因∠BAD =∠BCD =90°,故A 、B 、C 、D 四点共圆.延长BA 、CD 交于P ,则∠ADP =∠ABC =60°.设AD =x ,有AP =3x ,DP =2x .由割线定理得(2+3x )3x =2x (1+2x ).A B GC D FE 图1ABCD PO图2解得AD =x =23-2,BC =2BP =4-3. 由托勒密定理有 BD ·CA =(4-3)(23-2)+2×1=103-12.又S ABCD =S △ABD +S △BCD =233. 故sin ∠AOB =263615+. 例3 已知:如图3,AB =BC =CA =AD ,AH ⊥CD 于H ,CP ⊥BC ,CP 交AH 于P .求证:△ABC 的面积S =43AP ·BD .分析:因S △ABC =43BC 2=43AC ·BC ,只 须证AC ·BC =AP ·BD ,转化为证△APC ∽△BCD .这由A 、B 、C 、Q 四点共圆易证(Q 为BD 与AH 交点).证明:记BD 与AH 交于点Q ,则由AC =AD ,AH ⊥CD 得∠ACQ =∠ADQ . 又AB =AD ,故∠ADQ =∠ABQ .从而,∠ABQ =∠ACQ .可知A 、B 、C 、Q 四点共圆. ∵∠APC =90°+∠PCH =∠BCD ,∠CBQ =∠CAQ , ∴△APC ∽△BCD . ∴AC ·BC =AP ·BD . 于是,S =43AC ·BC =43AP ·BD . 2 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决. 2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长. 分析:由“AD =DC =DB =p ”可知A 、B 、C 在半径为p 的⊙D 上.利用圆的性质即可找到AC 与p 、q 的关系. 解:延长CD 交半径为p 的⊙D 于E 点,连结AE .显然A 、B 、C 在⊙D 上. ∵AB ∥CD ,∴BC AE .从而,BC =AE =q .在△ACE 中,∠CAE =90°,CE =2p ,AE =q ,故 AC =22AE CE -=224q p -.2.2 联想直径的性质构造辅助圆例5 已知抛物线y =-x 2+2x +8与x 轴交于B 、C 两点,点D 平分BC .若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____.分析:由“∠BAC 为锐角”可知点A 在以定线段BC 为直径的圆外,又点A 在x 轴上 侧,从而可确定动点A 的范围,进而确定AD 的取值范围.解:如图5,所给抛物线的顶点为A 0(1,9),对称轴为x =1,与x 轴交于两点B (-2,0)、 C (4,0).分别以BC 、DA 为直径作⊙D 、⊙E ,则两圆与抛物线均交于两点P (1-22,1)A图3BP QDHC A EDC B图4图5、Q (1+22,1).可知,点A 在不含端点的抛物线PA 0Q 内时,∠BAC <90°.且有3=DP =DQ <AD ≤DA 0=9,即AD 的取值范围是3<AD ≤9.2.3 联想圆幂定理构造辅助圆例6 AD 是Rt △ABC 斜边BC 上的高,∠B 的平行线交AD 于M ,交AC 于N .求证:AB 2-AN 2=BM ·BN . 分析:因AB 2-AN 2=(AB +AN )(AB -AN )=BM ·BN ,而由题设易知AM =AN ,联想割线定理,构造辅助圆即可证得结论.证明:如图6,∵∠2+∠3=∠4+∠5=90°,又∠3=∠4,∠1=∠5,∴∠1=∠2.从而,AM =AN .以AM 长为半径作⊙A ,交AB 于F ,交BA 的延长线于E .则AE =AF =AN . 由割线定理有 BM ·BN =BF ·BE =(AB +AE )(AB -AF )=(AB +AN )(AB -AN ) =AB 2-AN 2, 即 AB 2-AN 2=BM ·BN .例7 如图7,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证:EP 2+FQ 2=EF 2.分析:因EP 和FQ 是⊙O 的切线,由结论联想到切割线定理,构造辅助圆使EP 、FQ 向EF 转化. 证明:如图7,作△BCE 的外接圆交EF 于G ,连结CG .因∠FDC =∠ABC =∠CGE ,故F 、D 、C 、G 四点共圆.由切割线定理,有 EF 2=(EG +GF )·EF =EG ·EF +GF ·EF =EC ·ED +FC ·FB =EC ·ED +FC ·FB =EP 2+FQ 2, 即 EP 2+FQ 2=EF 2.2.4 联想托勒密定理构造辅助圆例8 如图8,△ABC 与△A 'B 'C '的三边分别为a 、b 、c 与a '、 b '、c ',且∠B =∠B ',∠A +∠A =180°.试证:aa '=bb '+cc '. 分析:因∠B =∠B ',∠A +∠A '=180°,由结论联想到托勒密定理,构造圆内接四边形加以证明.证明:作△ABC 的外接圆,过C 作CD ∥AB 交圆于D ,连结AD 和BD , 如图9所示. ∵∠A +∠A '=180°=∠A +∠D , ∠BCD =∠B =∠B ', ∴∠A '=∠D ,∠B '=∠BCD . ∴△A 'B 'C '∽△DCB . 有DC B A ''=CB C B ''=DBC A '',即 DC c '=aa '=DBb '. 故DC =''a ac ,DB =''a ab .又AB ∥DC ,可知BD =AC =b ,BC =AD =a .从而,由托勒密定理,得 AD ·BC =AB ·DC +AC ·BD , 即 a 2=c ·''a ac +b ·''a ab . 故aa '=bb '+cc '.练习题E AN D BFM12345图6(1)(2)图8AB C A'B'c b c'b'A BCDa bb c 图91. 作一个辅助圆证明:△ABC 中,若AD 平分∠A ,则AC =DC. (提示:不妨设AB ≥AC ,作△ADC 的外接圆交AB 于E ,证△ABC ∽△DBE ,从而AC AB =DE BD =DCBD.) 2. 已知凸五边形ABCDE 中,∠BAE =3a ,BC =CD =DE ,∠BCD =∠CDE =180°-2a .求证:∠BAC =∠CAD =∠DAE .(提示:由已知证明∠BCE =∠BDE =180°-3a ,从而A 、B 、C 、D 、E 共圆,得∠BAC =∠CAD =∠DAE .) 3. 在△ABC 中AB =BC ,∠ABC =20°,在AB 边上取一点M ,使BM =AC .求∠AMC 的度数. (提示:以BC 为边在△ABC 外作正△KBC ,连结KM ,证B 、M 、C 共圆,从而∠BCM =21∠BKM =10°,得∠AMC =30°.) 4.如图10,AC 是ABCD 较长的对角线,过C 作CF ⊥AF ,CE ⊥AE . 求证:AB ·AE +AD ·AF =AC 2. (提示:分别以BC 和CD 为直径作圆交AC 于点 G 、H .则CG =AH ,由割线定理可证得结论.)5. 如图11.已知⊙O 1和⊙O 2相交于A 、B ,直线CD 过A 交⊙O 1和⊙O 2于C 、D , 且AC =AD ,EC 、ED 分别切两圆于C 、D .求证:AC 2=AB ·AE . (提示:作△BCD 的外接圆⊙O 3,延长BA 交⊙O 3于F ,证E 在⊙O 3上, 得△ACE ≌△ADF ,从而AE =AF ,由相交弦定理即得结论.) 6.已知E 是△ABC 的外接圆之劣弧BC 的中点.求证:AB ·AC =AE 2-BE 2. (提示:以BE 为半径作辅助圆⊙E ,交AE 及其延长线于N 、M ,由△ANC ∽△ABM 证AB ·AC =AN ·AM .) 7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba=1. (提示:证b 2=a 2+ab ,联想托勒密定理作出五边形的外接圆即可证得.)第三讲 点共线、线共点在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用。
奥林匹克数学竞赛题

奥林匹克数学竞赛题
中国数学奥林匹克竞赛也称“全国高中数学联赛”创办于1981年,是教育部批准,由中国科协主管,中国数学会主办的一项传统竞赛活动,联赛每年9月份举行,分为一试和二试,由各省、市、自治区数学竞赛组织机构轮流承办,至今已举办20多年。
自2010年起,全国高中数学联赛试题新规则如下:
联赛分为一试、加试(即俗称的“二试”)。
各个省份自己组织的“初赛”、“初试”、“复赛”等等,都不是正式的全国联赛名称及程序。
一试和加试均在每年9月中旬的第一个周日举行。
一试考试时间为8:00—9:20,共80分钟,包括8道填空题(每题8分)和3道解答题(分别为16分、20分、20分),满分120分。
二试考试时间为9:40—12:10,共150分钟,包括4道解答题,涉及平面几何、代数、数论、组合四个方面。
前两题每题40分,后两题每题50分,满分180分。
高中联赛难度几何题100道(精华双图版)

高中联赛难度几何题100道(精华双图版)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F ,线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆。
第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ ⊥。
第六题:证明线段相等已知:BC 、BD 是⊙O 切线,C 、D 是切点,BJA 是割线,A 、J 在圆上,J 离B 较近,AO DE ⊥于E ,交AB 于F ,AC 交DE 于G ,求证:FG DF =。
第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
高中联赛难度几何100题及其解答(修订版)

高中联赛难度几何 100 题及其解答解答人:文武光华数学工作室 田开斌第一题、如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于 A 、B ,PCD 为⊙O 一条割线,CO 交⊙O 于另一点 E ,AC 、EB 交于点 F ,证明:CD 平分∠ADF。
F证明方法一:如图,延长 ED 交 CA 于 K ,根据条件知四边形 CADB 为调和四边形,故ED 、EC 、EA 、EB 构成一组调和线束,进而知 K 、C 、A 、F 构成一组调和点列。
而 KD⊥CD, 故 CD 平分∠ADF 。
PF证明方法二:如图,连结 OA 、OB 、AB 、BC ,因为∠AFB = ∠ACE − ∠BEC =∠AOE−∠BOC=180°−∠AOC−∠BOC=∠APC,且PA = PB ,故点 P 为△ABF 的外心。
于是知222∠PFA = ∠PAC = ∠PDA ,所以 P 、A 、D 、F 四点共圆。
又PA = PF ,故 CD 平分∠ADF。
F第二题、如图,AB 为⊙O直径,C、D 为⊙O上两点,且在 AB 同侧,⊙O在C、D 两处的切线交于点 E,BC、AD 交于点 F,EF 交AB 于M,证明:E、C、M、D 四点共圆。
B证明:如图,延长 AC、BD 交于点 K,则BC⊥AK,AD⊥BK,从而知 F 为△KAB 的垂心。
又在圆内接六边形 CCADDB 中使用帕斯卡定理,知 K、E、F 三点共线,从而KM⊥AB于M。
于是知∠CMF = ∠CAF = ∠CDE,所以 E、C、M、D 四点共圆。
B第三题、如图,AB 为⊙O 直径,C 、D 为⊙O 上两点,且在 AB 同侧,⊙O 在 C 、D 两处的切线交于点 E ,BC 、AD 交于点 F ,EB 交⊙O 于点 G ,证明:∠CEF = 2∠AGF 。
B证明:如图,根据条件知∠CFD =AB +CD =(180°−A C )+(180°−BD ) = ∠CAB + ∠DBA =22∠ECF + ∠EDF ,且EC = ED ,故点 E 为△CFD 外心。
高级中学联赛难度几何题100道(精华双图版)

高中联赛难度几何题100道(精华双图版)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F ,线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆。
第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ ⊥。
第六题:证明线段相等已知:BC 、BD 是⊙O 切线,C 、D 是切点,BJA 是割线,A 、J 在圆上,J 离B 较近,AO DE ⊥于E ,交AB 于F ,AC 交DE 于G ,求证:FG DF =。
第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
数学奥赛平面几何

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理:1、梅涅劳斯定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
2、塞瓦定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
3、托勒密定理:四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理:设P 是ABC ∆外接圆上任一点,过P 向ABC ∆的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
5、斯德瓦特定理:设P 是ABC ∆的边BC 边上的任一点,则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理:设ABC ∆和C B A '''∆中有一个角相等或互补(不妨设A=A ')则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理:设ABC ∆和C B A '''∆中有一个边相等,则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明:1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点,且AM:AC=CN:CE=k,如果BMN 三点共线,试求k 。
(IMO23,1982)2、在四边形ABCD 中,ABD ∆、BCD ∆、ABC ∆的面积之比为3:4:1,点M 、N 分别 是AC 、CD 上的点,且AM:AC=CN:CD, 并且BMN 三点共线,求证:M 、N 分别是AC 、 CD 的中点。
历年全国高中数学联赛《平面几何》专题真题汇编

历年全国高中数学联赛《平面几何》专题真题汇编1、如图,在锐角三角形ABC 的BC 边上有两点E 、F ,满足∠BAE =∠CAF ,作FM ⊥AB ,FN ⊥AC (M 、N 是垂足),延长AE 交三角形ABC 的外接圆于D .证明:四边形AMDN 与三角形ABC 的面积相等.2、如图:⊿ABC 中,O 为外心,三条高AD 、BE 、CF 交于点H ,直线ED 和AB 交于点M ,FD 和AC 交于点N 。
求证:(1)OB ⊥DF ,OC ⊥DE ;(2)OH ⊥MN 。
【解析】证明:(1)∵A 、C 、D 、F 四点共圆 ∴∠BDF =∠BAC又∠OBC =21(180°-∠BOC )=90°-∠BAC∴OB ⊥DF . (2)∵CF ⊥MA∴MC 2-MH 2=AC 2-AH 2 ① ∵BE ⊥NA∴NB 2-NH 2=AB 2-AH 2 ② ∵DA ⊥BC∴BD 2-CD 2=BA 2-AC 2 ③ ∵OB ⊥DF∴BN 2-BD 2=ON 2-OD 2 ④ ∵OC ⊥DE∴CM 2-CD 2=OM 2-OD 2 ⑤ ①-②+③+④-⑤,得NH 2-MH 2=ON 2-OM 2 MO 2-MH 2=NO 2-NH 2 ∴OH ⊥MN∵1-=DF OB k k ∴OB ⊥DF 同理可证OC ⊥DE . 在直线BE 的方程)(b x a cy -=中令x =0得H (0,a bc -)∴ac ab bc a c b a bc a a bc k OH++=+++=32222直线DF 的方程为x bc a acab y +-=2由⎪⎪⎩⎪⎪⎨⎧--=+-=)(2c x c a y x bc a ac ab y 得N (22222222,2c bc a ac abc c bc a bc c a -+--++) 同理可得M (22222222,2b bc a ab abc b bc a c b b a -+--++) ∴bc a ac ab bc a bc a b c bc a c b a k MN3)3)()(())((222222++-=++-+-=∵k OH ·k MN =-1,∴OH ⊥MN .3、如图,在⊿ABC 中,∠A=60°,AB>AC ,点O 是外心,两条高BE 、CF 交于H点,点M 、N 分别在线段BH 、HF 上,且满足BM=CN ,求OH NH MH +的值。
数学奥林匹克高中训练题100

合{1 ,2 , …, n}的不同子集 ,满足下列条件 :
(i) i ∈Ai 且 Card ( Ai ) ≥3 , i = 1 ,2 , …, n ;
(ii) i ∈Aj 的充要条件是 j ∈ Ai ( i ≠j ,
i 、j = 1 ,2 , …, n) .
试回答下列问题 :
n
∑ (1) 求 Card ( Ai ) ; i =1
(A) 0 < a < b
(B) a < 0 < b
(C) a < b < 0
(D)
a<
1 2
<
b
2. 已知不等式 22x + a2 x + b ≥0 解的最
小值为 2. 则 a 的取值范围是 ( ) .
(A) ( - ∞,0)
(B) [ 0 , + ∞)
(C) [ 2 , + ∞)
(D) [ - 4 , + ∞)
>
sin (α+β) sinα·sin β
-
2sin (α+β) ·cos(αsin 2α·sin 2β
β)
=
2sin (α+β)
[2cos α·cos sin 2α·sin
β2β
cos (α-
β)
]
=
2sin
(α+ sin
β) ·cos 2α·sin
(α+β) 2β
> 0.
5. B. 由韦达定理得 α+β= - p ,αβ= q. 则 m = (α+β) 2 + 4αβ= 2 (α+β) 2 - (α- β) 2 . 又| α+β| ≤| α| + | β| ≤1 , | α- β| ≤| α| + | β| ≤1 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中奥林匹克竞赛数学平面几何100题——珍藏版高中数学联赛的几何题目有100道,难度较高。
这些题目涉及到各种不同的几何概念和定理,需要考生具备扎实的数学基础和丰富的解题经验。
在这些题目中,有许多需要考生进行证明,需要考生熟练掌握各种证明方法和技巧。
同时,还有一些需要考生进行画图,需要考生具备良好的几何直观和手绘能力。
这些几何题目的难度不仅仅在于其题目本身,还在于考试的时间限制。
考生需要在有限的时间内解决尽可能多的问题,因此需要考生具备快速解题的能力和良好的时间管理能力。
为了更好地应对这些几何题目,考生需要在平时的研究中注重基础知识的掌握和解题技巧的训练。
同时,还需要多做一些类似的练题目,以提高自己的解题水平和应对能力。
总之,高中数学联赛的几何题目难度较高,需要考生具备扎实的数学基础、丰富的解题经验、良好的几何直观和手绘能力、快速解题的能力和良好的时间管理能力。
考生需要在平时的研究中注重基础知识的掌握和解题技巧的训练,并多做类似的练题目,以提高自己的解题水平和应对能力。
1.研究证明角平分在这一部分中,我们将研究如何证明一个角被平分。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角平分线的定义、角度相等、相似三角形等。
2.研究证明四点共圆在这一部分中,我们将研究如何证明四个点共圆。
这个问题也是几何学中的基础问题之一。
我们将介绍几种不同的证明方法,包括使用圆的定义、圆心角、垂直等。
3.研究证明角的倍数关系在这一部分中,我们将研究如何证明角的倍数关系。
这是一个非常重要的几何问题,因为它在许多几何证明中都有应用。
我们将介绍几种不同的证明方法,包括使用角度相等、相似三角形等。
4.证明线与圆相切在这一部分中,我们将研究如何证明一条线与一个圆相切。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用切线的定义、圆心角等。
5.证明垂直在这一部分中,我们将研究如何证明两条线段垂直。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用垂直的定义、垂直角等。
6.证明线段相等在这一部分中,我们将研究如何证明两条线段相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用线段相等的定义、相似三角形等。
7.证明线段为比例中项在这一部分中,我们将研究如何证明一条线段是两个线段的比例中项。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用比例中项的定义、相似三角形等。
8.证明垂直在这一部分中,我们将研究如何证明两条线段垂直。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用垂直的定义、垂直角等。
9.证明线段相等在这一部分中,我们将研究如何证明两条线段相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用线段相等的定义、相似三角形等。
10.证明角平分在这一部分中,我们将研究如何证明一个角被平分。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角平分线的定义、角度相等、相似三角形等。
11.证明垂直在这一部分中,我们将研究如何证明两条线段垂直。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用垂直的定义、垂直角等。
12.证明线段相等在这一部分中,我们将研究如何证明两条线段相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用线段相等的定义、相似三角形等。
13.证明角相等在这一部分中,我们将研究如何证明两个角相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角度相等、相似三角形等。
14.证明中点在这一部分中,我们将研究如何证明一个点是一条线段的中点。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用中点的定义、相似三角形等。
15.证明线段的二次等式在这一部分中,我们将研究如何证明两条线段的平方和等于另一条线段的平方。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用勾股定理、相似三角形等。
16.证明角平分在这一部分中,我们将研究如何证明一个角被平分。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角平分线的定义、角度相等、相似三角形等。
17.证明中点在这一部分中,我们将研究如何证明一个点是一条线段的中点。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用中点的定义、相似三角形等。
18.证明角相等在这一部分中,我们将研究如何证明两个角相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角度相等、相似三角形等。
19.证明中点在这一部分中,我们将研究如何证明一个点是一条线段的中点。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用中点的定义、相似三角形等。
20.证明线段相等在这一部分中,我们将研究如何证明两条线段相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用线段相等的定义、相似三角形等。
21.证明垂直在这一部分中,我们将研究如何证明两条线段垂直。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用垂直的定义、垂直角等。
22.证明角相等在这一部分中,我们将研究如何证明两个角相等。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用角度相等、相似三角形等。
23.证明四点共圆在这一部分中,我们将研究如何证明四个点共圆。
这个问题也是几何学中的基础问题之一。
我们将介绍几种不同的证明方法,包括使用圆的定义、圆心角、垂直等。
24.证明两圆相切在这一部分中,我们将研究如何证明两个圆相切。
这是一个非常基础的几何问题,但是它的应用非常广泛。
我们将介绍几种不同的证明方法,包括使用切线的定义、圆心角等。
25.证明线段相等在这一部分中,我们将第一题:证明角平分已知PE、PF是圆O的切线,A、B是圆O的直径点,PB 交圆O于另一点C,直线AF、BE交于D点。
要证明:∠PCD=∠PCE。
证明:首先由圆的性质可知,∠PCE=∠PEB,∠PCD=∠PBC,因此只需证明∠PEB=∠PBC即可。
由于PA、PB是圆O的切线,因此∠PAB=∠PBA=90°,又因为A、B是圆O的直径点,所以∠APB=180°,因此三角形APB是直角三角形。
又因为PE、PF是圆O的切线,所以∠PBE=∠PBF=90°,因此四边形BPEF是矩形,所以∠PEB=∠PBF。
又因为PB交圆O于点C,所以∠PBC=∠PCB,因此我们只需证明∠PBF=∠PCB即可。
由于AF、BE交于点D,所以∠FDE=∠BDE,又因为DE是圆O的切线,所以∠BDE=∠PBC,因此∠FDE=∠PBC。
又因为CF⊥AB,所以∠FDE=∠DFC+∠EFC,代入上式得到∠PBC=∠PBF+∠DFC+∠EFC,即∠PBF=∠PCB,证毕。
第二题:证明四点共圆如图,AB是圆O的直径,C、D是圆O上异于A、B且在AB同侧的两点,分别过C、D作圆O的切线,它们交于点E,线段AD与BC的交点为F,线段AB与EF的交点为M。
要证明:E、C、M、D四点共圆。
证明:首先由圆的性质可知,AB是圆O的直径,因此∠ACB=90°,又因为C、D是圆O上异于A、B且在AB同侧的两点,所以∠CED=∠CBD,因此四边形CDEB是一个梯形。
又因为CD是圆O的切线,所以∠CED=∠CBE,因此四边形CDEB是一个等腰梯形。
又因为AD与BC相交于点F,所以线段EF是AB的中线,因此M是AB的中点。
又因为AB是圆O的直径,所以∠AMB=90°,又因为EF是AB的中线,所以∠EMB=90°,因此四边形AEMB是一个矩形,即AE=MB。
又因为C、D是圆O上的点,所以CE=DE,又因为CDEB是一个等腰梯形,所以CE=BD,因此AE=MB=BD,即四边形ABD是一个等腰三角形。
又因为∠ACB=90°,所以∠AFB=90°,因此四边形ABDF是一个矩形,即AF=BD。
又因为AE=BD,所以AE=AF,因此四边形AEFD是一个平行四边形,即EF∥AD。
又因为EF是AB的中线,所以EF⊥CD,又因为CD是圆O的切线,所以∠CED=∠CBE,因此∠CEM=∠CBM,即MC与MB在圆O上对应的弧相等。
同理可证MD与MA在圆O上对应的弧相等,因此E、C、M、D四点共圆,证毕。
第三题:证明角的倍数关系如图,PE、PF是以AB为直径圆的切线,E、F是切点,PB交圆于C点,AF、BE交于D点,AB是直径。
要证明:∠DPE=2∠ACD。
证明:首先由圆的性质可知,∠APE=90°,∠BPE=90°,因此∠APE+∠BPE=180°,即APBE是一个矩形,所以AE=BP。
又因为PE、PF是以AB为直径圆的切线,所以∠APE=∠ECD,∠BPE=∠DCF,因此∠ECD+∠DCF=∠APE+∠BPE=180°,即四边形CDEF是一个平行四边形,因此CD∥EF。
又因为AF、BE交于点D,所以∠AFD+∠BED=180°,又因为APBE是一个矩形,所以∠AFD=∠APE=90°,因此∠BED=90°-∠ACB。
又因为CD∥EF,所以∠ACD=∠ECD,∠BDC=∠DCF,因此∠BDE=∠ACD-∠DCF=∠ACD-∠BDC。
又因为AB是直径,所以∠ADB=90°,因此∠DAB=90°-∠ACB,又因为AE=BP,所以∠AEB=∠BPA,因此∠DAB=∠DPA,即三角形DAB与三角形DPA相似。
又因为∠BDE=∠ACD-∠BDC=∠ACD-∠ADB,所以∠DPE=∠DPA-∠EPA=∠DAB-∠ECD=∠ACB+∠BED-∠ECD=∠ACB+90°-∠ACB-∠ECD-∠BDC=90°-∠ECD-∠BDC=2∠ACD,证毕。
第四题:证明线与圆相切已知:三角形ABC中,∠A=90°,AD切圆ABC,AD交BC延长线于D,E是A关于BC的对称点,AY⊥BE于Y,X是AY中点,延长BX交圆ABC于J。
