svm的损失函数
minist数据集常用损失函数

minist数据集常用损失函数
MNIST(手写数字识别)数据集常用于图像分类任务,对于这类任务,以下是一些常用的损失函数:
交叉熵损失函数(Cross-Entropy Loss):
适用于多类别分类任务,是最常用的损失函数之一。
在MNIST 数据集中,通常使用softmax 函数来将模型的原始输出转换为类别概率分布,然后计算交叉熵损失。
多类别对数损失函数(Categorical Cross-Entropy Loss):
类似于交叉熵损失,用于多类别分类。
在MNIST 中,输入是一个样本的真实标签和模型输出的概率分布,通过对数变换来计算损失。
稀疏多类别对数损失函数(Sparse Categorical Cross-Entropy Loss):类似于多类别对数损失,但适用于标签是整数形式的情况。
在MNIST 中,标签是0 到9 的整数,因此可以使用稀疏多类别对数损失。
Hinge 损失函数:
适用于支持向量机(SVM)等任务。
在MNIST 中,这通常不是最优选择,因为该数据集更适合使用softmax 损失。
这些损失函数的选择通常取决于模型的输出形式以及任务的性质。
对于MNIST 数据集,由于是多类别分类任务,交叉熵损失函数是一个常见的选择。
在实际应用中,建议根据具体情况进行实验和调整。
1。
svm梯度下降法

svm梯度下降法支持向量机(Support Vector Machine, SVM)是一种常用的分类算法,广泛应用于机器学习领域。
在SVM中,我们常用梯度下降法来求解模型的参数,以优化分类效果。
本文将介绍SVM梯度下降法的原理和步骤,并探讨其在实际应用中的一些注意事项。
一、SVM梯度下降法的原理SVM旨在找到一个超平面,将不同类别的样本点分开。
为了找到最佳的超平面,我们需要优化SVM模型中的参数。
梯度下降法是一种常用的优化算法,其思想是通过不断迭代调整参数值,直到达到使损失函数最小化的目标。
二、SVM梯度下降法的步骤1. 数据预处理:在应用SVM梯度下降法之前,我们需要对数据进行预处理,如去除异常值、缺失值处理、特征标准化等。
这样可以提高模型训练的稳定性和效果。
2. 定义损失函数:SVM梯度下降法的目标是最小化损失函数。
在SVM中,常用的损失函数是hinge损失函数。
损失函数的定义会直接影响到模型的训练效果,需要根据具体的问题进行选择。
3. 计算梯度:根据损失函数,我们计算梯度,即对参数进行求导。
梯度指示了损失函数沿着参数方向的变化率,通过梯度可以确定参数的更新方向。
4. 参数更新:通过梯度下降法,不断迭代更新参数,使损失函数逐渐减小。
更新的方式可以使用批量梯度下降法(Batch Gradient Descent)、随机梯度下降法(Stochastic Gradient Descent)或者小批量梯度下降法(Mini-batch Gradient Descent)等。
5. 收敛判定:在迭代过程中,我们需要设置一个收敛条件,即当损失函数变化足够小或迭代次数达到预设值时,停止迭代,得到最终的参数值。
三、实际应用中的注意事项1. 学习率选择:梯度下降法中的学习率是一个重要的超参数,它决定了参数每次更新的幅度。
学习率过大会导致参数在更新过程中发散,学习率过小会导致收敛速度过慢。
通常需要通过实验找到最优的学习率。
常用的损失函数 与损失函数的梯度

常用的损失函数与损失函数的梯度1. 引言在机器学习和深度学习领域,损失函数是一个非常重要的概念。
它用来衡量模型预测结果与真实数据之间的差异,是优化算法的核心部分。
在训练模型的过程中,我们需要通过最小化损失函数来不断调整模型的参数,使得模型可以更好地拟合数据。
本文将介绍常用的损失函数以及它们的梯度计算方法。
2. 常用的损失函数(1)均方误差损失函数(MSE)均方误差损失函数是回归任务中常用的损失函数,它衡量模型预测值与真实值之间的差异。
其计算公式如下:MSE = 1/n * Σ(yi - y^i)^2其中,n表示样本数量,yi表示真实值,y^i表示模型的预测值。
对于均方误差损失函数,我们需要计算其关于模型参数的梯度,以便进行参数的更新。
(2)交叉熵损失函数交叉熵损失函数是分类任务中常用的损失函数,特别适用于多分类问题。
它的计算公式如下:Cross-Entropy = -Σ(yi * log(y^i))其中,yi表示真实标签的概率分布,y^i表示模型的预测概率分布。
与均方误差损失函数类似,我们也需要计算交叉熵损失函数的梯度,以便进行参数的更新。
(3)Hinge损失函数Hinge损失函数通常用于支持向量机(SVM)中,它在二分类问题中表现良好。
其计算公式如下:Hinge = Σ(max(0, 1 - yi * y^i))其中,yi表示真实标签,y^i表示模型的预测值。
Hinge损失函数的梯度计算相对复杂,但可以通过数值方法或者约束优化方法进行求解。
3. 损失函数的梯度损失函数的梯度是优化算法中至关重要的一部分,它决定了参数更新的方向和步长。
在深度学习中,我们通常使用梯度下降算法来最小化损失函数,因此需要计算损失函数关于参数的梯度。
(1)均方误差损失函数的梯度对于均方误差损失函数,其关于模型参数的梯度计算相对简单。
以单个参数θ为例,其梯度可以通过以下公式计算得出:∂MSE/∂θ = 2/n * Σ(yi - y^i) * ∂y^i/∂θ其中,∂y^i/∂θ表示模型预测值关于参数θ的梯度。
svm损失函数

SVM损失函数引言SVM(Support Vector Machines,支持向量机)是一种常用的监督学习算法,广泛应用于分类和回归问题。
其核心思想是寻找一个能够划分不同类别样本的超平面,使得样本与超平面的距离尽可能大。
在求解SVM模型时,需要定义一个损失函数,用于衡量超平面的优劣程度并进行模型优化。
本文将重点探讨SVM的损失函数及其特点。
二级标题1:SVM的基本原理SVM是一种二分类模型,用于处理线性可分和线性不可分的分类问题。
其基本原理如下:1.基于线性可分的情况:假设训练样本集可以完美地被一个超平面分割为两个类别。
在这种情况下,SVM的目标是找到一个超平面,使得正负样本分别在超平面的两侧,并且使得超平面到最近样本的距离最大。
2.基于线性不可分的情况:实际数据中,样本往往无法被一个线性超平面分割开。
为了解决这一问题,SVM引入了松弛变量,允许部分样本被错误分类。
松弛变量的引入使得SVM的分类变得更加灵活。
二级标题2:SVM的优化目标SVM的优化目标是选择一个合适的超平面,使得正负样本离超平面的距离最大。
为了实现这一目标,我们需要定义一个损失函数,通过最小化损失函数来求解超平面的参数。
SVM常用的损失函数有Hinge Loss和平方和损失函数。
其中,Hinge Loss是SVM 模型最常用的损失函数。
三级标题1:Hinge LossHinge Loss是一种合页损失函数,常用于支持向量机模型的优化。
Hinge Loss可以保证学习的模型具有良好的泛化能力,对异常值具有一定的容忍性,适用于处理非线性可分问题。
Hinge Loss的数学表达式如下:loss(x)=max(0,1−y⋅f(x))其中,y是样本的真实标签,f(x)是超平面函数对样本x的预测结果。
Hinge Loss的特点是当样本被正确分类时,损失函数的值为0;当样本被错误分类时,损失函数的值与预测错误的程度成正比。
这个特性使得SVM的优化目标变成了“最小化错误分类的样本到超平面的距离”。
向量机参数列表

向量机参数列表向量机(SVM)是一种强大的机器学习算法,用于分类和回归分析。
在SVM中,参数的选择对模型的性能和结果有很大的影响。
以下是一些常用的SVM参数:1. 核函数:这是SVM中最重要的参数之一。
常用的核函数有线性核、多项式核、径向基函数(RBF)和sigmoid核。
选择哪种核函数取决于你的数据和问题。
2. 惩罚系数C:这是正则化参数,用于控制模型复杂度和防止过拟合。
较大的C值会导致模型复杂度增加,而较小的C值会导致模型简单。
3. 核函数参数:对于某些核函数(如多项式核和RBF核),需要额外的参数。
例如,多项式核的参数是degree(多项式的最高次数),RBF核的参数是gamma(决定了RBF核函数的宽度)。
4. 松弛变量:这是用于处理分类问题中的噪声和异常值的参数。
它允许模型在必要时违反约束,以提高泛化能力。
5. 不敏感损失函数:这是用于处理回归问题的参数。
它决定了模型对训练误差的容忍程度。
6. 迭代次数:这是优化算法的迭代次数。
如果迭代次数太少,优化算法可能无法找到全局最优解;如果迭代次数太多,可能会导致过拟合。
7. 正则化项:这是用于控制模型复杂度和防止过拟合的参数。
常用的正则化项有L1正则化和L2正则化。
8. 特征缩放:在某些情况下,特征的尺度会对模型的性能产生影响。
如果特征的尺度差异很大,可能需要使用特征缩放来提高模型的性能。
9. 初始化参数:这些参数用于控制优化算法的初始状态,如随机种子和初始解。
请注意,对于不同的数据集和问题,可能需要调整这些参数以获得最佳性能。
因此,建议使用交叉验证和网格搜索等技术来选择最佳的参数组合。
深度学习六十问(基础题)

深度学习六⼗问(基础题)数据类问题1.样本不平衡的处理⽅法①⽋采样 - 随机删除观测数量⾜够多的类,使得两个类别间的相对⽐例是显著的。
虽然这种⽅法使⽤起来⾮常简单,但很有可能被我们删除了的数据包含着预测类的重要信息。
②过采样 - 对于不平衡的类别,我们使⽤拷贝现有样本的⽅法随机增加观测数量。
理想情况下这种⽅法给了我们⾜够的样本数,但过采样可能导致过拟合训练数据。
③合成采样( SMOTE )-该技术要求我们⽤合成⽅法得到不平衡类别的观测,该技术与现有的使⽤最近邻分类⽅法很类似。
问题在于当⼀个类别的观测数量极度稀少时该怎么做。
⽐如说,我们想⽤图⽚分类问题确定⼀个稀有物种,但我们可能只有⼀幅这个稀有物种的图⽚。
④在loss⽅⾯,采⽤focal loss等loss进⾏控制不平衡样本。
不平衡类别会造成问题有两个主要原因: 1.对于不平衡类别,我们不能得到实时的最优结果,因为模型/算法从来没有充分地考察隐含类。
2.它对验证和测试样本的获取造成了⼀个问题,因为在⼀些类观测极少的情况下,很难在类中有代表性。
2.讲下数据增强有哪些⽅法(重点)翻转,旋转,缩放,裁剪,平移,添加噪声,有监督裁剪,mixup,上下采样,增加不同惩罚解决图像细节不⾜问题(增强特征提取⾻⼲⽹络的表达能⼒)3.过拟合的解决办法(重点)数据扩充/数据增强/更换⼩⽹络(⽹络太复杂)/正则化/dropout/batch normalization增加训练数据、减⼩模型复杂度、正则化,L1/L2正则化、集成学习、早期停⽌什么是过拟合过拟合(overfitting)是指在模型参数拟合过程中的问题,由于训练数据包含抽样误差,训练时,复杂的模型将抽样误差也考虑在内,将抽样误差也进⾏了很好的拟合。
产⽣过拟合根本原因:观察值与真实值存在偏差, 训练数据不⾜,数据太少,导致⽆法描述问题的真实分布, 数据有噪声, 训练模型过度,导致模型⾮常复杂什么是⽋拟合:训练的模型在训练集上⾯的表现很差,在验证集上⾯的表现也很差原因:训练的模型太简单,最通⽤的特征模型都没有学习到正则化正则化的原理:在损失函数上加上某些规则(限制),缩⼩解空间,从⽽减少求出过拟合解的可能性。
sklearn oneclass svm 损失函数 -回复

sklearn oneclass svm 损失函数-回复Sklearn OneClassSVM: Understanding the Loss FunctionIntroduction:In machine learning, one of the primary goals is to accurately classify data into different categories. However, there are instances where identifying outliers or anomalies is equally important.One-class SVM is a popular method used for anomaly detection, specifically when the data available for training contains only the normal class. In this article, we will focus on the loss function used in the OneClassSVM implementation provided by the sklearn library.1. One-Class SVM:One-Class SVM is a type of Support Vector Machine (SVM) algorithm used for unsupervised learning. Unlike traditional SVM models that aim to separate multiple classes, one-class SVM is designed to identify a boundary that encompasses the normal class while minimizing the influence of outliers. This makes it particularly useful in anomaly detection tasks, such as fraud detection, network intrusion detection, or medical diagnosis.2. The Loss Function:The loss function plays a crucial role in any machine learning algorithm, as it measures the model's accuracy and guides the optimization process. In the case of the OneClassSVM, the loss function is tailored to capture the characteristics of anomaly detection problems effectively.2.1. Hinge Loss:The primary component of the One-Class SVM loss function is the hinge loss. The hinge loss can be understood as a penalty imposed on misclassified samples in traditional SVMs. It measures the distance between the sample and the decision boundary, as well as the margin set by the user. Samples with a distance larger than the margin will not contribute to the loss, while samples within the margin or incorrectly classified will have non-zero loss.2.2. Nuclear Norm Regularization:OneClassSVM also utilizes a regularization term called "nuclear norm" to improve the model's generalization and prevent overfitting. The nuclear norm regularization adds a penalty term on the singular values of the kernel matrix, encouraging the model to find a more robust and generalized solution. This term helps themodel adapt to variations and noise in the data by reducing sensitivity to individual data points.3. Model Training:The OneClassSVM implementation in sklearn provides several parameters that allow users to control the loss function and regularization. These parameters include:- `nu`: Represents the upper boundary proportion of outliers accepted. The model aims to obtain a fraction `nu` of training samples that are classified as outliers.- `gamma`: Controls the influence of individual training samples. Higher values of gamma result in higher sensitivity to individual samples, potentially leading to overfitting.- `kernel`: Specifies the kernel function to be used to map the input data into a higher-dimensional space.4. Outlier Detection:Once the OneClassSVM model is trained, it can be used for outlier detection on unseen data. The model calculates the anomaly score for each sample, which represents the distance from the decision boundary. A higher score indicates a higher likelihood of being an outlier. By setting a threshold on the anomaly scores, we canidentify abnormal data points.5. Model Evaluation:Evaluating the effectiveness of an anomaly detection model is challenging due to the lack of labeled anomalous data. Common evaluation metrics for one-class SVM models include precision, recall, and the F1-score. Precision measures the proportion of correctly classified anomalies out of all identified anomalies. Recall measures the proportion of correctly identified anomalies out of all actual anomalies. The F1-score is the harmonic mean of precision and recall, providing an overall measure of the model's performance.Conclusion:The OneClassSVM implementation in sklearn utilizes a loss function composed of hinge loss and nuclear norm regularization. By minimizing the hinge loss, the model aims to identify the boundary that encompasses the normal class while minimizing the influence of outliers. The regularization term helps the model adapt to variations and reduces overfitting. Understanding the loss function and its components is essential for effectively utilizing theOneClassSVM model from the sklearn library in anomaly detection tasks.。
多类 svm 的损失计算题例题

多类 svm 的损失计算题例题多类支持向量机(SVM)的损失计算涉及到多个方面,包括多类别分类、间隔和决策函数等。
首先,让我们来看一个例题。
假设我们有一个3类分类问题,用线性SVM进行分类。
我们有一组训练数据,每个数据点都有相应的特征向量和类别标签。
我们的目标是找到一个超平面,将这些数据点正确地分类到三个类别中。
在这个问题中,我们可以使用多类别SVM来解决。
首先,我们需要定义决策函数。
对于多类别SVM,我们可以使用“one-vs-rest”或者“one-vs-one”策略。
在这个例子中,我们使用“one-vs-rest”策略。
对于每个类别,我们训练一个SVM分类器,将该类别与其他所有类别区分开来。
训练完成后,我们得到三个决策函数,分别对应三个类别。
接下来,我们需要计算损失。
在多类别SVM中,常用的损失函数是hinge loss。
对于每个类别,我们计算其对应的hinge loss,并将其累加起来作为最终的损失值。
具体计算公式如下:对于第i个数据点(xi, yi),其中xi是特征向量,yi是类别标签,我们的决策函数为f(x)。
那么第i个数据点的hinge loss可以表示为:Li = Σmax(0, maxj≠yi(fj(xi) fi(xi) + Δ))。
其中,j表示除了yi以外的其他类别,Δ是一个margin的阈值,用来控制分类器的间隔。
如果fi(xi)与正确类别yi的决策函数值加上Δ小于其他类别的决策函数值,则损失为0,否则损失为这个差值。
然后对所有数据点的损失进行累加,得到最终的损失值。
在实际计算中,我们通常会加入正则化项,来平衡损失函数和模型复杂度。
总结来说,多类别SVM的损失计算涉及到决策函数的定义和hinge loss的计算。
我们需要针对每个类别训练一个SVM分类器,并计算每个数据点的hinge loss,并将其累加起来得到最终的损失值。
同时,我们也可以加入正则化项来平衡损失函数和模型复杂度。
损失函数总结以及python实现:hingeloss(合页损失)、softmaxloss、。。。

损失函数总结以及python实现:hingeloss(合页损失)、softmaxloss、。
损失函数在机器学习中的模型⾮常重要的⼀部分,它代表了评价模型的好坏程度的标准,最终的优化⽬标就是通过调整参数去使得损失函数尽可能的⼩,如果损失函数定义错误或者不符合实际意义的话,训练模型只是在浪费时间。
所以先来了解⼀下常⽤的⼏个损失函数hinge loss(合页损失)、softmax loss、cross_entropy loss(交叉熵损失):1:hinge loss(合页损失)⼜叫Multiclass SVM loss。
⾄于为什么叫合页或者折页函数,可能是因为函数图像的缘故。
s=WX,表⽰最后⼀层的输出,维度为(C,None),L_i表⽰每⼀类的损失,⼀个样例的损失是所有类的损失的总和。
L_i=\sum_{j!=y_i}\left \{ ^{0 \ \ \ \ \ \ \ \ if \ s_{y_i}\geq s_j+1}_{s_j-s_{y_i}+1 \ otherwise} \right \}=\sum_{j!=y_i}max(0,s_{y_i}-s_j+1)函数图像长这样:举个例⼦:假设我们只有3个类别,上⾯的图⽚表⽰输⼊,下⾯3个数字表⽰最后⼀层每个类别的分数。
对于第⼀张猫的图⽚,L_i=max(0, 5.1 - 3.2 + 1) +max(0, -1.7 - 3.2 + 1)=2.9+0=2.9对于第⼆张汽车的图⽚,L_i=max(0, 1.3 - 4.9 + 1) +max(0, 2.0 - 4.9 + 1)=0+0=0可以看到对于分类错误的样例,最后有⼀个损失产⽣,对于正确分类的样例,其损失为0.其实该损失函数不仅仅只是要求正确类别的分数最⾼,还要⾼出⼀定程度。
也就是说即使分类正确了也有可能会产⽣损失,因为有可能正确的类别的分数没有超过错误类别⼀定的阈值(这⾥设为1)。
但是不管阈值设多少,好像并没有什么太⼤的意义,只是对应着W的放缩⽽已。
支持向量机 损失函数

支持向量机损失函数支持向量机(Support Vector Machine)是一种有监督学习算法,可以用于二分类或多分类问题。
在分类模型中,SVM选择一个最优的超平面将数据集分为两个部分,并尽可能地将两个类别分开。
SVM使用的损失函数是Hinge Loss,它可以让SVM对于误分类的点付出更高的代价,从而使得分类面更加鲁棒。
Hinge Loss也被称为最大间隔损失函数,可以被视为一个函数和阈值之间的描述。
对于一个二元分类问题,分类模型输出$\hat{y}$是一个连续值,该值可以被视为是一个数据点被分配到正类的概率。
将输出$\hat{y}$与阈值比较可以生成分类。
Hinge Loss为:$\mathrm{L}=\sum_{i=1}^{n}\left(\max (0,1-y_{i}\hat{y_{i}})\right)$其中,$n$表示训练数据集的大小,$y_{i}$是数据点的类别,$\hat{y_{i}}$是分类器对第$i$个数据点的预测值。
如果$h_{\theta}(x_{i})$与$y_{i}$符号相同(即$h_{\theta}(x_{i})y_{i}>0$),则$\max(0, 1-y_{i}h_{\theta}(x_{i})) = 0$,损失值为$0$,否则损失值大于$0$。
通过最小化Hinge Loss可以得到最优的分界超平面,使得分界超平面到最近样本点集的距离最大。
为了防止过拟合,原始的SVM模型在Hinge Loss函数中加入了正则化项。
正则化项的目的是使模型的复杂度受到限制,从而避免对训练数据集过拟合。
在SVM中,我们通常使用$L2$正则化项:$\mathrm{L}=\frac{1}{n} \sum_{i=1}^{n}\left[\max (0,1-y_{i}\hat{y_{i}})\right]+\alpha \sum_{j=1}^{m} \theta_{j}^{2}$其中,$m$表示特征数,$\alpha$是一个常数,$\theta_{j}$是特征权重。
SVM的损失函数(HingeLoss)

SVM的损失函数(HingeLoss)
损失函数
是⽤来衡量⼀个预测器在对输⼊数据进⾏分类预测时的质量好坏。
损失值越⼩,分类器的效果越好,越能反映输⼊数据与输出类别标签的关系(虽然我们的模型有时候会过拟合——这是由于训练数据被过度拟合,导致我们的模型失去了泛化能⼒)。
相反,损失值越⼤,我们需要花更多的精⼒来提升模型的准确率。
就参数化学习⽽⾔,这涉及到调整参数,⽐如需要调节权重矩阵W或偏置向量B,以提⾼分类的精度。
Hinge Loss
多分类svm:
损失函数的计算⽅法为:,其中i代表第i个样品,j代表第j个种类,那么y_i代表第i个
样品的真实种类。
其中,常⽤的数学表达式为:,但为了与代码中的统⼀,从⽽稍微变动以下,对于y_i来说同理。
计算正确类的预测值,和其他类的预测值之间的差距,如果正确类的预测值⼤于所有不正确的预测值则损失函数为0,证明当前的W和b所计算得到的效果很好。
当把损失值推⼴到整个训练数据集,则应为:
两分类SVM:
在⼆分类情况下,铰链函数公式如下:
L(y) = max(0 , 1 – t⋅y)
其中,y是预测值(-1到1之间),t为⽬标值(1或 -1)。
其含义为:y的值在 -1到1之间即可,并不⿎励 |y|>1,即让某个样本能够正确分类就可以了,不⿎励分类器过度⾃信,当样本与分割线的距离超过1时并不会有任何奖励。
⽬的在于使分类器更专注于整体的分类误差。
计算案例
三个图⽚的损失和整体损失:。
svm损失函数

svm损失函数支持向量机(Support Vector Machine,SVM)是一种常见的机器学习算法,它在分类和回归问题中都有广泛的应用。
在SVM中,我们通过最小化一个损失函数来找到一个最优的超平面将不同类别的数据分开。
SVM的损失函数有多种形式,其中最常见的是Hinge Loss。
Hinge Loss是一种基于边界距离的损失函数,在SVM中被用来衡量样本点是否被正确分类。
具体来说,对于一个给定的样本点(xi,yi),其中xi表示输入特征向量,yi表示标签(+1或-1),我们可以计算它与超平面w·x+b之间的距离d:d = yi(w·xi + b) / ||w||其中||w||表示权重向量w的模长。
如果样本点被正确分类,则其边界距离d应该大于1;否则,我们需要对其进行惩罚。
Hinge Loss可以定义为:L(yi, w·xi + b) = max(0, 1 - yi(w·xi + b))其中max(0, x)表示取x和0中较大的那个值。
这个函数可以看作是一个分段函数,在d≥1时为0,在0<d<1时为1-d,在d≤0时为1。
我们可以将所有样本点的Hinge Loss相加,并加上一个正则化项来得到SVM的目标函数:minimize 1/2||w||^2 + C∑i=1^n L(yi, w·xi + b)其中C是一个正则化参数,用来平衡模型的复杂度和训练误差。
这个目标函数可以通过梯度下降等优化算法来求解。
Hinge Loss的优点是它能够对误分类的样本点进行惩罚,并且在超平面附近有一定的缓冲区,使得模型更加鲁棒。
此外,由于它只关注边界距离,因此对于高维数据具有较好的表现。
然而,Hinge Loss也存在一些缺点。
首先,它不能够直接处理多类别分类问题,需要通过一些技巧来实现。
其次,在样本不平衡或噪声较多的情况下容易受到影响。
最后,由于它是一个分段函数,在梯度为0时会出现不可导点,使得优化算法变得困难。
分类问题损失函数

分类问题损失函数一、引言在机器学习中,分类问题是一个重要的问题,它涉及到将数据分成不同的类别。
为了解决这个问题,我们需要选择一个合适的损失函数来评估模型的性能。
本文将介绍常见的分类问题损失函数,并提供相应的代码实现。
二、常见的分类问题损失函数1. 交叉熵损失函数交叉熵损失函数是最常见的分类问题损失函数之一。
它是基于信息论中熵的概念而来。
对于二分类问题,交叉熵损失函数可以表示为:$$L=-ylog(p)-(1-y)log(1-p)$$其中,$y$表示真实标签,$p$表示预测标签。
对于多分类问题,交叉熵损失函数可以表示为:$$L=-\sum_{i=1}^{n}\sum_{j=1}^{m}y_{ij}log(p_{ij})$$其中,$n$表示样本数,$m$表示类别数,$y_{ij}$表示第$i$个样本是否属于第$j$个类别(0或1),$p_{ij}$表示第$i$个样本属于第$j$个类别的概率。
2. Hinge Loss(合页损失)函数Hinge Loss是用于支持向量机(SVM)中的一种常见损失函数。
对于二分类问题,Hinge Loss可以表示为:$$L=max(0,1-yp)$$其中,$y$表示真实标签,$p$表示预测标签。
对于多分类问题,Hinge Loss可以表示为:$$L=\sum_{i=1}^{n}\sum_{j\neq y_i}max(0,s_j-s_{y_i}+1)$$其中,$n$表示样本数,$y_i$表示第$i$个样本的真实类别,$s_j$表示第$i$个样本属于第$j$个类别的得分。
3. Softmax Loss函数Softmax Loss函数是用于多分类问题中的一种常见损失函数。
它通过将每个类别的得分转化为概率来计算损失。
对于多分类问题,Softmax Loss可以表示为:$$L=-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{m}y_{ij}log(p_{ij})$$ 其中,$n$表示样本数,$m$表示类别数,$y_{ij}$表示第$i$个样本是否属于第$j$个类别(0或1), $p_{ij}$ 表示第$i $个样本属于第$j $个类别的概率。
最大边界损失和交叉熵损失

最大边界损失和交叉熵损失
最大边界损失和交叉熵损失是神经网络中常用的两种损失函数。
最大边界损失函数是一种支持向量机(SVM)训练中的损失函数,主要用于二分类问题。
它的目标是最大化两个类别之间的边界,即使得两个类别之间的距离尽可能大。
在训练过程中,最大边界损失函数会将错误分类的样本惩罚得更加严重,以便更好地学习边界。
交叉熵损失函数是一种用于分类问题的损失函数,它的目标是最小化预测值和真实值之间的差异。
在训练过程中,交叉熵损失函数会根据样本的真实标签和神经网络预测的标签之间的距离来计算损失值,进而更新模型参数,使得预测结果更加准确。
两种损失函数在神经网络中都有广泛应用,但是在不同的场景下可能会有不同的表现。
最大边界损失函数在处理线性可分问题时表现良好,而交叉熵损失函数在处理非线性可分问题时更为适用。
因此,在选择损失函数时,需要根据具体的问题特点进行选择,以取得更好的效果。
- 1 -。
002-神经网络基础-得分函数,SVM损失函数,正则化惩罚项,softmax函数,交叉熵损失函数
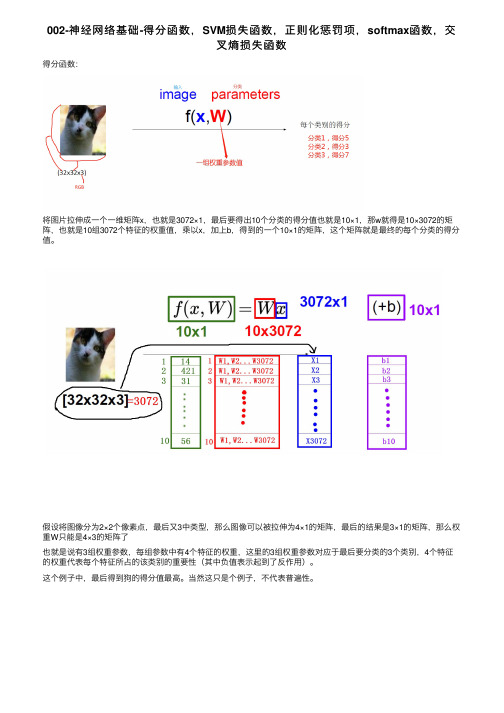
002-神经⽹络基础-得分函数,SVM损失函数,正则化惩罚项,softmax函数,交叉熵损失函数得分函数:将图⽚拉伸成⼀个⼀维矩阵x,也就是3072×1,最后要得出10个分类的得分值也就是10×1,那w就得是10×3072的矩阵,也就是10组3072个特征的权重值,乘以x,加上b,得到的⼀个10×1的矩阵,这个矩阵就是最终的每个分类的得分值。
假设将图像分为2×2个像素点,最后⼜3中类型,那么图像可以被拉伸为4×1的矩阵,最后的结果是3×1的矩阵,那么权重W只能是4×3的矩阵了也就是说有3组权重参数,每组参数中有4个特征的权重,这⾥的3组权重参数对应于最后要分类的3个类别,4个特征的权重代表每个特征所占的该类别的重要性(其中负值表⽰起到了反作⽤)。
这个例⼦中,最后得到狗的得分值最⾼。
当然这只是个例⼦,不代表普遍性。
--------------------------2018年10⽉14⽇02:52:49--睡觉--------------------------------------- --------------------------2018年10⽉14⽇16:41:09--继续---------------------------------------相当于做了这么⼀件事:利⽤⼀个直线作为决策边界,将样本进⾏分类b表⽰与Y轴的焦点。
损失函数:输⼊猫的图像,输出类别得分,猫:3.2,车5.1,青蛙:-1.75.1-3.2表⽰输⼊猫判断为车与输⼊猫判断为猫的得分差异,再加上1,表⽰对损失函数的容忍程度,这⾥的1可以换成任何实数,可以⽤△表⽰。
意义在于看看判断错误的情况下,得分与判断正确的情况下的最⼤差异通过损失函数可以衡量当前的模型到底是怎么样的。
绿⾊表⽰错误的得分值,蓝⾊表⽰正确的得分值。
delta表⽰容忍程度。
svm 损失函数

svm 损失函数
SVM(支持向量机)是一种常见的监督学习模型,用于分类和回归问题。
在SVM模型中,我们最常用的是线性SVM,它是一种线性分类器,通过寻找最佳的超平面来将数据点分为不同的类别。
SVM模型的损失函数是非常重要的,因为它决定了模型的优化方式。
在SVM中,常用的损失函数是Hinge Loss(铰链损失),它可以使模型更加关注分类错误的点,从而提高模型的准确性。
Hinge Loss的公式如下:
L(y, f(x)) = max(0, 1 - y*f(x))
其中,y是真实的类别标签,f(x)是模型对样本x的预测值。
如果y*f(x) > 1,则说明模型预测正确,损失为0;如果y*f(x) < 1,则说明模型预测错误,损失为1-y*f(x)。
这个损失函数的意义是,如果模型预测错误,我们就希望损失更大,以鼓励模型更加关注分类错误的点。
在训练SVM模型时,我们的目标是最小化总损失,即:
min Σi max(0, 1 - y(i)*f(x(i))) + αΣw(i)^2
其中,第一项是Hinge Loss,第二项是正则化项,用于控制模型的复杂度。
正则化参数α越大,模型的复杂度越低,对训练数据的拟合就越差,但是对新数据的泛化能力更好。
在实际应用中,我们可以使用梯度下降等优化算法来求解这个损失函数的最小值,从而得到最佳的超平面和模型参数w。
- 1 -。
【转载】铰链损失函数(HingeLoss)的理解
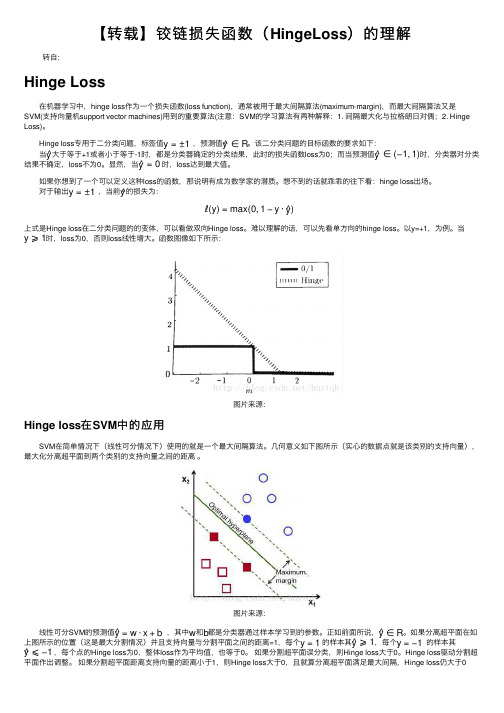
【转载】铰链损失函数(HingeLoss )的理解转⾃:Hinge Loss 在机器学习中,hinge loss 作为⼀个损失函数(loss function),通常被⽤于最⼤间隔算法(maximum-margin),⽽最⼤间隔算法⼜是SVM(⽀持向量机support vector machines)⽤到的重要算法(注意:SVM 的学习算法有两种解释:1. 间隔最⼤化与拉格朗⽇对偶;2. Hinge Loss)。
Hinge loss 专⽤于⼆分类问题,标签值,预测值。
该⼆分类问题的⽬标函数的要求如下: 当⼤于等于+1或者⼩于等于-1时,都是分类器确定的分类结果,此时的损失函数loss 为0;⽽当预测值时,分类器对分类结果不确定,loss 不为0。
显然,当时,loss 达到最⼤值。
如果你想到了⼀个可以定义这种loss 的函数,那说明有成为数学家的潜质。
想不到的话就乖乖的往下看:hinge loss 出场。
对于输出,当前的损失为:上式是Hinge loss 在⼆分类问题的的变体,可以看做双向Hinge loss 。
难以理解的话,可以先看单⽅向的hinge loss 。
以y=+1,为例。
当时,loss 为0,否则loss 线性增⼤。
函数图像如下所⽰:图⽚来源:Hinge loss 在SVM 中的应⽤ SVM 在简单情况下(线性可分情况下)使⽤的就是⼀个最⼤间隔算法。
⼏何意义如下图所⽰(实⼼的数据点就是该类别的⽀持向量),最⼤化分离超平⾯到两个类别的⽀持向量之间的距离 。
图⽚来源: 线性可分SVM 的预测值,其中和都是分类器通过样本学习到的参数。
正如前⾯所说,。
如果分离超平⾯在如上图所⽰的位置(这是最⼤分割情况)并且⽀持向量与分割平⾯之间的距离=1,每个的样本其,每个的样本其,每个点的Hinge loss 为0,整体loss 作为平均值,也等于0。
如果分割超平⾯误分类,则Hinge loss ⼤于0。
svm损失函数 合页损失

svm损失函数合页损失SVM(Support Vector Machine)是一种常用的机器学习算法,其通过寻找一个最优的超平面来对数据进行分类。
在SVM中,损失函数是非常重要的一部分,其中合页损失函数(Hinge Loss)是SVM中常用的一种损失函数。
合页损失函数可以用来衡量分类模型的性能,特别适用于二分类问题。
它的定义为:对于一个样本,如果它被正确分类,并且距离超平面的距离小于等于1,那么损失为0;如果它被正确分类,但是距离超平面的距离大于1,那么损失为距离超平面的距离;如果它被错误分类,那么损失为1。
合页损失函数的核心思想是希望将样本正确分类,并且使得分类结果与真实标签的间隔尽可能大。
对于正确分类的样本,合页损失函数的值是逐渐增大的,而对于错误分类的样本,合页损失函数的值恒定为1。
这样的设计使得合页损失函数能够鼓励模型学习到更好的分类边界,提高分类的准确性。
合页损失函数的优化可以通过梯度下降等方法进行。
梯度下降的基本思想是通过不断迭代调整模型参数来最小化损失函数。
在每一次迭代中,根据当前模型参数计算损失函数的梯度,并更新模型参数。
通过多次迭代,模型逐渐收敛到损失函数的最小值,从而得到最优的分类模型。
与其他损失函数相比,合页损失函数在一些场景下具有一定的优势。
例如,在处理具有不平衡数据集的情况下,合页损失函数能够更好地处理样本不平衡的问题。
合页损失函数对误分类的样本惩罚较大,可以减少误分类样本对模型的影响,提高模型的鲁棒性。
合页损失函数还可以与正则化项结合使用,进一步提高模型的泛化能力。
正则化项可以防止模型过拟合,避免在训练集上表现良好但在测试集上泛化能力差的情况。
总结来说,合页损失函数是SVM中常用的一种损失函数,它能够有效地衡量分类模型的性能,并通过梯度下降等方法进行优化。
合页损失函数的设计使得模型能够学习到更好的分类边界,提高分类的准确性。
在处理不平衡数据集和结合正则化项等方面,合页损失函数也具有一定的优势。
svm one class skclern 公式

svm one class skclern 公式
SVM One-Class SVM (也称为One-Class SVM 或OCSVM) 是一种特殊的支持向量机(SVM),它用于学习数据的非球形边界,并预测新数据是否属于这个边界。
这通常用于异常检测、无监督学习或聚类等任务。
以下是One-Class SVM 的基础公式:
1.决策函数:
(f(x) = \nu - \rho)
其中,(x) 是输入数据,(\nu) 是超球体的半径,而(\rho) 是数据到超球体中心的平均距离。
2.损失函数:
(L = \frac{1}{2} \nu^2 + \frac{1}{2} \sum_{i=1}^{N} \xi_i^2)
其中,(\xi_i) 是松弛变量,代表数据点到超球体边界的距离。
3.目标函数:
(J = \frac{1}{2} \nu^2 + \frac{1}{2} \sum_{i=1}^{N} \xi_i^2 - \frac{1}{2} \nu^2)
这是一个二次规划问题,可以使用各种优化算法(如SMO、SVM-LIGHT 等)来解决。
4.约束条件:
(\nu - \rho - \xi_i \geq 0)
(\xi_i \geq 0)
这表示数据点要么位于超球体内部((\rho - \xi_i > 0)), 要么位于超球体边界上((\xi_i = 0))。
简而言之,One-Class SVM 通过最小化数据点到超球体中心的平均距离和超球体的体积来学习数据的非球形边界。
这样,新数据可以根据其与这个边界的距离被分类为正常或异常。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
svm的损失函数
损失函数是机器学习中的一个重要组成部分,它可以理解为预测结果与真实结果之间的差异。
SVM的损失函数用来衡量样本分类的准确性,它可以帮助优化模型的参数,最终使模型在新样本上能更好地进行分类。
其实,SVM的损失函数就是分类问题中的交叉熵损失函数,该损失函数对于多分类问题具有很大的普遍性。
它通过计算模型预测结果与真实结果之间的差异,来度量模型的准确性。
交叉熵损失函数的公式如下:
$$L(y,f(x))=- \sum_{k=1}^K y_k\ln{f(x_k)}$$
其中,y=(y_1,y_2…y_k)是真实结果,f(x) =
(f(x_1),f(x_2)…f(x_k))是模型预测结果,K是类别数。
当模型预测结果f(x)与真实标签y相同时,损失函数L(y,f(x))达到最小值0,此时模型预测准确度最高;当模型预测结果f(x)与真实标签y不同时,损失函数
L(y,f(x))即可以概括为较大的负值,此时模型的预测准确度较低。
SVM的损失函数还可以分为线性损失函数和非线性损失函数,这两种损失函数的主要区别在于它们对模型预测结果的惩罚程度不同。
线性损失函数,也称为线性支持向量机(Linear SVM),它将模型预测结果f(x)与真实标签y之间的差异用一条直线表示,它的公式如下:
$$L(y,f(x))=||y-f(x)||^2$$
其中,||y-f(x)||表示模型预测结果f(x)与真实标签y之间的差异,若模型预测结果f(x)与真实标签y之间存在差异,损失函数L(y,f(x))会变大,此时模型的预测准确度较低。
非线性损失函数,也称为非线性支持向量机(Nonlinear SVM),它将模型预测结果f(x)与真实标签y 之间的差异用多项式函数表示,它的公式如下:
$$L(y,f(x))=(1-yf(x))_+$$
其中,(1-yf(x))_+表示模型预测结果f(x)与真实标签y之间的差异,若模型预测结果f(x)与真实标签y之间存在差异,损失函数L(y,f(x))会变大,此时模型的预测准确度较低。
总的来说,SVM的损失函数可以帮助优化模型的参数,使模型在新样本上能更好地进行分类。
它通过计算模型预测结果与真实结果之间的差异,来衡量模型的准确性,从而帮助模型更好地去学习训练样本,从而提高模型的泛化性能。
