四升五暑期奥数培优
四升五暑期奥数培优讲义——5-01-熟悉分数1-讲义-学生

第1讲 熟悉分数【例1】用分数表示下列各图中阴影部分的面积。
【趁热打铁-1】用分数表示下列各图中阴影部分的面积:【例2】填空:(1)把一根5米长的绳子平均分成3段,每段占全长的____,每段长____米。
(2)把5米长的绳子平均剪成8段,每段长是____米,每段是全长的____。
(3)76的分数单位是____,它有____个这样的分数单位,再添上____个这样的分数单位就是最小的假分数。
(4)851的分数单位是____,它有____个这样的分数单位,它比4少____个这样的分数单位。
(5)分数a 7,当a____时,a 7是真分数;当a____时,a 7是假分数;当a____时,a 7等于1。
(6)95的分数单位是_____,8个71是_____,65里有_____个61。
(7)把94的分子加上8,要使分数的大小不变,分母应该加上 。
(8)一个分数,如果分子加上1,结果是1;如果分母加上1,结果是87,原来这个分数是 。
(1)把4米长的绳子平均剪成5段,每段长是____米,每段长占全长的____。
(2)把8米长的绳子平均剪成5段,每段长____米,每段绳子是全长的____。
(3)971的分数单位是____,它再添上____个这样的单位就是4。
(4)531的分数单位是____,再添上____个这样的分数单位就变成2。
(5)分数x 9,当x ____时,x 9是真分数;当x ____时,x 9是假分数;当x ____时,x9等于1。
(6)5个17是 ;334里面有 个14; 个18是1。
(7)把83的分子增加18,要使分数的大小不变,分母应增加 。
(8)一个分数的分子扩大到原来的2倍,分母缩小到原来的21后得到41,原分数是 。
【例3】互换:(1)在直线上面的□里填上合适的分数,在下面的□里填上合适的小数。
(2)在下图的方框中填适当的数,直线上面填假分数,下面填带分数.(3) ÷ =34= ( )24= (填小数)。
四升五暑期奥数培优讲义——5-15-综合复习1-学生

第15讲 综合复习一、填空:(1)把3.2平均分成4份,每份是____;5.6里面有____个0.7;15是2.5的____倍;一个数的9倍是1.8,这个数是____。
(2)0.3856856…是____小数,循环节是____,用简便记法写作____,保留三位小数约是____。
(3)9.12÷0.24的商的最高位是____位。
(4)20÷6的商是____小数,用简便方法表示为____,保留两位小数是____。
(5)在4.555,2.333…,0.1717…,0.686868中,循环小数有 。
(6)甲数的小数点向右移1位后就和乙数相等,乙数比甲数多42.3,甲数是____。
(7)细心读题,谨慎填写。
0.125÷0.25=____÷25 ____÷0.03=1870÷38.01÷1.8=____÷____ 15÷0.04=____÷____(8)在横线处填上“>”“<”或“=”。
5.4÷9____5.4 2.8÷0.75____2.8 2.05÷0.5____20.5÷5 0.72×0.25____0.72 0.6÷0.03____6÷0.3 0.72÷2.5____0.72(9)把一根5米长的绳子平均分成3段,每段占全长的____,每段长____米。
(10)853的分数单位是____,它有____个这样的分数单位,它比4少____个这样的分数单位。
(11)把94的分子乘4,要使分数的大小不变,分母应____。
(12)94的分数单位是____,它有____个这样的分数单位。
(13)4个51是____,137里面有____个131,____个111是1。
(14)分母为6的最简真分数有____,它们的分数单位是____,分子是3的假分数有____个。
第02讲 整除问题进阶(学生版)-四升五暑期数学奥数培优讲义

一、整除问题进阶(五上)一、 两位截断与三位截断1、在1234,1144,17456789,35442,153153中,(1)哪些是7的倍数?(2)哪些是13的倍数?(3)哪些是99的倍数?2、六位数2008□□能同时被9和11整除.这个六位数是多少?第2讲 整除问题进阶知识点课堂例题3、已知九位数1234789□□能被99整除,这个九位数是__________.4、卡莉娅写了一个两位数59,墨莫写了一个两位数89,他们让小高写一个一位数放在59与89之间拼成一个五位数5989□,使得这个五位数能被7整除.请问:小高写的数是多少?□是13的倍数,□中的数字是().5、已知六位数20279A.1B.5C.7D.96、小高写了一个五位数,用方格盖住了两个数字后变成365□□,并告诉墨莫说这个五位数既是7的倍数,又是125的倍数.那么小高写的五位数可能是__________.7、用数字6,7,8各两个,要组成能同时被6,7,8整除的六位数.请写出一个满足要求的六位数.二、综合应用8、已知51位数255259555999个个□能被13整除,中间方格内的数字是多少?9、已知52位数255255555555个个□□能被13整除,中间方格内的数字是__________.10、(2011年四中入学)一个五位数abcba (相同字母表示相同数字)是7的倍数.若将它的十位和个位互换,新数是11的倍数,若将它的十位和百位互换,新数是13的倍数.那么原五位数是________.11、萱萱的爸爸买回来两箱杯子.两个箱子上各贴有一张价签,分别写着“总价117.□△元”、“总价127.○◇元”(□、△、○、◇四个数字已辨认不清,但是它们互不相同).爸爸告诉萱萱,其中一箱装了99只A 型杯子,另一箱装了75只B 型杯子,每只杯子的价格都是整数分.但是爸爸记不清每个价签具体是多少钱,也不记得哪个箱子装的是A 型杯子,哪个箱子装的是B 型杯子了.爸爸知道萱萱的数学水平很厉害,于是他想考考萱萱.萱萱看了看,说:“这可难不倒我,我刚好学了一些复杂的整除性质,这下可以派上用场了.”同学们,你能像萱萱一样把价签上的数分辨出来吗?12、能同时被7、9、11整除的最小三位数是,最大四位数是?13、一个整数能被15整除,这个整数的最后三位是215,那么这样的整数中最小是多少?14、一个五位数,它的末三位为999.如果这个数能被23整除,那么这个五位数最小是多少?1、四位数23□□能同时被9和11整除,这个四位数是__________.2、已知八位数123678□□能被99整除,这个八位数是__________.3、四位数572□能被7整除,那么这个四位数可能是__________.4、已知多位数 2010120103111333 个个能被13整除,那么中间方格内的数字是多少?1、有一个六位数,前四位是2857,即2857□□,这六位数能被143整除,则这个数的后组成的两位数为().A .12B .14C .21D .412、66ab ab 是77的倍数,则ab 最大为(). A .16B .93C .98D.99随堂练习课后作业3、在7315,58674,325702,96723,360360中,7的倍数有__________个.4、四位数33□□能同时被9和11整除,这个四位数是__________.5、四位数278□能被7整除,那么这个四位数是__________.6、(龙校五年级春季)(1)一个六位数2356□□是88的倍数,这个数除以88所得的商是________或________.(2)在□内填上适当的数字,使五位数236□□既能被3整除又能被5整除.7、(2011希望杯五年级初赛)如果六位数2011□□能被90整除,那么它的最后两位数是_________.8、已知多位数201225881258258258 个□能同时被7和13整除,方格内的数字是__________.9、已知多位数 2011120113111333 个个□能被7整除,那么中间方格内的数字是__________.10、八位数1235678a 能被7整除,a 等于多少?。
四升五奥数暑期培优考核

(0405)奥数暑期培优考核
姓名:
1.四年级和五年级一共有540人,四年级的人数是五年级的2倍。
两个年级各
有多少人?
2.买一套西服需要800元,其中裤子比上衣便宜200元。
裤子和上衣各需要多
少元?
3.简便计算:
125×32×25 1+2+3+……+20 41×24+82×88
4.一列火车车长240米,以60千米/时的速度通过一个隧道,共用2分钟。
这
个隧道长多少米?
5.挂钟5时整敲5下,20秒敲完。
那么10时整敲10下,几秒敲完?
6.把一个周长160厘米的正方形分成两个大小、形状完全一样的长方形,每个
长方形的周长是多少厘米?
7.篮子里有一些鸡蛋,4个4个数,多3个;5个5个数,多3个,篮子里至少
有多少个鸡蛋?
8.用红黄蓝绿四种信号灯组成信号,可以组成多少种不同的信号?
9.一个等腰三角形的顶角是50°,则这个三角形的底角是多少度?
10.一桶油第一次用去一半多4千克,第二次用去余下的一半少1千克,桶里还
有2千克。
这桶油原来有多少千克?。
四升五暑期奥数培优讲义——5-12-排列组合3-讲义-学生

第12讲排列组合【学习目标】1、进一步理解和应用分步计数原理和分类计数原理;2、掌握解决排列组合问题的常用策略;3、学会应用数学思想和方法解决排列组合问题。
【知识梳理】1、排列:不同元素中任意取出 m 个(m≤n)元素,按照一定的顺序排成一列,叫做从 n个不同元素中取出 m 个元素的一个排列。
2、组合:从 n 个不同元素中任意取出 m 个(m≤n)元素组成一组,不计较组内各元素的顺序,叫做从 n 个不同元素中取出 m 个元素的一个组合。
3、常用方法:(1)优先排序法——特殊位置或特殊元素(2)捆绑法——必须在一起,先捆再排(3)插空法——不能在一起,先排再插(4)排除法——正难则反(5)隔板法——相同物品放在不同位置 (或分给不同的人)【典例精析】【例1】六个人排成一排照相,有多少种排法?【趁热打铁-1】若把英语单词hero的字母写错了,则可能出现的错误共有多少种?【例2】六个人排成一排照相,若小明必须与小丽排在一起,有多少种排法?【趁热打铁-2】若小明和小丽不能排在一起,有多少种排法?【例3】正六边形的中心和顶点共 7 个点,以其中 3 个点为顶点的三角形共有多少个?【趁热打铁-3】现在有4根木棒,长度分别是4分米、6分米、8分米和10分米,从中任意取出3根木棒,能组成三角形的情况有种。
【例4】从5枚面值为1元的邮票和4枚面值为1.60元的邮票中任取1枚或若干枚,可组成不同的邮资种。
【趁热打铁-4】某学校四、五、六三个年级组织了一场文艺演出,共演出18个节目,如果每个年级至少演出4个节目,那么这三个年级演出节目数的所有不同情况共有种。
【例5】从15名同学选出5人,上场参加篮球比赛。
如果甲、乙、丙三人中恰好入选一人,共有多少种选法?【趁热打铁-5】如果甲、乙、丙不能同时都入选,共有多少种选法?【例6】从10名男生,8 名女生中选出 8 人参加游泳比赛。
在下列条件下,分别有多少种选法?(1)恰有 3 名女生入选;(2)至少有两名女生入选;【趁热打铁-6】(3)某两名女生,某两名男生必须入选;(4)某两名女生,某两名男生不能同时入选;(5)某两名女生,某两名男生最多入选两人。
四升五暑期奥数培优讲义——5-13-推理问题3-讲义-学生

第13讲推理问题【学习目标】1、掌握推理问题常用解题方法;2、通过学习推理问题,提高逻辑思维能力。
【知识梳理】我们把涉及一些相互关联的条件和因果关系的问题称为逻辑推理问题。
在解决这类问题时,我们要理解题目给的条件和导出的结论,通过分析、判断排除不合理的成分或者不可能的情况,从而做出正确的判断,找出问题的答案,通常用的方法有:①利用逻辑思维进行推理;②借助图表法进行分析推理;③对可能出现的情况进行假设,然后根据条件推理,如果推得结果和条件不矛盾,说明假设成立,如果推得结果和条件矛盾,说明假设不成立,再重新提出假设,再一次进行推理。
【典例精析】【例1】有13个外观完全相同的球,其中有一个是次品,它的重量比其余12个合格的球轻一些(合格品的重量是想等的)。
你能否用一架没有砝码的天平称三次,将次品找出来?【趁热打铁-1】老师有8个同样大小的球,其中有一个球的重量要轻一些,其他的球重量完全一样,现在有一台天平,如果只能称两次,能能找出重量最轻的球吗?【例2】标有1、2、3、4、5、6六个数字的正方体的三种不同的摆放如下图所示,请问三个正方体朝左那一面数字之和是多少?【趁热打铁-2】有一个正方体,每个面上分别写着:数、学、奥、林、匹、克,三个人从不同的角度观察的结果如图所示,请问每个汉字对面各是什么字?【例3】培培去参加奥数竞赛,她的四位同学新新、文文、雅雅、翰翰对她的分数进行了猜测。
新新说:“培培得了60分。
”文文说:“培培至少得了80分。
”雅雅说:“培培的分数不到100分。
”翰翰说:“培培最少得了50分。
”这四个猜测中只有一个猜测是对的。
请问培培究竟得了多少分?【趁热打铁-3】培培、新新、文文三位同学中有一位同学自觉将教室打扫干净。
老师问他们三人是谁打扫的教室。
培培说:“文文做的。
”文文说:“不是我打扫的。
”新新说:“也不是我扫的。
”现在只知道他们三人中只有一人说了真话,请问到底是谁打扫的教室呢?【例4】我国有“三山五岳”之说,其中五岳是指“东岳泰山,南岳衡山,西岳华山,北岳恒山和中岳嵩山.”一位老师拿出这一组山岳的图片,并在图片上标出数字,他让五位学生来识别,每人说出两个,学生回答如下:甲:2是衡山,3是华山乙:4是衡山,2是嵩山丙:1是衡山,5是恒山丁:4是恒山,3是嵩山戊:2是华山,5是泰山老师发现五个学生都只说对了一半,那么正确的说法1、2、3、4、5分别是?【趁热打铁-4】从前有三个和尚,一个讲真话,一个讲假话,另一个有时讲真话,有时讲假话,一天,一位智者遇到这三个和尚,他问第一位和尚:“你后面是哪位各尚?”和尚回答:“讲真话的.”他又问第二位和尚:“你是哪一位?”得到的回答是:“有时讲真话,有时讲假话.”他问第三位和尚:“你前面的是哪位和尚?”第三位和尚回答说:“讲假话.”根据他们的回答,智者马上分清了他们各是哪一位和尚,请你说出智者的答案.【例5】A、B、C、D、E五只球队打比赛,每两只球队之间只比赛一场。
四升五数学暑假奥数培优—页码问题3

页码问题例1、一本书共有205页,编印这本书的页码,一共要用多少个数字?例2、一本小说的页码,在排版时必须用2211个数码,这本书共有多少页?例3、一本书的页码为1至62,即共有62页。
在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次,结果得到的页码和为2000。
问:这个被多加了一次的页码是几?例4、有一本48页的书,中间缺了1张,小明将残书的页码相加,得到1131,老师说小明计算错了,你知道为什么吗?例5、排一本400页的书的页码,一共需要多少个数码"0”?例6、世界上最古老的拍卖行“苏富比”即将拍卖一本稀世的古藉。
古藉正文182页。
由于年代久远,书的16页至27页,62页至83页都被虫蛀了。
这本书中没有被虫蛀的有多少页?随堂练习1、一本书共288页,那么共需要多少个数字编页码?2、排一本小说的页码,需要用2202个数码,这本书共有多少页?3、一本书的页码为1至62,即共有62页。
在把这本书的各页的页码累加起来时,有一个页码漏加了。
结果,得到的和数为1939。
问:这个被漏加的页码是几?4、有一本96页的书,中间缺了一张。
如果将残书的所有页码相加,那么可能得到偶数吗?5、一本书有580页,问:数字“1”在页码中一共出现多少次?6、图书馆中有一本破旧不堪的书,共208页。
书的4页至8页111页至123页都因时间久远而被虫蛀掉。
这本书一共被蛀了多少页?基础拔高1、一本书共有40页,那么共需要多少个数码编页码?2、一本科幻小说共有100页,那么共需要多少个数码编页码?3、排版工人给一本书编排页码,共用去942个数字,这本书有多少页?4、小同打开数学书做作业时发现,这时左右两页的页码和是165,你知道小同打开的是哪一页吗?5、一本书共399页,编上页码:1,2,3,4,…,398,399,数字“2“在页码中共现多少次?6、从1数到456,一共数了多少个“5"?7、小刚从一本书的54页阅读到67页,苏明从95页阅读到135页,小强从180页阅到237页,他们总共阅读了多少页?8、给一本书编页码一共用了666个数字,这本书一共多少页?9、给一本书编页码,在印刷时必须用到2010个铅字(一个铅字代表一个数字)。
四升五暑期奥数培优讲义——5-05-实际应用(一)3-讲义-学生

第5讲实际应用题(一)【学习目标】1、回顾归一归总、植树、平均数等问题;2、进一步强化解题方法。
【知识梳理】1、归一问题:知道了单位数量(如:每小时行50千米,每天植5棵树,每天做10个零件),然后把它作为固定不变的量,进行相关问题的计算这种类型的应用问题,叫做归一问题。
(1)工作总量=每份的工作量(单一量)×份数(2)份数=工作总量÷每一份的工作量(3)每一份的工作量=总工作量÷份数2、归总问题:已知单位数量和计量单位数量的个数,以及不同的单位数量(或单位数量的个数),通过求总数量求得单位数量的个数(或单位数量)。
3、植树问题:这类应用题是以“植树”为内容。
研究总路程、株距、段数、棵数四种数量关系的应用题,叫作植树问题。
(1)段数=总长÷每段长(2)两端种树:棵数=段数+1(3)两端都不种:棵数=段数-1(4)一端种,一端不种:棵数=段数(5)封闭图形种树:棵数=段数4、平均数的问题:把一个总数平均分成几个相等的数,这个相等的数值就叫做平均数。
(1)平均数=总数÷份数;(2)移多补少(基准数法)。
【典例精析】【例1】服装厂加工一批校服,计划每天加工260套,25天完成,现在要提前5天完成,现在每天加工多少件?【趁热打铁-1】一辆汽车从南充到成都每小时行驶80千米,花一个半小时行驶了一半路程。
为了提前到达目的地,时速提高到100千米。
这样行完全程共用多少小时?【例2】8个工人3小时制作机器零件360个,如果人数缩小了2倍,时间增加了5小时,可制作机器零件多少个?【趁热打铁-2】红星粮食加工厂,3台磨面机4小时可磨面粉16.8吨,现在增加到8台磨面机,要磨面粉72.8吨,需要多少小时?【例3】一件工程原计划20个人36天完成,现在要提前6天完成,需要增加人。
【趁热打铁-3】一项工程,6人每天工作4小时要5天才能完成,照这样计算,如果增加4人,每天工作减少1小时,可提前 天完成。
四升五暑期奥数培优讲义——5-09-容斥原理4-讲义-教师

第9讲 容斥原理【学习目标】1、理解容斥原理的研究的范围;2、掌握容斥原理的分析方法;3、学会利用相关分析方法解题。
【知识梳理】1、容斥原理:对n 个事物,如果采用不同的分类标准,按性质a 分类与性质b 分类(如图),那么具有性质a 或性质b 的事物的个数=N a +N b -N ab 。
2、常用工具:韦恩图,线段图,方程,高斯记号3、常见题型:数论,几何。
【典例精析】【例1】五年级的学生一共有42人,参加奥数补习的有30人,参加语文补习的有25人,所有五年级学生都至少补习奥数和语文中的一门。
请问五年级中两门都补习的学生有多少人?30+25-42=13(人)【趁热打铁-1】实验小学五年级一班共有40名同学采集标本,每个同学至少要采集一种标本。
采集昆虫标本的有28人,采集植物标本的有19人,两种都采集的有多少人?28+19-40=7(人)【例2】星星艺术团有32名同学,其中有14人会拉小提琴,有21人会弹钢琴,小提琴和钢Nab NbNa琴都会的8人,既不会小提琴又不会弹钢琴的有多少人?32-(14+21-8)=5(人)【趁热打铁-2】学校组织100名家长去香港旅游,其中有10人既不懂英语又不懂粤语,有75人懂英语,83人懂粤语。
既懂英语又懂粤语的有多少人?(75+83)-(100-10)=68(人)【例3】在1到100的自然数中,既不是5的倍数也不是6的倍数的数有多少个?5的倍数:100÷5=20(个)6的倍数:100÷6≈16(个).5和6的倍数:100÷30≈3(个)100-(20+16-3)=67(个)【趁热打铁-3】在1到200的全部自然数中,既不是5的倍数又不是8的倍数的数有多少个?5的倍数:200÷5=40(个)8的倍数:200÷8=25(个)5和8的倍数:200÷40=5(个)200-(40+25-5)=140(个)【例4】奥斑马、小美、欧欧给100盆花浇水.奥斑马浇了78盆,小美浇了68盆,欧欧浇了85盆.那么,至少有______盆花被浇了三次水。
四升五年级暑假 奥数培优训练年龄问题

8x4=32(岁)
答:孩子8岁,爸爸妈妈都为32岁.
4、爷爷今年72岁,孙子今年12岁,几年后爷爷的年龄是孙子的
5倍?几年前爷爷的年龄是孙子的13倍?
解:①爷爷是孙子年龄5倍时,孙子的年龄:
(72-12)÷(5-1)=15(岁)
②几年后:15-12=3(年)
③爷爷年龄是孙子的13倍时,孙子的年龄:
(72-12)÷(13-1)=5(岁)
④几年前:12-5=7(年)
答:3年后,爷爷是孙子年龄的5倍;7年前,爷爷年龄是孙子的13倍.
5、兄弟二人三年后的年龄和是26岁,弟弟今年的年龄恰好是兄弟二人年龄差的2倍.请问3年后兄弟二人各几岁?
解:年龄差:(26-3-3)÷(2+2+1)=4(岁)
哥哥:(26+4)÷2=15(岁)
弟弟:26-15=11(岁)
答:3年后哥哥15岁,弟弟11岁.
6、小明今年9岁,父亲39岁,再过多少年父亲的年龄正好是小明年龄的2倍?。
四升五暑期奥数培优讲义——5-06-实际应用(二)3-讲义-学生

第6讲实际应用题(二)【例1【趁热打铁-1】两个桶里共盛水32.6斤,若把第一个桶里的水倒2.7斤到第二个桶里,两个桶里的水就一样多,则第一个桶原有斤水。
【例2】甲、乙两筐共装苹果76.8千克,从甲筐取出5.2千克苹果放人乙筐里,甲筐苹果还比乙筐多3.4千克.甲、乙两筐原各有苹果多少千克?【趁热打铁-2】哥哥和弟弟共有零花钱62.8元,哥哥给了弟弟13.3元后,弟弟就比哥哥多4.2元,哥哥与弟弟原有零花钱多少元?【例3】丽丽沿着学校长方形操场四周跑了3圈,共跑了1440米.已知这个长方形操场的长宽相差60米,那么操场的面积是____平方米.【趁热打铁-3】把一个减法算式的被减数、减数、差加起来和是180,已知减数比差大26,被减数、减数和差各是多少?【例4】一个两位小数,若去掉它的小数点,得到的新数比原数多47.52,这个两位小数是。
【趁热打铁-4】小雨今年12岁,爸爸今年40岁,再过年,爸爸的年龄正好是小雨的3倍。
【例5】甲厂人数比乙厂少540人,若从两厂各调走600人,乙厂人数恰好是甲厂人数的4倍.求甲厂原有多少人?【趁热打铁-5】今年小春的年龄比他哥哥的年龄小18岁,再过3年小春的年龄将是他哥哥年龄的一半,那么小春今年____岁.【例6】已知被除数比除数大78,并且商是 6,余数是 3,求被除数与除数之积.【趁热打铁-6】一个整除算式,被除数比商大126,除数是7,求被除数.【例7】甲、乙两数之和是473,已知乙数的末尾是0,如果把末尾的0去掉,正好等于甲数,则甲数是。
【趁热打铁-7】一个减法算式里,被减数、减数、差的和等于160,并且差是减数的3倍,则差是_____。
【例8】一个小数,如果把它的小数部分扩大5倍,它就变成17.92;如果把它的小数部分扩大8倍,它就变成20.38,则这个小数是多少?【趁热打铁-8】一桶油,连桶重 36.5千克,把油加到原来的3倍,连桶重104.6千克,原来桶中有油______千克,桶重_____千克。
四升五数学暑假奥数培优—用假设法解应用题4

用假设法解决问题例1、李师傅要给超市运送200千克的水果,每千克运费10元,但是因为天气炎热,双方约定了要是水果腐烂了,每千克腐烂的水果不但不给运费,还要赔偿超市3元。
运完后,李师傅一共赚得1636元,问运送过程中共有多少千克水果腐烂了?练一练1.小王是大巴车司机,晴天每天可载客10次,雨天每天可载客8次,这一周他一共载客66次。
这一周中有几天是雨天?2.有甲、乙两个工程队一起修建一段公路,要是甲工程队单独修的话要12天完成,乙程队单独修的话要24天完成,两队一起修建了几天后,甲工程队临时有事不能来修建,所以能由乙工程队来继续修建,一共修建了14天完成,请问两队一起修建了几天?例2、小明、小华、小芳、小新四人上山摘苹果,他们一共摘了61个苹果,小华比小芳少摘5个,小芳比小明多摘10个,小新比小芳少摘4个,问他们每人摘了多少个苹果?练一练1.六一儿童节到了,老师给学习小组的同学发礼物,老师准备了笔记本和铅笔,笔记本和铅笔的数量的比是4:9,给每个同学发2本笔记本和3支铅笔,结果发现笔记本刚好发完,但是铅笔还剩6支,学习小组一共有多少个同学?2.王叔根买了一些牛奶,放在甲乙两个桶里,两个桶都未装满。
如果把甲桶里的牛奶倒入乙桶,乙桶装满后,甲桶还剩10升;如果把乙桶牛奶全部倒进甲桶,甲桶还能再装20升。
已知甲桶的容量是乙桶的3倍。
请问:王叔叔一共买回多少升牛奶?例3、母亲节小明出去卖牡丹花,20元一束,但是买的人不太多,所以小明为了不亏本,把价格降低了,降价后,来买的人翻了倍,赚的4问小明把花价降了多少钱?钱多了原来的5练一练题得5分,做错一1.今天语文考试,卷子里有20道选择题,做对一题倒扣2分,若某同学得了86分,那么他做对多少题,做错多少题?2.有5元、10元和100元的纸币59张,共计2755元。
其中5元的和10元的张数相等,种纸币分别有多少张?例4、小明和小华都喜欢打篮球,今天他们准备进行投球比赛,约定每投中一次计2分,投不中倒扣1分,两人各投了20次,两人共计62分,其中小华比小明多得12分,同小明、小华两人各投中了多少次?练一练1.宏程公司现有甲、乙两个仓库存储水泥,甲仓库储存的水泥是乙仓库的3倍还多20袋,为了平衡两个仓库的存储,现从甲仓库运210袋水泥到乙仓库,此时甲、乙仓库存储的水泥数量相同,请问甲、乙两仓库各自原有水泥多少袋?2.小红喜欢集邮,而且喜欢按价值把邮票分开放。
四升五数学暑假奥数培优—还原问题5

还原问题例1、一个数减24加上15,再乘以8得432,求这个数是多少?练一练1.某数加上3,乘以5,再减去8,等于12。
求某数是多少?2.某数加2,乘5,再减3得27。
这个数是几?例2、小马虎在做一道加法题目时,把个位上的1看成了7,十位上的9看成了4,结果得到的和是148。
问正确的结果应是多少?练一练1.小明在做一道加法计算题时,把个位上的4看成7,十位上的8看成2,结果和是306。
正确的答案应该是多少?2.小英在做一道整数减法题时,把减数个位上的1看成7,把减数十位上的?7看成1,结果得出差是111问:正确答案是几?例3、工人们修一段路,第一天修的公路比全长的一半还多1千米,第二天修的比余下的一半还少3千米,还剩15千米没有修。
问公路的全长是多少千米?练一练1.一捆电线,第一次用去了全长的一半多3米,第二次用去余下的一半多5米,还剩下7米。
这捆电线原来长多少米?2、仓库里有一批大米,第一天售出的质量比总数的一半多12吨,第二天售出的质量比剩下的一半多12吨,结果还剩下12吨。
问这个仓库原有大米多少吨?例4、李奶奶卖鸡蛋,她上午卖出总数的一半多10个,下年又卖出剩下的一半多10个,最后还剩65个鸡蛋没有卖出。
李奶奶原来有多少个鸡蛋?练一练1.竹篮内有若干个李子,取它的一半又ー个给第一人,再取余下的一半又两个给第二人,剩下的李子平均分给余下的两个人,每人3个。
竹篮内原有李子多少个?2.兄弟俩争着挑26块砖,弟弟抢着装了一些,哥哥看弟弟挑得太多,就抢去一半,弟弟不服,哥哥就还给弟弟5块,这时两人一样多。
问弟弟最初准备挑多少块?例5、树林里放着一堆苹果,有50个小朋友轮流从苹果堆里取苹果,取的规则是:每次都要拿出这堆苹果总数的一半,然后再放回一个,直到所有的小朋友都取过为止,地上还剩两个苹果,问地上原有多少个苹果?练一练1.有一篮鸡蛋,第一次取出一半多2个,第二次取出余下的一半多2个,第三次取出8个,篮里还剩下2个鸡蛋。
四升五暑期奥数培优讲义——5-02-小数除法3-讲义-学生

第2讲小数除法【例1】列竖式计算并验算:25.2÷60= 34.5÷1.5= 5.6÷0.04=【趁热打铁-1】列竖式计算并验算:1.8÷12= 1.8÷1.2= 7.83÷9=【例2】计算下面各题,商保留一位小数。
(1)14.36÷2.7≈(2)8.33÷6.2≈(3)1.7÷0.03≈【趁热打铁-2】计算下面各题,商保留两位小数。
(1)32÷42≈(2)1.25÷1.2≈(3)2.41÷0.7≈【例3】循环小数:(1)在0.6666、1.5353……、3.1415926……、••3641.3、•52.2、••72.4、••92754.6、0.19292、0.32727……中,是有限小数,是无限小数,是循环小数。
(2)0.586÷0.11的商是小数,商的最高位是位,保留两位小数取商的近似值是,保留四位小数取商的近似值是。
【趁热打铁-3】(1)在0.333…,0.555,2.6363,3.9595…,5.233434…中,是循环小数的、。
(把循环小数改写成简写形式)(2)5.8÷4.5的商用循环小数表示是,循环节是,商的最高位是位,保留三位小数取商的近似值是。
(3)把•13.2、••13.2、••2132.、••212.3按从小到大的顺序排列:。
【例4】下面各题的商是循环小数的用循环小数表示,不是循环小数的保留两位小数:17.6÷2.7= 35.5÷4.6≈【趁热打铁-4】下面各题的商是循环小数的用循环小数表示,不是循环小数的保留两位小数: 100÷6 3.38÷1.8≈【例5】先说说运算顺序,再进行计算:7.85÷0.25÷4 9.37-13.05÷2.9【趁热打铁-5】先说说运算顺序,再进行计算:5.04÷(12.54-4.14) 0.64÷1.6+8.4÷2.1【例6】培培去美国旅游,带了5000元人民币,能换多少美元?(美元兑换人民币6.31元)(得数保留两位小数)【趁热打铁-6】新新到香港旅游,买了一台3800港元的学习机,折合成人民币多少元?(1港元兑换人民币0.79元)【例7】一辆摩托车每小时行42km,一辆小轿车的速度是它的2倍。
四升五数学暑假奥数培优—测试练习题

阶段测试一、填一填1、平平期末考试语文、数学、英语的平均成绩是94分,已知语文得了95分,英语得了92分,数学得了()分。
2、一个三位小数四舍五入为5.00,这个数最小是(),最大是()。
3、2分和5分的硬币共15枚,币值共51分,2分硬币()枚,5分硬币()枚。
4、如果A*B表示(A-2)×B,那么6*7=()5、有一列数:1,4,3,5,1,4,3,5,1,4,3,5⋯⋯第125个数是()。
6、一个数加上5,减去3,乘以4,除以6,等于24,这个数是()。
7、找规律填空。
3、5、9、15()、()。
二、计算(能简算的要简算,前4题每题3分,后2题每题4分)96×47+96×52+96 56×8+88×4125×64×25 9+99+999+9999+99999 1+2+3+4+5+6+7+8+9+⋯⋯+69+7050-49+48-47+46-45+⋯⋯+4-3+2-1三、解决问题1、学校需买一些足球和排球,若买1个足球和3个排球需要100元,若买2个足球和3个排球则需要140元。
买一个足球和一个排球共需要多少钱?2、王琳在商店买筷子10双、碗5个共付50元,已知每双筷子是每个碗价格的2倍,每双筷子和每个碗各多少元?3、修一条马路。
第一天修的长度比马路总长的一半少5米,第二天修的长度比余下的一半多2米,还剩25米没有修,这条路总共多少米?4、小青在做一道加法题目时,把其中一个加数个位上的6看成了9,把十位上的的8看成了3,结果得到的和是196,问正确的结果应是多少?5、鸡兔同笼,鸡比兔多12只,共有脚204,求鸡兔各有几只?6、有红、紫、蓝三块布,共长98米,红布比紫布多7米,蓝布比紫布少8米,求这三块布分别长多少米?7、小红、小丽、小敏三个人各有年历片若干张。
如果小红给小丽13张,小丽给小敏23张,小敏给小红3张,那么她们每人各有40张。
四升五暑期奥数培优讲义——5-03-加减巧算3-讲义-学生

第3讲加减巧算【学习目标】1、掌握加法中的速算技巧;2、熟悉整数、小数、分数在计算时的联系。
【知识梳理】1、加减法或者乘除法中的巧算:(1)移数凑整法:(2)借数凑整法:(3)拆数凑整法:(4)找“基准数”法:(5)分组凑整法。
2、等差数列:(1)等差数列的和=(首项+末项)×项数÷2(2)末项=首项+公差×(项数-1)(3)项数=(末项-首项)÷公差+13、公式计算:(1)1+2+3+……+n=(1+n)n÷2(2)1+3+5+……+(2n-1)=n²(3)1+2+3+……+(n-1)+n+(n-1)+(n-2)+……+3+2+1=n²【典例精析】【例1】用简便方法计算下面各题:(1)866-201 (2)3568-(199+568)(3)3842﹣1567﹣433﹣842 【趁热打铁-1】用简便方法计算下面各题:(1)30.1-19.9 (2)356.45-(19.9+56.45)(3)564.65-45.54-54.46-64.65【例2】怎样简便就怎样计算。
(1)9+99+999+9999+99999 (2)8+18+28+38+48+58+68+78+88+98【趁热打铁-2】怎样简便就怎样计算。
(1)0.9+9.9+99.9+999.9+9999.9 (2)1991+199.1+19.91+1.991【例3】计算:60+65+59+58+57+62+61+60+55+64【趁热打铁-3】计算:59.8+60.1+59.5+58.4+60.2+60.5+59.9+59.7+61.6+60.9 【例4】计算:1234+2345+3456+4567+5678+6789【趁热打铁-4】计算:12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.23【例5】计算:2000-111-89-112-88-113-87-114-86-115-85-116-84【趁热打铁-5】计算:0.0625+0.125+0.1875+0.25+0.3125+0.375+0.4375+0.5+0.875+0.625+0.6875+0.75+0.8125 【例6】计算:2+4+6+8+…+98+100【趁热打铁-6】计算:1.001+1.005+1.009+1.013+…+1.197.【例7】一个等差数列的第1项是4.1,公差是3.1,其中最后一项是50.6,求所有项的和。
四升五数学暑假奥数培优—复习练习题2

复习题二1、孙佳有2分、5分硬币共40枚,共是1元7角。
两和硬币各有多少枚?2、有一元、二元、五元的汽车票50张,总面值116元。
已知一元的比五元的多2张,问三种面值的汽车票各有几张?3、有3元、5元、7元的汽车票400张,总面值1920元。
其中7元的和5元的张数相等,三种面值的汽车票各有多少张?4、小兔妈采姑,晴天每天可采32个,雨天每天具能采22个,它一共采了390个,平均每天采26个。
这些天中有几天下雨?5、搬运1000只玻璃瓶,规定安全送到一只可得到运费3角。
如果打碎一只,不仅不给运费,还要赔偿5角。
如果运完后共得运费260元,那么搬运中打碎了多少只玻璃瓶?6、一批水泥,用小车装载,要用45辆:用大车装载,只要36辆。
已知每辆大车比小车多装4吨,问这批水泥有多少吨?7、12张兵乓球台上同时有34人在进行兵乓球比赛,正在进行单打的球台有多少张?8、某次数学竞共20道题,评分标准是毎做对一道题得5分,每做错一题道題1分。
刘亮参加了这次竞赛,得了64分,刘亮做对了多少道题?9、人民路小学的教师和学生共100人去栽树,教师每人栽3棵,学生平均每3人栽1棵,一共栽树100棵。
那么,有多少名学生参加栽树?10、甲、乙、内、丁四人上山摘桃子,已知他们共摘了80个桃子,甲比乙少摘8个,丙比甲少摘14个,丁和丙摘的一样多,他们每人摘了多少个桃子?1、王叔叔拿工资若干元,从工资中拿出一半多10元存入银行,又拿出余下的一半多5元买米、油,剩下80元买菜。
王叔叔拿工资多少元?2、联通公司出售手机,第・个月售了的比总数的・半多2部,第二个月售出的比第一个月剩下的一半多15部,还剩75部。
原有手机多少部?3、耕一块地,第一天耕的比整块地的一半少5公顷,第二天耕的比余下的一半多2公頃,第三大耕了20公顷后还剩下5公顷。
这块地有多少公顷?4、小芳在做一道加法题时,由于粗心,将个位上的5看作9,把位上的8看作3,结果所得的和是123。
四升五暑假奥数提优综合训练
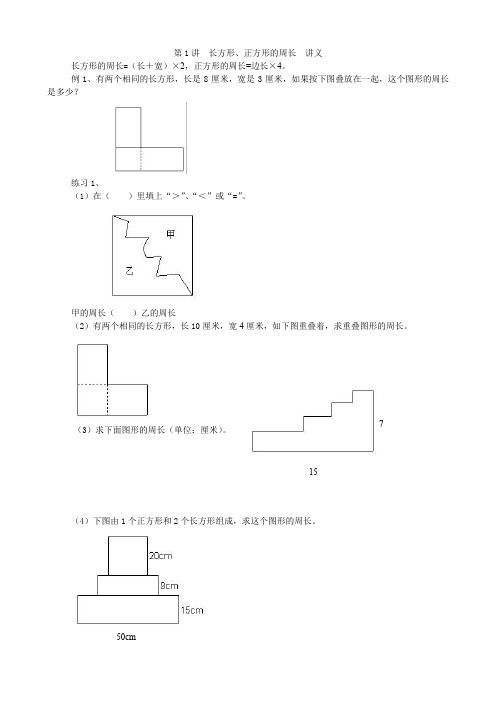
第1讲 长方形、正方形的周长 讲义长方形的周长=(长+宽)×2,正方形的周长=边长×4。
例1、有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是多少?练习1、(1)在( )里填上“>”、“<”或“=”。
甲的周长( )乙的周长(2)有两个相同的长方形,长10厘米,宽4厘米,如下图重叠着,求重叠图形的周长。
(3)求下面图形的周长(单位:厘米)。
(4)下图由1个正方形和2个长方形组成,求这个图形的周长。
715例2 有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
思路与导航根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。
因此,所求周长是18×4=72厘米。
练习2、(1)、有6块边长是2厘米的正方形,如例题中所说的这样重叠着,求重叠后图形的周长。
(2)下图中的每一小段的长度都相等,求图形的周长。
例3、下图由8个边长都是2厘米的正方形组成,求这个图形的周长。
练习3、(1)求下面图形的周长(单位:厘米)。
(2)下面是一个零件的平面图,图中每条短线段都是5厘米,零件长35厘米,高30厘米。
这个零件的周长是多少厘米?例4 已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?练习4、(1)下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
(2)有一张长40厘米,宽30厘米的硬纸板,在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒,求被剪后硬纸板的周长。
(3)下面三个正方形的面积相等,剪去阴影部分的面积也相等,求原来正方形的周长发生了什么变化?(单位:厘米)例5 一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?练习5、(1)一个长12厘米,宽2厘米的长方形和两个正方形正好拼成下图(1)所示长方形,求所拼长方形的周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四升五暑期奥数培优
二、和差问题
例题一、三四年级共植树128棵,四年级比三年级多植树20棵,求三、四年级各植树多少棵?
1、两堆石子共有800吨,第一堆比第二堆多200吨,两堆各有多少吨?
2、用锡和铝混合制成600千克的合金,铝的质量比锡多400千克,锡和铝各是
多少千克?
3、养鸡场养了540只鸡,其中母鸡比公鸡多50只,养鸡场养的公鸡和母鸡各
有多少只?
例题二、今年小勇和妈妈两个人年龄的和是38岁;3年前,小勇比妈妈小26岁。
问今年妈妈和小勇各多少岁?
1、今年小刚和小强两个人的年龄和是21岁;1年前,小刚比小强小3岁。
问今
年小强和小刚各多少岁?
2、黄茜和胡敏两人今年的年龄和是23岁,4年后,黄茜将比胡敏大3岁。
问她
们4年后各多少岁?
例题三、甲乙两个仓库共有大米800袋,如从甲仓库中取出25袋放到乙仓库中,则甲仓库比乙仓库还多8袋。
求两个仓库原来各有多少袋大米?
1、一个书架分上下两层,共放有图书100本。
如果从上层取出5本放入下层,
那么上层比下层还多6本。
问原来上、下两层各有图书多少本?
2、两箱零件共102个,从甲箱拿出24个放入乙箱后,甲箱还比乙箱多4个。
原来两箱各放有多少个零件?
例题四、小东的图书中有58本书不是故事书,有42本不是科技书,小东故事书和科技书共有60本。
问小东科技书有多少本?
1、一篇树林里有很多种树,有1500棵树不是松树,1200棵树不是树,松树和
树共有700棵。
树有多少棵?
2、某次数学测验中,四(2)班有16人不是考的九十几分,有40人不是考的
八十几分,考八十几分和九十几分的共50人,考八十几分的有多少人?
三、还原问题
例题一、有一个数,把它乘4以后减去46,再把所得的差除以3,然后减去10,最后得4.你知道这个数是多少吗?
1、一个数加上6,乘6,减去6,其结果等于36.求这个数。
2、一个数的3倍加上6,再减去9,最后乘以2,结果等于60.求这个数。
3、有一个数加上11,减去12,乘13,除以14,结果是26.这个数是多少?
例题二、某商场出售洗衣机,上午售出总数的一半多10台,下午售出剩下的一半多20台,还剩95台。
这个商场原来有洗衣机多少台?
1、粮库里有一批大米,第一次运出总数的一半多3吨,第二次运出剩下的一半
多5吨,还剩下4吨,问粮库原来有大米多少吨?
2、爸爸买了一些橘子,全家人第一天吃了这些橘子的一半多1个,第二天吃了
剩下的一半多1个,第三天又吃掉了剩下的一半多1个,还剩下1个,问爸爸买了多少个橘子?
例题三、小明、小强和小勇三人共有故事书60本。
如果小强向小明借3本后,又借给小勇5本,结果三人拥有故事书的本数相等。
这三人原来各有故事书多少本?
1、甲乙丙三个小朋友共有贺卡90,如果甲给乙3,乙又送给丙5,
那么三人的
贺卡数正好相同。
甲乙丙三个小朋友原来各有贺卡多少?
2、小红、小丽、小敏三个人各有年历片若干。
如果小红给小丽13,小丽给小敏
23,小敏给小红3,那么她们每人各有40。
原来三人各有年历片多少?
例题四、甲乙两桶油各有若干千克。
如果要从甲桶中倒出和乙桶同样多的油放入乙桶,再从乙桶倒出和甲桶同样多的油放入甲桶,这时两桶油恰好都是36千克,问两桶油原来各有多少千克?
1、王亮和强各有画片若干,如果王亮拿出和强同样多的画片送给强,强再拿出
和王亮同样多的画片给王亮,这时两个人都有24。
问王亮和强原来各有
画片多少?
2、甲、乙、丙三个小朋友各有玻璃球若干个,如甲按乙现有的玻璃球个数给乙,
再按丙现有的个数给丙之后,乙也按甲、丙现有的个数分别给甲、丙。
最后,丙也按同样的方法给甲和乙,这是他们三个人都有32个玻璃球,问
原来每个人各有多少个玻璃球?
四、植树问题
例题一、城中小学在一条大路边从头至尾栽28棵树,每隔6米栽一棵,这条大路长多少米?
1、在一条马路一边从头到尾植36棵树,没相邻两棵树间隔8米,这条马路有
多长?
2、同学们在做早操,21个同学排成一排,每相邻两个同学之间的距离相等,第
一个人到最后一个人的距离是40米。
相邻两个人间隔多少米?
3、一条路长200米,在路的一旁从头至尾每隔5米植一棵树,一
共要植树多少
棵?
例题二、在一个周长是240米的游泳池周围栽树,每隔5米栽一棵,一共要栽多少棵树?
1、一个鱼塘的周长是1500米,沿鱼塘周围每隔6米栽一棵树,需要栽多少棵
树?
2、在圆形水池边,每隔3米种一棵树,共种60棵,这个水池的周长是多少米?
例题三、在一座长800米的大桥两边挂彩灯,起点和终点都挂,一共挂了202盏,相邻两盏之间的距离都相等。
求相邻两盏灯之间的距离。
1、在一条长100米的大路两边各栽一行树,起点和终点都栽,一共栽52棵,
每相邻两棵树之间的距离相等。
求相邻两棵树之间的距离。
2、一座长400米的大桥两边挂彩灯,每两盏相隔4米,从桥头到桥尾一共装了
多少盏灯?
例题四、一位木工锯一根长19米的木料,他先把一头损坏部分锯下来1米,然后锯了5次,锯成同样长的短木条。
每条短木条长多少米?
1、有一位工人把长12米的圆钢锯成了3米长的小段,锯断一次要5分钟。
共
需要多少分钟?
2、有一根圆钢长22米,先锯下2米,剩下的锯成每根都是4米的小段,又锯
了几次?
例题五、有一栋十层的大楼,由于停电,电梯停开,某人从1层走到3层需要30秒,照这样计算,他从3层走到10层需要多少分钟?
1、把6米长的木料平均锯成3段要6分钟,照这样计算,如果锯
成6段需要几
分钟?
2、时钟4点钟敲4下,6秒钟敲完,那么12点钟敲12下,多少秒钟敲完?
五、盈亏问题
例题一、学校将一批铅笔奖给三好学生。
如果每人奖9支,则缺45支;如果每人奖7支,则缺7支。
三好学生有多少人?铅笔有多少支?
1、将月季花插入一些花瓶中。
如果每瓶插8朵,则缺少15朵;如果每瓶插6
朵,则缺少朵。
求花瓶的只数和月季花的朵数。
2、老师将一些练习本发给班上的学生。
如果每人发10本,则有两名学生没分
到;如果每人发8本,则正好发完。
问有多少名学生?多少本练习本?
例题二、学校给一批新入学的学生分配宿舍。
如果每个房间住12人,则34人没有位置;如果每个房间住14人,则空出4个房间。
求学生宿舍有多少间?住宿学生有多少人?
1、某校有若干学生寄宿学校,若每间宿舍住6人,则多出34人;若每间宿舍
住7人,则多出4间宿舍。
问宿舍多少间?寄宿学生有多少人?
2、学校分配宿舍。
如果每个房间住6人,则少2间宿舍;如果每个房间住9人,
则空出2个房间。
问学生宿舍有多少间?住宿学生有多少人?
3、三一班学生去公园划船,如果每条船坐4人,则少1条船;如果每条船坐6人,则多出4条船。
公园里有多少条船?三一班有多少个学生?。
