2015年希望杯四年级第一试试题解析
2015年第十三届小学希望杯全国数学邀请赛四年级第一试决赛试题及答案详解

2015年全国数学竞赛试题用7棵树栽6排,使每排3棵,用图来表示。
四年级数学奥数“希望杯”测试题(第一试)学校:班级:姓名:号次:一、我是计算小能手。
(6+6 共12分)四、解答。
(每15分一题共60分)列递等式计算: 1.在12÷( )=( )……()中,可能1.(7777+8888)÷5-(888-777)×3 出现余数多少?2 .100-98+96-94+92-90+…+4-2 2.四位数的四个数字都是偶数,百位数字是2,则这样的四位数有多少个?二、填空。
(7+7+7 共21分)1.故事书共160页,在它的页码中,数字“2”出现了 3.最大的三位数与最小的三位数的差是( )次。
合数还是质数?2.在16时16分,钟表上时针和分针的夹角为()。
3.盒子中有4个球,编号分别为1、2、3、4每次摸出两个球,将其编号相减(大减小),则差是() 4.若P和P+5都是质数,求(24P+1).的可能性大。
(20P+1)的值。
三、我是绘画小高手。
(7分)希望杯试题1 希望杯试题22015年全国数学竞赛试题答案120°+8°-96°=32°四年级数学奥数“希望杯”测试题(第一试)三、略一、50.3000 四、1.0、1、2、3、4、5、12详解: 2.1001、原式=(100+96+92+…+4)-(98+94+90+…+2) 3.合数,详解:999-100=899=29=25×(100+4)÷2-25×(98+2)÷2 ×31=25×(104-100)÷2 4.2009=25×4÷2=502、原式=16665÷5-111×3=3333-333=3000二、36.32°.1详解:2、360°÷12×4=120°360°÷60×16=96°360°÷(12×60)×16=8°。
2015小学四年级希望杯数学竞赛答案(1)

2015小学四年级希望杯数学竞赛及答案第十三届“希望杯”全国数学邀请赛四年级第1试来是9,百位是4,所以是在1492年。
一、1.49 2.46 3.3.844 10、周六4.23 5.16 6.11 二、111095 61050 21 497.630 8.6 9.1492 10.六详解:详解: 1.原式=7+97+997+9997+999971.原式=7×7=49 =(10-3)+(100-3)+(1000-3)+(10000-3)+(100000-3)2.除周围4个小圆外,中间小圆的规律是1×2,2 =(10+100+1000+10000+100000)-3×5×3,3×4,……,第6个图有6×7+4=46个小圆。
=111110-15=1110953. 3.844亿米2、4.略4.和23,差1,所以商是23。
附说明和*差=23,而 3.原式=(1+5+9+...+41)-(3+7+11+ (39)23只能是=23*1 =231-210=215.原来8个数的和是8×8=64,后来变成了7×8=56,小了8,所以原数是8+8=166.有10种属相,10+1=11人就可以满足条件。
抽屉问题7.要保持母鸡是公鸡的6倍,母鸡增加60,公鸡就要增加360,所以360-60=300就是差的2倍,现在有150只母鸡,原来有90只母鸡,一共养了630只鸡。
8.对于图c来说,每个小方块都摞了2层,最多有6块。
9、肯定是1×××年,16-1=15,百位,十位与个位和是15,十位加1后,数字和是15+1=16,此时十位和个位和是6的倍数,个位不是1,只能是2,十位原。
2011-2015希望杯四年级第1试解析

第九届“希望杯”全国数学邀请赛四年级 第1试2011年3月13日 以下每题6分,共120分。
1. 计算:(7777+8888)÷5—(888—777)×3= .2. 计算:1+11+21+…+1991+2001+2011= .3. 在小于30的质数中,加3以后是4的倍数的是 .4. 小于100的最大的自然数与大于300的最小的自然数的和,是不大于200的最大的自然数的 倍.5. 既是6的倍数又是8的倍数的所有两位数的和是 .6. 四年级一班2个小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会打乒乓球又会下象棋,那么这两个小组中既不会打乒乓球又不会下象棋的有 人.7. 按照左侧四个图中数的规律,在第五个图中填上适当的数:6135241642534253161642538. 已知9个数的乘积是800,将其中一个数改为4,这9个数的乘积是200,若再将另外一个数改为30,则这9个数的乘积变为1200.则这两个被改动的数以外的7个数的乘积是 .9. 如图1,△ABC 的面积为36,点D 在AB 上,BD=2AD ,点E 在DC 上,DE=2EC ,则△BEC 的面积是 .E DC B AO 60︒20︒E DC B AF B图1 图2 图310.今年,李林和他爸爸的年龄的和是50岁,4年后,他爸爸的年龄比他的年龄的3倍小2岁,则李林的爸爸比他大 岁.11.某次考试,A 、B 、C 、D 、E 五人的平均分是90分.若A 、B 、C 的平均分是86分,B 、D 、E 的平均分是95分,则B 的得分是 .12.如图2,已知直线AB 和CD 交于点O ,若∠AOC=20°,∠EOD=60°,则∠AOE= °,∠BOC= °13.如图3,四边形ABCD 与CEFG 是边长相等的正方形,且B 、C 、G 在一条直线上,则图中共有 个正方形, 个等腰直角三角形.14.一个水桶里有水,若将水加到原来的4倍,桶和水共重16千克;若将水加到原来的6倍,桶和水共重22千克.则桶内原有水 千克,桶重 千克.15.某个两位数的个位数字和十位数字的和是12,个位数字和十位数字交换后所得两位数比原数小36,则原数是 .16.王强步行去公园,回来时坐车,往返用了一个半小时,如果他来回都步行,则需要2个半小时,那么他来回都坐车,则需 分钟.17.图4中“C ”形图形的周长是 厘米.图4 18.如图5,从1,2,3,4,5,6,中选出5个数填在图中的空格内,使填好的格内的数右边的比左边的大,下边的比上边的大,则共有 种不同的填法.19.三个连续自然数中最小的数是9的倍数,中间的数是8的倍数,最大的数是7的倍数,则这三个数的和最小是 .20.甲、乙、丙、丁、戊五人猜测全班个人学科总成绩的前五名:甲:“第一名是D ,第五名是E .” 乙:“第二名是A ,第四名是C .”丙:“第三名是D ,第四名是A .” 丁:“第一名是C ,第三名是B .”戊:“第二名是C ,第四名是B .”若每个人都只猜对一个人的名次,且每个名次只有一个人猜对,则第一、二、三、四、五名分别是 .2012年“希望杯”全国数学邀请赛四年级初试试题1. 小慧从开始站立的A 点向西走了15米,到达B 点,接着从B 点向东走了23米,到达C 点,那么从C 点到A 点的距离是______米。
小学四年级希望杯历年数学竞赛试题与答案1_14届(最新全套完整版)

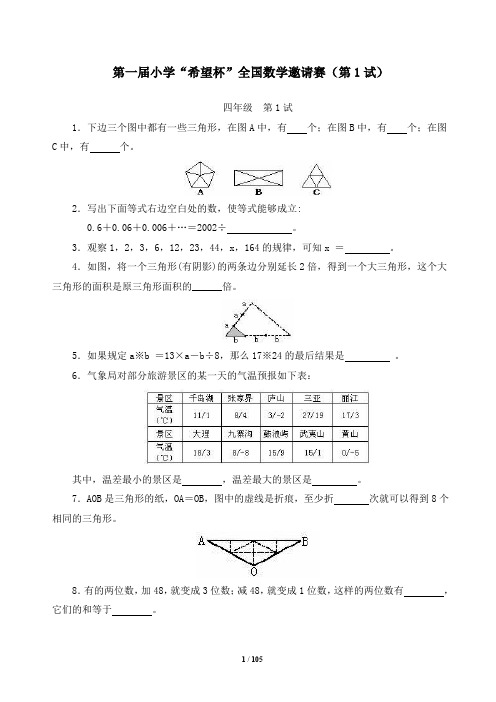
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
希望杯数学竞赛第一届至十三历届四年级全部试题与答案打

教育精品资料目录1.第一届小学“希望杯”全国数学邀请赛〔第1试〕 (2)2. 第一届小学“希望杯”全国数学邀请赛〔第2试〕 (5)3. 第二届小学“希望杯”全国数学邀请赛〔第1试〕 (7)4. 第二届小学“希望杯”全国数学邀请赛〔第2试〕 (10)5. 第三届小学“希望杯”全国数学邀请赛〔第1试〕 (12)6. 第三届小学“希望杯”全国数学邀请赛〔第2试〕 (15)7. 第四届小学“希望杯”全国数学邀请赛〔第1试〕 (17)8. 第四届小学“希望杯”全国数学邀请赛〔第2试〕 (20)9. 第五届小学“希望杯”全国数学邀请赛〔第1试〕 (22)10. 第五届小学“希望杯”全国数学邀请赛〔第2试〕 (24)11. 第六届小学“希望杯”全国数学邀请赛〔第1试〕 (26)12. 第六届小学“希望杯”全国数学邀请赛〔第2试〕 (28)13. 第七届小学“希望杯”全国数学邀请赛〔第1试〕 (30)14. 第七届小学“希望杯”全国数学邀请赛〔第2试〕 (34)15. 第八届小学“希望杯”全国数学邀请赛〔第1试〕 (37)16. 第八届小学“希望杯”全国数学邀请赛〔第2试〕 (39)17. 第九届小学“希望杯”全国数学邀请赛〔第1试〕 (41)18. 第九届小学“希望杯”全国数学邀请赛〔第2试〕 (43)19. 第十届小学“希望杯”全国数学邀请赛〔第1试〕 (45)20. 第十届小学“希望杯”全国数学邀请赛〔第2试〕 (47)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛〔第1试〕四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C 中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
2020年第十三届小学数学“梦想杯”全国数学邀请赛试卷(四年级第1试)

2015年第十三届小学“希望杯”全国数学邀请赛试卷(四年级第1试)一、填空题:1.(3分)计算:2468×629÷(1234×37)=.2.(3分)有一个除法算式,被除数和除数的和是136,商是7,则除数是.3.(3分)定义:a⊕b=a+b+ab,则(2⊕3)⊕4的值为.4.(3分)买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔支.5.(3分)王雷是国庆节那天出生的,若他年龄的3倍减去8刚好是他出生那月的总天数,则王雷今年岁.6.(3分)数一数,图中共有个三角形.7.(3分)某班30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,后来这4位同学赶到了比赛场地,分别跳了26,27,28,29个.这时全班同学的平均成绩是个.8.(3分)明明临摹一本字帖练习毛笔字,临摹第一遍时,他每天写25个字,临摹第二遍时,他每天多写3个字,结果刚好比第一遍少用了3天,则这本字帖共有字.9.(3分)如图有16个1×1的小正方形组成,图中△ABC的面积是.10.(3分)乌龟和兔子在全长为1000米的赛道上比赛,兔子的速度是乌龟速度的15倍.但兔子在比赛的过程中休息了一会儿,醒来时发现乌龟刚好到达终点,而此时兔子还差100米才到终点.则兔子休息期间乌龟爬行了米.11.(3分)任意一个一位奇数与任意一个一位偶数相乘,不同的乘积有个.12.(3分)一个长方形的相框长为40厘米,宽为32厘米,放入一张长为32厘米宽为28厘米的相片,则相框中没有被照片覆盖的部分的面积是平方厘米.13.(3分)爷爷,爸爸,小明的年龄分别是60岁,35岁,11岁,则再过年爷爷的年龄等于小明和爸爸年龄的和.14.(3分)一个长方形的长和宽都增加3厘米后,面积增加了90平方厘米,则原长方形的周长是厘米.15.(3分)甲筐和乙筐内原来分别放有54个和63个鸡蛋,若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍,那么应从乙筐内取出个鸡蛋放入甲筐.16.(3分)王蕾和姐姐从家步行去体育馆打羽毛球,已知姐姐每分钟比王蕾多走20米,25分钟后姐姐到体育馆,这时姐姐发现没有带球拍,于是立即按原路返回取球拍,在离体育馆300米的地方遇到了王蕾,则王蕾家到体育馆的路程是米.17.(3分)如图,用小正方形摆成下列图形,按摆放规律,第25个图形需要小正方形个.18.(3分)若abc+cba=1069,则这样的abc有个.19.(3分)某地希望杯组委会给参加希望杯考试的考生安排考场,若每个考场安排30名考生,则会有一个考场有26名考生;若每个考场安排26个考生,则会有一个考场有20名考生,并且要比前一种方案多用9个考场,则该地区参加考试的考生有个.20.(3分)如图有3个边长是6的正方形组成,则图中阴影部分的面积是.2015年第十三届小学“希望杯”全国数学邀请赛试卷(四年级第1试)参考答案与试题解析一、填空题:1.(3分)计算:2468×629÷(1234×37)=34.【分析】根据除法的性质进行简便计算.【解答】解:2468×629÷(1234×37)=2468×629÷1234÷37=2468÷1234×(629÷37)=2×17=34故答案为:34.【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.2.(3分)有一个除法算式,被除数和除数的和是136,商是7,则除数是17.【分析】方法一:被除数和除数的和是136,商是7,说明被除数是除数的7倍,被除数与除数的和就是除数的(7+1)倍,用136除以(7+1)即可求出除数,由此求解;方法二:根据被除数=商×除数,设除数是x,则被除数就是7x,再根据“被除数与除数的和是136”,列出方程并解方程即可.【解答】解:方法一:136÷(7+1)=136÷8=17答:除数是17.方法二:设除数是x,被除数是7x,由题意得:7x+x=1368x=136x=17答:除数是17.故答案为:17.【点评】解决本题可以看成和倍问题进行求解:两数和÷倍数和=1倍的数;也可以设出未知数,根据被除数、除数和商三者之间的关系找出等量关系列出方程求解.3.(3分)定义:a⊕b=a+b+ab,则(2⊕3)⊕4的值为59.【分析】根据题意得出a⊕b等于a加上b再加上a与b的积,由此利用此方法计算(2⊕3)⊕4的值,据此解答.【解答】解:(2⊕3)⊕4=(2+3+2×3)⊕4=11⊕4=11+4+11×4=59故答案为:59.【点评】先理解新运算的计算方法,然后按照先算小括号再算括号外的顺序带入数据计算即可.4.(3分)买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔8支.【分析】1元7角=1.7角,求用15元钱最多可以买这样的水彩笔多少支,就是求15里面有几个1.7,用除法解答即可.【解答】解:1元7角=1.7角15÷1.7≈8(支)答:用15元钱最多可以买这样的水彩笔8支.故答案为:8.【点评】本题考查了有余数除法应用题,要注意得数用“去尾法”求值.5.(3分)王雷是国庆节那天出生的,若他年龄的3倍减去8刚好是他出生那月的总天数,则王雷今年13岁.【分析】因为国庆节在10月,10月有31天,所以根据“他年龄的3倍减去8刚好是他出生那月的总天数,”知道王雷的年龄的3倍再减去8等于31,由此先求出王雷年龄的3倍,再求出王雷的年龄.【解答】解:(31+8)÷3=39÷3=13(岁);答:王雷今年13岁.故答案为:13.【点评】解答此题的关键是知道10月有31天,再根据“王雷的年龄的3倍再减去8等于31”这个数量关系解决问题.6.(3分)数一数,图中共有24个三角形.【分析】不在同一直线上三点可以确定一个三角形,据此即可求解.【解答】解:(5+1+1+1+1)+(4+2+2+1)+3+2+1=9+9+3+2+1=24(个)答:图中共有24个三角形.故答案为:24.【点评】本题主要考查了三角形的认识,按正确的顺序计算三角形的个数是解决本题的关键.7.(3分)某班30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,后来这4位同学赶到了比赛场地,分别跳了26,27,28,29个.这时全班同学的平均成绩是21个.【分析】根据30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,先算出30﹣4=26人的成绩,(30﹣4)×20=520,然后再加上26、27、28、29,再除以30即可解答.【解答】解:(30﹣4)×20=520(个)520+26+27+28+29=630(个)630÷30=21(个)答:这时全班同学的平均成绩是21个.故答案为:21.【点评】本题考查了平均数的含义以及应用.8.(3分)明明临摹一本字帖练习毛笔字,临摹第一遍时,他每天写25个字,临摹第二遍时,他每天多写3个字,结果刚好比第一遍少用了3天,则这本字帖共有700字.【分析】设临摹第一遍时,用了x天,则临摹第二遍时用了x﹣3天,根据等量关系:临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字,列方程解答即可得临摹第一遍时天数,再求这本字帖共有多少页即可.【解答】解:设临摹第一遍时,用了x天,25x=(25+3)×(x﹣3)25x=28x﹣843x=84x=28,28×25=700(字)答:这本字帖共有700字.故答案为:700.【点评】本题考查了列方程解应用题,关键是根据等量关系:临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字,列方程.9.(3分)如图有16个1×1的小正方形组成,图中△ABC的面积是7.【分析】正方形减去边上三个直角三角形的面积即可求解;正方形的边长4,左上角三角形的底是4,高是2;右下角三角形的底是1,高是4;左下角三角形的底是3,高是2,把这些数据代入正方形和三角形的面积公式求解即可.【解答】解:4×4﹣4×2÷2﹣4×1÷2﹣3×2÷2=16﹣4﹣2﹣3=7答:图中△ABC的面积是7.故答案为:7.【点评】此题解答的关键在于把要求三角形的面积转化成正方形的面积与另外三个三角形的面积差,再分别根据它们的面积公式求解.10.(3分)乌龟和兔子在全长为1000米的赛道上比赛,兔子的速度是乌龟速度的15倍.但兔子在比赛的过程中休息了一会儿,醒来时发现乌龟刚好到达终点,而此时兔子还差100米才到终点.则兔子休息期间乌龟爬行了940米.科技新闻网:##科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料,我们是国内外最新的科技新闻网。
【杯赛真题】2015年第十三届小学希望杯四年级一试真题详解

真题
答案
详解
奥数网∣择校、杯赛、教育
为了大家更好的备考杯赛奥数君从今天起会陆续发布一些杯赛的历年真题给大家真题是杯赛复习的一个重要参考家一起学习起来吧
【杯赛真题】2015年第十三届小学希望杯四年级一试真题详解
希望杯作为全国性杯赛之一,在小升初择校中起着举足轻重的作用,大家需要重视起来。
第十二--十五届小学“希望杯”邀请赛四年级第1试赛及答案

第十二届小学“希望杯”全国数学邀请赛四年级第Ⅰ试试题2014年3月16日上午8:30至10:00以下每题6分,共120分1、过元旦时,班委会用730元为全班同学每人买了一份价值17元的纪念品,剩余16元,那么,这个班共有学生()名。
2、买5斤黄瓜用了11元8角,比买4斤西红柿少用1元4角,那么,每斤西红柿的价格是()元()角。
3、图1是4×4的方格图,有3个小正方形有阴影,若再将一个小正方形涂阴影,使方格图成为轴对称图形,则不同的涂法有()种。
4、小东和小荣同时从甲地出发到乙地,小东每分钟行50米,小荣每分钟行60米,小荣到达乙地后立即返回,若两人从出发到相遇用了10分钟,则甲、乙两地相距()米。
5、如图2,从一张长50厘米、宽20厘米的长方形纸片上剪去边长分别是12厘米和4厘米的两个正方形,则剩余部分图形的周长是()厘米。
6、图3是长方形,将它分成7部分,至少要画()条直线。
7、甲、乙两个油桶中共有100千克油,将乙桶中的15千克油注入甲桶,此时甲桶中的油是乙桶中的油的4倍。
那么,原来甲桶中油比乙桶中的油多()千克。
8、甲、乙、丙三校合办画展,参展的画中,有41幅不是甲校的,有38幅不是乙校的,甲、乙两校参展的画共43幅,那么,丙校参展的画有()幅。
9、一个正方形的面积与一个长方形的面积相等,若长方形的长是1024,宽是1,则正方形的周长是()。
10、如图4,每个小正方形的边长都是1,那么。
图中面积为2的阴影长方形共有()个。
11、如图5,将一张圆形纸片对折,再对折,又对折,……,到第六次对折后,得到的扇形的面积是5,那么,圆形纸片的面积是()。
12、自然数a 是3的倍数,a -1是4的倍数,a -2是5的倍数,则a 最小是()。
13、四年级的两个班共有学生72人,其中有女生35人,四(1)班有学生36人,四(2)班有男生19人,则四(1)班有女生()人。
14、如图6,阴影小正方形的边长是2,最外边的大正方形的边长是6,则正方形 ABCD 的面积是()。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【通用】小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【推荐】小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
(完整版)全国四年级希望杯数学竞赛全部试题与答案

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
2015年第十三届小学“希望杯”全国数学邀请赛试卷(四年级第1试)

2015年第十三届小学“希望杯”全国数学邀请赛试卷(四年级第1试)一、填空题:1.(3分)计算:2468×629÷(1234×37)=.2.(3分)有一个除法算式,被除数和除数的和是136,商是7,则除数是.3.(3分)定义:a⊕b=a+b+ab,则(2⊕3)⊕4的值为.4.(3分)买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔支.5.(3分)王雷是国庆节那天出生的,若他年龄的3倍减去8刚好是他出生那月的总天数,则王雷今年岁.6.(3分)数一数,图中共有个三角形.7.(3分)某班30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,后来这4位同学赶到了比赛场地,分别跳了26,27,28,29个.这时全班同学的平均成绩是个.8.(3分)明明临摹一本字帖练习毛笔字,临摹第一遍时,他每天写25个字,临摹第二遍时,他每天多写3个字,结果刚好比第一遍少用了3天,则这本字帖共有字.9.(3分)如图有16个1×1的小正方形组成,图中△ABC的面积是.10.(3分)乌龟和兔子在全长为1000米的赛道上比赛,兔子的速度是乌龟速度的15倍.但兔子在比赛的过程中休息了一会儿,醒来时发现乌龟刚好到达终点,而此时兔子还差100米才到终点.则兔子休息期间乌龟爬行了米.11.(3分)任意一个一位奇数与任意一个一位偶数相乘,不同的乘积有个.12.(3分)一个长方形的相框长为40厘米,宽为32厘米,放入一张长为32厘米宽为28厘米的相片,则相框中没有被照片覆盖的部分的面积是平方厘米.13.(3分)爷爷,爸爸,小明的年龄分别是60岁,35岁,11岁,则再过年爷爷的年龄等于小明和爸爸年龄的和.14.(3分)一个长方形的长和宽都增加3厘米后,面积增加了90平方厘米,则原长方形的周长是厘米.15.(3分)甲筐和乙筐内原来分别放有54个和63个鸡蛋,若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍,那么应从乙筐内取出个鸡蛋放入甲筐.16.(3分)王蕾和姐姐从家步行去体育馆打羽毛球,已知姐姐每分钟比王蕾多走20米,25分钟后姐姐到体育馆,这时姐姐发现没有带球拍,于是立即按原路返回取球拍,在离体育馆300米的地方遇到了王蕾,则王蕾家到体育馆的路程是米.17.(3分)如图,用小正方形摆成下列图形,按摆放规律,第25个图形需要小正方形个.18.(3分)若abc+cba=1069,则这样的abc有个.19.(3分)某地希望杯组委会给参加希望杯考试的考生安排考场,若每个考场安排30名考生,则会有一个考场有26名考生;若每个考场安排26个考生,则会有一个考场有20名考生,并且要比前一种方案多用9个考场,则该地区参加考试的考生有个.20.(3分)如图有3个边长是6的正方形组成,则图中阴影部分的面积是.2015年第十三届小学“希望杯”全国数学邀请赛试卷(四年级第1试)参考答案与试题解析一、填空题:1.(3分)计算:2468×629÷(1234×37)=34.【分析】根据除法的性质进行简便计算.【解答】解:2468×629÷(1234×37)=2468×629÷1234÷37=2468÷1234×(629÷37)=2×17=34故答案为:34.【点评】完成本题要注意分析式中数据,运用合适的简便方法计算.2.(3分)有一个除法算式,被除数和除数的和是136,商是7,则除数是17.【分析】方法一:被除数和除数的和是136,商是7,说明被除数是除数的7倍,被除数与除数的和就是除数的(7+1)倍,用136除以(7+1)即可求出除数,由此求解;方法二:根据被除数=商×除数,设除数是x,则被除数就是7x,再根据“被除数与除数的和是136”,列出方程并解方程即可.【解答】解:方法一:136÷(7+1)=136÷8=17答:除数是17.方法二:设除数是x,被除数是7x,由题意得:7x+x=1368x=136x=17答:除数是17.故答案为:17.【点评】解决本题可以看成和倍问题进行求解:两数和÷倍数和=1倍的数;也可以设出未知数,根据被除数、除数和商三者之间的关系找出等量关系列出方程求解.3.(3分)定义:a⊕b=a+b+ab,则(2⊕3)⊕4的值为59.【分析】根据题意得出a⊕b等于a加上b再加上a与b的积,由此利用此方法计算(2⊕3)⊕4的值,据此解答.【解答】解:(2⊕3)⊕4=(2+3+2×3)⊕4=11⊕4=11+4+11×4=59故答案为:59.【点评】先理解新运算的计算方法,然后按照先算小括号再算括号外的顺序带入数据计算即可.4.(3分)买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔8支.【分析】1元7角=1.7角,求用15元钱最多可以买这样的水彩笔多少支,就是求15里面有几个1.7,用除法解答即可.【解答】解:1元7角=1.7角15÷1.7≈8(支)答:用15元钱最多可以买这样的水彩笔8支.故答案为:8.【点评】本题考查了有余数除法应用题,要注意得数用“去尾法”求值.5.(3分)王雷是国庆节那天出生的,若他年龄的3倍减去8刚好是他出生那月的总天数,则王雷今年13岁.【分析】因为国庆节在10月,10月有31天,所以根据“他年龄的3倍减去8刚好是他出生那月的总天数,”知道王雷的年龄的3倍再减去8等于31,由此先求出王雷年龄的3倍,再求出王雷的年龄.【解答】解:(31+8)÷3=39÷3=13(岁);答:王雷今年13岁.故答案为:13.【点评】解答此题的关键是知道10月有31天,再根据“王雷的年龄的3倍再减去8等于31”这个数量关系解决问题.6.(3分)数一数,图中共有24个三角形.【分析】不在同一直线上三点可以确定一个三角形,据此即可求解.【解答】解:(5+1+1+1+1)+(4+2+2+1)+3+2+1=9+9+3+2+1=24(个)答:图中共有24个三角形.故答案为:24.【点评】本题主要考查了三角形的认识,按正确的顺序计算三角形的个数是解决本题的关键.7.(3分)某班30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,后来这4位同学赶到了比赛场地,分别跳了26,27,28,29个.这时全班同学的平均成绩是21个.【分析】根据30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个,先算出30﹣4=26人的成绩,(30﹣4)×20=520,然后再加上26、27、28、29,再除以30即可解答.【解答】解:(30﹣4)×20=520(个)520+26+27+28+29=630(个)630÷30=21(个)答:这时全班同学的平均成绩是21个.故答案为:21.【点评】本题考查了平均数的含义以及应用.8.(3分)明明临摹一本字帖练习毛笔字,临摹第一遍时,他每天写25个字,临摹第二遍时,他每天多写3个字,结果刚好比第一遍少用了3天,则这本字帖共有700字.【分析】设临摹第一遍时,用了x天,则临摹第二遍时用了x﹣3天,根据等量关系:临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字,列方程解答即可得临摹第一遍时天数,再求这本字帖共有多少页即可.【解答】解:设临摹第一遍时,用了x天,25x=(25+3)×(x﹣3)25x=28x﹣843x=84x=28,28×25=700(字)答:这本字帖共有700字.故答案为:700.【点评】本题考查了列方程解应用题,关键是根据等量关系:临摹第一遍的时间×每天写25个字=临摹第二遍的时间×第二遍时每天写的字,列方程.9.(3分)如图有16个1×1的小正方形组成,图中△ABC的面积是7.【分析】正方形减去边上三个直角三角形的面积即可求解;正方形的边长4,左上角三角形的底是4,高是2;右下角三角形的底是1,高是4;左下角三角形的底是3,高是2,把这些数据代入正方形和三角形的面积公式求解即可.【解答】解:4×4﹣4×2÷2﹣4×1÷2﹣3×2÷2=16﹣4﹣2﹣3=7答:图中△ABC的面积是7.故答案为:7.【点评】此题解答的关键在于把要求三角形的面积转化成正方形的面积与另外三个三角形的面积差,再分别根据它们的面积公式求解.10.(3分)乌龟和兔子在全长为1000米的赛道上比赛,兔子的速度是乌龟速度的15倍.但兔子在比赛的过程中休息了一会儿,醒来时发现乌龟刚好到达终点,而此时兔子还差100米才到终点.则兔子休息期间乌龟爬行了940米.【分析】根据题意,兔子一共跑了1000﹣100=900(米),因为兔子的速度是乌龟的15倍,所以在兔子跑的同时乌龟跑了900÷15=60(米),而实际乌龟跑了1000米,所以它在兔子睡着的时候乌龟跑了1000﹣60=940(米),解决问题.【解答】解:1000﹣(1000﹣100)÷15=1000﹣900÷15=1000﹣60=940(米);答:兔子休息期间乌龟爬行了940米.故答案为:940.【点评】此题的解答思路:先求出兔子一共跑的路程,再根据兔子速度是乌龟的5倍,求出在兔子跑的同时乌龟跑的路程,进而解决问题.11.(3分)任意一个一位奇数与任意一个一位偶数相乘,不同的乘积有19个.【分析】因为0是最小的偶数,5个奇数(1,3,5,7,9)乘4个偶数(2、4、6、8)一共是4×5=20个数,去掉得数是18和得数是6的两个相同的,还有18个,再加上0,就是19个,据此解答.【解答】解:5个奇数(1,3,5,7,9)乘偶数(2、4、6、8)一共是5×4=20个得数,去掉3×6=2×9,2×3=1×6两个相同的,还有18个,再加上0,就是19个;答:不同的乘积有19个;故答案为:19.【点评】关键是别忘记把相同的乘积给减去,注意0是偶数.12.(3分)一个长方形的相框长为40厘米,宽为32厘米,放入一张长为32厘米宽为28厘米的相片,则相框中没有被照片覆盖的部分的面积是384平方厘米.【分析】放入一张长为32厘米宽为28厘米的相片,则被照片覆盖的部分的面积是这张相片的面积,分别求出相框和相片的面积,然后用相框的面积减去相片的面积即可.【解答】解:40×32﹣32×28=32×(40﹣28)=32×12=384(平方厘米)答:相框中没有被照片覆盖的部分的面积是384平方厘米.故答案为:384.【点评】此题考查了长方形面积公式的灵活运用.13.(3分)爷爷,爸爸,小明的年龄分别是60岁,35岁,11岁,则再过14年爷爷的年龄等于小明和爸爸年龄的和.【分析】设经过x年后爷爷的年龄等于小明和爸爸年龄的和,那么经过x年后,爷爷,爸爸,小明的年龄分别是:60+x,35+x,11+x,根据“爷爷的年龄等于小明和爸爸年龄的和”列出方程解答即可【解答】解:设经过x年后爷爷的年龄等于小明和爸爸年龄的和,由题意得:35+x+11+x=60+x2x+46=60+xx=14,答:经过14年后爷爷的年龄等于小明和爸爸年龄的和.故答案为:14.【点评】本题等量关系明显,用方程较易解决.14.(3分)一个长方形的长和宽都增加3厘米后,面积增加了90平方厘米,则原长方形的周长是54厘米.【分析】根据题意,长和宽分别增加了3厘米,这个长方形的面积就增加了90平方米(如下图):增加的面积包括2部分,下面的长方形,面积是3(3+a),右上角的小长方形,面积是3b,它们的和是3(3+a)+3b等于90,求出a+b的和,再用(a+b)×2计算即可.【解答】解:设长方形原来的长是a厘米,宽是b厘米,现在的长是a+3厘米,宽是b+3厘米,图下图:3(3+a)+3b=909+3a+3b=90a+b=2727×2=54(平方厘米)答:原长方形的周长是54厘米.【点评】此题主要考查长方形周长的计算,关键是求出原来长方形的长与宽的和,再根据长方形的公式解答.15.(3分)甲筐和乙筐内原来分别放有54个和63个鸡蛋,若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍,那么应从乙筐内取出24个鸡蛋放入甲筐.【分析】甲筐和乙筐内原来分别放有54个和63个鸡蛋,总共有54+63=117个鸡蛋;若要使甲筐内的鸡蛋个数变为乙筐内的鸡蛋个数的两倍,这两筐的鸡蛋总数不变,还是117个,根据和倍公式求出这时乙筐的鸡蛋个数,即117÷(2+1)=39个,那么乙筐比原来少的就是放入甲筐的个数,即63﹣39=24个.【解答】解:54+63=117(个)117÷(2+1)=117÷3=39(个);63﹣39=24(个).答:应从乙筐内取出24个鸡蛋放入甲筐.故答案为:24.【点评】本题关键是两筐鸡蛋总个数不变,根据倍数关系,由和倍公式求出后来乙筐鸡蛋的个数,然后再进一步解答.16.(3分)王蕾和姐姐从家步行去体育馆打羽毛球,已知姐姐每分钟比王蕾多走20米,25分钟后姐姐到体育馆,这时姐姐发现没有带球拍,于是立即按原路返回取球拍,在离体育馆300米的地方遇到了王蕾,则王蕾家到体育馆的路程是1500米.【分析】在离图书馆300米处相遇时,王蕾和姐姐的路程差为300×2=600米,由于姐姐每分钟比王蕾多走20米,因此两人相遇时经历的时间是=30分钟,然后可得姐姐走300米的时间,进而可得姐姐的速度,从而可求得王蕾家到图书馆的路程.【解答】解:在离图书馆300米处相遇时,王蕾和姐姐的路程差为300×2=600(米),两人相遇时经历的时间==30(分钟),姐姐返回走的300米花费的时间=30﹣25=5(分钟),姐姐的速度==60(米/分钟),王雷家到图书馆的路程=60×25=1500(米)答:王蕾家到体育馆的路程是1500米.故答案为:1500.【点评】本题考查了相遇问题,关键在于能根据相遇时两人的路程差求出相遇时经历的时间.17.(3分)如图,用小正方形摆成下列图形,按摆放规律,第25个图形需要小正方形625个.【分析】观察得知:第一个图有1个正方形形组成,即12个;第二个图有1+3=4个正方形形组成,即22个;第三个图有1+3+5=9个正方形形组成,即32个;第四个图有1+3+5+7=16个正方形形组成,即42个;…以此类推:第n个图有1+3+5+7+…+.2n﹣1=n2个正方形形组成.据此解答即可.【解答】解:由分析可得:第25个图形需要小正方形:1+3+5+7+…+49=252=625(个)答:第25个图形需要小正方形625个.故答案为:625.【点评】解答本题的关键是:正确找出第几个图与所含正方形形个数的关系,进而得出它们之间的关系.18.(3分)若abc+cba=1069,则这样的abc有8个.【分析】解:(1)abc+cba=100a+10b+c+100c+10b+a=101a+101c+20b=101×(a+c)+20b=1069;(2)根据101×(a+c)+20b=1069的个位数字9可知:a+c 的个位一定是9;又因为a、c最大值均不超过9,因此a+c=9,可得b一定是8;(3)分析a+c=9有多少种情况:因为a、c 都出现在第一位上,因此均不可能为0.然后推出当a=1、2、3、4、5、6、7、8 时c的值,解决问题.【解答】解:(1)由abc+cba=1069,可得abc+cba=100a+10b+c+100c+10b+a=101a+101c+20b=101×(a+c)+20b=1069;(2)因为101×(a+c)+20b=1069的个位数字9,a+c 的个位一定是9;又因为a、c最大值均不超过9,因此a+c=9,可得b一定是8;(3)因为a+c=9,因为a、c 都出现在第一位上,因此均不可能为0.当a=1 时,c=8;当a=2 时,c=7;当a=3时,c=6;当a=4时,c=5;当a=5时,c=4;当a=6时,c=3;当a=7时,c=2;当a=8时,c=9;因此每种组合对应着一种情况,故abc存在8个不同的数.综上,这样的abc有8个.故答案为:8.【点评】此题由关系式入手,101×(a+c)+20b=1069的个位数字9,从而得出a+c 的个位一定是9,这是解题的关键.19.(3分)某地希望杯组委会给参加希望杯考试的考生安排考场,若每个考场安排30名考生,则会有一个考场有26名考生;若每个考场安排26个考生,则会有一个考场有20名考生,并且要比前一种方案多用9个考场,则该地区参加考试的考生有1736个.【分析】首先分析把题意转换为标准的盈亏问题,转换为30人的考场则少4人,26人的考场则多26×8+20=228人即可求解.【解答】解:依题意可知:题意转换为30人的考场则少4人,26人的考场则多26×8+20=228人.考场个数为(228+4)÷(30﹣26)=58(场).学生共58×30﹣4=1736(人)故答案为:1736【点评】本题考查对盈亏问题的理解和运用,关键问题是分析出两次的盈亏数字,问题解决.20.(3分)如图有3个边长是6的正方形组成,则图中阴影部分的面积是36.【分析】如图,灰色小长方形加上灰色直角三角形加上阴影部分正好是一个梯形.梯形的上底等于小正方形边长的,下底和高都等于正方形边长的2倍,由此可求出梯形的面积;灰色长方形的长等于小正方形的边长,宽等于长的一半,由此可求出小长方形的面积;灰色直角三角形的面积两直角边分别是小正方形边长的2倍、小正方形边长,由此可求出这个直角三角形的面积;梯形面积﹣灰色长方形面积﹣灰色三角形面积=阴影部分面积.【解答】解:如图,(6×+6×2)×(6×2)÷2﹣6××6﹣6×2×6÷2=(3+12)×12÷2﹣6××6﹣6×2×6÷2=15×12÷2﹣6××6﹣6×2×6÷2=90﹣18﹣36=36,故答案为:36.【点评】此题是考查组成图形的面积,通过辅助部分组成一直角梯形,面积可求,两辅助部分面积也可求,梯形面积减去两辅助部分面积就是阴影部分面积.。
第十三届希望杯四年级试题及详解

.
.、
那么 2 3 4=11 4=11+4+11 4=59
4.
买一支水彩笔需要 1 元 7 角,用 15 元钱最多可以买这样的水彩笔 【出处】2015 希望杯四年级初赛第 4 题 【考点】应用题 【难度】☆☆ 【答案】8 【解析】1 元 7 角相当 17 角,15 元相当于 150 角. 可列出如下算式: 150 17=8...14 故最多可赛第 11 题 【考点】加乘原理——计数 【难度】☆☆☆☆ 【答案】19 【解析】(1)一位数奇数有:1、3、5、7、9;一位数偶数有 0、2、4、6、8. (2)0 和任意数相乘得数相同,因此 0 与奇数相乘的不同乘积有:1 个; 2、4、6、8 和奇数相乘得意得到的乘积有: 4 5 20 个. 法一:计算找相同乘积 通过计算可知: 2 3 6 1;2 9 6 3 重复了 2 个; 因此不同的乘积有: 20 1 2 19 个. 法二:通过因数分析找相同乘积 (i) 8 里面有 3 个 2 相乘,而 2、4、6 均没有 3 个 2,奇数里没有 2,故 8 和任 意奇数相乘的结果不会和其他偶数与奇数相乘的结果相同. (ii) 4 里面有 2 个 2,而 2、6、8 均不是有 2 个 2,奇数里没有 2,故 4 和任意 奇数相乘的结果不会和其他偶数与奇数相乘的结果相同. (iii) 2 和 6 里面都有 1 个 2 因数,因此可能会出现相同的乘积; 6 里面还有 3 这个因数,因此要想相同,2 乘的另一个奇数一定是 3 的倍 数,因此可以很快检验出 2 3 6 1;2 9 6 3 这两个乘积结果重复了. 因此不同的乘积有: 20 1 2 19 个. 12. 一个长方形的相框长为 40 厘米,宽为 32 厘米,放入一张长为 32 厘米宽为 28 厘米的相片,则相框 中没有被照片覆盖的部分的面积是______平方厘米. 【出处】2015 希望杯四年级初赛第 12 题 【考点】面积——几何 【难度】☆☆ 【答案】384 【解析】由题意可知: 40 32 32 28 32 40 28 384 平方厘米. 13. 爷爷,爸爸,小明今年的年龄分别是 60 岁,35 岁,11 岁,则再过_______年爷爷的年龄等于小明和 爸爸年龄的和.
小学四年级希望杯历年数学竞赛试题与答案1-13届

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
全国四年级希望杯数学竞赛全部试题与答案

第一届小学“盼望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式可以成立:0.6+0.06+0.006+…=2002÷。
3.视察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的倍。
5.假如规定a※b =13×a-b÷8,那么17※24的最终结果是。
6.气象局对局部旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.是三角形的纸,=,图中的虚线是折痕,至少折次就可以得到8个一样的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任教师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园教师给几组小挚友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小挚友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比拟小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影局部的面积是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 相遇时,姐姐比王蕾多走了: 300 2=600 米. (2) 姐姐和王蕾花费的时间相同,姐姐每分钟比王蕾多走 20 米,相遇时一共多走了 600 米, 因此他们从家到体育馆花费了: 600 20=30 分钟. (3) 25 分钟姐姐到达体育馆,可知后来的 300 米姐姐花费了 30 25=5 分钟;因此姐姐的速 度为: 300 5 60 (米/分). (4) 家到体育馆的距离为: 60 25 1500 米. 17. 如图 3,用小正方形摆成下列图形,按摆放规律,第 25 个图形需要小正方形______个.
【出处】2015 希望杯四年级初赛第 18 题 【考点】位置原理——数论 【难度】☆☆☆ 【答案】8 【解析】(1)通过位值原理可得:
abc cba 100a 10b c 100c 10b a 101a 101c 20b 101 a c 20b 1069
【出处】2015 希望杯四年级初赛第 10 题 【考点】行程问题 【难度】☆☆☆ 【答案】940 【解析】(1)乌龟走 1000 米,兔子走了: 1000 100 900 米; (2)因为兔子是乌龟速度的 15 倍,那么兔子爬 900 米,乌龟应该爬: 900 15 60 米; 而乌龟爬了 1000 米,所以乌龟多爬的 1000 60 940 米是在兔子休息期间进行的。 11. 任意一个一位奇数与任意一个一位偶数相乘,不同的乘积有______个.
6.
数一数,图 1 中共有
个三角形.
图1
【出处】2015 希望杯四年级初赛第 6 题 【考点】图形计数——计数 【难度】☆☆☆ 【答案】24 【解析】(1)有一个小单元组成的三角形有:8 个; (2)有两个小单元组成的三角形有: 3 2 2 8 个;
2
(3)有三个小单元组成的三角形有: 2 2 4 个; (4)有四个小单元组成的三角形有: 2 2 4 个; (5)有五、六、七、八个小单元组成的三角形都不存在. 因此图中共有: 8 8 4 4 24 个. 7. 某班 30 个人参加跳绳比赛,开始时有 4 人迟到没有参加比赛,这时平均成绩为 20 个,后来这 4 位同 学赶到了比赛场地,分别跳了 26,27,28,29 个.这时全班同学的平均成绩是 【出处】2015 希望杯四年级初赛第 7 题 【考点】平均数——应用题 【难度】☆☆ 【答案】21 【解析】(1)刚开始来到的 26 人跳的总个数: 30 4 20 520 个; (2)30 人跳的总个数: 520 26 27 28 29 630 个; (3)全班平均成绩为: 630 30 21 个. 8. 明明临摹一本练习毛笔字,临摹第一遍时,他每天写 25 个字,临摹第二遍时,他每天多写 3 个字, 结果恰好比第一遍少用了 3 天,则这本字帖共有 【出处】2015 希望杯四年级初赛第 8 题 【考点】盈亏问题——应用题 【难度】☆☆☆ 【答案】700 【解析】法一:盈亏方法解应用题 第一遍比第二遍多用了 3 天, 又因为每天写 25 个字, 因此这三天多写了 3 25 75 个字. 因为这两遍写的字数是一样的,因此第二遍用的天数: 75 3 25 天. 所以字帖共有: 25 25 3 700 个. 法二:列方程解应用题 设第一遍摹了 x 天,那么第二遍摹了 x 3 天,根据题意可列方程如下: 字. 个.
x 25 x 3 28
解方程得: x 28 因此共有字: 28 25 700 个.
3
9.
图 2 由 16 个 1 1 的小正方形组成,图中 ABC 的面积是
.
A
B
图2
C
【出处】2015 希望杯四年级初赛第 9 题 【考点】毕克定理、图形分割——几何 【难度】☆☆ 【答案】7 【解析】法一:毕克定理 由正方形格点下的毕克定理可知:面积=内点数+边点数÷2-1 那么 ABC 的面积为: 6 4 2 1 7 法二:图形分割
5
【出处】2015 希望杯四年级初赛第 13 题 【考点】年龄问题——应用题 【难度】☆☆ 【答案】14 【解析】(1)要想爷爷的年龄等于小明和爸爸年龄的和,则小明和爸爸增加的总和要比爷爷增加的多:
60 35 11 14 岁.
(2)每过一年,小明、爸爸、爷爷都增加 1 岁,小明和爸爸的增加的总和比爷爷多增加了 1 岁;因此要再过: 14 1 14 年,小明和爸爸的年龄和等于爷爷的年龄. 14. 一个长方形的长和宽都增加 3 厘米后,面积增加了 90 平方厘米,则原长方形的周长是_____厘米. 【出处】2015 希望杯四年级初赛第 14 题 【考点】面积问题——几何 【难度】☆☆☆ 【答案】54 【解析】根据题意可画出下图:
7
(1)
(2)
(3) 图3
(4)
【出处】2015 希望杯四年级初赛第 17 题 【考点】等差数列——计算 【难度】☆☆ 【答案】625 【解析】通过观察可知第 25 个图形的小正方形总数为: 1 3 5 7 ... 47 25 2 1 法一:等差数列 计算该等差数列得: 1 49 25 2 625 个. 因此第 25 个图形需要 625 个小正方形. 法二:特殊计算(天下无双,个数平方) 总和: 1 3 5 7 ... 47 25 2 1 25 25 625 个. 因此第 25 个图形需要 625 个小正方形. 18. 若 abc cba 1069 ,则这样的 abc 有 _____个.
6
【难度】☆ 【答案】24 【解析】最终想让甲筐内的鸡蛋是乙筐内的两倍,如果把乙筐的数量看成 1 份,那么甲筐的就是 2 份, 总数不变,因此 3 份量等于: 54 63=117 个 1 份量为: 117 3=39 个 后来的乙的数量为 1 份量也就是 39 个,因此需要拿出: 63 39=24 个放到甲筐内. 16. 王蕾和姐姐从家步行去体育馆打羽毛球, 已知姐姐每分钟比王蕾多走 20 米, 25 分钟后姐姐到体育馆, 这时姐姐发现没有带球拍,于是立即按原路返回取球拍,在离体育馆 300 米的地方遇到了王蕾,则 王蕾家到体育馆的路程是______米. 【出处】2015 希望杯四年级初赛第 16 题 【考点】行程问题 【难度】☆☆☆ 【答案】1500 【解析】根据题意可画下图:
4
【出处】2015 希望杯四年级初赛第 11 题 【考点】加乘原理——计数 【难度】☆☆☆☆ 【答案】19 【解析】(1)一位数奇数有:1、3、5、7、9;一位数偶数有 0、2、4、6、8. (2)0 和任意数相乘得数相同,因此 0 与奇数相乘的不同乘积有:1 个; 2、4、6、8 和奇数相乘得意得到的乘积有: 4 5 20 个. 法一:计算找相同乘积 通过计算可知: 2 3 6 1;2 9 6 3 重复了 2 个; 因此不同的乘积有: 20 1 2 19 个. 法二:通过因数分析找相同乘积 (i) 8 里面有 3 个 2 相乘,而 2、4、6 均没有 3 个 2,奇数里没有 2,故 8 和任 意奇数相乘的结果不会和其他偶数与奇数相乘的结果相同. (ii) 4 里面有 2 个 2,而 2、6、8 均不是有 2 个 2,奇数里没有 2,故 4 和任意 奇数相乘的结果不会和其他偶数与奇数相乘的结果相同. (iii) 2 和 6 里面都有 1 个 2 因数,因此可能会出现相同的乘积; 6 里面还有 3 这个因数,因此要想相同,2 乘的另一个奇数一定是 3 的倍 数,因此可以很快检验出 2 3 6 1;2 9 6 3 这两个乘积结果重复了. 因此不同的乘积有: 20 1 2 19 个. 12. 一个长方形的相框长为 40 厘米,宽为 32 厘米,放入一张长为 32 厘米宽为 28 厘米的相片,则相框 中没有被照片覆盖的部分的面积是______平方厘米. 【出处】2015 希望杯四年级初赛第 12 题 【考点】面积——几何 【难度】☆☆ 【答案】384 【解析】由题意可知: 40 32 32 28 32 40 28 384 平方厘米. 13. 爷爷,爸爸,小明今年的年龄分别是 60 岁,35 岁,11 岁,则再过_______年爷爷的年龄等于小明和 爸爸年龄的和.
阴影部分的面积是 90 平方厘米,通过变形把 3×宽的阴影部分移动到右下角空白长方形 处.因此: 90 3 长 3 宽 . 那么: 长 3 宽=90 3=30=90 3=30 厘米
长+宽= 3 0 3 = 厘米 27
故原长方形的周长为: 27 2=54 厘米. 15. 甲筐和乙筐内原来分别放有 54 个和 63 个鸡蛋,若要使甲筐内的鸡蛋的个数变为乙筐内鸡蛋个数的 两倍,那么应从乙筐内取出_______个鸡蛋放入甲筐. 【出处】2015 希望杯四年级初赛第 15 题 【考点】应用题
第十三届小学“希望杯”全国数学邀请赛 四年级
2015 年 3 月 15 日
第 1 试试题
上午 8:30 至 10:00
以下每题 6 分,共 120 分. 1. 计算: 2468 629 1234 37 .
【出处】2015 希望杯四年级初赛第 1 题 【考点】计算 【难度】☆ 【答案】34 【解析】原式 =2468 629 1234 37 =2468 1234 629 37 =2 17 =34 2. 有一个除法算式,被除数和除数的和是 136,商是 7,则除数是 【出处】2015 希望杯四年级初赛第 2 题 【考点】计算 【难度】☆☆ 【答案】17 【解析】(1)被除数÷除数=7,因此我们能得到被除数是除数得 7 倍. (2)如果设除数是 1 份,那么被除数就是 7 份,它们的和是 136. 所以每份量为: 136 8=17 .即除数是 17. 3. 定义 a b a b 3 题 【考点】定义新运算——计算 【难度】☆☆ 【答案】59 【解析】有括号先算括号: 2 3 =2+3+2 3=11
