材料力学专项习题练习 6弯曲内力
弯曲内力习题与答案

弯曲力1. 长l的梁用绳向上吊起,如图所示。
钢绳绑扎处离梁端部的距离为x。
梁由自重引起的最大弯矩|M|max为最小时的x值为:(A) /2l;(B) /6l;(C…) 1)/2l。
l;(D) 1)/22. 多跨静定梁的两种受载情况如图(a)、(b)所示。
下列结论中哪个是正确的?(A) 两者的剪力图相同,弯矩图也相同;(B) 两者的剪力图相同,弯矩图不同;(C) 两者的剪力图不同,弯矩图相同;(D….) 两者的剪力图不同,弯矩图也不同。
3. 图示(a)、(b)两根梁,它们的(A) 剪力图、弯矩图都相同;(B…) 剪力图相同,弯矩图不同;(C) 剪力图不同,弯矩图相同;(D) 剪力图、弯矩图都不同。
4. 图示梁,当力偶M e的位置改变时,有下列结论:(A) 剪力图、弯矩图都改变;(B…) 剪力图不变,只弯矩图改变;(C) 弯矩图不变,只剪力图改变;(D) 剪力图、弯矩图都不变。
5. 图示梁C截面弯矩M C = ;为使M C =0,则M e= ;为使全梁不出现正弯矩,则M e≥。
6. 图示梁,已知F、l、a。
使梁的最大弯矩为最小时,梁端重量P= 。
7. 图示梁受分布力偶作用,其值沿轴线按线性规律分布,则B端支反力为,弯矩图为 次曲线,|M |max 发生在 处。
8. 图示梁,m (x )为沿梁长每单位长度上的力偶矩值,m (x )、q (x )、F S (x )和M (x )之间的微分关系为:S d ();d F x x = d ()d M x x = 。
9. 外伸梁受载如图,欲使AB 中点的弯矩等于零时,需在B 端加多大的集中力偶矩(将大小和方向标在图上)。
10. 简支梁受载如图,欲使A 截面弯矩等于零时,则=e21e /M M 。
1-10题答案:1. C 2. D 3. B 4. B 5. 28e2M ql -;42ql ;22ql 6. ⎪⎭⎫⎝⎛-a l a F 24 7. m 0/2;二;l /28. q (x );F S (x )+ m (x ) 9. 10. 1/211-60题. 作图示梁的剪力图和弯矩图。
材料力学第六章弯曲内力

上弯为正
二、数值计算
[例2]:求图(a)所示梁1--1、2--2截面处的内力。 q 2 解:截面法求内力。 qL 1 1--1截面处截取的分离体 1 a y qL A M1 x1 Q1 图(b) 2 b 如图(b)示。
x
图(a)
Y qL Q1 0 Q1 qL
mA( Fi ) qLx1 M1 0 M1 qLx1
+
1m 3 – 2m
+
1m
x
5kN
1kN
q=2kN/m
M(kN· m) 1 + 1.25 x
–
1
35
§6–6 平面刚架和曲杆的弯曲内力
一、平面刚架
1. 平面刚架:同一平面内,不同取向的杆件,通过杆端相
互刚性连接而组成的结构。 特点:刚架各杆的内力有:Q、M、N。
连接处夹角不变, 即两部分无相对转动.
q B
qa2
RA
§6–5 按叠加原理作弯矩图
一、叠加原理: 多个载荷同时作用于结构而引起的内力等于每个载荷单独作
用于结构而引起的内力的代数和。
Q( P , P2 Pn ) Q1 ( P ) Q2 ( P2 ) Qn ( Pn ) 1 1
m C
Q Q 图 特 征 M 图 特 征
水平直线
Q Q
斜直线
Q
自左向右突变
Q
无变化
Q C
Q1 C x
x
Q<0
x
x
x
Q>0
斜直线
M x M x
增函数 降函数 自左向右折角 自左向右突变 曲线
M M x M x
弯曲内力例题(0509)

和
M max 及其所
P
y
m=Pa
1、列出梁的剪力方程和弯矩方程
AB段:
A
x
x a
B a
C
x
FQ ( x) 0
(0 x a )
M ( x) m Pa (0 x a)
材料力学
弯曲内力/剪力方程和弯矩方程 剪力图和弯矩图 BC段: m=Pa P
FQ ( x) P
( a x 2a )
弯矩 立柱弯矩图为抛物线,左侧受压,1、2截面的弯矩值为
M1 0,
qa2/2
3
qa/2
4
2M4 0
qa/2
1
FAy
材料力学
M
FAx
1 2 1 2 M 2 qa a qa qa , 2 2 1 2 M 3 qa , M 4 0 2
作弯矩图。
弯曲内力/平面刚架内力图
x 3.1m
1 M E F 3.1 FAy 2.1 q 2.12 2
(-)
材料力学
1.41kN.m (+)
-3kN.m
(-)
-2.2kN.m
1.41kN.m M D左 2.2kN.m
q
P qa q
qa qa
a
FQ
a
a 2qa qa
M
qa 2 qa / 2
材料力学
弯曲内力/剪力和弯矩
M1 2qa
A
2
q
M 2 2qa2
B
C
a a 4a
FAy
FBy
取左段梁为研究对象:
取右段梁为研究对象:
FQc FAy q 2a qa
《材料力学》弯曲计算-习题

②无均布载荷段弯矩图均为直线。有均布载荷段,弯矩图为
抛物线,其开口与均布载荷方向相同。
(3)弯矩、剪力、载荷集度的关系
①
M '(x) F S (x) F S'(x) q(x)
② FS=0的点是M图的取极值的点,FS=0的段M图是平行
于轴线的直线。
注意: 内力图上要注明控制面值、特殊点纵坐标值。
利用微分关系绘内力图
y
B截面 30.3 +
z
C截面 15.1 z
-
+
69
34.5
(d) 单位:MPa
Engineering Mechanics
四、弯曲 弯曲强度计算
例3 之二
解:(1)求截面形心轴,即中性轴z轴。
yC
( yi Ai ) Ai
170 30 170 30 200 (170 30)
2
2
17030 30 200
解:(1)外力分析,判变形。
10kN
50kN
(a) A
CD
B
z
4m
2m
4m
求得支坐反力
FA 26kN ,FB 34kN
荷载与梁轴垂直,梁将发
26kN 26 16
34kN
生平面弯曲。中性轴z过形心
+ (b)
与载荷垂直,沿水平方向。
FQ(kN)
104 136
34
(2)内力分析,判危险面。剪力
+
(c)
⑤解题步骤:
1)外力分析,判变形、中性轴,求截面的几何性质、支反力。 2)内力分析,判危险面,画剪力图、弯矩图(可只画弯矩图)
3)应力分析,判危险点。 4)强度计算。
最新弯曲的内力与强度计算习题

弯曲的内力与强度计算一、判断题1.如图1示截面上,弯矩M和剪力Q的符号是:M为正,Q为负。
()图12.取不同的坐标系时,弯曲内力的符号情况是M不同,Q相同。
()3、在集中力作用的截面处,Q图有突变,M连续但不光滑。
()4、梁在集中力偶作用截面处,M图有突变,Q图无变化。
()5.梁在某截面处,若剪力Q=0,则该截面的M值一定为零值。
()6.在梁的某一段上,若无荷载作用,则该梁段上的剪力为常数。
()7.梁的内力图通常与横截面面积有关。
()8.应用理论力学中的外力定理,将梁的横向集中力左右平移时,梁的Q 图,M图都不变。
()9.将梁上集中力偶左右平移时,梁的Q图不变,M图变化。
()10.图2所示简支梁跨中截面上的内力为M≠0,Q=0。
()图 2 图 311.梁的剪力图如图3所示,则梁的BC段有均布荷载,AB段没有。
()12.上题中,作用于B处的集中力大小为6KN,方向向上。
()13.右端固定的悬臂梁,长为4m,M图如图示,则在x=2m处,既有集中力又有集中力偶。
()图 4 图 514.上题中,作用在x=2m处的集中力偶大小为6KN·m,转向为顺时针。
()15.图5所示梁中,AB跨间剪力为零。
()16.中性轴是中性层与横截面的交线。
()17.梁任意截面上的剪力,在数值上等于截面一侧所有外力的代数和。
()18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况,是分析梁的危险截面的依据之一。
()19.梁上某段无荷载作用,即q=0,此段剪力图为平行x的直线;弯矩图也为平行x轴的直线。
()20.梁上某段有均布荷载作用,即q=常数,故剪力图为斜直线;弯矩图为二次抛物线。
()21.极值弯矩一定是梁上最大的弯矩。
()22.最大弯矩Mmax只可能发生在集中力F作用处,因此只需校核此截面强度是否满足梁的强度条件。
()23.截面积相等,抗弯截面模量必相等,截面积不等,抗弯截面模量必不相等。
()24.大多数梁都只进行弯曲正应力强度核算,而不作弯曲剪应力核算,这是因为它们横截面上只有正应力存在。
材料力学B试题6弯曲变形
弯曲变形1。
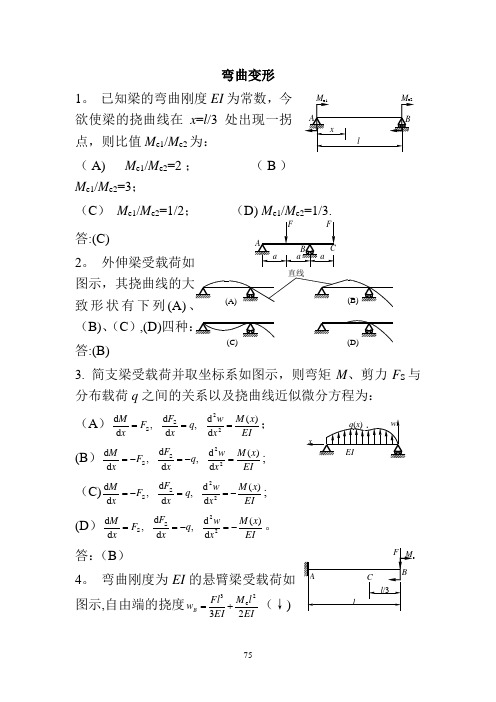
已知梁的弯曲刚度EI 为常数,今欲使梁的挠曲线在x =l /3处出现一拐点,则比值M e1/M e2为:(A) M e1/M e2=2; (B ) M e1/M e2=3;(C ) M e1/M e2=1/2; (D) M e1/M e2=1/3.答:(C)2。
外伸梁受载荷如致形状有下列(A)(B)、(C ),(D)答:(B)3. 简支梁受载荷并取坐标系如图示,则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为: (A )EI x M xw q xF FxM )(d d ,d d ,d d 22SS ===;(B )EI x M x w q x F F x M )(d d ,d d ,d d 22S S =-=-=; (C)EI x M xw q x F F x M )(d d ,d d ,d d 22S S -==-=;(D )EI x M xw q x F F x M )(d d ,d d ,d d 22S S -=-==。
答:(B )4。
弯曲刚度为EI 的悬臂梁受载荷如图示,自由端的挠度EIl M EI Flw B 232e3+=(↓)则截面C 处挠度为:(A )2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛l EI M l EI F (↓);(B )233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F (↓); (C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛l EI Fl M l EI F (↓);(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F (↓).答:(C )5. 画出(a )、(b)、(c )三种梁的挠曲线大致形状。
答:6.7.(a )、(b)刚度关系为下列中的哪一种: (A) (a)>(b ); (B) (a)<(b);(C ) (a)=(b ); (D) 不一定. 答:(C)8。
材料力学弯曲内力习题课

qL/2
qL/2
qx 2 MA 2
L L qL L MC q ( x) 2 4 2 2
M A MC
4 x 2 4 Lx L2 0
1 2 x L 2
x 0.207 L
(x为负值无意义)
( -)
x
在梁上行走的小车如图所示,两轮的轮压力均为F,设小 车的车轮距为c,大梁的跨度为l。试求小车行至何位置时, 梁内的弯矩最大?且求出最大弯矩的值。 x F c F
l
某工字型截面梁如图所示,一活动荷载P可以在全梁L上 移动。试问,如何布置中间铰B和可动铰C,才能充分利 用材料抗力。 P A B C D L
等截面杆AB,未受力时长L。将它竖起,上下端固定。当 上下端距离等于原长L时,求在自重作用下,(1)应力表 达式;(2)受拉区的位移表达式。设截面面积为A,材 料比重为γ,拉伸和压缩弹性模量分别为 E+ 和 E-。 A L B
作图示具有中间铰的组合梁的FS、M图。
qa2 qa2 /2
试画出图示有中间铰梁的 剪力图和弯矩图。
FDy qa / 2 FBy 3qa / 2 FAy qa / 2
M A qa 2 / 2
Fs qa/2
( +)AqaDBqC
a
a
a
qa
( +)
qa/2
qa2/2
( -)
M
( -)
qa2/2
弯曲的内力与强度计算 习题

弯曲的内力与强度计算一、判断题1.如图1示截面上,弯矩M和剪力Q的符号是:M为正,Q为负。
()图12.取不同的坐标系时,弯曲内力的符号情况是M不同,Q相同。
()3、在集中力作用的截面处,Q图有突变,M连续但不光滑。
()4、梁在集中力偶作用截面处,M图有突变,Q图无变化。
()5.梁在某截面处,若剪力Q=0,则该截面的M值一定为零值。
()6.在梁的某一段上,若无荷载作用,则该梁段上的剪力为常数。
()7.梁的内力图通常与横截面面积有关。
()8.应用理论力学中的外力定理,将梁的横向集中力左右平移时,梁的Q图,M图都不变。
()9.将梁上集中力偶左右平移时,梁的Q图不变,M图变化。
()10.图2所示简支梁跨中截面上的内力为M≠0,Q=0。
()图 2 图 311.梁的剪力图如图3所示,则梁的BC段有均布荷载,AB段没有。
()12.上题中,作用于B处的集中力大小为6KN,方向向上。
()13.右端固定的悬臂梁,长为4m,M图如图示,则在x=2m处,既有集中力又有集中力偶。
()图 4 图 514.上题中,作用在x=2m处的集中力偶大小为6KN·m,转向为顺时针。
()15.图5所示梁中,AB跨间剪力为零。
()16.中性轴是中性层与横截面的交线。
()17.梁任意截面上的剪力,在数值上等于截面一侧所有外力的代数和。
()18.弯矩图表示梁的各横截面上弯矩沿轴线变化的情况,是分析梁的危险截面的依据之一。
()19.梁上某段无荷载作用,即q=0,此段剪力图为平行x的直线;弯矩图也为平行x轴的直线。
()20.梁上某段有均布荷载作用,即q=常数,故剪力图为斜直线;弯矩图为二次抛物线。
()21.极值弯矩一定是梁上最大的弯矩。
()22.最大弯矩Mmax只可能发生在集中力F作用处,因此只需校核此截面强度是否满足梁的强度条件。
()23.截面积相等,抗弯截面模量必相等,截面积不等,抗弯截面模量必不相等。
()24.大多数梁都只进行弯曲正应力强度核算,而不作弯曲剪应力核算,这是因为它们横截面上只有正应力存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选文档
弯曲内力
1. 长l 的梁用绳向上吊起,如图所示。
离为x 。
梁内由自重引起的最大弯矩|M |max 为最小时的x (A) /2l ; (B) /6l ; (C) 1)/2l
; (D) 1)/2l 。
2. 多跨静定梁的两种受载情况如图(a)、(b)所示。
下列结论中哪个是正确的? (A) 两者的剪力图相同,弯矩图也相同; (B) 两者的剪力图相同,弯矩图不同; (C) 两者的剪力图不同,弯矩图相同; (D) 两者的剪力图不同,弯矩图也不同。
3. 图示(a)、
(b)两根梁,它们的 (A) 剪力图、弯矩图都相同; (B) 剪力图相同,弯矩图不同; (C) 剪力图不同,弯矩图相同; (D) 剪力图、弯矩图都不同。
4. 图示梁,当力偶M e 的位置改变时,有下列结论: (A) 剪力图、弯矩图都改变; (B) 剪力图不变,只弯矩图改变; (C) 弯矩图不变,只剪力图改变; (D) 剪力图、弯矩图都不变。
5. 图示梁C 截面弯矩M C = ;为使M C =0,则M e =
;为使全梁不出现正弯矩,则M e ≥ 。
6. 图示梁,已知F 、l 、a 。
使梁的最大弯矩为最小时,梁端重量P = 。
7. 图示梁受分布力偶作用,其值沿轴线按线性规律分布,则B 端支反力为 ,弯矩图为 次曲线,|M |max 发生在 处。
8. 图示梁,m (x )为沿梁长每单位长度上的力偶矩值,
m (x )、q (x )、F S (x )和M (x )之间的微分关系为:
S d ()
;
d F x x
=
d ()
d M x x
= 。
9. 外伸梁受载如图,欲使AB 中点的弯矩等于零时,需在B 端加多大的集中力偶矩(将大小和方向标在图上)。
10. 简支梁受载如图,欲使A 截面弯矩等于零时,则
=e21e /M M 。
1-10题答案:1. C 2. D 3. B 4. B
5. 28e 2M ql -;42ql ;22ql
6. ⎪⎭
⎫
⎝⎛-a l a F 24 7. m 0/2;
二;l /2 8. q (x );F S (x )+ m (x ) 9. 10. 1/2
11-60题. 作图示梁的剪力图和弯矩图。
解:
2
2
F qa 2
2
qa
解:
解:
解:
2
F
F F
F
2
F
精选文档
解: 解: 解:
F
/24
2
F /2
F
F
⋅
2
F
.
解:
解:
解:
2
F
F
F
M
F
M
解:解:解:
F
F
F
/12
F
F
F
精选文档
解:
F
2
F
F
解:
解:
解:
F
kN
F
F
F
2
F
F ⋅F 2
F 0F
F
36 3
2
F
F
2
F
F
2
F
.
61. 图示结构,作梁ABC
62. 作图示刚架的轴力、剪力和弯矩图。
63.
解:
/2
F
F 图
N
F 图
S
M图
qa /22
qa /22
qa2 2
2
2
qa2
q
a
a
2qa
F 图
N
F 图
S
M图
qa 2
64. 作图示刚架的轴力、剪力和弯矩图。
65. 作图示刚架的轴力、剪力和弯矩图。
66.
F 图
N
F 图
S
M图
N S
q
图
N
F 图
S
M图
qa
qa
qa 2 2
qa
F 图
N
F 图
S
M图
解:
67. 作图示刚架的轴力、剪力和弯矩图。
解:
F 图
S M 图
q
qa /23qa F 图
N F 图
S M 图
2a
3qa /2
qa 2M 图
7qa
68. 作图示刚架的轴力、剪力和弯矩图。
解:
69-70. 梁的剪力图如图所示,作弯矩图及载荷图。
已知梁上没有作用集中力偶。
2
32
/22/22
F 图
N F 图
S M 图
F qa /2
F 3qa qa /2
71-72. 梁的剪力图如图所示,作弯矩图及载荷图。
已知梁上B 截面作用一集中力偶。
解:
73-74. 已知梁的弯矩图如图所示,作梁的载荷图和剪力图。
解:
F
2
2
F
3qa
a
a
F
a
a qa a
a 2
F
75-76. 已知梁的弯矩图如图所示,作梁的载荷图和剪力图。
解:
77. 处于xy平面内的开口圆环,半径为R,A
C端受F x=F、F z=F(垂直纸面向里)力作用,则
截面的扭矩T= ;弯矩M x= ,
M z= 。
(z轴垂直纸面向里)
答:FR;FR;-FR。
78. 一结构由直杆AB和曲杆BC在B点刚结而
成,支承和受载如图所示。
作结构的剪力图和弯
矩图。
对于曲杆段要求先写出剪力方程和弯矩方
程,然后作图。
解:BC段剪力方程和弯矩方程分别为
S
()sin;()(1cos)
2
F Fa
F M
ϕϕϕϕ
=-=--
a
a a
2
F
F
79. 写出图示曲杆的内力方程,并作内力图(轴力、剪力、弯矩图)。
解:N (1cos )cos F qR ϕϕ=-; S (1cos )sin F qR ϕϕ=-;
2
2(1cos )2
qR
M ϕ=-。
80. 图示梁上,作用有集度为q =q (x )的分布载荷及m =m (x )的分布力偶。
试建立力偶矩集度
m (x )、分布载荷集度q (x )、剪力F S (x )和弯矩M (x )间的微分关系。
解:
微段d x 的平衡方程为
S S S 0,()()d [()d ()]0y F F x q x x F x F x ∑=+-+= (a)
S d 0,()d ()()d ()d ()()d 02
C x
M M x M x q x x
F x x M x m x x ∑=+----= (b) 由式(a)得 S d ()
()d F x q x x
= 由式(b)并略去二阶微量,得
S d ()
()()d M x F x m x x
=+ R
B q
A
O
F 图
N M 图
F 图
S
M ((x )+d M (x ))+d F (x )S。
