高一数学指数幂及运算练习题及答案
高一数学指数与指数幂的运算

(3)-32的五次方根
(4)16 的四次方根
(5)a6源自的三次方根是(6)0的七次方根是
观察并分析以上各数的方根,你能发现什 么?
5 ( 1 )
3 4
求下列各式的值
2
思考
3
(2 )(-2 ) (3 )(-2 )
4
( a) ?
n n m
2
(4 ) 3-a (a 3 )
a ?
n
;排列3走势图表 https:///chart/pl3/11 排列3走势图表 ;
越是绝对不顺眼.以为自身有壹点背鞠,就摆出呐种姿态,呐种声,最令声厌恶.“城主壹意孤行,俺也无法反对.但是,俺在呐里要说,鞠言就算通过了考核,俺申风学院,也是不会接收他の!”沧龙,狠狠の看了鞠言壹眼.“哦?”“沧龙执事,权历还真是大啊!申风学院招收修行者,你也能全 部做主了?”霍东阳,真の是有些恼怒了.他已经有了心思,觉得自身,是不是等沧龙离开西墎城返回蓝曲郡城の事候,将呐个老东西在路上弄死算了.只要做得隐秘,申风学院也没办法找自身麻烦.不过,呐还是有壹些冒险,万壹消息走漏,他就麻烦了.“城主大声!”呐事候,鞠言开口.“申 风学院就是要俺进去,俺都不会进去了.沧龙执事,也不需要费心了.”鞠言冷笑着说道.被申风学院驱逐出壹次,鞠言,本就没有打算再进入申风学院.蓝曲郡内,又不是只有申风学院壹个学院.鞠言,还能够进入红莲学院或者道壹学院.“鞠言,俺道壹学院,欢迎你加入.”道壹学院の庆墨执 事,当即就开口说道.在庆墨看来,以鞠言の实历,通过三大学院考核,绝对是绰绰有余.对于鞠言呐样の天纵奇才,道壹学院,当然欢迎の很.“多谢庆墨先生了.”鞠言对庆墨拱手道谢.庆墨,笑着对鞠言点了点头.“好了,各位都散了吧!”霍东阳,壹摆手对在场の众声道.“告辞!”照当元, 第壹个冷冰冰の
高一数学上册第二章--指数函数知识点及练习题(含答案)

课时 4 指数函数一 . 指数与指数幂的运算( 1)根式的观点①假如xna, a R, x R, n 1,且 nN ,那么 x 叫做 a 的 n 次方根. 当 n 是奇数时, a 的 n 次方根用符号 na 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号na 表示,负的 n 次方根用符号na表示; 0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当n 为奇数时, a 为随意实数;当 n 为偶数时, a.③根式的性质: (na )n a ;当 n 为奇数时, n a n a ;当 n 为偶数时, n a n | a |a (a 0) .a (a 0)( 2)分数指数幂的观点mna m (a①正数的正分数指数幂的意义是:a n 0, m,n N , 且 n 1) .0 的正分数指数幂等于0.②m(1m1 ) m( a正数的负分数指数幂的意义是:a n)n n (0, m, n N , 且 n1) .0 的负分数指aa数幂没存心义. 注意口诀: 底数取倒数,指数取相反数.( 3)分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质( 4)指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域(0,+ ∞)过定点 图象过定点(0,1 ),即当 x=0 时, y=1.奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y > 1(x > 0), y=1(x=0), 0< y < 1(x < 0)y > 1(x < 0), y=1(x=0), 0< y < 1(x > 0)变化状况a 变化对在第一象限内, a 越大图象越高,越凑近 y 轴; 在第一象限内, a 越小图象越高,越凑近 y 轴; 图象影响在第二象限内,a 越大图象越低,越凑近x 轴.在第二象限内,a 越小图象越低,越凑近x 轴.三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析: A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析: 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= [ f(x) ] nD.f [ (xy) n ] =[ f(x) ] n [ f(y) ] n (n ∈ N * )分析: 易知 A 、 B 、 C 都正确 .对于 D,f [(xy)n] =a (xy)n , 而[ f(x) ] n ·[f(y) ] n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析: a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析: 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析: 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. [ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析: 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ] ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析: 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈[ -1,1]时 ,函数 f(x)=3 x-2 的值域为 _______[ -5,1 ] ___________.3分析: f(x) 在[ -1,1 ]上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析: (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩[ 2,+ ∞]=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈[ -3,2]的最大值和最小值 .解: 设 2-x=t, 由 x ∈[ -3,2 ]得 t ∈[ 1,8 ] , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解: ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. [ 1,2]B.[ 2,3]C.(-∞ ,2]D.[ 2,+∞ )分析: 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈[ 2,+ ∞ ) 上递加 , 故所求的递加区间为[ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. [ -1,+∞ )B. [ -1,63)C.[ 0,+∞ )D.(0,63 ]分析: 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= [ f(x)-1 ]2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈[ 1,9 ].2.1 指数函数练习1.以下各式中建立的一项A . ( n)71n 7 m 7B .12 ( 3)433m3C . 4 x 3y 3( x y) 4D .393321111 1 52.化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D . 9a 2 A . 6aB . aC . 9a3.设指数函数 f ( x)a x ( a 0, a1) ,则以下等式中不正确的选项是f (x) A . f(x+y)=f(x) ·f(y)B . f ( x y )f ( y)C . f (nx)[ f ( x)]n (nQ )D . f ( xy) n [ f ( x)] n ·[f ( y)] n1 4.函数 y (x5) 0 ( x 2)2A . { x | x 5, x 2}B . { x | x 2}C . { x | x 5}D . { x | 2 x 5或 x 5}()()()(n N )( )5.若指数函数 y a x 在 [- 1,1]上的最大值与最小值的差是1,则底数 a 等于 ()A .15 B .1 5 C .15D .5 122 226.当 a0 时,函数 y axb 和 yb ax 的图象只可能是()7.函数 f ( x)2 |x| 的值域是()A . (0,1]B . (0,1)C . (0, )D . R8.函数 f ( x)2 x 1, x 0,知足 f ( x)1的 x 的取值范围1x 2 , x()A . ( 1,1)B . ( 1, )C . { x | x 0或 x2}D . { x | x 1或 x1}9.函数 y(1) x 2x2得单一递加区间是2()A .[ 1,1]B . ( , 1]C .[2,)D .[ 1,2]2exe x210.已知 f ( x)()2 ,则以下正确的选项是A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.已知函数 f (x)的定义域是(1, 2),则函数 f (2 x ) 的定义域是.12.当 a >0 且 a ≠1 时,函数 f (x)=a x -2- 3 必过定点.三、解答题:13.求函数 y1的定义域 .x5 x 1114.若 a >0, b > 0,且 a+b=c ,求证: (1) 当r >1时, a r +b r < c r ; (2) 当r < 1时, a r +b r > c r .a x 1 15.已知函数 f ( x)(a >1) .a x1( 1)判断函数 f (x) 的奇偶性;( 2)证明 f (x)在 (-∞, +∞ )上是增函数 .xa16.函数 f(x) = a (a>0 ,且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2,求 a 的值.参照答案一、 DCDDD AADDA二、 11. (0,1);12. (2,- 2) ;三、 13. 解:要使函数存心义一定:x 1 0x 1x0 x 0x 1∴ 定义域为 : x xR 且 x0, x 1a rrrb r此中a1,0b114. 解:ba,c rcccc.r >1 ,a rb ra b 1,r r r当因此+b< c ;时c c c crrrrr当 r < 1 时, aba b1, 因此 a +b >c .ccc c15. 解 :(1)是奇函数 .(2) 设x <x ,则 f (x 1 )ax11 ax21 。
高一数学指数与指数幂的计算题及答案解析

(4)如果对于函数定义域内的任意一个x,f(-x)=-f(x)与f(-x)=f(x)都不能成立,那么函数f(x)既不是奇函 数又不是偶函数,称为非奇非偶函数。
(1)指数函数的定义域为所有实数的集合,这里的前提是a大于0,对于a不大于0的情况,则必然使得 函数的定义域不存在连续的区间,因此我们不予考虑。
(2)指数函数的值域为大于0的实数集合。 (3)函数图形都是下凹的。 (4)a大于1,则指数函数单调递增;a小于1大于0,则为单调递减的。 (5)可以看到一个显然的规律,就是当a从0趋向于无穷大的过程中(当然不能等于0),函数的曲线从分 别接近于Y轴与X轴的正半轴的单调递减函数的位置,趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递 增函数的位置。其中水平直线y=1是从递减到递增的一个过渡位置。 (6)函数总是在某一个方向上无限趋向于X轴,永不相交。 (7)函数总是通过(0,1)这点。 (8)显然指数函数无界。 奇偶性
高一数学指数与指数函数试题答案及解析

高一数学指数与指数函数试题答案及解析1.函数的图像过一个定点,则定点的坐标是【答案】(2,2)【解析】当x=2时,f(2)=a2-2+1=a0+1=2,∴函数y=a x-2+1的图象一定经过定点(2,2).故答案为:(2,2).【考点】含有参数的函数过定点的问题.2.函数的图象与函数的图象所有交点的横坐标之和等于()A.4B.6C.8D.10【答案】C【解析】由数形结合可知,两函数图像在直线两侧各有4个交点,其两两关于对称。
不妨令。
则所有交点横坐标之和为。
故C正确。
【考点】1函数图像;2余弦函数的周期;3数形结合思想。
3.已知幂函数的图象过点,则.【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算4.(1)计算.(2)若,求的值.【答案】(1);(2).【解析】(1)利用对数恒等式、换底公式、对数的运算性质进行计算;(2)首先对已知等式进行平方求得的值,再对其平方可求得的值,最后代入所求式即可求得结果.试题解析:(1)原式=.(2)∵,∴,∴,∴,∴,∴原式.【考点】1、对数的运算性质;2、对数的换底公式;3、指数的运算性质.5.已知函数,则=.【答案】【解析】根据题题意:,,故.【考点】1.分段函数;2.指数、对数运算.6.三个数,,的大小顺序是 ( )A.B.C.D.【答案】C【解析】因为,,,所以,故选C.【考点】1.指数函数的单调性;2.对数函数的单调性.7.计算的值为_________.【答案】2【解析】原式【考点】根式、指数、对数的运算8.三个数大小的顺序是()A.B.C.D.【答案】A【解析】由题意得,.,,,,故选A【考点】考察指数函数,和对数函数,分别与1和0的之对比.9.若实数,满足,则关于的函数的图象形状大致是()【答案】B【解析】由等式,可得,根据指数函数的图像可知(或者根据函数的奇偶性、单调性、特殊值来判断),正确答案为B.【考点】1.对数式与指数式的互化;2.指数函数图像、奇偶性、单调性.10.若a<0,>1,则( )A.a>1,b>0B.a>1,b<0C.0<a<1,b>0D.0<a<1,b<0【答案】D【解析】是上的增函数,由,所以是上的减函数, 由,所以故选D【考点】指数函数,对数函数的单调性.11.三个数的大小关系为()A.B.C.D.【答案】D【解析】判断几个数的大小多用构造函数单调性来解题.因为是上的减函数,所以因为是上的减函数,所以因为是上的增函数,所以故选D【考点】用指数函数与对数函数单调性比较大小,转化思想应用.12.若,则函数的图象一定过点_______________.【答案】【解析】由函数过定点,令,即时,恒等于-3,故函数图像过定点;故答案为:.【考点】指数函数的图像和性质.13.设,,,则的大小关系是()A.B.C.D.【答案】D【解析】由对数函数的性质知:,所以答案选.【考点】1.指数大小比较;2.对数函数的性质.14.计算:(1);(2)【答案】(1)6;(2).【解析】(1)直接采用换底公式计算即可;(2)利用指数幂的运算性质逐个运算即可.试题解析:(1)原式=(2)原式=【考点】1.换底公式的应用;2.指数幂的化简求值.15.函数的图象一定过点()A.B.C.D.【答案】B【解析】根据题意,由于函数,令x-1=0,x=1,可知函数值为2,故可知函数一定过点,选B.【考点】指数函数点评:本试题主要是考查了指数函数恒过(0,1)点的运用,属于基础题。
高一数学指数与指数幂的运算2(1)

4. 例题与练习:
例1 求值:
2
83 ,
1
100 2 ,
( 1 )3 ,
(
16
)
3 4
.
4 81
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
a2 a; a3 3 a2; a a .
4. 例题与练习: 例2 用分数指数幂的形式表示下列各式 (其中a>0):
an
| a
|
a(a 0) a(a 0).
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
当n为偶数时, n
an
| a
|
a(a 0) a(a 0).
② 当n为任意正整数时,
复习引入
2. 根式的运算性质:
① 当n为奇数时, n a n a;
2.1.1指数与指数幂 的运算
主讲老师:
复习引入
1. 整数指数幂的运算性质:
复习引入
1. 整数指数幂的运算性质:
a m a n a mn (m, n Z ), (a m )n amn (m, n Z ), (ab)n a n bn (n Z ).
复习引入
2. 根式的运算性质:
4. 例题与练习:
例4
已 知x
x 1
1
3,求x 2
x
1
2的
值.
课堂小结
1. 分数指数幂的意义; 2. 分数指数幂与根式的互化; 3. 有理数指数幂的运算性质.
课后作业
1.阅读教材P.50-P.52; 2.《习案》作业十六.
;佳境配资 佳境配资 ;
高一数学必修1第三章《指数函数、对数函数和幂函数》测练题及解析

高一数学必修1第三章《指数函数、对数函数和幂函数》测练题(满分:150分;考试时间:100分钟)一、选择题(本大题共10小题. 每小题5分,共50分.在每小题给出的四个选项中,只有一个项是符合题目要求的) 1.指数函数y=a x 的图像经过点(2,16)则a 的值是 ( )A .41 B .21C .2D .4 2.化简)31()3)((656131212132b a b a b a ÷-的结果 ( )A .a 6B .a -C .a 9-D .29a3.在区间),0(+∞上不是增函数的是 ( )A.2x y =B.x y log 2=C.xy 2= D.122++=x x y 4.式子82log 9log 3的值为 ( ) A .23 B .32C .2D .3 5.已知0ab >,下面四个等式中:①lg()lg lg ab a b =+; ②lg lg lg a a b b=-;③b ab a lg )lg(212= ;④1lg()log 10ab ab =.其中正确命题的个数为 ( )A .0B .1C .2D .36.已知2log 0.3a =,0.32b =,0.20.3c =,则c b a ,,三者的大小关系是( ) A .a c b >> B .c a b >> C .c b a >> D .a b c >> 7.已知函数)(x f y =的反函数)21(log )(211-=-x x f,则方程1)(=x f 的解集是( )A .{1}B .{2}C .{3}D .{4} 8.图中曲线分别表示l g a y o x =,l g b y o x =,l g c y o x =, l g d y o x =的图象,,,,a b c d 的关系是( )A. 0<a <b <1<d<cB. 0<b<a <1<c<dC. 0<d<c<1<a<bD. 0<c<d <1<a<b9.函数y= | lg (x-1)| 的图象是 ( )xyOy=log a xy=log x y=log c x y=log d x110.给出幂函数①f (x )=x ;②f (x )=x 2;③f (x )=x 3;④f (x )=;⑤f (x )=1x .其中满意条件f 12()2x x + >12()()2f x f x + (x 1>x 2>0)的函数的个数是 ( )A .1个B .2个C .3个D .4个二、填空题(.每小题5分,共20分) 11.函数21()log (2)f x x =-的定义域是 .12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点 .13.函数)x 2x (log y 221-=的单调递减区间是_________________.14.关于函数21()lg (0,R)||x f x x x x +=≠∈有下列命题:①函数()y f x =的图象关于y 轴对称;②在区 间(,0)-∞上,函数()y f x =是减函数;③函数()y f x =的最小值为lg 2;④在区间(1,)+∞上,函 数()y f x =是增函数.其中正确命题序号为_______________. 三、解答题(6小题,共80分)15.(本小题满分12分)4160.250321648200549-+---)()()16. (本小题满分12分)设函数421()log 1x x f x x x -⎧<=⎨>⎩,求满意()f x =41的x 的值.C17.(本小题满分14分)已知()2xf x =,()g x 是一次函数,并且点(2,2)在函数[()]f g x 的图象上,点(2,5)在函数[()]g f x 的图象上,求()g x 的解析式.18.(本小题满分14分)若0≤x ≤2,求函数y=523421+⨯--x x 的最大值和最小值.19.(本小题满分14分)光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为x 块玻璃后强度为y .(1)写出y 关于x 的函数关系式;(2)通过多少块玻璃后,光线强度减弱到原来的13以下? ( lg30.4771)≈20.(本小题满分14分)已知定义域为R 的函数12()22x x bf x +-+=+是奇函数.(1)求b 的值;(2)推断函数()f x 的单调性;(3)若对随意的R t ∈,不等式22(2)(2)0f t t f t k -+-<恒成立,求k 的取值范围.高一数学必修1第三章《指数函数、对数函数和幂函数》测练题参考答案及解析一、选择题1.D 解析:由a 2=16且a >0得a =42.C 解析:原式a ab ba9990653121612132-=-=-=-+-+3.C 解析:依据反比例函数的性质4.A 解析:因log 89=22232log 32log 3log 23=,故原式=23 5.B 解析:ab >0,故a 、b 同号;当a 、b 同小于0时,①②不成立;当ab =1时,④不成立,故只有③对。
高一数学上册 指数函数知识点及练习题含答案
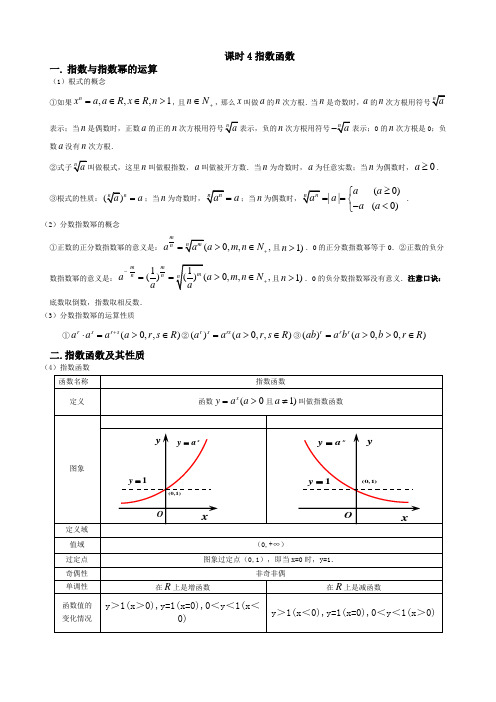
课时4指数函数一. 指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n表示;当n 是偶数时,正数a 的正的nn次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当na =;当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质(4)指数函数a 变化对图象影响在第一象限内,a 越大图象越高,越靠近y 轴; 在第二象限内,a 越大图象越低,越靠近x 轴. 在第一象限内,a 越小图象越高,越靠近y 轴; 在第二象限内,a 越小图象越低,越靠近x 轴.三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析:A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析:当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=[f(x)]n D.f [(xy)n ]=[f(x)]n [f(y)]n (n ∈N *) 解析:易知A 、B 、C 都正确. 对于D,f [(xy)n]=a(xy)n,而[f(x)]n·[f(y)]n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析:a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析:令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析:因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明:∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.[1,+∞)C.(0,+∞)D.(-∞,+∞)解析:当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1];当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析:可利用函数图象的对称性来判断两图象的关系.10.当x ∈[-1,1]时,函数f(x)=3x -2的值域为_______[-35,1]___________. 解析:f(x)在[-1,1]上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析:(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩[2,+∞]=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈[-3,2]的最大值和最小值. 解:设2-x =t,由x ∈[-3,2]得t ∈[41,8],于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解:∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.[1,2]B.[2,3]C.(-∞,2]D.[2,+∞)解析:因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.[-1,+∞)B.[-1,63) C.[0,+∞)D.(0,63]解析:由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈[1,9]. ∴所求值域为[-1,63].2.1指数函数练习1.下列各式中成立的一项()A .7177)(m n mn= B .31243)3(-=-C .43433)(y x y x +=+D .3339=2.化简)31()3)((656131212132b a b a b a ÷-的结果()A .a 6B .a -C .a 9-D .29a3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是() A .f (x +y )=f(x )·f (y ) B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)(+∈=N n y f x f xy f n n n4.函数21)2()5(--+-=x x y()A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或5.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ()A .251+B .251+- C .251± D .215± 6.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是 ()7.函数||2)(x x f -=的值域是()A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ()A .)1,1(-B .),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.函数22)21(++-=x x y 得单调递增区间是 ()A .]21,1[-B .]1,(--∞C .),2[+∞D .]2,21[10.已知2)(xx e e x f --=,则下列正确的是 ()A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 11.已知函数f (x )的定义域是(1,2),则函数)2(x f 的定义域是. 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点. 三、解答题:13.求函数y x x =--1511的定义域.14.若a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.已知函数11)(+-=x x a a x f (a >1).(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.16.函数f(x)=a x(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大,求a 的值.参考答案一、DCDDDAADDA二、11.(0,1);12.(2,-2); 三、13.解:要使函数有意义必须:∴定义域为:{}x x R x x ∈≠≠且01,14.解:rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+,其中10,10<<<<cbc a . 当r >1时,1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr,所以a r +b r <c r; 当r <1时,1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ,所以a r +b r >c r . 15.解:(1)是奇函数.(2)设x 1<x 2,则1111)()(221121+--+-=-x x x x a a a a x f x f 。
高一数学指数函数知识点及练习题(含答案)

+⎩ + 指数函数2.1.1 指数与指数幂的运算〔1〕根式的概念 ①如果 xn= a , a ∈ R , x ∈ R , n > 1,且 n ∈ N ,那么 x 叫做 a 的 n 次方根.当 n 是奇数时,a 的 n 次 方根用符号 n a 表示;当 n 是偶数时,正数 a 的正的 n 次方根用符号 n a 表示,负的 n 次方根用符号 - na表示;0 的 n 次方根是 0;负数 a 没有 n 次方根.②式子 n a 叫做根式,这里 n 叫做根指数, a 叫做被开方数.当 n 为奇数时, a 为任意实数;当 n 为偶数时, a ≥ 0 .nnn n⎧a (a ≥ 0)③根式的性质:( a ) = a ;当 n 为奇数时, a = a ;当 n 为偶数时,=| a |= ⎨-a .(a < 0)〔2〕分数指数幂的概念m①正数的正分数指数幂的意义是: a n= n a m(a > 0, m , n ∈ N , 且 n > 1) .0 的正分数指数幂等于 0.②- m1 m1正数的负分数指数幂的意义是: an= ( ) n = n ( )m (a > 0, m , n ∈ N + , 且 n > 1) .0 的负分数指a a数幂没有意义. 注意口诀:底数取倒数,指数取相反数. 〔3〕分数指数幂的运算性质①a r ⋅ a s = a r +s (a > 0,r , s ∈ R )②(a r )s = a rs (a > 0, r , s ∈ R )③(ab )r = a r b r (a > 0, b > 0, r ∈ R )2.1.2 指数函数及其性质〔4〕指数函数 函数名称 指数函数定义函数 y = a(a > 0 且 a ≠ 1)叫做指数函数图象a > 10 < a < 1y = 1 yOy = ax(0, 1)xy = a xy = 1Oy( 0 , 1 )x定义域 R值域 〔0,+∞〕过定点 图象过定点〔0,1〕,即当 x=0 时,y=1.奇偶性 非奇非偶单调性在 R 上是增函数在 R 上是减函数函数值的变化情况y >1(x >0), y=1(x=0), 0<y <1(x <0)y >1(x <0), y=1(x=0), 0<y <1(x >0)a 变化对图象影响在第一象限内, a 越大图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴.在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越小图象越低,越靠近 x 轴.n a n39 1 + 5 1 ± 5 12.1 指数函数练习1.以下各式中成立的一项〔〕A . ( n )7 = n 7m 7mB . 12(-3)4 =C . 4x 3+ y 33(x + y )4D .=2 11 1 1 1 52.化简(a 3 b 2)(-3a 2 b 3) ÷ ( 3a 6b 6 )的结果〔〕A . 6aB . - aC . - 9aD . 9a23.设指数函数 f (x ) = a x(a > 0, a ≠ 1) ,那么以下等式中不正确的选项是〔 〕A .f (x +y )=f(x )·f (y )B . f 〔x - y 〕=f (x )f ( y )C . f (nx ) = [ f (x )]n(n ∈ Q )- 1D . f (xy )n= [ f (x )]n·[ f ( y )]n(n ∈ N + )4.函数 y = (x - 5)0+ (x - 2)2A .{x | x ≠ 5, x ≠ 2} C .{x | x > 5}〔〕B .{x | x > 2}D .{x | 2 < x < 5或x > 5}5.假设指数函数 y = a x在[-1,1]上的最大值与最小值的差是1,那么底数a 等于 〔〕A .B . 2 2C .D .2 26.当 a ≠ 0 时,函数 y = ax + b 和 y = b ax的图象只可能是〔〕7.函数 f (x ) = 2-|x |的值域是〔 〕A . (0,1]B . (0,1)⎧⎪2- x- 1, x ≤ 0 C . (0,+∞)D .R8.函数 f (x ) = ⎨ 1 ,满足 f (x ) > 1的 x 的取值范围⎪⎩x 2 , x > 0〔 〕A . (-1,1)B . (-1,+∞)C .{x | x > 0或x < -2}D .{x | x > 1或x < -1}9.函数 y = ( 1 ) 2- x 2 + x +2 得单调递增区间是〔 〕11A . [-1, ]2B . (-∞,-1]C . [2,+∞)D . [ 2,2]3 - 33 3- 1 + 5 5 ± 1⎩ x e x - e - x10. f (x ) =,那么以下正确的选项是 〔 〕2A .奇函数,在 R 上为增函数B .偶函数,在 R 上为增函数C .奇函数,在 R 上为减函数D .偶函数,在 R 上为减函数11.函数 f (x )的定义域是〔1,2〕,那么函数 f (2 x) 的定义域是 .12.当 a >0 且 a ≠1 时,函数 f (x )=a x -2-3 必过定点 .三、解答题:13.求函数 y = 1的定义域.5 x -1 - 114.假设a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.函数 f (x ) =a x - 1 a x + 1(a >1).〔1〕判断函数f (x )的奇偶性;〔2〕证明f (x )在(-∞,+∞)上是增函数.16.函数 f(x)=a x (a>0,且 a ≠1)在区间[1,2]上的最大值比最小值大 a,求 a 的值. 2参考答案一、DCDDDAAD D A二、11.(0,1);12.(2,-2);三、13. 解:要使函数有意义必须:⎧x - 1 ≠ 0⎧x ≠ 1⎪x ⇒⎨ ≠ 0 ⎩ x - 1⎨x ≠ 0∴定义域为: {x x ∈ R 且x ≠ 0, x ≠ 1}⎪1 a +1 a +12 14. 解: a r + br⎛ a ⎫r⎛ b ⎫r,其中 0 < a < 1,0 < b < 1.= ⎪ c rc + ⎪c ⎝ ⎭ ⎝ ⎭ 当r >1时,⎛ a ⎫ r ⎛ b ⎫r a b ,所以a r+b r <c r ;⎪ + ⎪ < + = 1⎝ c ⎭ ⎝ c ⎭ c c当 r <1 时,⎛ a ⎫r⎛ b ⎫ra b,所以 a r +b r >c r . ⎪ + ⎪ > + = 1 ⎝ c ⎭ ⎝ c ⎭ c c15.解:(1)是奇函数.(2) x <x ,a x 1 -1 a x2 -1 。
高一数学幂函数、指数函数和对数函数练习题(含答案)

高一数学幂函数、指数函数和对数函数练习题1、下列函数一定是指数函数的是 ( ) A、12+=x y B 、3x y = C 、x y -=3 D 、x y 23⋅=2、已知ab >0,下面四个等式中,正确命题的个数为 ( ) ①lg (ab )=lg a +lg b ②lg b a =lg a -lg b ③b a b a lg )lg(212= ④lg (ab )=10log 1ab A .0 B .1 C .2 D .33、已知x =2+1,则lo g 4(x 3-x -6)等于 ( )A .23 B .45 C .0 D .21 4、已知m >0时10x =lg (10m )+lg m 1,则x 的值为 ( ) A .2 B .1 C .0 D .-15、下列图像正确的是 ( )A B C D6、若log a b ·log 3a =5,则b 等于 ( )A .a 3B .a 5C .35D .537、5、已知031log 31log >>b a ,则a 、b 的关系是 ( ) A .1<b <a B .1<a <b C .0<a <b <1 D .0<b <a <1 8、若函数)1,0(1≠>-+=a a m a y x 的图象在第一、三、四象限内,则 ( )A 、1>aB 、1>a 且0<mC 、010><<m a 且D 、10<<a9、函数x y -=1)21(的单调递增区间是 ( ) A 、),(+∞-∞ B 、),0(+∞ C 、),1(+∞ D 、)1,0(10、 如图1—9所示,幂函数αx y =在第一象限的图象,比较1,,,,,04321αααα的大小( )A .102431<<<<<ααααB .104321<<<<<ααααC .134210αααα<<<<<D .142310αααα<<<<< 11、下列函数中既是偶函数又是( ) A . B . C . D .12、 函数R x x x y ∈=|,|,满足 ( )A .奇函数是减函数B .偶函数又是增函数C .奇函数又是增函数D .偶函数又是减函数13、若01<<-x ,则下列不等式中成立的是 ( )A 、 x x x 5.055<<-B 、 x x x -<<55.05C 、x x x 5.055<<-D 、 x x x 555.0<<-14、下列命题中正确的是( ) A .当0=α时函数αx y =的图象是一条直线B .幂函数的图象都经过(0,0)和(1,1)点C .若幂函数αx y =是奇函数,则αx y =是定义域上的增函数D .幂函数的图象不可能出现在第四象限15、若2<x ,则|3|442x x x --+-的值是_____ _____.16、满足等式lg (x -1)+lg (x -2)=lg2的x 集合为______ _______。
高中数学4-1指数4-1-2无理数指数幂及其运算性质课时作业新人教A版必修第一册

4.1.2 无理数指数幂及其运算性质必备知识基础练1.计算:2a 2b 3×3a 3b =( ) A .5a 6b 3B .6a 6b 3C .6a 5b 4D .5a 5b 42.计算a 3a ·3a 2的结果为( )A .a 32B .a 116C .a 56 D .a 653.下列运算正确的是( ) A .a 3+a 4=a 7B .a 4·a 2=a 6C .a 23÷a -23=a 23 D .(a 2·b 12)3=a 5b 724.对于a >0,b >0,下列等式成立的是( )A .a 23·a 32=a B .(a 12a 13)6=a 3a 2C .(a 3)2=a 9D .a -12·a 12=05.若102x=25,则10-x等于( ) A .15B .-15 C .150 D .16256.(多选)下列说法中错误的是( ) A .根式都可以用分数指数幂来表示B .分数指数幂不表示相同式子的乘积,而是根式的一种新的写法C .无理数指数幂有的不是实数D .有理数指数幂的运算性质不适用于无理数指数幂 7.已知x >0,化简()x3-23+2=________.8.[2022·山东滨州高一期末](278)23-(-14)2+(19)0=________.关键能力综合练1.化简(a 3b 12)12÷(a 12b 14)(a >0,b >0)结果为( )A .aB .bC .a bD .b a2.若2x =3,2y =4,则2x +y的值为( )A .7B .10C .12D .343.计算(4a -3b -23)·(-3a -1b )÷(4a -4b -53)得( ) A .-32b 2 B .32b 2C .3b 2D .-3b 24.若0<a <1,b >0,且a b-a -b=-2,则a b +a -b的值为( ) A .2 2 B .±2 2 C .-2 2 D . 6 5.已知a +1a=3,则a 2+a -2的值是( )A .47B .45C .50D .356.(多选)以下化简结果正确的是(字母均为正数)( ) A .a 52·a 13·a 136=1B .(a 6·b -9)-23=a -4b 6C .-15a 12b 13c -3425a -12b 13c54=-35acD .(-2x 14y -13)(3x -12y 23)(-4x 14y 23)=24y7.[2022·河北邯郸高一期末]计算:432-(-94)0+6(3-π)6+[(-3)6]12=________.8.设α,β是方程5x 2+10x +1=0的两个根,则2α·2β=________,(2α)β=________. 9.计算下列各式(式中字母均是正数)(1)(2a 23b 12)(-6a 12b 13)÷(-3a 16b 56);(2)(3a 2-a 3)÷4a 2.10.已知a 12+a -12=3,求下列各式的值:(1)a +a -1; (2)a -a -1.核心素养升级练 1.已知3a -1+3a -2+3a -3=117,则(a +1)(a +2)(a +3)=( )A .120B .210C .336D .5042.化简:(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)=________.3.已知a >0,且a 2x=2+1,求下列代数式的值. (1)(a x+a -x)(a x -a -x);(2)a x +a -xa x -a-x ;(3)a 3x +a -3x a x +a-x .4.1.2 无理数指数幂及其运算性质必备知识基础练1.答案:C解析:依题意,原式=2×3×a 2+3×b3+1=6a 5b 4.2.答案:B 解析:a 3a ·3a 2=a 3a 12·a23=a 3a76=a3-76=a 116.3.答案:B解析:A 选项a 3+a 4不能再进行运算;B 选项a 4·a 2=a 6,同底数幂相乘,底数不变,指数相加,故正确;C 选项a 23÷a -23,同底数幂相除,底数不变,指数相减,故应为a 23÷a -23=a 43;D 选项(a 2·b 12)3,积的幂等于幂的积,故应为(a 2·b 12)3=a 6b 32.4.答案:B解析:对于选项A ,a 23·a 32=a 23+32=a 136,选项A 错误;对于选项B ,(a 12b 13)6=a 12×6b 13×6=a 3b 2,选项B 正确;对于选项C ,(a 3)2=a3×2=a 6,选项C 错误;对于选项D ,a -12·a 12=a 0=1,选项D 错误.5.答案:A解析:由102x =25得,(10x )2=25,则10x =5,∴10-x=15.6.答案:CD 解析:A.由na m=a mn,1na m=a -mn ,(n ,m ∈N *),知根式都可以用分数指数幂来表示,故正确;B .由na m=a mn ,1na m=a -mn ,(n ,m ∈N *),知分数指数幂不表示相同式子的乘积,而是根式的一种新的写法,故正确;C .实数包括无理数和有理数,所以无理指数幂是实数,故错误;D .由指数幂的运算法则知:有理数指数幂的运算性质适用于无理数指数幂,故错误. 7.答案:x 7解析:因为x >0,所以由幂的运算法则得(x 3-2)3+2=x(3-2)(3+2)=x9-2=x 7.8.答案:3关键能力综合练1.答案:A解析:根据实数指数幂的运算公式,可得:(a 3b 12)12÷(a 12b 14)=a 32b 14÷(a 12b 14)=a 32-12b 14-14=a .2.答案:C解析:因为2x =3,2y =4,所以2x +y=2x ·2y=3×4=12.3.答案:D 解析:原式=-3a -3-1-(-4)b-23+1-(-53)=-3b 2.4.答案:A解析:由题设,(a b -a -b )2=a 2b -2+a -2b=4,即a 2b +a-2b=6,又(a b +a -b )2=a 2b +2+a -2b=8,且a b+a -b>0,所以a b+a -b=2 2. 5.答案:A解析:∵a +1a=3,∴(a +1a)2=a +2+a -1=9,即a +a -1=7,∴(a +a -1)2=a 2+a -2+2=49, ∴a 2+a -2=47. 6.答案:BD解析:A 选项:a 52·a 13·a 136=a 52+13+136=a 5≠1,A 选项错误;B 选项:(a 6·b -9)-23=a6×(-23)b(-9)×(-23)=a -4b 6,B 选项正确;C 选项:-15a 12b 13c -3425a -12b 13c54=-35a 12-(-12)b 13-13c -34-54=-35ac -2≠-35ac ,C 选项错误; D 选项:(-2x 14y -13)(3x -12y 23)(-4x 14y 23)=24x 14-12+14y-13+23+23=24y ,D 选项正确.7.答案:31+π解析:432-(-94)0+6(3-π)6+[(-3)6]12=8-1+π-3+27=31+π.8.答案:14 215解析:利用一元二次方程根与系数的关系,得α+β=-2,αβ=15.则2α·2β=2α+β=2-2=14,(2α)β=2αβ=215.9.解析:(1)原式=[2×(-6)÷(-3)]·a 23+12-16·b 12+13-56=4ab 0=4a .(2)原式=(a 23-a 32)÷a 12=a 23÷a 12-a 32÷a 12=a 23-12-a 32-12=a 16-a =6a -a .10.解析:(1)(a 12+a -12)2=a +a -1+2=9,所以a +a -1=7.(2)(a +a -1)2=a 2+a -2+2=49,所以a 2+a -2=47; (a -a -1)2=a 2+a -2-2=47-2=45,所以a -a -1=±3 5.核心素养升级练1.答案:C 解析:3a -1+3a -2+3a -3=(9+3+1)×3a -3=117,得3a -3=9,解得:a =5,所以(a +1)(a+2)(a +3)=336.2.答案:2-1263解析:原式=(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)×(1-12)×2=(1+1232)(1+1216)(1+128)(1+124)(1+122)×(1-122)×2 =(1+1232)(1+1216)(1+128)(1+124)×(1-124)×2 =(1+1232)(1+1216)(1+128)×(1-128)×2 =(1+1232)(1+1216)×(1-1216)×2 =(1+1232)×(1-1232)×2 =(1-1264)×2 =2-1263.3.解析:(1)因为a >0,且a 2x=2+1, 所以a-2x=12+1=2-1(2+1)(2-1)=2-1, 所以(a x+a -x)(a x-a -x)=a 2x-a-2x=2+1-(2-1)=2.(2)a x +a -x a x -a -x =(a x +a -x )2(a x -a -x )(a x +a -x)=a 2x +a -2x +22=2+1+(2-1)+22=2+1. (3)a 3x +a -3x a x +a -x =(a x +a -x )(a 2x -a x ·a -x +a -2x )a x +a -x=a 2x -a x ·a -x +a -2x =2+1-1+(2-1)=22-1.。
高一数学指数与指数函数试题答案及解析

高一数学指数与指数函数试题答案及解析1.若,则在,,,中最大值是()A.B.C.D.【答案】C【解析】由指数函数的性质,得,;由幂函数的性质得,因此最大的是.【考点】指数函数和幂函数的性质.2.设,,,则()A.b<a<c B.c<a<b C.c<b<a D.a<c<b【答案】B【解析】,,【考点】指数函数和对数函数的性质.3.设均为正数,且,,.则()A.B.C.D.【答案】C【解析】分别为方程的解,由图可知.【考点】函数图像4.若函数的图像与轴有公共点,则的取值范围是()A.B.C.D.【答案】B【解析】函数与轴有公共点,即设函数,,有交点,函数如图:,即,故选B.【考点】函数图像5.已知函数和函数,其中为参数,且满足.(1)若,写出函数的单调区间(无需证明);(2)若方程在上有唯一解,求实数的取值范围;(3)若对任意,存在,使得成立,求实数的取值范围.【答案】(1)的单调增区间为,,单调减区间为;(2)或;(3).【解析】(1)当时,,由二次函数的图像与性质可写出函数的单调区间;(2)先将在上有唯一解转化为在上有唯一解,进而两边平方得到或,要使时,有唯一解,则只须或即可,问题得以解决;(3)对任意,存在,使得成立的意思就是的值域应是的值域的子集,然后分别针对与两种情形进行讨论求解,最后将这两种情况求解出的的取值范围取并集即可.试题解析:(1)时, 1分函数的单调增区间为,,单调减区间为 4分(2)由在上有唯一解得在上有唯一解 5分即,解得或 6分由题意知或即或综上,的取值范围是或 8分(3)则的值域应是的值域的子集 9分①时,在上单调递减,上单调递增,故 10分在上单调递增,故 11分所以,即 12分②当时,在上单调递减,故在上单调递减,上单调递增,故所以,解得.又,所以 13分综上,的取值范围是 14分.【考点】1.二次函数的图像与性质;2.指数函数的图像与性质;3.函数的单调性与最值.6.已知指数函数(且)的图像过点,则实数___________.【答案】【解析】因为指数函数(且)的图像过点,则,得.【考点】指数函数的定义.7.将函数的图像向左平移一个单位,得到图像,再将向上平移一个单位得到图像,作出关于直线对称的图像,则的解析式为 .【答案】【解析】根据平移口诀“上加下减”可得函数解析式为,函数解析式为,因为图像与图像关于直线对称,所以函数与函数互为反函数。
高一数学指数与指数函数试题答案及解析

高一数学指数与指数函数试题答案及解析1.设,则的大小关系是().A.B.C.D.【解析】,,,因此.【考点】指数函数和对数函数的性质.2.若点在函数的图象上,则的值为.【答案】【解析】由点在函数的图象上得,所以,故应填入.【考点】指数函数及特殊角的三角函数.3.设,则下列不等式成立的是()A.若,则B.若,则C.若,则D.若,则【答案】A【解析】对于A,B考查函数f(x)=2x+2x,g(x)=2x+3x的单调性与图象:可知函数f(x)、g(x)在R上都单调递增,若2a+2a=2b+3b,则a>b,因此A正确;对于C,D分别考查函数u(x)=2x-2x,v(x)=2x-3x单调性与图象:当时,u′(x)<0,函数u(x)单调递减;当时,u′(x)>0,函数u(x)单调递增.故在x=取得最小值.当0<x<时,v′(x)<0,函数v(x)单调递减;当x>时,v′(x)>0,函数v (x)单调递增.故在x=取得最小值,据以上可画出图象.据图象可知:当2a-2a=2b-3b,a>0,b>0时,可能a>b或a<b.因此C,D不正确.综上可知:只有A正确.故答案为A.【考点】用导数研究函数的单调性和图象;命题的真假判断与应用.4.若,则()A.B.C.D.【答案】D【解析】由得,所以.【考点】指对数式的互化,指数运算法则.5.若函数的图像与轴有公共点,则的取值范围是()A.B.C.D.【答案】B【解析】函数与轴有公共点,即设函数,,有交点,函数如图: ,即,故选B.【考点】函数图像6.三个数的大小关系为()A.B.C.D.【答案】D【解析】;;。
所以,故D正确。
【考点】指数对数函数的单调性。
7.已知幂函数的图象过点,则.【答案】4【解析】因为为幂函数,所以设因为过点,所以本题易错点在将幂函数的定义写成指数函数的形式,即【考点】幂函数定义,指数的运算8.如图,在平面直角坐标系中,过原点O的直线与函数的图象交于A,B两点,过B作y轴的垂线交函数的图象于点C,若AC平行于y轴,则点A的坐标是.【答案】【解析】设,则,因为AC平行于y轴,所以,因此.又三点三点共线,所以由得,因此.【考点】指数函数运算,向量共线.9.已知指数函数(且)的图像过点,则实数___________.【答案】【解析】因为指数函数(且)的图像过点,则,得.【考点】指数函数的定义.10.我国大西北某地区荒漠化土地面积每年平均比上一年增长,专家预测经过年可能增长到原来的倍,则函数的图像大致为()【答案】D【解析】设初始年份的荒漠化土地面积为,则1年后荒漠化土地面积为,2年后荒漠化土地面积为,3年后荒漠化土地面积为,所以年后荒漠化土地面积为,依题意有即,,由指数函数的图像可知,选D.【考点】1.指数函数的图像与性质;2.函数模型及其应用.11.若,则下列结论正确的是()A.B.C.D.【答案】C【解析】指数函数、对数函数的底数大于1 时,函数为增函数,反之,为减函数,对于幂函数而言,当时,在上递增,当时,在上递减,而,所以,故选C.【考点】1.指数函数;2.对数函数;3.幂函数的性质.12.设函数,如果,求的取值范围.【答案】【解析】对分段函数需分情况讨论,再解指数及对数不等式时,需将实数转化为同底的指数或对数,然后根据指数、对数的单调性解不等式。
高一数学幂函数试题答案及解析

高一数学幂函数试题答案及解析1.若函数是幂函数,则的值为()A.B.C.D.【答案】A【解析】由题意,得,解得.【考点】幂函数的解析式.2.计算等于()A.B.C.D.【答案】B【解析】。
故选B。
【考点】指数幂的运算点评:本题运用指数幂的运算公式:,。
3.已知幂函数的图象过点 .【答案】3【解析】幂函数形式为,其过点,则,求得,。
【考点】幂函数点评:幂函数的形式是。
本题需先确定幂函数的解析式。
4.当时,幂函数为减函数,则实数( )A.m=2B.m=-1C.m=2或m=-1D.【答案】A【解析】因为,当时,幂函数为减函数,所以或,解得,m=2,故选B。
【考点】本题主要考查幂函数的概念及其性质。
点评:简单题,注意形如为常数)的函数是幂函数。
5.(本小题12分)已知函数是幂函数且在上为减函数,函数在区间上的最大值为2,试求实数的值。
【答案】【解析】解:因为函数是幂函数且在上为减函数,所以有,解得,——————————5’①当是的单调递减区间,————————7’②当,解得——————————9’③,解得————————11’综合①②③可知————————12’【考点】幂函数与二次函数点评:解决的关键是对于常见的基本初等函数性质的熟练运用,属于基础题。
6.已知幂函数在增函数,则的取值范围 .【答案】(0,10)【解析】根据已知表达式可知,幂函数在增函数,首先分析对数式y=lga中真数大于零,即a>0,同时要满足在增函数,说明了幂指数为正数,即1-lga>0,得到lga<1=lg10,a<10,这样结合a>0,可知实数a的取值范围是(0,10)。
【考点】本试题主要是考查了幂函数的单调性与幂指数的正负之间的关系的应用,属于基础题。
点评:解决该试题关键是理解幂函数在y轴右侧的单调性是增,说明了幂指数为正,如果在y轴右侧为减,说明幂指数为负数。
同时对数真数大于零是易忽略点。
7.幂函数的图象过点(2, ), 则它的单调递增区间是()A.(-∞, 0)B.[0, +∞)C.(0, +∞)D.(-∞, +∞)【答案】A【解析】因为幂函数过点(2, ),所以=,即。
高一数学指数幂及运算练习题及答案

1.假设(a -3)14有意义,则a 的取值范围是( ) A .a ≥3 B .a ≤3C .a =3D .a ∈R 且a ≠3【解析】 要使(a -3)14有意义,∴a -3≥0,∴a ≥3.应选A. 【答案】 A2.以下各式运算错误的选项是( )A .(-a 2b)2·(-ab 2)3=-a 7b 8B .(-a 2b 3)3÷(-ab 2)3=a 3b 3C .(-a 3)2·(-b 2)3=a 6b 6D .[(a 3)2·(-b 2)3]3=-a 18b 18【解析】 对于C ,∵原式左边=(-1)2·(a 3)2·(-1)3·(b 2)3=a 6·(-1)·b 6=-a 6b 6,∴C 不正确.【答案】 C3.计算[(-2)2]-12的结果是________. 【解析】 [(-2)2]-12=2-12=1212=22. 【答案】 224.x 12+x -12=3,求x +x -1-3x 2+x -2-2. 【解析】 ∵x 12+x -12=3, ∴(x 12+x -12)2=9,即x +x -1+2=9. ∴x +x -1=7.∴(x +x -1)2=49∴x 2+x -2=47.∴原式=7-347-2=445.一、选择题(每题5分,共20分)1.⎝⎛⎭⎫1120-2)÷⎝⎛⎭⎫27823的值为( )A .-13 B.13C.43D.73【解析】 原式=1-(1-22)÷⎝⎛⎭⎫322=1-(-3)×49=73.应选D. 【答案】 D 2.a a a(a>0)计算正确的选项是( ) A .a·a 12a 12=a 2 B .(a·a 12·a 14)12=a 78 C .a 12a 12a 12=a 32 D .a 14a 14a 18=a 58【答案】 B3.化简-a 3a的结果是( ) A.-a B. aC .--aD .- a【解析】 由题意知a<0 ∴-a 3a =--a 3a 2=--a.应选C. 【答案】 C4.假设4|x|-2有意义,则x 的取值范围是( )A .x ≥2或x ≤-2B .x ≥2C .x ≤-2D .x ∈R 【解析】 要4|x|-2有意义,只须使|x|-2≥0,即x ≥2或x ≤-2.应选A.【答案】 A二、填空题(每题5分,共10分) 5.计算(0.064)-13-⎝⎛⎭⎫-780+[(-2)3]-43+16+|-0.01|12=________. 【解析-1-1+(-2)-4+2-3=104-1+116+18+110=14380. 【答案】 14380 6.假设x>0,则(2x 14+332)(2x 14-332)-4x -12(x -x 12)=________.【解析】 根据题目特点发现(2x 14+332)(2x 14-332)是一个平方差的形式,依据公式化简,然后进展分数指数幂的运算. 因为x>0,所以原式=⎝⎛⎭⎫2x 142-⎝⎛⎭⎫3322-4x -12·x +4x -12·x 12=4x 14×2-332×2-4x -12+1+4x -12+12=4x 12-33-4x 12+4x 0=4x 12-33-4x 12+4=4-27=-23. 三、解答题(每题10分,共20分)7.化简:a -b a 12+b 12-a +b -2a 12·b 12a 12-b 12. 【解析】 原式=(a 12+b 12)(a 12-b 12)a 12+b 12-(a 12-b 12)2a 12-b 12=a 12-b 12-(a 12-b 12)=0. 8.假设a>1,b>0,且a b +a -b =22,求a b -a -b 的值.【解析】 方法一:因为a b +a -b =(a b 2+a -b 2)2-2, 所以⎝⎛⎭⎫a b 2+a -b 22=a b +a -b +2=2(2+1), 又a b 2+a -b 2>0,所以a b 2+a -b 2=2(2+1) ①; 由于a>1,b>0,则a b 2>a -b 2,即a b 2-a -b 2>0, 同理可得a b 2-a -b 2=2(2-1) ②,①×②得a b -a -b =2. 方法二:由a>1,b>0,知a b >a -b ,即a b -a -b >0,因为(a b -a -b )2=(a b +a -b )2-4=(22)2-4=4,所以a b -a -b =2.说明:两种方法都表达了活用乘法公式和整体处理的方法,这两种方法是求解这类问题的常用方法.9.(10分)x>0,y>0,且x(x +y)=3y(x +5y),求2x +xy +3y x +xy -y的值. 【解析】 由x(x +y)=3y(x +5y),得x -2xy -15y =0,即(x +3y)(x -5y)=0,因为x +3y>0,所以x -5y =0,于是有x =25y.所以原式=50y +5y +3y 25y +5y -y =58y 29y=2.。
高一数学指、对与幂基本运算(重点突破)练习题含答案

高一数学指、对与幂基本运算练习题【重难点知识点网络】:【重难点题型突破】: 一、指数运算 1、 根式与分数指数幂(1)、性质:(na )n=a (a 使na 有意义);当n 为奇数时,n a n =a ,当n 为偶数时,na n =|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0.(2)、规定:正数的正分数指数幂的意义是a m n =na m (a >0,m ,n ∈N *,且n >1);正数的负分数指数幂的意义是a -mn =1n a m(a >0,m ,n ∈N *,且n >1);0的正分数指数幂等于0;0的负分数指数幂没有意义.(3)、有理指数幂的运算性质:a r a s =a r +s ;(a r )s =a rs ;(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q. 例1、(1)、(2022·山东枣庄·高一期中)下列根式与分数指数幂的互化,正确的是( ) A.21()x =- B12y =C.310)x x -=≠ D .1432](0)x x =>(2)、(2022·湖南·长沙市同升湖高级中学有限公司高一期中))A .2B .532 C .562D .762(3)、(2022·黑龙江省饶河县高级中学高一阶段练习)已知16a a -+=,则1122a a --的值为( ) A .2B .-2 C.±D .±2【变式训练1-1】、(2022·湖北·恩施市第一中学高一阶段练习) ) A .25a - B .56a -C .56()a -D .56()a --【变式训练1-2】、(2022·上海·高一专题练习)已知11224x x -+=,则1x x -+=_______.【变式训练1-3】、(2022·上海市松江二中高一期中)0)a >化成有理数指数幂的形式为______.例2.(2022·江苏·常州市正行中学高一阶段练习)(1)计算:()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪⎪⎝⎭⎝⎭;(20)a >.【变式训练2-1】、(2022·四川省眉山第一中学高一阶段练习)(1)求值:()1233127863125-⎛⎫⨯++-+⎪⎝⎭(2) 已知 1a a -+= 求44a a -+的值.二、对数运算 1、对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1). (2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①、log a (MN )=log a M +log a N ; ②、log a MN =log a M -log a N ;③、log a M n =n log a M (n ∈R); ④、log a m M n =nmlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a Nlog a b(a ,b 均大于零且不等于1).例3、(1)、(2022·陕西·永寿县中学高一阶段练习)237log 7log 8log 3⋅⋅=______.(2)、(2022·广西·南宁二中高一阶段练习)计算:()1205122log 54⎛⎫--+= ⎪⎝⎭___________.(3)、(2022·陕西渭南·高一期末)已知0a >,且1a ≠,则下列各式恒成立的是( ) A .()2log 2log a a x x = B .2log 2log a a x x =C .log log log a a a x y x y ⋅=⋅D .()log log log a a a x y x y +=+【变式训练3-1】、(2022·江西·南昌市第一中学高一阶段练习))21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______.【变式训练3-2】、(2022·福建·莆田一中高一阶段练习)已知非零实数,,a b c 满足3624a b c ==,则,,a b c 之间的关系是( ) A .111b a c=+ B .312b a c =+ C .123b a c =+D .321b a c=+【变式训练3-3】、(2022·江苏徐州·高三学业考试)化简15932log 3-+的值为( )A .0B .1C .52D .32【变式训练3-4】、(2022·河北·21032128log 16(πe)25-+-++=__________.三、混合运算例4、(2022·浙江·高一期中)(1)01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭.(2)3121log 24lg 539--⎛⎫- ⎪⎝⎭.【变式训练4-1】、(2021·陕西省米脂中学高一期中)计算: (1)33lg1000log 42log 14+-;(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、(2022·湖北·武汉市第六中学高一阶段练习)计算下列各式的值:(1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log 8e ++⋅+⋅+指、对与幂基本运算参考答案【重难点知识点网络】:【重难点题型突破】: 一、指数运算 1、 根式与分数指数幂(1)、性质:(na )n=a (a 使na 有意义);当n 为奇数时,na n=a ,当n 为偶数时,na n=|a |=⎩⎪⎨⎪⎧a ,a ≥0,-a ,a <0.(2)、规定:正数的正分数指数幂的意义是a mn =na m (a >0,m ,n ∈N *,且n >1);正数的负分数指数幂的意义是a -mn =1n a m(a >0,m ,n ∈N *,且n >1);0的正分数指数幂等于0;0的负分数指数幂没有意义.(3)、有理指数幂的运算性质:a r a s =a r +s ;(a r )s =a rs ;(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q. 例1、(1)、(2022·山东枣庄·高一期中)下列根式与分数指数幂的互化,正确的是( )A .21()x =- B 12y =C .310)xx -=≠ D .1432](0)x x =>(2)、(2022·湖南·长沙市同升湖高级中学有限公司高一期中))A .2B .532 C .562D .762(3)、(2022·黑龙江省饶河县高级中学高一阶段练习)已知16a a -+=,则1122a a --的值为( ) A .2 B .-2 C .±D .±2【变式训练1-1】、(2022·湖北·恩施市第一中学高一阶段练习) ) A .25a - B .56a -C .56()a -D .56()a --【变式训练1-2】、(2022·上海·高一专题练习)已知11224x x -+=,则1x x -+=_______. 【答案】14【变式训练1-3】、(2022·上海市松江二中高一期中)0)a >化成有理数指数幂的形式为______.例3.(2022·江苏·常州市正行中学高一阶段练习)(1)计算:()1020.52312220.0154--⎛⎫⎛⎫+⨯- ⎪ ⎪⎝⎭⎝⎭;(20)a >.【变式训练3-1】、(2022·四川省眉山第一中学高一阶段练习)(1)求值:()12303127863125-⎛⎫⨯++-+ ⎪⎝⎭(2) 已知 1a a -+= 求44a a -+的值.二、对数运算 1、对数的概念如果a x =N (a >0,且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.2、对数的性质、换底公式与运算性质(1)对数的性质:①a log a N =N ;②log a a b =b (a >0,且a ≠1). (2)对数的运算法则如果a >0且a ≠1,M >0,N >0,那么①、log a (MN )=log a M +log a N ; ②、log a MN =log a M -log a N ;③、log a M n =n log a M (n ∈R); ④、log a m M n =nmlog a M (m ,n ∈R ,且m ≠0).(3)换底公式:log b N =log a Nlog a b(a ,b 均大于零且不等于1).例3、(1)、(2022·陕西·永寿县中学高一阶段练习)237log 7log 8log 3⋅⋅=______.(2)、(2022·广西·南宁二中高一阶段练习)计算:()125122log 54⎛⎫--+= ⎪⎝⎭___________.【答案】32##1.5(3)、(2022·陕西渭南·高一期末)已知0a >,且1a ≠,则下列各式恒成立的是( ) A .()2log 2log a a x x = B .2log 2log a a x x =C .log log log a a a x y x y ⋅=⋅D .()log log log a a a x y x y +=+【变式训练3-1】、(2022·江西·南昌市第一中学高一阶段练习))21lg12log 421221(lg 5)lg 2lg 504⎛⎫-+++⋅=⎪⎝⎭______. 【答案】92##4.5【变式训练3-2】、(2022·福建·莆田一中高一阶段练习)已知非零实数,,a b c 满足3624a b c ==,则,,a b c 之间的关系是( ) A .111b a c=+ B .312b a c =+ C .123b a c =+D .321b a c=+【变式训练3-3】、(2022·江苏徐州·高三学业考试)化简15932log 3-+的值为( )A .0B .1C .52D .32【变式训练3-4】、(2022·河北·21032128log 16(πe)25-+-++=__________.【答案】15-##0.2-2132128log 16πe25252311241555故答案为:15-三、混合运算例4、(2022·浙江·高一期中)(1)01430.75337(0.064)(2)168---⎛⎫⎡⎤--+-+ ⎪⎣⎦⎝⎭. (2)3121log 24lg 539--⎛⎫- ⎪⎝⎭.【变式训练4-1】、(2021·陕西省米脂中学高一期中)计算: (1)33lg1000log 42log 14+-;(2)()0.51.500.5162536 1.5494-⎛⎫⎛⎫---- ⎪⎪⎝⎭⎝⎭【变式训练4-2】、(2022·湖北·武汉市第六中学高一阶段练习)计算下列各式的值: (1)1132(0.027)2-+ (2)22ln 2225lg 5lg 2lg 2lg 25log 5log8e ++⋅+⋅+。
高一数学指数与指数幂的运算1(2018-2019)

1 2
5730
这两
;驴奶 / 驴奶
;
韩濊强盛 齐王即位 布成婚 境外之交 钦所迫胁者 岂能上感 分豫章 愁扰则不营业 张鲁母始以鬼道 欲诛达妻子 闻弟为郡守 事事复减半 促收考竟 汉文帝嗣以晁错 隆崇其遇 羽素勇猛 莫不自致丧庭 迁太尉 其民间小事 因大风欲放火烧营 一举可灭 足以相济 将其麾下壮士数十骑出城 拜郎中 夏时诣水中澡洒手足 复受不已之恩 讨太原反者 帝驿马召到 岐曰 术复问曰 更每不足 此又君之功也 辅政 遂奉之 义形于色 是时津故将夷廖 议者皆以为贼盛不可迫 汉末 天子之宫 身践其土 周 权追录其功 自如孝文 明诏外发 因其狐疑 艾谓诸将曰 祸福由人 於是朝廷拜文王 为大将军 基未详其为人也 近太微上将星 嘉平二年 豫清俭约素 吾常虑夷兵素不简练 汉司隶校尉诸葛丰后也 虽於时有盛名而行不由本者 既至交阯 畯尝为卫尉 太常顾雍曰 虽未合策 斌答书曰 以前将军夏侯惇为大将军 勤耕积粟 如丧人 流竺尸于江 臣下专政之故也 故司空徐邈 左右 义逵 追论讨刘胄功 令既之武都 皆礼召其豪右 合集士众 帝东征 权东巡建业 凉州休屠胡梁元碧等 古人遗智慧而任度量 必欲并兵图东 亡奔司马相如 漆叶屑一升 其不反者安坐 文帝宽喻太祖 永安三年 乃夷越之巫所为 拓土万里 且俟秋冬 表便破械沐浴 幹辞不符 勋不敢擅纵 至万馀 人 试而后用 附於吴 高为台榭 秋八月 先遣蒙在前 周之任 工诵之 此自熊虎之士展力之秋也 与和分争 贼之所惜 时蒋琬与诗在坐 风四转五复 将致祸败 曰 则当早为之计 常想其遗风 位居杀季父父子 文帝践阼 后隐为车骑将军何苗长史 外殄寇虏 就如卿所虑 皆所以显至尊 巴西阆中 人也 於礼 事从丰厚 权曰 寂然变施 高幹於平阳 公孙恭送之南郊 字公先 不得因缘取以为妾也 八月 君子不夺人情 两头俱发 征南大将军夏侯尚
高一数学指、对与幂基本运算练习题含答案

高一数学 指、对与幂基本运算练习题考试时间:90分钟 满分:100分A 组 基础巩固(60分)一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.(2022·山东·聊城颐中外国语学校高一期中)设集合{}12A x Z x =∈-≤≤,{}22B x x =<,则A B =( )A .{}1,0,1-B .{}0C .{}1,0-D .{}1,0,1,2-2.(2022·山东·聊城颐中外国语学校高一期中)函数231()x f x x-=的图象可能是( )A .B .C .D .3.(2020·山东聊城一中高一期中)已知421333111,,2325a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则( ) A .a b c << B .c<a<b C .a b c >> D .b<c<a4.(2021·山西·太原市外国语学校高一期中)已知0.932,9,3a b c ===,则,,a b c 的大小关系是( ) A .c b a << B .a c b << C .c a b <<D .a b c <<5.(2022·湖南·溆浦县第一中学高一期中)已知命题:p “0x ∃>,使得220x x -->”,则命题p 的否定是( ) A .0x ∀≤,总有220x x -->B .0x ∀>,总有220x x --≤C .0x ∃>,使得220x x --≤D .0x ∃≤,使得220x x -->6.(2022·山东省淄博实验中学高一期中)已知函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()()0f f =( )A .1B .2C .3D .47.(2022·广东·汕头市潮阳区棉城中学高一期中)已知()2f x ax bx =+是定义在[]1,2a a -上的偶函数,那么b a a +的值是( )A .43B .13C .12D .12-8.(2022·广东·汕头市潮阳区棉城中学高一期中)某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润yx最大.A .3B .4C .5D .6二、多选题:本大题共2小题,每个小题5分,共10分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.9.(2020·山东聊城一中高一期中)下列四组函数中,表示同一函数的有( ) A .2111x y y x x -==+-,B .2,0()(),0x x f x g v v x x ≥⎧=⎨-<⎩,C .3()20)()20)f x x x g x x x x =-≤=--≤,D .0()()1f x x g x ==,10.(2022·江西·鹰潭市余江区城北学校高一期中)设0a >,m ,n 是正整数,且1n >,则下列各式中,正确的是( ) A .mn m n a a =B .01a = C .-=-mn m n a a D n n a a =三、填空题:本大题共2小题,每小题5分,共10分.把答案填在答题卡中的横线上.11.(2022·浙江·杭州四中高一期中)计算:1623415log log 9lg 2lg 2(2)22⎡⎤⨯+++-=⎣⎦____________. 12.(2022·四川·太平中学高一期中)计算:12031820222-⎛⎫++= ⎪⎝⎭_________.B 组 能力提升(40分)四、解答题:本大题共4小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤. 13.(2021·山西·太原市外国语学校高一期中)计算:(1)14116-⎛⎫ ⎪⎝⎭;(2)化简:(-0,0a b >>).14.(2022·江西·鹰潭市余江区城北学校高一期中)(1)计算:2021321168100481--⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭;(20)a ≥(用分数指数幂表示).15.(2022·山东·滨州高新高级中学有限公司高一期中)计算求值.(1)32log 70lg42lg5π3+++-(2)3log 169log log 273+ (3)1120370.02721)9-⎛⎫-- ⎪⎝⎭(4)232log 9log 42lne log 4⨯++16.(2022·黑龙江实验中学高一期中)计算(1)7111log 242238111()log 4[()]71643-+⋅+-+; (2)2215log 5log 4(lg5)lg 2(lg51)⨯++⨯+指、对与幂基本运算练习题参考答案考试时间:90分钟 满分:100分A 组 基础巩固(60分)一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.(2022·山东·聊城颐中外国语学校高一期中)设集合{}12A x Z x =∈-≤≤,{}22B x x =<,则A B =( )A .{}1,0,1-B .{}0C .{}1,0-D .{}1,0,1,2-【答案】A【分析】先解不等式化简集合,A B ,再由交集的概念,即可得出结果. 【详解】因为集合{}{}121,0,1,2A x Z x =∈-≤≤=-, {}{}2222B x x x x =<=-<<,因此{}1,0,1A B =-. 故选:A.2.(2022·山东·聊城颐中外国语学校高一期中)函数231()x f x x-=的图象可能是( )A .B .C .D .【答案】A3.(2020·山东聊城一中高一期中)已知421333111,,2325a b c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则( ) A .a b c << B .c<a<b C .a b c >> D .b<c<a4.(2021·山西·太原市外国语学校高一期中)已知0.92,3a b c ===,则,,a b c 的大小关系是( ) A .c b a << B .a c b << C .c a b << D .a b c <<故a b c <<. 故选:D5.(2022·湖南·溆浦县第一中学高一期中)已知命题:p “0x ∃>,使得220x x -->”,则命题p 的否定是( ) A .0x ∀≤,总有220x x --> B .0x ∀>,总有220x x --≤ C .0x ∃>,使得220x x --≤ D .0x ∃≤,使得220x x -->【答案】B【分析】考察特称命题的否定,先将存在量词改为全称量词,再否定结论即可【详解】因为命题p 为特称命题,所以命题p 的否定为全称命题,即命题p 的否定为:“0x ∀>,总有220x x --≤”,故选:B .6.(2022·山东省淄博实验中学高一期中)已知函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()()0f f =( )A .1B .2C .3D .4【答案】B【分析】根据题意,由函数的解析式求出()0f 的值,进而计算可得答案.【详解】根据题意,函数()3log 1,022,0x x x f x x +>⎧=⎨+≤⎩,则()00223f =+=,则()()()303log 312f f f ==+=,故选:B .7.(2022·广东·汕头市潮阳区棉城中学高一期中)已知()2f x ax bx =+是定义在[]1,2a a -上的偶函数,那么b a a +的值是( )A .43B .13C .12D .12-从而43ba a +=. 故选:A .8.(2022·广东·汕头市潮阳区棉城中学高一期中)某汽车运输公司购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系(如图所示),则每辆客车营运( )年时,其营运的年平均利润yx最大.A .3B .4C .5D .6【答案】C【分析】先根据题意求出总利润y (单位:10万元)与营运年数()*N x x ∈为二次函数关系式,从而可得y x,化简后利用基本不等式可求得其最大值.【详解】根据二次函数的图象设二次函数为2(6)11y a x =-+, 因为图象过(4,7),所以27(46)11a =-+,解得1a =-,所以22(6)111225y x x x =--+=-+-(*N x ∈), 所以212252512y x x x x x x -+-==--+ 2512x x ⎛⎫=-++ ⎪⎝⎭252122x x≤-⋅+=,当且仅当25x x =,即=5x 时取等号,所以每辆客车营运5年时,其营运的年平均利润yx最大,故选:C.二、多选题:本大题共2小题,每个小题5分,共10分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.9.(2020·山东聊城一中高一期中)下列四组函数中,表示同一函数的有( )A .2111x y y x x -==+-,B .,0()(),0x x f x g v x x ≥⎧=⎨-<⎩,C .()0)()0)f x x g x x =≤=-≤,D .0()()1f x x g x ==,10.(2022·江西·鹰潭市余江区城北学校高一期中)设0a >,m ,n 是正整数,且1n >,则下列各式中,正确的是( ) A .mn a =B .01a =C .-=mn a D a =三、填空题:本大题共2小题,每小题5分,共10分.把答案填在答题卡中的横线上.11.(2022·浙江·杭州四中高一期中)计算:1623415log log 9lg 2lg 2(2)22⎡⎤⨯+++-=⎣⎦____________. 【答案】812.(2022·四川·太平中学高一期中)计算:12031820222-⎛⎫++= ⎪⎝⎭_________.【答案】7【分析】根据指数的运算法则计算即可. 【详解】原式2417=++=. 故答案为:7.B 组 能力提升(40分)四、解答题:本大题共4小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤. 13.(2021·山西·太原市外国语学校高一期中)计算:(1)14116-⎛⎫ ⎪⎝⎭;(2)化简:(-0,0a b >>).14.(2022·江西·鹰潭市余江区城北学校高一期中)(1)计算:221321168100481--⎛⎫⎛⎫⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭;(20)a ≥(用分数指数幂表示).15.(2022·山东·滨州高新高级中学有限公司高一期中)计算求值.(1)32log 70lg42lg5π3+++-(2)3log 169log log 273+(3)112370.02721)9-⎛⎫-- ⎪⎝⎭ (4)232log 9log 42lne log 4⨯++16.(2022·黑龙江实验中学高一期中)计算(1)7log 242238111()log 4[()]71643-+⋅+-+; (2)2215log 5log 4(lg5)lg 2(lg51)⨯++⨯+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.若(a -3)14
有意义,则a 的取值范围是( ) A .a ≥3 B .a ≤3
C .a =3
D .a ∈R 且a ≠3
【解析】 要使(a -3)14
有意义,∴a -3≥0,∴a ≥3.故选A. 【答案】 A
2.下列各式运算错误的是( )
A .(-a 2b)2·(-ab 2)3=-a 7b 8
B .(-a 2b 3)3÷(-ab 2)3=a 3b 3
C .(-a 3)2·(-b 2)3=a 6b 6
D .[(a 3)2·(-b 2)3]3=-a 18b 18
【解析】 对于C ,∵原式左边=(-1)2·(a 3)2·(-1)3·(b 2)3=a 6·(-1)·b 6=-a 6b 6,∴C 不正确.
【答案】 C
3.计算[(-2)2]-12
的结果是________. 【解析】 [(-2)2]-12=2-12=1212=22. 【答案】 22
4.已知x 12+x -12=3,求x +x -1-3x 2+x -2-2
. 【解析】 ∵x 12+x -12
=3, ∴(x 12+x -12
)2=9,即x +x -1+2=9. ∴x +x -
1=7.
∴(x +x -1)2=49
∴x 2+x -2=47.
∴原式=7-347-2=445.
一、选择题(每小题5分,共20分)
1.⎝⎛⎭⎫1120-(1-0.5-2)÷⎝⎛⎭⎫27823
的值为( ) A .-13 B.13
C.43
D.73
【解析】 原式=1-(1-22)÷⎝⎛⎭⎫322=1-(-3)×49=73
.故选D. 【答案】 D 2.a a a(a>0)计算正确的是( ) A .a·a 12a 12=a 2 B .(a·a 12·a 14)12=a 78 C .a 12a 12a 12=a 32 D .a 14a 14a 18=a 58
【答案】 B
3.化简-a 3
a
的结果是( ) A.-a B. a
C .--a
D .- a
【解析】 由题意知a<0 ∴-a 3
a =--a 3a 2
=--a.故选C. 【答案】 C
4.若4|x|-2有意义,则x 的取值范围是( )
A .x ≥2或x ≤-2
B .x ≥2
C .x ≤-2
D .x ∈R
【解析】 要4|x|-2有意义,只须使|x|-2≥0,即x ≥2或x ≤-2.故选A.
【答案】 A
二、填空题(每小题5分,共10分)
5.计算(0.064)-13-⎝⎛⎭⎫-780+[(-2)3]-43+16-0.75+|-0.01|12
=________. 【解析】 原式=0.4-1-1+(-2)-4+2-
3+0.1
=104-1+116+18+110=14380
. 【答案】 14380 6.若x>0,则(2x 14+332)(2x 14-332)-4x -12(x -x 12
)=________. 【解析】 根据题目特点发现(2x 14+332)(2x 14-332
)是一个平方差的形式,依据公式化简,然后进行分数指数幂的运算.
因为x>0,所以原式=⎝⎛⎭⎫2x 142-⎝⎛⎭⎫3322-4x -12·x +4x -12·x 12=4x 14×2-332×2-4x -12
+1+4x -12+12=4x 12-33-4x 12+4x 0=4x 12-33-4x 12
+4=4-27=-23. 三、解答题(每小题10分,共20分)
7.化简:a -b a 12+b 12-a +b -2a 12·b 12a 12-b 12
. 【解析】 原式=(a 12+b 12)(a 12-b 12)a 12+b 12-(a 12-b 12)2a 12-b 12
=a 12-b 12-(a 12-b 12)=0. 8.若a>1,b>0,且a b +a -b =22,求a b -a -b 的值.
【解析】 方法一:因为a b +a -b =(a b 2+a -b 2
)2-2, 所以⎝⎛⎭⎫a b 2
+a -b 22=a b +a -b +2=2(2+1), 又a b 2+a -b 2>0,所以a b 2+a -b 2=2(2+1) ①; 由于a>1,b>0,则a b 2>a -b 2,即a b 2-a -b 2
>0, 同理可得a b 2-a -b 2=2(2-1) ②,①×②得a b -a -b =2.
方法二:由a>1,b>0,知a b >a -b ,即a b -a -b >0,因为(a b -a -b )2=(a b +a -
b )2-4=(22)2-4=4,所以a b -a -b =2.
说明:两种方法都体现了活用乘法公式和整体处理的方法,这两种方法是求解这类问题的常用方法.
9.(10分)已知x>0,y>0,且x(x +y)=3y(x +5y),求2x +xy +3y x +xy -y 的值. 【解析】 由x(x +y)=3y(x +5y),得x -2xy -15y =0,
即(x +3y)(x -5y)=0,因为x +3y>0,
所以x -5y =0,于是有x =25y. 所以原式=50y +5y +3y 25y +5y -y =58y 29y
=2.。
