牛顿环数据处理表
牛顿环测透镜曲率半径实验的数据处理方法

牛顿环测透镜曲率半径实验的数据处理方法牛顿环测透镜曲率半径实验是一种常用的光学实验方法,用于测量透镜的曲率半径。
本文将介绍牛顿环测量方法以及常用的数据处理方法,帮助读者了解该实验并正确进行数据处理。
一、牛顿环测量方法牛顿环测量方法是通过观察牛顿环的圆心与边缘的环形干涉图案来确定透镜的曲率半径。
具体步骤如下:1. 实验准备首先,我们需要准备一块光滑的透镜和一块玻璃基片。
将透镜和基片放在光源下方,保证光线垂直照射。
2. 形成干涉图案调整透镜和基片的间距,使得玻璃基片上形成一组明暗相间的圆环。
这个圆环就是我们所说的牛顿环。
3. 测量半径使用读数显微镜或目镜放大牛顿环图案。
从内环的直径开始,分别测量每个环的直径。
通常情况下,选取3-5个环作为测量点。
4. 记录数据将每个环的直径数据记录下来。
为了减小误差,需要重复多次测量。
二、数据处理方法牛顿环测量实验会得到一系列环的直径数据,我们需要对这些数据进行处理才能得到透镜的曲率半径。
下面介绍两种常用的数据处理方法。
1. 计算平均值首先,将每次测量得到的环直径求平均值。
这样可以减小由于实验误差导致的数据波动。
2. 曲线拟合通过拟合实验数据的曲线,我们可以得到更精确的透镜曲率半径。
常用的拟合方法有最小二乘法和直线拟合法。
最小二乘法是通过最小化实验数据与拟合曲线之间的距离来确定最优的拟合曲线。
直线拟合法则是将实验数据作为点,通过拟合直线的斜率来得到曲率半径。
三、实验注意事项在进行牛顿环测量实验时,需要注意以下几点。
1. 保持环境稳定实验环境应尽量保持稳定,避免外界震动和温度变化对实验结果的影响。
2. 测量精度使用高精度仪器进行测量,并尽量减小读数误差。
对于每个环的直径测量,应进行多次重复以提高精度。
3. 数据处理准确性在数据处理过程中,需要严格按照公式进行计算,并保留足够的有效数字。
避免舍入误差对最终结果的影响。
四、实验结果的分析与讨论根据实验得到的透镜曲率半径数据,可以进行结果的分析与讨论。
牛顿环实验数据处理方法
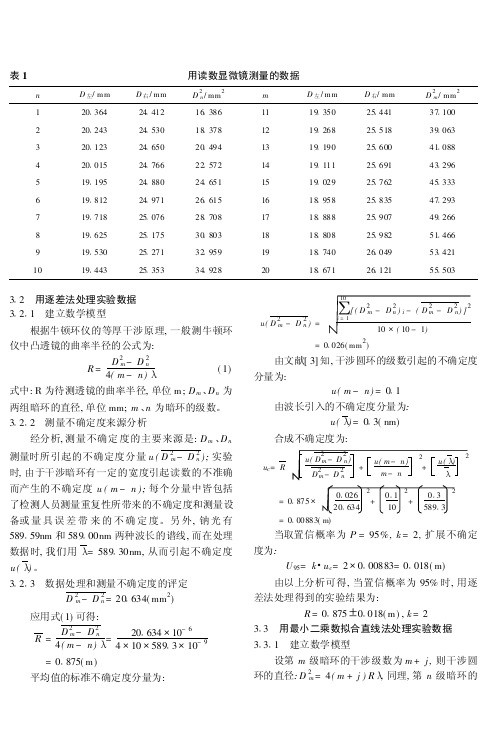
=
n
x
2 i
-
i= 1
关联系数为:
n
x iyi
i= 1
n
n
x
2 i
i= 1
= 2 062( mm2)
n
n
n
x iy i
x iyi -
i= 1
i= 1
n
=
n
n
n
x
2 i
y
2 i
x
2 i
-
i= 1
i= 1
n
y
2 i
-
i= 1
i= 1
n
= 0 9999
应用式( 2) 可得:
R= 4 = 4
2 58 9
用读数显微镜测量的数据
D
2 n
/
m
m
2
m
D左/ mm
16 386
11
19 350
18 378
12
19 268
20 494
13
19 190
22 572
14
19 111
24 651
15
19 029
26 615
16
18 958
28 708
17
18 888
30 803
18
18 808
32 959
19
18 740
34 928
20
18 671
D 右/ mm 25 441 25 518 25 600 25 691 25 762 25 835 25 907 25 982 26 049 26 121
D
2 m
/
mm2
37 100
牛顿环

一、检验项目:牛顿环
二、定义:两层ITO导电层之间产生干涉之光学现象,使得待测物(以下简称为试片)
表面形成彩虹状光环。
此现象系牛顿所发现,故称为「牛顿环」。
三、适用范围:本标准检验方法适用于公司所有须检视外观之试片。
四、目的:由于光学现象的影响,在某种角度下可观测到试片表面有牛顿环产生,可能
造成成品品质的不良,所以须做牛顿环之检测。
五、样品准备:制备试片,规格300mm ×300mm以上;组合的半成品;成品
六、使用装置及材料:
七、操作步骤:
1. 以标准目视检验方法(请参考表面脏污标准检验方法RY-STD-01-001),检查试片表面是否有牛顿环。
2. 以ITO玻璃法检测:用试片的ITO膜面与玻璃的ITO膜面相接触,用手触控膜面,从
玻璃背面观察是否有牛顿环。
八、评定准则:试片表面有任何牛顿环的情形皆”不允许”。
九、检验数据处理:表(一):牛顿环记录表。
十、注意事项:无
十一、参考文献:无
牛顿环检验记录及报告
检验日期:年月日 室温:
检验批号: 湿度:
待测物材质:
牛顿环检验记录:。
牛顿环实验报告.

精选ppt
北方民族大学物理实验中心 Fundamental physics experim2ent
内容
1 2 3 4
5 6
实验目的 实验仪器 实验原理 实验内容和要求
数据记录和处理
思考题
精选ppt
北方民族大学物理实验中心 Fundamental physics experim3ent
实验目的
1. 观察等厚现象,考察其特点。 2. 掌握一种测量透镜曲率半径的 方法。 3. 学习使用读数显微镜。
将一曲率半径相 当大的平凸玻璃透镜 放在一平面玻璃的上 面,则在两者之间形 成一个厚度随直径变 化的空气隙。
空气隙的等厚干
涉条纹是一组明暗相
间的同心环。该干涉
条纹最早被牛顿发现 , 北方民族大学物理实验中心
精选ppt
Fundamental physics experim9ent
实验原理
空气薄层中,任一厚度e处上下表面反射光的干涉条件:
精选ppt
北方民族大学物理实验中心 Fundamental physics experi1m2ent
实验内容与要求
3. 取m=15,n=5。横向改变显微镜筒位置,使叉 丝由第15圈外向第15圈移动直至叉丝交点与之重 合,读取C15,继续朝同一方向移动叉丝至第5圈 读取C5 ;仍按原方向移动叉丝(为防止产生空程 差),越过中央暗环,按同样方法读取C'5 、C'15 。 4. 将牛顿环旋转若干角度,重复以上测量共6次。
2
r k R
k0,1,2暗条纹
R
Dm2
4m
Dn2
n
如波长已知,可用此法求出透镜曲率半径;
反之亦然。
精选ppt
光的等厚干涉牛顿环实验数据

光的等厚干涉牛顿环实验数据光的等厚干涉是一种通过观察干涉条纹来研究光的性质和干涉现象的实验方法。
牛顿环是一种经典的光的等厚干涉实验,它由英国科学家艾萨克·牛顿于17世纪末发现并研究。
牛顿环实验使用了一块平行玻璃板和一个凸透镜。
首先,在平行玻璃板上滴上一滴液体,使其形成一个薄膜。
然后将凸透镜轻轻压在玻璃板上,使液体薄膜变得均匀且等厚。
当光通过液体薄膜时,会发生反射和折射,产生干涉现象。
观察牛顿环时,可以看到一系列明暗相间的圆环。
这些圆环由于液体薄膜的等厚性而形成,每个圆环都对应着液体薄膜的等厚线。
在中心圆环处,由于光程差最小,所以明亮;而在其他圆环处,光程差逐渐增大,因此呈现出暗纹。
通过测量牛顿环的半径,可以得到液体薄膜的厚度。
根据干涉理论,牛顿环的半径r与液体薄膜的厚度t之间满足以下关系式:r² = t × λ × N其中,λ为入射光的波长,N为干涉的级数。
在实际测量中,可以通过调节凸透镜和平行玻璃板之间的距离,使得干涉条纹清晰可见,然后使用显微镜测量各级圆环的半径。
通过测量不同级数下的圆环半径,可以得到液体薄膜的厚度。
光的等厚干涉牛顿环实验不仅可以用于测量液体薄膜的厚度,还可以用于研究光的干涉现象。
通过观察干涉条纹的分布和变化,可以得到关于光的干涉性质的重要信息。
除了液体薄膜,牛顿环实验还可以用于测量其他材料的厚度。
例如,可以用它来测量透明薄膜、光学元件等的厚度。
通过将待测物品放置在平行玻璃板和凸透镜之间,调节距离使得干涉条纹清晰可见,然后测量圆环半径,就可以得到待测物品的厚度。
光的等厚干涉牛顿环实验在科学研究和工程应用中具有重要意义。
它不仅可以用于测量物体的厚度,还可以用于研究光的干涉现象。
通过对光的干涉现象的研究,可以深入理解光的波动性质和光的相干性。
光的等厚干涉牛顿环实验是一种重要的实验方法,通过观察干涉条纹来研究光的性质和干涉现象。
它可以用于测量物体的厚度,也可以用于研究光的干涉现象。
用牛顿环测量透镜的曲率半径(附数据处理)

007大学实验报告评分:课程: 学期: 指导老师: 007 年级专业: 学号: 姓名: 习惯一个人007实验3-11 用牛顿环测量透镜的曲率半径一.实验目的1. 进一步熟悉移测显微镜使用, 观察牛顿环的条纹特征。
2. 利用等厚干涉测量平凸透镜曲率半径。
3.学习用逐差法处理实验数据的方法。
二. 实验仪器三.牛顿环仪, 移测显微镜, 低压钠灯四.实验原理牛顿环装置是由一块曲率半径较大的平凸玻璃透镜, 以其凸面放在一块光学玻璃平板(平晶)上构成的, 如图1所示。
平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加, 若以平行单色光垂直照射到牛顿环上, 则经空气层上、下表面反射的二光束存在光程差, 它们在平凸透镜的凸面相遇后, 将发生干涉。
从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环(如图2所示), 称为牛顿环。
由于同一干涉环上各处的空气层厚度是相同的, 因此它属于等厚干涉。
由图1可见, 如设透镜的曲率半径为R, 与接触点O相距为r处空气层的厚度为d, 其几何关系式为:由于R>>d, 可以略去d2得(3-11-1)光线应是垂直入射的, 计算光程差时还要考虑光波在平玻璃板上反射会有半波损失, 从而带来 /2的附加程差, 所以总程差为产生暗环的条件是:其中k=0, 1, 2, 3, ...为干涉暗条纹的级数。
综合(23-1)、(23-2)和(23-3)式可得第k级暗环的半径为:(3-11-2)由(4)式可知, 如果单色光源的波长 已知, 测出第m级的暗环半径rm, 即可得出平凸透镜的曲率半径R;反之, 如果R已知, 测出rm 后, 就可计算出入射单色光波的波长 。
但是用此测量关系式往往误差很大, 原因在于凸面和平面不可能是理想的点接触;接触压力会引起局部形变, 使接触处成为一个圆形平面, 干涉环中心为一暗斑。
或者空气间隙层中有了尘埃, 附加了光程差, 干涉环中心为一亮(或暗)斑, 均无法确定环的几何中心。
牛顿环法测平凸透镜曲率半径的数据处理

牛顿环法测平凸透镜曲率半径的数据处理
牛顿环法测平凸透镜曲率半径时,直接测量量为牛顿环的直径,而这一直径的测量为不等精度测量,本文采用了一种特殊的方法,使测量直径时的不确定度传措至变量替换后的一元线性方程中的时,使Y的不确定度与无关.即的测量(间接测量)为等精度测量.这样使这一测量的数据处理变为等精度测量的数据处理. 关键词牛顿环法,最,1,=乘法,等精度. 分类号.蚰一其中D.,Dl为牛顿环第m,级直径,为入射光的波长,R 为待测曲率半径,近来不少人&qu。
等厚干涉牛顿环实验报告数据处理

等厚干涉牛顿环实验报告数据处理等厚干涉牛顿环实验报告数据处理1. 引言等厚干涉牛顿环实验是光学实验中常见的一种实验方法,通过观察光的干涉现象来研究光的性质。
在这个实验中,我们通过使用等倾干涉仪,观察到一系列的干涉圆环。
本报告将详细介绍数据处理过程以及从实验中得出的结论。
2. 实验方法2.1 准备工作在进行实验之前,我们需要准备一台等倾干涉仪以及一台显微镜。
我们将干涉仪放置在实验台上,并确保其调节好水平。
此外,我们也需要一盒含有波长为546nm的绿光滤光片。
2.2 实验步骤(1) 调节光源: 首先,我们会使用黑白干涉仪,调节光源,使其尽可能的亮。
确保光线的入射角为45度。
(2) 安装滤光片: 在干涉仪的透镜后面插入绿光滤光片。
(3) 调节显微镜: 使用显微镜,将其中一眼调节到最清晰的焦平面。
(4) 观察干涉图像: 通过调节显微镜的焦距,观察到一系列的圆环。
我们将拍摄每一个圆环的直径,并记录其观察到的次数。
3. 数据处理3.1 数据记录我们使用尺子或显微镜目镜的刻度标定每个圆环的直径。
然后,我们将直径与观察到的次数一一对应,以便后续的数据处理。
3.2 数据处理方法根据物体与目镜之间的距离关系,可以得到测得的圆环直径d与真实圆环半径R的关系式:d = 2Rtanθ其中,θ为物体与目镜的角度。
为了使数据处理更加准确,我们需要对θ进行校正。
我们可以使用标准样品来进行校准。
首先,我们选择一个知名的样品,比如一根细丝,或者一个精确制作的薄片,用它替换我们的样品。
通过测量标准样品的圆环直径,并对比已知的半径,我们可以得到校准因子K。
经过校准,我们就可以得到实际的圆环半径R。
接下来,我们可以根据实际圆环半径R和观察到的次数n,来计算每个圆环的空间角度Δθ和角度差Δθ的平方。
4. 结论通过实验数据处理,我们得到了一系列的角度差Δθ的平方。
根据等厚干涉牛顿环实验原理,我们可以使用这些数据来研究光的干涉现象以及光的性质。
【word】对牛顿环实验的数据处理及不确定度评定

【word】对牛顿环实验的数据处理及不确定度评定对牛顿环实验的数据处理及不确定度评定第33卷第2期延边大学(自然科学版)2007年6月JournalofYanbianUniversity(NaturalScience)Vo1.33No.2June2007文章编号:1004—4353(2007)02—0105—04对牛顿环实验的数据处理及不确定度评定金逢锡,索建彪(延边大学理学院物理系,吉林延吉133002)摘要:介绍了在牛顿环实验的数据处理过程中,对等精度和不等精度的测量进行不确定度的计算方法.通过等精度测量的数据处理及不确定度的评定后,加权取平均法即可以解决非线性的不等精度的数据处理问题及进行不确定度的评定.关键词:等精度;不确定度;牛顿环;不等精度;干涉条纹中图分类号:04—33文献标识码:A牛顿环实验测量球面曲率半径是普通物理实验中最常见的实验之一.在实验中,人们讨论了多种数据处理的方法,如逐差法,最小二乘法,等精度测量的数据处理法,加权取平均法等等.除此之外,通过等精度测量的数据处理及不确定度的评定后加权取平均法亦是一种切实可行的数据处理方法.以下我们用此方法讨论牛顿环实验的数据处理及不确定度的评定.1实验原理牛顿环装置是由一块曲率半径较大的平凸玻璃透镜,以其凸面放在一块光学玻璃平板(平晶)上构成的,如图1所示.平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加,若以平行单色光垂直照射到牛顿环上,则经空气层上,下表面反射的两光束存在光程差,它们在平凸透镜的凸面相遇后,将发生干涉.从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环(如图2所示),称为牛顿环llj.牛顿环第级暗环的半}\}llilj尺tl\\\<,r///,….1一d‘…_f图1牛顿环装置图2牛顿环径为厂2=R,可知,如果单色光源的波长已知,测出第级的暗环半径厂,即可得出平凸透镜的曲率半径R;反之,如果R已知,测出r后,就可计算出入射单色光波的波长.但是用此测量关系式往往误差很大,原因在于凸面和平面不可能是理想的点接触,接触压力会引起局部形变,使接触处成为一个圆形平面,干涉环中心为一暗斑,或者空气间隙层中有了尘埃,附加了光程差,干涉环中心为一亮(或暗)斑,这些均无法确定环的几何中心.实际收稿日期:2006—10—17作者简介:金逢锡(1963一),男(朝鲜族),吉林延吉人,副教授,研究方向为光信息106延边大学(自然科学版)第33卷测量时,我们可以通过测量距中心较远的两个暗环的半径r和的平方差来计算曲率半径R.因为r2=mR2,r2=nR2,两式相减可得r一r2=R(m一),所以R=或R=.由上式可知,只要测出.与.(分别为第与第条暗环的直径)的值,就能算出R或.2等精度的测量及数据处理测量干涉条纹的暗环直径采取等精度的测量,即测第k环和k+m环的直径,要求k取16,17,18,19,20,m取1O.在测这1O个环的直径时,至少要重复测量5次以上,测量数据见表1.所测数据分别代入公式:,:1,2,3,4,5,可分别算出5组等精度测量的透镜的平均曲率半径,计算结果见表2.表1各牛顿环直径的原始测量数据mm次数m+k左右D+k左右DkD…一D2130.29.10021.0178.0832028.40021.7086.69220.52223029.10121.0128.0892028.40321.7116.69220.64933029.10221.0158.0872028.40221.7126.69020.64343029.10221.0148.0892028.40221.7156.68720.71653029.10321.0198.0812028.40121.7136.68820.57312929.03821.0757.9631928.31721.7886.52920.78222929.03721.0807.9571928.31821.7916.52720.71232929.04021.0777.9631928.31321.7896.52420.84742929.04221.0817.9611928.32121.7856.53620.65852929.03921.0827.9571928.32021.7926.52820.69912828.97221.1407.8321828.23821.8646.37420.71222828.97921.1377.8421828.24221.8696.37320.88232828.97821.1467.8321828.23921.8736.36620.814.42828.97921.1527.8271828.24121.8716.37020.68552828.97021.1477.8291828.24021.8736.36720.75512728.90821.2127.6961728.15321.9506.20320.75122728.90921.2157.6941728.15121.9596.19220.85732728.91021.2177.6921728.16121.9566.20320.69042728.97221.2187.6951728.16221.9596.20220.74852728.90621.2197.6871728.15921.9616.20120.63812628.84121.2787.5631628.06122.0396.02220.93422628.83721.2797.5581628.06922.0426.02720.79932628.84221.2807.5621628.07222.0436.02920.83542628.84521.2857.5601628.07322.0496.02420.86552628.83921.2847.5551628.07222.0466.02620.7653等精度测量的不确定度的评定3.1标准A类不确定度的评定第2期金逢锡,等:对牛顿环实验的数据处理及不确定度评定107根据被测量的平均值的标准偏差,可得所测每一干涉暗环的A类标准不确定度的评定:S(D)=或S(D+)=A(D)=t0.683S(D)或A(D+)=t0.683S(D+).t0.683为与测量的次数有关的比例系数[](当7z=5时,t0.683=1.114),计算结果见表3.3.2标准B类不确定度的评定一般情况下,物理实验中的B类不确定度采用均匀分布,即B=?/?3,?为移测显微镜的极限误差,由此可得本实验所测的每一环直径的B类不确定度:B(D16):B(D17):…:B(D3.):会::0.00289mm.’?jj3.3合成标准不确定度根据所估算出的A类和B类标准的不确定度,可合成所测每一干涉条纹直径的标准不确定度:c(D):?(D)+(D)或c(D+)=?(D+)+?(D+),计算结果见表3.由于各干涉条纹直径是相互独立的,所以可分别得到各组平均曲率半径的不确定度c(R1)=R1『2D16,,].『2D26,r,,].『尘1:In,一n,Ckg16I十In,一n,”c\L126I【.J(R2/I2D,7]2+[D27)]+其中DD+卅,D+一D;均采用平均值.此时所测5组透镜的平均曲率半径可分别表示为1?ttC(1),…,一R5?ttC(5),P=0.683,它们分别为等精度测量的结果,数据记录见表2所示.表2各个环的半径及不确定度的计算结果mm表3各个环的直径及不确定度的计算结果mm108延边大学(自然科学版)第33卷4,非等精度测量的数据处理及不确定度的评定从牛顿环实验的干涉条纹第k级暗环半径公式=?kRA可知,除零级暗环外,各环的直径D的关系为D】:D2:D3_..?=1:?2:?3_..?.随着干涉条纹级数k的增大,干涉条纹变密,因此该测量是非线性的不等精度测量,直接用逐差法处理数据解决不了不等精度测量问题,也就不能进行不确定度的评定l2J.若通过等精度测量的数据处理及不确定度的评定后加权取平均法,即可以解决非线性的不等精度测量数据处理及进行不确定度的评定.由于R1,R2,R3,R4,R5为非等精度测量的结果,假设其权分别为P1,P2,P3,P4,P5且一R与P成反比[,则有P=,其中i=1,2,…,5,N为比例常数,所测透镜的平均曲U-cL55厂了———?_率半径__P?i=1880?086mm,不确定度)_1/?志316mm,测量结果为R?Uc(R)=880.086?1.316mm(P=0.683),若用Uc表示扩展不确定度,则Uc=kuc(R)=2.632mm(k=2时,P=0.95)l5J.5结束语采用此方法处理数据及进行不确定度的评定,解决了非线性的不等精度测量问题,所以它更具合理性和适用性,它既可适用于牛顿环测量透镜的曲率半径的实验,也可适用于牛顿环测液体折射率的实验,但目前用此方法处理数据的缺点是测量数据多且计算比较繁琐.如果能利用计算软件,将实验数据处理得到简化,那么就会节省整个实验时间,提高工作效率.参考文献:[1]任隆良,谷晋骐.物理实验[M].天津:天津大学出版社,2003:3-6.[2]虞仲博,屠全良.牛顿环实验等精度测量及其不确定度的评定与表示[J].物理实验,2000,20(5):17.19[3]刘才明大学物理实验中测量不确定度的评定与表示[J].大学物理,1997,16(8):21.23.[4]杨述武.普通物理实验(电磁学部分)[M].北京:高等教育出版社,2000:2.5.[5]刘智敏.不确定度与分布合成[J].物理实验,1999,19(5):58.6O.DataProcessingandEvaluationofUncertaintyDegreeintheExperimen tofNewton’SRingsJINFeng—xi,SUOJian—biao(DepartmentofPhysics,CollegeofScience,YanbianUniversity,YanjiJilin13 3002,China)Abstract:Computingmethodofuncertaintydegreeforthedataofequalprecisio nmeasurementintheexperi—mentofNewton’Sringsisintroduced.Andthe problemofunequalprecisiondata anduncertaintydegreeevaluationissolvedbythemethodthroughweightedmean.Keywords:equalprecision;degreeofuncertainty;Newton’Srings;unequalpr ecision;interferencefringe。
用牛顿环测透镜曲率半径的数据处理方法

用牛顿环测透镜曲率半径的数据处理方法步超100104103 机械工程及自动化摘要:牛顿环实验是大学物理实验中非常重要的实验,以单色平行光投射到牛顿环装置上,则由空气膜上下表面反射的光波将互相干涉,形成的干涉条纹为博的等厚各点的轨迹,这种干涉是一种等厚干涉。
处理该实验的测量数据常采用逐差法,最小二乘法,加权平均以及其它方法。
通过介绍用逐差法、线性回归法、加权平均法处理牛顿环测透镜曲率半径数据的方法和过程。
比较三种实验数据处理方法的优缺点,其中加权平均法既考虑了如何克服实验的系统误差, 又能按照处理原则去对待非等精度测量, 且建立在数理统计理论基础上。
该方法主要是比较相应的权, 进而求出加权平均值, 得出加权平均法为牛顿环实验数据处理的最佳方法,但加权平均法中要计算的数据较多,公式较多,较传统的方法要复杂的多。
故探讨如何简化加权平均法,利用Matlab 软件进行处理。
关键字:牛顿环实验、加权平均法、非等精度实验数据的处理、干涉条纹、加权平均值英文译文:Buchao 100104103 Mechanical engineering and automationNewton rings experiment is university physics experiment is very important experiment, deal with the experimentThe test data of the long through "gradual deduction method, the least square method, and the weighted average, and other methods. Through the detailed introduction is used by differential method, linear regression method, the weighted average method to deal with Newton ring the lens curvature radius the method and process of data. Compare three kind of experiment data processing and the advantages and disadvantages of the methods, of which the weighted average method takes into account both the how to overcome the experiment system error, and can according to principles of management to treat the measurement precision, and established in the mathematical statistics theory basis. This method is mainly to compare the corresponding rights, and seek the weighted average, draw the weighted average method for Newton rings experiment data processing the best method, but the weighted average method to compute the data in the more, the formula is more, more traditional method is more complicated. Discusses how to simplify the weighted average method, use of Matlab software for processing.Key word: of Newton ring's experiments, weighted average method, the accuracy of experimental data processing, the interference fringes,weighted average引言:牛顿环是牛顿在1675 年所做的著名实验。
牛顿环实验数据处理分析-牛顿环实验报告数据处理
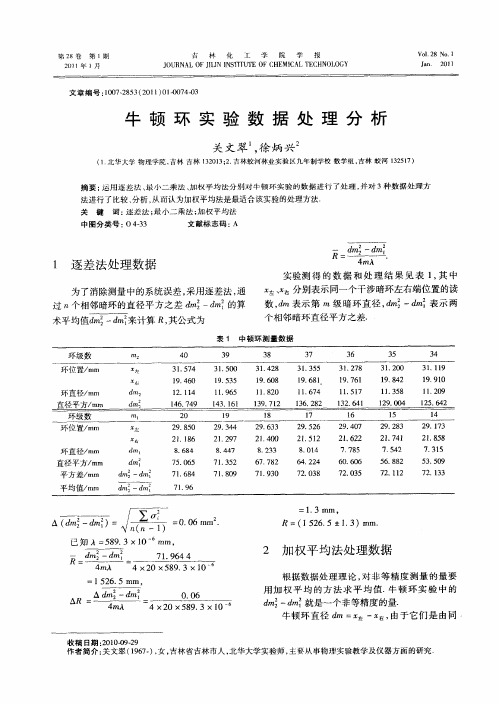
=
0. 5 n, 7 7 ml
=
.
…
R=( 5 6 2± . ) m 12 . 0 8 m
的 方 误 = 均 根差 √
=
3 用 最 小 二 乘 法 进 行 直 线 拟 合
根据干涉产生暗环的条件有 d m= , g 2+ / 2  ̄ 4
s 其 中 s 为 无 限 小 量.令 Y=d = 尺, m, ,
6:
。 :
一
。
一
,
× o. …
…
mm ,
=石 b 2=
=1 6 8984 m , 3 m 5
.
=百 = 104 =00 0 8, a .3 0
.
a= = 去 R -
R = (5 4 ±6 16 )mm .
× = … o 5 . .
这里的d ; d m 一 m 是菲等精度的, 因此, 在处理牛
△ : r = o
0 .
0 丽6 3
表 3 最小二乘法运算项 数据
吉
林
化
工
学
院
学
报
案 ( ): 751 :2m n 一 × 86 1 ∑ ∑ 2 ・ .m 9 19 9 , 一 1 0 5 “ n2∑ ) : 7 29 0 :391 ∑ 51 而1:3m ( 丢 6 1 .m . 0. 4 4 1 1 1 19 一8 1 ・ 19 ・3 t 露 :.xs. , /90 o — - …m 1 — 71 0
4,A n
=
4 0 ×58 3 × 0 一。 —X 2 9 — 1
.
=
15 6. 2 5 mm ,
:
△ 可d  ̄ d 2 尺: m - i A n 1
等厚干涉牛顿环实验报告数据处理

等厚干涉牛顿环实验报告数据处理牛顿环实验是一种常用的光学实验,用于测量透明薄片的厚度。
实验中,通过观察牛顿环的干涉现象,可以得到薄片的厚度和光的波长之间的关系。
本报告将详细介绍牛顿环实验的原理、实验装置、数据处理方法以及实验结果的分析。
一、实验原理牛顿环是由光的干涉现象产生的一组同心圆环。
在牛顿环实验中,使用一个透明薄片覆盖在平板玻璃上,然后将平板玻璃和一反射银镜组合在一起形成一个实验装置。
通过在实验装置上放置一个小透镜,并使用一照明光源,可以观察到牛顿环的干涉现象。
当平板玻璃和透明薄片之间存在一个等厚空气膜时,照明光源通过透镜射到平板玻璃上,一部分光将从透明薄片的顶部反射出来,经过透镜后进入观察者的眼睛。
另一部分光将进入透明薄片内部,经过多次反射和折射,最终也进入观察者的眼睛。
根据干涉理论,当透明薄片的厚度不同时,反射出来的光和穿过透明薄片的光之间会形成干涉条纹。
而牛顿环实验中观察到的干涉条纹的图案,正是由这种干涉现象形成的。
二、实验装置1.平板玻璃:一块平整透明的平板玻璃,用作实验基座。
2.透明薄片:一块薄而透明的样品,放置在平板玻璃上。
3.反射镜:一块光洁的反射银镜,与平板玻璃倒插在一起。
4.透镜:一块小透镜,用于观察牛顿环的干涉现象。
5.照明装置:一光源,用于照明整个实验装置。
6.目镜:用于观察牛顿环的干涉现象。
三、数据处理方法在进行牛顿环实验时,可以通过调节透镜与样品间的距离,使得干涉条纹清晰可见。
实验过程中,需要记录透镜与样品间的距离以及对应的干涉条纹的序号。
通过对多组数据的处理,可以得到透镜与样品间的距离与干涉条纹的序号之间的关系。
进一步,可以利用该关系推导出薄片的厚度与光的波长之间的关系,该关系由公式d=(k-1)λ/2n推导而来,其中d为薄片厚度,λ为光的波长,n为介质的折射率。
四、实验结果与分析根据实验记录的数据,可以绘制透镜与样品间的距离与干涉条纹的序号之间的关系曲线。
通过对这些数据的拟合,可以得到一条直线,进而可以通过直线的截距和斜率计算出薄片的厚度和光的波长之间的关系。
大学物理实验牛顿环实验报告含数据

大学物理实验牛顿环实验报告含数据一、实验目的1、观察等厚干涉现象——牛顿环。
2、掌握用牛顿环测量平凸透镜曲率半径的方法。
3、学习使用读数显微镜。
二、实验原理牛顿环是将一块曲率半径较大的平凸透镜放在一块平面玻璃上,在透镜凸面和玻璃平面之间形成一空气薄层,其厚度从中心接触点到边缘逐渐增加。
当一束单色平行光垂直照射到牛顿环装置上时,在空气薄层的上、下表面反射的两束光将产生干涉。
在反射光中,由于空气薄层的厚度不同,会形成以接触点为中心的一系列明暗相间的同心圆环,即牛顿环。
设透镜的曲率半径为$R$,形成的第$m$ 级暗环的半径为$r_m$,对应的空气薄层厚度为$d_m$。
由于暗环处光程差为半波长的奇数倍,所以有:\\begin{align}2d_m +\frac{\lambda}{2} &=(2m + 1)\frac{\lambda}{2}\\2d_m &= m\lambda\\d_m &=\frac{m\lambda}{2}\end{align}\又因为$d_m$ 可以近似表示为:\d_m = R \sqrt{R^2 r_m^2} \approx \frac{r_m^2}{2R}\将其代入上式可得:\r_m^2 = mR\lambda\则透镜的曲率半径为:\R =\frac{r_m^2}{m\lambda}\三、实验仪器1、读数显微镜2、钠光灯3、牛顿环装置四、实验步骤1、调节读数显微镜调节目镜,使十字叉丝清晰。
转动调焦手轮,使镜筒自下而上缓慢移动,直至从目镜中看到清晰的牛顿环图像。
移动牛顿环装置,使十字叉丝交点对准牛顿环中心。
2、测量牛顿环直径转动测微鼓轮,使叉丝从牛顿环中心向左移动,依次记下第 30 到21 级暗环的位置读数。
继续转动鼓轮,越过干涉圆环中心,记下第 20 到 11 级暗环的位置读数。
3、重复测量重复上述测量步骤 3 次。
4、数据处理计算各级暗环直径$D_m =|X_{m右} X_{m左}|$。
