架空线路线长计算.doc
架空线的弧垂线长及应力计算

架空线的弧垂、线长及应力计算1 弧垂、线长计算架空线由于档距很大,材料的刚性影响可忽略不计,架空线的形状就像一条两端悬挂的柔软的索链。
所以,可以按悬链线进行计算其弧垂和线成,其方程为:弧垂 f = σ/g〔ch(gl/2σ)-1〕线长L = 2σ/g〔sh(gl/2σ)〕上二式写成级数形式展开后为:f = σ/g{〔1+(L12g2/8σ2)+(L14g4/38σ4)+……〕-1}= (L12g/8σ)+(L14g3/38σ3)+……L = 2σ/g{(L1g/2σ)+(L13g3/48σ3)+(L15g5/3840σ5)+……}= L1+(L13g2/24σ2)+(L15g4/1920σ4)+……为了简化计算,工程上取f第一项计算弧垂,取L前二项计算线长(即用抛物线方程代替悬链线方程近似计算):f = L12g/8σL = L1+(L13g2/24σ2)= L1+(8 f2/3 L1)式中,L1—档距,m;g —架空线的比载,N/m·mm2g = W/S其中,W —单位长度导线重量,N/m;S —导线截面积,mm2σ—架空线最低点应力(水平应力),N/mm2。
按上式计算的误差:当弧垂不大于档距的5%时,线长误差率小于15×10-4%。
几种情况弧垂计算:①在交叉跨越档距中一般需计算被跨越物上面任一点导线的弧垂f x,以便校验交叉跨越距离。
档距中任一点导线的弧垂按下式计算:f x = x(L1-x)g/2σ= 4 f x(1-x/L1)/L1式中,x—从悬挂点至计算坐标点的水平距离,m。
②在悬挂点具有高差的档距中架空线的计算需用斜抛物线法,即:L =(L1/cosφ)+(L13g2 cosφ/24σ2)f = L12g/8σcosφf x = x(L1-x)g/2σcosφ式中,φ—高差角,φ = arc tg(h/L1)其中,h —高差;L1—档距。
2 应力计算①架空线任一点处的应力架空线各点所受应力的方向是沿架空线切线方向变化的,最低点处的应力称为水平应力,只要知道最低点应力,架空线上任一点的应力都可以用下式计算求得:σX= σ+(f-f x)g式中,σX—架空线任一点处的应力,N/mm2;σ—架空线最低点应力(水平应力),N/mm2;f —架空线弧垂,m;f x—计算点导线的弧垂,m;g —架空线比载,N/m·mm2。
农村架空配电线路施工中常用的一些数据估算

农村架空配电线路施工中常用的一些数据估算在农村,进行架空配电线路的施工,经常要遇到一些实际问题,只有通过现场实际计算才能确定,为了比较准确迅速地决定施工中经常遇到的—些问题,笔者根据多年来经验,摸索出在农村架空配电线路施工中常用的一些数据的估算,供广大工人在实际工作中的参考。
一、锥形(环形)钢筋混凝土电杆重心的确定:电杆重心点(距杆底)=0.4H十0.5 (米)H——电杆长度(米)例如:一根稍径为190毫米长为12米的环形钢筋混凝土电杆的重心点应在距杆底面的0.4×12十0.5=5.3米处。
二、电杆埋深的估算:H——电杆长度 (米)例如:12米环形钢筋混凝土电杆一般埋没。
深度应为:×12米=2米。
三、锥形电柱各部直径的确定;(毫米)фx——电杆从顶部至x米处的直径(毫米)ф稍——电杆稍径(毫米)X——电杆从顶部至需测算处的长度(毫米)例如:欲知稍径为ф190毫米的锥形杆,从杆顶下0.75米处的直径应为:фo.75=190十=200毫米。
四、拉线底锚埋深的佑算:拉线底锚埋深(米)=80×拉线棒直径(米)例如:拉线棒直径为ф16毫米,其埋没深度应为:80×16=1280毫米=1.28米五、拉线长度的估算:拉线长度L(米)=1.4×杆中心至拉线坑中心的距离(米)例如:杆中心至拉线坑中心距离为8米,则拉线长度应为1.4×8=11.2米六、高压配电线路线间距离的佑算:线间距离D=0.06U十0.3 (米)H——配电线路的额定电压(千伏)UH例如:——条10千伏的配电线路,导线间距离应为:0.06×10十0。
3=0.9米七、低压配电线路导线截面选择的估算:S——选择的低压导线截面(平方毫米)例如:在距变压器500米处欲安装20千瓦的水泵应选用多少平方毫米的导线?因此可选用LJ一35导线八、导线重量的估算,铜导线重量G=导线截面(平方毫米)×导线长度(米)×9铝导线重量G=导线截面(平方毫米)×导线长度(米)×2.7钢芯铝线重量=导线截面(平方毫米)×导线长度(千米)×4 .例如:欲估算120平方毫米长度为2公里的铜导线、铝导线、钢芯铝线的重量分别为:铜导线重=120×2×9=2160公斤;铝导线重量=120×2×27=648公斤;钢芯铝线重量=120×2×4=960公斤。
架空线计算公式

类别 参数
悬链线公式
斜抛物线公式 (大高差 0.1<h/l<0.25)
平抛物线公式 (小高差 h/l<0.1)
y
悬 挂 曲 线 方 程
0 ( x a) a [ch ch ] 0 0
y
2 0 x ( x 2a) sh sh 2 0 2 0
l a h sh arcsh 0 Lh 0 2 0 l b h sh arcsh 0 Lh 0 2 0
1 1 a 0 sin ; b 0 sin 2 2
发生在档距中央。
发生在档距中央。
xm a
发生在:
0 h arcsh l
l 0 h h arcsh arcsh 2 l Lh 0
2
L LH 0 h 2
档内 线长
2 l l 2a 0 sh ch 2 0 2 0
yB 0 sh
两点 应力 关系
2 1 y 2 y1
2 1 y 2 y1
2 1 y 2 y1
最低点至 两悬点的 水平距离
a
1 0 h 1 h arcsh ; b 0 arcsh 2 Lh 0 2 Lh 0
注: Lh 0
L
2 0 l sh 2 0
l 2 l 3 cos 2 cos 24 0
Ll L
h2 2l 3 2l 24 0 2
l 2l 3 (修正式) cos 24 0 2
任一 点 应力
工程量计算-架空线路

第十二节 10KV以下架空线路一、本章定额适用于10KV以下的配电线路安装工程,是按平原条件编制,如在其他地形条件施工时,其人工和机械定额按下表乘以地形系数。
表8 地形系数表项目丘陵一般山地、泥沼地地形系数二、地形划分1、平原地带:指地形比较平坦,地面比较干燥的地带。
2、丘陵地带:指地形起伏的矮岗,土丘等(在1公里以内地形起伏相对高差在30-50m范围以内的地带)3、一般山地:指一般山岭、沟谷(在250m以内地形起伏相对高差在30-50m范围内的地带)。
4、泥沼地带:指有水的庄稼田地或泥水淤积的地带。
三、线路一次施工工程量是按5根以上电杆考虑的。
如在5根以内者,其人工和机械乘以的系数。
架空线路的地形系数与主杆5根以内的人工、机械增加系数为连乘的关系。
四、10KV架空线路的电杆定位执行第三册“送电线路工程”中的土石方工程施工定额的相应子目。
五、挖土(石)方套用第三册“送电线路工程”中的“电杆、拉线塔、拉线坑挖填”定额的相应子目。
1、土石方工程量的计算公式:V=(a+2c+KH)×(b+2c+KH)+(1/3)K2H2式中:V——地坑体积 a——坑底净长b——坑底净宽 K——放坡系数取H——坑的深度 c——工作面取米B C C BV=B/H B=KH如设计无规定时,可按表9计算方量表9 杆坑土方量参考表放坡系数杆高(m)7 8 9 10 11 12 13 15埋深(m)底盘规格(mm)600×600800×8001000×1000带底盘土方量(M3)不带底盘土方量(M3)注:①土方量计算公式亦用于拉线坑。
②双接腿坑,按带底盘的土方量计算。
③木杆按不带底盘的土方量计算。
3、电杆埋深可按下式取整数计算:埋深h=H/6六、10KV架空线路的工地运输可套用第三册“送电线路工程”中的工地运输中的相应子目及有关规定。
七、电杆组立,按电杆的长度及不同的材质以“根”为单位套用定额。
架空线常用计算公式和应用举例_图文

架空线常用计算公式和应用举例前言在基层电力部门从事输电线路专业工作的技术人员,需要掌握导线的基本的计算方法。
这些方法可以从教材或手册中找到。
但是,教材一般从原理开始叙述,用于实际计算的公式夹在大量的文字和推导公式中,手册的计算实例较少,给应用带来一些不便。
本书根据个人在实际工作中的经验,摘取了一些常用公式,并主要应用Excel工作表编制了一些例子,以供相关人员参考。
本书的基本内容主要取材于参考文献,部分取材于网络。
所用参考文献如下:1. GB50545 -2010 《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电力线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线力学计算,中国电力出版社,2003。
5. 刘增良、杨泽江主编,输配电线路设计, 中国水利水电出版社,2004。
6.李瑞祥编,高压输电线路设计基础,水利电力出版社,1994。
7.电机工程手册编辑委员会,电机工程手册,机械工业出版社,1982。
8.张殿生主编,电力工程高压送电线路设计手册,中国电力出版社,2003。
9.浙西电力技工学校主编,输电线路设计基础,水利电力出版社,1988。
10.建筑电气设计手册编写组,建筑电气设计手册,中国建筑工业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国水利水电出版社,2003。
由于个人水平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久 2015-9-16目录第一章电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式二、导线截面选择与校验的方法三、地线的选择第二节架空电力线路的设计气象条件一、设计气象条件的选用二、气象条件的换算第二章导线(地线)张力(应力)弧垂计算第一节导线和地线的机械物理特性与单位荷载一、导线的机械物理特性二、导线的单位荷载第二节导线的最大使用张力和平均运行张力一、导线的最大使用张力二、导线的平均运行张力第三节导线张力弧垂的精确计算一、导线的悬链线解析方程式二、导线的张力、弧垂与线长三、导线的允许档距和允许高差四、导线悬挂点等高时的张力弧垂计算五、架空线的等效张力(平均张力)第四节导线张力弧垂的近似计算一、导线的抛物线解析方程式二、导线的张力、弧垂与线长第五节水平档距和垂直档距一、水平档距和水平荷载二、垂直档距和垂直荷载第六节导线的状态方程式一、孤立档的状态方程式二、连续档的状态方程式和代表档距第七节临界档距一、用斜抛物线状态方程式求临界档二、用临界档距判别控制条件所控制的档距范围第八节导线张力弧垂计算步骤第九节导线应力弧垂分析一、导线和地线的破坏应力与比载二、导线的悬链线公式三、导线应力弧垂的近似计算四、水平档距和垂直档距五、导线的斜抛物线状态方程式六、临界档距第三章特殊情况导线张力弧垂的计算第一节档距中有一个集中荷载时导线张力弧垂的计算一、档距中有一个集中荷载的弧垂和张力二、导线强度及对地或交叉跨越物距离的校验第二节孤立档导线的计算一、耐张绝缘子串的单位荷载二、孤立档导线的张力和弧垂三、孤立档的临界档距第三节导线紧线时的过牵引计算一、紧线施工方法与过牵引长度二、过牵引引起的伸长和变形三、不考虑耐张绝缘子串的导线过牵引计算四、孤立档考虑耐张绝缘子串的导线过牵引计算第四节连续倾斜档的安装计算一、连续倾斜档导线安装时的受力分析二、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘子串倒挂的校验第六节悬垂线夹悬垂角的计算第四章导线和地线的防振计算第一节防振锤和阻尼线一、防振锤的安装二、阻尼线的安装第二节分裂导线的防振第五章架空线的不平衡张力计算第一节刚性杆塔固定横担线路不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时的不平衡张力求解方法三、断线张力求解方法四、导线从悬垂线夹松落时的不平衡张力第二节固定横担线路考虑杆塔挠度时不平衡张力的计算一、线路产生不平衡张力时的几种关系二、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张力求解方法三、考虑杆塔挠度时的断线张力求解方法第三节转动型横担线路断线张力的计算一、断线张力的求解方程二、断线张力的计算机试凑求解方法第四节相分裂导线不平衡张力的计算一、计算分裂导线的不平衡张力的公式二、计算公式中几个参数的取值与计算三、不平衡张力的求解方法四、用Excel工作表进行计算的方法第五节地线支持力的计算一、电杆的刚度和刚度系数二、电杆的挠度三、地线支持力的计算四、地线支持力的计算机试凑求解方法第六章架空线弧垂观测计算第一节弧垂观测概述一、观测档的选择二、导线初伸长的处理三、弧垂的观测方法四、弧垂的调整与检查五、观测弧垂时应该注意的问题第二节均布荷载下的弧垂的观测参数计算一、用悬链线法求弧垂观测参数二、弧垂观测角的近似计算公式三、用异长法和等长法观测弧垂时a、b与弧垂f的关系第三节观测档内联有耐张绝缘子串时弧垂的观测参数计算一、观测档弧垂的计算公式二、用等长法和异长法观测弧垂三、用角度法观测弧垂架空线常用计算公式和应用举例 安岳供电公司 李荣久第一章 电力线路的导线和设计气象条件第一节导线和地线的型式和截面的选择一、导线型式常用导线的型号和名称如表1-1-1。
工程量计算-架空线路

工程量计算-架空线路(总5页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第十二节 10KV以下架空线路一、本章定额适用于10KV以下的配电线路安装工程,是按平原条件编制,如在其他地形条件施工时,其人工和机械定额按下表乘以地形系数。
表8 地形系数表项目丘陵一般山地、泥沼地地形系数二、地形划分1、平原地带:指地形比较平坦,地面比较干燥的地带。
2、丘陵地带:指地形起伏的矮岗,土丘等(在1公里以内地形起伏相对高差在30-50m范围以内的地带)3、一般山地:指一般山岭、沟谷(在250m以内地形起伏相对高差在30-50m范围内的地带)。
4、泥沼地带:指有水的庄稼田地或泥水淤积的地带。
三、线路一次施工工程量是按5根以上电杆考虑的。
如在5根以内者,其人工和机械乘以的系数。
架空线路的地形系数与主杆5根以内的人工、机械增加系数为连乘的关系。
四、10KV架空线路的电杆定位执行第三册“送电线路工程”中的土石方工程施工定额的相应子目。
五、挖土(石)方套用第三册“送电线路工程”中的“电杆、拉线塔、拉线坑挖填”定额的相应子目。
1、土石方工程量的计算公式:V=(a+2c+KH)×(b+2c+KH)+(1/3)K2H2式中:V——地坑体积 a——坑底净长b——坑底净宽 K——放坡系数取H——坑的深度 c——工作面取米B C C BV=B/H B=KH如设计无规定时,可按表9计算方量表9 杆坑土方量参考表放坡系数杆高(m)7 8 9 10 11 12 13 15埋深(m)底盘规格(mm)600×600800×8001000×1000带底盘土方量(M3)不带底盘土方量(M3)注:①土方量计算公式亦用于拉线坑。
②双接腿坑,按带底盘的土方量计算。
③木杆按不带底盘的土方量计算。
3、电杆埋深可按下式取整数计算:埋深h=H/6六、10KV架空线路的工地运输可套用第三册“送电线路工程”中的工地运输中的相应子目及有关规定。
4 均布菏载下架空线的计算

图4-3 不等高悬点架空线的悬链线
斜抛物线 悬挂曲线方程 任一点弧垂 任一点应力 斜抛物线线长
图4-4 架空线斜抛物线下的受力图
图4-5 等高悬点与不等高悬点架空线弧垂间的关系
图4-6 架空线平抛物线下的受力图
图4-7 线长计算公式误差曲线
图4-8
弧垂误差曲线
(b)斜抛物线弧垂误差百分数
(a)平抛物线弧垂误差百分数
架空线的平均高度 架空线的平均应力
图4-9
架空线的平均高度
等高悬点架空线的悬链线方程
y
0 (ch x 1) 0
2 0
(4-6)
等高悬点架空线任意一点x处的弧垂
f x yB y
sh
x1 (l x1 ) sh 2 0 2 0
(4-8)
等高悬点架空线档距中央弧垂(最大弧垂) 2 l l f y B 0 (ch 1) 0 sh 2 2 0 4 0 等高悬点架空线线长 2 x l Lx 0 sh L 0 sh 0 2 0 等高悬点架空线任一点应力
2
0 cos
2 2
(4-52) (4-53)
x l (y yl )
架空线斜抛物线线长
L
0
l
dy 2 1 2 cos2 l l 2l 3 cos 1 ( ) dx [l ] 2 2 dx cos 3 cos 8 0 24 0
f x |h 0 2 0
sh
x (l x) sh 2 0 2 0
不等高悬点架空线一档内的最大弧垂
d fx l h h 0 xm 0 (arcsh arcsh ) dx 2 l Lh0
(标准)架空输电线路电气参数计算

架空输电线路电气参数计算专业整理知识分享一、提资参数表格式专业整理知识分享二、线路参数的计算:1.3倍。
导线的直流电阻可在导线产品样本中查到。
当线路的相导线为两分裂导线时,相当于两根导线并联,则其电阻应除以2。
多分裂导线以此类推。
X1=0.0029f lg(d m/r e) Ω/km式中 f-频率(Hz);d m-相导线间的几何均距,(m);dm=3√(d ab d bc d ca)d ab d bc d ca -分别为三相导线间的距离,(m);r e-导线的有效半径,(m);r e≈0.779r专业整理知识分享r-导线的半径,(m)。
2)单回路相分裂导线的正序电抗:X1=0.0029f lg(d m/R e) Ω/km 式中 f-频率(Hz);d m-相导线间的几何均距,(m);dm=3√(d ab d bc d ca)d ab d bc d ca -分别为三相导线间的距离,(m);R e-相分裂导线的有效半径,(m);n=2 R e=(r e S)1/2n=4 R e=1.091(r e S3)1/4n=6 R e=1.349(r e S5)1/6S-分裂间距,(m)。
专业整理知识分享3)双回路线路的正序电抗:X1=0.0029f lg (d m/R e) Ω/km式中 f-频率(Hz);d m-相导线间的几何均距,(m); a 。
c′。
dm=12√(d ab d ac d ab′d ac′‵d ba d bc d ba′d bc′d ca d cb d ca′d cb′) b 。
b′。
d ab d bc ……分别为三相双回路导线间的轮换距离,(m); c 。
a′。
R e-相分裂导线的有效半径,(m);R e=6√(r e3 d aa′d bb′d cc′)国内常用导线的线路正序电抗查《电力工程高压送电线路设计手册》第二版 P18~P19查表时注意: 1)弄清计算线路有代表性的塔型(用得多的塔型),或有两种塔型时,用加权平均计算出线路的几何均距。
架空线路公式

导线截面的选择1、按经济电流密度选择线路的投资总费用Z1式中Z1 =(F0+αΑ)LF0—与导线截面无关的线路单位长费用;α—与导线截面相关的线路单位长度单位截面的费用;Α—导线的截面积;L—线路长度。
线路的年运行费用包括折旧费,检修维护费和管理费等,可用百分比b 表示为线路的年电能损耗费用(不考虑电晕损失):若投资回收年限为n得到导线的经济截面A n经济电流密度J n我国的经济电流密度可以按表查取。
2、按电压损耗校验在不考虑线路电压损耗的横分量时,线路电压、输送功率、功率因数、电压损耗百分数、导线电阻率以及线路长度与导线截面的关系,可用下式表示3、按导线允许电流校验(1)按导线的允许最大工作电流校验导线的允许最大工作电流为其中(2)按短路电流校验根据短路电流的热效应,要求导线的最小截面为4、按电晕条件校验超高压输电线路的导线表面电场强度很高,以至超过周围空气的放电强度,使空气电离形成局部放电,这种现象称为电晕。
电晕可以引起无线电干扰、可听噪声、导线震动等,还会产生有功功率损耗。
导线的电晕随外加电压的升高而出现、加剧。
导线表面开始发生局部放电时的电压,称为起始电晕电压。
导线表面全面发生电晕时的电压,称为临界电晕电压,相应的电场强度称为临界电场强。
倒显得临界电晕电场强,与其直径、表面状况及大气条件等有关。
根据理论分析及试验所的结果,海拔不超过1000m 的地区,如导线直径不小于下表所列数值,一般不必验算电晕。
绝缘子和绝缘子串1、绝缘子的许用荷载绝缘子的许用荷载当绝缘子所受荷载大于其许用荷载时,除可更换大吨位绝缘子外,还可以采取双串和多串联解决。
所需串数N悬垂串片数计算:一般地区单位工作电压所要求的泄露电流(泄露比距):海拔高度1000m~3500m 的地区悬垂串的绝缘子数量按下式计算。
气象参数1、风速的此时换算欲将 4 次定时2 分钟平均风速V2换算成连续自记10 分钟平均风速V10,v需要搜集到两种观测方法的平行观测记录,然后通过相关分析建立二者之间的回归方程式。
架空线路线长计算.doc

第四章 均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此,设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节 架空线悬链线方程的积分普遍形式图4-1 架空线悬挂曲线受力图(a )分离体受力图;(b )整档架空线受力图;图4-1(b )所示为某档架空线,A 、B 均为两悬挂点。
沿架空线线长作用有均布比载γ,方向垂直向下。
在比载γ作用下,架空线呈曲线形状,其最低位置在ο点,在悬挂点A 、B处,架空线的轴向应力分别为A σ和B σ。
选取线路方向(垂直于比载)为坐标系的x 轴,平行于比载方向为y 轴。
在架空线上任选一点C ,取长为OC L 的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有0cos ,0σθσ==∑XX (4- 1)OC XL Y γθσ==∑sin ,0 (4- 2)式(4-1)表明,架空线上任一点C 处的轴向应力X σ的水平分量等于弧垂最低点处的轴向应力0σ,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长OC L 与比载γ之积。
以上两式相除可得tg θ=OCL 0σγdx dy =OC L 0σγ(4- 3)上式为悬链线方程的徽分形式。
从中可以看出,当比值γ/0σ一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
架空送电线路工程架线施工常用计算公式集锦
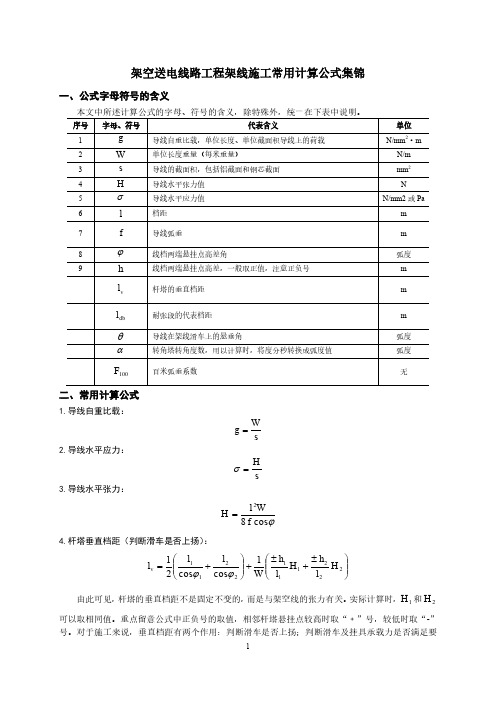
6
1
求,是否需要悬挂双滑车或者采取其他补强措施。 5.耐张段代表档距:
l db
l cos l cos
3 i i i 3 i 2 i
i
(李庆林版)
l db
l cos l cos
i
i
(李博之版)
注:地形平坦情况下,两者计算结果相差不大,为了确保精确度,建议采用李博之版。 6.导线在滑车上的悬垂角:
2
当包络角大于 30°时,需要悬挂双滑车,对于光缆来说,可以放大到 60°。 8.相邻导线挂点高差角:
tg 1
9.导线一档线长计算公式
h l
l W 2l 3 L (平抛物线计算公式) cos 24H 2 L
10.弧垂(驰度)计算公式
l W 2 l 3 cos (斜抛物线计算公式) cos 24H 2
lv
l 1 l1 2 2 cos1 cos 2
由此可见, 杆塔的垂直档距不是固定不变的, 而是与架空线的张力有关。 实际计算时,H 1 和 H 2 可以取相同值。重点留意公式中正负号的取值,相邻杆塔悬挂点较高时取“﹢”号,较低时取“-” 号。对于施工来说,垂直档距有两个作用:判断滑车是否上扬;判断滑车及挂具承载力是否满足要
其中: l 为控制档档距,m; x 为障碍物到高悬挂点水平距离,m; y 为高悬挂点到障碍物顶部的垂直净空距离,m。
4
y 0 为导线对正下方障碍物垂直净空距离,即安全距离,m;
为控制档两侧挂点高差角。
16.出口张力计算
T0 1i H i W (h1 1h2 2 h3 1i hi 1i f i )
3
-1 -1
架空线路弧垂应力及线长计算

架空线路弧垂、应力及线长计算1、导线的机械特性和荷载 1.1导线的机械特性导线的特性参数是指导线的瞬时破坏应力σp 、弹性系数E 、温度线膨胀系数α以及密度γ等数据。
这些特性参数是对导线进行机械计算的重要依据,一般可从有关资料或手册中得到。
1.1.1导线的瞬时破坏应力σp 。
对导线做拉伸试验时,将测得的瞬时拉断力除以导线的截面积,即得导线的瞬时破坏应力σp ,计算公式为σp =AT p (N/mm 2) (ZY0400201002-1)式中:T p —导线的瞬时拉断力,N ;A —导线的截面积,mm 2。
对于钢芯铝绞线来说,指的是的综合瞬时破坏应力σp ,可以通过下面的经验公式求得σp =sa sps s ap a a A A σA σA η++η(N/mm 2) (ZY0400201002-2)式中:ηa —铝线绞合引起的强度损失系数,37股以下绞线ηa =0.95,37股以上绞线ηa =0.9; ηs —钢绞线绞合引起的强度损失系数,取ηa =0.85; σap —铝单线的抗拉强度,N /mm 2; σsp —钢线的抗拉强度,N /mm 2; A a —铝部的截面积; A s —钢部的截面积。
1.1.2导线弹性系数E 。
是指在弹性限度内,导线受拉力作用时,其应力σ与应变ε的比例系数E 。
钢芯铝绞线的弹性系数是一个综合弹性系数E ,可按下式计算aaE E E ++=1a s (N/mm 2) (ZY0400201002-3)式中:E s —单股钢线的弹性系数,N /mm 2; E a —单股铝线的弹性系数,N /mm 2;a —导线铝和钢的截面比,LGJ 型a =5.3~6.0,LGJQ 型a =8.0,LGJJ 型a =4.3~4.4。
1.1.3导线温度线膨胀系数α。
是指导线温度升高1℃时长度伸长的相对值,用公式表示为α=tΔε(1/℃) (ZY0400201002-4)式中:ε—温度变化引起的导线相对变形量;∆t —温度变化量,℃。
架空线路线长计算

架空线路线长计算第四章均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此,设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节架空线悬链线方程的积分普遍形式图4-1 架空线悬挂曲线受力图(a )分离体受力图;(b )整档架空线受力图;图4-1(b )所示为某档架空线,A 、B 均为两悬挂点。
沿架空线线长作用有均布比载γ,方向垂直向下。
在比载γ作用下,架空线呈曲线形状,其最低位置在ο点,在悬挂点A 、B 处,架空线的轴向应力分别为Aσ和Bσ。
选取线路方向(垂直于比载)为坐标系的x 轴,平行于比载方向为y 轴。
在架空线上任选一点C ,取长为OCL 的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有0cos ,0σθσ==∑XX (4- 1)OC XL Y γθσ==∑sin ,0 (4- 2)式(4-1)表明,架空线上任一点C 处的轴向应力Xσ的水平分量等于弧垂最低点处的轴向应力0σ,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长OCL 与比载γ之积。
以上两式相除可得tg θ=OCL 0σγdx dy =OC L 0σγ(4- 3)上式为悬链线方程的徽分形式。
从中可以看出,当比值γ/0σ一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
2020年(班组长管理)架空线路线长计算

(班组长管理)架空线路线长计算第四章均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此,设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节架空线悬链线方程的积分普遍形式图4-1架空线悬挂曲线受力图(a)分离体受力图;(b)整档架空线受力图;图4-1(b)所示为某档架空线,A、B均为两悬挂点。
沿架空线线长作用有均布比载,方向垂直向下。
在比载作用下,架空线呈曲线形状,其最低位置在点,在悬挂点A、B处,架空线的轴向应力分别为和。
选取线路方向(垂直于比载)为坐标系的x轴,平行于比载方向为y轴。
在架空线上任选一点C,取长为的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有(4-1)(4-2) 式(4-1)表明,架空线上任一点C处的轴向应力的水平分量等于弧垂最低点处的轴向应力,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长与比载之积。
以上两式相除可得tg==(4-3) 上式为悬链线方程的徽分形式。
从中可以看出,当比值/一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
在弧垂最低点O处,曲线的斜率为零,即=0,将式(4-3)写成两边微份分离变量后两端积分或写成=sh(4-4) 上式两端积分,得y=ch(4-5) 式(4-5)是架空线悬链线方程的积分普遍形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 均布荷载下架空线的计算在架空输电线路的设计中,不同气象条件下架空线的弧垂、应力和线长占有十分重要的位置,是输电线路力学研究的主要内容。
这是因为架空线的弧垂和应力直接影响着线路的正常安全运行,而架空线线长的微小变化和误差都会引起弧垂和应力相当大的改变。
设计弧垂小,架空线的拉应力就大,振动现象加剧,安全系数减小,同时杆塔荷载增大因而要求强度提高。
设计弧垂过大,满足对地安全距离所需杆塔高度增加,线路投资增大,而且架空线的风摆、舞动和跳跃会造成线路停电事故,若加大塔头尺寸,必然会使投资再度提高。
因此,设计合适的弧垂是十分重要的。
本章研究垂直均布荷载和水平均布荷载作用下的架空线有关计算问题。
第一节 架空线悬链线方程的积分普遍形式图4-1 架空线悬挂曲线受力图(a )分离体受力图;(b )整档架空线受力图;图4-1(b )所示为某档架空线,A 、B 均为两悬挂点。
沿架空线线长作用有均布比载γ,方向垂直向下。
在比载γ作用下,架空线呈曲线形状,其最低位置在ο点,在悬挂点A 、B处,架空线的轴向应力分别为A σ和B σ。
选取线路方向(垂直于比载)为坐标系的x 轴,平行于比载方向为y 轴。
在架空线上任选一点C ,取长为OC L 的一段架空线作为研究对象,受力分析如图4-1(a)所示。
列研究对象的力平衡方程式,有0cos ,0σθσ==∑XX (4- 1)OC XL Y γθσ==∑sin ,0 (4- 2)式(4-1)表明,架空线上任一点C 处的轴向应力X σ的水平分量等于弧垂最低点处的轴向应力0σ,即架空线上轴向应力的水平分量处处相等,式(4-2)表明,架空线上任一点轴向应力的垂向分量等于该点到弧垂最低点间线长OC L 与比载γ之积。
以上两式相除可得tg θ=OCL 0σγdx dy =OC L 0σγ(4- 3)上式为悬链线方程的徽分形式。
从中可以看出,当比值γ/0σ一定时,架空线上任一点处的斜率与该点至弧垂最低点之间的线长成正比。
在弧垂最低点O 处,曲线的斜率为零,即θ=0,将式(4- 3)写成OC L y 0σγ=' 两边微份()()dx y dy dx L d y d C 2020001)(2'±=+=='σγσγσγ 分离变量后两端积分⎰⎰='+'dx y y d 021σγ)()(10C x y arcsh +='σγ或写成dxdy=sh )(10C x +σγ (4- 4) 上式两端积分,得y=γσ0ch 210)(C C x ++σγ(4- 5)式(4- 5)是架空线悬链线方程的积分普遍形式。
其中1C 、2C 为积分常数,其值取决于坐标系的原点位置。
第二节 等高悬点架空线的弧垂、线长和应力一、等高悬点架空线的悬链线方程等高悬点是指架空线的两个悬挂点高度相同。
由于对称性,等高悬点架空线的弧垂最低点位于档距中央,将坐标原为取在该点,如图4-2所示。
图4-2 等高悬点架空线的悬链线当x=0时,dxdy=0,代入式(4- 4)可解得1C =0;当x=0时,y=0,代入式(4- 5)并利用1C =0,解得γσ01-=C ,将1C 、2C 的值代回式(4- 5),并加以整理即可得到架空线的悬链线方程 y=γσ0)1(ch 0-x σγ (4- 6)由式(4- 6)可以看出,架空线的悬链线具体形状完全由比值γσ/0决定,即无论是何种架空线,何种气象条件,只要γσ/0相同,架空线的悬挂曲线形状就相同。
在比载γ一定的情况下,架空线的水平应力0σ是决定悬链线形状的唯一因素,所以架线时的水平张力对架空线的空间形状有着决定性的影响。
在导出式(4- 6)的过程中,并没有用到等高悬点的限定条件,因此式(4- 6)同样可用于不等高悬点的情况。
二、等高悬点架空线的弧垂架空线上任一点的弧垂是指该点距两悬挂点连线的垂向距离。
在架空输电线路设计中,需计算架空线任一点x 处的弧垂X f ,以验算架空线对地安全距离,参见图4-2,显然y y f B X -=而=B y γσ0(ch 120-σrl) 所以=X f ]2)2(2[]2[0100000σσγγσσγσγγσx l r ch lch x ch l ch --=- (4- 7) 利用恒等式ch α-ch β=2sh22shβαβα-+ 对上式进行变换,可以得到=X f 010102)(22σσγσx l r sh rx sh- (4- 8) 在档距中央,弧垂有最大值f ,此时x=0或x1=2l,所以有 0200042]12(σγγσσγγσl sh l ch y f B =-== (4-9)除非特别说明,架空线的弧垂一般指的是最大弧垂。
最大弧垂在线路的设计、施工中占有十分重要的位置。
三、等高悬点架空线的线长弧垂最低点O 与任一点C 之间的架空线长度OC L (参见图4-1)可由式(4-3)和式(4-4)联立求解,并考虑到01=C 而得到。
线长OC L 计算式为0σγσrx sh L OC =或记为0σγσrx sh L X =将2/l X =代入上式,可得到半档距架空线的长度2/l X L =,整档架空线的线长L 是2/l X L =的2倍,即===2/2l X L L 022σγσrlsh(4- 10)上式表明,在档距l 一定时,架空线的线长随比载γ和水平应力0σ的变化而改变,即架空线的线长是其比载的应力的函数。
应该指出,式(4- 10)计算得出的是按架空线的悬挂曲线几何形状的计算长度,与架空线的制造长度不尽相同。
四、等高悬点架空线的应力架空线上任一点C 处的应力指的是该点的轴向应力,其方向同该点线轴方向,如图4-1(a )所示。
轴向应力x σ可视为水平应力0σ和垂向应力0σ的合成。
0σ是架空线最低点处的应力,工程上常作为已知条件。
当架空线的比载γ也已知时,任一点的应力为()020002020122σσσσσσσrx sh rx sh rL OC x +=⎪⎪⎭⎫ ⎝⎛+=+= 根据恒等变换ch αα21sh += ,可得0σσσrxchx = (4- 11)在两等高悬挂点A 、B 处,有02σσσσrlchB A == (4- 12) 如果用弧垂表示,则为rf B A +==0σσσ上式表明,等高悬点处架空线的应力等于其水平应力和作用在其上的比载与中央弧垂的乘积的和。
必须指出,悬挂点处的应力除按式(4- 12)计算的静态应力外,还有线夹的横向挤压应力,考虑刚度时的附加弯曲应力和振动时产生的附加动应力等。
第三节 不等高悬点架空线的弧垂、线长和应力地形的起伏不平或杆塔高度的不同,将造成架空线悬挂高度不相等。
同一档距两悬挂点间的高度差简称为高差,两悬挂点连线与水平面的夹角称为高差角。
一、 不等高悬点架空线的悬链线方程为应用方便起见,取坐标原点位于左侧悬挂点处,如图4-3所示。
图4-3 不等高悬点架空线的悬链线在所选坐标系中,当x=a 时,0/=x y d d ,代入式(4-4)求得a C -=1;当x=0时,y=0,代入式(4-5)并注意到a C -=1,求得02σσrachrC -= ,将C1、C2之值再代回到式(4-5),有000002)2(22])([σγσγγσσσγγσa x sh x sh ra ch a x ch y -=--=(4- 13) 上式即为不等高悬点架空线的悬链线方程,但式中架空线最低点至左侧低悬挂点的水平距离a 待求。
将x=l 时y=h 的边界条件代入式(4- 13),可以得到00222σγσσx sh r h arcsh rl a -=上式中反双曲线函数一项的分母,实际上就是式(4-10)表示的等高悬点架空线的档内悬链线长度,记为0=h L ,即022σγγσl shL h == (4- 10/) 所以02=-=h L h arcsh r l a σ (4- 14) 相应地,弧垂最低点距右侧高悬挂点的水平距离为02=+=h L h arcsh r l b σ (4- 15) 由于200000200000002)()(12)(2)()(12)(]2)([]2[2)2(σγσγσγσγσγσγσγσγx l sh L h x l ch L h L hl x ch L h l x sh L h arcsh l x sh a x sh a x shh h h h h -+--=-++-=+-=-=-=====上式代入式(4-13),便可得到坐标原点位于左悬点时的不等高悬点架空线的悬链线方程为]2)(22[)(1]2)(22[]2)()(12)([22]2)2(22000200000020000000σσγγσσσγγσσγσσγγσσγσγγσx l r sh x sh L h x l r ch x sh L h x l sh L h x l r ch L h x sha x sh x sh y h h h h -+--=-+--=-===== (4- 16)当h =0时,即得到坐标原点位于左悬挂点时的等高悬点的架空线悬链线方程002)(22σγσγγσx l sh x shy --= (4- 17)二、 不等高悬点架空线的弧垂根据弧垂的定义,不等高悬点架空线任一点处的弧垂为]2)(22[)(1]2)(22[2)2(22000200000000σσγγσσγσγγσσγσγγσx l r sh x sh L h x l ch x sh L h x l h a x sh x sh x l h y x l h f h h x -++--=--=-=== (4-18)等高悬点h =0时,有00)0(2)(22σγσγγσx l sh x shf h x --== 这与式(4-8)是一致的。
架空输电线路最常用的是档距中央弧垂,最低点弧垂和最大弧垂(斜切点弧垂),在档距中央x=l /2,代入式(4-18)并化简后得到档距中央弧垂的计算式)12()(1002021-+==σγσrl ch L h f h (4- 19) 最低点弧垂出现在x=a 处,代入任一点弧垂公式(4-18)并注意到式(4-4),适当整理后得)12)(1[002000--+===h h L h arcsh l h rl ch L h f σγσ (4- 20) 同式(4-19)相比较,上式可写成200210)(11[==+-+-=h h L h L h sh arc l h f f γσ (4- 20/)最大弧垂出现在0=dxdf x处,即 0)()])(([)(0000=--=---=-=σσσσa x r sh l h rach a x r ch r x l h dx d y x lhdx d dx df x 解得出现最大弧垂的位置)(2000=-+=+=h m L h arcsh l h arcsh r l l h arcshra x σσ (4- 21) 从上式可以看出,不等高悬点架空线的最大弧垂不在档距中央。
