大学物理2作业题1-3

合集下载

大连理工大学大学物理作业2(静电场二)及答案详解

1．如图所示，把点电荷q +从高斯面外P 移到R 处()OP OR =，O 为S 上一点，则[ ].A 穿过S 的电通量e φ发生改变，O 处E变.B e φ不变，E 变。

.C e φ变，E 不变。

.D e φ不变，E不变。

答案：【B 】[解]闭合面外的电荷对穿过闭合面的电通量无贡献，或者说，闭合面外的电荷产生的电场，穿过闭合面的电通量的代数和为零；移动点电荷，会使电荷重新分布，或者说改变电荷的分布，因此改变了O 点的场强。

2．半径为R 的均匀带电球面上，电荷面密度为σ，在球面上取小面元S ∆，则S ∆上的电荷受到的电场力为[ ]。

.A 0 .B 22Sσε∆ .C2S σε∆ .D2204SRσπε∆答案：【B 】解：应用高斯定理和叠加原理求解。

如图所示。

面元S ∆上的电荷受到的库仑力是其他电荷在面元S ∆处产生的总电场强度1E与面元S ∆上的电荷量S Q ∆=∆σ的乘积：111E S E Q F∆=∆=σ。

面元S ∆处电场强度E是面元S ∆电荷在此产生的电场强度2E 与其他电荷在面元S∆处产生的总电场强度1E 的矢量和，21E E E+=。

首先，由高斯定理求得全部球面分布电荷在面元S ∆处产生的总电场强度 R E ˆ0εσ=其次，面元S ∆上的电荷量S Q ∆=∆σ对于面元S ∆来说，相当于无限大带电平面，因此，面元S ∆上的电荷量S Q ∆=∆σ在面元S ∆处产生的电场强度为R E ˆ202εσ=由叠加原理，其他电荷在面元S ∆处产生的总电场强度为 R E E E ˆ2021εσ=-=面元S ∆上的电荷量S Q ∆=∆σ受到的库仑力为RS R S E S E Q F ˆ2ˆ2020111εσεσσσ∆=∆=∆=∆= 注：本题可以用叠加原理直接进行计算，太麻烦。

3．如图所示，一个带电量为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于[ ]。

.A06q ε .B 012q ε .C24qε .D48q ε答案：【C 】[解] ：如果以A 为中心，再补充上7个相同大小的立方体，则组成一个边长为小立方体边长2倍大立方体，点电荷q 位于大立方体的中心。

07-08(二)大学物理Ⅱ重修班试卷及解答 (1)

07/08（二）大学物理Ⅱ 重修班试卷（A ）一选择题（共24分） 1.（本题3分）（2018）边长为L 的一个导体方框上通有电流I ，则此框中心的磁感强度 (A) 与L 无关． (B) 正比于L 2． (C) 与L 成正比． (D) 与L 成反比．(E) 与I 2有关．［ D ］【提示】0O 124(cos cos )4I B r μθθπ=⨯-， =2Lr ，145θ=︒，2135θ=︒ 2.（本题3分）（2125）如图，长度为l 的直导线ab 在均匀磁场B中以速度v移动，直导线ab 中的电动势为 (A) Bl v ．(B) Bl v sin α． (C) Bl v cos α． (D) 0．［ D ］【提示】没有切割磁感应线。

()B L ε=⨯⋅v ，()B ⨯v 的方向垂直于纸面，与L 点积后等于零。

3.（本题3分）（5138）在一自感线圈中通过的电流I 随时间t 的变化规律如图(a)所示，若以I 的正流向作为ε的正方向，则代表线圈内自感电动势ε随时间t 变化规律的曲线应为图(b)中(A)、(B)、(C)、(D)中的哪一个？[ D ]【提示】d d L I L t ε=-，d d It为I —t 曲线上的斜率；还有一负号。

4.（本题3分）（2420）在圆柱形空间内有一磁感强度为B 的均匀磁场，如图所示．B的大小以速率d B /d t 变化．在磁场中有A 、B 两点，其间可放直导线AB 和弯曲的导线AB ，则 (A) 电动势只在AB 导线中产生． (B) 电动势只在AB 导线中产生． (C) 电动势在AB 和AB 中都产生，且两者大小相等．(D) AB 导线中的电动势小于AB 导线中的电动势．［ D ］【提示】作径向辅助线后构成一个回路，则AB 的电动势等于该回路的电动势，而回路的电vttt动势与回路的面积成正比。

所以，面积大的，电动势就大。

5.（本题3分）（3356）在如图所示的单缝夫琅禾费衍射实验中，若将单缝沿透镜光轴方向向透镜平移，则屏幕上的衍射条纹 (A) 间距变大．(B) 间距变小．(C) 不发生变化． (D) 间距不变，但明暗条纹的位置交替变化．［ C ］6.（本题3分）（3361）某元素的特征光谱中含有波长分别为λ1＝450 nm 和λ2＝750 nm (1 nm ＝10-9 m)的光谱线．在光栅光谱中，这两种波长的谱线有重叠现象，重叠处λ2的谱线的级数将是 (A) 2 ，3 ，4 ，5 ．．．．．． (B) 2 ，5 ，8 ，11．．．．．． (C) 2 ，4 ，6 ，8 ．．．．．． (D) 3 ，6 ，9 ，12．．．．．．［ D ］【提示】1122sin d k k θλλ==，2133,6,9,......5k k == 7.（本题3分）（3368）一束光强为I 0的自然光垂直穿过两个偏振片，且此两偏振片的偏振化方向成45°角，则穿过两个偏振片后的光强I 为 (A) 4/0I 2 ． (B) I 0 / 4．(C) I 0 / 2． (D)2I 0 / 2．［ B ］【提示】自然光通过一个偏振片后，为光强2I 的线偏振光，再通过第二个偏振片后，光强为200cos 4524I I I ⎛⎫=︒=⎪⎝⎭8.（本题3分）（3544）一束自然光自空气射向一块平板玻璃(如图)，设入射角等于布儒斯特角i 0，则在界面2的反射光 (A) 是自然光． (B) 是线偏振光且光矢量的振动方向垂直于入射面． (C) 是线偏振光且光矢量的振动方向平行于入射面． (D) 是部分偏振光．［ B ］【提示】0090=+γi ，r 为界面2上的布儒斯特角，所以，在界面2的反射光是线偏振光且光矢量的振动方向垂直于入射面．二填空题（共26分） 9.（本题4分）（2065）两个带电粒子，以相同的速度垂直磁感线飞入匀强磁场，它们的质量之比是1∶4，电屏幕荷之比是1∶2，它们所受的磁场力之比是____________，运动轨迹半径之比是______________．1∶2 2分 1∶2 2分【提示】磁场力F q B =v ，1212::1:2F F q q ==2q B m R =v v →m R qB =v ，112221121==412R m q R m q ⎛⎫⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭10.（本题3分）（2584）有一半径为a ，流过稳恒电流为I 的1/4圆弧形载流导线bc ，按图示方式置于均匀外磁场B中，则该载流导线所受的安培力大小为______ ． aIB【提示】均匀外磁场中，弯曲导线的受力=从起点到终点通以同样电流的直导线的受力。

大学物理第二版习题答案

13级应用化学（2）班物理习题详解习题精解1-1某质点的速度为j t i v 82-=，已知t=0时它经过点（3，7），则该质点的运动方程为（）A.j t i t 242-B.()()j t i t 74322+-+ C.j 8- D.不能确定解：本题答案为B.因为 dt rd v =所以 ()dt j t i r d82-=于是有()d t j t i r d t rr ⎰⎰-=0820即 j t i t r r2042-=-亦即 ()j t i t j i r 24273-=-- 故 ()()j t i t r 74322+-+=1-2 一质点在平面上作曲线运动,1t 时刻位置矢量为j i r 621+-=，2t 时刻的位置矢量为j i r 422+=，求：（1）在12t t t -=∆时间内质点的位移矢量式;(2)该段时间内位移的大小和方向；（3）在坐标图上画出21,r r及r∆。

解（1）在12t t t -=∆时间内质点的位移矢量式为()()m j i r r r 2412-=-=∆ （2）该段时间内位移的大小 ()()m r 522422=+=∆该段时间内位移的方向与轴的夹角为 ︒-=⎪⎭⎫⎝⎛-=-6.2642tan 1α （3）坐标图上的表示如图1.1所示1-3某质点作直线运动，其运动方程为214x t t =+- ，其中x 以m 计，t 以s 计，求：（1）第3s 末质点的位置；（2）头3s 的位移大小；（3）头3s 内经过的路程。

解（1）第3s 末质点的位置为2(3)14334()x m =+⨯-=（2）头3s 的位移大小为 ()(3)03()x x m -=（3）因为质点做反向运动是有()0v t =，所以令0dxdt=，即420,2t t s -==因此头3s 内经过的路程为 (3)(2)(2)(0)45515()x x x x m -+-=-+-=1-4 已知某质点的运动方程为22,2x t y t ==-，式中t 以s 计，x 和y 以m 计。

大学物理课后习题答案(上下册全)武汉大学出版社习题3详解

3-1 有一半径为R 的水平圆转台，可绕通过其中心的竖直固定光滑轴转动，转动惯量为J ，开始时转台以匀角速度ω0转动，此时有一质量为m 的人站在转台中心，随后人沿半径向外跑去，当人到达转台边缘时，转台的角速度为 [ ] A.2ωmR J J + B. 02)(ωR m J J+ C.02ωmR JD. 0ω 答案：A3-2 如题3-2图所示，圆盘绕O 轴转动。

若同时射来两颗质量相同,速度大小相同,方向相反并在一直线上运动的子弹,子弹射入圆盘后均留在盘内,则子弹射入后圆盘的角速度ω将：[ ]A. 增大.B. 不变.C. 减小.D. 无法判断. 题3-2 图答案： C3-3 芭蕾舞演员可绕过脚尖的铅直轴旋转,当她伸长两手时的转动惯量为J 0，角速度为ω0,当她突然收臂使转动惯量减小为J 0 / 2时,其角速度应为：[ ] A. 2ω0 . B. ω0 . C. 4ω0 . D. ω 0/2. 答案：A3-4 如题3-4图所示，一个小物体，位于光滑的水平桌面上，与一绳的一端相连结，绳的另一端穿过桌面中心的小孔O . 该物体原以角速度ω 在半径为R 的圆周上绕O 旋转，今将绳从小孔缓慢往下拉．则物体：[ ]A. 动量不变，动能改变；题3-4图B. 角动量不变，动量不变；C. 角动量改变，动量改变；D. 角动量不变，动能、动量都改变。

答案：D3-5 在XOY 平面内的三个质点,质量分别为m 1 = 1kg, m 2 = 2kg,和 m 3 = 3kg,位置坐标(以米为单位)分别为m 1 (－3,－2)、m 2 (－2,1)和m 3 (1,2),则这三个质点构成的质点组对Z 轴的转动惯量J z = .答案： 38kg ·m 23-6 如题3-6图所示，一匀质木球固结在一细棒下端，且可绕水平光滑固定轴O 转动，今有一子弹沿着与水平面成一角度的方向击中木球并嵌于其中，则在此击中过程中，木球、子弹、细棒系统对o 轴的守恒。

大学物理基础教程答案1-3力-3

v = v +( + ) v ' mv mv m m v v ' = ( v − v ) /( + ) v mv mv m m
O f 1 2 C C O f 1 2
300 m1
x
v v 1 v 1 v −1 = m(2i − 1j) /(4 + 2) = i − j(m.s ) 6 12
( Vc’是子系统质心速度）是子系统质心速度）
2
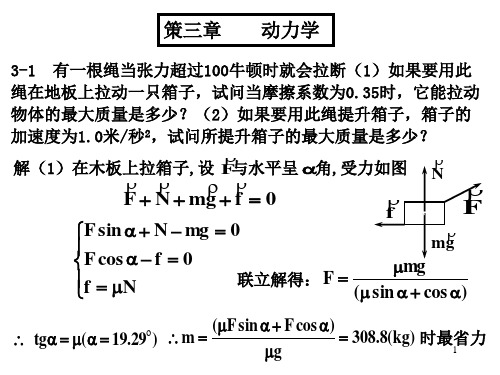
(2)绳中张力处处近似相等,如图: (2)绳中张力处处近似相等,如图: − 2F cos θ + mg = ma , 绳中张力处处近似相等
v l dv d v0 l a= )=− = (− 3 dt dt 2 x 16 x m 0l2 (x2 + l2 4)1/ 2 v2 F = (m + g ) 3 16x 2x
走了多远. 走了多远水平方向合外力为零,故水平方向动量守恒故水平方向动量守恒: 解: 水平方向合外力为零故水平方向动量守恒 (M+m) xc=Mx1+mx2 Vc=0 △xc=0 m ∆x2 (M+m) △xc=M△x1+m△x2=0 ∆x1 = − △ △ M 由相对运动可知 △x1+ l =△x2 m M
（2）若用此绳提升箱子，则有若用此绳提升箱子，
F−m = m g a
F ∴ m= = 92.6(kg) (g + a)
如题图所示，使木箱上升，若绳端的下降速度不变， 3-2 如题图所示，用力F使木箱上升，若绳端的下降速度不变，定滑轮和绳的固定端在同一高度上，木箱质量为m，定滑轮和绳的固定端在同一高度上，且相距为l，动滑轮、定滑轮和绳的质量以及绳的伸长量都忽略不及，(1)以动滑轮、定滑轮和绳的质量以及绳的伸长量都忽略不及，(1)以x (2)求F(x)。为变量表示m的速率v； (2)求F(x)。

大学物理2习题参考答案

题1-3图第一章流体力学1.概念（3）理想流体：完全不可压缩又无黏性的流体。

（4）连续性原理：理想流体在管道中定常流动时，根据质量守恒定律，流体在管道内既不能增多，也不能减少，因此单位时间内流入管道的质量应恒等于流出管道的质量。

（6）伯努利方程：C gh v P =++ρρ221（7）泊肃叶公式：LPR Q ηπ84∆=2、从水龙头徐徐流出的水流，下落时逐渐变细，其原因是（ A ）。

A. 压强不变，速度变大； B. 压强不变，速度变小；C. 压强变小，流速变大；D. 压强变大，速度变大。

3、如图所示，土壤中的悬着水，其上下两个液面都与大气相同，如果两个页面的曲率半径分别为R A 和R B (R A <R B )，水的表面张力系数为α，密度为ρ，则悬着水的高度h 为___)11(2BA R R g -ρα__。

(解题：BB A A A B R P P R P P gh P P ααρ2,2,00-=-==-) 4、已知动物的某根动脉的半径为R, 血管中通过的血液流量为Q ，单位长度血管两端的压强差为ΔP ，则在单位长度的血管中维持上述流量需要的功率为____ΔPQ ___。

5、城市自来水管网的供水方式为：自来水从主管道到片区支管道再到居民家的进户管道。

一般说来，进户管道的总横截面积大于片区支管的总横截面积，主水管道的横截面积最小。

不考虑各类管道的海拔高差（即假设所有管道处于同水平面），假设所有管道均有水流，则主水管道中的水流速度大，进户管道中的水流速度小。

10、如图所示，虹吸管的粗细均匀，略去水的粘滞性，求水流速度及A 、B 、C 三处的压强。

221.2 理想流体的定常流动'2gh v C =∴222121'CC D D v P v gh P ρρρ+=++0,0≈==D C D v P P P 练习5：如图，虹吸管粗细均匀，略去水的粘滞性，求管中水流流速及A 、B 、C 三处的压强。

大学物理习题(下)

习题课（一）1-1 在边长为a 的正方体中心处放置一点电荷Q ，设无穷远处为电势零点，则在正方体顶角处的电势为（A ）aQ 034πε （B ）a Q 032πε （C ）a Q 06πε （D ）a Q 012πε1-2 选无穷远处为电势零点，半径为R 的导体球带电后，其电势为U 0，则球外离球心距离为r 处的电场强度的大小为（A ）302r U R （B ）R U 0 （C ）20r RU （D ）rU1-3 在一个孤立的导体球壳内，若在偏离球中心处放一个点电荷，则在球壳内、外表面上将出现感应电荷，其分布将是（A ）内表面均匀，外表面也均匀。

（B ）内表面不均匀，外表面均匀。

（C ）内表面均匀，外表面不均匀。

（D ）内表面不均匀，外表面也不均匀。

1-4 一平行板电容器充电后仍与电源连接，若用绝缘手柄将电容器两极板间距离拉大，则极板上的电量Q 、电场强度的大小E 和电场能量W 将发生如下变化（A ）Q 增大，E 增大，W 增大。

（B ）Q 减小，E 减小，W 减小。

（C ）Q 增大，E 减小，W 增大。

（D ）Q 增大，E 增大，W 减小。

1-5 一半径为R 的均匀带电圆盘，电荷面密度为，设无穷远处为电势零点，则圆盘中心O 点的电势U 0 = 。

1-6 图示BCD 是以O 点为圆心，以R 为半径的半圆弧，在A 点有一电量为+q 的点电荷，O 点有一电量为q 的点电荷，线段BA = R ，现将一单位正电荷从B 点沿半圆弧轨道BCD 移到D 点，则电场力所做的功为。

1-7 两个电容器1和2，串联后接上电源充电。

在电源保证连接的情况下，若把电介质充入电容器2中，则电容器1上的电势差，电容器极板上的电量。

（填增大、减小、不变）1-8 如图所示为一个均匀带电的球层，其电荷体密度为，球层内表面半径为R 1，外表面半径为R 2，设无穷远处为电势零点，求空腔内任一点的电势。

1-9 如图所示，半径分别为R 1和R 2（R 2 > R 1）的两个同心导体薄球壳，分别带电量Q 1和Q 2，今将内球壳用细导线与远处半径为r 的导体球相连，导体球原来不带电，试求相连后导体球所带电量q 。

大学物理作业题2

M dm dx l
x
dx

f
M dt L L f 2 1 0 L 0
2 m ( v1 v 2 ) t Mg
1 Mglt ml (v1 v 2 ) 2
17、空心圆环可绕竖直轴AC自由转动，如图所示，其转动惯量为I0，环半径为R，初始角速度为0．质量为m的小球，原来静置于A点，由于微小的干扰，小球向下滑动．设圆环内壁是光滑的，问小球滑到B点与C点时，小球相对于环的速率各为多少?

L y v2 L x 1 2 c
v2 0.5 1 2 0.866 c
把 = 45°及Lx ',Ly '代入，得
v 0.816 c
(2)在S系中测得米尺长度为
L
Ly sin 45
0.707 m
3、在惯性系S中，有两事件发生于同一地点，且第二事件比第一事件晚发生t =2s；而在另一惯性系S＇中，观测第二事件比第一事件晚发生t'=3s．那么在S＇系中发生两事件的地点之间的距离是多少？解: 令S＇系与S系的相对速度为v，有
2
1 1 ( v / c )2
1)
代入题干中的具体数值，解得平均寿命为
v = 0.91c
t
t0
1 (v / c)
2
5.31 10 8
9、一正负电子对撞机可以把电子加速到动能＝2.8×109eV．这种电子速率比光速差多少? 这样的一个电子动量是多大?(与电子静止质量相应的能量为＝0.511×106eV ) 解:
解 : （ 1）
t
t 0 v2 1 2 c
t 0 2 10 6 s
d vt 9470 m
因d>6000m，故该介子能到达地球

哈工大大学物理第二章作业题+答案

方向向下。
T1 m1 ( g a1 ) 0.2 (9.8 1.96) 1.57 N 1 T2 T1 0.785 N 2 m g T2 0.1 9.8 0.785 a2 2 1.95 m s 2 m2 0.1
方向向下。
a3
方向向上。
m3 g T2 0.05 9.8 0.785 5.9 m s 2 m3 0.05
5
物体受力：真实力：重力 mg, 、斜面对它的正压力 N 惯性力： ma0
mg N ( ma0 ) mar
mgsin ma0sin mar mgcos N ma0cos 0
解得
N m ( g 0a) c o s; ar (g a0 ) sin
A

mg N ma
x 方向： mg sin max m(ar a0 sin ) y 方向： ma y N mg cos ma0 cos 解得
N m ( g 0a) c o s; ar (g a0 ) sin
解法二：以升降机为参考系（非惯性系），建立坐标系如图，
解当雨滴均匀运动时得所以当速率为 4.0 m s 时
1
mg k v 2 k mg / 25
F ma mg k v 2 mg
得
16 9 mg mg 25 25 a 9 g / 25
12. 2-12 质量为 m 的物体系于长度为 R 的绳子的一个端点上，在竖直平面内绕绳子另一端点（固定）作圆周运动．设时刻物体瞬时速度的大小为，绳子与竖直向上的方向成 θ 角，如图所示。(1) 求ｔ时刻绳中的张力 T 和物体的切向加速度 at；(2) 说明在物体运动过程中 at 的大小和方向如何变化？

大学物理第二章练习及答案

一、判断题1. 根据冲量的定义21d t t I F t =⋅⎰知，I 与F 的方向相同. ······················································· [×]2. 在应用动量定理时，物体的始末动量应由同一个惯性系来确定. ···································· [√]3. 外力在某一方向的分量之和为零，总动量在该方向的分量守恒. ···································· [√]4. 系统的内力可以改变系统的总动量，也可改变系统内质点的动量. ································ [×]5. 保守力做功等于势能的增量. ································································································ [×]6. 系统的势能的量值只有相对意义，而势能差值具有绝对意义. ········································ [√]7. 系统的外力做功等于系统动能的增量. ················································································ [×]8. 非保守力做功一定为负值. ···································································································· [×]9. 势能属于整个物体系统，不为单个物体拥有. ···································································· [√] 10. 质点受有心力作用下绕定点转动，质点对定点的角动量守恒. ········································ [√] 二、选择题11. 质量为m 的质点，以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动。

大学物理习题2

《普通物理》作业：动量与角动量 No.2序号姓名院系. 专业. 年级成绩你最感兴趣的题目是你认为最困难的题目是一. 选择题[ ] 1. A. B 两木块质量分别为m A 和m B ，且m B ＝2m A ，两者用一轻弹簧连接后静止于光滑水平桌面上，如图所示，若用外力将两木块压近使弹簧被压缩，然后将外力撤去，则此后两木块运动动能之比E KA ／E KB 为 (A)21。

(B) 2。

(D) 2/2。

解：以m A . m B 及弹簧为研究对象，系统所受合外力为零，动量守恒 0=+B B A A v m v m分量式为0=-B B A A v m v m∴ 2==AB B A m m v v ∴ 222121212222=⨯=⎪⎪⎭⎫ ⎝⎛==B A B A B B A A KB KAv v m m v m v m E E ∴选B[ ] 2. 粒子B 的质量是粒子A 的质量的4倍，开始时粒子A 的速度为)43(j i +，粒子B的速度为)72(j i -，由于两者的相互作用，粒子A 的速度变为)47(j i -，此时粒子B 的速度等于(A) j i 5-。

(B)j i 72-。

(D)j i 35-。

解：以两个粒子为研究对象，无外力作用，动量守恒，即：B B A B A v m j i m j i m j i m +-=-++)47()72()43(∴ B AB A B v m m j i j i m m j i +-=-++47)72(43 将4=AB m m 代入，得j i v B 5-=，选A 。

[ ] 3. 如图所示，砂子从h ＝0.8m 高处落到以3m ／s 的速率水平向右运动的传送带上，取重力加速度g ＝10m ／s 2，传送带给予砂子的作用力的方向为(A) 与水平夹角 53向下。

(B) 与水平夹角 53向上。

(D) 与水平夹角 37向下。

大学物理考试试题及答案3套

大学物理考试试题及答案3套2011 年12 月考试大学物理第一次作业一、判断题(本大题共30 分，共10 小题，每小题3 分) 1. 物体运动的速度越大，它具有的功也越大( ) 2. 物体处于一定的高度，就具有一定的重力势能( ) 3. 若刚体所受到的合外力为零，则刚体对定轴的角动量守恒( ) 4. 一物体的加速度恒定，而其速度方向不断改变( ) 5. 不可逆过程一定找不到另一过程使系统和外界同时复原( ) 6. 气体的温度表示每个分子的冷热程度( ) 7. 弹性势能和重力势能的零势点均可任意选择( ) 8. 气体的温度是分子平均动能的量度( ) 9. a 变化但质点作直线运动是可能的( ) 10. 在封闭容器中有一定量的理想气体，若气体各部分压强相等，分子数密度也相同，则该气体处于平衡态( )二、填空题(本大题共40 分，共8 小题，每小题5 分) 1. 质量为M 的车以速度v 沿光滑水平地面直线前进，车上的人将一质量为m 的物体相对于车以速度u 竖直上抛，则此时车的速度为______ 2. 温度27 ℃时，1mol 氢气具有的平动动能为______ ，转动动能为______ 3. 一质点沿x 轴运动，速度与位置的关系为v=kx，其中k 为一正常量，则质点在任意x 处的加速度为______ 4. 一圆运动质点的轨迹半径R=1.24，质点的角加速度α =2t，若t=0 时质点角速度为=0.32，t=1 时质点的角速度为______ 、切向加速度为______ 何法向加速度为______ 5. 一质点运动的速度与路程关系为v=4+3s ，则切向加速度与路程的关系为______ 6. 一星球可看作绕轴转动的匀质球体，若在一个演化过程中它的半径缩小为原来的一半，它的自转周期为原来的______ 倍，它赤道上一点的速率是原来的______ 倍7. 有氦气、氢气和水蒸气混合处于平衡态，若氦分子的平均动能为0.03eV，则氢分子的平均动能为______ eV，水分子的平均平动动能为______ eV，平均转动动能为______ eV 8. 一质点沿半径为R 的圆周运动，角速度，其中k 为一正常量。

1力学(1-3章)

大学物理习题解答——力学部分 11—2 一质点的运动方程为 k t j t i r ++=24，式中r 、t 分别以m 、s 为单位。

试求：（1）它的速度与加速度；（2）它的轨迹方程。

解 ⑴ j dtd a k j t dt r d 8 8==+==υυ ⑵ t z t y x === ,4 ,12 所以轨道方程为 ⎩⎨⎧==241zy x l —3 一质点自原点开始沿抛物线2bx y =运动，它在O x 轴上的分速度为一恒量，值为10.4-⋅=s m x υ,15.0-=m b 。

求质点位于m x 0.2=处的速度和加速度。

解抛物线2bx y =是质点的轨迹方程，它是参数方程)(t x x =和)(t y y =合成的结果．由于x υ是已知的，可得x 方向上的运动方程)(t x x =及加速度分量x a ，由)(t x x =和轨迹方程)(x f y =，求得运动方程在y 方向上的分量式)(t y y =及其加速度分量y a ，再由速度和加速度的分量可得其矢量表达式．因10.4-⋅=s m x υ为一常量，故0=x a ．当0=t 时，0=x ，由dt dx x =υ积分可得 t x x υ= (1)又由质点的抛物线方程，有22)(t b bx y x υ== (2)由y 方向的运动方程可得该方向的速度和加速度分量分别为t b dt dy x y 22υυ== (3) 2222xy b dt y d a υ== （4）当质点位于m x 0.2=时，由上述各式可得→-→-→→→⋅+⋅=+=j sm i s m j i y x 110.80.4υυυ； →-→→→⋅=+=j s m j a i a a y x 216． 1—5 质点的运动方程为230)10(t t x +-=；22015t t y -=．试求：(1)初速度的大小和方向；(2)加速度的大小和方向。

解由运动方程的分量式可分别求出速度、加速度的分量，再由运动合成算出速度和加速度的大小和方向．(1)速度的分量式为t dt dx x 6010+-==υ；t dt dy y 4015-==υ；当0=t 时，1010-⋅-=s m x υ，1015-⋅=s m y υ，则初速度大小为1202000.18-⋅=+=s m y x υυυ；设0→υ与x 轴的夹角为α，则2300-==x tg y υυα，/041123=α；(2)加速度的分量式为 260-⋅==s m dt d a x x υ；240-⋅-==s m dtd a y y υ．则加速度的大小为 2221.72-⋅=+=s m a a a y x设→a 与x 轴的夹角为β，则 32-==x y a a tg β，)19326(4133/0/0或-=β 1—9 一半径为0.50m 的飞轮在启动时的短时间内，角速度与时间的平方成正比。

大学物理2期末作业题

⼤学物理2期末作业题1、⼀均匀带电球⾯，电荷⾯密度为σ，球⾯内电场强度处处为零，球⾯上⾯元d S 的⼀个带电量为σd S 的电荷元，在球⾯内各点产⽣的电场强度()A 处处为零 ()B 不⼀定都为零 ()C 处处不为零()D ⽆法判定〔〕2、空间某处附近的正电荷越多，那么有：〔〕()A 位于该处的点电荷所受的⼒越⼤；()B 该处的电场强度越⼤；()C 该处的电场强度不可能为零； ()D 以上说法都不正确；3、两条⽆限长载流导线，间距厘⽶，电流10A ，电流⽅向相同，在两导线间距中点处磁场强度⼤⼩为〔〕（A ）0 （B ）πµ02000T （C ）πµ04000 T （D ）πµ0400T 4、⼀根长为L ，载流I 的直导线置于均匀磁场B 中，计算安培⼒⼤⼩的公式是θsin IBL F =,这个式中的θ代表（A ）直导线L 和磁场B 的夹⾓（B ）直导线中电流⽅向和磁场B 的夹⾓（C ）直导线L 的法线和磁场B 的夹⾓（D ）因为是直导线和均匀磁场，则可令θ=900[]5、如图所⽰，光滑固定导轨M 、N ⽔平放置，两根导体棒P 和Q 平⾏放在导轨上，形成⼀个闭合回路，当⼀条形磁铁从⾼处下落接近回路时 [ ]（A）P和Q将互相靠近；（B）P和Q均向左运动；（C）P和Q将互相远离；（D）P和Q均向右运动。

6、在感⽣电场是（）（A）由电荷激发，是⽆源场；（B）由电荷激发，是有源场；（C）由变化的磁场激发，是⽆源场；（D）由变化的磁场激发，是有源场。

7、关于感应电动势的正确说法是：（）（A）导体回路中的感应电动势的⼤⼩与穿过回路的磁感应通量成正⽐；（B）当导体回路所构成的平⾯与磁场垂直时，平移导体回路不会产⽣感应电动势；（C）只要导体回路所在处的磁场发⽣变化，回路中⼀定产⽣感应电动势；（D）将导体回路改为绝缘体环，通过环的磁通量发⽣变化时，环中有可能产⽣感应电动势。

8、在双缝⼲涉实验中，若单⾊光源S到两缝1S、2S距离相等，则观察屏上中央明纹中⼼位于图中O处，现将光源S向下移动到⽰意图中的S'位置，则（）（A）中央明条纹向下移动，且条纹间距不变；（B）中央明条纹向上移动，且条纹间距增⼤；（C）中央明条纹向下移动，且条纹间距增⼤；SS（D ）中央明条纹向上移动，且条纹间距不变。

理学大学物理C2练习题新1

电学练习题（一）学习目标1．掌握静电场的库仑定律、掌握电场强度和电势、电势能的概念。

2．学会计算点电荷系电场的电场强度和电势。

3．理解静电力做功与电势差的关系。

一、选择题1.下列哪一说法正确？（）A 电荷在电场中某点受到的电场力很大，该点的电场强度一定很大；B 在某一点电荷附近的任一点，如果没有把试验电荷放进去，则这点的电场强度为零；C 如果把质量为m的点电荷q放在一电场中，由静止释放，电荷一定沿电场线运动；D电场线上任一点的切线方向，代表正电荷q在该点处获得的加速度的方向。

2.如图所示，一个带负电荷的质点，在电场力的作用下从A点经C点运动到B点，其运动轨迹如图所示。

已知质点运动的速率是递减的，下面关于C点场强方向的四个图示中正确的是：（）3.一电量为的点电荷位于圆心O处，A、B、C、D为同一圆周上的四点，现将一试验电荷从A点分别移动到BCD各点则（）A 从A至B电场力作功最大B 从A到C电场力作功最大。

C 从A到D电场力作功最大D 从A到各点电场力作功相等。

二、填空题1.如图所示，在直角三角形ABC的A点上有电荷911.810q C-=⨯，B点上有电荷924.810q C-=-⨯。

则C点的电场强度大小为E=________，方向__________。

C点的电势为_________。

2.如图所示静电场中，把一正电荷从P点移到Q点，则电场力作_____功（以正、负作答），它的电势能PQ______（以增加、减少作答），______点的电势高。

3. 一点电荷q = 10-9 C ，A 、B 、C 三点分别距该点电荷10 cm 、20 cm 、30 cm 。

若选B 点的电势为零，则A 点的电势为__________，C 点的电势为__________。

三、计算题1. 如图所示，四个电量均为+q 的点电荷，固定于水平面内边长为a 的正方形的四个顶点上，O 为正方形的两对角线的交点，P 在O 点的正上方（即PO 垂直于正方形所在平面），PO=a ，求：（1）O 点的电场强度和电势；（2）P 点的电场强度和电势。

大学物理第2章质点动力学习题答案

第二章质点动力学2－1一物体从一倾角为30︒的斜面底部以初速v 0=10m·s -1向斜面上方冲去，到最高点后又沿斜面滑下，当滑到底部时速率v =7m·s -1,求该物体与斜面间的摩擦系数。

解：物体与斜面间的摩擦力f ＝uN ＝umgcos30︒物体向斜面上方冲去又回到斜面底部的过程由动能定理得220112(1)22mv mv f s -=-⋅物体向斜面上方冲到最高点的过程由动能定理得2010sin 302mv f s mgh f s mgs -=-⋅-=-⋅-20(2)(31)v s g u ∴=-把式（2）代入式（1）得，()222200.1983v v u v v-==+2－2如本题图，一质量为m 的小球最初位于光滑圆形凹槽的A 点，然后沿圆弧ADCB 下滑，试求小球在C 点时的角速度和对圆弧表面的作用力，圆弧半径为r 。

解：小球在运动的过程中受到重力G 和轨道对它的支持力T .取如图所示的自然坐标系，由牛顿定律得22sin (1)cos (2)t n dv F mg mdt v F T mg mR αα=-==-=由,,1ds rd rd v dt dt dt vαα===得代入式（）， A 并根据小球从点运动到点C 始末条件进行积分有，902n (sin )2cos 2cos /m cos 3cos '3cos ,e v vdv rg d v gr vg rrv mg mg rmg ααααωαααα=-===+==-=-⎰⎰得则小球在点C 的角速度为＝由式（2）得 T 由此可得小球对园轨道得作用力为T T 方向与反向2－3如本题图，一倾角为θ的斜面置于光滑桌面上，斜面上放一质量为m 的木块，两者间摩擦系数为μ，为使木块相对斜面静止，求斜面的加速度a 应满足的条件。

习题2－2图Ao B r DCT α解：如图所示()1212minmax sin ,cos cos sin (1)sin cos 2(1)(2)(sin cos )(cos sin )(sin cos )()(cos sin )1(2)(1)(sin cos )(cos sin )(sin cos a a a a N mg ma ma mg uN m a ma u g u a u g u g tg u a u utg u g u a u g u a θθθθθθθθθθθθθθθθθθθθθ==∴-==±==⨯+-=+--∴==++-⨯+=-+∴=得，得，)()(cos sin )1()()11g tg u u utg g tg u g tg u a utg utg θθθθθθθθθ+=---+∴≤≤+-2－4如本题图，A 、B 两物体质量均为m ，用质量不计的滑轮和细绳连接，并不计摩擦，则A 和B 的加速度大小各为多少。

大学物理(下册)习题与答案

大学物理练习册物理教研室遍热力学（一）一、选择题：1、如图所示，当汽缸中的活塞迅速向外移动从而使汽缸膨胀时，气体所经历的过程（A）是平衡过程，它能用P—V图上的一条曲线表示。

（B）不是平衡过程，但它能用P—V图上的一条曲线表示。

（C）不是平衡过程，它不能用P—V图上的一条曲线表示。

（D）是平衡过程，但它不能用P—V图上的一条曲线表示。

[ ]2、在下列各种说法中，哪些是正确的？[ ]（1）热平衡就是无摩擦的、平衡力作用的过程。

（2）热平衡过程一定是可逆过程。

（3）热平衡过程是无限多个连续变化的平衡态的连接。

（4）热平衡过程在P—V图上可用一连续曲线表示。

（A）（1）、（2）（B）（3）、（4）（C）（2）、（3）、（4）（D）（1）、（2）、（3）、（4）3、设有下列过程：[ ]（1）用活塞缓慢的压缩绝热容器中的理想气体。

（设活塞与器壁无摩擦）（2）用缓慢地旋转的叶片使绝热容器中的水温上升。

（3）冰溶解为水。

（4）一个不受空气阻力及其它摩擦力作用的单摆的摆动。

其中是逆过程的为（A）（1）、（2）、（4）（B）（1）、（2）、（3）（C）（1）、（3）、（4）（D）（1）、（4）4、关于可逆过程和不可逆过程的判断：[ ]（1）可逆热力学过程一定是准静态过程。

（2）准静态过程一定是可逆过程。

（3）不可逆过程就是不能向相反方向进行的过程。

（4）凡有摩擦的过程，一定是不可逆过程。

以上四种判断，其中正确的是（A）（1）、（2）、（3）（B）（1）、（2）、（4）（C）（2）、（4）（D）（1）、（4）5、在下列说法中，哪些是正确的？[ ]（1）可逆过程一定是平衡过程。

（2）平衡过程一定是可逆的。

（3）不可逆过程一定是非平衡过程。

（4）非平衡过程一定是不可逆的。

（A）（1）、（4）（B）（2）、（3）（C）（1）、（2）、（3）、（4）（D）（1）、（3）6、置于容器的气体，如果气体各处压强相等，或气体各处温度相同，则这两种情况下气体的状态 [ ]（A ）一定都是平衡态。

理三大学物理期末练习题

大学物理（2）期末练习题（）一、选择1．依照高斯定理的数学表达式⎰∑⋅=Sεq S E 0/d可知下述各类说法中，正确的选项是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强必然为零． (B) 闭合面内的电荷代数和不为零时，闭合面上各点场强必然处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不必然处处为零．(D) 闭合面上各点场强均为零时，闭合面内必然处处无电荷．［］ 2．一“无穷大”均匀带电平面A ，其周围放一与它平行的有必然厚度的“无穷大”平面导体板B ，如下图。

已知A 上的电荷面密度为+σ ，那么在导体板B 的两个表面1和2上的感生电荷面密度为：(A) σ 1 = - σ， σ 2 = + σ．(B) σ 1 = σ21-， σ 2 =σ21+．(C) σ 1 = σ21-， σ 1 = σ21-．(D) σ 1 = - σ， σ 2 = 0．［］ 3. 真空中一根无穷长直细导线上通电流I ，那么距导线垂直距离为a 的空间某点处的磁能密度为(A)200)2(21a I πμμ (B) 200)2(21aI πμμ (C) 20)2(21I a μπ (D) 200)2(21aI μμ ［］4. 在圆柱形空间内有一磁感强度为B的均匀磁场，如下图．B的大小以速度d B /d t 转变．在磁场中有A 、B 两点，其间可放直导线AB 和弯曲的导线B A，那么(A) 电动势只在直导线AB 中产生。

(B) 电动势只在弯曲的导线B A中产生。

(D) AB 导线中的电动势小于B A导线中的电动势。

［］5．有两个大小不相同的金属球，大球直径是小球的两倍，大球带电，小球不带电，二者相距很远．今用细长导线将二者相连，在忽略导线的阻碍下，大球与小球的带电之比为：［］(A) 2； (B) 1； (C) 1/2； (D) 0。

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

作业题一（静止电荷的电场）班级:_____________ 姓名:_____________ 学号:_____________ 一、选择题1. 一均匀带电球面，电荷面密度为σ，球面内电场强度处处为零，球面上面元d S 带有σ d S 的电荷，该电荷在球面内各点产生的电场强度(A) 处处为零． (B) 不一定都为零． (C) 处处不为零． (D) 无法判定．[ ］ 2. 电荷面密度均为＋σ的两块“无限大”均匀带电的平行平板如图放置，其周围空间各点电场强度E随位置坐标x 变化的关系曲线为：(设场强方向向右为正、向左为负) ［］3. 将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处(如图)，测得它所受的力为F ．若考虑到电荷q 0不是足够小，则 (A) F / q 0比P 点处原先的场强数值大． (B) F / q 0比P 点处原先的场强数值小． (C) F / q 0等于P 点处原先场强的数值． (D) F / q 0与P 点处原先场强的数值哪个大无法确定．［］4. 如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd 的电场强度通量等于：(A)06εq ． (B) 012εq． (C) 024εq ． (D) 048εq ．［］5. 高斯定理 ⎰⎰⋅=VSV S E 0/d d ερ(A) 适用于任何静电场．02εP 0(B) 只适用于真空中的静电场． (C) 只适用于具有球对称性、轴对称性和平面对称性的静电场．(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场．［］6. 如图所示，两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为λ1和λ2，则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E 为：(A) r0212ελλπ+． (B) 20210122R R ελελπ+π(C) 1012R ελπ． (D) 0．［］7. 点电荷Q 被曲面S 所包围，从无穷远处引入另一点电荷q至曲面外一点，如图所示，则引入前后： (A) 曲面S 的电场强度通量不变，曲面上各点场强不变． (B) 曲面S 的电场强度通量变化，曲面上各点场强不变． (C) 曲面S 的电场强度通量变化，曲面上各点场强变化． (D) 曲面S 的电场强度通量不变，曲面上各点场强变化．［］8. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中，正确的是：(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零． (C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电［］二、填空题9. A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．则A 、B 两平面上的电荷面密度分别为σA ＝_______________, σB ＝____________________．qABE 0E 0/3E 0/310. 三个平行的“无限大”均匀带电平面，其电荷面密度都是＋σ，如图所示，则A 、B 、C 、D 三个区域的电场强度分别为：E A ＝_________________，E B ＝_____________， E C ＝_________，E D =___________ (设方向向右为正)．11. 一半径为R 的带有一缺口的细圆环，缺口长度为d (d<<R)环上均匀带有正电，电荷为q ，如图所示．则圆心O 处的场强大小E ＝__________________ __________，场强方向为______________________．12. 如图所示，真空中两个正点电荷Q ，相距2R ．若以其中一点电荷所在处O 点为中心，以R 为半径作高斯球面S ，则通过该球面的电场强度通量＝______________；若以 0r 表示高斯面外法线方向的单位矢量，则高斯面上a 、b 两点的电场强度分别为________________________．三、计算题13. 带电细线弯成半径为R 的半圆形，电荷线密度为λ=λ0sin φ，式中λ0为一常数，φ为半径R 与x 轴所成的夹角，如图所示．试求环心O 处的电场强度．14. “无限长”均匀带电的半圆柱面，半径为R ，设半圆柱面沿轴线OO'单位长度上的电荷为λ，试求轴线上一点的电场强度．+σ+σ+σABCD15. 一半径为R 的带电球体，其电荷体密度分布为ρ =Ar (r ≤R ) ， ρ =0 (r ＞R )A 为一常量．试求球体内外的场强分布．16. 图中虚线所示为一立方形的高斯面，已知空间的场强分布为： E x ＝bx ， E y ＝0， E z ＝0．高斯面边长a ＝0.1 m ，常量b ＝1000 N/(C ·m)．试求该闭合面中包含的净电荷．(真空介电常数ε0＝8.85×10-12 C 2·N -1·m -2 )答案作业题 (一）一、1-8 CBACADDC 二、9. －2ε0E 0 / 3; 4ε0E 0 / 310. －3σ / (2ε0); －σ / (2ε0); σ / (2ε0); 3σ / (2ε0) 11.()30220824R qdd R R qd εεπ≈-ππ; 从O 点指向缺口中心点．12. Q / ε0;a E ＝0，()20018/5R r Q E b επ=aa aaxzyO三、13. 解：在φ处取电荷元，其电荷为d q =λd l = λ0R sin φ d φ它在O 点产生的场强为R Rq E 00204d sin 4d d εφφλεπ=π= 3分在x 、y 轴上的二个分量 d E x =－d E cos φ d E y =－d E sin φ 对各分量分别求和 ⎰ππ=000d cos sin 4φφφελRE x ＝0 RR E y 0002008d sin 4ελφφελ-=π=⎰π∴ j Rj E i E E yx 008ελ-=+= 14. 解:设坐标系如图所示．将半圆柱面划分成许多窄条．d l 宽的窄条的电荷线密度为θλλλd d d π=π=l R取θ位置处的一条，它在轴线上一点产生的场强为 θελελd 22d d 020RR E π=π=如图所示. 它在x 、y 轴上的二个分量为：d E x =d E sin θ , d E y =－d E cos θ对各分量分别积分 R R E x 02002d sin 2ελθθελππ=π=⎰ 0d cos 2002=π-=⎰πθθελR E y 场强 i Rj E i E E y x02ελπ=+= 15. 解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为r r Ar V q d 4d d 2π⋅==ρ 在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rVπ=π==⎰⎰ρ (r ≤R)以该球面为高斯面，按高斯定理有 0421/4εAr r E π=π⋅ 得到()0214/εAr E =， (r ≤R )方向沿径向，A >0时向外, A <0时向里．在球体外作一半径为r 的同心高斯球面，按高斯定理有 0422/4εAR r E π=π⋅ 得到 ()20424/r AR E ε=， (r >R )方向沿径向，A >0时向外，A <0时向里． 16. 解：设闭合面内包含净电荷为Q ．因场强只有x 分量不为零，故只是二个垂直于x 轴的平面上电场强度通量不为零．由高斯定理得：-E 1S 1+ E 2S 2=Q / ε0 ( S 1 = S 2 =S ) 3分则 Q = ε0S (E 2- E 1) = ε0Sb (x 2- x 1)= ε0ba 2(2a －a ) =ε0ba 3 = 8.85×10-12 C作业题二（电势）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1.(1019) 在点电荷+q 的电场中，若取图中P 点处为电势零点，则M 点的电势为 (A)a q 04επ． (B) a q 08επ． (C) a q 04επ-． (D) aq08επ-．［］2. 如图所示，两个同心球壳．内球壳半径为R 1，均匀带有电荷Q ；外球壳半径为R 2，壳的厚度忽略，原先不带电，但与地相连接．设地为电势零点，则在内球壳里面，距离球心为r 处的P 点的场强大小及电势分别为： (A) E ＝0，U ＝104R Q επ． (B) E ＝0，U ＝⎪⎪⎭⎫ ⎝⎛-π21114R R Qε．(C) E ＝204r Q επ，U ＝r Q04επ (D) E ＝204r Q επ，U ＝104R Q επ．[ ] 3. 关于静电场中某点电势值的正负，下列说法中正确的是： (A) 电势值的正负取决于置于该点的试验电荷的正负． (B) 电势值的正负取决于电场力对试验电荷作功的正负． (C) 电势值的正负取决于电势零点的选取． (D) 电势值的正负取决于产生电场的电荷的正负．［］4. 点电荷-q 位于圆心O 处，A 、B 、C 、D 为同一圆周上的四点，如图所示．现将一试验电荷从A 点分别移动到B 、C 、D 各点，则(A) 从A 到B ，电场力作功最大．(B) 从A 到C ，电场力作功最大． (C) 从A 到D ，电场力作功最大．(D) 从A 到各点，电场力作功相等．［］ 5. 如图所示，直线MN 长为2l ，弧OCD 是以N 点为中心，l 为半径的半圆弧，N 点有正电荷＋q ，M 点有负电荷-q ．今将一试验电荷＋q 0从O 点出发沿路径OCDP 移到无穷远处，设无穷远处电势为零，则电场力作功A7.(A) A ＜0 , 且为有限常量． (B) A ＞0 ,且为有限常量．(C) A ＝∞． (D) A ＝0．［］ 6. 半径为r 的均匀带电球面1，带有电荷q ，其外有一同心的半径为R 的均匀带电球面2，带有电荷Q ，则此两球面之间的电势差U 1-U 2为： (A)⎪⎭⎫⎝⎛-πR r q 1140ε . (B) ⎪⎭⎫ ⎝⎛-πr R Q 1140ε .(C) ⎪⎭⎫ ⎝⎛-πR Q r q 041ε . (D)rq04επ . [ ] 7. 两块面积均为S 的金属平板A 和B 彼此平行放置，板间距离为d (d 远小于板的线度)，设A 板带有电荷q 1，B 板带有电荷q 2，则AB 两板间的电势差U AB 为(A)d S q q 0212ε+． (B) d Sq q 0214ε+． (C)d S q q 0212ε-． (D) d Sq q 0214ε-．［］ 8. 面积为S 的空气平行板电容器，极板上分别带电量±q ，若不考虑边缘效应，则两极板间的相互作用力为(A)S q 02ε． (B) S q 022ε．(C) 2022S q ε． (D) 202Sq ε．［］二、填空题9. 如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8 C ；外球面半径为r 2＝20 cm ，带电荷q 2＝－6×108C ，设无穷远处电势为零，则空间另一电势为零的球面半径r ＝ __________________．10. 真空中一半径为R 的均匀带电球面，总电荷为Q ．今在球面上挖去很小一块面积△S (连同其上电荷)，若电荷分布不改变，则挖去小块后球心处电势(设无穷远处电势为零)为________________．11. 把一个均匀带有电荷+Q 的球形肥皂泡由半径r 1吹胀到r 2，则半径为R (r 1＜R ＜r 2)的球面上任一点的场强大小E 由______________变为______________；电势U 由 __________________________变为________________(选无穷远处为电势零点)．12. 静电场的环路定理的数学表示式为：______________________．该式的物理意义是：____________________________________________________________．该定理表明，静电场是______ _________场．BAS q 1q 2三、计算题13. 一“无限大”平面，中部有一半径为R 的圆孔，设平面上均匀带电，电荷面密度为σ．如图所示，试求通过小孔中心O 并与平面垂直的直线上各点的场强和电势(选O 点的电势为零)．14. 图示为一个均匀带电的球层，其电荷体密度为ρ，球层内表面半径为R 1，外表面半径为R 2．设无穷远处为电势零点，求空腔内任一点的电势．15.两个带等量异号电荷的均匀带电同心球面，半径分别为R 1＝0.03 m 和R 2＝0.10 m ．已知两者的电势差为450 V ，求内球面上所带的电荷．16. 有两根半径都是R 的“无限长”直导线，彼此平行放置，两者轴线的距离是d (d ≥2R )，沿轴线方向单位长度上分别带有＋λ和－λ的电荷，如图所示．设两带电导线之间的相互作用不影响它们的电荷分布，试求两导线间的电势差．作业题（二）一、1-8 DBCDDACB 二、9. 10cm 10.⎪⎭⎫⎝⎛π∆-π20414R SR Q ε 11. Q / (4πε0R 2); 0 ; Q / (4πε0R ); Q / (4πε0r 2)12. 0d =⋅⎰Ll E单位正电荷在静电场中沿任意闭合路径绕行一周，电场力作功等于零有势（或保守力）三、13. 解：将题中的电荷分布看作为面密度为σ的大平面和面密度为－σ的圆盘叠加的结果．选x 轴垂直于平面，坐标原点Ｏ在圆盘中心，大平面在x 处产生的场强为ixx E 012εσ=圆盘在该处的场强为i x R x x E ⎪⎪⎭⎫ ⎝⎛+--=2202112εσ ∴ i x R xE E E 220212+=+=εσ该点电势为 ()22002202d 2x R R x R x x U x +-=+=⎰εσεσ 14. 解: 由高斯定理可知空腔内E ＝0，故带电球层的空腔是等势区，各点电势均为U .在球层内取半径为r →r ＋d r 的薄球层．其电荷为 d q = ρ 4πr 2d r该薄层电荷在球心处产生的电势为 ()00/d 4/d d ερεr r r q U =π= 整个带电球层在球心处产生的电势为()212200002d d 21R R r r U U R R -===⎰⎰ερερ 因为空腔内为等势区所以空腔内任一点的电势U 为()2122002R R U U -==ερ 若根据电势定义⎰⋅=l E Ud 计算同样给分.15.解：设内球上所带电荷为Q ，则两球间的电场强度的大小为204r QE επ= (R 1＜r ＜R 2)两球的电势差⎰⎰π==212120124d R R R R r dr Qr E U ε⎪⎪⎭⎫ ⎝⎛-π=21114R R Q ε∴ 12122104R R U R R Q -π=ε＝2.14×10-9 CO x P16. 解：设原点O 在左边导线的轴线上，x 轴通过两导线轴线并与之垂直．在两轴线组成的平面上，在R ＜x ＜(d －R )区域内，离原点距离x 处的P 点场强为()x d x E E E -π+π=+=-+0022ελελ 则两导线间的电势差 ⎰-=R d Rx E U d ⎰-⎪⎭⎫ ⎝⎛-+π=Rd Rx x d x d 1120ελ()[]R d Rx d x ---π=ln ln 20ελ⎪⎭⎫ ⎝⎛---π=R d R R R d ln ln 20ελ RR d -π=ln 0ελ+λ作业题三（导体和电介质）班级:_____________ 姓名:_____________ 学号:_____________一、选择题1. A 、B 为两导体大平板，面积均为S ，平行放置，如图所示．A 板带电荷+Q 1，B 板带电荷+Q 2，如果使B 板接地，则AB 间电场强度的大小E 为［］(A) S Q 012ε ．(B) SQ Q 0212ε-．(C)SQ 01ε． (D) S Q Q 0212ε+．2. 一带正电荷的物体M ，靠近一原不带电的金属导体N ，N 的左端感生出负电荷，右端感生出正电荷．若将N 的左端接地，如图所示，则(A) N 上有负电荷入地．(B) N 上有正电荷入地（地面负电荷进入导体）． (C ) N 上的电荷不动．(D) N 上所有电荷都入地．［］ 3. 一导体球外充满相对介电常量为εr 的均匀电介质，若测得导体表面附近场强为E ，则导体球面上的自由电荷面密度σ为［］ (A) ε 0 E ． (B) ε 0 ε r E ． (C) ε r E ． (D) (ε 0 ε r - ε 0)E ．4. 一平行板电容器始终与端电压一定的电源相联．当电容器两极板间为真空时，电场强度为0E ，电位移为0D，而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时，电场强度为E ，电位移为D，则［］(A) r E E ε/0 =，0D D =． (B) 0E E =，0D D rε=．(C) r E E ε/0 =，r D D ε/0 =． (D) 0E E =，0D D=．5. 在静电场中，作闭合曲面S ，若有0d =⎰⋅SS D (式中D为电位移矢量)，则S面内必定［］(A) 既无自由电荷，也无束缚电荷． (B) 没有自由电荷． (C) 自由电荷和束缚电荷的代数和为零．(D) 自由电荷的代数和为零．1+Q 2B6. 一个大平行板电容器水平放置，两极板间的一半空间充有各向同性均匀电介质，另一半为空气，如图．当两极板带上恒定的等量异号电荷时，有一个质量为m 、带电荷为+q 的质点，在极板间的空气区域中处于平衡．此后，若把电介质抽去，则该质点［］(A) 保持不动． (B) 向上运动． (C) 向下运动． (D) 是否运动不能确定．7.一个平行板电容器，充电后与电源断开，当用绝缘手柄将电容器两极板间距离拉大，则两极板间的电势差U 12、电场强度的大小E 、电场能量W 将发生如下变化：［］(A) U 12减小，E 减小，W 减小．(B) U 12增大，E 增大，W 增大． (C) U 12增大，E 不变，W 增大．(D) U 12减小，E 不变，W 不变． 8. 如图所示, 一球形导体，带有电荷q ，置于一任意形状的空腔导体中．当用导线将两者连接后，则与未连接前相比系统静电场能量将 (A) 增大． (B) 减小．(C) 不变． (D) 如何变化无法确定．［］二、填空题9. 半径为R 1和R 2的两个同轴金属圆筒，其间充满着相对介电常量为εr 的均匀介质．设两筒上单位长度带有的电荷分别为+λ和-λ，则介质中离轴线的距离为r 处的电位移矢量的大小D =____________，电场强度的大小 E =____________．10. 一平行板电容器，充电后与电源保持联接，然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质，这时两极板上的电荷是原来的______倍；电场强度是原来的 _________倍；电场能量是原来的_________倍．11. 一平行板电容器，充电后切断电源，然后使两极板间充满相对介电常量为εr的各向同性均匀电介质．此时两极板间的电场强度是原来的____________倍；电场能量是原来的___________ 倍．12. 分子的正负电荷中心重合的电介质叫做_______________ 电介质．在外电场作用下，分子的正负电荷中心发生相对位移，形成________________________．三、计算题13. 如图所示，一内半径为a 、外半径为b 的金属球壳，带有电荷Q ，在球壳空腔内距离球心r 处有一点电荷q ．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷． (2) 球心O 点处，由球壳内表面上电荷产生的电势．(3) 球心O 点处的总电势．+Q14. 半径分别为R1和R2 (R2 > R1 )的两个同心导体薄球相联后导体球所带电荷q．15. 假想从无限远处陆续移来微量电荷使一半径为R 的导体球带电． (1) 当球上已带有电荷q 时，再将一个电荷元d q 从无限远处移到球上的过程中，外力作多少功？(2) 使球上电荷从零开始增加到Q 的过程中，外力共作多少功？16. 一电容器由两个很长的同轴薄圆筒组成，内、外圆筒半径分别为R 1 = 2 cm ，R 2 = 5 cm ，其间充满相对介电常量为εr 的各向同性、均匀电介质．电容器接在电压U = 32 V 的电源上，(如图所示)，试求距离轴线R = 3.5 cm 处的A 点的电场强度和A 点与外筒间的电势差．参考答案一、1-8 CBBBDBCB 二、9. λ/(2πr )；λ/(2π ε0 εr r ) 10. ,1,r r εε 11.1r ε;1rε12. 无极分子;电偶极子三、13. 解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q ，外表面上带电荷q +Q ．(2) 不论球壳内表面上的感生电荷是如何分布的，因为任一电荷元离O 点的距离都是a ，所以由这些电荷在O 点产生的电势为adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和 q Q q q O U U U U +-++= r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+ 14. 解：设导体球带电q ，取无穷远处为电势零点，则导体球电势：r qU 004επ=内球壳电势： 10114R q Q U επ-=2024R Q επ+二者等电势，即 r q04επ1014R q Q επ-=2024R Q επ+ 解得 )()(122112r R R Q R Q R r q ++=15. 解：(1) 令无限远处电势为零，则带电荷为q 的导体球，其电势为R qU 04επ=将d q 从无限远处搬到球上过程中，外力作的功等于该电荷元在球上所具有的电势能 q RqW A d 4d d 0επ== (2) 带电球体的电荷从零增加到Q 的过程中，外力作功为⎰⎰==QR q q A A 004d d πεR Q 028επ=16. 解：设内外圆筒沿轴向单位长度上分别带有电荷+λ和-λ, 根据高斯定理可求得两圆筒间任一点的电场强度为 rE r εελ02π=则两圆筒的电势差为 1200ln 22d d 2121R R r r r E U r R R r R R εελεελπ=π==⎰⎰⋅解得 120ln 2R R Ur εελπ=于是可求得Ａ点的电场强度为 A E )/ln(12R R R U== 998 V/m 方向沿径向向外A 点与外筒间的电势差： ⎰⎰=='22d )/ln(d 12RR R Rr rR R U r E U RR R R U212ln )/ln(== 12.5 V。