三角及反三角函数
三角函数值与反三角函数值

三角函数值与反三角函数值三角函数是数学中常见的函数之一,它与三角形的边长和角度之间存在着密切的关系。
而反三角函数则是对三角函数的逆运算,用来求解角度。
在数学和物理等领域中,三角函数和反三角函数都有着广泛的应用。
三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。
这些函数的值与角度之间有着明确的对应关系。
例如,对于一个角度为θ的三角形,其正弦值sin(θ)定义为对边与斜边的比值,余弦值cos(θ)定义为邻边与斜边的比值,正切值tan(θ)定义为对边与邻边的比值。
正弦函数的值域在[-1, 1]之间,在数学和物理中经常用于描述波动和振动现象。
例如,当我们观察到一种周期性的波动或振动时,可以利用正弦函数来描述其变化规律。
正弦函数的图像呈现出周期性的波形,振幅决定了波动的强度,周期决定了波动的频率。
余弦函数与正弦函数类似,也是一种周期性函数,其图像与正弦函数的图像相似,只是相位不同。
余弦函数的值域同样在[-1, 1]之间,它可以用来描述角度的变化规律。
在几何学和物理学中,经常会用到余弦函数来计算两个向量之间的夹角,或者描述物体在运动过程中的轨迹。
正切函数是另一种重要的三角函数,其定义为正弦值与余弦值的比值。
正切函数的图像呈现出周期性的波动,但与正弦函数和余弦函数不同的是,正切函数在某些点上会出现无穷大的值。
这意味着在一些特殊的角度下,正切函数的值变得非常大,甚至无法表示。
因此,在实际应用中,我们需要注意正切函数的定义域,并避免出现无意义的结果。
与三角函数相对应的是反三角函数,它是对三角函数的逆运算。
反三角函数用来求解角度,将已知的三角函数值转化为对应的角度值。
常见的反三角函数包括反正弦函数(arcsin)、反余弦函数(arccos)、反正切函数(arctan)等。
这些函数的定义域和值域与对应的三角函数相反,例如反正弦函数的定义域为[-1, 1],值域为[-π/2, π/2]。
反三角函数在几何学、物理学和工程学等领域中有着广泛的应用。
角函数反三角函数公式大全

角函数反三角函数公式大全角函数是数学中的一种常见函数,它描述了角的变化与函数值之间的关系。
而反三角函数则是角函数的逆函数。
在三角函数和反三角函数之间有很多重要的公式和关系。
以下是一些常用的角函数和反三角函数公式的介绍:1. 正弦函数(sine function):正弦函数是一个周期性函数,可以表示为:f(x) = sin(x)。
正弦函数的一些重要公式包括:- 周期性:sin(x + 2π) = sin(x)。
- 奇偶性:sin(-x) = -sin(x)。
- 值域:-1 ≤ sin(x) ≤ 1- 三角恒等式:sin^2(x) + cos^2(x) = 12. 余弦函数(cosine function):余弦函数也是一个周期性函数,可以表示为:f(x) = cos(x)。
余弦函数的一些重要公式包括:- 周期性:cos(x + 2π) = cos(x)。
- 奇偶性:cos(-x) = cos(x)。
- 值域:-1 ≤ cos(x) ≤ 1- 三角恒等式:sin^2(x) + cos^2(x) = 13. 正切函数(tangent function):正切函数是正弦函数和余弦函数的比值,可以表示为:f(x) = tan(x) = sin(x) / cos(x)。
正切函数的一些重要公式包括:- 周期性:tan(x + π) = tan(x)。
- 奇偶性:tan(-x) = -tan(x)。
- 无穷性:tan(π/2) = ∞,tan(-π/2) = -∞。
- 三角恒等式:tan(x) = sin(x) / cos(x)。
4. 反正弦函数(arcsine function):反正弦函数是正弦函数的反函数,可以表示为:f(x) = arcsin(x)。
反正弦函数的一些重要公式包括:- 值域:-π/2 ≤ arcsin(x) ≤ π/2- 奇偶性:arcsin(-x) = -arcsin(x)。
- 反函数恒等式:arcsin(sin(x)) = x。
三角函数与反三角函数的关系公式

三角函数与反三角函数的关系公式
三角函数与反三角函数的关系
三角函数是指使用角度作为变量的函数,在很多领域都发挥着重要作用,比如几何学、物理学和工程学。
反三角函数也是一种函数,它们和三角函数有着密切的联系。
在数学中,三角函数的反函数可以定义为反三角函数,它们之间的关系可以总结为:如果y=f(x)是一个三角函数,那么反三角函数x=f-1(y)就是y=f(x)的反函数。
换句话说,反三角函数的参数是三角函数的结果,而三角函数的参数是反三角函数的结果。
另外,三角函数与反三角函数之间还有一种重要的关系,即函数反演定理。
根据函数反演定理,如果y=f(x)是一个三角函数,那么反三角函数x=f-1(y)也是一个三角函数,而且两个函数之间满足如下关系:f-1(f(x))=x。
总之,三角函数和反三角函数之间有着密切的关系,函数反演定理是它们之间最重要的关系。
三角函数的反函数就是反三角函数,而反三角函数的参数是三角函数的结果,反之亦然。
另外,反三角函数也是一种三角函数,两个函数之间满足f-1(f(x))=x的关系。
三角函数及反三角函数图像性质、知识点总结

千里之行,始于足下。
三角函数及反三角函数图像性质、知识点总结三角函数是数学中的重要概念,它研究角和三角形之间的关系。
在解决各种几何和物理问题时,三角函数经常被用于描述和计算角度的大小和位置,具有广泛的应用。
而反三角函数则是对三角函数的运算结果进行逆运算,可以将三角函数的值转化为角度的大小。
三角函数包括正弦函数、余弦函数、正切函数等。
它们的图像性质对于理解和使用三角函数非常重要。
首先,正弦函数的图像为一条连续的曲线,其振幅为1,但其值域在[-1, 1]之间变化。
在0到2π的区间上,正弦函数的图像呈现周期性变化,即在每个周期内重复出现相同的形状。
正弦函数在0、π、2π等处的值为0,而在π/2和3π/2等处的值达到最大值1和最小值-1。
余弦函数的图像与正弦函数非常相似,也是连续的曲线,振幅为1,值域在[-1, 1]之间变化。
与正弦函数不同的是,余弦函数在0处达到最大值1,在π/2和3π/2处达到最小值-1,并且在π处到达最小值-1时的斜率大于其他点。
正切函数的图像则比正弦函数和余弦函数复杂一些。
正切函数的值在整个实数轴上变化,但在某些点上出现垂直渐近线。
正切函数在0处为0,并且在π/2处存在一个不可取的点,其他点上的斜率变化也比较剧烈。
反三角函数是三角函数的逆运算。
对于给定的角度值,反三角函数可以计算出与之对应的三角函数的值。
反正弦函数、反余弦函数和反正切函数是最常用的反三角函数。
第1页/共2页锲而不舍,金石可镂。
反正弦函数的图像是一段弧线,其定义域为[-1, 1],值域为[-π/2, π/2]。
在定义域范围内的每个值,它的反正弦函数都会返回一组对应的弧度值。
反余弦函数的图像也是一段弧线,其定义域为[-1, 1],值域为[0, π]。
与反正弦函数不同,反余弦函数的值域比较大,因此可以返回更多的角度值。
反正切函数的图像是一条连续的曲线,其定义域为整个实数轴,值域为(-π/2, π/2)。
反正切函数的图像在x轴与正y轴的交点是原点,其斜率在各点上的变化没有正切函数那么剧烈。
三角函数及反三角函数

半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin—--·cos—-—2 2α+βα-βsinα-sinβ=2cos—--·sin—-—2 2α+βα-βcosα+cosβ=2cos—--·cos—-—2 2α+βα-βcosα-cosβ=-2sin—--·sin—-—2 2 si nα·cosβ=1/2sinα+β+sinα-βcosα·sinβ=1/2sinα+β-sinα-βcosα·cosβ=1/2cosα+β+cosα-βsinα·sinβ=-1/2cosα+β-cosα-β化asinα ±bcosα为一个角的一个三角函数的形式辅助角的三角函数的公式函数变换反三角函数三角函数的反函数;是多值函数..它们是反正弦Arcsin x;反余弦Arccos x;反正切Arctan x;反余切Arccot x等;各自表示其正弦、余弦、正切、余切、正割、余割为x的角..为限制反三角函数为单值函数;将反正弦函数的值y限在y=-π/2≤y≤π/2;将y为反正弦函数的主值;记为y=arcsin x;相应地;反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x 的主值限在-π/2<y<π/2;反余切函数y=arccot x的主值限在0<y<π..反三角函数实际上并不能叫做函数;因为它并不满足一个自变量对应一个函数值的要求;其图像与其原函数关于函数y=x对称..其概念首先由欧拉提出;并且首先使用了arc+函数名的形式表示反三角函数;而不是f-1x.反三角函数主要是三个:y=arcsinx;定义域-1;1;值域-π/2;π/2;图象用红色线条;y=arccosx;定义域-1;1;值域0;π;图象用兰色线条;y=arctanx;定义域-∞;+∞;值域-π/2;π/2;图象用绿色线条;sinarcsinx=x;定义域-1;1;值域-π/2;π/2证明方法如下:设arcsinx=y;则siny=x ;将这两个式子代如上式即可得为限制反三角函数为单值函数;将反正弦函数的值y限在y=-π/2≤y≤π/2;将y为反正弦函数的主值;记为y=arcsin x;相应地;反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2<y<π/2;反余切函数y=arccot x的主值限在0<y<π..反三角函数实际上并不能叫做函数;因为它并不满足一个自变量对应一个函数值的要求;其图像与其原函数关于函数y=x对称..其概念首先由欧拉提出;并且首先使用了arc+函数名的形式表示反三角函数;而不是f-1x.1正弦函数y=sin x在-π/2;π/2上的反函数;叫做反正弦函数..arcsin x表示一个正弦值为x的角;该角的范围在-π/2;π/2区间内..2余弦函数y=cos x在0;π上的反函数;叫做反余弦函数..arccos x表示一个余弦值为x 的角;该角的范围在0;π区间内..3正切函数y=tan x在-π/2;π/2上的反函数;叫做反正切函数..arctan x表示一个正切值为x的角;该角的范围在-π/2;π/2区间内..反三角函数主要是三个:y=arcsinx;定义域-1;1 ;值域-π/2;π/2图象用红色线条;y=arccosx;定义域-1;1 ; 值域0;π;图象用蓝色线条;y=arctanx;定义域-∞;+∞;值域-π/2;π/2;图象用绿色线条;sinarcsin x=x;定义域-1;1;值域-1;1 arcsin-x=-arcsinx证明方法如下:设arcsinx=y;则siny=x ;将这两个式子代入上式即可得其他几个用类似方法可得cosarccos x=x; arccos-x=π-arccos xtanarctan x=x; arctan-x=-arctanx反三角函数其他公式arcsin-x=-arcsinxarccos-x=π-arccosxarctan-x=-arctanxarccot-x=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsinarcsinx=x=cosarccosx=tanarctanx=cotarccotx当x∈—π/2;π/2时;有arcsinsinx=x当x∈0;π;arccoscosx=xx∈—π/2;π/2;arctantanx=xx∈0;π;arccotcotx=xx〉0;arctanx=π/2-arctan1/x;arccotx类似若arctanx+arctany∈—π/2;π/2;则arctanx+arctany=arctanx+y/1-xy。
三角函数-反三角函数公式大全

三角函数-反三角函数公式大全tan (π+α)= tanα cot (π+α)= cotα 公式三:任意角α与 -α的三角函数值之间的关系: sin (-α)= -sinα cos (-α)= cosα tan (-α)= -tanα cot (-α)= -cotα 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα cos (π-α)= -cosα tan (π-α)= -tanα cot (π-α)= -cotα 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα 公式六:2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =;余切函数cos cot sin xx x =; 正割函数1sec cos x x =;余割函数1csc sin x x= 三角函数奇偶、周期性sin x ,tan x ,cot x 奇函数;cos x 偶函数;sin x,cos x 周期2π;sin()t ωϕ+ 周期2πω;tan x ,cot x 周期π常用三角函数公式:22cos sin 1x x += 22cos sin cos2x x x -=2s i n c o ssx x x = 21cos 22sin x x -= 21c o s 22c o sx x +=22211tan sec cos x x x+== 22211cotcsc sin x x x +==1sin sin [cos()cos()]2x y x y x y =-+-- 1c o sc o s[c o s ()c o s ()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数:a r c s i na r c c o s 2x x π+=a r c t a na r c c o t2x x π+=arcsin x:定义域[1,1]-,值域[,]22ππ-;arccos x :定义域[1,1]-,值域[0,]π;arctan x:定义域(,)-∞+∞,值域(,)22ππ-;arccot x :定义域(,)-∞+∞,值域(0,)π式中n为任意整数.arc sin x = arc cos x = arc tan x = arc cot x =。
三角函数与反三角函数公式大全

三角函数与反三角函数公式大全三角函数和反三角函数是高中数学中的重要内容,也是数学和物理学中广泛应用的数学工具。
下面我们将介绍一些常用的三角函数和反三角函数的公式。
1. 正弦函数(sin)和余弦函数(cos)的关系:sin^2x + cos^2x = 12. 正切函数(tan)与正弦函数(sin)和余弦函数(cos)的关系:tanx = sinx / cosx3. 余切函数(cot)和正弦函数(sin)和余弦函数(cos)的关系:cotx = cosx / sinx4. 正弦函数(sin)和余弦函数(cos)的周期性:sin(x + 2π) = sinxcos(x + 2π) = cosx5. 正弦函数(sin)和余弦函数(cos)的奇偶性:sin(-x) = -sinxcos(-x) = cosx6. 正切函数(tan)和余切函数(cot)的奇偶性:tan(-x) = -tanxcot(-x) = -cotx7. 正弦函数(sin)和余弦函数(cos)的对称性:sin(π - x) = sinxcos(π - x) = -cosx8. 正切函数(tan)和余切函数(cot)的对称性:tan(π - x) = -tanxcot(π - x) = -cotx9. 正弦函数(sin)和余弦函数(cos)的双角和差公式:sin(x ± y) = sinxcosy ± cosxsinycos(x ± y) = cosxcosy ∓ sinxsiny10. 正切函数(tan)和余切函数(cot)的双角和差公式:tan(x ± y) = (tanx ± tany) / (1 ∓ tanxtany)cot(x ± y) = (cotxcoty ∓1) / (coty ± cotx)11. 正弦函数(sin)和余弦函数(cos)的和差化积公式:sinx + siny = 2sin[(x + y) / 2]cos[(x - y) / 2]sinx - siny = 2sin[(x - y) / 2]cos[(x + y) / 2]cosx + cosy = 2cos[(x + y) / 2]cos[(x - y) / 2]cosx - cosy = -2sin[(x + y) / 2]sin[(x - y) / 2] 12. 正切函数(tan)和余切函数(cot)的和差化积公式:tanx + tany = (tanx + tany) / (1 - tanxtany)tanx - tany = (tanx - tany) / (1 + tanxtany)cotx + coty = (cotx + coty) / (cotxcoty - 1)cotx - coty = (cotx - coty) / (cotxcoty + 1)13. 正弦函数(sin)和余弦函数(cos)的倍角公式:sin2x = 2sinxcosxcos2x = cos^2x - sin^2x = 2cos^2x - 1 = 1 - 2sin^2x14. 正弦函数(sin)和余弦函数(cos)的半角公式:sin(x/2) = ±√[(1 - cosx) / 2]cos(x/2) = ±√[(1 + cosx) / 2]15. 反正弦函数(arcsin)和反余弦函数(arccos)的范围:-π/2 ≤ arcsinx ≤ π/20 ≤ arccosx ≤ π16. 反正弦函数(arcsin)和反余弦函数(arccos)的负值关系:arcsin(-x) = -arcsinxarccos(-x) = π - arccosx17. 反正弦函数(arcsin)和反余弦函数(arccos)的和、差关系:arcsin(x) ± arccos(x) = π/2这些公式是三角函数和反三角函数的基本关系,掌握它们对于理解和解决三角函数相关的问题非常重要。
三角函数和反三角函数详解

[三角函数的定义和符号变化][三角函数的图形与特征]标准正弦曲线周期:π2=T与x 轴交点(同拐点):,2,1,0),0,(±±=k k B k π极值点(极大点或极小点):,2,1,0,)1(,)21(±±=⎪⎭⎫⎝⎛-+k k A k k π余弦曲线周期:π2=T与x 轴交点(同拐点):,2,1,0,0,)21(±±=⎪⎭⎫⎝⎛+k k B k π极值点:,2,1,0),)1(,(±±=-k k A kk π 一般正弦曲线)sin(0ϕω+=x A y 周期:ωπ2=T式中A >0为振幅,ω为角频率,0ϕ为初相 与x 轴交点(同拐点):,2,1,0,0,0±±=⎪⎭⎫⎝⎛-k k B k ωϕπ 极值点:,)1(,)21(0⎪⎪⎪⎪⎭⎫ ⎝⎛--+A k A k k ωϕπ ,2,1,0±±=k同时,)cos(1ϕω+=x A y 也属于一般正弦曲线(设210πϕϕ+=,可化为))2sin(1πϕω++x A ,它是将标准正弦曲线在y 轴方向上伸长A 倍,在x 轴方向上压缩ω倍,并向左平移ωϕ0一段距离而得到.正切曲线 y =tan x周期:π=T与x 轴交点(同拐点): ,2,1,0),0,(±±=k k A k π, 该点切线斜率为1.渐近线:π)21(+=k x 余切曲线:周期:π=T与x 轴交点(同拐点):,2,1,0,0,)21(±±=⎪⎭⎫⎝⎛+k k A k π,该点切线斜率为-1.渐近线:πk x = 正割曲线周 期:π2=T 极大点:)1,)12((-+πk A k 极小点:,2,1,0),1,2(±±=k k B k π渐近线:π)21(+=k x 余割曲线周 期:π2=T极大点:⎪⎭⎫ ⎝⎛-+1,)232(πk A k 极小点:⎪⎭⎫⎝⎛+1,)212(πk B k,2,1,0±±=k渐近线:πk x =3. 特殊角的三角函数值表中02 π表示02 πϕ→,(即左、右极限).一个锐角的余角的三角函数值等于这个角的余三角函数值,例如︒=︒15sin 75cos ,︒=︒18cot 72tan ,︒=︒5.22sec 5.67csc .4. 三角函数的基本关系和公式 [诱导公式]三角函数的诱导公式表表中n 为整数. [基本关系]sin cos 221αα+=αααcos sin tan =αααsin cos cot =1cot tan =⋅αα sin csc αα⋅=1cos sec αα⋅=11tan sec 22=-αα 1cot csc 22=-αα三角函数的相互关系表例如,若sin α=x ,则cos α=±-12x[加法公式]αββαβαβαβαβαβαβαβαβαβαβαcot cot 1cot cot )cot(tan tan 1tan tan )tan(sin sin cos cos )cos(sin cos cos sin )sin(±=±±=±=±±=±[和差与积互化公式]βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαsin cos )cos(cot tan sin sin )sin(cot cot cos cos )sin(tan tan 2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos2sin sin 2cos2sin2sin sin ±=±±±=±±=±-+-=--+=+-+=--+=+sin sin [cos()cos()]cos cos [cos()cos()]sin cos [sin()sin()]αβαβαβαβαβαβαβαβαβ=-+--=++-=++-121212[倍角公式]αααααααααααααααααααααααααtan cot tan cot tan 1sec 2sec cot 21cot 2cot tan 1tan 22tan tan 1tan 1sin 211cos 2sin cos 2cos tan 1tan 2cos sin 22sin 22222222222-+=-=-=-=+-=-=-=-=+== 1cot 3cot 3cot 3cot tan 31tan tan 33tan cos 3cos 43cos sin 3sin 43sin )cot (tan 21csc sec 212csc 232333--=--=-=+-=+==ααααααααααααααααααα[半角公式]下列公式中根号所取符号与等号左边的符号一致.1sec sec 22csc 1sec sec 22sec cos 1sin sin cos 1cos 1cos 12cot cos 1sin sin cos 1cos 1cos 12tan 2cos 12cos 2cos 12sin -±=+±=-=+=-+±=+=-=+-±=+±=-±=αααααααααααααααααααααααα[降幂公式]sin (cos )sin (sin sin )sin (cos cos )sin ()cos()sin()sin()2342212012212210121214331834241212212121221αααααααααααα=-=-=-+=--+⎡⎣⎢⎤⎦⎥=--+-+=-+++=∑∑nn n k n k k n n n n nn k n kk nC n k C C n kcos (cos )cos (cos cos )cos (cos cos )cos cos()coscos()2342212012212211212143318342412221212221αααααααααααα=+=+=++=-+⎡⎣⎢⎤⎦⎥=-+-=-++=∑∑nn n k k n n n n nn k k nC n k C Cn k以上式中的n 为正整数.5. 反三角函数定义[反三角函数的定义域与主值范围]一般反三角函数与主值的关系为x n x xn x xn x n tan arc tan Arc arccos 2Arccos arcsin )1(sin Arc +=±=-+=πππ式中n 为任意整数.[反三角函数的图形与特征]反正弦曲线 反余弦曲线拐点(同曲线对称中心): 拐点(同曲线对称中心):)0,0(O ,该点切线斜率为1 )2,0(πA ,该点切线斜率为-1反正切曲线 反余切曲线拐点(同曲线对称中心): 拐点:)0,0(O ,该点切线斜率为1)2,0(πA ,该点切线斜率为-1 渐进线:2π±=y曲线对称中心:)2,0(πA 渐近线:π==y y ,0反正割曲线 反余割曲线顶点:),1(),0,1(π-B A 顶点:)2,1(),2,1(ππ--B A渐近线:2π=y渐近线:0=y6. 反三角函数的相互关系与基本公式[反三角函数的相互关系]带有*号者只当x为正值时适用. [反三角函数基本公式]7. 三角形基本定理[正弦定理]a Ab B cC R sin sin sin ===2式中R 为∆ABC 的外接圆半径(图1.3). [余弦定理]a b c bc A b c a ca B c a b ab C 222222222222=+-=+-=+-cos cos cos[勾股定理]在直角三角形(C 为直角)中,勾方加股方等于弦方(图1.4),即a b c 222+=勾股定理也称商高定理,外国书刊中称毕达哥拉斯定理.8. 斜三角形解法。
三角函数及反三角函数
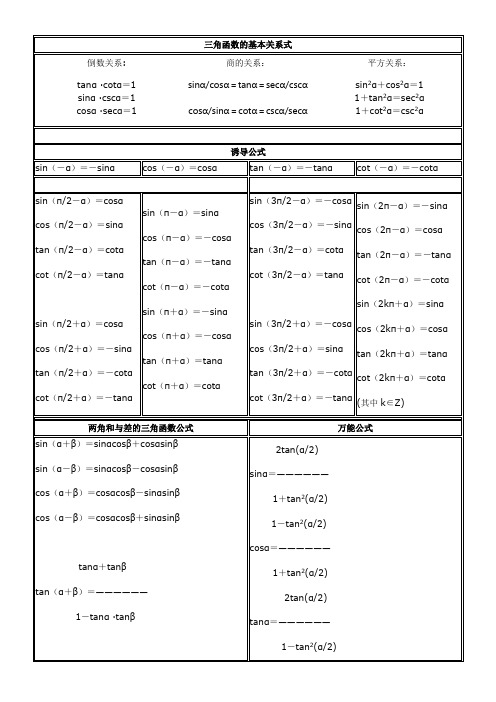
tanα-tanβtan(α-β)=——————1+tanα ·tanβ半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin—--·cos—-—2 2α+βα-βsinα-sinβ=2cos—--·sin—-—2 2α+βα-βcosα+cosβ=2cos—--·cos—-—2 2α+βα-βcosα-cosβ=-2sin—--·sin—-—2 2sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)函数变换360k+αsinαcosαtanαcotαsecαcscα90°-αcosαsinαcotαtanαcscαsecα90°+αcosα-sinα-cotα-tanα-cscαsecα180°-αsinα-cosα-tanα-cotα-secαcscα180°+α-sinα-cosαtanαcotα-secα-cscα270°-α-cosα-sinαcotαtanα-cscα-secα270°+α-cosαsinα-cotα-tanαcscα-secα360°-α-sinαcosα-tanα-cotαsecα-cscα﹣α-sinαcosα-tanα-cotαsecα-cscα反三角函数三角函数的,是多值函数。
三角函数与反三角函数公式大全

三角函数与反三角函数公式大全1. 正弦函数(sine function)的公式:- 基本关系式:sinθ = 对边/斜边- 余角关系式:sin(90°-θ) = cosθ- 二倍角关系式:sin2θ = 2sinθcosθ- 半角关系式:sin(θ/2) = ±√[(1-cosθ)/2]- 三倍角关系式:sin3θ = 3sinθ - 4sin^3θ- 和差关系式:sin(α±β) = sinαcosβ ± cosαsinβ2. 余弦函数(cosine function)的公式:- 基本关系式:cosθ = 邻边/斜边- 余角关系式:cos(90°-θ) = sinθ- 二倍角关系式:cos2θ = cos^2θ - sin^2θ- 半角关系式:cos(θ/2) = ±√[(1+cosθ)/2]- 三倍角关系式:cos3θ = 4cos^3θ - 3cosθ- 和差关系式:cos(α±β) = cosαcosβ ∓ sinαsinβ3. 正切函数(tangent function)的公式:- 基本关系式:tanθ = 对边/邻边= sinθ/cosθ- 余角关系式:t an(90°-θ) = 1/tanθ- 二倍角关系式:tan2θ = (2tanθ)/(1-tan^2θ)- 半角关系式:tan(θ/2) = ±√[(1-cosθ)/(1+cosθ)]- 三倍角关系式:tan3θ = (3tanθ-tan^3θ)/(1-3tan^2θ)- 和差关系式:tan(α±β) = (tanα±tanβ)/(1∓tanαtanβ) 4. 余切函数(cotangent function)的公式:- 基本关系式:cotθ = 邻边/对边= 1/tanθ- 余角关系式:co t(90°-θ) = tanθ- 二倍角关系式:cot2θ = (cot^2θ-1)/(2cotθ)- 半角关系式:cot(θ/2) = ±√[(1+cosθ)/(1-cosθ)]- 三倍角关系式:cot3θ = (3cotθ-cot^3θ)/(1-3cot^2θ)- 和差关系式:cot(α±β) = (cotαcotβ-1)/(cotβ±cotα) 1. 反正弦函数(arcsine function)的公式:- 基本关系式:sinθ = arcsin(x)- 余角关系式:arcsin(x) = 90° - arccos(x)- 二倍角关系式:arcsin(2x√(1-x^2)) = 2arcsin(x)- 和差关系式:arcsin(x ± y) ≠ arcsin(x) ± arcsin(y) 2. 反余弦函数(arccosine function)的公式:- 基本关系式:cosθ = arccos(x)- 余角关系式:arccos(x) = 90° - arcsin(x)- 二倍角关系式:arccos(2x^2 - 1) = 2arccos(x)- 和差关系式:arccos(x ± y) ≠ arccos(x) ± arccos(y) 3. 反正切函数(arctangent function)的公式:- 基本关系式:tanθ = arctan(x)- 余角关系式:arctan(x) = 90° - arctan(1/x)- 二倍角关系式:arctan(2x/(1-x^2)) = 2arctan(x)- 和差关系式:arctan(x ± y) ≠ arctan(x) ± arctan(y)。
(完整)三角函数及反三角函数

半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=————-1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=----——1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin—--·cos—-—2 2α+βα-βsinα-sinβ=2cos—--·sin—-—2 2α+βα-βcosα+cosβ=2cos---·cos--—2 2α+βα-βcosα-cosβ=-2sin—--·sin—-—22sinα·cosβ=(1/2)[sin (α+β)+sin(α—β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos (α+β)+cos(α-β)]sinα·sinβ=—(1/2)[cos(α+β)-cos(α—β)]化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)函数变换360k+αsinαcosαtanαcotαsecαcscα90°-αcosαsinαcotαtanαcscαsecα90°+αcosα-sinα-cotα—tanα—cscαsecαsinα—cosα—tanα-cotα—secαcscα180°—α180°+-sinα-cosαtanαcotα-secα—cscαα—cosα-sinαcotαtanα-cscα—secα270°-α270°+—cosαsinα-cotα—tanαcscα—secαα—sinαcosα—tanα-cotαsecα—cscα360°-α﹣α—sinαcosα-tanα-cotαsecα-cscα反三角函数三角函数的反函数,是多值函数。
三角函数与反三角函数

三角函数与反三角函数三角函数是数学中一个重要的概念,它们在解决几何问题、物理问题以及工程问题等方面起着不可替代的作用。
与之相对应的,反三角函数是解三角函数方程时经常使用的工具。
本文将介绍三角函数和反三角函数的定义、性质以及它们在实际问题中的应用。
一、三角函数的定义与性质三角函数是利用一个角的弧度或角度值,计算该角对应三角比值的函数。
常见的三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。
1. 正弦函数正弦函数sin(x)的定义是:在单位圆上,角x所对应点的纵坐标值。
正弦函数的性质有:- 周期性:sin(x)的周期是2π,即sin(x + 2π) = sin(x)。
- 奇偶性:正弦函数是奇函数,即sin(-x) = -sin(x)。
2. 余弦函数余弦函数cos(x)的定义是:在单位圆上,角x所对应点的横坐标值。
余弦函数的性质有:- 周期性:cos(x)的周期是2π,即cos(x + 2π) = cos(x)。
- 偶性:余弦函数是偶函数,即cos(-x) = cos(x)。
3. 正切函数正切函数tan(x)的定义是:在单位圆上,角x所对应点的纵坐标值与横坐标值的比值。
正切函数的性质有:- 周期性:tan(x)的周期是π,即tan(x + π) = tan(x)。
- 奇偶性:正切函数是奇函数,即tan(-x) = -tan(x)。
除了这三个常见的三角函数,还有诸如余割函数csc(x)、正割函数sec(x)和余切函数cot(x)等函数,它们的性质可以通过正弦函数和余弦函数的倒数关系得到。
二、反三角函数的定义与性质反三角函数是三角函数的反函数。
在实际问题中,我们经常需要求解三角函数方程,即已知三角函数的值,求解相应角的值。
此时就需要用到反三角函数。
常见的反三角函数包括反正弦函数arcsin(x)、反余弦函数arccos(x)、反正切函数arctan(x)等。
1. 反正弦函数反正弦函数arcsin(x)的定义是:满足sin(y) = x的角y,其中y的取值范围是[-π/2, π/2]。
三角函数及反三角函数公式大全

三角函数是数学中的一种基本函数,它可以描述角度与直角三角形的边长之间的关系。
而反三角函数则是三角函数的逆运算,它可以用来求解角度或直角三角形的边长。
在数学和物理等领域中,三角函数和反三角函数广泛应用,包括圆的运动、波的传播、信号处理等。
本文将介绍三角函数及反三角函数的定义、性质和公式,希望能够对读者有所帮助。
一、三角函数的定义与性质1. 正弦函数(sin)正弦函数可以用来描述直角三角形中某个角的正弦值,定义为对边与斜边的比值。
正弦函数的性质包括周期性、奇偶性、界值等,它在数学和物理中有着重要的应用。
2. 余弦函数(cos)余弦函数是描述直角三角形中某个角的余弦值的函数,定义为邻边与斜边的比值。
余弦函数也具有周期性、奇偶性、界值等性质,它与正弦函数有着密切的关系。
3. 正切函数(tan)正切函数可以用来描述直角三角形中某个角的正切值,定义为对边与邻边的比值。
正切函数的性质包括周期性、奇偶性、界值等,它在数学和工程中有着广泛的应用。
4. 余切函数(cot)余切函数是描述直角三角形中某个角的余切值的函数,定义为邻边与对边的比值。
余切函数也具有周期性、奇偶性、界值等性质,它与正切函数有着密切的关系。
5. 正割函数(sec)正割函数可以用来描述直角三角形中某个角的正割值,定义为斜边与邻边的比值。
正割函数的性质包括周期性、奇偶性、界值等,它在数学和物理中有着重要的应用。
6. 余割函数(csc)余割函数是描述直角三角形中某个角的余割值的函数,定义为斜边与对边的比值。
余割函数也具有周期性、奇偶性、界值等性质,它与正割函数有着密切的关系。
二、反三角函数的定义与性质1. 反正弦函数(arcsin)反正弦函数是正弦函数的逆运算,可以用来求解某个数值的角度。
反正弦函数的定义域和值域、奇偶性、单调性等性质是求解问题时需要考虑的重要因素。
2. 反余弦函数(arccos)反余弦函数是余弦函数的逆运算,可以用来求解某个数值的角度。
三角函数、反三角函数

定义直角三角形三角函数定义在直角三角形中,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个直角三角形,其中∠ACB为直角。
对∠BAC而言,对边(opposite)a=BC、斜边(hypotenuse)c=AB、邻边(adjacent)b=AC,则存在以下关系:基本函数英文缩写表达式语言描述正弦函数sine sin a/c ∠A的对边比斜边余弦函数cosine cos b/c ∠A的邻边比斜边正切函数tangent tan a/b ∠A的对边比邻边余切函数cotangent cot b/a ∠A的邻边比对边正割函数secant sec c/b ∠A的斜边比邻边余割函数cosecant csc c/a ∠A的斜边比对边注:正切函数、余切函数曾被写作tg、ctg,现已不用这种写法。
secx=1/cosx、cscx=1/sinx变化规律正弦值随着角度的增大(或减小)而增大(或减小),余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小),余切值随着角度的增大(或减小)而减小(或增大);正割值随着角度的增大(或减小)而增大(或减小),余割值随着角度的增大(或减小)而减小(或增大)。
特殊角在三角函数中,有一些特殊角,例如30°、45°、60°,这些角的三角函数值为简单单项式,计算中可以直接求出具体的值。
这些函数的值参见下表格:角度0°15°30°45°60°90°120°135°150°180°270°弧度sin值cos值tan 值不存在不存在cot 值不存在不存在几何性质函数图象函数对称轴对称中心图象无(kπ/2+π/2,0)正切三角函数图像无最小正周期如果一个函数f (x )的所有周期中存在一个最小的正数,那么这个最小的正数就叫做f (x )的最小正周期(minimal positive period ).例如,正弦函数的最小正周期是2π.对于正弦函数y=sinx, 自变量x 只要并且至少增加到x+2π时,函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。
数学中的三角函数与反三角函数的关系

数学中的三角函数与反三角函数的关系三角函数和反三角函数是数学中非常重要的概念和工具,它们在解决几何、物理、工程等问题中起着至关重要的作用。
本文将探讨三角函数和反三角函数之间的关系。
一、三角函数的定义三角函数是以角作为自变量的函数,常见的三角函数有正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。
它们的定义如下:1. 正弦函数sin(x):在单位圆上,角度x所对应的点在直角坐标系中的y坐标值。
2. 余弦函数cos(x):在单位圆上,角度x所对应的点在直角坐标系中的x坐标值。
3. 正切函数tan(x):正弦函数与余弦函数的比值,即tan(x) = sin(x) / cos(x)。
二、反三角函数的定义反三角函数是三角函数的逆运算,用来求解角度的函数。
常见的反三角函数有反正弦函数arcsin(x)、反余弦函数arccos(x)、反正切函数arctan(x)等。
它们的定义如下:1. 反正弦函数arcsin(x):满足sin(arcsin(x)) = x,其中x的值范围为[-1, 1],返回的结果是角度值。
2. 反余弦函数arccos(x):满足cos(arccos(x)) = x,其中x的值范围为[-1, 1],返回的结果是角度值。
3. 反正切函数arctan(x):满足tan(arctan(x)) = x,返回的结果是角度值。
三、三角函数与反三角函数的关系三角函数和反三角函数之间存在着紧密的联系和互为逆运算的关系。
1. 正弦函数与反正弦函数的关系若sin(x) = y ,则有arcsin(y) = x + 2kπ 或π - x + 2kπ,其中k为整数。
反正弦函数的结果是角度值。
2. 余弦函数与反余弦函数的关系若cos(x) = y ,则有arccos(y) = x + 2kπ 或 -x + 2kπ,其中k为整数。
反余弦函数的结果是角度值。
3. 正切函数与反正切函数的关系若tan(x) = y ,则有arctan(y) = x + kπ,其中k为整数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角、反三角函数
一、考纲要求
1.理解任意角的概念、弧度的意义,能正确进行弧度和角度的互换。
2.掌握任意角的正弦、余弦、正切的定义,了解余切、正割、余割的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义。
3.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式。
4.能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式的证明。
5.了解正弦函数、余弦函数,正切函数的图像和性质,会用“五点法”画正弦函数,余弦函数和函数y=Asin(wx+ϕ)的简图,理解A 、w 、ϕ的物理意义。
6.会由已知三角函数值求角,并会用符号arcsinx 、arccosx 、arcotx 表示。
7.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决三角形的计算问题。
8.理解反三角函数的概念,能由反三角函数的图像得出反三角函数的性质,能运用反三角函数的定义、性质解决一些简单问题。
9.能够熟练地写出最简单的三角方程的解集。
二、知识结构
1.角的概念的推广:
(1)定义:一条射线OA 由原来的位置OA ,绕着它的端点O 按一定方向旋转到另一位置OB ,就形成了角α。
其中射线OA 叫角α的始边,射线OB 叫角α的终边,O 叫角α的顶点。
(2)正角、零角、负角:由始边的旋转方向而定。
(3)象限角:由角的终边所在位置确定。
第一象限角:2k π<α<2k π+2
π
,k ∈Z 第二象限角:2k π+
2
π
<α<2k π+π,k ∈Z 第三象限角:2k π+π<α<2k π+2
3π
,k ∈Z
第四象限角:2k π+2
3π
<α<2k π+2π,k ∈Z
(4)终边相同的角:一般地,所有与α角终边相同的角,连同α角在内(而且只有这样的角),可以表示为k ²360°+α,k ∈Z 。
(5)特殊角的集合:
终边在坐标轴上的角的集合{α|α=
2
π
k ,k ∈Z } 终边在一、三象限角平分线上角的集合{α|α=k π+4π
,k ∈Z } 终边在二、四象限角平分线上角的集合{α|α=k π-4π
,k ∈Z }
终边在四个象限角平分线上角的集合{α|α=k π-4
π
,k ∈Z }
2.弧度制:
(1)定义:用“弧度”做单位来度量角的制度,叫做弧度制。
(2)角度与弧度的互化:
1°=
180
π
弧度,1弧度=(
π
180
)°
(3)两个公式:(R 为圆弧半径,α为圆心角弧度数)。
弧长公式:l=|α|R 扇形面积公式:S=
21lR=2
1|α|R 2
3.周期函数:
(1)定义:对于函数y=f(x),如果存在一个非零常数T ,使得x 取定义域内的任意值时,都有f(x+T)=f(x),那么函数y=f(x)叫做周期函数,其中非零常数T 叫做这个函数的一个周期,如果T 中存在一个最小的正数,则这个最小正
数叫做这个函数的最小正周期。
(2)几个常见结论:
①如果T 是函数y=f(x)的一个周期,那么kT(k ∈Z ,且k ≠0)也是y=f(x)的周期。
(1)
②如果T 是函数y=f(x)的一个周期,那么
ω
T
也是y=f(wx)(w ≠0)的周期。
③一个周期函数不一定有最小正周期,如常函数y=f(x)=c 。
4.三角函数定义: (1)定义:设α是一个任意大小的角,P(x ,y)是角α终边上任意一点,它与原点的距离|PO |=r,那么角α的正弦、余弦、正切、余切、正割、余弦分别是sin α=
r
y ,cos α=r x
,tan
α=
y r ,cot α=y
x
,Sec α=r x ,csc α=r y (如图(1))。
(2)六个三角函数值在每个象限的符号:(如图(2))
(3)同角三角函数的基本关系式:
倒数关系:sin α²csc α=1,cos α²sec α=1,tan α²cot α=1 商数关系:tan α=
ααcos sin ,cot α=α
α
sin cos 平方关系:sin 2
α+cos 2
α=1,1+tan 2
α=sec 2
α,1+cot 2
α=csc 2
α
5.已知三角函数值求角
6.三角函数的图象和性质: (1)三角函数线:
如图(3),sin α=MP,cos α=OM,tan α=AT,cot α=BS
(2)三角函数的图像和性质:
函数y=Asin(wx+ϕ)的图像可以通过下列两种方式得到: ϕ>0,图像左移ϕ
(1)y=sinx y=sin(x+ϕ) ϕ<0,图像右移|ϕ| w >1,横坐标缩短为原来的
w
1倍
y=sin(wx+ϕ)
0<w <1,横坐标伸长为原来的
w
1倍 A >1,纵坐标伸长为原来的A 倍
y=Asin(wx+ϕ) 0<A <1,纵坐标缩短为原来的A 倍 w >1,横坐标缩短为原来的
w 1倍 (2)y=sinx 0<w <1,横坐标伸长为原来的
w
1倍 ϕ>0,图像左移w
ϕ y=sin(wx)
ϕ<0,图像右移w
ϕ
A >1,纵坐标伸长为原来A 倍
y=sin(wx+ϕ) y=Asin(wx+ϕ) 0<A <1,纵坐标缩短为原来A 倍 8.两角和与差的三角函数: (1)常用公式:
两角和与差的公式:
sin(α±β)=sin αcos β±cos αsin β, cos(α±β)=cos αcos β sin αsin β, tan(α±β)=
β
αβ
αtg tg tg tg 1±
倍角公式:
sin2α=2sin αcos α,
cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2
α, tan2α=
α
α
2
12tg tg -. 半角公式: sin
2α=±2cos 1α-, cos
2α=±2
cos 1α+, tan
2α=±ααcos 1cos 1+-=α
αcos 1sin +=ααsin cos 1-.
积化和差公式:
sin αcos β=21
〔sin(α+β)+sin(α-β)〕, cos αsin β=21
〔sin(α+β)-sin(α-β)〕
cos αcos β=21
〔cos(α+β)+cos(α-β)〕,
sin αsin β=-2
1
〔cos(α+β)-cos(α-β)〕
和差化积公式: sin α+sin β=2sin
2β
α+cos
2β
α-,
sin α-sin β=2cos 2βα+sin 2β
α-
cos α+cos β=2cos 2βα+cos 2β
α- ,
cos α-cos β=-2sin 2βα+sin 2
β
α-
万能公式:
sin α=
2
12
22
α
α
tg tg
+,cos α=
2
12122
α
αtg tg +-,tan α=2
12
22
α
α
tg tg
-
(2)各公式间的内在联系:
(3)应注意的几个问题:
①凡使公式中某个式子没有意义的角,都不适合公式。
②灵活理解各公式间的和差倍半的关系。
③在半角公式中,根号前的符号由半角所在像限来决定。
④常具的变形公式有:cos α=
ααsin 22sin ,sin 2α=22cos 1α-,cos 2
α=2
2cos 1α+,tan α+tan
β=tan(α+β)(1-tan αtan β).
⑤asin α+bcos α=22b a +sin(α+ϕ).(其中ϕ所在位置由a ,b 的符号确定,ϕ的值由tan ϕ=
a
b
确定)。
9.解斜三角形:
在解三角形时,常用定理及公式如下表:
10.反三角函数:
[-1,1] [-1,1] (-∞,+∞) (-∞,+∞) [-
2π,2π] [0,π] (-
2π,2
π) (0,π) 在(-∞,+∞)上是增
11.三角方程:
(1) (2)三、知识点、能力点提示
三角函数是中学数学的主要内容之一,也是每年高考的必考内容,其主要内容由以下三
部分构成:三角函数的定义,图像和性质;三角恒等变形;反三角函数。
在高考中,第二部分为主要内容,进行重点考查,当然也不放弃前后两部的考查,对近几年高考试题进行分析后,可以看出:对三角函数的考查主要有两种方式:单独考查三角函数或与其它学科综合考查,前一部分通常是容易题或中等题,而后一部分有一定难度。
