最新5种基本平曲线线型

平曲线的基本形式

平曲线的基本形式
平曲线是一种经济学上常用的图表类型，用于展示不同替代方案之间成本与收益之间的关系和平衡点。

平曲线的基本形式有以下两种：
1. U 型曲线：U 型曲线表明当成本（如固定成本和可变成本总和）增加的时候，单位产品的成本会降低而单位利润率会增加。

这种曲线形状类似于大写的U 字母，因此称作U 型曲线。

这表明当产量增加时，边际收益（即额外收益）总是大于边际成本（即额外成本），比如适用于生产高质量产品或提供高质量服务的公司。

2. 反U 型曲线：反U 型曲线表明当成本增加时，单位产品的成本会上升并且单位利润率会下降。

这种曲线形状类似于倒过来的U 字母，因此称作反U 型曲线。

这表示当产量增加时，边际成本增加快于边际收益，比如适用于一些制造行业中。

它们会在大规模生产期间面临较高的固定成本，当生产达到饱和状态时，它们将面临较高的可变成本并出现反向趋势。

需要注意的是，实际情况可能比理论曲线更为复杂，因此在使用平曲线进行分析时，需要考虑到实际情况和数据的差异，进行合理的解释和分析。

道路线形的基本组合及特点（不转可惜哦！）

道路线形的基本组合及特点（不转可惜哦！）1．道路中线组成及其特点1.1 道路中线的组成道路的中线，包括立交匝道的中线，不论看上去多么复杂，都不外乎由直线、圆曲线和缓和曲线三个基本线形要素组成，如图所示。

圆曲线：具有固定的曲率半径。

直线：具有固定的曲率半径，且曲率为0（半径无穷大），可理解为一种特殊的圆曲线；缓和曲线：又称为回旋曲线，曲率半径是变化的，用于两种不同曲率圆曲线（直线）之间的过渡。

缓和曲线的作用为：①曲率的逐渐变化，便于驾驶与路线顺杨，构成美观及视觉协调的最佳线形；②离心加速度的逐渐变化，使汽车不致产生侧向滑移；③作为行车道横坡变化的过渡段，以减少行车震荡。

缓和曲线是协调平面线形变化的主要线形要素。

1.2 道路中线常用的曲线组合类型在道路及立交匝道设计中，实际采用的线形往往是由直线、圆曲线、缓和曲线中的一种或几种组合而成。

主要有以下几种：(1)基本型曲线是按“直线－回旋曲线－圆曲线－回旋曲线－直线”的顺序组合起来的线型。

基本型中，又可以根据其中两个回旋曲线参数相等与否而分为对称式和不对称式两种。

(2)S 型曲线把两个反向圆曲线用回旋曲线连接起来的线型。

两个反向回旋曲线的参数可以相等，也可以不相等。

(3)C 型曲线同向曲线的两回旋曲线在曲率为0 处径相衔接的形式。

C 型曲线连接处的曲率为0，即，相当于两同向曲线中间直线长度为0，对行车和线形都有一定影响，所以C 型曲线只有在特殊地形条件下方可使用。

(4)卵型曲线用一个回旋曲线连接两个同向圆曲线的线型。

为了只用一个回旋曲线连成卵形，就要求圆曲线延长后，大的圆曲线能完全包含小的圆曲线，并且圆曲线不同圆心，而回旋曲线的曲率半径是从 R1 到R 2。

(5)凸型曲线在两个同向回旋曲线间不插入圆曲线而径相衔接而成的线型。

分对称型和非对称型两种。

凸型曲线尽管在各衔接处的曲率是连续的，但因中间圆曲线的长度为0，对驾驶操纵亦造成一些不利因素，所以只有在路线严格受地形、地物限制方可采用。

认识平面曲线形

认识平面曲线形平面曲线形是数学中的一个重要概念，它包含了很多数学中的基础理论，比如解析几何、微积分等。

在现实生活中，平面曲线形也经常可以被用来描述自然界中物体的形状和运动状态。

本文将简要介绍平面曲线形的相关概念与性质。

一、平面曲线形是什么在数学中，平面曲线形是指在二维平面上的曲线，它可以被用函数方程或者参数方程等形式来表示。

常见的曲线包括直线、圆、椭圆、抛物线、双曲线等，它们都是平面曲线形的特殊形式。

二、平面曲线形的表示方式平面曲线形可以被用多种方式来表示，比如点的坐标、函数方程、参数方程等等。

1.点的坐标对于平面上的直线，可以用两点坐标来表示。

比如，直线AB可以用点A(x1,y1)和点B(x2,y2)来表示。

同理，对于曲线，也可以用点的坐标来表示，但是这种方式比较麻烦且不直观，通常并不常用。

2.函数方程函数方程是指y与x之间的函数关系式，其中y是曲线上的点的纵坐标，x是曲线上的点的横坐标。

例如，圆的方程是x²+y²=r²。

3.参数方程参数方程是指x和y都作为参数的一元函数，通常表示为x=f(t),y=g(t)。

比如，双曲线的参数方程是x=a*t,y=b/sqrt(t²+1)。

三、平面曲线形的性质平面曲线形具有很多重要的性质，下面列举几个常见的性质。

1.切线和法线在曲线上任意一点P处，有一条切线和一条法线。

切线是与曲线相切的直线，法线是与切线垂直的直线。

2.斜率曲线的斜率是切线的斜率，表示曲线在某一点的变化率。

斜率可以用微积分的概念来计算。

3.弧长曲线的弧长是从起点到终点沿曲线走过的距离。

弧长可以用微积分的概念来计算。

4.曲率曲线在某一点的曲率是切线在该点附近的弯曲程度。

曲率可以用微积分的概念来计算。

综上所述，平面曲线形是数学中的基础概念之一，它可以被用来描述自然界中物体的形状和运动状态。

对于平面曲线形的认识和理解，对于学习数学的人来说尤为重要。

平曲线

平曲线、超高、竖曲线、超高在线形设计时，各级公路（高速公路和一级公路除外）的视距应不小于两倍停车视距；并应根据需要，结合地形设置保证超车视距的路段。

平曲线半径：当汽车在平曲线上行驶时，所产生的横向力应不超过轮胎与路面摩阻力所允许的界限，并使驾驶员无不顺适感觉。

平曲线半径、行车速度、路面超高和横向摩阻系数[kg2]的关系式为[147-01],[kg2]其中(+) 直接关系到汽车在平曲线上行驶时的安全和顺适感。

极限最小半径：是公路受到地形或地物等限制所允许采用的最小半径。

其计算的条件是：为0.10（=120公里/小时）～0.15（=40公里/小时），这时驾驶员仍感顺适；是路面超高允许最大值，一般用6％，个别用8％，特殊情况下用10％。

一般最小半径：为使公路平面线型在整体组合上不致不协调，驾驶员感到较为顺适的常用的最小半径。

这时，为0.05～0.06；为6％～8％，不用10％。

不设超高的最小半径公路的平曲线保持直线上的路拱（即不设超高），驾驶员不感到有弯道的最小半径，这时，为0.035；为－2％或－1.5％。

回头曲线：当公路需要展线以争取高程，而又受地形限制不能继续前进而须折返展线时，在折返处设转角一般大于180°的平曲线,称为回头曲线。

回头曲线因受地形限制，常采用极限甚至小于极限的最小半径。

超高：汽车在平曲线上行驶时产生离心力，设置超高，可抵消其部分离心力，使汽车不致向外倾覆。

超高值过大不利于驾驶操作和行车安全，也不利于公路养护、施工;过小则不利于排水。

专供汽车行驶的高速公路,一级公路的超高横坡度不超过10％，其他各级公路不超过8％。

在积雪寒冷地区，最大超高横坡度不超过6％。

平曲线加宽：汽车在平曲线上行驶时，后轮的轨迹在前轮的内侧,其车轮所占有宽度比在直线上的要宽,因此车道内侧应予加宽。

加宽值视车型和平曲线半径()而定,[kg2]一般可按/2计算。

式中为汽车前后轴距；如为半挂车时，可分别按牵引车和挂车的前后轴距[kg2],计算。

5种基本平曲线线型

For personal use only in study and research; not for commercial use??? 在进行道路平面线形设计时，一般会遵循下列原则：1、平面线形应直捷、连接、顺适，并与地形地物相适应，与周围环境相协调；2、必须满足行驶力学要求，视觉和心理上的要求对高速路应尽量满足；3、保持平面线形的均衡与连贯；4、应避免连续急弯的线形；5、平曲线应有足够的长度。

一般来说道路线型分为以下六类：1、基本型直线+缓和曲线+圆曲线+缓和曲线+直线，这种线型和地铁平曲线里的大部分线型是一样的。

2、S型缓和曲线1+圆曲线1+缓和曲线1+（反向）+缓和曲线2+圆曲线2+缓和曲线2S型曲线几点注意：（1）相邻两个回旋参数A1和A2宜相等，当采用不同参数时，A1/A2<2.0，有条件时应<1.5；（2）两反向曲线之间不设直线，不得已插入直线时，必须尽量短，其直线长度或重合段的长度应满足L≤（A1+A2）/40。

（3）S型两圆曲线半径之比不宜过大，宜为：R2/R1=11/3。

3、卵型缓和曲线1+圆曲线1+缓和曲线（过渡）+圆曲线2+缓和曲线2卵型曲线的几点注意：（1）卵型上的回旋参数A不应小于该级公路关于回旋线最小参数的规定，同时宜在下列界限内：R2/2≤ A≤ R2（R2为小圆半径）；（2）两圆曲线半径之比宜在下列界限之内：0.2≤R2/R1≤ 0.8（R1为大圆半径）；（3）两圆曲线的间距，宜在下列界限之内：0.003≤D/R2≤ 0.03（D为两圆曲线最小间距）。

4、凸型直线+缓和曲线1+（同向）缓和曲线2+直线5、复合型直线+缓和曲线1+（同向）缓和曲线2+圆曲线+……圆曲线1+缓和曲线1+（同向）缓和曲线2+圆曲线2仅供个人用于学习、研究；不得用于商业用途。

For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей,которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文。

曲线的基本类型及性质

曲线的基本类型及性质曲线一直是数学中的重要概念，广泛应用于各个领域。

在数学中，曲线可以通过方程、参数方程、极坐标方程等多种形式来表示。

本文将介绍曲线的基本类型以及它们的性质。

一、直线直线是最基本的一种曲线类型，其特点是在平面上无限延伸，始终保持直线状。

直线可以由一元一次方程来表示，形如 y = kx + b，其中k 和 b 是常数。

直线具有以下性质：1. 直线上的任意两点可以唯一确定一条直线；2. 直线的斜率等于直线与 x 轴的夹角的正切值；3. 直线的斜率为正表示直线向上倾斜，斜率为负表示直线向下倾斜；4. 直线的斜率为零表示直线水平，斜率不存在表示直线垂直于 x 轴。

二、抛物线抛物线是一种常见的平面曲线，具有形状如同开口向上或开口向下的弧线。

抛物线可以由一元二次方程来表示，形如 y = ax^2 + bx + c，其中 a、b、c 是常数，且 a 不等于零。

抛物线具有以下性质：1. 抛物线的开口方向由二次项的系数a 决定，a 大于零时开口向上，a 小于零时开口向下；2. 抛物线的顶点是抛物线的最值点，其 x 坐标为 -b/2a；3. 抛物线关于顶点对称；4. 当 a 的绝对值越大时，抛物线的形状越扁平。

三、椭圆椭圆是一种闭合曲线，其形状类似于“椭圆”这个几何图形。

椭圆可以由参数方程来表示，形如 x = a cos(t)，y = b sin(t)，其中 a 和 b 是正数，且 a 大于 b。

椭圆具有以下性质：1. 椭圆的长轴在 x 轴上，短轴在 y 轴上；2. 椭圆的离心率小于 1，且离心率等于 0 时为圆形；3. 椭圆的焦点到椭圆上任意点的距离之和是一个常数；4. 椭圆具有对称性，关于 x 轴和 y 轴都对称。

四、双曲线双曲线是一种开口朝外或朝内的曲线，在数学和物理学中有着广泛的应用。

双曲线可以由参数方程来表示，形如 x = a sec(t)，y = b tan(t)，其中 a 和 b 是正数。

平曲线认识

第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物，它的中线是一个空间曲线，叫路线，其在水平面的投影就是平面线形。

道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。

在路线平面方向的转折处为满足行车要求，需要用适当的曲线把前、后直线连接起来，这种曲线称为平曲线。

平曲线包括圆曲线和缓和曲线。

①圆曲线要素主点桩号计算：ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2（校核）②缓和曲线要素切线长：外距：曲线长：()s s 18022180l aR l a R L h +=+-=πβπ切线加长：q =/2－3/(240R2)圆曲线相对切线内移量：p = 2/(24R)切曲差 Dh = 2T －Lh上式中：α 为线路转向角；β0为缓和曲线角；其中q 、p 、β0缓和曲线参数。

ZH 桩号 = JD 桩号－T HY 桩号 = ZH 桩号＋QZ 桩号 = HY 桩号＋L/2YH 桩号 = QZ 桩号＋L/2 = HY 桩号＋L = ZH 桩号＋＋LHZ 桩号 = YH 桩号＋= ZH 桩号＋LhJD 桩号 = ZY 桩号－Th ＋Dh （检核）m)2)(（q tgp R T ++=α）（m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意：上面计算需要大家掌握主点桩号计算，五大主点：ZH、HY、QZ、YH、HZ，还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。

可以判断下图即可。

重点知识必须掌握（线元法基础）：直线：曲率为0，起终点半径无穷大。

圆曲线：具有一定曲率半径的圆弧，半径为固定值。

缓和曲线：在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线（指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段），我国公路缓和曲线的形式采用回旋线。

（曲率为半径的倒数）A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式：A²=R x Ls1，A²=R x Ls2入缓和曲线：从ZH点到HY点，A固定不变，随着Ls1的增大，半径从∞减小到R出缓和曲线：从YH点到HZ点，A固定不变，随着Ls2的减小，半径从R增大到∞如果A²≠R x Ls，那么这段缓和曲线是不完整的，叫做不完整缓和曲线。

曲线调整中常用的16种的曲线形状

曲线调整中常用的16种的曲线形状1. 输入输出值相等。

就是说，人还没有来得及对图像做任何手脚。

2. 除最暗的一点外，均匀提亮全图。

精确地说，输入色阶225的点A是分界点，这个点提亮的幅度最大，所有其他的点，离点A越远的，提亮幅度越小。

虽说如此，在图像的高亮部分即所有输入色阶大于225的点，实际上也已经提亮到最大限度了。

由本图，不难做出除最亮一点外压暗全图的曲线。

3. 除最亮、最暗点外，以中间亮度为主均匀提亮全图。

请注意这不是一个弧。

弧是圆的一部分，但在这里，无论什么圆都不可能同这条曲线相吻合。

看上去这应该是一条摆线，动力学中所谓“最速降落线”。

请与下面真实的弧暗影比较一下，显然曲线两端是不对称的。

由本图，不难做出依图像的灰阶特性压暗全图的曲线（以下这类直接相对的曲线形态不再做特别说明）。

4. 均匀压暗全图，最亮的部分压暗的幅度最大，以下这幅度逐渐减少，到最暗的一点等于零（因为已经无可再暗了，只能等于零）。

5. 全图呈无差别中性灰（中性灰在图像的叠加模式下和图像的灰平衡理论中都很重要）。

6. 全图反相。

7. 极暗点不变，极亮点压成极暗点，但是把中间部分均匀提亮。

这种类型的曲线在照片调整中极少使用。

8. 稍稍提亮亮部，同时造成暗部的代偿性压暗。

9. 稍稍提亮中间部分，同时在亮部和暗部都造成代偿性压暗。

10. 加锁定点，避免一部分代偿性压暗。

11. 以点A（色阶192）为界，压暗右侧所有部分，同时提亮左侧所有部分。

12. 三峰调整。

这种曲线在做金属效果的时候经常用到。

13. 夹杂着手动曲线。

14. 平滑手动曲线。

15. 调出曲线对话框以后，按下Alt，“自动”键就变成了“选项”键，单击选项键，便能指定自动范围。

[按：自动曲线，相当于自动色阶。

]此问题比较深，不说也罢。

16. 不可能曲线（因为对一个输入值，不可能有不同的输出值）。

曲线形状是无法穷举的，这里只能是例举。

诸公举一反三可也。

三个吸管，都是点图吸管。

线路类型的总结

线路类型的总结
一、平曲线
平曲线（圆曲线段长度）指的是道路平面走向改变方向或竖向改变坡度时所设置的连接两相邻直线段的圆弧形曲线。

基本类型
单曲线：由一个圆曲线组成的曲线称为单曲线。

复曲线：由两个或两个以上同向圆曲线组成的曲线，
同向曲线：转向相同的两相邻曲线连同其间的直线段所组成的曲线称为同向曲线；
反向曲线：转向相反的两相邻曲线连同其间的直线段所组成的曲线称为反向曲线。

平面曲线的组合
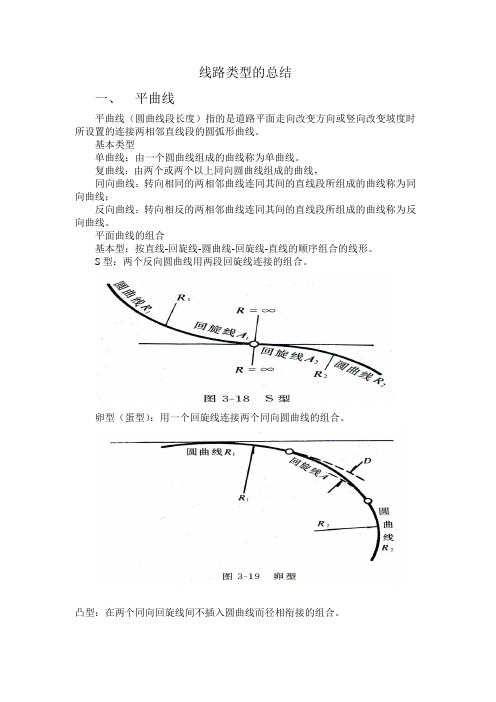
基本型：按直线-回旋线-圆曲线-回旋线-直线的顺序组合的线形。

S型：两个反向圆曲线用两段回旋线连接的组合。

卵型（蛋型）：用一个回旋线连接两个同向圆曲线的组合。

凸型：在两个同向回旋线间不插入圆曲线而径相衔接的组合。

复合型：两个以上同向回旋线间在曲率相等处相互连接的线形。

C型：同向曲线的两回旋线在曲率为零处径相衔接的线形。

二、竖曲线
竖曲线在线路纵断面上，以变坡点为交点，连接两相邻坡段的曲线称为竖
曲线。

竖曲线有凸形和凹形两种。

鐵路線路採用的豎曲綫，按其形狀可分為一下三種：
1 圓曲綫形豎曲綫
2 抛物線形豎曲綫
3 連續短坡（鏈條坡）
三、缓和曲线
缓和曲线的基本线型分为：
三次抛物线形：曲率和线路横坡是按照直线规律变化的。

三次抛物线余弦改善形：在三次抛物线缓和曲线超高的起、终点处，插入一定长度的余弦曲线圆顺坡。

三次抛物线圆改善型：在三次抛物线缓和曲线超高的起、终点处，插入一定长度的圆曲线顺坡。

七次四项式
半波正弦形：曲率和线路横坡是按照正弦规律变化的。

一波正弦形。

基本型曲线组合

基本型曲线组合一、三种基本型曲线介绍在数学中，曲线是指在坐标平面上的一条连续的线。

基本型曲线是指具有特定形状和性质的曲线，下面将介绍三种常见的基本型曲线。

1. 直线曲线直线曲线是最简单的曲线类型之一，它由无数个点连成的直线段组成。

直线曲线具有线性关系，其特点是斜率恒定。

在数学表示中，直线曲线可以用一元线性方程 y = kx + b 来表示，其中 k 表示斜率，b 表示截距。

直线曲线广泛应用于物理学、几何学等领域中。

2. 抛物线曲线抛物线曲线是一种呈现对称形状的曲线，它由一些特定的二次函数方程描述。

抛物线曲线的形状像一个碗或者一个喷泉，其特点是顶点和对称轴。

一元二次方程 y = ax^2 + bx + c 描述了抛物线曲线的形状，其中 a 是一个非零常数，控制了抛物线的开口方向和形状。

3. 正弦曲线正弦曲线是以正弦函数为基础的曲线类型。

它的形状呈现周期性波动，可以用来描述振动和波动现象。

正弦曲线有很多应用，例如在信号处理、物理学、音乐等领域中被广泛使用。

正弦曲线的数学表示是 y = A*sin(Bx + C) + D，其中 A、B、C、D 是参数，控制了振幅、周期、相位和垂直平移。

二、基本型曲线的组合运用基本型曲线的组合运用是指将两个或多个基本型曲线结合起来，形成新的复合曲线。

通过调整基本型曲线的参数和组合方式，可以获得不同形状和特性的复合曲线。

以下是几种常见的基本型曲线组合运用示例。

1. 直线与抛物线的组合直线和抛物线是常见的基本型曲线，它们可以通过组合产生新的复合曲线。

一种常见的组合方式是将直线和抛物线的方程分别加在一起，形成一个复合方程。

例如 y = kx + b，同时又有 y = ax^2 + bx+ c，将两个方程相加得到 y = ax^2 + (kx + b)x + c，这样就得到了直线和抛物线组合的复合曲线。

2. 抛物线与正弦曲线的组合抛物线和正弦曲线也可以组合产生新的复合曲线。

一种常见的组合方式是将抛物线的方程嵌入到正弦曲线的方程中，形成一个复合方程。

平曲线

平曲线、超高、竖曲线、超高在线形设计时，各级公路（高速公路和一级公路除外）的视距应不小于两倍停车视距；并应根据需要，结合地形设置保证超车视距的路段。

平曲线半径：当汽车在平曲线上行驶时，所产生的横向力应不超过轮胎与路面摩阻力所允许的界限，并使驾驶员无不顺适感觉。

平曲线半径、行车速度、路面超高和横向摩阻系数[kg2]的关系式为[147-01],[kg2]其中(+) 直接关系到汽车在平曲线上行驶时的安全和顺适感。

极限最小半径：是公路受到地形或地物等限制所允许采用的最小半径。

其计算的条件是：为0.10（=120公里/小时）～0.15（=40公里/小时），这时驾驶员仍感顺适；是路面超高允许最大值，一般用6％，个别用8％，特殊情况下用10％。

一般最小半径：为使公路平面线型在整体组合上不致不协调，驾驶员感到较为顺适的常用的最小半径。

这时，为0.05～0.06；为6％～8％，不用10％。

不设超高的最小半径公路的平曲线保持直线上的路拱（即不设超高），驾驶员不感到有弯道的最小半径，这时，为0.035；为－2％或－1.5％。

回头曲线：当公路需要展线以争取高程，而又受地形限制不能继续前进而须折返展线时，在折返处设转角一般大于180°的平曲线,称为回头曲线。

回头曲线因受地形限制，常采用极限甚至小于极限的最小半径。

超高：汽车在平曲线上行驶时产生离心力，设置超高，可抵消其部分离心力，使汽车不致向外倾覆。

超高值过大不利于驾驶操作和行车安全，也不利于公路养护、施工;过小则不利于排水。

专供汽车行驶的高速公路,一级公路的超高横坡度不超过10％，其他各级公路不超过8％。

在积雪寒冷地区，最大超高横坡度不超过6％。

平曲线加宽：汽车在平曲线上行驶时，后轮的轨迹在前轮的内侧,其车轮所占有宽度比在直线上的要宽,因此车道内侧应予加宽。

加宽值视车型和平曲线半径()而定,[kg2]一般可按/2计算。

式中为汽车前后轴距；如为半挂车时，可分别按牵引车和挂车的前后轴距[kg2],计算。

平面曲线的性质与分类解析

平面曲线的性质与分类解析平面曲线是一个重要的数学概念，广泛应用于几何学、物理学以及工程学等领域。

了解平面曲线的性质和分类对于深入理解曲线的特点以及解决实际问题具有重要意义。

本文将对平面曲线的性质和分类进行解析。

1. 曲线的性质曲线是由点按照一定的规律在平面上绘制出来的，具有以下几个基本性质：1.1 曲线长度：曲线长度是指从曲线上任意两点之间的弧长。

对于光滑曲线，可以通过积分计算得到曲线长度。

1.2 曲率：曲线在任意一点的曲率是指曲线在该点处的曲率圆半径的倒数。

曲率越大，曲线越弯曲。

1.3 弯曲的方向：曲线的弯曲方向可以通过曲率的正负来确定。

当曲率为正时，曲线向凸侧弯曲，当曲率为负时，曲线向凹侧弯曲。

2. 平面曲线的分类平面曲线可以根据其数学表达式、图形特征以及几何性质进行分类。

下面将介绍几种常见的平面曲线分类。

2.1 直线直线是一种最简单的曲线，它由无数个点按照同一方向上等距离排列而成。

直线的数学表达式可以用线性方程表示，例如y = kx + b。

直线的特点是具有恒定的斜率，不会弯曲。

2.2 抛物线抛物线是一种开口朝上或开口朝下的曲线，它具有对称轴和焦点。

抛物线的数学表达式可以用二次方程表示，例如y = ax^2 + bx + c。

抛物线的特点是在焦点处反射光线呈现出特殊的性质。

2.3 椭圆椭圆是一种闭合曲线，它由离两个焦点的距离之和恒定的点构成。

椭圆的数学表达式可以用标准方程表示，例如(x^2/a^2) + (y^2/b^2) = 1。

椭圆的特点是具有两个焦点，离焦点越远的点离椭圆越远。

2.4 双曲线双曲线是一种开口朝左和开口朝右的曲线，它由离两个焦点的距离之差恒定的点构成。

双曲线的数学表达式可以用标准方程表示，例如(x^2/a^2) - (y^2/b^2) = 1。

双曲线的特点是具有两个独立的分支。

2.5 阿基米德螺线阿基米德螺线是由一个定点绕着一根直线旋转而成的曲线。

阿基米德螺线的数学表达式可以用极坐标表示，例如r = aθ。

平曲线认识

第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物，它的中线是一个空间曲线，叫路线，其在水平面的投影就是平面线形。

道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。

在路线平面方向的转折处为满足行车要求，需要用适当的曲线把前、后直线连接起来，这种曲线称为平曲线。

平曲线包括圆曲线和缓和曲线。

①圆曲线要素主点桩号计算：ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2（校核）②缓和曲线要素切线长：外距：曲线长：()s s 18022180l aR l a R L h +=+-=πβπ切线加长：q =/2－3/(240R2)圆曲线相对切线内移量：p = 2/(24R)切曲差 Dh = 2T －Lh上式中：α 为线路转向角；β0为缓和曲线角；其中q 、p 、β0缓和曲线参数。

ZH 桩号 = JD 桩号－T HY 桩号 = ZH 桩号＋QZ 桩号 = HY 桩号＋L/2YH 桩号 = QZ 桩号＋L/2 = HY 桩号＋L = ZH 桩号＋＋LHZ 桩号 = YH 桩号＋= ZH 桩号＋LhJD 桩号 = ZY 桩号－Th ＋Dh （检核）m)2)(（q tgp R T ++=α）（m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意：上面计算需要大家掌握主点桩号计算，五大主点：ZH、HY、QZ、YH、HZ，还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。

可以判断下图即可。

重点知识必须掌握（线元法基础）：直线：曲率为0，起终点半径无穷大。

圆曲线：具有一定曲率半径的圆弧，半径为固定值。

缓和曲线：在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线（指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段），我国公路缓和曲线的形式采用回旋线。

（曲率为半径的倒数）A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式：A²=R x Ls1，A²=R x Ls2入缓和曲线：从ZH点到HY点，A固定不变，随着Ls1的增大，半径从∞减小到R出缓和曲线：从YH点到HZ点，A固定不变，随着Ls2的减小，半径从R增大到∞如果A²≠R x Ls，那么这段缓和曲线是不完整的，叫做不完整缓和曲线。

道路平曲线概念讲解

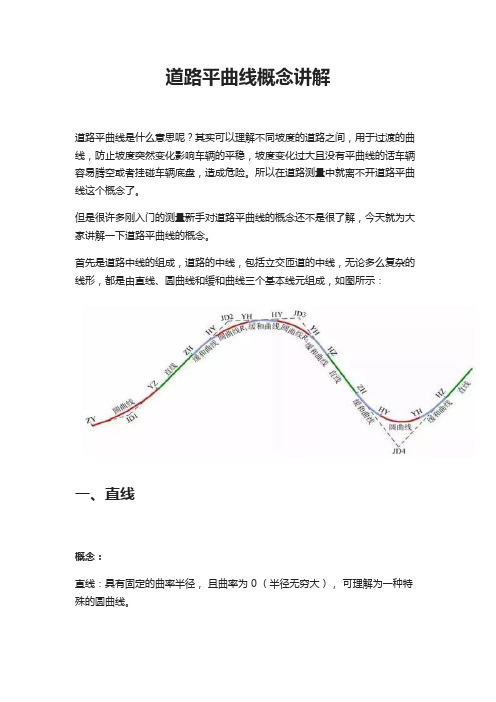
道路平曲线概念讲解道路平曲线是什么意思呢？其实可以理解不同坡度的道路之间，用于过渡的曲线，防止坡度突然变化影响车辆的平稳，坡度变化过大且没有平曲线的话车辆容易腾空或者挂碰车辆底盘，造成危险。

所以在道路测量中就离不开道路平曲线这个概念了。

但是很许多刚入门的测量新手对道路平曲线的概念还不是很了解，今天就为大家讲解一下道路平曲线的概念。

首先是道路中线的组成，道路的中线，包括立交匝道的中线，无论多么复杂的线形，都是由直线、圆曲线和缓和曲线三个基本线元组成，如图所示：一、直线概念：直线：具有固定的曲率半径，且曲率为 0 （半径无穷大），可理解为一种特殊的圆曲线。

特点：1）两点之间以直线为最短。

2）笔直的道路给人以短捷、直达的良好印象。

3）汽车在直线上行驶受力简单，方向明确，驾驶操作简易。

4）测设施工方便。

二、缓和曲线概念：缓和曲线 :为了使路线的平面线形更加符合汽车的行驶轨迹、离心力逐渐变化，确保行车的安全和舒适，需要在直线和圆曲线之间或半径相差较大的两个同向圆曲线之间设置一段曲率连续变化的曲线，此曲线称为缓和曲线。

目前我国公路设计中，以回旋线作为缓和曲线。

缓和曲线类型：1.完整缓和曲线 :判断标准： A²=R x Ls2、非完整缓和曲线：判断标准： A²≠R x LsA= 缓和曲线参数缓和曲线三、圆曲线概念：圆曲线：即圆的一部分（圆弧），具有固定的曲率半径。

特点1、曲线上任一点曲率半径R为常数2、大半径的圆曲线线形美观、顺适、行车舒适，是公路上常采用的线形。

四、道路中常见的线形组合在道路及立交匝道设计中，实际采用的线形往往是直线、圆曲线、缓和曲线中的一种或几种组合而成。

主要有以下几种：(1)基本型曲线是按“直线－回旋曲线－圆曲线－回旋曲线－直线”的顺序组合起来的线型。

基本型中，又可以根据其中两个回旋曲线参数相等与否而分为对称式和不对称式两种。

(2)S 型曲线把两个反向圆曲线用回旋曲线连接起来的线型,GQ处R=∞。

s型平曲线线型组合要求

s型平曲线线型组合要求
1.线型：S型平曲线线型组合要求使用S型曲线作为主要线型，辅助线型为直线或圆弧线型。

2. 曲线半径：S型曲线半径应根据道路等级、速度要求等因素合理选定，并满足道路设计规范中相关要求。

3. 联接部分：S型曲线与直线或圆弧线型的联接部分应平滑过渡，避免出现急转弯或突变的情况。

4. 转向角度：S型曲线的转向角度应根据实际情况和设计要求进行合理选定，避免出现转弯过大或过小导致的安全隐患。

5. 辅助线型选择：辅助线型的选择应根据设计需要和实际情况选定，确保设计合理、安全稳定。

6. 设计标准：S型平曲线线型组合设计应符合相关道路设计规范和标准要求，确保设计质量和安全可靠性。

- 1 -。

平面线形的组合类型

1、基本形
当按直线—回旋线（A1）—圆曲线—回旋线（A2 ）—直线的顺序组合而成线形。

2、S形定义
两个反向圆曲线用两段反向回旋线连接的组合形式。

3.卵形
（1）定义：两同向的平曲线，按直线—缓和曲线（A1）—圆曲线（R1）—缓和曲线（AF）—圆曲线（R2）—缓和曲线（A2）—直线的顺序组合而成的线形。

4.凸形
两段同向缓和曲线之间不插入圆曲线而径相衔接的组合形式（圆曲线长度为零）。

5.复合形
将两个以上的同向回旋线在曲率相等处相互连接的线形。

6.C形
两同向回旋线在曲率为零处径相连接（即连接处曲率为0，半径为）的组合线形。