高二数学课件 导数及其应用
合集下载
3.2导数的计算(27张PPT)
;
(7) y 3 x; 2
例3 :日常生活中的饮用水通常是经过净化的，随着水纯
净度的提高，所需净化费用不断增加。已知1吨水净化
到纯净度为x%时所需费用（单位:元）为：
c(x)= 5284 (80 x 100). 100 x
求净化到下列纯净度时，所需净化费用的瞬时变化率;
(1)90%;
(2)98%.
x
x
f (x) (x2) ' lim y lim 2x x x2 lim (2x x) 2x.
x x0
x0
x
x0
公式三：（x2）' 2x
二、几种常见函数的导数
4) 函数y=f(x)=1/x的导数.
解: y f (x) 1 , x
y f (x x) f (x) 1 1 x x x x (x x)x
y
'
1 x2
探究：
表示y=C图象上每一点处的切线 斜率都为0
表示y=x图象上每一点处的切线 斜率都为1
这又说明什么?
这又说明什么?
画出函数y=1/x的图像。根据图像， 描述它的变化情况。并求出曲线在 点（1,1）处的切线方程。
x+y-2=0
3.2.2基本初等函数 的导数公式及导数 的运算法则
高二数学 选修1-1
y f (x x) f (x) C C 0,
y 0, x
f (x) C lim y 0. x0 x
公式一：C 0 (C为常数)
二、几种常见函数的导数
2) 函数y=f(x)=x的导数. 解: y f (x) x,
y f (x x) f (x) (x x) x x,
(1) c '(90) 5284 52.84 (100 90)2
高二数学ppt课件 导数及其应用课件3(1)
2．导数的几何意义 函数 y＝f(x)在 x＝x0 处的导数，就是曲线 y＝f(x)在 x＝x0
fx0＋Δx－fx0 lim Δx 切线的斜率 Δx→0 处的____________，即 k＝f ′(x0)＝____________________.
3．函数的导数 对于函数 y＝f(x)，当 x＝x0 时，f ′(x0)是一个确定的数．当 x 变化时，f ′(x)便是一个关于 x 的函数，我们称它为函数 y＝
1 [解析] 由 x＋2y－3＝0 知斜率 k＝－2， 1 ∴f ′(x0)＝－2&在 x＝1 处的切线方程为__________.
• [答案] x＋y－2＝0
f1＋Δx－f1 [解析] y′|x＝1＝f ′(1)＝ lim Δx Δx→0 1 －1 1＋Δx －1 ＝ lim ＝ lim ＝－1， Δx Δx→0 Δx→0 1＋Δx 则切线方程为 y－1＝－(x－1)，即 x＋y－2＝0.
典例探究学案
•导数几何意义的理解 • 若函数y＝f(x)的导函数在区间[a， b]上是增函数，则函数y＝f(x)在区间[a，b]上的 图象可能是( )
• [分析] (1)导数的几何意义是什么？(2)y＝f(x) 的导函数在区间[a，b]上是增函数，说明y＝ f(x)图象的切线有什么特点？
• [解析] 因为函数y＝f(x)的导函数y＝f ′(x)在 [a，b]上是增函数，由导数的几何意义可知， 在区间[a，b]上各点处的切线斜率是逐渐增 大的，只有A选项符合． • [答案] A
• 牛刀小试 • 1．设f ′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0)) 处的切线( ) • A．不存在 B．与x轴平行或重合 • C．与x轴垂直 D．与x轴斜交 • [答案] B • [解析] 曲线在点(x0，f(x0))的切线斜率为0， 切线平行或重合于x轴．
导数及其应用PPT课件
解：(1)
4.已知a>0,n为正整数。 (1)设y=(x-a)n, 证明y’=n(x-a)n-1; (2)设fn(x)=xn-(x-a)n , 对任意n≥a,证明：
小
求函数单调区间的步骤：
求函数极值的步骤：
结
(1)求导函数f ’(xቤተ መጻሕፍቲ ባይዱ; (2)求方程f ’(x)=0的根；(3)检查f ’(x)在 方程根左右的符号，如果左正右负，那么f(x)在这个根处 取得最大值，如果左负右正，那么f(x)在这个根处取得最 小值。 求闭区间上函数的最值的方法：
y
极大值
极大值
x0
极小值
0
x
极小值
显然在极值处函数的导数为０．
【知识在线】:
１．函数ｙ＝２ｘ３＋４ｘ２＋１的导数是_____________. ２.函数y=f(x)的导数y/>0是函数f(x)单调递增的 （B ）
A.充要条件
C.必要不充分条件
B.充分不必要条件
D.既不充分也不必要条件
(0,2) 单调递增区 ３.函数y=x2 (x-3),则f(x)的单调递减区间是_____, (-∞,0) , (2,+∞) 。 间为______________
x
f(x)
极大值 极小值
由此可得，函数在ｘ＝－ ，处取得极大值２＋ ２
在ｘ＝ ，处取得极小值２- ２ ．草图如图
y
∵ａ＞０，显然极大值必为正，
故只要看极小值的正负即可。
－
０
x
y
方程x3-3ax+2=0有惟一的实根；
－
０ y
x
方程x3-3ax+2=0有二个不同的实根 （其中有一个为二重根）；
导数的应用(第1课时)利用导数研究函数的单调性(课件)高二数学(沪教版2020选择性必修第二册)
图 （ １ ） 中的曲线越来越 “ 陡峭 ”， 在区间 （ ０ ， １ ） 上各点处 的切线斜率始终大于 １ ； 图 （ ２ ） 中的曲线由 “ 陡峭 ” 变得 “ 平缓 ”， 在区间 （ ０ ， １ ） 的右半段的切线斜率小于 １ ； 图 （ ３ ） 中的曲线由 “ 平缓 ” 变得 “ 陡峭 ”， 在区间 （ ０ ， １ ） 的左半段的切线斜率小于 １ ； 图 （ ４ ） 中的曲线越来越 “ 平缓 ”， 在区间 （ ０ ， １ ） 上各点处 的切线斜率始终小于 １． 因此 ， 只有图 ５-３-１ （ １ ） 中的图像有可能表示函数 y ＝ f（ 可能成为严格递增区间与严格 递减区间的分界点 ．
例4.确定函数（f x）＝x2的单调区间 ．
解函数在x 0处没有定义 ．当x 0时，f (x)=-2x3，
方程f′（ x )＝０ 无解 ， 所以函数 f（ x ）没有驻点 ． 但当 x ＞０ 时 ，f′（ x ） ＜０ ，f（ x ） 单调递减 ； 当 x ＜０ 时 ，f′（ x） ＞０ ， f（ x ） 单调递增 ． 可 见 ， 函数 f （ x ） 的严格递增区间为 （－∞，０）， 严格 递减区间为（０，＋∞）
课本练习 宋老师数学精品工作室
１． 利用导数研究下列函数的单调性 ， 并说明所得结果与你 之前的认识是否一致 ：
宋老师数学精品工作室 ２． 确定下列函数的单调区间 ：
随堂检测 宋老师数学精品工作室
1、函数y＝x2cos 2x的导数为（ ）
A．y′＝2xcos 2x－x2sin 2x
B．y′＝2xcos 2x－2x2sin 2x
上面我们用导数值的正负判断函数在某区间的单调性 ． 但导数值还可 以进一步用以判断函数变化速度的快慢 ： 导数f′（ x ０ ） 是函数 f（ x ） 在点 x ０ 的切线的斜率 ， 所以它描述了曲线 y＝f（ x ） 在点 x０ 附近相 对于x轴的倾斜程度 ： 当f′（ x ０ ） ＞０ 时 ，f′（ x０ ） 越大 ， 曲线 y ＝ f （ x ） 在点 x ０ 附近相对于 x 轴倾斜得越厉害 ，f（ x ） 递增得 越快 ； 而当f′（ x ０ ） ＜０ 时 ，f′（ x ０ ） 越小 ， 曲线y ＝ f （ x ） 在点 x０ 附近相对于x轴倾斜得越厉害 ， f （ x ） 递减得越快 ． 综合这 两个方面 ， 导数的绝对值越大 ， 函数图像就越 “ 陡峭 ”， 也就是 函数值变化速度越快 ．
高二导数ppt课件
指数函数和对数函数导数
指数函数f(x)=ex的导数为f'(x)=ex，对数函数f(x)=lnx的导数为 f'(x)=1/x。
导数四则运算法则
加法法则
[f(x)+g(x)]'=f'(x)+g'(x)，即两个函数的和的导数等于各 自导数之和。
减法法则
[f(x)-g(x)]'=f'(x)-g'(x)，即两个函数的差的导数等于被减 数导数减去减数导数。
导数在图像变换中的应用
02
利用导数的性质，研究函数图像的平移、伸缩、对称等变换规
律。
导数在曲线绘制中的应用
03
通过计算函数的导数，确定曲线的切线斜率，从而绘制出函数
的图像。
04
高阶导数及其应用
高阶导数概念引入
定义与性质
高阶导数表示函数在某一点附近 的变化速率，具有局部性、线性
性和求导法则等基本性质。
微分在近似计算中应用举例
利用微分进行函数值的近似计算
通过计算函数在某一点的导数，可以估算函数在该点附近的函数值。
利用微分求最值问题
通过求解函数的导数，可以确定函数的单调区间和极值点，进而求出函数的最值。
THANKS
感谢观看
乘法法则
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)，即两个函数的积的导数等 于第一个函数导数乘以第二个函数加上第一个函数乘以第 二个函数导数。
除法法则
[f(x)/g(x)]'=[f'(x)g(x)-f(x)g'(x)]/g²(x)，即两个函数的商 的导数等于分子中第一个函数导数乘以分母减去分子乘以 分母导数再除以分母平方。
指数函数f(x)=ex的导数为f'(x)=ex，对数函数f(x)=lnx的导数为 f'(x)=1/x。
导数四则运算法则
加法法则
[f(x)+g(x)]'=f'(x)+g'(x)，即两个函数的和的导数等于各 自导数之和。
减法法则
[f(x)-g(x)]'=f'(x)-g'(x)，即两个函数的差的导数等于被减 数导数减去减数导数。
导数在图像变换中的应用
02
利用导数的性质，研究函数图像的平移、伸缩、对称等变换规
律。
导数在曲线绘制中的应用
03
通过计算函数的导数，确定曲线的切线斜率，从而绘制出函数
的图像。
04
高阶导数及其应用
高阶导数概念引入
定义与性质
高阶导数表示函数在某一点附近 的变化速率，具有局部性、线性
性和求导法则等基本性质。
微分在近似计算中应用举例
利用微分进行函数值的近似计算
通过计算函数在某一点的导数，可以估算函数在该点附近的函数值。
利用微分求最值问题
通过求解函数的导数，可以确定函数的单调区间和极值点，进而求出函数的最值。
THANKS
感谢观看
乘法法则
[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)，即两个函数的积的导数等 于第一个函数导数乘以第二个函数加上第一个函数乘以第 二个函数导数。
除法法则
[f(x)/g(x)]'=[f'(x)g(x)-f(x)g'(x)]/g²(x)，即两个函数的商 的导数等于分子中第一个函数导数乘以分母减去分子乘以 分母导数再除以分母平方。
导数的概念及其意义(课件)高二数学(人教A版2019选择性必修第二册)
=
=
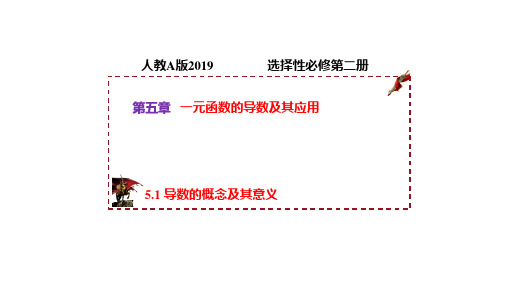
−1
1 + ∆ − 1
= ∆ + 2
切线的斜率
− 1
1 + ∆ 2 − 1
=
=
= ∆ + 2
−1
1 + ∆ − 1
当∆无限趋近于0，即无论x从小于1的一边，还是从大于1
的一边无限趋近于1时，割线0 的斜率k都无限趋近于2
由 =
1+∆ −(1)
∆
= ∆ + 2
但 ∆可正、可负；
∆ = (2 ) − (1 )是函数值的改变量，可正、
可负，也可为0， 因此平均变化率可正、可负，也可为零
函数的平均变化率为0，并不一定说明函数f(x)没有变化
瞬时变化率
函数 f(x) 在 x = x0 处的 瞬时变化率
是函数 f(x) 从 x0 到 x0 + ∆x 的平均变化率
A.0
B.-1 C.3
D.-6
答案 D
解析
(0+Δ)-(0)
Δ
则切线斜率
=
(Δ)2 -6Δ-0
=Δx-6,
Δ
f(0+x)-f(0)
k= lim
x
Δ→0
= (Δx-6)=-6.
x→0
)
规律方法 求曲线上某点(x0,f(x0))处的割线或切线斜率的步骤
f(x 0 +x)-f(x 0 )
例2 将原油精炼为汽油、柴油、塑胶等各种不同产品，需要对原油进行冷却和加热.
已知在第 x h时，原油的温度（单位：℃）为
= = 2 − 7 + 15(0 ≤ ≤ 8) .
计算第 2 h 与第 6 h 时，原油温度的瞬时变化率，并说明它们的意义.
=
−1
1 + ∆ − 1
= ∆ + 2
切线的斜率
− 1
1 + ∆ 2 − 1
=
=
= ∆ + 2
−1
1 + ∆ − 1
当∆无限趋近于0，即无论x从小于1的一边，还是从大于1
的一边无限趋近于1时，割线0 的斜率k都无限趋近于2
由 =
1+∆ −(1)
∆
= ∆ + 2
但 ∆可正、可负；
∆ = (2 ) − (1 )是函数值的改变量，可正、
可负，也可为0， 因此平均变化率可正、可负，也可为零
函数的平均变化率为0，并不一定说明函数f(x)没有变化
瞬时变化率
函数 f(x) 在 x = x0 处的 瞬时变化率
是函数 f(x) 从 x0 到 x0 + ∆x 的平均变化率
A.0
B.-1 C.3
D.-6
答案 D
解析
(0+Δ)-(0)
Δ
则切线斜率
=
(Δ)2 -6Δ-0
=Δx-6,
Δ
f(0+x)-f(0)
k= lim
x
Δ→0
= (Δx-6)=-6.
x→0
)
规律方法 求曲线上某点(x0,f(x0))处的割线或切线斜率的步骤
f(x 0 +x)-f(x 0 )
例2 将原油精炼为汽油、柴油、塑胶等各种不同产品，需要对原油进行冷却和加热.
已知在第 x h时，原油的温度（单位：℃）为
= = 2 − 7 + 15(0 ≤ ≤ 8) .
计算第 2 h 与第 6 h 时，原油温度的瞬时变化率，并说明它们的意义.
高二数学ppt课件 导数应用课件13
思考：观察图中的函数y=f(x)的图像，对f′(2)， f′(3)，f(3)-f(2)与0的大小进行排序. 提示：f′(2)，f′(3)是x分别为 2，3时对应图像上点的切线斜率，
f 3 f 2 f 3 f 2 3 2
是图像上x为2和3对应点两点连 线的斜率，故f′(2)＞f(3)-f(2)＞f′(3)＞0.
f (x) 0 如果在某个区间内，函数y=f(x)的导数_________,
减少的 则在这个区间上，函数y=f(x)是_______.
图像表示如下： y
y=f(x)
f '(x)>0
y
y=f(x)
f '(x)<0
o
a
b
x
o a
减少的
b
x
增加的
特别提醒：如果在某个区间内恒有 f (x) 0 ,则 f (x) 为常数.
2.若在区间(a，b)内有f′(x)＞0，且f(a) ≥0， 则在(a，b)内有 ( A ) A.f(x)＞0 B.f(x)＜0
C.f(x)＝0
D.不能确定
3．函数f(x)=xlnx在区间(0，1)上是(
A.单调增函数
C
)
B.单调减函数
1 C.在(0, )上是减函数，在( 1 , 1)上是增函数 e e 1 1 D.在( , 1)上是减函数，在(0, )上是增函数 e e
y
当x∈(-∞,0)时, f (x) 2x 0,
函数y=x2在区间(-∞,0)上是
o
1 1 -1
x
减少的.
思考：通过上面三个实例思考导函数的符号与函数的单 调性之间具有什么关系？
f (x) 0 , 结论：如果在某个区间内，函数y=f(x)的导数_______
第三章 导数及其应用3-4定积分与微积分基本定理(理)
9 4
＝
2 3 1 x ＋ x249 3 2 2
2 3 2 3 1 2 1 1 2 ＝ ×9 － ×4 ＋ ×9 － ×4 ＝45 . 3 2 3 2 2 2 6 1＋cosx (4) cos dx＝ dx 2 2
π 0
2x
π 0
1 0
1 1 3 1 －3 2 (2) x ＋x4dx＝ 3x －3x 1
2 1
2
8 1 1 1 21 ＝ － － ＋ ＝ . 3 3 3×8 3 8
(3)
9 4
1 x(1＋ x)dx＝ (x ＋x)dx 2
b a b a
n －1 i ＝0
分下限与积分上限，区间[a，b]叫做积分区间，函数 f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积 式．此时称函数f(x)在区间[a，b]上可积．
对定义的几点说明：
(1)定积分bf(x)dx是一个常数． a
(2)用定义求定积分的一般方法是： ①分割区间：将区间分为n个小区间，实际应用 中常常是n等分区间[a，b]； ②近似代替：取点ξi∈[xi－1，xi]；
1，xi]上任取一点ζi(i＝1,2，…，n)，作和
式
n f(ζi)Δx，记λ为每个小区间Δxi＝xi＋1－xi i＝ 1
(i＝0,1,2，…，n－1)中的长度最大者，当λ 趋近于0时，所有小区间的长度都趋近于0.
当λ→0时，此和式如果无限接近某个常数，这个 常数叫做函数f(x)在区间[a，b]上的定积分，记作 f(x)dx. 即 f(x)dx＝ lim f (ξi)Δxi，这里a与b分别叫做积 λ→0
在曲线y＝x2(x≥0)上某一点A处作一切线使之 1 与曲线以及x轴所围成的面积为 .则 12 (1)切点A的坐标为________． (2)过切点A的切线方程为________．
＝
2 3 1 x ＋ x249 3 2 2
2 3 2 3 1 2 1 1 2 ＝ ×9 － ×4 ＋ ×9 － ×4 ＝45 . 3 2 3 2 2 2 6 1＋cosx (4) cos dx＝ dx 2 2
π 0
2x
π 0
1 0
1 1 3 1 －3 2 (2) x ＋x4dx＝ 3x －3x 1
2 1
2
8 1 1 1 21 ＝ － － ＋ ＝ . 3 3 3×8 3 8
(3)
9 4
1 x(1＋ x)dx＝ (x ＋x)dx 2
b a b a
n －1 i ＝0
分下限与积分上限，区间[a，b]叫做积分区间，函数 f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积 式．此时称函数f(x)在区间[a，b]上可积．
对定义的几点说明：
(1)定积分bf(x)dx是一个常数． a
(2)用定义求定积分的一般方法是： ①分割区间：将区间分为n个小区间，实际应用 中常常是n等分区间[a，b]； ②近似代替：取点ξi∈[xi－1，xi]；
1，xi]上任取一点ζi(i＝1,2，…，n)，作和
式
n f(ζi)Δx，记λ为每个小区间Δxi＝xi＋1－xi i＝ 1
(i＝0,1,2，…，n－1)中的长度最大者，当λ 趋近于0时，所有小区间的长度都趋近于0.
当λ→0时，此和式如果无限接近某个常数，这个 常数叫做函数f(x)在区间[a，b]上的定积分，记作 f(x)dx. 即 f(x)dx＝ lim f (ξi)Δxi，这里a与b分别叫做积 λ→0
在曲线y＝x2(x≥0)上某一点A处作一切线使之 1 与曲线以及x轴所围成的面积为 .则 12 (1)切点A的坐标为________． (2)过切点A的切线方程为________．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
略解：如图直线 y 2x 3与抛物线 y x 2
的交点坐标为（－1，1）
和（3，9），则
S＝
（ 3 2x＋3－x2 )dx
1
（x 2
3x
x3 3
) |31
32 3
2、求由抛物线 y x 2 4 x 3 及其在点
M的（图0形，的－面3）积和。N（3，0）处的两条y 切线所围成
略解： y / 2x 4
（3/2，3）
则在M、N点、 处的切线方程
分别为 y 4x 3 y 2x 6o
x
S＝
3
2 [(4x 3) (x2 4x 3)]dx
y=－x2+4x-3
0
3
3 [(2x
2
6)
(
x2
4x
3)]dx
9 4
x 3、在曲线y x2
一切线使之与曲线以及
(
x
轴 所0)围上成的的某面点积A为处作1
课题：定积分的应用
我行 我能 我要成功 我能成功
几种常见的曲边梯形面积的计算方法：
(1)曲线 y f (x)(f (x) 0）与直线 x a, x b(a b)
以及x 轴所围成的曲边梯形的面积：S＝
b
f ( x)dx
(2)曲线
y
f (x)(f (x)
0）与直线
x
a,
a
x
b(a
b)
以及x 轴所围成的曲边梯形的面积：S＝ －
y f2(x)
a
y f1( x)
b
平面图形的面积
b
A a [ f2( x) f1( x)]dx
特别注意图形面积与定积分不一定相等,
如函数y sin x x ［０,2］的图像与 x
轴围成的图形的面积为4,而其定积分为0.
1、求直线 y 2x 3与抛物线 y x 2
所围成的图形面积。
知 识 结 构
Ⅰ、导数的概念
Ⅱ、几种常见函数的导数公式
c 0 （c为常数） （xn） nxn1 （n Q） （sin x） cosx ，（cosx） sin x
（ln
x）
1 x
（ex） ex
，（log
a
x）
1 x
log a
e
， （ax） ax ln a
Ⅲ、求导法则
Ⅳ、复合函数求导 Ⅴ、导数的几何意义
b
f ( x)dx
y
ya
a
b
y f (x)
x
b
a
bx
y f (x)
(3)两条曲线 y f ( x)，y g( x)(其中f ( x) g( x)）
与直线 x a, x b(a b)围成的曲边梯形的面积: y
y f (x)
y g(x)
a
b
S＝ b[f (x)－g(x)]dx a
x sin x
x sin x
(4)
y
x
1 2
1
log
3
e (x2
1)
2x log 3 e x2 1
例3、已知f (x) =2x2+3x f (1), f (0)=
解:由已知得: f (x)=4x+3 f (1), ∴ f (1)=4+3 f (1), ∴ f (1)=-2 ∴ f (0)= 4×0+3 f (1)=3×(-2)=-6
解得a=-3
小结： •导数的应用主要表现在：
1. 利用导数的几何意义求切线的斜率；
2. 求函数的单调区间，只要解不等式f(x) ＞0或f(x)＜ 0即可；
3. 求函数f(x)的极值，首先求f `(x),在求f `(x)=0的根， 然后检查方程根左右两侧的导数符号而作出判定；
4. 函数f(x)在［a,b］内的最值求法：①求f(x)在（a,b） 内的极值；②将f(x)的各极值与f(a),f(b)比较，其中 最大的是最大值，最小的为最小值。
x0 2 )dx
x03 12
1 12
x0 1 所以切点坐标与切线方程分别为
A(1,1), y 2x 1
y
y=x2
(另解 :
S
x0 0
x 2dx
1 2
x0 2
x
2 0
x
3 0
1
)
A
12 12
OB C x
小结:求平面图形面积的方法与步骤：
（1）画图,并将图形分割为若干个 曲边梯形； （2）对每个曲边梯形确定其存在 的范围,从而确定积分的上、下限； （3）确定被积函数； （4）求出各曲边梯形的面积和,即 各积分的绝对值的和。
则所求图形的面积为
S＝ 【1 g(y) f (y)]dy 1(4 2 2y )dy
0
0
（4 y 2 2 y log 2 e) |10 4 2 log 2 e
bx
y
y f (x)
a
bx
y g(x)
4、求曲线 y log 2 x与曲线y log 2 (4 x)
x 以及 轴所围成的图形面积。
略解：如图由 y log 2 x 得
x f ( y) 2 y 由 y log 2 (4 x)
得 x g( y) 4 2 y 当 y (0,1) 时，g(y) f (y)
f
' (1)
0
a
1 3
,
b
1 2
单增区间为（-∞，-1/3）和（1，+∞） 单间区间为（-1/3，1）
练习巩固： 设函数y=x3+ax2+bx+c的图象如图所示，且与y=0在 原点相切，若函数的极小值为-4 （1）求a、b、c的值 （2）求函数的单调区间
答案（1）a=-3,b=0,c=0 （2）单增区间为(-∞,0)和(2,+∞)
b
a
f
(x)dx，即即b b aa
nn
ff((xx))ddxxlimlim f n0i1i1
b(xni)aDxfi。(xi
)
定积分的定义：
即
b a
f
( x)dx
lim
n
n i1
b
n
a
f
(xi )
定积分的相关名称：
———叫做积分号， f(x) ——叫做被积函数，
y
y f (x)
f(x)dx —叫做被积表达式，
.试求：切点A的坐标以及切线方程.
12
略解：
y
y=x2
设切点坐标为（x0 , x0 2 )
y / 2x 则切线方程为
A
O
(
x0B,0)
C(x0 , 0) x
2
y 2x0 x x02
切线与x轴的交点坐标为
( x0 ,0) 2
则由题可知有
S
x0
2 x2dx
0
x0 x0
(
x
2
2
2x0 x
（4）y= log 3 (x 2 1)
解(1)y′=
1
(x
1
2) 2
(3x
1)2
x 2 2 (3x 1) 3
2
(3x 1)2 6(3x 1) x 2 2 x2
(2) y 2e2x cos x e2x sin x
(3) y 1 (x sin x) 1 cosx
▪ 解:由已知,函数f (x)过原点(0,0), ∴ f (0) =c=0
∵ f (x)=3x2+2ax+b 且函数f (x)与y=0在原点相切， ∴ f (0)=b=0 即f (x)=x3+ax2
由由已f知(xf)=332xa2+ 2ax4=0,得x1=0,x2=(-2/3)a
即 8 a3 4 a3 4 27 9
bx
平面图形的面积
b
A a f ( x)dx
平面图形的面积
A
b[ a
f2(x)
f1( x)]dx
a
b
y f (x)
平面图形的面积
b
A a f ( x)dx
y f2(x)
பைடு நூலகம்
a b
y f1( x)
平面图形的面积
b
b
A a f2( x)dx a f1( x)dx
b
a [ f2( x) f1( x)]dx
x ———叫做积分变量，
a ———叫做积分下限， b ———叫做积分上限， O a
bx
[a, b] —叫做积分区间。
积分上限
b
f ( x)dx
a
I
n
lim 0 i1
f (xi )Dxi
被
被
积
积分下限
积
积
分
函
表
变
数
达
量
式
定积分的定义：
即
b a
f
( x)dx
lim
n
n i1
b
n
a
f
(xi )
1、求曲边梯形的思想方法是什么？ 2、定积分的几何意义、物理是什么？ 3、微积分基本定理是什么？
求由连续曲线yf(x)对应的曲边梯形面积的方法
(1)分割:在区间[0,1]上等间隔地插入n-1个点,将它等分成
n个小区间:a, x1,x1, x2, xi1, xi , ,xn1,b,
每个小区间宽度⊿x b a
按定积分的定义，有
(1) 由连续曲线yf(x) (f(x)0) ，直线xa、xb及x轴 所围成的曲边梯形的面积为
b
S
f (x)dx；
a
(2) 设物体运动的速度vv(t)，则此物体在时间区间
[a, b]内运动的距离s为
v