《管理运筹学》第二课后习题答案
卫生管理运筹学第二版第二章课后答案

卫生管理运筹学第二版第二章课后答案1、3.高龄产妇中有()都是剖腹产。
[单选题] *A.50%B.60%(正确答案)C.70%D.80%2、92、Ⅲ度烧伤面积达80%的病人,创面处理建议采取(? ?) *A、暴露疗法(正确答案)B、分次实施切痂植皮手术(正确答案)C、功能部位力争恢复功能(正确答案)D、肢体部位采取包扎疗法3、34.不属于全血标本检测的项目的是()[单选题] *A.血常规B.血糖C.肌酐D.脂类(正确答案)4、46. 下列哪项食物不富含维生素A:()[单选题] *A. 动物肝脏B. 全奶C. 豆类(正确答案)D. 水果5、56.使用心电监护最常用于观察的导联是()[单选题] *A.Ⅰ导联B.Ⅱ导联(正确答案)C.Ⅲ导联D.Ⅳ导联6、1.进行口腔护理操作时昏迷、吞咽功能障碍的病人应采取什么体位()[单选题] * A.坐位B.侧卧位(正确答案)C.仰卧位D.头高足低位7、46.乳房发生乳腺癌最常见的部位为(? ) [单选题] *A、乳头部位B、内上象限C、外上象限(正确答案)D、内下象限8、48.对尿失禁患者护理应()*A.加强皮肤与心理护理(正确答案)B.指导患者多饮水,促进排尿反射(正确答案)C.长期尿失禁者可用留置尿管(正确答案)D.可轻轻按摩或热敷下腹部9、381.婴幼儿的1个睡眠周期只有()个小时。
[单选题] *A.1~2(正确答案)B.2~3C.3~4D.4~510、14.尿失禁预防,可进行缩肛锻炼,即做收缩肛门的动作,每天()次左右。
[单选题] *A.20B.30(正确答案)C.40D.5011、37. 成分输血的优点不包括:()[单选题] *A. 一血多用B. 针对性强C. 无须进行交叉配血(正确答案)D. 便于运输和保存12、22.散步一小时可以帮助消耗大约()千卡的能量。
[单选题] *A.200B.300C.400D.500(正确答案)13、15、下列饮食中属于基本饮食的是()[单选题] *A.高热量饮食B.低盐饮食C.半流质饮食(正确答案)D.高纤维饮食14、86.频发室是指每分钟发生室早多于()[单选题] *A. 1次B. 5次(正确答案)C. 10次D. 20次15、73.下列哪类患者的尿液中有烂苹果味: ()[单选题] *A.前列腺炎B.尿道炎C.膀胱炎D.糖尿病酸中毒(正确答案)16、12.关于乳管内乳头状瘤,下列哪一条不正确: ()[单选题] * A.肿瘤小,常不能触及B.多见于经产妇C.可从乳头溢出血性液D.属于良性病变,不会恶变(正确答案)17、33.一般()乳汁充盈最旺盛,是挤母乳的最好时间。
《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社,超详细版

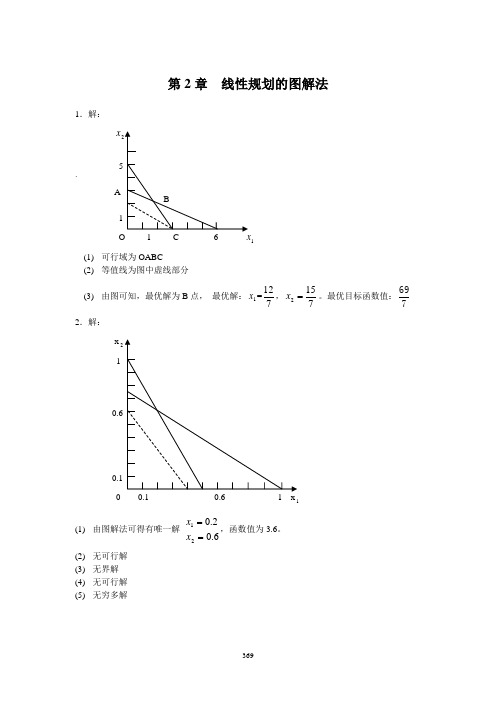
《管理运筹学》第二版习题答案(韩伯棠教授)高等教育出版社第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
《管理运筹学》第2版习题答案_韩伯棠

第一章是没有的第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解 x 1 = 0.2 函数值为 3.6 x 2 = 0.6 b 无可行解 c 无界解 d 无可行解 e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 =3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 30 3x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 = −4 x 1 − 6x 3 − 0s 1 − 0s 2 3x 1 − x 2 − s 1 = 6 x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x '− 2 x '' − 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 702 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 −2x 2 − s 2 = 30 ' ' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 20 3x 1 + 3x 2 − s 2 = 184 x 1 + 9x 2 − s 3 = 36x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
《管理运筹学》课后习题答案

《管理运筹学》课后习题答案第2章线性规划的图解法1.解决方案:X25`a1bo1c6x1可行的区域是oabc等值线为图中虚线部分从图中可以看出,最优解是B点,最优解是x1=121569,x2?。
最优目标函数值:7772.解:x21零点六0.100.10.61x1有唯一解、无可行解、无界解、无可行解和无限解x1?0.2x2?0.6,函数值为3.6。
三百六十九20923有唯一解,函数值为。
83x2?3x1?3.解决方案:(1).标准形式:麦克斯夫?3x1?2x2?0s1?0s2?0s39x1?2x2?s1?303x1?2x2?s2?132x1?2x2?s3?9x1,x2,s1,s2,s3?0(2).标准形式:明夫?4x1?6x2?0s1?0s23x1?x2?s1?6x1?2x2?s2?107x1?6x2?4x1,x2,s1,s2?0(3).标准形式:明夫?x1?2x2?2x2?0s1?0s2“”?3x1?5x2?5x2?s1?七十 '''2x1'?5x2?5x2?503x?2x?2x?s2?30'''x1',x2,x2,s1,s2?0'1'2''2标准形式:麦克斯?10x1?5x2?0s1?0s23x1?4x2?s1?95x1?2x2?s2?8x1,x2,s1,s2?0松弛变量(0,0)的最优解为X1=1,X2=3/23705.解决方案:标准形式:明夫?11x1?8x2?0s1?0s2?0s310x1?2x2?s1?203x1?3x2?s2?184x1?9x2?s3?36x1,x2,s1,s2,s3?0剩余变量(0.0.13)最优解为x1=1,x2=5.6.解决方案:(10)最优解为x1=3,x2=7.(11)1?c1?3(12)2?c2?6(13)x1?6x2?四(14)最优解为x1=8,x2=0.(15)不变化。
《管理运筹学》课后习题答案
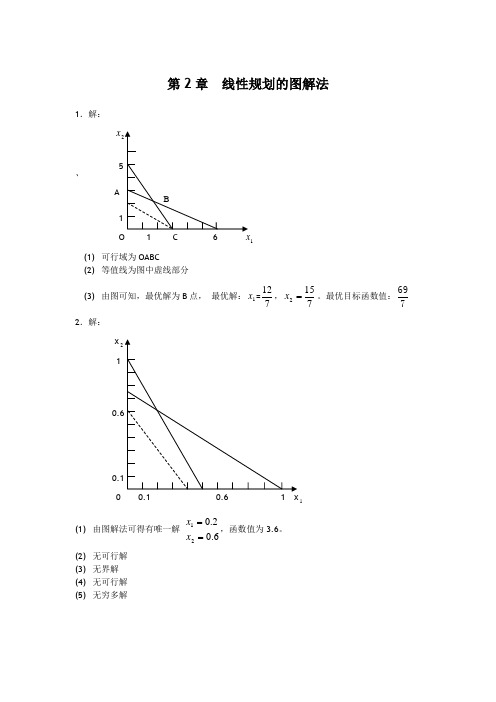
min f=25x11+20x12+30x21+24x22
s.t.x11+x12+x21+x22 2000
x11+x12=x21+x22
约束条件2:年回报额增加1个单位,风险系数升高2.167;
约束条件3:基金B的投资额增加1个单位,风险系数不变。
(3)约束条件1的松弛变量是0,表示投资额正好为1200000;约束条件2的剩余变量是0,表示投资回报率正好是60000;约束条件3的松弛变量为700000,表示投资B基金的投资额为370000。
总成本最小为264元,能比第一问节省:320-264=56元。
3.解:设生产A、B、C三种产品的数量分别为x1,x2,x3,则可建立下面的
数学模型:
max z=10 x1+12x2+14x3
s.t. x1+1.5x2+4x3 2000
2x1+1.2x2+x3 1000
x1 200
x2 250
x3 100
3.解:
(1).式:
4.解:
标准形式:
松弛变量(0,0)
最优解为 =1,x =3/2.
5.解:
标准形式:
剩余变量(0.0.13)
最优解为x1=1,x2=5.
6.解:
(1)最优解为x1=3,x2=7.
(2)
(3)
(4)
(5)最优解为x1=8,x2=0.
(6)不变化。因为当斜率 ,最优解不变,变化后斜率为1,所以最优解不变.
(5)约束条件1的右边值在300000到正无穷的范围内变化,对偶价格仍为0.1;
《管理运筹学》第二版习题答案(韩伯棠教授

x2+x3+x4+x5+1 ≥ 3
x3+x4+x5+x6+2 ≥ 3
x4+x5+x6+x7+1 ≥ 6
x5+x6+x7+x8+2 ≥ 12
x6+x7+x8+x9+2 ≥ 12
x7+x8+x9+x10+1 ≥ 7
x8+x9+x10+x11+1 ≥ 7
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥ 0
第
3章线性规划问题的计算机求解
1、解:
a x1 =
150 x2 =
70 目标函数最优值
103000
b 1,3使用完 2,4没用完 0,330,0,15
c 50,0,200,0
含义: 1车间每增加
1工时,总利润增加
50元
3车间每增加
1工时,总利润增加
约束条件
2:年回报额增加
1个单位,风险系数升高
2.167
c约束条件
1的松弛变量是
0,约束条件
2的剩余变量是
0
约束条件
3为大于等于,故其剩余变量为
700000
d当
c2不变时,
c1在
3.75到正无穷的范围内变化,最优解不变
当
c1不变时,
i=1 i=1
S.T
不变
8 、解:
a 模型:
min f =
8xa +
3xb
50xa +100xb ≤
1200000
5xa +
4xb ≥
60000
100xb ≥
300000
xa , xb ≥
管理运筹学第二章课后答案

管理运筹学(谢家平)第二章课后答案1 解maxZ=200x1+240x260x1+50x2≤420030x1+40x2≤300060x1+50x2≤4500化成标准型为:maxZ=200x1+240x2+0x3+0x4+0x560x1+50x2+x3=420030x1+40x2+x4=300060x1+50x2+x5=4500**********************最优解如下*************************目标函数最优值为: 18400变量最优解相差值------- -------- --------x1 20 0x2 60 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .8892 0 4.8893 300 0目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 180 200 288x2 166.667 240266.667常数项数范围:约束下限当前值上限------- -------- -------- --------1 3750 4200 45002 2100 3000 33603 4200 4500 无上限最优生产方案是生产甲产品20,生产乙产品60。
x3=0,x4=0,x5=300说明:生产甲乙产品的材料为瓶颈材料增加材料会增加甲乙二设备D为富余设备。
因为甲产品上升100大于88所以甲需要调整,而乙产品下降的60小于73.33所以不需要调整。
由表可知非紧缺资源最多可以减少300,紧缺资源分别可以增加300,360。
2 设项目第一二三年年初投资为x1,x5x6;项目I第一年年初投资x2项目III第二年年初投资为x3项目IV第三年年初投资为x4MaxZ=0.2x1+0.5x2+0.6x3+0.4x4+0.2x5+0.2x6+30X1+X2≤30X2≤20X5+x3≤30—(x1+x2)+1.2x1X3≤15X6+x4≤30-(x1+x2)+1.2x1-x5-x3+1.5x2X4≤10X1,x2,x3,x4,x5,x6≥0**********************最优解如下*************************目标函数最优值为: 27.5变量最优解相差值------- -------- --------x1 12.5 0x2 17.5 0x3 15 0x4 10 0x5 0 .3x6 16.25 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .32 2.5 03 0 .34 0 .15 0 .26 0 .2目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 .08 .2 .56x2 .14 .5 .62x3 .5 .6 无上限x4 .2 .4 无上限x5 无下限.2 .5x6 0 .2 .28常数项数范围:约束下限当前值上限------- -------- -------- --------1 15 30 452 17.5 20 无上限3 9 30 334 12 15 285 13.75 30 无上限6 0 10 26.25项目一一二三年年初投资为12.5, 0,16.25项目二第一年初投资为17.5项目三第二年年初投资为15项目四年初投资为10 万元3设五种家具分别为x1,x2,x3,x4,x5。
《管理运筹学》第二课后习题答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学第二版习题答案

12-2《管理运筹学》课后习题详解 第2章 线性规划的图解法1. ( 1)可行域为0, 3, A ,3围成的区域。
(2) 等值线为图中虚线所示。
(3) 如图,最优解为 A 点(12/7,15/7 ),对应最 优目标函数值 Z=69/7。
2.( 1)有唯一最优解 A 点,对应最优目标函数 值 Z=3.6。
(2)无可行解。
(3)有无界解。
40.7 0-33X 1+ X2(4)无可行解。
9y -F 2.r, + 6 = 30 3x x+2X2 + s2 =13 2x{—2xi+6=9 gx”片宀宀二0max f = 一4形—— 0町—Os2(5)无可行解。
X22max最优解A点最优函数值3. (1)标准形式(2)标准形式Xj + 2X2 H-S2 = 107,v:—6.v* = 4M , .Y2 , % 出> O(3)标准形式|!_|_fifmax f = —x 1 + 2 屯—2 込—0® — 0^2—3x x * 5X 2 — 5X 2 + s x = 70 2x x — 5X 2 + 5X 2 = 50 3xj + 2X 2 — 2X 2 —=305x ;,歩1 .s 2 土 0max z = 10.^! + 5.Y 2 \ 0^t 1 0©3x 】十 4X 2 + S J = 95.巧 +2.Y 2 -b >s 2 = 8 x t ,x 2 ^s lr>s 2 > 04.解: (1)标准形式求解:3X 〔 4X 2 9 5X 〔 2X 28X , 1 X 21.5S , S 25.标准形式:x , x 2 6 x , 3.6 S 3 S 2 0 4x , 9x 2 16x 2 2.4s , 11.27. 模型: (1) X 1=150, X 2=150;最优目标函数值 Z=103000。
(2) 第2、4车间有剩余。
剩余分别为: 330、15,均为松弛变量。
《管理运筹学》(第二版)课后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划线性规划的三要素是什么答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型松弛变量和剩余变量的管理含义是什么答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
.解:标准化.列出单纯形表412b02[8]2 /80868 /641241/41/81/8]/8(1/4/(1/813/265/4/43/4(13/2/(1/4 0-1/23/21/222806-221-12-502故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
管理运筹学后习题参考答案汇总

《管理运筹学》(第二版)课后习题参考答案第1章线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误?答:(1)唯一最优解:只有一个最优点;(2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s.t.解:标准化s.t .列出单纯形表4 12b0 2 [8]2/80 8 68/64 1 241/41/8 1/8] /8(1/4/(1/813/265/4 /4 3/4(13/2/(1/4-1/23/21/22 2 80 6 -22 1-12-52故最优解为,即,此时最优值为.6.表1—15中给出了求极大化问题的单纯形表,问表中为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以代替基变量;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
《管理运筹学》课后习题参考标准答案

《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么就是线性规划?线性规划的三要素就是什么?答:线性规划(Linear Programming,LP)就是运筹学中最成熟的一个分支,并且就是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,就是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量就是决策问题待定的量值,取值一般为非负;约束条件就是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数就是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解; (3)无界解:可行域无界,目标值无限增大;(4)没有可行解:线性规划问题的可行域就是空集。
当无界解与没有可行解时,可能就是建模时有错。
3.什么就是线性规划的标准型?松弛变量与剩余变量的管理含义就是什么? 答:线性规划的标准型就是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不就是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
管理运筹学第二章习题答案

第二章补充作业习题:用大M 法和两阶段法求解下面LP 问题:⎪⎪⎩⎪⎪⎨⎧≥≥+-≥-+=0,3232s.t.42min 21212121x x x x x x x x z解: 标准化为⎪⎪⎩⎪⎪⎨⎧≥=-+-=----='0,,,3232s.t.42max 432142132121x x x x x x x x x x x x z(1)大M 法引入人工变量65,x x ,得到下面的LP 问题⎪⎪⎪⎪⎨⎧=≥=+-+-=+------=6,,1,03232s.t.42max 642153216521 j x x x x x x x x x Mx Mx x x z j因为人工变量6x 为4>0,所以原问题没有可行解。
(2)两阶段法:增加人工变量65,x x ,得到辅助LP 问题⎪⎪⎩⎪⎪⎨⎧=≥=+-+-=+----=6,,1,03232s.t.max 6421532165 j x x x x x x x x x x x g j初始表因为辅助LP 问题的最优值为4>0,所以原问题没有可行解。
习2.1 解:设1x 为每天生产甲产品的数量,2x 为每天生产乙产品的数量,则数学模型为,5183202..200300max 211212121≥≤≤+≤++=x x x x x x x t s x x z最优解为:()TX 4.8,2.3*=,最优值为:z = 2640。
(1)最优解为:()TX 5.0,5.1*=,最优值为:z = 4.5。
(2)无可行解有无穷多最优解,其中一个为:TX⎪⎭⎫⎝⎛=0,310*1,另一个为:()TX10,0*2=,最优值为:z = 20。
(4)无界解解:A B资源限额会议室115桌子3212货架3618工资2522设1x为雇佣A的天数,2x为雇佣B的天数,则数学模型为,186312235..2225min2121212121≥≥+≥+≥++=xxxxxxxxt sxxz最优解为:()TX3,2*=,最优值为:z = 116。
《管理运筹学》第二版习题答案(韩伯棠教授)1

3第 2 章 线性规划的图解法1、解:x 26A B1O 01C6x 1a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O0.1 0.6x 1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
管理运筹学课后习题答案
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 21(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》(第二版)课后习题参考答案第1章 线性规划(复习思考题)1.什么是线性规划?线性规划的三要素是什么?答:线性规划(Linear Programming ,LP )是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
建立线性规划问题要具备三要素:决策变量、约束条件、目标函数。
决策变量是决策问题待定的量值,取值一般为非负;约束条件是指决策变量取值时受到的各种资源条件的限制,保障决策方案的可行性;目标函数是决策者希望实现的目标,为决策变量的线性函数表达式,有的目标要实现极大值,有的则要求极小值。
2.求解线性规划问题时可能出现几种结果,哪种结果说明建模时有错误? 答:(1)唯一最优解:只有一个最优点; (2)多重最优解:无穷多个最优解;(3)无界解:可行域无界,目标值无限增大; (4)没有可行解:线性规划问题的可行域是空集。
当无界解和没有可行解时,可能是建模时有错。
3.什么是线性规划的标准型?松弛变量和剩余变量的管理含义是什么?答:线性规划的标准型是:目标函数极大化,约束条件为等式,右端常数项0≥i b ,决策变量满足非负性。
如果加入的这个非负变量取值为非零的话,则说明该约束限定没有约束力,对企业来说不是紧缺资源,所以称为松弛变量;剩余变量取值为非零的话,则说明“≥”型约束的左边取值大于右边规划值,出现剩余量。
4.试述线性规划问题的可行解、基础解、基可行解、最优解的概念及其相互关系。
答:可行解:满足约束条件0≥=X b AX ,的解,称为可行解。
基可行解:满足非负性约束的基解,称为基可行解。
可行基:对应于基可行解的基,称为可行基。
最优解:使目标函数最优的可行解,称为最优解。
最优基:最优解对应的基矩阵,称为最优基。
它们的相互关系如右图所示:5.用表格单纯形法求解如下线性规划。
s .t . ⎪⎩⎪⎨⎧≥≤++≤++0,,86238321321321x x x x x x x x x解:标准化 32124m a xx x x Z ++= s .t . ⎪⎩⎪⎨⎧≥=+++=+++0,,,,862385432153214321x x x x x x x x x x x x x 列出单纯形表故最优解为T X )6,0,2,0,0(*=,即2,0,0321===x x x ,此时最优值为4*)(=X Z . 6.表1—15中给出了求极大化问题的单纯形表,问表中d c c a a ,,,,2121为何值及变量属于哪一类型时有:(1)表中解为唯一最优解;(2)表中解为无穷多最优解之一;(3)下一步迭代将以1x 代替基变量5x ;(4)该线性规划问题具有无界解;(5)该线性规划问题无可行解。
表1—15 某极大化问题的单纯形表解:(1)0,0,021<<≥c c d ;(2)中至少有一个为零)(2121,0,0,0c c c c d ≤≤≥; (3)22134,0,0a d a c >>>; (4)0,012≤>a c ;(5)1x 为人工变量,且1c 为包含M 的大于零的数,234a d >;或者2x 为人工变量,且2c 为包含M 的大于零的数,0,01>>d a .7.用大M 法求解如下线性规划。
s .t . ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≤++0,,101632182321321321321x x x x x x x x x x x x解:加入人工变量,进行人造基后的数学模型如下:s .t . ⎪⎪⎩⎪⎪⎨⎧=≥=+++=+++=+++)6,,2,1(0101632182632153214321 i x x x x x x x x x x x x x i列出单纯形表故最优解为T X )0,0,4,0,4,6(*=,即0,4,6321===x x x ,此时最优值为42*)(=X Z . 8.A ,B ,C 三个城市每年需分别供应电力320,250和350单位,由I ,II 两个电站提供,它们的最大可供电量分别为400单位和450单位,单位费用如表1—16所示。
由于需要量大于可供量,决定城市A 的供应量可减少0~30单位,城市B 的供应量不变,城市C 的供应量不能少于270单位。
试建立线性规划模型,求将可供电量用完的最低总费用分配方案。
表1—16 单位电力输电费(单位:元)解:设ij x 为“第i 电站向第j 城市分配的电量”(i =1,2; j =1,2,3),建立模型如下:s .t . ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥≤+≥+=+≤+≥+=++=++3,2,1;2,1,035027025032029045040023132313221221112111232221131211j i x x x x x x x x x x x x x x x x x ij9.某公司在3年的计划期内,有4个建设项目可以投资:项目I 从第一年到第三年年初都可以投资。
预计每年年初投资,年末可收回本利120%,每年又可以重新将所获本利纳入投资计划;项目II 需要在第一年初投资,经过两年可收回本利150%,又可以重新将所获本利纳入投资计划,但用于该项目的最大投资不得超过20万元;项目III 需要在第二年年初投资,经过两年可收回本利160%,但用于该项目的最大投资不得超过15万元;项目IV 需要在第三年年初投资,年末可收回本利140%,但用于该项目的最大投资不得超过10万元。
在这个计划期内,该公司第一年可供投资的资金有30万元。
问怎样的投资方案,才能使该公司在这个计划期获得最大利润?解:设)1(i x 表示第一次投资项目i ,设)2(i x 表示第二次投资项目i ,设)3(i x 表示第三次投资项目i ,(i =1,2,3,4),则建立的线性规划模型为s .t . ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤≤≤----+++=+--+≤+≤+4,3,2,1,0,,101520302.15.12.1302.130)3()2()1()1(4)1(3)1(2)1(3)2(1)1(2)1(1)1(1)1(2)2(1)1(4)3(1)1(2)1(1)1(1)1(3)2(1)1(2)1(1i x x x x x x x x x x x x x x x x x x x x x x i i i 通过LINGO 软件计算得:44,12,0,20,10)2(1)2(1)1(3)1(2)1(1=====x x x x x . 10.某家具制造厂生产五种不同规格的家具。
每种家具都要经过机械成型、打磨、上漆几道重要工序。
每种家具的每道工序所用的时间、每道工序的可用时间、每种家具的利润由表1—17给出。
问工厂应如何安排生产,使总利润最大?表1—17 家具生产工艺耗时和利润表解:设i x 表示第i 种规格的家具的生产量(i =1,2,…,5),则s .t . ⎪⎪⎩⎪⎪⎨⎧=≥≤++++≤++++≤++++5,,2,1,0280034332395046534360032643543215432154321 i x x x x x x x x x x x x x x x x i通过LINGO 软件计算得:3181,642,0,254,38,054321======Z x x x x x .11.某厂生产甲、乙、丙三种产品,分别经过A ,B ,C 三种设备加工。
已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表2—10所示。
表1—18 产品生产工艺消耗系数(1)建立线性规划模型,求该厂获利最大的生产计划。
(2)产品丙每件的利润增加到多大时才值得安排生产?如产品丙每件的利润增加到6,求最优生产计划。
(3)产品甲的利润在多大范围内变化时,原最优计划保持不变?(4)设备A 的能力如为100+10q ,确定保持原最优基不变的q 的变化范围。
(5)如合同规定该厂至少生产10件产品丙,试确定最优计划的变化。
解:(1)设321,,x x x 分别表示甲、乙、丙产品的生产量,建立线性规划模型s .t . ⎪⎪⎩⎪⎪⎨⎧≥≤++≤++≤++0,,3006226005410100321321321321x x x x x x x x x x x x标准化得s .t . ⎪⎪⎩⎪⎪⎨⎧≥=+++=+++=+++0,,,,,3006226005410100654321632153214321x x x x x x x x x x x x x x x x x x列出单纯形表故最优解为0,3/200,3/100321===x x x ,又由于321,,x x x 取整数,故四舍五入可得最优解为0,67,33321===x x x ,732max =Z .(2)产品丙的利润3c 变化的单纯形法迭代表如下:要使原最优计划保持不变,只要0333≤-=c σ,即67.6363≈≤c .故当产品丙每件的利润增加到大于6.67时,才值得安排生产。
如产品丙每件的利润增加到6时,此时6<6.67,故原最优计划不变。
(3)由最末单纯形表计算出0611,03210,0611151413≤-=≤+-=≤--=c c c σσσ,解得1561≤≤c ,即当产品甲的利润1c 在]15,6[范围内变化时,原最优计划保持不变。
(4)由最末单纯形表找出最优基的逆为⎪⎪⎪⎭⎫⎝⎛---=-10206/13/206/13/51B ,新的最优解为 解得54≤≤-q ,故要保持原最优基不变的q 的变化范围为]5,4[-.(5)如合同规定该厂至少生产10件产品丙,则线性规划模型变成s .t . ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤++≤++≤++0,,1030062260054101003213321321321x x x x x x x x x x x x x通过LINGO 软件计算得到:708,10,58,32321====Z x x x .第2章 对偶规划(复习思考题)1.对偶问题和对偶向量(即影子价值)的经济意义是什么?答:原问题和对偶问题从不同的角度来分析同一个问题,前者从产品产量的角度来考察利润,后者则从形成产品本身所需要的各种资源的角度来考察利润,即利润是产品生产带来的,同时又是资源消耗带来的。
对偶变量的值i y 表示第i 种资源的边际价值,称为影子价值。
可以把对偶问题的解Y 定义为每增加一个单位的资源引起的目标函数值的增量。
2.什么是资源的影子价格?它与相应的市场价格有什么区别?答:若以产值为目标,则i y 是增加单位资源i 对产值的贡献,称为资源的影子价格(Shadow Price )。
即有“影子价格=资源成本+影子利润”。
