专题01 三角形全等-手拉手模型(解析版)-初中数学几何专题之冲刺2022年满分突破大全
专题 全等三角形模型——手拉手模型与半角模型(解析版)

全等三角形模型——手拉手模型与半角模型手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点,如图所示结论:(1)△ABD ≌△AEC(2)∠α+∠BOC=180°(3)OA 平分∠BOC变形:1.如图,以ABC D 的边AB ,AC 为边,向外作等边ABD D 和等边ACE D ,连接BE ,CD 相交于点F .(1)求证:DC BE =.(2)求DFE Ð的度数.(3)求证:FA 平分DFE Ð.(4)求证:DF AF BF =+.【分析】(1)根据等边三角形的性质和全等三角形的判定和性质得出DC BE =即可;(2)根据全等三角形的性质和角的关系得出120DFE Ð=°即可;(3)过点A 作AP DC ^于P ,AQ BE ^于Q ,根据三角形面积公式和角平分线的性质解答即可;(4)在DF 上截取DM BF =,连接AM ,根据全等三角形的判定和性质解答即可.【解答】证明:(1)ABD D Q 和ACE D 是等边三角形,AD AB \=,AE AC =,60DAB EAC AEC ACE Ð=Ð=Ð=Ð=°,DAB BAC EAC BAC \Ð+Ð=Ð+Ð,即DAC BAE Ð=Ð,在DAC D 与BAE D 中,AD AB DAC BAE AC AE =ìïÐ=Ðíï=î,()DAC BAE SAS \D @D ,DC BE \=;(2)DAC BAE D @D Q ,ADF ABF \Ð=Ð,AGD FGB Ð=ÐQ ,60BFG DAG \Ð=Ð=°,120DFE \Ð=°;(3)过点A 作AP DC ^于P ,AQ BE ^于Q ,DAC BAE D @D Q ,\1122DAC BAE S DC AP S BE AQ D D =×==×,DC BE =Q ,AP AQ \=,AP DC ^Q ,AQ BE ^,FA \平分DFE Ð;(4)在DF 上截取DM BF =,连接AM ,在ADM D 与ABF D 中,AD AB ADM ABF DM BF =ìïÐ=Ðíï=î,()ADM ABF SAS \D @D ,AM AF \=,DAM BAF Ð=Ð,60DAB Ð=°Q ,60DAM MAG \Ð+Ð=°,60BAF MAG \Ð+Ð=°,即60MAF Ð=°,AMF \D 是等边三角形,MF AF \=,DF DM MF AF BF \=+=+.2.等边ABD D 和等边BCE D 如图所示,连接AE 与CD ,证明:(1)AE DC =;(2)AE 与DC 的夹角为60°;(3)AE 延长线与DC 的交点设为H ,求证:BH 平分AHC Ð.【分析】(1)根据ABD D 和BCE D 都是等边三角形,即可得到()ABE DBC SAS D @D ,进而得出AE DC =;(2)根据全等三角形的性质以及三角形内角和定理,即可得到ADH D 中,60AHD Ð=°,进而得到AE 与DC 的夹角为60°;(3)过B 作BF DC ^于F ,BG AH ^于G ,根据全等三角形的面积相等,即可得到BG BF =,再根据BF DC ^于F ,BG AH ^于G ,可得BH 平分AHC Ð.【解答】证明:(1)ABD D Q 和BCE D 都是等边三角形,AB DB \=,EB CB =,ABD EBC Ð=Ð,ABE DBC \Ð=Ð,在ABE D 和DBC D 中,AB DB ABE DBC EB CB =ìïÐ=Ðíï=î,()ABE DBC SAS \D @D ,AE DC \=;(2)ABE DBC D @D Q ,BAE BDC \Ð=Ð,又120BAE HAD ADB Ð+Ð+Ð=°Q ,120BDC HAD ADB \Ð+Ð+Ð=°,ADH \D 中,18012060AHD Ð=°-°=°,即AE 与DC 的夹角为60°;(3)如图,过B 作BF DC ^于F ,BG AH ^于G ,ABE DBC D @D Q ,ABE DBC S S D D \=,即1122AE BG DC BF ´=´,又AE DC =Q ,BG BF \=,又BF DC ^Q 于F ,BG AH ^于G ,BH \平分AHC Ð.3.(2021春•宁阳县期末)如图两个等腰直角ADC D 与EDG D ,90ADC EDG Ð=Ð=°,连接AG ,CE 交于点H .证明:(1)AG CE =;(2)AG CE ^.【分析】(1)由两个等腰直角ADC D 与EDG D ,可得AD CD =,DG DE =,90ADC GDE Ð=Ð=°,进而得出ADG CDE Ð=Ð,然后由SAS 即可判定ADG CDE D @D ,进而可得结论;(2)根据全等三角形的性质则可证得DAG DCE Ð=Ð,再根据直角三角形的两锐角互余进而证出90CHA Ð=°即可得解.【解答】解:(1)证明:ADC D Q 与EDG D 是等腰直角三角形,AD CD \=,DG DE =,且90ADC GDE Ð=Ð=°,ADC CDG GDE CDG \Ð+Ð=Ð+Ð,即ADG CDE Ð=Ð,在ADG D 与CDE D 中,AD CD ADG CDEDG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,AG CE \=;(2)证明:设CD 与AG 相交于点P ,由(1)知,ADG CDE D @D,DAG DCE \Ð=Ð,90ADC Ð=°Q ,90DAG APD \Ð+Ð=°,APD CPH Ð=ÐQ ,90DCE CPH \Ð+Ð=°,90CHP \Ð=°,AG CE \^.4.如图,两个等腰Rt ADC D 与Rt EDG D ,连接AG ,CE 交于点H ,连接HD .求证:AHD EHD Ð=Ð.【分析】由“SAS ”可证ADG CDE D @D ,可得AG CE =,ADG CDE S S D D =,由面积公式可得DN DM =,由角平分线的判定定理可得结论.【解答】证明:如图,过点D 作DN AG ^于N ,DM CE ^于M ,90ADC GDE Ð=Ð=°Q ,ADG EDC \Ð=Ð,在ADG D 和CDE D 中,AD CD ADG CDE DG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,AG CE \=,ADG CDE S S D D =,\1122AG DN CE DM ´´=´´,DN DM \=,又DN AG ^Q ,DM CE ^,AHD EHD \Ð=Ð.5.如图,两个正方形ABCD 和DEFG ,连接AG 与CE ,二者相交于H .问:(1)求证:ADG CDE D @D .(2)AG 与CE 的关系?并说明理由.(3)求证:HD 平分AHE Ð.【分析】(1)由四边形ABCD 与DEFG 是正方形,可得AD CD =,90ADC GDE Ð=Ð=°,进而得出ADG CDE Ð=Ð,DG DE =,然后由SAS 即可判定ADG CDE D @D ;(2)根据全等三角形的性质则可证得AG CE =,DAG DCE Ð=Ð,进而证出90CHA Ð=°即可;(3)根据全等三角形的性质和三角形的面积解答即可.【解答】(1)证明:Q 四边形ABCD 和四边形DEFG 是正方形,AD CD \=,DG DE =,且90ADC GDE Ð=Ð=°,ADG CDE \Ð=Ð,在ADG D 与CDE D 中,AD CD ADG CDE DG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,(2)解:AG CE =,AG CE ^,理由如下:由(1)得:ADG CDE D @D ,AG CE \=,DAG DCE Ð=Ð,DCE CHA DAG ADC Ð+Ð=Ð+ÐQ ,90CHA ADC \Ð=Ð=°,AG CE \^;(3)证明:过点D 作DM AG ^于M ,DN CE ^于N ,如图:ADG CDE D @D Q ,DCE ADG S S D D \=,\1122CE DN AG DM ´´=´´,DM DN \=,MD AG ^Q ,DN CE ^,DH \平分AHE Ð.6.(2021秋•南岗区校级期中)已知:AB AC =,AD AE =,BAC DAE Ð=Ð.(1)如图1,求证:BD CE =;(2)如图2,当60BAC Ð=°时,BD 、CE 交于点P ,连接PA ,求证:PB PC PA -=;(3)如图3,在(2)的条件下,过E 作EH PA ^于H ,在PE 上取点F ,连接FH 并延长至G ,使GH FH =,连接GE ,若2HGE HEG Ð=Ð,求EHF Ð的度数.【分析】(1)证明BAD CAE D @D 即可;(2)作AF BD ^,AG CE ^,截取PH PA =,证明ABF ACG D @D ,可推出60APF APG Ð=Ð=°,从而可证ACH ABP D @D ,进而得证;(3)作HQ CE ^于Q ,作HM GH =交GE 于M ,作MN AE ^于N ,证明HQF ENM D @D ,可推出15AEG Ð=°,进而求得结果.【解答】(1)证明:如图1,BAC DAE Ð=ÐQ ,BAC CAD DAE CAD \Ð+Ð=Ð+Ð,BAD CAE \Ð=Ð,AB AC =Q ,AD AE =,()BAD CAE SAS \D @D ,BD CE \=;(2)证明:如图2,设AC 与PB 交于I ,作AF BD ^于F ,AG CE ^于G ,在PE 上截取PH PA =,90AFB AGC \Ð=Ð=°,由(1)知:BAD CAE D @D ,B C \Ð=Ð,PIC AIB Ð=ÐQ ,60CPF BAC \Ð=Ð=°,AB AC =Q ,()AFB AGC AAS \D @D ,AF AG \=,11(180)(18060)6022APF APG CPF \Ð=Ð=°-Ð=°-°=°,PAH \D 是等边三角形,60AHC \Ð=°,AHC APB \Ð=Ð,()ABP ACH AAS \D @D ,PB CH PC PH PC PA \==+=+,即:PB PC PA -=;(3)解:如图3,作HQ CE ^于Q ,作HM GH =交GE 于M ,作MN AE ^于N ,90HQF MNE \Ð=Ð=°,AMG G Ð=Ð,2G AEG Ð=ÐQ ,2AMG AEG \Ð=Ð,AMG AEG EHM Ð=Ð+ÐQ ,AEG EHM \Ð=Ð,MH ME \=,12EN AN EH \==,GH FH =Q ,ME FH \=,PH HE ^Q ,90PHE \Ð=°,由(2)知:60APF Ð=°,30HEP \Ð=°,12HQ EH \=,HQ NE \=,()HQF ENM HL \D @D ,AEG QHF \Ð=Ð,EHF G AEG Ð=Ð+ÐQ ,3FHE AEG \Ð=Ð,4QHE QHF FHE AEG \Ð=Ð+Ð=Ð,90HQE \Ð=°,30HEP Ð=°,60HQE \Ð=°,460AEG \Ð=°,15AEG \Ð=°,345EHF AEG \Ð=Ð=°.7.(2021秋•天河区期末)ABC D 是等边三角形,点D 是AC 边上动点,(030)CBD ααÐ=°<<°,把ABDD 沿BD 对折,得到△A BD ¢.(1)如图1,若15α=°,则CBA Т= .(2)如图2,点P 在BD 延长线上,且DAP DBC αÐ=Ð=.①试探究AP ,BP ,CP 之间是否存在一定数量关系,猜想并说明理由.②若10BP =,CP m =,求CA ¢的长.(用含m 的式子表示)【分析】(1)由ABC D 是等边三角形知,60ABC Ð=°,由15CBD αÐ==°,知A BD ABD ABC α¢Ð=Ð=Ð-,2602CBA A BD ABC ααα¢¢Ð=Ð-=Ð-=°-,代入α值即可;(2)①连接CP ,在BP 上取一点P ¢,使BP AP ¢=,根据SAS 证△BP C APC ¢@D ,得CP CP ¢=,再证CPP ¢D 是等边三角形,即可得出BP AP CP =+;②先证180BCP BCA ¢Ð+Ð=°,即A ¢、C 、P 三点在同一直线上,得出PA PC CA ¢¢=+,根据SAS 证ADP D @△A DP ¢,得出A P AP ¢=,即可求出CA ¢的值.【解答】解:(1)ABC D Q 是等边三角形,60ABC \Ð=°,CBD αÐ=Q ,A BD ABD ABC α¢\Ð=Ð=Ð-,2602CBA A BD ABC ααα¢¢\Ð=Ð-=Ð-=°-,15α=°Q ,6021530CBA ¢\Ð=°-´°=°,故答案为:30°;(2)①BP AP CP =+,理由如下:连接CP ,在BP 上取一点P ¢,使BP AP ¢=,ABC D Q 是等边三角形,60ACB \Ð=°,BC AC =,DAP DBC αÐ=Ð=Q ,\△()BP C APC SAS ¢@D ,CP CP ¢\=,BCP ACP ¢Ð=Ð,60PCP ACP ACP BCP ACP ACB ¢¢¢¢\Ð=Ð+=Ð+Ð=Ð=°,CP CP ¢=Q ,CPP ¢\D 是等边三角形,60CPB \Ð=°,PP CP ¢=,BP BP PP AP CP ¢¢\=+=+,即BP AP CP =+;②如下图,由①知,60BPC Ð=°,180********BCP BPC PBC αα\Ð=°-Ð-Ð=°-°-=°-,由(1)知,602CBA α¢Ð=°-,由折叠知,BA BA ¢=,BA BC =Q ,BA BC ¢\=,11(180)[180(602)]6022BCA CBA αα¢¢\Ð=°-Ð=°-°-=°+,12060180BCP BCA αα¢\Ð+Ð=°-+°+=°,\点A ¢、C 、P 在同一直线上,即PA PC CA ¢¢=+,由折叠知,BA BA ¢=,ADB A DB ¢Ð=Ð,180180ADB A DB ¢\°-Ð=°-Ð,ADP A DP ¢\Ð=Ð,DP DP =Q ,ADP \D @△()A DP SAS ¢,A P AP ¢\=,由①知,BP AP CP =+,10BP =Q ,CP m =,10AP BP CP m \=-=-,10A P AP m ¢\==-,10102CA A P CP m m m ¢¢\=-=--=-.半角模型图形中,往往出现90°套45°的情况,或者120°套60°的情况。
专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)(解析版)

专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。
3)双等腰三角形型条件:△ABC 和△DCE 均为等腰三角形,C 为公共点;连接BE ,AD 交于点F 。
结论:①△ACD ≌△BCE ;②BE =AD ;③∠ACM =∠BFM ;④CF 平分∠AFD 。
4)双正方形形型条件:△ABCFD 和△CEFG 都是正方形,C 为公共点;连接BG ,ED 交于点N 。
结论:①△△BCG ≌△DCE ;②BG =DE ;③∠BCM =∠DNM=90°;④CN 平分∠BNE 。
例1.(2022·黑龙江·中考真题)ABC V 和ADE V 都是等边三角形.(1)将ADE V 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE V 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE V 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC+=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,PA =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明CAP BAF ≌△△(SAS ),得CAP BAF Ð=Ð,AF AP =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明BAP CAF ≌△△(SAS ),得出CAF BAP Ð=Ð,AP AF =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∵△ABC 是等边三角形,∴AB =AC ,∵点P 与点A 重合,∴PB =AB ,PC =AC ,PA =0,∴PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC=+证明:在BP 上截取BF CP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AC =AB ,CP =BF , ∴CAP BAF ≌△△(SAS ),∴CAP BAF Ð=Ð,AF AP =,∴CAP CAF BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AB =AC ,BP =CF ,∴BAP CAF ≌△△(SAS ),∴CAF BAP Ð=Ð,AP AF =,∴BAF BAP BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.例2.(2023·湖南·长沙市八年级阶段练习)如图1,在Rt △ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE .(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长;(3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.例3.(2023·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B 重合时,如图2,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论.【详解】解:(1)CD 2+DB 2=2DF 2证明:∵DF =EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF = 连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =,CF AB ^,即90CFB Ð=° ∴45FCB FBC Ð=Ð=°,90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =,45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2 证明:连接CF 、BE∵CF =BF ,DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ,∠DCF =∠EBF =135°∵∠EBD =∠EBF -∠FBD =135°-45°=90° 在Rt △DBE 中,BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例4.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC V 和ADE V 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE V 均为等腰直角三角形,90ACB DCE Ð=Ð=°,点A ,D ,E 在同一条直线上,CM 为DCE V 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°;2AE AD DE BE CM=+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ≌△CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ≌△CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∵ABC V 和ADE V 是顶角相等的等腰三角形,∴AB AC =,AD AE =,BAC DAE Ð=Ð,∴BAC CAD DAE CAD Ð-Ð=Ð-Ð,∴BAD CAE Ð=Ð.在BAD V 和CAE V 中,AB AC BAD CAE AD AE =ìïÐ=Ðíï=î,∴()BAD CAE SAS ≌△△,∴BD CE =.(2)解:90AEB =°∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE V V ,∴AD BE =,ADC BEC ÐÐ=,∵CDE △是等腰直角三角形,∴45CDE CED Ð=Ð=°,∴180135ADC CDE Ð=°-Ð=°,∴135BEC ADC Ð=Ð=°,∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°.∵CD CE =,CM DE ^,∴DM ME =.∵90DCE Ð=°,∴DM ME CM ==,∴2DE CM =.∴2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ≌△BCE 是解本题的关键.3)15°模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④D AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
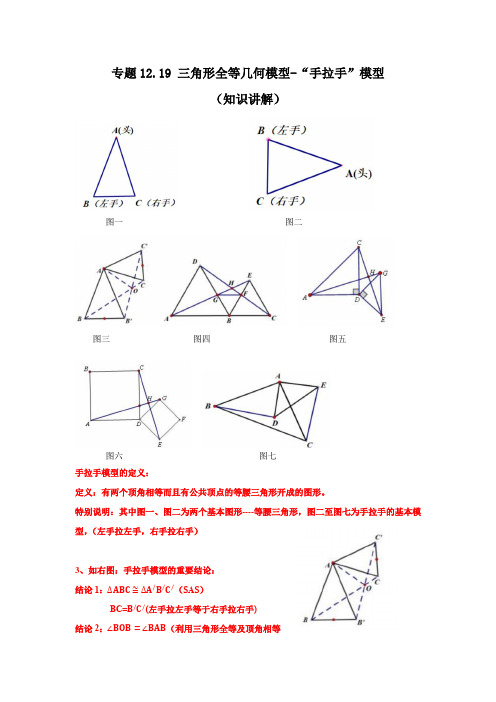
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
全等三角形中“手拉手”模型-2023年新八年级数学暑假精品课(苏科版)(解析版)

重难点:全等三角形中“手拉手”模型1.识别几何模型。
2.利用“手拉手”模型解决问题【基本模型】一、等边三角形手拉手-出全等二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有:①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;例1、如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点. 若DE=13,BD=12,求线段AB的长.∵△ACE≌△BCD∴AE=BD,∠EAC=∠B=45°∵BD=12∴∠EAD=45°+45°=90°,AE=12在Rt△EAD中,∠EAD=90°,DE=13,AE=12,由勾股定理得:AD=5∴AB=BD+AD=12+5=17【变式1】某校八年级数学兴趣小组的同学在研究三角形时,把两个大小不同的等腰直角三角板按图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);(2)试说明:DC与BE的位置关系.【分析】(1)利用SAS定理证明△BAE≌△CAD;(2)根据全等三角形的性质得到∠B=∠ACB=45°,根据垂直的定义证明结论.【解答】解:(1)△BAE≌△CAD,理由如下:∵∠BAC=∠EAD=90°,∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD在△BAE和△CAD中,,∴△BAE≌△CAD(SAS);(2)DC⊥BE,理由如下:∵△BAC为等腰直角三角形,∴∠B=∠ACB=45°,∵△BAE≌△CAD,∴∠CAD=∠B=45°,∴∠ACD=∠ACB+∠CAD=90°,∴DC⊥BE.【点评】本题考查的是全等三角形的判定和性质、等腰直角三角形的性质,掌握三角形全等的判定定理和性质定理是解题的关键.【变式2】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连结AE,BD交于点O,AE与DC 交于点0,AE与DC交于点M,BD与AC交于点N.解析:∵△ACB和△DCE都是等腰三角形∠ACB=∠DCE=90°∴AC=BC,DC=EC∴∠ACB+∠ACD=∠DCE+∠ACD∴∠BCD=∠ACE在△ACE和△BCD中AC=BC∠ACE=∠BCDCE=CD∴△ACE≌△BCD(SAS)∴AE=BD例2.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.如图1,当点D在边BC上时,求证:△ABD≌△ACE;直接判断结论BC=DC+CE是否成立(不需要证明);如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC、DC、CE之间存在的数量关系,并写出证明过程.解析:(1)∵△ABC和△ADE是等边三角形∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE∴∠BAC-∠DAC=∠DAE-∠DAC∴∠BAD=∠EAC在△ABD和△ACE中AB=AC∠BAD=∠EACAD=AE∴△ABD≌△ACE(SAS)[来源:学科网ZXXK]∵△ABD≌△ACE∴BD=CE∵BC=BD+CD∴BC=CE+CD(2)∵△ABC和△ADE是等边三角形∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE∴∠BAC+∠DAC=∠DAE+∠DAC∴∠BAD=∠EAC在△ABD和△ACE中AB=AC∠BAD=∠EACAD=AE∴△ABD≌△ACE(SAS)∴BD=CE∵BD=BC+CD∴CE=BC+CD【变式1】如图,点C在线段AB上,△DAC和△DBE都是等边三角形,求证:△DAB≌△DCE;DA∥EC.解析:(1)△DAC和△DBE都是等边三角形.∴DA=DC,DB=DE,∠ADC=∠BDE=60°.∴DA=DC,DB=DE,∠ADC=∠BDE=60°∴∠ADC+∠CDB=∠BDE+∠CDB,即∠ADB=∠CDE在△DAB和△DCE中,DA=DC∠ADB=∠CDEDB=DE∴△DAB≌△DCE.(2)∵△DAB≌△DCE∴∠A=∠DCE=60°∵∠ADC=60°∴∠DCE=∠ADC∴DA∥EC.【变式2】如图,在△AOB和△COD中,OA=OB,OC=OD,若∠AOB=∠COD=60°.(1)求证:AC=BD.(2)求∠APB的度数.【分析】(1)先∠AOB=∠COD=60°,OA=OB,OC=OD得到∠AOC=∠BOD,然后得证△AOC≌△BOD,从而得到AC=BD;(2)先由△AOC≌△BOD得到∠OAC=∠OBD,从而得到∠PAB+∠PBA=∠OAB+∠OBA,然后由OA =OB,∠AOB=60°得到△AOB是等边三角形,从而得到∠PAB+∠PBA=120°,最后得到∠APB的度数.【解答】(1)证明:∵∠AOB=∠COD,∴∠AOC=∠BOD,在△AOC和△BOD中,,∴△AOC≌△BOD(SAS),∴AC=BD.(2)解:∵△AOC≌△BOD,∴∠OAC=∠OBD,∵∠OAC+∠BAC=∠OAB,∠ABO+∠OBD=∠ABP,∴∠PAB+∠PBA=∠OAB+∠OBA,∵OA=OB,∠AOB=60°,∴△AOB是等边三角形,∴∠PAB+∠PBA=120°,∴∠APB=180°﹣(∠PAB+∠PBA)=180°﹣120°=60°.【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质,解题的关键是熟练掌握SAS定理判定三角形全等.例3、已知,在△ABC中,AB=AC,点P平面内一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,⑴若点P在△ABC内部,求证BQ=CP;⑵若点P在△ABC外部,以上结论还成立吗?解析:(1)∵∠QAP=∠BAC∴∠QAP-∠B AP=∠BAC-∠BAP[来源:Z#xx#]即∠QAB=∠PAC另由旋转得AQ=AP在△AQB和△APC中AQ=AP∠QAB=∠PACAB=AC∴△AQB≌△APC∴BQ=CP(2)∵∠QAP=∠BAC∴∠QAP+∠BAP=∠BAC+∠BAP[来源:学科网]即∠QAB=∠PAC另由旋转得AQ=AP在△AQB和△APC中AQ=AP∠QAB=∠PACAB=AC∴△AQB≌△APC∴BQ=CP【变式】(1)如图1,在Rt△ABC中,AB=AC,D是直线BC上的一点,将线段AD绕点A逆时针旋转90°至AE,连接CE,求证:△ABD≌△ACE;(2)如图2,A是△BDC内一点,∠ABC=∠ADB=45°,∠BAC=90°,BD=6,线段AD绕点A逆时针旋转90°至AE,点D、E、B恰好共线,求△BDC的面积;(3)如图3,在图1的条件下,延长DE,AC交于点G,BF⊥AB交DE于点F,求证:FG AE.【分析】(1)如图1,根据SAS证明三角形全等即可.(2)过点A作AE⊥AD交BD于E,连接CE.利用全等三角形的性质证明CE=BD,CE⊥BD即可.(3)过点D作DK⊥DC交FB K.证明△ECG≌△DKF(AAS),推出DF=EG,再证明FG=DE AE即可.【解答】(1)证明:如图1,∵∠BAC=∠DAE=90°,∴∠DAB=∠EAC,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).(2)解:如图2,过点A作AE⊥AD交BD于E,连接CE.∵∠ADB=45°,∠DAE=90°,∴△ADE与△ABC都是等腰直角三角形,同法可证△ABD≌△ACE,∴CE=BD=6,∵∠AEC=∠ADB=45°,∴∠CED=∠CEB=90°,∴S△BDC•BD•CE6×6=18.(3)证明:如图3,过点D作DK⊥DC交FB的延长线于K.∵DK⊥CD,BF⊥AB,∴∠BDK=∠ABK=90°,∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∴∠DBK=∠K=45°,∴DK=DB,∵△ABD≌△ACE,∴∠ABD=∠ACE=135°,DB=EC=DK,∴∠ECG=45°,∵BF⊥AB,CA⊥AB,∴AG∥BF,∴∠G=∠DFK,在△ECG和△DKF中,,∴△ECG≌△DKF(AAS),∴DF=EG,∵DE AE,∴DF+EF AE,∴EG+EF AE,即FG AE.【点评】本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.一.填空题(共4小题)1.(2020秋•工业园区月考)在△ABC中,∠ABC=45°,AD、BE分别为BC、AC边上的高,AD、BE 相交于点F,连接CF.下列结论:(1)∠FCD=45°;②AE=EC;③S△ABF:S△AFC=BD:CD,④若BF =2EC,则△FDC的周长等于AB的长.正确的是(填序号).【分析】首先在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,由此可以得到∠BAD=45°,接着得到AD=BD,又∠DAC和∠FBD都是∠ACD的余角,所以可以证明△BDF ≌△ADC,根据全等三角形的性质可以得到FD=CD,进一步得到①;若AE=EC,则由BE⊥AC,推出BA=BC,显然不可能,故②错误,根据三角形面积公式和它们有一条公共边可以得到③;若BF=2EC,根据①可以得到E是AC的中点,然后可以推出EF是AC的垂直平分线,最后由线段垂直平分线的性质即可得到④.【解答】解:∵△ABC中,AD,BE分别为BC、AC边上的高,∴AD⊥BC,而△ABF和△ACF有一条公共边,∴S△ABF:S△AFC=BD:CD,∴③正确;∵∠ABC=45°,∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,而∠ADB=∠ADC=90°,∴△BDF≌△ADC,∴FD=CD,∴∠FCD=∠CFD=45°,∴①正确;若AE=EC,则∵BE⊥AC,∴BA=BC,显然不可能,故②错误,若BF=2EC,根据①得BF=AC,∴AC=2EC,即E为AC的中点,∴BE为线段AC的垂直平分线,∴AF=CF,BA=BC,∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,即△FDC周长等于AB的长,∴④正确.故答案为①③④【点评】本题考查了全等三角形的性质与判定,也考查了线段的垂直平分线的性质与判定,也利用了三角形的周长公式解题,综合性比较强,对学生的能力要求比较高.2.(2022秋•通州区期中)如图,在△ABC中,∠C=90°,∠BAC=60°.P是BC边上一点,CP=CA,连接AP,以AP为边在AP的右上方作等边三角形APQ.若AB=5,则点Q到边AB的距离为.【分析】过点Q作QD⊥AB,垂足为D,根据垂直定义可得∠ADQ=90°,再利用直角三角形的两个锐角互余可得∠ABC=30°,从而利用含30度角的直角三角形的性质可得CP=AC=AB=2.5,然后证明手拉手模型﹣旋转型全等△ACP≌△ADQ,从而利用全等三角形的性质即可解答.【解答】解:过点Q作QD⊥AB,垂足为D,∴∠ADQ=90°,∵∠C=90°,∠BAC=60°,∴∠ABC=90°﹣∠BAC=30°,∵AB=5,∴AC=AB=2.5,∵AC=CP,∴AC=CP=2.5,∵△AQP是等边三角形,∴AP=AQ,∠QAP=60°,∴∠QAP﹣∠PAB=∠BAC﹣∠PAB,∴∠CAP=∠DAQ,∵∠C=∠ADQ=90°,∴△ACP≌△ADQ(AAS),∴QD=CP=2.5,∴点Q到边AB的距离为2.5,故答案为:2.5.【点评】本题考查了全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形,熟练掌握手拉手模型﹣旋转型全等是解题的关键.3.(2021秋•滨湖区期末)如图,在△ABC中,∠ACB=90°,AC=BC=.D是边AB上一动点,连接CD,以CD为直角边在CD左侧作等腰直角△CDE,且∠DCE=90°,连接AE,则DE长度的最小值为;△ADE面积的最大值为.【分析】要求DE最小值,只需求出CD的最小值,过点C作CF⊥AB于点F,根据垂线短最短即可得出CF即为CD的最小值,然后用勾股定理求出DE的最小值;利用手拉手全等模型可得△ACE≌△BCD(SAS),从而得∠DAE=90°,设AE=x,则AD=2﹣x,从而表示出△ADE面积,即可求解.【解答】解:∵△CDE是等腰直角三角形,∴DE=,∴CD取得最小值时,DE取得最小值,如图,过点C作CF⊥AB于点F,此时CF即为CD的最小值,∵∠ACB=90°,AC=BC=,∴CF=1,AB=2,∴CD的最小值为1,∴DE的最小值为.∵∠ACB=∠DCE=90°,∴∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴∠EAC=∠B=45°,AE=BD,∴∠EAD=90°,设BD=x,则AE=x,AD=2﹣x,∴S△ADE==,∴当x=1时,S△ADE的最大值为,故答案为,.【点评】本题考查等腰三角形的性质、垂线段最短、全等三角形,其中判断出手拉手模型得全等是解题关键.4.(2021秋•常州期末)如图,两条互相垂直的直线m、n交于点O,一块等腰直角三角尺的直角顶点A 在直线m上,锐角顶点B在直线n上,D是斜边BC的中点.已知OD=,BC=4,则S△AOB=.【分析】利用等腰三角形的三线合一想到连接AD,根据已知可得∠ADB=90°,AD=DB=BC=2,因为OD=,想到构造手拉手﹣旋转性全等,所以过点D作ED⊥DO,交直线n于点E,证明△DAO≌△DBE,可得DO=DE=,OA=BE,然后在Rt△OAB中,利用勾股定理进行计算即可解答.【解答】解:连接AD,过点D作ED⊥DO,交直线n于点E,∴∠EDO=90°,∵△ABC是等腰直角三角形,∠CAB=90°,∴AB=AC,∵D是斜边BC的中点,∴∠ADB=90°,AD==DB=BC=2,∴AB===2,∵∠ADB﹣∠BDO=∠EDO﹣∠BDO,∴∠ADO=∠BDE,∵m⊥n,∴∠AOB=90°,∴∠DAO+∠DBO=360°﹣∠ADB﹣∠AOB=180°,∵∠DBO+∠DBE=180°,∴∠DAO=∠DBE,∴△DAO≌△DBE(ASA),∴DO=DE=,OA=BE,∴OE===,∴OB+BE=,∴OB+OA=,∴(OB+OA)2=14,∴OA2+OB2+2OA•OB=14,在Rt△OAB中,OA2+OB2=AB2,∴OA2+OB2=(2)2=8,∴2OA•OB=14﹣8=6,∴OA•OB=3,∴△AOB的面积=OA•OB=,故答案为:.【点评】本题考查了勾股定理,全等三角形的判定与性质,等腰直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.二.解答题(共13小题)5.(2022秋•宜兴市月考)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.(1)求证:AE=CD;(2)证明:∠1=∠3.【分析】(1)由已知角相等,利用等式的性质得到夹角相等,利用SAS即可得证;(2)利用全等三角形对应角相等得到一对角相等,再由对顶角相等及内角和定理即可得证.【解答】(1)证明:∵∠1=∠2,∴∠ABE=∠CBD,在△ABE和△CBD中,,∴△ABE≌△CBD(SAS),∴AE=CD;(2)证明:由(1)知,△ABE≌△CBD,∴∠A=∠C,又∵∠AFB=∠CFE,∴∠1=∠3.【点评】此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.6.(2021秋•丹阳市期末)如图,△ABC中,∠ACB=90°,AC=BC,延长AB到D,使得DB=AB,连接CD,以CD为直角边作等腰Rt△CDE,其中∠DCE=90°,连接BE.(1)猜想线段BE与AD的数量和位置关系,并说明理由;(2)若AC=cm,则BE=cm,DE=cm.【分析】(1)根据等腰直角三角形的性质得到CD=CE,CA=CB,然后利用“SAS”可判断△ACD≌△BCE;根据全等三角形的性质得到∠1=∠2,而∠3=∠4,然后根据三角形内角和定理即可得到∠EBD=∠ECD =90°;(2)根据全等三角形的性质得到AD=BE,而DB=AB=2cm,所以BE=4cm;在Rt△DBE中,利用勾股定理求出DE的长.【解答】解:(1)BE⊥AD且BE=AD.理由如下:∵△ACB和△DCE都是等腰直角三角形,∴CD=CE,CA=CB,∵∠ACB=90°,∠DCE=90°,∴∠ECD+∠DCB=∠DCB+∠ACB,即∠ECB=∠ACD,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS);∴∠1=∠BEC,而∠3=∠4,∴∠EBD=∠ECD=90°,∴BE⊥AD且BE=AD.(2)∵若AC=BC=cm,∴AB==2(cm),∵△ACD≌△BCE,∴AD=BE,∵DB=AB=2cm,∴BE=2×2=4(cm),在Rt△DBE中,DE=(cm).故答案为4,2.【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.7.(2020秋•崇川区期末)如图,AB=AD,∠B=∠D,∠BAD=∠CAE=60°.(1)求证:△ABC≌△ADE;(2)若AE=5,求CE的长.【分析】(1)根据等式的性质和全等三角形的判定解答即可;(2)根据全等三角形的性质解答即可.【解答】证明:(1)∵∠BAD=∠=60°.∴∠BAD+∠BAE=∠CAE+∠BAE,∴∠DAE=∠BAC,在△DAE与△BAC中,,∴△ABC≌△ADE(ASA);(2)∵△ABC≌△ADE,∴AE=AC,∵∠CAE=60°.∴△ACE是等边三角形,∴CE=AE=5.【点评】此题考查全等三角形的判定和性质,关键是根据等式的性质和全等三角形的判定解答.8.(2021秋•江阴市校级月考)如图,△ABC是等边三角形,点D为BC上一点(与点B不重合),过点C作∠ACE=60°,且CE=BD(点E与点A在射线BC同侧),连接AD,ED.求证:AD=DE.【分析】连接AE,根据等边三角形的性质可得AB=AC,∠B=∠BAC=60°,从而利用SAS可证△ABD ≌△ACE,然后利用全等三角形的性质可得AD=AE,∠BAD=∠CAE,从而可得∠DAE=60°,进而可得△ADE是等边三角形,最后利用等边三角形的性质即可解答.【解答】证明:连接AE,∵△ABC是等边三角形,∴AB=AC,∠B=∠BAC=60°,∵∠ACE=60°,∴∠B=∠ACE=60°∵BD=CE,∴△ABD≌△ACE(SAS),∴AD=AE,∠BAD=∠CAE,∵∠BAC=60°,∴∠BAD+∠DAC=60°,∴∠CAE+∠DAC=60°,∴∠DAE=60°,∴△ADE是等边三角形,∴AD=DE.【点评】本题考查了全等三角形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.9.(2022秋•崇川区校级月考)在△ABC中,AB=AC,点D是直线BC上的一点(不与点B、C重合),以AD为腰右侧作等腰三角形△ADE,且AD=AE,∠BAC=∠DAE,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度.(2)设∠BAC=α,∠BCE=β.①点D是在线段BC上移动时,如图2,则α、β之间有怎样的数量关系?试说明理由.②点D是在射线CB上移动时,则α、β之间有怎样的数量关系?试直接写出结论.【分析】(1)证明△BAD≌△CAE,得∠B=∠ACE,即可证明;(2)①与(1)同理证明△BAD≌△CAE,得∠ABD=∠ACE,则∠BAC+∠BCE=∠BAC+∠BCA+∠ACE =∠BAC+∠BCA+∠B=180°;②同理证明△ADB≌△AEC,得∠ABD=∠ACE,由∠ABD=∠BAC+∠ACB,则∠BAC=∠BCE.【解答】解:(1)∵∠BAC=∠,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠B=∠ACE,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;(2)①α+β=180°,理由如下:∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△BAD与△CAE中,,∴△BAD≌△CAE(SAS),∴∠ABD=∠ACE,∵∠BAC+∠ABD+∠BCA=180°,∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,∴α+β=180°;②α=β,理由如下:∵∠DAE=∠BAC,∴∠DAB=∠EAC,在△ADB与△AEC中,,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE,∵∠ABD=∠BAC+∠ACB,∴∠BAC=∠BCE,∴α=β.【点评】本题主要考查了等腰三角形的性质,全等三角形的判定与性质,三角形外角的性质等知识,证明△ADB≌△AEC是解题的关键.10.(2022秋•徐州期中)在△ABC中,AB=AC,∠BAC=90°.将一个含45°角的直角三角尺DEF按图1所示放置,使直角三角尺的直角顶点D恰好落在BC边的中点处,将直角三角尺DEF绕点D旋转,设AB交DF于点N,AC交DE于点M,示意图如图2所示.(1)[证明推断]求证:DN=DM;小明给出的思路:若要证明DN=DM,只需证明△BDN≌△ADM即可,请你根据小明的思路完成证明过程;(2)[延伸发现]连接AE,BF,如图3所示,求证:AE=BF;(3)[迁移应用]延长EA交DF于点P,交BF于点Q.在图3中完成如上作图过程,猜想并证明AE和BF 的位置关系.【分析】(1)D是BC的中点,则AD=BD=CD,∠ABC=∠DAC=45°,再证明∠FDB=∠ADE,得到△BDN≌△ADM(ASA),即可求解;(2)△DEF为等腰直角三角形,则DE=DF,由(1)知:∠FDB=∠EDA,BD=AD,可以证明△FDB ≌△EDA(SAS),即可求解;(3)由△FDB≌△EDA,得到∠BFD=∠AED,进而求解.【解答】证明:(1)如图2,在Rt△ABC中,∵D是BC的中点,即BD是△ABC的中线,∴AD=BD=CD,∠ABC=∠45°,∵∠FDB+∠FDA=90°,∠FDA+∠ADE=90°,∴∠FDB=∠ADE,在△BDN和△ADM中,,∴△BDN≌△ADM(ASA),∴DN=DM;(2)∵△DEF为等腰直角三角形,∴DE=DF,由(1)知:∠FDB=∠EDA,BD=AD,在△BDF和△ADE中,,∴△FDB≌△EDA(SAS),∴AE=BF;(3)作图如下,AE和BF的位置关系为:相互垂直,理由如下:由(2)知△FDB≌△EDA,∴∠BFD=∠AED,又∵∠FPQ=∠EPD,∴∠FQP=∠PDE=90°,即AE⊥BF,故AE和BF【点评】本题属于几何变换综合题,考查了旋转变换、等腰直角三角形的性质、全等三角形的判定和性质等,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.11.(2022秋•东海县期中)【问题呈现】在Rt△ABC中,∠ACB=90°,CA=CB,点D是斜边AB上的一点,连接CD,试说明AD、BD、CD之间的数量关系,并说明理由.【解决策略】小敏同学思考后是这样做的:将△CAD绕点C逆时针旋转90°,得到对应的△CBE,连接DE,如图1经过推理使问题得到解决.请回答:(1)△DBE的形状是,△DCE的形状是;(2)直接写出AD、BD、CD之间的数量关系是;【方法感悟】在解决问题时,条件中若出现“等边三角形”、“等腰直角三角形”字样,可以考虑旋转某个三角形,把分散的条件或结论集中到一起,从而使问题得到解决.(3)如图2,在四边形ABCD中,∠BCD=45°,连接对角线AC、BD,∠ADB=90°,AD=BD,若CB =2,CD=4,求CA的长;(4)如图3,在四边形ABCD中,∠BAD=60°,AB=AD,若BC=5,CD=2,求A、C两点之间的最大距离.【分析】【解决策略】(1)由旋转的性质得出△DCE是等腰直角三角形,证明△ACD≌△BCE(SAS),由全等三角形的性质得出∠A=∠CBE=45°,则可得出结论;(2)由全等三角形的性质得出结论;【方法感悟】(3)过点D作DE⊥DC,交CB的延长线于E,连接AE,证出∠AEC=∠AED+∠DEC=90°,由勾股定理可得出答案;(4)将△ADC绕点A顺时针旋转90°,得到对应的△ABE,连接CE,则CD=BE=2,证出AC=CE,求出CE的最大值可得出答案.【解答】【解决策略】解:(1)∵将△CAD绕点C逆时针旋转90°,得到对应的△CBE,∴CD=CE,∠DCE=90°,∴△DCE是等腰直角三角形,∵∠ACB=90°=∠ACD+∠DCB,∴∠ACD=∠ECB,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠A=∠CBE=45°,∵∠ABC=45°,∴∠ABE=∠ABC+∠CBE=45°+45°=90°,∴△DBE是直角三角形,故答案为:直角三角形,等腰直角三角形;(2)∵△ACD≌△BCE,∴AD=BE,∵∠DBE=90°,∴DB2+BE2=DE2,∵∠DCE=90°,∴CD2+CE2=2CD2=DE2,∴DB2+AD2=2CD2;故答案为:DB2+AD2=2CD2;【方法感悟】(3)过点D作DE⊥DC,交CB的延长线于E,连接AE,如图2,∵∠BCD=45°,∴△DCE是直角三角形,由(1)可知△ADE≌△BDC,∴∠AED=∠BCD=45°,AE=BC,∵∠DEC=45°,∴∠AEC=∠AED+∠DEC=90°,∵DC=4,BC=2,∴CE=DC=4,AE=2,∴AC===6;(4)将△ADC绕点A顺时针旋转90°,得到对应的△ABE,连接CE,如图3,∴CD=BE=2,∵AC=AE,∠CAE=60°,∴△ACE是等边三角形,∴AC=CE,∵CE≤BC+BE=5+2=7,∴当C,B,E三点共线时,CE最大,∴A、C两点之间的最大距离是7.【点评】本题是四边形综合题,考查了全等三角形的判定与性质,旋转的性质,等腰直角三角形的性质,勾股定理,熟练掌握全等三角形的判定与性质是解题的关键.12.(2021秋•淮安期末)如图1,AC=BC,CD=CE,∠ACB=∠DCE=α.(1)AD、BE相交于点M.①求证:AD=BE;②用含α的式子表示∠AMB的度数;(2)如图2,点P、Q分别是AD、BE的中点,连接CP、CQ,判断△CPQ的形状,并加以证明;(3)如图3,在△ABC中,∠ACB=45°,BC=,AC=3,以AB为直角边,B为直角顶点作等腰Rt △ABD,则CD=(直接写出结果).【分析】(1)①由“SAS”可证△ACD≌△BCE,可得BE=AD;②由三角形内角和定理可求解;(2)由“SAS”可证△ACP≌△BCQ,可得CP=CQ,可得结论;(3)将△BCD绕着点B逆时针旋转90°得到△AEB,连接BE,CE,根据旋转的性质得到BE=BC=,∠CBE=∠ABD=90°,AE=CD,可得出△BCE是等腰直角三角形,根据勾股定理即可得到结论.【解答】(1)①证明:如图1,∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE;②解:如图1,∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠BAC+∠ABC=180°﹣α,∴∠BAM+∠ABM=180°﹣α,∴∠AMB=180°﹣(180°﹣α)=α;(2)△CPQ为等腰三角形,理由如下:如图2,由(1)可得,BE=AD,∵AD,BE的中点分别为点P、Q,∴AP=BQ,∵△ACD≌△BCE,∴∠CAP=∠CBQ,在△ACP和△BCQ中,,∴△ACP≌△BCQ(SAS),∴CP=CQ,∴△CPQ为等腰三角形.(3)将△BCD绕着点B逆时针旋转90°得到△AEB,连接BE,CE,则BE=BC=,∠CBE=∠ABD=90°,AE=CD,∴△BCE是等腰直角三角形,∴∠BCE=45°,CE=BC=4,∵∠ACB=45°,∴∠ACE=90°,∴AE===5,∴CD=AE=5.故答案为:5.【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,旋转的性质,勾股定理等,运用旋转的性质构造全等三角形是解题的关键.13.(2022秋•亭湖区校级月考)【阅读材料】小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD =AE,则△ABD≌△ACE.【材料理解】(1)在图1中证明小明的发现.【深入探究】(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有(将所有正确的序号填在横线上).【延伸应用】(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.【分析】(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;(2)同(1)的方法判断出△ABD≌△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF≌△ACO,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF<CF,进而判断出∠OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP(SAS),即可得出结论.【解答】(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)如图2,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE,①正确,∠ADB=∠AEC,记AD与CE的交点为G,∵∠AGE=∠DGO,∴180°﹣∠ADB﹣∠DGO=180°﹣∠AEC﹣∠AGE,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB上取一点F,使OF=OC,连接CF,∴△OCF是等边三角形,∴CF=OC,∠OFC=∠OCF=60°=∠ACB,∴∠BCF=∠ACO,∵AB=AC,∴△BCF≌△ACO(SAS),∴∠AOC=∠BFC=180°﹣∠OFC=120°,∴∠AOE=180°﹣∠AOC=60°,③正确,连接AF,要使OC=OE,则有OC=CE,∵BD=CE,∴CF=OF=BD,∴OF=BF+OD,∴BF<CF,∴∠OBC>∠BCF,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC>30°,而没办法判断∠OBC大于30度,所以,④不一定正确,即:正确的有①②③,故答案为:①②③;(3)如图3,延长DC至P,使DP=DB,∵∠BDC=60°,∴△BDP是等边三角形,∴BD=BP,∠DBP=60°,∵∠ABC=60°=∠DBP,∴∠ABD=∠CBP,∵AB=CB,∴△ABD≌△CBP(SAS),∴∠BCP=∠A,∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.【点评】此题是三角形综合题,主要考查了等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解本题的关键.14.(2021秋•沭阳县月考)在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD 为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=°.(2)如图2,设∠BAC=α,∠BCE=β.当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;(3)如图2,当点D在线段BC上,如果∠BAC=60°,D点为△ABC中BC边上的一个动点(D与B、C 均不重合),当点D运动到什么位置时,△DCE的周长最小?请探求点D的位置,并求出此时∠EDC的度数,直接写出你的结论.【分析】(1)由等腰直角△ABC、△ADE易证△ABD≌△ACD,即可得出∠ECA=∠B=45°,进而求出∠ECD=90°,(2)证明△BAD≌△CAE(SAS),推出∠ACE=∠B,则可得出结论;(3)由全等三角形的性质可得出BD=CE,可推出CD+EC=CD+BD=BC,由△ECD的周长=DE+CD+CE =DE+BC,BC为定值,推出DE定值最小时,△DCE得到周长最小,根据此线段最短即可解决问题.【解答】解:(1)如图1中,∵AB=AC,AD=AE,∠BAC=∠ADE=90°,∴∠BAD=∠CAE,∠B=∠ACB=45°,∴△BAD≌△CAE(SAS),∴∠B=∠ACE=45°,∴∠BCE=45°+45°=90°.故答案为:90.(2)α+β=180°.理由如下:如图2中,∵AB=AC,AD=AE,∠BAC=∠ADE,∴∠BAD=∠CAE,∠B=∠ACB,∴△BAD≌△CAE(SAS),∴∠ACE=∠B,β=∠ABC+∠ACB,∴α+β=180°.(3)∵△BAD≌△CAE(SAS),∴BD=EC,∴CD+EC=CD+BD=BC,∵△ECD的周长=DE+CD+CE=DE+BC,∵BC为定值,∴DE定值最小时,△DCE得到周长最小,∵DE=AD,∴AD⊥BC时,AD定值最小,此时BD=CD=CE,∴∠EDC=(180°﹣120°)=30°,∴当点D运动到BC的中点时,△DEC是周长最小,此时∠EDC=30°.【点评】本题属于三角形综合题,考查了等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题.15.(2022秋•江阴市期中)在学习全等三角形的知识时,数学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成的,在相对位置变化的同时,始终存在一对全等三角形.兴趣小组成员经过研讨给出定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,可以形象地看作两双手,所以通常称为“手拉手模型”.(1)如图1,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,则有.(2)如图2,已知△ABC,以AB、AC为边分别向外作等边△ABD和等边△ACE,并连接BE,CD,则∠BOD=°.(3)如图3,在两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,∠BAC=∠DAE=90°,连接BD,CE,交于点P,请判断BD和CE的关系,并说明理由.【分析】(1)由“SAS”可证△BAD≌△CAE;(2)由“SAS”可证△DAC≌△BAE,可得∠ADC=∠ABE,由外角的性质可求解;(3)由“SAS”可证△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,由余角的性质可求解.【解答】解:(1)∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),故答案为:△BAD,△CAE;(2)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=60°,∴∠DAC=∠BAE,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ADC+∠BDC+∠ABD+∠DAB=180°,∠ABE+∠BDC+∠ABD+∠DOB=180°,∴∠DAB=∠BOD=60°,故答案为:60;(3)BD=CE,BD⊥CE,理由如下:∵∠BAC=∠DAE=90°,∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠BAD,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵∠BPC+∠ABD=∠BAC+∠ACE,∴∠BPC=∠BAC=90°,∴BD⊥CE.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,等边三角形的性质,灵活运用这些性质解决问题是解题的关键.16.(2022秋•阜宁县期中)【问题发现】(1)如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一直线上,连接CE,容易发现:①∠BEC 的度数为;②线段BD、CE之间的数量关系为;【类比探究】(2)如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,连接CE,试探究∠BEC的度数及线段BE、CE、DE之间的数量关系,并说明理由;【问题解决】(3)如图3,∠AOB=∠ACB=90°,OA=3,OB=7,AC=BC,求OC2的值.【分析】(1)由等边三角形的性质得到AB=AC,AD=AE,∠BAC=∠DAE=∠ADE=60°,则∠BAD =∠CAE,再证△BAD≌△CAE(SAS),即可解决问题;(2)由“SAS”可证△ABD≌△ACE,得BD=CE,∠AEC=∠ADB=135°,即可求解;(3)过点C作EF∥OB,交AO的延长线于点F,过点B作BE⊥EF于点E,由“AAS”证△ACF≌△CBE,得BE=CF,AF=CE,设OF=x,再由AF=CE列方程得x的值,然后由勾股定理可求解.【解答】解:(1)①∵△ABC和△ADE为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠ADE=60°,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴∠AEC=∠ADB=180°﹣∠ADE=120°,∴∠BEC=∠AEC﹣∠AED=120°﹣60°=60°,故答案为:60°;②由①可知,△BAD≌△CAE,∴BD=CE,故答案为:BD=CE;(2)∠BEC=90°,BE=CE+DE,理由如下:∵∠BAC=∠DAE=90°,△ABC和△ADE均为等腰直角三角形,∴AB=AC,AD=AE,∠ADE=∠AED=45°,∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE,∠AEC=∠ADB=180°﹣∠ADE=135°,∴∠BEC=∠AEC﹣∠AED=135°﹣45°=90°,∵BE=BD+DE,∴BE=CE+DE;(3)如图3,过点C作EF∥OB,交AO的延长线于点F,过点B作BE⊥EF于点E,则∠BOF=180°﹣∠AOB=90°,∠BEC=∠CFA=90°,∴四边形BOFE是矩形,∴OB=EF=7,BE=OF,∵∠ACB=90°,∴∠BCE+∠ACF=90°,∵∠ACF+∠CAF=90°,∴∠CAF=∠BCE,∵∠F=∠E=90°,AC=BC,∴△ACF≌△CBE(AAS),∴CF=BE,AF=CE,设OF=x,则CF=BE=OF=x,AF=3+x,CE=7﹣x,∴3+x=7﹣x,∴x=2,∴OF=CF=2,在Rt△OCF中,由勾股定理得:OC2=OF2+CF2=22+22=8,故答案为:8.【点评】本题是三角形的综合题,考查的是等边三角形的性质、等腰直角三角形的性质、全等三角形的判定和性质以及勾股定理等知识,本题综合性强,掌握全等三角形的判定与性质是解题的关键,属于中考常考题型.17.(2021秋•兴化市期末)如图1,△ABC与△ADE是共顶点A的两个等腰三角形,其中AB=AC,AD =AE,∠BAC=∠DAE,连接CE、BD.(1)求证:CE=BD;(2)如图2,固定△ABC,将△ADE绕点A旋转,若AD=25,BC=20,S△ABC=240,当点D旋转到线段BC上时,求CE的长;(3)如图3,设F为BD、CE的交点,G、H分别为BD、CE的中点,∠BFC=α,∠AGH=β,试探究α与β的数量关系,并说明理由.【分析】(1)由等腰三角形的性质可知AB=AC,AD=AE,∠BAD=∠CAE,再利用SAS可证明△BAD ≌△CAE,得CE=BD;(2)过点A作AP⊥BC于P,连接CE,根据BC=20,S△ABC=240,得AP=24,可知点D在CP或BP 上,利用勾股定理解决问题;(3)连接AH,由(1)同理知,△BAD≌△CAE(SAS),得∠ADB=∠AEC,BD=CE,再利用SAS证明△ADG≌△AEH,得∠AHE=∠AGD=∠AGH+∠FGH,AG=AH,从而解决问题.【解答】(1)证明:∵∠BAC=∠DAE,∠BAC=∠BAD+∠CAD,∠DAE=∠CAE+∠CAD,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴CE=BD;(2)解:如图,过点A作AP⊥BC于P,连接CE,由(1)同理知,△BAD≌△CAE(SAS),∴CE=BD,∵BC=20,S△ABC=240,∴AP=24,当点D在CP上时,在Rt△APD中,PD2=AD2﹣AP2=49,∴PD=7,∵AB=AC,AP⊥BC,∴P为BC的中点,∴BP=CP,∵BC=20,∴BP=10,∴BD=17,∴CE=BD=17,当点D在BP上时,同理可知CE=BD=10﹣7=3,综上所述:CE=3或17;(3)解:α+2β=180°,理由如下:如图,连接AH,由(1)同理知,△BAD≌△CAE(SAS),∴∠ADB=∠AEC,BD=CE,∵G,H分别为BD,CE的中点,∴DG=EH,∵∠ADB=∠AEC,DG=EH,AD=AE,∴△ADG≌△AEH(SAS),∴∠AHE=∠AGD=∠AGH+∠FGH,AG=AH,∴∠AGH=∠AHG,∵∠FHG+∠AHG+∠AHE=180°,∴∠FHG+∠AGH+∠AGH+∠FGH=180°,∵∠BFC=∠FGH+∠FHG,∠BFC=α,∠AGH=β,∴α+2β=180°.【点评】本题主要考查了等腰三角形的性质,旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟悉基本模型证明△BAD≌△CAE是解题的关键.。
中考数学几何专题——手拉手模型一

手拉手模型一、手拉手模型1.手的判别:人站在等腰三角形顶角的位置,张开双臂,左手边的腰为左手,右手边的腰为右手。
2.手拉手模型的定义:两个等顶角的等腰三角形组成的图形,且顶角的顶点为公共顶点。
(顶角相等、等腰三角形、共顶点)条件模型结论特殊结论△ABC与△CDE是等腰三角形,且∠ACB=∠DCE (1)D ACD@D BCE (SSS)(2)AD=BE(左手拉左手,右手拉右手)(3)ÐBHA=ÐBCA(4)HC平分ÐAHE△ABC与△CDE是等腰直角三角形,且∠ACB=∠DCE=90°(5)S D BCD=S D ACE(6)BD2+AE2=AB2+DE2正方形ACBP与正方形CEQD是正方形△ABC 与△CDE是等边三角形(5)D ACM@D BCND DCM@D ECN(6) CM=CN(7)D CMN是等边三角形(8)MN∥AE,CD∥AB, CB∥DE(9) BH+CH=AHDH+CH=EH二、手拉手模型的变形:(两三角形相似,且对应角共顶点)条件模型结论D BAC∽D DAE,且ÐDAE=ÐBAC (1)D BAD∽D CAE(两边对应成比例且夹角相等) (2)BDCE=BACA(3) ÐBHC=ÐBAC【巩固练习】1、如图所示,若△ABC、△ADE都是正三角形,试比较线段BD与线段CE的大小.2、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是()3、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,四边形ADEF是菱形?(4)当△ABC满足什么条件时,四边形ADEF是正方形?(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?4、问题情境:如图1,已知△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC=2,CD=CE=1,点D在AC 边上,点E 在BC 延长线上。
专题01 全等三角形(解析版)

2021-2022学年人教版数学八年级上册压轴题专题精选汇编专题01 全等三角形一.选择题1.(2020秋•东城区期末)如图所示,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=20,则△AOB的面积是( )A.20B.30C.50D.100【思路引导】根据角平分线的性质求出OE,最后用三角形的面积公式即可解答.【完整解答】解:过O作OE⊥AB于点E,∵BO平分∠ABC,OD⊥BC于点D,∴OE=OD=5,∴△AOB的面积=,故选:C.2.(2020秋•定西期末)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )A.4B.3C.2D.1【思路引导】根据垂线段最短得出当DP⊥BC时,DP的长最小,求出∠ABD=∠CBD,根据角平分线的性质得出此时DP=AD,再得出选项即可.【完整解答】解:当DP⊥BC时,DP的长最小,∵BD⊥CD,∴∠BDC=90°,∵∠A=90°,∠ADB=∠C,∠A+∠ADB+∠ABD=180°,∠BDC+∠C+∠CBD=180°,∴∠ABD=∠CBD,∵∠A=90°,∴当DP⊥BC时,DP=AD,∵AD=4,∴DP的最小值是4,故选:A.3.(2020秋•莫旗期末)如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,则PE的最小值为( )A.8B.5C.4D.2【思路引导】过E作EP⊥BC于P,此时PE的值最小,求出AD⊥CD,根据角平分线的性质求出AE=DE=PE,求出AE的长即可.【完整解答】解:过E作EP⊥BC于P,此时PE的值最小,∵AB∥CD,AD⊥AB,∴AD⊥CD,∵BE和CE分别平分∠ABC和∠BCD,∴AE=PE,ED=PE,∴AE=ED=PE,∵AD=8,∴PE=4,即PE的最小值是4,故选:C.4.(2020秋•鞍山期末)如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点D作DF⊥AB,垂足为点F,点E在边AC上,若DE=DB,则下列结论不正确的是( )A.DC=DF B.DE=BF C.AC=AF D.AB=AC+CE【思路引导】根据全等三角形的判定和性质解答即可.【完整解答】解:∵Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点D作DF⊥AB,垂足为点F,∴DC=DF,故A正确,在Rt△DCE与Rt△DFB中,,∴Rt△DCE≌Rt△DFB(HL),∴CE=BF,故B错误,在Rt△ADC与Rt△ADF中,,∴Rt△ADC≌Rt△ADF(HL),∴AC=AF,故C正确,∴AB=AF+BF=AC+CE,故D正确,故选:B.5.(2020秋•新宾县期末)如图,AB=AD,AC=AE,∠DAB=∠CAE=50°,以下四个结论:①△ADC≌△ABE;②CD=BE;③∠DOB=50°;④点A在∠DOE的平分线上,其中结论正确的个数是( )A.1B.2C.3D.4【思路引导】证明△ADC≌△ABE(SAS),可得出CD=BE,∠ADC=∠ABE,则得出∠DOB=50°,连接OA,过点A作AM⊥CD于点M,AN⊥BE于点N,证明△ABN≌△ADM(AAS),则可得出点A在∠DOE的平分线上.【完整解答】解:∵∠DAB=∠CAE=50°,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE,在△ADC与△ABE中,,∴△ADC≌△ABE(SAS),∴CD=BE;故①,②正确;如图1,若AB与CD相交于点F,∵△ABE≌△ADC,∴∠ADC=∠ABE,∵∠AFD=∠CFB,∴∠DOB=∠DAB=50°.故③正确.如图2,连接OA,过点A作AM⊥CD于点M,AN⊥BE于点N,∴∠AMD=∠ANB=90°,∵△ABE≌△ADC,∴∠ABN=∠ADM,在△ABN和△ADM中,,∴△ABN≌△ADM(AAS),∴AN=AM,∴点A在∠DOE的平分线上.故④正确.故选:D.6.(2020秋•金昌期末)如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=30°,∠B=55°,则∠BDE的度数为( )A.35°B.40°C.45°D.50°【思路引导】根据三角形的内角和求出∠ACB=95°,利用三角形全等,求出DC=DE,再利用外角求出答案.【完整解答】解:∵∠CAB=30°,∠B=55°,∴∠ACB=180°﹣30°﹣55°=95°,∵CE⊥AD,∴∠AFC=∠AFE=90°,∵AD是△ABC的角平分线,∴∠CAD=∠EAD=×30°=15°,又∵AF=AF,∴△ACF≌△AEF(ASA)∴AC=AE,∵AD=AD,∠CAD=∠EAD,∴△ACD≌△AED(SAS),∴DC=DE,∴∠DCE=∠DEC,∵∠ACE=90°﹣15°=75°,∴∠DCE=∠DEC=∠ACB﹣∠ACE=95°﹣75°=20°,∴∠BDE=∠DCE+∠DEC=20°+20°=40°,故选:B.7.(2020秋•宜兴市期中)如图,在△ABC中,AB=4,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )A.B.C.D.【思路引导】把要求的最大值的两条线段经过平移后形成一条线段,然后再根据垂线段最短来进行计算即可.【完整解答】解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,在Rt△AHB中,∵∠ABC=60°,AB=4,∴BH=2,AH=2,在Rt△AHC中,∠ACB=45°,∴AH=CH=2,∴AC===2,∵点D为BC中点,∴BD=CD,在△BFD与△CKD中,,∴△BFD≌△CKD(AAS),∴BF=CK,延长AE,过点C作CN⊥AE于点N,得矩形ENCK,∴CK=EN,∴AE+BF=AE+CK=AE+EN=AN,在Rt△ACN中,AN<AC,当直线l⊥AC时,最大值为2,综上所述,AE+BF的最大值为2.故选:B.8.(2020秋•江岸区校级月考)如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)A.28B.29C.30D.31【思路引导】当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,由此即可判断.【完整解答】解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,∴一共有:8+24﹣1=31(个)三角形与△ABC全等,故选:D.二.填空题9.(2020秋•南岗区校级月考)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=5,则CH的长为 2 .【思路引导】先由AD⊥BC,CE⊥AB,判断出∠ADB=∠AEH=90°,再判断出∠BAD=∠BCE,进而判断出△HEA≌△BEC,得出AE=EC=5,即可得出结论.【完整解答】解:∵AD⊥BC,CE⊥AB,∴∠ADB=∠AEH=90°,∵∠AHE=∠CHD,∴∠BAD=∠BCE,在△HEA和△BEC中,,∴△HEA≌△BEC(AAS),∴AE=EC=5,则CH=EC﹣EH=AE﹣EH=5﹣3=2.故答案为:2.10.(2020•松北区一模)在△ABC中,点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD= 2 .【思路引导】延长CE于F,使CE=EF,交AB于点G,根据SAS证明△BEF与△DEC全等,进而利用全等三角形的性质解答即可.【完整解答】解:延长CE于F,使CE=EF,交AB于点G,∵E是BD的中点,∴BE=DE,在△BEF与△DEC中,,∴△BEF≌△DEC(SAS),∴∠F=∠DCE,BF=DC,∵∠ACB=∠ABC+2∠BCE,∴∠DCE=∠ACB﹣∠BCE=∠ABC+∠BCE,∵∠AGC=∠ABC+∠BCE,∴∠AGC=∠DCE,∴∠F=∠DCE=∠AGC=∠BGF,AG=AC,∴BF=BG=CD,设BF=BG=CD=x,∵AD=5,AB+AC=16,∴,解得:x=2,∴CD=2,故答案为:2.11.(2020•荷塘区模拟)在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为 4 .【思路引导】如图,延长BP交AC于D,先说明△ABD是等腰直角三角形,△ADP是30°的直角三角形,可得PD和AD的长,根据费马点的定义可得∠APC=120°,从而可知△PDC也是30°的直角三角形,可得CD的长,根据三角形的面积公式可得结论.【完整解答】解:如图,延长BP交AC于D,∵∠BAC=∠PBA=45°,∴∠ADB=90°,AD=BD,∵P为△ABC的费马点,∴∠APB=∠CPA=120°,∴∠BAP=180°﹣120°﹣45°=15°,∴∠PAC=45°﹣15°=30°,∴∠APD=60°,Rt△PAD中,∵PA=4,∴PD=2,AD=2,∵∠APC=120°,∴∠CPD=120°﹣60°=60°,Rt△PDC中,∠PCD=30°,∴CD=2,∴AC=AD+CD=2+2=4,∴△PAC的面积为==4.故答案为:4.12.(2020秋•海珠区校级期中)如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG,△ADG 和△ADE的面积分别为50和39,则△EDF的面积为 5.5 .【思路引导】在线段AC上取一点M,使DM=DE,过点D作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.【完整解答】解:如图,在线段AC上取一点M,使DM=DE,过点D作DN⊥AC于点N,∵DE=DG,∴DM=DG,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DN,在Rt△DEF和Rt△DMN中,,∴Rt△DEF≌Rt△DMN(HL),∵△ADG和△AED的面积分别为50和39,∴S△MDG =S△ADG﹣S△ADM=50﹣39=11,∴S△DNM =S△EDF=S△MDG=×11=5.5.故答案是:5.5.13.(2020秋•青羊区校级月考)如图,在△ABC中,∠C=90°,D是AB中点,FD⊥ED于D,BE=,AF=,则EF= 3 .【思路引导】延长DE到H,使DH=DE,连接FH,先证△BED≌△AHD(SAS),得AH=BE,∠B=∠DAH,再求出∠FAH=90°,然后由勾股定理求出FH=3,最后由线段垂直平分线上的性质即可得出答案.【完整解答】解:如图,延长DE到H,使DH=DE,连接FH,∵D是AB中点,∴AD=BD,在△BED和△AHD中,,∴△BED≌△AHD(SAS),∴AH=BE=,∠B=∠DAH,∵∠C=90°,∴∠FAH=∠BAC+∠DAH=∠BAC+∠B=180°﹣90°=90°,由勾股定理得,FH===3,∵FD⊥ED,DE=DH,∴EF=FH=3,故答案为:3.14.(2020秋•温岭市期中)如图,AD是△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,给出下列结论:①DE=DF;②△ADF≌△ADE;③△ABD和△ACD的面积相等.其中正确结论的序号是 ①② .【思路引导】根据角平分线的性质和全等三角形的判定和性质解答即可.【完整解答】解:∵AD是△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,∴DE=DF,故①正确;在Rt△ADF与Rt△ADE中,,∴Rt△ADF≌Rt△ADE(HL),故②正确;∵得不出AB=AC,∴△ABD和△ACD的面积无法判断相等,故③错误;故答案为:①②.15.(2019秋•南岗区校级月考)如图,在△ABC中,∠ACB=90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为 4 .【思路引导】设∠BCD=α,延长AC到点G,使AG=AB,连接BG,延长EF和CA交于点H,根据已知条件证明△CEH≌△CGB,即可解决问题.【完整解答】解:设∠BCD=α,∵∠ACB=90°,∴∠ACD=90°﹣α,∵AD=AC,∴∠ADC=∠ACD=90°﹣α,∴∠CAB=180°﹣2∠ACD=2α,∴∠ABC=90°﹣2α,∵EF⊥CD,∴∠CKF=90°,∴∠DFK=90°﹣(90°﹣α)=α,∴∠CEF=90°﹣α,如图,延长AC到点G,使AG=AB,连接BG,∵AD=AC,∴CD∥GB,BD=CG=CE,∴∠GBC=∠BCD=α,∴∠G=90°﹣α,∴∠G=∠CEF,延长EF和CA交于点H,∴∠H=α=∠GBC,∵∠CAB=2α,∴∠AFH=α,∴∠H=∠AFH,∴AH=AF=2,在△CEH和△CGB中,,∴△CEH≌△CGB(ASA),∴CH=CB=8,∴DF=AD﹣AF=AC﹣AH=CH﹣2AH=8﹣4=4.故答案为:4.16.(2019秋•江汉区期中)如图,AB⊥CD于点E,且AB=CD=AC,若点I是△ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=135°;②BD=BI;③S△AIC =S△BID;④IF⊥AC.其中正确的是 ①③④ (填序号).【思路引导】如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.利用全等三角形的判定和性质,平行四边形的判定和性质一一判断即可.【完整解答】解:如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.∵AB ⊥CD ,∴∠AEC =90°,∴∠EAC +∠ECA =90°,∴∠IAC +∠ICA =∠EAC +∠ECA =45°,∴∠AIC =180°﹣45°=135°,故①正确,∵AB =AC ,∠IAB =∠IAC ,AI =AI ,∴△AIB ≌△AIC (SAS ),∴∠AIB =∠AIC =135°,IA =ID ,∴∠BIC =360°﹣135°﹣135°=90°,同法可证:△ICA ≌△ICD (SAS ),∴∠AIC =∠CID =135°,IA =ID ,∴∠AID =360°﹣135°﹣135°=90°,∴∠DIB +∠AIC =180°,∵DF =FB ,IF =FG ,∴四边形IBGD 是平行四边形,∴ID =BG =AI ,ID ∥BG ,∴∠DIB +∠IBG =180°,∴∠AIC =∠IBG ,∵IA =ID ,IC =IB ,∴△AIC ≌△GBI (SAS ),∴∠GIB =∠ACI ,S △AIC =S △BGI =S 平行四边形DGBI =S △BDI ,故③正确,∵∠GIB +∠CIK =90°,∴∠CIK +∠ICK =90°,∴∠IKC =90°,即IF ⊥AC ,故④正确,不妨设BI =BD ,则△BDI 是等腰直角三角形,显然ID =IB ,即AI =IC ,显然题目不满足这个条件,故②错误.故答案为①③④.17.(2018秋•襄城县期末)如图,△ABC 的内角∠ABC 和外角∠ACD 的平分线相交于点E ,BE 交AC 于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:①∠BEC=∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有 ①③④ (将所有正确答案的序号填写在横线上).【思路引导】①根据角平分线的定义得到∠EBC=∠ABC,∠DCE=ACD,根据外角的性质即可得到结论;②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;③由BG=GE,CH=EH,于是得到BG﹣CH=GE﹣EH=GH.即可得到结论;④由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.【完整解答】解:①BE平分∠ABC,∴∠EBC=∠ABC,∵CE平分∠ACD,∴∠DCE=ACD,∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,∴∠EBC+∠BEC=(∠BAC+∠ABC)=∠EBC+BAC,∴∠BEC=∠BAC,故①正确;∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.③BE平分∠ABC,∴∠ABE=∠CBE,∵GE∥BC,∴∠CBE=∠GEB,∴∠ABE=∠GEB,∴BG=GE,同理CH=HE,∴BG﹣CH=GE﹣EH=GH,故③正确.④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,∵BE平分∠ABC,∴EM=ED,∵CE平分∠ACD,∴EN=ED,∴EN=EM,∴AE平分∠CAM,设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,则∠BAC=180°﹣2z,∠ACB=180﹣2x,∵∠ABC+∠ACB+∠BAC=180°,∴2y+180°﹣2z+180°﹣2x=180°,∴x+z=y+90°,∵z=y+∠AEB,∴x+y+∠AEB=y+90°,∴x+∠AEB=90°,即∠ACE+∠AEB=90°,故④正确;故答案为:①③④.18.(2019秋•潍坊月考)如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于 5.5 .【思路引导】可通过作辅助线,即延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,从而利用角之间的关系转化为线段之间的关系,进而最终可得出结论.【完整解答】解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,∵M是BC中点,∴BM=CM,∠BMN=∠CMF,∴△BMN≌△CMF,∴BN=CF,∠N=∠MFC,又∵∠BAD=∠CAD,MF∥AD,∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,∴AE=AF,BN=BE,∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,∴FC=(AB+AC)=5.5.故答案为5.5.三.解答题19.(2021春•铁岭月考)如图,在四边形ABCD中,∠B+∠ADC=180°,CE平分∠BCD交AB于点E,连接DE.(1)若∠A=50°,∠B=70°,求∠BEC的度数;(2)若∠A=∠1,试说明∠CDE=∠DCE.【思路引导】(1)求出∠A+∠BCD=180°,求出∠BCD,求出∠BCE,根据三角形内角和定理求出即可;(2)根据三角形内角和定理和∠A+∠BCD=180°求出∠CDE=∠BCE,即可得出答案.【完整解答】解:(1)∵∠A+∠B+∠BCD+∠ADC=360°,∠B+∠ADC=180°,∴∠A+∠BCD=180°,∵∠A=50°,∴∠BCD=130°,∵CE平分∠BCD∴∠BCE=∠BCD=×130°=65°,∵∠B=70°,∴∠BEC=180°﹣65°﹣70°=45°,(2)证明:由(1)知∠A+∠BCD=180°,∴∠A+∠BCE+∠DCE=180°,∵∠CDE+∠DCE+∠1=180°,∠1=∠A,∴∠BCE=∠CDE,∵CE平分∠BCD,∴∠DCE=∠BCE,∴∠CDE=∠DCE.20.(2021•南岗区模拟)已知:点E,F在BC上,AF=DE,BE=CF,∠AFE=∠DEF.(1)如图1,求证:AB=CD;(2)如图2,连接AC,BD,AE,DF,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.【思路引导】(1)证△ABF≌△DCE(SAS),即可得出结论;(2)由全等三角形的性质得∠B=∠C,得AB∥CD,再证四边形ABDC是平行四边形,得AC∥BD,同理证出AF∥DE,AE∥DF.【完整解答】(1)证明:∵BE=CF,∴BE﹣EF=CF﹣EF,即BF=CE,∵∠AFE=∠DEF,∴∠AFB=∠DEC,在△ABF和△DCE中,,∴△ABF≌△DCE(SAS),∴AB=CD;(2)解:图2中的四组平行线为:AB∥CD,AC∥BD,AF∥DE,AE∥DF,理由如下:由(1)得:△ABF≌△DCE,∴AB=DC,∠B=∠C,∴AB∥CD,∴四边形ABDC是平行四边形,∴AC∥BD,∵∠AFE=∠DEF,∴AF∥DE,∵AF=DE,∴四边形AEDF是平行四边形,∴AE∥DF.21.(2020秋•来宾期末)如图,在五边形ABCDE中,AB=DE,AC=AD.(1)请你添加一个与角有关的条件,使得△ABC≌△DEA,并说明理由;(2)在(1)的条件下,若∠CAD =65°,∠B =110°,求∠BAE 的度数.【思路引导】(1)添加∠BAC =∠EDA ,根据SAS 即可判定两个三角形全等;(2)根据全等三角形对应角相等,运用三角形内角和定理,即可得到∠BAE 的度数.【完整解答】解:(1)添加一个角方面的条件为:∠BAC =∠EDA ,使得△ABC ≌△DEA ,理由如下:在△ABC 和△DEA 中,,∴△ABC ≌△DEA (SAS ),(2)在(1)的条件下,∵△ABC ≌△DEA ,∴∠ACB =∠DAE ,∵∠CAD =65°,∠B =110°,∴∠ACB +∠BAC =180°﹣∠B =70°,∴∠DAE +∠BAC =∠ACB +∠BAC =70°,∴∠BAE =∠DAE +∠BAC +∠CAD =70°+65°=135°.22.(2020秋•云南期末)如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是152cm 2,AB =20cm ,AC =18cm ,求DE 的长.【思路引导】根据S △ABC =S △ABD +S △ACD ,再利用角平分线的性质即可解决问题.【完整解答】解:∵AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,∴DE =DF ,∵S △ABC =S △ABD +S △ACD ,∴S △ABC =,∵△ABC 面积是152cm 2,AB =20cm ,AC =18cm ,∴152=,∴10DE +9DF =152,∵DE =DF ,∴19DE =152,∴DE =8.23.(2021春•萧山区月考)如图,在△ABC 中,OE ⊥AB 与点E ,OF ⊥AC 与点F ,且OE =OF .(1)如图①,当O 为BC 中点时,试说明AB =AC ;(2)如图②,当点O 在△ABC 内部,且OB =OC ,试判断AB 与AC 的关系.【思路引导】(1)证Rt △OBE ≌Rt △OCF (HL ),得∠B =∠C ,即可得出AB =AC ;(2)由等腰三角形的性质得∠OBC =∠OCB ,再证Rt △OBE ≌Rt △OCF (HL ),得∠ABO =∠ACO ,则∠ABC =∠ACB ,即可得出结论.【完整解答】(1)说明如下:∵O 为BC 中点,∴BO =CO ,∵OE ⊥AB ,OF ⊥AC ,∴∠OEB =∠OFC =90°,在Rt △OBE 和Rt △OCF 中,,∴Rt △OBE ≌Rt △OCF (HL ),∴∠B =∠C ,∴AB =AC ;(2)解:AB=AC,理由如下:∵OB=OC,∴∠OBC=∠OCB,∵OE⊥AB,OF⊥AC,∴∠OEB=∠OFC=90°,在Rt△OBE和Rt△OCF中,,∴Rt△OBE≌Rt△OCF(HL),∴∠ABO=∠ACO,∴∠ABC=∠ACB,∴AB=AC.24.(2021春•南山区校级期中)如图,在△ABC中,AB=AC=3,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC= 30° ,∠AED= 70° .(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.【思路引导】(1)由平角的定义和三角形外角的性质可求∠EDC,∠DEC的度数;(2)当DC=3时,由“AAS”可证△ABD≌△DCE;(3)分AD=DE,DE=AE,AE=AD三种情况讨论,由三角形内角和和三角形外角的性质可求∠BDA 的度数.【完整解答】解:(1)∵∠ADB+∠ADE+∠EDC=180°,且∠ADE=40°,∠BDA=110°,∴∠EDC=180°﹣110°﹣40°=30°,∵AB=AC,∴∠B=∠C=40°,∴∠AED=∠EDC+∠C=30°+40°=70°,故答案为:30°,70°;(2)当DC=3时,△ABD≌△DCE,理由如下:∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠B=∠ADE=40°,∴∠BAD=∠CDE,且AB=CD=3,∠B=∠C=40°,∴△ABD≌△DCE(ASA);(3)若AD=DE时,∵AD=DE,∠ADE=40°,∴∠DEA=∠DAE=70°,∵∠DEA=∠C+∠EDC,∴∠EDC=30°,∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣30°=110°,若AE=DE时,∵AE=DE,∠ADE=40°,∴∠ADE=∠DAE=40°,∴∠AED=100°,∵∠DEA=∠C+∠EDC,∴∠EDC=60°,∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣60°=80°,若AE=AD时,∠AED=∠ADE=40°,∠DAE=180°﹣40°﹣40°=100°,此时D与B重合,不合题意,舍去.综上所述:当∠BDA=80°或110°时,△ADE的形状可以是等腰三角形.25.(2021春•沂源县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC 上,且BD=DF.(1)求证:CF=EB;(2)请你判断AE、AF与BE之间的数量关系,并说明理由.【思路引导】(1)根据角平分线的性质得到DC=DE,根据直角三角形全等的判定定理得到Rt△DCF≌Rt△DEB,根据全等三角形的性质定理得到答案;(2)根据全等三角形的性质定理得到AC=AE,根据(1)的结论得到答案.【完整解答】证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,∴DC=DE,在Rt△DCF和Rt△DEB中,,∴Rt△DCF≌Rt△DEB,∴CF=EB;(2)AF+BE=AE.∵Rt△DCF≌Rt△DEB,∴AC=AE,∴AF+FC=AE,即AF+BE=AE.26.(2020秋•腾冲市期末)(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.【思路引导】(1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;(2)由条件可知∠BAD+∠CAE=180°﹣α,且∠DBA+∠BAD=180°﹣α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论;(3)由条件可知EM=AH=GN,可得EM=GN,结合条件可证明△EMI≌△GNI,可得出结论I是EG 的中点.【完整解答】解:(1)如图1,∵BD⊥直线l,CE⊥直线l,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)DE=BD+CE.如图2,证明如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠DBA=∠CAE,在△ADB和△CEA中..∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE(3)如图3,过E作EM⊥HI于M,GN⊥HI的延长线于N.∴∠EMI=GNI=90°由(1)和(2)的结论可知EM=AH=GN∴EM=GN在△EMI和△GNI中,,∴△EMI≌△GNI(AAS),∴EI=GI,∴I是EG的中点.27.(2020秋•大武口区期末)如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,(1)求证:△ABC≌△ADE;(2)若AE∥BC,且∠E=∠CAD,求∠C的度数.【思路引导】(1)由∠1=∠2=∠3,可得∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,又∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,已知AC=AE,即可证得:△ABC≌△ADE;(2)由题意可得,∠ADB=∠ABD=4x,在△ABD中,可得x+4x+4x=180°,解答处即可;【完整解答】解:(1)∵∠1=∠2=∠3,∴∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,又∵∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,在△ABC和△ADE中,∴△ABC≌△ADE(AAS);(2)∵AE∥BC,∴∠E=∠3,∠DAE=∠ADB,∠2=∠C,又∵∠3=∠2=∠1,令∠E=x,则有:∠DAE=3x+x=4x=∠ADB,又∵由(1)得AD=AB,∠E=∠C,∴∠ABD=4x,∴在△ABD中有:x+4x+4x=180°,∴x=20°,∴∠E=∠C=20°.28.(2020秋•船营区期末)如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.【思路引导】已知等边及垂直,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.【完整解答】解:影子一样长.证明:∵AB⊥BC,A′B′⊥B′C′∴∠ABC=∠A′B′C′=90°∵AC∥A′C′∴∠ACB=∠A′C′B′在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS)∴BC=B′C′即影子一样长.。
【中】全等三角形手拉手模型(解析版)
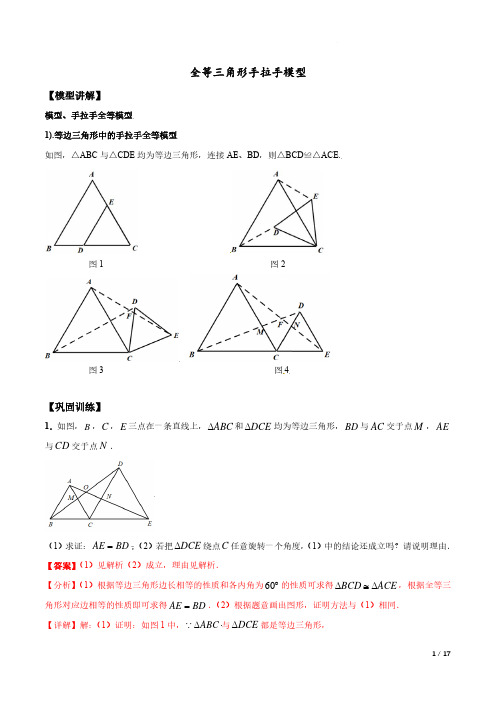
全等三角形手拉手模型【模型讲解】模型、手拉手全等模型1).等边三角形中的手拉手全等模型如图,△ABC 与△CDE 均为等边三角形,连接AE 、BD ,则△BCD ≌△ACE.图1图2图3图4【巩固训练】1.如图,B ,C ,E 三点在一条直线上,ABC ∆和DCE ∆均为等边三角形,BD 与AC 交于点M ,AE 与CD 交于点N .(1)求证:AE BD =;(2)若把DCE ∆绕点C 任意旋转一个角度,(1)中的结论还成立吗?请说明理由.【答案】(1)见解析(2)成立,理由见解析.【分析】(1)根据等边三角形边长相等的性质和各内角为60︒的性质可求得BCD ACE ∆≅∆,根据全等三角形对应边相等的性质即可求得AE BD =.(2)根据题意画出图形,证明方法与(1)相同.【详解】解:(1)证明:如图1中,ABC ∆ 与DCE ∆都是等边三角形,AC BC ∴=,CD CE =,60ACB DCE ∠=∠=︒,180ACB ACD DCE ∠+∠+∠= ,60ACD ∴∠=︒,ACB ACD ACD DCE ∠+∠=∠+∠,即BCD ACE ∠=∠.在BCD ∆和ACE ∆中,BC AC BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,BCD ACE ∴∆≅∆(SAS).BD AE ∴=.即AE=BD ,(2)成立AE BD =;理由如下:如图2中,ABC ∆ 、DCE ∆均为等边三角形,BC AC ∴=,CD CE =,60BCA DCE ∠=∠=︒,BCA ACD DCE ACD ∴∠+∠=∠+∠,即BCD ACE ∠=∠,在ACE ∆和BCD ∆中,AC BC BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,()ACE BCD SAS ∴∆≅∆,AE BD ∴=.【点睛】本题考查了等边三角形的性质的运用及全等三角形的判定和性质的运用.解决本题的关键是证明三角形全等,属于中考常考题型.2.如图1,若点P 是线段AB 上的动点(P 不与A ,B 重合),分别以AP 、PB 为边向线段AB 的同一侧作等边APC ∆和等边PBD ∆.(1)图1中,连接AD 、BC ,相交于点Q ,设AQC α∠=,那么α=o ;(2)如图2,若点P 固定,将PBD ∆绕点P 按顺时针方向旋转(旋转角小于180 ),此时α的大小是否发生变化?请说明理由.【答案】(1)60α= ;(2)此时α的大小不会发生改变,始终等于60 ,理由见解析【分析】(1)首先证得△APD ≌△CPB ,然后根据三角形的外角的性质即可求解;(2)旋转的过程中,(1)中得两个三角形的全等关系不变,因而角度不会变化.【详解】(1)60α= ,理由:∵△APC 是等边三角形,∴PA=PC ,∠APC=60°,∵△BDP 是等边三角形,∴PB=PD ,∠BPD=60°,∴∠APC=∠BPD ,∴∠APD=∠CPB ,∴△APD ≌△CPB ,∴∠PAD=∠PCB ,∵∠QAP+∠QAC+∠ACP=120°,∴∠QCP+∠QAC+∠ACP=120°,∴∠AQC=180°-120°=60°;(2)此时α的大小不会发生改变,始终等于60 .理由:∵APC ∆是等边三角形,∴PA PC =,60APC ∠=∵BDP ∆是等边三角形∴PB PD =,60BPD ∠= ∴APC BPD∠=∠∴APD CPB ∠=∠∴APD ∆≌CPB ∆∴PAD PCB∠=∠∵120QAP QAC ACP ∠+∠+∠= ∴120QCP QAC ACP ∠+∠+∠= ∴18012060AQC ∠=-=【点睛】本题考查旋转的性质、全等三角形的判定与性质,正确证明两个三角形全等是解题的关键.3.如图,AB=CB,BD=BE,∠ABC=∠DBE=α.(1)当α=60°,如图①则,∠DPE 的度数______________(2)若△BDE 绕点B 旋转一定角度,如图②所示,求∠DPE (用α表示)【答案】(1)60°;(2)∠DPE=α【分析】(1)利用SAAS 证得△ABE ≌△CBD ,利用全等三角形的性质得到∠AEB=∠CDB ,再利用三角形内角和定义以及等边三角形的性质即可解答;(2)利用SAAS 证得△ABE ≌△CBD ,利用全等三角形的性质得到∠AEB=∠BDC ,再利用三角形内角和定理即可完成.【详解】(1)解:∵∠ABC=∠DBE ∴∠ABC+∠CBE=∠DBE+∠CBE 即∠ABE=∠CBD在△ABE 和△CBD 中AB BC ABE CBD BE BD =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴∠AEB=∠CDB∵∠ABC=∠DBE ,AB=CB,BD=BE ∴△ABC 和△EBD 是等边三角形∴∠BDE=∠EDB=60°∵∠EDP+∠CDB=60°∴∠EDP+∠AEB=60°∵∠DPE+∠AEB+∠BED+∠EDP=180°∴∠DPE=60°故答案为:60°(2)如图:∵∠ABC=∠DBE=α∴∠ABC ﹣∠EBC=∠DBE ﹣∠EBC 即∠ABE=∠CBD在△ABE 和△CBD 中AB BC ABE CBD BE BD =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴∠AEB=∠BDC∵∠DQB+∠DBE+∠BDC=180°∠EQP+∠DPE+∠AEB=180°又∵∠DQB=∠EQP ∴∠DBE=∠DPE∴∠DPE=α【点睛】本题主要考查全等三角形的判定及性质,还涉及了等边三角形的判定及性质、三角形内角和定理等知识点,熟练掌握相关性质定理是解题关键.4.如图,△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB =∠COD =90°,AC 、BD 交于点M .(1)如图1,求证:AC=BD ,判断AC 与BD 的位置关系并说明理由;(2)如图2,∠AOB =∠COD =60°时,∠AMD 的度数为___________.【答案】(1)答案见解析;(2)120. 【分析】()1易证.BOD AOC ≌,,AMD ABM BAM ∠=∠+∠.BAM BAO OAC ∠=∠+∠.AMD ABM BAO OBD OBA BAO ∠=∠+∠+∠=∠+∠90.AOB ∠= 即可求得90.AMD ∠= 即可判断AC 与BD 的位置关系()2同理可得.=120.AMD OBA BAO ∠=∠+∠ 【详解】()190AOB COD ∠∠ ==,.AOB AOD COD AOD ∠+∠∠+∠=即:.BOD AOC ∠∠=,,OA OB OC OD ==易证.BOD AOC ≌.OBD OAC ∴∠=∠AC=BD∵,AMD ABM BAM ∠=∠+∠.BAM BAO OAC ∠=∠+∠∴.AMD ABM BAO OBD OBA BAO ∠=∠+∠+∠=∠+∠∵90.AOB ∠= ∴90.OBA BAO ∠+∠= 90.AMD ∴∠= ∴AC ⊥BD (2)同理可得..AMD OBA BAO ∠=∠+∠60.AOB ∠= 120.OBA BAO ∠+∠= 120.AMD ∴∠= 故答案为:120. 【点睛】本题考查了全等三角形的判定及性质,掌握全等三角形的判定及性质是解题的关键.2).等腰(直角)三角形中的手拉手全等模型1.如图,△ABC 与△ADE 均为等腰三角形,且∠BAC =∠DAE ,连接BD 、CE ,则△ABD ≌△ACE.2.两个共直角顶点的等腰直角三角形,绕点C 旋转过程中(B 、C 、D 不共线)始终有:①△BCD ≌△ACE ;②BD ⊥AE (位置关系)且BD=AE (数量关系);③FC 平分∠BFE【巩固训练】1.问题发现:(1)如图1,已知C 为线段AB 上一点,分别以线段AC ,BC 为直角边作等腰直角三角形,90ACD ∠=︒,CA CD =,CB CE =,连接AE ,BD ,线段AE ,BD 之间的数量关系为______;位置关系为_______.拓展探究:(2)如图2,把Rt ACD △绕点C 逆时针旋转,线段AE ,BD 交于点F ,则AE 与BD 之间的关系是否仍然成立?请说明理由.【答案】问题发现:(1)AE BD =;AE BD ⊥;拓展探究:(2)成立,理由见解析;拓展延伸:(3)5+【分析】问题发现:(1)根据题目条件证△ACE ≌△DCB ,再根据全等三角形的性质即可得出答案;拓展探究:(2)依然用SAS 证ACE DCB ∆≅∆,根据全等三角形的性质即可证得;【详解】解:问题发现:(1)如下图,延长BD ,交AE 于点F ,∵90ACD ∠=︒∴90,ACE DCB ︒∠=∠=又∵,CA CD CB CE ==∴B ACE DC ≅∆ (SAS ),∴AE=BD ,∠CAE=∠CDB∵90CDB CBD ∠+∠=︒∴90CAE CBD ∠+∠=︒∴90AFD ∠=︒∴AF FB ⊥∴AE ⊥BD ,故答案为:AE BD =,AE BD ⊥拓展探究:(2)成立.理由:如图1,设CE 与BD 相交于点G .∵90ACD BCE ∠=∠=︒,∴ACE BCD ∠=∠.又∵CB CE =,AC CD =,∴()ACE DCB SAS ≌,∴AE BD =,AEC DBC ∠=∠.∵90CBD CGB ∠+∠=︒,∴90AEC EGF∠+∠=︒,∴90AFB ∠=︒,∴BD AE ⊥.【点睛】本题考查了全等三角形的判定和性质,三角形三边关系,有2个形状相同的图形,有一个公共点,就是手拉手模型,手拉手模型必有全等,证明方法都是用“SAS”,所以熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.2.如图1,在线段BE 上取一点C ,分别以CB ,CE 为腰作等腰直角△BCA 和等腰直角△DCE ,连接BD 和AE.(1)请判断线段BD 和线段AE 的数量关系,并说明理由;(2)如图2,若B ,C ,E 三点不共线,(1)中的结论还成立吗?请说明理由.【答案】(1)BD =AE ,理由见解析;(2)成立,理由见解析【分析】(1)依据等腰直角三角形的性质可得到BC =AC ,DC =CE ,∠BCD =∠ACE =90°,然后依据SAS 证明△BCD ≌△ACE ,接下来,依据全等三角形的性质可得到BD =AE ;(2)依据等腰直角三角形的性质可得到BC =AC ,DC =CE ,∠BCD =∠ACE =90°,然后利用等式的性质证明∠BCD =∠ACE ,然后依据SAS 证明△BCD ≌△ACE ,接下来,依据全等三角形的性质可得到BD =AE .【详解】解:(1)∵△BCA 和△DCE 均为等腰直角三角形,∴BC =AC ,DC =CE ,∠BCD =∠ACE =90°.在△BCD 和△ACE 中,,,BC AC BCD ACE DC CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△ACE .∴BD =AE .(2)成立.∵△BCA 和△DCE 均为等腰直角三角形,∴BC =AC ,DC =CE ,∠BCD =∠ACE =90°.∴∠BCA +∠ACD =∠DCE +∠ACD ,即∠BCD =∠ACE .在△BCD 和△ACE 中,,,,BC AC BCD ACE DC CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△ACE .∴BD =AE .【点睛】本题主要考查的是全等三角形的性质和判定、等腰直角三角形的性质,熟练掌握相关知识是解题的关键.3.如图,将两块含45°角的大小不同的直角三角板△COD 和△AOB 如图①摆放,连结AC ,BD .(1)如图①,猜想线段AC 与BD 存在怎样的数量关系和位置关系,请写出结论并证明;(2)将图①中的△COD 绕点O 顺时针旋转一定的角度(如图②),连结AC ,BD ,其他条件不变,线段AC 与BD 存在(1)中的关系吗?请写出结论并说明理由.(3)将图①中的△COD 绕点O 逆时针旋转一定的角度(如图③),连结AC ,BD ,其他条件不变,线段AC 与BD存在怎样的关系?请直接写出结论.【答案】(1)AC=BD ,AC ⊥BD ,证明见解析;(2)存在,AC=BD ,AC ⊥BD ,证明见解析;(3)AC=BD ,AC ⊥BD【分析】(1)延长BD 交AC 于点E .易证△AOC ≌△BOD (SAS ),可得AC=BD ,∠OAC=∠OBD ,由∠ADE=∠BDO ,可证∠AED=∠BOD=90º即可;(2)延长BD 交AC 于点F ,交AO 于点G .易证△AOC ≌△BOD (SAS ),可得AC=BD ,∠OAC=∠OBD ,由∠AGF=∠BGO ,可得∠AFG=∠BOG=90º即可;(3)BD 交AC 于点H ,AO 于M ,可证△AOC ≌△BOD (SAS ),可得AC=BD ,∠OAC=∠OBD ,由∠AMH=∠BMO ,可得∠AHM=∠BOH=90º即可.【详解】(1)AC=BD ,AC ⊥BD ,证明:延长BD 交AC 于点E .∵△COD和△AOB均为等腰直角三角形,∴OC=OD,OA=OB,∠COA=∠BOD=90º,∴△AOC≌△BOD(SAS),∴AC=BD,∴∠OAC=∠OBD,∵∠ADE=∠BDO,∴∠AED=∠BOD=90º,∴AC⊥BD;(2)存在,证明:延长BD交AC于点F,交AO于点G.∵△COD和△AOB均为等腰直角三角形,∴OC=OD,OA=OB,∠DOC=BOA=90º,∵∠AOC=∠DOC-∠DOA,∠BOD=∠BOA-∠DOA,∴∠AOC=∠BOD,∴△AOC≌△BOD(SAS),∴AC=BD,∠OAC=∠OBD,∵∠AGF=∠BGO,∴∠AFG=∠BOG=90º,∴AC⊥BD;(3)AC=BD,AC⊥BD.证明:BD交AC于点H,AO于M,∵△COD和△AOB均为等腰直角三角形,∴OC=OD,OA=OB,∠DOC=BOA=90º,∵∠AOC=∠DOC+∠DOA,∠BOD=∠BOA+∠DOA,∴∠AOC=∠BOD,∴△AOC≌△BOD(SAS),∴AC=BD,∠OAC=∠OBD,∵∠AMH=∠BMO,∴∠AHM=∠BOH=90º,∴AC⊥BD.【点睛】本题考查三角形旋转变换中对应相等的位置与数量关系,掌握三角形全等的证明方法,及其角度计算是解题关键.3).其他手拉手全等模型如图1,在任意△ABC中,分别以AB、AC为边作等边△ADB、△ACE,连接DC、BE,则△ADC≌△ACE.如图2,在任意△ABC中,分别以AB、AC为边作正方形ABDE、ACFG,连接EC、BG,则△AEC≌△ABG.【巩固训练】1.已知:如图1,在ABC ∆和ADE ∆中,C E ∠=∠,CAE DAB ∠=∠,BC DE =.(1)证明ABC ADE ∆∆≌.(2)如图2,连接CE 和BD ,DE ,AD 与BC 分别交于点M 和N ,56DMB ∠=︒,求ACE ∠的度数.(3)在(2)的条件下,若CN EM =,请直接写出CBA ∠的度数.【答案】(1)证明见解析;(2)∠ACE =62°;(3)∠CBA =6°.【分析】(1)根据已知条件可以确定∠CAB =∠EAD ,结合已知条件,用AAS 可判定△ABC ≌△ADE ;(2)由(1)中△ABC ≌△ADE 可得∠CBA=∠EDA ,AC=AE ,在△MND 和△ANB 中,用三角形内角和定理由∠MND=∠ANB 可得∠DAB=∠DMB=56°,即∠CAE =∠DAB=56°,由AC=AE ,可得∠ACE=∠AEC=1(18056)622︒-︒=︒;(3)连接AM ,先证NCA MEA ≅V V (SAS),得到AM=AN,EAM CAN ∠=∠,进而可得EAC MAN ∠=∠,由(2)可知=56EAC MAN ︒∠=∠,根据等腰三角形内角和可得ANM ∠=1(18056)622︒︒︒-=,由三角形外角定理可得CBA ANM DAB ∠=∠-∠=62︒-56︒=6︒.【详解】解:(1)∵∠CAE =∠DAB ,∴∠CAE +∠CAD =∠DAB +∠CAD ,即∠CAB =∠EAD ,在△ABC 和△ADE 中,C E CAB EAD BC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (AAS ),(2)∵△ABC ≌△ADE ,∴∠CBA=∠EDA ,AC=AE ,在△MND 和△ANB 中,∵∠EDA +∠MND+∠DMB =180︒,∠CBA +∠ANB +∠DAB =180︒,又∵∠MND=∠ANB ,∴∠DAB=∠DMB=56︒,∴∠CAE =∠DAB=56︒,∵AC=AE ,∴∠ACE =∠AEC=1(18056)622︒︒︒-=,∴∠ACE =62︒,(3)∠CBA=6︒,如图所示,连接AM , NCA MEA ∠=∠,CN=EM,CA=EA,∴NCA MEA ≅V V (SAS),∴AM=AN,EAM CAN ∠=∠,∴EAM CAM ∠-∠=CAN CAM ∠-∠即EAC MAN ∠=∠,由(2)可得:=56EAC MAN ︒∠=∠,∴ANM ∠=1(18056)622︒︒︒-=, ∠CAE =∠DAB=56︒∴CBA ANM DAB ∠=∠-∠=62︒-56︒=6︒.【点睛】本题综合考查了三角形的相关定理与证明,较为综合,熟练掌握三角形的内角和定理,外角定理,全等三角形的判定与性质是解题的关键.2.如图,ABD 和AEC 均为等边三角形,连接BE 、CD .(1)请判断:线段BE 与CD 的大小关系是;(2)观察图,当ABD 和AEC 分别绕点A 旋转时,BE 、CD 之间的大小关系是否会改变?(3)观察如图和4,若四边形ABCD 、DEFG 都是正方形,猜想类似的结论是___________,在如图中证明你的猜想.【答案】(1)BE=CD (2)线段BE 与CD 的大小关系不会改变(3)AE =CG ,证明见解析(4)这些结论可以推广到任意正多边形.如图5,BB 1=EE 1,它们分别在△AE 1E 和△AB 1B 中,如图6,连接FF 1,可证△AB 1B ≌△AF 1F .图形见解析.【分析】本题是变式拓展题,图形由简单到复杂,需要从简单图形中探讨解题方法,并借鉴用到复杂图形中;证明三角形全等时,用旋转变换寻找三角形全等的条件.【详解】(1)线段BE 与CD 的大小关系是BE=CD ;(2)线段BE 与CD 的大小关系不会改变;(3)AE=CG .证明:如图4,正方形ABCD 与正方形DEFG 中,∵AD=CD ,DE=DG ,∠ADC=∠GDE=90°,又∠CDG=90°+∠ADG=∠ADE ,∴△ADE ≌△CDG ,∴AE=CG .【点睛】本题综合考查全等三角形、等边三角形和多边形有关知识.注意对三角形全等的证明方法的发散.3.如图,P 为等边ABC 的边BC 延长线上的一动点,以AP 为边向上作等边APD △,连接CD .(1)求证:ABP ACD ≌△△;(2)当PC AC =时,求PDC ∠的度数;(3)PDC ∠与PAC ∠有怎样的数量关系?随着点P 位置的变化,PDC ∠与PAC ∠的数量关系是否会发生变化?请说明理由.【答案】1)证明见解析;(2)30PDC ∠=︒;(3)PDC PAC ∠=∠;数量关系不变;理由见解析【分析】(1)先根据等边三角形的性质得出∠BAC =∠PAQ =60°,AB =AC ,AP =AQ ,再由SAS 定理即可得出结论;(2)由∠APC=∠CAP ,∠B=∠BAC ,∠B+∠BAC+∠APC+∠CAP=180°,得∠BAP=90°,再结合ABP ACD ≌△△,进而即可求解;(3)设CD 与AP 交于点O ,由ABP ACD ≌△△,得∠ACD=∠APD ,结合∠AOC=∠DOP ,三角形内角和定理,即可得到结论.【详解】(1)证明:∵△ABC 与△APD 是等边三角形,∴∠BAC =∠PAD =60°,AB =AC ,AP =AD ,∴∠BAP =∠DAC ,在△ABP 与△ACD 中,AB AC BAP CAD AP AD ⎧⎪∠∠⎨⎪⎩===,∴ABP ACD ≌△△(SAS );(2)∵PC AC =,∴∠APC=∠CAP ,∵△ABC 是等边三角形,∴∠B=∠BAC=60°,又∵∠B+∠BAC+∠APC+∠CAP=180°,∴∠BAC+∠CAP=12×180°=90°,即:∠BAP=90°,∴∠APB=90°-60°=30°,∴∠ADC=∠APB=30°,∵△APD 是等边三角形,∴PDC ∠=60°-∠ADC=60°-30°=30°;(3)PDC ∠=PAC ∠,随着点P 位置的变化,PDC ∠与PAC ∠的数量关系不会发生变化,理由如下:设CD 与AP 交于点O ,∵ABP ACD ≌△△,∴∠ACD=∠ABP=60°,∵∠APD=60°,∴∠ACD=∠APD ,又∵∠AOC=∠DOP ,∠AOC+∠ACD+∠PAC=180°,∠DOP+∠APD+∠PDC=180°,∴PDC ∠=PAC ∠.【点睛】本题主要考查全等三角形的判定和性质,等边三角形的性质,直角三角形的判定,熟练掌握全等三角形的判定和性质,是解题的关键.4.(1)作图发现:如图1,已知ABC ∆,小涵同学以AB 、AC 为边向ABC ∆外作等边ABD ∆和等边ACE ∆,连接BE ,CD .这时他发现BE 与CD 的数量关系是.(2)拓展探究:如图2,已知ABC ∆,小涵同学以AB 、AC 为边向外作正方形ABFD 和正方形ACGE ,连接BE ,CD ,试判断BE 与CD之间的数量关系,并说明理由.【答案】(1)BE=CD ;(2)BE=CD ,理由见解析;【分析】(1)利用等边三角形的性质得出,,60AD AB AC AE BAD CAE ==∠=∠=°,然后有CAD EAB ∠=∠,再利用SAS 即可证明CAD EAB ∆∆≌,则有BE CD =;(2)利用正方形的性质得出,,90AD AB AC AE BAD CAE ==∠=∠=°,然后有CAD EAB ∠=∠,再利用SAS 即可证明CAD EAB ∆∆≌,则有BE CD =;【详解】(1)如图1所示:ABD ∆ 和ACE ∆都是等边三角形,,,60AD AB AC AE BAD CAE ==∠=∠=∴°,BAD BAC CAE BAC ∴∠+∠=∠+∠,即CAD EAB ∠=∠,在CAD ∆和EAB ∆中,AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,()CAD EAB SAS ∆∆∴≌BE CD ∴=.(2)BE CD =, 四边形ABFD 和ACGE 均为正方形,AD AB ∴=,AC AE =,90BAD CAE ∠=∠=︒,BAD BAC CAE BAC ∴∠+∠=∠+∠CAD EAB ∠=∠∴,在CAD ∆和EAB ∆中,AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,()CAD EAB SAS ∆∆∴≌,BE CD ∴=。
专题01 全等三角形中的手拉手旋转模型(解析版)
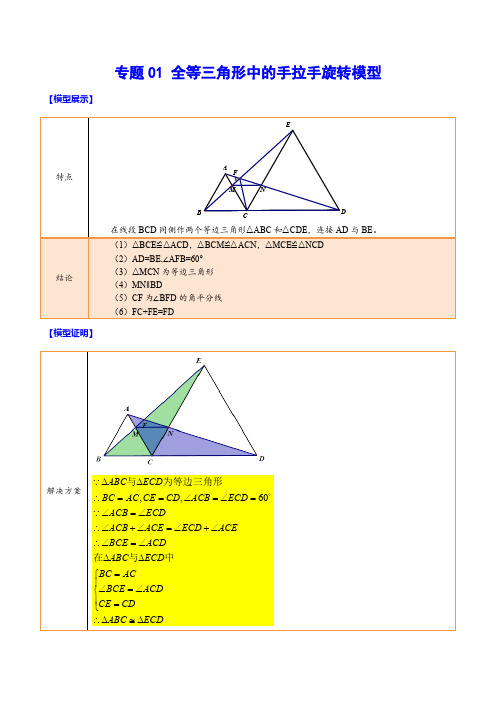
专题01 全等三角形中的手拉手旋转模型【模型展示】【模型证明】ECDABC CD CE ACD BCE AC BC ECD ABC ACD BCE ACE ECD ACE ACB ECDACB ECD ACB CD CE AC BC ECD ABC ∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∴∠+∠=∠+∠∴∠=∠=∠=∠==∴∆∆中与在为等边三角形与 60,,BDMN NCD MNC NCD MNC MCN MCN MCN CN CM ACN BCM AFB AFM BCM AFM BMC AMF MAF AFM BMC CBM BCM AFM AMF MAF BCM BMC CBM CADCBE ACD BCE ADBE ACD BCE //60606060,60)(180)(180180180∴∠=∠∴=∠=∠∴∆∆∴=∠=∴∆≅∆=∠=∠=∠∴∠=∠∠+∠-=∠∠+∠-=∠∴=∠+∠+∠=∠+∠+∠∠=∠∴∆≅∆=∴∆≅∆为等边三角形为等边三角形即P Q NMFECABD【模型拓展】【题型演练】一、单选题1.如图,在ABCV中,90ABC∠=°,分别以AB,AC为边作等边ABD△和等边ACEV,连结DE,若3AB=,5AC=,则ED=()A.B.C.4D.【答案】C【分析】在Rt△ABC中可直接运用勾股定理求出BC,然后结合“手拉手”模型证得△ABC≌△ADE,即可得到DE=BC,从而求解即可.【详解】解:在Rt△ABC中,AB=3,AC=5,∴由勾股定理得:BC=4,∵ABD △和ACE V 均为等边三角形,∴AB =AD ,AC =AE ,∠BAD =∠CAE =60°,∴∠BAD -∠CAD =∠CAE -∠CAD ,即:∠BAC =∠DAE ,在△ABC 和△ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS ),∴DE =BC =4,故选:C .【点睛】本题考查全等三角形的判定与性质,勾股定理的应用,掌握全等三角形的判定与性质,熟练运用勾股定理解三角形是解题关键.2.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论错误的是( )A .∠AOB =60°B .AP =BQC .PQ ∥AED .DE =DP【答案】D【分析】利用等边三角形的性质,BC ∥DE ,再根据平行线的性质得到∠CBE =∠DEO ,于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,得出A 正确;根据△CQB ≌△CPA (ASA ),得出B 正确;由△ACD ≌△BCE 得∠CBE =∠DAC ,加之∠ACB =∠DCE =60°,AC =BC ,得到△CQB ≌△CPA (ASA ),再根据∠PCQ =60°推出△PCQ 为等边三角形,又由∠PQC =∠DCE ,根据内错角相等,两直线平行,得出C 正确;根据∠CDE =60°,∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,可知∠DQE ≠∠CDE ,得出D 错误.【详解】解:∵等边△ABC 和等边△CDE ,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠BCD =∠DCE +∠BCD ,即∠ACD =∠BCE,在△ACD 与△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠DAC ,又∵∠ACB =∠DCE =60°,∴∠BCD =60°,即∠ACP =∠BCQ ,又∵AC =BC ,在△CQB 与△CPA 中,ACP BCQ AC BCPAC CBQ ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△CQB ≌△CPA (ASA ),∴CP =CQ ,又∵∠PCQ =60°可知△PCQ 为等边三角形,∴∠PQC =∠DCE =60°,∴PQ ∥AE ,故C 正确,∵△CQB ≌△CPA ,∴AP =BQ ,故B 正确,∵AD =BE ,AP =BQ ,∴AD -AP =BE -BQ ,即DP =QE ,∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE =60°,∴∠DQE ≠∠CDE ,故D 错误;∵∠ACB =∠DCE =60°,∴∠BCD =60°,∵等边△DCE ,∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,故A正确.故选:D.【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,解题的关键是找到不变量.3.如图,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC=5,AD=AE=2,点P,Q,R分别是BC,DC,DE的中点.把△ADE绕点A在平面自由旋转,则△PQR的面积不可能是()A.8B.6C.4D.2【答案】A【分析】连接BD、CE,BD的延长线交CE的延长线于O,AC交BO于H.证明△BAD≌△CAE,然后可推出△PQR是等腰直角三角形,S△PQR=12•PQ2,由AB=5,AD=2可知3≤BD≤7,从而得到32≤PQ≤72,那么9 8≤12•PQ2≤498,即可得出答案.【详解】解:连接BD、CE,BD的延长线交CE的延长线于O,AC交BO于H.∵AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴BD=CE,∠ABH=∠OCH,∵∠AHB=∠CHO,∴∠O=∠BAH=90°,∵点P ,Q ,R 分别是BC ,DC ,DE 的中点,∴PQ =12BD ,PQ ∥BO ,QR =12EC ,QR ∥CO ,∵BO ⊥OC ,∴PQ ⊥RQ ,PQ =QR ,∴△PQR 是等腰直角三角形,∴S △PQR =12•PQ 2,∵AB =5,AD =2,∴3≤BD ≤7,∴32≤PQ ≤72,∴98≤12•PQ 2≤498,∴△PQR 的面积不可能是8,故答案为:A .【点睛】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的判定和性质,三角形的中位线定理,解题的关键是灵活运用所学知识解决问题.4.如图,在ABC V 中,AB AC =,点D 、F 是射线BC 上两点,且AD AF ⊥,若AE AD =,15BAD CAF ∠=∠=°;则下列结论中正确的有( )①CE BF ⊥;②ABD ACE △≌△;③ABC ADCE S S =四边形△;④122BC EF AD CF-=-A .1个B .2个C .3个D .4个【答案】D【分析】由AD ⊥AF ,∠BAD=∠CAF ,得出∠BAC=90°,由等腰直角三角形的性质得出∠B=∠ACB=45°,由SAS 证得△ABD ≌△ACE (SAS ),得出BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,则∠ECB=90°,即EC ⊥BF ,易证∠ADF=60°,∠F=30°,由含30°直角三角形的性质得出EF=2CE=2BD ,DF=2AD ,则BD=12EF ,由BC-BD=DF-CF ,得出BC-12EF=2AD-CF ,即可得出结果.【详解】∵AD ⊥AF ,∠BAD=∠CAF ,∴∠BAC=90°,∵AB=AC ,∴∠B=∠ACB=45°,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩,∴△ABD ≌△ACE (SAS ),∴BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,∴∠ECB=90°,∴EC ⊥BF ,∵∠B=45°,∠BAD=15°,∴∠ADF=60°,∴∠F=30°,∴EF=2CE=2BD ,DF=2AD ,∴BD=12EF ,∵BC-BD=DF-CF ,∴BC-12EF=2AD-CF ,∴①、②、③、④正确.故选:D .【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、含30°角直角三角形的性质、外角的定义等知识,熟练掌握直角三角形的性质、证明三角形全等是解题的关键.5.如图,正ABC V 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有( )个①60AFB ∠=° ②连接FC ,则CF 平分BFD ∠ ③3BF DF = ④BF AF FC=+A .4B .3C .2D .1【答案】A【分析】根据“手拉手”模型证明BCE ACD V V ≌,从而得到CBE CAD ∠=∠,再结合三角形的外角性质即可求解60AFB ACB ∠=∠=°,即可证明①;作CM BE ⊥于M 点,CN AD ⊥于N 点,证明CEM CDN V V ≌,结合角平分线的判定定理即可证明②;利用面积法表示BCF △和DCF V 的面积,然后利用比值即可证明③;利用“截长补短”的思想,在AD 上取点Q ,使得FC FQ =,首先判断出FCQ V 为等边三角形,再结合“手拉手”模型推出BCF ACQ V V ≌即可证明④.【详解】解:①∵ABC V 和CDE △均为等边三角形,∴60ACB ECD ∠=∠=°,AC BC =,EC DC =,∴ACB ACE ECD ACE ∠+∠=∠+∠,∴BCE ACD ∠=∠,在BCE V 和ACD △中,BC AC BCE ACDEC DC =⎧⎪∠=∠⎨⎪=⎩∴()BCE ACD SAS V V ≌,∴CBE CAD ∠=∠,∵AFB CBE CDA ∠=∠+∠,ACB CDA CAD ∠=∠+∠,∴60AFB ACB ∠=∠=°,故①正确;②如图所示,作CM BE ⊥于M 点,CN AD ⊥于N 点,则90CME CND ∠=∠=°,∵BCE ACD V V ≌,∴CEM CDN ∠=∠,在CEM V 和CDN △中,CME CND CEM CDNCE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CEM CDN AAS V V ≌,∴CM CN =,∴CF 平分BFD ∠,故②正确;③如图所示,作FP BD ⊥于P 点,∵1122BCF S BF CM BC FP ==V g g ,1122DCF S DF CN CD FP ==V g g ,∴11221122BCFDCF BF CM BC FP S S DF CN CD FP ==V V g g g g ,∵CM CN =,∴整理得:BF BC DF CD=,∵3BC CD =,∴33BF CD DF CD==,∴3BF DF =,故③正确;④如图所示,在AD 上取点Q ,使得FC FQ =,∵60AFB ACB ∠=∠=°,CF 平分BFD ∠,∴120BFD ∠=°,1602CFD BFD ∠=∠=°,∴FCQ V 为等边三角形,∴60FCQ ∠=°,CF CQ =,∵60ACB ∠=°,∴ACB ACF FCQ ACF ∠+∠=∠+∠,∴BCF ACQ ∠=∠,在BCF △和ACQ V 中,BC AC BCF ACQCF CQ =⎧⎪∠=∠⎨⎪=⎩∴()BCF ACQ SAS V V ≌,∴BF AQ =,∵AQ AF FQ =+,FQ FC =,∴BF AF FC =+,故④正确;综上,①②③④均正确;故选:A .【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质等,理解等边三角形的基本性质,掌握全等三角形中的辅助线的基本模型,包括“手拉手”模型,截长补短的思想等是解题关键.6.如图,点C 是线段AE 上一动点(不与A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,有以下5个结论:①AD=BE ;②PQ ∥AE ;③AP=BQ ;④DE=DP ;⑤∠AOB=60°.其中一定成立的结论有( )个A .1B .2C .3D .4【答案】D 【分析】①由于△ABC 和△CDE 是等边三角形,可知AC=BC ,CD=CE ,∠ACB=∠DCE=60°,从而证出△ACD ≌△BCE ,可推知AD=BE;③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;②根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.【详解】①∵等边△ABC和等边△DCE,∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60∘,∴∠ACD=∠BCE,在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,DC=CE,∴△ACD≌△BCE(SAS),∴AD=BE;故①正确;③∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°(已证),∴∠BCQ=180°-60°×2=60°,∴∠ACB=∠BCQ=60°,在△ACP与△BCQ中,∠CAD=∠CBE,AC=BC,∠ACB=∠BCQ=60°,∴△ACP≌△BCQ(ASA),∴AP=BQ;故③正确;②∵△ACP≌△BCQ,∴PC=QC,∴△PCQ是等边三角形,∴∠CPQ=60∘,∴∠ACB=∠CPQ ,∴PQ ∥AE ;故②正确;④∵AD=BE ,AP=BQ ,∴AD−AP=BE−BQ ,即DP=QE ,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ ,∠CDE=60°,∴∠DQE≠∠CDE ,∴DE≠QE ,则DP≠DE ,故④错误;⑤∵∠ACB=∠DCE=60°,∴∠BCD=60°,∵等边△DCE ,∠EDC=60°=∠BCD ,∴BC ∥DE ,∴∠CBE=∠DEO ,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故⑤正确;综上所述,正确的结论有:①②③⑤,错误的结论只有④,故选D .【点睛】本题考查全等三角形的判定和性质,以及等边三角形的判定和性质,此图形是典型的“手拉手”模型,熟练掌握此模型的特点是解题的关键.二、填空题7.如图,ABD △、CDE △是两个等边三角形,连接BC 、BE .若30DBC ∠=°,6BD =,8BC =,则BE =________.【答案】BE =10【分析】连接AC ,根据题意易证△ACD ≌△BED(SAS),根据全等三角形的性质可得AC=BE ,再根据勾股定理求出AC 的值即可得出结论.【详解】如图,连接AC ,∵ABD △、CDE △是两个等边三角形,∴AB=BD=AD=2,CD=DE ,∠ABD=∠ADB=∠CDE=60,∴∠ADB+∠BDC=∠CDE+∠BDC ,∴∠ADC=∠BDE ,在△ACD 与△BDE 中AD BD ADC BDE CD DE =⎧⎪=⎨⎪=⎩∠∠,∴△ACD ≌△BED (SAS ),∴AC=BE ,∵30DBC ∠=°,∴∠ABC=∠ABD+∠DBC=60°+30°=90°,在Rt △ABC 中,AB=6,BC=8,∴10=,∴BE=10,故答案为:10.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,勾股定理,孰练的掌握知识点是解题关键.8.如图,△ABC 中,∠C =90°,AC =BC =△ABC 绕点A 顺时针方向旋转60°到△AB 'C '的位置,连接BC ',BC '的延长线交AB '于点D ,则BD 的长为 _____.【分析】连接BB ′,根据旋转的性质可得AB =AB ′,判断出△ABB ′是等边三角形,根据等边三角形的三条边都相等可得AB =BB ′,然后利用“边边边”证明△ABC ′和△B ′BC ′全等,根据全等三角形对应角相等可得∠ABC ′=∠B ′BC ′,延长BC ′交AB ′于D ,根据等边三角形的性质可得BD ⊥AB ′,利用勾股定理列式求出AB ,然后根据等边三角形的性质和等腰直角三角形的性质求出BD .【详解】解:如图,连接BB ′,∵△ABC 绕点A 顺时针方向旋转60°得到△AB ′C ′,∴AB =AB ′,∠BAB ′=60°,∴△ABB ′是等边三角形,∴AB =BB ′,在△ABC ′和△B ′BC ′中,AB BB AC B C BC BC =¢⎧⎪¢=¢¢⎨⎪¢=¢⎩,∴△ABC ′≌△B ′BC ′(SSS ),∴∠ABC ′=∠B ′BC ′30=° ,延长BC ′交AB ′于D ,则BD ⊥AB ′,∵∠C =90°,AC =BC ,∴AB 2=AB ’,∴AD =112AB =∴BD =,【点睛】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC ′在等边三角形的高上是解题的关键,也是本题的难点.9.如图,ABC V 是边长为5的等边三角形,BD CD =,120BDC ∠=°.E 、F 分别在AB 、AC 上,且60EDF ∠=°,则三角形AEF 的周长为______.【答案】10【分析】延长AB 到N ,使BN =CF ,连接DN ,求出∠FCD =∠EBD =∠NBD =90°,根据SAS 证△NBD ≌△FCD ,推出DN =DF ,∠NDB =∠FDC ,求出∠EDF =∠EDN ,根据SAS 证△EDF ≌△EDN ,推出EF =EN ,易得△AEF 的周长等于AB +AC .【详解】解:延长AB 到N ,使BN =CF ,连接DN ,∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,∵BD =CD ,∠BDC =120°,∴∠DBC =∠DCB =30°,∴∠ACD =∠ABD =30°+60°=90°=∠NBD ,∵在△NBD 和△FCD 中,BD DC NBD FCD BN CF =⎧⎪∠=∠⎨⎪=⎩,∴△NBD ≌△FCD (SAS ),∴DN =DF ,∠NDB =∠FDC ,∵∠BDC =120°,∠EDF =60°,∴∠EDB +∠FDC =60°,∴∠EDB +∠BDN =60°,即∠EDF =∠EDN ,在△EDN 和△EDF 中,DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩,∴△EDN ≌△EDF (SAS ),∴EF =EN =BE +BN =BE +CF ,即BE +CF =EF .∵△ABC 是边长为5的等边三角形,∴AB =AC =5,∵BE +CF =EF ,∴△AEF 的周长为:AE +EF +AF =AE +EB +FC +AF =AB +AC =10,故答案为:10.【点睛】本题考查了等边三角形性质和判定,等腰三角形的性质,三角形的内角和定理,全等三角形的性质和判定的综合运用.注意掌握辅助线的作法,注意掌握数形结合思想的应用.10.如图,C 为线段AE 上一动点(不与点A 、E 重合),在AE 同侧分别作正△ABC 和正△CDE ,AD 与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ P AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有_____.(把你认为正确的序号都填上)【答案】①②③⑤为等边三角形,再证【分析】根据等边三角形的性质及SAS即可证明;根据全等三角形的性质证明MCN明△ACD≌△BCE即可求解.【详解】解:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,∴AC=BC,EC=DC,∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE,故本选项正确,符合题意;②∵△ACD≌△ECB∴∠CBQ=∠CAP,又∵∠PCQ=∠ACB=60°,CB=AC,∴△BCQ≌△ACP,∴CQ=CP,又∠PCQ=60°,∴△PCQ为等边三角形,∴∠QPC=60°=∠ACB,∴PQ P AE,故本选项正确,符合题意;③∵∠ACB=∠DCE=60°,∴∠BCD=60°,∴∠ACP=∠BCQ,∵AC=BC,∠DAC=∠QBC,∴△ACP≌△BCQ(ASA),∴CP=CQ,AP=BQ,故本选项正确,符合题意;④已知△ABC 、△DCE 为正三角形,故∠DCE =∠BCA =60°⇒∠DCB =60°,又因为∠DPC =∠DAC +∠BCA ,∠BCA =60°⇒∠DPC >60°,故DP 不等于DE ,故本选项错误,不符合题意;⑤∵△ABC 、△DCE 为正三角形,∴∠ACB =∠DCE =60°,AC =BC ,DC =EC ,∴∠ACB +∠BCD =∠DCE +∠BCD ,∴∠ACD =∠BCE ,∴△ACD ≌△BCE (SAS ),∴∠CAD =∠CBE ,∴∠AOB =∠CAD +∠CEB =∠CBE +∠CEB ,∵∠ACB =∠CBE +∠CEB =60°,∴∠AOB =60°,故本选项正确,符合题意.综上所述,正确的结论是①②③⑤.三、解答题11.如图,ACB △和ECD V 都是等腰直角三角形,,,CA CB CD CE ACB ==△的顶点A 在ECD V 的斜边DE 上,连接BD .(1)求证:BD AE =.(2)若3cm,6cm AE AD ==,求AC 的长.【答案】(1)证明见解析;(2)AC =.【分析】(1)根据同角的余角相等得出∠BCD=∠ACE ,然后根据SAS 定理证明△BCD ≌△ACE ,从而得出结论;(2)根据全等三角形的性质得出∠BDC=∠AEC ,然后结合等腰直角三角形的性质求得∠BDA 是直角三角形,从而利用勾股定理求解.【详解】(1)∵ACB △和ECD V 都是等腰直角三角形,∴90ACB ECD ∠=∠=°,∴90,90ACD BCD ACD ACE ∠+∠=°∠+∠=°,∴BCD ACE ∠=∠,在BCD △和ACB △中,CB CA BCD ACECD CE =⎧⎪∠=∠⎨⎪=⎩∴()BCD ACE SAS V V ≌,∴BD AE =.(2)∵BCD ACE V V ≌,∴BDC AEC ∠=∠,又∵ECD V 是等腰直角三角形,∴45CDE CED ∠=∠=°,∴45BDC ∠=°,∴90BDC CDE ∠+∠=°,∴BDA ∠是直角三角形,∴22222223645AB BD AD AE AD =+=+=+=,在等腰直角三角形ACB 中,22222AB AC BC AC =+=,∴AC =【点睛】本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键.12.如图,A 、B 、C 在同一直线上,且△ABD ,△BCE 都是等边三角形,AE 交BD 于点M ,CD 交BE 于点N ,MN ∥AC ,求证:(1)∠BDN=∠BAM ;(2)△BMN 是等边三角形.【答案】(1)证明过程见详解;(2)证明过程见详解。
相似三角形重要模型-手拉手模型(解析版)-初中数学

相似三角形重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC =∠DAE =α,AD AB =AE AC=k ;结论:△ADE ∽△ABC ,△ABD ∽△ACE ;EC BD =k .2)手拉手相似模型(直角三角形)条件:如图,∠AOB =∠COD =90°,OC OA =OD OB =k (即△COD ∽△AOB );结论:△AOC ∽△BOD ;BD AC =k ,AC ⊥BD ,S ABCD =12AB ×CD .3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点;结论:△BME ∽△CMF ;BE CF =3.条件:△ABC 和ADE 是等腰直角三角形;结论:△ABD ∽△ACE .1(2023秋·福建泉州·九年级校考期末)问题背景:(1)如图①,已知△ABC ∽△ADE ,求证:△ABD ∽△ACE ;尝试应用:(2)如图②,在△ABC 和△ADE 中,∠BAC =∠DAE =90°,∠ABC =∠ADE =60°,AC 与DE相交于点F ,点D 在BC 边上,DF CF=233,求AD BD 的值;拓展创新:(3)如图③,D 是△ABC 内一点,∠BAD =∠CBD =30°,∠BDC =90°,AB =4,AC =23,求AD 的长.【答案】(1)见解析;(2)AD BD =2;(3)AD =5【分析】问题背景(1)由题意得出AB AD =AC AE ,∠BAC =∠DAE ,则∠BAD =∠CAE ,可证得结论;尝试应用(2)连接EC ,证明△ABC ∽△ADE ,由(1)知△ABD ∽△ACE ,由相似三角形的性质得出AE AD =EC BD =3,∠ACE =∠ABD =∠ADE ,可证明△ADF ∽△ECF ,得出DF CF =AD CE=233,则可求出答案.拓展创新(3)过点A 作AB 的垂线,过点D 作AD 的垂线,两垂线交于点M ,连接BM ,证明△BDC ∽△MDA ,由相似三角形的性质得出BD MD =DC DA ,证明△BDM ∽△CDA ,得出BM CA =DM AD=3,求出BM =6,由勾股定理求出AM ,最后由直角三角形的性质可求出AD 的长.【详解】问题背景(1)证明:∵△ABC ∽△ADE ,∴AB AD =AC AE ,∠BAC =∠DAE ,∴∠BAD =∠CAE ,AB AC =AD AE,∴△ABD ∽△ACE ;尝试应用(2)解:如图,连接EC ,∵∠BAC=∠DAE=90°,∠ABC=∠ADE=60°,∴△ABC∽△ADE,AE=3AD由(1)知△ABD∽△ACE,∴AEAD=ECBD=3,∠ACE=∠ABD=∠ADE=60°,∴AEEC=ADBD,∵∠AFD=∠AEFC∴△ADF∽△ECF∴DFCF =ADCE∵DF CF =233∴DFCF=ADCE=233∴AD=233CE∴AE=3AD=2CE∴ADBD=AEEC=2,拓展创新(3)解:如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,∵∠BAD=30°,∴∠DAM=60°,∴∠AMD=30°,∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴BDMD=DCDA,又∠BDC=∠ADM,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM=∠CDA,∴△BDM∽△CDA,∴BMCA=DMAD=3,∵AC=23,∴BM=23×3=6,∴AM=BM2-AB2=62-42=25,∴AD=12AM=5.【点睛】此题是相似形综合题,考查了直角三角形的性质,勾股定理,相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.2(2023秋·江苏无锡·九年级校考阶段练习)【模型呈现:材料阅读】如图,点B,C,E在同一直线上,点A,D在直线CE的同侧,△ABC和△CDE均为等边三角形,AE,BD 交于点F,对于上述问题,存在结论(不用证明):(1)△BCD≌△ACE(2)△ACE可以看作是由△BCD绕点C旋转而成;⋯【模型改编:问题解决】点A ,D 在直线CE 的同侧,AB =AC ,ED =EC ,∠BAC =∠DEC =50°,直线AE ,BD 交于F ,如图1:点B 在直线CE 上,①求证:△BCD ∽△ACE ; ②求∠AFB 的度数. 如图2:将△ABC 绕点C 顺时针旋转一定角度.③补全图形,则∠AFB 的度数为;④若将“∠BAC =∠DEC =50°”改为“∠BAC =∠DEC =m °”,则∠AFB 的度数为.(直接写结论)【模型拓广:问题延伸】如图3:在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =23,DG =6,连接AG ,BF ,求BF AG 的值.图1 图2 图3【答案】【模型改编:问题解决】①见解析;②65°;③图见解析,115°;④90°+m °2【模型拓广:问题延伸】233【分析】【模型改编:问题解决】①先证明△ABC ∽△EDC ,可得AC EC =BC DC,再证明∠ACE =∠BCD ,可得△BCD ∽△ACE ;②由△BCD ∽△ACE ,可得∠DBC =∠EAC ,再结合三角形的外角可得答案;③连接EA 并延长交BD 于F ,同理可得:△BCD ∽△ACE ,∠CEF =∠BDC ,再结合三角形的外角可得答案;④先求解∠CDE =∠DCE =12180°-m ° =90°-12m °,结合③的思路可得答案;【模型拓广:问题延伸】连接BD 、DF ,先证明△ADB ∽△GDF ,可得∠ADB =∠GDF ,AD DG =BD DF ,证明∠ADG =∠BDF ,可得△BDF ∽△ADG ,可得BF AG =BD AD,从而可得答案.【详解】【模型改编:问题解决】①∵AB =AC ,ED =EC ,∠BAC =∠DEC =50°,∴∠ABC =∠ACB =180°-50° ÷2=65°,∠EDC =∠ECD =180°-50° ÷2=65°,∴△ABC ∽△EDC ,∴AC EC =BC DC,∵∠ACE =180°-∠ACB =115°,∠BCD =180°-∠DCE =115°,∴∠ACE =∠BCD ,∴△BCD ∽△ACE ;②由①知,△BCD ∽△ACE ,∴∠DBC =∠EAC ,∴∠AFB =∠DBC +∠CEA =∠EAC +∠CEA =∠ACB =65°③补图如下:连接EA 并延长交BD 于F ,图2同理可得:△BCD ∽△ACE ∴∠CEF =∠BDC ,∴∠AFB =∠BDC +∠CDE +∠DEF =∠CEF +∠CDE +∠DEF =∠CED +∠CDE =50°+65°=115°,④∵∠BAC =∠DEC =m °,CE =DE ,∴∠CDE =∠DCE =12180°-m ° =90°-12m °,同理③可得∠AFB =∠CED +∠CDE =m °+90°-12m °=90°+m °2,故答案为:90°+m °2;【模型拓广:问题延伸】连接BD 、DF ,图3∵在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =FG =23,DG =6,∴AB AD =GF DG =33,又∵∠BAD =∠DGF =90°,∴△ADB ∽△GDF ,∴∠ADB =∠GDF ,AD DG=BD DF ,∵∠ADG =∠GDF +∠ADF ,∠BDF =∠ADB +∠ADF ,∴∠ADG =∠BDF ,∴△BDF ∽△ADG ,∴BF AG =BD AD,∵AD =23,AB =2,∴BD =AB 2+AD 2=4,∴BF AG =BD AD =423=233.【点睛】本题考查的是等腰三角形的性质,矩形的性质,勾股定理的应用,相似三角形的判定与性质,熟练的证明三角形相似是解本题的关键.3(2023春·湖北黄冈·九年级专题练习)【问题呈现】△CAB 和△CDE 都是直角三角形,∠ACB =∠DCE =90°,CB =mCA ,CE =mCD ,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当m =1时,直接写出AD ,BE 的位置关系:;(2)如图2,当m ≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当m =3,AB =47,DE =4时,将△CDE 绕点C 旋转,使A ,D ,E 三点恰好在同一直线上,求BE 的长.【答案】(1)BE ⊥AD (2)成立;理由见解析(3)BE =63或43【分析】(1)根据m =1,得出AC =BC ,DC =EC ,证明△DCA ≌△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(2)证明△DCA ∽△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(3)分两种情况,当点E 在线段AD 上时,当点D 在线段AE 上时,分别画出图形,根据勾股定理求出结果即可.【详解】(1)解:∵m =1,∴AC =BC ,DC =EC ,∵∠DCE =∠ACB =90°,∴∠DCA +∠ACE =∠ACE +∠ECB =90°,∴∠DCA =∠ECB ,∴△DCA ≌△ECB ,∴∠DAC =∠CBE ,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;故答案为:BE⊥AD.(2)解:成立;理由如下:∵∠DCE=∠ACB=90°,∴∠DCA+∠ACE=∠ACE+∠ECB=90°,∴∠DCA=∠ECB,∵DC CE =ACBC=1m,∴△DCA∽△ECB,∴∠DAC=∠CBE,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG =∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;(3)解:当点E在线段AD上时,连接BE,如图所示:设AE=x,则AD=AE+DE=x+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3x+4=3x+43,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE2+BE2=AB2,即x2+3x+432=472,解得:x=2或x=-8(舍去),∴此时BE=3x+43=63;当点D在线段AE上时,连接BE,如图所示:设AD=y,则AE=AD+DE=y+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3y,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE 2+BE 2=AB 2,即y +4 2+3y 2=47 2,解得:y =4或y =-6(舍去),∴此时BE =3y =43;综上分析可知,BE =63或43.【点睛】本题主要考查了全等三角形的判定和性质,相似三角形的判定和性质,三角形内角和定理的应用,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.4(2023秋·福建泉州·九年级校考阶段练习)如图,已知△ABC 中,AB =AC ,∠BAC =α.点D 是△ABC 所在平面内不与点A 、C 重合的任意一点,连接CD ,将线段CD 绕点D 顺时针旋转α得到线段DE ,连接AD 、BE .(1)如图1,当α=60°时,求证:BE =AD .(2)当α=120°时,请判断线段BE 与AD 之间的数量关系是,并仅就图2的情形说明理由.(3)当α=90°时,且BE ⊥AB 时,若AB =8,BE =2,点E 在BC 上方,求CD 的长.【答案】(1)见解析,(2)BE =3AD ,理由见解析(3)82【分析】(1)先证明△ABC 和△DCE 是等边三角形,再证明△ADC ≌△BEC ,可推出BE =AD ;(2)过A 作AH ⊥BC 与H ,先根据含30°的直角三角形的性质,等腰三角形的性质以及勾股定理可求出BC =3AC ,同理求出CE =3CD ,可得出BC EC =3AC 3DC=AC DC ,证明∠DCA =∠BCE ,然后证明△EBC ∽△DAC 即可求解;(3)过E 作EF ⊥BC 于F ,可判断△BEF 是等腰直角三角形,然后可求出EF ,BF ,CF 的长度,由(2)同理可证出△EBC ∽△DAC ,最后根据相似三角形的性质即可求解.【详解】(1)解:∵旋转,∴CD =ED ,当α=60°时,又AB =AC ,∴△ABC 和△DCE 是等边三角形,∴AC =BC ,DC =EC ,∠DCE =∠ACB =60°,∴∠ACD =∠BCE ,∴△ADC ≌△BEC ,∴AD =BE ;(2)解:BE =3AD 过A 作AH ⊥BC 与H ,∵AB =AC ,∠BAC =α=120°,∴∠ACB =30°,CH =12BC ,∴AC =2AH ,又由勾股定理得AH 2+CH 2=AC 2,∴CH =32AC ,∴BC =3AC ,同理CE =3CD ,∵DC =EC ,∠CDE =α=120°,∴∠DCE =30°=∠ACB ,∴∠DCA =∠BCE ,∵BC =3AC ,CE =3CD ,∴BC EC =3AC 3DC =AC DC ,∴△EBC ∽△DAC ,∴BE AD =BC AC =3,即BE =3AD (3)解:如图,过E 作EF ⊥BC 于F ,当α=90°时,∵AC =AB =8,∴∠ACB =45°,BC =AB 2+AC 2=2AC =82,∵BE ⊥AB ,∴∠EBF =45°=∠BEF ,∴BF =EF ,∵BE =EF 2+BF 2=2EF =2,∴EF =BF =2,∴CF =BF +BC =92,∴CE =EF 2+CF 2=241,由(2)同理可证△EBC ∽△DAC ,∴EC DC =BC AC=2,即241DC =2,∴DC =82.【点睛】本题属于三角形综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键在于正确寻找全等三角形或相似三角形.5(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠BAC =∠EAF =30°,连接BE ,CF,延长BE交CF于点D.则BE与CF的数量关系:,∠BDC=°;(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:;(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP=.【答案】(1)BE=CF,30(2)BE=CF,∠BDC=60°,证明见解析(3)BF=CF+2AM(4)7+74或7-74【分析】(1)根据已知得出∠BAE=∠CAF,即可证明△BAE≌△CAF,得出BE=CF,∠ABE=∠ACF,进而根据三角形的外角的性质即可求解;(2)同(1)的方法即可得证;(3)同(1)的方法证明△BAE≌△CAF SAS,根据等腰直角三角形的性质得出AM=12EF=EM=MF,即可得出结论;(4)根据题意画出图形,连接BD,以BD为直径,BD的中点为圆心作圆,以D点为圆心,1为半径作圆,两圆交于点P,P1,延长BP至M,使得PM=DP=1,证明△ADP∽△BDM,得出PA=22BM,勾股定理求得PB,进而求得BM,根据相似三角形的性质即可得出PA=221+7=2+142,勾股定理求得BQ,PQ,进而根据三角形的面积公式即可求解.【详解】(1)解:∵∠BAC=∠EAF=30°,∴∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF,∴BE=CF,∠ABE=∠ACF设AC,BD交于点O,∵∠AOD=∠ACF+∠BDC=∠ABE+∠BAO∴∠BDC=∠BAO=∠BAC=30°,故答案为:BE= CF,30.(2)结论:BE=CF,∠BDC=60°;证明:∵∠BAC=∠EAF=120°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF∴BE=CF,∠AEB=∠AFC∵∠EAF=120°,AE=AF,∴∠AEF=∠AFE=30°,∴∠BDC=∠BEF-∠EFD=∠AEB+30°-∠AFC-30°=60°,(3)BF=CF+2AM,理由如下,∵∠BAC=∠EAF=90°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵△ABC和△AEF均为等腰直角三角形∴AB=AC,AE=AF,∴△BAE≌△CAF SAS,∴BE= CF,在Rt △AEF 中,AM ⊥BF ,∴AM =12EF =EM =MF ,∴BF =BE +EF =CF +2AM ;(4)解:如图所示,连接BD ,以BD 为直径,BD 的中点为圆心作圆,以D 点为圆心,1为半径作圆,两圆交于点P ,P 1,延长BP 至M ,使得PM =DP =1,则△MDP 是等腰直角三角形,∠MDP =45°∵∠CDB =45°,∴∠MDB =∠MDP +∠PDC +∠CDB =90°+∠PDC =∠ADP ,∵AD DB =12,DP DM =12,∴△ADP ∽△BDM ∴PA BM =12=22,∴PA =22BM ,∵AB =2,在Rt △DPB 中,PB =DB 2-DP 2=22 2-12=7,∴BM =BP +PM =7+1∴PA =221+7 =2+142过点P 作PQ ⊥AB 于点Q ,设QB =x ,则AQ =2-x ,在Rt △APQ 中,PQ 2=AP 2-AQ 2,在Rt △PBQ 中,PQ 2=PB 2-BQ 2∴AP 2-AQ 2=PB 2-BQ 2∴2+142 2-2-x 2=7 2-x 2解得:x =7-74,则BQ =7-74,设PQ ,BD 交于点G ,则△BQG 是等腰直角三角形,∴QG =QB =7-74在Rt △DPB ,Rt △DP 1B 中,DP =DP 1DB =DB ∴Rt △DPB ≌Rt △DP 1B ∴∠PDB =∠P 1DB又PD =P 1D =1,DG =DG ∴△PGD ≌△P 1DG ∴∠PGD =∠P 1GD =45°∴∠PGP 1=90°,∴P 1G ∥AB ∴S △ABP 1=12AB ×QG =12×2×7-74=7-74,在Rt △PQB 中,PQ =PB 2-BQ 2=7 2-7-74 2=7+74∴S△ABP =12AB ×PQ =12×2×7+74=7+74,综上所述,S△ABP=7+74或7-74故答案为:7+74或7-74.【点睛】本题考查了全等三角形的性质与判定,相似三角形的性质与判定,正方形的性质,勾股定理,直径所对的圆周角是直角,熟练运用已知模型是解题的关键.6(2023·山东济南·九年级统考期中)问题背景:一次小组合作探究课上,小明将一个正方形ABCD和等腰Rt△CEF按如图1所示的位置摆放(点B、C、E在同一条直线上),其中∠ECF=90°.小组同学进行了如下探究,请你帮助解答:初步探究(1)如图2,将等腰Rt△CEF绕点C按顺时针方向旋转,连接BF,DE.请直接写出BF与DE的关系;(2)如图3,将(1)中的正方形ABCD和等腰Rt△CEF分别改成菱形ABCD和等腰△CEF,其中CE=CF,∠BCD=∠FCE,其他条件不变,求证:BF=DE;深入探究:(3)如图4,将(1)中的正方形ABCD和等腰Rt△CEF分别改成矩形ABCD和Rt△CEF,其中∠ECF=90°且CECF =CDBC=34,其它条件不变.①探索线段BF与DE的关系,说明理由;②连接DF,BE若CE=6,AB=12,直接写出DF2+BE2=.【答案】(1)BF=DE,BF⊥DE;(2)见解析;(3)①DEBF=34,DE⊥BF,见解析;②500【分析】(1)由正方形的性质,等腰直角三角形的性质,得到BC=CD,CE=CF,证明△BCF≌DCE,得到BF=DE,∠CBF=∠CDE,结合对顶角相等,即可得到BF⊥DE;(2)由菱形的性质,旋转的性质,先证明ΔBCF≌ΔDCE,即可得到结论成立;(3)①由矩形的性质,直角三角形的性质,先证明ΔBCF∽ΔDCE,得到BF与DE的数量关系,再由余角的性质证明位置关系即可;②连接BD,先求出矩形的边长,直角三角形的边长,与(1)同理先证明BF⊥DE,然后利用勾股定理,等量代换,即可得到DF2+BE2=500.【详解】解:(1)如图:∵正方形ABCD和等腰Rt△CEF中,∴BC=CD,CE=CF,∠BCD=∠ECF=90°,∴∠BCD+∠DCF=∠ECF+∠DCF,即∠BCF=∠DCE,∴△BCF≌DCE,∴BF=DE,∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DFG=90°∴BF⊥DE.(2)证明:如图:∵∠BCD=∠FCE,∴∠BCF=∠DCE,∵四边形ABCD为菱形∴BC=CD,又∵CE=CF∴△BCF≌△DCE(SAS),∴BF=DE;(3)①∵在矩形ABCD中,∠BCD=90°,∴∠BCD=∠FCE∴∠BCF=∠DCE,又∵CECF=CDBC=34∴△BCF∽△DCE,∴DEBF=CECF=34;∴∠CBF=∠CDE,设CD与BF交于点G∵∠BGC=∠DGF∴180°-∠CBF-∠BGC=180°-∠CDE-∠DGF,∴∠DQB=∠BCD=90°∴DE⊥BF.②如图:连接BD在矩形ABCD中,CD=AB=12,∵CE=6,6CF =12BC=34,∴CF=8,BC=16,∵△BCF∽△DCE,∴∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DQG=90°,∴BF⊥DE;在直角△BCD中,有BD2=BC2+CD2=162+122=400,在直角△BDQ中,BD2=BQ2+DQ2=400;在直角△CEF中,EF2=CE2+CF2=62+82=100,在直角△EFQ中,EF2=EQ2+FQ2=100;∴BQ2+DQ2+EQ2+FQ2=400+100=500;在直角△BEQ和直角△DFQ中,由勾股定理,则∵BQ2+EQ2=BE2,DQ2+FQ2=DF2,∴DF2+BE2=BQ2+DQ2+EQ2+FQ2=500;故答案为:500.【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,旋转的性质,勾股定理,以及等腰直角三角形的性质等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线,找到证明三角形相似和三角形全等的条件进行解题.7(2023春·广东·九年级专题练习)已知在△ABC中,O为BC边的中点,连接AO,将△AOC绕点O顺时针方向旋转(旋转角为钝角),得到△EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)如图2,当∠BAC =90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.【答案】(1)AE=CF;(2)成立,证明见解析;(3)511 3【分析】(1)结论AE=CF.证明ΔAOE≅ΔCOF(SAS),可得结论.(2)结论成立.证明方法类似(1).(3)首先证明∠AED=90°,再利用相似三角形的性质求出AE,利用勾股定理求出DE即可.【详解】解:(1)结论:AE=CF.理由:如图1中,∵AB=AC,∠BAC=90°,OC=OB,∴OA=OC=OB,AO⊥BC,∵∠AOC=∠EOF=90°,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(2)结论成立.理由:如图2中,∵∠BAC=90°,OC=OB,∴OA=OC=OB,∵∠AOC=∠EOF,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(3)如图3中,由旋转的性质可知OE =OA ,∵OA =OD ,∴OE =OA =OD =5,∴∠AED =90°,∵OA =OE ,OC =OF ,∠AOE =∠COF ,∴OA OC =OE OF ,∴ΔAOE ∽ΔCOF ,∴AE CF =OA OC,∵CF =OA =5,∴AE 5=53,∴AE =253,∴DE =AD 2-AE 2=102-253 2=5113.【点睛】本题属于几何变换综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.课后专项训练1(2023秋·北京顺义·九年级校考期中)如图,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .则BD CE的值为()A.12B.22C.2D.2【答案】B 【分析】由等腰直角三角形的性质可推出∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,从而可得出∠EAC =∠DAB ,AE AD =AC AB=2,证明△DAB ∽△EAC 即可得出结论.【详解】解:∵△ABC 和△ADE 都是等腰直角三角形,∴∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,∴∠EAC =∠DAB ,AE AD =AC AB =2,∴△DAB ∽△EAC ,∴BD CE =AD AE=22.故选B .【点睛】本题考查等腰直角三角形的性质,勾股定理,相似三角形的判定和性质.掌握三角形相似的判定条件是解题关键.2(2023春·浙江金华·九年级校考期中)如图,在Rt △ABC 中,∠ABC =90°,以AB ,AC 为边分别向外作正方形ABFG 和正方形ACDE ,CG 交AB 于点M ,BD 交AC 于点N .若GM CM =12,则CG BD=() A.12 B.34 C.255 D.13013【答案】D【分析】设AG =a =AB ,BC =2a ,由“AAS ”可证△ABC ≌△CHD ,可得AB =CH =a ,DH =BC =2a ,利用勾股定理分别求出CG ,BD 的长,即可求解.【详解】解:如图,过点D 作DP ⊥BC ,交AC 的延长线于点P,交BC 的延长线于点H ,∵AG ∥BF ,∴△AGM ∽△BCM ,∴AG BC =GM CM=12,∴设AG =a =AB ,BC =2a ,∴CG =GF 2+FC 2=a 2+(3a )2=10a ,∵DH ⊥BC ,AB ⊥BC ,∴∠DHC =∠ABC =∠ACD =90°,AB ∥DH ,∴∠DCH +∠ACB =90°=∠ACB +∠BAC ,∴∠DCH =∠BAC ,在△ABC 和△CHD 中,∠ABC =∠DHC ∠BAC =∠DCH AC =CD,∴△ABC ≌△CHD (AAS ),∴AB =CH =a ,DH =BC =2a ,∴BD =BH 2+DH 2=(3a )2+(2a )2=13a ,∴CG BD =10a 13a =13013.故选:D .【点睛】本题考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定和性质,添加恰当辅助线构造相似三角形是解题的关键.3(2023春·浙江丽水·九年级专题练习)如图,在△ABC 中,过点C 作CD ⊥AB ,垂足为点D ,过点D 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E ,F .连接EF 交线段CD 于点O ,若CO =22,CD =32,则EO ⋅FO 的值为( ).A.63B.4C.56D.6【答案】B【分析】由题意易得出∠DEC=∠DFC=90°,即说明点C,E,D,F四点共圆,得出∠DEO=∠FCO,从而易证△DOE∽△FOC,得出EOCO=DOFO.由题意可求出DO=CD-CO=2,即可求出EO⋅FO=CO⋅DO=4.【详解】解:∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°,∴点C,E,D,F四点共圆,∴∠DEF=∠FCD,即∠DEO=∠FCO.又∵∠DOE=∠FOC,∴△DOE∽△FOC,∴EOCO=DOFO,∴EO⋅FO=CO⋅DO.∵CO=22,CD=32,∴DO=CD-CO=2,∴EO⋅FO=CO⋅DO=22×2=4.故选B.【点睛】本题考查相似三角形的判定和性质,四点共圆的知识,圆周角定理.确定点C,E,D,F四点共圆,从而可得出证明△DOE∽△FOC的条件是解题关键.4(2022·广西梧州·统考一模)如图,在△ABC中,∠C=45°,将△ABC绕着点B逆时针方向旋转,使点C的对应点C′落在CA的延长线上,得到△A′BC′,连接AA′,交BC′于点O.下列结论:①∠AC′A′= 90°;②AA′=BC′;③∠A′BC′=∠A′AC′;④△A′OC′∽△BOA.其中正确结论的个数是()A.1B.2C.3D.4【答案】C【分析】利用旋转的性质和等腰三角形的性质推出∠AC A =90°,即可判断①的正确性;通过点A 、B、A、C 四点共圆可以判断出②③④的正确性.【详解】解:由题意可得:BC=BC ,∠C=∠A C B∵∠C=45°∴∠BC A=45°∵∠AC A =∠A C B+∠BC A∴∠AC A =90°,故①正确;∵∠BC A=∠C=45°∴∠C BC=90°∵∠ABC=∠A BC ∴∠A BA=90°∴∠A BA+∠AC A =180°,∠C AB+∠C A B=180°∴点A 、B、A、C 四点共圆∵∠AC A =90°,∠BAC ≠90°∴A A是直径,BC 不是直径∴A A≠BC ,故②错误;∵点A 、B、A、C 四点共圆∴∠A BC =∠A AC ,故③正确;∵点A 、B、A、C 四点共圆∴∠AA C =∠ABC ,∠A C B=∠A AB∴△A OC ∽△BOA,故④正确;∴正确结论的个数是3个故选C.【点睛】本题考查了图形的旋转、等腰三角形的性质、四点共圆、圆周角定理的推论以及相似的判定等知识点,灵活运用这些知识点是解题的关键.5(2023·广东深圳·校联考模拟预测)如图,已知▱ABCD ,AB =3,AD =8,将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,延长AB 交EF 于点H ,则FH 的长为.【答案】558【分析】先利用平行四边形的性质得到CD =AB =3,BC =AD =8,∠D =∠ABC ,再根据旋转的性质得到∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,接着证明△ADC ∽△AEH ,然后利用相似比求出EH ,从而得到FH 的长.【详解】解:∵四边形ABCD 为平行四边形,∴CD =AB =3,BC =AD =8,∠D =∠ABC ,∵将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,∴∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,∴∠E =∠D ,∵∠DAC =∠HAE ,∴△ADC ∽△AEH ,∴AD AE =DC EH ,∴83=3EH ,∴EH =98,∴FH =EF -EH =8-98=558,故答案为:558.【点睛】本题考查了平行四边形的性质,旋转、三角形相似的判定利用三角形相似比求线段的长,根据旋转的性质得到∠DAG =∠BAE ,然后根据两组对应角分别相等的两三角形相似得出AD AE=DC EH 是本题的关键.6(2022·安徽·模拟预测)如图,将边长为3的菱形ABCD 绕点A 逆时针旋转到菱形AB C D 的位置,使点B 落在BC 上,B C 与CD 交于点E .若BB =1,则CE 的长为.【答案】34/0.75【分析】延长D D 交BC 的延长线于点M ,过点C 作CN ∥DM 交B C 于点N ,根据菱形的性质和旋转的性质证明△ABB ≌△ADD ≌△DCM ≌B C M ,求得C D =B C =2,CM =C M =1,再根据CN ∥DM ,得CN MC =B C B M ,CN DC=CE DE ,代入即可求解.【详解】解:如图,延长D D 交BC 的延长线于点M ,过点C 作CN ∥DN 交B C 于点N ,∵四边形ABCD是菱形∴AB=BC=CD=AD=3,∠B=∠ADC=∠D ,AB∥CD∴∠DCM=∠B由旋转的性质得:AB =AB=3,AD =AD=3,∠BAB =∠DAD =∠MB C ,B C =D C =3,∠ADC=∠D ,∴△ABB ≌△ADD ∴DD =BB =1∴DC =D C -DD =2∵∠CDM+∠ADC=∠DAD +∠D ∴∠BAB =∠DAD =∠CDM∴△ABB ≌△DCM≌B C M,∴DM=AB =3,∠M=∠AB B∴C M=CM=3-2=1∵CN∥DM∴△B CN∽△B MC ∴CNMC =B CB M∵B C=BC-BB =2∴CN1=23∴CN=23∵CN∥DM∴△CNE∽△DC E∴CNDC =CEDE∴232=CE3-CE∴CE=34故答案为:34【点睛】本题考查菱形的性质,旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质,综合性较强,作辅助线构造全等三角形和相似三角形是解题的关键.7(2021·湖南益阳·统考中考真题)如图,Rt△ABC中,∠BAC=90°,tan∠ABC=32,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB C ,连接BB ,CC ,则△CAC 与△BAB 的面积之比等于.【答案】9:4【分析】先根据正切三角函数的定义可得ACAB=32,再根据旋转的性质可得AB=AB,AC=AC ,∠BAB=∠CAC =α,从而可得ACAC =ABAB=1,然后根据相似三角形的判定可得△CAC ∼△BAB ,最后根据相似三角形的性质即可得.【详解】解:∵在Rt△ABC中,∠BAC=90°,tan∠ABC=32,∴ACAB=32,由旋转的性质得:AB=AB ,AC=AC ,∠BAB =∠CAC =α,∴ACAC=ABAB=1,在△CAC 和△BAB 中,ACAC=ABAB∠CAC =∠BAB,∴△CAC ∼△BAB ,∴S△CACS△BAB=ACAB2=94,即△CAC 与△BAB 的面积之比等于9:4,故答案为:9:4.【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.8(2023秋·山东济南·九年级校考阶段练习)如图,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°.(1)求证:△ACD∽△BCE;(2)若AC=3,AE=8,求AD.【答案】(1)见详解(2)AD=103 3【分析】(1)根据30°的正切值得ACBC=DCEC,即可证明相似.(2)先证明∠BAE=90°,进而求出BE=10,再根据△ACD∽△BCE得出ADBE=ACBC=DCEC=33,即可求出AD=33BE=1033.【详解】(1)∵∠ACB=∠DCE=90°∴∠ACD=∠BCE∵∠ABC=∠CED=∠CAE=30°∴tan∠ABC=ACBC =33,tan∠CED=DCEC=33∴AC BC =DCEC∴△ACD∽△BCE(2)∵由(1),△ACD∽△BCE∴ADBE =ACBC=DCEC=33∵∠ABC=∠CED=∠CAE=30°∴∠BAC=60°∴∠BAE=90°∵AC=3,∠ABC=30°∴AB=2AC=6∵AE=8∴BE=10∴AD=33BE=1033【点睛】本题考查相似三角形的判定、特殊角三角函数值及勾股定理,根据特殊角得出对应线段成比例是解题关键.9(2023·安徽滁州·九年级校考阶段练习)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P、M.求证:(1)△BAE∽△CAD;(2)MP⋅MD=MA⋅ME.【答案】(1)证明见解析(2)证明见解析【分析】(1)由题意可得AC=2AB,AD=2AE,∠BAE=∠CAD=135°,即可证△BAE∽△CAD;(2)由△BAE∽△CAD可得∠BEA=∠CDA,即可证△PME∽△AMD,可得MP⋅MD=MA⋅ME.【详解】(1)证明:∵等腰Rt △ABC 和等腰Rt △ADE ,∴AB =BC ,AE =DE ,∠BAC =∠DAE =45°,∴AC =2AB ,AD =2AE ,∠BAE =∠CAD =135°,∴AC AB =AD AE=2,∴△BAE ∽△CAD ,(2)∵△BAE ∽△CAD ,∴∠BEA =∠CDA ,且∠PME =∠AMD ,∴△PME ∽△AMD ,∴ME MD =MP AM,∴MP ⋅MD =MA ⋅ME .【点睛】本题考查了相似三角形的判定和性质,等腰直角三角形性质,勾股定理的应用,熟练运用相似三角形的判定是本题的关键.10(2023秋·湖北孝感·九年级校联考阶段练习)问题背景:如图1,在△ABC 中,∠ACB =90°,AC =BC ,AD 是BC 边上的中线,E 是AD 上一点,将△CAE 绕点C 逆时针旋转90°得到△CBF ,AD 的延长线交BF 于点P .问题探究:(1)当点P 在线段BF 上时,证明EP +FP =2BP .①先将问题特殊化,如图2,当CE ⊥AD 时,证明:EP +FP =2BP ;②再探究一般情形,如图1,当CE 不垂直AD 时,证明:EP +FP =2BP ;拓展探究:(2)如图3,若AD 的延长线交BF 的延长线于点P 时,直接写出一个等式,表示EP ,FP ,BP 之间的数量关系.【答案】(1)①见解析,②见解析(2)EP -FP =2PB【分析】①结论:PE +PF =2PB .根据旋转的性质△ACE ≌△BCF ,再证明四边形CEPF 是正方形,可得结论.②结论不变,如图2中,过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .证明△CHF ≌△CGE ,可以推出FH =EG ,再利用正方形的性质解决问题即可.(2)结论:EP -FP =2PB ,证明方法类似②.【详解】(1)①证明:∵CE ⊥AD ,∴∠AEC =∠PEC =90°,在△ABC 中,∠ACB =90°,AC =AB ,∵将△CAE 绕点C 逆时针旋转90°得到△CBF ,∴△ACE ≌△BCF ,CF =CE ,∠ECF =90°,∠BFC =∠AEC =90°,∴∠BFC =∠ECF =∠PEC =90°,∴四边形CEPF 是矩形,∵CE =CF ,∴四边形CEPF 是正方形,∴CE =EP =FP =CF ,∠EPF =90°,∴∠BPD =90°=∠CED ,∵AD 是△ABC 中BC 边上的中线,∴BD =CD =12BC ,在△CED 和△BPD 中,∴∠CED =∠BPD∠CDE =∠BDP CD =BD,∴△CED ≌△BPD (AAS ),∴CE =BP ,∴BP =EP =CE =FP ,∴EP +FP =2BP②结论成立,证明:过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .则∠CGE =∠CGD =∠CHF =90°.由旋转性质可知,△CBF≌△CAE,∴CF=CE,∠CFB=∠CEA,∠ACE=∠BCF,∵∠CFH=180°-∠CFB,∠CEG=180°-∠CEA,∴∠CFH=∠CEG,∴△CHF≌△CGE,∴∠FCH=∠ECG,CH=CG,FH=EG.∴∠FCH+∠BCF+∠DCG=∠ECG+∠ACF+∠DCG=90°.∴∠HCG=90°.∴四边形CGPH是正方形.∴CG=GP=PH,∴EP+FP=GP+PH=2CG.∵CD=BD,∠CGD=∠BPD=90°,∠CDG=∠BDP,∴△CDG≌△BDP.∴CG=BP.∴EP+FP=2PB.(2)解:EP-FP=2PB.理由:如下图所示,过C作CN∥BP交AP于点N,CM∥DP交BP的延长线于点M,则四边形CNPM是平行四边形,△BPD∽△BMC,∴CN=PM,CM=PN,BPBM =BDBC=12,∴BM=2BP,∴PM=BP,∵∠APB=90°,∴∠NPM=90°,∴四边形CNPM是矩形,∴∠M=∠CNE=∠CNP=90°,在△CFM和△CEN中,∠H=∠CNE=90°∠CFH=∠CEN CF=CE,∴△CFM≌△CEN(AAS),∴CM=CN,FM=EN,∴四边形CNPM是正方形,∴PM=CN=PN,∴EP-FP=PN+EN-FP=PN+FM-FP=PN +PM=2PM,∴EP-FP=2BP.【点睛】本题属于几何变换综合题,考查相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质等知识,解题关键是正确寻找全等三角形解决问题,属于中考压轴题.11(2022·河南·九年级专题练习)规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.(1)问题联想:如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为,位置关系为;(2)类比探究:如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗?若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;(3)拓展延伸:如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.【答案】(1)BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由见解析;(3)BM =2DN ,BM ⊥DN .【分析】(1)根据SAS证明△ABM'≌△AND',进而得到BM =DN ,∠ABM'=∠ADN',再利用三角形内角和可推出∠BOD=90°,即BM ⊥DN ;(2)根据旋转和菱形的性质证明ΔABM ≌ΔADN ,再推出∠BOD=∠BAD=60°,故可求解;(3)根据旋转和矩形的性质证明ΔABM ∼ΔADN ,得到BM =2DN ,再推出∠BOD=∠BAD=90°即可求解.【详解】(1)如图设AB,DN 交于点H,,∵四边形ABCD,AMPN都是正方形,把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',∴AB=AD,AM'=AD', ∠BAM =∠DAN =150°∴△ABM'≌△AND',∴BM =DN ,∠ABM'=∠ADN',∵∠ADN'+∠DHA+∠DAH=180°,∠ABM'+∠BHO+∠BOD=180°,又∠DHA=∠BHO∴∠BOD=∠BAD=90°,即BM ⊥DN 故答案为:BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由:设AB,DN 交于点E,由旋转的性质可得∠BAM =∠DAN =150°.∵四边形ABCD,AM P N 都是菱形,∴AB=AD,AM =AN ,∴ΔABM ≌ΔADN ,∴BM =DN ,∠ABM =∠ADN .。
初中数学几何模型之——手拉手模型,跟我学-应对中考轻松自如
初中数学几何模型之——手拉手模型,跟我学-应对中考轻松自
如
一、模型一:手拉手模型----旋转型全等
(1)等边三角形
手拉手-等边旋转
【条件】:△OAB和△OCD均为等边三角形;
【结论】:①△OAC≌△OBD;②∠AEB=60°;③OE平分∠AED
(2)等腰直角三角形
手拉手-等腰直角旋转
【条件】:△OAB和△OCD均为等腰直角三角形;
【结论】:①△OAC≌△OBD;②∠AEB=90°;③OE平分∠AED
(3)顶角相等的两任意等腰三角形
手拉手-等腰旋转
【条件】:△OAB和△OCD均为等腰三角形;且∠COD=∠AOB
【结论】:①△OAC≌△OBD;②∠AEB=∠AOB;③OE平分∠AED
二、模型二:手拉手模型----旋转型相似
(1)一般情况
【条件】:CD∥AB,将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA
(2)特殊情况
【条件】:CD∥AB,∠AOB=90° 将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA;
③BD/AC=OD/OC=OB/OA=tan∠OCD;
④BD⊥AC;
⑤连接AD、BC,必有AD2+BC2=AB2+CD2;
⑥S△BCD=1/2AC×BD。
初中数学专题一 旋转中的几何模型(手拉手模型、对角互补模型)(解析版)

专题一旋转中的几何模型模型一 “手拉手”模型模型特征:两个等边三角形或等腰直角三角形或正方形共顶点.模型说明:如图1,△ABE,△ACF都是等边三角形,可证△AEC≌△ABF.如图2,△ABD,△ACE都是等腰直角三角形,可证△ADC≌△ABE.如图3,四边形ABEF,四边形ACHD都是正方形,可证△ABD≌△AFC.图1 图2 图3等腰图形有旋转,辩清共点旋转边,关注三边旋转角,全等思考边角边。
1【问题提出】(1)如图①,△ABC,△ADE均为等边三角形,点D,E分别在边AB,AC上.将△ADE绕点A沿顺时针方向旋转,连结BD,CE.在图②中证明△ADB≅△AEC.[学以致用](2)在(1)的条件下,当点D,E,C在同一条直线上时,∠EDB的大小为度.[拓展延伸](3)在(1)的条件下,连结CD.若BC=6,AD=4直接写出△DBC的面积S的取值范围.【思路点拨】(1)根据“手拉手”模型,证明△ADB≅△AEC即可;(2)分“当点E在线段CD上”和“当点E在线段CD的延长线上”两种情况,再根据“手拉手”模型中的结论即可求得∠EDB的大小;(3)分别求出△DBC的面积最大值和最小值即可得到结论【详解】(1)∵ABC,ADE均为等边三角形,∴AD=AE,AB=AC,∴∠DAE-∠BAE=∠BAC-∠BAE,即∠BAD=∠CAE在△ADB和△AEC中,AD=AE∠BAD=∠CAE AB=AC∴ABD ≅ACE (SAS );(2)当D ,E ,C 在同一条直线上时,分两种情况:①当点E 在线段CD 上时,如图,∵△ADE 是等边三角形,∴∠ADE =∠AED =60°,∴∠AEC =180°-∠AED =120°,由(1)可知,△ADB ≅△AEC ,∴∠ADB =∠AEC =120°,∴∠EDB =∠ADB -∠ADE =120°-60°=60°②当点E 在线段CD 的延长线上时,如图,∵△ADE 是等边三角形,∴∠ADE =∠AED =60°∴∠ADC =180°-∠ADE =120°,由(1)可知,△ADB ≅△AEC∴∠ADB =∠AEC =60°,∴∠EDB =∠ADB +∠ADE =60°+60°=120°综上所述,∠EDB 的大小为60°或120°(3)过点A 作AF ⊥BC 于点F ,当点D 在线段AF 上时,点D 到BC 的距离最短,此时,点D 到BC 的距离为线段DF 的长,如图:∵ΔABC 是等边三角形,AF ⊥BC ,BC =6∴AB =BC =6,BF =12BC =3∴AF =AB 2-BF 2=62-32=33∴DF =33-4此时S .DBC =12BC ⋅DF =12×6×(33-4)=93-12;当D 在线段FA 的延长线上时,点D 到BC 的距离最大,此时点D 到BC 的距离为线段DF 的长,如图,∵ΔABC 是等边三角形,AF ⊥BC ,BC =6∴AB =BC =6,BF =12BC =3,∴AF =AB 2-BF 2=62-32=33∵AD =4∴DF =AF +AD =33+4此时,S .DBC =12BC ⋅DF =12×6×(33+4)=93+12;综上所述,△DBC 的面积S 取值是93-12≤5≤93+12【点评】 利用“手拉手”模型,构造对应边“拉手线”组成的两个三角形全等是解题关键2已知正方形ABCD 和等腰直角三角形BEF ,BE =EF ,∠BEF =90°,按图1放置,使点F 在BC 上,取DF 的中点G ,连接EG ,CG .(1)探索EG,CG的数量关系和位置关系并证明;(2)将图(1)中△BEF绕点B顺时针旋转45°,再连接DF,取DF中点G(见图2),(1)中的结论是否仍然成立?证明你的结论;(3)将图(1)中△BEF绕点B顺时针转动任意角度(旋转角在0°到90°之间),再连接DF,取DF中点G(见图3),(1)中的结论是否仍然成立?证明你的结论.【思路点拨】(1)首先证明B、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG= GF=CG,得到∠EGF=2∠EDG,∠CGF=2∠CDG,从而证得∠EGC=90°;(2)首先证明△FEG≌△DHG,然后证明△ECH为等腰直角三角形.可以证得:EG=CG且EG⊥CG;(3)首先证明:△BEC≌△FEH,即可证得:△ECH为等腰直角三角形,从而得到:EG=CG且EG⊥CG.【解题过程】解:(1)EG=CG且EG⊥CG.证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.∴∠EGF=2∠EDG,∠CGF=2∠CDG.∴∠EGF+∠CGF=2∠EDC=90°,即∠EGC=90°,∴EG⊥CG.(2)仍然成立,证明如下:如图②,延长EG交CD于点H.∵BE⊥EF,∴EF∥CD,∴∠1=∠2.又∵∠3=∠4,FG=DG,∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,∴△HFG≌△CDG,∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,∴HE=EC,∠BEC=∠FEH,∴∠BEF=∠HEC=90°,∴△ECH为等腰直角三角形.又∵CG=GH,∴EG=CG且EG⊥CG.针对训练11已知ΔABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF,CF,AF.(1)问题发现:如图1,当点E在线段AD上时,且∠AFC=35°,则∠FAC的度数是;(2)结论证明:如图2,当点E 在线段AD 的延长线上时,请判断∠AFC 和∠FAC 的数量关系,并证明你的结论;(3)拓展延伸:若点E 在直线AD 上运动,若存在一个位置,使得ΔACF 是等腰直角三角形,请直接写出此时∠EBC 的度数.【答案】(1)55°;(2)∠AFC +∠FAC =90°,见解析;(3)15°或75°【解析】(1)55°,理由:∵ΔABC 是等边三角形,∴AB =AC =BC ,∠ABC =∠BAC =∠ACB =60°,∵AB =AC ,AD ⊥BC ,∴∠BAD =30°,∵将BE 绕点B 顺时针方向旋转60°得到BF ,∴BE =BF ,∠EBF =60°,∴∠EBF =∠ABC ,在△ADC 和△BDA 中,AB =BC∠ABE =∠FBC BE =BF,∴ΔABE ≌ΔCBF SAS ,∴∠BAE =∠BCF =30°,∴∠ACF =90°,∴∠AFC +∠FAC =90°;∵∠AFC =35°,∴∠FAC =55°;(2)结论:∠AFC +∠FAC =90°,理由如下:∵ΔABC 是等边三角形,∴AB =AC =BC ,∠ABC =∠BAC =∠ACB =60°,∵AB =AC ,AD ⊥BC ,∴∠BAD =30°,∵将BE 绕点B 顺时针方向旋转60°得到BF ,∴BE =BF ,∠EBF =60°,∴∠EBF =∠ABC ,在△ADC 和△BDA 中,AB =BC∠ABE =∠FBC BE =BF,∴ΔABE ≌ΔCBF SAS ,∴∠BAE =∠BCF =30°,∴∠ACF =90°,∴∠AFC +∠FAC =90°;(3)∠EBC =15°或75°分两种情况:①点E 在点A 的下方时,如图:∵ΔACF 是等腰直角三角形,∴AC =CF ,由(2)得ΔABE ≌ΔCBF ,∴CF =AE ,∴AC =AE =AB ,∴∠ABE =180°-30°2=75°,∴∠EBC =∠ABE -∠ABC =75°-60°=15°;②点E 在和点A 的上方时,如图:同理可得∠EBC =∠ABE +∠ABC =75°.2已知四边形ABCD 是正方形,将线段CD 绕点C 逆时针旋转α(0°<α<90°),得到线段CE ,联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F .(1)如图,当BE =CE 时,求旋转角α的度数;(2)当旋转角α的大小发生变化时,∠BEF 的度数是否发生变化?如果变化,请用含α的代数式表示;如果不变,请求出∠BEF 的度数;(3)联结AF ,求证:DE =2AF .【答案】(1)30°;(2)不变;45°;(3)见解析【解析】(1)证明:在正方形ABCD 中, BC =CD .由旋转知,CE=CD,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形,∴∠BCE=60°.又∵∠BCD=90°,∴α=∠DCE=30°.(2)∠BEF的度数不发生变化.在△CED中,CE=CD,∴∠CED=∠CDE=180°-α2=90°-α2,在△CEB中,CE=CB,∠BCE=90°-α,∴∠CEB=∠CBE=180°-∠BCE2=45°+α2,∴∠BEF=180°-∠CED-∠CEB=45°.(3)过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于点H,过点C作CI⊥DF于点I易知四边形AGFH是平行四边形,又∵BF⊥DF,∴平行四边形AGFH是矩形.∵∠BAD=∠BGF=90°,∠BPF=∠APD,∴∠ABG=∠ADH.又∵∠AGB=∠AHD=90°,AB=AD,∴△ABG≌△ADH.∴AG=AH,∴矩形AGFH是正方形.∴∠AFH=∠FAH=45°,∴AH=AF∵∠DAH+∠ADH=∠CDI+∠ADH=90°∴∠DAH=∠CDI又∵∠AHD=∠DIC=90°,AD=DC,∴△AHD≌△DIC∴AH=DI,∵DE=2DI,∴DE=2AH=2AF模型二 对角互补模型对角互补模型的特征:外观呈现四边形,且对角和为180°。
中考数学几何模型复习 专题 手拉手模型(学生版+解析版)

中考数学几何模型复习手拉手模型一、方法突破问题一:构成手拉手的必要条件.当对一个几何图形记忆并不深刻的时候,可以尝试用文字取总结要点,比如手拉手:四线共点,两两相等,夹角相等.条件:如图,OA=OB,OC=OD(四线共点,两两相等),∠AOB=∠COD(夹角相等)结论:△OAC≌△OBD(SAS)证明无需赘述,关于条件中的OA=OB,OC=OD,有时候会直接以特殊几何图形的形式给出,比如我们都很熟悉的等边三角形和正方形.1.等边三角形手拉手(1)如图,B、C、D三点共线,△ABC和△CDE是等边三角形,连接AD、BE,交于点P:结论一:△ACD≌△BCE证明:AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩→ △ACD≌△BCE(SAS)ABCDOD(2)记AC 、BE 交点为M ,AD 、CE 交点为N :结论二:△ACN ≌△BCM ;△MCE ≌△NCD证明:MBC NAC BC AC BCM ACN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △ACN ≌△BCM (SAS );MCE NCD CE CDCEM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △MCE ≌△NCD (ASA ) (3)连接MN :结论三:△MNC 是等边三角形.证明:60CM CNMCN =⎧⎨∠=︒⎩→△MCN 是等边三角形.(4)记AD 、BE 交点为P ,连接PC :结论四:PC 平分∠BPD证明:△BCE ≌△ACD → CG =CH → PC 平分∠BPD .DDHG ααEDCBAP(5)结论五:∠APB =∠BPC =∠CPD =∠DPE =60°.(6)连接AE :结论六:P 点是△ACE 的费马点(P A +PC +PE 值最小)2.正方形手拉手如图,四边形ABCD 和四边形CEFG 均为正方形,连接BE 、DG :结论一:△BCE ≌△DCG证明:CB CD BCE DCG CE CG =⎧⎪∠=∠⎨⎪=⎩→ △BCE ≌△DCG (SAS )结论二:BE =DG ,BE ⊥DG证明:△BCE ≌△DCG → BE =DG ;∠CBE =∠CDG → ∠DHB =∠BCD =90°(旋转角都相等)【重点概述】手拉手模型是一种基本的旋转型全等,与其说看图找模型,不如是“找条件、定模型”.60°60°60°60°PABCDEEDCBAPF问题二:条件与结论如何设计?设计一:我们可以给出手拉手模型条件,得到一组全等来解决问题,就像问题一中所得出的结论那样; 设计二:如果题目已知△ABC ≌△ADE 外,则还可得△ABD 和△ACE 均为等腰三角形,且有△ABD ∽△ACE ,AB AD BDAC AE CE==.问题三:如何构造手拉手?如何构造手拉手?换句话说,如何构造旋转?当我们在思考这个问题的时候,不妨先问一句,旋转能带来什么?图形位置的改变,这一点就够了,因为,若有数量关系,则先有位置关系.二、典例精析例一:如图,等边三角形ABC 的边长为4,点O 是ABC ∆的中心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①OD OE =;②ODE BDE S S ∆∆=;③四边形ODBEBDE ∆周长的最小值为6.上述结论中正确的个数是( )A .1B .2C .3D .4例二:如图,点P 在等边ABC ∆的内部,且6PC =,8PA =,10PB =,将线段PC 绕点C 顺时针旋转60︒得到P C ',连接AP ',则sin PAP '∠的值为 .EDCBAC例三:如图,P 是等边三角形ABC 内一点,将线段AP 绕点A 顺时针旋转60︒得到线段AQ ,连接BQ .若6PA =,8PB =,10PC =,则四边形APBQ 的面积为 .例四:如图,等边三角形ABC 内有一点P ,分別连结AP 、BP 、CP ,若6AP =,8BP =,10CP =.则ABP BPC S S ∆∆+= .例五:如图,P 为等边三角形ABC 内的一点,且P 到三个顶点A ,B ,C 的距离分别为3,4,5,则ABC∆的面积为( )A.9 B.9 C.18+D.18 例六:在Rt △ABC 中,AB =AC ,点P 是三角形内一点且∠APB =135°,PC =AC 的最大值为_________.QPABCPABCPABCABCP三、中考真题演练1.(2021•日照)问题背景:如图1,在矩形ABCD中,AB=30ABD∠=︒,点E是边AB的中点,过点E作EF AB⊥交BD于点F.实验探究:(1)在一次数学活动中,小王同学将图1中的BEF∆绕点B按逆时针方向旋转90︒,如图2所示,得到结论:①AEDF=;②直线AE与DF所夹锐角的度数为.(2)小王同学继续将BEF∆绕点B按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.拓展延伸:在以上探究中,当BEF∆旋转至D、E、F三点共线时,则ADE∆的面积为.2.(2021•贵港)已知在ABC∆中,O为BC边的中点,连接AO,将AOC∆绕点O顺时针方向旋转(旋转角为钝角),得到EOF∆,连接AE,CF.(1)如图1,当90=;=时,则AE与CF满足的数量关系是AE CF∠=︒且AB ACBAC(2)如图2,当90≠时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若∠=︒且AB ACBAC不成立,请说明理由.(3)如图3,延长AO到点D,使OD OABC=时,求DE的长.=,连接DE,当5==,6AO CF3.(2021•黑龙江)在等腰ADE ∆中,AE DE =,ABC ∆是直角三角形,90CAB ∠=︒,12ABC AED ∠=∠,连接CD 、BD ,点F 是BD 的中点,连接EF .(1)当45EAD ∠=︒,点B 在边AE 上时,如图①所示,求证:12EF CD =;(2)当45EAD ∠=︒,把ABC ∆绕点A 逆时针旋转,顶点B 落在边AD 上时,如图②所示,当60EAD ∠=︒,点B 在边AE 上时,如图③所示,猜想图②、图③中线段EF 和CD 又有怎样的数量关系?请直接写出你的猜想,不需证明.4.(2021•通辽)已知AOB ∆和MON ∆都是等腰直角三角形)OM OA <<,90AOB MON ∠=∠=︒.(1)如图1,连接AM ,BN ,求证:AM BN =; (2)将MON ∆绕点O 顺时针旋转.①如图2,当点M 恰好在AB 边上时,求证:2222AM BM OM +=;②当点A ,M ,N 在同一条直线上时,若4OA =,3OM =,请直接写出线段AM 的长.5.(2021•十堰)已知等边三角形ABC,过A点作AC的垂线l,点P为l上一动点(不与点A重合),连接CP,把线段CP绕点C逆时针方向旋转60︒得到CQ,连QB.(1)如图1,直接写出线段AP与BQ的数量关系;(2)如图2,当点P、B在AC同侧且AP AC=时,求证:直线PB垂直平分线段CQ;∆,(3)如图3,若等边三角形ABC的边长为4,点P、B分别位于直线AC异侧,且APQ求线段AP的长度.6.(2020•沈阳)在ABC ∆中,AB AC =,BAC α∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接DB ,DC . (1)如图1,当60α=︒时, ①求证:PA DC =; ②求DCP ∠的度数;(2)如图2,当120α=︒时,请直接写出PA 和DC 的数量关系.(3)当120α=︒时,若6AB =,BP D 到CP 的距离为 .中考数学几何模型复习手拉手模型一、方法突破问题一:构成手拉手的必要条件.当对一个几何图形记忆并不深刻的时候,可以尝试用文字取总结要点,比如手拉手:四线共点,两两相等,夹角相等.条件:如图,OA=OB,OC=OD(四线共点,两两相等),∠AOB=∠COD(夹角相等)结论:△OAC≌△OBD(SAS)证明无需赘述,关于条件中的OA=OB,OC=OD,有时候会直接以特殊几何图形的形式给出,比如我们都很熟悉的等边三角形和正方形.3.等边三角形手拉手(1)如图,B、C、D三点共线,△ABC和△CDE是等边三角形,连接AD、BE,交于点P:结论一:△ACD≌△BCE证明:AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩→ △ACD≌△BCE(SAS)ABCDOD(2)记AC 、BE 交点为M ,AD 、CE 交点为N :结论二:△ACN ≌△BCM ;△MCE ≌△NCD证明:MBC NAC BC AC BCM ACN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △ACN ≌△BCM (SAS );MCE NCD CE CDCEM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △MCE ≌△NCD (ASA ) (3)连接MN :结论三:△MNC 是等边三角形.证明:60CM CNMCN =⎧⎨∠=︒⎩→△MCN 是等边三角形.(4)记AD 、BE 交点为P ,连接PC :结论四:PC 平分∠BPD证明:△BCE ≌△ACD → CG =CH → PC 平分∠BPD .DDDHG ααEDCBAP(5)结论五:∠APB =∠BPC =∠CPD =∠DPE =60°.(6)连接AE :结论六:P 点是△ACE 的费马点(P A +PC +PE 值最小)4.正方形手拉手如图,四边形ABCD 和四边形CEFG 均为正方形,连接BE 、DG :结论一:△BCE ≌△DCG证明:CB CD BCE DCG CE CG =⎧⎪∠=∠⎨⎪=⎩→ △BCE ≌△DCG (SAS )结论二:BE =DG ,BE ⊥DG证明:△BCE ≌△DCG → BE =DG ;∠CBE =∠CDG → ∠DHB =∠BCD =90°(旋转角都相等)【重点概述】手拉手模型是一种基本的旋转型全等,与其说看图找模型,不如是“找条件、定模型”.60°60°60°60°PAB CDEEDCBAPF问题二:条件与结论如何设计?设计一:我们可以给出手拉手模型条件,得到一组全等来解决问题,就像问题一中所得出的结论那样; 设计二:如果题目已知△ABC ≌△ADE 外,则还可得△ABD 和△ACE 均为等腰三角形,且有△ABD ∽△ACE ,AB AD BDAC AE CE==.问题三:如何构造手拉手?如何构造手拉手?换句话说,如何构造旋转?当我们在思考这个问题的时候,不妨先问一句,旋转能带来什么?图形位置的改变,这一点就够了,因为,若有数量关系,则先有位置关系.二、典例精析例一:如图,等边三角形ABC 的边长为4,点O 是ABC ∆的中心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①OD OE =;②ODE BDE S S ∆∆=;③四边形ODBEBDE ∆周长的最小值为6.上述结论中正确的个数是( )A .1B .2C .3D .4 【分析】等边三角形中的旋转型全等连接OB 、OC ,易证△OBD ≌△OCE ,∴OD =OE ,结论①正确;考虑∠FOG 是可以旋转的,△ODE 面积和△BDE 面积并非始终相等,故结论②错误;ECBACC∵△OBD ≌△OCE ,∴四边形ODBE 的面积等于△OBC的面积,142OBCS=⨯=,故结论③正确;考虑BD =CE ,∴BD +BE =CE +BE =4,只要DE 最小,△BDE 周长就最小,△ODE 是顶角为120°的等腰三角形,故OD 最小,DE 便最小, 当OD ⊥AB 时,OD此时2DE ==,∴周长最小值为6,故结论④正确. 综上,选C ,正确的有①③④.【小结】所谓全等,实际就是将△ODB 绕点O 旋转到△OEC 的位置.等等,好像和某个图有点神似,如下:当然这个图形还可以简化一下,毕竟和D 点及F 点并没有什么关系.结论与证明不多赘述,题型可以换,但旋转是一样的旋转.例二:如图,点P 在等边ABC ∆的内部,且6PC =,8PA =,10PB =,将线段PC 绕点C 顺时针旋转60︒得到P C ',连接AP ',则sin PAP '∠的值为 .【分析】连接PP ',则CPP '△是等边三角形,故6PP PC '==,易证△CPB ≌CP A '△,∴10AP BP '==, 又AP =8,∴APP '△是直角三角形,∴3sin 5PAP '∠=.D例三:如图,P 是等边三角形ABC 内一点,将线段AP 绕点A 顺时针旋转60︒得到线段AQ ,连接BQ .若6PA =,8PB =,10PC =,则四边形APBQ 的面积为 .【分析】分四边形为三角形.连接PQ ,易证△APQ 是等边三角形,△BPQ 是直角三角形,26APQS=168242BPQS =⨯⨯=, ∴四边形APBQ的面积为(.例四:如图,等边三角形ABC 内有一点P ,分別连结AP 、BP 、CP ,若6AP =,8BP =,10CP =.则ABP BPC S S ∆∆+= .【分析】构造旋转.如图,将△BPC 绕点B 逆时针旋转60°得△BEA ,连接EP , 可得△AEP 是直角三角形,△BEP 是等边三角形,21688242APBBPCAEPBEPSSSS+=+=⨯⨯+=+ 所以本题答案为24+QPABCQPABCPABCC搭配一:若222PA PB PC+=,则可任意旋转,得等边+直角.且两条较短边夹角(∠APB)为150°.搭配二:若∠APB=150°,则有222PA PB PC+=.例五:如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则ABC∆的面积为()A.9B.9C.18+D.18【分析】(3,4,5)是一组勾股数,通过旋转构造直角三角形.法一:如图,将三个小三角形面积分别123S S S、、考虑到△ABC是等边三角形,可将△APB 旋转到△ADC位置,可得:21331334642ADP PCDS S S S+=+=+⨯⨯=,同理可得:212143462S S++⨯⨯=,223153462S S+=+⨯⨯=,∴()123218S S S++,∴1239S S S++,故选A.CC CPABCS3S2S1PAB CC法二:如图,易证∠APB =150°,过点A 作BP 的垂线交BP 延长线于点H ,则1322AH AP ==,PH,4BH =)2229271625944S AH BH ==+=+++=+=⎝. 【思考】如果放在正方形里,条件与结论又该如何搭配?作旋转之后,可得△AEP 是等腰直角三角形,若使△PEB 也为直角三角形, 则原∠APD =135°,而线段PA 、PB 、PD 之间的关系为:2222PA PD PB +=.搭配一:若∠APD =135°,则2222PA PD PB +=;搭配二:若2222PA PD PB +=,则∠APD =135°.另外,其实这个图和点C 并没有什么关系,所以也可以将正方形换成等腰直角三角形. 大概如下图:抓主要条件,舍弃无用条件,也是理解几何图形的一种方式.例六:在Rt △ABC 中,AB =AC ,点P 是三角形内一点且∠APB =135°,PC =AC 的最大值为_________.【分析】显然根据∠APB =135,构造旋转.可得:△APQ 是等腰直角三角形,△PQC 是直角三角形,且∠PQC =90°,另外还有条件PC =HPABC EAB CDEPABCPC重新梳理下条件,(1)有一条线段PC =(2)∠PQC =90°,则Q 点轨迹是个圆弧,(3)以PQ 为斜边在PC 异侧作等腰直角三角形,点A 是直角顶点.∴A 点轨迹是什么?瓜豆原理啦,也是个圆弧:∴AC22=.三、中考真题演练1.(2021•日照)问题背景:如图1,在矩形ABCD 中,AB =30ABD ∠=︒,点E 是边AB 的中点,过点E 作EF AB ⊥交BD 于点F . 实验探究:(1)在一次数学活动中,小王同学将图1中的BEF ∆绕点B 按逆时针方向旋转90︒,如图2所示,得到结论:①AEDF= ;②直线AE 与DF 所夹锐角的度数为 . (2)小王同学继续将BEF ∆绕点B 按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由. 拓展延伸:在以上探究中,当BEF ∆旋转至D 、E 、F 三点共线时,则ADE ∆的面积为 .CPP PCCC【解答】解:(1)如图1,30ABD ∠=︒,90DAB ∠=︒,EF BA ⊥,cos BE AB ABD BF DB ∴∠==, 如图2,设AB 与DF 交于点O ,AE 与DF 交于点H ,BEF ∆绕点B 按逆时针方向旋转90︒,90DBF ABE ∴∠=∠=︒,FBD EBA ∴∆∆∽,∴AE BE DF BF ==,BDF BAE ∠=∠, 又DOB AOF ∠=∠,30DBA AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30︒,,30︒;(2)结论仍然成立,理由如下:如图3,设AE 与BD 交于点O ,AE 与DF 交于点H ,将BEF ∆绕点B 按逆时针方向旋转,ABE DBF ∴∠=∠,又BE AB BF DB ==, ABE DBF ∴∆∆∽,∴AE BE DF BF ==,BDF BAE ∠=∠, 又DOH AOB ∠=∠,30ABD AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30︒.拓展延伸:如图4,当点E 在AB 的上方时,过点D 作DG AE ⊥于G ,2AB =30ABD ∠=︒,点E 是边AB 的中点,90DAB ∠=︒,BE ∴2AD =,4DB =,30EBF ∠=︒,EF BE ⊥,1EF ∴=,D 、E 、F 三点共线,90DEB BEF ∴∠=∠=︒,DE ∴30DEA ∠=︒,12DG DE ∴==由(2)可得:AE BE DF BF ==,∴=AE ∴,ADE ∴∆的面积1122AE DG =⨯⨯==; 如图5,当点E 在AB 的下方时,过点D 作DG AE ⊥,交EA 的延长线于G ,同理可求:ADE ∆的面积1122AE DG =⨯⨯==2.(2021•贵港)已知在ABC ∆中,O 为BC 边的中点,连接AO ,将AOC ∆绕点O 顺时针方向旋转(旋转角为钝角),得到EOF ∆,连接AE ,CF .(1)如图1,当90BAC ∠=︒且AB AC =时,则AE 与CF 满足的数量关系是 ;(2)如图2,当90BAC ∠=︒且AB AC ≠时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)如图3,延长AO 到点D ,使OD OA =,连接DE ,当5AO CF ==,6BC =时,求DE 的长.【解答】解:(1)结论:AE CF=.理由:如图1中,=,∠=︒,OC OB AB ACBAC=,90⊥,∴==,AO BCOA OC OB∠=∠=︒,AOC EOF90∴∠=∠,AOE COF=,=,OE OFOA OCAOE COF SAS∴∆≅∆,()∴=.AE CF(2)结论成立.理由:如图2中,=,∠=︒,OC OBBAC90∴==,OA OC OB∠=∠,AOC EOF∴∠=∠,AOE COF=,=,OE OFOA OC∴∆≅∆,AOE COF SAS()∴=.AE CF(3)如图3中,由旋转的性质可知OE OA=,OA OD=,5OE OA OD∴===,90AED∴∠=︒,OA OE=,OC OF=,AOE COF∠=∠,∴OA OEOC OF=,AOE COF∴∆∆∽,∴AE OACF OC=,5 CF OA==,∴5 53 AE=,253 AE∴=,DE∴=.3.(2021•黑龙江)在等腰ADE ∆中,AE DE =,ABC ∆是直角三角形,90CAB ∠=︒,12ABC AED ∠=∠,连接CD 、BD ,点F 是BD 的中点,连接EF .(1)当45EAD ∠=︒,点B 在边AE 上时,如图①所示,求证:12EF CD =; (2)当45EAD ∠=︒,把ABC ∆绕点A 逆时针旋转,顶点B 落在边AD 上时,如图②所示,当60EAD ∠=︒,点B 在边AE 上时,如图③所示,猜想图②、图③中线段EF 和CD 又有怎样的数量关系?请直接写出你的猜想,不需证明.【解答】(1)证明:如图①中,EA ED =,45EAD ∠=︒,45EAD EDA ∴∠=∠=︒,90AED ∴∠=︒,BF FD =,12EF DB ∴=, 90CAB ∠=︒,45CAD BAD ∴∠=∠=︒,1452ABC AED ∠=∠=︒, 45ACB ABC ∴∠=∠=︒,AC AB ∴=,AD ∴垂直平分线段BC ,DC DB ∴=,12EF CD ∴=. (2)解:如图②中,结论:12EF CD =.理由:取CD 的中点T ,连接AT ,TF ,ET ,TE 交AD 于点O . 90CAD ∠=︒,CT DT =,AT CT DT ∴==,EA ED =,ET ∴垂直平分线段AD ,AO OD ∴=,90AED ∠=︒,OE OA OD ∴==,CT TD =,BF DF =,//BC FT ∴,45ABC OFT ∴∠=∠=︒,90TOF ∠=︒,45OTF OFT ∴∠=∠=︒,OT OF ∴=,AF ET ∴=,FT TF =,AFT ETF ∠=∠,FA TE =,()AFT ETF SAS ∴∆≅∆,EF AT ∴=,12EF CD ∴=.如图③中,结论:EF =.理由:取AD 的中点O ,连接OF ,OE .EA ED =,60AED ∠=︒,ADE ∴∆是等边三角形,AO OD =,OE AD ∴⊥,30AEO OED ∠=∠=︒,tan AO AEO OE ∴∠==∴OEAD =1302ABC AED ∠=∠=︒,90BAC ∠=︒,AB ∴,AO OD =,BF FD =,12OF AB ∴=,∴OF AC =, ∴OE OFAD AC =,//OF AB ,DOF DAB ∴∠=∠,90DOF EOF ∠+∠=︒,90DAB DAC ∠+∠=︒,EOF DAC ∴∠=∠,EOF DAC ∴∆∆∽,∴EFOECD AD =,EF ∴.4.(2021•通辽)已知AOB ∆和MON ∆都是等腰直角三角形)OM OA <<,90AOB MON ∠=∠=︒. (1)如图1,连接AM ,BN ,求证:AM BN =;(2)将MON ∆绕点O 顺时针旋转. ①如图2,当点M 恰好在AB 边上时,求证:2222AM BM OM +=; ②当点A ,M ,N 在同一条直线上时,若4OA =,3OM =,请直接写出线段AM 的长.【解答】(1)证明:90AOB MON ∠=∠=︒, AOB AON MON AON ∴∠+∠=∠+∠,即AOM BON ∠=∠,AOB ∆和MON ∆都是等腰直角三角形,OA OB ∴=,OM ON =,()AOM BON SAS ∴∆≅∆,AM BN ∴=;(2)①证明:连接BN ,90AOB MON ∠=∠=︒,AOB BOM MON BOM ∴∠-∠=∠-∠,即AOM BON ∠=∠,AOB ∆和MON ∆都是等腰直角三角形,OA OB ∴=,OM ON =,()AOM BON SAS ∴∆≅∆,45MAO NBO ∴∠=∠=︒,AM BN =,90MBN ∴∠=︒,222MB BN MN ∴+=,MON ∆都是等腰直角三角形,222MN ON ∴=,2222AM BM OM ∴+=;②解:如图3,当点N 在线段AM 上时,连接BN ,设BN x =, 由(1)可知AOM BON ∆≅∆,可得AM BN =且AM BN ⊥, 在Rt ABN ∆中,222AN BN AB +=,AOB ∆和MON ∆都是等腰直角三角形,4OA =,3OM =,MN ∴=,AB =222(x x ∴-+=,解得:x =,AM BN ∴= 如图4,当点M 在线段AN 上时,连接BN ,设BN x =, 由(1)可知AOM BON ∆≅∆,可得AM BN =且AM BN ⊥, 在Rt ABN ∆中,222AN BN AB +=,AOB ∆和MON ∆都是等腰直角三角形,4OA =,3OM =,MN ∴=,AB =222(x x ∴++=,解得:x =,AM BN ∴=,综上所述,线段AM . 5.(2021•十堰)已知等边三角形ABC ,过A 点作AC 的垂线l ,点P 为l 上一动点(不与点A 重合),连接CP ,把线段CP 绕点C 逆时针方向旋转60︒得到CQ ,连QB .(1)如图1,直接写出线段AP 与BQ 的数量关系;(2)如图2,当点P 、B 在AC 同侧且AP AC =时,求证:直线PB 垂直平分线段CQ ;(3)如图3,若等边三角形ABC 的边长为4,点P 、B 分别位于直线AC 异侧,且APQ ∆,求线段AP 的长度.【解答】解:(1)在等边ABC ∆中,AC BC =,60ACB ∠=︒, 由旋转可得,CP CQ =,60PCQ ∠=︒, ACB PCQ ∴∠=∠,ACB PCB PCQ PCB ∴∠-∠=∠-∠,即ACP BCQ ∠=∠, ()ACP BCQ SAS ∴∆≅∆,AP BQ ∴=.(2)在等边ABC ∆中,AC BC =,60ACB ∠=︒, 由旋转可得,CP CQ =,60PCQ ∠=︒,ACB PCQ ∴∠=∠,ACB PCB PCQ PCB ∴∠-∠=∠-∠,即ACP BCQ ∠=∠, ()ACP BCQ SAS ∴∆≅∆,AP BQ ∴=,90CBQ CAP ∠=∠=︒;BQ AP AC BC ∴===,AP AC =,90CAP ∠=︒,30BAP ∴∠=︒,75ABP APB ∠=∠=︒,135CBP ABC ABP ∴∠=∠+∠=︒,45CBD ∴∠=︒,45QBD ∴∠=︒,CBD QBD ∴∠=∠,即BD 平分CBQ ∠,BD CQ ∴⊥且点D 是CQ 的中点,即直线PB 垂直平分线段CQ .(3)①当点Q 在直线l 上方时,如图所示,延长BQ 交l 于点E ,过点Q 作QF l ⊥于点F ,由题意可得AC BC =,PC CQ =,60PCQ ACB ∠=∠=︒, ACP BCQ ∴∠=∠,()APC BCQ SAS ∴∆≅∆,AP BQ ∴=,90CBQ CAP ∠=∠=︒,60CAB ABC ∠=∠=︒,30BAE ABE ∴∠=∠=︒,4AB AC ==,AE BE ∴=, 60BEF ∴∠=︒,设AP t =,则BQ t =,EQ t ∴=-,在Rt EFQ ∆中,)QF t =-,12APQ S AP QF ∆∴=⋅=,即1)2t ⋅-=,解得t =t .即AP . ②当点Q 在直线l 下方时,如图所示,设BQ 交l 于点E ,过点Q 作QF l ⊥于点F ,由题意可得AC BC =,PC CQ =,60PCQ ACB ∠=∠=︒,ACP BCQ ∴∠=∠,()APC BCQ SAS ∴∆≅∆,AP BQ ∴=,90CBQ CAP ∠=∠=︒,60CAB ABC ∠=∠=︒,30BAE ABE ∴∠=∠=︒,120BEF ∴∠=︒,60QEF ∠=︒,4AB AC ==,AE BE ∴=, 设AP m =,则BQ m =,EQ m ∴=-,在Rt EFQ ∆中,QF m =,12APQ S AP QF ∆∴=⋅=,即12m m ⋅-解得m m ==.综上可得,AP 6.(2020•沈阳)在ABC ∆中,AB AC =,BAC α∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接DB ,DC .(1)如图1,当60α=︒时,①求证:PA DC =;②求DCP ∠的度数;(2)如图2,当120α=︒时,请直接写出PA 和DC 的数量关系.(3)当120α=︒时,若6AB =,BP D 到CP 的距离为 .【解答】(1)①证明:如图1中,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD , PB PD ∴=,AB AC =,PB PD =,60BAC BPD ∠=∠=︒, ABC ∴∆,PBD ∆是等边三角形,60ABC PBD ∴∠=∠=︒,PBA DBC ∴∠=∠,BP BD =,BA BC =,()PBA DBC SAS ∴∆≅∆,PA DC ∴=.②解:如图1中,设BD 交PC 于点O .PBA DBC ∆≅∆,BPA BDC ∴∠=∠,BOP COD ∠=∠,60OBP OCD ∴∠=∠=︒,即60DCP ∠=︒.(2)解:结论:CD =.理由:如图2中,AB AC =,PB PD =,120BAC BPD ∠=∠=︒,2cos30BC AB ∴=⋅⋅︒,2cos30BD BP =⋅︒=,∴BC BD BA BP= 30ABC PBD ∠=∠=︒,ABP CBD ∴∠=∠,CBD ABP ∴∆∆∽,∴CD BC PA AB=CD ∴=.(3)过点D 作DM PC ⊥于M ,过点B 作BN CP ⊥交CP 的延长线于N . 如图31-中,当PBA ∆是钝角三角形时,在Rt ABN ∆中,90N ∠=︒,6AB =,60BAN ∠=︒,cos603AN AB ∴=⋅︒=,sin 60BN AB =⋅︒=2PN PB ==, 321PA ∴=-=,由(2)可知,CD = BPA BDC ∠=∠,30DCA PBD ∴∠=∠=︒, DM PC ⊥,12DM CD ∴=如图32-中,当ABP ∆是锐角三角形时,同法可得235PA =+=,CD =12DM CD ==综上所述,满足条件的DM ..。
2022年人教版中考数学复习第一部分考点讲解-第四章三角形-微专题-手拉手模型

第6题解图
在△ABE和△DBC中,
AB DB ABE DBC BE BC
∴△ABE≌△DBC.∴∠EAB=∠CDB.
第2题图
又∵∠OAB+∠OBA=∠ODH+∠OHD,∴∠AHD=∠ABD=60°;
微专题 手拉手模型
(2)连接HB,求证:HB平分∠AHC.
(2)如解图,过点B作AH、DC的垂线,垂足分别为点M、N.
结论:△ABD≌△AEC;△ABE∽△ADC;
微专题 手拉手模型
模型应用 5. 如图,在△ABC中,∠ABC=60°,AB=2 3 ,BC=8,以AC为腰,点A为顶点 作等腰△ACD,且∠DAC=120°,则BD的长为_1_0__.
第5题图
微专题 手拉手模型
6. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°, 求BD的长.
∵△ABE ≌△DBC,
∴S△ABE=S△DBC. 即AE·BM=CD·BN.
又∵AE=CD,
∴BM=BN. ∴HB平分∠AHC.
第2题解图
微专题 手拉手模型 模型二 相似型手拉手模型
模型分析
模型展示
微专题 手拉手模型
△AOB∽△COD,且绕公共顶点O旋转, 简记为:非等腰,共顶点, 模型特点 顶角相等,旋转得相似
第1题图
微专题 手拉手模型
微专题 手拉手模型
微专题 手拉手模型
2. 如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点H,
交BD于点O.
(1)求证:∠AHD=60°;
证明:(1)∵∠ABE=∠ABD-∠EBD,∠DBC=∠EBC-∠EBD,
∠ABD=∠EBC=60°,∴∠ABE=∠DBC.
2024中考数学总复习冲刺专题:手拉手模型(全等与相似)通用版

《“手拉手”模型常用结论的证明及应用》手拉手模型,也叫整体旋转法,是中考最重要的模型之一,全国一年176套中考卷中,有40%的卷子考到此模型。
手拉手模型分为“全等手拉手”和“相似手拉手”,在解决手拉手模型的问题时,需要灵活运用全等三角性和相似三角形的性质与判定方法,以及轴对称的性质和判定方法来进行证明。
同时,还需要掌握基本的手拉手模型形式及其变形情况,才能更好的解决相关问题。
一、教学目标知识与技能:了解手拉手模型的组成条件,探究“全等手拉手”模型和“相似手拉手”模型的常用结论,会利用手拉手模型来解决几何问题;过程与方法:在探究手拉手模型常用结论的过程中,培养分析问题、解决问题的能力,培养模型思想;情感态度与价值观:养成主动探索、获取知识的习惯,感受探索的乐趣和成功的体验,激发学生学好数学的愿望和信心.二、重点难点重点:探索全等手拉手模型、相似手拉手模型的常用结论;难点:利用旋转、全等、相似等知识解决手拉手模型的相关问题.三、教学过程(一)全等手拉手模型精典例题例1:如图,在线段BD上取一点A,在同侧作等边△ABC和等边△ADE,连接BE、CD,求证:(1)△ABE≌△ACD;(2)BE=CD;(3)△AFB≌△AGC;(4)△AFE≌△AGD;(5)△AFG是等边三角形;(6)∠COB=∠CAB;(7)OA平分∠BOD;(8)FG//BD.例2:如图,已知正方形ABCD和正方形DEFG有公共顶点D,连接AG,CE,相交于点H.求证:(1)△ADG≌△CDE;(2)AG⟂CE;(3)HD平分∠AHE;(4)AC2+EG2=AE2+CG2.跟踪练习1.(2022秋•界首市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE,∠BAD=30°,∠ACE=25°,则∠ADE的度数为()A.50°B.55°C.60°D.65°2.(2023秋•江阳区校级月考)已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是()A.1B.2C.3D.43.(2020春•富县期末)如图,已知四边形ABCD和四边形CEFG都是正方形,且AB>CE,连接BG,DE.(1)求证:BG=DE;(2)连接BD,若CG∥BD,BG=BD,求∠BDE 的度数.4.(2019秋•新都区期末如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.(1)求证:AE=BD;(2)试探究线段AD、BD与CD之间的数量关系;(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2,CD=,求线段AB的长.(二)相似手拉手模型精典例题例3:如图,已知△ABC∽△ADE,求证:(1)△ABD∽△ACE;(2)∠BFC=∠BAC.跟踪练习1.如图,四边形ABCD中,AB=3,BC=2,AC=AD,∠ACD=60°,则对角线BD长的最大值为()A.5B.2C.2D.12.如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D 的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=()A.5B.5.5C.6D.73.两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并把它们的底角顶点连接起来,形成一组全等的三角形,那么把具有这个规律的图形称为“手拉手”图形.(1)如图1,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,则有△BAD≌.(2)如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一条直线上,连接CE,试探究线段BE,CE,DE之间的数量关系,并说明理由.(3)如图3,△ABC为等腰直角三角形,∠BAC=90°,∠AEC=135°,求证:BE⊥CE.(三)手拉手综合题例5:(2019•玄武区一模)如图,四边形ABCD和四边形AEFG均为正方形,连接CF,DG,则=()A.B.C.D.例6:(2022•深圳中考)已知△ABC是直角三角形,∠ABC=90°,AB=3,BC=5,AE =2,连接CE,以CE为底作直角三角形CDE,且CD=DE.F是AE边上的一点,连接BD和BF,且∠FBD=45°,则AF长为.跟综练习1.(2022•无锡)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.2.(2023•成都)探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.在Rt△ABC中,∠C=90°,AC=BC,D是AB边上一点,且=(n为正整数),E 是AC边上的动点,过点D作DE的垂线交直线BC于点F.【初步感知】(1)如图1,当n=1时,兴趣小组探究得出结论:AE+BF=AB,请写出证明过程.【深入探究】(2)①如图2,当n=2,且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).【拓展运用】(3)如图3,连接EF,设EF的中点为M,若AB=2,求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).四、教学反思本节课从全等手拉手模型、相似手拉手模型、手拉手综合题三个模块进行探索,题目从易到难,每个模块都有两个精典例题,2-4道跟综练习。
手拉手模型——全等三角形常见模型介绍一[实用]
![手拉手模型——全等三角形常见模型介绍一[实用]](https://img.taocdn.com/s3/m/31fdc131f342336c1eb91a37f111f18582d00c46.png)
手拉手模型——全等三角形常见模型介绍(一)[实用]手拉手模型,也被称为全等三角形模型,是一种在几何证明中常见的模型。
这个模型的关键在于,两个或多个全等三角形通过对应边和对应角的对应关系,形成了一种特定的几何形状。
下面我们将详细介绍这个模型的构造和运用。
首先,我们需要了解全等三角形的定义。
全等三角形是指具有完全相同形状和大小的三角形。
全等三角形的对应边相等,对应角也相等。
全等三角形的证明通常是通过边角边(SAS)、角边角(ASA)或角角边(AAS)等公理来完成的。
在手拉手模型中,我们需要构造两个或多个全等三角形,并通过对应边和对应角的对应关系来证明其他几何结论。
手拉手模型的构造通常是通过旋转、平移或翻转三角形来完成的。
在这个过程中,我们需要确定旋转中心、旋转角度和旋转方向,以及平移或翻转的距离和方向。
例如,在下面的证明题中,我们需要在两个全等三角形ABC和A'B'C'中,证明AB平行于A'B'。
首先,我们可以通过旋转三角形ABC来得到三角形A'B'C'。
假设旋转中心为点A,旋转角度为∠BAC。
由于三角形ABC和A'B'C'是全等三角形,因此对应边AB 和A'B'相等,且对应角∠B和∠B'相等。
因此,我们可以得出AB平行于A'B'的结论。
手拉手模型的应用非常广泛,它可以用于证明各种几何结论,例如平行线、等腰三角形、直角三角形等等。
在实际应用中,我们还需要结合其他几何定理和性质,例如平行线的传递性、等腰三角形的轴对称性等等来证明更复杂的结论。
此外,手拉手模型还可以用于解决实际问题。
例如,在测量两个不可到达点之间的距离时,我们可以将一个点向另一个点平移,然后通过全等三角形的性质来证明距离相等。
或者在解谜题中,我们可以使用手拉手模型来构造全等三角形,从而证明两个几何图形之间的关系。
专题01 三角形-2021-2022学年八年级数学上学期期末解答题必刷专题训练(人教版)(解析版)

三角形1.如图,在四边形ABCD 中,90A C Ð=Ð=°,BE 平分ABC Ð,DF 平分ADC Ð.(1)求ABC ADC Ð+Ð的度数;(2)求证:BE DF ∥.【答案】(1)∠ABC +∠ADC =180°;(2)见解析.【分析】(1)根据四边形的内角和定理求出即可;(2)求出∠2=∠DFC ,根据平行线的判定推出即可.【详解】(1)解:∵∠A =∠C =90°,∴∠ABC +∠ADC =360°-90°-90°=180°;(2)证明:∵BE 平分∠ABC ,DF 平分∠ADC ,∴∠2=12∠ABC ,∠4=12∠ADC ,∵四边形ABCD 中,∠A =∠C =90°,∴∠4+∠DFC =90°,由(1)得∠ABC +∠ADC =180°,∴∠2+∠4=90°,∵∠4+∠DFC =90°,∴∠2=∠DFC ,∴BE ∥DF ..【点睛】本题考查了平行线的判定,角平分线定义,三角形的内角和定理,四边形的内角和定理的应用,解此题的关键是求出∠EBC =∠DFC .2.如图,在△ABC中,AE是角平分线,AD是高,∠BAC=70°,∠EAD=10°,求∠B的度数.【答案】45°【分析】∠BAC=35°,那么∠BAD=∠BAE+∠EAD=45°.根据AD是△ABC的高,根据AE是角平分线,得∠BAE=12得∠ADC=90°.根据三角形外角的性质,得∠ADC=∠B+∠BAD,那么∠B=∠ADC−∠BAD=45°.【详解】解:∵AE是角平分线,∴∠BAE=1∠BAC=35°.2∴∠BAD=∠BAE+∠EAD=35°+10°=45°.∵AD是△ABC的高,∴∠ADC=90°.∵∠ADC=∠B+∠BAD,∴∠B=∠ADC−∠BAD=90°−45°=45°.【点睛】本题主要考查三角形的高、角平分线的定义、三角形外角的性质,熟练掌握三角形的高、角平分线的定义、三角形外角的性质是解决本题的关键.3.如图,AD为V ABC中线,AB=12cm,AC=9cm,V ACD的周长为27cm,求V ABD的周长.【答案】△ABD的周长为30cm【分析】利用中线定义可得BD=CD,进而可得AD+DC=AD+BD,然后再求△ABD的周长即可.【详解】解:∵△ACD的周长为27cm,∴AC+DC+AD=27cm,∵AC=9cm,∴AD+CD=18cm,∵AD为△ABC的中线,∴BD=CD,∴AD+BD=18cm,∵AB=12cm,∴AB+AD+BD=30cm,∴△ABD的周长为30cm.【点睛】此题主要考查了三角形的中线,关键是掌握三角形的中线定义.4.如图①,V ABC的角平分线BD、CE相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,过P点作直线MN,分别交AB和AC于点M和N,且MN平行于BC,则有∠MPB+∠NPC=90°﹣12∠A.①若将直线MN绕点P旋转,如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立,并说明理由;②当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问①中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.【答案】(1)130°;(2)①仍然成立,见解析;②不成立,∠MPB﹣∠NPC=90°﹣12∠A,见解析【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠1+∠2,进而求出∠BPC即可解决问题.(2)运用(1)中的结论,结合三角形的内角和定理逐一分类解析,即可解决问题.【详解】解:(1)如图①∵在△ABC中,∠A+∠ABC+∠ACB=180°,且∠A=80°,∴∠ABC+∠ACB=100°,∵∠1=12∠ABC,∠2=12∠ACB,∴∠1+∠2=12(∠ABC+∠ACB)=12×100°=50°,∴∠BPC =180°﹣(∠1+∠2)=180°﹣50°=130°.(2)①如图③,由(1)知:∠BPC =180°﹣(∠1+∠2);∵∠1+∠2=12(180°﹣∠A )=90°-12∠A ,∴∠BPC =180°﹣(90°﹣12∠A )=90°+12∠A ;∴∠MPB +∠NPC =180°﹣∠BPC =180°﹣(90°+12∠A )=90°﹣12∠A .②不成立,∠MPB ﹣∠NPC =90°﹣12∠A .如图④,由①知:∠BPC =90°+12∠A ,∴∠MPB ﹣∠NPC =180°﹣∠BPC=180°﹣(90°+12∠A )=90°﹣12∠A .【点睛】该题主要考查了三角形的内角和定理、角平分线的定义等几何知识点及其应用问题;牢固掌握三角形的内角和定理、角平分线的定义等几何知识点是基础,灵活运用是关键.5.如图,在△ABC 中,AE 是BC 边上的高,AD 是角平分线,∠B =42°,∠C =68°.①求∠DAE 的度数;②若∠B =α,∠C =β(α<β),用含α,β的代数式表示∠DAE .(直接写出结论)【答案】(1)13°(2)2b a -【分析】(1)根据三角形内角和定理求出∠BAC ,求出∠DAC ,根据三角形内角和定理求出∠AC ,代入∠DAE =∠DAC −∠EAC 求出即可.(2)同(1)的方法即可求解.【详解】解:(1)∵∠B =42°,∠C =68°,∴∠BAC =180°−∠B −∠C =70°,∵AD 是∠BAC 的平分线,∴∠DAC =12∠BAC =35°,∵AE 是BC 边上的高,∴∠AEC =90°,∵∠C =68°,∴∠EAC =180°−∠AEC −∠C =22°,∴∠DAE =∠DAC −∠EAC =35°−22°=13°.(2)∵∠B =α,∠C =β,∴∠BAC =180°−∠B −∠C =180°−α−β,D 是∠BAC 的平分线,∴∠DAC =12∠BAC =90°−12α−12β,AE 是BC 边上的高,∴∠AEC =90°,∵∠C =β,∴∠EAC =180°−∠AEC −∠C =90°−β,∠DAE =∠DAC −∠EAC =(90°−12α−12β)−(90°−β)=2b a -.【点睛】本题考查了三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力.6.如图,在ABC V 中,BF 平分ABC Ð,CF 平分ACB Ð,65A Ð=°,求F Ð的度数.【答案】122.5°【分析】由题意直接根据三角形内角和定理和角平分线的定义进行分析,并利用角的等量替换即可得出答案.【详解】解:在ABC V 中,∵65A Ð=°(已知),∴180115ABC ACB A Ð+Ð=°-Ð=°(三角形内角和定理).∵BF 平分ABC Ð,CF 平分ACB Ð(已知),∴12FBC ABC Ð=Ð,12FCB ACB Ð=Ð(角平分线的定义).在FBC V 中,∵180F FBC FCB Ð+Ð+Ð=°(三角形内角和定理),∴(180)F FBC FCB Ð=°-Ð+Ð1118022ABC ACB æö=°-Ð+Ðç÷èø1180()2ABC ACB =°-Ð+Ð11801152=-´°122.5=°.【点睛】本题考查三角形内角和定理和角平分线的定义,熟练掌握三角形内角和定理和角平分线的定义是解题的关键.7.阅读下列材料:阳阳同学遇到这样一个问题:如图1,在ABC D 中AB AC =,BD 是ABC D 的高,P 是BC 边上一点,PM 、PN 分别与直线AB ,AC 垂直,垂足分别为点M 、N .求证:BD PM PN =+.阳阳发现,连接AP ,有ABC ABP ACP S S S D D D =+,即111222AC BD AB PM AC PN ×=×+×.由AB AC =,可得BD PM PN =+.他又画出了当点P 在CB 的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时BD 、PM 、PN 之间的数量关系是:BD PN PM =-.请回答:(1)请补全阳阳同学证明猜想的过程;证明:连接AP .ABC APC S S D D =-Q ________,1122AC BD AC \×=×________12AB -×________.AB AC =Q ,BD PN PM \=-.(2)参考阳阳同学思考问题的方法,解决下列问题:在ABC D 中,AB AC BC ==,BD 是ABC D 的高.P 是ABC D 所在平面上一点,PM 、PN 、PQ 分别与直线AB 、AC 、BC 垂直,垂足分别为点M 、N 、Q .①如图3,若点P 在ABC D 的内部,猜想BD 、PM 、PN 、PQ 之间的数量关系并写出推理过程.②若点P 在如图4所示的位置,利用图4探究得此时BD 、PM 、PN 、PQ 之间的数量关系是:_______.(直接写出结论即可)【答案】(1)S △APB ;PN ;PM ;(2)①BD =PM +PN +PQ ,证明见解析②BD =PM +PQ −PN .【分析】(1)根据图形,结合阅读材料填写即可;(2)①连接AP 、BP 、CP ,根据S △ABC =S △APC +S △APB +S △BPC 得出12AC •BD =12AC •PN +12AB •PM +12BC •PQ ,由AB =AC =BC ,即可得出BD =PM +PN +PQ ;②连接AP 、BP 、CP ,根据S △ABC =S △APB +S △BPC −S △APC ,得出12AC •BD =12AB •PM +12BC •PQ −12AC •PN ,由于AB =AC =BC ,即可证得BD =PM +PQ −PN .【详解】解:(1)证明:连接AP .∵S △ABC =S △APC −S △APB ,∴12AC •BD =12AC •PN −12AB •PM .∵AB =AC ,∴BD =PN −PM .故答案为:S △APB ;PN ;PM ;(2)①BD =PM +PN +PQ ;如图3,连接AP 、BP 、CP ,∵S △ABC =S △APC +S △APB +S △BPC ∴12AC •BD =12AC •PN +12AB •PM +12BC •PQ ,∵AB =AC =BC ,∴BD =PM +PN +PQ ;②BD =PM +PQ −PN ;如图4,连接AP 、BP 、CP ,∵S △ABC =S △APB +S △BPC −S △APC .∴12AC •BD =12AB •PM +12BC •PQ −12AC •PN ,∵AB =AC =BC ,∴BD =PM +PQ −PN .【点睛】本题考查了等边三角形的性质,三角形的面积等,作出辅助线构建三个三角形是解题的关键.8.(1)如图1,在ABC V 中,BP 平分ABC Ð,CP 平分ACB Ð,求证:1902P A Ð=°+Ð;(2)如图2,在ABC V 中,BP 平分ABC Ð,CP 平分外角ACE Ð,猜想P Ð和A Ð有何数量关系,并证明你的结论.【答案】(1)见解析;(2)12P A Ð=Ð,证明见解析【分析】(1)根据三角形内角和定理以及角平分线的定义进行证明即可:(2)根据一个三角形的外角等于与它不相邻的两个内角和,可求出A ACE ABC Ð=Ð-Ð,P PCE PBC Ð=Ð-Ð,再由角平分线的定义得到12PBC ABC Ð=Ð,12PCE ACE Ð=Ð, 则()11112222P ACE ABC ACE ABC A Ð=Ð-Ð=Ð-Ð=Ð.【详解】(1)证明:()180P PBC PCB Ð=-Ð+Ðo ,∵BP 平分ABC Ð,CP 平分ACB Ð,∴12PBC ABC Ð=Ð,12PCB ACB Ð=Ð,∴()111222PBC PCB ABC ACB ABC ACB Ð+Ð=Ð+Ð=Ð+Ð∴()11801802P PBC PCB ABC ACB Ð=--=-Ð+Ðo o ∠∠,∵=180ABC ACB A+-o ∠∠∠()11180180=9022P A A \Ð=--+Ðo o o ∠;(2)猜想:12P A Ð=Ð,证明:ACE A ABC Ð=Ð+ÐQ ,A ACE ABC \Ð=Ð-Ð,∵PCE P PBC Ð=Ð+Ð,∴P PCE PBC Ð=Ð-Ð,又BP 平分ABC Ð,CP 平分ACE Ð,∴12PBC ABC Ð=Ð,12PCE ACE Ð=Ð,()11112222P ACE ABC ACE ABC A \Ð=Ð-Ð=Ð-Ð=Ð,12P A \Ð=Ð.【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,角平分线的定义,解题的关键在于能够熟练掌握角平分线的定义.9.如图,在ABC V 中,75A Ð=°,45C Ð=°,BE 是ABC V 的角平分线,BD 是边AC 上的高.(1)求CBE Ð的度数;(2)求DBE Ð的度数.【答案】(1)∠CBE =30°;(2)∠DBE =15°.【分析】(1)根据三角形内角和可求∠ABC =180°-∠A -∠C =180°-75°-45°=60°,然后根据角平分线∠CBE =11603022ABC Ð=´°=°;(2)先求∠DBC =90°-∠C=90°-45°=45°,再利用两角之差计算即可.【详解】解:(1)∵∠ABC +∠A +∠C =180°,75A Ð=°,45C Ð=°,∴∠ABC =180°-∠A -∠C =180°-75°-45°=60°,∵BE 是ABC V 的角平分线,∴∠CBE =11603022ABC Ð=´°=°;(2)∵BD ⊥AC ,∴∠BDC =90°,∴∠DBC +∠C =90°,∵45C Ð=°∴∠DBC =90°-∠C=90°-45°=45°,∴∠DBE =∠DBC -∠CBE =45°-30°=15°.【点睛】本题考查三角形内角和,角平分线定义,直角三角形两锐角互余,角的和差,掌握三角形内角和,角平分线定义,直角三角形两锐角互余,角的和差是解题关键.10.如图,在V ABC中,∠1=∠2=∠3.(1)求证:∠ABC=∠EDF;(2)若∠ABC=45°,∠DFE=50°,求∠BAC的度数.【答案】(1)见解析;(2)85°【分析】(1)利用三角形的外角的性质可得∠EDF=∠1+∠ABD,再结合∠ABC=∠2+∠ABD,∠1=∠2即可证得∠ABC =∠EDF;(2)先根据三角形的内角和定理求得∠DEF=85°,再利用三角形的外角的性质结合∠1=∠3即可求得答案.【详解】(1)证明:∵∠1=∠2,∴∠1+∠ABD=∠2+∠ABD,又∵∠EDF=∠1+∠ABD,∠ABC=∠2+∠ABD,∴∠ABC=∠EDF;(2)解:∵∠ABC=∠EDF,∠ABC=45°,∴∠EDF=45°,又∵∠DFE=50°,∴∠DEF=180°-∠DFE-∠EDF=85°,∴∠EAC+∠3=∠DEF=85°,又∵∠1=∠3,∴∠BAC=∠EAC+∠1=∠EAC+∠3=85°.【点睛】本题考查三角形内角和定理,三角形外角的性质等知识,解题的关键是熟练掌握三角形内角和定理,属于中考常考题型.11.如图,在V ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=56°,∠C=70°.(1)求∠DAE的度数;(2)求∠BOA的度数.【答案】(1)8°;(2)125°【分析】(1)根据角平分线的定义求出∠CAE ,根据直角三角形两锐角互补可得CAD Ð,根据DAE CAE CAD Ð=Ð-Ð计算即可;(2)根据三角形内角和求出ABC Ð,根据角平分线的定义求出,BAO ABO ÐÐ的度数,然后根据三角形内角和可得结果.【详解】解:(1)∵∠BAC =56°,∠C =70°,AE 是∠BAC 的平分线,∴∠CAE =1282BAC Ð=°∵AD 是BC 边上的高,∴90ADC Ð=°,∴∠CAD =907020°-°=°,∴28208DAE CAE CAD Ð=Ð-Ð=°-°=°;(2)∵∠C =70°,∠BAC =56°,∴∠ABC =180°−70°−56°=54°,∵BF 平分∠ABC ,∴1272ABO ABC Ð=Ð=°,∵AE 平分∠BAC ,1282OAB BAC Ð=Ð=°,∴∠BOA 180125ABO OAB =°-Ð-Ð=°.【点睛】本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.12.如图,△ABC 中,角平分线AD 、BE 、CF 相交于点H ,过H 点作HG ⊥AC ,垂足为G ,如果∠AHE=50度,求∠CHG 的度数.【答案】∠CHG =50°【分析】根据角平分线的定义可设可设=BAD CAD x =∠∠,=ABE CBE y Ð=Ð,=BCF ACF z Ð=Ð,则由三角形内角和定理可得90x y z ++=o ,再由三角形外角的性质可得==90AHE BAD ABE x y z ++=-o ∠∠∠,=90AGH ACF CHG +=o ∠∠∠,从而可以推出50CHG AHE Ð=Ð=o .【详解】解:∵AD ,BE ,CF 为△ABC 的角平分线,∴可设=BAD CAD x =∠∠,=ABE CBE y Ð=Ð,=BCF ACF z Ð=Ð,∵=180ABC BAC ACB ++o ∠∠∠,∴222180x y z ++=o ,即90x y z ++=o ,∵==90AHE BAD ABE x y z ++=-o ∠∠∠,=90AGH ACF CHG +=o ∠∠∠,∴==90CHG AGH ACF z --o ∠∠∠,∴50CHG AHE Ð=Ð=o .【点睛】本题主要考查了角平分线的定义,三角形内角和定理,三角形外角的性质,解题的关键在于能够熟练掌握角平分线的定义.13.已知,Rt △ABC 中,∠C =90°,点D 、E 分别是边AC ,BC 上的点,点P 是斜边AB 上一动点.令∠PDA =∠1,∠PEB =∠2,∠DPE =∠α.(1)如图①所示,当点P 运动至∠α=50°时,则∠1+∠2= ;(2)如图②所示,当P 运动至AB 上任意位置时,试探求∠α,∠1,∠2之间的关系,并说明理由.【答案】(1)12140Ð+Ð=°;(2)1290a Ð+Ð=Ð+°,理由见解析【分析】(1)根据平角的定义求得1180,2180PDC PEC Ð+Ð=°Ð+Ð=°,进而根据四边形的内角和等于360°,以及∠α=50°,即可求得∠1+∠2的值;(2)方法同(1).【详解】(1)Q 1180,2180PDC PEC Ð+Ð=°Ð+Ð=°,12360PDC PEC \Ð+Ð+Ð+Ð=°,在四边形CEPD 中,360C PDC PEC a Ð+Ð+Ð+Ð=°,12C a \Ð+Ð=Ð+Ð,Q ∠α=50°,90C Ð=°,\12140Ð+Ð=°,故答案为:140°(2)1290a Ð+Ð=Ð+°,理由如下,Q Q 1180,2180PDC PEC Ð+Ð=°Ð+Ð=°,12360PDC PEC \Ð+Ð+Ð+Ð=°,在四边形CEPD 中,360C PDC PEC a Ð+Ð+Ð+Ð=°,12C a \Ð+Ð=Ð+Ð,Q 90C Ð=°,\1290a Ð+Ð=Ð+°【点睛】本题考查了平角的定义,四边形内角和为360°,掌握四边形的内角和是解题的关键.14.如图,AD 是△ABC 的角平分线,CE 是△ABC 的高,∠BAC =50°,∠BCE =25°,求∠AOC 和∠ADB 的度数.【答案】∠AOC 的度数为115°,∠ADB 的度数为90°【分析】根据AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°可得∠BAD=∠CAD=25°,∠CEA=90°,从而求得∠ACE的度数,由此可得∠AOC的度数,又因为∠BCE=25°,∠ADB=∠BCE+∠ACE+∠CAD,从而求得∠ADB的度数.【详解】解:∵AD是△ABC的角平分线,∠BAC=50°,∴∠BAD=∠CAD=12∠BAC=25°,∵CE是△ABC的高,∴∠CEA=90°,∴∠ACE=90°-∠BAC=40°,∴∠AOC=180°-∠ACE-∠CAD=180°-40°-25°=115°,∵∠BCE=25°,∠ACE=40°,∠CAD=25°,∴∠ADB=∠BCE+∠ACE+∠CAD=25°+40°+25°=90°,答:∠AOC的度数为115°,∠ADB的度数为90°.【点睛】本题考查三角形的内角和、三角形的平分线和高的定义以及三角形的一个外角等于和它不相邻的内角的和,关键是根据具体目中的信息,灵活变化,求出相应的问题的答案.15.如图,在△ABC中,∠ACB=90°,CD,CE分别是△ABC的高和中线,F是CB的延长线上一点.(1)若∠ACD=53°,求∠ABF的度数;(2)若BC=6 cm,AC=8 cm,AB=10 cm,求CD的长和△BCE的面积.【答案】(1)127°;(2)24cm5CD=,212cmBCES=V【分析】(1)结合CD为△ABC的高,先求出∠A,然后结合三角形的外角定理求解即可;(2)先根据等面积法求出CD,然后结合中线的性质求出BE,从而利用三角形的面积公式求解即可.【详解】解:(1)∵CD 为△ABC 的高,∴CD ⊥AB ,∠ADC =90°,∵∠ACD =53°,∴∠A =180°-90°-53°=37°,∵∠ABF 为△ABC 的外角,∴∠ABF =∠A +∠ACB =37°+90°=127°;(2)由题意,1122ABC S AC BC AB CD ==V g g ,∴6824cm 105AC BC CD AB ´===g ,∵CE 是△ABC 的中线,∴E 为AB 的中点,即:152AE BE AB ===,∴21124512cm 225BCE S BE CD ==´´=V g .【点睛】本题考查三角形中线,高相关的定义与计算,理解三角形中重要线段的定义与性质,熟悉等面积法是解题关键.16.如图,在△ABC 中,30A Ð=°,60B Ð=°,CF 平分ACB Ð交AB 于点E .(1)求ACE Ð的度数:(2)若CD AB ^于点D ,75CDF Ð=°.判断△CFD 的形状,并说明理由.【答案】(1)45ACE Ð=°;(2)CFD △是直角三角形,理由见解析.【分析】(1)依据三角形内角和定理以及角平分线的定义,即可得到ACE Ð的度数.(2)依据三角形内角和定理以及直角三角形的性质,即可得到DCF Ð的度数,进而得出CFD Ð的度数.【详解】解:(1)ABC QV 中,30A Ð=°,60B Ð=°,180306090ACB \Ð=°-°-°=°,又CE Q 平分ACB Ð,1452ACE ACB \Ð=Ð=°,即45ACE Ð=°;(2)CFD △是直角三角形,理由:CD AB ^Q 于点D ,60B Ð=°,906030BCD \Ð=°-°=°,又45BCE ACE Ð=Ð=°Q ,15DCF BCE BCD \Ð=Ð-Ð=°,又75CDF Ð=°Q ,180751590CFD \Ð=°-°-°=°,CFD \△是直角三角形.【点睛】本题考查了三角形的内角和定理,直角三角形的性质,角平分线定义等知识点,关键是求出各个角的度数.17.已知,如图,在△ABC 中,AD ,AE 分别是△ABC 的高和角平分线,若∠B =30°,∠C =50°.(1)求∠DAE 的度数.(2)试写出∠DAE 与∠C -∠B 有何关系,给出证明.【答案】(1)10°;(2)()1,2DAE C B Ð=Ð-Ð证明见解析【分析】(1)先求解,,BAC CAE ÐÐ 再求解,CAD Ð 再利用角的和差可得答案;(2)先求解()190,90,2CAE B C DAC C Ð=°-Ð+ÐÐ=°-Ð 再利用角的和差可得结论.【详解】解:(1)Q ∠B =30°,∠C =50°,180100,BAC B C \Ð=°-Ð-Ð=°Q AD ,AE 分别是 △ ABC 的高和角平分线,150,90,2BAE CAE BAC ADE ADC \Ð=Ð=Ð=°Ð=Ð=° 905040,DAC \Ð=°-°=°504010.DAE EAC DAC \Ð=Ð-Ð=°-°=°(2)()1,2DAE C B Ð=Ð-Ð 理由如下:Q AD ,AE 分别是 △ ABC 的高和角平分线。
专题01 手拉手模型大全(解析版)

B专题01 手拉手模型大全等边三角形模型一、△ACE 与△DBC 是等边三角形。
当B 、C 、E 三点不共线时 1.△ACE ≅△BCD 2.BD=CE 3.∠APB=60°思路引领:由:∠ACB=∠E CD=60°⇒∠BCD=∠ACE 又∵AB=AC, CD=CE ∴△ACE ≅△BCD∴BD=AE, ∠CAE=∠CBD (法一)∴点A,B,C,P 四点共圆. ∴∠APB=∠ACB= 60°(法二) ∠APB+∠CAE=∠ACB +∠BCD=∠AGB ∴∠APB=∠ACB= 60°模型二、△ACE 与△DBC 是等边三角形。
当B 、C 、E 三点共线时,则有以下10个结论 (可借助右边备用图) 1.△ACE ≅△BCD 2.BD=CE 3.∠APB=60° 以上证法同一.4.△HCA ≅△BGC由△ACE ≅△BCD 可得∠CAE=∠CBD, 又∵AB=AC, ∠ACH=∠BCG=60°, ∴△HCA ≅△BGC5.△GCH 是等边三角形. △HCA ≅△BGC ⇒CG=CH 又由于∠BCG=60°,所以△GCH 是等边三角形. 6.△GDC ≅△HCE△HCA ≅△BGC ⇒CG=CH又由于DC=ED,∠ACH=∠BCG=60° 可得△GDC ≅△HCE 7.GH∥BE由△GCH 是等边三角形. 可得∠CHG=∠H CE=60° GH∥BEBB8.PC 平分∠EPB思路:过点C 作CM,CN 分别垂直于BD,AE,垂足为 M,N∵△ACE ≅△BCD ∴CM=CN ∴PC 平分∠EPB9.BP=AP+PC,EP=PD+PC 如图,截取BQ=AP 易证△APC ≅△BQC 得∠BCQ=∠ACP,CP=CQ 可证: ∠QCP=60° 得△CPQ 为等边三角形. 则CP=QP.∴BP=BQ+QP=AP+AC 同法可证: EP=PD+PC10.△GCB∽△APG,△DPH∽△HCE由上述结论中的:∠CBG=∠PAG, ∠APG=∠GCB,可证△GCB∽△APG 同理可证△DPH∽△HCE等腰篇模型三、若△ACE 与△DBC 是等腰三角形。
手拉手模型(解析版)--全等三角形的七大模型全攻略 (1)
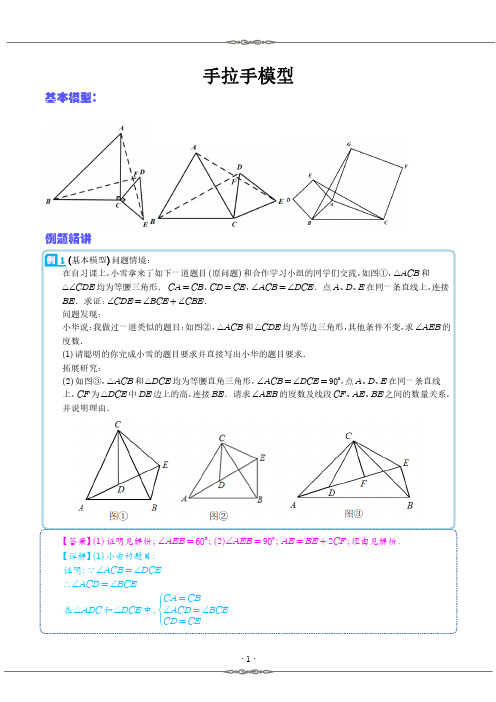
手拉手模型基本模型:例题精讲1(基本模型)问题情境:在自习课上,小雪拿来了如下一道题目(原问题)和合作学习小组的同学们交流,如图①,△ACB和△∠CDE均为等腰三角形.CA=CB,CD=CE,∠ACB=∠DCE.点A、D、E在同一条直线上,连接BE.求证:∠CDE=∠BCE+∠CBE.问题发现:小华说:我做过一道类似的题目:如图②,△ACB和△CDE均为等边三角形,其他条件不变,求∠AEB的度数.(1)请聪明的你完成小雪的题目要求并直接写出小华的题目要求.拓展研究:(2)如图③,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CF为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CF、AE、BE之间的数量关系,并说明理由.【答案】(1)证明见解析;∠AEB=60°;(2)∠AEB=90°;AE=BE+2CF;理由见解析.【详解】(1)小雪的题目:证明:∵∠ACB=∠DCE∴∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCECD=CE∴△ADC≅△BEC SAS∴∠CAD=∠CBE又∵∠ACD=∠BCE,∠CDE=∠CAD+∠ACD ∴∠CDE=∠CBE+∠BCE;小华的题目:解:∵∠ACB=∠DCE∴∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCE CD=CE∴△ADC≅△BEC SAS∴∠ADC=∠BEC∵△CDE为等边三角形∴∠CDE=∠CED=60°又∵点A、D、E在同一条直线上∴∠ADC=∠BEC=120°∴∠AEB=∠BEC-∠CED=60°(2)∠AEB=90°;AE=BE+2CF;理由如下:∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,∴∠ACB-∠DCB=∠DCE-∠DCB即∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCE CD=CE∴△ADC≅△BEC SAS∴BE=AD,∠BEC=∠ADC,∵点A、D、E在同一直线上∴∠ADC=180°-45°=135°∴∠BEC=135°∴∠AEB=∠BEC-∠CED=135°-45°=90°∵∠DCE=90°,CD=CE,CF⊥DE∴CF=DF=EF∴DE=DF+EF=2CF∴AE=AD+DE=BE+2CF .2(培优综合)(1)如图1,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在△BCD中,若∠BCD<120°,分别以BC,CD和BD为边在△BCD外部作等边△ABC,等边△CDE,等边△BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.【答案】(1)详见解析;(2)①详见解析;②PB+PC+PD=BE,理由详见解析【详解】(1)证明:∵△ABC和△DCE都是等边三角形,∴BC=AC,CE=CD,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴BE=AD;(2)①证明:∵△ABC和△DCE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,同理:△ABD≌△CBF(SAS),∴AD=CF,即AD=BE=CF;②解:结论:PB+PC+PD=BE,理由:如图2,AD与BC的交点记作点Q,则∠AQC=∠BQP,由①知,△ACD≌△BCE,∴∠CAD=∠CBE,在△ACQ中,∠CAD+∠AQC=180°-∠ACB=120°,∴∠CBE+∠BQP=120°,在△BPQ中,∠APB=180°-(∠CBE+∠BQP)=60°,∴∠DPE=60°,同理:∠APC=60°,∴∠CPE=60°, ∠CPD=120°,在PE上取一点M,使PM=PC,∴△CPM是等边三角形,∴CP=CM=PM,∠PCM=∠CMP=60°,∴∠CME=120°=∠CPD,∵△CDE是等边三角形,∴CD=CE,∠DCE=60°=∠PCM,∴∠PCD=∠MCE,∴△PCD≌△MCE(SAS),∴PD=ME,∴BE=PB+PM+ME=PB+PC+PD.【变式训练】1现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA所在直线上.以MN为边作如图所示的等边△MNP.(1)如图1,当M在线段OA上时,证明:AM-AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.【答案】(1)见解析;(2)AM+AN=AP,理由见解析【详解】证:(1)由题意可知,∠BAO=60°,如图所示,在AB上取点C,使得AC=AM,则△ACM为等边三角形,MC=MA,∠CMA=60°,∵△NMP为等边三角形,∴MN=MP,∠NMP=60°,∴∠CMA=∠NMP,∴∠CMA-∠NMA=∠NMP-∠NMA,∴∠CMN=∠AMP,在△CMN和△AMP中,MC=MA∠CMN=∠AMP MN=MP∴△CMN≌△AMP(SAS),∴CN=AP,∴CN+AN=AP+AN=AC,∵AC=AM,∴AP+AN=AM,∴AM-AN=AP;(2)AM+AN=AP,理由如下:如图所示,在射线AO上取点D,使得AN=AD,∵∠BAO=60°,∴△AND 为等边三角形,ND =NA ,∠DNA =60°,∵△NMP 为等边三角形,∴NM =NP ,∠MNP =60°,∴∠DNA =∠MNP ,∴∠DNA +∠ANM =∠MNP +∠ANM ,∴∠DNM =∠ANP ,在△DNM 和△ANP 中,ND =NA∠DNM =∠ANPNM =NP∴△DNM ≌△ANP (SAS ),∴AP =DM ,∵AN =AD ,DA +AM =DM ,∴AN +AM =AP .2如图1,在△ABC 中,AE ⊥BC 于E ,AE =BE ,D 是AE 上一点,且DE =CE ,连接BD ,CD .(1)判断BD 与AC 的位置关系和数量关系,并证明;(2)如图2,若将△DCE 绕点E 旋转一定的角度后,BD 与AC 的位置关系和数量关系是否发生变化?并证明;(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD 与AC夹角的度数.【答案】(1)BD ⊥AC ,BD =AC ;(2)BD ⊥AC ,BD =AC ;(3)60°.【详解】解:(1)BD 与AC 的位置关系是:BD ⊥AC ,数量关系是BD =AC .理由如下:如图1,延长BD 交AC 于点F .∵AE ⊥BC 于E ,∴∠BED =∠AEC =90°.∵AE =BE ,DE =CE ,∴△DBE ≅△CAE ,∴BD =AC ,∠DBE =∠CAE ,∠BDE =∠ACE .∵∠BDE =∠ADF ,∴∠ADF =∠ACE .∵AE ⊥BC∴∠ACE +∠CAE =90°,∴∠ADF +∠CAE =90°,∴BD ⊥AC .(2)BD 与AC 的位置关系是:BD ⊥AC ,数量关系是BD =AC .如图,线段AC 与线段BD 交于点F ,线段AE 与线段BD 交于点G,∵∠AEB =∠DEC =90°,∴∠AEB +∠AED =∠DEC +∠AED ,即∠BED =∠AEC .∵AE =BE ,DE =CE ,∴△BED ≅△AEC ,∴BD =AC ,∠DBE =∠CAE .∵AE ⊥BC∴∠DBE +∠BGE =90°,又∵∠FGA =∠BGE∴∠FGA +∠CAE =90°,∴BD ⊥AC .(3)如图,线段AC 与线段BD 交于点F ,∵△ABE 和△DEC 是等边三角形,∴AE =BE ,DE =EC ,∠EDC =∠DCE =60°,∠BEA =∠DEC =60°,∴∠BEA +∠AED =∠DEC +∠AED ,∴∠BED =∠AEC ,在△BED 和△AEC 中,BE =AE∠BED =∠AECDE =EC∴△BED ≅△AEC ,∴∠BDE =∠ACE ,∴∠BED +∠ACD =∠ACE +∠ACD =60°,∴∠DFC =180°-(∠EDC +∠BDE +∠ACD )=60°∴BD 与AC 的夹角度数为60°.3在△ABC 中,AB =AC ,点D 是直线BC 上一点(不与B ,C 重合),以AD 为一边在AD 的右侧作△ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE.(1)(请直接写出你的结论)如图1,当点D 在线段BC 上:①如果∠BAC =90°,则∠BCE =°;②如果∠BAC =100°,则∠BCE =°;(2)设∠BAC =α,∠BCE =β.①如图2,当点D 在线段BC 上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D 在直线BC 上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.【答案】(1)①90;②80;(2)①α+β=180°,理由见解析;②图见解析,α+β=180°或α=β【详解】解:(1)①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;②∵∠BAC=100°,AB=AC,∴∠ABD=∠ACB=40°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=40°,∴∠BCE=∠ACE+∠ACB=40°+40°=80°,故答案为:80.(2)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC.即∠BAD=∠CAE.在△ABD与△ACE中,AB=AC∠BAD=∠CAE AD=AE,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°.②如图1:当点D在射线BC上时,α+β=180°,连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD 和△ACE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,在△ABC 中,∠BAC +∠B +∠ACB =180°,∴∠BAC +∠ACE +∠ACB =∠BAC +∠BCE =180°,即:∠BCE +∠BAC =180°,∴α+β=180°,如图2:当点D 在射线BC 的反向延长线上时,α=β.连接BE ,∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,∴∠ABD =∠ACE =∠ACB +∠BCE ,∴∠ABD +∠ABC =∠ACE +∠ABC =∠ACB +∠BCE +∠ABC =180°,∵∠BAC =180°-∠ABC -∠ACB ,∴∠BAC =∠BCE .∴α=β;综上所述:点D 在直线BC 上移动,α+β=180°或α=β.4如图1,在△ABC 中,CA =CB ,∠ACB =90°.点D 是AC 中点,连接BD ,过点A 作AE ⊥BD 交BD 的延长线于点E ,过点C 作CF ⊥BD 于点F .(1)求证:∠EAD =∠CBD ;(2)求证:BF =2AE ;(3)如图2,将△BCF 沿BC 翻折得到△BCG ,连接AG ,请猜想并证明线段AG 和AB的数量关系.【答案】(1)见解析;(2)见解析;(3):AG =AB ,理由见解析【详解】(1)证明:∵AE ⊥BD ,∴∠AED =90°,∴∠EAD +∠ADE =90°,∵∠ADE =∠BDC ,∴∠EAD +∠BDC =90°,∵∠ACB=90°,∴∠CBD+∠BDC=90°,∴∠EAD=∠CBD;(2)证明:如图1,连接CE,在BF上截取BP=AE,连接CP,∵∠EAD=∠CBD,AC=BC,∴△AEC≌△BPC(SAS),∴CE=CP,∠ACE=∠BCP,∴∠ACE+∠DCP=∠BCP+∠DCP,∴∠ECP=∠DCB=90°,∵CE=CP,CF⊥BD,∴∠CEP=∠CPF=∠PCF=45°,∴CF=PF,∵点D是AC的中点,∴AD=CD,∵∠AED=∠CFD=90°,∠ADE=∠CDF,∴△AED≌△CFD(AAS),∴AE=CF,∴AE=PF,∴BF=BP+PF=2AE;(3)结论:AG=AB,证明如下:如图2,取BG的中点H,连接CE,CH,AH,∴BH=12BG=12BF=AE,∵∠HBC=∠PBC=∠EAC,∴∠EAC+∠CAB=∠HBC+∠CBA,∴∠EAB=∠HBA,∵AB=BA,∴△AEB≌△BHA(SAS),∴∠BHA=∠AEB=90°,∴AH⊥BG,∵BH=HG,∴AG=AB.课后训练5如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D为三角形右侧外一点.且∠BDC=45°.连接AD,若△ACD的面积为98,则线段CD的长度为.【答案】32【详解】解:过点B 作BE ⊥BD ,交DC 的延长线于点E ,连接AE ,如图所示:∵∠ABC =90°,∴∠ABE +∠EBC =∠EBC +∠CBD =90°,∴∠ABE =∠CBD ,∵∠BDC =45°,∠EBD =90°,∴△EBD 是等腰直角三角形,∴∠BDC =∠BED =45°,BE =BD ,∵AB =BC ,∴△BCD ≌△BAE (SAS ),∴∠BDC =∠BEA =45°,AE =CD ,∴∠AED =∠AEB +∠BED =90°,∵S △ACD =12CD ⋅AE =98,∴CD 2=94,∴CD =32;故答案为32.6如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图中,线段PM 与PN 的数量关系是,位置关系是;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.【答案】(1)PM =PN ,PM ⊥PN(2)△PMN 是等腰直角三角形(3)S △PMN 最大=492【详解】(1)∵点P ,N 是BC ,CD 的中点,∴PN ∥BD ,PN =12BD ,∵点P,M是CD,DE的中点,∴PM∥CE,PM=12CE,∴AB=AC,AD=AE,∴BD=CE,∴PM=PN,∵PN∥BD,∴∠DPN=∠ADC,∵PM∥CE,∴∠DPM=∠DCA,∵∠BAC=90°,∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,∴PM⊥PN,故答案为:PM=PN,PM⊥PN;(2)△PMN是等腰直角三角形,理由如下:由旋转知,∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≅△ACE(SAS),∴∠ABD=∠ACE,BD=CE,利用三角形的中位线得,PN=12BD,PM=12CE,∴PM=PN,∴△PMN是等腰三角形,同(1)的方法得,PM∥CE,∴∠DPM=∠DCE,同(1)的方法得,PN∥BD,∴∠PNC=∠DBC,∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形;(3)由(2)知,△PMN是等腰直角三角形,PM=PN=12BD,∴PM最大时,△PMN面积最大,∴点D在BA的延长线上,∴BD=AB+AD=14,∴PM=7,∴S △PMN 最大=12PM 2=12×72=492.7【问题发现】(1)如图1,△ABC 和△ADE 均为等边三角形,点B ,D ,E 在同一直线上,连接CE ,容易发现:①∠BEC 的度数为;②线段BD 、CE 之间的数量关系为;【类比探究】(2)如图2,△ABC 和△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,点B ,D ,E 在同一直线上,连接CE ,试判断∠BEC 的度数以及线段BE 、CE 、DE 之间的数量关系,并说明理由;【问题解决】(3)如图3,∠AOB =∠ACB =90°,OA =4,OB =8,AC =BC ,则OC 2的值为.【答案】(1)①60°;②BD =CE ;(2)∠BEC =90°,BE =CE +DE ,见解析;(3)8【详解】解:(1)∵△ABC 和△ADE 均为等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =60°,∴∠BAC -∠DAC =∠DAE -∠DAC ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴BD =CE ,∠AEC =∠ADB =180°-∠ADE =120°,∴∠BEC =∠AEC -∠AED =120°-60°=60°,故答案为:60°,BD =CE ;(2)∠BEC =90°,BE =CE +DE ,理由如下:∵∠BAC =∠DAE =90°,△ABC 和△ADE 均为等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =90°,∠ADE =∠AED =45°∠BAC -∠DAC =∠DAE -∠DAC ,即∠BAD =∠CAE ,在△ABD 和△ACE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴BD =CE ,∠AEC =∠ADB =135°,∴∠BEC =∠AEC -∠AED =135°-45°=90°,∵BE =BD +DE ,∴BE =CE +DE ;(3)如图3,过点C 作EF ∥OB ,交AO 的延长线于F ,过点B 作BE ⊥EF 于E ,∴∠F=∠AOB=∠BOF=90°,∠E=90°,∴四边形BOFE是矩形,∴OB=EF=8,BE=OF,∵∠ACB=90°,∴∠BCE+∠ACF=90°,∵∠ACF+∠CAF=90°,∴∠CAF=∠BCE,∵∠F=∠E=90°,AC=BC,∴△ACF≌△CBE(AAS),∴CF=BE,AF=CE,设OF=x,则AF=4+x,CE=8-x,∴4+x=8-x∴x=2,∴OF=2,AF=CE=6,∴CF=BE=OF=2,∴在Rt△COF中,OC2=OF2+CF2=22+22=8.故答案为:8.8已知在△ABC中,AB=AC,过点B引一条射线BM,D是BM上一点【问题解决】(1)如图1,若∠ABC=60°,射线BM在∠ABC内部,∠ADB=60°,求证:∠BDC=60°,小明同学展示的做法是:在BM上取一点E使得AE=AD,通过已知的条件,从而求得∠BDC的度数,请你帮助小明写出证明过程;【类比探究】(2)如图2,已知∠ABC=∠ADB=30°.①当射线BM在∠ABC内,求∠BDC的度数②当射线BM在BC下方,如图3所示,请问∠BDC的度数会变化吗?若不变,请说明理由,若改变,请求出∠BDC的度数;【答案】(1)见解析(2)①∠BDC=120°②;∠BDC的度数会变化,理由见解析【详解】(1)证明:如图1,在BM上取一点E,使AE=AD,∵∠ADB=60°,∴△ADE是等边三角形,∴∠EAD=60°,∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,∴∠BAC=∠EAD,∴∠BAC-∠EAC=∠EAD-∠EAC,即∠BAE=∠CAD,∵在△BAE和△CAD中AB=AC∠BAE=∠CAD AE=AD,∴△BAE≌△CAD SAS,∴∠ADC =∠AEB =120°,∴∠BDC =120°-60°=60°;(2)证明:①在BD 上取一点E ,AE =AD ,如图所示:∵∠ABC =∠ADB =30°,AB =AC ,∴∠ABC =∠ACB =30°,∠AED =∠ADE =30°,∴∠BAC =∠EAD =120°,∴∠BAE =∠CAD ,∵在△BAE 和△CAD 中AB =AC∠BAE =∠CAD AE =AD,∴△BAE ≌△CAD SAS ,∴∠ADC =∠AEB =180°-30°=150°,∴∠BDC =150°-30°=120°;②∠BDC 的度数会变化,理由如下:在DB 延长线上取一点E ,使得AE =AD ,如图所示:同理①的方法可证:△BAE ≌△CAD ,∴∠ADC =∠E =30°,∴∠BDC =∠ADE +∠ADC =30°+30°=60°.9(1)如图1,△ABC 与△CDE 均为等腰直角三角形,∠ACB =∠DCE =90°,猜想并证明:线段AE 、BD的数量关系和位置关系.(2)在(1)的条件下,若点A ,E ,D 在同一直线上,CM 为△DCE 中DE 边上的高,请判断∠ADB 的度数及线段CM ,AD ,BD 之间的数量关系,并说明理由.【答案】(1)AE =BD ,AE ⊥BD ,证明见解析.(2)∠ADB =90°,AD =2CM +BD .证明见解析【详解】解:(1)如图1中,延长AE 交BD 于点H ,AH 交BC 于点O ,∵△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,∴AC =BC ,CD =CE ,∴∠ACE =∠BCD ,∴△ACE ≌△BCD (SAS ),∴AE =BD ,∠CAE =∠CBD,∵∠CAE+∠AOC=90°,∠AOC=∠BOH,∴∠BOH+∠CBD=90°.∴∠AHB=90°,∴AE⊥BD.故答案为AE=BD,AE⊥BD;(2)∠ADB=90°,AD=2CM+BD,理由如下:如图2中,∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,∴∠CDE=∠CED=45°,∴∠AEC=180°-∠CED=135°,由(2)可知:△ACE≌△BCD,∴AE=BD,∠BDC=∠AEC=135°,∴∠ADB=∠BDC-∠CDE=135°-45°=90°;在等腰直角三角形DCE中,CM为斜边DE上的高,∴CM=DM=ME,∴DE=2CM,∴AD=DE+AE=2CM+BD .10已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.(1)如图1,若∠DAB=60°,则∠AFG=;(2)如图2,若∠DAB=90°,则∠AFG=;(3)如图3,若∠DAB=α,试探究∠AFG与α的数量关系,并给予证明.【答案】(1)60°;(2)45°;(3)12(180°-α),证明见解析【解析】(1)连接AG.∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.在△ADC和△ABE中,AD=AB∠DAC=∠BAE AC=AE,∴△ADC≌△ABE(SAS),∴DC =BE ,∠ADC =∠ABE .∵G 、F 分别是DC 与BE 的中点,∴DG =12DC ,BF =12BE ,∴DG =BF .在△ADG 和△ABF 中,AD =AB∠ADC =∠ABE DG =BF,∴△ADG ≌△ABF (SAS ),∴AG =AF ,∠DAG =∠BAF ,∴∠AGF =∠AFG ,∠DAG -∠BAG =∠BAF -∠BAG ,∴∠DAB =∠GAF .∵∠DAB =60°,∴∠GAF =60°.∵∠GAF +∠AFG +∠AGF =180°,∴∠AFG =60°;故答案为60°,(2)连接AG ,如图2,∵∠DAB =90°,∠DAB =∠GAF ,(已证)∴∠GAF =90°,∵AG =AF ,∴∠AFG =12×(180°-90°)=45°;故答案为45°,(3)连接AG ,如图3,∵∠DAB =α,∠DAB =∠GAF ,(已证)∴∠GAF =α,∵AG =AF ,∴∠AFG =12(180°-α).11△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形.(1)问题发现:如图1,若点A,D,E在同一直线上,连接AE,BE.①求证:△ACD≌△BCE;②求∠AEB的度数.(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.【答案】(1)①见解析;②∠AEB=60°;(2)∠ADB=60°,2DM+BD=AD,理由见解析;(3)α=60°,证明见解析【解析】(1)①证明:∵△ACB和△DCE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=60°-∠DCB=∠BCE,∴△ACD≌△BCE(SAS);②∵△ACD≌△BCE,∴∠ADC=∠BEC=180°-∠CDE=120°,又∵∠CED=60°,∴∠AEB=60°;(2)解:∠ADB=60°,2DM+BD=AD,理由如下;∵AC=BC,CD=CE,∠ACD=60°+∠DCB=∠BCE,∴△ACD≌△BCE(SAS),∴∠CDA=∠CED=60°;∵∠ADB+∠CDA=∠DCE+∠CED,∴∠ADB=60°;又∵CM⊥BE,且△CDE为等边三角形,∴DE=2DM,∴2DM+BD=BE=AD;(3)解:α=60°,理由如下:同理可证△ACD≌△BCE,∴∠BEC=∠ADC,∴∠CDF+∠CEF=180°,∴∠ECD+∠DFE=180°,而α+∠DFE=180°,∴α=∠ECD=60°.12(1)问题发现:如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD,BE,点A、D、E在同一条直线上,则∠AEB的度数为,线段AD、BE之间的数量关系;(2)拓展探究:如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由.(3)解决问题:如图3,△ACB 和△DCE 均为等腰三角形,∠ACB =∠DCE =α,则直线AD 和BE 的夹角为.(请用含α的式子表示)【答案】(1)90°,AD =BE ;(2)AD =BE ,AD ⊥BE ;(3)α【详解】(1)∵△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,∴AC =BC ,CD =CE ,∠CDE =45°∴∠CDA =135°∵∠ACB -∠DCB =∠DCE -∠DCB ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC =BC∠ACD =∠BCE CD =CE,∴△ACD ≌△BCE (SAS ),∴∠BEC =∠ADC =135°,AD =BE∴∠AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ⊥BE ,理由如下,同理可得△ACD ≌△BCE ,则AD =BE ,延长AD 交BE 于点F ,设∠FAB =α,则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠FAB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE(3)如图,延长BE 交AD 于点G ,∵△ACB 和△DCE 均为等腰三角形,∴AC =BC ,CD =CE ,∵∠ACB =∠DCE =α,∵∠ACB +∠ACE =∠DCE +∠ACE ,∴∠ACD =∠BCE .CD =CE∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD∵∠ACB =∠DCE =α∴∠CBA =∠CAB =12180°-α =90°-12α∴∠GAB +∠GBA =∠CAD +∠CAB +∠ABC -∠CBE ,=∠ABC +∠CAB =180°-α,∴∠AGB =180°-(∠GAB +∠GBA )=α,即直线AD 和BE 的夹角为α.故答案为:α.13已知,在△ABC 中,∠A =90°,AB =AC ,点D 为BC 的中点.(1)观察猜想如图①,若点E 、F 分别是AB 、AC 的中点,则线段DE 与DF 的数量关系是;线段DE 与DF 的位置关系是.(2)类比探究如图②,若点E 、F 分别是AB 、AC 上的点,且BE =AF ,上述结论是否仍然成立,若成立,请证明:若不成立,请说明理由;(3)解决问题如图③,若点E 、F 分别为AB 、CA 延长线的点,且BE =AF =13AB =2,请直接写出△DEF 的面积.【答案】(1)DE =DF ,DE ⊥DF ;(2)成立,证明见解析;(3)17【详解】解:(1)∵点E 、F 、D 分别是AB 、AC 、BC 的中点,∴ED =12AC ,DF =12AB ,ED ∥AC ,DF ∥AB ,∵AB =AC ,∠A =90°,∴DE =DF ,∠BDE =∠FDC =∠C =45°,∴∠EDF =90°即DE ⊥DF ,故答案为:DE =DF ,DE ⊥DF ;(2)结论成立:DE =DF ,DE ⊥DF ,证明:如图所示,连接AD ,∵AB =AC ,∠BAC =90°,D 为BC 的中点,∴AD =12BC =BD =CD ,且AD 平分∠BAC ,∠B =∠C =45°,∴∠BAD =∠CAD =45°,BE =AF∴△BDE ≌△ADF SAS ,∴DE =DF ,∠BDE =∠ADF ,∵∠BDE +∠ADE =90°,∴∠ADF +∠ADE =90°,即∠EDF =90°,即DE ⊥DF ;(3)如图所示,连接AD ,∵AB =AC ,∠BAC =90°,D 为BC 的中点,∴AD =12BC =BD =CD ,且AD 平分∠BAC ,∠ABC =∠C =45°,∴∠BAD =∠CAD =45°,∴∠FAD =180°-∠CAD =135°,∠EBD =180°-∠ABC =135°,∴∠FAD =∠EBD ,在在△BDE 和△ADF 中,BD =AD∠EBD =∠FAD BE =AF,∴△BDE ≌△ADF (SAS ),∴S △BDE =S △ADF ,∴S △DEF =S △ABD +S △AEF =12S △ABC +S △AEF,∵BE =AF =13AB =2,∴AB =AC =6,∴AE =AB +BE =8,∴S △DEF =12S △ABC +S △AEF =12×2×8+12×12×6×6=1714如图,在等边三角形ABC 右侧作射线CP ,∠ACP =α<60°,点A 关于射线CP 的对称点为点D ,连接BD 交CP 于点E ,连接AD ,CD ,AE .(1)用含α的式子表示∠BCD ;(2)求∠BEC 的度数;(3)试探究线段BD 、AE 、CE 之间的数量关系,并证明.【答案】(1)∠BCD =60°+2α;(2)60°;(3)BD =2AE +CE ,证明见解析【详解】(1)∵点A 关于射线CP 的对称点为点D ,∴PC 垂直平分AD ,∴AC=DC,∠ACP=∠DCP=α,∴∠ACD=2α,∵△ABC是等边三角形,∴∠ACB=60°,∴∠BCD=∠BCA+∠ACD=60°+2α,(2)由(1)得∠BCD=60°+2α,∵△ABC是等边三角形,∴BC=AC,又∵AC=DC,∴BC=DC,∴∠DBC=∠BDC=180°-60°-2α2=60°-α,∴∠BEC=180°-∠DBC-∠BCE=180°-(60°-α)-(60°+α)=60°;(3)答:BD=2AE+CE;证明:在BE上取点F,使得EF=EC,连接FC,∵∠BEC=60º,∴△EFC是等边三角形,∴∠ECF=∠ACB=60°,EF=FC=EC,∴∠ECF-∠ACF=∠ACB-∠ACF即∠BCF=∠ACE,在△BCF和△ACE中,AC=BC∠ACE=∠BCF FC=EC,∴△BCF≌△ACE(SAS),∴BF=AE,∵PC垂直平分AD,∴DE=AE,∴BD=BF+EF+DE,即BD=2AE+CE.·21·。
《探索三角形全等》几何模型-“手拉手”(专项练习)(基础篇)-2021-2022学年八年级数学上册

专题1.20 《探索三角形全等》几何模型-“手拉手”(专项练习)(基础篇)一、单选题1.如图所示,C 是线段BD 上一点,分别以BC ,CD 为边在BD 同侧作等边ABC D 和等边CDE D ,AD 交CE 于F ,BE 交AC 于G ,则图中可通过旋转而得到的全等三角形的对数为( )对.A .1B .2C .3D .42.如图,AB=AD ,AC=AE ,ÐDAB=ÐCAE=50° ,以下四个结论:①△ADC ≌△ABE ;②CD=BE ;③ÐDOB=50°;④点A 在ÐDOE 的平分线上,其中结论正确的个数是( )A .1B .2C .3D .4二、填空题3.如图,点B 、C 、E 在同一条直线上,ABC V 与CDE △都是等边三角形,下列结论:①AE=BD ;②DGC EFC V V ≌;③线段AE 和BD 所夹锐角为80°;④FG ∥BE .其中正确的是______.(填序号)三、解答题4.如图,AC BC ^,DC EC ^,AC BC =.DC EC =,AE 与BD 交于点F .(1)求证:AE BD =;(2)求AFD Ð的度数.5.在ABC V 中,AB AC =,点D 是直线BC 上一点(点D 不与点B ,C 重合),以AD 为一边在AD 的右侧作ADE V ,使AD AE =,DAE BAC Ð=Ð,连接CE .(1)如图(1),若点D 在线段BC 上,BCE Ð和BAC Ð之间有怎样的数量关系?(不必说明理由)(2)若60BAC й°,当点D 在射线BC 上移动时,如图(2),BCE Ð和BAC Ð之间有怎样的数量关系?说明理由.6.如图,△ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°,点A ,D ,E 在同一条直线上,连接BE .(1)求证:AD=BE ;(2)若∠CAE=15°,AD=4,求AB 的长.7.如图,A 、B 、C 在同一直线上,且△ABD ,△BCE 都是等边三角形,AE 交BD 于点M ,CD 交BE 于点N ,MN ∥AC ,求证:(1)∠BDN=∠BAM ;(2)△BMN 是等边三角形.8.如图,若ABD △和ACE △都是等边三角形,求BOC Ð的度数.9.如图,在△ABC 中,AB =BC ,∠ABC =120°,点D 在边AC 上,且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,点F 是ED 与AB 的交点.(1)求证:AE =CD ;(2)若∠DBC =45°,求∠BFE 的度数.10.如图,ABC V 中,AC BC =,DCE V 中,DC EC =,且DCE ACB Ð=Ð,当把两个三角形如图①放置时,有AD BE =.(不需证明)(1)当把DCE V 绕点C 旋转到图②③④的情况,其他条件不变,AD 和BE 还相等吗?请在图②③中选择一种情况进行证明;(2)若图④中AD 和BE 交于点P ,连接PC ,求证:PC 平分BPD Ð.11.如图,在等边三角形ABC 中,点P 在BA 的延长线上,以AP 为边在射线BA 的右侧作等边三角形PAD ,连接CP ,BD ,求证:CP BD =.12.如图,以ABC V 的边AB 、AC 向外作等边ABD △和等边ACE △,连接BE 、CD .问:线段BE 和CD 有什么数量关系?试证明你的结论.13.如图所示,ABC D 和ADE D 都是等边三角形,且B A E 、、在同一直线上,连结BD 交AC 于M ,连接CE 交AD 于N ,连结MN .求证:(1)BD CE =;D@D;(2)ABM ACND是等边三角形.(3)AMN14.如图,点C是线段AB上任意一点(点C与点A,B不重合),分别以AC,BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE 相交于点N.连接MN.证明:(1)△ACE≌△DCB;(2)△ACM≌△DCN;(3)MN∥AB.15.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)线段AN与线段BM交于点O,求∠AOM的度数;(3)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.16.如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上.若∠B=60°,求证:CE=AC+CD.17.如图,△ABD和△BCE都为等边三角形,连接AE、CD.求证:AE=DC.参考答案1.C【解析】本题考查的是全等三角形的判定、等边三角形的性质以及旋转的性质的综合运用.根据等边三角形的三边相等、三个角都是60°,以及全等三角形的判定方法(SSS、SAS、ASA、AAS),进行证明.解:△EBC≌△ACD,△GCE≌△FCD,△BCG≌△ACF.理由如下:BC=AC,EC=CD,∠ACB=∠ECD,∠ACE是共同角⇒△EBC≌△ACD.CD=EC,∠FCD=ECG,∠GEC=∠CDF⇒△GCE≌△FCD.BC=AC,∠GBC=∠FAC,∠FCA=∠GCB⇒△BCG≌△ACF.故选C.2.D【分析】根据全等三角形的判定及角平分线的性质即可依次判断.【详解】∵ÐDAB=ÐCAE∴ÐDAB+ÐBAC=ÐCAE+ÐBAC∴ÐDAC=ÐEAB∵AB=AD,AC=AE∴△ADC≌△ABE∴CD=BE,故①②正确;∵△ADC≌△ABE∴ÐADC =ÐABE设AB与CD交于G点,∵ÐAGD =ÐBGC∴ÐDOB=ÐDAB=50°,故③正确;过点A作AF⊥CD于F点,过点A作AH⊥BE于H点,则AF、AH分别是△ADC与△ABE边上的高∵△ADC≌△ABE∴点A 在ÐDOE 的平分线上,④正确故选D .【点拨】此题主要考查全等三角形的判定与性质,解题的关键是熟知角平分线的性质与判定.3.①②④【分析】利用等边三角形的性质证明BCD ACE V V ≌可判断①,利用BCD ACE V V ≌,可得,BDC AEC Ð=Ð利用三角形的外角的性质可得60,AHB Ð=° 从而可判断③, 再结合等边三角形的性质证明DGC EFC V V ≌可判断②, 由DGC EFC V V ≌可得:CG CF =,结合60,ACD Ð=°可得60CFG Ð=°,从而可判断④.【详解】解:如图,记AE 与BD 的交点为H ,∵ABC V 与CDE △都是等边三角形,∴AC=BC ,CD=CE ,∠BCA=∠DCE=60°∵点B 、C 、E 在同一条直线上,∴∠ACD=60°,∴∠BCD=∠ACE=120°在BCD V 和ACE △中,BCD ACECD CE ïÐ=Ðíï=î∴BCD ACE V V ≌,,BD AE \= 所以结论①正确;∵BCD ACE V V ≌,∴∠BDC=∠CEA ,∵∠AHB=∠DBE+∠BEA=∠DBE+∠BDC=180°-∠BCD=60°, 所以③错误;在GCD V 和FCE △中,GCD DCE CE CDCDB CEA Ð=Ðìï=íïÐ=Ðî, ∴GCD FCE V V ≌,∴所以②正确;GCD FCE QV V ≌,∵CG=CF ,∠ACD=60°,∴∠GFC=60,又∵∠DCE=60°,∴∠GFC=∠DCE ,∴GF ∥BC ,所以④正确.故答案为:①②④.【点拨】本题考查了全等三角形的判定和性质、等边三角形的性质和判定,平行线的判定,解决本题的关键是找到判定三角形全等的条件.4.(1)见解析(2)90°【分析】(1)根据题意证明△ACE ≌△BCD 即可求解;(2)根据三角形的内角和及全等三角形的性质即可得到AFD Ð的度数.【详解】(1)∵AC BC ^,DC EC ^,∴∠ACB=∠ECD=90°∴∠ACB+∠BCE=∠ECD+∠BCE即∠ACE=∠BCD又AC BC =.DC EC=∴△ACE ≌△BCD∴AE BD=(2)∵△ACE ≌△BCD∴∠A=∠B设AE 与BC 交于O 点,∴∠AOC=∠BOF∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°∴∠BFO=∠ACO=90°故AFD Ð=180°-∠BFO=90°.【点拨】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定定理.5.(1)180BCE BAC Ð+Ð=°;(2)180BCE BAC Ð+Ð=°,理由见解析【分析】(1)根据题意证明ABD ACE △≌△,根据三角形的内角和即可求解;(2)设AD 与CE 交于F 点,根据题意证明ABD ACE △≌△,根据平角的性质即可求解.【详解】(1)180BCE BAC Ð+Ð=°.理由如下:BAC DAE Ð=ÐQ ,BAD CAE \Ð=Ð.AB AC =Q ,AD AE =,ABD ACE \V V ≌,ABC ACE \Ð=Ð,∴BCE BCA ACE Ð=Ð+Ð=BCA ABCÐ+Ð∵180ABC BAC ACB Ð+Ð+Ð=°∴180BCE BAC Ð+Ð=°;(2)180BCE BAC Ð+Ð=°.理由如下:设AD 与CE 交于F 点.BAC DAE Ð=ÐQ ,BAD CAE \Ð=Ð.AB AC =Q ,AD AE =,ABD ACE \V V ≌,ADB AEC \Ð=Ð.AFE CFD Ð=ÐQ ,EAF ECD \Ð=Ð.BAC FAE Ð=ÐQ ,180BCE ECD Ð+Ð=°,180BCE BAC \Ð+Ð=°.【点拨】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定定理.6.(1)见解析;(2)8【分析】(1)直接证明≌ACD BCE V V ,即可得出结论;(2)由(1)可进一步推出AEB △为直角三角形,且30EAB Ð=°,从而由2AB BE =求解即可.【详解】(1)Q △ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°,ADC BCE \Ð=Ð,在ACD △与BCE V 中,AC BC ACD BCEDC EC =ìïÐ=Ðíï=î()ACD BCE SAS \V V ≌,AD BE \=;(2)ABC QV 是等腰直角三角形,45ABC \Ð=°,由(1)可知,15CAE CBE Ð=Ð=°,4BE AD ==,451560ABE ABC CBE \Ð=Ð+Ð=°+°=°,90ABE ACB \Ð=Ð=°,则在Rt AEB V 中,30EAB Ð=°,28AB BE \==.【点拨】本题考查全等三角形的判定与性质,及含30°角的直角三角形的性质,根据“手拉手”模型证明全等,并推导出直角三角形是解题关键.7.(1)证明过程见详解;(2)证明过程见详解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍长中线模型模型讲解【结论】已知△ABC中,∠ACB=∠DCE,AC=BC,DC=EC,且点A、D、E 在同一直线上,AE与BC相交于点F,连接BE.(1)△ACD≌△BCE(2)∠CAD=∠CBE;∠AEB=∠ACF【证明】(1)∵∠ACB=∠DCE,CA=CB,CD=CE,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,∵∠CF A=∠BFE,∴∠AEB=∠ACF△BCE可看成△ACD绕C点顺时针旋转一定角度而得到的;△ACD可看成△BCE绕C点逆时针旋转一定角度而得到的。
所以,通常用旋转的思想来构造全等三角形手拉手模型的关键:AC=BC(线段相等、有公共点且此三点不共线)那么,哪些图形满足这些特征呢?1【等边三角形类】等边△ABD、△BCE,则:(1)△ABC≌△BDE (2)∠ACB=∠DEB已知等边△BCE,将△ABC绕B点旋转60°到△BDE,那么会得到一个新的△ABD也为等边三角形。
【等腰直角三角形类】等腰Rt△ABD、△BCE,则:(1)△ABC≌△BDE (2)∠ACB=∠DEB已知等腰Rt△BCE,将△ABC绕B点旋转90°到△BDE,那么会得到一个新的△ABD也为等腰Rt△。
方法点拨例题演练1.(2021春•鄄城县期末)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=()A.55°B.50°C.45°D.60°【解答】解:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴∠2=∠ABD=30°,∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°,故选:A.2.(2016春•威海期末)如图,△ABC和△CDE均为等边三角形,且AB=DE,AC⊥CD,连接AE,BD,分别交CD,AC于点G,连接FG,BE.下列结论:①AE=BD=BE;②BC平分∠DBE;③直线EC⊥AB;④FG∥BE.其中正确结论的个数为()A.1个B.2个C.3个D.4个【解答】解:∵△ABC和△CDE均为等边三角形,且AB=DE,∴∠ACB=∠DCE=60°,∵AC⊥CD,∴∠ACD=90°,∴∠ACE=∠BCD=150°,∴∠BCE=150°,在△ACE与△BCD与△BCE中,,∴△ACE≌△BCD≌△BCE,∴AE=BD=BE,故①正确,∠DBC=∠EBC,故②正确;∴∠BEC=∠AEC,∵BE=AE,∴直线EC⊥AB;故③正确;在△BCF与△ECG中,,∴△BCF≌△ECG,∴BF=EG,设AE,BD交于H,∵∠FBC=∠GEC,∠CBE=∠CEB,∴∠HBE=∠HEB,∴BH=EH,∴HF=HG,∴,∴FG∥BE,故④正确,故选:D.3.(2018秋•海珠区校级期中)如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,下列结论:①∠FCD=45°;②AE=EC;③S△ABF:S△AFC=BD:CD;④若BF=2EC,则△FCD的周长等于AB的长,正确的有()个.A.1B.2C.3D.4【解答】解:∵△ABC中,AD,BE分别为BC、AC边上的高,∴AD⊥BC,而△ABF和△ACF有一条公共边,∴S△ABF:S△AFC=BD:CD,∴③正确;∵∠ABC=45°,∴AD=BD,∠DAC和∠FBD都是∠ACD的余角,而∠ADB=∠ADC=90°,∴△BDF≌△ADC,∴FD=CD,∴∠FCD=∠CFD=45°,∴①正确;若AE=EC,BE⊥AC,可得AB=BC,与题意不符合,故②错误.若BF=2EC,根据①得BF=AC,∴AC=2EC,即E为AC的中点,∴BE为线段AC的垂直平分线,∴AF=CF,BA=BC,∴AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD,即△FDC周长等于AB的长,∴④正确.强化训练故选:C.1.(2021春•北碚区校级期末)如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA =ED.(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:EC平分∠BCD;(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD =AB=4.求点E到BC的距离.【解答】(1)证明:延长CD到T,使得DT=BA,连接ET.∵∠CDE=120°,∴∠EDT=180°﹣120°=60°,∵∠A=60°,∴∠A=∠EDT,在△EAB和△EDT中,,∴△EAB≌△EDT(SAS),∴EB=ET,∴CB=CD+BA=CD+DT=CT,在△ECB和△ECT中,,∴△ECB≌△ECT(SSS),∴∠ECB=∠ECD.(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,∴∠A=∠EDQ,在△AEB和△DEQ中,,∴△AEB≌△DEQ(ASA),∴EB=EQ,∵∠AED=2∠BEC,∴∠AEB+∠CED=∠BEC,∴∠CED+∠DEQ=∠BEC,∴∠CEB=∠CEQ,在△CEB和△CEQ中,,∴△ECB≌△ECQ(SAS),∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30,∴S△EBC=15,∵CD=AB=4,∴AB=6,CD=4,∴BC=CD+QD=CD+AB=10,∴×10×EH=15,∴EH=3,∴点E到BC的距离为3.2.(2021春•松江区期末)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E、F分别在直线BC、CD上,且∠EAF=∠BAD.(1)当点E、F分别在边BC、CD上时(如图1),请说明EF=BE+FD的理由;(2)当点E、F分别在边BC、CD延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF、BE、FD之间的数量关系,并说明理由.【解答】解:(1)EF=BE+DF,理由:延长EB至G,使BG=DF,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,∴∠ADC=∠ABG,在△ABG和△ADF中,,∴△ABG≌△ADF(SAS),∴AG=AF,∠BAG=∠DAF,∵∠EAF=∠BAD,∴∠BAE+∠DAF=∠BAE+∠BAG=∠EAF,即∠EAG=∠EAF,在△EAG和△EAF中,,∴△EAG≌△EAF(SAS),∴GE=EF,∴EF=BE+DF;(2)(1)中结论不成立,EF=BE﹣FD,在BE上截取BM=DF,连接AM,∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,∴∠ABC=∠ADF,在△ABM和△ADF中,,∴△ABM≌△ADF(SAS),∴AM=AF,∠BAM=∠DAF,∵∠BAM+∠MAD=∠DAF+∠MAD,∴∠BAD=∠MAF,∵∠EAF=∠BAD,∴∠EAF=∠MAF,∴∠EAF=∠EAM,在△AME和△AFE中,,∴△AME≌△AFE(SAS),∴ME=BE﹣BM=BE﹣DF,∴EF=BE﹣FD.3.(2017•南岸区二模)如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBD,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.(1)若AE=2,求CE的长度;(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:F A+FB=FE.【解答】解:(1)延长CE交AB于G,∵△BAC是等腰直角三角形,CE平分∠ACB,∴CG⊥AB,∴∠AGC=90°,∵CA=CB,∠ACB=90°,∴∠CAB=45°,∴△CAG是等腰直角三角形,∵△BCD是等边三角形,∴BC=CD=AC,∠BCD=60°,∴∠CAD=∠CDA,∴∠ACD=∠ACB+∠BCD=150°,∴∠CAD=∠CDA=15°,∴∠EAB=∠CAB﹣∠CAD=30°,在Rt△AEG中,∠EAG=30°,AE=2,∴AG=,EG=1,∵CG=AG=,∴CE=CG﹣EG=﹣1.(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.由(1)可知:AC=BC,CE平分∠ACB,∴∠ACE=∠BCE,∴△ACE≌△BCE,∴AE=BE,∴∠EAB=∠EBA=30°,在△AFB中,∠AFB=60°,∴∠F AB+∠FBA=120°,∴∠F AE=∠EAB+∠F AB=30°+∠F AB,∠EBH=180°﹣∠EBA﹣∠ABF=150°﹣(120°﹣∠F AB)=30°+∠F AB,∴∠EBH=∠F AE,∴△AFE≌△BHE,∴∠AFE=∠BHE,EF=EH,∴∠EFB=∠EHB=∠AFE=30°,∵EI⊥FH,∴EI=IH,在Rt△FEI中,∠EFI=30°,∴FI=FE,∴FH=BH+FB=FE,∴F A+FB=FE.4.(2021春•南岸区期末)如图,已知∠BAD=∠CAE=90°,AB=AD,AE=AC.(1)△ABC与△ADE全等吗?请说明理由;(2)若AF⊥CB,垂足为F,请说明线段2CF=CE;(3)在(2)的基础上,猜想线段BF,DE,CD存在的数量关系,并直接写出结论.【解答】解:(1)△ABC≌△ADE,理由如下:如图1,∵∠BAD=∠CAE=90°,∴∠BAC=∠DAE=90°﹣∠CAD,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS).(2)如图2,作AG⊥BC于点G,则∠AGC=∠AGE=90°,∵AC=AE,AG=AG,∴Rt△AGC≌Rt△AGE(HL),∴CG=EG=CE,∠CAG=∠EAG=∠CAE=45°,∴∠ACG=∠E=45°,∵△ABC≌△ADE,∴∠ACF=∠E=45°,∵AF⊥CB,∴∠F=90°,∴∠CAF=45°,∵∠ACF=∠ACG=45°,AC=AC,∠CAF=∠CAG=45°,∴△CAF≌△CAG,∴CF=CG=CE,∴2CF=CE.(3)BF=(CD﹣DE),理由如下:如图2,由(2)得,CF=CG=EG,∵△ABC≌△ADE,∴BC=DE,∴CF﹣BC=EG﹣DE,∴BF=DG,∵DG=EG﹣DE=CE﹣DE=(CD+DE)﹣DE=(CD﹣DE),∴BF=(CD﹣DE).5.(2021春•沙坪坝区校级期末)如图,C为AB上一点,△ACD和△BCE为等边三角形,AE交CD于M,DB交CE于N.求证:(1)AE=DB;(2)MN∥AB;(3)PC平分∠APB;(4)PC+PE=PB.【解答】证明:(1)∵△ACD和△BCE是等边三角形,∴∠ACD=∠BCE=60°,AC=DC,EC=BC,∴∠ACD+∠DCE=∠DCE+∠ECB,即∠ACE=∠DCB,∴△ACE≌△DCB(SAS),∴AE=BD;(2)∵△ACE≌△DCB,∴∠EAC=∠BDC,∵∠ACD=∠BCE=60°,∴∠DCE=60°,∴∠ACD=∠MCN=60°,且∠EAC=∠BDC,AC=DC,∴△ACM≌△DCN(ASA),∴CM=CN,又∵∠MCN=60°,∴△MCN是等边三角形,∴∠NMC=∠ACD=60°,∴MN∥AB;(3)如图,过点C作CG⊥AE于G,作CH⊥BD于H,∵∠EAC=∠BDC,AC=DC,∠AGC=∠DHC=90°,∴△AGC≌△DHC(AAS),∴CG=CH,且CG⊥AE,CH⊥BD,∴PC平分∠APB;(4)如图,在PB上截取PF=PC,连接CF,∵△ACE≌△DCB,∴∠CAE=∠BDC,∠AEC=∠DBC,∵∠ACD=∠BDC+∠CBD=60°,∴∠DOA=∠CAE+∠CBD=60°,∴∠APB=120°,∵PC平分∠APB,∴∠CPF=APB=60°,∴△CPF为等边三角形,∴CF=CP,∠CFP=60°,∴∠CFB=∠CPE=120°,∴△CFB≌△CPE(AAS),∴BF=PE,∴PB=BF+PF=PE+PC.6.(2013秋•沙坪坝区校级月考)如图,等边△ABC中,点E、F分别是AB、AC的中点,P为BC上一点,连接EP,作等边△EPQ,连接FQ,EF.(1)若等边△ABC的边长为20,且∠BPE=45°,求等边△EPQ的边长;(2)求证:BP=EF+FQ.【解答】(1)解:过点E作EM⊥BC于M∵等边△ABC,∴∠B=60°,∵E为AB的中点,∴BE=AB=10,在Rt△BEM中,sin B=,∴=,∴EM=5,在Rt△EMP中,sin∠EPM=,∴=,∴EP=5,即等边△EPQ的边长为5;(2)证明:取BC的中点N,连接NE,∵等边△ABC,∴AB=BC,∵E为AB的中点,F为AC的中点,N为BC的中点,∴EF=BC,BE=AB,BN=BC,EF∥BC,∴EF=BE=BN,∵∠B=60°,∴△EBN是等边三角形,∴EN=BN=EF,∠ENB=60°,∵EF∥BC,∴∠FEN=60°,∴∠1+∠2=60°,∵等边△EPQ,∴EP=EQ,∠PEQ=60°,∴∠2+∠3=60°,∴∠1=∠3,在△ENP和△EFQ中,,∴△ENP≌△EFQ(SAS),∴NP=FQ,∴BP=BN+NP=EF+FQ.7.(2020秋•斗门区校级期中)如图,在Rt△ABC中,∠A=90°,AB=AC,D、E分别在AB,AC上,且AD=AE.若△ADE绕点A逆时针旋转,得到AD1E1,设旋转角为a(0°<a≤180°),记直线BD1与CE1的交点为P.(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求旋转角为a的度数.【解答】解:(1)在△ABD1和△ACE1中,,∴△ABD1≌△ACE1 (SAS),∴BD1=CE1;(2)设AC与BP交于点G,由(1)知△ABD1≌△ACE1,∴∠ABD1=∠ACE1,∵∠AGB=∠CGP,∴∠CPG=∠BAG=90°,∴∠CPD1=90°,∵∠CPD1=2∠CAD1,∴∠CAD1=∠CPD1=45°,∴旋转角α=90°+∠CAD1=135°.8.(2021春•渝中区校级期末)如图,△CAB与△CDE为等腰直角三角形,∠ACB=∠DCE =90°,CA=CB,CD=CE,∠CAB=∠CBA=45°,∠CDE=∠CED=45°,连接AD、BE.(1)如图1,若∠CAD=28°,∠DCB=10°,则∠DEB的度数为27度;(2)如图2,若A、D、E三点共线,AE与BC交于点F,且CF=BF,AD=3,求△CEF 的面积;(3)如图3,BE与AC的延长线交于点G,若CD⊥AD,延长CD与AB交于点N,在BC上有一点M且BM=CG,连接NM,请猜想CN、NM、BG之间的数量关系并证明你的猜想.【解答】解:(1)如图1中,∵△ACB,△CDE都是等腰直角三角形,∴∠ACB=∠DCE=90°,CA=CB,CD=CE,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE=28°,∵∠DCB=10°,∴∠ECB=90°﹣10°=80°,∴∠CEB=180°﹣80°﹣28°=72°,∵∠CED=45°,∴∠DEB=72°﹣45°=27°.故答案为:27.(2)如图2中,过点C作CQ⊥DE于Q.∵△ACD≌△BCE,∴∠ADC=∠CEB,AD=BE=3,∵∠CDE=∠CED=45°,∴∠ADC=∠CEB=135°,∴∠AEB=90°,在△CFQ和∠BFE中,,∴△CQF≌△BEF(AAS),∴CQ=BE=3,QF=EF,∵CQ=EQ=3,∴EF=EQ=,∴S△CEF=•EF•CQ=××3=.(3)如图3中,结论:CN+MN=BG.理由:如图过点B作BT⊥BC交CN的延长线于T∵AD⊥CD,∴∠ADC=90°,∵△ACD≌△BCE,∴∠ADC=∠BEC=90°,∵∠BCT+∠ECB=90°,∠ECB+∠CBG=90°,∴BCT=∠CBG,在△CBT和△BCG中,,∴△CBT≌△BCG(ASA),∴BT=CG,CT=BG,∵BM=CG,∴BM=BT,在△BNM和△BNT中,,∴△BNM≌△BNT(SAS),∴MN=NT,∴CN+MN=CN+NT=CT=BG.9.(2021春•楚雄州期末)已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.(1)如图1,当α=60°时,求出∠AEB的度数.(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=4+2,求△ABF的面积.【解答】解:(1)∵∠ACB=∠DCE=60°,CA=CB,CD=CE,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,∵∠CF A=∠BFE,∴∠AEB=∠ACF=60°.(2)同理可证△ACD≌△BCE,∴∠CAF=∠CBE,∵∠CBE=∠BAE,∴∠CAF=∠BAE,∴AF平分∠CAB,∵FC⊥AC,CF=2,∴点F到AB的距离=CF=2,∴S△ABF=•AB•CF=×(4+2)×2=4+2.10.(2012秋•渝北区期末)如图,△ABC中,AC=BC,∠ACB=90°,点D在△ABC的外部,且AD⊥BD,AD交BC于点E,连接CD,过点C作CG⊥CD,交AD于点G.(1)若CG=4,求DG的长;(2)若CG=BD,求证:AB=AC+CE.【解答】(1)解:∵AD⊥BD,∴∠ADB=90°,∵∠ACB=90°,而∠AEC=∠BED,∴∠CAE=∠EBD,∵CG⊥CD,∴∠GCD=90°,即∠GCE+∠ECD=90°,而∠GCE+∠ACG=90°,∴∠ACG=∠ECD,在△ACG和△BCD中,∴△ACG≌△BCD,∴CG=CD,∴△CDG为等腰直角三角形,∴DG=CG=4;(2)证明:延长AC、BD,它们相交于点H,如图,∵CG=BD,而CG=CD,∴BD=CD,∴∠DCB=∠DBC,∵∠H+∠CBH=90°,∠CHD+∠DCB=90°,∴∠H=∠HCD,∴CD=HD,∴DH=DB,而AD⊥BH,∴AB=AH,在△ACE和△BCH中,∴△ACE≌△BCH,∴CE=CH,∴AB=AC+CH=AC+CE.11.已知△BAC和△BDE都是等腰直角三角形,∠BAC=∠BDE=90°.(1)如图1,点E、B、C三点在一条直线上,连接AE,若∠AEC=30°,BC=4,求BE的长.(2)如图2,将△BDE以点B为旋转中心顺时针旋转,当C在ED延长线上时,EC交AB于点H.求证:∠BAE=2∠BCH.【解答】(1)解:如图1中,作AH⊥BC于H.∵AB=AC,∠BAC=90°,AH⊥BC,∴AH=BH=HC=2,在Rt△AEH中,∵∠AHE=90°,AH=2,∠AEH=30°,∴EH==2,∴BE=EH﹣BH=2﹣2.(2)证明:如图2中,连接AD.∵∠BDH=∠HAC,∠BHD=∠CHA,∴△BHD∽△CHA,∴=,∴=,∵∠AHD=∠CHB,∴△AHD∽△CHB,∴∠ADH=∠CBH=45°,∠DAH=∠BCH,∴∠ADB=90°+45°=135°,∴∠ADE=360°﹣90°﹣135°=135°,∴∠ADE=∠ADB,在△ADE和△ADB中,,∴△ADE≌△ADB,∴∠DAE=∠DAB,∵∠DAB=∠BCH,∴∠BAE=2∠BCH.12.(2021•鄂尔多斯)旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.(1)尝试解决:如图①,在等腰Rt△ABC中,∠BAC=90°,AB=AC,点M是BC上的一点,BM=1cm,CM=2cm,将△ABM绕点A旋转后得到△ACN,连接MN,则AM =cm.(2)类比探究:如图②,在“筝形”四边形ABCD中,AB=AD=a,CB=CD,AB⊥BC 于点B,AD⊥CD于点D,点P、Q分别是AB、AD上的点,且∠PCB+∠QCD=∠PCQ,求△APQ的周长.(结果用a表示)(3)拓展应用:如图③,已知四边形ABCD,AD=CD,∠ADC=60°,∠ABC=75°,AB=2,BC=2,求四边形ABCD的面积.【解答】解:(1)如图①,∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,由旋转得:CN=BM=1,∠ACN=∠B=45°,∠MAN=∠BAC=90°,AM=AN,∴∠MCN=∠ACB+∠ACN=45°+45°=90°,△AMN是等腰直角三角形,∵CM=2,∴MN==,∴AM=MN=(cm);故答案为:;(2)如图②,延长AB到E,使BE=DQ,连接CE,∵AB⊥BC,AD⊥CD,∴∠ADC=∠ABC=90°,∴∠CBE=∠CDQ=90°,在△CDQ和△CBE中,,∴△CDQ≌△CBE(SAS),∴∠DCQ=∠BCE,CQ=CE,∵∠PCB+∠QCD=∠PCQ,∴∠PCB+∠BCE=∠PCQ=∠PCE,在△QCP和△ECP中,,∴△QCP≌△ECP(SAS),∴PQ=PE,∴△APQ的周长=AQ+PQ+AP=AQ+PE+AP=AQ+BE+PB+AP=AQ+DQ+AB=2AB=2a;(3)如图③,连接BD,由于AD=CD,所以可将△BCD绕点D顺时针方向旋转60°,得到△DAB′,连接BB′,延长BA,作B′E⊥BA于E,由旋转得:△BCD≌△B′AD,∴BD=B'D,∠BDB'=60°,∠CBD=∠AB'D,∴S四边形ABCD=S四边形BDB′A,△BDB'是等边三角形,∵∠ABC=75°,∠ADC=60°,∴∠BAB′=∠BDB'+∠AB'D+∠ABD=135°,∴∠B′AE=45°,∵B′A=BC=2,∴B′E=AE=,∴BE=AB+AE=2+=3,∴BB′==2,设等边三角形的高为h,则勾股定理得:h==,∴S四边形ABCD =S四边形BDB′A=S△BDB′﹣S△ABB′=×2×﹣××=5﹣2.。
