11年北京石景山区初三数学一模试题及答案
北京市石景山中考一模数学试卷(含答案)

北京市石景山区2022年中考一模数学试卷一、选择题〔此题共16分,每题2分〕1.以下各式计算正确的选项是〔〕A2C3L5r 2 3A. a 2a 5aB. a a a2•实数a , b在数轴上的位置如下列图,以下说法正确的选项是〔# ft1TIF.BCD5 .如图,AD // BC, AC 平分/ BAD,假设/ B = 40 °A. 40°B. 65°C. 70°D.80°2D D4.以下博物院的标识中不是.轴对称图形的是〔〕ab C. a6 a2 a3D. (a2)3 a5MJ ^rl M那么/ C的度数是〔6.如图,在平面直角坐标系 xOy 中,点C , B , E 在y 轴上,Rt △ ABC 经过变化得到 Rt △ EDO ,假设点 B 的坐标为(0,1),OD=2,那么这种变化可以是〔 〕 7•甲、乙两地相距 300千米,一辆货车和一辆轿车分别从甲地开往乙地〔轿车的平均速度大于货车的平均速度〕,如图线段OA 和折线BCD 分别表示两车离甲地的距离 y 〔单位:千米〕与时间 x 〔单位:小时〕 之间的函数关系•那么以下说法正确的选项是〔 〕&罚球是篮球比赛中得分的一个组成局部,罚球命中率的上下对篮球比赛的结果影响很大•以下列图是对 某球员罚球训练时命中情况的统计:下面三个推断:① 当罚球次数是500时,该球员命中次数是 411,所以 罚球命中〞的概率是0.822 ; ② 随着罚球次数的增加, 罚球命中〞的频率总在0.812附近摆动,显示出一定的稳定 性,可以估计该球员 罚球命中〞的概率是0.812 ;③ 由于该球员 罚球命中〞的频率的平均值是 0.809,所以 罚球命中〞的概率是0.809. 其中合理的是〔 〕 A .①B .②C .①③D .②③A . △ ABC 绕点B . △ ABC 绕点 C . △ ABC 绕点D . △ ABC 绕点 C 顺时针旋转 C 逆时针旋转 O 顺时针旋转 O 逆时针旋转 90 °再向下平移 90 °再向下平移 90 °再向左平移 90 °再向右平移5个单位长度 5个单位长度 3个单位长度 1个单位长度A .两车同时到达乙地C .货车出发3小时后,轿车追上货车B .轿车在行驶过程中进行了提速 D .两车在前80千米的速度相等0.822 0.8120 100 200 300 400 500 600 700 800 900 1000 1100 1200 罚球次数二、填空题〔此题共 16分,每题2分〕9 •对于函数y —,假设x 2,那么y _________ 3〔填“ >或 “<〕x10•假设正多边形的一个外角是 45 °那么该正多边形的边数是 _______ •11•如果x y 5,那么代数式〔1 + 丄〕2X 2的值是 _____________________ •x y x y12•我国古代数学名著?孙子算经?中记载了一道题,大意是: 100匹马恰好拉了 100片瓦,3匹小 马能拉1片瓦,1匹大马能拉3片瓦,求小马、大马各有多少匹.假设设小马有 x 匹,大马有y 匹,依题 意,可列方程组为 _____________ •14・ 如图,在△ ABC 中,D , E 分别是AB , AC 边上的点, DE // BC •假设AD — , BD 2 , DE 3,那么 BC ______________________ •15 •某学校组织学生到首钢西十冬奥广场开展综合实践活动, 数学小组的同学们在距奥组委办公楼 钢老厂区的筒仓〕20m 的点B m 的测角仪测得筒仓顶点 C 的仰角为63°贝U 筒仓CD 的高约为13 .如图, AB 是O O 的直径, CD 是弦,CDAE ____________ • AB 于点E ,假设O O 的半径是5 , CD 8,那么〔原首E1.9—〕16.小林在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图,(1) 利用刻度尺在AOB的两边OA, OB上分别取OM ON ;(2) 利用两个三角板,分别过点M,N画OM,ON的垂线,交点为P ;(3) 画射线OP .那么射线OP为AOB的平分线.请写出小林的画法的依据___________________________________________________ 三、解答题〔此题共68分,第17、18题,每题5分;第19题4分;第20-23题,每题5分;第24、25 题,每题6分;第26、27题,每题7分;第28题8分〕17.计算:2sin45° 5 (-尽.33(x 1) 4x 5,18•解不等式组:x 62x219•问题:将菱形的面积五等分.小红发现只要将菱形周长五等分,再将各分点与菱形的对角线交点连接即可解决问题•如图,点 形ABCD 的对角线交点,AB 5 ,下面是小红将菱形 ABCD 面积五等分的操作与证明思路,O 是菱 请补充完整〔1〕在AB 边上取点E ,使AE〔2〕在BC 边上取点F ,使BF〔3〕在CD 边上取点G ,使CG〔4〕在DA 边上取点H ,使DH由于AE _____ + ______ _4,连接 0A , OE ; _______ ,连接OF ; _______ ,连接OG ; _______ ,连接OH • _+ _____ + _____ 可证S A AOE S 四边形EOFBS四边形FOGC 1S四边形GOHD=S A HOA.220.关于x 的一元二次方程 mx (3m 2)x 6 0 .〔1〕当m 为何值时,方程有两个不相等的实数根;〔2〕当m 为何整数时,此方程的两个根都为负整21.如图,在四边形 〔1〕求证:AE 〔2〕假设 tan D ABCD 中, ACE ;3,求AB 的长.BCD 90 ° BC CD 2局,CE AD 于点 E .a22 .在平面直角坐标系xOy中,函数y 〔x 0〕的图象与直线h: y x b交于点A(3,a 2).x〔1〕求a,b的值;〔2〕直线l2:y x m与x轴交于点B,与直线h交于点C,假设S △ ABC > 6,求m的取值范围.23.如图,AB是O O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交O O于点C ,连接BC , 过点D作FD丄OC交O O的切线EF于点F .1〔1〕求证:CBE — F ;2〔2〕假设O O的半径是2韶,点D是OC中点,CBE 15° ,求线段EF的长.24.某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了他们的10次测验, 10次成绩如下〔单位:分〕:整理、分析过程如下,请补充完整.〔1〕按如下分数段整理、描述这两组数据〔示〔3〕假设从甲、乙两人中选择一人参加知识竞赛,你会选〔填甲〞或乙〕,25 .如图,半圆0的直径AB 5cm,点M在AB上且AM 1cm,点P是半圆0上的动点,过点B作BQ PM交PM〔或PM的延长线〕于点Q •设PM x cm, BQ ycm •〔当点P与点A或点B重合时,y的值为0〕小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究下面是小石的探究过程,请补充完整:〔1〕通过取点、画图、测量,得到了x与y的几组值,如下表:〔2〔3〕结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60时,PM的长度约为__________________ c m.26. 在平面直角坐标系xOy中,将抛物线G-i:y mx2 2 3〔m 0〕向右平移.3个单位长度后得到抛物线G2,点A是抛物线G2的顶点.〔1〕直接写出点A的坐标;〔2〕过点〔0, 3〕且平行于x轴的直线I与抛物线G2交于B , C两点.①当BAC =90。
北京初三数学2011年各区一模二模12题汇总(含答案)
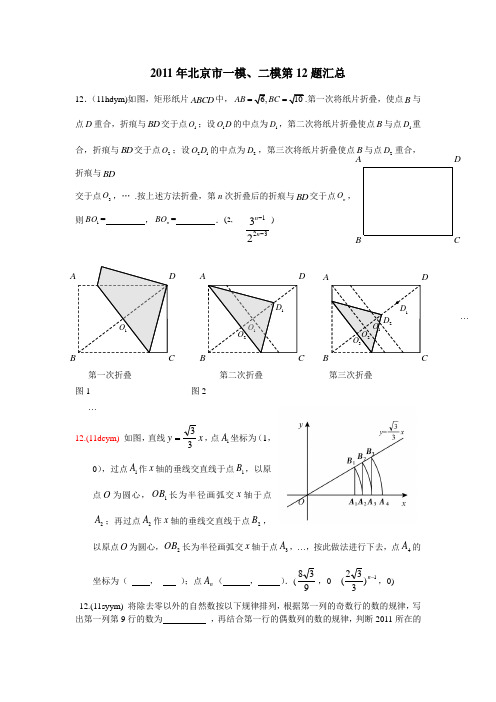
2011年北京市一模、二模第12题汇总12.(11hdym)如图,矩形纸片ABC D 中,6,10AB BC ==.第一次将纸片折叠,使点B 与点D 重合,折痕与BD 交于点1O ;设1O D 的中点为1D ,第二次将纸片折叠使点B 与点1D 重合,折痕与BD 交于点2O ;设21O D 的中点为2D ,第三次将纸片折叠使点B 与点2D 重合,折痕与BD交于点3O ,… .按上述方法折叠,第n 次折叠后的折痕与BD 交于点n O , 则1BO = ,n BO = .(2,12332n n --)…第一次折叠 第二次折叠 第三次折叠 图1 图2 …12.(11dcym) 如图,直线x y 33=,点1A 坐标为(1,0),过点1A 作x 轴的垂线交直线于点1B ,以原点O 为圆心,1O B 长为半径画弧交x 轴于点2A ;再过点2A 作x 轴的垂线交直线于点2B ,以原点O 为圆心,2O B 长为半径画弧交x 轴于点3A ,…,按此做法进行下去,点4A 的坐标为( , );点n A ( , ).(938,0 1)332(-n ,0)12.(11syym) 将除去零以外的自然数按以下规律排列,根据第一列的奇数行的数的规律,写出第一列第9行的数为 ,再结合第一行的偶数列的数的规律,判断2011所在的BADCBA DC1O 1O 2O 1D 1D 2D 1O 2O 3O B ADCB ADC…① ② ③ ④位置是第 行第 列.(6,121n n +)12.(11fsym)如图,以边长为1的正方形的四边中点为顶点作四边形, 再以所得四边形四边中点为顶点作四边形,......依次作下去, 图中所作的第三个四边形的周长为________;所作的第n个四边形的周长为_________________.(2,42()2n)12.(11yqym)如图,图①是一块边长为1,周长记为1P 的正三角形纸板,沿图①的底边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第)3(≥n n块纸板的周长为n P ,则=-34P P ;1--n n P P = .(81, 121-⎪⎭⎫ ⎝⎛n )12.(11myym) 如图,一个空间几何体的主视图和左视图都是边长为1的正 三角形,俯视图是一个圆,那么这个几何体的侧面积是 . (12π)12.(11dxym).将一个面积为1的等边三角形挖去连接三边中点所组成的三角形(如第①图)后,继续挖去连接剩余各个三角形三边中点所成的三角形(如第②图、第③图)…如此进行挖下去,第④个图中,剩余图形的面积为 ,那么第n(n 为正整数)个图中,挖去的所有三角形形的面积和为 (用含n 的代数式表示). ⎪⎭⎫⎝⎛25681)43(4或, n )(431-.(12题图)12.(11sjsym)已知:如图,在平面直角坐标系xOy 中,点1B 、点1C 的坐标分别为()0,1,()31,,将△11C OB绕原点O 逆时针旋转︒60,再将其各边都扩大为原来的m 倍,使12OC OB =,得到△22C OB .将△22C OB 绕原点O 逆时针旋转︒60,再将其各边都扩大为原来的m 倍,使23OC OB =,得到△33C OB ,如此下去,得到△n n C OB . (1)m 的值是_______________;(2)△20112011C OB 中,点2011C 的坐标:_____________.(2;(32,220102010)) 12.(11ysym)已知:点F 在正方形纸片ABCD 的边CD 上,AB=2,∠FBC=30°(如图1);沿BF 折叠纸片,使点C 落在纸片内点C '处(如图2);再继续以BC '为轴折叠纸片,把点A 落在纸片上的位置记作A '(如图3),则点D 和A '之间的距离为_________. (2-6)12.(11mtgym)已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图所示).当n = 8时,共向外作出了个小等边三角形; 当n = k 时,共向外作出了 个小等边三角形,这些小等边三角形的面积和是 (用 含k 的式子表示).183(-2)k23(2)k sk-A D A D D C 'F F F A 'B C B B图1 图2 图3n =3n =5……n =4D 4D 1D 2D 3ABCE 3E 2E 112.(11tongzym )已知ABC AB AC m ∆==中,,72A B C ∠=︒,1BB 平分A B C ∠交A C 于1B ,过1B 作12B B //B C 交AB 于2B ,作23B B 平分21A B B ∠,交A C 于3B ,过3B 作34//B B BC ,交AB 于4B ……依次进行下去,则910B B 线段的长度用含有m 的代数式可以表示为 .212332n n --12.(11changpem)如图,点E 、D 分别是正三角形ABC 、正四边形ABCM 、正五边形ABCMN 中以C 点为顶点的一边延长线和另一边反向延长线上的点,且BE =CD ,DB 的延长线交AE 于点F ,则图1中∠AFB 的度数为 ;若将条件“正三角形、正四边形、正五边形”改为“正n 边形”,其他条件不变,则∠AFB 的度数为 .(用n 的代数式表示,其中,n ≥3,且n 为整数)(0°,2180n n-⋅())图1E FB ADC图2AC DB FEM图3NAC DB F EM12.(11fangsem)如图,正方形ABCD ,E 为AB 上的动点,(E 不与A 、B 重合)联结DE ,作DE 的中垂线,交AD 于点F . (1)若E 为AB 中点,则D F A E=.(2)若E 为AB 的n 等分点(靠近点A),则D FA E = .(251,42n n+) 12. (11fengtem)已知:如图,在R t ABC △中,点1D 是斜边A B 的中点,过点1D 作11D E AC ⊥于点E 1,联结1B E 交1C D 于点2D ;过点2D 作22D E AC ⊥于点2E ,联结2BE交1C D 于点3D ;过点3D 作33D E AC ⊥于点3E ,如此继续,可以依次得到点45、D D 、…、n D ,分别记112233△、△、△、BD E BD E BD E …、n nBD E △的面积为123、、、S S S …n S .设△ABC 的面积是1, 则S 1= ,n S = (用含n 的代数式表示)(211,4(1)n +)12. (11huairem)如图7所示,P 1(x 1,y 1)、P 2(x 2,y 2),……P n (x n ,y n )在函数y =x4(x >0)的图象上,⊿OP 1A 1,⊿P 2A 1A 2,⊿P 3A 2A 3……⊿P n A n -1A n ……都是等腰三角形,斜边OA 1,A 1A 2……A n -1A n ,都在x 轴上,则y 1= .y 1+y 2+…y n = . (2, 2n )12.(11shijsem)如图平面内有公共端点的五条射线,,,,,OE OD OC OB OA 从射线OA 开始,在射线上写出数字1,2,3,4,5; 6,7,8,9,10;….按此规律,则“12”在射线 上;“2011”在射线 上.(OC ;OB ) 12.(11yanqem)正方形ABCD 的位置如图所示,点A 的坐标为)0,1(,点D 的坐标为)2,0(. 延长CB 交x 轴于点1A ,作正方形C C B A 111; 延长11B C 交x 轴于点2A ,作正方形1222C C B A … 按这样的规律进行下去,第3个正方形的面积为________; 第n 个正方形的面积为_____________(用含n 的代数式表示).4235)( , 22235-⎪⎭⎫ ⎝⎛nyo xAAAB B B CC CD 第12题图。
北京西城区初三一模数学试题含答案.doc

2011年北京西城区初三一模数学试题(含答案)
参考答案
一、选择题ACAB CCDB
二、填空题9.2(3)y x - 10.8 11.①③ 12.5;5n 三、解答题
13.1
2- 14.-3<x ≤1
;x = 15.2y x =-+;1AOP S =
17.由根的判别式得22b a =,代入原式化简得2 18.(1)300;60;99;132;9 (2)72°
19.抢险车20km/时,吉普车30km/时。
注意分式方程要检验
20.(1)BN=5;(2)163
(25)922
S =+⨯=
21.(1)连接BO ,证明略;
(2)易证△ABO 为正三角形,于是∠E=∠C=30°,所以△BFE ∽△AFC 由cos ∠BFA=
2
3
BF AF = 设△AOC 面积为S ,因此有239
()824
S ==,解得S=18 22.(1)1:2;121 (2)正三角形、正六边形 (3)如图
24.(1)30°;60°
(2)21
82
y x =-+;
(3)5个;22
)3;22(
)3;16()3
25.(1)如图,
E
F
C D
过点E 作EF ⊥AE ,使EF=BD ,构造全等三角形,易证△DCA ≌△AEF (SAS )从而△AFD 是等腰直角三角形 再利用四边形EFDB 是平行四边形得EB ∥FD ,于是∠APE=∠ADF=45°
(2)如图
F
D
C
方法同(1),构造相似,判断含30°的直角三角形,从而得∠APE 是30°。
9.2011初三数学一模题-西城

北京市西城区2011年初三一模试卷数 学 2011. 5一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. -2的相反数为( ).A .2B .-2C .12D .-122.上海世博会是我国第一次举办的综合类世界博览会.据统计自2010年5月1日开幕至 5月31日,累计参观人数约为8 030 000人.将8 030 000用科学记数法表示应为 ( ) .A . 480310⨯B .580.310⨯C .68.0310⨯ D. 70.80310⨯3.以方程组21y x y x =-+⎧⎨=-⎩的解为坐标的点(,)x y 在( ). A .第一象限 B .第二象限 C .第三象限 D .第四象限4. 右图是正方体的展开图,原正方体相对两个面上的数字和最小是( ). A. 4B. 6C. 7D. 8 5.有四张形状、大小和质地完全相同的卡片,每张卡片的正面写有一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.则抽取的两张卡片上的算式都正确的概率是().A .12B .14C .18D . 16 6.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图.则这组数据的众数和中位数分别是( ).A .7,7B . 8,7.5C .7,7.5D . 8,61 42 5 367.如图,在梯形ABCD 中,AB ∥CD ,∠A =60°,∠B =30°,若AD =CD =6,则AB 的长等于( ).A .9B .12C .6+D .188.如图,点A 在半径为3的⊙O 内,,P 为⊙O 上一点,当∠OP A 取最大值时,P A 的长等于( ).A .32 B C D .二、填空题(本题共16分,每小题4分)9.分解因式:y xy y x 962+-= .10.如图,甲、乙两盏路灯相距20米. 一天晚上,当小明从路灯甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为 米.11. 定义[,,a b c ]为函数2y ax bx c =++的特征数,下面给出特征数为[2m ,14m -,21m -] 的函数的一些结论:①当12m =时,函数图象的顶点坐标是11()24-,;②当1-=m 时,函数在1x >时,y 随x 的增大而减小;③无论m 取何值,函数图象都经过同一个点. 其中所有的正确结论有 .(填写正确结论的序号)12. 如图1,小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形1111D C B A ,正方形1111D C B A 的面积为 ;再把正方形1111D C B A 的各边延长一倍得到正方形2222D C B A (如图2),如此进行下去,正方形n n n n D C B A 的面积为 .(用含有n 的式子表示,n 为正整数)图1 图2三、解答题(本题共30分,每小题5分)13.计算:1024sin 60(-︒- .14.解不等式组 302(1)33,x x x +>⎧⎨-+⎩,≥ 并判断3=x 是否为该不等式组的解.15. 如图,在平面直角坐标系xOy 中,一条直线l 与x 轴相交于点A ,与y 轴相交于点(0,2)B ,与正比例函数 y =mx (m ≠0)的图象相交于点(1,1)P .(1)求直线l 的解析式;(2)求△AOP 的面积.16. 如图,在四边形ABCD 中,AB =BC ,BF 平分∠ABC ,AF ∥DC ,连接AC ,CF . 求证:(1)AF =CF ;(2)CA 平分∠DCF .17. 已知关于x 的一元二次方程)0(0212≠=++a bx ax 有两个相等的实数根,求()()()11122-++-b b a ab 的值.18.某中学就到校的方式问题对初三年级的所有学生进行了一次调查,并将调查结果制成了表格和扇形统计图,请你根据图表信息完成下列各题:(1)补全下表:(2)在扇形统计图中,“步行”对应的圆心角的度数为 °.四、解答题(本题共20分,每小题5分)19.在2011年春运期间,我国南方发生大范围冻雨灾害,导致某地电路出现故障,该地供电局组织电工进行抢修.供电局距离抢修工地15千米,抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车每小时分别行驶多少千米.20.如图,四边形ABCD 是边长为9的正方形纸片,B '为CD 边上的点,C B '=3.将纸片沿某条直线折叠,使点B 落在点B '处,点A的对应点为A ',折痕分别与AD ,BC 边交于点M ,N .(1)求BN 的长;(2)求四边形ABNM 的面积.21.如图,D 是⊙O 的直径CA 延长线上一点,点 B 在⊙O 上,且AB =AD =AO .(1)求证:BD 是⊙O 的切线;(2)若E 是劣弧BC 上一点,AE 与BC 相交于点F ,△BEF 的面积为8,且cos ∠BF A =32, 求△ACF 的面积.22.我们约定,若一个三角形(记为△A 1)是由另一个三角形(记为△A )通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A 1是由△A 复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A 复制出△A 1,又由△A 1复制出△A 2,再由△A 2复制出△A 3,形成了一个大三角形,记作△B .以下各题中的复制均是由△A 开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A 全等的三角形)之间既无缝隙也无重叠.(1)图1中标出的是一种可能的复制结果,小明发现△A ∽△B ,其相似比为_________.在图1的基础上继续复制下去得到△C ,若△C 的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C 中含有______个小三角形;(2)若△A 是正三角形,你认为通过复制能形成的正多边形是________;(3)请你用两次旋转和一次平移复制形成一个四边形,在图2的方框内画出草图,并仿照图1作出标记.图1图2五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.抛物线2y ax bx c =++,a >0,c <0,2360a b c ++=.(1)求证:1023b a +>; (2)抛物线经过点1(,)2P m ,Q (1,)n . ① 判断mn 的符号; ② 若抛物线与x 轴的两个交点分别为点A 1(,0)x ,点B 2(,0)x (点A 在点B 左侧),请说明116x <,2112x <<.24.如图1,平面直角坐标系xOy 中,A ,B (4,0).将△OAB 绕点O 顺时针旋转α角(0°<α<90°)得到△OCD (O ,A ,B 的对应点分别为O ,C ,D ),将△OAB 沿x 轴负方向...平移m 个单位得到△EFG (m >0,O ,A ,B 的对应点分别为E ,F ,G ),α,m 的值恰使点C ,D ,F 落在同一反比例函数k y x=(k ≠0)的图象上. (1)∠AOB= °,α= °;(2)求经过点A ,B ,F 的抛物线的解析式;(3)若(2)中抛物线的顶点为M ,抛物线与直线EF 的另一个交点为H ,抛物线上的点P 满足以P ,M ,F ,A 为顶点的四边形的面积与四边形MF AH 的面积相等(点P 不与点H 重合),请直接写出满足条件的点P 的个数,并求位于直线EF25.在Rt △ABC 中,∠C =90°,D ,E 分别为CB ,CA 延长线上的点,BE 与AD 的交点为P .(1)若BD=AC ,AE=CD ,在图1中画出符合题意的图形,并直接写出∠APE 的度数;(2)若AC =,CD =,求∠APE 的度数.。
北京市石景山区九年级数学第一次统一练习

石景山区2012年初三第一次统一练习暨毕业考试数 学 试 卷第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.31-的相反数是 A .31 B .31- C .3 D .3- 2.农历龙年春节黄金周,北京旅游市场迎来经济和社会效益双丰收.黄金 周7天,北京市各主要景区、公园共接待中外游客约8270000人次. 将 8270000用科学记数法表示为A .71027.8⨯ B .710827.0⨯ C .61027.8⨯ D .5107.82⨯ 3.下列图形中可以由一个基础图形通过平移变换得到的是A B C D4.一个不透明的盒子里装有2个白球,2个红球,若干个黄球,这些球除了颜色外,没有任何其他区别.若从这个盒子中随机摸出一个是黄球的概率是53,则盒子中黄球的个数是 A .2 B .4 C .6 D .85.如图,在△ABC 中,DE BC ∥,2AD =,3AE =,4BD =,则AC 的长为 A.9B.8 C .7 D . 66.如图,弦AB 和CD 相交于点P ,︒=∠30B ,︒=∠80APC ,则BAD ∠的度数为A CD EBP DCBA第5题图 第6题图120,设这组P以每秒切,设点P数关系图:第行的第个数是.三、解答题(本题共30分,每小题5分)13.计算:()()0201231260tan11-+-︒-+-14.解不等式1312523-+≥-x x ,并把解集表示在数轴上.15.已知422=+a a ,求121111122+-+÷--+a a a a a 的值.16.如图,∠ACB =∠CDE =90°,B 是CE 的中点,∠DCE =30°,AC =CD . 求证:AB ∥DE .17.已知一次函数b kx y +=的图像经过点A (1,0)和B ()a a -,3(0>a ),且点B 在反比例函数xy 3-=的图像上. (1)求一次函数的解析式;(2)若点M 是y 轴上一点,且满足△ABM 是直角三角形,请直接写出点M 的坐标.18.小明从A 地出发向B 地行走,同时晓阳从B地出发向A 地行走,如图所示,相交于点M 的两条线段12l l 、分别表示小明、晓阳离A 地的距离y(千米)与已用时间x (分钟)之间的关系, (1)小明与晓阳相遇时,晓阳出发的时间是 ;(2)求小明与晓阳的速度。
石景山区2024届初三一模数学试题及答案

石景山区2024年初三统一练习数 学 试 卷第一部分 选择题一、选择题(共16分,每题2分) 第1-8题均有四个选项,符合题意的选项只有一个.1.下列几何体中,主视图是三角形的是2.2023年10月26日,搭载神州十七号载人飞船的长征二号F 摇十七运载火箭在酒泉卫星发射中心成功发射.长征二号F (代号:CZ 2F −,简称:长二F ,绰号:神箭)主要用于发射神州飞船和大型目标飞行器到近地轨道,其近地轨道运载能力是8500千克.将8500用科学记数法表示应为 (A )28510⨯(B )28.510⨯(C )38.510⨯(D )40.8510⨯3.下列图书馆标志图形中,是轴对称图形的是(A )(B )(C )(D )4.如图,直线a b ∥,直线l 与a b ,分别交于点A B ,,过 点A作AC b ⊥于点C .若155∠=°,则2∠的大小为 (A )35° (B )45° (C )55° (D )125°(A )(B )(C )(D )21lba A BC5.已知30m +<,则下列结论正确的是 (A )33m m −<<−< (B )33m m <−<−< (C )33m m −<<<−(D )33m m <−<<−6.若一个多边形的内角和是720°,则该多边形的边数是 (A )4(B )5(C )6(D )77.不透明的袋子中装有两个黄球和一个红球,除颜色外三个小球无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么两次都摸到黄球的概率是 (A )29(B )13(C )49(D )238.如图,90ABC BA BC ∠==°,,BM 是ABC ∠内部的射线且45CBM ∠<°,过点A 作AD BM ⊥于点D ,过点C 作CE BM ⊥于点E , 在DA 上取点F ,使得DF DE =,连接EF . 设CE a BE b EF c ===,,,给出下面三个结论:①c b a =−);②a c +<;>.上述结论中,所有正确结论的序号是 (A )①②(B )①③(C )②③(D )①②③第二部分 非选择题二、填空题(共16分,每题2分)9x 的取值范围是 .10.分解因式:24xy x −= .11.如图,在□ABCD 中,点E 在BC 上且2EB EC =,AE 与BD 交于点F .若5BD =,则BF 的长为 . 12.方程21375x x=+的解为 . FA BECDMFCA D EB13.在平面直角坐标系xOy 中,若点11A y (,),23B y (,)在反比例函数0ky k x=>()的 图象上,则1y 2y (填“>”“<”或“=”).14.若关于x 的一元二次方程220x x m −−=有两个相等的实数根,则实数m 的值为 .15.如图,AB 是O ⊙的直径,P 是AB 延长线上一点,PC与O ⊙相切于点C .若40P ∠=°,则A ∠= °.16.某酒店在客人退房后清洁客房需打扫卫生、整理床铺、更换客用物品、检查设备共四个步骤.某清洁小组有甲、乙、丙三名工作人员,工作要求如下:①“打扫卫生”只能由甲完成;每间客房“打扫卫生”完成后,才能进行该客房的其他三个步骤,这三个步骤可由任意工作人员完成并可同时进行;②一个步骤只能由一名工作人员完成,此步骤完成后该工作人员才能进行其他步骤;在不考虑其他因素的前提下,若由甲单独完成一间客房的清洁工作,需要分钟;若由甲、乙、丙合作完成四间客房的清洁工作,则最少需要 分钟.三、解答题(共68分,第17-19题,每题5分,第20-21题,每题6分,第22-23题,每题5分,第24题6分,第25题5分,第26题6分,第27-28题,每题7分) 解答应写出文字说明、演算步骤或证明过程. 171122sin 605−++°().18.解不等式组:4178523x x x x −<+−>⎧⎪⎨⎪⎩,.19.已知2360x x −−=,求代数式2926x x x x +−÷()的值.20.如图,在四边形ABCD 中,AD BC AB AD =∥,,AE 平分BAD ∠交BC 于点E ,连接DE .(1)求证:四边形ABED 是菱形;(2)连接BD 交AE 于点F .若90BCD ∠=°,6cos 3DBC ∠=,26BD =,求EC 的长.21.为了保护水资源,提倡节约用水,北京市居民用水实行阶梯水价,实施细则如下表:北京市居民用水阶梯水价表(单位:元/立方米)供水 类型阶梯 户年用水量 (立方米) 水价 其中水费 水资源费污水处理费自来水第一阶梯0—180(含) 5 2.07 1.571.36第二阶梯 181—260(含) 7 4.07 第三阶梯260以上96.07某户居民2023年用水共缴纳1040元,求这户居民2023年的用水量.22.在平面直角坐标系xOy 中,函数0y k x b k =+≠()的图象过点03A (,)和21B −(,),与过点05(,)且平行于x 轴的直线交于点C . (1)求该函数的解析式及点C 的坐标;(2)当2x <时,对于x 的每一个值,函数0y mx m =≠()的值小于0y k x b k =+≠()的值,直接写出m 的取值范围.xyO–1–2–3–4–5–6123456–1–2–3–4–5–6123456备用图CDEBA23.为了培养学生的爱国情感,某校在每周一或特定活动日举行庄严的升国旗仪式.该校的国旗护卫队共有18名学生,测量并获取了所有学生的身高(单位:cm ),数据整理如下:a .18名学生的身高:170,174,174,175,176,177,177,177,178, 178,179,179,179,179,181,182,183,186 b .18(1)写出表中m ,n 的值;(2)该校的国旗护卫队由升旗手、护旗手、执旗手组成,其中12名执旗手分为两组:对于不同组的学生,如果一组学生的身高的方差越小,则认为该组的执旗效果越好. 据此推断:在以上两组学生中,执旗效果更好的是 (填“甲组”或“乙组”); (3)该校运动会开幕式的升国旗环节需要6名执旗手,因甲组部分学生另有任务,已确定四名执旗手的身高分别为175,177,178,178.在乙组选另外两名执旗手时,要求所选的两名学生与已确定的四名学生所组成的六名执旗手的身高的方差最小,则选出的另外两名学生的身高分别为 和 .24.如图,AB 是O ⊙的直径,CD 是O ⊙的弦,CD AB ⊥于点E ,点F 在O ⊙上且CF CA =,连接AF .(1)求证:AF CD =;(2)连接BF BD ,.若26AE BF ==,,求BD 的长.25.某农科所的科研小组在同一果园研究了甲、乙两种果树的生长规律.记果树的生长时间为 x (单位:年),甲种果树的平均高度为1y (单位:米),乙种果树的平均高度为2y (单位:米).记录的部分数据如下:对以上数据进行分析,补充完成以下内容.(1)可以用函数刻画1y 与x ,2y 与x 之间的关系,在同一平面直角坐标系xOy 中,已经画出1y 与x 的函数图象,请画出2y 与x 的函数图象;(2)当甲种果树的平均高度达到8.00米时,生长时间约为 年(结果保留小数点后一位);当乙种果树的平均高度为5.00米时,两年后平均高度约为 米(结果保留小数点后两位);(3)当甲、乙两种果树的平均高度相等时,生长时间约为 年(结果保留小数点后一位).26.在平面直角坐标系xOy 中,抛物线222y x m x m =−++()的对称轴为直线x t =. (1)求t 的值(用含m 的代数式表示);(2)点1A t y −(,),2B t y (,),31C t y +(,)在该抛物线上.若抛物线与x 轴的一个交点为00x (,),其中002x <<,比较1y ,2y ,3y 的大小,并说明理由.27.在ABC △中,AB AC =,060BAC <∠<°°,将线段BC 绕点B 逆时针旋转60°得到线段BD ,连接AD .将线段AD 绕点A 顺时针旋转90°得到线段AE ,连接DE . (1)如图1,求证:EA ∥BC ;(2)延长BC 到点F ,使得CF CB =,连接DF 交AC 于点M ,依题意补全图2 .若点M 是AC 的中点,用等式表示线段MF ,MD ,DE 之间的数量关系, 并证明.EADCB EDC B A 图1 图228.对于线段MN 和点P 给出如下定义:点P 在线段MN 的垂直平分线上,若以点P 为圆心,PM 为半径的优弧M mN 上存在三个点A B C ,,,使得ABC △是等边三角形,则称点P 是线段MN 的“关联点”.例如,图1中的点P 是线段MN 的一个“关联点”. 特别地,若这样的等边三角形有且只有一个,则称点P 是线段MN 的“强关联点”.在平面直角坐标系xOy 中,点A 的坐标为20(,).(1)如图2,在点1234313101213C C C C −(,),(,),(,),(,)中,是线段OA 的“关 联点”的是 ;(2)点B 在直线33y x =上.存在点P ,是线段OA 的“关联点”,也是线段OB 的“强关联点”.①直接写出点B 的坐标;②动点D 在第四象限且2AD =,记OAD α∠=.若存在点Q ,使得点Q 是线 段AD 的“关联点”,也是OB 的“关联点”,直接写出α及线段AQ 的取值范围.AmPCB MN图1 图2xy-3 -2 -1-1-32311 2 3-2OC 1C 3C 4C 2A石景山区2024年初三统一练习数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可。
2011年北京市石景山区初三数学二模试题及答案

A
D C
20.已知:如图, AF为△ABC 的角平分线,以 BC 为直径的圆与边 AB 交于点 D, 点E 为弧 BD 的中点, 联结 CE 交 AB 于 H , AH AC . (1)求证: AC 与⊙ O 相切; (2)若 AC 6 , AB 10 ,求 EC 的长. 解:
A E H B O F C D
四、解答题(本题共 20 分,每小题 5 分) 19.已知:等腰梯形 ABCD 中, AD ∥ BC , AD 2 , BC 6 ,将线段 DC 绕点 D 逆 时针旋转 90 , . 得到线段 DC . (1)求△ AD C 的面积; (2)若 tan DA C 解:
2 ,求 AB 的长. 5
工学20%
(1 ) 请你根据统计图计算出 2009 年——2011 年这三年全国硕士研究生入学考试报考人数比上年增加值的 平均数为 万人(结果保留整数) ; (2)为了调查各专业报考人数,某网站进行了网上调查,并将调查结果绘制成扇形统计图,请你补全扇 ... 形统计图 并计算图中表示金融专业的扇形的圆心角为 .... 度;若 2012 年全国硕士研究生报考人数按照(1)中的平均数增长,各专业报考人数所占比例 与 2011 年相比基本保持不变,请你预测 2012 年全国硕士研究生入学考试报考金融专业的考生约有 万人(结果保留整数).
二
三
四
五
六
七
总分Βιβλιοθήκη 第Ⅰ卷(共 32 分)一、选择题(本题共 32 分,每小题 4 分) 在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在第 1-8 题的相应位置上. 1. 2 的算术平方根是( A. 2 B. )
2
北京2011年石景山初中毕业考试数学(一模)试卷及答案

m ( x 0 )的图象交于点 x P .PA x 轴于点 A ,PB y 轴于点 B . 一次函数的图象分别交 x 轴、y 轴于点 C 、 OC 1 . 点 D ,且 S△DBP 27 , CA 2 (1)求点 D 的坐标;
(2)求一次函数与反比例函数的解析式; (3)根据图象写出当 x 取何值时,一次函数的值小于反比例函数的值?
FR
1 FQ BD ,则 的值为_____________. 2 QR
2
五、解答题(本题满分 7 分)
23.已知抛物线 C : y x m 1x 1 的顶点在坐标轴 上. ...
初三数学试卷 第 页5(共 6 页)
(1)求 m 的值; (2) m 0 时,抛物线 C 向下平移 nn 0 个单位后与抛物线 C1 : y ax2 bx c 关 (3) 3 m 0 时,抛物线 C 的顶点为 M ,且过点 P1, y0 .问在直线 x 1 上是 否存在一点 Q 使得△ QPM 的周长最小, 如果存在, 求出点 Q 的坐标, 如果不存在, 请说明理由. 于 y 轴对称,且 C1 过点 n,3 ,求 C1 的函数关系式;
1 3
一 二 等 等 奖 奖 三等奖 二等奖
B.
2 7
C.
3 16
H
D.
1 8
G F Q
三等奖 一等奖 三等奖
E
D A
P C B
第 8 题图
第 7 题图
8.已知:如图,无盖无底的正方体纸盒 ABCD EFGH , P , Q 分别为棱 FB , GC 上 的点,且 FP 2 PB, GQ 展开,得到的平面图形是 A.一个六边形 C.两个直角三角形 B.一个平行四边形 D. 一个直角三角形和一个直角梯形
2011初三数学二模题答案-石景山

石景山区2011年初三第二次统一练习考试试卷阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共32分,每小题4分)题 号12345678答 案ADDBCCBA二、填空题(本题共16分,每小题4分)9.; 10.2; 11.1); 12.;21≤x 2)12(-a a ,65(πOC .OB 三、解答题(本题共30分,每小题5分)13.解:原式= …………………………………… 4分2241223⨯--+= ……………………………………………………………… 5分122-14.解:原方程化为: …………………………………………1分 03122=--x x ………………………………………………2分131122+=+-x x………………………………………………3分()341-2=x ∴ ………………………………………………5分3321,332121-=+=x x 15.证明: ∵ 是等边三角形,∴ PBC △︒=∠60PCB 又 ∵ 四边形是矩形 ∴ ABCD ︒=∠90DCB ∴ …………………… 1分︒=∠30DCP 同理 ︒=∠30QCB ︒=∠30ABP ∴ …………………… 2分︒=∠30PCQ ∵ 是等边三角形,∴PBC △PC PB =∵是等边三角形 ∴QCD △QCCD = 四边形是矩形 ∴ ∴……………… 3分ABCD DC AB =QC AB =在△和△中PBA PCQ ⎪⎩⎪⎨⎧=∠=∠=CQ AB PCQ PBA PC BP ∴ △≌△(SAS ) ……… 4分PBA PCQ ∴ ……………………………………………… 5分QPC APB ∠=∠QDCB AP16.解:∵且 211=+yx 0≠xy ∴ ……………………………………… 1分 xy y x 2=+= …………………………………… 3分y xy x y xy x +++-353xy y x xyy x ++-+5)(3= …………………………………… 4分xy xy xy xy +-256= …………… 5分 3117.解:(1)解法一:由图表知:抛物线的顶点为……………………… 1分c bx ax y ++=2()4,1设抛物线解析式为()412+-=x a y ∵抛物线交轴于点y ()3,0∴34=+a 解得: 1-=a ∴()412+--=x y 即: …………………………………………………… 2分322++-=x x y 解法二:由图表知:抛物线的对称轴为c bx ax y ++=21=x 抛物线与轴交于点x ()0,1-∴由抛物线的轴对称性可求抛物线与轴另一交点为 ……………… 1分x ()0,3设抛物线解析式为()()13+-=x x a y ∵抛物线过点()3,0∴33=-a ∴1-=a ∴此二次函数的解析式为…………………………… 2分322++-=x x y (2) ,,, ……………… 5分()0,11E ()0,42E ()0,1103-E ()0,1104--E 18. 解:设平均每次下调的百分率为x ; ………1分依题意,得: ……………………3分20250)1(250002=-⨯x 解得:1.0,9.121==x x 由题意得 ……………………4分1.0=x 答:平均每次下调的百分率为10%(2) 方案一优惠费用: 20250×100×1%=20250方案二物业费: 100×2.3×12×5=13800 20250>13800答:选择方案一 …………………………………5分19.解:(1)作出线段 ………………………………… 1分C D ' 过点作于,过点作于D BC DF ⊥F A BC AH ⊥H∵四边形是等腰梯形,∥ABCD AD BC 易证()22-621===BH FC ︒=∠=∠90ADF EDF 过点作垂直于的延长线于点'C E C 'AD E∴︒=∠='∠90DFC C DE ∵线段绕点逆时针旋转90°,得到线段DC D C D '∴,︒='∠90C CD C D DC '=∴,︒=∠+∠9031︒=∠+∠9032∴21∠=∠∴≌ ………………………… 2分CFD ∆ED C '∆∴2=='FC C E ∴…………………… 3分=∆'ADC S 2222121'=⨯⨯=⋅E C AD (2)在中,,'AEC Rt ∆52tan ='∠C DA 2='C E ∴5=EA ∵2=AD ∴ …………………………… 4分3=ED 由≌得:CFD ∆ED C '∆3==ED DF 在中,由勾股定理得:DFC Rt ∆13=CD ∴ ……………………………5分13==CD AB 20.解:(1)证明:联结 ………………………………1分 BE ∵ 为直径 ∴=90°BC E ∠∴︒=∠+∠90EHB EBH ∵, 的角平分线AC AH =ABC AF 为△∴ACH AHC ∠=∠∵EHB AHC ∠=∠∴ACHEHB ∠=∠∵为弧的中点E 点BD ∴DBEECB ∠=∠ ∴ ……………2分︒=∠+∠90ACH ECB ∴ 是⊙的切线AC O (2) ∵ 是⊙的切线 ∴AC O ︒=∠90ACB ∵ ∴10,6==AB AC 8=BC ∵ ∴ …………………………………………3分AC AH =4=BH 又∵,为公共角DBE ECB ∠=∠E ∠∴∽BEH △CEB△321H EFC 'ABCD∴…………………………………………4分 ∴2184===CB BH EC BE 在中,可得EBC Rt △, ………………………………5分222)21(BC EC EC =+5516=EC 21.(1)10万 (2);126°; 56万%3522.(1) ………………………………………………………………1分3 ………………………………………………………2分212S S S ⋅= (2) ………………………………………………………………4分481五、解答题(本题满分7分)23.设抛物线解析式为)4)(2(-+=x x a y ∵C 点坐标为(0,4)∴a= ………………………………1分21-∴解析式为,4212++-=x x y 顶点D 坐标为(1,)……2分29(2)直线CD 解析式为y=kx+b.则 ∴⎪⎩⎪⎨⎧=+=294b k b ⎪⎩⎪⎨⎧==214k b ∴直线CD 解析式为y=x+4……………………………3分21E (-8,0) F(4,6)若抛物线向下移m 个单位,其解析式)0(4212>-++-=m m x x y 由消去y,得⎪⎪⎩⎪⎪⎨⎧+=-++-=4214212x y m x x y 021212=-+-m x x ∵△=∴0<m ≤ 0241≥-m 81∴向下最多可平移个单位.……………………5分81F若抛物线向上移m 个单位,其解析式)0(4212>+++-=m m x x y 方法一:当x=-8时,y=-36+m 当x=4时,y=m要使抛物线与EF 有公共点,则-36+m ≤0或 m ≤6∴0<m ≤36…………………………7分方法二: 当平移后的抛物线过点E (-8,0)时,解得 36=m 当平移后的抛物线过点时,()6,4F 6=m 由题意知:抛物线向上最多可以平移36个单位长度……………………7分综上,要使抛物线与EF 有公共点,向上最多可平移36个单位,向下最多可平移81个单位.六、解答题(本题满分7分)24.(1)猜想结论:……………………………………………1分AD OM 21=(2)①结论仍成立……………………………………2分证明:延长BO 到F,使FO=BO.联结CF,∵ M 为BC 中点,O 为BF 中点,∴MO 为中位线BCF ∆∴ MO= …………3分CF 21∵===90°AOB ∠AOF ∠COD ∠∴=AOD ∠COF ∠AO =OF,CO=DO∴≌…………4分AOD △FOC △∴CF=AD∴MO=………………………………………5分AD 21②∵MO 为中位线BCF ∆∴MO ∥CF∴=………………………………………………6分MOB ∠F ∠又∵≌∴=AOD △FOC △DAO ∠F∠∵+=90°∴+=90°………………………7分MOB ∠AOM ∠DAO ∠AOM ∠即ADOM ⊥七、解答题(本题满分8分)25. 解:(1)如图,由抛物线得:22-+=bx ax y ()2,0-C ∴∴2==OC OA ()0,2A ∵△的面积为2ABC ∴2=AB ∴………………………………1分()0,4B ∴设抛物线的解析式为,代入点()()42--=x x a y ()2,0-C ∴抛物线的解析式为; ……2分()()2234142412-+-=---=x x x x y(2)由题意:tCE =,t PB 2=t OP 24-=∵∥ED BA可证CO CEOB ED = 即24CEED =∴ ………………………………3分t CE ED 22==① …………………4分()tt t t t t OP ED 21242424121112+-=-=-+=+∵当时有最大值11=t t t 22+-∴当时的值最小,最小值为1.……………………5分1=t OPED 11+② 由题意可求:,t CD 5=52=CB ∴ ………………………………6分t BD 552-=∵∠=∠PBD ABC∴以 为顶点的三角形与△相似有两种情况D B P 、、ABC 当时,即BC BD AB BP =5255222tt -=解得: ………………………………7分32=t 当时,即BA BC BD BP =2525522=-tt 解得: ………………………………8分710=t ∴当或时,以为顶点的三角形与△相似.32=t 710=t D B P 、、ABC。
石景山区初三数学一模试卷及答案

石景山区初三第一次统一练习暨毕业考试数 学 试 卷考 生 须 知1.本试卷共8页.全卷共五道大题,25道小题. 2.本试卷满分120分,考试时间120分钟.3.在试卷密封线内准确填写区(县)名称、毕业学校、姓名和准考证号. 4.考试结束后,将试卷和答题纸一并交回.题号 一 二 三 四五 总分 分数第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.-1.5的倒数是 A .32-B .23-C .5.1D . -3 2.今年财政部公布的最新数据显示,1至2月累计,全国公共财政收入22426亿元,比去年同期增加1508亿元,数字1508用科学记数法表示为A .410508.1⨯B .4101508.0⨯C .21008.15⨯D .310508.1⨯ 3.无理数6在哪两个整数之间 A .1和2 B .2和3 C .3和4 D . 4与5 4.函数1-=x x y 中自变量x 的取值范围是A .x ≥1B .1x <且 0≠xC .1>xD .x ≥1且 0≠x 5.某班有10名学生参加篮球的“定点投篮”比赛,每人投10次,他们的进球数分别为:6,1,4,2,6,4,8,6,4,6.这组数据的极差和中位数分别是A .7、5B .5、5C .5、4D . 7、46.如图,AM 为⊙O 的切线,A 为切点,BD ⊥AM 于点D ,BD 交⊙O 于点C ,OC 平分∠AOB .则∠OCD 的度数为 A .︒110 B .︒115 C .︒120 D .︒1257.把同一副扑克牌中的红桃6、红桃7、红桃9三张牌背面朝上放在桌子上,从 中随机抽取两张,牌面的数字之和为奇数的概率为A .31 B .32 C .21 D .61 8.已知:如图,正方形ABCD 的边长为2,E 、F 分别为AB 、AD 的中点, G 为线段CE 上的一个动点,设x CECG=,y S GDF =∆,则y 与x第6题图D AC EB的函数关系图象大致是第Ⅱ卷(共88分)二、填空题(本题共16分,每小题4分)9.将二次函数762++=x x y 配方为k h x y +-=2)(形式,则=h ___,=k ________.10.分解因式:3244x x x -+=_______________.11. 如图,在正方形网格(图中每个小正方形的边长均为1)中,一段圆弧经过网格的格点A 、B 、C.则弧AC 所在圆的半径长为 ;弧AC 的长为 . 12.将全体正整数排成一个三角形数阵:1 2 3 4 5 6 7 8 9 10. . . . . . . 按照以上排列的规律,第5行从左到右的第3个数为_______;第n 行(n ≥3)从左到右的第3个数为 .(用含n 的代数式表示) 三、解答题(本题共30分,每小题5分)13.131274cos3082-⎛⎫+-︒+- ⎪⎝⎭.14.解不等式组并把解集在数轴上表示出来.3(2) 4 1214x x xx --≤⎧⎪⎨-<-⎪⎩①,②.15.已知:如图,点C 是AB 的中点,CD ∥BE ,且CD =BE . 求证:△ACD ≌△CBE .16.已知:24510x x +-=,求代数式()()()()221122x x x x x +--++-的值.A B C D第11题图17.已知:一次函数3+=x y 与反比例函数3m y x-=(0<x ,m 为常数)的图象交于点A (a ,2)、B 两点.(1)求m 的值和B 点坐标;(2)过A 点作y 轴的平行线,过B 点作x 轴的平行线,这两条直线交于点E ,若反比例函数ky x=的图象与△ABE 有公共点,请直接写出k 的取值范围.18.如图,一架飞机由A 向B 沿水平直线方向飞行,在航线AB 的正下方有两个山头C 、D .飞机在A 处时,测得山头D 恰好在飞机的正下方,山头C 在飞机前方,俯角为30°.飞机飞行了6千米到B 处时,往后测得山头C 、D 的俯角分别为60°和30°.已知山头D 的海拔高度为1千米,求山头C 的海拔高度. (精确到0.01 1.732≈)四、解答题(本题共20分,每小题5分)19. 已知:如图,在四边形ABCD 中,AD DC ⊥,△DBC 是等边三角形,︒=∠45ABD ,2=AD .求四边形ABCD 的周长.20.如图,BD 为⊙O 的直径,AB =AC ,AD 交B C 于点E ,AE =1,ED =2. (1)求证:∠ABC =∠ADB ;| (2)求AB 的长;(3)延长DB 到F ,使得BF =BO ,连接F A ,试判断直线F A 与⊙O 的位置关系,并说明理由.DCBABACD21.以下是根据北京市国民经济和社会发展统计公报中的相关数据绘制成的统计表和统计图的一部分.电话用户包括固定电话用户和移动电话用户两种.-全国电话用户到达数和净增数统计表年份全国电话用户到达数(单位:万户)98160 106095 115335 127135 139031净增数(单位:万户)6866 7935 9240 a11896请根据以上信息,解答下列问题(注意:所求数据均保留整数):(1)统计表中的数据a的值为_________;(2)通过计算补全条形统计图并注明相应数据;(3),全国移动电话用户净增约12591万户,求该年固定电话用户减少了多少万户. wwW .2008-2012年全国移动电话用户统计图2008-2012年全国移动电话用户占电话用户的百分比22.问题解决:已知:如图,D为AB上一动点,分别过点A、B作ABCA⊥于点A,ABEB⊥于点B,联结CD、DE.(1)请问:点D满足什么条件时,DECD+的值最小?(2)若8=AB,4=AC,2=BE,设xAD=.用含x的代数式表示DECD+的长(直接写出结果).拓展应用:参考上述问题解决的方法,请构造图形,并求出代数式()22144x x++-+的最小值.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23. 如图,直线33y x=-+交轴于A点,交轴于B点,过A、B两点的抛物线1C交轴于另一点M(-3,0).(1)求抛物线1C的解析式;(2)直接写出抛物线1C关于y轴的对称图形2C的解析式;(3)如果点'A是点A关于原点的对称点,点D是图形2C的顶点,那么在x轴上是否存在点P,使得△PAD与△'A BO是相似三角形?若存在,求出符合条件的P点坐标;若不存在,请说明理由. wwW .24.如图,△ABC中,∠90ACB=︒,2=AC,以AC为边向右侧作等边三角形ACD.(1)如图24-1,将线段AB绕点A逆时针旋转︒60,得到线段1AB,联结1DB,则与1DB长度相等的线段为(直接写出结论);(2)如图24-2,若P是线段BC上任意一点(不与点C重合),点P绕点A逆时针旋转︒60得到点Q,求ADQ∠的度数;(3)画图并探究:若P是直线BC上任意一点(不与点C重合),点P绕点A逆时针旋x y xA BCDEODA yC x B (E ) FJ转 60得到点Q ,是否存在点P ,使得以 A 、 C 、 Q 、 D 为顶点的四边形是梯形,若存在,请指出点P 的位置,并求出PC 的长;若不存在,请说明理由.25.如图,把两个全等的Rt △AOB 和Rt △ECD 分别置于平面直角坐标系xOy 中,使点E 与点B 重合,直角边OB 、BC 在y 轴上.已知点D (4,2),过A 、D 两点的直线交y 轴于点F .若△ECD 沿DA 方向以每秒2个单位长度的速度匀速平移,设平移的时间为t (秒),记△ECD 在平移过程中某时刻为△'''E C D , ''E D 与AB 交于点M ,与y 轴交于点N ,''C D 与AB 交于点Q ,与y 轴交于点P (注:平移过程中,点'D 始终在线段DA 上,且不与点A 重合).(1)求直线AD 的函数解析式;(2)试探究在△ECD 平移过程中,四边形MNPQ 的面积是否存在最大值?若存在,求出这个最大值及t 的取值;若不存在,请说明理由;(3)以MN 为边,在''E D 的下方作正方形MNRH ,求正方形MNRH 与坐标轴有两个公共点时t 的取值范围.石景山区初三第一次统一练习暨毕业考试 数学参考答案阅卷须知:备用图备用图DAC EB1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)w W w.9. 32--,;10.()22-x x ; 11. ; 12.13, 262n n -+.三、解答题(本题共6道小题,每小题5分,共30分)13-114cos302⎛⎫-︒+ ⎪⎝⎭=242-- ……………………………4分=3 …………………………………………………5分14.解:解不等式①, 1≥x …………………………………………2分解不等式②, 23<x ……………………………………………4分原不等式组的解集为231<≤x ,在数轴上表示为:……5分15.证明:∵C 是AB 的中点∴CB AC = …………………………… 1分 又∵CD ∥BE∴B ACD ∠=∠…………………………… 2分 在△ACD 和△CBE 中⎪⎩⎪⎨⎧=∠=∠=BE CD B ACD CB AC …………………………… 4分 ∴△ACD ≌△CBE …………………………………………………… 5分16.解:原式4144222-++-++=x x x x x …………………………………2分2453x x =+- ………………………… 3分当01542=-+x x 时,1542=+x x …………………………… 4分 原式132=-=-.………………………………5分17.解:(1)∵一次函数3+=x y 与反比例函数xm y 3-=(0<x ) (m 为常数)的图象交于点A (a ,2)、B 两点 ∴ 3223a a m +=⎧⎨=-⎩解得11a m =-⎧⎨=⎩ …………………………………2分∴反比例函数3m y x -=(0<x )的解析式为2y x =- 由题意解23y x y x ⎧=-⎪⎨⎪=+⎩得1112x y =-⎧⎨=⎩,2221x y =-⎧⎨=⎩………………………………3分 ∵A (1-,2),∴B (2-,1) ………………………………4分(2)914k -≤≤- ………………………………5分18.解:在Rt △ABD 中,∵∠ ABD = 30°,∴AD = AB ·tan30° = 6 × 33 = 23.……………1分∵∠ABC = 60°,∠BAC = 30°,∴∠ACB = 90°, …………………………………2分 ∴AC = AB ·cos30° = 6 ×32= 33.……………3分 过点C 作CE ⊥AD 于点E , 则∠CAE = 60°,AE = AC ·cos60°=2.……………4分 ∴DE = AD − AE = 2 3 −332 = 32 w W w. ∴山头C 的海拔高度为1+32≈1.87千米. …………5分19. 解:过点A 作BD AE ⊥于点E (1)分∵AD DC ⊥∴︒=∠90ADC∵△DBC 是等边三角形 ∴︒=∠60BDC∴︒=∠30ADB ………………… 2分 在Rt △AED 中,2=AD∴121==AD AE由勾股定理得:3=DE ………………………………3分 在Rt △AEB 中,︒=∠45ABD ∴1==AE BE ∴2=AB ………………………………4分ABCDEBACDE∴31+=BD∴31+===BD BC DC即四边形ABCD 的周长为3224++.20. (1)证明:∵AB =AC ,∴∠ABC =∠C , 又∵∠C =∠D ,∴∠ABC =∠ADB . …………1分(2) ∵∠ABC =∠ADB 又∵∠BAE =∠DAB , ∴△ABE ∽△ADB , …………………………2分 ∴AB AEAD AB=, ∴AB 2=AD ·AE =(AE +ED )·AE =(1+2)×1=3,∴AB 3分 (3) 直线F A 与⊙O 相切,理由如下:联结OA ,∵BD 为⊙O 的直径,∴∠BAD =90°,∴BD 4分BF =BO =12BD∵AB BF =BO =AB ,可证∠OAF =90°,∴直线F A 与⊙O 相切.………………………………………5分21.解:(1)11800; …………………… 1分(2)1112258.11122480%139031≈=⨯ …………………2分图略 …………………4分 (3)69511896-12591= …………………………5分22. 解:(1)当点D 、C 、E 三点在一条直线上时,DE CD +的值最小………1分(2) CD DE +=……………………2分(3)如图,令4=AB ,1=AC ,2=BE ,设x AD =,则x BD -=4,CD DE + = ……………………3分∵D 、C 、E 三点在一条直线上时,DE CD +的值最小 ∴CE 的最小值.过点E 作AB 的平行线交CA 的延长线于点F∵AB CA ⊥于A ,AB EB ⊥于B .∴AF ∥BE∴四边形AFEB 是矩形 ……………………4分∴2AF BE ==,4EF AB ==在Rt △CFE 中,90F ∠=︒, 3CF =……………5分F EDCBA23.解:(1)设抛物线的解析式为:2(0)y ax bx c a =++≠ ∵直线33y x =-+交轴于A 点,交轴于B 点,∴A 点坐标为(1,0)、B 点坐标为(0,3). ………………1分 又∵抛物线经过A 、B 、M 三点,∴0,930,3.a b c a b c c ++=⎧⎪-+=⎨⎪=⎩ 解得:123a b c =-⎧⎪=-⎨⎪=⎩. ∴抛物线1C 的解析式为:223y x x =--+.………………2分(2)抛物线1C 关于y 轴的对称图形2C 的解析式为:223y x x =-++. ……3分(3)'A 点的坐标为(-1,0),∵223y x x =-++=2(1)4x --+,wwW . ∴该抛物线的顶点为(1,4)D .………………………………4分 若△PAD 与△'A BO 相似,①当DA AP =3'BO OA =时,43AP =,P 点坐标为1(,0)3-或7(,0)3……………5分 ②当DA AP =1'3BO OA =时,12AP =,P 点坐标为(11,0)-或(13,0)…………6分 ∴当△PAD 与△'A BO 是相似三角形时,P 点坐标为1(,0)3-或7(,0)3或(11,0)-或(13,0) ………………7分24.解:(1) BC …………………………… 1分 (2由作图知AQ AP =,∠︒=06PAQ ∵△ACD 是等边三角形.∴AD AC =,PAQ CAD ∠=︒=∠06 ∴QAD PAC ∠=∠ 在△PAC 和△QAD 中⎪⎩⎪⎨⎧=∠=∠=AD AC QAD PAC AQ AP ∴△PAC ≌△QAD∴︒=∠=∠90ACP ADQ …………………………… 3分 (3)如图3,同①可证△PAC ≌△QAD ,︒=∠=∠90ACP ADQx y当AD ∥CQ 时,︒=∠-︒=∠90180ADQ CQD∵︒=∠60ADC∴︒=∠30QDC∵2==AC CD | ∴31==DQ CQ , ∴3==DQ PC 且AD CQ ≠…………………………… 5分∴此时四边形ACQD 是梯形.如图4,同理可证△PAC ≌△QAD ,︒=∠=∠90ACP ADQ当AQ ∥CD 时,︒=∠=∠60ADC QAD ,︒=∠30AQD∵2==AC AD∴4AQ DQ ==,∴PC DQ ==此时DQ 与AC 不平行,四边形ACDQ 是梯形.综上所述,这样的点P 有两个,分别在C 点两侧,当P 点在C 点左侧时,3=PC ;当P 点在C 点右侧时,PC =…………………………… 7分25.解:(1)由题意A (2.0) …………………………………………………………………1分由D (4,2),可得直线AD 解析式:2-=x y …………………………………………………2分 由B (0,4),可得直线AB 解析式:42+-=x y ,直线BD 解析式:421+-=x y ,J (21,). (2)在△ECD 平移t 秒时,由∠CDF =45°, 可得D’(t t --24,),N (t 2340-,) 设直线E’D’解析式为:13422y x t =-+- 可得M (t t 24,-),…………………………………………………3分Q (t t -+222,),P (t -20,)由△MQ D’∽△BJD ,得2)3233't S S BJD MQD -=∆∆(,可得 S △MQD ’ 2)211(3t -=…………………………………………………4分 S 梯形E’C’ PN t t t t 241)2122(212+-=-+=………………………………………5分 23)1(2112122+--=++-=t t t ∴当1=t 时,S 最大=23…………………………………………………6分 (3)当点H 在x 轴上时,有M (t t 24,-)横纵坐标相等 即t t 24-=∴34=t ∴340<<t .…………………………………………………8分|。
石景山区初三第一次统一练习暨毕业考试数学试卷

石景山区2009年初三第一次统一练习暨毕业考试数学试卷考 生 须 知1.本试卷共6页.全卷共九道大题,25道小题. 2.本试卷满分120分,考试时间120分钟.3.在试卷密封线内准确填写区(县)名称、毕业学校、姓名、报名号和准考证号.4.考试结束后,将试卷和答题纸一并交回.一、选择题(共8个小题,每小题4分,共32分) 在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.27的立方根是A .9B .3C .9±D .3±2.北京奥组委和国际奥委会在新闻发布上说:“中国有8亿4千万(840000000)人观看了奥运会开幕式,这确实是一个令人惊讶的数字.” 840000000这个数字用科学记数法可表示为A .90.8410⨯B .98.410⨯C .78410⨯D .88.410⨯3.如果两圆半径分别为3和4,圆心距为6,那么这两圆的位置关系是A .相交B .内切C .外离D .外切4. 在一个暗箱里,装有3个红球、5个黄球和7个绿球,它们除颜色外都相同,搅拌均匀后,从中任意摸出一个球是红球的概率是A .31 B .41 C .51 D .157 5x 的取值必须满足A .23->x B .23-≥x C .23>x D .23≥x 6. 某校初三(1该组女生体重的平均数、众数、中位数分别是 A .45、44、44 B .45、3、2C .45、3、44D .45、44、467. 已知:如图,在ABC ∆中,D 是AB 边上的一点,且AD BD 2=, 10=CD , 53sin =∠BCD ,则BC 边上的高AE 的长为 A .5.4 B .6C .8D .9第7题EA B CD8.若正方形网格中的每个小正方形的边长都是1,则把每个小格的顶点叫做格点.现有一个表面积为12的正方体,沿着一些棱将它剪开,展成以格点为顶点的平面图形,下列四个图形中,能满足题意的是DCBA二、填空题(共4个小题,每小题4分,共16分)9.分解因式:=++aaxax22.10.若关于x的方程0222=-+-aaxx有两个相等的实根,则a的值是.11.三角形纸片ABC中,55A∠=︒,75B∠=︒,将纸片的一角折叠,使点C落在ABC∆内(如图),则12∠+∠=_________°.12.将一副三角板如图放置,则上下两块三角板面积之比1A:2A等于________.三、解答题(共5个小题,每小题5分,共25分)13.计算:02)722(60sin41122-+︒-+--π.14.解不等式组⎩⎨⎧+<->-22413xxx,并把它的解集表示在数轴上.15.解方程:021211=-++-xxxx.16.已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得DFBE=,联结EC、FC.求证:FCEC=.FCDBA第16题A2A1第12题第11题17.已知062=-+x x ,求代数式7)1()1(22---+x x x x 的值.四、解答题(共2个小题,每小题5分,共10分)18.如图,等腰梯形ABCD 中,BC AD //,︒=∠45DBC ,翻折梯形ABCD ,使点B 与点D 重合,折痕分别交边AB 、BC 于点F 、E ,若2=AD ,8=BC . (1)求BE 的长;(2)求CDE ∠的正切值.第18题19.已知:如图,点A 是⊙O 上一点,半径OC 的延长线与过点A 的直线交于点B ,BC OC =,OB AC 21=. (1)求证:AB 是⊙O 的切线;(2)若︒=∠45ACD ,2=OC ,求弦CD 的长.A第19题五、解答题(本题满分6分)20.在我国,除夕之夜,全家一起看春节联欢晚会是人们传统的娱乐活动,尤其是小品类节目为我们带来了很多的欢乐.为了统计观众对2009年春晚小品类节目的喜好,中央电视台在网上进行了“2009年春晚我最喜爱的小品”调查问卷,并将统计结果绘制成两幅统计图,请你结合图中所给信息解答下列问题:(1)求参加调查的观众喜欢小品《暖冬》的人数占总投票人数的百分比; (2)求参加调查的观众喜欢小品《黄豆黄》的人数并补全条形图; (3)若北京市共有1200万人收看了春晚节目,请你估算北京市喜欢小品《不差钱》 的观众约有多少人?“2009年春晚我最喜爱的小品节目”调查结果条形统计图(单位:人)“2009年春晚我最喜爱的小品节目”调查结果扇形统计图(说明:A :《吉祥三宝》;B :《黄豆黄》;C :《水下除夕夜》; D :《北京欢迎你》;E :《暖冬》;F :《不差钱》) 六、解答题(共2个小题,第21题4分,第22题5分,共9分)21.已知:如图,直角三角形AOB 的两直角边、分别在x 轴的正半轴和轴的负半轴上,C 为线段OA 上一点,OB OC =,且1>m )经过A 、C 两点.(1)求出A 、B 两点的坐标(可用含m (2)若AOB ∆的面积为2,求m 的值.22直线l ,在直线l 两边各放一粒跳棋子A 、B ,在图中1P 处有一粒跳棋子,1P 距A 点b厘米、与直线l 的距离c 厘米,按以下程序起跳:第1次,从1P 点以A 为对称中心跳至2P 点;第2次,从2P 点以l 为对称轴跳至3P 点;第3次,从3P 点以B 为对称中心跳至4P 点;第4次,从4P 点以l 为对称轴跳至1P 点. (1)画出跳棋子这4次跳过的路径并标注出各点字母(画图工具不限); (2)棋子按上述程序跳跃15次后停下,假设8=a ,6=b ,3=c ,计算这时它与 点A 的距离.第22题七、解答题(本题满分7分) 23.两个反比例函数xk y 1=和x k y 2=(021>>k k )在第一象限内的图象如图所示,动点P 在xky 1=的图象上,x PC ⊥轴于点C ,交x k y 2=的图象于点A ,y PD ⊥轴于点D ,交xky 2=的图象于点B .(1)求证:四边形PAOB 的面积是定值;(2)当32=PC PA 时,求BPDB的值; (3)若点P 的坐标为(5,2),OAB ∆、ABP ∆的面积分别记为OAB S ∆、ABP S ∆,设ABP OAB S S S ∆∆-=.①求1k 的值;②当2k 为何值时,S 有最大值,最大值为多少?第23题八、解答题(本题满分7分) 24.已知:如图,半圆O 的直径cm DE 12=,在ABC ∆中,︒=∠90ACB ,︒=∠30ABC ,cm BC 12=.半圆O 以每秒cm 2的速度从左向右运动,在运动过程中,点D 、E 始终在直线BC 上.设运动时间为t (秒),当0=t (秒)时,半圆O 在ABC ∆的左侧,cm OC 8=.(1)当t 为何值时,ABC ∆的一边所在直线与半圆O 所在的圆相切?(2)当ABC ∆的一边所在直线与半圆O 所在的圆相切时,如果半圆O 与直线DE 围成的区域与ABC ∆三边围成的区域有重叠部分,求重叠部分的面积.第24题九、解答题(本题满分8分)25.已知:如图(1),射线//AM 射线BN ,AB 是它们的公垂线,点D 、C 分别在AM 、BN 上运动(点D 与点A 不重合、点C 与点B 不重合),E 是AB 边上的动点(点E 与A 、B 不重合),在运动过程中始终保持EC DE ⊥,且a AB DE AD ==+. (1)求证:ADE ∆∽BEC ∆;(2)如图(2),当点E 为AB 边的中点时,求证:CD BC AD =+;(3)设m AE =,请探究:BEC ∆的周长是否与m 值有关?若有关,请用含有m 的代数式表示BEC ∆的周长;若无关,请说明理由.第25题(1) 第25题(2)石景山区2009年初三第一次统一练习暨毕业考试数学试卷参考答案及评分标准阅卷须知:1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分)三、解答题(共5个小题,每小题5分,共25分)13. 解:02)722(60sin 41122-+︒-+--π 1|2341|324+⨯-+--= …………………………………3分1132324+-+--=4-=. …………………………………5分14. 解:由不等式413->-x ,得1->x . …………………………………1分 由不等式22+<x x ,得2<x . …………………………………2分 ∴ 原不等式组的解集是21<<-x . …………………………………3分 在数轴上表示为:…………………………………5分15. 解:去分母,得0)1(2)21)(1(=++--x x x x . …………………………………2分去括号,整理,得015=-x .解得 51=x . …………………………………4分 经检验,51=x 是原方程的根. …………………………………5分 所以,原方程的根为51=x .16.证明:∵ 四边形ABCD 是菱形,∴ DC BC =,ADC ABC ∠=∠.∴ FDC EBC ∠=∠. …………………2分 在EBC ∆和FDC ∆中,⎪⎩⎪⎨⎧=∠=∠=,,,DC BC FDC EBC DF BE ∴ EBC ∆≌FDC ∆. …………………………………4分 ∴ FC EC =. …………………………………5分17.解:7)1()1(22---+x x x x 7323-+-+=x x x xFC DBA第16题72-+=x x . …………………………………3分∵ 062=-+x x , ∴ 172-=-+x x .即 7)1()1(22---+x x x x 1-=. …………………………………5分 四、解答题(共2个小题,每小题5分,共10分)18. 解:(1)由题意得BFE ∆≌DFE ∆,所以,BE DE =.∵ 在BDE ∆中,BE DE =,︒=∠45DBE , ∴ ︒=∠=∠45DBE BDE .∴ ︒=∠90DEB .即BC DE ⊥. …………………………………1分 在等腰梯形ABCD 中,2=AD ,8=BC ,∴ 3)(21=-=AD BC EC . ∴ 5=BE . …………………………………3分 (2)由(1)得,5==BE DE .在DEC ∆中,︒=∠90DEC ,5=DE ,3=EC ,所以,53tan ==∠ED EC CDE . …………………………………5分19.(1)证明:如图,联结OA . …………………………………1分∵ BC OC =,OB AC 21=, ∴ OA AC BC OC ===.∴ ACO ∆是等边三角形. ∴ ︒=∠60O ,︒=∠60OCA . ∴ ︒=∠30B .∴ ︒=∠90OAB . …………………………………2分 所以,AB 是⊙O 的切线. …………………………………3分 (2)解:作CD AE ⊥于E 点. ∵ ︒=∠60O ,∴ ︒=∠30D .又︒=∠45ACD ,2==OC AC ,所以在ACE Rt ∆中,2==AE CE .在ADE Rt ∆中,∵ ︒=∠30D ,∴ 22=AD . 由勾股定理,可求6=DE .第19题所以,CE DE CD +=26+=. …………………………………5分五、解答题(本题满分6分) 20. 解:(1)10%. ……………………2分 (2)340人,见右图.……………………4分 (3)约660万人. ……………………6分六、解答题(共2个小题,第21题4分,第22题5分,共9分)21. 解:(1)在抛物线m x m x y ++-=)1(2中,令0=y ,得0)1(2=++-m x m x , 解得1=x 或m x =(1>m ).所以,1=OC ,m OA =. ∵ OB OC =,∴ 1=OB .所以,A 点的坐标为(m ,0), …………………………………1分 B 点的坐标为(0,1-). …………………………………2分 (2)AOB ∆的面积OB OA S ⋅=21m 21=,所以,当2=S 时,4=m . …………………………………4分22. 解:(1)跳棋子跳过路径及各点字母如图. ………………3分 (2)跳跃15次后,停在4P 处, 过4P 作⊥C P 4AB ,垂足为C 点, 则C P 435136=-=;由7=AC ,∴ A P 4212844935==+=.…………………………………5分七、解答题(本题满分7分)23.(1)证明:设),(11y x A ,),(22y x B ,),(33y x P ,AOC ∆与BOD ∆的面积分别为1S,第22题2S ,矩形PCOD 的面积为3S .由题意,得 121x k y =,222x k y =,313x k y =. ∴ 21112121k y x S ==,22222121k y x S ==,1333k y x S ==.∴ 21213)(k k S S S S PAOB -=+-=四边形.∴ 四边形PAOB 的面积是定值. …………………………………2分 (2)解:由(1)可知21S S =,则AC OC BD OD ⋅=⋅. 又∵ PC PA 32=, ∴ PC AC 31=. ∵ OC DP =,PC OD =,∴ DP BD 31=.∴ 21=BP DB . …………………………………4分(3)解:①由题意知:101==P P y x k . …………………………………5分②A 、B 两点坐标分别为)5,5(2k A ,)2,2(2k B ,∴ )25)(52(212122k k BP AP S ABP --=⋅=∆. ∴ )25)(52(212102222k k k S S S ABP PAOB --⨯--=-=∆四边形. ∴ 222101k k S +-=. ∴ 当52=k 时,S 有最大值25. …………………………………7分 八、解答题(本题满分7分)24.解:(1)如图(1),当1=t 时,ABC ∆的AC 边与⊙O 相切; 如图(2),当4=t 时,ABC ∆的AB 边与⊙O 相切; 如图(3),当7=t 时,ABC ∆的AC 边与⊙O 相切;如图(4),当16=t 时,ABC ∆的AB 边所在直线与⊙O 相切. …………………………………4分第23题(2)由(1),可知,当4=t 和7=t 时,半圆O 与直线DE 围成的区域与ABC ∆ 三边围成的区域有重叠部分,如图(2)、(3)的阴影部分所示,重叠部分的面积分别为29cm π和2)639(cm π+.…………………………………7分九、解答题(本题满分8分) 25.(1)证明:∵ EC DE ⊥,∴ ︒=∠90DEC .∴ ︒=∠+∠90BEC AED . 又∵ ︒=∠=∠90B A ,∴ ︒=∠+∠90EDA AED .∴ EDA BEC ∠=∠.∴ ADE ∆∽BEC ∆. …………………………………2分(2)证明:如图,过点E 作EF BC //,交CD 于点F ,∵ E 是AB 的中点,容易证明)(21BC AD EF +=. 在DEC Rt ∆中,∵ CF DF =,∴ CD EF 21=. ∴ )(21BC AD +CD 21=. ∴ CD BC AD =+. …………………………………5分(3)解:AED ∆的周长DE AD AE ++=m a +=,m a BE -=.设x AD =,则x a DE -=.第24题(4)第24题(1)第24题(2)第24题(3) 第25题∵ ︒=∠90A ,∴ 222AD AE DE +=.即22222x m x ax a +=+-. ∴ am a x 222-=. 由(1)知ADE ∆∽BEC ∆,∴ 的周长的周长BEC ∆∆ADE BE AD =m a a m a --=222am a 2+=. ∴ BEC ∆的周长⋅+=ma a 2ADE ∆的周长a 2=. ∴ BEC ∆的周长与m 值无关. …………………………………8分。
北京市石景山区中考一模数学试题及答案

北京市石景山区初三统一练习暨毕业考试数学试卷一、选择题(本题共32分,每小题4分) 1.32-的相反数是 A .23- B .23C .32-D .32 2.清明小长假本市150家景区接待游客约5245000人,数字5245000用科学记数法表示为 A .3105.245⨯B .6105.245⨯ C .7100.5245⨯ D .3105245⨯3.正五边形的每个内角等于 A .72°B .108°C .54°D .36°4.为了解居民用水情况,晓娜在某小区随机抽查了10户家庭的月用水量,结果如下表:则这10户家庭的月用水量的平均数和众数分别是A .7.8,9B .7.8,3C .4.5,9D .4.5,3 5.将二次函数1822--=x x y 化成k h x a y +-=2)(的形式,结果为 A .1)2(22--=x y B .32)4(22+-=x yC .9)2(22--=x yD . 33)4(22--=x y6.如图,△ABC 内接于⊙O ,BA =BC ,∠ACB =25°,AD 为⊙O 的直径,则∠DAC 的度数是 A .25 B .30° C .40° D .50°7.转盘上有六个全等的区域,颜色分布如图所示,若指针固定不动,转动转盘, 当转盘停止后,则指针对准红色区域的概率是 A .21 B .31 C .41 D .61 8.如图,边长为1的正方形ABCD 中有两个动点P , Q ,点P 从点B 出发沿BD 作匀速运动,到达点D 后停止;同时点Q 从点B 出发,沿折线BC →CD 作匀速运动,P ,Q 两个点的速度都为每秒1个单位,如果其中一点停止运动,则另一点也停止运动.设P ,Q 两点的运动时间为x 秒,两点之间的距离为y ,下列图象中,能表示y 与x 的函数关系的图象大致是月用水量(吨)5 6 7 8 9 10 户数112231第8题图QPC DAB第6题图 第7题图红黄 蓝 红 蓝 蓝O DCBAyAy O x 1 2 y O x12 yOx12 y O x12 A BC D二、填空题(本题共16分,每小题4分)9. 分解因式:ax ax 163-=_______________.10. 如图,CD AB //,AC 与BD 相交于点O ,3=AB , 若3:1:=BD BO ,则CD 等于_____.11.如图所示,小明同学在距离某建筑物6米的点A 处测得条幅两端B 点、C 点的仰角分别为60°和30°,则条幅的高度BC 为 米(结果可以保留根号).12.在平面直角坐标系xOy 中,已知直线l :x y =,作1A (1,0)关于x y =的对称点1B ,将点1B 向右水平平移2个单位得到点2A ;再作2A 关于x y =的对称点2B ,将点2B 向右水平平移2个单位得到点3A ;….请继续操作并探究:点3A 的坐标是 ,点2014B 的坐标是 .三、解答题(本题共30分,每小题5分)13.02014130tan 3512)(-︒+--.14.解方程:xx x -=+--53153. 15.如图,在△ABC 和△ADE 中,AC AB =, AE AD =,DAE BAC ∠=∠,点C 在DE 上. 求证:(1)△ABD ≌△ACE ;(2)ADC BDA ∠=∠.16.已知:23=y x ,求代数式yx yx 3294+-的值.17.如图,一次函数21+=kx y 的图象与x 轴交于点B (0 2-,),与函数xmy =2(0>x )的图象交于点A (a 1,). ECBAD BDC第11题图OCD BA第10题图CB A D(1)求k 和m 的值; (2)将函数xmy =2(0x >)的图象沿y 轴向下平移3个单位后交x 轴于点C .若点D 是平移后函数图象上一点,且△BCD 的面积是3,直接写出点D 的坐标.18.某公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台. (1)求该公司至少购买甲型显示器多少台?(2)若要求甲型显示器的台数不超过乙型显示器的台数,问有哪些购买方案? 四、解答题(本题共20分,每小题5分)19.如图,在四边形ABCD 中,2AB =,︒=∠=∠60C A ,DB AB ⊥于点B ,45DBC ∠=︒,求BC 的长.20.为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.(1)请根据以上信息,直接补全条形统计图和扇形统计图;(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史? (3)若该校共有学生540人,请估算全校有多少学生选修篮球课? 21.如图,⊙O 是△ABC 的外接圆,AC AB =,连结CO 并延长交⊙O 的切线AP 于点P .(1)求证:BCP APC ∠=∠;三个班级参加选修课的 初二(5)班参加各类选修课的人数统计图 人数分布统计图 人数 音乐史 管乐 篮球 健美操 油画 课程 10 9 8 7 6 5 4 3 2 1(2)若53sin =∠APC ,4=BC ,求AP 的长.22.实验操作(1)如图1,在平面直角坐标系xOy 中,△ABC 的顶点的横、纵坐标都是整数,若所经过的路线长为 .(1)求m 的值;(2)将抛物线1C :1)1(22-+-+=m x m mx y 向右平移a 个单位,再向上平移b 个单位得到抛物线2C ,若抛物线2C 过点),(b A 2和点),(12 4+b B ,求抛物线2C 的表达式;(3)将抛物线2C 绕点(n n ,1+)旋转︒180得到抛物线3C ,若抛物线3C 与直线121+=x y 有两个交点且交点在其对称轴两侧,求n 的取值范围.BPCO A24.在矩形ABCD 中,AD =12,AB =8,点F 是AD 边上一点,过点F 作∠AFE =∠DFC ,交射线AB 于点E ,交射线CB 于点G . (1) 若82FG =,则_____CFG ∠=︒;(2) 当以F ,G ,C 为顶点的三角形是等边三角形时,画出图形并求GB 的长;(3)过点E 作EH//CF 交射线CB 于点H ,请探究:当GB 为何值时,以F ,H ,E ,C 为顶点的四边形是平行四边形.25.在平面直角坐标系xOy 中,对于任意三点A ,B ,C 的“矩面积”,给出如下定义: “水平底”a :任意两点横坐标差的最大值,“铅垂高”h :任意两点纵坐标差的最大值,则“矩面积”=S ah .例如:三点坐标分别为)2,1(A ,)1,3(-B ,)2,2(-C ,则“水平底”5=a ,“铅垂高”4=h ,“矩面积”20==S ah . (1)已知点)2,1(A ,)1,3(-B ,),0(t P .①若A ,B ,P 三点的“矩面积”为12,求点P 的坐标; ②直接写出A ,B ,P 三点的“矩面积”的最小值. (2)已知点)0,4(E ,)2,0(F ,)4,(m m M ,)16,(nn N ,其中0>m ,0>n . ①若E ,F ,M 三点的“矩面积”为8,求m 的取值范围;②直接写出E ,F ,N 三点的“矩面积”的最小值及对应n 的取值范围.D A 备用图E DA F北京市石景山区初三统一练习暨毕业考试数学参考答案阅卷须知:1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分) 题 号 1 2 3 4 5 6 7 8 答 案 D B B A C CBA二、填空题(本题共4道小题,每小题4分,共16分)9.)4)(4(-+x x ax ; 10.6; 11.34; 12.(3,2),(,). 三、解答题(本题共30分,每小题5分) 13.解:02014130tan 3512)(-︒+-- =1333532-⨯+- ………………………………………4分 =6-33 ………………………………………5分 14. 解:方程两边同乘以)5(-x ,得 ………………………………………1分3)5(3-=-+-x x . ………………………………………2分解得25=x . ………………………………………3分 经检验:25=x 是原分式方程的解. ………………………………4分所以25=x 是原方程的解. ………………………………………5分15.证明:(1)DAE BAC ∠=∠ ,DAC DAE DAC BAC ∠-∠=∠-∠∴.CAE BAD ∠=∠∴. …………………………1分 在△ABD 和△ACE 中,⎪⎩⎪⎨⎧=∠=∠=AE AD EAC BAD AC AB , ……………2分 ∴△ABD ≌△ACE . ………………………3分 (2)AEC ADB ∠=∠∴. AE AD = ,AEC ADC ∠=∠∴. …………………………4分 ADC BDA ∠=∠∴. …………………………5分16.解:由已知y x 32=, ………………………………………2分 ∴原式yy yy 3396+-=………………………………………4分21-=. ………………………………………5分 17.解:(1)根据题意,将点B (0 2-,)代入21+=kx y ,∴22-0+=k . ………………………………………………………1分∴1=k . …………………………………………………2分∴A (3 1,).将其代入x my =2,可得:3=m …………………3分(2)(2 53,)或(2 3-,). ………………………………………5分18.解:设该公司购进甲型显示器x 台, 则购进乙型显示器()50-x 台.(1)依题意可列不等式:77000)50(20001000≤-+x x ……………2分解得:23≥x …………………………………………………………3分∴该公司至少购进甲型显示器23台.(2)依题意可列不等式:x x -≤50解得:25≤x ………………………………………………………4分 ∵23≥x∴x 为23,24,25. 答:购买方案有:①甲型显示器23台,乙型显示器27台; ②甲型显示器24台,乙型显示器26台;③甲型显示器25台,乙型显示器25台. …………5分四、解答题(本题共20分,每小题5分)19. 解:过点D 作BC DE ⊥于点E . ……………………1分︒=∠=⊥60 2,A AB AB DB ,,∴3260tan =︒⨯=AB BD . ………………2分 45DBC ∠=︒,BC DE ⊥, ∴645sin =︒⨯==BD DE BE …………3分︒=∠︒=∠=∠9060DEC A C ,260tan =︒=∴DECE . ……………………4分62+=∴BC .………………………………5分20.解:(1)条形统计图补充数据:6(图略). ………………………………………1分扇形统计图补充数据:20. ……………………………2分(2)180×308=48(人). ………………………………………………3分 (3)()1543030303020866=++÷⎪⎭⎫⎝⎛⨯++. ……………4分 EBAD144540154=⨯(人). …………………………………………5分 21.(1)证明:连结AO 并延长交BC 于D 、⋂BC 于EAP 切⊙O 于点AAPBC BC EA AC AB ACAB PA EA //∴⊥∴=∴=⊥∴⋂⋂…………………1分 BCP APC ∠=∠∴…………………………2分(2)解:BC AE ⊥221==∴BC CD53sin ==∠PO AO APC ∴设k OP k OA 5,3==,则k OA OC 3==………………3分AP BC //∴△PAO ∽△CDO …………………………4分 COPOCD PA =∴ kkPA 352=∴∴310=PA …………………………5分22. 解:()画出点P …………………..1分画出△DEF ………………..2分 () x y–5–4–3–2–112345–5–4–3–2–112345P F E D C B A O BPCO E DEG D A B CF°A'C'B'PCA C B…………………………….4分34π=⋂AB ……………………………………………………5分 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.解:(1)∵方程01)1(22=-+-+m x mmx有两个实数根, ∴0≠m 且0≥∆, ……………………1分则有0)1(4-)1(42≥--m m m 且0≠m ∴1≤m 且0≠m又∵m 为非负整数,∴1=m . ………………………………2分(2)抛物线1C :2x y =平移后,得到抛物线2C :b a x y +-=2)(,……3分 ∵抛物线2C 过),2(b A 点,b a b +-=2)2(,可得2=a ,同理:b a b +-=+2)4(12,可得3=b , …………………………4分∴2C :()322+-=x y)(或742+-=x x y . …………5分(3)将抛物线2C :3)2(2+-=x y 绕点(n n ,1+)旋转180°后得到的抛物线3C 顶点为(322-n n ,), (6)分当n x 2=时,11221+=+⨯=n n y , 由题意,132+>-n n ,即:4>n . ……………………………7分24.解:(1)90° ………………………………………………2分 (2)正确画图 ………………………………………………3分四边形ABCD 是矩形, ∴∠D=90°.△FGC 是等边三角形,=60GFC ∴∠︒ . ∠DFC =∠AFE ,∴∠DFC =60°. …………4分 DC =8 ,∴331660sin =︒=DC FC .△FGC 是等边三角形,∴GC =FC =1633. BC=AD =12, ∴GB=12-1633.………………………………5分 (3)过点F 作FK ⊥BC 于点K四边形ABCD 是矩形∴∠ABC =90°,AD//BC∴∠DFC =∠KCF ,∠AFG =∠KGF∠DFC =∠AFG∴∠KCF =∠KGF∴FG =FC ……………………………………………………………6分∴GK =CK四边形FHEC 是平行四边形∴FG =EG ……………………………………………………………7分 ∠FGK =∠EGB, ∠FKG =∠EBG=90°∴△FGK ≌△EGB∴BG =GK=KC=4312=……………………………………………8分25.解:(1)由题意:4=a .①当2>t 时,1-=t h ,则12)1(4=-t ,可得4=t ,故点P 的坐标为(0,4);……………1分 当1<t 时,t h -=2,则12)2(4=-t ,可得1-=t ,故点P 的坐标为(0,1)-.…………2分②A ,B ,P 三点的“矩面积”的最小值为4. ……………………3分(2)①∵E ,F ,M 三点的“矩面积”的最小值为8,∴⎩⎨⎧≤≤≤≤24040m m .∴210≤≤m . K H E G D A B C F∵0>m ,∴210≤<m . ………………………………………………………4分 ②E ,F ,N 三点的“矩面积”的最小值为16,…………………………5分 n 的取值范围为84≤≤n ………………………………………………7分F E。
北京市石景山区中考数学一模试卷

.
15.(3 分)2014 年 5 月 1 日起,北京市居民用水实施阶梯水价.按年度用水量
计算,将居民家庭全年用水量划分为三档,水价分档递增,水量分档和水价
标准如下:第一阶梯用水量不超过 180 立方米,水价为每立方米 5 元;第二
阶梯用水量在 180(不含)﹣260(含)立方米之间,超出 180 立方米的部分
第6页(共8页)
(2)将图 1 中的直线 A′B 沿着 EC 方向平移,与直线 EC 交于点 D,与直线 BC 交 于点 F,过点 F 作直线 AB 的垂线,垂足为点 H.
①如图 2,若点 D 在线段 EC 上,请猜想线段 FH,DF,AC 之间的数量关系,并 证明;
②若点 D 在线段 EC 的延长线上,直接写出线段 FH,DF,AC 之间的数量关系.
上,满足 OA= ,OC=1.将矩形 OABC 绕原点 O 以每秒 15°的速度逆时针旋
转.设运动时间为 t 秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为 S,
表示 S 与 t 的函数关系的图象大致如图所示,则矩形 OABC 的初始位置是
()
第2页(共8页)
A.
B.
C.
D.
二、填空题(本题共 18 分,每小题 3 分)
请回答以下问题:
(1)此次调查对象共
人,扇形统计图中 m 的值为
;
(2)请补全条形统计图并在图上标出数据;
(3)据统计,该市某大学有学生 15000 人,请根据上述调查结果估计这所大学
2014﹣2015 学年度第一学期参加过至少两次公益活动的大约有
人.
25.(5 分)如图,AB 是⊙O 的直径,C 是⊙O 上一点,D 是 OB 中点,过点 D 作
北京市石景山区中考数学一模试题

石景山区2011年初三第一次统一练习暨毕业考试数 学 试 卷第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.12-的绝对值是 A .12B . 12-C .2D .2-2.据《北京日报》报道,去年北京批准约209亿元公积金贷款投入保障房建设,数字209用科学记数法可表示为 A .10.920⨯B .2109.02⨯ C .31009.20⨯D . 3109.02⨯3.已知:如图,m l ∥,等边ABC △的顶点B 在直线m 上,边BC 与直线m 所夹锐角为︒20,则α∠的度数为 A .︒60 B .︒45 C .︒40 D .︒304.函数12y x =-的自变量x 的取值范围是A .0x ≠B .2x ≠C .2x ≥D .2x >5.下列数据是某班六位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,9,8,4,0,3,这组数据的平均数、中位数和极差分别是A .6,6,9B .6,5,9C .5,6,6D .5,5,96.已知:⊙O 的半径为2cm ,圆心到直线l 的距离为1cm ,将直线l 沿垂直于l 的方向平移,使l 与⊙O 相切,则平移的距离是 A .1 cmB .2 cmC .3cmD .1 cm 或3cm第3题图l 20︒mBA αC7.为吸引顾客,石景山万达广场某餐饮店推出转盘抽奖打折活动,如图是可以自由转动的转盘,转盘被分成若干个扇形,转动转盘,转盘停止后,指针所指区域内的奖项可作为打折等级(若指针指向两个扇形的交线时,重新转动转盘),其中一等奖打九折,二等奖打九五折,三等奖赠送小礼品.小明和同学周六去就餐,他们转动一次转盘能够得到九折优惠的概率是 A .31B .72 C .163 D .81 QPHG FED C BA8.已知:如图,无盖无底的正方体纸盒ABCD EFGH -,P ,Q 分别为棱FB ,GC 上的点,且12,2FP PB GQ QC ==,若将这个正方体纸盒沿折线AP PQ QH --裁剪并展开,得到的平面图形是A .一个六边形B .一个平行四边形C .两个直角三角形D . 一个直角三角形和一个直角梯形第Ⅱ卷(共88分)二、填空题(本题共16分,每小题4分)9.将二次函数562++=x x y 配方为k h x y +-=2)(形式,则=h ____,=k ________. 10.分解因式:=-234xy x _______________.11.已知:如图,AB ,BC 为⊙O 的弦,点D 在AB 上,若4=OD ,10=BC ,︒=∠=∠60B ODB ,则DB 的长为 . 第7题图 第8题图第11题图 第12题图C 1B 112.已知:如图,在平面直角坐标系xOy 中,点1B 、点1C 的坐标分别为()0,1,()31,,将△11C OB 绕原点O 逆时针旋转︒60,再将其各边都扩大为原来的m 倍,使12OC OB =,得到△22C OB .将△22C OB 绕原点O 逆时针旋转︒60,再将其各边都扩大为原来的m 倍,使23OC OB =,得到△33C OB ,如此下去,得到△n n C OB . (1)m 的值是_______________;(2)△20112011C OB 中,点2011C 的坐标:_____________.三、解答题(本题共30分,每小题5分)13.103130tan 12)2011(-⨯︒--+-)(.14.解不等式组⎪⎩⎪⎨⎧⋅-≥++->-②)1(517,①4113x x x x 并把解集在数轴上表示出来.15.如图,在△ABC 中,BC AB ⊥,AC BE ⊥于E ,点F 在线段BE 上,21∠=∠,点D 在线段EC 上,请你从以下两个条件中选择一个作为条件,证明△AFD ≌△AFB . (1)DF ∥BC ; (2)DF BF =.16.已知:04622=-+x x ,求代数式)225(4232---÷--x x x x x 的值.17.已知:如图,一次函数3+=kx y 的图象与反比例函数xmy =(0>x )的图象交于点P .x PA ⊥轴于点A ,y PB ⊥轴于点B .一次函数的图象分别交x 轴、y 轴于点C 、点D ,且27=DBP S △,21=CA OC .(1)求点D 的坐标;(2)求一次函数与反比例函数的解析式;(3)根据图象写出当x 取何值时,一次函数的值小于反比例函数的值?18.为继续进行旅游景区公共服务改造,某市今年预算用资金41万元在200余家A 级景区配备两种轮椅1100台,其中普通轮椅每台360元,轻便型轮椅每台500元. (1) 若恰好全部用完预算资金,能购买两种轮椅各多少台?(2) 由于获得了不超过4万元的社会捐助,问轻便型轮椅最多可以买多少台?四、解答题(本题共20分,每小题5分) 19.已知:如图,直角梯形ABCD 中,AD AB CDA BCD =︒=∠︒=∠,,6090,4,2AB DF ==,求BF 的长.20.已知:如图,在矩形ABCD 中,点O 在对角线BD 上,以OD 的长为半径的⊙O 与AD ,BD分别交于点E 、点F ,且∠ABE =∠DBC .(1)判断直线BE 与⊙O 的位置关系,并证明你的结论;(2)若33sin =∠ABE ,2=CD ,求⊙O 的半径. 21.远洋电器城中,某品牌电视有D C B A ,,,四种不同型号供顾客选择,它们每台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,商场调查了一周内这四种不同型号电视的销售情况,并根据销售情况,将所得的数据制成统计图,现已知该请根据以上信息,解答下列问题: (1)请补全统计图;(2)通过计算,说明商场这一周内该品牌哪种型号的电视总销售利润最大; (3)谈谈你的建议.22.在边长为1的正方形网格中,正方形ABFE 与正方形EFCD 的位置如图所示. (1)请你按下列要求画图: ① 联结BD 交EF 于点M ;② 在AE 上取一点P ,联结BP ,MP ,使△PEM 与△PMB 相似;(2)若Q 是线段BD 上一点,连结FQ 并延长交四边形ABCD 的一边于点R ,且满足某商场四种型号电视一周的销售量统计图 销售量(台) 型号BD FR 21=,则QR FQ 的值为_____________. 五、解答题(本题满分7分)23.已知抛物线C :()112++-=x m x y 的顶点在坐标轴...上. (1)求m 的值;(2)0>m 时,抛物线C 向下平移()0>n n 个单位后与抛物线1C :c bx ax y ++=2关于y 轴对称,且1C 过点()3,n ,求1C 的函数关系式;(3)03<<-m 时,抛物线C 的顶点为M ,且过点()0,1y P .问在直线1-=x 上是否存在一点Q 使得△QPM 的周长最小,如果存在,求出点Q 的坐标, 如果不存在,请说明理由.六、解答题(本题满分7分)24.已知:如图,正方形ABCD 中,,AC BD 为对角线,将BAC ∠绕顶点A 逆时针旋转α°(045α<<),旋转后角的两边分别交BD 于点P 、点Q ,交,BC CD 于点E 、点F ,联结,EF EQ .(1)在BAC ∠的旋转过程中,AEQ ∠的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);(2)探究△APQ 与△AEF 的面积的数量关系,写出结论并加以证明.七、解答题(本题满分8分)25.已知二次函数23332-+-=mx mx y 的图象与x 轴交于点A (0)、点B ,与y 轴交于点C .(1)求点B 坐标;(2)点P 从点C 出发以每秒1个单位的速度沿线段CO 向O 点运动,到达点O 后停止运动,过点P 作AC PQ //交OA 于点Q ,将四边形PQAC 沿PQ 翻 折,得到四边形''C PQA ,设点P 的运动时间为t .①当t 为何值时,点'A 恰好落在二次函数23332-+-=mx mx y 图象的对称轴上; ②设四边形''C PQA 落在第一象限内的图形面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.石景山区2011年初三第一次统一练习暨毕业考试试卷初三数学参考答案阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共32分,每小题4分)9.4,3--; 10.)2)(2(y x y x x -+; 11.6; 12.2;(32,220102010).三、解答题(本题共30分,每小题5分) 13.解:原式333321⨯-+= …………………………………………4分 31+= …………………………………………5分14.解:解不等式① 3<x …………………………………………1分解不等式② 3-≥x …………………………………………2分 原不等式组的解集为33<x ≤- …………………………………………4分在数轴上表示为:…………………………………………5分15.情况一、添加条件:DF //BC证明: ∵ DF ∥BC∴ C FDE ∠=∠ ………………………………… 1分 ∵BC AB ⊥,AC BE ⊥∴︒=∠+∠=∠+∠90EBC C EBC ABF∴C ABF ∠=∠ ……………… …………2分 ∴ADF ABF ∠=∠ ……………… …………3分在ABF ∆和ADF ∆中 ⎪⎩⎪⎨⎧=∠=∠∠=∠AFAF ADF ABF 21 ∴AFD ∆≌AFB ∆ ……………………………………………… 5分 情况二、添加条件:DF BF =证明:过点F 作AB FG ⊥于G …………………………………………… 1分∵ AC BE ⊥,21∠=∠ ∴ EF FG =………………………………… 2分在BGF Rt ∆和DEF Rt ∆中 ︒=∠=∠90DEF BGF∵⎩⎨⎧==DFBF EF FG∴BGF Rt ∆≌()HL DEF Rt ∆ ………………………………………… 3分 ∴EDF GBF ∠=∠………………………………………………………… 4分 在ABF ∆和ADF ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠AF AF ADF ABF 21 ∴AFD ∆≌AFB ∆ ………………………………………………………… 5分21FA B C D E16.解:原式)1225(4232+--÷---=x x x x x ……………………………………1分)29(42322-+-÷---=x x xx x ………………………………………… 2分x x 6212+= ………………………………………………… 3分 当04622=-+x x 时,4622=+x x …………………………… 4分原式41= ………………………………………………………5分17.解:(1)根据题意,得:)3,0(D …………………………………1分 (2)在Rt △COD 和Rt △CAP 中, 21=CA OC ,3=OD ∴,6=AP 6=OB ∴9=DBRt △DBP 中,∴,272=⨯BPDB ∴6=BP ,)6,6(-P …………………2分一次函数的解析式为:323+-=x y ……………………………………………………………3分反比例函数解析式为:xy 36-= …………………………………4分(3)如图可得:6>x ………………………………5分 18.解:(1)设能买普通轮椅x 台,轻便型轮椅()x -1100台 …………………1分根据题意得:()4100001100500360=-+x x …………………………2分 解得:1000=x经检验1000=x 符合实际意义且1001100=-x …………………………3分答:能买普通轮椅1000台,轻便型轮椅100台.(2) 根据题意得:()4500001100500360≤-+x x ………………………4分 解得:72714≥x 753851100≤-x符合题意的整数值为385 ………………………………5分 答:轻便型轮椅最多可以买385台.四、解答题(本题共20分,每小题5分)19.解:如图,过A 作AH ⊥FC 于H ………………1分 则四边形ABCH 为矩形AB CH AH BC ==, ……………………… ………2分∵60,4CDA AD AB ===∠∴AH ==︒60sin AD HD ==︒60cos AD 2 …………………………4分∴CF =CH +HD +DF =4+2+2=8,∴BF =………………………………………………5分F E D CB AH20.解:(1)直线BE 与⊙O 相切……………………………………………………1分证明:联结OE在矩形ABCD 中, AD ∥BC∴∠ADB =∠DBC ∵OE OD =∴∠OED =∠ODE又∵∠ABE =∠DBC∴∠ABE =∠OED ……………………………………………………………2分 ∵矩形ABDC ,∠︒=90A ∴︒=∠+∠90AEB ABE ∴︒=∠+∠90AEB OED∴︒=∠90BEO ………………………………………………………………3分 ∴直线BE 与⊙O 相切 (2) 联结EF 方法1:∵四边形ABCD 是矩形,2=CD ∴︒=∠=∠90C A ,2==CD AB ∵∠ABE =∠DBC∴=∠CBD sin 33sin =∠ABE ∴32sin =∠=CBDDCBD …………………………………………………4分在AEB Rt ∆中,可求2=AE ∴勾股定理求得6=BE在BEO Rt ∆中,︒=∠90BEO 222OB EB EO =+ 设⊙O 的半径为r则()()222326r r -=+∴r =23……………………………………………………………………5分 方法2:∵DF 是⊙O 的直径 ∴︒=∠90DEF∵四边形ABCD 是矩形∴︒=∠=∠90C A ,2==CD AB∵∠ABE =∠DBC∴=∠CBD sin 33sin =∠ABE设x BD x DC 3,==,则x BC 2= ∵2=CD∴22=BC ……………………………………………………………4分 ∵ABE CBD ∠=∠tan tan ∴AB AEBC DC = ∴2222AE =∴2=AE∴E 为AD 中点.∵DF 为直径,∠︒=90FED ∴AB EF // ∴321==BD DF ∴⊙O 的半径为23……………………………………………………………5分21. 解:(1)补全统计图如下…………2分(2)12500502500%10=⨯⨯ ,480001004000%12=⨯⨯,63000706000%15=⨯⨯,400002010000%20=⨯⨯∴商场在这一周内该品牌C 型号的电视总销售利润最大………………4分(3)从进货角度、宣传角度等方面答对即可. ……………………………5分 22.(1)如图所示…………………………2分(2)1、32或2 ………………………………………………………………5分 五、解答题(本题满分7分)23.解:当抛物线C 的顶点在x 轴上时()[]0412=-+-=∆m解得1=m 或3-=m ………………………………1分 当抛物线C 的顶点在y 轴上时 ()01=+-m∴1-=m ………………………………2分 综上1±=m 或3-=m . (2)当0>m 时,1=m抛物线C 为122+-=x x y .向下平移()0>n n 个单位后得到n x x y -122+-=抛物线n x x y -122+-=与抛物线1C : c bx ax y ++=2关于y 轴对称∴1=a ,2=b ,n c -=1 …………………………………3分 ∴抛物线1C : n x x y -++=122 ∵1C 过点()3,n∴3122=-++n n n ,即022=-+n n ……………………………………4分P M F E D C B A 型号销售量(台)解得2,121-==n n (由题意0>n ,舍去)∴1=n ∴抛物线1C : x x y 22+=. ………………………………………………5分 (3)当03<<-m 时1-=m抛物线C :12+=x y 顶点()1,0M ∵过点()0,1y P ∴2110=+=y∴()2,1P ………………6分作点()1,0M 关于直线1-=x 的对称点()1,2'-M直线'PM 的解析式为3531+=x y ∴⎪⎭⎫ ⎝⎛-34,1Q ………………………………………7分六、解答题(本题满分7分) 24. 解:(1)不变; ……………………………………………………………………1分45°;………………………………………………………………………2分(2)结论:S △AEF =2 S △APQ ………………………………………………………………3分 证明:∵AEQ ∠=45°,45EAF ∠=︒∴90EQA ∠=︒ ……………………∴AE = …………………… ………4分同理AF = …………………… ………5分 过点P 作PH AF ⊥于H …………… ………6分∴S △AEF 1122AF EQ AQ =⋅=⋅2AP AQ PH AQ S =⋅=⋅=△APQ …………………………………7分七、解答题(本题满分8分)25. 解:(1)将A (0)代入23332-+-=mx mx y 解得m =………1分 ∴函数的解析式为23312-+-=x x y令0=y ,解得:32,321==x x∴B 0) ……………………………………………………………………2分 (2)①由解析式可得点)2,0(-C二次函数图象的对称轴方程为x =Rt △AOC 中 ∵32,2==OA OC ∴︒=∠︒=∠60,30OCA OAC∴︒=∠︒=∠60',150QH A PQA ,Q A AQ '= 过点A ′作'A H x ⊥轴于点H ,则QH AH =HQ PFE DC B A∴2OQ QH OQ QH ⎧+=⎪⎨⎪+=⎩………………………3分解得2QH =则AQ =1CP =∴1=t ……………………………………………………4分 ②分两种情况:ⅰ)当10≤<t 时,四边形PQA ′C ′落在第一象限内的图形为等腰三角形QA ’N .'NQ A Q ==t t AQ H A 2323360sin '=⋅=︒= 2'43323321t t t S NQ A =⋅=△ 当1=t 时,有最大值S 433= ⅱ)当21<<t 时,设四边形PQA ′C ′落在第一象限内的图形为四边形M O QA ′.''''2222))224OPQ PC MMOQA QA C S S S S t t ∆∆=--⎡⎤=----⎢⎥⎣⎦=+-四边形梯形P 当85t =时,有最大值'MOQA S =四边形 综上:当85t =时,四边形PQA ’ C.。
石景山区2010-2011学年度第一学期初三期末数学答案_题库_初中数学新_更

石景山区2010-2011学年度第一学期期末考试试卷初三数学参考答案阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)题 号 1 2 3 4 5 6 7 8 答 案BDCCADDB二、填空题(本题共4道小题,每小题4分,共16分)9.40; 10.4)3(2+--=x y ; 11.()5,3; 12.32π. 三、解答题(本题共5道小题,每小题5分,共25分) 13.解:︒+︒︒-60tan 45tan 60sin 12=32332+- ……………………………………………………………4分 =325……………………………………………………………………5分 14. 解:过D 作AC DE ⊥于E ……………………………1分 在Rt △ABC 中,∵90B ∠=,AB =BC =22,∴45C ∠=…………………………………………2分 ∵点D 为BC 的中点,∴122BD DC BC ===∴2222(22)(2)10AD AB BD =+=+=………………………………3分在Rt △DCE 中,sin 451DE DC =⋅︒=………………………………4分∴10sin 10DAC ∠=…………………………5分 EDCBA15.解:(1)不同类型的正确结论有:①PC =PD ②CD ⊥BA ③∠CEP =90° ④∠CPO =∠DP A ⑤ ……2分 (2)联结OC∵PC 、PD 分别切⊙O 于点D C 、 ∴PC =PD , ∠CPO =∠DP A ∴CD ⊥AB ∵CD=12∴DE =CE =12CD =6.………………………3分 ∵21tan =∠CPO∴在Rt △EPC 中 , PE=12∴勾股得36=CP ………………………4分 ∵PC 切⊙O 于点C ∴ 90=∠OCP 在Rt △OPC 中, ∵21tan =∠CPO ∴21=PC OC ∴33=OC∴()()15336332222=+=+=PC OC OP ………………………………5分16.解:由题意得:D (4,2)- ………………………1分∵双曲线经过点D ∴24k -=∴8k =- ………………………2分∴8y x=-设点C ),8(n ………………………3分 ∴818n =-=- ………………………4分 ∴点C )1,8(- ………………………5分y第16题xODABCE ODCBAP第18题 第18题17. 解:(1)解法一:用列表法 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5678910列表正确 …………………………………………………3分解法二:画树状图画树状图正确 ………………………………………………………3分 (2)31248)3(==的倍数和为P ………………………………………………5分四、画图题(本题满分4分) 18.解:注:正确画出一条得2分,正确画出两条得4分.开始1 2 3 4 789 10六面体4651 2 3 4 678 91 2 3 4 567 831 2 3 4 456 7212 3 4 345 611 2 3 4 234 5四面体H五、解答题(本题共4道小题,每小题6分,共24分) 19.解:(1)由已知,抛物线过)8,1(-A 和点)7,2(-,得⎩⎨⎧=++-=+-78484c a c a ………………………1分 解这个方程组,得5,1-==c a∴ 所求抛物线的解析式为542--=x x y ………………………2分 (2)令0y =,则0542=--x x ………………………3分 解方程,得51=x ,21x =-. ………………………4分∴二次函数图象与x 轴的两个交点坐标分别为)0,5(和(10)-,.∴二次函数图象向左平移5个单位后经过坐标原点. ………………………5分 平移后所得图象与x 轴的另一个交点坐标为)0,6(- ………………………6分 20.解:过F 作BC FH ⊥于H ……………………………1分 ∵∠BFH =︒30,∠BEH =︒60,∠BHF =︒90 ∴∠EBF =∠EBC =︒30………………………2分 ∴BE = EF = 20 ………………………3分 在Rt △BHE 中, )(3.17232060sin m BE BH ≈⨯=︒⋅= ………………………4分 )(197.13.17m =+ ………………………5分答:宣传条幅BC 的长是19米.………………………6分 21.解:(1)如图,连结OA ……………………………1分 ∵AD 是⊙O 的切线 ∴︒=∠90OAD设D α∠=,则90DOA α∠=︒-,2B α∠=,4AOC α∠=………………2分∴︒=+-︒180490αα ∴︒=30α∴ ︒=∠30D …………………………3分 (2)解:OA OC =∵,︒==∠1204αAOC . ∴D ACO ∠=︒=∠30.∴=AD 34=AC . ……………………………5分在Rt ADO △中,3tan 4343AO AD D =⨯∠=⨯=………………………6分 ∴⊙O 的半径是4.DCBA O第21题图22.解:(1)设抛物线解析式为2ax y =………………………………………1分 设点),10(n B ,点)3,10(+n D ………………………………………………2分 由题意:⎩⎨⎧=+=an an 253100 解得⎪⎩⎪⎨⎧-=-=2514a n ………………………………………………3分∴2251x y -= ………………………………………………4分 (2)方法一:当3=x 时,9251⨯-=y ∵3)4(259>---.6 ………………………………………………5分 ∴在正常水位时,此船能顺利通过这座拱桥.…………………………………6分方法二: 当5246.3-=-=y 时,225152x -=- ∴10±=x∵310>± ......................................................5分 ∴在正常水位时,此船能顺利通过这座拱桥. (6)六、解答题(本题满分6分)23. 解:(1)90α︒+ ……………………………………………………………1分 (2)图中两对相似三角形:①△ABB '∽△AC C ' ,②△ACE ∽△FBE ;……… 3分 证明①:∵△ABC 绕点A 顺时针旋转角β得到△AB 'C '∴∠CA C '=∠BAB '=β,AC=A C ' ,AB=AB ' ………………………………4分 ∴''AB AC AB AC = ……………………………………………………5分 ∴△ABB '∽△AC C ' ……………………………………………………6分证明②:∵△ABC 绕点A 顺时针旋转角β得到△AB 'C '∴∠CA C '=∠BAB '=β,AC=A C ' ,AB=AB ' ………………………………4分∴∠AC C '=∠ABB '=2180β- ………………………………5分又∠A E C =∠FEB∴△ACE ∽△FBE ……………………………………………………6分 七、解答题(本题满分6分)24.解:(1)依题意,得[]()0363634)3(22≥+-=+--=∆a a a a ……………1分解得1≤a又0≠a 且a 为非负整数∴1=a ………………………………………………………………2分 ∴442+-=x x y (2)解法一:抛物线442+-=x x y 过点(1,1),(2,0),向下平移()0>m m 个单位后得到点()n ,1和点()12,2+n ……………………………3分∴()⎩⎨⎧=-=+-mn mn 1120, 解得3=m . ……………………………4分解法二:抛物线442+-=x x y 向下平移()0>m m 个单位后得:m x x y -+-=442,将点()n ,1和点()12,2+n 代入解析式得⎩⎨⎧+=-=-121n m nm …………………3分解得3=m . ……………………………4分 (3)设()00,y x P ,则()00,y x Q -- ……………………………5分 ∵Q P 、在抛物线k x x y ++-=442上,将Q P 、两点坐标分别代入得:⎩⎨⎧-=+++=++-002000204444y k x x y k x x ,将两方程相加得: 028220=++k x 即0420=++k x ∵()044'≥+-=∆k∴4-≤k当 4-=k 时,Q P 、两点重合,不合题意舍去∴4-<k . ……………………………6分八、解答题(本题满分7分) 25.解:(1)∵对称轴122-=-=ax ∴1a = ……………………………………………………1分∵()0,3-A∴3c =-设直线AC 的解析式为y kx b =+ ∵()0,3-A ,()3,0-C , 代入得:直线AC 的解析式为 3--=x y ………………………………………2分 (2)代数方法一:过点D 作DM ∥y 轴分别交线段AC 和x 轴于点M 、N .设()32,2-+x x x D ,则()3,--x x M …………………………………3分∵ABC ACD ABCD S S S ∆∆+四边形= 136()622DM AN ON DM +⨯⨯+=+= ()[()]3232362+-----+=x x x629232+--=x x87523232+⎪⎭⎫ ⎝⎛+-=x ……………………………………5分∴当23-=x 时,四边形ABCD 面积有最大值875. 代数方法二:O BC AD N S S ∆∆++=S S N D CO A D CB 梯形四边形 =()()()()23332213232122+-++--++--+x x x x x x = 87523236292322+⎪⎭⎫ ⎝⎛+-=+--x x x ……………………………………5分∴当23-=x 时,四边形ABCD 面积有最大值875.几何方法:过点D 作AC 的平行线l ,设直线l 的解析式为b x y +-=.由⎩⎨⎧+-=-+=bx y x x y 322得:0332=--+b x x ………………………………3分当()03432=---=∆b 时,直线l 与抛物线只有一个公共点即:当421-=b 时,△ADC 的面积最大,四边形ABCD 面积最大 此时公共点D 的坐标为⎪⎭⎫⎝⎛--415,23 ………………………………4分 O BC AD N S S ∆∆++=S S N D CO A D CB 梯形四边形()312123321415321212121212121⨯⨯+⨯⨯+⨯⨯=⋅+⋅+⋅=⋅+++⋅=OCOB ON OC DN OA OC OB ON OC DN DN AN =875 ………………………………5分 即:当23-=x 时,四边形ABCD 面积有最大值875.(3)如图所示,由抛物线的轴对称性可求得B (1,0)∵以线段PB 为直径的圆与直线BC 切于点B∴过点B 作BC 的垂线交抛物线于一点,则此点必为点P . 过点P 作x PE ⊥轴于点E , 可证Rt △PEB ∽Rt △BOC∴BOOC PEEB =,故EB =3PE ,……………………………………………………6分设()32,2-+x x x P , ∵B (1,0)∴BE =1-x ,PE =322-+x x()32312-+=-x x x ,解得11=x (不合题意舍去),,3102-=x ∴P 点的坐标为: ⎪⎭⎫⎝⎛-913310,.………………………………………………7分。
石景山区2010—2011学年九年级上期末考试数学试卷及答案

石景山区2010—2011学年第一学期期末考试试卷初三数学第Ⅰ卷(共32分)一、选择题(本题共8道小题,每小题4分,共32分)在每道小题给出的四个备选答案中,只有一个是符合题目要求的,请把所选答案的字母填在下面的表格中. 1.如果4:7:2x =,那么x 的值是A .14B .78 C .67 D .722.正方形网格中,α ∠的位置如右图所示,则tan α的值是A .21B .552C . 5D . 23.在一个不透明的布袋中装有2个白球和3个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一球,摸到白球的概率是 A .51B .21 C .52 D .324.已知:ABC △中,︒=∠90C ,52cos =B ,15=AB ,则BC 的长是 A . 213B .293C .6D . 325.如图,AB 为O ⊙的直径,CD 为O ⊙的弦,︒=∠53ABD ,则BCD ∠为 A . ︒37 B .︒47 C .︒45 D . ︒536. 如图,平行四边形ABCD 中,E 为DC 的中点,DEF △的面积为2,则△ABF 的面积为α第2题图A .2B .4C .6D .87.函数y =bx +1(b ≠0)与y =ax 2+bx +1(a ≠0)的图象可能是8...已知:点....()m m A ,在反比例函数......xy 4=的.图.象上,点....B .与点..A .关于坐标轴对称,以.........AB ..为边作正方形,则满足条件的正方形的个数是....................A . 4B . 5C . 3D .8第Ⅱ卷(共88分)二、填空题(本题共4道小题,每小题4分,共16分) 9.已知()310cos 2=︒-α,则锐角α的度数是 °.10.将二次函数562-+-=x x y 化为()k h x a y +-=2的形式为 .11.已知:如图,⊙C 与坐标轴交于A (1,0)、B (5,0)两点,⊙C 的半径为3 则圆心C的坐标为 .第5题 第6题第11题 第12题A B CD第7题图12.如图,⊙O 的半径为2,4=OA ,AB 切⊙O 于B ,弦BC OA ∥,连结AC , 图中阴影部分的面积为 .三、解答题(本题共5道小题,每小题5分,共25分) 13.计算:︒+︒︒-60tan 45tan 60sin 12.14.如图,已知:Rt △ABC 中,90B ∠=,AB =BC=点D 为BC 的中点,求sin DAC ∠.15.如图,已知:射线PO 与⊙O 交于B A 、两点, PC 、PD 分别切⊙O 于点D C 、.(1)请写出两个不同类型的正确结论;(2)若12=CD ,21tan =∠CPO ,求PO 的长.16.如图,已知:双曲线(0)ky x x=>经过直角三角形OAB斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为)4,8(-,求点C 的坐标.17.正四面体各面分别标有数字1、2、3、4,正六面体各面分别标有数字1、2、3、4、5、6,同时掷这两个正多面体,并将它们朝下面上的数字相加. (1)请用树状图或列表的方法表示可能出现的所有结果; (2)求两个正多面体朝下面上的数字之和是3的倍数的概率.四、画图题(本题满分4分)18.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知,ABC △的顶点都在格点上,︒=∠90C ,8=AC ,4=BC ,若在边AC 上以某个格点E为端点画出长是52的线段EF ,使线段另一端点F 恰好落在边BC 上,且线段EF 与点C 构成的三角形与ABC △相似,请你在图中画出线段EF (不必说明理由).DCBA 第14题图第15题五、解答题(本题共4道小题,每小题6分,共24分)19.已知:二次函数c x ax y +-=42的图象经过点)8,1(-A 和点)7,2(-.(1)求该二次函数的解析式;(2)将该二次函数图象向左平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x 轴的另一个交点的坐标.20.如图,在某建筑物AC 上,挂着宣传条幅BC ,小明站在点F 处,看条幅顶端B ,测得的仰角为︒30,再往条幅方向前行20米到达点E 处,看条幅顶端B ,测得的仰角为︒60,若小明的身高约1.7米,求宣传条幅BC 的长(结果精确到1米).21.如图,已知:ABC △内接于⊙O ,AD 是⊙O 的切线,CO 的延长线交AD 于点D . (1)若∠B =2∠D ,求∠D 的度数;(2)在(1)的条件下,若34=AC ,求⊙O22.如图,有一座抛物线形拱桥,在正常水位时水面AB 的宽为20米,如果水位上升3米,则水面CD 的宽是10米.(1)建立如图所示的直角坐标系,求此抛物线的解析式;(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?第18题ACB第21题图六、解答题(本题满分6分)23.如图①,△ABC 中,90ACB ∠=︒,∠ABC =α,将△ABC 绕点A 顺时针旋转得到△AB'C ' ,设旋转的角度是β.(1)如图②,当β= °(用含α的代数式表示)时,点B '恰好落在CA 的延长线上;(2)如图③,连结BB ' 、CC ', CC ' 的延长线交斜边AB 于点E ,交BB '于点F .请写出图中两对相似三角形 , (不含全等三角形),并选一对证明.七、解答题(本题满分6分)24.已知:关于x 的一元二次方程03)3(22=++-+a x a ax 有两个实数根,且a 为非负整数.(1)求a 的值;(2)若抛物线3)3(22++-+=a x a ax y 向下平移()0>m m 个单位后过点 ()n ,1和点()12,2+n ,求m 的值;(3)若抛物线k a x a ax y +++-+=3)3(22上存在两个不同的点Q P 、关于原点对称,求k 的取值范围.八、解答题(本题满分7分)25.已知:抛物线c x ax y ++=22,对称轴为直线1-=x ,抛物线与y 轴交于点C ,与x 轴交于()0,3-A 、B 两点. (1)求直线AC 的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值; (3)P 为抛物线上一点,若以线段PB 为直径的圆与直线BC 切于点B ,求点P 的坐标.第22题图C 'B 'CBAFE C 'B 'CBA第23题① 第23题②第23题③ C 'B 'CBA石景山区2010-2011学年度第一学期期末考试试卷初三数学参考答案阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)二、填空题(本题共4道小题,每小题4分,共16分)9.40; 10.4)3(2+--=x y ; 11.()5,3; 12.32π. 三、解答题(本题共5道小题,每小题5分,共25分) 13.解:︒+︒︒-60tan 45tan 60sin 12=32332+- ……………………………………………………………4分 =325……………………………………………………………………5分 14. 解:过D 作AC DE ⊥于E ……………………………1分 在Rt △ABC 中,∵90B ∠=,AB =BC=,∴.45C ∠=…………………………………………2.................分. ∵点..D .为.BC ..的中点,.... ∴.12BD DC BC === ∴.AD ===........…………3.....分.在Rt △DCE 中,sin 451DE DC =⋅︒=………………………………4分∴.sin 10DAC ∠=…………………………5...........分. 15.解:(1)不同类型的正确结论有:①.PC ..=.PD .. ②.CD ..⊥.BA ..③∠..CEP ...=90° ...④∠..CPO ...=.∠.DPA ...⑤. ……2...分.(.2.)联结...OC ..∵.PC ..、.PD ..分别切...⊙.O 于点..D C 、∴.PC ..=.PD .., .∠.CPO ...=.∠.DPA ... ∴.CD ..⊥.AB .. ∵.CD=...12..∴.DE ..=.CE ..=.12CD ..=6....………………………3..........分.∵.21tan =∠CPO ∴.在.Rt ..△.EPC ...中. ,. PE=...12..∴.勾股得...36=CP ………………………4..........分. ∵.PC ..切.⊙.O 于点..C∴.90=∠OCPEDCBA在.Rt ..△.OPC ...中., . ∵.21tan =∠CPO ∴.21=PC OC ∴.33=OC∴.()()15336332222=+=+=PC OC OP ………………………………5.............分.16.解:由题意得:D (4,2)- ………………………1分∵双曲线经过点D∴24k -=∴8k =- ………………………2分 ∴8y x=-设点C ),8(n ………………………3分 ∴818n =-=- ………………………4分 ∴点C )1,8(- ………………………5分17. 解:(1)解法一:用列表法列表正确 …………………………………………………3分解法二:画树状图开始12 3 4 789 10六面体 4651 2 3 4 678 91 2 3 4 567 831 2 3 4 456 721 2 3 4 345 611 2 3 4 234 5四面体第18题第18题H画树状图正确 ………………………………………………………3分 (2)31248)3(==的倍数和为P ………………………………………………5分四、画图题(本题满分4分) 18.解:注:正确画出一条得2分,正确画出两条得4分. 五、解答题(本题共4道小题,每小题6分,共24分) 19.解:(1)由已知,抛物线过)8,1(-A 和点)7,2(-,得⎩⎨⎧=++-=+-78484c a c a ………………………1分 解这个方程组,得5,1-==c a∴ 所求抛物线的解析式为542--=x x y ………………………2分 (2)令0y =,则0542=--x x ………………………3分 解方程,得51=x ,21x =-. ………………………4分∴二次函数图象与x 轴的两个交点坐标分别为)0,5(和(10)-,.∴二次函数图象向左平移5个单位后经过坐标原点. ………………………5分 平移后所得图象与x 轴的另一个交点坐标为)0,6(- ………………………6分 20.解:过F 作BC FH ⊥于H ……………………………1分 ∵∠BFH =︒30,∠BEH =︒60,∠BHF =︒90 ∴∠EBF =∠EBC =︒30………………………2分 ∴BE = EF = 20 ………………………3分 在Rt △BHE 中, )(3.17232060sin m BE BH ≈⨯=︒⋅= ………………………4分 )(197.13.17m =+ ………………………5分答:宣传条幅BC 的长是19米.………………………6分 21.解:(1)如图,连结OA ……………………………1分∵AD 是⊙O 的切线 ∴︒=∠90OAD设D α∠=,则90DOA α∠=︒-,2B α∠=,4AOC α∠=………………2分∴︒=+-︒180490αα ∴︒=30α∴ ︒=∠30D …………………………3分 (2)解:OA OC =∵,︒==∠1204αAOC . ∴D ACO ∠=︒=∠30.∴=AD 34=AC . ……………………………5分 在Rt ADO △中,tan 43AO AD D =⨯∠==………………………6分 ∴⊙O 的半径是4.22.解:(1)设抛物线解析式为2ax y =………………………………………1分 设点),10(n B ,点)3,10(+n D ………………………………………………2分 由题意:⎩⎨⎧=+=an an 253100 解得⎪⎩⎪⎨⎧-=-=2514a n ………………………………………………3分∴2251x y -= ………………………………………………4分 (2)方法一:当3=x 时,9251⨯-=y ∵3)4(259>---.6 ………………………………………………5分 ∴在正常水位时,此船能顺利通过这座拱桥.…………………………………6分方法二: 当5246.3-=-=y 时,225152x -=- ∴10±=x∵310>± ......................................................5分 ∴在正常水位时,此船能顺利通过这座拱桥. (6)六、解答题(本题满分6分)23. 解:(1)90α︒+ ……………………………………………………………1分第21题图(2)图中两对相似三角形:①△ABB '∽△AC C ' ,②△ACE ∽△FBE ;……… 3分 证明①:∵△ABC 绕点A 顺时针旋转角β得到△AB 'C '∴∠CA C '=∠BAB '=β,AC=A C ' ,AB=AB ' ………………………………4分 ∴''AB AC AB AC = ……………………………………………………5分 ∴△ABB '∽△AC C ' ……………………………………………………6分证明②:∵△ABC 绕点A 顺时针旋转角β得到△AB 'C '∴∠CA C '=∠BAB '=β,AC=A C ' ,AB=AB ' ………………………………4分∴∠AC C '=∠ABB '=2180β- ………………………………5分 又∠A E C =∠FEB∴△ACE ∽△FBE ……………………………………………………6分七、解答题(本题满分6分)24.解:(1)依题意,得[]()0363634)3(22≥+-=+--=∆a a a a ……………1分 解得1≤a又0≠a 且a 为非负整数∴1=a ………………………………………………………………2分∴442+-=x x y(2)解法一:抛物线442+-=x x y 过点(1,1),(2,0),向下平移()0>m m 个单位后得到点 ()n ,1和点()12,2+n ……………………………3分 ∴()⎩⎨⎧=-=+-mn mn 1120, 解得3=m . ……………………………4分 解法二: 抛物线442+-=x x y 向下平移()0>m m 个单位后得:m x x y -+-=442,将点()n ,1和点()12,2+n 代入解析式得⎩⎨⎧+=-=-121n m n m …………………3分 解得3=m . ……………………………4分(3)设()00,y x P ,则()00,y x Q -- ……………………………5分∵Q P 、在抛物线k x x y ++-=442上,将Q P 、两点坐标分别代入得: ⎩⎨⎧-=+++=++-0020********y k x x y k x x ,将两方程相加得: 028220=++k x 即0420=++k x∵()044'≥+-=∆k ∴4-≤k当 4-=k 时,Q P 、两点重合,不合题意舍去∴4-<k . ……………………………6分八、解答题(本题满分7分)25.解:(1)∵对称轴122-=-=a x∴1a = ……………………………………………………1分∵()0,3-A∴3c =-设直线AC 的解析式为y kx b =+∵()0,3-A ,()3,0-C , 代入得: 直线AC 的解析式为 3--=x y ………………………………………2分(2)代数方法一: 过点D 作DM ∥y 轴分别交线段AC 和x 轴于点M 、N .设()32,2-+x x x D ,则()3,--x x M …………………………………3分 ∵ABC ACD ABCD S S S ∆∆+四边形=136()622DM AN ON DM +⨯⨯+=+= ()[()]3232362+-----+=x x x 629232+--=x x 87523232+⎪⎭⎫ ⎝⎛+-=x ……………………………………5分 ∴当23-=x 时,四边形ABCD 面积有最大值875. 代数方法二:OBC ADN S S ∆∆++=S S NDCO ADCB 梯形四边形=()()()()23332213232122+-++--++--+x x x x x x = 87523236292322+⎪⎭⎫ ⎝⎛+-=+--x x x ……………………………………5分 ∴当23-=x 时,四边形ABCD 面积有最大值875.几何方法:过点D 作AC 的平行线l ,设直线l 的解析式为b x y +-=.由⎩⎨⎧+-=-+=bx y x x y 322得:0332=--+b x x ………………………………3分 当()03432=---=∆b 时,直线l 与抛物线只有一个公共点 即:当421-=b 时,△ADC 的面积最大,四边形ABCD 面积最大 此时公共点D 的坐标为⎪⎭⎫ ⎝⎛--415,23 ………………………………4分 OBC ADN S S ∆∆++=S S NDCO ADCB 梯形四边形()312123321415321212121212121⨯⨯+⨯⨯+⨯⨯=⋅+⋅+⋅=⋅+++⋅=OC OB ON OC DN OA OC OB ON OC DN DN AN =875 ………………………………5分 即:当23-=x 时,四边形ABCD 面积有最大值875. (3)如图所示,由抛物线的轴对称性可求得B (1,0)∵以线段PB 为直径的圆与直线BC 切于点B∴过点B 作BC 的垂线交抛物线于一点,则此点必为点P . 过点P 作x PE ⊥轴于点E , 可证Rt △PEB ∽Rt △BOC ∴BO OC PEEB =,故EB =3PE ,……………………………………………………6分设()32,2-+x x x P ,∵B (1,0)∴BE =1-x ,PE =322-+x x()32312-+=-x x x ,解得11=x (不合题意舍去),,3102-=x ∴P 点的坐标为: ⎪⎭⎫ ⎝⎛-913310,.………………………………………………7分。
石景山区2011—2012学年第一学期期末考试试卷初三数学

CB AO EBA石景山区2011—2012学年第一学期期末考试试卷初三数学考 生 须 知1.本试卷共6页.全卷共五道大题,25道小题. 2.本试卷满分120分,考试时间120分钟.3.在试卷密封线内准确填写区(县)名称、学校、姓名和准考证号. 4.考试结束后,将试卷和答题纸一并交回.第Ⅰ卷(共32分)一、选择题(本题共8道小题,每小题4分,共32分)在每道小题给出的四个备选答案中,只有一个是符合题目要求的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.如图,在Rt △ABC 中,∠C =90°,BC =3,AC =2, 则tan B 的值是A .23B .32C .255D .21313第1题 第2题2.如图,⊙O 的弦AB =8,OE ⊥AB 于点E ,且OE =3,则⊙O 的半径是A .7B . 2C . 10D . 53.对于反比例函数2y x=,下列说法正确的是A .图象经过点(2,-1)B .图象位于第二、四象限C .图象是中心对称图形D .当x <0时,y 随x 的增大而增大 4.一枚质地均匀的正方体骰子,其六个面上分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字大于4的概率是 A .21 B .31 C .32 D .615.在平面直角坐标系中,将二次函数22x y =的图象向上平移2个单位,所得图象的解析式为A .222+=x y B .222-=x y C .2)2(2+=x y D .2)2(2-=x y 6.如图,在△ABC 中,DE ∥BC ,AD =2,AB =6,AE =3,则CE 的长为 A .9 B .6 C .3 D .4CBA P DyxCB A O F EDCBA第6题 第7题7.如图,若AD 是⊙O 的直径,AB 是⊙O 的弦,∠DAB =50°,点C 在圆上,则 ∠ACB 的度数是A .100°B .50°C .40°D .20° 8.如图,动点P 从点A 出发,沿线段AB 运动至点B .点P 在运动过程中速度大小不变.则以点A 为圆心,线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致是A B C D第Ⅱ卷(共88分) 二、填空题(本题共4道小题,每小题4分,共16分)9.如图,是河堤的横断面,堤高BC =5米,迎水坡AB 的坡比1:3(坡比是坡面的铅直高度BC 与水平宽度AC 之比),则AC 的长是 米. 10.已知抛物线2y ax bx c =++(a >0)过O (0,0)、A (2,0)、B (3-,1y )、C (4,2y )四点,则1y 2y (填“>”、“<”或“=”). 11.如图,有一边长为4的等边三角形纸片,要从中剪出三个面积相等的扇形,那么剪下的其中一个..扇形ADE (阴影部分)的面积为 ;若用剪下的一个扇形围成一个圆锥,该圆锥的底面圆的半径r 是 .第9题 第11题 第12题12.如图,⊙A 与x 轴交于B (2,0)、C (4,0)两点,OA =3,点P 是y 轴上的一个动点,PD 切⊙O 于点D ,则PD 的最小值是 .BA C ED CODBA 第8题三、解答题(本题共8道小题,每小题5分,共40分) 13.计算:030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.14.已知:函数5413-+=-x mxy m 是二次函数.(1)求m 的值;(2)写出这个二次函数图象的对称轴: ,顶点坐标: ; (3)求图象与x 轴的交点坐标.15.如图,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,∠EBC =45°,BE =6,CD =63,求∠DCB 的度数.16.如图,一次函数3y x =+的图象与x 轴、y 轴分别交于点A 、点B ,与反比例函数()04>=x xy 的图象交于点C ,CD ⊥x 轴于点D ,求四边形OBCD 的面积.17.如图,在△ABC 中,︒=∠90C ,点O 在BC 上,CD 为⊙O 的直径,⊙O 切AB于E ,若178==AB AC ,,求⊙O 的半径.EDCBA Dy xCB AO A O DE BC18.袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,记下编号.将两次编号作为数字求和.(1)请用树状图或列表的方法表示可能出现的所有结果; (2)求两次所取球的编号之和是偶数的概率.19.如图,河两岸a ,b 互相平行,C ,D 是河岸a 上间隔40米的两根电线杆,某人在河岸b 上的A 处,测得∠DAE =45°,然后沿河岸走了30米到达B 处,测得∠CBE =60°,求河的宽度(结果精确到1米,7.13,4.12≈≈ ).20.某超市按每袋20元的价格购进某种干果.销售过程中发现,每月销售量y (袋)与销售单价x (元)之间的关系可近似地看作一次函数:10500y x =-+(2050x <<).(1)当x=45元时,y= 袋;当y=200袋时,x= 元;(2)设这种干果每月获得的利润为w (元),当销售单价定为多少元时,每月可获得最大利润?最大利润是多少?四、解答题(本题共3道小题,每小题6分,共18分)21.如图,抛物线与x 轴交于A (1,0),B (3-,0)两点,与y 轴交于点C (0,3).(1)求此抛物线的解析式;(2)在x 轴上找一点D ,使得以点A 、C 、D 为顶点的三角形是直角三角形,求点D 的坐标.EDCBAa bθAA 'CBB '30︒B 'A 'CB A22. 如图, △ABC 中,以AB 为直径的⊙O 交AC 于点E ,OD ⊥AC 于D ,∠AOD =∠C .(1)求证:BC 为⊙O 的切线; (2)若32cos 12==C AE ,,求OD 的长.23.如图1,在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转30°,得到△A ′B ′C .联结A ′A 、B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′ 和S △BC B′.(1)直接写出S △ACA ′ ︰S △BC B′ 的值 ;(2)如图2,当旋转角为θ(0°<θ<180°)时,S △ACA ′ 与S △BC B′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含θ的代数式表示).图1 图2五、解答题(本题共2道小题,每小题7分,共14分) 24.已知函数232+-=x mxy (m 是常数).(1)求证:不论m 为何值,该函数的图象都经过y 轴上的一个定点; (2)若一次函数1+=x y 的图象与该函数的图象恰好只有一个交点,求m 的值及这个交点的坐标.25.如图,矩形'''O BC A 是矩形ABCO 绕点B 顺时针旋转得到的.其中点C O ,'在x 轴负半轴上,线段OA 在y 轴正半轴上,B 点的坐标为()3,1-.(1)如果二次函数()02≠++=a c bx ax y 的图象经过'O O 、两点且图象顶点M 的纵坐标为1-.求这个二次函数的解析式;(2)求边''A O 所在直线的解析式;(3)在(1)中求出的二次函数图象上是否存在点P ,使得D CO M PO S S ''3∆∆=,若存在,请求出点P 的坐标,若不存在,请说明理由.石景山区2011-2012学年度第一学期期末考试试卷初三数学参考答案阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)题 号 1 2 3 4 5 6 7 8 答 案ADCBABCC二、填空题(本题共4道小题,每小题4分,共16分)9.35; 10.>; 11.π32;31 12.22三、解答题(本题共8道小题,每小题5分,共40分) 13.解:132cos 60sin 45(tan 30)22+︒+︒-︒=12221222-+⨯+ (4)分=1223- (5)分14. 解:(1)m =1; ……………………………………………………………………1分(2)2-=x ;)9,2(--;……………………………………………………………3分(3)由0542=-+x x ,解得;5,121-==x x∴ ),,(,05)01(- …………………………………………………………5分15. 解:在Rt △BEC 中,∠BEC =90°,∠EBC =45°∴2622645sin =÷=︒÷=BE BC …………… ………………2分EDA在Rt △BDC 中,∠BDC =90°,232663cos ===∠BCDC DCB ……………… ……4分∴︒=∠30DCB ……………………………………………………………………5分 16.解:由题意:43x x+=…………………………………………………………1分 解得:121,4x x ==-(舍) ………………………………………………………3分∴C (1,4),又()3,0B …………………………………………………………4分()2714321=⨯+=OBCDS 四边形 (5)分17.解:联结OE (1)分在Rt △ABC 中,︒=∠90C ∵178==AB AC ,∴由勾股定理得15=BC …………………2分 又∵⊙O 切AB 于E∴︒=∠=∠90C BEO …………………3分 在Rt △BOE 和Rt △BAC 中 ∵C BEO ∠=∠ B B ∠=∠∴△BOE ∽△BAC …………………4分∴BABOAC OE =, 即 17158OE OE -= ∴524=OE …………………5分18. 解:(1)用列表法(树状图略):编号一和 编号二123AO DEBC1 2 3 4 2 3 4 5 34 5 6 (3)分(2)P=95 (5)分19.解:分别过A 作DC AM ⊥于M ,过C 作AB CN ⊥于N ……………………1分在Rt △CNB 中,∠CNB =︒90,∠CBN =︒60,设BN =x ,则CN =x 3 ………………………………………………………2分在Rt △DMA 中,∠DMA =︒90,∠DAM =︒45,DM =AM =CN =x 3 ………………………………………………………………3分∴x x 34030-=- (4)分解得≈x 14,x 3≈24 ……………………………………………………5分答:河的宽度约为24米.20.(1)当x=45元时,y=50袋;当y=200袋时,x=30元;………………………2分(2)由题意,得:w = (x -20)y=(x -20)(10500x -+) 21070010000x x =-+- (4)分352b x a=-=时,2250=最大y (5)分答:当销售单价定为35元时,每月可获得最大利润,最大利润是2250元. 四、解答题(本题共3道小题,每小题6分,共18分) 21.解:(1)设此抛物线的解析式为:))((21x x x x a y --=∵抛物线与x 轴交于A (1,0)、B ()0,3-两点, ∴)3)(1(+-=x x a y又∵抛物线与y 轴交于点C (0,3)∴3)30)(10(=+-a ,解得1-=a∴)3)(1(+--=x x y …………………………………………………………3分即322+--=x x y (2)有两种情况:当AC 是斜边时,显然点D 与点O 重合,即D (0,0); ………………4分当AC 是直角边时,过点C 作CD ⊥AC 交x 轴于点D ∵点A (1,0),点C (0,3) ∴OA =1,OC =3,由勾股定理AC =10 Rt △ACD 中∴ACOA CAD ADAC =∠=cos解得AD =10, ∴OD =9即:D (-9,0) ……………………………………………………………6分22.(1)证明:∵OD ⊥AC ∴∠ADO =90°又∵∠AOD =∠C ,∠A =∠A ∴∠ABC =∠ADO = 90°∴BC 是⊙O 的切线. ………………………………2分(2)解:∵OD ⊥AE ,∴D 为AE 中点∴1AD =AE=62 (3)分由2cos 3C =,可得5tan 2C = (4)分∴25tan tan ==∠=C DOA ODAD , (5)分∴1255O D =. ……………………………………………………………6分23.解:(1)S △ACA ′ ︰S △BC B′ = 9︰16 ; …………………………………………2分(2)S △ACA ′ 与S △BC B′ 的比值不变;证明:∵△ABC 绕点C 顺时针旋转角θ得到△A 'B 'C∴∠AC A '=∠BCB '=θ, …………………………………………3分AC=A 'C ,BC =B ' C ,∴CB C A BCAC ''=, (4)分∴△AC A '∽△BCB ', ……………………………………………………5分∴S △ACA ′ ︰S △BC B′ =(A C ︰BC )2= 9︰16. (6)分五、解答题(本题共2道小题,每小题7分,共14分) 24.解:(1)当x=0时,2y =.∴不论m 为何值,该函数图象过y 轴上的一个定点(0,2) (2)分(2)①当0m =时,函数232+-=x mx y 为一次函数23+-=x y ,令:123+=+-x x ,解得14x =, (3)分 ∴交点为(15,44);………………………………………………………………4分②当0m ≠时,函数232+-=x mxy 为二次函数.若一次函数1+=x y 的图象与函数232+-=x mxy 的图象只有一个交点,令2321mx x x -+=+,即2410m x x -+=,…………………………………5分由△=0,得4m =, ………………………………………………………………6分 此时交点为(13,22).………………………………………………………………7分25.解:(1)联结'BO 、BO ,由旋转知BO BO ='……………………………………1分OC BC ⊥∴OC C O =' ∵ ()3,1-B∴()()110,2'---,,M O ∴⎪⎩⎪⎨⎧=+--=+-=02410c b a c b a c ∴⎪⎩⎪⎨⎧===021c b a∴这个二次函数的解析式为:x x y 22+= ……………………………………2分(2)设()D y D A O BC ,1''-交于点与 显然CD O Rt D BA Rt ''∆≅∆ 在CD O Rt '∆中 ()2231y y -=+,解得34=y ………………………………………………3分∴⎪⎭⎫⎝⎛-341,D∴可求边O ’A ’所在直线的解析式为: 3834+=x y (4)分(3)由⎪⎭⎫⎝⎛-341,D ,易求323412121''=⨯⨯=⋅=∆CD C O S C DO若存在点P ,使得D CO M PO S S ''3∆∆=,则有23''==∆∆D CO M PO S S …………………………………………………………5分方法一(代数法):由()()110,2'---,,M O ,可得2:'--=x y l M O 设()x x x P 2,2+过P 作直线x PQ ⊥轴,交直线M O '于Q ,则()2,--x x Q ,''PQO PQM M PO S S S ∆∆∆-=()[]()[]()232121222122++=---⋅---+=x xx x x23'==∆DCOS即:4232=++x x ,解得2173±-=x∴⎪⎪⎭⎫ ⎝⎛-+-217721731,P , ⎪⎪⎭⎫⎝⎛+-2177217-32,P .…………………7分方法二(几何法): ∵()()110,2'---,,M O ∴ 1'==CM C O 在CM O Rt '∆中, 可求︒=∠=452''M CO M O ,设M PO '∆的边M O '上的高为h 则2221=⋅⋅h ,求得22=h过点'O 作M O '的垂线交y 轴于点E ,则︒=∠45'O EO 且2'=OO 在O EO Rt '∆中,2245cos 2'=︒=E O ,2=OE∴()2,0E ,2'=∆MEOS过点E 作M O '的平行线l 交抛物线于两点21,P P 则直线l 的解析式为2+-=x y解方程组⎩⎨⎧+=+-=x x y x y 222 得⎪⎪⎩⎪⎪⎨⎧-=+-=21772173y x 或⎪⎪⎩⎪⎪⎨⎧+=--=21772173y x ∴二次函数图象上存在点P ,使得D CO M PO S S ''3∆∆=, 且点⎪⎪⎭⎫ ⎝⎛-+-217721731,P ,⎪⎪⎭⎫⎝⎛+-2177217-32,P …………………………7分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
石景山区2009年初三第一次统一练习暨毕业考试数学试卷一、选择题(共8个小题,每小题4分,共32分) 在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上. 1.27的立方根是A .9B .3C .9±D .3±2.北京奥组委和国际奥委会在新闻发布上说:“中国有8亿4千万(840000000)人观看了奥运会开幕式,这确实是一个令人惊讶的数字.” 840000000这个数字用科学记数法可表示为A .90.8410⨯B .98.410⨯C .78410⨯D .88.410⨯3.如果两圆半径分别为3和4,圆心距为6,那么这两圆的位置关系是A .相交B.内切C .外离D .外切4. 在一个暗箱里,装有3个红球、5个黄球和7个绿球,它们除颜色外都相同,搅拌均匀后,从中任意摸出一个球是红球的概率是A .31 B .41 C .51 D .157 5x 的取值必须满足A .23->x B .23-≥x C .23>x D .23≥x 6. 某校初三(1A .45、44、44B .45、3、2C .45、3、44D .45、44、467. 已知:如图,在ABC ∆中,D 是AB 边上的一点,且AD BD 2=, 10=CD , 53sin =∠BCD ,则BC 边上的高AE 的长为 A .5.4 B .6C .8D .9第7题EA B CD8.若正方形网格中的每个小正方形的边长都是1,则把每个小格的顶点叫做格点.现有一个表面积为12的正方体,沿着一些棱将它剪开,展成以格点为顶点的平面图形,下列四个图形中,能满足题意的是DCBA二、填空题(共4个小题,每小题4分,共16分)9.分解因式:=++aaxax22.10.若关于x的方程0222=-+-aaxx有两个相等的实根,则a的值是.11.三角形纸片ABC中,55A∠=︒,75B∠=︒,将纸片的一角折叠,使点C落在ABC∆内(如图),则12∠+∠=_________°.12.将一副三角板如图放置,则上下两块三角板面积之比1A:2A等于________.三、解答题(共5个小题,每小题5分,共25分)13.计算:02)722(60sin41122-+︒-+--π.14.解不等式组⎩⎨⎧+<->-22413xxx,并把它的解集表示在数轴上.15.解方程:021211=-++-xxxx.16.已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得DFBE=,联结EC、FC.求证:FCEC=.FCDBA第16题A2A1第12题第11题17.已知062=-+x x ,求代数式7)1()1(22---+x x x x 的值.四、解答题(共2个小题,每小题5分,共10分)18.如图,等腰梯形ABCD 中,BC AD //,︒=∠45DBC ,翻折梯形ABCD ,使点B 与点D 重合,折痕分别交边AB 、BC 于点F 、E ,若2=AD ,8=BC . (1)求BE 的长;(2)求CDE ∠的正切值.第18题19.已知:如图,点A 是⊙O 上一点,半径OC 的延长线与过点A 的直线交于点B ,BC OC =,OB AC 21=. (1)求证:AB 是⊙O 的切线;(2)若︒=∠45ACD ,2=OC ,求弦CD 的长.A第19题五、解答题(本题满分6分)20.在我国,除夕之夜,全家一起看春节联欢晚会是人们传统的娱乐活动,尤其是小品类节目为我们带来了很多的欢乐.为了统计观众对2009年春晚小品类节目的喜好,中央电视台在网上进行了“2009年春晚我最喜爱的小品”调查问卷,并将统计结果绘制成两幅统计图,请你结合图中所给信息解答下列问题:(1)求参加调查的观众喜欢小品《暖冬》的人数占总投票人数的百分比; (2)求参加调查的观众喜欢小品《黄豆黄》的人数并补全条形图; (3)若北京市共有1200万人收看了春晚节目,请你估算北京市喜欢小品《不差钱》 的观众约有多少人?“2009年春晚我最喜爱的小品节目”调查结果条形统计图(单位:人)“2009年春晚我最喜爱的小品节目”调查结果扇形统计图(说明:A :《吉祥三宝》;B :《黄豆黄》;C :《水下除夕夜》; D :《北京欢迎你》;E :《暖冬》;F :《不差钱》)六、解答题(共2个小题,第21题4分,第22题5分,共9分)21.已知:如图,直角三角形AOB 的两直角边OA 、OB 分别在轴的正半轴和y 轴的负半轴上,C 为线段OA 上一点,OB OC =,且1>m )经过A 、C 两点.(1)求出A 、B 两点的坐标(可用含m (2)若AOB ∆的面积为2,求m 的值.22直线l ,在直线l 两边各放一粒跳棋子A 、B ,在图中1P 处有一粒跳棋子,1P 距A 点b 厘米、与直线l 的距离c厘米,按以下程序起跳:第1次,从1P 点以A 为对称中心跳至2P 点;第2次,从2P 点以l 为对称轴跳至3P 点;第3次,从3P 点以B 为对称中心跳至4P 点;第4次,从4P 点以l 为对称轴跳至1P 点. (1)画出跳棋子这4次跳过的路径并标注出各点字母(画图工具不限); (2)棋子按上述程序跳跃15次后停下,假设8=a ,6=b ,3=c ,计算这时它与 点A 的距离.第22题七、解答题(本题满分7分) 23.两个反比例函数xk y 1=和x ky 2=(021>>k k )在第一象限内的图象如图所示,动点P 在xk y 1=的图象上,x PC ⊥轴于点C ,交x ky 2=的图象于点A ,y PD ⊥轴于点D ,交xky 2=的图象于点B .(1)求证:四边形PAOB 的面积是定值;(2)当32=PC PA 时,求BPDB的值; (3)若点P 的坐标为(5,2),OA B ∆、ABP ∆的面积分别记为OAB S ∆、ABP S ∆,设ABP OAB S S S ∆∆-=.①求1k 的值;②当2k 为何值时,S 有最大值,最大值为多少?第23题八、解答题(本题满分7分) 24.已知:如图,半圆O 的直径cm DE 12=,在ABC ∆中,︒=∠90ACB ,︒=∠30ABC ,cm BC 12=.半圆O 以每秒cm 2的速度从左向右运动,在运动过程中,点D 、E 始终在直线BC 上.设运动时间为t (秒),当0=t (秒)时,半圆O 在ABC ∆的左侧,cm OC 8=.(1)当t 为何值时,ABC ∆的一边所在直线与半圆O 所在的圆相切?(2)当ABC ∆的一边所在直线与半圆O 所在的圆相切时,如果半圆O 与直线DE 围成的区域与ABC ∆三边围成的区域有重叠部分,求重叠部分的面积.第24题九、解答题(本题满分8分) 25.已知:如图(1),射线//AM 射线BN ,AB 是它们的公垂线,点D 、C 分别在AM 、BN 上运动(点D 与点A 不重合、点C 与点B 不重合),E 是AB 边上的动点(点E 与A 、B 不重合),在运动过程中始终保持EC DE ⊥,且a AB DE AD ==+. (1)求证:ADE ∆∽BEC ∆; (2)如图(2),当点E 为AB 边的中点时,求证:CD BC AD =+;(3)设m AE =,请探究:BEC ∆的周长是否与m 值有关?若有关,请用含有m 的代数式表示BEC ∆的周长;若无关,请说明理由.第25题(1) 第25题(2)石景山区2009年初三第一次统一练习暨毕业考试数学试卷参考答案及评分标准阅卷须知:1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分)三、解答题(共5个小题,每小题5分,共25分) 13. 解:02)722(60sin 41122-+︒-+--π 1|2341|324+⨯-+--= …………………………………3分1132324+-+--=4-=. …………………………………5分14. 解:由不等式413->-x ,得1->x . …………………………………1分 由不等式22+<x x ,得2<x . …………………………………2分 ∴ 原不等式组的解集是21<<-x . …………………………………3分 在数轴上表示为:…………………………………5分15. 解:去分母,得0)1(2)21)(1(=++--x x x x . …………………………………2分去括号,整理,得015=-x .解得 51=x . …………………………………4分 经检验,51=x 是原方程的根. …………………………………5分 所以,原方程的根为51=x .16.证明:∵ 四边形ABCD 是菱形,∴ DC BC =,ADC ABC ∠=∠.∴ FDC EBC ∠=∠. …………………2分 在EBC ∆和FDC ∆中,⎪⎩⎪⎨⎧=∠=∠=,,,DC BC FDC EBC DF BE ∴ EBC ∆≌FDC ∆. …………………………………4分 ∴ FC EC =. …………………………………5分17.解:7)1()1(22---+x x x x 7323-+-+=x x x x72-+=x x . …………………………………3分FC DBA第16题∵ 062=-+x x , ∴ 172-=-+x x .即 7)1()1(22---+x x x x 1-=. …………………………………5分 四、解答题(共2个小题,每小题5分,共10分)18. 解:(1)由题意得BFE ∆≌DFE ∆,所以,BE DE =.∵ 在BDE ∆中,BE DE =,︒=∠45DBE , ∴ ︒=∠=∠45DBE BDE .∴ ︒=∠90DEB .即BC DE ⊥. …………………………………1分 在等腰梯形ABCD 中,2=AD ,8=BC ,∴ 3)(21=-=AD BC EC . ∴ 5=BE . …………………………………3分 (2)由(1)得,5==BE DE .在DEC ∆中,︒=∠90DEC ,5=DE ,3=EC ,所以,53tan ==∠ED EC CDE . …………………………………5分19.(1)证明:如图,联结OA . …………………………………1分∵ BC OC =,OB AC 21=, ∴ OA AC BC OC ===.∴ ACO ∆是等边三角形. ∴ ︒=∠60O ,︒=∠60OCA . ∴ ︒=∠30B .∴ ︒=∠90OAB . …………………………………2分 所以,AB 是⊙O 的切线. …………………………………3分 (2)解:作CD AE ⊥于E 点. ∵ ︒=∠60O ,∴ ︒=∠30D .又︒=∠45ACD ,2==OC AC ,所以在ACE Rt ∆中,2==AE CE .在ADE Rt ∆中,∵ ︒=∠30D ,∴ 22=AD . 由勾股定理,可求6=DE . 所以,CE DE CD +=26+=. …………………………………5分第19题五、解答题(本题满分6分) 20. 解:(1)10%. ……………………2分 (2)340人,见右图.……………………4分 (3)约660万人. ……………………6分六、解答题(共2个小题,第21题4分,第22题5分,共9分)21. 解:(1)在抛物线m x m x y ++-=)1(2中,令0=y ,得0)1(2=++-m x m x , 解得1=x 或m x =(1>m ).所以,1=OC ,m OA =. ∵ OB OC =,∴ 1=OB .所以,A 点的坐标为(m ,0), …………………………………1分 B 点的坐标为(0,1-). …………………………………2分 (2)AOB ∆的面积OB OA S ⋅=21m 21=,所以,当2=S 时,4=m . …………………………………4分22. 解:(1)跳棋子跳过路径及各点字母如图. ………………3分 (2)跳跃15次后,停在4P 处, 过4P 作⊥C P 4AB ,垂足为C 点, 则C P 435136=-=;由7=AC ,∴ A P 4212844935==+=.…………………………………5分七、解答题(本题满分7分)23.(1)证明:设),(11y x A ,),(22y x B ,),(33y x P ,AOC ∆与BOD ∆的面积分别为1S ,2S ,矩形PCOD 的面积为3S .第22题由题意,得 121x k y =,222x k y =,313x k y =. ∴ 21112121k y x S ==,22222121k y x S ==,1333k y x S ==.∴ 21213)(k k S S S S PAO B -=+-=四边形.∴ 四边形PAOB 的面积是定值. …………………………………2分 (2)解:由(1)可知21S S =,则AC OC BD OD ⋅=⋅. 又∵ PC PA 32=, ∴ PC AC 31=. ∵ OC DP =,PC OD =,∴ DP BD 31=.∴21=BP DB . …………………………………4分 (3)解:①由题意知:101==P P y x k . …………………………………5分②A 、B 两点坐标分别为)5,5(2k A ,)2,2(2kB ,∴ )25)(52(212122k k BP AP S ABP --=⋅=∆. ∴ )25)(52(212102222k k k S S S ABP PAOB --⨯--=-=∆四边形. ∴ 222101k k S +-=. ∴ 当52=k 时,S 有最大值25. …………………………………7分 八、解答题(本题满分7分)24.解:(1)如图(1),当1=t 时,ABC ∆的AC 边与⊙O 相切; 如图(2),当4=t 时,ABC ∆的AB 边与⊙O 相切; 如图(3),当7=t 时,ABC ∆的AC 边与⊙O 相切;如图(4),当16=t 时,ABC ∆的AB 边所在直线与⊙O 相切.…………………………………4分 (2)由(1),可知,当4=t 和7=t 时,半圆O 与直线DE 围成的区域与ABC ∆第23题三边围成的区域有重叠部分,如图(2)、(3)的阴影部分所示,重叠部分的面积分别为29cm π和2)639(cm π+.…………………………………7分九、解答题(本题满分8分) 25.(1)证明:∵ EC DE ⊥,∴ ︒=∠90DEC .∴ ︒=∠+∠90BEC AED . 又∵ ︒=∠=∠90B A ,∴ ︒=∠+∠90EDA AED .∴ EDA BEC ∠=∠.∴ ADE ∆∽BEC ∆. …………………………………2分(2)证明:如图,过点E 作EF BC //,交CD 于点F ,∵ E 是AB 的中点,容易证明)(21BC AD EF +=. 在DEC Rt ∆中,∵ CF DF =,∴ CD EF 21=. ∴ )(21BC AD +CD 21=. ∴ CD BC AD =+. …………………………………5分(3)解:AED ∆的周长DE AD AE ++=m a +=,m a BE -=.设x AD =,则x a DE -=.∵ ︒=∠90A ,∴ 222AD AE DE +=.即22222x m x ax a +=+-.第24题(4)第24题(1)第24题(2)第24题(3) 第25题∴ am a x 222-=. 由(1)知ADE ∆∽BEC ∆,∴ 的周长的周长BEC ∆∆ADE BEAD =m a a m a --=222a m a 2+=. ∴ BEC ∆的周长⋅+=ma a 2ADE ∆的周长a 2=. ∴ BEC ∆的周长与m 值无关. …………………………………8分。
