中考数学切割线定理
切割线定理

定理
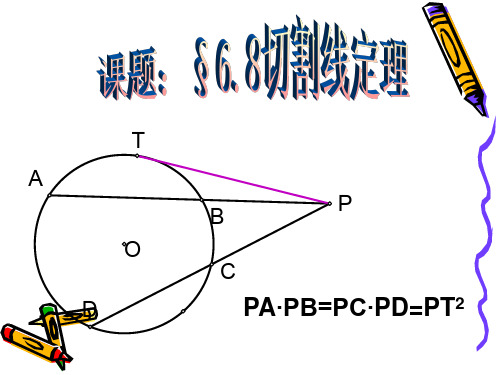
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幂定理的一种。
切割线定理示意图几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT 的平方=PA·PB(切割线定理)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线,PBA,PDC 是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT ∧2(平方)=PA·PB=PC·PD
证明
切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT^2=PA·PB
证明:连接A T, BT ∵∠PTB=∠PAT(弦切角定理) 切割线定理的证明∠P=∠P(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB:PT=PT:AP 即:PT^2=PB·PA
比较
相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。
一般用于求直线段长度。
2020年中考数学提优专题:《圆:切割线定理》(含答案)

《圆:切割线定理》知识梳理:(1)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT的平方=PA•PB(切割线定理)(2)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何语言:∵PBA,PDC是⊙O的割线∴PD•PC=PA•PB(切割线定理推论)(割线定理)由上可知:PT2=PA•PB=PC•PD.一.选择题1.如图,P是⊙O的直径BC延长线上一点,PA切⊙O 于点A,若PC=2,BC=6,则切线PA的长为()A.无限长B.C.4 D.2.如图,PT是⊙O的切线,T为切点,PBA是割线,交⊙O于A、B两点,与直径CT交于点D,已知CD=2,AD=3,BD=4,那么PB等于()A.6 B.C.7 D.203.设H为锐角△ABC的三条高AD、BE、CF的交点,若BC=a,AC=b,AB=c,则AH•AD+BH•BE+CH•CF 等于()A.(ab+bc+ca)B.(a2+b2+c2)C.(ab+bc+ca) D.(a2+b2+c2)4.如图,MN切⊙O于A点,AC为弦,BC为直径,那么下列命题中假命题是()A.∠MAB和∠ABC互余B.∠CAN=∠ABC C.OA=BC D.MA2=MB•BC5.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于()A.B.C.8 D.56.如图,AB是⊙O直径,AC是⊙O的弦,过弧BC 的中点D作AC的垂线交AC的延长于E,若DE=2,EC=1,则⊙O的直径为()A. B.C.5 D.47.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,AB=PC=2,则PD的长是()A.3 B.7.5 C.5 D.5.58.如图,已知⊙O的弦A B、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=cm,则PE的长为()A.4cm B.3cm C.5cm D.cm9.如图,⊙O1与⊙O2相交于A、B两点,PQ切⊙O1于点P,交⊙O2于点Q、M,交AB的延长线于点N.若MN=1,MQ=3,则NP等于()A.1 B.C.2 D.310.同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆上一点,GE、GF 分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为()A.①③B.②③C.③④D.②④二.填空题11.如图,AB为⊙O的直径,P点在AB的延长线上,PM切⊙O于点M.若OA=a,PM=,那么△PMB 的周长是.12.已知:如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=4,PB=8,则PA =,sin∠P=,CD=.13.如图,PA、PB与⊙O分别相切于点A、点B,AC 是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为.14.如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,若PA=6,PB=4,弧AB的度数为60°,则BC =,∠PCA=度,∠PAB=度.15.如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=.16.如图,AC为⊙O的直径,PA是⊙O的切线,切点为A,PBC是⊙O的割线,∠BAC的平分线交BC于D 点,PF交AC于F点,交AB于E点,要使AE=AF,则PF应满足的条件是(只需填一个条件).17.由⊙O外一点F作⊙O的两条切线,切点分别为B、D,AB是⊙O的直径,连接AD、BD,线段OF交⊙O 于E,交BD于C,连接DE、BE.有下列序号为①~④的四个结论:①BE=DE;②∠EBD=∠EDB;③DE∥AB;④BD2=2AD•FC其中正确的结论有.(把你认为正确结论的序号全部填上)三.解答题18.已知:如图,在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆.(1)求证:AC是⊙O的切线;(2)若AD=6,AE=6,求DE的长.19.如图,圆O是以AB为直径的△ABC的外接圆,D 是劣弧的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;(1)求证:OE=AC;(2)求证:;(3)当AC=6,AB=10时,求切线PC的长.20.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;(2)当∠BOP=30°,P点为的中点时,求D、E、F、P四个点的坐标及S△DEF.参考答案一.选择题1.解:∵PC=2,BC=6,∴PB=8,∵PA2=PC•PB=16,∴PA=4.故选:C.2.解:∵TD•CD=AD•BD,CD=2,AD=3,BD=4,∴TD=6,∵PT2=PD2﹣TD2,∴PT2=PB•PA=(PD﹣BD)(PD+AD),∴PD=24,∴PB=PD﹣BD=24﹣4=20.故选:D.3.解:AH•AD=AC•AE=AC•AB•cos∠BAE=(b2+c2﹣a2),同理BH•BE=(a2+c2﹣b2),CH•CF=(a2+b2﹣c2),故AH•AD+BH•BE+CH•CF=(a2+b2+c2).故选:B.4.解:∵BC是⊙O的直径,∴∠BAC=90°,∴∠MAB+∠CA N=90°;∵MN切⊙O于A,∴MA2=MB•MC,(故D错误)∠CAN=∠CBA,(故B正确)∴∠MAB+∠CBA=90°;(故A正确)∵OA是⊙O的半径,BC是⊙O的直径,∴BC=2OA;(故C正确)故选:D.5.解:∵3x2﹣10x+3=0,∴x=3(不合题意,舍去)或x=.∴cosD=AD:BD=1:3,设A D=x,则BD=3x.∴AB==2x,BC=2x﹣4.∴(2x)2=(2x﹣4)•x.∴x=0(舍去),或x=2.∴AB=2×2=8.故选:C.6.解:连接OD,∵点D是弧BC的中点,∴OD⊥BC,∠OFC=90°,AB是直径,∴∠ACB=90°,DE⊥AE,∴∠E=90°,∴四边形CFDE是矩形,∴∠ODE=90°,∴ED是圆的切线.作OG⊥AC,则OG=CF=ED=2.∵DE2=EC•AE,∴AE=4,AC=3,AG=,∴AO=,∴AB=5.故选:C.7.解:∵PA=3,AB=PC=2,∴PB=5,∵PA•PB=PC•PD,∴PD=7.5,故选:B.8.解:∵PA•PB=PC•PD,PA=4cm,PB=3cm,PC=6cm,∴PD=2;设DE=x,∵AE2=ED•EC,∴x(x+8)=20,∴x=2或x=﹣10(负值舍去),∴PE=2+2=4.故选:A.9.解:∵PN2=NB•NA,NB•NA=NM•NQ,∴PN2=NM•NQ=4,∴PN=2.故选:C.10.解:连接OK,∵EF切小圆于K,∴OK⊥EF,根据垂径定理得EK=FK,∵EP切小圆于P,FQ切小圆于Q,∴EP=EK,FQ=FK,∴EP=FQ,故③正确;∴由切割线定理得,FK2=FN•FG,EK2=EM•EG,∴FN•FG=EM•EG,故④正确;故选:C.二.填空题(共7小题)11.解:连接OM;∵PM切⊙O于点M,∴∠OMP=90°,∵OA=OM=a,PM=,∴tan∠MOP=MP:OM=,∴∠MOP=60°,∴OP=2a,∴PB=OP﹣OB=a;∵OM=OB,∴△OMB是等边三角形,MB=OB=a,∴△PMB的周长是(+2)a.12.解:∵PC切⊙O于点C,割线PAB经过圆心O,PC=4,PB=8,∴PC2=PA•PB.∴PA==2.∴AB=6.∴圆的半径是3.连接OC.∵OC=3,OP=5,∴sin∠P=.∴CE=,∴CD=.13.解:连接AD,OB,OP;∵PA、PB与⊙O分别相切于点A、点B,∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,∴∠AOP=60°,AP=AOtan60°=,∴PC=;∵PA2=PD•PC,∴PD=,∴CD=.14.解:∵PA2=PB•PC,PA=6,PB=4;∴PC=9,∴BC=5;∵弧AB的度数为60°,∴∠PCA=30°,∴∠PAB=30°.15.解:由切割线定理得PB•PA=PC•PD,则有8×20=PC(PC+6).解得PC=10.在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.从而AD是圆的直径.由勾股定理,得AD2=AC2+CD2=(PA2﹣PC2)+CD2=202﹣102+62=336.∴AD==4∴R=AD=2.故答案为2.16.解:∵∠PAC=90°,∠ABC=90°,∴90°﹣∠AFP=90°﹣∠BEP,∴∠APF=∠CPF,∴PF平分∠APC.17.解:∵BF,DF是⊙O的两条切线∴OF是∠DFB的角平分线,DF=FB,FO⊥BD,CD=CB∴=∴BE=DE(①正确)∵=∴∠EBD=∠EDB(②正确)∵FB切⊙O于B∴FB⊥OB∵BC⊥OF∵BC2=OC•FC∴(BD)2=OC•CE∵OC为△ABD的中位线∴OC=AD∴(BD)2=AD•CE∴BD2=2AD•FC(④正确)故其中正确的结论有①②④.三.解答题(共3小题)18.(1)证明:连接OE;(1分)∵⊙O是△BDE的外接圆,∠DEB=90°,∴BD是⊙O的直径,(不证直径,不扣分)∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,(2分)∴∠OEB=∠CBE,∴OE∥BC,(3分)∵∠C=90°,∴∠AEO=90°,∴AC是⊙O的切线;(4分)(2)解:∵AE是⊙O的切线,AD=6,AE=6,∴AE2=AD•AB,(5分)∴AB===12,∴BD=AB﹣AD=12﹣6=6;∵∠AED=∠ABE,∠A=∠A,∴△AED∽△ABE,(6分)∴;设DE=x,BE=2x,∵DE2+BE2=BD2,(7分)∴2x2+4x2=36,解得x=±(负的舍去),∴DE=2.(8分)19.(1)证明:∵AB为直径∴∠ACB=90°∴AC⊥BC又D为中点,∴OD⊥BC,OD∥AC,又O为AB中点,∴;(4分)(2)证明:连接CD,PC为切线,由∠PCD=∠CAP,∠P为公共角,∴△PCD∽△PAC,(6分)∴,又CD=BD,∴;(8分)(3)解:∵AC=6,AB=10,∴BC=8,BE=4,OE=3,∴DE=2,∴BD2=DE2+BE2=20,(9分)∴AD2=AB2﹣BD2=80,∴AD=4,(10分)CD=BD=2,由(2),∴,(11分)∴CP2=DP•AP=45×5,∴切线PC=15.(12分)20.(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)解:连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a,a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,过E作EM⊥x轴于M,∵AO切⊙O1于O,∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a,a),∵E(﹣a,a),D(﹣a,a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为:a,∴S△DEF=×a×a=a2.故答案为:D(﹣a,a),E(﹣a,a),F(﹣a,0),P(﹣a,);S△DEF=a2.。
切割线定理和割线定理

切割线定理和割线定理
切割线定理和割线定理是几何学中重要的概念,它们在解决几何问题和证明几何定理中起着至关重要的作用。
让我们来谈谈切割线定理。
切割线定理是指,如果一条直线与两条平行线相交,那么这条直线被称为切割线,它将平行线分割成相似三角形。
这个定理在解决三角形相似性问题时非常有用,通过切割线定理,我们可以证明两个三角形的某些角度相等,从而推导出它们是相似的。
接下来,让我们来看看割线定理。
割线定理是指,如果一条直线与一个圆相交,那么这条直线被称为割线,它将圆分割成两个不相交的部分。
割线定理在解决圆的性质和相关定理时非常重要,通过割线定理,我们可以推导出圆内角和弧的关系,以及切线与半径的垂直关系等。
总的来说,切割线定理和割线定理都是几何学中基础而重要的概念,它们为我们理解几何形状和解决几何问题提供了重要的线索。
通过运用切割线定理和割线定理,我们可以更好地理解几何学知识,推导几何定理,解决几何难题。
在实际应用中,切割线定理和割线定理也有着广泛的应用。
比如在建筑设计中,我们需要根据建筑物的不同形状和结构来设计合适的切割线和割线,以确保建筑物的稳固和美观。
在工程测量中,切割
线和割线也经常被用来确定地表的坡度和地势的高低,为工程施工提供重要的参考依据。
总的来说,切割线定理和割线定理是几何学中重要的概念,它们在理论研究和实际应用中都具有重要意义。
通过深入理解和应用切割线定理和割线定理,我们可以更好地掌握几何学知识,解决实际问题,推动科学技术的发展。
希望通过本文的介绍,读者能对切割线定理和割线定理有更深入的了解,进一步探索几何学的奥秘。
切割线定理的证明

切割线定理的证明切割线定理,也被称为Severi's定理或Sokhotski–Plemelj定理,是复变函数理论中的一个重要定理。
它描述了圆周上的切割线是满足特定条件的函数的积分路径。
首先,我们先来了解一下切割线的概念。
在复平面上考虑一个圆周C,设C的圆心为a,半径为r。
我们将这个圆周与平面割开,然后选择一个切割线L,使得它与圆周C只有一个交点。
切割线L可以看作是一个无限细长的线,在我们的讨论中,我们主要关注切割线与圆周交点的位置。
切割线定理可以被描述为:如果f(z)是一个在圆周C内解析的复变函数,那么对于切割线L上的任意点z0,方向由内指向外,切割线对应的复函数f(L)在点z0处的值可以通过下面的积分得到:f(L) = \frac{1}{2πi}\int_{C}\frac{f(z)}{z-z_0}dz其中,f(z)是圆周C内的解析函数,z0是切割线L上的点,C是切割线L与圆周C之间的路径。
这个定理的证明可以按照以下步骤进行。
首先,我们可以将切割线L与圆周C之间的路径C分为两段:一段位于切割线L外部,另一段位于切割线L内部。
接下来,我们需要通过引入一个小的参数ε来表示L的位置。
当我们让ε趋近于零时,切割线L就会趋近于圆周C上的一个点。
在圆周C上选择一个点Z,通过C上的路径积分,我们可以得到f(L)在点Z处的值。
根据留数定理,我们可以将路径积分转换为圆周C 内的留数求和。
但是由于该定理的前提条件是f(z)是圆周C内的解析函数,因此留数求和等于零。
因此,我们得到了f(L)在点Z处的值为零。
接下来,我们将点Z沿着圆周C移动至点z0处。
根据解析函数的性质,在点Z和点z0之间的圆周C上,函数f(z)也是解析的。
因此,我们可以得到f(L)在点z0处的值也为零。
最后,我们让点z0沿着切割线L变动。
根据切割线L的定义,我们可以观察到f(L)在点z0处的值是连续变化的。
根据复变函数理论中的连续性原理,我们可以得出结论:f(L)在点z0处的值是切割线L上所有点值的极限。
切割线定理公式及证明

切割线定理公式及证明
切割线定理公式:假设$V=\{v_i\}_{i=1}^{n}$是多边形$P$的一个顶点集合,$L=\{l_i\}_{i=1}^{n}$是从$v_1$出发,从$v_i$开始绕$P$沿顺时针方向绕一圈,途经定点$v_{i+1}$与$v_i$之间的一条射线,则定理结论如下:将射线$L$在多边形$P$内部切割,给出的n段子线段的总长度
T(L)与多边形面积S(P)满足:
$T(L)=2S(P)$
证明:
考虑多边形$P$包围面积S(P)中最后一个三角形,设其三个顶点分别为$v_i,v_{i+1},v_{i+2}$,以$v_i,v_{i+1}$为基线,$v_{i+2}$为外顶点。
将射线$l_i$投射到$v_i,v_{i+1}$的基线上,形成一个新的顶点
$v'_{i+2}$,由$v_i,v'_{i+2}$组成的新的三角形,与原来的三角形
$v_i,v_{i+1},v_{i+2}$完全相同,只不过替换了一个顶点,而新三角形的面积仍然为S(P),且$v'_{i+2}$是射线$l_i$与多边形$P$之间的一个公共点,即射线$l_i$将多边形$P$内部切割,形成了两段新线段,令这两段新线段为$s_1$与$s_2$,则有:
$T(L)=s_1+s_2=2S(P)$
因此,得证切割线定理。
切割线定理推论

切割线定理推论切割线定理是高等数学中非常重要的一个定理,其在数学和物理学中都有广泛的应用。
本文将从切割线定理的定义、推论以及实际应用等方面进行阐述。
一、切割线定理的定义切割线定理是指:若一曲线上有一点P,并且该曲线在P点处有一条切线,那么该曲线可以被这条切线分成两部分,其中一部分包含点P,而另一部分则不包含点P。
二、切割线定理的推论1.推论一若一曲线上有一点P,并且该曲线在P点处有一条切线,那么该曲线在P点处的斜率等于该曲线在P点处的切线的斜率。
2.推论二若一曲线上有一点P,并且该曲线在P点处有一条切线,那么在点P处,该曲线的导数等于该曲线在P点处的切线的斜率。
3.推论三若一曲线上有一点P,并且该曲线在P点处有一条切线,那么在点P处,该曲线的凹凸性与该曲线在P点处的切线的斜率变化的方向相同。
三、切割线定理的实际应用切割线定理在实际应用中有着广泛的应用,下面介绍几个具体的实例。
1.曲线的最大值和最小值通过对曲线进行分割,可以确定曲线的最大值和最小值。
具体的方法是,找到曲线的拐点,然后将拐点作为切割线,从而得出曲线的最大值和最小值。
2.曲线的优化在工程和科学研究中,经常需要对曲线进行优化,以达到最佳效果。
通过切割线定理,可以找到曲线的拐点,从而确定曲线的优化方向。
3.曲线的积分在计算曲线的积分时,切割线定理也有着重要的作用。
通过将曲线进行分割,可以将曲线的积分分为多个小段,从而更加方便地进行计算。
切割线定理是高等数学中非常重要的一个定理,其具有广泛的应用。
通过对切割线定理的理解和应用,我们可以更好地理解和掌握高等数学的知识,为实际应用提供更加准确和有效的数学支持。
初中数学重点梳理:切线和割线

切线和割线知识定位切割线定理是初中平面几何中的重要定理,它应用广泛,各地的中考题有相当多的题目都用到它,竞赛题也不例外.且题目新颖,灵活多变,学生往往甚感困难。
因此有计划、有目的、有步骤地对切割线定理进行补充、演化无疑是十分有益的。
知识梳理知识梳理1:切割线定理切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幂定理的之一。
几何语言:∵PT切⊙O于点T,PDC是⊙O的割线∴PT²=PD·PC(切割线定理)知识梳理2:割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线,PBA、PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT²=PA·PB=PC·PD例题精讲【试题来源】【题目】如图,等边三角形ABC中,边AB与⊙O相切于点H,边BC,CA与⊙O交于点D,E,F,G。
已知AG=2,GF=6,FC=1.则DE=_______.【答案】21【解析】2由切割线定理可知16:4又AH AG AF,AHAC AG=•=∴==2又99故5则25又7,9,AC AG GF FCAB ACBHBD BE BHCE CD CF CG BC AC=++=∴===•==•=•===【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,⊙O和⊙O′都经过点A和B,PQ切⊙O于P,交⊙O′于Q,M,交AB的延长线于N.求证:2PN MN NQ=⋅.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,已知点P是O外一点,PS,PT是O的两条切线,过点P作O的割线PAB,交O于A.B两点,并交ST于点C,求证:1111()2PC PA PB=+.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC。
九年级数学切割线定理

B
推论: 如果弦与直径垂直相交,那么弦的一半
是它分直径所成的两条线段的比例中项. PC2=PA· PB
• 练习 : ⊙o的弦 CD平分AB于P, 且AB=12cm,CD=13cm • 试求: PC 和 PD 的长.
A
C P •O
B
D
A
D P • C
PA · PB = PD · PC
B
G
O•
F
思考题: 若延长PE交圆O于F,BF交CD于G 求证: PC•BG=PD • BC
C
交端×交端=交端×交端
PA· PB = PD· PC 相 交 弦 定 理 PT2 =PA· PB 切 割 线 定 理
PA AB PC CD 2 PT PA AB
PC· PD =PA· PB
P
PM· PN =PC2
练习四:如图,圆o1和圆o2都经过点A和 B,点P在BA
的延长线上。过点P作圆O1的切线PC切圆O1于C,作 圆O2的切线PD切圆O2于D。求证:PC =PD。
B o1 • A C
o2
•
D
P
是BA的延长线上一点。PC,PD,PE …分别与圆o1,圆o2,圆 o3 …相切于C,D,E … ,求证:C,D,E … 在同一个圆上。
T
练习一: 如下图,圆o的两条弦AB和CD相交于点E,AC和DB 的延长线交于P,下列结论成立的是( D ). (A) PC • CA=PB • BD (B) CE • AE=BE • ED (C) CE • CD=BE • BA (D) PB • PD=PC • PA
PA· PB = PD· PC
PB = 4
切割线定理的证明

切割线定理的证明引言切割线定理是数学中的一个重要定理,它在几何学和分析学中有广泛的应用。
本文将详细探讨切割线定理的证明过程,以及其在不同领域中的应用。
切割线定理的定义在数学中,切割线定理是指:对于任意一个凸多边形,存在一条直线,将该多边形分割成两个面积相等的部分。
证明过程证明切割线定理的过程如下:步骤一:连接多边形的两个不相邻的顶点首先,我们连接多边形的两个不相邻的顶点,得到一条直线。
步骤二:计算两边的面积我们计算连接线两边的面积。
设连接线两边的长度分别为a和b,相应的面积分别为S1和S2。
步骤三:判断面积大小判断S1和S2的大小。
如果S1等于S2,则证明切割线定理成立。
如果S1不等于S2,则我们需要调整连接线的位置。
步骤四:调整连接线的位置调整连接线的位置,使得S1和S2的面积尽可能接近。
我们可以通过改变连接线的倾斜角度或者位置来实现。
步骤五:重新计算面积重新计算连接线两边的面积,并判断它们是否相等。
如果相等,则证明切割线定理成立。
如果不相等,则继续调整连接线的位置,重复步骤四和步骤五,直到找到满足条件的连接线。
切割线定理的应用切割线定理在几何学和分析学中有广泛的应用。
以下是一些常见的应用场景:圆的切割线在圆的几何中,切割线定理可以用来证明圆内任意两点之间连线的长度小于等于圆的直径。
多边形的分割切割线定理可以用来将一个凸多边形分割成两个面积相等的部分。
这在计算几何学中有重要的应用,例如计算多边形的重心或者质心。
积分的应用在分析学中,切割线定理可以用来证明积分的性质。
通过将函数曲线分割成两个等面积的部分,可以推导出积分的对称性和平均值定理等重要结论。
优化问题切割线定理可以用来解决一些优化问题。
例如,在给定一定面积的情况下,如何找到一个凸多边形使得周长最小,或者如何找到一个凸多边形使得某个属性的值最大化。
总结切割线定理是数学中的一个重要定理,它可以用来将一个凸多边形分割成两个面积相等的部分。
本文通过详细的证明过程和应用场景的介绍,希望读者对切割线定理有更深入的理解。
中考数学切割线定理

【课堂练习】
1.已知 、 分别切 于 、 , 是劣弧 上任意一点,过 作 的切线和 、 分别交于 、 ,若 , 半径为 ,则 的周长为()
A. B. C. D.不确定
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
4.弦切角定理:弦切角等于其所夹的弧所对的圆周角;
5.切割线定理:已知 中, 切 于 ,割线 交 于 ,则有 。证明方法:连结 、 ,证:
6.切割线定理推论:已知 、 为 的两条割线,交 于 、 ,则有 ,证明方法:过 作 切 于 ,用两次切割线定理。
【经典例题】
【例1】已知:如图, 切圆于 , 为圆直径, , , 。求 的长。
【例2】如图所示, 中, ,以 为直径的 交 于点 ,切线 交 于 。求证: 。
【例3】如图所示, 、 是 的切线, 、 为切点, 于 ,交 于 ,求证: 。
【例4】已知, 为 的直径,过 点作 的切线 , 交 于点 , 的延长线交 于 。
9.已知:如图, 与 切于 , 为直径, , 为 一弦。求 与 的度数。
10.已知: , 与 分别切于 、 两点,延长 到 ,使 ,求证: 。
【课外练习】
1. 切 于 , 是过 点的割线,且 ,则 的度数为()
A. B. C. D.
2.过 外一点 引圆的两切线 、 , 、 是切点, , ,则 半径的长为()
5. 、 分别切 于 、 , 交 于 ,连结 、 ,则圆中的直角三角形共有()个
A.3B.4C.5D.6
6.已知:如图1,直线 切 于 点, , ,那么 ____.
7.已知:如图2,直线 与 相切于点 , 为 直径, 于 , ,则 ____.
九年级数学切割线定理

例3 已知:如图, ⊙O的割线PAB交
解:设⊙O的半径为r,PO和它的延长线交⊙O于
C、D,由切割线定理的推论,有:
⊙O于点A和B,PA=6cm,AB=8 cm, PO=10.9cm,求⊙O的半径。
PA· PB = PD· PC
PA=6 PB=6+8=14 PC=10.9-r
8
10.9
切 割 线 定 理
四川省阆中东风中学校
宋兴军
D
已知:线段a,b. 求作:线段c,使c2=ab.
A
c
a B b C
反思:这个作图题是作两
已知线段的比例中项的问 题,可以当作基本作图加 以应用.请同学们想一想, 这到题还有别的作法吗?
C
c
A
O
a
D
b
B
相交弦定理: 圆内的两条相交弦, 被交点分成的两条线段长的积相 等. PA· PB = PD· PC
B
G
O•
F
思考题: 若延长PE交圆O于F,BF交CD于G 求证: PC•BG=PD • BC
C
交端×交端=交端×交端
PA· PB = PD· PC 相 交 弦 定 理 PT2 =PA· PB 切 割 线 定 理
PA AB PC CD 2 PT PA AB
PC· PD =PA· PB
PT2 =PA· PB
PC· PD =PA· PB
练习二:
• 1. 过圆O外一点P, 作两条割线PAB和PCD, 已知PA=1, PB=3, PC=0.6。则CD= ? CD = 4.4 • 2。 已知PT切圆O于T,PAB为圆O的割线, PA : AB =1 : 3 , PT=2 , 则PB= ?
初中数学课件《切割线定理》
E D
解:(1)由切割线定理,得 PE2=PC ∙ PD=PA ∙ PB ∵AB=3cm,PA=2cm ∴PB=AB+PA=5(cm) ∵CD=4cm ∴PD=PC+CD=PC+4 ∴PC(PC+4)=2X5 化简,整理得:PC2+4PC−10=0
解得: PC 2
14
( 负数不合题意,舍去)
B
已知:(如图)点P为⊙O外一点,PC切 ⊙O于点C,割线PBA 交⊙O于A、B 求证:PC2=PA∙PB
C P A O B
切割线定理: 从圆外一点引圆的两切线和条割线,切 线长是这点到割线与圆的交点的两条线段长 的比例中项。
证明: 连接AC、BC, ∵PC切⊙O于点C ∴∠B= ∠PCA, 又 ∠P=∠P ∴ △PCA∽ △ PBC ∴ PC :PA=PB :PC ∴PC2= PA∙PB
A B
P
割线PCD、PAB交⊙O于点C、D和A、B => PA∙PB=PC∙PD
已知:(如图)过⊙O外一点P作两条割线,分别交 ⊙O 于点A、B和C、D,再作⊙O的切线PE,E为切点, 连接CE、DE。 已知AB=3cm,PA=2cm,CD=4cm. (1)求PC的长 (2)设CE=a,试用含a的代数式表示DE。
T A B O C D P
PA∙PB=PC∙PD=PT2
复习: 1、如图在⊙O中弦AB、CD相交于点P,则有 怎样的结论? 答:PA ∙ PB=PC ∙ PD 怎样证明上述结论? 答:连接BC、AD证明 A △PBC∽ △ PDA 2、设OP=d、 ⊙O 的半径为r 则PA ∙ PB=PC ∙ PD的值 D 为多少? 答:PA ∙ PB=PC ∙ PD=r2—d2
切割线定理

P DB
(1)如图⊙O1与⊙O2相交于A、B两点,P是 AB的延长线上的一点,过P点的割线分
别与⊙O1、⊙O2交于D、C;E,F。 试判断PD•PC是否和PF•PE相等。
为什么?
F
.
O1
.O2
E
CA
(2)如图A、B是⊙O割线上的两点,AS切 ⊙O于S,BT切⊙O于T。若AC=BD,则AS和TB 有什么关系?
由切割线定理,得PE2=PA•PB
∴PE2= 2×5=10 ∴PE= 10(cm).
由切割线定理推论得,PC•PD=PA•PB
∴x(x+4)=2×5
化简,整理得 x2+4x-10=0
解得 x= - 2 ± 14(负数不合题意,舍去)
∴ x= ( 14-2)(cm) 答:PC长是PC=( 14- 2)cm
(3) 若PT=2,PA=4,BT=1则AT= 2 .
PT切圆O于T PT2=PB•PA
P
1
2
B
D
6
1
3
5 •O
2.过圆外一点P引圆的两条割线分别与圆 交于 A、B和C 、D两点. (1)若PA=6,PB=1,PD=2则PC= 3 .
(2)若AB=5,PB=1,PC=3则PD= 2 .
C (3)若PA=6,PD=2,BD=1则AC=
例1 如图过圆外一点P作两条割线,分别交⊙O于A、B和C、D.再作⊙O 切线PE,E为切点,连结CE、DE.已知AB=3cm,PA=2cm,CD=4cm
. (2) 设CE=a,试用含a的代数式表示DE
B
3
4
D
A2
x
C
10
a
E
解: 由弦切角定理,得∠CEP= ∠D
人教版九年级数学课件:切割线定理

作
业
PT2 =PA· PB 切 割 线 定 理
PT =PB· BA × PA· = PD· AB CD
2
PC· =PA· PD PB
切 割 推 线 定 论 理
×
作业 P132
11 , P133 12 ,13.
PT2 =PA· PB
PC· =PA· PD PB
练习二:
1.
过圆O外一点P, 作两条割线PAB和PCD, 已知PA=1, PB=3, PC=0.6.则CD= ? CD = 4.4 2.
已知PT切圆O于T,PAB为圆O的割线, PA : AB =1 : 3 , PT=2 , 则PB= ?
PB = 4
法二: 连接CD ,射影定理. A D •O
BC2=BD•BA
Rt△ABC中 AC=3; BC=4. BD=3.2 (cm) AB=5 BC=4
B
C
提高题:如图,PA切圆O于A,PBC是圆O的割线,D是
PA的中点,DC交圆O于E. 求证:1)PD2=DE•DC;2) ∠1= ∠C.
分析: 1. PD=DA
PA· = PM· PB PN
P
PM· =PC2 PN
练习四:如图,圆o1和圆o2都经过点A和 B,点P在BA
的延长线上.过点P作圆O1的切线PC切圆O1于C,作 圆O2的切线PD切圆O2于D.求证:PC =PD.
B o1 • A C
o2
•
D
P
提示:PC = PD = PE …
B o1 • A D E P o2 • o3•
P P
D 1
E
A
且DA2=DE • DC 2. PD:DE=DC:PD ∠ PDE= ∠ CDP 则: △PDE∽ △CDP 从而: ∠ 1= ∠ C
中考数学知识考点整理:定理、公式4_考点解析

中考数学知识考点整理:定理、公式4_考点解析
中考数学知识考点整理:定理、公式4
1切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项
2 推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等
3 如果两个圆相切,那么切点一定在连心线上
4 定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
5 同角或等角的余角相等
6过一点有且只有一条直线和已知直线垂直
7 直线外一点与直线上各点连接的所有线段中,垂线段最短
8 两直线平行,内错角相等
9 定理1:关于某条直线对称的两个图形是全等形
10 定理2:如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线。
初三数学切割线定理(“定理”相关文档)共7张

讲课人:王兆群
复习:相交弦定理:
弦AB, CD相交于P AP•BP=CP•DP
B C
P
A
D
AP•BP=CP•DP
(2)已知:PAB是圆O的割线,
PAAP=•B4P,=CPPT=•D6P,
则PA圆=4O,的P面T积=6=,
。
A则P圆•BOP的=C面P积•D=P
。
(31)已知PATB是、圆POC的D是切圆线O,的割线,
B
PA=6 ,AB=4 ,PO=
D A O
(3)已知PT是圆O的切线,
T
PA=4, PT=6 , 则圆O的面积=
O
。
A P
C
P
P
例3 已知:弦AB 、CD相交于E,过点E作BC的平行 线PE交AD延长线于点P,PG与圆O相交于点G 求证:PG=PE
P
D G
A
B
E
C
(12)已知P:APBA、BP是C圆DO是的圆割O线的,割线,
(AP2•)BP已=知CP:•DPPAB是圆O的割线,
(3)已知PT是圆O的切线,
弦AB, CD相交于P
切割线定理的应用
例1 、 填空
B
(1)已知PAB、PCD是圆O的割线,
PA=3 , AB==5 CD=2,则PC=
(2)已知:PAB是圆O的割线,
(PA2=)4,已知PT:=6PA,B是圆O的割线,
(AP1•)BP已=知CPP•ADBP、PCD是圆O的割线,
APAP=•B4P,=CPPT=•D6P,
(PA2=)6 已,知AB:=P4A,BP是O圆=1O0的,割线,
(则3圆)O已的知面P积T=是圆O的切线,。
P(A2=)4,已知PT:=6PA,B是圆O的割线,
初中数学课件《切割线定理》

切割线定理的相关概念介绍
为了帮助大家更好地理解切割线定理,我们在这里先来介绍一下它的相关概念。
扇形
扇形是圆心角对应的圆弧及其 圆心所组成的图形,它是切割 线重要概念。
弓形
弓形指的是圆上一个扇形所截 下来的圆弧部分,是能够帮助 我们理解切割线定理的重要概 念。
弦长
弦是连接圆上两点的线段,弦 长是线段长度,是切割线定理 中常用的量。
解决切割线定理中的常见错误和误区
学习切割线定理的时候,常见错误和误区包括对图形理解不够溜,计算公式没有掌握好,套路不熟练等 等,下面是一些错误率较高的问题。
• 画图不规范,不能很好地说明切线、割线、交点的位置关系 • 公式记忆不清,导致计算错误 • 理解不深刻,只会套用公式,难以发挥应有的思考能力
切割线定理在各国数学教育中的地位
切割线定理作为数学中非常重要的一个知识点,它在不同国家的数学教育中都占据着重要地位,是不容 忽视的。下面介绍几个国家中切割线定理的教学情况。
• 中国:在初中阶段的几何课程中必须学习切割线定理。 • 美国:在高中阶段的几何学里也会涉及切割线定理的知识点。 • 日本:从小学到高中,切割线定理都是几何学习的重点。
具体表述
具体来说,若AB与CD是两条割线,交于点E,那么∠AEB=∠CED,∠BEC=1/2∠BAD。
套路示范
判断两条线段是否相互垂直的时候,可以用切割线定理进行证明。
切割线定理的含义和意义
切割线定理是数学中一条很重要的定理。它在几何解题中的应用非常广泛,可以帮助我们更好地理 解和应用各种几何概念。
切割线定理的进阶应用
掌握好了切割线定理的基础知识之后,还可以进一步拓展应用,例如: • 推导出更复杂的几何公式 • 应用切割线定理解决更高级的几何问题 • 将切割线定理与其他定理的知识点相关联,挖掘其更多潜力
切割线定理公式及证明

切割线定理公式及证明【公式】切割线定理可以表示为以下比例关系:设有两条平行线L和M,一条切割线N与这两条平行线相交,相交点分别为A、B、C。
那么,切割线N所生成的线段AB与AC的长度之比等于线段BC与AC的长度之比,即:AB/AC=BC/AC【证明】为了证明切割线定理,我们可以通过几何方法或代数方法来进行证明。
下面将给出一种几何方法证明的详细步骤。
1.设有两条平行线L和M,一条切割线N与这两条平行线相交,相交点分别为A、B、C。
2.连接线段AC和BC,使得△ABC成为一个三角形。
3.观察△ABC,我们可以发现该三角形有两个平行边AB和MN,因此,在△ABC中可以使用平行线性质来进行推导证明。
4.运用同位角性质,我们可以得到角ABN=ABC,角BCA=ACN,并且这两个角是同位角。
5.根据相交线与平行线的同位角性质,我们可以得到三角形△ABN和△ACN的两个角是对应角,即角ABN=ANB,角ACN=ANC。
6.观察△ABN和△ACN,我们可以得出结论,这两个三角形相似(AA相似性质),因为它们有一个对应角相等,且由于线段AB和AC平行,所以角BAN=CAN。
7.根据相似三角形的性质,我们可以得到△ABN和△ACN的边长之比等于对应边长之比,即AB/AC=AN/AN。
8.由于AN=AC+CN,可将上式作进一步化简,得到AB/AC=AC/AC+CN/AC。
9.同理,通过相似三角形的性质,我们可以得到△BCN和△ACN的边长之比等于对应边长之比,即BC/AC=CN/AC。
10.把式子10代入式子9中,我们可以得到AB/AC=BC/AC+111.化简以上等式,得到AB/AC-BC/AC=112.进一步化简可得到AB/AC=BC/AC,即切割线定理的公式。
通过以上证明,我们可以看到切割线定理的正确性。
根据这个定理,我们可以在平面几何问题中应用切割线定理来解决一些相关的比例问题,特别是在梯形、三角形和平行四边形等图形的相似性问题中,起到重要的指导作用。
中考数学 切割线定理

切割线定理:已知O中,PT切O于T,割线交O于A,则有PTB PAT
∆
切割线定理推论:已知PB、为O的两条割线,交O于A、
切O于T,用两次切割线定理。
T
O B O
O交BC O的切线,
为O的直径,过点作O的切线交O于点E
如图所示,O是∆ABC O于E,O的切线。
求证:2
AE=
O于A、O的切线和O半径为3,则∆
B.8 C
.圆外切四边形一组对边和为12,圆的半径为)
B.12 C
.外心、内心、垂心、重心这四心重合的三角形是(E
B D O
O 于B 、
C ,直线BC 切O 于B 点,O 相切于点O 直径,O 切于B 点,割线O 交于C 和PT 与O 切于C ,为直径,60BAC ∠=O 一弦。
求O 分别切于O 于B ,A
D
C
O 图
O 外一点O 半径的长为(
B B
C 是O 的直径,O 的切线,3=,则O 半径为
B ..O 是AB
C ∆的直径,O 的切线,
3=,则O 半径为 ( ) .40︒
B ..已知:如图3,AB
C ∆的三边分别切于
D 、56DF
E ∠=B ∠=____O 于C 点,O 于A ,O 于B 、平分APC ∠O 于A 、O 于C 、
O半径,O于C,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学内容
【知一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2.切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
2.圆外切四边形一组对边和为12,圆的半径为2,则这个四边形的面积为()
A.6 B.12C.24 D.48
3.外心、内心、垂心、重心这四心重合的三角形是()
A.任意三角形B.直角三角形C.等腰三角形D.等边三角形
4. 、 分别切圆于 、 , 、 两点分圆所得两弧比为 ,则 的度数为()
A. B. C. D.
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
4.弦切角定理:弦切角等于其所夹的弧所对的圆周角;
5.切割线定理:已知 中, 切 于 ,割线 交 于 ,则有 。证明方法:连结 、 ,证:
6.切割线定理推论:已知 、 为 的两条割线,交 于 、 ,则有 ,证明方法:过 作 切 于 ,用两次切割线定理。
9.已知:如图, 与 切于 , 为直径, , 为 一弦。求 与 的度数。
10. 已知: , 与 分别切于 、 两点,延长 到 ,使 ,求证: 。
【课外练习】
1. 切 于 , 是过 点的割线,且 ,则 的度数为()
A. B. C. D.
2.过 外一点 引圆的两切线 、 , 、 是切点, , ,则 半径的长为()
5. 、 分别切 于 、 , 交 于 ,连结 、 ,则圆中的直角三角形共有()个
A.3 B.4C.5 D.6
图1
6.已知:如图1,直线 切 于 点, , ,那么 ____.
图2
7.已知:如图2,直线 与 相切于点 , 为 直径, 于 , ,则 ____.
8.已知:直线 与 切于 点,割线 与 交于 和 两点, , ,则 ;
(1)求证: ;
(2)若 ,求 、 的长。
【例5】如图所示, 是 的外接圆, 的平分线 交 于 ,交 于 , 的切线 交 的延长线于 。求证: 。
【课堂练习】
1.已知 、 分别切 于 、 , 是劣弧 上任意一点,过 作 的切线和 、 分别交于 、 ,若 , 半径为 ,则 的周长为()
A. B. C. D.不确定
6.已知:如图4,圆 为 外接圆, 为直径, 切 于 点, ,那么 ____.
7.已知:如图, 切 于 , 交 于 、 , 平分 ,求 的度数。
8.已知:如图, 、 分别切 于 、 , 为割线交 于 、 ,若 , , ,求 的长。
9.已知:如图, 是 半径, 是 延长线上一点, 切 于 , 于 。求证: 平分 .
重点、难点
重点:理解切线长的概念,掌握切线长定理并会运用它解决有关问题;理解弦切角的概念,掌握弦切角定理及其推论,并会运用它们解决有关问题,通过弦切角定理的证明,进一步了解分情况证明数学命题的思想和方法;
难点:切割线定理的综合运用
考点及考试要求
理解切线长的概念,掌握切线长定理并会运用它解决有关问题;了解切割线定理及其推论间的相互关系,并能综合运用它们解决有关问题;
【经典例题】
【例1】已知:如图, 切圆于 , 为圆直径, , , 。求 的长。
【例2】如图所示, 中, ,以 为直径的 交 于点 ,切线 交 于 。求证: 。
【例3】如图所示, 、 是 的切线, 、 为切点, 于 ,交 于 ,求证: 。
【例4】已知, 为 的直径,过 点作 的切线 , 交 于点 , 的延长线交 于 。
A. B. C. D.
3. 是 的直径, 是 延长线上一点,且 , 是 的切线,且 ,则 半径为()
A. B. C. D.
4. 是 的直径, 是 延长线上一点,且 , 是 的切线,且 ,则 半径为( )
A. B. C. D.
图3
图4
5.已知:如图3, 的 ,内切圆 与 的三边分别切于 、 、 三点, ,那么 ____.
中考数学切割线定理
课 题
切割线定理
教学目标
1.理解切线长的概念,掌握切线长定理并会运用它解决有关问题;
2.理解弦切角的概念,掌握弦切角定理及其推论,并会运用它们解决有关问题,通过弦切角定理的证明,进一步了解分情况证明数学命题的思想和方法;
3.使学生理解切割线定理及其推论间的相互关系,并能综合运用它们解决有关问题;
