九年级数学切割线定理.ppt
合集下载
人教版九年级数学切线长定理PPT共29页

55、 为 中 华 之 崛起而 读书。 ——周 恩来Βιβλιοθήκη 人教版九年级数学切线长定理
56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
60、人民的幸福是至高无个的法。— —西塞 罗
谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
60、人民的幸福是至高无个的法。— —西塞 罗
谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
切割线定理课件

推论三:切线和切平面的性质
总结词
切线和切平面的性质
详细描述
切线和切平面的性质是切割线定理的最后一个重要推论。这个定理指出,过圆外一点作圆的切线,则 该点和圆心的连线与切点的连线垂直于过该点和圆心的平面。这个性质在三维几何中尤其重要,因为 它涉及到平面和空间的关系。
04 切割线定理的应用实例
应用实例一:求圆的切线方程
证明方法三:利用向量积的性质
总结词
通过向量运算和向量的外积性质,证明切割线定理。
详细描述
第三种证明方法是利用向量运算和向量的外积性质。首 先,我们需要理解向量的外积性质,即两个向量的外积 等于它们所夹的平行四边形的面积的两倍。在切割线定 理的情境中,我们可以将切割线视为一个向量,并利用 向量的外积性质来计算它与半径之间的比例关系。通过 适当的数学推导,我们可以证明切割线定理。这种方法 基于向量运算和向量的外积性质,通过向量运算来证明 定理。
范围,我们可以发现更多有趣的应用场景。
对切割线定理的进一步研究与探索
深入研究切割线定理的细节
虽然我们已经对切割线定理有了基本的理解,但还有 很多细节值得深入研究。例如,我们可以探索不同条 件下切割线定理的表现形式,或者研究这个定理在其 他几何图形中的应用。通过深入研究,我们可以更深 入地理解这个定理的本质。
切割线定理的几何意义
证明相似三角形
通过切割线定理,可以证明两个三角形相似,从而用于解决 几何问题。
Hale Waihona Puke 计算线段长度利用切割线定理,可以计算出给定条件下某条线段的长度。
切割线定理的应用场景
建筑设计
在建筑设计领域,切割线定理常被用 于确定建筑物的位置和尺寸,以确保 建筑物的外观和结构符合设计要求。
初三数学切割线定理 人教版优选PPT

小结 作业 思考题: 圆O2的切线PC交圆O2于C。
o1•
已知PT切圆O于T,PAB为圆O的割线,
PD:DE=DC:PD
• PA : AB =1 : 3 , PT=2 , 则PB= ? o2
PC2 = PA·PB
切割线定理:从圆外一点引圆的切线和割线,切线长是
思考题:
A 练习 :
⊙o的弦 CD平分AB于P, 且AB=12cm,CD=13cm 试求: PC 和 PD 的长.
1
已知:如下图,点P是⊙o外一点,PT是切线,T是切点,
证明:连结TA,TB P ∠ 1= ∠ B
过点P作圆O1的割线PMN交圆O1于M . PA ·PB = PD ·PC
∠ P= ∠ P
PA·PB = PD·PC
PT2 =PA·PB
A
△PTA∽ △PBT
PA:PT=PT:PB
PT2 =PA·PB B
这点到割线与圆交点的两条线段长的比例
中项。 即 PT =PA·PB 求证:PM·PN =PC2。
2
(C) CE • CD=BE • BA (D) PB • PD=PC • PA
PA的中点,DC交圆O于E。 PA·AB = PD·CD ×
T
练习三:如图,圆o1和圆o2都经过点A和 B,点P在BA
练习六 P128 2. PT2 =PA·PB
PA是割线 , 点A和B是它与⊙o的交点。 求证:PM·PN =PC2。
证明:
o3 …相切于C,D,E … ,求证:C,D,E … 在同一个圆上。
即 PT2 =PA·PB
N PA•PB=PC•PD 吗?
且DA2=DE • DC
B
问题:如下图,点P是⊙o外一点,过P点向圆作两条
切割线定理课件

A O
得到∵PPP∴又CAC∠是?∠BPPP=⊙CB=∠∠O?PPCCC的BAA切,线
B
∴ P∴C△2=PPCAA?∽PB△ PBC
∴ PC :PA=PB :PC
切割线定理:
∴PC2= PA?PB
从圆外一点引圆的切线和条割线 切线长
是这点到割线与圆的交点的两条线段长的 比
例中项。
C
O
A
B
C
P
D
P
O
A T
1050
B
已知:(如图)点 P为⊙O外一点, PC切 ⊙O于点C,割线PBA 交⊙O于A、B
C
P
O
A
B
答:PC2=PA?PB 怎样证明结论?
已知:(如图)点P为⊙O外一点,PC切
⊙O于点C,割线PBA 交⊙O于A、B
求证:PC2=PA?PB
证明:
C
图P形这几利也何连∵用是P语接△C今A言切P后CC⊙描、A做O∽述B于题C△:点,的PC一BC个基本
B
割线PCD、PAB 交⊙O于点C、D和A、B
=> PA?PB=PC?PD
已知:PT是⊙O的切线,且 PT=500km, 直径AB=1050km,求PA=?
P
∵PT是⊙O 的切线
A
∴ PT2=PA?PB
设PA=x,则5002=x(x+1050)
T
(x+1250)(x-200) =0
O
x=200 或x=-1250( 舍去)
B O
D
A
P
解:(1)由切割线定理,得
C
PC ? PD=PA ? PB
∵AB=3cm,PA=2cm
∴PB=AB+PA=5 (cm ) ∵CD=4cm
《切割线定理》课件

掌握这些性质和特点,可以帮助我们在解决问题和应用中更加灵活和准确地 使用切割线。
切割线的应用领域
切割线在各个领域都有广泛的应用,如建筑设计、地理学、艺术和工程等。它们可以帮助我们理解和解决与形 状和空间相关的问题。
通过学习切割线的应用领域,我们可以将数学和几何知识与实际情境相结合,培养创造性思维和解决问题的能 力。
《切割线定理》课件
欢迎来到本次《切割线定理》的课件!在这个课件中,我们将一起探索切割 线的定义和原理,并了解其在数学和几何中的重要性。
切割线的定义和原理
切割线是指在平面上两个或多个形状之间切割的直线。它们可以将不同的区 域或形状分割开来,从而产生新的图形。
通过研究切割线的定义和原理,我们可以深入了解它们在几何学中的重要性 和应用。
结论和要点
通过本课件,我们对《切割线定理》有了全面的了解。切割线的定义和原理、性质和特点、应用领域、计算方 法以及实验验证,都是我们学习和探索的重点。 希望这些知识对你掌握切割线的概念和应用有所帮助,并启发你在数学和几何领域的研究和实践。
切割线的重要性
切割线在数学和几何中起着关键的作用。它们帮助我们分析和理解各种形状之间的关系,解决问题,并推动数 学和几何的发展。 熟练掌握切割线的基本概念和性质,能够帮助我们在实际生活中应用几何学的知识。
切割线的性质和特点
切性质 可以帮助我们更好地理解切割线的行为和影响。
切割线的计算方法
在具体应用中,我们需要计算切割线的长度、角度和位置等参数。通过掌握 计算方法,我们可以准确地确定切割线的属性。
学习切割线的计算方法有助于我们在实际问题中应用几何学的知识,解决相 关的计算和设计难题。
切割线的实验验证
通过实验验证,我们可以观察和验证切割线的性质和特点。通过亲身体验,我们可以更加深入地理解切割线的 行为和应用。 实验验证也是巩固和应用几何学知识的重要方法,让我们深入探索切割线的奥秘。
切割线的应用领域
切割线在各个领域都有广泛的应用,如建筑设计、地理学、艺术和工程等。它们可以帮助我们理解和解决与形 状和空间相关的问题。
通过学习切割线的应用领域,我们可以将数学和几何知识与实际情境相结合,培养创造性思维和解决问题的能 力。
《切割线定理》课件
欢迎来到本次《切割线定理》的课件!在这个课件中,我们将一起探索切割 线的定义和原理,并了解其在数学和几何中的重要性。
切割线的定义和原理
切割线是指在平面上两个或多个形状之间切割的直线。它们可以将不同的区 域或形状分割开来,从而产生新的图形。
通过研究切割线的定义和原理,我们可以深入了解它们在几何学中的重要性 和应用。
结论和要点
通过本课件,我们对《切割线定理》有了全面的了解。切割线的定义和原理、性质和特点、应用领域、计算方 法以及实验验证,都是我们学习和探索的重点。 希望这些知识对你掌握切割线的概念和应用有所帮助,并启发你在数学和几何领域的研究和实践。
切割线的重要性
切割线在数学和几何中起着关键的作用。它们帮助我们分析和理解各种形状之间的关系,解决问题,并推动数 学和几何的发展。 熟练掌握切割线的基本概念和性质,能够帮助我们在实际生活中应用几何学的知识。
切割线的性质和特点
切性质 可以帮助我们更好地理解切割线的行为和影响。
切割线的计算方法
在具体应用中,我们需要计算切割线的长度、角度和位置等参数。通过掌握 计算方法,我们可以准确地确定切割线的属性。
学习切割线的计算方法有助于我们在实际问题中应用几何学的知识,解决相 关的计算和设计难题。
切割线的实验验证
通过实验验证,我们可以观察和验证切割线的性质和特点。通过亲身体验,我们可以更加深入地理解切割线的 行为和应用。 实验验证也是巩固和应用几何学知识的重要方法,让我们深入探索切割线的奥秘。
初中数学课件《切割线定理》
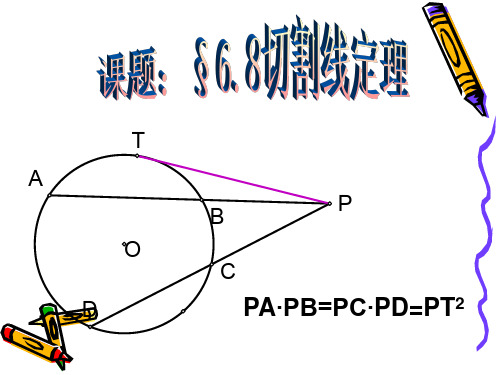
B O A C P
E D
解:(1)由切割线定理,得 PE2=PC ∙ PD=PA ∙ PB ∵AB=3cm,PA=2cm ∴PB=AB+PA=5(cm) ∵CD=4cm ∴PD=PC+CD=PC+4 ∴PC(PC+4)=2X5 化简,整理得:PC2+4PC−10=0
解得: PC 2
14
( 负数不合题意,舍去)
B
已知:(如图)点P为⊙O外一点,PC切 ⊙O于点C,割线PBA 交⊙O于A、B 求证:PC2=PA∙PB
C P A O B
切割线定理: 从圆外一点引圆的两切线和条割线,切 线长是这点到割线与圆的交点的两条线段长 的比例中项。
证明: 连接AC、BC, ∵PC切⊙O于点C ∴∠B= ∠PCA, 又 ∠P=∠P ∴ △PCA∽ △ PBC ∴ PC :PA=PB :PC ∴PC2= PA∙PB
A B
P
割线PCD、PAB交⊙O于点C、D和A、B => PA∙PB=PC∙PD
已知:(如图)过⊙O外一点P作两条割线,分别交 ⊙O 于点A、B和C、D,再作⊙O的切线PE,E为切点, 连接CE、DE。 已知AB=3cm,PA=2cm,CD=4cm. (1)求PC的长 (2)设CE=a,试用含a的代数式表示DE。
T A B O C D P
PA∙PB=PC∙PD=PT2
复习: 1、如图在⊙O中弦AB、CD相交于点P,则有 怎样的结论? 答:PA ∙ PB=PC ∙ PD 怎样证明上述结论? 答:连接BC、AD证明 A △PBC∽ △ PDA 2、设OP=d、 ⊙O 的半径为r 则PA ∙ PB=PC ∙ PD的值 D 为多少? 答:PA ∙ PB=PC ∙ PD=r2—d2
E D
解:(1)由切割线定理,得 PE2=PC ∙ PD=PA ∙ PB ∵AB=3cm,PA=2cm ∴PB=AB+PA=5(cm) ∵CD=4cm ∴PD=PC+CD=PC+4 ∴PC(PC+4)=2X5 化简,整理得:PC2+4PC−10=0
解得: PC 2
14
( 负数不合题意,舍去)
B
已知:(如图)点P为⊙O外一点,PC切 ⊙O于点C,割线PBA 交⊙O于A、B 求证:PC2=PA∙PB
C P A O B
切割线定理: 从圆外一点引圆的两切线和条割线,切 线长是这点到割线与圆的交点的两条线段长 的比例中项。
证明: 连接AC、BC, ∵PC切⊙O于点C ∴∠B= ∠PCA, 又 ∠P=∠P ∴ △PCA∽ △ PBC ∴ PC :PA=PB :PC ∴PC2= PA∙PB
A B
P
割线PCD、PAB交⊙O于点C、D和A、B => PA∙PB=PC∙PD
已知:(如图)过⊙O外一点P作两条割线,分别交 ⊙O 于点A、B和C、D,再作⊙O的切线PE,E为切点, 连接CE、DE。 已知AB=3cm,PA=2cm,CD=4cm. (1)求PC的长 (2)设CE=a,试用含a的代数式表示DE。
T A B O C D P
PA∙PB=PC∙PD=PT2
复习: 1、如图在⊙O中弦AB、CD相交于点P,则有 怎样的结论? 答:PA ∙ PB=PC ∙ PD 怎样证明上述结论? 答:连接BC、AD证明 A △PBC∽ △ PDA 2、设OP=d、 ⊙O 的半径为r 则PA ∙ PB=PC ∙ PD的值 D 为多少? 答:PA ∙ PB=PC ∙ PD=r2—d2
人教版九年级数学课件:切割线定理

作
业
PT2 =PA· PB 切 割 线 定 理
PT =PB· BA × PA· = PD· AB CD
2
PC· =PA· PD PB
切 割 推 线 定 论 理
×
作业 P132
11 , P133 12 ,13.
PT2 =PA· PB
PC· =PA· PD PB
练习二:
1.
过圆O外一点P, 作两条割线PAB和PCD, 已知PA=1, PB=3, PC=0.6.则CD= ? CD = 4.4 2.
已知PT切圆O于T,PAB为圆O的割线, PA : AB =1 : 3 , PT=2 , 则PB= ?
PB = 4
法二: 连接CD ,射影定理. A D •O
BC2=BD•BA
Rt△ABC中 AC=3; BC=4. BD=3.2 (cm) AB=5 BC=4
B
C
提高题:如图,PA切圆O于A,PBC是圆O的割线,D是
PA的中点,DC交圆O于E. 求证:1)PD2=DE•DC;2) ∠1= ∠C.
分析: 1. PD=DA
PA· = PM· PB PN
P
PM· =PC2 PN
练习四:如图,圆o1和圆o2都经过点A和 B,点P在BA
的延长线上.过点P作圆O1的切线PC切圆O1于C,作 圆O2的切线PD切圆O2于D.求证:PC =PD.
B o1 • A C
o2
•
D
P
提示:PC = PD = PE …
B o1 • A D E P o2 • o3•
P P
D 1
E
A
且DA2=DE • DC 2. PD:DE=DC:PD ∠ PDE= ∠ CDP 则: △PDE∽ △CDP 从而: ∠ 1= ∠ C
初中数学课件《切割线定理》

切割线定理的相关概念介绍
为了帮助大家更好地理解切割线定理,我们在这里先来介绍一下它的相关概念。
扇形
扇形是圆心角对应的圆弧及其 圆心所组成的图形,它是切割 线重要概念。
弓形
弓形指的是圆上一个扇形所截 下来的圆弧部分,是能够帮助 我们理解切割线定理的重要概 念。
弦长
弦是连接圆上两点的线段,弦 长是线段长度,是切割线定理 中常用的量。
解决切割线定理中的常见错误和误区
学习切割线定理的时候,常见错误和误区包括对图形理解不够溜,计算公式没有掌握好,套路不熟练等 等,下面是一些错误率较高的问题。
• 画图不规范,不能很好地说明切线、割线、交点的位置关系 • 公式记忆不清,导致计算错误 • 理解不深刻,只会套用公式,难以发挥应有的思考能力
切割线定理在各国数学教育中的地位
切割线定理作为数学中非常重要的一个知识点,它在不同国家的数学教育中都占据着重要地位,是不容 忽视的。下面介绍几个国家中切割线定理的教学情况。
• 中国:在初中阶段的几何课程中必须学习切割线定理。 • 美国:在高中阶段的几何学里也会涉及切割线定理的知识点。 • 日本:从小学到高中,切割线定理都是几何学习的重点。
具体表述
具体来说,若AB与CD是两条割线,交于点E,那么∠AEB=∠CED,∠BEC=1/2∠BAD。
套路示范
判断两条线段是否相互垂直的时候,可以用切割线定理进行证明。
切割线定理的含义和意义
切割线定理是数学中一条很重要的定理。它在几何解题中的应用非常广泛,可以帮助我们更好地理 解和应用各种几何概念。
切割线定理的进阶应用
掌握好了切割线定理的基础知识之后,还可以进一步拓展应用,例如: • 推导出更复杂的几何公式 • 应用切割线定理解决更高级的几何问题 • 将切割线定理与其他定理的知识点相关联,挖掘其更多潜力
九年级数学相交弦定理切割线定理PPT优秀课件

3. ⊙O中弦AB和CD相交于 P,CP=2.5,PD=6,AB=8,那么AP,PB的长是 那个一元两次方程的两个根( )
A. x2 8 x 1 5 0B. x28x 1 5 0
C. x28x 1 5 0 D. x28x 1 5 0
4.如图:⊙O的弦AB,CD相交于 P,PA=4,PB=3,PC=6,EA切⊙O 于点A,AE与CD的延长交于点
复习之四
相交弦定理 切割线定理
一.复习目标:
1.掌握相交弦定理及其应用.2.掌握切割 线定理及其应用.
3.了解相交弦,切割线定理的证明.4.掌 握割线定理及其应用.
二、复习指导:回忆知识点,会的直接 填写,不会的可翻书填写,边填边记, 比谁能正确填写,并能运用它们做对习 题.
三,知识要点:
1.圆内的两条相交弦,被交点分成的两条线
E,AE=2 5 ,求PE的长?
B
C
E DP
A
5.如图:⊙O的两条弦AB与CD相交
于点M,且OM⊥CD,作ON⊥AB,N
为垂足,已知CD=6,BM=9,ON= 11, 求⊙O的半径和OM的长.
A
C
M
DN
O
B
6、M是⊙O1与⊙O2的公共弦AB上的 一点,CE,DF分别是⊙O1, ⊙O2的弦, 它们相交于M,
的两条割线,连结AE交PC于F,用数学
式子表示上述定理:(1)相交弦定
理
,(2)切割线定理 ,(3)割
线定理Leabharlann .E DP
B O•
FC
A
1、过⊙O外一点P的一条割线 PAB交⊙O于A、B两点,PO交 ⊙O于C,且AB=7,PA=4,设 ⊙O半径为10,求PO的长
A
B
A. x2 8 x 1 5 0B. x28x 1 5 0
C. x28x 1 5 0 D. x28x 1 5 0
4.如图:⊙O的弦AB,CD相交于 P,PA=4,PB=3,PC=6,EA切⊙O 于点A,AE与CD的延长交于点
复习之四
相交弦定理 切割线定理
一.复习目标:
1.掌握相交弦定理及其应用.2.掌握切割 线定理及其应用.
3.了解相交弦,切割线定理的证明.4.掌 握割线定理及其应用.
二、复习指导:回忆知识点,会的直接 填写,不会的可翻书填写,边填边记, 比谁能正确填写,并能运用它们做对习 题.
三,知识要点:
1.圆内的两条相交弦,被交点分成的两条线
E,AE=2 5 ,求PE的长?
B
C
E DP
A
5.如图:⊙O的两条弦AB与CD相交
于点M,且OM⊥CD,作ON⊥AB,N
为垂足,已知CD=6,BM=9,ON= 11, 求⊙O的半径和OM的长.
A
C
M
DN
O
B
6、M是⊙O1与⊙O2的公共弦AB上的 一点,CE,DF分别是⊙O1, ⊙O2的弦, 它们相交于M,
的两条割线,连结AE交PC于F,用数学
式子表示上述定理:(1)相交弦定
理
,(2)切割线定理 ,(3)割
线定理Leabharlann .E DP
B O•
FC
A
1、过⊙O外一点P的一条割线 PAB交⊙O于A、B两点,PO交 ⊙O于C,且AB=7,PA=4,设 ⊙O半径为10,求PO的长
A
B
