11.3逻辑变量与基本运算2
合集下载
基本逻辑门电路
基本逻辑门电路————————————————————————————————作者：————————————————————————————————日期：第一节基本逻辑门电路1.1 门电路的概念：实现基本和常用逻辑运算的电子电路，叫逻辑门电路。
实现与运算的叫与门，实现或运算的叫或门，实现非运算的叫非门，也叫做反相器，等等（用逻辑1表示高电平；用逻辑0表示低电平）11.2 与门：逻辑表达式F＝A B即只有当输入端A和B均为1时,输出端Y才为1,不然Y为0.与门的常用芯片型号有:74LS08,74LS09等.11.3 或门：逻辑表达式F＝A+ B即当输入端A和B有一个为1时,输出端Y即为1,所以输入端A和B均为0时,Y才会为O.或门的常用芯片型号有:74LS32等.11.4．非门逻辑表达式F=A即输出端总是与输入端相反.非门的常用芯片型号有:74LS04,74LS05,74LS06,74LS14等.11.5．与非门 逻辑表达式 F=AB即只有当所有输入端A 和B 均为1时,输出端Y 才为0,不然Y 为1.与非门的常用芯片型号有:74LS00,74LS03,74S31,74LS132等.11.6．或非门： 逻辑表达式 F=A+B即只要输入端A 和B 中有一个为1时,输出端Y 即为0.所以输入端A 和B 均为0时,Y 才会为1.或非门常见的芯片型号有:74LS02等.11.7．同或门: 逻辑表达式F=A B+A BA F B11.8.异或门：逻辑表达式F=A B+A B=AF B11.9.与或非门：逻辑表逻辑表达式F=AB+CD AB C F D11.10.RS 触发器：电路结构把两个与非门G1、G2的输入、输出端交叉连接，即可构成基本RS 触发器，其逻辑电路如图7.2.1.(a)所示。
它有两个输入端R 、S 和两个输出端Q 、Q 。
工作原理 :基本RS 触发器的逻辑方程为：根据上述两个式子得到它的四种输入与输出的关系:1.当R=1、S=0时，则Q=0,Q=1,触发器置1。
11.3逻辑变量与基本运算
L
A、B是两个逻辑变量 L是运算结果
“与”运算的真值表
A
B
A ·B（或AB）
1 1 0 0
1 0 1 0
1 1=1
1 0=0 0 1=0 0 0=0
“与”的运算法则:有0出0，全1出1
例2.写出下列各式的运算结果
（） 1 1 0 （2） 0 0
解: （） 1 1 0 0
(3) 11
相当于集合中的并集
p q
或门电路(或)
Hale Waihona Puke p∨q形式复合命题的真值表
p
q
洗衣机在甩干时,到达预订时间或机盖被打 开就会停机,即当两个条件至少有一个满足 时,就会停机.相应的电路叫做“或门电路”
真 真 假 假
真 假 真 假
p∨q 真 真 真 假
“全假为假,有真即真”
复习回顾：
填表：
A
B
1 1 0
0
0 1 0
1
A+B 1 0
1 1
A· B 0 0 1
0
A
0
0 1 1
B
1
0 1 0
A
1 1 0 0
AB
0 0 1 0
A AB
1 1 1 0
三、课堂小结
1、逻辑变量和逻辑关系的基本概念 2、“与、或、非”及“与、或、非复合逻辑运算”的概 念与运算
作业： P8—9 练习册
温故知新
3、“非”运算
一件事件的发生依赖于一个条件，当这个条件成立，这个事件不发生；当这个 条件不成立，这个事件发生，这种逻辑关系称为“非”逻辑关系。 如图，灯L亮否取决于开关A的状态，当A断开时，灯L亮； 当A合上时，因为短路，灯L就不亮。这里灯L和开关A的关系就 是逻辑非，就做
A、B是两个逻辑变量 L是运算结果
“与”运算的真值表
A
B
A ·B（或AB）
1 1 0 0
1 0 1 0
1 1=1
1 0=0 0 1=0 0 0=0
“与”的运算法则:有0出0，全1出1
例2.写出下列各式的运算结果
（） 1 1 0 （2） 0 0
解: （） 1 1 0 0
(3) 11
相当于集合中的并集
p q
或门电路(或)
Hale Waihona Puke p∨q形式复合命题的真值表
p
q
洗衣机在甩干时,到达预订时间或机盖被打 开就会停机,即当两个条件至少有一个满足 时,就会停机.相应的电路叫做“或门电路”
真 真 假 假
真 假 真 假
p∨q 真 真 真 假
“全假为假,有真即真”
复习回顾：
填表：
A
B
1 1 0
0
0 1 0
1
A+B 1 0
1 1
A· B 0 0 1
0
A
0
0 1 1
B
1
0 1 0
A
1 1 0 0
AB
0 0 1 0
A AB
1 1 1 0
三、课堂小结
1、逻辑变量和逻辑关系的基本概念 2、“与、或、非”及“与、或、非复合逻辑运算”的概 念与运算
作业： P8—9 练习册
温故知新
3、“非”运算
一件事件的发生依赖于一个条件，当这个条件成立，这个事件不发生；当这个 条件不成立，这个事件发生，这种逻辑关系称为“非”逻辑关系。 如图，灯L亮否取决于开关A的状态，当A断开时，灯L亮； 当A合上时，因为短路，灯L就不亮。这里灯L和开关A的关系就 是逻辑非，就做
逻辑变量与基本运算
用0和1分别表示开关的“断开”和“闭合”、灯泡的 “灭”和“亮”，完成开关A、B与电灯P的状态列表（表 4）： 开关A 开关B 灯泡P
讨
论
0
0 1
0
1 0
1
1
表4
（三）师生合作
A 0 0 1 1 B 1 概 0 念 1 0 P 0
共探新知
（2）逻辑乘法运算（“与”运算）
当开关A和开关B同时合上时，电灯Ｐ才会亮。 0 我们把这种逻辑关系叫做变量A与变量B的逻辑乘法 0 运算(“与”运算)，并把P叫做A、B的逻辑积，记作 1 A· B=P（或A∧B=P），简记为AB=P。
讨
开关A 灯泡D 0 1
表6
论
（三）师生合作
（3）逻辑非运算
A 0 D 1 0
共探新知
概 1念
当开关A合上时，电灯灭；当开关A断开时，电 灯亮。我们把这种逻辑关系叫做变量A的逻辑非运 算，并把D叫做A的逻辑非，记作 。
这里 0 的意思 是“非0”，既然不 能否从表6总结出逻辑非运算的 讨 论 运算规则？ 为0，那么只能是
逻辑变量与基本运算
（一）创设情境
问 题
兴趣导入
我们可以用0和1两个符号 分别表示两种不同的状态，就 状态的量”的数学模型。
在日常生产、生活中，有很多事物变化只表 可以建立这种“只有两种对立 现为两种对应的状态，你能举出一些吗？
事物的 答 案
对 真
错 假 绿灯行 闭合 灭
交通灯的 开关的 灯泡的
红灯停 断开 亮
答
亮，这种逻辑运算叫逻辑乘法运算，又叫“与运算”；
在开关与灯泡并联的电路中，开关不闭合，灯泡D才 亮，这种逻辑运算叫逻辑非运算。 联系：三种逻辑运算中的0和1的各种运算，都并非数 字的运算，而是逻辑状态的运算，表示的是逻辑代数所 研究的因果逻辑关系。
逻辑变量与基本运算图文
助简化逻辑函数，通过观 察输入与输出之间的关系，可以更容易 地识别出最小项和最大项，从而简化逻 辑函数表达式。
3
卡诺图还可以用于检测逻辑错误和优化 逻辑电路设计。通过观察卡诺图，可以 快速发现输入与输出之间的不正确关系 ，从而及时纠正错误。
逻辑函数表达式与真值表的关系
逻辑函数表达式是描述输入与输出之间逻辑关系的数 学表达式。真值表则是一种表格形式，列出输入变量
逻辑变量与基本运算图文
目录
• 逻辑变量的概念与表示 • 基本逻辑运算 • 逻辑运算的复合与扩展 • 逻辑运算的应用 • 逻辑运算的图形表示
01
逻辑变量的概念与表示
逻辑变量的定义
逻辑变量是用于表示逻辑值的符号或 标记，通常用于逻辑运算和逻辑推理 中。
逻辑变量可以是任何符号，如字母、 数字或特定的符号，只要它们能够表 示逻辑值即可。
算法设计
算法设计是数字系统设计的核心，需要根据系统 需求设计合适的算法，以满足性能、精度和稳定 性等方面的要求。
硬件平台选择
数字系统设计需要考虑硬件平台的选择，包括处 理器、存储器、输入输出接口等硬件资源的配置 和优化。
05
逻辑运算的图形表示
卡诺图（Karnaugh Map）
1
卡诺图是一种用于表示逻辑函数输入与 输出之间关系的图形表示方法。它通过 将输入变量和输出变量的所有可能组合 表示为小方格，并使用特定的符号来表 示逻辑函数的值。
(land) 表示逻辑与运算。
3
在逻辑或-与复合运算中，首先进行括号内的逻辑与运算
(B land C)，然后再与 (A) 进行逻辑或运算。
4
逻辑或-与复合运算的运算优先级高于单纯的逻辑或和
逻辑与运算。
多重逻辑运算的扩展
3
卡诺图还可以用于检测逻辑错误和优化 逻辑电路设计。通过观察卡诺图，可以 快速发现输入与输出之间的不正确关系 ，从而及时纠正错误。
逻辑函数表达式与真值表的关系
逻辑函数表达式是描述输入与输出之间逻辑关系的数 学表达式。真值表则是一种表格形式，列出输入变量
逻辑变量与基本运算图文
目录
• 逻辑变量的概念与表示 • 基本逻辑运算 • 逻辑运算的复合与扩展 • 逻辑运算的应用 • 逻辑运算的图形表示
01
逻辑变量的概念与表示
逻辑变量的定义
逻辑变量是用于表示逻辑值的符号或 标记，通常用于逻辑运算和逻辑推理 中。
逻辑变量可以是任何符号，如字母、 数字或特定的符号，只要它们能够表 示逻辑值即可。
算法设计
算法设计是数字系统设计的核心，需要根据系统 需求设计合适的算法，以满足性能、精度和稳定 性等方面的要求。
硬件平台选择
数字系统设计需要考虑硬件平台的选择，包括处 理器、存储器、输入输出接口等硬件资源的配置 和优化。
05
逻辑运算的图形表示
卡诺图（Karnaugh Map）
1
卡诺图是一种用于表示逻辑函数输入与 输出之间关系的图形表示方法。它通过 将输入变量和输出变量的所有可能组合 表示为小方格，并使用特定的符号来表 示逻辑函数的值。
(land) 表示逻辑与运算。
3
在逻辑或-与复合运算中，首先进行括号内的逻辑与运算
(B land C)，然后再与 (A) 进行逻辑或运算。
4
逻辑或-与复合运算的运算优先级高于单纯的逻辑或和
逻辑与运算。
多重逻辑运算的扩展
逻辑代数基本公式及定律
（11）
图2.2.3 复合逻辑的图形符号和运算符号
现在您浏览到是十二页，共二十九页。
（12）
与非逻辑真值表
A BC Y 00 0 1 00 1 1 01 0 1 01 1 1 10 0 1 10 1 1 11 0 1 11 1 0
异或逻辑真值表
A BY 00 0 01 1 10 1 11 0
现在您浏览到是十三页，共二十九页。
现在您浏览到是二十五页，共二十九页。
（25）
例1： F 1A•BC•D0
注意
注意括号
括号 F1(AB )•(CD )•1
F 1A C B C A D B D
与或式
现在您浏览到是二十六页，共二十九页。
（26）
例2：F2ABCDE
反号不动
F2A•B•C•D•E 反号不动 A •(B C D E )
互为反变量
3.混合变量的吸收： A B + A C + BC=AB+AC
证明：左式 AB ACBC AB AC(AA)BC
A B A C AB A B CC 添加 口诀：
添冗余因子
正负相对,
(A B AB )(C A CA B)C 余全完。
ABAC =右式
（消冗余项）
现在您浏览到是二十一页，共二十九页。
（21）
4. A ·A ·B=A ·B A ·A ·B=A
证明：
A·A·B = A·(A+B) =A ·B
A ·A ·B= A·(A+B)=A
Hale Waihona Puke √ × A ·A ·B= ? A
A
× × A·B A·B
现在您浏览到是二十二页，共二十九页。
二值逻辑变量与基本逻辑运算康华光数字电子技术第六版ppt课件
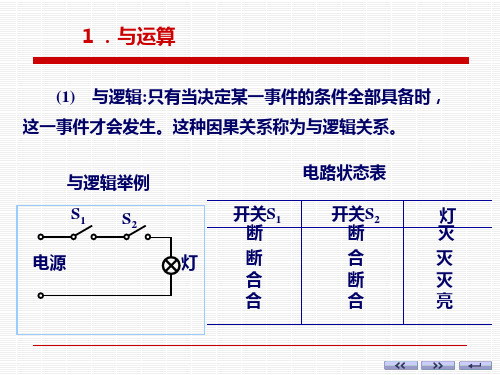
4 ) 同或运算
若两个输入变量的值相同，输出为1，否则为0。
同或逻辑真值表
同或逻辑逻辑符号
AB
L
0
0
1
0
1
0
1
0
0
1
1
1
同或逻辑表达式
A
B
L
A
=
L B
L=AB+ A B =AB
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
１．与运算
(1) 与逻辑:只有当决定某一事件的条件全部具备时， 这一事件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例
电路状态表
S1
S2
开关S1
开关S2
灯
1
A
&L
B
逻辑表达式
与逻辑： L = A ·Ｂ= AB
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
２、或运算
只要在决定某一事件的各种条件中，有一个或几个条件具 备时，这一事件就会发生。这种因果关系称为或逻辑关系。
或逻辑举例
S1 S2 电源
电路状态表
开关S1
开关S2
灯
断
断
灭
灯
断
合
亮
合断亮合源自合亮为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
２、或运算
或逻辑举例状态表
开关
开关S2
中职教材 11.3 逻辑变量与基本运算
（2）0+0· 1+0；
3、非运算 一个事件的发生依赖于一个条件，当这个 条件成立时，这个事件不发生；反之，当这个条 件不成立时，这个事件发生。我们称这种逻辑关 系为“非”逻辑关系。 如图的串联电路中，灯L亮否取 R 决于开关A的状态，当A “合上” L 时，灯L就不亮；当A “断开”时， A 灯L就亮。 灯L与开关A的关系就是逻辑非， L= A
11.3 逻辑变量与基本运算
1、逻辑变量概念、逻辑运算的运算 2、逻辑或、逻辑非、逻辑与的运算法则及 其复合运算
探究
观察如图所示的并联电路： （1）完成开关A、B与灯L的关状态 表1。
开关A 合上 合上 断开 断开 开关B 合上 断开 合上 断开 灯L 亮 亮 亮 熄
A B L
（2）如果规定“合上”用1表示， “断开”用0表示；灯“亮”用1表 示，灯“熄”用0表示，那么请你将 上表改写成下表2。
与运算的运算规则 1· 1=1 1· 0=0 0· 1=0 0· 0=0
例2 写出下列各式的运算结果
（1）1· 0；
1。 （ 2） 0· 0； （ 3 ） 1 ·
例3 写出下列各式的运算结果 （1）1· 1+0；（2）1+0· 1+0。
练习 写出下列各式的运算结果
（1）1+1· 0；
（3）0+0· 1+0· 0；
开关A 开关B 灯L
A B L
1
1
1
0
1
1
0
0
1
0
1
0
逻辑关系：
灯L是否亮，取决于开关A、B的状态，就说 它们之间具有因果逻辑关系。 逻辑变量：
灯L、开关A、B的状态会发生变化，且只有 两种变化的状态，这样的量叫做逻辑变量，常用 大写字母A，B，C，· · · 表示. 逻辑常量： 逻辑变量只有两种状态，只能取值0和1。0和1 只是一种符号，表示两种对立状态，没有数的大 小关系。 0和1叫做逻辑常量。 逻辑代数：研究逻辑关系
逻辑代数中的三种基本运算
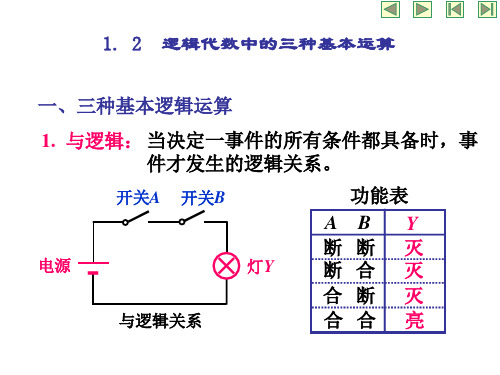
& ≥1
Y3
(真值表略 真值表略) 真值表略
(4) 异或逻辑
A (Exclusive—OR) B
=1
Y4
Y4 = A ⊕ B = AB + AB
(5) 同或逻辑 (异或非) 异或非) A B =1
(Exclusive—NOR)
A 0 0 1 1
B 0 1 0 1
Y4 0 1 1 0
Y5 = A⊕ B
1. 2
逻辑代数中的三种基本运算
一、三种基本逻辑运算 1. 与逻辑： 当决定一事件的所有条件都具备时，事 与逻辑： 当决定一事件的所有条件都具备时， 件才发生的逻辑关系。 件才发生的逻辑关系。
开关A 开关 开关B 开关
电源
灯Y
与逻辑关系
A 断 断 合 合
功能表 B Y 断 灭 合 灭 断 灭 合 亮
2. 几种常用复合逻辑运算 (1) 与非逻辑
(NAND)
Y1 = AB
(2) 或非逻辑
(NOR)
A B A B
&
Y1
Y1、Y2 的真值表 A 0 0 1 1 B 0 1 0 1 Y1 Y2 1 1 1 0 1 0 0 0
≥1
Y2
Y2 = A + B
(3) 与或非逻辑
A (AND – OR – INVERT) B C D Y3 = AB + CD
= AB + AC + ABC + ABC = AB+ A + C
推论
AB + A + BCD = AB + A C C
AB + AB = A B + AB
证明： 公式 (5) 证明：
中职第三册教案：逻辑变量与基本运算(第二课时)
【练习巩固】
填写表格
A
B
A+B
AB
0
0
0
1
1
0
1
1
A
B
AB
+AB
·B
0
0
0
1
1
0
1
1
【课堂总结】
学习本课时，主要重点掌握三种运算的运算法则和复合运算。
【作业布置】
课后习题
复习逻辑关系、逻辑变量、逻辑常量、逻辑加(逻辑或)、或运算规则等知识
口算完成
阅读了解与逻辑关系
掌握与运算的规则：“有0出0，全1出1”
课题
逻辑变量与基本运算（2）
课型
新授
学时
1
教学目标
1、培养学生的逻辑思维能力
2、理解与运算、非运算并掌握其运算规则
3、了解逻辑运算的运算顺序，能求出一些由逻辑常量组成的式子的运算结果。
4、培养学生用逻辑运算表示简单电路的能力。
教学重点
与运算、非运算的运算规则、能求出一些由逻辑常量组成的式子的运算结果
教学难点
与运算、非运算的运算规则
教学方法
讲探练结合
学习方法
探究、讲授、练习
教学设备
触摸式一体机
教学过程
教学活动内容及时间
学生活动内容及时间
【组织教学】
清点人数
【复习导入】
1、逻辑关系
2、逻辑变量
3、逻辑常量
4、逻辑加(逻辑或)
5、或运算规则
6、写出下列各式的运算结果
（1）1+1（2）1+1+0
（3）0+0（4）0+1+0
【新课讲解】
填写表格
A
B
A+B
AB
0
0
0
1
1
0
1
1
A
B
AB
+AB
·B
0
0
0
1
1
0
1
1
【课堂总结】
学习本课时，主要重点掌握三种运算的运算法则和复合运算。
【作业布置】
课后习题
复习逻辑关系、逻辑变量、逻辑常量、逻辑加(逻辑或)、或运算规则等知识
口算完成
阅读了解与逻辑关系
掌握与运算的规则：“有0出0，全1出1”
课题
逻辑变量与基本运算（2）
课型
新授
学时
1
教学目标
1、培养学生的逻辑思维能力
2、理解与运算、非运算并掌握其运算规则
3、了解逻辑运算的运算顺序，能求出一些由逻辑常量组成的式子的运算结果。
4、培养学生用逻辑运算表示简单电路的能力。
教学重点
与运算、非运算的运算规则、能求出一些由逻辑常量组成的式子的运算结果
教学难点
与运算、非运算的运算规则
教学方法
讲探练结合
学习方法
探究、讲授、练习
教学设备
触摸式一体机
教学过程
教学活动内容及时间
学生活动内容及时间
【组织教学】
清点人数
【复习导入】
1、逻辑关系
2、逻辑变量
3、逻辑常量
4、逻辑加(逻辑或)
5、或运算规则
6、写出下列各式的运算结果
（1）1+1（2）1+1+0
（3）0+0（4）0+1+0
【新课讲解】
第11章 逻辑代数的三种基本运算
表1-9 与非逻辑的真值表 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Y 1 1 1 1 1 1 1 0
图1-4 与非逻辑的逻辑符号 “有0必1，全1才0” 2011-6-15
21
（2） 或非运算 “或”和“非”的复合运算称为或非运算。 逻辑表达式：
ABC ABC ABC ABC ABC ABC ABC ABC 最小项 二进制数 000 001 010 011 100 101 110 111 十进制数 0 1 2 3 4 5 6 7
编号
2011-6-15
m0
m1
m2
m3
m4
m5
m6Байду номын сангаас
m7
28
最小项的性质： 任意一组变量取值，只有一个最小 最小项的性质： • 任意一组变量取值，只有一个最小 项 的值为1，其它最小项的值均为0 的值为 ，其它最小项的值均为 • 同一组变量取值任意两个不同最小项 同一组变量取值任意两个不同最小项 两个不同 乘积为 。 的乘积为0。即mi×mj=0 (i≠j) 2 −1 • 全部最小项之和为1，即 全部最小项之 最小项之和 ， m = 1
2011-6-15
26
1 函数表达式的常用形式
• 五种常用表达式 F(A、 F(A、B、C)= AB + AC
= (A + C)(A + B)
“与―或”式 与 “或―与”式 或 “与非―与非”式 与非―与非” 与非 基本形式
= AB • AC
或非― 或非 或非” = A + C + A + B “或非―或非”式 “与―或― 与 = A • 利用还原律 利用反演律 非”式 C+A•B • 表达式形式转换
图1-4 与非逻辑的逻辑符号 “有0必1，全1才0” 2011-6-15
21
（2） 或非运算 “或”和“非”的复合运算称为或非运算。 逻辑表达式：
ABC ABC ABC ABC ABC ABC ABC ABC 最小项 二进制数 000 001 010 011 100 101 110 111 十进制数 0 1 2 3 4 5 6 7
编号
2011-6-15
m0
m1
m2
m3
m4
m5
m6Байду номын сангаас
m7
28
最小项的性质： 任意一组变量取值，只有一个最小 最小项的性质： • 任意一组变量取值，只有一个最小 项 的值为1，其它最小项的值均为0 的值为 ，其它最小项的值均为 • 同一组变量取值任意两个不同最小项 同一组变量取值任意两个不同最小项 两个不同 乘积为 。 的乘积为0。即mi×mj=0 (i≠j) 2 −1 • 全部最小项之和为1，即 全部最小项之 最小项之和 ， m = 1
2011-6-15
26
1 函数表达式的常用形式
• 五种常用表达式 F(A、 F(A、B、C)= AB + AC
= (A + C)(A + B)
“与―或”式 与 “或―与”式 或 “与非―与非”式 与非―与非” 与非 基本形式
= AB • AC
或非― 或非 或非” = A + C + A + B “或非―或非”式 “与―或― 与 = A • 利用还原律 利用反演律 非”式 C+A•B • 表达式形式转换
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课题名称11.3逻辑变量和基本
运算
授课班级
授课时间
12机电1、2
课题序号授课课时第到授课形式启发、引导使用教具
教学目的（1）通过具体的问题情境，了解逻辑常量、逻辑变量及其取值的问题。
（2）通过具体的电路图，理解三种基本的逻辑运算及相应的运算规则。
（3）了解逻辑运算的运算顺序，能求出一些由逻辑常量组成的式子的运算结果。
（4）培养学生用逻辑运算表示简单电路的能力。
教学重点通过具体的电路图，理解三种基本的逻辑运算及相应的运算规则。
教学难点通过具体的电路图，理解三种基本的逻辑运算及相应的运算规则。
更新、补
充、删减
内容
课外作业P16习题1,2
授课主要内容或板书设计
11.3逻辑变量和基本运算
1.或运算及其真值表
例题例题
2.与运算及其真值表
3.非运算及其真值表练习练习
4.“或”“与”“非”的复合运算
教学后记。