年普通高中创新素养培养实验班招生考试试卷及答案

合集下载

宁波市2014年普通高中创新素养培养实验班招生考试试卷及参考答案

宁波市2014年普通高中创新素养培养实验班招生考试试卷数学试题一、选择题（共6题，每题4分，共24分） 1、从1，2，3，4，5这五个数字任取两个数字，使其乘积为偶数的概率为（）（A ）54 （B ）107（C ）53（D ）21 2、已知锐角△ABC 角平分线AD 与高线BE 交于点M ，△CDE 是等边三角形，则S △DEM ：S △ABM 的值为（）（A ）2:2 （B ）2:1（C ）3:1（D ）4:13、在平面直角坐标系中，O 为坐标原点，点A 在第二象限，点B 在x 轴负半轴上，△OAB 的面积是9，P 是AB 重点，若函数xk y =（x<0）的图像经过点A 、P ，则k 的值为（）（A ）-6 （B ）-4（C ）-3（D ）-24、对于任意的有理数a ，方程0)43()1(222=+--++b a a x a x 的根总是有理数，则b 的值为（）（A ）1 （B ）-1（C ）2（D ）05、如图，△ABC 内接于⊙O ，过BC 的中点D 作直线l ∥AC ，l 与AB 交于点E ，与⊙O 交于点G 、F ，与⊙O 在点A 处的切线交于点P ，若PE=3，ED=2，EF=3，则PA 的长度为（）（A ）2 （B ）5（C ）6（D ）7第5题第6题6、如图，已知锐角∠A=∠B ，AA 1、PP 1、BB 1均垂直于A 1B 1，垂足分别是A 1、P 1、B 1，且AA 1=17，AP+PB=13，BB 1=20，A 1B 1=12，则PP 1的长度为（）（A ）13 （B ）14（C ）15（D ）16二、填空题（共6题，每题4分，共24分）7、已知a 是方程0132=+-x x 的根，则1325222++--a a a 的值为 . 8、“*”表示一种运算，规定))(1(11*A y x xy y x ++-=。

若1213*1=，则2013*2014= . 9、如图，Rt △ABC 的硬纸片，∠BAC=90°，AB=3，BC=5，AD 为BC 边上的高，从这张硬纸片上剪下一个如图所示的内接正方形EFGH ，则正方形EFGH 的边长为 .10、如图，在△ABC 中，AB=AC ，CM 平分∠ACB ，与AB 交于点M ，A D ⊥BC 于点D ，ME ⊥BC 于点E ，MF ⊥MC 与BC 交于点F ，若CF=10，则DE= .BBBC A第9题第10题11、已知b a ,是不为零的实数，对于任意实数y x ,，都有02888))((22222≥++-++++k k ay bx y x b a ，其中k 是实数，则k 的最大值为 .12、一个平面把空间分为2个部分，两个平面最多把空间分成4个部分，三个平面最多把空间分为个部分，四个平面最多把空间分成个部分.三、解答题（共4题，每题13分，共52分）13、二次函数)0(2>++=a c bx ax y 的图像与x 轴有两个交点A(-1,0)，B （n ，0），交y 轴于点C （0，p ），已知)2(3--=n a p .（1）求点B 坐标（2）若抛物线上存在点M ，使△ABM 为直角三角形，求a 的取值范围.14、某学生为了培养自己的自主学习能力，采用级别制的自我激励方法管理，级别标志是：全天自主学习时间累计满2小时就算学习1天，学习满5天时，级别标志为1颗星星：又满7天时，再增加1颗星星，级别标志为2颗星星；……（得到第n 颗星星要比得到第n-1颗星星时多耗时2天）.每够4颗星星就改用1个月亮，每够4个月亮就改用1个太阳（即16颗星星为1个太阳）。

2022年福建省厦门市重点大学附属中学创新班化学试题(含答案)

厦门重点大学附属中学2022年创新实验班招生考试化学试卷考试时间：45分钟满分：100分注意事项：1.本科考试试题卷共4页9题。

2.答案一律写在答题卷上，写在试题卷上无效。

请在答题卷上填写毕业学校、姓名、准考证号。

3.可能用到的相对原子质量：H1O16Mg24A127S32Cl35.5Fe56Cu64一、选择题（每小题只有1个正确选项，每题5分，共25分）1.化学与生活、生产密切相关，下列说法正确的是（）A.《物理小识》记载“青矾厂气熏人，衣服当之易烂，栽木不茂。

”其中“青矾厂气”是CO 和B.《内经》记载“五谷为养、五果为助、五禽为益、五菜为充”，文中涉及糖类、维生素、蛋白质等人体所需营养素C.《梦溪笔谈》中对宝剑的记载：“古人以剂钢为刃，柔铁为茎干，不尔则多断折。

”说明铁的合金硬度比纯铁的大，熔点比纯铁的高D.“春蚕到死丝方尽，蜡炬成灰泪始干”中的“丝”灼烧后有烧纸的气味2.60℃时，向100g 水中加入一定量形成溶液，再降温至20℃，析出固体质量的变化如图1。

结合图2，下列说法正确的是（）A.加入的质量为41.6gB.降温过程中溶液始终为饱和溶液C.蒸发溶剂可将M 点的溶液转化到N 点D.20℃时，100g 饱和溶液中有31.6g 溶质3.室温下足量镁片、铝片（已去除氧化膜）分别与40g 溶质质量分数为7.3%的稀盐酸反应（装置如图甲），用压强传感器测得装置内压强随时间的变化关系如图乙。

已知：相同温度下，装置内压强与产生气体的体积成正比。

下列说法错误的是（）2CO 3KNO 3KNO 3KNO 3KNOA.曲线①为镁与盐酸反应的压强变化曲线B.AB 段下降的原因是随反应的进行盐酸浓度逐渐减小C.反应结束时消耗镁片与铝片的质量比为4：3D.反应结束后二者产生氢气的质量相等4.为探究一瓶久置的NaOH 溶液的变质情况，设计了如图方案。

下列说法错误的是（）A.由步骤①的现象可知该溶液已变质B.若“现象Ⅰ”为产生白色沉淀，则该溶液部分变质C.“通入”可改为“滴加酚酞溶液”D.“溶液”可用“溶液”代替5.往100g 和的混合溶液中加入铁粉。

四川省高二下学期(创新班数学试题)入学考试试题(解析版)

高二（下）创新班入学考试理科数学一､单选题（本大题共12小题，共60分）1. 椭圆的长轴长是 2228x y +=A. 2 B.C. 4D.【答案】D 【解析】【分析】现将椭圆的方程化为标准方程，由此求得的值，进而求得长轴长.a 2a 【详解】椭圆方程变形为，，∴.故选D.22148x y +=28a =a =2a =【点睛】本小题主要考查椭圆的标准方程，考查椭圆的几何性质.要注意长轴是而不是.属于基础题. 2a a 2. 在复平面内，设z=1+i （i 是虚数单位），则复数+z 2对应的点位于 A. 第一象限 B.第二象限C. 第三象限D. 第四象限【答案】A 【解析】【详解】试题分析：根据复数的四则运算进行化简，结合复数的几何意义即可得到结论．解：∵z=1+i ， ∴+z 2=+（1+i ）2==1﹣i+2i=1+i ，对应的点为（1，1），位于第一象限，故选A ．点评：本题主要考查复数的几何意义，利用复数的基本运算进行化简是解决本题的关键．3. 已知，，则（）(2,2,3)a =--(2,0,4)= b cos ,a b〈〉=A.B. C. 0 D. 1【答案】B 【解析】【分析】利用空间向量的夹角余弦值公式即可求得. cos ,||||a b a b a b ⋅<>=⋅【详解】解：，，(2,2,3)a =--(2,0,4)= b.cos ,||||a b a b a b ⋅∴<>===⋅故选：B. 4. 函数的单调递减区间为（） ()21ln 2f x x x =-A. B.C.D.()1,1-(),1∞-()0,1()1,+∞【答案】C 【解析】【分析】求出导函数，然后由确定减区间． ()f x '()0f x '<【详解】函数定义域是， (0,)+∞由已知， 1(1)(1)()x x f x x x x+-'=-=当时，，时，，所以减区间是． 01x <<()0f x '<1x >()0f x '>(0,1)故选：C ．5. “”是“为双曲线”的（） 0mn <221mx ny +=A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】C 【解析】【分析】先求方程表示双曲线的条件，再根据两者相等关系确定充要关系. 221mx ny +=【详解】因为方程表示双曲线，所以， 221mx ny +=0mn <又当时，方程表示双曲线，0mn <221mx ny +=因此“”是“方程表示双曲线”的充要条件. 0mn <221mx ny +=故选：C6. 甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中至少有1门不相同的选法共有 A. 6种 B. 12种C. 30种D. 36种【答案】C【解析】【详解】由=30选C.222444c c c -7. 如图，在直三棱柱中，面，，则直线与直线夹111ABC A B C -BC ⊥11ACC A 12CA CC CB ==1BC 1AB 角的余弦值为（）A.B.C.D.35【答案】C 【解析】【分析】连接交于，若是的中点，连接，易得，即直线与直线1CB 1BC D E AC ,BE ED 1//ED AB 1BC 夹角为或补角，进而求其余弦值.1AB BDE ∠【详解】连接交于，若是的中点，连接，1CB 1BC D E AC ,BE ED由为直棱柱，各侧面四边形为矩形，易知：是的中点，111ABC A B C -D 1CB 所以，故直线与直线夹角，即为与的夹角或补角， 1//ED AB 1BC 1AB ED 1BC BDE ∠若，则，， 1BC =1CE =BD CD ==面，面，则，BC ⊥11ACC A EC ⊂11ACC A CB CE ⊥而，又，面，故面， 1EC CC ⊥1BC CC C ⋂=1,BC CC ⊂11BCC B EC ⊥11BCC B 又面，所以. CD ⊂11BCC B CE CD ⊥所以，，32ED ==BE ==在△中.BDE 222cos 2BD ED BE BDE BD ED +-∠===⋅故选：C8. 点P 在曲线上移动，设点P 处切线的倾斜角为，则角的范围是（） 323y x x =-+ααA. B. C.D. π[0,]2ππ0,,022⎡⎤⎛⎫⋃- ⎪⎢⎥⎣⎦⎝⎭3π,π4⎡⎤⎢⎥⎣⎦3π[0,)[)2π,π4⋃【答案】D 【解析】【分析】先由导数的几何意义，求出切线的斜率的范围，再求出倾斜角的范围即可. 【详解】由可得， 323y x x =-+231y x '=-，即，[)1,y ∞∴∈-+'[)[)tan 1,,0,πk α∞α=∈-+∈当时，； [)tan 0,α∈+∞π0,2α⎡⎫∈⎪⎢⎣⎭当时，.[)tan 1,0α∈-3π,π4⎡⎫∈⎪⎢⎣⎭α，π30,,π24πα⎡⎫⎡⎫∴∈⎪⎪⎢⎢⎣⎭⎣⎭故选：.D 9. 已知是椭圆上的点，､分别是椭圆的左､右焦点，若，则P 221259x y +=1F 2F 1212PF PF PF PF⋅=⋅1212F PF △的面积为（） A. B.C.D.【答案】A 【解析】【分析】由条件根据向量夹角公式求，然后利用余弦定理和椭圆定义列方程组可解.12F PF ∠【详解】设椭圆的长半轴为，短半轴为，半焦距为，221259x y +=a b c 则，，5,3a b==4c ==即.1228F F c ==设，所以由椭圆的定义可得：①.12,F P m F P n ==10m n +=因为，所以由数量积的公式可得：121212PF PF PF PF ⋅=⋅ ，所以.121cos 2,PF PF = 12π,3PF PF = 在中，12F PF △12π3F PF ∠=所以由余弦定理可得：②， 22π642cos 3m n mn =+-由①②可得：，所以12mn =121πsin 23F PF S mn ==A 故选：A.10. 随机变量X 的分布列如表所示，若，则（） ()13E X =()32D X -=X1-0 1 P16abA. 9B. 7C. 5D. 3【答案】C 【解析】【分析】由，利用随机变量的分布列列出方程组，求出，，由此能求出，再由1()3E X =X 13a =12b =()D X ，能求出结果．(32)9()D X D X -=【详解】， 1()3E X =由随机变量的分布列得：∴X，解得，， 1161163a b b ⎧++=⎪⎪⎨⎪-+=⎪⎩13a =12b =．2221111115()(1)(0)(1)3633329D X ∴=--⨯+-⨯+-⨯=． 5(32)9()959D X D X ∴-==⨯=故选：．C 【点睛】本题考查方差的求法，考查离散型随机变量的分布列、数学期望、方差等基础知识，考查运算求解能力，考查函数与方程思想，是常考题．11. 已知A ，B为双曲线E 的左，右顶点，点M 在E 上，∆ABM 为等腰三角形，且顶角为120°，则E 的离心率为 A.B. C.D.2【答案】D 【解析】【详解】设双曲线方程为，如图所示，，，过点22221(0,0)x y a b a b-=>>AB BM =作轴，垂足为，在中，，，故点的坐标为M MNx ⊥N Rt BMN ∆BN a =MN =M ，代入双曲线方程得，即，所以D ．(2)M a 2222a b a c ==-222c a =e =考点：双曲线的标准方程和简单几何性质．12. 已知函数与图象上存在关于轴对称的点，则的取21()(0)2xf x x e x =+-<2()ln()g x x x a =++值范围是A. B.C. D. (-∞(-∞((【答案】B 【解析】【详解】由题可得存在满足()0,0x ∈-∞()()00f x g x =- ∴()()0220001ln 2x x e x x a +-=-+-+,()001ln 2x e x a ∴--+-0=令,()()1ln 2xh x e x a =--+-因为函数和在定义域内都是单调递增的, x y e =()ln y x a =--+所以函数在定义域内是单调递增的, ()()1ln 2xh x e x a =--+-又因为趋近于时,函数且在上有解(即函数有零点), x -∞()h x 0<()0h x =(),0-∞()h x所以()()010ln 002h e a =-+->ln a a ⇒<<故选：B.考点：指对数函数方程单调性二､填空题：（本大题共4小题，每小题5分，共20分.）13. 的展开式中的系数为______（用数字作答）. 61()x x y y ⎛⎫-+ ⎪⎝⎭24x y 【答案】9 【解析】【分析】根据二项式定理求出含的项，即可得其系数.24x y 【详解】由的展开式通项为，6()x y +616C r rr r T xy -+=当时，当时，4r =42456C T x y ==5r 5566C T xy =所以含的项为. 24x y 424554524246666C ()C (C C )9x x y xy x y x y y+-⋅=-=故的系数为9. 24x y 故答案为：914. 抛物线与过焦点的直线交于两点，为原点，则________.22y x =,A B O OA OB ⋅=【答案】 34-【解析】【详解】(1)当直线AB 轴时,在中,令,有,则 ⊥x 22y x =12x =1y =±,得.11(,1),(,1)22A B -(2)当直线AB 与轴不互相垂直时,设AB 的方程为:x 1()2y k x =-由,消去,整理得,显然.21(){22=-=y k x y xy 22221(2)04k x k x k -++=0k ≠设,则,得 1122(,),(,)A x y B x y 21212221,4k x x x x k ++=⋅==+=+1122(,)(,)x y x y ⋅12x x ⋅1y 2y 12x x ⋅11()2k x -21()2k x ⋅-===.22212121(1)()24k k x x x x k +⋅-++22222121(1)424k k k k k ++-⋅+34-综(1),(2)所述,有．15. 已知函数有两个零点，a 的取值范围是_____； 2()(2)e (1)x f x x a x =-+-【答案】 (0,)+∞【解析】【分析】首先求出函数的导函数，再对参数分类讨论，结合单调性和函数值的变化特点，即可得到所求a 范围．【详解】解：因为 2()(2)e (1)x f x x a x =-+-所以． ()(1)2(1)(1)(2)x x f x x e a x x e a '=-+-=-+（i ）设，则，只有一个零点．0a =()(2)x f x x e =-()f x （ii ）设，则当时，；当时，． 0a >(,1)x ∈-∞()0f x '<(1,)x ∈+∞()0f x '>所以在上单调递减，在上单调递增． ()f x (,1)-∞(1,)+∞又，，取满足且，则 (1)e f =-(2)f a =b 0b <ln2ab <，故存在两个零点． 223()(2)(1)()022a fb b a b a b b >-+-=->()f x （iii ）设，由得或． a<0'()0f x =1x =ln(2)x a =-若，则，故当时，， 2ea ≥-ln(2)1a -≤(1,)x ∈+∞'()0f x >因此在上单调递增．又当时，， ()f x (1,)+∞1x ≤()0f x <所以不存在两个零点． ()f x 若，则，故当时，； 2ea <-ln(2)1a ->(1,ln(2))x a ∈-'()0f x <当时，．因此在上单调递减， (ln(2),)x a ∈-+∞()0f x '>()f x (1,ln(2))a -在上单调递增．又当时，， (ln(2),)a -+∞1x ≤()0f x <所以不存在两个零点．综上可得的取值范围为． ()f x a (0,)+∞故答案为：(0,)+∞16. 若双曲线上存在两个点关于直线对称，则实数的取值范围为2213y x -=:4(0)l y kx k =+>k ______.【答案】 10,2⎫⎛⎫+∞⎪ ⎪⎪⎝⎭⎭【解析】【分析】设双曲线上两点，，，，直线的方程是，代入双曲线方程化简1(A x 1)y 2(B x 2)y AB x ky n =-+得，的中点是，，利用判别式大于0，韦达定理结合的中点222(1)230k y kny n --+-=AB 0(D x 0)y AB 在直线上，转化求解的范围即可．D :4(0)l y kx k =+>k 【详解】解：依题意，双曲线上两点，，，， 1(A x 1)y 2(B x 2)y 若点A 、B 关于直线对称，则:4(0)l y kx k =+>设直线的方程是，代入双曲线方程化简得：AB x ky n =-+2213y x -=，222(31)6330k y kny n --+-=则，且，解得，且2222364(31)(33)0k n k n ∆=--->2310k -≠22310k n -+>2310k -≠又，设的中点是，， 122631kny y k +=-AB 0(D x 0)y 所以，． 12023231y y kn y k +==-00231nx ky n k =-+=--因为的中点在直线上， AB D :4(0)l y kx k =+>所以，所以，又 22343131kn n k k k -=⋅+--231nk k =-2310k -≠所以，即，所以 0nk ≠0,0k n ≠≠231k n k-=所以，整理得，22231310k k k ⎛⎫--+> ⎪⎝⎭22(31)(41)0k k -->所以或 102k <<k >实数的取值范围为： k 10,2⎫⎛⎫+∞⎪ ⎪⎪⎝⎭⎭故答案为：. 10,2⎫⎛⎫+∞⎪ ⎪⎪⎝⎭⎭三､解答题：（本大题共6小题，共70分，解答应写出文字说明､证明过程或演算步骤.）17. 2022年北京冬奥会即第24届冬季奥林匹克运动会在2022年2月4日至2月20日在北京和张家口举行.某研究机构为了解大学生对冰壶运动是否有兴趣，从某大学随机抽取男生、女生各200人，对冰壶运动有兴趣的人数占总数的，女生中有80人对冰壶运动没有兴趣. 2740有兴趣没有兴趣合计男女80 合计（1）完成上面2×2列联表，并判断是否有99%的把握认为对冰壶运动是否有兴趣与性别有关？（2）按性别用分层抽样的方法从对冰壶运动有兴趣的学生中抽取9人，若从这9人中随机选出2人作为冰壶运动的宣传员，设X 表示选出的2人中女生的人数，求X 的分布列和数学期望.附：.22()()()()()()n ad bc K n a b c d a b c d a c b d -==+++++++()20P K k ≥0.100 0.050 0.025 0.010 0.0010k 2.706 3.841 5.024 6.635 10.828【答案】（1）列联表见解析，有的把握认为对冰壶运动是否有兴趣与性别有关．99%（2）分布列见解析，. 8()9E X =【解析】【分析】（1）根据题干所给数据求出冰壶运动有兴趣的男女人数，即可得到列联表，再计算出卡方，即可判断；（2）首先利用分层抽样求出男、女抽取的人数，依题意的所有可能取值为，，，求出所对应的X 012概率，即可得到分布列与数学期望；【小问1详解】解：依题意对冰壶运动有兴趣的人数为人， ()2720020027040⨯+=则女生中对冰壶运动有兴趣的有人，20080120-=男生中对冰壶运动有兴趣的有人，270120150-=所以男生中对冰壶运动无兴趣的有人，20015050-=所以列联表：22⨯有兴趣没有兴趣合计男150 50 200女120 80 200合计270 130 400， 22400(1508050120)40010.256 6.63527013020020039K ⨯⨯-⨯==≈>⨯⨯⨯有的把握认为对冰壶运动是否有兴趣与性别有关．∴99%【小问2详解】解：从对冰壶运动有兴趣的学生中抽取人，抽到的男生人数、女生人数分别为：（人，915095270⨯=)（人， 12094270⨯=)则的所有可能取值为，，，X 012所以， 2529C 105(0)C 3618P X ====， 114529C C 205(1)C 369P X ====， 4292C 61(2)C 366P X ====故的分布列是：XX 0 1 2 P 518 59 16故． 5518()01218969E X =⨯+⨯+⨯=18. 在中，，，与BC 斜率的积是． ABC A (2,0)A -(2,0)B AC 14-（1）求点的轨迹方程；C （2），求PC 的中点的轨迹方程．(4,0)P M 【答案】（1） 221(2)4x y x +=≠±（2） ()22241(0)x y y -+=≠【解析】【分析】（1）设点C 坐标，根据题意直接列方程可得；（2）由相关点法可得.【小问1详解】设点C 坐标为，由题知 (,)x y 1224AC BC y y k k x x ⋅=⨯=-+-整理得点的轨迹方程为 C 221(2)4x y x +=≠±【小问2详解】设点M 坐标为，点C 坐标为(,)x y 00(,)x y由中点坐标公式得，即 00422y x x y +⎧=⎪⎪⎨⎪=⎪⎩00242x x y y =-⎧⎨=⎩将代入得点的轨迹方程为：，即00242x x y y =-⎧⎨=⎩221(2)4x y x +=≠±M ()()222421(0)4x y y -+=≠()22241(0)x y y -+=≠19. 四棱锥中，底面ABCD 是边长为2的菱形，侧面底面，，P ABCD -PAD ⊥ABCD 60BCD ∠=︒是BC 的中点，点在侧棱PC 上.PA PD ==E Q（1）若Q 是PC 的中点，求二面角的余弦值；E DQ C --（2）是否存在，使平面DEQ ?若存在，求出的值；若不存在，说明理由. Q //PA PQ PC【答案】（1；（2）时，平面. 23PQ PC =//PA DEQ 【解析】【分析】（1）以为坐标原点，建立空间直角坐标系利用向量法能求出二面角的余O O xyz -E DQ C --弦值．（2）设，，，，推导出，利用向量法能求出当(01)PQ PC λλ= ……(Q x y )z (2,1)Q λλ--+23λ=时，平面．//PA DEQ 【小问1详解】解：取中点，连接，，．AD O OP OB BD 因为，所以．PA PD =PO AD ⊥因为侧面底面，且平面底面，PAD ⊥ABCD PAD ⋂ABCD AD =所以底面．可知，，，PO ⊥ABCD BO AD ⊥PO AD ⊥以为坐标原点，如图建立空间直角坐标系．O O xyz-则，(1,0,0),((0,0,1),(D E P C ---因为为中点，所以． QPC 1(2Q -所以，12DE DQ == 所以平面的法向量为．DEQ 1(1,0,0)n = 因为，1()2DC DQ =-= 设平面的法向量为，DQC 2(,,)n x y z = 则，即． 22·0·0DC n DQ n ⎧=⎪⎨=⎪⎩0102x y z ⎧-=+=令．x=1,y z ==2n = 所以． 121212cos ,||||n n n n n n <>== A由图可知，二面角． E DQ C --【小问2详解】解：设(01)PQ PC λλ= ……由（1）可知．(1),(1,0,1)PC PA =--=- 设，，，则，(Q x y )z (,,1)PQ x y z =-又因为，(2,)PQ PC λλλ==-- 所以，即．21x y z λλ=-⎧⎪=⎨⎪=-+⎩(2,1)Q λλ--+所以在平面中，，DEQ (12,1)DE DQ λλ==-- 所以平面的法向量为，DEQ 1(1,0,21)n λλ=-- 又因为平面，所以，//PA DEQ 10PA n = A 即，解得． (1)(1)(21)0λλ-+--=23λ=所以当时，即，平面． 23λ=23PQ PC =//PA DEQ 20. 已知函数．()e cos x f x x x =-（Ⅰ）求曲线在点处的切线方程；()y f x =(0,(0))f （Ⅱ）求函数在区间上的最大值和最小值．()f x π[0,]2【答案】(Ⅰ)；（Ⅱ）最大值1；最小值. 1y =2π-【解析】【详解】试题分析：（Ⅰ）根据导数的几何意义，先求斜率，再代入切线方程公式中即可；（Ⅱ）设，求，根据确定函数的()()()000y f f x ¢-=-()()h x f x ='()h x '()0h x '<()h x 单调性，根据单调性求函数的最大值为，从而可以知道恒成立，所以函数()00h =()()0h x f x '=<是单调递减函数，再根据单调性求最值.()f x 试题解析：（Ⅰ）因为，所以.()e cos x f x x x =-()()()e cos sin 1,00x f x x x f -''=-=又因为，所以曲线在点处的切线方程为.()01f =()y f x =()()0,0f 1y =（Ⅱ）设，则. ()()ecos sin 1x h x x x =--()()e cos sin sin cos 2e sin x x h x x x x x x =--=-'-当时，， π0,2x ⎛⎫∈ ⎪⎝⎭()0h x '<所以在区间上单调递减. ()h x π0,2⎡⎤⎢⎥⎣⎦所以对任意有，即. π0,2x ⎛⎤∈ ⎥⎝⎦()()00h x h <=()0f x '<所以函数在区间上单调递减. ()f x π0,2⎡⎤⎢⎥⎣⎦因此在区间上的最大值为，最小值为. ()f x π0,2⎡⎤⎢⎥⎣⎦()01f =22f ππ⎛⎫=- ⎪⎝⎭【名师点睛】这道导数题并不难，比一般意义上的压轴题要简单很多，第二问比较有特点的是需要两次求导数，因为通过不能直接判断函数的单调性，所以需要再求一次导数，设，再求()f x '()()h x f x ='，一般这时就可求得函数的零点，或是()恒成立，这样就能知道函数()h x '()h x '()0h x '>()0h x '<的单调性，再根据单调性求其最值，从而判断的单调性，最后求得结果.()h x ()y f x =21. 已知椭圆的左，右焦点分别为、，上下顶点分别为M 、N ，点的2222:1(0)x y E a b a b+=>>1F 2F M坐标为，在下列两个条件中任选一个：①离心率；②四边形的面积为4，解M e =12F MF N 答下列各题.（1）求椭圆的方程；E （2）设直线交椭圆于A 、B 两点，判断点与以线段AB 为直径的圆的:1(R)l x my m =-∈E 9,04G ⎛⎫-⎪⎝⎭位置关系，并说明理由. 【答案】（1）； 22142x y +=（2）G 在以AB 为直径的圆外，理由见解析.【解析】【分析】（1）根据所选条件及，结合椭圆参数关系求出椭圆方程. c e a=（2）联立直线与椭圆方程，应用韦达定理求、，利用向量的数量积的坐标运算判断A B y y +A B y y 符号，即可判断点圆的位置关系.GA GB ⋅ 【小问1详解】选①：由上顶点，即，M b =由，且，可得， c e a ==22222a b a c -=-=24a =所以椭圆的方程为. E 22142x y +=选②：由题设，，即，而， 12242b c ⨯⨯=2bc =b =所以，c =2224a b c =+=所以椭圆的方程为. E 22142x y +=【小问2详解】联立与， :1(R)l x my m =-∈22142x y +=并整理可得：，则，， 22(2)230m y my +--=222A B m y y m +=+232A B y y m =-+所以， 24()22A B A B x x m y y m +=+-=-+， 22224(1)(1)()12A B A B A B A B m x x my my m y y m y y m -=--=-++=+由，， 9(,)4A A GA x y =+ 9(,)4B B GB x y =+ 所以 99981(()44416A B A B A B A B A B GA GB x x y y x x x x y y ⋅=+++=++++ ， 22222224981317202216216(2)m m m m m m -+=-+-=>++++故，故且不共线，故为锐角，||||cos 0GA GB AGB ∠> [0,]AGB π∠∈,GA GB AGB ∠所以G 在以AB 为直径的圆外.22. 已知函数(),()ln ,x f x e g x x a x a R ==+∈（1）讨论g (x )的单调性；（2）若，对任意恒成立，求a 的最大值； ()()2af x xg x x ++…(1,)x ∈+∞【答案】（1）见解析；（2）e【解析】【分析】（1）对求导，然后分及讨论得出单调性情况；()g x 0a …a<0（2）原不等式可转化为，设，求出的单调性，可知当ln ln x x a a e e x x ++…()ln (0)h x x x x =+>()h x 1x >时，，设，求出的最小值即可得解． ln x a x …()(1)ln x x x xϕ=>()ϕx 【详解】解：（1）， ()1(0)a x a g x x x x +'=+=>当时，，在上单调递增；0a …()0g x '>()g x (0,)+∞当时，令，解得，令，解得，a<0()0g x '>x a >-()0g x '<0x a <<-在上单调递减，在上单调递增；()g x ∴(0,)a -(,)a -+∞综上，当时，在上单调递增；0a …()g x (0,)+∞当时，在上单调递减，在上单调递增；a<0()g x (0,)a -(,)a -+∞（2）即为，即，()2()a f x x g x x ++…ln x a e x a x x ++…ln ln x x a a e e x x ++…设，则， ()ln (0)h x x x x =+>11()1x h x x x+'=+=易知函数在上单调递增，()h x (0,)+∞而，所以，即，当时，即为， ()()x a h e h x …x a e x …ln x a x …1x >ln x a x…设，则， ()(1)ln x x x x ϕ=>2ln 1()ln x x x ϕ-'=易知函数在上单调递减，在上单调递增，()ϕx (0,)e (,)e +∞（e ），()x ϕϕ∴…e =，即的最大值为．a e ∴…a e 【点睛】本题考查利用导数研究函数的单调性，考查不等式的恒成立问题，考查构造函数思想，考查运算求解能力，属于难题．。

年普通高中创新素养培养实验班招生考试试卷及答案

E D CBA 2014年普通高中创新素养培养实验班招生考试试卷数学试题一、选择题（共6题，每题4分，共24分）1、从1，2，3，4，5这五个数字任取两个数字，使其乘积为偶数的概率为（）（A ）45 （B ）710 （C ）35 （D ）12解：总数=4+3+2+1=10，符合条件的为：2×1；2×3；2×4；2×5；4×1；4×3；4×5共7个（或只有1×3；1×5；3×5共3个例外），∴概率为710或1－310＝710 2、已知锐角△ABC 角平分线AD 与高线BE 交于点M ，△CDE 是等边三角形，则S △DEM ∶S △ABM 的值为（）（A ）2∶2 （B ）1∶2 （C ）1∶3 （D ）1∶4∵∠C =600，∠BEC =900，∴∠EBC =300，又∠CDE =600，∴∠BED =300， ∴ED =BD =CD ，∴AD 即是∠BAC 的平分线，又是BC 上的中线， ∴AB =AC ，∴△ABC 为正三角形，∴AD 与BE 的交点为△的重心 ∴S △DEM ∶S △ABM =1∶4。

3、在平面直角坐标系中，O为坐标原点，点A在第二象限，点B在x轴负半轴上，△OAB的面积是9，P是AB中点，若函数y＝kx（x<0）的图像经过点A、P，则k的值为（）（A）－6 （B）－4 （C）－3 （D）－2设点A坐标为（m，n），点B（a，0），∵S△OAB=9，∴－12an＝9，∵P是AB的中点，∴点P坐标为（m＋a2，n2），∵k＝xy，∴代入A、P坐标得：k＝mn，k＝(m＋a)n4，∴mn＝(m＋a)n4，∴3mn＝an，∵－an＝18，∴mn＝－6∴k＝－6（本例考点为点与函数的关系、中点坐标的应用，中点坐标是解压轴题的重要工具）※ 同类测试题：如在直角坐标系中，存在一个平行四边形，其中平行四边形的三个项点的坐标为（1，3），（2，2）和（3，4），求另一顶点的坐标？4、对于任意的有理数a，方程2x2＋(a＋1)x－(3a2－4a＋b)＝0的根总是有理数，则b的值为（）（A）1 （B）－1 （C）2 （D）0解：方程的△＝(a＋1)2＋8(3a2－4a＋b)＝(5a－3)2＋8b－8≥0，∴当8b－8≥0时，PG FED C B A 必定△≥0，即方程必有实根，∴b ≥1，当b ＝1时，3a 2－4a ＋1＝(3a －1)(a －1)， ∴十字因式分解得方程为（(x －a ＋1)(2x ＋3a －1)＝0，∴b ＝1成立，当b ＝2时，3a 2－4a ＋b ＝3a 2－4a ＋2不能因式分解，∴方程有可能为无理数解，（在一元二次方程中，运用方程的判别式和因式分解是解决方程有理根和整数根重要工具，）※同类测试题：使得m 2＋m ＋7是完全平方数的所有整数m 的积的值。

衢州初升高创新班试卷及答案

衢州初升高创新班试卷及答案一、语文（共40分）1. 阅读理解（20分）阅读下面的文章，回答下列问题。

（文章内容略）（1）文章中提到的“创新”一词，作者主要强调了哪些方面？（5分）（2）请分析文中主人公面对挑战时的心态变化。

（5分）（3）文章最后一段中，作者提出了哪些对未来的展望？（5分）（4）根据文章内容，你认为创新对于个人成长的意义是什么？（5分）2. 作文（20分）请以“创新的力量”为题，写一篇不少于800字的议论文。

二、数学（共30分）1. 选择题（10分，每题2分）（1）下列哪个选项是二次方程的解？A. x = 1B. x = -1C. x = 2D. x = 3（2）-3的相反数是：A. 3B. -3C. 0D. 1（3）若a > b，下列哪个不等式是正确的？A. a < bB. a > bC. a ≤ bD. a ≥ b（4）下列哪个选项是圆的面积公式？A. πr²B. 2πrC. πd²D. πr² + 2πr（5）下列哪个选项是勾股定理的表达式？A. a² + b² = c²B. a + b = cC. a × b = cD. a - b = c2. 填空题（10分，每题2分）（1）若一个三角形的三边长分别为3, 4, 5，则这个三角形是____。

（2）若一个圆的半径为7，则它的周长是____。

（3）若一个数的平方根是2，则这个数是____。

（4）若一个数的立方根是3，则这个数是____。

（5）若一个数的绝对值是5，则这个数可以是____或____。

3. 解答题（10分）已知一个等差数列的首项为2，公差为3，求这个数列的前10项的和。

三、英语（共30分）1. 阅读理解（20分）阅读下面的文章，回答下列问题。

（文章内容略）（1）What is the main idea of the passage?（5分）（2）What does the author suggest about the future of technology?（5分）（3）What is the author's opinion on the importance of innovation?（5分）（4）What are the examples given to illustrate the importance of innovation?（5分）2. 完形填空（10分）（文章内容略）衢州初升高创新班试卷答案一、语文1. 阅读理解（1）略（2）略（3）略（4）略2. 作文略二、数学1. 选择题（1）B（2）A（3）B（4）A（5）A2. 填空题（1）直角三角形（2）44π（3）4（4）27（5）5，-53. 解答题等差数列的前10项和为：S = n/2 * (a1 + an) = 10/2 * (2 + 2 + 9*3) = 10 * 31 = 310三、英语1. 阅读理解（1）略（2）略（3）略（4）略2. 完形填空略试卷到此结束，祝各位考生考试顺利！。

2014年普通高中创新素养培养实验班招生考试试卷及答案

2014年普通高中创新素养培养实验班招生考试试卷数学试题一、选择题（共6题，每题4分，共24分）1、从1，2，3，4，5这五个数字任取两个数字，使其乘积为偶数的概率为（）（A）45（B）710（C）35（D）12解：总数=4+3+2+1=10，符合条件的为：2×1；2×3；2×4；2×5；4×1；4×3；4×5共7个（或只有1×3；1×5；3×5共3个例外），∴概率为710或1－310＝71023AB中点，2，2）和（3，4），求另一顶点的坐标？4、对于任意的有理数a，方程2x2＋(a＋1)x－(3a2－4a＋b)＝0的根总是有理数，则b的值为（）（A）1 （B）－1 （C）2 （D）0解：方程的△＝(a＋1)2＋8(3a2－4a＋b)＝(5a－3)2＋8b－8≥0，∴当8b－8≥0时，必定△≥0，即方程必有实根，∴b≥1，当b＝1时，3a2－4a＋1＝(3a－1)(a－1)，∴十字因式分解得方程为（(x－a＋1)(2x＋3a－1)＝0，∴b＝1成立，当b＝2时，3a2－4a＋b＝3a2－4a＋2不能因式分解，∴方程有可能为无理数解，（在一元二次方程中，运用方程的判别式和因式分解是解决方程有理根和整数根重要工具，）※同类测试题：使得m2＋m＋7是完全平方数的所有整数m的积的值。

5、如图，△ABC内接于⊙O，过BC的中点D作直线l∥AC，l与AB交于点E，与⊙O交于点G、F，与⊙O在点A处的切线交于点P，若PE=3，ED=2，EF=3，则PA的长度为（）（A） 2 （B） 5 （C） 6 （D）76，BB1=20，A1（7∵8、“*”表示一种运算，规定x*y＝1xy－1(x＋1)(y＋A)。

若1*3＝112，则2013*2014= 。

1*3＝11×3－1(1＋1)(3＋A)＝112，解得A＝－1，2013*2014=12013×2014－1(2013＋1)(2014－1)＝09、如图，Rt△ABC的硬纸片，∠BAC=90°，AB=3，BC=5，AD为BC边上的高，从这张硬纸片上剪下一个如图所示的内接正方形EFGH，则正方形EFGH的边长为.解：由勾股定理得AC=4，由面积公式得AB·AC=BC·AD，H G F E DC B A∴AD =125，设正方形的边长为x ，∵HG ∥BC ，∴HG BC ＝AH AB ， ∵HE ∥AD ，∴HE AD ＝BH AD ，两式相加得：x 5＋x 125＝AH ＋BH AB ＝1，解得x ＝6037。

创新教育实验班(高中)招生试卷[1]

第一届(1999年)创新教育实验班(高中)招生试卷考生须知：全卷满分1 2 0分，考试时间1 00分钟。

其中数学部分有2大题，6小题，满分6O 分；自然科学部分为2大题，1 3小题，满分6 O 分。

数学部分一、选择题(本题有3小题，每小题5分，共15分。

选出各题中1个符合题意的正确选项，填在题后的括号内。

不选：多选、错选均不给分)1．有一个盛水的容器．现匀速地向容器内注水，最后把容器注满：在注水过程的任何时刻，容器中水面的高度如图所示，图中PQ 为一线段，这个容器的形状是 ( )2．如图，相离的两个圆⊙O 1和⊙O 2在直线l 的同侧。

一条光线跟⊙O 1相切射向l 后反射，反射线又跟⊙O 2相切，则满足条件的光线共有 ( )A ．1条B ．2．条C ．3条D ．4条3．甲、乙两位同学在环形跑道上从同一点G 出发，按相反方向沿跑道而行。

已知甲每分钟跑240米，乙每分钟跑1 80米，如果他们同时出发，并且当他们在出发点G 第一次相遇时结束跑步，则他们从出发到结束之间中途相遇的次数是 ( )A ．6B ．7C ．8D ．不能确定二、解答题(本题有3小题，共45分)4．(本题12分)已知a ，b 为实数，且满足16a 2+2a+8ab+b 2—1=O ，求3a+b 的最小值。

5．(本题1 6分)已知抛物线y=2x 2—4mx+21 与x 轴有2个不同的交点A ，B ，抛物线的顶点为C ， (1)当△ABC 为等边三角形时，试确定点C 的位置。

(2)如何平移符合条件(1)的抛物线，使AC=23AB ； (3)设点D ，E 分别是AC ，BC 的中点，点F ，G 分别是DC ，EC 的中点，问四边形DFGE 的面积S 的大小与m 的取值是否有关?若有关，写出其关系式；若无关，请说明理由。

6．(本题1 7分)某校新组建一支足球队，共有队员n 人，其中每一个人恰与3个人互相认识。

(1)证明：n是偶数。

(2)如果用点表示队员，两点间连线表示这两名队员互相认识，试画出n=16时，这个球队队员间相互认识关系的一个示意图。

创新人才实验班招生考试思想品德

创新人才实验班招生考试思想品德【注意事项】1．本试卷共8页，总分100分，答题时长90分钟，请掌握好时间。

2．先将自己的姓名、准考证号用钢笔或圆珠笔填写在答题卷的相应位置上。

考试结束后，应将试卷和答题卷一并交回。

3．考生务必将答案写在答题卷上，在试卷上作答无效。

注意字迹清楚，卷面整洁。

第Ⅰ卷选择题（共40分）下列各题四个备选答案中，只有一个是最符合题意的，请选出正确答案，并将其序号填入答题卷中的表格内。

（共20题，每题2分）1．2011年3月14日，十一届全国人大四次会议通过的“十二五”规划纲要指出，“十二五”期间，我国经济和社会的发展要以为主题，以为主线。

A.保持社会稳定实现经济又快又好发展B. 科学发展加快转变经济发展方式C.保持社会稳定加快转变经济发展方式D. 科学发展实现经济又好又快发展2．2011年6月30日，全国人大常委会表决通过了关于修改个人所得税法的决定，将个税起征点提高到元，从2011年9月1日起正式施行。

A. 2800 B． 3000 C．3500 D．40003．2010年中国GDP总量超过日本,成为全球第大经济体,这一成就说明。

A．一我国已经实现共同富裕 B．一社会主义制度具有优越性C．二我国已经实现共同富裕 D．二社会主义制度具有优越性4．“‘娜’可不简单！”北京时间2011年6月4日，2011 女单决赛，李娜夺得单打冠军，在中国网球史上划下石破天惊的一笔，成为第一个大满贯的亚洲选手。

A．澳网 B．法网C．温网 D．美网5．如下图所示，两个球靠在一起，看似很紧，其实接触的只是一个点，不够紧密；如果两个球都削去一片，接触的就是一个面，会十分紧密。

这对我们适应新环境的启示在于A.学会让别人帮助自己B.在与他人的交往中认识自我C.要学会主动调节自己D.学会在逆境中保持独特个性6．多年来，马鞍山二中设立“心理咨询中心”、“学生信箱”，组织学生开展心理辅导讲座。

学校这样做①是学校的事，跟我们无关②是老师为了窥视我们的隐私③是尊重、珍爱生命的表现④有助于我们遇到问题及时求助A．①② B．②③ C．②④ D．③④7.“好说己长便是短，自知己短便是长。

湖南省衡阳县2020年高一创新实验班招生物理试卷(Word版含答案)

湖南省衡阳县2020年高一创新实验班招生物理试卷考生注意:1、本试卷共四大题，考试时间为90分钟，满分为100分。

2、计算题要求写出必要的文字说明、公式及重要的演算步骤，只写出最后答案不能得分。

3、所有答案都必须写到答题卡相应位置，写在试题卷和草稿纸上无效。

一、选择题(共32分，1-8小题为单选题，每小题2分, 9-12小题为多选题，每小题4分。

多选题全部选对得4分，选对但不全的得2分，有错选的得0分)1、下列数据中，最接近实际情况的是( )A.将一瓶500ml的普通矿泉水从地面拿起举过头顶做功约为10JB.大学生游泳的速度约为10m/sC.从冷库刚拿出的冻肉温度约为20℃D.台灯调到最亮通过的电流约为10A2、下列说法正确的是( )A.用水平力推水平地面上的箱子没推动，是因为推力小于箱子受到的摩擦力B.从枪膛射出的子弹容易射进墙壁而抛出的实心球下落后不容易陷入地面，说明子弹比实心球惯性大C.手提重物时，手上出现了压痕，是由于重物的重力作用在手上引起的D.石油、煤、天然气、可燃冰都属于不可再生能源3、下列物品中，通常情况可以导电的是( )A.普通毛笔杆B.订书钉C.硅胶D.粉笔4、夜深人静时，小明突然被- -阵轰隆隆的发动机声音惊醒，哎，又有人骑“小绵羊”在飙车，请问惊醒他和他辨别出“小绵羊”的分别是因为声音的什么特性( )A.音调响度B.响度音色C.音色音调D.音色响度5、甲、乙两车分别从P、Q两点同时沿同一直线同向运动，它们的s-t图像分别如图所示，经过6s甲在乙前方10m处，则下列说法正确的是( )A.V甲>V乙B.P、Q两点相距8mC.甲、乙两车不会相遇D.甲、乙从出发经13. 5s相遇6、公园的健身区有跷跷板，两个成年人坐在跷跷板两端，忽略一切阻力，当跷跷板处于水平静止时( )A.两人到支点的距离一定相等B.两人的重量一定相等C.重的人离支点近一些D.轻的人离支点近一些7、如图所示，A、B分别为地球人造卫星，绕行方向相同，周期分别为2h和1.5h,某时刻A、B两卫星相距最近(0、B、A在同一直线上)，0为地球中心，则A B 两卫星再一次相距最近至少需要经过的时间为( )A.1.5hB.3hC.6hD.9h8、如图甲所示，A、B两个质量相等的小球用两根等长的细线竖直悬挂，现在在A、B小球上分别施加m水平向左向右等大的拉力F,待两球再次保持静止状态时，可能是图中的( )9、下列说法正确的是( )A.房间安装隔音玻璃可以减弱外界噪音对房内的影响B.青藏高原的上气温通常比衡阳低，在青藏高原上烧水时90℃就能沸腾，说明水的沸点与气温有关C.有时白天天色较暗时，教室内也要开灯，如果拉上窗帘，我们感觉教室内更亮，这是因为光的漫反射D.“一粒老鼠屎坏了一锅粥”是因为热传递10、一辆汽车以108km/h的速度在水平路面上匀速行驶了1h，消耗汽油10kg,若已知该汽车发动机的功率(即牵引力的功率)为30kw,汽车总质量为2t,汽油的密度为0.725g/ml,热值为4.5×107J/kg,g=10N/kg.则下列对汽车在这段路.上的行驶分析正确的是( )A.该汽车这段路的百公里油耗约为12.8LB.该汽车克服阻力做的功是1.0×108JC.该汽车的牵引力是2.0×103ND.该汽车发动机的效率是24%11、如图所示，电源电压不变，电表均为理想表，当电键S由断开到闭合时，下列变化正确的是( )A.电流表A示数变小示数变为0B.电压表V1示数与电流表A示数的比值不变C.电压表V2D.电压表V示数与电流表A示数的比值不变112、如图所示，粗糙的水平地面上放置相同材料制成的2个木块A、B,质量分别为2kg和3kg,木块间用一不可伸长的水平轻绳相连，现用水平向右的拉力F=20N 拉其中B木块，使A、B一起水平向右匀速运动，则( )A. A与地面间的摩擦力大小为0B. B与地面间的摩擦力大小为12NC.轻绳对A的拉力大小为10ND.轻绳对B的拉力大小为8N二、作图及填空题(共20分)13、(4分)如图所示，若小磁针静止时的北极指向右，当滑动变阻器滑片向B端移动时，通电螺线管的磁性减弱，在不改变原有导线情况下，请用笔画线代替导线将图示的实物图补充完整。

高一创新班物理、化学考试题及答案

高一创新班物理、化学考试题物理试题试卷说明：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分120分，考试时间90分钟。

2．答第Ⅰ卷前，考生务必将准考证号、考试科目用2B铅笔涂写在答题卡上，并同时将班级、姓名、学号填写在规定的地方。

3．选择题选出答案后，用2B铅笔把答题卡上对应题目的正确答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案，答案写在试卷上无效。

4．非选择题答题时，务必书写于指定位置，笔迹清晰。

5.考试结束后，应将本试卷和答题卡一并交给监考教师。

可能用到的相对原子质量：H-1 C-12 N-14 O-16 S-32 Cl -35.5 Na-23 Mg-24 Ca-40 Fe-56 Cu-64 Zn-65 Ag-108 Ba-137第Ⅰ卷选择题一、单项选择题（共16题，每题32分）1.发酵法制乙醇（C2H5OH）是最常用的工业方法。

发酵法的原料是含淀粉的农产品，如谷类、薯类或野生植物果实等或者是含纤维素的木屑、植物茎秆等。

这些物质经一定的预处理后，经水解、发酵，即可制得乙醇。

车用乙醇汽油是由乙醇与汽油按1：9的比例混合而成。

下列有关推广使用乙醇汽油的说法不正确的是（）A．乙醇属于有机化合物B．有助于减轻大气污染，改善大气环境C．乙醇是一种不可再生的能源D．有助于促进麦秸秆等农作物转化，提高农民收入2. 生物体死亡后，体内含有的碳-14会逐渐减少（称为衰变）。

因此科学家可通过测量生物体遗骸中碳-14的含量，来计算它存活的年代，这种方法称之为放射性碳测年法。

碳-14原子核中含6个质子与8个中子，在衰变时，一个中子变成质子，形成新的原子核。

下列关于新原子核的说法正确的是（）。

A．碳原子核，含7个质子，8个中子B．氧原子核，含7个质子，8个中子C．碳原子核，含6个质子，7个中子D．氮原子核，含7个质子，7个中子3. 化学与生活密切相关，从化学的角度认识生活中的问题，下列说法正确的是( )A．地沟油经化学方法处理制成航空燃油，实现变废为宝B．食品添加剂符合国家许可，制作食品过程中可随意添加C．脂肪、糖类、动物蛋白都是人体必须的营养素，吃得越多越好D．生活污水不是化工废水，可向江河湖泊里任意排放4. 现有3种无色溶液，溶质分别为硫酸铵、氯化钠和碳酸钾。

年普通高中创新素养培养实验班招生考试试卷及答案

年普通高中创新素养培养实验班招生考试试卷及答案The following text is amended on 12 November 2020.E DCBA 2014年普通高中创新素养培养实验班招生考试试卷数学试题一、选择题（共6题，每题4分，共24分）1、从1，2，3，4，5这五个数字任取两个数字，使其乘积为偶数的概率为（）（A ）45 （B ）710 （C ）35 （D ）12解：总数=4+3+2+1=10，符合条件的为：2×1；2×3；2×4；2×5；4×1；4×3；4×5共7个（或只有1×3；1×5；3×5共3个例外），∴概率为710或1－310＝7102、已知锐角△ABC 角平分线AD 与高线BE 交于点M ，△CDE 是等边三角形，则S △DEM ∶S △ABM 的值为（）（A ）2∶2 （B ）1∶2 （C ）1∶3 （D ）1∶4∵∠C=600，∠BEC=900，∴∠EBC=300，又∠CDE=600，∴∠BED=300，∴ED=BD=CD，∴AD即是∠BAC的平分线，又是BC上的中线，∴AB=AC，∴△ABC为正三角形，∴AD与BE的交点为△的重心∴S△DEM∶S△ABM=1∶4。

3、在平面直角坐标系中，O为坐标原点，点A在第二象限，点B在x轴负半轴上，△OAB的面积是9，P是AB中点，若函数y＝kx（x<0）的图像经过点A、P，则k的值为（）（A）－6 （B）－4 （C）－3 （D）－2设点A坐标为（m，n），点B（a，0），∵S△OAB=9，∴－12an＝9，∵P是AB的中点，∴点P坐标为（m＋a2，n2），∵k＝xy，∴代入A、P坐标得：k＝mn，k＝(m＋a)n4，∴mn＝(m＋a)n4，∴3mn＝an，∵－an＝18，∴mn＝－6∴k＝－6（本例考点为点与函数的关系、中点坐标的应用，中点坐标是解压轴题的重要工具）※ 同类测试题：如在直角坐标系中，存在一个平行四边形，其中平行四边形的三个项点的坐标为（1，3），（2，2）和（3，4），求另一顶点的坐标4、对于任意的有理数a，方程2x2＋(a＋1)x－(3a2－4a＋b)＝0的根总是有理数，则b的值为（）（A）1 （B）－1 （C）2 （D）0解：方程的△＝(a＋1)2＋8(3a2－4a＋b)＝(5a－3)2＋8b－8≥0，∴当8b－8≥0时，必定△≥0，即方程必有实根，∴b≥1，当b＝1时，3a2－4a＋1＝(3a－1)(a－1)，∴十字因式分解得方程为（(x－a＋1)(2x＋3a－1)＝0，∴b＝1成立，当b＝2时，3a2－4a＋b＝3a2－4a＋2不能因式分解，∴方程有可能为无理数解，（在一元二次方程中，运用方程的判别式和因式分解是解决方程有理根和整数根重要工具，）※同类测试题：使得m2＋m＋7是完全平方数的所有整数m的积的值。

创新班招生考试卷语文

一、选择题（每题2分，共20分）1. 下列词语中，字形、字音、字义完全正确的是：A. 沉鱼落雁眉清目秀美轮美奂B. 惊弓之鸟塞翁失马美中不足C. 雕梁画栋鹤立鸡群画蛇添足D. 美不胜收红颜薄命色厉内荏2. 下列句子中，没有语病的是：A. 他不仅学习成绩好，而且具备良好的品德。

B. 通过这次活动，同学们不仅增强了团队协作能力，还丰富了业余生活。

C. 他的歌声如泉水般清澈，如黄鹂般婉转。

D. 我喜欢看书，尤其是科幻小说。

3. 下列成语中，意思与其他三项不同的一项是：A. 胸有成竹B. 背水一战C. 班门弄斧D. 画龙点睛4. 下列句子中，使用了比喻修辞手法的是：A. 小明长得像他爸爸。

B. 雨后的彩虹犹如一条七彩丝带。

C. 这本书对我来说是至关重要的。

D. 他勤劳肯干，是公司的顶梁柱。

5. 下列词语中，属于双音节叠词的是：A. 沉默B. 跳跃C. 欣喜D. 悲伤二、填空题（每题2分，共20分）1. 我国古代四大名著分别是《》、《》、《》、《》。

（填书名）2. 下列词语中，含有“自”字的有：自满、自高自大、自言自语、自力更生。

（填词语）3. 《水浒传》中，智取生辰纲的人物是（填姓名）。

4. 《红楼梦》中，贾宝玉的通灵宝玉是（填物品）。

5. 《西游记》中，孙悟空的武器是（填武器）。

三、阅读题（每题10分，共30分）阅读下面的文章，完成题目。

秋天的田野秋天，是一个收获的季节，也是一个美丽的季节。

走在乡间的田野上，我看到了一幅幅美丽的画卷。

金色的稻田里，稻穗沉甸甸的，像一颗颗金黄的珍珠。

农民伯伯们弯着腰，忙碌地收割着稻谷。

他们的脸上洋溢着幸福的笑容，仿佛在说：“看，我们丰收了！”果园里，果实累累。

苹果红彤彤的，像一个个小灯笼；葡萄紫溜溜的，像一串串珍珠；柿子红艳艳的，像一个个小红灯笼。

果农们正在采摘果实，他们的脸上洋溢着喜悦，仿佛在说：“看，我们的果实熟了！”菜地里，蔬菜长得郁郁葱葱。

黄瓜、西红柿、豆角等各种蔬菜应有尽有。

甘肃省民乐一中2020-2021学年高一创新实验班招生考试化学试题含答案

民乐一中2021级创新实验班招生考试化学试卷相对原子质量C:12 O:16 H:1 Na:23 N：14（全卷80分）一、选择题（本题25小题，1～10小题，每小题1分，11～25小题，每小题2分，共40分。

每小题所列的四个选项中，只有一个选项符合题目要求。

）1.下列典故中，从物质变化的角度分析，主要体现化学变化的是（）A．煤的干馏B．分离液态空气C．石油的分馏D．品红遇水变红色2. 有关下列实验的说法中，不合理的是（）甲乙丙丁A．甲实验中左试管放出气泡快，说明MnO2比CuO的催化效果好B．乙实验中水中长导管口冒气泡，说明此装置气密性良好C．丙实验中低的蜡烛先熄灭，说明CO2的密度大于空气D．丁实验中生成氢气和氧气，说明水是由氢氧元素组成3．把A克的二氧化锰放入B克的过氧化氢中，完全反应后，剩余的质量为C克，则生成氧气的质量为（）A．（B-C）g B．（A+B-C）g C．（A-B）g D．（C-B）g4.下列实验操作中能达到实验目的的是（）选项目的主要实验操作A 鉴别硬水和蒸馏水加入肥皂水，振荡，观察现象B 检验人呼出的气体中的O2伸入带火星的木条，观察是否复燃C 自来水的杀菌消毒加入明矾，充分搅拌，静置D 排空气法收集CO2时验满把燃着的木条伸入集气瓶中，观察是否熄灭5.如图是关于氧气的部分知识网络，关于该图说法正确的是（）A．实验室制氧气的原料都是纯净物B．Ⅰ类反应都是化合反应C．Ⅱ类反应中可以添加光合作用D．Ⅰ、Ⅱ两类反应都放出热量6.在某氮的氧化物里，氮元素与氧元素的质量比为7：4，则该氧化物的化学式为（）A. NOB. N2O5C. NO2D. N2O7.下列图形能正确反映对应变化关系的是（）A B C DA.加热一定质量氯酸钾和二氧化锰混合物B.在密闭容器中甲烷完全燃烧C.碳在盛有氧气的密闭集气瓶内燃烧D.电解水8. 下列对一些事实的解释错误的是（）事实解释A 书写档案规定必须使用碳素墨水碳的化学性质稳定B 二氧化碳能使浸有紫色石蕊溶液的纸花变红二氧化碳和水反应生成碳酸C 焦炭可以把铁从它的氧化物矿石里还原出来焦炭具有氧化性D 金刚石、石墨和C60的化学性质相似但物理性质差异很大金刚石、石墨和C60都是由碳元素组成的单质,但它们的原子排列方式不同9. 右下图是反映某个化学反应里各物质质量与时间的变化关系，下列对此变化的描述中，正确的是（）A．充分反应后，乙+丙=甲的质量B．物质甲的相对分子质量大于乙C．此化学反应中，不遵守质量守恒定律D．反映了此化学反应是分解反应10.一定条件下，甲、乙、丙、丁四种物质在密闭容器中反应，测得反应前后各物质的质量分数如图所示，下列说法正确的是（）A．丁是该反应的催化剂B. 甲、乙的质量之和一定等于生成丙的质量C. 该反应中甲、丙的质量比为7：10D．该反应中乙、丙的质量比为3：1711．电解质是溶于水溶液中或在熔融状态下就能够导电的化合物，则下列说法正确的是（）A．NaCl固体不导电，NaCl是非电解质B．CO2的水溶液能导电，所以CO2是电解质C．铜、石墨均能导电，所以它们都是电解质D．蔗糖在水溶液或熔化时均不导电，所以它是非电解质12．下列各组中的两物质作用时，反应温度或反应物用量的改变，对生成物没有影响的是（）A．H2O2与MnO 2B．Fe与O2C．NaOH与CO2D．C与O2,13．在Fe+CuSO₄=FeSO₄+Cu反应中，Cu被Fe还原了出来，则根据下列反应：（1）2ACl3＋3B＝2A＋3BCl2（2）3DCl2＋2A＝2ACl3＋3D（3）BCl2＋C＝CCl2＋B，判断A、B、C、D的还原性由强到弱的顺序是（）A.A＞B＞C＞DB.D＞C＞B＞AC.C＞B＞A＞DD.B＞A＞C＞D14.常用燃烧法测定有机物的组成。

河北省高一(创新班)下学期入学考试数学试题(解析版)

2022－2023学年度高一（下）期创新班入学考试题一、单选题（满分40分，每小题5分）1. 已知集合，集合，则（） {}3,2,1,0,1A =---{N23}B x x =∈-≤<∣A B = A. B.C.D.{3,2,1,0,1}---{}2,1,0,1--{}0,1{}2,1,0--【答案】C 【解析】【分析】由交集运算求解即可.【详解】因为，所以. {}{N23}0,1,2B x x =∈-≤<=∣A B = {}0,1故选：C2. 若函数的定义域为，值域为，则的取值范围是（） 234y x x =--[]0,m 25,44⎡⎤--⎢⎥⎣⎦m A. B.C.D.(]0,43,32⎡⎤⎢⎥⎣⎦3,42⎡⎤⎢⎥⎣⎦3,2⎡⎫+∞⎪⎢⎣⎭【答案】B 【解析】【分析】画出二次函数图象，结合对称轴和值域可判断取值范围. m 【详解】的对称轴为，当时，，时， 234y x x =--32x =32x =254y =-0x =4y =-故当时，设另一根为，解得，要使定义域为时，值域为，故4y =-2x 23x =[]0,m 25,44⎡⎤--⎢⎥⎣⎦.3,32m ⎡⎤∈⎢⎥⎣⎦故选：B3. 已知函数是奇函数，是偶函数，且，则（） ()f x ()g x ()()232f xg x x x +=+-()f x =A. B. C. D. 2464xx x --2464xx x +-2334xx x --2234xx x +-【答案】D 【解析】【分析】根据函数的奇偶性可得出关于、的等式组，由此可解得函数的解析式. ()f x ()g x ()f x 【详解】因为是奇函数，是偶函数，所以，．()f x ()g x ()()f x f x -=-()()g x g x -=所以，，即，()()()()232232f x g x x x f x g x x x ⎧+=+⎪⎪-⎨⎪-+-=-+⎪--⎩()()()()232232f x g x x x f x g x x x ⎧+=+⎪⎪-⎨⎪-+=--⎪+⎩因此，. ()2234xf x x x =+-故选：D.4. 下述正确的是（）A. “，”是“”的充要条件 ππ4k θ=+k ∈Z sin cos θθ=B. 若，则cos 0θ=π2θ=C. 若的终边为第三象限平分线，则 θtan 1θ=-D. 若为第四象限角，则 θsin 0θ>【答案】A 【解析】【分析】根据充分条件和必要条件的定义结合三角函数的定义即可判断A ；根据特殊角的余弦函数值即可判断B ；根据第三象限正切值的符号即可判断C ；根据第四象限正弦值的符号即可判断D. 【详解】对于A ，若，， 4k θπ=π+k ∈Z 当为奇数时，kππππsin sin πsin cos πcos 4444k k θθ⎛⎫⎛⎫=+=-==+=-= ⎪ ⎪⎝⎭⎝⎭当为偶数时，k， ππππsin sin πsin cos πcos 4444k k θθ⎛⎫⎛⎫=+===+==⎪ ⎪⎝⎭⎝⎭综上，，sin cos θθ=若，则， sin cos θθ=sin cos 0θθ-=π04θ⎛⎫-= ⎪⎝⎭所以，所以，， ππ4k θ-=ππ4k θ=+k ∈Z 所以“，”是“”的充要条件，故A 正确；ππ4k θ=+k ∈Z sin cos θθ=对于B ，若，则，故B 错误；cos 0θ=ππ,Z 2k k θ=+∈对于C ，若的终边为第三象限平分线，则，故C 错误； θtan 1θ=对于D ，若为第四象限角，则，故D 错误. θsin 0θ<故选：A.5. 已知函数，若，且，则的取值范围是（） ()lg f x x =0a b <<()()f a f b =a b +A. B.C.D.()1,+∞[)1,+∞()2,+∞[)2,+∞【答案】C 【解析】【分析】将函数化成分段函数的形式，可得且时，必有成立，利用对勾函0a b <<()()f a f b =1ab =数的单调性即可算出答案【详解】因为函数，且时， lg ,1()lg lg ,01x x f x x x x >⎧==⎨-<≤⎩0a b <<()(),f a f b =所以，， 01a b <<<lg lg 1a b ab -=⇔=所以，由对勾函数在区间单调递减可得， 1a b a a +=+1y x x =+()0,111121a a +>+=所以的取值范围是 ab +()2,+∞故选：C6. 某正四棱锥的侧棱与底面所成的角为45°，则该正四棱锥的侧面与底面的面积之比为（）A.B.C.D.【答案】D【分析】设底面边长为，由线面角的定义可得侧棱长,然后分别求侧面的面积和底面的面积即可得解. a 【详解】如图，是正四棱锥的高，PO P ABCD-设底面边长为，则底面积为， a 21S a =因为正四棱锥的侧棱与底面所成的角为， 45︒所以，又，所以， 45PAO ∠=︒AO=PA a ==所以是正三角形，面积为， PAB22S =所以214S S ==故选：D.7. 已知的内角所对的边分别为，下列四个命题中正确的命题是（） ABC A B C ，，a b c ，，A. 若，则一定是等边三角形 cos cos cos a b cA B C==ABC B. 若，则一定是等腰三角形 cos cos a A b B =ABC C. 若，则一定是等腰三角形 cos cos b C B b +=ABC D. 若，则一定是锐角三角形 2220a b c +->ABC 【答案】A 【解析】【分析】由正弦定理化边为角变形判断AB ，举特例判断C ，由余弦定理及锐角三角形的定义判断D ．【详解】由正弦定理，若，则，sin sin sin a b cA B C ==cos cos cos a b c A B C==tan tan tan A B C ==为三角形内角，所以，三角形是等边三角形，A 正确；,,A B C A B C ==若，由正弦定理得，即， cos cos a A b B =sin cos sin cos A A B B =sin 2sin 2A B =，则或，即或，三角形为等腰三角形或直角三角,(0,π)A B ∈22A B =22πA B +=A B =π2A B +=例如，，，满足，但此时不是等腰三角形，C 错；b =π3C =π6B =cos cos b C B b +=ABC 时，由余弦定理可得，即为锐角，但是否都是锐角，不2220a b c +->222cos 02a b c C ab+-=>C ,A B 能保证，因此该三角形不一定是锐角三角形，D 错．故选：A ．【点睛】易错点睛：本题考查三角形形状的判断，解题时利用正弦定理、余弦定理进行边角转换后再进行变形判断是常用方法，解题时注意三角函数性质的正确应用，如选项B ，在由得结论sin 2sin 2A B =时不能直接得出，否则会出现漏解，在判断三角形形状时，锐角三角形需要三个内角都是锐22A B =角，直角三角形只有一个角是直角，钝角三角形只有一个角是钝角，它们判断方法有一些区别，这些是易错点．8. 已知正方体的棱长为分别是棱的中点，动点在正方形1111ABCD A B C D -1,,M N 1,BC CCP 11BCC B （包括边界）内运动，若平面，则线段的长度范围是（）1//PA AMN1PAA. B.C. D.【答案】B 【解析】【分析】先过点画出与平面平行的平面，然后得出点的轨迹，最后计算的长度取值范围1A AMN P 1PA 即可.【详解】如图，分别作的中点,连接111,B C BB ,E F 11,,EF A E A F显然,//EF MN 1//A E AM 且平面，；平面, 1,A E EF ⊂1A EF 1A E EF E ⋂=,AM MN ⊂AMN AM MN M ⋂=所以平面平面 1A EF //AMN 平面平面1A EF 11BCC B EF =所以动点在正方形的轨迹为线段P 11BCC B EF在三角形中，，1A EF 112EF BC ==11A E A F ===所以点到点的最大距离为，最小距离为等腰三角形在边上的高为P 1A 11A E A F ==1A EF EF=故选：B二、多选题（满分20分，每小题5分，选对但不全得2分，有错得0分，全对得5分） 9. 已知平面向量，，，则（）．(),1a m = ()2,b n = ()1,2c =-A. 若，则B. 若，则a c ∥12m =-bc ⊥1n =C. 若与的夹角为锐角，则D. 的最小值为4b c1n <2a c -【答案】ABD 【解析】【分析】根据向量的平行和垂直的坐标表示，列式计算，可判断A,B;根据向量的夹角公式求出与的bc夹角为锐角时的n 的范围，要考虑向量同向情况，判断C;根据向量的模的坐标计算可判断D.【详解】由题意平面向量，，，(),1a m = ()2,b n = ()1,2c =-若，则，A 正确； a c∥1210,2m m --=∴=-若，则，B 正确； b c ⊥220,1n n -=∴=若与的夹角为锐角，则，即，bc220b c n ⋅=->1n <但时，与同向，满足，但夹角为，不是锐角，故C 错误；n =-4bc220b c n ⋅=->，2a c -===当，故的最小值为4，D 正确， 12m =4=2a c - 故选：ABD.10. 已知复数，则下列说法正确的是（）()21(1)i()z m m m m =-+++∈R A. 若，则的共轭复数 B. 若复数，则 0m =z 1z =--2z=m =C.若复数为纯虚数，则 D. 若，则z 1m =±0m =2420z z ++=【答案】ABD 【解析】【分析】根据每个选项里的条件，求出相应的结果，即可判断选项的正误. 【详解】对于A ，时，，则，故A 正确；0m =1z =-+1z =-对于B ，若复数，则满足，解得，故B 正确；2z =(()21210m m m ⎧-=⎪⎨++=⎪⎩m =对于C ，若复数z 为纯虚数，则满足，解得，故C 错误；(()21010mm m ⎧-=⎪⎨++≠⎪⎩1m =对于D ，若，则，0m =1z =-，故D 正确.()()2211424242130z z ++=++=-++-+--=-故选：ABD.11. 已知函数（，，）的部分图象如图所示，则下列结论正确()()sin f x A x =+ωϕ0A >0ω>π2ϕ<的是（）A. ()π2cos 23f x x ⎛⎫=-⎪⎝⎭B. 满足的的取值范围为（） ()1f x >x ππ,π3k k ⎛⎫+ ⎪⎝⎭k ∈Z C. 将函数的图象向右平移个单位长度，得到的图象的一条对称轴()f x π12π3x =D. 函数与的图象关于直线对称 ()f x ()2cos 2g x x =-π3x =【答案】ABD 【解析】【分析】根据图象求出的解析式，然后运用三角函数的知识逐一判断即可.()f x 【详解】由图可得，， ()max 1152,2πππ1212f x T ⎛⎫==⨯-=⎪⎝⎭所以，因为，所以， 2,2A ω==ππ2sin 201212f ϕ⎛⎫⎛⎫-=-⨯+= ⎪ ⎪⎝⎭⎝⎭π2π,Z 6k k ϕ-+=∈所以，因为，所以 π2π+,Z 6k k ϕ=∈π2ϕ<π,6ϕ=，故A 正确；()=π2c 2π2sin o 26s 3f x x x ⎛⎫- ⎪⎪⎝⎛⎫=+ ⎝⎭⎭由可得， ()π2sin 216f x x ⎛⎫=+> ⎪⎝⎭π1sin 262x ⎛⎫+> ⎪⎝⎭所以，解得，，故B 正确；ππ5π2π22π,Z 666k x k k +<+<+∈ππ,π3x k k ⎛⎫∈+ ⎪⎝⎭k ∈Z 将函数的图象向右平移个单位长度，得到的是函数的图()f x π12ππ2sin 22sin 2126y x x ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦象，直线不是其对称轴，故C 错误； π3x =因为，()2π3π2sin 22cos 232f x x x g x ⎛⎫⎛⎫-=-+=-=⎪ ⎪⎝⎭⎝⎭所以函数与的图象关于直线对称，故D 正确； ()f x ()2cos 2g x x =-π3x =故选：ABD12. 如图，棱长为2的正方体中，P 为线段上动点（包括端点）.则下列结论正确1111ABCD A B C D -11B D 的是（）A. 当点P 在线段上运动时，三棱锥的体积为定值11B D 1P A BD -B. 记过点P 平行于平面的平面为，截正方体截得多边形的周长为 1A BD αα1111ABCD A B C D -C. 当点P 为中点时，异面直线与所成角为11B D 1A P BD π2D. 当点P 为中点时，三棱锥的外接球表面积为 11B D 1P A BD -11π【答案】ACD 【解析】【分析】对A ，显然平面，所以在任何位置时到平面的距离相等，即可得解； 11B D ∥1A BD P 1A BD 对B ，由在上且，故截面为，算出周长即可；P 11B D 11B D BD ∥11B CD 对C ，当点P 为中点时，由于为正方形，所以，即可得到垂直；11B D 1111D C B A 111A P B D ⊥对D ，是线面垂直型的外接球问题，当点P 为中点时，，设外接圆直径，所11B D 111A P B D ⊥BPD △2r以三棱锥的外接球的直径，即可得解.1P A BD -2R =【详解】对A ，由于，显然平面， 11B D BD ∥11B D ∥1A BD 又，所以在任何位置时到平面的距离相等， 11P B D ∈P 1A BD 所以三棱锥的体积为定值，故A 正确； 1P A BD -对B ，由在上且，故截面为，P 11B D 11B D BD ∥11B CD所以截面周长为B 错误；对C ，当点P 为中点时，由于为正方形，11B D 1111D C B A 所以，又，所以，故C 正确； 111A P B D ⊥11BD B D ∥1A P BD ⊥对D ，当点P 为中点时，， 11B D 111A P B D ⊥所以在正方体中平面，1A P⊥BDP 由，，BD =BP DP ==所以，22241cos 2123BP DP BD BPD BP DP +-∠===⋅⋅sin BPD ∠=所以外接圆直径， BPD△23r ==所以三棱锥的外接球的直径，1P A BD -2R ===所以三棱锥的外接球表面积为，故D 正确； 1P A BD -2411ππ=故选：ACD三、填空题（满分20分，每小题5分）13. 已知向量，，，若A ，B ，D 三点共线，则_________．()2,1AB = ()7,BC m = ()3,1CD =-m =【答案】6 【解析】【分析】根据给定条件，求出，再利用共线向量的坐标表示计算作答.BD【详解】因，，则，()7,BC m = ()3,1CD =-(10,1)BD BC CD m =+=- 又，且A ，B ，D 三点共线，即，因此，解得，()2,1AB = //AB BD2(1)1100m --⨯=6m =所以. 6m =故答案为：614. 设，且，则________． 25a b m ==211a b+=m =【答案】20 【解析】【分析】显然用对数式表示出后代入，运用对数的运算法则化简可得答案. 0,m >,a b 211a b+=【详解】依题意有0,m > 2525,log ,log ,a b m a m b m ==∴==. 25212112log 2log 5log 20,20log log m m m m a b m m=+=+=+=∴=故答案为：2015. 如图，在三棱锥木块中，VA ，VB ，VC 两两垂直，，点P 为的重V ABC -1VA VB VC ===VAC 心，沿过点P 的平面将木块锯开，且使截面平行于直线VC 和AB ，则该截面的面积为______．【解析】【分析】如图作出平面，根据线面平行的判定定理，可证平面，平面EFMH AB ∕∕EFMH VC ∕∕，则平面即为所求，根据线面平行的判定定理、性质定理，可证四边形为平行EFMH EFMH EFMH 四边形，根据线面垂直的判定定理、性质定理，可证四边形为矩形，根据三角形相似，可求得EFMH 的值，即可得答案.,HE EF 【详解】由VA ，VB ，VC 两两垂直，，1VA VB VC ===则可将三棱锥补形到正方体中，连接AP 并延长，交VC 于D ，过P 作VC 的平行线，交AV 于E ，交AC 与F ，过E 作，交VB 于H ，过H 作，交BC 于M ，连接MF ，如图所示EH AB ∕∕HM VC ∕∕因为，所以E 、F 、M 、H 四点共面， MH VC EF ∕∕∕∕因为，平面，平面， EF VC ∕∕VC ⊄EFMH EF ⊂EFMH 所以平面，VC ∕∕EFMH 因为，平面，平面， EH AB ∕∕AB ⊄EFMH HE ⊂EFMH 所以平面， AB ∕∕EFMH 则平面即为所求，EFMH 因为，平面，平面， EH AB ∕∕EH ⊄ABC AB ⊂ABC 所以平面，EH ∕∕ABC 又平面，平面平面， EH ⊂EFMH EFMH ⋂ABC MF =所以，EH MF ∕∕所以四边形为平行四边形，EFMH 又，平面VAB ， ,VC VB VC VA ⊥⊥,VA VB ⊂所以平面VAB ， VC ⊥所以平面VAB ， EF ⊥因为平面VAB ，EH ⊂所以，即四边形为矩形， EF EH ⊥EFMH 因为， EF VC ∕∕所以， AEF AVC ∽因为P 为的重心， VAC 所以，则， 23EF AE AP VC AV AD ===23AE EF ==同理可证，VEH VAB ∽所以，则， 13VE HE VA AB ==HE =所以矩形EFMH 23=16. 已知函数，，以，，的值为边长()()222221x k x f x x x +++=++()0x >∀,,0a b c >()f a ()f b ()f c 可构成一个三角形，则实数的取值范围为______． k 【答案】 []3,6-【解析】【分析】根据题意可知, 恒成立,再分情况讨论函数的最值即可. ∀,,0a b c >()()()f a f b f c +>()f x 【详解】根据题意可知, 恒成立,∀,,0a b c >()()()f a f b f c +>又. ()()222222222222211111x k x x x kx kx k f x x x x x x x x x++++++===+=+++++++++()0x >1.当时, 显然成立. 0k =()2f x =2.当时,因为函数在上单调递减,在上单调递增, 0k >11y x x=++()0,1[)1,+∞故.所以.[)113,y x x=++∈+∞22,2131k k y x x⎛⎤=+∈+ ⎥⎝⎦++又恒成立,所以.此时 ∀,,0a b c >()()()f a f b f c +>22263kk +≥+⇒≤06k <≤3. 当时,同2有,所以 0k <[]113,y x x=++∈+∞222131k k y x x⎡⎫=+∈+⎪⎢⎣⎭++，此时.此时 22233k k ⎛⎫⨯+≥⇒≥- ⎪⎝⎭30k -≤<综上所述, 的取值范围为k []3,6-【点睛】本题主要考查了函数的值域综合问题,需要根据题意求函数的最值并列出函数最值满足的关系式,同时也需要对函数的分离常数化简等有所掌握.属于难题.四、解答题（满分70分）17. 若不等式的解集是． 2(1)460a x x --+>{31}x x -<<（1）解不等式；22(2)0x a x a +-->（2）b 为何值时，的解集为R ． 230ax bx ++≥【答案】（1）或{1x x <-}32x >（2） []6,6-【解析】【分析】（1）由题意可得和1是方程的两个根，则有，求出的3-2(1)460a x x --+=43116311a a ⎧-+=⎪⎪-⎨⎪-⨯=⎪-⎩a 值，然后解不等式即可，22(2)0x a x a +-->（2）由（1）可知的解集为R ，从而可得，进而可求出的取值范围 2330x bx ++≥0∆≤b 【小问1详解】由题意得和1是方程的两个根，则有，解得，3-2(1)460a x x --+=43116311a a ⎧-+=⎪⎪-⎨⎪-⨯=⎪-⎩3a =所以不等式化为，， 22(2)0x a x a +-->2230x x -->(1)(23)0x x +->解得或， 1x <-32x >所以不等式的解集为或{1x x <-}32x >【小问2详解】由（1）可知的解集为R ， 2330x bx ++≥所以，解得， 24330b ∆=-⨯⨯≤66b -≤≤所以的取值范围为b []6,6-18. 函数.()22cos cos 2f x x x x =-+（1）求的单调递增区间； ()f x （2）求在上的值域.()f x π0,2⎡⎤⎢⎥⎣⎦【答案】（1），2πππ,π36k k ⎡⎤-+-+⎢⎥⎣⎦Z k ∈（2） []1,4【解析】【分析】（2）由已知，根据题意，对原函数化简，得到函数，()22cos cos 2f x x x x =-+，然后根据余弦函数单调区间，解不等式，即可完π()2cos 233f x x ⎛⎫=++ ⎪⎝⎭ππ2π22π3k x k -+≤+≤成求解；（2）由已知，可令，根据x 的范围，求解出t 的范围，先求解出，然后再求解函数3π2t x =+cos t 的值域.()f x 【小问1详解】cos 223x x =+π2cos 233x ⎛⎫=++ ⎪⎝⎭，， ππ2π22π3k x k -+≤+≤Z k ∈，； 2ππππ36k x k -+≤≤-+Z k ∈∴的单调增区间为，；()f x 2πππ,π36k k ⎡⎤-+-+⎢⎥⎣⎦Z k ∈【小问2详解】因为，令，所以，π0,2x ⎡⎤∈⎢⎥⎣⎦3π2t x =+π4π,33t ⎡⎤∈⎢⎥⎣⎦∴，所以，1cos 1,2t ⎡⎤∈-⎢⎥⎣⎦[]π()2cos 231,43f x x ⎛⎫=++∈ ⎪⎝⎭∴. ()[]1,4f x ∈19. 已知是定义域为R 的奇函数． ()221xf x a =-+（1）求a 的值；（2）判断的单调性并证明你的结论；()f x （3）若恒成立，求实数k 的取值范围． ()()22220f x x f x k -++--<【答案】（1）；1a =（2）单调递增，证明见解析；（3）. 116k >【解析】【分析】（1）利用奇函数定义，列式计算作答.（2）判断单调性，再利用函数单调性定义按步骤推理作答.（3）利用函数的奇偶性、单调性脱去法则“f ”，再分离参数求出最值作答. 【小问1详解】因为函数是定义域为R 的奇函数，则有，解得， ()221xf x a =-+02(0)1021f a a =-=-=+1a =此时，，函数是奇函数， ()22112121x x x f x -=-=++()211221()211221x x x x xx f x f x ------===-=-+++()f x 所以. 1a =【小问2详解】函数在R 上单调递增，()f x 任意，1212,R,x x x x ∈<121221*********(22)()()(1)(121212121(21)(21)x x xx x x x x f x f x --=---=-=++++++，因为函数在R 上单调递增，，则有，即有，即2x y =12x x <12022x x <<12())0(f x f x -<，12()()f x f x <所以函数在R 上单调递增. ()f x 【小问3详解】由（2）知，函数在R 上单调递增，又是R 上的奇函数，()f x ()f x不等式恒成立，等价于， ()()22220f x x f x k -++--<()()()222222f x x f x k f x k -+<---=+即恒成立，而，当且仅当时222224x x x k k x x -+<+⇔>-+2211144(81616x x x -+=--+≤18x =取等号，则， 116k >所以实数k 的取值范围是. 116k >20. 在①，②，③，5cos cos cos 4a C c A b B +=π5sin()5sin()12B B ++-=π(0,2B ∈13cos 2cos 25B B =-．这三个条件中任进一个，补充在下面问题中并作答．已知中，内角所对的边分别为，且________． ABC ,,A B C ,,a b c （1）求的值; tan2B （2）若，求的周长与面积． 1211tan ,54A c =-=ABC 【答案】（1）247（2）周长为11，面积为 338【解析】【分析】（1）若选①，利用正弦定理边化角及诱导公式求出，再求出，由正切的二倍角4cos 5B =tan B 公式即可求出的值；若选②，由诱导公式化简，再结合三角函数的平方和，可求出，tan2B sin B tan B ，再由正切的二倍角公式可求出的值；若选③，由余弦的二倍角公式代入化简求出，再tan2B 4cos 5B =求出，由正切的二倍角公式可求出的值； tan B tan2B （2）由，求出，由正弦定理求出，最后根据三角形的面积公式和周长即可12tan 5A =-cos ,sin A A ,a b 得出答案. 【小问1详解】若选①:由正弦定理得，5sin cos sin cos sin cos 4A C C A B B +=故，5sin()sin cos 4A CB B +=而在中，， ABC sin()sin(π)sin A C B B +=-=故，又，5sin sin cos 4B B B =(0,π)B ∈所以，则， sin 0B ≠4cos 5B =则， 3sin 3sin ,tan 5cos 4B B B B ====故．22tan 24tan 21tan 7B B B ==-若选②:由，化简得，代入中，整理得π5sin()5sin()12B B ++-=1cos sin 5B B -=22cos sin 1B B +=，225sin 5sin 120B B +-=即，(5sin 3)(5sin 4)0B B -+=因为，所以，所以， (0,π)B ∈sin 0B >3sin 5B =则， 4sin 3cos ,tan 5cos 4B B B B ===故．22tan 24tan 21tan 7B B B ==-若选③:因为， 13cos 2cos 25B B =-所以，即，则． 2132cos 1cos 25B B -=-2122cos cos 025B B --=34(2cos )055B B +-=因为，所以， π(0,)2B ∈4cos 5B =则， 3sin 3sin ,tan 5cos 4B B B B ====故．22tan 24tan 21tan 7B B B ==-【小问2详解】因为，且， sin 12tan cos 5A A A ==-22sin cos 1,(0,π)A A A +=∈所以． 512cos ,sin 1313A A =-=由（1）得，则 43cos ,sin 55==B B ， 1245333sin sin()sin cos cos sin 13513565C A B A B A B =+=+=⨯-⨯=由正弦定理得，则． 65sin sin sin 12a b c A B C ===135,4a b ==故的周长为，ABC 11a b c ++=的面积为． ABC 11133333sin 5224658ABC S ab C ==⨯⨯⨯=V 21. 如图所示，四棱锥中，底面为矩形，平面，，P ABCD -ABCD PA ⊥ABCD 2PA AB ==，点是的中点．AD =E PB（1）证明：； AE PC ⊥（2）求点到的距离； D CE （3）求二面角的大小． C AE D --【答案】（1）证明见解析；（2；（3）. π4【解析】【分析】（1）由已知位置关系推出，即可证明异面直线；AE PBC ⊥平面AE PC ⊥（2）由（1）中，，得，，求解各边长AE PBC ⊥平面BC PAB ⊥平面AE EC ⊥AD AE ⊥ECD 度，得为等边三角形，利用等边三角形的性质即得点到的距离； ECD D CE （3）利用二面角定义求解即可. 【小问1详解】证明：平面，底面为矩形PA ⊥ ABCD ABCD ，又 ,PA BC BC AB ∴⊥⊥,,PA AB A PA AB PAB =⊂ 平面，又BC PAB ∴⊥平面AE PAB ⊂ 平面，，点是的中点．BC AE ∴⊥PA AB = E PB ，又AE PB ∴⊥,,PB BC B PB BC PBC =⊂ 平面AE PBC ∴⊥平面AE PC ∴⊥【小问2详解】解：由（1）得：AE PBC ⊥平面AE EC ⊥又，，，即 BC PAB ⊥平面BC AD ∥AD PAB ∴⊥平面AD AE ⊥因为，2PA AB ==AD =所以，，，故AE =2DE =AC =2EC =即，三角形是边长为2的正三角形， 2EC DE CD ===ECD 点到的距离为,则，所以D CE d 1π122sin 2232ECD S d =⨯⨯⨯==⨯⨯d =所以点到. D CE 【小问3详解】解：由（2）知，，故取中点M ，连接EM ，DM .AD AE ⊥AE EC ⊥PC因为分别为中点，所以，即，故 ,E M ,PB PC EM BC ∥EMAD EM AE ⊥则为二面角的平面角 MEC ∠C AE D --又在中，EMC△1112,222ECEM BC MC PC ======所以，又 2222cos MEC +-∠==(0,π)MEC ∠∈所以.π4MEC ∠=即二面角的大小为.C AED --π422. 如图，在三棱柱中，点在平面上的射影为的中点，，111ABC A B C -A 1A BC BC D 2BAC π∠=，.BC =11A B A C =12A A a =（1）求证：平面；1A D ⊥ABC （2）若，求直线与平面所成角的正弦值的取值范围.12a ≤≤1AC 11BCC B【答案】（1）证明见解析；（2）． 12⎤⎥⎦【解析】【分析】（1）先由面面垂直的判定定理证出平面平面，再由面面垂直的性质定理证出结论ABC ⊥1A BC 成立；（2）取中点，可证出四边形是平行四边形，由已知结合（1）的证明，可得平面11B C 1D 11A D DA BC ⊥，进而得出平面平面，作于，利用线面角的定义找出线面角的11AA D D 11BB C C ⊥11AA D D 11A E D D ⊥E 平面角，求出各棱的长度，由二次函数的性质得出正弦值的取值范围．【详解】（1）证明：因为平面，平面，所以平面平面.AD ⊥1A BC AD ⊂ABC ABC ⊥1A BC 因为，，所以. 11=AC A B BD CD =1A D BC ⊥又因为平面平面，平面平面，平面， ABC ⊥1A BC ABC 1A BC BC =1A D ⊂1A BC 所以平面1A D ⊥ABC （2）解：取中点，连接，，则，所以四边形是平行四边形. 11B C 1D 11A D 1DD 111DD BB AA 11A D DA 因为，，，，平面，BC AD ⊥1BC A D ⊥1AD A D D ⋂=AD 1A D ⊂11AA D D所以平面，又平面 BC ⊥11AA D D BC ⊂11BB C C 所以平面平面. 11BB C C ⊥11AA D D 作于，则平面， 11A E D D ⊥E 1A E ⊥11BB C C 连接，则为直线与平面所成的角. CE 1A CE ∠1AC 11BCC B 由，，2BAC π∠=BD CD =BC =AD BD CD ===又由（1）知平面，1A D ⊥ABC 所以，，1A D =1111A D A D E DD ⨯===. 12AC a ==则. 111sin A E A CE A C ∠====由于，所以. 12a ≤≤21114a ≤≤11sin 2A CE ≤∠≤故直线与平面所成角的正弦值的取值范围为. 1AC 11BCCB 12⎤⎥⎦。

年普通高中创新素养培养实验班招生考试试卷及答案

3、在平面直角坐标系中，O为坐标原点，点A在第二象限，点B在x轴负半轴上，△OAB的面积是9，P是AB中点，若函数y＝kx（x<0）的图像经过点A、P，则k的值为（）（A）－6 （B）－4 （C）－3 （D）－2设点A坐标为（m，n），点B（a，0），∵S△OAB=9，∴－12an＝9，∵P是AB的中点，∴点P坐标为（m＋a2，n2），∵k＝xy，∴代入A、P坐标得：k＝mn，k＝(m＋a)n4，∴mn＝(m＋a)n4，∴3mn＝an，∵－an＝18，∴mn＝－6∴k＝－6（本例考点为点与函数的关系、中点坐标的应用，中点坐标是解压轴题的重要工具）※ 同类测试题：如在直角坐标系中，存在一个平行四边形，其中平行四边形的三个项点的坐标为（1，3），（2，2）和（3，4），求另一顶点的坐标4、对于任意的有理数a，方程2x2＋(a＋1)x－(3a2－4a＋b)＝0的根总是有理数，则b的值为（）（A）1 （B）－1 （C）2 （D）0解：方程的△＝(a＋1)2＋8(3a2－4a＋b)＝(5a－3)2＋8b－8≥0，∴当8b－8≥0时，PG FED C B A 必定△≥0，即方程必有实根，∴b ≥1，当b ＝1时，3a 2－4a ＋1＝(3a －1)(a －1)， ∴十字因式分解得方程为（(x －a ＋1)(2x ＋3a －1)＝0，∴b ＝1成立，当b ＝2时，3a 2－4a ＋b ＝3a 2－4a ＋2不能因式分解，∴方程有可能为无理数解，（在一元二次方程中，运用方程的判别式和因式分解是解决方程有理根和整数根重要工具，）※同类测试题：使得m 2＋m ＋7是完全平方数的所有整数m 的积的值。

甘肃省民乐一中2020-2021学年高一创新实验班招生考试数学试题含答案

民乐一中2021级创新实验班招生考试数学试卷一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数2x y x-=中，自变量x 的取值范围是（） A ．x ＞2 B ．x≥2 C.x≥2且x ≠0 D. x ≠02.化简算式+ 等于（）A ．1B ． 1+２C ．D ．3. 如图是六个棱长为1的正方块组成的一个几何体，它的左视图的面积是 ( )A ．6B ．5C ．4D ．34．若函数y 1＝x+1与函数y 2＝的图象相交于点M （1，m ），N （﹣2，n ）．若y 1<y 2，则x 的取值范围是（）A ．x ＜﹣2或0＜x ＜1B ．x ＜﹣2或x ＞1C ．﹣2＜x ＜0或0＜x ＜1D ．﹣2＜x ＜0或x ＞15.如图，在3×3的网格中，每个小正方形的边长均为1，点A ，B ，C 都在格点上，若BD 是△ABC 的高，则BD 的长为（）A ．B ．C ．D ．6. 定义运算：m ☆n ＝mn 2﹣mn ﹣1．例如：4☆2＝4×22﹣4×2﹣1＝7．则方程1☆x ＝0的根的情况为（）A ．有两个不相等的实数根B ．有两个相等的实数根C ．无实数根D ．只有一个实数根7. 用换元法解方程+＝2时，若设＝y ，则原方程可化为关于y 的方程是( )A ．y 2﹣2y+1＝0B ．y 2+2y+1＝0C ．y 2+y+2＝0D ．y 2+y ﹣2＝08.如图，等腰直角三角形ABC 中，∠ABC=90°，BA=BC ，将BC 绕点B 顺时针旋转θ(0°<θ<90°)，得到BP ，连结CP ，过点A 作AH⊥CP 交CP 的延长线于点H ，连结AP ，则∠PAH 的度数（）A ．随着θ的增大而增大B ．随着θ的增大而减小C ．不变D ．随着θ的增大，先增大后减小9.已知抛物线（其中a ，b ，c 是常数,0a ≠，1c >）经过点（2,0），其对称轴是第 3题图第8题图 B C P HA 第5题图直线．有下列结论：① ， ②关于x 的方程有两个不等的实数根，③a<- .其中正确结论的个数是（）A ．0B ．1C ．2D ．310.如图，在等腰△ABC 中，AB=AC,直线l 垂直于底边BC 于点F ，现将直线l 沿线段BC 从B 点匀速平移至C 点，直线l与△ABC 的边相交于E ，F 两点．设线段EF 的长度为y ，平移时间为t ，则下图中能较好反映y 与t 的函数关系的图象是（）二、填空题（本大题共8小题,每小题4分,共32分.）11. 因式分解：3a 4﹣3b 4＝．12.埃及胡夫金字塔是世界古代建筑奇迹之一，其底面是正方形、侧面是全等的等腰三角形.底面正方形的边长与侧面等腰三角形底边上的高的比值是（﹣1），它介于整数n 和n+1之间，则n 的值是．13.把抛物线y ＝ax 2+bx+c 的图象先向右平移3个单位，再向下平移2个单位，所得的抛物线的解析式是y ＝x 2-3x+5，则a+b+c=__________.14. 我国古代有这样一道数学问题:“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何?”题意是:如图所示，把枯木看作一个圆柱体，因为一丈等于十尺，则该圆柱的高为 20 尺，底面周长为 3 尺，有葛藤自点 A 处缠绕而上，绕五周后其末端恰好到达点B 处，则问题中葛藤的最短长度是尺．15.如图，AB 是圆O 的弦，点C 在过点B 的切线上，OC ⊥OA ，OC 交AB 于点P ．若∠BPC=70°，则∠ABC 的度数等于 .16．如图都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第个图形中共有210个小球．第14题图第15题图第10题图 A B C D17.如图，已知直线y ＝kx （k ＞0）分别交反比例函数y ＝和y ＝在第一象限的图象于点A ，B ，过点B 作BD ⊥x 轴于点D ，交y ＝的图象于点C ，连接AC ．若△ABC 是等腰三角形，则k 的值是．18.如图，动点M 在边长为2的正方形ABCD 内，且AM ⊥BM ，P 是DC 边上的一个动点，E 是AD 边的中点,则线段PE,PM 的和PE+PM 的最小值是 .三、解答题：本大题共10小题,共78分.解答时写出必要的文字说明、证明过程或演算步骤.19．（5分）初中数学教科书告诉我们一种作已知角的平分线的方法：已知：,求作：的平分线作法：（1）以O 为圆心，适当长为半径画弧，交OA 于点M ，交OB 于点N ；（2）分别以点M ，N 为圆心，以大于的长为半径画弧，两弧在AOB 的内部相交于点C ；（3）画射线OC ，射线OC 即为所求．请你根据提供的材料完成下面问题：（1）这种作已知角平分线的方法的依据是__________________(填序号)．①SSS ② ③ ④（2）请你证明OC 为的平分线．20.(5分)先化简，再从-2，-1，0，1，2中选一个合适的数作为x 的值代入求值．21. (6分) 如下是学习分式方程的应用时，老师板书的问题和两名同学所列的方程．一艘轮船在静水中的最大航速为30 km/h ，它以最大航速沿江顺流航行90 km 所用时间，与以最大航速逆流航行60 km 所用时间相等，求江水的流速为多少？甲：；乙：根据以上信息，解答下列问题：（1）甲同学所列方程中的x 表示_________ ________ _____；乙同学所列方程中的y 表示________________________________________；(2)两个方程中任选一个，解方程并回答老师提出的问题．22.(6分)如图，某楼房AB 顶部有一根天线BE ，为了测量天线的高度，在地面上取同一条直线上的三点C,D,A ，在点C处测得天线顶端E 的仰角为，从点C 走到点D ，测得CD=5m ，P A D M C 第18题图 B E 第17题图从点D测得天线底端B的仰角为，已知A,B,E在同一条垂直于地面的直线上，AB=25m.求天线BE的高度．（结果保留根号）23.(8分)暑期将至，某健身俱乐部面向学生推出两种暑期优惠活动方案．方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；方案二：不购买学生暑期专享卡，每次健身费用按八折优惠．设某学生暑期健身x（次），按照方案一所需费用为y1（元），且y1＝k1x+b；按照方案二所需费用为y2（元），且y2＝k2x．其函数图象如图所示．（1）求k1和b的值，并说明它们的实际意义；（2）求打折前的每次健身费用和k2的值；（3）学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少？说明理由．24. (7分)如图，已知一次函数=x-1的图象与反比例函数=(x＞0)的图象相交于点A （3，m），与y轴交于点B.（1）求m和k的值；（2）设点P（x,y）(x＞3)是反比例函数图象上的一点，过点P作直线PC⊥x 轴于点C,交=x-1的图象于点D，连接BP，OA，若,求点P的坐标.25. (9分)某商店销售一种商品，经市场调查发现，该商品的周销售量y(件)是售价x(元/件)的一次函数，其售价、周销售量、周销售利润w(元)的三组对应值如下表:售价x(元/件) 50 60 80周销售量y(件) 100 80 40周销售利润w(元) 1000 1600 1600OBCPADxy注:周销售利润=周销售量×(售价-进价).(1)①求y 关于x 的函数解析式(不要求写出自变量的取值范围);②该商品进价是元/件;当售价是元/件时，周销售利润最大，最大利润是元;(2)由于某种原因，该商品进价提高了m 元/件(m>0)，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元，求m 的值.26.(10分)如图1，在平面直角坐标系中，矩形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，且OA=4,OC=6,点O 为原点，将矩形OABC 绕O 点顺时针旋转45°后停止.（1）求矩形OABC 在整个旋转过程中所扫过的面积；（2）如图2，在旋转过程中，是否存在某一位置，使得BC 边与x 轴的交点N A 的坐标；若不存在，请说明理由.27．（10分）如图，在△ABC 中，AB ＝AC ，以AB 为直径的⊙O 分别交AC,BC 于点D,E ，点F 在AC 的延长线上，且∠CBF ＝∠CAB ．（1）求证：直线BF 是⊙O 的切线；（2）若AB ＝5，sin ∠BAD ＝，求AD 和CF 的长；28．（12分）如图，抛物线的顶点为A （h ，﹣1），与y 轴交于点B （0，﹣），点F （2，1）为抛物线对称轴上的一个定点．（1）求这条抛物线的解析式；（2）已知直线l 是过点C （0，﹣3）且垂直于y 轴的定直线，若抛物线上的任意一点P （m ，n ）到直线l 的距离为d ，求证：PF ＝d ；（3）已知坐标平面内的点D （4，3），请在抛物线上找一点Q ，使△DFQ 的周长最小，并求此时△DFQ 周长的最小值及点Q 的坐标．O x y A B CN 图2 W O x yA BC 图1·创新实验班数学参考答案一、选择题（每题4分，共40分）1. B2. B3.D4. A5. D6. A7.A8. C9.C 10.B二、填空题（每题4分，共32分）11.3（a2+b2）(a+b)(a-b) 12.1 13. 11 14. 25 15. 70° 16. 2017. 或．（缺一个答案扣2分，若有错解不得分） 18. -1三、解答题（共78分）19．（1）①……… 1分（2）如图，连接MC，NC．根据作图的过程知，在△MOC与△NOC中，，………3分∴△MOC≌△NOC（SSS），………4分的平分线．………5分∠AOC=∠BOC，∴OC为AOB20.原式=. ........1分===== ..........3分在-2，-1，0，1，2中，只有当x=-2时，原分式有意义，即x只能取-2 . ...4分当x=-2时，原式==-1 ....................................5分21. (1)江水的流速; .......... 1分轮船以最大航速沿江顺流航行90 km所用时间,或以最大航速逆流航行60 km所用时间 ............................2分(2)选第一个方程：由得， ....................3分90-3x=60+2x,x=6 ....................4分经检验，x=6是原方程的解 ....................5分答：江水的流速为6km/h. ..............6分选第二个方程求解如下，参考上面步骤给分：由得y=2.5,经检验符合原方程，于是船逆流航行的速度为602.5=24 km/h，水流速度为30-24=6 km/h。

创新教育实验班(高中)招生试卷数学6(含答案)

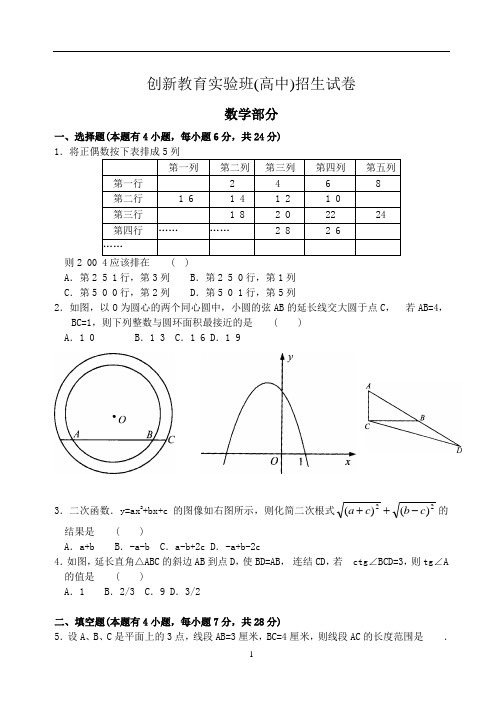
创新教育实验班(高中)招生试卷数学部分一、选择题(本题有4小题，每小题6分，共24分) 1则2 00 4应该排在 ( )A ．第2 5 1行，第3列B ．第2 5 0行，第1列C ．第5 0 0行，第2列D ．第5 0 1行，第5列2．如图，以O 为圆心的两个同心圆中，小圆的弦AB 的延长线交大圆于点C ，若AB=4，BC=1，则下列整数与圆环面积最接近的是 ( ) A ．1 0 B ．1 3 C ．1 6 D ．1 93．二次函数．y=ax 2+bx+c 的图像如右图所示，则化简二次根式22)()(c b c a -++的结果是 ( )A ．a+bB ．-a-bC ．a-b+2cD ．-a+b-2c 4．如图，延长直角△ABC 的斜边AB 到点D ，使BD=AB ，连结CD ，若 ctg∠BCD=3，则tg∠A 的值是 ( )A ．1B ．2/3C ．9D ．3/2二、填空题(本题有4小题，每小题7分，共28分)5．设A 、B 、C 是平面上的3点，线段AB=3厘米，BC=4厘米，则线段AC 的长度范围是．6．若5条直线两两相交，则交点的个数有． 7．4位数5xy9是某个自然数的平方，则2x+y= ．8．在边长为4 6厘米的正方形铁皮上按如图所示剪取一块圆形和一块扇形铁皮，恰好做成一个圆锥模型，则该圆锥模型的底面半径是．三、解答题(本题有3小题，共48分) 9．(本题1 5分)如图，有5张同样大小的小正方形纸片，用它们拼成轴对称图形，要求相邻两张正方形纸片有一条边相连接，你有几种拼法?请画出示意图．(画出草图即可，每拼对一个得3分，满分不超过1 5分)10．(本题1 6分)某食品公司欲用这3种食物混合研制1 0 0千克食品，要求研制成的食品中至少含3 6 00 0单位的维生素A 和4 00 00单位的维生素B ．(1)研制这1 0 0千克食品，至少要用甲种食物多少千克?丙种食物至多能用多少千克? (2)若限定甲种食物用5 O 千克，则研制这1 00千克食品的总成本S 的取值范围是多少? 11．(本题1 7分)对于某一自变量为x 的函数，若当x=x 0时，其函数值也为x 0，则称点(x 0，x 0)为此函数的不动点．现有函数y=bx ax ++3， (1)若y=bx ax ++3有不动点(4，4)，(一4，-4)，求a ，b ． (2)若函数y=bx ax ++3的图像上有两个关于原点对称的不动点，求实数a ，b 应满足的条件．(3)已知a=4时，函数y=b x a x ++3仍有两个关于原点对称的不动点，则此时函数y=b x ax ++3的图像与函数y=35+-x 的图像有什么关系?与函数y=x5- 的图像又有什么关系?创新教育实验班(高中)招生试卷参考答案数学部分一、选择题(本题有4小题，每小题6分，共24分) 1．A 2．C 3．C 4．D二、填空题(本题有4小题，每小题7分，共28分) 5．1厘米≤Ac≤7厘米6．或1个，或5个，或6个，或8个，或10个 7．8或2 0 8．(102 -4)厘米三、解答题(本题有3小题，共48分)9．解：如图，每个给3分(全等图形视作一个)．1 O ．解：设研制1 00千克食品用甲种、乙种和丙种食物各x 千克，y 千克和z 千克， (1)由题意，得由①z=100-x-y,代入②③，得⎩⎨⎧≥-≥50y 2x 20y∴ 2x ≥y+5 O≥7 O，x≥3 5，即至少要用甲种食物3 5千克．将①变形为y=100-x-z ，代入②，得z≤8O—x≤8 O -3 5=4 5，即丙种食物至多能用4 5千克． (2)研制1 OO 千克食品的总成本S=6x+4y+3z ，将z=100-x —y 代入，得S=3x+y+300．当x=5O 时，S=y+450， 20≤y≤50．∴ 47O≤S≤500．11．解：(1)由题意，得解得(2)令bx a x ++3=x ，得3x+a=x 2+bx(x≠-b) 即 x 2+(b —3)x-a=O ．设方程的两根为x 1，x 2，则两个不动点(x 1，x 2)，(x 2，x 2)，由于它们关于原点对称，所以x 1+x 2=0， ∴⎩⎨⎧>=-=-04)3(032a b b ，解得⎩⎨⎧=>3b a ，又因为x≠-b ，即 x≠-3，所以以a≠9，因此a ，b 满足条件a>0且a≠9，b=3． (3)由(2)知b=3，此时函数为y=343++x x ，即y=3-35+x ． ∴ 函数y=343++x x 的图像可由y=-35+x 的图像向上平移3个单位得到．又函数y=-35+x 的图像可由函数y=-x 5的图像向左平移3个单位得到，所以函数y=343++x x 的图像可由函数y=-x5的图像向左平移3个单位，再向上平移3个单位得到．。