图论算法与编程实例
图论算法详解(C++版)

1.1、prim算法:无向图的生成树就是从图的边集中选择一些边,使得这些边构成一个连通无环图,也就是树。
如果给每一条边加一个权,所有生成树中权和最小的生成树称为最小生成树。
【Prim算法思想】任意时刻的中间结果都是一棵树,每次花费最小的代价,用一条边把不在树中的结点加进来。
【最小生成树算法实例】现有一张城市地图,图中的顶点为城市,无向边代表两个城市间的连通关系,边上的权代表公路造价。
在分析了这张图后发现,任一对城市都是连通的。
现在要求用公路把所有城市联系起来,如何设计可使得工程的总造价最少?【输入】第一行两个数v(v<=200),e,分别代表城市数和边数以下e行,每行为两个顶点和它们之间的边权w(w<1000)。
【输出】连通所有城市的公路最小造价。
【输入样例】6 101 2 101 5 191 6 212 3 52 4 62 6 113 4 64 5 184 6 145 6 33【输出样例】50 原图最小生成树#include<cstdio>#include<string>#include<cstring>#include<climits>using namespace std;int i,j,k,n,m,mi,t,s,a[1000][1000]; void prim(){int mi,p,f,k,d[1000];bool v[1000];memset(v,false,sizeof(v));f=1;for (i=2;i<=n;i++){d[i]=INT_MAX;}d[f]=0;s=0;for(i=1;i<=n;i++){mi=INT_MAX;for (j=1;j<=n;j++)if ((v[j]==false) && (d[j]<mi)){p=j;mi=d[j];}s+=mi;v[p]=true;for(j=1;j<=n;j++){if (a[p][j]<d[j]) d[j]=a[p][j];}}}int main(){memset(a,0,sizeof(a));scanf("%d%d",&n,&m);mi=INT_MAX;for (i=1;i<=n;i++){for (j=1;j<=n;j++){a[i][j]=INT_MAX;}}for (i=1;i<=m;i++){scanf("%d%d%d",&k,&j,&t);if ((t<a[k][j])||(t<a[j][k])){a[k][j]=t;a[j][k]=a[k][j];}}prim();printf("%d",s);return 0;}1.2、克鲁斯卡尔算法假设N=(V,{E})是连通网,将N中的边按权值从小到大的顺序排列;①、将n个顶点看成n个集合;②、按权值小到大的顺序选择边,所选边应满足两个顶点不在同一个顶点集合内,将该边放到生成树边的集合中。
图论及其应用

图论及其应用简介图论是计算机科学中的一个重要分支,研究的对象是由边与顶点组成的图形结构以及与其相关的问题和算法。
图论的应用广泛,涵盖了计算机科学、网络科学、物理学、社会学、生物学等多个领域。
本文将介绍图论的基本概念、常用算法以及一些实际的应用案例。
图的基本概念图由顶点(Vertex)和边(Edge)组成,记作G=(V, E),其中V为顶点的集合,E为边的集合。
图可以分为有向图和无向图两种类型。
有向图有向图中的边具有方向性,即从一个顶点到另一个顶点的边有明确的起点和终点。
有向图可以表示一种有序的关系,比如A到B有一条边,但B到A可能没有边。
有向图的表示可以用邻接矩阵或邻接表来表示。
无向图无向图中的边没有方向性,任意两个顶点之间都有相互连接的边。
无向图可以表示一种无序的关系,比如A与B有一条边,那么B与A之间也有一条边。
无向图的表示通常使用邻接矩阵或邻接表。
常用图论算法图论中有许多经典的算法,其中一些常用的算法包括:深度优先搜索(DFS)深度优先搜索是一种用于遍历或搜索图的算法。
通过从起始顶点开始,沿着一条路径尽可能深入图中的顶点,直到无法再继续前进时,返回上一个顶点并尝试下一条路径的方式。
DFS可以用于判断图是否连通,寻找路径以及检测环等。
广度优先搜索(BFS)广度优先搜索也是一种用于遍历或搜索图的算法。
不同于深度优先搜索,广度优先搜索逐层遍历顶点,先访问离起始顶点最近的顶点,然后依次访问与起始顶点距离为2的顶点,以此类推。
BFS可以用于寻找最短路径、搜索最近的节点等。
最短路径算法最短路径算法用于计算图中两个顶点之间的最短路径。
其中最著名的算法是迪杰斯特拉算法(Dijkstra’s A lgorithm)和弗洛伊德算法(Floyd’s Algorithm)。
迪杰斯特拉算法适用于没有负权边的图,而弗洛伊德算法可以处理带有负权边的图。
最小生成树算法最小生成树算法用于找到一个连通图的最小的生成树。
其中最常用的算法是普里姆算法(Prim’s Algorithm)和克鲁斯卡尔算法(Kruskal’s Algorithm)。
图论及其应用
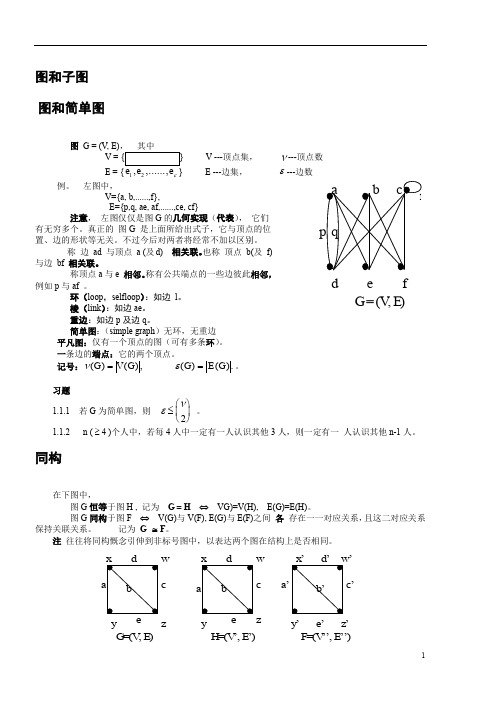
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
matlab图论程序算法大全

图论算法matlab实现求最小费用最大流算法的 MATLAB 程序代码如下:n=5;C=[0 15 16 0 00 0 0 13 140 11 0 17 00 0 0 0 80 0 0 0 0]; %弧容量b=[0 4 1 0 00 0 0 6 10 2 0 3 00 0 0 0 20 0 0 0 0]; %弧上单位流量的费用wf=0;wf0=Inf; %wf 表示最大流量, wf0 表示预定的流量值for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流while(1)for(i=1:n)for(j=1:n)if(j~=i)a(i,j)=Inf;end;end;end%构造有向赋权图for(i=1:n)for(j=1:n)if(C(i,j)>0&f(i,j)==0)a(i,j)=b(i,j); elseif(C(i,j)>0&f(i,j)==C(i,j))a(j,i)=-b(i,j);elseif(C(i,j)>0)a(i,j)=b(i,j);a(j,i)=-b(i,j);end;end;end for(i=2:n)p(i)=Inf;s(i)=i;end %用Ford 算法求最短路, 赋初值for(k=1:n)pd=1; %求有向赋权图中vs 到vt 的最短路for(i=2:n)for(j=1:n)if(p(i)>p(j)+a(j,i))p(i)=p(j)+a(j,i);s( i)=j;pd=0;end;end;endif(pd)break;end;end %求最短路的Ford 算法结束if(p(n)==Inf)break;end %不存在vs 到vt 的最短路, 算法终止. 注意在求最小费用最大流时构造有向赋权图中不会含负权回路, 所以不会出现k=ndvt=Inf;t=n; %进入调整过程, dvt 表示调整量while(1) %计算调整量if(a(s(t),t)>0)dvtt=C(s(t),t)-f(s(t),t); %前向弧调整量elseif(a(s(t),t)<0)dvtt=f(t,s(t));end %后向弧调整量if(dvt>dvtt)dvt=dvtt;endif(s(t)==1)break;end %当t 的标号为vs 时, 终止计算调整量t=s(t);end %继续调整前一段弧上的流fpd=0;if(wf+dvt>=wf0)dvt=wf0-wf;pd=1;end%如果最大流量大于或等于预定的流量值t=n;while(1) %调整过程if(a(s(t),t)>0)f(s(t),t)=f(s(t),t)+dvt; %前向弧调整elseif(a(s(t),t)<0)f(t,s(t))=f(t,s(t))-dvt;end %后向弧调整if(s(t)==1)break;end %当t 的标号为vs 时, 终止调整过程t=s(t);endif(pd)break;end%如果最大流量达到预定的流量值wf=0; for(j=1:n)wf=wf+f(1,j);end;end %计算最大流量zwf=0;for(i=1:n)for(j=1:n)zwf=zwf+b(i,j)*f(i,j);end;end%计算最小费用f %显示最小费用最大流图 6-22wf %显示最小费用最大流量zwf %显示最小费用, 程序结束__Kruskal 避圈法:Kruskal 避圈法的MATLAB 程序代码如下:n=8;A=[0 2 8 1 0 0 0 02 0 6 0 1 0 0 08 6 0 7 5 1 2 01 0 7 0 0 0 9 00 1 5 0 0 3 0 80 0 1 0 3 0 4 60 0 2 9 0 4 0 30 0 0 0 8 6 3 0];k=1; %记录A中不同正数的个数for(i=1:n-1)for(j=i+1:n) %此循环是查找A中所有不同的正数if(A(i,j)>0)x(k)=A(i,j); %数组x 记录A中不同的正数kk=1; %临时变量for(s=1:k-1)if(x(k)==x(s))kk=0;break;end;end %排除相同的正数k=k+kk;end;end;endk=k-1 %显示A中所有不同正数的个数for(i=1:k-1)for(j=i+1:k) %将x 中不同的正数从小到大排序if(x(j)<x(i))xx=x(j);x(j)=x(i);x(i)=xx;end;end;endT(n,n)=0; %将矩阵T 中所有的元素赋值为0q=0; %记录加入到树T 中的边数for(s=1:k)if(q==n)break;end %获得最小生成树T, 算法终止for(i=1:n-1)for(j=i+1:n)if(A(i,j)==x(s))T(i,j)=x(s);T(j,i)=x(s); %加入边到树T 中TT=T; %临时记录Twhile(1)pd=1; %砍掉TT 中所有的树枝for(y=1:n)kk=0;for(z=1:n)if(TT(y,z)>0)kk=kk+1;zz=z;end;end %寻找TT 中的树枝if(kk==1)TT(y,zz)=0;TT(zz,y)=0;pd=0;end;end %砍掉TT 中的树枝if(pd)break;end;end %已砍掉了TT 中所有的树枝pd=0; %判断TT 中是否有圈for(y=1:n-1)for(z=y+1:n)if(TT(y,z)>0)pd=1;break;end;end;end if(pd)T(i,j)=0;T(j,i)=0; %假如TT 中有圈else q=q+1;end;end;end;end;endT %显示近似最小生成树T, 程序结束用Warshall-Floyd 算法求任意两点间的最短路.n=8;A=[0 2 8 1 Inf Inf Inf Inf2 0 6 Inf 1 Inf Inf Inf8 6 0 7 5 1 2 Inf1 Inf 7 0 Inf Inf 9 Inf Inf 1 5 Inf 0 3 Inf 8 Inf Inf 1 Inf 3 0 4 6Inf Inf 2 9 Inf 4 0 3Inf Inf Inf Inf 8 6 3 0]; % MATLAB 中, Inf 表示∞D=A; %赋初值for(i=1:n)for(j=1:n)R(i,j)=j;end;end %赋路径初值for(k=1:n)for(i=1:n)for(j=1:n)if(D(i,k)+D(k,j)<D(i,j))D(i,j )=D(i,k)+D(k,j); %更新dijR(i,j)=k;end;end;end %更新rijk %显示迭代步数D %显示每步迭代后的路长R %显示每步迭代后的路径pd=0;for i=1:n %含有负权时if(D(i,i)<0)pd=1;break;end;end %存在一条含有顶点vi 的负回路if(pd)break;end %存在一条负回路, 终止程序end %程序结束利用 Ford--Fulkerson 标号法求最大流算法的MATLAB 程序代码如下:n=8;C=[0 5 4 3 0 0 0 00 0 0 0 5 3 0 00 0 0 0 0 3 2 00 0 0 0 0 0 2 00 0 0 0 0 0 0 40 0 0 0 0 0 0 30 0 0 0 0 0 0 50 0 0 0 0 0 0 0]; %弧容量for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流for(i=1:n)No(i)=0;d(i)=0;end %No,d 记录标号图 6-19while(1)No(1)=n+1;d(1)=Inf; %给发点vs 标号while(1)pd=1; %标号过程for(i=1:n)if(No(i)) %选择一个已标号的点vifor(j=1:n)if(No(j)==0&f(i,j)<C(i,j)) %对于未给标号的点vj, 当vivj 为非饱和弧时No(j)=i;d(j)=C(i,j)-f(i,j);pd=0;if(d(j)>d(i))d(j)=d(i);endelseif(No(j)==0&f(j,i)>0) %对于未给标号的点vj, 当vjvi 为非零流弧时No(j)=-i;d(j)=f(j,i);pd=0;if(d(j)>d(i))d(j)=d(i);end;end;end;end;endif(No(n)|pd)break;end;end%若收点vt 得到标号或者无法标号, 终止标号过程if(pd)break;end %vt 未得到标号, f 已是最大流, 算法终止dvt=d(n);t=n; %进入调整过程, dvt 表示调整量while(1)if(No(t)>0)f(No(t),t)=f(No(t),t)+dvt; %前向弧调整elseif(No(t)<0)f(No(t),t)=f(No(t),t)-dvt;end %后向弧调整if(No(t)==1)for(i=1:n)No(i)=0;d(i)=0; end;break;end %当t 的标号为vs 时, 终止调整过程t=No(t);end;end; %继续调整前一段弧上的流fwf=0;for(j=1:n)wf=wf+f(1,j);end %计算最大流量f %显示最大流wf %显示最大流量No %显示标号, 由此可得最小割, 程序结束图论程序大全程序一:关联矩阵和邻接矩阵互换算法function W=incandadf(F,f)if f==0m=sum(sum(F))/2;n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=i:nif F(i,j)~=0W(i,k)=1;W(j,k)=1;k=k+1;endendendelseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);W(a(1),a(2))=1;W(a(2),a(1))=1;endelsefprint('Please imput the right value of f');endW;程序二:可达矩阵算法function P=dgraf(A) n=size(A,1);P=A;for i=2:nP=P+A^i;endP(P~=0)=1;P;程序三:有向图关联矩阵和邻接矩阵互换算法function W=mattransf(F,f)if f==0m=sum(sum(F));n=size(F,1);W=zeros(n,m);k=1;for i=1:nfor j=i:nif F(i,j)~=0W(i,k)=1;W(j,k)=-1;k=k+1;endendendelseif f==1m=size(F,2);n=size(F,1);W=zeros(n,n);for i=1:ma=find(F(:,i)~=0);if F(a(1),i)==1W(a(1),a(2))=1;elseW(a(2),a(1))=1;endendelsefprint('Please imput the right value of f');endW;第二讲:最短路问题程序一:Dijkstra算法(计算两点间的最短路)function [l,z]=Dijkstra(W)n = size (W,1); for i = 1 :nl(i)=W(1,i);z(i)=0;endi=1;while i<=nfor j =1 :nif l(i)>l(j)+W(j,i)l(i)=l(j)+W(j,i);z(i)=j-1;if j<ii=j-1;endendendi=i+1;end程序二:floyd算法(计算任意两点间的最短距离)function [d,r]=floyd(a)n=size(a,1);d=a;for i=1:nfor j=1:nr(i,j)=j;endendr;for k=1:nfor i=1:nfor j=1:nif d(i,k)+d(k,j)<d(i,j)d(i,j)=d(i,k)+d(k,j);r(i,j)=r(i,k);endendendend程序三:n2short.m 计算指定两点间的最短距离function [P u]=n2short(W,k1,k2)n=length(W);U=W;m=1;while m<=nfor i=1:nfor j=1:nif U(i,j)>U(i,m)+U(m,j)U(i,j)=U(i,m)+U(m,j);endendendm=m+1;endu=U(k1,k2);P1=zeros(1,n);k=1;P1(k)=k2;V=ones(1,n)*inf;kk=k2;while kk~=k1for i=1:nV(1,i)=U(k1,kk)-W(i,kk);if V(1,i)==U(k1,i)P1(k+1)=i;kk=i;k=k+1;endendendk=1;wrow=find(P1~=0);for j=length(wrow):-1:1P(k)=P1(wrow(j));k=k+1;endP;程序四、n1short.m(计算某点到其它所有点的最短距离)function[Pm D]=n1short(W,k)n=size(W,1);D=zeros(1,n);for i=1:n[P d]=n2short(W,k,i);Pm{i}=P;D(i)=d;end程序五:pass2short.m(计算经过某两点的最短距离)function [P d]=pass2short(W,k1,k2,t1,t2)[p1 d1]=n2short(W,k1,t1);[p2 d2]=n2short(W,t1,t2);[p3 d3]=n2short(W,t2,k2);dt1=d1+d2+d3;[p4 d4]=n2short(W,k1,t2);[p5 d5]=n2short(W,t2,t1);[p6 d6]=n2short(W,t1,k2);dt2=d4+d5+d6;if dt1<dt2d=dt1;P=[p1 p2(2:length(p2)) p3(2:length(p3))];elsed=dt1;p=[p4 p5(2:length(p5)) p6(2:length(p6))];endP;d;第三讲:最小生成树程序一:最小生成树的Kruskal算法function [T c]=krusf(d,flag)if nargin==1n=size(d,2);m=sum(sum(d~=0))/2;b=zeros(3,m);k=1;for i=1:nfor j=(i+1):nif d(i,j)~=0b(1,k)=i;b(2,k)=j;b(3,k)=d(i,j);k=k+1;endendendelseb=d;endn=max(max(b(1:2,:)));m=size(b,2);[B,i]=sortrows(b',3);B=B';c=0;T=[];k=1;t=1:n;for i=1:mif t(B(1,i))~=t(B(2,i))T(1:2,k)=B(1:2,i);c=c+B(3,i);k=k+1;tmin=min(t(B(1,i)),t(B(2,i)));tmax=max(t(B(1,i)),t(B(2,i)));for j=1:nif t(j)==tmaxt(j)=tmin;endendendif k==nbreak;endendT;c;程序二:最小生成树的Prim算法function [T c]=Primf(a)l=length(a);a(a==0)=inf;k=1:l;listV(k)=0;listV(1)=1;e=1;while (e<l)min=inf;for i=1:lif listV(i)==1for j=1:lif listV(j)==0 & min>a(i,j)min=a(i,j);b=a(i,j);s=i;d=j;endendendendlistV(d)=1;distance(e)=b;source(e)=s;destination(e)=d;e=e+1;endT=[source;destination]; for g=1:e-1c(g)=a(T(1,g),T(2,g));endc;另外两种程序最小生成树程序1(prim 算法构造最小生成树)a=[inf 50 60 inf inf inf inf;50 inf inf 65 40 inf inf;60 inf inf 52 inf inf 45;...inf 65 52 inf 50 30 42;inf 40 inf 50 inf 70 inf;inf inf inf 30 70 inf inf;...inf inf 45 42 inf inf inf];result=[];p=1;tb=2:length(a);while length(result)~=length(a)-1temp=a(p,tb);temp=temp(:);d=min(temp);[jb,kb]=find(a(p,tb)==d);j=p(jb(1));k=tb(kb(1));result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[];endresult最小生成树程序2(Kruskal 算法构造最小生成树)clc;clear;a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40;a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;a(4,7)=42; a(5,6)=70;[i,j,b]=find(a);data=[i';j';b'];index=data(1:2,:);loop=max(size(a))-1;result=[];while length(result)<looptemp=min(data(3,:));flag=find(data(3,:)==temp);flag=flag(1);v1=data(1,flag);v2=data(2,flag);if index(1,flag)~=index(2,flag)result=[result,data(:,flag)];endindex(find(index==v2))=v1;data(:,flag)=[];index(:,flag)=[];endresult第四讲:Euler图和Hamilton图程序一:Fleury算法(在一个Euler图中找出Euler环游)注:包括三个文件;fleuf1.m, edf.m, flecvexf.mfunction [T c]=fleuf1(d)%注:必须保证是Euler环游,否则输出T=0,c=0 n=length(d);b=d;b(b==inf)=0;b(b~=0)=1;m=0;a=sum(b);eds=sum(a)/2;ed=zeros(2,eds);vexs=zeros(1,eds+1);matr=b;for i=1:nif mod(a(i),2)==1m=m+1;endendif m~=0fprintf('there is not exit Euler path.\n')T=0;c=0;endif m==0vet=1;flag=0;t1=find(matr(vet,:)==1);for ii=1:length(t1)ed(:,1)=[vet,t1(ii)];vexs(1,1)=vet;vexs(1,2)=t1(ii);matr(vexs(1,2),vexs(1,1))=0;flagg=1;tem=1;while flagg[flagg ed]=edf(matr,eds,vexs,ed,tem); tem=tem+1;if ed(1,eds)~=0 & ed(2,eds)~=0T=ed;T(2,eds)=1;c=0;for g=1:edsc=c+d(T(1,g),T(2,g));endflagg=0;break;endendendendfunction[flag ed]=edf(matr,eds,vexs,ed,tem)flag=1;for i=2:eds[dvex f]=flecvexf(matr,i,vexs,eds,ed,tem);if f==1flag=0;break;endif dvex~=0ed(:,i)=[vexs(1,i) dvex];vexs(1,i+1)=dvex;matr(vexs(1,i+1),vexs(1,i))=0;elsebreak;endendfunction [dvex f]=flecvexf(matr,i,vexs,eds,ed,temp) f=0;edd=find(matr(vexs(1,i),:)==1);dvex=0;dvex1=[];ded=[];if length(edd)==1dvex=edd;elsedd=1;dd1=0;kkk=0;for kk=1:length(edd)m1=find(vexs==edd(kk));if sum(m1)==0dvex1(dd)=edd(kk);dd=dd+1;dd1=1;elsekkk=kkk+1;endendif kkk==length(edd)tem=vexs(1,i)*ones(1,kkk);edd1=[tem;edd];for l1=1:kkklt=0;ddd=1;for l2=1:edsif edd1(1:2,l1)==ed(1:2,l2)lt=lt+1;endendif lt==0ded(ddd)=edd(l1); ddd=ddd+1;endendendif temp<=length(dvex1)dvex=dvex1(temp);elseif temp>length(dvex1) & temp<=length(ded)dvex=ded(temp);elsef=1;endend程序二:Hamilton改良圈算法(找出比较好的Hamilton路)function [C d1]= hamiltonglf(v)%d表示权值矩阵%C表示算法最终找到的Hamilton圈。
图论中的最短路径算法

图论中的最短路径算法图论是数学的一个分支,研究图的性质和图之间的关系。
在图论中,最短路径算法是一类重要的算法,用于寻找图中两个顶点之间的最短路径。
本文将介绍图论中的几种常见的最短路径算法。
一、Dijkstra算法Dijkstra算法是最短路径算法中最常用的一种。
它基于贪心策略,通过逐步扩展路径来求解最短路径。
算法的基本思想是,从一个起始顶点开始,逐步扩展到其他顶点,每次选择当前路径中距离起始顶点最近的顶点进行扩展,直到扩展到目标顶点或者所有顶点都被扩展完毕。
Dijkstra算法的步骤如下:1. 初始化起始顶点的距离为0,其他顶点的距离为无穷大。
2. 选择距离起始顶点最近的顶点,将其加入已扩展顶点集合。
3. 更新与新加入顶点相邻的顶点的距离,如果新的距离比原来的距离小,则更新距离。
4. 重复步骤2和步骤3,直到扩展到目标顶点或者所有顶点都被扩展完毕。
5. 根据更新后的距离,可以得到最短路径。
二、Bellman-Ford算法Bellman-Ford算法是另一种常用的最短路径算法。
它可以处理带有负权边的图,而Dijkstra算法只适用于非负权边的图。
Bellman-Ford算法的基本思想是通过对所有边进行松弛操作,逐步减小起始顶点到其他顶点的估计距离,直到得到最短路径。
Bellman-Ford算法的步骤如下:1. 初始化起始顶点的距离为0,其他顶点的距离为无穷大。
2. 对所有边进行松弛操作,即如果存在一条边(u, v),使得从起始顶点到v的距离大于从起始顶点到u的距离加上边(u, v)的权值,则更新距离。
3. 重复步骤2,直到没有顶点的距离发生变化。
4. 根据更新后的距离,可以得到最短路径。
三、Floyd-Warshall算法Floyd-Warshall算法是一种多源最短路径算法,可以求解图中任意两个顶点之间的最短路径。
该算法通过动态规划的方式,逐步更新顶点之间的距离,直到得到最短路径。
Floyd-Warshall算法的步骤如下:1. 初始化顶点之间的距离矩阵,如果两个顶点之间存在边,则距离为边的权值,否则距离为无穷大。
【转】彻底弄懂最短路径问题(图论)

【转】彻底弄懂最短路径问题(图论)P.S.根据个⼈需要,我删改了不少问题引⼊问题:从某顶点出发,沿图的边到达另⼀顶点所经过的路径中,各边上权值之和最⼩的⼀条路径——最短路径。
解决最短路的问题有以下算法,Dijkstra算法,Bellman-Ford算法,Floyd算法和SPFA算法,另外还有著名的启发式搜索算法A*,不过A*准备单独出⼀篇,其中Floyd算法可以求解任意两点间的最短路径的长度。
笔者认为任意⼀个最短路算法都是基于这样⼀个事实:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若⼲个节点到B。
⼀.Dijkstra算法该算法在《数据结构》课本⾥是以贪⼼的形式讲解的,不过在《运筹学》教材⾥被编排在动态规划章节,建议读者两篇都看看。
(1) 迪杰斯特拉(Dijkstra)算法按路径长度递增次序产⽣最短路径。
先把V分成两组:S:已求出最短路径的顶点的集合V-S=T:尚未确定最短路径的顶点集合将T中顶点按最短路径递增的次序加⼊到S中,依据:可以证明V0到T中顶点Vk的最短路径,或是从V0到Vk的直接路径的权值或是从V0经S中顶点到Vk的路径权值之和(反证法可证)。
(2) 求最短路径步骤1. 初使时令 S={V0},T={其余顶点},T中顶点对应的距离值,若存在<V0,Vi>,为<V0,Vi>弧上的权值(和SPFA初始化⽅式不同),若不存在<V0,Vi>,为Inf。
2. 从T中选取⼀个其距离值为最⼩的顶点W(贪⼼体现在此处),加⼊S(注意不是直接从S集合中选取,理解这个对于理解vis数组的作⽤⾄关重要),对T中顶点的距离值进⾏修改:若加进W作中间顶点,从V0到Vi的距离值⽐不加W的路径要短,则修改此距离值(上⾯两个并列for循环,使⽤最⼩点更新)。
3. 重复上述步骤,直到S中包含所有顶点,即S=V为⽌(说明最外层是除起点外的遍历)。
图论及其应用

Prim算法及思想
• • • • • 首先我们将V分成两部分U,S U∩S=∅ U∪S=V 一开始S中只有任意以个节点 每次我们枚举每条U,S之间的边权最小的边S中 这条边的端点 删除并加入U • 我们可以每次更新S中点的这个值不需要每次枚 举边复杂度O(n^2) • 如果使用堆优化可以做到O(nlogn+nlogm)
tarjan算法
tarjan算法
拓扑排序
• 每次选择一个入度为0的点加入队列,然后 删掉这个点的所有出度
小试身手
• APIO2009 atm • 有一个城市有若干条有向道路 • 一个小偷从一个点出发想偷这个城ATM机, 他从一个点出发,最后偷完之后需要到一 个酒吧庆祝,给定道路情况,每个路口atm 的钱数和有没有酒吧,求最多能偷多少钱。 • n<=100000
小试身手
对于n<=1000我们依然可以直接暴力建出图 来进行Dijsktra算法但是对于n<=10000的测 试点,所有边一共有10^10条,我们无法存下 来但是我们发现,只有x坐标相邻和y坐标相 邻的边才有意义(为什么?),然后就可以建出 图来用堆优化的Dij或者spfa过掉
小试身手
• 给你一个n个点的图,小Q有q个询问,每次 询问任意两点之间的最短路 • n<=200,q<=4000000
Байду номын сангаас
最短路算法
• 如果我们需要知道所有的点对之间的最短 路,可以使用floyed的传递闭包方法。 • floyed算法思想: • 我们每次选择一个中间点,然后枚举起点 和终点,用通过中间点的最短路径更新起 点和终点之间的最短路径时间复杂度O(n^3)
floyed代码实现
• 代码非常简单 • 注意枚举顺序
Python编程实例:计算图的连通分量

06
总结与展望
总结连通分量计算的重要性和应用场景
连通分量计算是图论中的基本问题,对于理解图的结构和性质至关重 要。
连通分量计算在社交网络分析、网页排名、图像分割等领域有着广泛 的应用。
连通分量计算可以帮助我们更好地理解数据的分布和关联,从而为实 际问题提供有效的解决方案。
未来,随着图数据的不断增加,连通分量计算的重要性和应用场景将 会更加广泛。
计算连通分量:使用 networkx库的
connected_compon ents函数
输出结果:将计算 结果打印或保存到 文件中
05
连通分量计算的应用
在社交网络分析中的应用
社交网络中的连通分量:表 示社交网络中相互连接的用 户群体
连通分量的应用:分析社交 网络的结构和特性,例如找 出核心用户群、检测社交网 络中的社区结构等
添加标题
顶点表:存储图中所有顶点的信息,如顶点编号 、顶点名称等
添加标题
边表:存储图中所有边的信息,如起始顶点、终 止顶点、边的权重等
添加标题
邻接表表示法的优点:易于实现图的基本操作, 如添加顶点、删除顶点、添加边、删除边等
添加标题
邻接表表示法的缺点:占用空间较大,不适合表 示稀疏图
添加标题
Python实现图的连通分量计算时,可以使用邻接 表表示法来存储图结构,方便地进行图的遍历和 操作。
在交通运输网络中的应用
计算图的连通分量可以帮助我们理解交通运输网络的结构
通过计算连通分量,可以找出交通网络的关键节点和关键路径
在交通网络优化中,连通分量的计算可以帮助我们找到最优的交通路 线
连通分量的计算还可以帮助我们预测交通网络的拥堵情况,并采取相 应的措施进行缓解
图论算法介绍

if (a[i,k]=1)and (a[k,j]=1) then a[i,j]=1 (a[i,j]=1表示i可达j,a[i,j]=0表示i不可达j)。
var
link,longlink:array[1..20,1..20] of boolean;{ 无向图和无向图的传递闭包。其
中
l o n g l i n k[i,
例如:公路交通图,边以距离w为权。
例
2
2
1
3
1
3
有向完全图 例
245
无向完全图 5
1
例 1
3
6
图与子图
57
32
46
G2
顶点5的度:3 顶点2的度:4
3
6
例 245
1
3
6
G1
顶点2入度:1 出度:3 顶点4入度:1 出度:0
例
路径:1,2,3,5,6,3 路径长度:5
245
简单路径:1,2,3,5
❖ 图 G = (V, E)
V = 顶点集 E = 边集 = V V的子集
结点集V={a, b, c, d} 边集E={e1, e2, e3, e4, e5} 其中e1=(a, b), e2=(a, c),
e3=(a, d), e4=(b, c), e5=(c, d)。
(一)、计算无向图的传递闭包
v1→v2→v4→v8→v5 →v3→v6→v7
算法结构:
调用一次dfs(i), 可按深度优先搜索 的顺序访问处理结 点i所在的连通分 支(或强连通分 支),dfs(i)的时 间复杂度为W(n2)。 整个图按深度优先 搜索顺序遍历的过 程如下:
显然,为了避免重复访问同一个顶点,必须 记住每个顶点是否被访问过。为此,可设置 一个布尔向量visited[1..n],它的初值为 false,一旦访问了顶点vi,便将visited[i] 置为ture。 图的深度优先搜索是一个递归过程,可以使 用栈来存储那些暂时不访问的邻接点.类似于 树的前序遍历,它的特点是尽可能先对纵深 方向进行搜索,故称之深度优先搜索。
图论的常用算法及应用

例题2 解法2
如何产生这样的一一映射呢?如何产生排列? Nhomakorabea
例题2 循环法
for m[1]:=1 to 4 do for m[2]:=1 to 4 do if m[1] <> m[2] then for m[3]:=1 to 4 do if (m[3] <> m[2]) and (m[3] <> m[1]) then for m[4]:=1 to 4 do if (m[4] <> m[3]) and (m[4] <> m[2]) and (m[4] <> m[1]) then 调用judge且判断;
广度优先搜索算法程序1
procedure bfs(which: integer); var i: integer; begin queue[1] := which; ql:=1; qh:=1; visited[which] :=1;
广度优先搜索算法程序2
while qh<=ql do begin for i:=1 to n do if (visited[i] = 0) and (data[queue[qh]][i]) then begin inc(ql); queue[ql] := i; visited[i] := 1; end; inc(qh); end; end;
Bellman – Ford 思考题
如何进一步提高算法的效率 如何判断一个图存在负圈 应用举例
两个基本算法
深度优先搜索(Depth First Search) 广度优先搜索(Breadth First Search)
深度优先搜索
图论经典问题
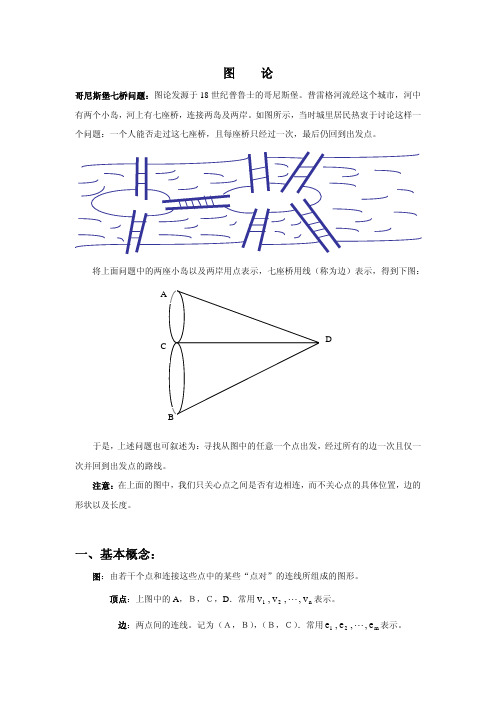
图 论哥尼斯堡七桥问题:图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市,河中有两个小岛,河上有七座桥,连接两岛及两岸。
如图所示,当时城里居民热衷于讨论这样一个问题:一个人能否走过这七座桥,且每座桥只经过一次,最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示,七座桥用线(称为边)表示,得到下图:于是,上述问题也可叙述为:寻找从图中的任意一个点出发,经过所有的边一次且仅一次并回到出发点的路线。
注意:在上面的图中,我们只关心点之间是否有边相连,而不关心点的具体位置,边的形状以及长度。
一、基本概念:图:由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点:上图中的A ,B,C,D .常用表示。
n 21 v , , v , v 边:两点间的连线。
记为(A,B),(B,C).常用表示。
m 21e , , e , e次:一个点所连的边数。
定点v的次记为d(v).图的常用记号:G=(V,E),其中,}{v V i =,}{e E i =子图:图G的部分点和部分边构成的图,成为其子图。
路:图G中的点边交错序列,若每条边都是其前后两点的关联边,则称该点边序列为图G的一条链。
圈(回路):一条路中所含边点均不相同,且起点和终点是同一点,则称该路为圈(回路)。
有向图:,其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合,A a 称为G 的弧集合。
G {(,)ij i j }n n ==若,则称为的前驱, 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图(网络):设是一个图,若对G 的每一条边(弧)都赋予一个实数,称为边的权,。
记为。
G (,,)G N E W =两个结论:1、图中所有顶点度数之和等于边数的二倍; 2、图中奇点个数必为偶数。
二、图的计算机存储:1. 关联矩阵简单图:,对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图:,对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图:,对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵:简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用:例:如图,用点代表7个村庄,边上的权代表村庄之间的路长,现在要在这7个村庄中布电话线,如何布线,使材料最省?分析:需要将图中的边进行删减,使得最终留下的图仍然连通,并且使总的权值最小。
图论(C++版)

对于带权值的网图,可以在边表结点定义中再 增加一个数据域来存储权值即可:
邻接表(网)
在进行邻接表的输入时,可以直接使用邻接表的定义方式直接输入; 也可由别的输入方式进行演变,课本上的就是利用边的顶点及其权值进行输入的
• 以下是用数组模拟邻接表存储的参考程序段:
const int N=maxn; // maxn表示图中最大顶 点数 const int E=maxe ; // maxe图中最大边数 struct Edge{ int u,v; //边所邻接的两个顶点 int w; //边的权值 int next; //边指针,指向下一条边的内存地址 }edge[E]; // 静态内存,用于分配边 int head[N]; // 表头 int num; // 内存的指针 void init() { for(int i=0;i<E;i++) head[i]=-1; //这里为什么 要设为-1 num= 0; } void addedge(int b,int e,int w) { edge[num].u=b; edge[num].v=e; edge[num].w=w; edge[num].next=head[b]; head[b]=num++; }
图的各种定义
• 无向边:若顶点Vi到Vj之间的边没有方向,则 称这条边为无向边(Edge),用无序偶数对(Vi,Vj) 来表示。 • 无向图:图中所有顶点间的边均是无向的。
上图G1是一个无向图,G1={V1,E1},其中 V1={A,B,C,D}, E1={(A,B),(B,C),(C,D),(D,A),(A,C)}
无向图中的极大连通子图称为连通分量。 注意以下概念: 首先要是子图,并且子图是要连通的; 连通子图含有极大顶点数; “极大”的含义:指的是对子 图再增加图G中的其它顶点,子图就不再连通。 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
组合图论图论及其算法课件

4. 实例:求下列赋权完全图的最优Hamilton回路.
A
解:ACEBDA: 权和 25 BACEDB: 权和 25 CABEDC: 权和 22 DACEBD: 权和 25 EACDBE: 权和 27
21 B
9 10
34 5E 7 6
C8D 所选初始点不同,得到的近似解也不同.
5. 修改方法:最邻近插入法
(2)不允许高速路在所研究的城市以外的某点 处连接.
最短网络问题: 如何用最短的线路将三部电话连起来?
A
B
C
此问题可抽象为设△ABC为等边三角形,,连接三 顶点的路线(称为网络)。这种网络有许多个, 其中最短路线者显然是二边之和(如AB∪AC).
❖ 但若增加一个周转站(新点P),连接4点的新网 络的最短路线为PA+PB+PC。最短新路径之长N 比原来只连三点的最短路径O要短。
3). 重复2)过程直到汇y被标号,或不再有顶点可以标号为止. 若y得到标号,说明存在一条x y增广路P,进入步骤2调整过程; 若y未得到标号,标号过程无法进行,说明f 即为最大流.
(2) 调整过程
1).
令
min{ min (vi ,v j )P
(Cij
f
ij
),
(
min
vi ,v j )P
f ji},调整增广路P中
三. 中国邮递员问题(1962,管梅谷)
1. 问题:邮递员每天从邮局选好邮件,送到他所管辖 的邮区的客户手中,再返回邮局,他每天必须走过每 条街道至少一次,问如何选择邮递路线,使得他走过 的投递总行程最短?
2. 模型:非负赋权图G: 顶点----交叉口或终端,边----街道,权-----街道长 度,此即求图的通过每条边至少一次的闭途径,称为G 的环游.
图论的基本算法及性质

图论的基本算法及性质二分图(Is-Bipartite)一个图的所有顶点可以划分成两个子集,使所有的边的入度和出度顶点分别在这两个子集中。
这个问题可以转换为上篇提到过的图的着色问题,只要看图是否能着2个颜色就行了。
当然,可以回溯解决这个问题,不过对于着2个颜色可以BFS解决。
同样,一维数组colors表示节点已着的颜色。
伪代码:IS-BIPARTITE(g,colors)let queue be new Queuecolors[0] = 1queue.push(0)while queue.empty() == falselet v = queue.top()queue.pop()for i equal to every vertex in gif colors[i] == 0colors[i] = 3 - colors[v]queue.push(i)else if colors[i] == colors[v]return falseendendreturn true时间复杂度:Θ(V+E),V表示顶点的个数,E表示边的个数DFS改良(DFS-Improve)上篇文章提到过,搜索解空间是树形的,也就是在说BFS和DFS。
那么在对图进行BFS和DFS有什么区别呢,这个问题要从解空间角度去理解。
对图进行BFS的解空间是一颗树,可叫广度优先树。
而DFS是多棵树构成的森林,可叫深度优先森林。
这里要对DFS进行小小的改良,它的性质会对解多个问题会很有帮助。
原版DFS搜索的时候,会先遍历本顶点,再递归遍历临接的顶点。
DFS改良希望能先递归遍历临接的顶点,再遍历本顶点,并且按遍历顺序逆序存储起来。
伪代码:DFS-IMPROVE(v,visited,stack)visited[v] = truefor i equal to every vertex adjacent to vif visited[i] == falseDFS-IMPROVE(i,visited,stack)endstack.push(v)这个改良版DFS有个很有用的性质就是,对于两个顶点A、B,存在A到B的路径,而不存在B到A的路径,则从记录的顺序中取出的时候,一定会先取出顶点A,再取出顶点B。
与图论相关的算法

广度优先搜索
procedure bfs(i:integer); var p:arcptr;
closed,open:integer; q:array[1..maxn] of integer; begin 访问并处理顶点i; map[i].visited:=true; 顶点i进入队列q; closed:=0; open:=1; repeat
编号都不超过k的路径。 递推公式:
t(k)[i,j]= t(k-1)[i,j] or (t(k-1)[i,k] and t(k-1)[k,j])
Johnson算法
Johnson算法常用于求顶点个数较多的稀 疏图的每对点间最短路问题。
感兴趣的同学请参阅《国际信息学奥林 匹克竞赛指导——实用算法的分析与程 序设计》
inc(closed); v:=q[closed]; p:=map[v].firstarc; while p<>nil do begin
if map[p^.v].visited=false then begin 访问并处理顶点q^.v; map[q^.v].visited=true; inc(open); q[open]:=q^.v; end;
q:=q^.nextarc; end; until closed=open; end;
计算连通分支数
count:=0; for i:=1 to n do
map[i].visited:=false; for i:=1 to n do
if map[i].visited=false do begin inc(count); dfs(i); end;
图论及其算法

图的最短路
给定带权有向图G=(V,E),其中每条边的
权是非负实数,另外,再给定V中的一个顶点, 我们称之为源点。要计算从源点到其他各顶 点的最短路径长度。这个问题称为图论单源 最短路问题。 Dijkstra、spfa、floyd
Dijkstra
是一种贪心算法。
建立集合s,先将源点加入集合。把距源点最
图的遍历
图的遍历是对给定一个图,从其中的任一顶
点出发顺序访问图中的所有顶点,每个顶点 被访问一次。遍历的结果是将顶点排成一定 的序列。图的遍历是求解图的连通、拓扑排 序等算法的基础。通常有深度优先遍历和广 度优先遍历两种方法。
Spfa(邻接表实现) var zt:array[0..10000] of longint; pre,other,w:array[0..10000] of longint;//邻接表 last,d:array[0..100] of longint; v:array[0..100] of boolean; i,p,q,r,t,l,n,m:longint; procedure spfa; var p,q,l,r,i:longint; begin fillchar(v,sizeof(v),false); //初值设为未访问 for i:=1 to n do d[i]:=1000000; //初始距离设为最大 l:=0;r:=1;d[1]:=0; //源点的距离是0 zt[1]:=1;v[1]:=true; //源点入队 while l<r do begin inc(l); //取出队头元素 p:=zt[l];v[p]:=false;q:=last[p]; while q<>0 do begin //邻接表的循环 if d[other[q]]>d[p]+w[q] then begin d[other[q]]:=d[p]+w[q]; //更新 if not v[other[q]] then begin inc(r);v[other[q]]:=true; //如果能更新,则入队 zt[r]:=other[q]; end;
算法与程序框图

通过逐步构建解决方案,并在构建过程中进 行验证和剪枝的算法。
算法的应用场景
数学领域:诸如求解方程、优化 问题等。如牛顿迭代法、梯度下 降法等。
工程领域:包括信号处理、控制 系统等问题。如卡尔曼滤波算法 、PID控制算法等。
计算机科学领域:包括数据排序 、图形渲染、人工智能等问题。 如快速排序算法、Dijkstra最短路 径算法等。
KMP算法
通过预处理模式串,计算出一个next数组,用于在匹配失败时快速跳过一些不可能匹配的字符,从而 提高字符串匹配的效率。程序框图中可使用两个指针、一个循环结构和一个条件判断表示KMP算法过 程,同时需要额外的计算过程来预处理模式串并生成next数组。
06
算法与程序框图的未来 发展
量子计算对算法与程序框图的影响
程序框图的基本元素
01
起止框
表示程序的开始和结束。
处理框
02
03
判断/决策框
表示程序中的一个处理步骤或操 作。
表示程序中的条件判断或决策点 。
程序框图的基本元素
01
流程线:表示程序的执行流程或 控制流。
02
连接点:用于连接跨越较大空间 的流程线。
输入/输出框:表示程序的输入和 输出。
03
这些基本元素通过各种组合和连 接,可以描述出各种复杂的程序
快速排序
采用分治思想,选取一个基准元素,将列表中小于基准的元 素放到左侧,大于基准的元素放到右侧,然后递归地对左右 两侧子序列进行快速排序。程序框图中可使用递归和条件判 断表示快速排序过程。
图论算法的程序框图表示
深度优先搜索
从某个起始节点开始,沿着一条路径尽 可能深入地搜索,直到路径无法继续为 止,然后回溯到前一个节点,继续深度 优先搜索。程序框图中可使用栈和条件 判断表示深度优先搜索过程。
最短路径算法floyd代码

最短路径算法floyd代码1.引言1.1 概述最短路径算法是图论中一个重要的问题,它的目标是找到两个节点之间最短的路径。
在实际生活中,最短路径算法被广泛应用于交通规划、物流配送、通信网络等领域。
针对不同类型的图,有不同的最短路径算法可供选择,其中Floyd算法是一种被广泛使用的算法之一。
Floyd算法是一种动态规划算法,它通过逐步优化图中各个节点之间的最短路径长度来求解最短路径。
其基本思想是通过计算任意两个节点之间的中间节点,以确定最短路径的中间节点集合。
通过反复迭代更新中间节点集合,最终可以得到节点之间的最短路径长度。
本文将介绍Floyd算法的原理和实现代码。
首先,我们将详细解释Floyd算法的原理,包括其计算最短路径的思路和步骤。
接着,我们将给出Floyd算法的代码实现,通过具体的编程示例来展示算法的具体实现过程和运行结果。
本文的目的是帮助读者了解Floyd算法,并通过实例代码帮助读者理解算法的具体实现步骤。
读者可以通过学习和实践运用Floyd算法,为实际问题寻找最短路径提供一种有效的解决方案。
此外,本文还将总结Floyd 算法的优缺点,以及对该算法在实际应用中的一些考虑和限制。
通过阅读本文并实践代码,读者将能够更好地理解Floyd算法的原理和实现方法,并在实际问题中灵活运用该算法来解决最短路径问题。
无论是对于图论的研究者还是对于应用场景中的实际需求,本文都将提供一些有价值的参考和启示。
在接下来的章节中,我们将逐步介绍Floyd算法的详细原理和代码实现。
让我们一起开始这段有趣的学习之旅吧!文章结构(Article Structure)本篇文章主要围绕最短路径算法Floyd展开讨论,按照以下结构进行阐述。
1. 引言1.1 概述:对最短路径算法的背景和应用进行简要介绍,强调其在网络通信、路线规划和图论等领域的重要性。
1.2 文章结构:本节内容。
1.3 目的:明确本文旨在通过介绍Floyd算法的原理和代码实现,帮助读者理解和应用该算法。
matlab图论方法

哈密顿圈(环球旅行游戏)
问题3(四色问题): 对任何一张地图进行着色,两个共同边界的
国家染不同的颜色,则只需要四种颜色就够了.
问题4(关键路径问题): 一项工程任务,大到建造一座大坝,一座体育
中心,小至组装一台机床,一架电视机, 都要包括 许多工序.这些工序相互约束,只有在某些工序完 成之后, 一个工序才能开始. 即它们之间存在完 成的先后次序关系,一般认为这些关系是预知的, 而且也能够预计完成每个工序所需要的时间.
V = {v1 , v2 , v3 , v4}, E = { v1v2 , v1v3 , v1v4 , v2v3 , v2v4 , v3v4}.
今后将不计较这种外形上的差别,而用一个容 易理解的、确定的图解去表示一个图.
有边联结的两个点称为相邻的点, 有一个公共 端点的边称为相邻边. 边和它的端点称为互相关联. 常用d(v)表示图G中与顶点v关联的边的数目, d(v) 称为顶点v的度数. 用N(v)表示图G中所有与顶点v相 邻的顶点的集合.
这时工程领导人员迫切希望了解最少需要多 少时间才能够完成整个工程项目, 影响工程进度 的要害工序是哪几个?
6.1 图论的基本概念
图论中的“图”并不是通常意义下的几何图 形或物体的形状图, 而是以一种抽象的形式来表 达一些确定的事物之间的联系的一个数学系统.
定义1 一个有序二元组(V, E ) 称为一个图, 记 为G = (V, E ), 其中
(0,1,0,1) (0,1,0,0) (0,0,1,0) (0,0,0,1) (0,0,0,0) (1,0,1,0) (1,0,1,1) (1,1,0,1) (1,1,1,0) (1,1,1,1)
C语言技术与算法设计结合实例分享

C语言技术与算法设计结合实例分享在计算机科学领域中,C语言是一门被广泛应用的编程语言。
它的灵活性和高效性使得它成为许多软件和系统的首选语言。
然而,单纯的掌握C语言并不足以成为一名出色的程序员。
算法设计是计算机科学中至关重要的一部分,它涉及解决问题的方法和步骤。
本文将探讨C语言技术与算法设计的结合,并通过一些实例来分享这种结合的实际应用。
首先,让我们来看一个简单的实例。
假设我们需要编写一个程序来计算斐波那契数列的第n个数字。
斐波那契数列是一个经典的数学问题,其定义是每个数字都是前两个数字的和。
通过使用C语言的循环和条件语句,我们可以编写一个简单的程序来解决这个问题。
然而,这种方法的效率并不高,特别是当n的值很大时。
为了提高效率,我们可以使用递归算法来解决这个问题。
递归算法是一种将问题分解成更小的子问题并逐步解决的方法。
通过使用递归算法,我们可以大大减少计算时间,提高程序的效率。
接下来,让我们来看一个稍微复杂一些的实例。
假设我们需要编写一个程序来解决旅行商问题。
旅行商问题是一个经典的组合优化问题,其目标是找到一条路径,使得旅行商可以经过所有城市并返回起始城市,同时路径的总长度最短。
这个问题的解决方案需要使用图论和动态规划等算法。
在C语言中,我们可以使用图的数据结构和相关的算法来解决这个问题。
通过使用邻接矩阵或邻接表来表示城市之间的连接关系,并使用最短路径算法(如Dijkstra算法或Floyd-Warshall算法)来计算最短路径,我们可以编写一个高效的程序来解决旅行商问题。
除了以上两个实例,C语言技术与算法设计的结合在许多其他领域也有广泛的应用。
例如,在图像处理中,我们可以使用C语言编写算法来实现图像的滤波、边缘检测和图像压缩等操作。
在网络编程中,我们可以使用C语言编写算法来实现数据包的传输和路由选择等功能。
在人工智能和机器学习领域,我们可以使用C 语言编写算法来实现各种模型和算法,如神经网络、遗传算法和支持向量机等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 5
1 6 ??????????? 原??? 图
从第1点出发的最短路径
program dijkstra_example;
const
? vmax=100;
type
? path=record????????????????? {此记录类型用于记录每一个结点与v0的距离和其父结点}
??????????? if flag[k] then {找已在集合中的顶点}
????????????? for j:=1 to v do {求满足条件的边的最小值}
???????????????? if (not(flag[j])) and (w[k,j]<min) and (w[k,j]<>0)
??? 由于源结点V0是给定的,所谓称为单源最短路径。
【Dijkstra算法思想】
?? 把所有结点分为两组。
?? 第一组:包含已确定最短路径的结点。
?? 第二组:包含尚未确定最短路径的结点。
?? 按最短路径长度递增的顺序把第二组的结点加到第一组中去,直到V0可达的所有结点都包含于第一组中。在这个过程中,总保持从V0到第一组各结点的最短路径长度都不大于从V0到第二组任何结点的路径长度。
procedure init;
? begin
??? assign(input,'dijkstra.in');
??? reset(input);
??? assign(output,'dijkstra.out');
??? rewrite(output);
??? readln(v);
??? readln(e);
2 3 5
2 4 6
2 6 11
3 4 6
4 5 18
4 6 14
5 6 33
【输出样例】
1 2 10
2 3 5
2 4 6
2 6 11
4 5 18
原? 图
最小生成树
program prim_example;
Const
?? vmax=200
rewrite(output);
fillchar(w,sizeof(w),0);
readln(v);
for i:=1 to v do
readln(x[i],y[i]);
for i:=1 to v do {计算图的邻接矩阵}
【Prim算法思想】
任意时刻的中间结果都是一棵树,每次花费最小的代价,用一条边把不在树中的结点加进来。
【最小生成树算法实例】
??? 现有一张城市地图,图中的顶点为城市,无向边代表两个城市间的连通关系,边上的权代表公路造价。在分析了这张图后发现,任一对城市都是连通的。现在要求用公路把所有城市联系起来,如何设计可使得工程的总造价最少?
【输出】 v-1行,每行为两个城市的序号,表明这两个城市间建一条公路。
【输入样例】
6
10
1 2 10
1 5 19
1 6 21
2 3 5
2 4 6
2 6 11
3 4 6
4 5 18
4 6 14
5 6 33
【输出样例】
1 2
2 3
??? for i:=1 to v do
????? for j:=1 to v do
??????? if i<>j
????????? then w[i,j]:=30000
?? {30000只是一个较大的数的意思,实际应用于应该根据题目中给出的取值范围赋予一个充分大的数}
????????? else w[i,j]:=0;
prim(1);
writeln(sum:0:2);
close(input);
close(output);
end.
无向图的生成树就是从图的边集中选择一些边,使得这些边构成一个连通无环图,也就是树。如果给每一条边加一个权,所有生成树中权和最小的生成树称为最小生成树。
? begin
??? fillchar(flag,sizeof(flag),false);
??? flag[v0]:=true; {先选出v0}
??? for i:=1 to v-1 do {一共寻找v-1条边}
????? begin
??????? min:=maxint;
????????? for k:=1 to v do
??? for i:=1 to e do
????? begin
??????? read(x,y);
??????? readln(w[x,y]);
then begin
flag[nextk]:=true;
{writeln(prevk,' ',nextk,' ',min:0:2); 此部分输出每个结点对的距离,因题目不要求所以不输出。}
【输入】network.in
输入文件的第一行为一个正整数N(1≤N≤100)。
接下来N行,每行2个数U,V ,表示坐标。
【输出】network.out
输出最短路径距离(保留两位小数)
【样例数据】?
【输入】
5
0 0
0 1
0 -1
1 0
-1 0
【输出】
4.00
{思路分析:此题可以应用PRIM算法解决,关键是根据输入文件算出图的邻接矩阵,然后可以直接应用PRIM算法。}
begin
min:=1e38;
for k:=1 to v do
if flag[k] then
for j:=1 to v do
if (not flag[j]) and (w[k,j]<min) and (w[k,j]<>0)
????? readln(w[i,j]);
????? w[j,i]:=w[i,j];
??? end;
? prim(1);
? close(input);
? close(output);
end.
设图G=(V,E)是一个有向图,它的每一条边(U,V)都有一个非负权W(U,V),在G中指定一个结点V0,要求从V0到G的每一个结点Vj的最短路径找出来(或指出不存在)。
??????? length:integer;
??????? pre:0..vmax;
?????? end;
var
? w:array[1..vmax,1..vmax] of integer;
? dist:array[1..vmax] of path;
? v,e,u,i,j,x,y:integer;
【输入】 第一行两个数v(v<=200),e,分别代表城市数和边数 以下e行,每行为两个顶点和它们之间的边权w(w<1000)。
【输出】 v-1行,每行为两个城市的序号,表明这两个城市间建一条公路,再加该公路的造价。
【输入样例】
6 10
1 2 10
1 5 19
1 6 21
????????????????????????? writeln(prevk,' ',nextk,‘ ',min);
???????????????????????? end;
???????????? end;{for}
?? end;{prim}
begin
? assign(input,'prim.in');
图论算法
最小生成树算法(Prim算法)单源最短路径算法(Dijkstra算法)任意结点最短路径算法(Floyd算法)求有向带权图的所有环Bellman-Ford算法计算图的连通性计算最佳连通分支计算拓扑序列图论算法习题
网络建设问题最短变换问题挖地雷乌托邦城市乌托邦交通中心
某大学准备在校园网中构建校园网络,已知在校园网中选好了N(N<1000)个点,并准备在这些点安装网络设备和电脑。若要将N个点互相连接起来,问怎样布线才能使得总距离最短,两点间的布线长度等于这两个点的几何距离。
var
?? w:array[1..vmax,1..vmax]of integer;
?? i,j,k,v,e:integer;
procedure prim(v0:integer); {v0是开始结点}
? var
??? flag:array[1..vmax] of boolean;
??? min,prevk,nextk:integer;
var
flag:array[1..vmax] of boolean;
min:real;
prevk,nextk:integer;
Байду номын сангаасbegin
fillchar(flag,sizeof(flag),false);
flag[v0]:=true;
for i:=1 to v-1 do
? reset(input);
? assign(output,'prim.out');
? rewrite(output);
? fillchar(w,sizeof(w),0);
? readln(v,e);
? for k:=1 to e do
??? begin
????? read(i,j);
then begin
min:=w[k,j];
