中考数学压轴题典型题型精讲含答案
(完整)中考数学压轴题精选及答案
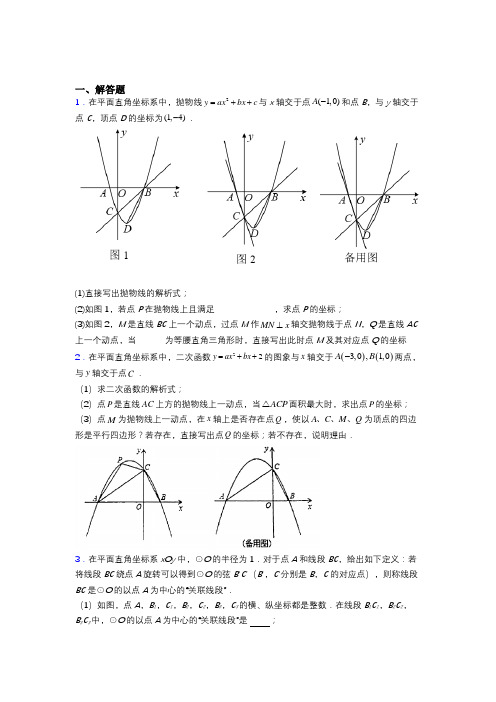
一、解答题1．在平面直角坐标系中，抛物线2y ax bx c =++与x 轴交于点(1,0)A -和点B ，与y 轴交于点C ，顶点D 的坐标为(1,4)-．(1)直接写出抛物线的解析式；(2)如图1，若点P 在抛物线上且满足，求点P 的坐标； (3)如图2，M 是直线BC 上一个动点，过点M 作MN x ⊥轴交抛物线于点N ，Q 是直线AC 上一个动点，当为等腰直角三角形时，直接写出此时点M 及其对应点Q 的坐标2．在平面直角坐标系中，二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点，与y 轴交于点C ．（1）求二次函数的解析式；（2）点P 是直线AC 上方的抛物线上一动点，当ACP △面积最大时，求出点P 的坐标；（3）点M 为抛物线上一动点，在x 轴上是否存在点Q ，使以A C M Q 、、、为顶点的四边形是平行四边形？若存在，直接写出点Q 的坐标；若不存在，说明理由．3．在平面直角坐标系xOy 中，⊙O 的半径为1．对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′（B ′，C ′分别是B ，C 的对应点），则称线段BC 是⊙O 的以点A 为中心的“关联线段”．（1）如图，点A ，B 1，C 1，B 2，C 2，B 3，C 3的横、纵坐标都是整数．在线段B 1C 1，B 2C 2，B 3C 3中，⊙O 的以点A 为中心的“关联线段”是 ；（2）△ABC 是边长为1的等边三角形，点A （0，t ），其中t ≠0．若BC 是⊙O 的以点A 为中心的“关联线段”，求t 的值；（3）在△ABC 中，AB ＝1，AC ＝2．若BC 是⊙O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．综合与探究如图，在平面直角坐标系中，点()0,10A ，点B 是x 轴的正半轴上的一个动点，连接AB ，取AB 的中点M ，将线段MB 绕着点B 按顺时针方向旋转90°，得到线段BC ．过点B 作x 轴的垂线交直线AC 于点D ．设点B 坐标是(),0t（1）当6t =时，点M 的坐标是 ；（2）用含t 的代数式表示点C 的坐标；（3）是否存在点B ，使四边形AOBD 为矩形？若存在，请求出点B 的坐标；若不存在，请说明理由；（4）在点B 的运动过程中，平面内是否存在一点N ，使得以A 、B 、N 、D 为顶点的四边形是菱形？若存在，请直接写出点N 的纵坐标（不必要写横坐标）；若不存在，请说明理由．5．如图（1），在菱形ABCD 中，∠ABC ＝60°，点E 在边CD 上（不与点C ，D 重合），连结AE ，交BD 于点F ．（1）如图（2），若点M 在BC 边上，且DE ＝CM ，连结AM ，EM ．求证：三角形AEM 为等边三角形；（2）设DF x BF=，求tan ∠AFB 的值（用x 的代数式表示）； （3）如图（3），若点G 在线段BF 上，且FG ＝2BG ，连结AG 、CG ，DF x BF =，四边形AGCE 的面积为S 1，ABG 的面积为S 2，求12S S 的最大值．6．如图，在平面直角坐标系中，ABC 的边AB 在x 轴上，且OB OA >，以AB 为直径的圆过点C ．若点C 的坐标为()0,4，10AB =，（1）求抛物线的解析式；（2）点P 为该函数在第一象限内的图象上一点（不与BC 重合)，过点P 作PQ BC ⊥，垂足为点Q ，连接PC ．若以点P 、C 、Q 为顶点的三角形与COA 相似，求点P 的坐标；（3）若ACB ∠平分线所在的直线l 交x 轴与点E ，过点E 任作一直线l '分别交射线CA ，CB （点C 除外）于点M ，N ．则11CM CN+的是否为定值？若是，求出该定值；若不是，请说明理由．7．如图1，⊙I 与直线a 相离，过圆心I 作直线a 的垂线，垂足为H ，且交⊙I 于P 、Q 两点（Q 在P 、H 之间）．我们把点Q 称为⊙I 关于直线a 的“近点”，点P 称为⊙I 关于直线a 的“远点”把PQ ·QH 的值称为⊙I 关于直线a 的“特征数”．（1）如图2，在平面直角坐标系xOy 中，点E 的坐标为（0，3）．半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D ．①过点E 画垂直于y 轴的直线m ，则⊙O 关于直线m 的“近点”“远点”分别是点_____和_____（填“A ”、“B ”、“C ”或“D ”），⊙O 关于直线m 的“特征数”为_____；②若直线n 的函数表达式为33y x =-+．求⊙O 关于直线n 的“特征数”；（2）在平面直角坐标系xOy 中，直线l 经过点M （1，2），点F 是坐标平面内一点，以F 5为半径作⊙F ．若⊙F 与直线l 相离，点N （1-，0）是⊙F 关于直线l 的“近点”．且⊙F 关于直线l 的“特征数”是6，求直线l 的函数表达式．8．如图，抛物线y＝－x2＋bx＋c与x轴交于A，B两点，其中A（3，0），B（－1，0），与y轴交于点C，抛物线的对称轴交x轴于点D，直线y＝kx＋b1经过点A、C，连接CD．（1）分别求抛物线和直线AC的解析式；（2）在直线AC下方的抛物线上，是否存在一点P，使得△ACP的面积是△ACD面积的2倍，若存在，请求出点P的坐标；若不存在，请说明理由；（3）在抛物线的对称轴上是否存在一点Q，使线段AQ绕Q点顺时针旋转90°得到线段QA1，且点A1恰好落在该抛物线上？若存在，求出点Q的坐标；若不存在，请说明理由．9．已知：如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，以OA，OC为边作矩形ABCO，矩形ABCO的面积是36．（1）求直线AC的解析式．（2）点P为线段AB上一点，点Q为第一象限内一点，连接PO，PQ，∠OPQ＝90°，且OP＝PQ，设AP的长为t，点Q的横坐标为d，求d与t的函数关系式．（不要求写出自变量t的取值范围）（3）在（2）的条件下，过点Q作QE∥PO交AB的延长线于点E，作∠POC的平分线OF 交PE于点F，交PQ于点K，若KQ＝2EF，求点Q的坐标．10．如图，平面直角坐标系中，点O为原点，抛物线交x轴于()2,05,0B两点，交y轴于点C．A-、()（1）求抛物线解析式；（2）点P在第一象限内的抛物线上，过点P作x轴的垂线，垂足为点H，连AP交y轴于点E，设P点横坐标为t，线段EC长为d，求d与t的函数解析式；（3）在（2）条件下，点M在CE上，点Q在第三象限内抛物线上，连接PC、PQ、PM，PQ与y轴交于W，若，，，求点Q的坐标．11．已知：如图1，点A（a，b），AB x⊥轴于点B2++-+=．a b a b24(8)0（1）试判断△AOB的形状，并说明理由；（2）如图2，若点C为线段AB的中点，连OC并作OD OC⊥，且OD OC=，连AD交x轴于点E，试求点E的坐标；（3）如图3，若点M为点B的左边x轴负半轴上一动点，以AM为一边作45∠=︒交MANy轴负半轴于点N，连MN，在点M运动过程中，试猜想式子OM MN ON+-的值是否发生变化？若不变，求这个不变的值；若发生变化，试求它变化的范围．12．直角三角板ABC的斜边AB的两个端点在⊙O上，已知∠BAC=30°，直角边AC与⊙O 相交于点D，且点D是劣弧AB的中点．(1)如图1，判断直角边BC所在直线与⊙O的位置关系，并说明理由；(2)如图2，点P是斜边AB上的一个动点（与A、B不重合），DP的延长线交⊙O于点Q，连接QA、QB．①AD=6，PD=4，则AB= ；PQ= ；②当点P在斜边AB上运动时，求证：QA+QB=3QD．13．如图，已知四边形ABCD内接于⊙O，直径DF交BC于点G．(1)如图1，求证：∠BAD－∠BCF＝90°；(2)如图2，连接AC，当∠BAC＝∠CFD＋∠ACD时，求证：CA＝CB；(3)如图3，在（2）的条件下，AC交DF于点H，∠BAC＝∠DGB，45CGBG，AC＝9，求△CDH的面积．14．同学们学过正方形与等腰三角形发现它们都是轴对称图形，它们之间有很多相似，在正边形ABCD中，E是对角线AC上一点（不与点A、C重合），以AD、AE为邻边作平行四边形AEGD，GE交CD于点M，连接CG．(1)如图1，当12AE AC<时，过点E作EF BE⊥交CD于点F，连接GF并延长交AC于点H．求证：EB EF=；(2)在ABC中，AB AC=，90BAC∠=︒．过点A作直线AP，点C关于直线AP的对称点为点D，连接BD，CD直线BD交直线AP于点E．如图2，①依题意补全图形；②请用等式表示线段EB，ED，BC之间的数量关系，并予以证明．15．如图，在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于点A和点B（1，0），与y轴交于点C（0，﹣3）．(1)求抛物线的函数表达式．(2)若点P为第三象限内抛物线上一动点，作PD⊥x轴于点D，交AC于点E，过点E作AC 的垂线与抛物线的对称轴和y轴分别交于点F、G，设点P的横坐标为m．①求PE2的最大值；②连接DF、DG，若∠FDG＝45°，求m的值．16．【问题提出】如图①，在△ABC中，若AB＝8，AC＝4，求BC边上的中线AD的取值范围．【问题解决】解决此问题可以用如下方法：延长AD 到点E ，使DE ＝AD ，再连结BE （或将△ACD 绕着点D 逆时针旋转180°得到△EBD ），把AB 、AC ，2AD 集中在△ABE 中，利用三角形三边的关系即可判断．由此得出中线AD 的取值范围是__________【应用】如图②，如图，在△ABC 中，D 为边BC 的中点、已知AB ＝10，AC ＝6，AD ＝4，求BC 的长．【拓展】如图③，在△ABC 中，∠A ＝90°，点D 是边BC 的中点，点E 在边AB 上，过点D 作D F⊥DE 交边AC 于点F ，连结EF ．已知BE ＝5，CF ＝6，则EF 的长为__________.17．已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B （1，0）两点，与y 轴交于点()03C -，．(1)求二次函数的表达式及A 点坐标；(2)D 是二次函数图象上位于第三象限内的点，若点D 的横坐标为m ，ACD △的面积为S ，求S 与m 之间的函数关系式，并写出ACD △的面积取得最大值时点D 的坐标；(3)M 是二次函数图象对称轴上的点，在二次函数图象上是否存在点N ．使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．18．如图，在平面直角坐标系中，已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ，点B 39(2,)16- 是一次函数5119216y x =+上一点．(1)当a ＝0时，求顶点P 坐标；(2)若a ＞0，且一次函数2y x b =-+的图象与此抛物线没有交点，请你写出一个符合条件的一次函数关系式（只需写一个，不必写出过程）；(3)作直线OC ：12y x =与一次函数5119216y x =+交于点C ．连结OB ，当抛物线与△OBC 的边有两个交点时，求a 的取值范围．19．已知O 为ABC ∆的外接圆，AC BC =，点D 是劣弧AB 上一点（不与点A ，B 重合），连接DA ，DB ，DC ．(1)如图1，若AB 是直径，将ACD ∆绕点C 逆时针旋转得到BCE ∆．若4CD =，求四边形ADBC 的面积；(2)如图2，若AB AC =，半径为2，设线段DC 的长为x ．四边形ADBC 的面积为S ． ①求S 与x 的函数关系式；②若点M ，N 分别在线段CA ，CB 上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置．DMN ∆的周长有最小值t ，随着点D 的运动，t 的值会发生变化．求所有t 值中的最大值，并求此时四边形ADBC 的面积S ．20．如图，在ABCD 中，90ABD ∠=︒，5cm AD =，8cm BD =．点P 从点A 出发，沿折线AB BC -向终点C 运动，点P 在AB 边、BC 边上的运动速度分别为1cm/s 、5cm /s ．在点P 的运动过程中，过点P 作AB 所在直线的垂线，交边AD 或边CD 于点Q ，以PQ 为一边作矩形PQMN ，且2QM PQ =，MN 与BD 在PQ 的同侧．设点P 的运动时间为t （秒），矩形PQMN 与ABCD 重叠部分的面积为()2cm S ．（1）求边AB 的长．（2）当04t <<时，PQ = ，当48t <<时，PQ = ．（用含t 的代数式表示）（3）当点M 落在BD 上时，求t 的值．（4）当矩形PQMN 与ABCD 重叠部分图形为四边形时，求S 与t 的函数关系式．【参考答案】参考答案**科目模拟测试一、解答题1．(1)223y x x =--；(2)，； (3)，；，；，；，； ，；，． 【解析】【分析】（1）根据顶点的坐标，设抛物线的解析式为y ＝a （x ﹣1）2﹣4，将点A （﹣1，0）代入，求出a 即可得出答案；（2）利用待定系数法求出直线BD 解析式为y ＝2x ﹣6，过点C 作CP 1∥BD ，交抛物线于点P 1，再运用待定系数法求出直线CP 1的解析式为y ＝2x ﹣3，联立方程组即可求出P 1（4，5），过点B 作y 轴平行线，过点C 作x 轴平行线交于点G ，证明△OCE ≌△GCF（ASA），运用待定系数法求出直线CF解析式为y＝12x﹣3，即可求出P2（52，﹣74）；（3）利用待定系数法求出直线AC解析式为y＝﹣3x﹣3，直线BC解析式为y＝x﹣3，再分以下三种情况：①当△QMN是以NQ为斜边的等腰直角三角形时，②当△QMN是以MQ为斜边的等腰直角三角形时，③当△QMN是以MN为斜边的等腰直角三角形时，分别画出图形结合图形进行计算即可．(1)解：∵顶点D的坐标为（1，﹣4），∴设抛物线的解析式为y＝a（x﹣1）2﹣4，将点A（﹣1，0）代入，得0＝a（﹣1﹣1）2﹣4，解得：a＝1，∴y＝（x﹣1）2﹣4＝x2﹣2x﹣3，∴该抛物线的解析式为y＝x2﹣2x﹣3；(2)解：∵抛物线对称轴为直线x＝1，A（﹣1，0），∴B（3，0），设直线BD解析式为y＝kx+e，∵B（3，0），D（1，﹣4），∴，解得：，∴直线BD解析式为y＝2x﹣6，过点C作CP1∥BD，交抛物线于点P1，设直线CP1的解析式为y＝2x+d，将C（0，﹣3）代入，得﹣3＝2×0+d，解得：d＝﹣3，∴直线CP1的解析式为y＝2x﹣3，结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝2x﹣3，解得：x1＝0（舍），x2＝4，故P1（4，5），过点B作y轴平行线，过点C作x轴平行线交于点G，∵OB＝OC，∠BOC＝∠OBG＝∠OCG＝90°，∴四边形OBGC是正方形，设CP1与x轴交于点E，则2x﹣3＝0，解得：x＝32，∴E（32，0），在x轴下方作∠BCF＝∠BCE交BG于点F，∵四边形OBGC是正方形，∴OC＝CG＝BG＝3，∠COE＝∠G＝90°，∠OCB＝∠GCB＝45°，∴∠OCB﹣∠BCE＝∠GCB﹣∠BCF，即∠OCE＝∠GCF，∴△OCE≌△GCF（ASA），∴FG＝OE＝32，∴BF＝BG﹣FG＝3﹣32＝32，∴F（3，﹣32），设直线CF解析式为y＝k1x+e1，∵C（0，﹣3），F（3，﹣32），∴，解得：，∴直线CF解析式为y＝12x﹣3，结合抛物线y＝x2﹣2x﹣3，可得x2﹣2x﹣3＝12x﹣3，解得：x1＝0（舍），x2＝52，∴P2（52，﹣74），综上所述，符合条件的P点坐标为：（4，5）或（52，﹣74）；(3)解：（3）设直线AC解析式为y＝m1x+n1，直线BC解析式为y＝m2x+n2，∵A（﹣1，0），C（0，﹣3），∴，解得：，∴直线AC解析式为y＝﹣3x﹣3，∵B（3，0），C（0，﹣3），∴，解得：，∴直线BC解析式为y＝x﹣3，设M（t，t﹣3），则N（t，t2﹣2t﹣3），∴MN＝|t2﹣2t﹣3﹣（t﹣3）|＝|t2﹣3t|，①当△QMN是以NQ为斜边的等腰直角三角形时，此时∠NMQ＝90°，MN＝MQ，如图2，∵MQ∥x轴，∴Q（﹣13t，t﹣3），∴|t2﹣3t|＝|t﹣（﹣13t）|，∴t2﹣3t＝±43t，解得：t＝0（舍）或t＝53或t＝133，∴，；，；②当△QMN是以MQ为斜边的等腰直角三角形时，此时∠MNQ＝90°，MN＝NQ，如图3，∵NQ∥x轴，∴Q（，t2﹣2t﹣3），∴NQ＝|t﹣|＝13|t2+t|，∴|t2﹣3t|＝13|t2+t|，解得：t＝0（舍）或t＝5或t＝2，∴M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；③当△QMN是以MN为斜边的等腰直角三角形时，此时∠MQN＝90°，MQ＝NQ，如图4，过点Q作QH⊥MN于H，则MH＝HN，∴H（t，），∴Q（，），∴QH＝|t﹣|＝16|t2+5t|，∵MQ＝NQ，∴MN＝2QH，∴|t2﹣3t|＝2×16|t2+5t|，解得：t＝7或1，∴M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）；综上所述，点M及其对应点Q的坐标为：，；，；M3（5，2），Q3（﹣5，12）；M4（2，﹣1），Q4（0，﹣3）；M5（7，4），Q5（﹣7，18）；M6（1，﹣2），Q6（0，﹣3）．【点睛】本题是二次函数综合题，主要考查了待定系数法求一次函数和二次函数解析式，求一次函数与二次函数图象交点坐标，全等三角形判定和性质，正方形判定和性质，等腰直角三角形性质等，本题属于中考压轴题，综合性强，难度较大，熟练掌握待定系数法、等腰直角三角形性质等相关知识，运用数形结合思想、分类讨论思想是解题关键．2．（1）224233y x x =--+；（2）35(,)22P -（3）存在，12(1,0),(5,0)Q Q --，34(27,0),(27,0)Q Q ．【解析】【分析】（1）根据待定系数法求抛物线解析式；（2）设224(,)33P t t --根据（1）的结论求得C 的坐标，进而求得AC 的解析式，过P 作PD ⊥x 轴交AC 于点D ，进而求得PD 的长，根据12APC C A S PD x x =⋅⋅-△求得APC S 的表达式，进而根据二次函数的性质求得取得最大值时，t 的值，进而求得P 点的坐标；（3）分情况讨论，①//CM AQ ，②//AC MQ ，根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标．【详解】（1）二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点，则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+ （2）抛物线224233y x x =--+与y 轴交于点C ，令0x =，则2y = (0,2)C ∴设直线AC 的解析式为y kx b =+，由(3,0)A -，(0,2)C ，则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的解析式为223y x =+， 如图，过P 作PD ⊥x 轴交AC 于点D ，设224(,)33P t t --，则2(,2)3D t t +， 2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APC C A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时，APC S 取得最大值，此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P - （3）存在，理由如下抛物线解析式为224233y x x =--+()228133x =-++ ∴抛物线的对称轴为直线1x =①如图，当//CM AQ 时，Q 点在x 轴上，//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称，(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时，如图，设M 的纵坐标为n ，四边形ACQM 是平行四边形，点A ,Q 在x 轴上，则,AQ MC 的交点也在x 轴上， 202n +∴= 解得2n =-设(,2)M m -，2242233x x ∴-=--+ 解得17x =-(17,2)M ∴--A 点到C 点是横坐标加3，纵坐标加2∴M 点到Q 点也是横坐标加3，纵坐标加2 即(173,0)Q -±34(27,0),(27,0)Q Q ∴综上所述，存在点Q ，使得以A C M Q 、、、为顶点的四边形是平行四边形，Q 点的坐标为12(1,0),(5,0)Q Q --，34(27,0),(27,0)Q Q ．【点睛】本题考查了二次函数综合，待定系数法，二次函数最值，二次函数的图象与性质，平行四边形的性质，综合运用以上知识是解题的关键．3．（1）B 2C 2；（233-3）OA 最小值为1，相应的3BC =OA 最大值为2，相应的6BC =【解析】【分析】（1）结合题意，根据旋转和圆的性质分析，即可得到答案；（2）根据题意，分B C ''在x 轴上方和x 轴上方两种情况；根据等边三角形、勾股定理、全等三角形的性质，得32AD OD ==，从而完成求解； （3）结合题意，得当AC '为⊙O 的直径时，OA 取最小值；当A 、B '、O 三点共线时，OA 取最大值；根据勾股定理、等腰三角形的性质计算，即可得到答案．【详解】（1）线段B 1C 1绕点A 旋转得到的11B C ''，均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”；线段B 2C 2绕点A 旋转得到的22B C ''，如下图：∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”；线段B 3C 3绕点A 旋转得到的33B C ''，均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”；故答案为：B 2C 2；（2）∵△ABC 是边长为1的等边三角形，点A （0，t ），⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况：当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：∵1OB OC ''==∴1122B D B C '''== ∴2232OD OB B D ''=-=∵△ABC 是边长为1的等边三角形，即△AB C ''是边长为1的等边三角形， ∴AC D OC D ''∠=∠，AD B C ''⊥ ∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =；当B C ''在x 轴上方时，B C ''与y 轴相交于点D ，见下图：同理，3AO AD OD =+=∴()0,3A -；∴t 3=-；∴3t =或3-；（3）当AC '为⊙O 的直径时，OA 取最小值，如下图：∴OA 最小值为1，90AB C ''∠=︒ ∴223BC B C AC AB ''''==-=；当A 、B '、O 三点共线时，OA 取最大值，2OA AC '== ，如下图：作AE OC '⊥交OC '于点E ，作C F AO '⊥交AO 于点F ，如下图∵2OA AC '==∴1122OE OC '==∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '==∴2214OF OC C F ''=-=∴34B F OB OF ''=-=∴262BC B C C F B F ''''==+=∴OA 最小值为1，相应的3BC =；OA 最大值为2，相应的62BC =． 【点睛】本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识；解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质，从而完成求解．4．（1）(3,5)M ，（2）1(5,)2C t t +；（3）(20,0)B ；（4）154或10． 【解析】 【分析】（1）利用中点坐标公式计算即可．（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．证明()MEB BFC AAS ∆≅∆，利用全等三角形的性质即可解决问题．（3）如图2中，存在．由题意当CF OA =时，可证四边形AOBD 是矩形，构建方程即可解决问题．（4）分三种情形：①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为6．③因为BD AB ≠，所以不存在以AD 为对角线的菱形． 【详解】解：（1）如图1中，(0,10)A ，(6,0)B ，AM BM =， (3,5)M ∴，（2）如图1中，作ME OB ⊥于E ，CF x ⊥轴于F ．//ME OA ，AM BM =， 12OE EB t ∴==，152ME OA ==，90MEB CFB CBM ∠=∠=∠=︒，90MBE CBF ∴∠+∠=︒，90MBE BME ∠+∠=︒， BME CBF ∴∠=∠，()MEB BFC AAS ∴∆≅∆，5BF ME ∴==，12CF BE t ==，5OF OB BF t ∴=+=+， 1(5,)2C t t ∴+．（3）存在．如图2中，作ME OB ⊥于E ，CF x ⊥轴于F ．理由：由题意当=10CF OA =时，//OA CF ， ∴四边形AOFC 是平行四边形，90AOF ∠=︒，∴四边形AOFC 是矩形，90DAO AOB DBO ∴∠=∠=∠=︒，∴四边形AOBD 是矩形，又∵由（2）得12CF BE t ==， 即：1102t =，解得：20t =．(20,0)B ∴．（4）①如图3中，当AD BD =时，以AB 为对角线可得菱形ADBN ，此时点N 在y 轴上．AD BD =， BAD ABD ∴∠=∠，OAB ABD ∴∠=∠，OAB BAD ∴∠=∠． tan tan OAB BAD ∴∠=∠， ∴12OB BC OA BA ==，即1102t =，5t ∴=，5OB ∴=，设AN NB m ==，在Rt OBN △中，则有2225(10)m m =+-， 解得254m =， 25151044ON OA AN ∴=-=-=， ∴点N 的纵坐标为154． ②如图4中，当AD AB =时，以BD 为对角线可得菱形ABND ．此时点N 的纵坐标为10．③BD AB ≠，∴不存在以AD 为对角线的菱形． 综上所述，满足条件的点N 的纵坐标为154或10． 【点睛】本题属于四边形综合题，考查了矩形的判定和性质，菱形的判定和性质，翻折变换，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．5．（1）证明见解析；（23333xx；（3）194【解析】 【分析】（1）如图，连接,AC 证明,ACB ACD 都为等边三角形，可得,AC AD = 再证明,ACM ADE ≌从而可得答案；（2）如图，记,AC BD 交于点,O 设,,DFa OFb 四边形ABCD 为菱形，60,ABC ∠=︒表示33,33OA OB a b 利用,2DF ax BF a b则2,1a xb x再利用三角函数的定义可得答案；（3）如图，设,DFESn 证明,DFE BFA ∽ 2,BFAnSx 再表示2222,,33ABGAGFn nSS S x x 结合菱形的轴对称的性质可得：2=,3CBG nS x 表示,AFDn S x可得2=,BCD ABDn n S Sxx 可得2212243334,3nn n S x x x x n S x 再利用二次函数的性质可得答案.【详解】证明：（1）如图，连接,AC 菱形ABCD 中，∠ABC ＝60°，,60,120,60,AB BC CDAD ABC ADC BAD BCD BAC CAD ACB,ACB ACD 都为等边三角形，,AC AD ∴=,60,DE CM ACM ADE,ACM ADE ≌ ,,AMAE MAC EAD 60,MACCAECAEEADAME ∴是等边三角形（2）如图，记,AC BD 交于点,O设,,DF a OF b 四边形ABCD 为菱形，60,ABC ∠=︒,,30,ACBD OB OD a b ABO33,33OAOB a b ,2DF a x BFa b1221,a b bx a a 11,22b ax 则2,1ax bx333tan 13a b OAa AFBOFbb32331,3133xxxx（3）如图，设,DFESn四边形ABCD 是平行四边形，,DFE BFA ∽22=,BFAn DF x S BF2,BFAn SxFG ＝2BG ， 2222,,33ABGAGFn n SS S xx根据菱形的轴对称的性质可得：2=,3CBG n S x ,AFD ABFS DF x SBF2,AFDn n S x x x 2=,BCDABD n n SSxx1222224=333n n n n n nS nn x x x x x x， 2212243334,3n n n S x x x x n S x 30,a所以12S S 有最大值， 当31232x时，最大值为：1119334.424【点睛】本题考查的是菱形的性质，全等三角形的判定与性质，等边三角形的判定与性质，相似三角形的判定与性质，列二次函数关系式，二次函数的性质，锐角三角函数的应用，灵活运用以上知识解题是解本题的关键.6．（1）213442y xx =-++；（2）点P 的坐标为：（6，41，2）；（3）11NC MC +=【解析】 【分析】（1）根据题意，先证明AOC ∆∽COB ∆，得到AO OCCO OB=，求出点A 、B 的坐标，然后利用待定系数法，即可求出抛物线解析式；（2）根据题意，可分为两种情况：AOC ∆∽PQC ∆或AOC ∆∽CQP ∆，结合解一元二次方程，相似三角形的判定和性质，分别求出点P 的坐标，即可得到答案；（3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，然后由角平分线的性质定理，得到EI =EJ ，再证明△MEI ∽△MNC ，△NEJ ∽△NMC ，得到111NC MC EI+=，然后求出EI 一个定值，即可进行判断． 【详解】解：（1）∵以AB 为直径的圆过点C ， ∴∠ACB =90°， ∵点C 的坐标为()0,4， ∴CO ⊥AB ，∴∠AOC =∠COB =90°，∴∠ACO +∠OCB =∠ACO +∠OAC =90°， ∴∠OCB =∠OAC , ∴AOC ∆∽COB ∆，∴AO OCCO OB=， ∵4CO =，10AO BO AB +==， ∴10AO OB =-， ∴1044OB OB-=， 解得：2OB =或8OB =， 经检验，满足题意， ∵OB OA >， ∴8OB =，∴点A 为（2-，0），点B 为（8，0）．设抛物线的解析式为2y ax bx c =++，把点A 、B 、C 三点的坐标代入，有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩，解得：14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式为213442y x x =-++；（2）根据题意，如图：当AOC ∆∽PQC ∆时， ∴ACO PCQ ∠=∠， ∵90ACO OCB ∠+∠=︒， ∴90PCQ OCB ∠+∠=︒， ∴PC ⊥OC ， ∴点P 的纵坐标为4，当4y =时，有2134442x x -++=，解得：16x =或20x =（舍去）； ∴点P 的坐标为（6，4）；当AOC ∆∽CQP ∆时，则此时BC 垂直平分OP ，作PG ⊥y 轴，垂足为G ，如上图， ∴90CQP AOC ∠=∠=︒，∴AC ∥OP ， ∴∠ACO =∠POG ， ∵90PGO AOC ∠=∠=︒， ∴AOC ∆∽PGO ∆， ∴AO OCPG GO=， 设点P 为（x ，213442x x -++）， ∴PG x =，213442GO x x =-++，∴22413442x x x =-++， 解得：171x =±-， ∵点P 在第一象限， ∴171x =-，∴2134217242x x -++=-，∴点P 的坐标为（171-，2172-）；综合上述，点P 的坐标为：（6，4）或（171-，2172-）； （3）过点E 作EI ⊥AC 于I ，EJ ⊥CN 于J ，如图：∵CE 是∠ACB 的角平分线， ∴EI =EJ ，∵EI ∥CN ，EJ ∥CM ，∴△MEI ∽△MNC ，△NEJ ∽△NMC ， ∴EI ME NC MN =，EJ NE MC MN =， ∴1EI EJ ME NENC MC MN MN +=+=， ∴1EI EI NC MC +=， ∴111NC MC EI+=， ∵△ACO ∽△AEI ，∴12AI AO EI CO ==，∵AC = ∵AC AI IC AI EI =+=+，12=，解得：EI =∴111NC MC EI +==∴11NC MC+是一个定值． 【点睛】本题考查了二次函数的综合应用，求二次函数的解析式，二次函数的性质，相似三角形的判定和性质，解一元二次方程，角平分线的性质定理等知识，解题的关键是熟练掌握题意，正确的作出辅助线，运用数形结合的思想进行解题．7．（1）①B ；D ；4；②1；（2）1522y x =-+或24y x =-+【解析】 【分析】（1）①根据“近点”、“远点”以及“ 特征数”的定义判断即可；②过点O 作OH ⊥直线n 于点H ，交O 于点Q ，P ．先分别求得点E 、F 的坐标，进而可求得EF 的长，再利用等积法求得OH 的长，进而即可解决问题；（2）如图，先求得“近点”N 到直线l 的距离NH AOB AHN △∽△即可求得答案． 【详解】解：（1）①由题意，点B 是O 关于直线m 的“近点”， 点D 是O 关于直线m 的“远点”， ∵点E 的坐标为（0，3）．⊙O 的半径为1， ∴OE ＝3，OB ＝OD ＝1，∴BE ＝OE －OB ＝2，DB ＝OB ＋OD ＝2，O 关于直线m 的特征数224DB BE =⋅=⨯=， 故答案为：B ；D ；4；②如图，过点O 作OH ⊥直线n 于点H ，交O 于点Q ，P ，设直线33y x =-+交x 轴于点F ，交y 轴于点E ， 令y ＝0，则x ＝3；令x ＝0，则y ＝3， ∴(3F ，0)，(0,3)E ，3OE ∴=，3OF =，22223(3)23EF OE OF ∴=+=+=，∵1122EOF S OE OF EF OH =⋅=⋅△， ∴11332322OH ⨯⨯=⨯⋅， 解得：32OH =， 12QH OH OQ ∴=-=， 又∵2PQ OQ OP =+=，O ∴关于直线n 的“特征数” 1212PQ QH =⋅=⨯=；（2）如图，设直线l 交x 轴于点A ，交y 轴于点B ，过点F 作FH ⊥直线l ，垂足为点H ，交⊙F 于N ，G ，∵⊙F 5，∴FN ＝FG 5，∴GN ＝FN ＋FG 5∵⊙F 关于直线l 的“特征数”是6， ∴GN·NH ＝6，NH ＝6， 解得：NH设直线l 的解析式是y kx b =+， ∵直线l 经过点M （1，2），∴将（1，2）代入y kx b =+，得：2k b +=， 2b k ∴=-，(2)y kx k ∴=+-，∴当0x =时，2y k =-，∴点B 坐标为（0，2－k ），|2|OB k ∴=-，当0y =时，(2)0kx k +-=， 解得：2k x k-=， ∴点A 坐标为（2k k-，0）， 2||k OA k -∴=，22|(1)||1|k k AN k k--=--=+，AB ∴2||k k-= BAO NAH ∠=∠，90AOB AHN ∠=∠=︒， AOB AHN ∴△∽△，∴NH ANOB AB=，∴|2|522|1|||k k k k k-=--+， 整理，得：22520k k ++=，解得：12k =-或2k =-，∴直线l 的解析式为1522y x =-+或24y x =-+．【点睛】本题属于圆综合题，考查了一次函数的性质，相似三角形的判定和性质运用以及勾股定理的运用，远点，近点，特征数等新定义等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．8．（1）y ＝－x 2+2x +3，y ＝-x +3；（2）存在，（－1，0）或（4，－5）；（3）存在，（1，2）或（1，－3） 【解析】 【分析】（1）将点A ，B 坐标代入抛物线解析式中，求出b ，c 得出抛物线的解析式，进而求出点C 的坐标，再将点A ，C 坐标代入直线AC 的解析式中，即可得出结论；（2）利用抛物线的对称性得出BD AD =，进而判断出ABC 的面积和ACP △的面积相等，即可得出结论；（3）分点Q 在x 轴上方和在x 轴下方，构造全等三角形即可得出结论． 【详解】（1）把(30)A ，、(10)B -，代入2y x bx c =-++， 解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为（0，3），又(30)A ，，代入1y kx b =+， 得1k =-，13b =， ∴直线AC 的解析式为3y x =-+， （2）如图，连接BC ，∵点D 是抛物线的对称轴与x 轴的交点， ∴AD BD =， ∴2ABCACDSS=，∵2ACP ACD S S =△△，∴ACP ABC S S =△△，此时，点P 与点B 重合， 即：(10)P -，， 过B 点作PB AC ∥交抛物线于点P ，则直线BP 的解析式为1y x =--①， ∵抛物线的解析式为2y x 2x 3=-++②，联立①②解得，10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩，∴P （4，﹣5），∴即点P 的坐标为（﹣1，0）或（4，﹣5）； （3）由（1）可知，抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ，如下图所示：22222BM AM ==+，4AB =即222BM AM AB +=则MAB △是等腰直角三角形，符合题意，M 点即为所求Q 点的一种情况，当Q 点在x 轴下方时，设Q 为(1,)m ，0m ＜， 因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点，则1ADQ QEA ≌ ∴2AD QE ==，1DQ EA m ==- ∴12(1)A m m --，∵点A1恰好落在抛物线2y x 2x 3=-++上， 代入，解得m=－3或2m = (舍去) ∴Q （1，－3）综上，Q 点坐标为（1,2）或（1，－3）， 【点睛】本题考查的是二次函数的综合题，涉及解析式的求解，与三角形面积有关的问题，全等三角形的判定与性质，解题的关键是利用数形结合的思想，设点坐标并结合几何图形的性质列式求解．9．（1）直线AC 的解析式为y ＝﹣x +6；（2）d =4-t ；（3）Q （212，1）． 【解析】 【分析】（1）先由解析式求出得A 、C 点的坐标，得OA =OC ，得四边形ABCO 为正方形，再根据正方形的面积求得边长，便可得b 的值；（2）过点Q 作QG ⊥AB 交AB 延长沿于点G ，证明Rt △AOP ≌Rt △GPQ （AAS ），得到AP =GQ ，进而求得结论便可；（3）过点P 作PH ⊥OF 于点H ，延长PH 交EQ 的延长线于点R ，EQ 的延长线与x 轴交于点N ，过Q 作QM ⊥x 轴于点M ．证明Rt △AOP ≌Rt △GPQ （CCS ），得PK =QR ，∠R=∠OKP，再证明∠R=∠FPR，得EP=ER，再证FE=NR，设FE=NR=k，NQ=m，在Rt△PQE中，由勾股定理列出方程，得到k与m的关系，解Rt△PQE得tan∠PEQ，进而把这个函数值运用到△OAP中，求得t的值，再运用（2）中结论得Q的纵坐标d的值，再运用到△QNM中求得NM，NQ的值，进而求得ON，便可得Q的横坐标的值．【详解】解：（1）∵直线y＝﹣x+b（b＞0）交x轴于点A，交y轴于点C，A b C b，∴(,0),(0,)∴OA=OC=b，∴矩形ABCO为正方形，∵矩形ABCO的面积是36．∴b=6，即直线AC的解析式为y＝﹣x+6；（2）如图，过点Q作QG⊥AB交AB延长沿于点G，∵∠OPQ=90°，∴∠APO+∠GPQ=90°，∵∠APO+∠AOP=90°，∴∠AOP=∠GPQ，∵在矩形ABCO，∠OAP=90°，QG⊥AB,∴∠QGP=∠OAP=90°，∵PQ=OP，∴Rt△AOP≌Rt△GPQ（AAS），∴AP=GQ，∵AP=t，∴GQ=t，∴d=4-t；（2）过点P作PH⊥OF于点H，延长PH交EQ的延长线于点R，EQ的延长线与y轴交于点N，过Q作QM⊥y轴于点M．则AP=t，QM=d，且d=6-t．∵OF 平分∠POC ， ∴∠POF =∠COF =∠PFO ， ∴PF =PO ，∵PH ⊥OF ，∠OPQ ＝90°， ∴∠OPH =∠FPH ，∠KPH =∠POH ， 在△OPK 和△PQR 中， 90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝， ∴△OPK ≌△PQR （ASA ）， ∴PK =QR ，∠R =∠OKP ，∵∠OKP +∠POK =∠POK +∠OPH =90°， ∴∠OKP =∠OPH ， ∴∠R =∠OPH ， ∵PO =PF ，PH ⊥OF ， ∴∠OPH =∠FPH ， ∴∠R =∠FPR ， ∴EP =ER ，∵PE ∥ON ，OP ∥EN ， ∴四边形OPEN 是平行四边形， ∴EN =PO =PF ， ∴PE -PF =ER -EN ， ∴FE =NR ，设FE =NR =k ，则KQ =2FE =2k ， 又设NQ =m ，∴PK=QR=m+k，∴PQ=m+3k，∴PO=EN=PF=m+3k，∴QE=EN-QR=m+3k-m=3k，PE=PF+FE=4k+m，在Rt△PQE中，∵PE2=PQ2+QE2，∴（4k+m）2=（3k+m）2+（3k）2，∴k1=0（舍去），k2=m，∴PQ=4m，QE=3m，∴tan∠PEN=43 PQQE=，∵OP∥EN，∴∠OPA=∠PEN，∴tan∠APO=43，∵AO=6，∴AP=4.5，∴t=4.5，∴QM=d=6-t=1.5，∵PE∥OC，∴∠QNM=∠PEN，∴tan∠QNM=tan∠PEN=43，∴NM=9 tan8QMQNM=∠，∴m=NQ158 =，∴PE=ON=4k+m=5m=758，∴OM=ON+NM=212，∴Q（212，1）．【点睛】本题是一次函数与四边形的综合题，主要考查了一次函数的图象与性质，全等三角形的性质与判定，正方形的性质，旋转的性质，解直角三角形的应用，等腰三角形的性质与判定，平行四边形的性质与判定，是一道综合性极强的题目，解决这类问题常用到数形结合、方程和转化等数学思想方法．构造全等三角形是解题的关键，也是问题的突破口．10．（1）；（2）；（3）【解析】 【分析】（1）由抛物线的二次项系数 再根据交点式可得抛物线为从而可得答案；（2）先画好图形，证明利用相似三角形的性质求解从而可得答案；（3）如图，过P 作轴于,K 过M 作于,N 证明即再求解则，再解方程可得 4,t = 再求解的解析式，再联立解析式解方程可得答案. 【详解】 解：（1） 抛物线交x 轴于()2,0A -、()5,0B 两点，所以可得抛物线为：（2）如图，过P 作于,H 连AP 交OC 于则，x 则令0,（3）如图，过P作轴于,K过M作于,N 由（2）得：，，轴，则轴，，即结合（1）可得：四边形为矩形，。
初中数学中考压轴题及答案详解(上海篇)
专题训练125．如图9，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC相交于点E，连结DE并延长，与线段BC的延长线交于点P.（1）当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；（2）若CE=2，BD=BC，求∠BPD的正切值；（3）若1tan3BPD∠=，设CE=x，△ABC的周长为y，求y关于x的函数关系式.图9 图10(备用)参考答案：（1）解：∵∠B＝30°∠ACB＝90°∴∠BAC＝60°∵AD=AE ∴∠AED＝60°=∠CEP ∴∠EPC＝30°∴三角形BDP为等腰三角形∵△AEP与△BDP相似∴∠EAP=∠EPA=∠DBP=∠DPB=30°∴AE=EP=1∴在RT△ECP中，EC=12EP=12（2）过点D作DQ⊥AC于点Q，且设AQ=a，BD=x ∵AE=1,EC=2∴QC=3-a∵∠ACB＝90°∴△ADQ与△ABC相似∴AD AQ AB AC=即113ax=+，∴31 ax=+∵在RT△ADQ中2222328111x x DQ AD AQx x+-⎛⎫=-=-=⎪++⎝⎭∵DQ AD BC AB=∴228111x x x x x +-+=+ 解之得x=4，即BC=4 过点C 作CF//DP∴△ADE 与△AFC 相似，∴AE ADAC AF=，即AF=AC ，即DF=EC=2, ∴BF=DF=2∵△BFC 与△BDP 相似 ∴2142BF BC BD BP ===，即：BC=CP=4 ∴tan ∠BPD=2142EC CP ==(3)过D 点作DQ ⊥AC 于点Q ，则△DQE 与△PCE 相似,设AQ=a ，则QE=1-a ∴QE DQEC CP =且1tan 3BPD ∠= ∴()31DQ a =-∵在Rt △ADQ 中，据勾股定理得：222AD AQ DQ =+ 即：()222131a a =+-⎡⎤⎣⎦，解之得41()5a a ==舍去 ∵△ADQ 与△ABC 相似∴445155AD DQ AQ AB BC AC x x====++ ∴5533,44x xAB BC ++==∴三角形ABC 的周长553313344x xy AB BC AC x x ++=++=+++=+ 即：33y x =+，其中x>0专题训练21．如图，在平面直角坐标系中，二次函数26y ax x c =++的图像经过点()4,0A 、()1,0B -，与y 轴交于点C ，点D 在线段OC 上，=OD t ，点E 在第二象限，∠=90ADE ，1=2tan DAE ∠，EF OD ⊥，垂足为F ．（1）求这个二次函数的解析式；（2）求线段EF 、OF 的长（用含t 的代数式表示）； （3）当∠ECA =∠OAC 时，求t 的值．参考答案：解：（1）二次函数y=ax 2+6x+c 的图象经过点A （4，0）、B （﹣1，0），∴，解得。
中考数学压轴题十大题型(含详细答案)
一、中考数学压轴题1．如图，在平面直角坐标系中，点O 为坐标原点，直线y =-x + m 交 y 轴的正半轴于点A ，交x 轴的正半轴于点B ，过点A 的直线AF 交x 轴的负半轴于点F ，∠AFO=45°． （1）求∠FAB 的度数；（2）点 P 是线段OB 上一点，过点P 作 PQ ⊥OB 交直线 FA 于点Q ，连接 BQ ，取 BQ 的中点C ，连接AP 、AC 、CP ，过点C 作 CR ⊥AP 于点R ，设 BQ 的长为d ，CR 的长为h ，求d 与 h 的函数关系式（不要求写出自变量h 的取值范围）；（3）在（2）的条件下，过点 C 作 CE ⊥OB 于点E ，CE 交 AB 于点D ，连接 AE ，∠AEC=2∠DAP ，EP=2，作线段 CD 关于直线AB 的对称线段DS ，求直线PS 与直线 AF 的交点K 的坐标．2．已知：如图，在平面直角坐标系中，点O 为坐标原点，()2,0C ．直线26y x =+与x 轴交于点A ，交y 轴于点B ．过C 点作直线AB 的垂线，垂足为E ，交y 轴于点D ． （1）求直线CD 的解析式；（2）点G 为y 轴负半轴上一点，连接EG ，过点E 作EH EG ⊥交x 轴于点H ．设点G 的坐标为()0,t ，线段AH 的长为d ．求d 与t 之间的函数关系式（不要求写出自变量的取值范围）（3）过点C 作x 轴的垂线，过点G 作y 轴的垂线，两线交于点M ，过点H 作HN GM ⊥于点N ，交直线CD 于点K ，连接MK ，若MK 平分NMB ∠，求t 的值．3．如图1，抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，点E 是BD 上方抛物线上的一点，连接AE 交DB 于点F ，若AF=2EF ，求出点E 的坐标．（3）如图3，点M 的坐标为（32，0），点P 是对称轴左侧抛物线上的一点，连接MP ，将MP 沿MD 折叠，若点P 恰好落在抛物线的对称轴CE 上，请求出点P 的横坐标．4．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．5．如图，在平面直角坐标系中，直线6y x =+与x 轴交于点A ，与y 轴交于点B ，点C 在x 轴正半轴上，2ABC ACB ∠=∠．（1）求直线BC 的解析式；（2）点D 是射线BC 上一点，连接AD ，设点D 的横坐标为t ，ACD ∆的面积为S ()0S ≠，求S 与t 的函数解析式，并直接写出自变量t 的取值范围；（3）在（2）的条件下，AD 与y 轴交于点E ，连接CE ，过点B 作AD 的垂线，垂足为点H ，直线BH 交x 轴于点F ，交线段CE 于点M ，直线DM 交x 轴于点N ，当:7:12NF FC =时，求直线DM 的解析式．6．在梯形ABCD 中，//AD BC ，90B ∠=︒，45C ∠=︒，8AB =，14BC =，点E 、F 分别在边AB 、CD 上，//EF AD ，点P 与AD 在直线EF 的两侧，90EPF ∠=︒，PE PF =，射线EP 、FP 与边BC 分别相交于点M 、N ，设AE x =，MN y =．（1）求边AD 的长；（2）如图，当点P 在梯形ABCD 内部时，求关于x 的函数解析式，并写出定义域； （3）如果MN 的长为2，求梯形AEFD 的面积．7．如图，已知正方形ABCD 中，4,BC AC BD =、相交于点O ，过点A 作射线AM AC ⊥，点E 是射线AM 上一动点，连接OE 交AB 于点F ，以OE 为一边，作正方形OEGH ，且点A 在正方形OEGH 的内部，连接DH ．（1）求证：EDO EAO ∆≅∆；（2）设BF x =，正方形OEGH 的边长为y ，求y 关于x 的函数关系式，并写出定义域；（3）连接AG ，当AEG ∆是等腰三角形时，求BF 的长．8．问题提出（1）如图①，在ABC 中，42,6,135AB AC BAC ==∠=，求ABC 的面积．问题探究（2）如图②，半圆O 的直径10AB =，C 是半圆AB 的中点，点D 在BC 上，且2CD BD =，点P 是AB 上的动点，试求PC PD +的最小值．问题解决（3）如图③，扇形AOB 的半径为20,45AOB ∠=在AB 选点P ，在边OA 上选点E ，在边OB 上选点F ，求PE EF FP ++的长度的最小值．9．如图，在ABC ∆中，14AB =，45B ∠=︒，4tan 3A =，点D 为AB 中点．动点P 从点D 出发，沿DA 方向以每秒1个单位长度的速度向终点A 运动，点P 关于点D 对称点为点Q ，以PQ 为边向上作正方形PQMN ．设点P 的运动时间为t 秒．（1）当t =_______秒时，点N 落在AC 边上．（2）设正方形PQMN 与ABC ∆重叠部分面积为S ，当点N 在ABC ∆内部时，求S 关于t 的函数关系式．（3）当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时，直接写出t 的值．10．对于平面直角坐标系xOy 中的任意点()P x y ，，如果满足x y a += (x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点(1,2),(1,3),(2.5,0)A B C 中，满足此条件的特征点为__________________；②⊙W 的圆心为(,0)W m ，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数()10Z x x x=+>，请利用特征点求出该函数的最小值．11．如图，在平面直角坐标系中，点(1,2)A ，(5,0)B ，抛物线22(0)y ax ax a =->交x 轴正半轴于点C ，连结AO ，AB ．（1）求点C 的坐标；（2）求直线AB 的表达式； （3）设抛物线22(0)y ax ax a =->分别交边BA ，BA 延长线于点D ，E ．①若2AE AO =，求抛物线表达式；②若CDB △与BOA △相似，则a 的值为 ．（直接写出答案）12．如图1，在平面直角坐标系中，抛物线239334y x x =--x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ． （1）过点C 的直线5334y x =-x 轴于点H ，若点P 是第四象限内抛物线上的一个动点，且在对称轴的右侧，过点P 作//PQ y 轴交直线CH 于点Q ，作//PN x 轴交对称轴于点N ，以PQ PN 、为邻边作矩形PQMN ，当矩形PQMN 的周长最大时，在y 轴上有一动点K ，x 轴上有一动点T ，一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ，再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动，求动点G 运动时间的最小值：（2）如图2， 将ABC ∆绕点B 顺时针旋转至A BC ''∆的位置， 点A C 、的对应点分别为A C ''、，且点C '恰好落在抛物线的对称轴上，连接AC '．点E 是y 轴上的一个动点，连接AE C E '、， 将AC E ∆'沿直线C E '翻折为A C E ∆''， 是否存在点E ， 使得BAA ∆'为等腰三角形?若存在，请求出点E 的坐标；若不存在，请说明理由．13．（1）如图1，A 是⊙O 上一动点，P 是⊙O 外一点，在图中作出PA 最小时的点A ． （2）如图2，Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，以点C 为圆心的⊙C 的半径是3.6，Q 是⊙C 上一动点，在线段AB 上确定点P 的位置，使PQ 的长最小，并求出其最小值． （3）如图3，矩形ABCD 中，AB ＝6，BC ＝9，以D 为圆心，3为半径作⊙D ，E 为⊙D 上一动点，连接AE ，以AE 为直角边作Rt △AEF ，∠EAF ＝90°，tan ∠AEF ＝13，试探究四边形ADCF 的面积是否有最大或最小值，如果有，请求出最大或最小值，否则，请说明理由．14．（问题探究）课堂上老师提出了这样的问题：“如图①，在ABC 中，108BAC ∠=︒，点D 是BC 边上的一点，7224BAD BD CD AD ∠=︒==，，，求AC 的长”．某同学做了如下的思考：如图②，过点C 作CE AB ∥，交AD 的延长线于点E ，进而求解，请回答下列问题：（1）ACE ∠=___________度；（2）求AC 的长．（拓展应用）如图③，在四边形ABCD 中，12075BAD ADC ∠=︒∠=︒，，对角线AC BD 、相交于点E ，且AC AB ⊥，22EB ED AE ==，，则BC 的长为_____________．15． 在平面直角坐标系中，点O 为坐标原点，直线y ＝﹣x+4与x 轴交于点A ，过点A 的抛物线y ＝ax 2+bx 与直线y ＝﹣x+4交于另一点B ，且点B 的横坐标为1．（1）该抛物线的解析式为；（2）如图1，Q 为抛物线上位于直线AB 上方的一动点（不与B 、A 重合），过Q 作QP ⊥x 轴，交x 轴于P ，连接AQ ，M 为AQ 中点，连接PM ，过M 作MN ⊥PM 交直线AB 于N ，若点P 的横坐标为t ，点N 的横坐标为n ，求n 与t 的函数关系式；在此条件下，如图2，连接QN 并延长，交y 轴于E ，连接AE ，求t 为何值时，MN ∥AE ．（3）如图3，将直线AB 绕点A 顺时针旋转15度交抛物线对称轴于点C ，点T 为线段OA 上的一动点（不与O 、A 重合），以点O 为圆心、以OT 为半径的圆弧与线段OC 交于点D ，以点A 为圆心、以AT 为半径的圆弧与线段AC 交于点F ，连接DF ．在点T 运动的过程中，四边形ODFA 的面积有最大值还是有最小值？请求出该值．16．如图，抛物线25y ax bx =+-交x 轴于点A 、B （A 在B 的左侧），交y 轴于点C ，且OB OC =，()2,0A -．（1）求抛物线的解析式；（2）点P 为第四象限抛物线上一点，过点P 作y 轴的平行线交BC 于点D ，设P 点横坐标为t ，线段PD 的长度为d ，求d 与t 的函数关系式．（不要求写出t 的取值范围） （3）在（2）的条件下，F 为BP 延长线上一点，且45PFC ∠=︒，连接OF 、CP 、PB ，FOB ∆的面积为3600169，求PBC ∆的面积．17．如图①，△ABC是等腰直角三角形，在两腰AB、AC外侧作两个等边三角形ABD和ACE，AM和AN分别是等边三角形ABD和ACE的角平分线，连接CM、BN，CM与AB交于点P．（1）求证：CM＝BN；（2）如图②，点F为角平分线AN上一点，且∠CPF＝30°，求证：△APF∽△AMC；（3）在（2）的条件下，求PFBN的值．18．如图，在⊙O中，直径AB＝10，tanA＝3．（1）求弦AC的长；（2）D是AB延长线上一点，且AB＝kBD，连接CD，若CD与⊙O相切，求k的值；（3）若动点P以3cm/s的速度从A点出发，沿AB方向运动，同时动点Q以32cm/s的速度从B点出发沿BC方向运动，设运动时间为t （0＜t＜103），连结PQ．当t为何值时，△BPQ为Rt△？19．如图，在矩形ABCD中，点E为BC的中点，连接AE，过点D作DF AE⊥于点F，过点C作CN DF⊥于点N，延长CN交AD于点M．（1）求证：AM MD=（2）连接CF，并延长CF交AB于G①若2AB=，求CF的长度；②探究当ABAD为何值时，点G恰好为AB的中点．20．在一次数学课上，李老师让同学们独立完成课本第23页第七题选择题（2）如图 1，如果 AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝（）A．180° B．270° C．360° D．540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB∥EF，请直接写出∠BAD，∠ADE，∠DEF之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示），当AD，ED分别平分∠BAC，∠CEF时，∠ACE与∠ADE之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB∥EF，当∠ACD=90°时，∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系？请你直接写出结果，不需要证明．21．如图1，以AB为直径作⊙O，点C是直径AB上方半圆上的一点，连结AC，BC，过点C作∠ACB的平分线交⊙O于点D，过点D作AB的平行线交CB的延长线于点E．（1）如图1，连结AD，求证：∠ADC＝∠DEC．（2）若⊙O的半径为5，求CA•CE的最大值．（3）如图2，连结AE，设tan∠ABC＝x，tan∠AEC＝y，①求y关于x的函数解析式；②若CBBE＝45，求y的值．22．发现来源于探究．小亮进行数学探究活动，作边长为a的正方形ABCD和边长为b的正方形AEFG（a>b），开始时，点E在AB上，如图1．将正方形AEFG绕点A逆时针方向旋转．（1）如图2，小亮将正方形AEFG 绕点A 逆时针方向旋转，连接BE 、DG ，当点G 恰好落在线段BE 上时，小亮发现DG ⊥BE ，请你帮他说明理由．当a=3，b=2时，请你帮他求此时DG 的长．（2）如图3，小亮旋转正方形AEFG ，点E 在DA 的延长线上，连接BF 、DF ．当FG 平分∠BFD 时，请你帮他求a ：b 及∠FBG 的度数．（3）如图4，BE 的延长线与直线DG 相交于点P ，a=2b ．当正方形AEFG 绕点A 从图1开始，逆时针方向旋转一周时，请你帮小亮求点P 运动的路线长（用含b 的代数式表示）．23．问题探究（1）如图1．在ABC 中，8BC =，D 为BC 上一点，6AD =．则ABC 面积的最大值是_______．（2）如图2，在ABC 中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC 的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值：若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．24．问题一：如图①，已知AC ＝160km ，甲，乙两人分别从相距30km 的A ，B 两地同时出发到C 地．若甲的速度为80km /h ，乙的速度为60km /h ，设乙行驶时间为x （h ），两车之间距离为y （km ）．（1）当甲追上乙时，x ＝ ．（2）请用x 的代数式表示y ．问题二：如图②，若将上述线段AC 弯曲后视作钟表外围的一部分，线段AB 正好对应钟表上的弧AB （1小时的间隔），易知∠AOB ＝30°．（3）分针OD 指向圆周上的点的速度为每分钟转动 km ，时针OE 指向圆周上的点的速度为每分钟转动 °；（4）若从2：00起计时，求几分钟后分针与时针第一次重合？25．在平面直角坐标系中，点O 为坐标原点，抛物线(2)()y a x x m =++与x 轴交于点A C 、（点A 在点C 的左侧），与y 轴正半轴交于点B ，24OC OB ==．（1）如图1，求a m 、的值；（2）如图2，抛物线的顶点坐标是M ，点D 是第一象限抛物线上的一点，连接AD 交抛物线的对称轴于点N ，设点D 的横坐标是t ，线段MN 的长为d ，求d 与t 的函数关系式；（3）如图3，在（2）的条件下，当154d =时，过点D 作DE x 轴交抛物线于点E ，点P 是x 轴下方抛物线上的一个动点，连接PE 交x 轴于点F ，直线211y x b =+经过点D 交EF 于点G ，连接CG ，过点E 作EH CG 交DG 于点H ，若3CFG EGH S S =△△，求点P 的坐标．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．F解析：（1）∠FAB=90°；（2）22d h =；（3）直线PS 与直线AF 的交点K(-2，6)．【解析】【分析】（1）通过直线AB 的解析式可求出点A 、B 的坐标，可知AOB 是等腰直角三角形，再结合已知条件即可确定90FAB ∠=︒；（2）根据已知条件证明CP=AC=QC=BC 从而得出△ACP 是等腰直角三角形，在Rt △CRP 中，利用sin ∠CPR 22CR CP ==，推出2CP CR =，继而得出22BQ CR =，得出答案； （3）过点 A 作AH ⊥CE 交 EC 的延长线于点 H ，延长 CH 到点 G ，使 HG=CH ，连接AG ，证明△AHC ≌△CEP ，设AH CE n ==，得出EG=CE+CH+GH=n+2+2=n+4，再通过角的等量代换，得出∠EAG=∠G ，从而有EG=EA=n+4，在Rt △AHE 中，通过勾股定理AE²=HE²+AH²可求出n 的值为6，从而得出直线AF 的解析式y = x + 8 ，再求出直线PS 的解析式为 y=-x+4，求交点即可．【详解】解：（1）如下图，y = -x + m ，当x=0时，y=m∴A （0，m ），OA=m当y=0时，0=-x+m ，x=m ，∴B （m ，0），OB=m∴OA=OB∴∠OAB=∠OBA=45°∵∠AFO=45°，∠FAB+∠FBA+∠AFB=180°∴∠FAB=90°（2）如下图 ，∵CP 、AC 分别是 Rt △QPB 和 Rt △QAB 的斜边上的中线∴CP= 12QB ，12AC QB =， ∴CP=AC=QC=BC∴∠CAB=∠CBA设∠CAB=∠CBA=α，∴∠CBP=45°+α∴∠CPB=∠CBP=45°+α∴∠PCB=180°-（∠CPB+∠CBP ）=90°-2α∵∠ACB=180°-∠CAB-∠CBA=180°-2α∴∠ACP=∠ACB-∠PCB=180°-2α-（90°-2α）=90°∵AC=CP∴△ACP 是等腰直角三角形∴∠CPA=∠CAP=45°∵CR ⊥AP ，∴∠CRP=90°，在Rt △CRP 中sin ∠CPR 22CR CP == ∴2CP CR =∵12CP BQ =， ∴22BQ CR =即22d h =（3）过点 A 作AH ⊥CE 交 EC 的延长线于点 H ，延长 CH 到点 G ，使 HG=CH ，连接AG ∴∠AHC=∠CEP=90°∴∠HAC+∠HCA=∠PCE+∠HCA∴∠HAC=∠PCE ，∵AC=CP∴△AHC ≌△CEP∴CH=PE=2，AH=CE ，∴GH=CH=2，AH CE n ==∴EG=CE+CH+GH=n+2+2=n+4设∠DAP=β，则∠AEG=2β∴α+β=45°∵∠EBD=∠EDB=∠HDA=∠HAD=45°∴∠CAH=∠HAD-α=45°-α=β∵AH 垂直平分 GC∴AG=AC∴∠GAH=∠CAH=β∴∠G=90°-β 在△EAG 中∠EAG=180°-∠G-∠AEG=180°-（90°-β）-2β =90°-β∴∠EAG=∠G∴EG=EA=n+4在 Rt △AHE 中，AE²=HE²+AH²222(4)(2)n n n +=++126,2n n ==-（舍）∴AH=OE=6，EP=EB=2∴OB=OE+BE=8∴m=8，∴A （0，8）∴OA=OF=8 ， ∴F （-8，0）∴直线 AF 的解析式为 y = x + 8∵CD=CE-DE=CE-BE=6-2=4∵线段 CD 关于直线 AB 的对称线段 DS∴SD=CD=4，∠CDA=∠SDA=45°∴∠CDS=90°，∴SD ∥x 轴过点 S 分别作 SM ⊥x 轴于点 M ，SN ⊥y 轴于点 N∴四边形 OMSN 、SMED 都是矩形∴OM=SN=OE-ME=2，ON=SM=DE=BE=2∴S(2，2)∵OP=OE-EP=6-2=4，∴P(4，0)设直线 PS 的解析式为 y=ax+b∴4022a b a b +=⎧⎨+=⎩，解得：14a b =-⎧⎨=⎩∴直线 PS 的解析式为 y=-x+4设直线PS 与直线AF 的交点K(x ，y)∴48y x y x =-+⎧⎨=+⎩解得26x y =-⎧⎨=⎩∴直线PS 与直线AF 的交点K(-2，6)．【点睛】本题考查的知识点是一次函数与几何图形，将一次函数的图象与几何图形综合在一起的问题，是考查学生综合素质和能力的热点题型，它充分体现了数学解题中的数形结合思想和整体转化思想．本题考查的知识点有一次函数图象与坐标轴的交点问题、等腰直角三角形的判定及性质、三角形内角和定理、全等三角形的判定及性质、矩形的性质、待定系数法求一次函数解析式、线段垂直平分线等．2．C解析：（1）112y x =-+；（2）1d t =-+；（3）6215t -= 【解析】【分析】（1）根据互相垂直两直线斜率积为-1，设出直线CE 的解析式，再将点C 坐标代入即可求解；（2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，通过解直角三角形可证EDM ≌EAN ，ENH ≌EMG ，得到AN =DM ，HN =GM ，进而得到AH DG =，再根据CE 解析式求出D 点坐标，即可找出d 与t 之间的函数关系式；（3）过点B 作BT CM ⊥于点T ，在直线BT 上截取TL NK =，证四边形BGMT 与四边形HNMC 均为矩形，得MN MT =，再进一步证明ENH ≌EMG ，利用全等三角形的性质通过角度计算，得出△BML 为等腰三角形且BM BL =，再用含有t 的代数式表示BM ，最后在Rt △BMG 中利用勾股定理建立等式，求出t 的值．【详解】解：（1）∵CE ⊥AB ，∴设直线CE 的解析式为：12y x c =-+， 把点C （2，0）代入上述解析式，得1c =，∴直线CD 的解析式为：112y x =-+； （2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，令26 112y xy x=+⎧⎪⎨=-+⎪⎩，解得22xy=-⎧⎨=⎩，∴()2,2E-，易证EDM≌EAN，ENH≌EMG，∴AN=DM ，HN=GM，∴AH DG=，由直线CE的解析式112y x=-+，可求点D（0，1）∴DG=1—t，∴1d t=-+；（3）过点B作BT CM⊥于点T，在直线BT上截取TL NK=，易证四边形BGMT与四边形HNMC均为矩形，由（2）问可知1tAH GD==-，则6tHC=-∴6tBG MT==-，∴MN MT=，∵90KNM LTM∠=∠=︒，∴ENH≌EMG，∴LNKM∠=∠，设KMNα∠=，则KMB KMNα∠=∠=，∴90NKM α∠=︒-，∴90NKM L α∠=∠=︒-，∵//BL MN ，∴2MBL BMN α∠=∠=，∴18090BML MBL L α∠=︒-∠-∠=︒-，∴BM BL =， ∵1tan 2KCH ∠=， ∴11322KH CH t ==-， ∴133322KN KH HN t t t TL =+=--=-=， ∴352BL BT TL t BM =+=-=， 在Rt BMG △中， 222BM BG GM =+，解得t =（不合题意舍去）或t =故，65t -=． 【点睛】本题一次函数综合题，考查了待定系数法求解析式，一次函数的性质，全等三角形的判定与性质，角平分线的性质，勾股定理等，利用已知条件求相等交，相等线段是解决本题的关键．3．E解析：（1）2y x 2x 3=-++；（2）E （2，3）或（1，4）；（3）P 点横坐标为118【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），设抛物线的解析式为2(1)4y a x =-+，由抛物线过点B,（3，0），即可求出a 的值，即可求得解析式； （2）过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x xx -++，求出A 、D 点的坐标，得到OM=x ，则AM=x+1，由AF=2EF 得到22(1)33x AN AM +==，从而推出点F 的坐标21210(,)3333x x --+，由23FN EM =，列出关于x 的方程求解即可；（3）先根据待定系数法求出直线DM 的解析式为y=-2x+3，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.证明△FGP ≌△FHQ ，得到FG=FH ，PT=45GH.设点P （m ，-m²+2m+3），则T （m ，-2m+3），则PT=m²-4m ，GH=1-m ， 可得m²-4m=45（1-m ），解方程即可. 【详解】（1）∵抛物线的顶点为C （1，4），∴设抛物线的解析式为2(1)4y a x =-+，∵抛物线过点B,（3，0），∴20(31)4a =-+，解得a=-1，∴设抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++；（2）如图，过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x x x -++，∵抛物线的解析式为2y x 2x 3=-++，当y=0时，2023x x =-++，解得x=-1或x=3，∴A （-1.0），∴点D （0,3），∴过点BD 的直线解析式为3y x =-+，点F 在直线BD 上，则OM=x ，AM=x+1，∴22(1)33x AN AM +==， ∴2(1)2111333x x ON AN +=-=-=-， ∴21210(,)3333x x F --+，∴2210332233FN EM x x x +--++==， 解得x=1或x=2， ∴点E 的坐标为（2，3）或（1，4）；（3）设直线DM 的解析式为y=kx+b ，过点D （0,3），M （32，0）， 可得，3023k b b ⎧+=⎪⎨⎪=⎩，解得k=-2，b=3，∴直线DM 的解析式为y=-2x+3，∴32OM =，3OD =， ∴tan ∠DMO=2， 如图，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.∵PQ ⊥MT ，∴∠TFG=∠TPF ，∴TG=2GF ，GF=2PG ，∴PT=25GF ， ∵PF=QF ，∴△FGP ≌△FHQ ，∴FG=FH ，∴PT=45GH. 设点P （m ，-m²+2m+3），则T （m ，-2m+3），∴PT=m²-4m ，GH=1-m ，∴m²-4m=45（1-m ）， 解得：1112018m -=，或2112018m +=（不合题意，舍去）， ∴点P 的横坐标为11201-. 【点睛】 本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识，解题的关键是学会用转化的思想思考问题，学会用数形结合的思想解决问题，有一定难度.4．D解析：（1）DF 的长为158；（2）MN 的长为5；（3）O 的半径长为258． 【解析】【分析】（1）作EH BM ⊥于H ，根据中位线定理得出四边形BMFA 是平行四边形，从而利用cos 45B =解直角三角形即可求算半径，再根据平行四边形的性质求FD 即可； （2）先证AMB CNM ∠=∠，再证MAD CNM ∠=∠，从而证明AFM NFD ∆~∆，得到AF MF AF DF NF MF NF DF=⇒=，再通过平行证明AFN DFM ∆~∆，从而得到AF NF AF MF NF DF DF MF=⇒=，通过两式相乘得出AF NF =再根据平行得出NF DF =， 从而得出答案．（3）通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒，再利用cos 45B =解三角函数即可得出答案． 【详解】（1）如图，作EH BM ⊥于H ：∵E 为AB 中点，45,cos 5AB AD DC B ====∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ，在Rt OEH ∆中：()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得：2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= （2）如图：连接MD AN ，∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN ∴AFN DFM ∆~∆∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5；（3）作如图：∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ，圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上 ∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得：254BM = O 的半径长为258【点睛】 本题是一道圆的综合题目，难度较大，掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键．5．A解析：（1）6y x =-+；（2）636S t =-，()6t >；（3）5599y x =+ 【解析】【分析】（1）求出点A 、B 的坐标，从而得出△ABO 是等腰直角三角形，再根据2ABC ACB ∠=∠可得△OCB 也是等腰直角三角形，从而可求得点C 的坐标，将点B 、C 代入可求得解析式；（2）存在2种情况，一种是点D 在线段BC 上，另一种是点D 在线段BC 的延长线上，分别利用三角形的面积公式可求得；（3）如下图，先证ACR CAD ∆≅∆，从而推导出//RD AC ，进而得到CF RG =，同理还可得NF DG =，RD CN =，然后利用:7:12NF FC =可得到N 、D 的坐标，代入即可求得．【详解】解：（1）直线6y x =+与x 轴交于点A ，与y 轴交于点B ，(6,0)A ∴-，(0,6)B ．6OA OB ∴==．45BAO ∴∠=︒，180BAO ABC BCO ∠+∠+∠=︒，2ABC ACB ∠=∠，45BCO ∴∠=︒6OC OB ∴==，()6,0C ∴．设直线BC 的解析式为y kx b =+，将B 、C 两点坐标代得606k b b +=⎧⎨=⎩ 解得16k b =-⎧⎨=⎩∴直线BC 的解析式为6y x =-+．（2）点D 是射线BC 上一点，点D 的横坐标为t ，(,6)D t t ∴-+，6(6)12AC =--=．如下图，过点D 作DK AC ⊥于点K ，当点D 在线段BC 上时，6DK t =-+，16362S AC DK t ∴=⋅=-+()06t ≤<； 如下图，当点D 在线段BC 的延长线上时，6DK t =-，636S t ∴=-()6t >．（3）如图，延长CE 交AB 于点R ，连接DR 交BF 于点G ，交y 轴于点P ．45BAO BCO ∠=∠=︒，BA BC ∴=．AO CO =，BO AC ⊥EA EC ∴=，EAC ECA ∴∠=∠．ACR CAD ∴∆≅∆．BAD BCR ∴∠=∠．AR CD ∴=．BR BD ∴=．//RD AC ∴．BH AD ⊥，HBD BAD BCR ∴∠=∠=∠．MB MC ∴=，∠MRB MRB MBR ∠=∠MR MB ∴=．CM MR ∴=．//RD AC ，::1:1CF RG CM RM ∴==．CF RG ∴=．同理NF DG =．RD CN =．∵:7:12NF FC =．:7:12DG RG ∴=．RP PD BP ==，5tan 19PG OF OBF BP OB∴==∠= 6OB ∴=，3019OF ∴=，6OC =，8419CF ∴=． 7RD GN ∴==．1ON ∴=，72PD =．52OP OB BP ∴=-=． (1,0)N ∴-，75,22D ⎛⎫ ⎪⎝⎭． 设直线 DN 的解析式为y ax c =+，将N 、D 两点代入，07522a c a c -+=⎧⎪⎨+=⎪⎩解得5959 ac⎧=⎪⎪⎨⎪=⎪⎩∴直线DM的解析式为5599y x=+．【点睛】本题考查了一次函数与图形的综合，需要用到全等、三角函数和平面直角坐标系的知识，解题关键是想办法确定函数图像上点的坐标．6．D解析：（1）6；（2）y=－3x+10(1≤x＜103)；（2）1769或32【解析】【分析】（1）如下图，利用等腰直角三角形DHC可得到HC的长度，从而得出HB的长，进而得出AD的长；（2）如下图，利用等腰直角三角形的性质，可得PQ、PR的长，然后利用EB=PQ+PR得去x、y的函数关系，最后根据图形特点得出取值范围；（3）存在2种情况，一种是点P在梯形内，一种是在梯形外，分别根y的值求出x的值，然后根据梯形面积求解即可．【详解】（1）如下图，过点D作BC的垂线，交BC于点H∵∠C=45°，DH⊥BC∴△DHC是等腰直角三角形∵四边形ABCD是梯形，∠B=90°∴四边形ABHD是矩形，∴DH=AB=8∴HC=8∴BH=BC－HC=6∴AD=6（2）如下图，过点P作EF的垂线，交EF于点Q，反向延长交BC于点R，DH与EF交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理，PR=12y ∵AB=8，∴EB=8－x∵EB=QR∴8－x=()11622x y ++ 化简得：y=－3x+10 ∵y ＞0，∴x ＜103 当点N 与点B 重合时，x 可取得最小值则BC=NM+MC=NM+EF=－3x+10+614x +=，解得x=1∴1≤x ＜103（3）情况一：点P 在梯形ABCD 内，即（2）中的图形 ∵MN=2，即y=2，代入（2）中的关系式可得：x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二：点P 在梯形ABCD 外，图形如下：与（2）相同，可得y=3x －10则当y=2时，x=4，即AE=4 ∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质，难点在于第（2）问中确定x 的取值范围，需要一定的空间想象能力． 7．A解析：（1）详见解析；（2）2448x x y -+=（04x <<）；（3）当AEG ∆是等腰三角形时，2BF =或43【解析】【分析】 （1）根据正方形的性质得到∠AOD=90°，AO=OD ，∠EOH=90°，OE=OH ，由全等三角形的性质即可得到结论；（2）如图1，过O 作ON ⊥AB 于N ，根据等腰直角三角形的性质得到122AN BN ON AB ====， 根据勾股定理得到()222222248OF FN ON x x x =+=-+=-+线段成比例定理即可得到结论；（3）①当AE=EG 时，△AEG 是等腰三角形，②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP ⊥EG 于P ③当GE=AG 时，△AEG 是等腰三角形，如图3，过G 作GQ ⊥AE 于Q ，根据相似三角形的性质或全等三角形的性质健即可得到结论．【详解】（1）∵四边形ABCD 是正方形，,OA OD AC BD ∴=⊥，90AOD ∴∠=︒，∵四边形OEGH 是正方形，,90OE OH EOH ∴=∠=︒，AOD EOH ∴∠=∠，AOD AOH EOH AOH ∴∠-∠=∠-∠，即HOD EOA ∠=∠，HDO EAO ∴∆≅∆．（2）如图1，过O 作ON⊥AB 于N ，则122AN BN ON AB ====， ∵BF=x，∴AF=4-x ，∴FN=2-x ， ∴()222222248OF FN ON x x x =+=-+=-+∴248EF y x x =-+ ∵AM⊥AC，∴AE∥OB，∴BF OF AF EF＝， ∴2248448x x x x y x x -+=---+， ∴)24804x x y x x-+≤＝＜； （3）①当AE=EG 时，△AEG 是等腰三角形，则AE=OE ，∵∠EAO=90°，∴这种情况不存在；②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP⊥EG 于P ，则AP∥OE，∴∠PAE=∠AEO，∴△APE∽△EAO，∴PE AE OA OE=，∵AE=AG，∴2421482x xxPE y-+==，()22248xAE yx-=-=，∴()22222224448448xx xxx xx---+=+，解得：x=2，②当GE=AG时，△AEG是等腰三角形，如图3，过G作GQ⊥AE于Q，∴∠GQE=∠EAO=90°，∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°，∴∠EGQ=∠AEO，∵GE=OE，∴△EGQ≌△OEA（AAS），∴22EQ AO==∴224242()xAE E Q-===∴43x =， ∴BF=2或43． 【点睛】本题考查了四边形的综合题，正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质，勾股定理，正确的作出辅助线构造全等三角形是解题的关键．8．B解析：（1）12；（2）3）【解析】【分析】（1）如图1中，过点B 作BD CA ⊥，交CA 延长线于点D ，通过构造直角三角形，求出BD 利用三角形面积公式求解即可.（2）如图示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ，确定点P 的位置，利用勾股定理与矩形的性质求出CQ 的长度即为答案.（3）解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、，通过轴对称性质的转化，最终确定最小值转化为SN 的长.【详解】（1）如解图1所示，过点B 作BD CA ⊥，交CA 延长线于点D ，135BAC ∠=，180********BAD BAC ∴∠=-∠=-=，BD CA ⊥，交CA 延长线于点D ，BAD ∴为等腰直角三角形，且90BDA ∠=，BD AD ∴=，在BAD 中，,90BD AD BDA =∠=，222BD AD AB ∴+=，即222BD AB =，4AB =222232BD AB ∴===，解得：4BD =，6AC =，11641222ABC S AC BD ∴=⋅=⨯⨯=．（2）如解图2所示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ， D 关于AB 的对称点Q ，CQ 交AB 于点P ，PD PQ ∴=，PC PD PC PQ CQ ∴+=+=，点P 为AB 上的动点，PC PD CQ ∴+≥，∴当点P 处于解图2中的位置，PC PD +取最小值，且最小值为CQ 的长度， 点C 为半圆AB 的中点，90COB ∴∠=，90BOD COD COB ∠+∠=∠=，11903033BOD COB ∴∠=∠=⨯=， 10AB =，1110522OD AB ∴==⨯=， 在Rt ODH △中，由作图知，90OHD ∠=，且30HOD BOD ∠=∠=， 155,222DH OD QH DH ∴==∴==， 222255352OH OD DH ⎛⎫∴=-=-= ⎪⎝⎭， 由作图知，四边形OMQH 为矩形，553,2OM QH MQ OH ∴==== 515522CM OM OC ∴=+=+=， 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，PC PD ∴+的最小值为53．（3）如解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、， 点P 关于OA 的对称点S ，点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，PE SE ∴=，FP FN =，SOA POA ∠=∠，,NOB POB OS OP ON ∠=∠==，．PE EF FP SE EF FN SN ∴++=++=，SOA NOB POA POB ∠+∠=∠+∠，E 为OA 上的点，F 为OB 上的点PE EF FP SN ∴++≥，∴当点E F 、处于解图3的位置时，PE EF FP ++的长度取最小值，最小值为SN 的长度，45POA POB AOB ∠+∠=∠=，45SOA NOB ∴∠+∠=，454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=．扇形AOB 的半径为20，20OS ON OP ∴===，在Rt SON 中，90SON ∠=，20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容，理解题意，作出辅助线是做题的关键.9．A解析：（1）145；（2）2274,0314971421,2235t tSt t t⎧⎛⎫<≤⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<<⎪⎪⎝⎭⎩；（3）t的值为477或727．【解析】【分析】（1）如下图，根据4tan3A=，可得出PN与AP的关系，从而求出t的值；（2）如下图，存在2种情况，一种是点M在△ABC内，另一种是点M在△ABC外部，分别根据正方形和三角形求面积的公式可求解；（3）如下图，存在2种情况，一种是PM所在的直线将△ABC的面积平分，另一种是QN 所在的直线将△ABC的面积平分．【详解】（1）如图1，点N在AC上图1由题意可知：PD=DQ=t ，AP=7－t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =，即2473t t =- 解得：t=145 （2）①如图2，图2四边形PQMN 是正方形，90BQM ∴∠=︒，45B ∠=︒，BQ MQ ∴=，即72t t -=解得73t =， 故当0t <≤73时，22(2)4S t t ==； ②如图3， 图390BQF ∠=︒，45B ∠=︒，7BQ FQ t ∴==-，45BFQ MFE ∠=∠=︒，则37MF MQ QF t =-=-，90M ∠=︒，37ME MF t ∴==-， 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭； 综上，2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩． （3）如下图，过点C 作AB 的垂线，交AB 于点G图4∵4tan 3A = ∴设CG=4x ，则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14，解得：x=2∴1148562ABC S== ∴1282ABCS = 情况一：PM 所在的直线平分△ABC 的面积，如下图，PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形，∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB－PA=14－(7－t)=7+t∴7+t=47t=477-情况二：如下图，QN所在线段平分△ABC的面积，QF交AC于点F，过点F作AB的垂线，交AB于点H图6同理，28AFQS=∵四边形PQMN是正方形，∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y，则AH=3y，HQ=FH=4y，∴AQ=7y∴174282AFQS y y==，解得：2∵AQ=AB－QB=14－(7－t)=7+t∴2解得：27∴综上得：t的值为477或727．【点睛】本题考查动点问题，解题关键是根据动点的变化情况，适当划分为几种不同的形式分别分析求解．10．A。
中考数学压轴题之一元二次方程组(中考题型整理,突破提升)附答案解析
（2）若方程两实根 x1 ， x2 满足 x1 x2 x1x2 1 0 ，求 k 的值.
【答案】(1) k＜ 1 ;(2) k=0. 4
【解析】 【分析】 （1）根据一元二次方程的根的判别式得出△ ＞0，求出不等式的解集即可； （2）根据根与系数的关系得出 x1+x2=-（2k-1）=1-2k，x1•x2=k2，代入 x1+x2+x1x2-1=0，即可 求出 k 值． 【详解】 解：（1）∵ 关于 x 的一元二次方程 x2+（2k-1）x+k2=0 有两个不等实根 x1，x2，
月份
用水量 （吨）
水费 （元）
四月
35
59.5
五月
80
151
【答案】
5．有一个人患了流感，经过两轮传染后共有 36 人患了流感． （1）求每轮传染中平均一个人传染了几个人？ （2）如果不及时控制，第三轮将又有多少人被传染？ 【答案】（1）5；（2）180 【解析】 【分析】 （1）设平均一人传染了 x 人，根据有一人患了流感，经过两轮传染后共有 36 人患了流 感，列方程求解即可； （2）根据每轮传染中平均一个人传染的人数和经过两轮传染后的人数，列出算式求解即 可． 【详解】 （1）设每轮传染中平均一个人传染了 x 个人，根据题意得： x+1+（x+1）x＝36， 解得：x＝5 或 x＝﹣7（舍去）． 答：每轮传染中平均一个人传染了 5 个人； （2）根据题意得：5×36＝180（个）， 答：第三轮将又有 180 人被传染．
2a
2 2
2
∴ x1＝－1＋ 6 ，x2＝－1－ 6
2
2
（2）(y＋2)2－(3y－1)2＝0
中考数学压轴题专题复习——反比例函数的综合及详细答案
的坐标是（7，﹣3）时，对应的函数解析式是 y=﹣ x2+ ； f、当点 A 在 x 轴负半轴上，点 B 在 y 轴负半轴上，点 C 坐标为（3，4）时，另一个顶点 D
3．已知点 A，B 分别是 x 轴、y 轴上的动点，点 C，D 是某个函数图象上的点，当四边形 ABCD（A，B，C，D 各点依次排列）为正方形时，我们称这个正方形为此函数图象的“伴侣 正方形”． 例如：在图 1 中，正方形 ABCD 是一次函数 y=x+1 图象的其中一个“伴侣正方形”．
（1）如图 1，若某函数是一次函数 y=x+1，求它的图象的所有“伴侣正方形”的边长；
∵ 反比例函数 ∴ k=1×2=2，
的图象过点 A（1，2）．
∴ 反比例函数关系式是：y=
（2）解：反比例函数 y= ，当 x＞0 时，y 随 x 的增大而减少， 而当 x=1 时，y=2，当
x=6 时，y= ，
∴ 当 1≤x≤6 时，反比例函数 y 的值： ≤y≤2 【解析】【分析】（1）根据题意首先把点 B（﹣1，0）代入一次函数 y=x+b 求出一次函数 解析式，又点 A（1，n）在一次函数 y=x+b 的图象上，再利用一次函数解析式求出点 A 的 坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出 当 x=1，x=6 时的 y 值，即可得到答案．
（3）解：∠ PAQ=∠ PBQ． 理由如下：
过点 Q 作 QT⊥x 轴于 T，设 AQ 交 x 轴于 D，QB 的延长线交 x 轴于 E，如图 3． 可设点 Q 为（c， ），直线 AQ 的解析式为 y=px+q，则有
初中数学试卷中考压轴题精选(含详细答案)
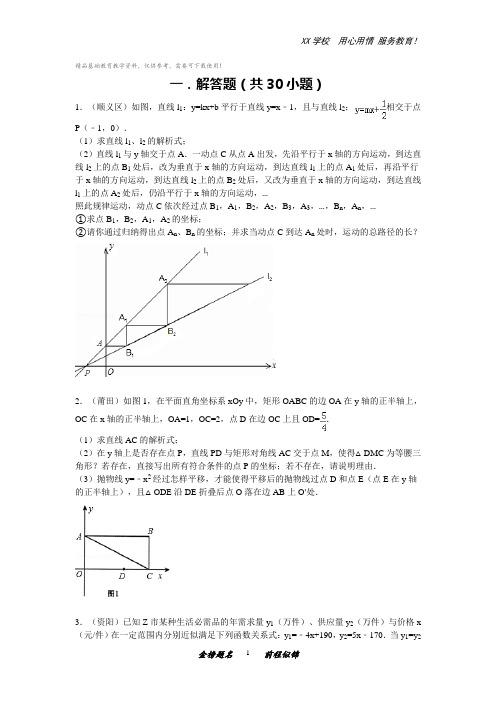
精品基础教育教学资料，仅供参考，需要可下载使用！一．解答题（共30小题）1．（顺义区）如图，直线l1：y=kx+b平行于直线y=x﹣1，且与直线l2：相交于点P（﹣1，0）．（1）求直线l1、l2的解析式；（2）直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，B n，A n，…①求点B1，B2，A1，A2的坐标；②请你通过归纳得出点A n、B n的坐标；并求当动点C到达A n处时，运动的总路径的长？2．（莆田）如图1，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=1，OC=2，点D在边OC上且OD=．（1）求直线AC的解析式；（2）在y轴上是否存在点P，直线PD与矩形对角线AC交于点M，使得△DMC为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．（3）抛物线y=﹣x2经过怎样平移，才能使得平移后的抛物线过点D和点E（点E在y轴的正半轴上），且△ODE沿DE折叠后点O落在边AB上O′处．3．（资阳）已知Z市某种生活必需品的年需求量y1（万件）、供应量y2（万件）与价格x （元/件）在一定范围内分别近似满足下列函数关系式：y1=﹣4x+190，y2=5x﹣170．当y1=y2时，称该商品的价格为稳定价格，需求量为稳定需求量；当y1＜y2时，称该商品的供求关系为供过于求；当y1＞y2时，称该商品的供求关系为供不应求．（1）求该商品的稳定价格和稳定需求量；（2）当价格为45（元/件）时，该商品的供求关系如何？为什么？4．（哈尔滨）如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．（1）求直线AC的解析式；（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；（3）在（2）的条件下，当t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．5．（桂林）如图已知直线L：y=x+3，它与x轴、y轴的交点分别为A、B两点．（1）求点A、点B的坐标．（2）设F为x轴上一动点，用尺规作图作出⊙P，使⊙P经过点B且与x轴相切于点F（不写作法，保留作图痕迹）．（3）设（2）中所作的⊙P的圆心坐标为P（x，y），求y关于x的函数关系式．（4）是否存在这样的⊙P，既与x轴相切又与直线L相切于点B？若存在，求出圆心P的坐标；若不存在，请说明理由．6．（防城港）如图，在平面直角坐标系，直线y=﹣（x﹣6）与x轴、y轴分别相交于A、D两点，点B在y轴上，现将△AOB沿AB翻折180°，使点O刚好落在直线AD的点C处．（1）求BD的长；（2）设点N是线段AD上的一个动点（与点A、D不重合），S△NBD=S1，S△NOA=S2，当点N运动到什么位置时，S1•S2的值最大，并求出此时点N的坐标；（3）在y轴上是否存在点M，使△MAC为直角三角形？若存在，请写出所有符合条件的点M的坐标，并选择一个写出其求解过程；若不存在，简述理由．7．（大兴安岭）直线y=kx+b（k≠0）与坐标轴分别交于A、B两点，OA、OB的长分别是方程x2﹣14x+48=0的两根（OA＞OB），动点P从O点出发，沿路线O⇒B⇒A以每秒1个单位长度的速度运动，到达A点时运动停止．（1）直接写出A、B两点的坐标；（2）设点P的运动时间为t（秒），△OPA的面积为S，求S与t之间的函数关系式（不必写出自变量的取值范围）；（3）当S=12时，直接写出点P的坐标，此时，在坐标轴上是否存在点M，使以O、A、P、M为顶点的四边形是梯形？若存在，请直接写出点M的坐标；若不存在，请说明理由．8．（云南）如图，在直角坐标系中，半圆直径为OC，半圆圆心D的坐标为（0，2），四边形OABC是矩形，点A的坐标为（6，0）．（1）若过点P（2，0）且与半圆D相切于点F的切线分别与y轴和BC边交于点H与点E，求切线PF所在直线的解析式；（2）若过点A和点B的切线分别与半圆相切于点P1和P2（点P1、P2与点O、C不重合），请求P1、P2点的坐标并说明理由．（注：第（2）问可利用备用图作答）．9．（厦门）如图，在直角梯形OABD中，DB∥OA，∠OAB=90°，点O为坐标原点，点A 在x轴的正半轴上，对角线OB，AD相交于点M．OA=2，AB=2，BM：MO=1：2．（1）求OB和OM的值；（2）求直线OD所对应的函数关系式；（3）已知点P在线段OB上（P不与点O，B重合），经过点A和点P的直线交梯形OABD 的边于点E（E异于点A），设OP=t，梯形OABD被夹在∠OAE内的部分的面积为S，求S关于t的函数关系式．10．（天门）如图①，在平面直角坐标系中，A点坐标为（3，0），B点坐标为（0，4）．动点M从点O出发，沿OA方向以每秒1个单位长度的速度向终点A运动；同时，动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动．设运动了x秒．（1）点N的坐标为（_________，_________）；（用含x的代数式表示）（2）当x为何值时，△AMN为等腰三角形；（3）如图②，连接ON得△OMN，△OMN可能为正三角形吗？若不能，点M的运动速度不变，试改变点N的运动速度，使△OMN为正三角形，并求出点N的运动速度．11．（乐山）如图，在平面直角坐标系中，△ABC的边AB在x轴上，且OA＞OB，以AB 为直径的圆过点C．若点C的坐标为（0，2），AB=5，A，B两点的横坐标x A，x B是关于x的方程x2﹣（m+2）x+n﹣1=0的两根．（1）求m，n的值；（2）若∠ACB平分线所在的直线l交x轴于点D，试求直线l对应的一次函数解析式；（3）过点D任作一直线l′分别交射线CA，CB（点C除外）于点M，N．则的是否为定值？若是，求出该定值；若不是，请说明理由．12．（黄冈）已知：如图，在直角梯形COAB中，OC∥AB，以O为原点建立平面直角坐标系，A，B，C三点的坐标分别为A（8，0），B（8，10），C（0，4），点D为线段BC 的中点，动点P从点O出发，以每秒1个单位的速度，沿折线OABD的路线移动，移动的时间为t秒．（1）求直线BC的解析式；（2）若动点P在线段OA上移动，当t为何值时，四边形OPDC的面积是梯形COAB面积的；（3）动点P从点O出发，沿折线OABD的路线移动过程中，设△OPD的面积为S，请直接写出S与t的函数关系式，并指出自变量t的取值范围；（4）试探究：当动点P在线段AB上移动时，能否在线段OA上找到一点Q，使四边形CQPD 为矩形？并求出此时动点P的坐标．13．（遵义）如图，已知一次函数的图象与x轴，y轴分别相交于A，B两点，点C在AB上以每秒1个单位的速度从点B向点A运动，同时点D在线段AO上以同样的速度从点A向点O运动，运动时间用t（单位：秒）表示．（1）求AB的长；（2）当t为何值时，△ACD与△AOB相似并直接写出此时点C的坐标；（3）△ACD的面积是否有最大值？若有，此时t为何值；若没有，请说明理由．14．（株洲）已知Rt△ABC，∠ACB=90°，AC=4，BC=3，CD⊥AB于点D，以D为坐标原点，CD所在直线为y轴建立如图所示平面直角坐标系．（1）求A，B，C三点的坐标；（2）若⊙O1，⊙O2分别为△ACD，△BCD的内切圆，求直线O1O2的解析式；（3）若直线O1O2分别交AC，BC于点M，N，判断CM与CN的大小关系，并证明你的结论．15．（镇江）探索、研究：下图是按照一定的规律画出的一列“树型”图，下表的n表示“树型”图的序号，a n表示第n个“树型”图中“树枝”的个数．图：表：n 1 2 3 4 …a n 1 3 7 15 …（1）根据“图”、“表”可以归纳出a n关于n的关系式为_________．若直线l1经过点（a1，a2）、（a2，a3），求直线l1对应的函数关系式，并说明对任意的正整数n，点（a n，a n+1）都在直线l1上．（2）设直线l2：y=﹣x+4与x轴相交于点A，与直线l1相交于点M，双曲线y=（x＞0）经过点M，且与直线l2相交于另一点N．①求点N的坐标，并在如图所示的直角坐标系中画出双曲线及直线l1、l2．②设H为双曲线在点M、N之间的部分（不包括点M、N），P为H上一个动点，点P的横坐标为t，直线MP与x轴相交于点Q，当t为何值时，△MQA的面积等于△PMA的面积的2倍又是否存在t的值，使得△PMA的面积等于1？若存在，求出t的值；若不存在，请说明理由．③在y轴上是否存在点G，使得△GMN的周长最小？若存在，求出点G的坐标；若不存在，请说明理由．16．（咸宁）如图，在平面直角坐标系xoy中，已知矩形ABCD的边AB、AD分别在x轴、y轴上，点A与坐标原点重合，且AB=2，AD=1．操作：将矩形ABCD折叠，使点A落在边DC上．探究：（1）我们发现折痕所在的直线与矩形的两边一定相交，那么相交的情形有几种请你画出每种情形的图形；（只要用矩形草稿纸动手折一折你会有发现的！）（2）当折痕所在的直线与矩形的边OD相交于点E，与边OB相交于点F时，设直线的解析式为y=kx+b．①求b与k的函数关系式；②求折痕EF的长（用含k的代数式表示），并写出k的取值范围．17．（厦门）已知点P（m，n）（m＞0）在直线y=x+b（0＜b＜3）上，点A、B在x轴上（点A在点B的左边），线段AB的长度为b，设△PAB的面积为S，且S=b2+b．（1）若b=，求S的值；（2）若S=4，求n的值；（3）若直线y=x+b（0＜b＜3）与y轴交于点C，△PAB是等腰三角形，当CA∥PB时，求b的值．18．（乌鲁木齐）如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，6），点B坐标为，BC∥y轴且与x轴交于点C，直线OB与直线AC相交于点P．（1）求点P的坐标；（2）若以点O为圆心，OP的长为半径作⊙O（如图2），求证：直线AC与⊙O相切于点P；（3）过点B作BD∥x轴与y轴相交于点D，以点O为圆心，r为半径作⊙O，使点D在⊙O 内，点C在⊙O外；以点B为圆心，R为半径作⊙B，若⊙O与⊙B相切，试分别求出r，R 的取值范围．19．（随州）如图，直角梯形ABCD的腰BC所在直线的解析式为y=﹣x﹣6，点A 与坐标原点O重合，点D的坐标为（0，﹣4），将直角梯形ABCD绕点O顺时针旋转180°，得到直角梯形OEFG（如图1）．（1）直接写出E，F两点的坐标及直角梯形OEFG的腰EF所在直线的解析式；（2）将图1中的直角梯形ABCD先沿x轴向右平移到点A与点E重合的位置，再让直角顶点A紧贴着EF，向上平移直角梯形ABCD（即梯形ABCD向上移动时，总保持着AB∥FG），当点A与点F重合时，梯形ABCD停止移动．观察得知：在梯形ABCD移动过程中，其腰BC始终经过坐标原点O．（如图2）①设点A的坐标为（a，b），梯形ABCD与梯形OEFG重合部分的面积为S，试求a与何值时，S的值恰好等于梯形OEFG面积的；②当点A在EF上滑动时，设AD与x轴的交点为M，试问：在y轴上是否存在点P，使得△PAM是底角为30°的等腰三角形？如果存在，请求出所有符合条件的点P的坐标；如果不存在，请说明理由．（利用图3进行探索）20．（邵阳）如图，直线y=﹣x+2与x轴，y轴分别相交于点A，B．将△AOB绕点O 按顺时针方向旋转α角（0°＜α≤360°），可得△COD．（1）求点A，B的坐标；（2）当点D落在直线AB上时，直线CD与OA相交于点E，△COD和△AOB的重叠部分为△ODE（图①）．求证：△ODE∽△ABO；（3）除了（2）中的情况外，是否还存在△COD和△AOB的重叠部分与△AOB相似，若存在，请指出旋转角α的度数；若不存在，请说明理由；（4）当α=30°时（图②），CD与OA，AB分别相交于点P，M，OD与AB相交于点N，试求△COD与△AOB的重叠部分（即四边形OPMN）的面积．21．（韶关）如图，在平面直角坐标系中，四边形OABC是矩形，OA=4，AB=2，直线与坐标轴交于D、E．设M是AB的中点，P是线段DE上的动点．（1）求M、D两点的坐标；（2）当P在什么位置时，PA=PB求出此时P点的坐标；（3）过P作PH⊥BC，垂足为H，当以PM为直径的⊙F与BC相切于点N时，求梯形PMBH 的面积．22．（衢州）如图，点B1（1，y1），B2（2，y2），B3（3，y3）…，B n（n，y n）（n是正整数）依次为一次函数y=x+的图象上的点，点A1（x1，0），A2（x2，0），A3（x3，0），…，A n（x n，0）（n是正整数）依次是x轴正半轴上的点，已知x1=a（0＜a＜1），△A1B1A2，△A2B2A3，△A3B3A4…△A n B n A n+1分别是以B1，B2，B3，…，B n为顶点的等腰三角形．（1）写出B2，B n两点的坐标；（2）求x2，x3（用含a的代数式表示）；分析图形中各等腰三角形底边长度之间的关系，写出你认为成立的两个结论；（3）当a（0＜a＜1）变化时，在上述所有的等腰三角形中，是否存在直角三角形？若存在，求出相应的a的值；若不存在，请说明理由．23．（黔东南州）某商厦试销一种成本为50元/件的商品，规定试销时的销售单价不低于成本，又不高于80元/件，试销中销售量y（件）与销售单价x（元/件）的关系可近似的看作一次函数（如图）．（1）求y与x的关系式；（2）设商厦获得的毛利润（毛利润=销售额﹣成本）为s（元），则销售单价定为多少时，该商厦获利最大，最大利润是多少？此时的销售量是多少件？24．（牡丹江）如图，在平面直角坐标系中，已知点A（﹣3，6），点B，点C分别在x轴的负半轴和正半轴上，OB，OC的长分别是方程x2﹣4x+3=0的两根（OB＜OC）．（1）求B，C两点的坐标；（2）在坐标平面内是否存在点Q和点P（点P在直线AC上），使以O、P、C、Q为顶点的四边形是正方形？若存在，请直接写出Q点的坐标；若不存在，请说明理由；（3）若平面内有M（1，﹣2），D为线段OC上一点，且满足∠DMC=∠BAC，∠MCD=45°，求直线AD的解析式．25．（梅州）如图，直角梯形ABCD中，AB∥CD，∠A=90°，AB=6，AD=4，DC=3，动点P从点A出发，沿A→D→C→B方向移动，动点Q从点A出发，在AB边上移动．设点P移动的路程为x，点Q移动的路程为y，线段PQ平分梯形ABCD的周长．（1）求y与x的函数关系式，并求出x，y的取值范围；（2）当PQ∥AC时，求x，y的值；（3）当P不在BC边上时，线段PQ能否平分梯形ABCD的面积？若能，求出此时x的值；若不能，说明理由．26．（聊城）某市为了进一步改善居民的生活环境，园林处决定增加公园A和公园B的绿化面积．已知公园A，B分别有如图1，图2所示的阴影部分需铺设草坪，在甲、乙两地分别有同种草皮1608m2和1200m2出售，且售价一样．若园林处向甲、乙两地购买草皮，其路程和运费单价见下表：公园A 公园B路程（千米）运费单价（元）路程（千米）运费单价（元）甲地30 0.25 32 0.25乙地22 0.3 30 0.3（注：运费单价指将每平方米草皮运送1千米所需的人民币）（1）分别求出公园A，B需铺设草坪的面积；（结果精确到1m2）（2）请设计出总运费最省的草皮运送方案，并说明理由．27．（佳木斯）如图，在平面直角坐标系中，已知点A（﹣3，6），点B，点C分别在x轴的负半轴和正半轴上，OB，OC的长分别是方程x2﹣4x+3=0的两根（OB＜OC）．（1）求点B，点C的坐标；（2）若平面内有M（1，﹣2），D为线段OC上一点，且满足∠DMC=∠BAC，求直线MD 的解析式；（3）在坐标平面内是否存在点Q和点P（点P在直线AC上），使以O，P，C，Q为顶点的四边形是正方形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．28．（济南）已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D 的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．29．（黑龙江）如图，点A为x轴负半轴上一点，点B为x轴正半轴上一点，OA，OB（OA ＜OB）的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根，C（0，3），且S△ABC=6 （1）求∠ABC的度数；（2）过点C作CD⊥AC交x轴于点D，求点D的坐标；（3）在第（2）问的条件下，y轴上是否存在点P，使∠PBA=∠ACB？若存在，请直接写出直线PD的解析式；若不存在，请说明理由．30．（哈尔滨）如图，梯形ABCD在平面直角坐标系中，上底AD平行于x轴，下底BC 交y轴于点E，点C（4，﹣2），点D（1，2），BC=9，sin∠ABC=．（1）求直线AB的解析式；（2）若点H的坐标为（﹣1，﹣1），动点G从B出发，以1个单位/秒的速度沿着BC边向C点运动（点G可以与点B或点C重合），求△HGE的面积S（S≠0）随动点G的运动时间t′秒变化的函数关系式（写出自变量t′的取值范围）；（3）在（2）的条件下，当秒时，点G停止运动，此时直线GH与y轴交于点N．另一动点P开始从B出发，以1个单位/秒的速度沿着梯形的各边运动一周，即由B到A，然后由A到D，再由D到C，最后由C回到B（点P可以与梯形的各顶点重合）．设动点P 的运动时间为t秒，点M为直线HE上任意一点（点M不与点H重合），在点P的整个运动过程中，求出所有能使∠PHM与∠HNE相等的t的值．答案与评分标准一．解答题（共30小题）1．（顺义区）如图，直线l1：y=kx+b平行于直线y=x﹣1，且与直线l2：相交于点P（﹣1，0）．（1）求直线l1、l2的解析式；（2）直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，B n，A n，…①求点B1，B2，A1，A2的坐标；②请你通过归纳得出点A n、B n的坐标；并求当动点C到达A n处时，运动的总路径的长？考点：一次函数综合题。
数学中考压轴题大全(含答案、详细解析版)
（ 2） A( 3，0) B (5，4)
C (0，4) ………… 5 分
C
1
A 01
B x
把点 A 坐标代入 y ax2 5ax 4 中，解得 a
1
……… 6 分
6
y
1 x2
5 x
4 …………………………………………
7分
66
y
Ｍ
（ 3）存在符合条件的点 P 共有 3 个．以下分三类情形探索．
A
1
Ｎ
令 x=20,y=60 ，得 k=60
①
令 x=100,y=100 ，得 a× 802＋ k=100
②
由①②解得
1 a
160 ， k 60
∴y
1
2
x 20 60 。……… 14 分
160
2 、（常州）已知 A( 1， m) 与 B(2， m 3 3) 是反比例函数
y
k
图象上的两个点．
x
（ 1）求 k 的值；
（ 3）过原点 O 的另一条直线 l 交双曲线 y k ( k 0) 于 P， Q 两 x
一象限），若由点 A， B， P， Q 为顶点组成的四边形面积为 24 ，求点
y A
解： (1) ∵点 A横坐标为 4 , ∴当 x = 4 时， y = 2 .
O B
点（ P 点在第 P 的坐标． x
∴ 点 A的坐标为（ 4 ， 2 ） .
∴ S = S 梯形 PEFA △POA = 6 .
∴ 1 (2
8 ) (m 4)
6，
2m
解得 m = 8 ， m = - 2 ( 舍去 ) .
∴ P（8， 1） .
∴ 点 P的坐标是 P（ 2，4）或 P（ 8， 1）.
中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)
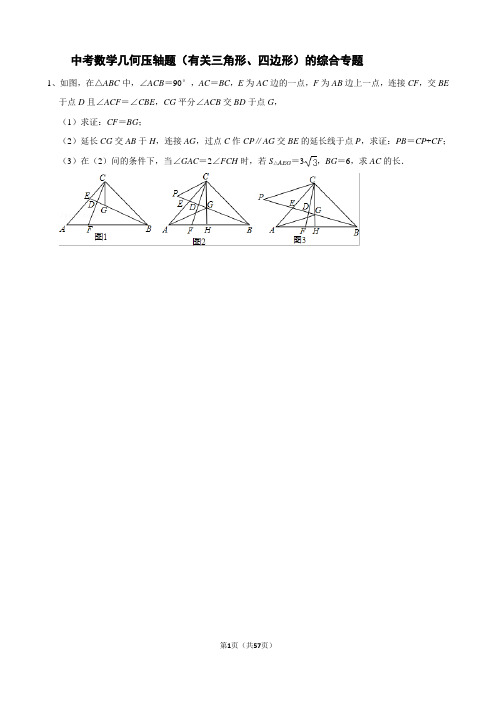
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2009年全国中考数学压轴题精选精析（四）41.（09年湖北恩施州）24.如图，在ABC ∆中，∠A 90=°，10=BC ,ABC ∆的面积为25，点D 为AB 边上的任意一点(D 不与A 、B 重合)，过点D 作DE ∥BC ，交AC 于点E ．设x DE =以DE 为折线将△ADE 翻折，所得的DE A '∆与梯形DBCE 重叠部分的面积记为y.（1）．用x 表示∆ADE 的面积; （2）．求出0﹤x ≤5时y 与x 的函数关系式； （3）．求出5﹤x ﹤10时y 与x 的函数关系式； （4）．当x 取何值时，y 的值最大？最大值是多少？（09年湖北恩施州24题解析）解:(1)∵ D E ∥BC ∴∠ADE=∠B,∠AED=∠C ∴△ADE ∽△ABC ∴2)(BC DE S S ABC ADE =∆∆即241x S ADE =∆ 3分 (2)∵BC=10 ∴BC 边所对的三角形的中位线长为5 ∴当0﹤5≤x 时 241x S y ADE ==∆ 6分 （3）x ≤5﹤10时，点A '落在三角形的外部,其重叠部分为梯形∵S △A 'DE =S △ADE =241x∴DE 边上的高AH=AH '=x 21 由已知求得AF=5 ∴A 'F=AA '-AF=x-5 由△A 'MN ∽△A 'DE 知2DE A'MN A')HA'F A'(=∆∆S SCBA2MN A')5(-=∆x S∴251043)5(41222-+-=--=x x x x y 9分 （4）在函数241x y =中∵0﹤x ≤5∴当x=5时y 最大为：42510分 在函数2510432-+-=x x y 中当3202=-=a b x 时y 最大为：32511分 ∵425﹤325∴当320=x 时，y 最大为：32512分39.（09年黑龙江绥化）28．(本小题满分lO 分)（09年黑龙江绥化28题解析）40.（09年湖北鄂州）27．如图所示，将矩形OABC 沿AE 折叠，使点O 恰好落在BC 上F处，以CF 为边作正方形CFGH ，延长BC 至M ，使CM ＝｜CF —EO ｜，再以CM 、CO 为边作矩形CMNO(1)试比较EO 、EC 的大小，并说明理由 (2)令；四边形四边形CNMN CFGHS S m，请问m 是否为定值？若是，请求出m 的值；若不是，请说明理由(3)在(2)的条件下，若CO ＝1，CE ＝31，Q 为AE 上一点且QF ＝32，抛物线y ＝mx 2+bx+c 经过C 、Q 两点，请求出此抛物线的解析式.(4)在(3)的条件下，若抛物线y ＝mx 2+bx+c 与线段AB 交于点P ，试问在直线BC 上是否存在点K ，使得以P 、B 、K 为顶点的三角形与△AEF 相似?若存在，请求直线KP 与y 轴的交点T 的坐标?若不存在，请说明理由。
（09年湖北鄂州27题解析）（1）EO ＞EC ，理由如下：由折叠知，EO=EF ，在Rt △EFC 中，EF 为斜边，∴EF ＞EC ， 故EO ＞EC …2分 （2）m 为定值∵S 四边形CFGH =CF 2=EF 2－EC 2=EO 2－EC 2=(EO+EC)(EO ―EC)=CO ·(EO ―EC)S 四边形CMNO =CM ·CO=|CE ―EO|·CO=(EO ―EC)·CO ∴1==CMNO CFGHS S m 四边形四边形……………………………………………………4分（3）∵CO=1，3231==QF CE ，∴EF=EO=QF ==-32311 ∴cos ∠FEC=21∴∠FEC=60°， ∴︒=∠∠=︒=︒-︒=∠3060260180EAO OEA FEA ，∴△EFQ 为等边三角形，32=EQ …………………………………………5分作QI ⊥EO 于I ，EI=3121=EQ ，IQ=3323=EQ ∴IO=313132=-∴Q 点坐标为)31,33(……………………………………6分∵抛物线y=mx 2+bx+c 过点C(0，1)， Q )31,33(，m=1 ∴可求得3-=b ，c=1∴抛物线解析式为132+-=x x y ……………………………………7分（4）由（3），3323==EO AO当332=x 时，3113323)332(2=+⨯-=y ＜AB ∴P 点坐标为)31,332(…………………8分 ∴BP=32311=-AO 方法1：若△PBK 与△AEF 相似，而△AEF ≌△AEO ，则分情况如下：①3323232=BK 时，932=BK ∴K 点坐标为)1,934(或)1,938( ②3232332=BK 时，332=BK ∴K 点坐标为)1,334(或)1,0(…………10分故直线KP 与y 轴交点T 的坐标为)1,0()31,0()37,0()35,0(或或或--…………………………………………12分方法2：若△BPK 与△AEF 相似，由（3）得：∠BPK=30°或60°，过P 作PR ⊥y 轴于R ，则∠RTP=60°或30° ①当∠RTP=30°时，23332=⨯=RT ②当∠RTP=60°时，323332=÷=RT∴)1,0()31,0()35,0()37,0(4321T T T T ，，，--……………………………12分42.（09年湖北黄冈）20．(满分14分)如图,在平面直角坐标系xoy 中,抛物线21410189y x x =--与x 轴的交点为点B ,过点B 作x 轴的平行线BC ,交抛物线于点C ,连结AC ．现有两动点P ,Q 分别从O,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于点E ,射线QE 交x 轴于点F ．设动点P ,Q 移动的时间为t (单位:秒)(1)求A,B,C 三点的坐标和抛物线的顶点的坐标; (2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程;(3)当0＜t ＜92时,△PQ F 的面积是否总为定值?若是,求出此定值,若不是,请说明理由;(4)当t 为何值时,△PQF 为等腰三角形?请写出解答过程．（09年湖北黄冈20题解析）解：（1）21(8180)18y x x =--，令0y =得281800x x --=，()()18100x x -+=∴18x =或10x =-∴(18,0)A ；………………………1′在21410189y x x =--中，令0x =得10y =即(0,10)B -；………………2′ 由于B C ∥OA ，故点C 的纵坐标为－10，由2141010189x x -=--得8x =或0x = 即(8,10)C -且易求出顶点坐标为98(4,)9-……………………………………3′于是，(18,0),(0,10),(8,10)A B C --，顶点坐标为98(4,)9-。
…………………4′（2）若四边形PQCA 为平行四边形，由于Q C ∥PA 。
故只要QC=PA 即可，而184,PA t CQ t =-=故184t t -=得185t =；……………………7′ （3）设点P 运动t 秒，则4,OP t CQ t ==，0 4.5t <<，说明P 在线段OA 上，且不与点OA 、重合，由于Q C ∥OP 知△QD C ∽△PDO ，故144QD QC t DP OP t === ∴4AF t OP ==∴18PF PA AF PA OP =+=+=…………………9′又点Q 到直线PF 的距离10d =，∴1118109022PQF S PF d ∆==⨯⨯=g g ，于是△PQF 的面积总为90。
…………………………10′（4）由上知，(4,0),(184,0),(8,10)P t F t Q t +--，0 4.5t <<。
构造直角三角形后易得2222(48)10(58)100PQ t t t =-++=-+，2222(1848)10(510)100FO t t t =+-++=++① 若FP=PQ ，即2218(58)100t =-+，故225(2)224t +=，∵22 6.5t +≤≤∴25t +==∴25t =-……………………11′ ② 若QP=QF ，即22(58)100(510)100t t -+=++，无0 4.5t ≤≤的t 满足条件；……………12′③ 若PQ=PF ，即22(58)10018t -+=，得2(58)224t -=，∴8 4.55t +=>或805t -=<都不满足0 4.5t ≤≤，故无0 4.5t ≤≤的t 满足方程；………………………13′综上所述：当25t =-时，△PQR 是等腰三角形。
…………………………14′ 43.（09年湖北黄石）25．（本小题满分10分）正方形ABCD 在如图所示的平面直角坐标系中，A 在x 轴正半轴上，D 在y 轴的负半轴上，AB 交y 轴正半轴于E BC ，交x 轴负半轴于F ，1OE =，抛物线24y ax bx =+-过A D F 、、三点．（1）求抛物线的解析式；（3分）（2）Q 是抛物线上D F 、间的一点，过Q 点作平行于x 轴的直线交边AD 于M ，交BC 所在直线于N ，若32FQN AFQM S S =△四边形，则判断四边形AFQM 的形状；（3分） （3）在射线DB 上是否存在动点P ，在射线CB 上是否存在动点H ，使得AP PH ⊥且AP PH =，若存在，请给予严格证明，若不存在，请说明理由．（4分）（09年湖北黄石25题解析）解：（1）依条件有(04)D -，，(01)E ，．由OEA ADO △∽△知24OA OE OD ==g． ∴(20)A ，由Rt Rt ADE ABF △≌△得DE AF =． ∴(30)F -，．将A F 、的坐标代入抛物线方程， 得42409340a b a b +-=⎧⎨--=⎩23a b ⇒==．∴抛物线的解析式为222433y x x =+-． ···························································· 3分 （2）设QM m =，1(5)||2Q AFQM S m y =+g 四边形，1(5)||2FQN Q S m y =-g △．∴3(5)||(5)||12Q Q m y m y m +=-⇒=g g设()Q a b ，，则(1)M a b +，∴222432(1)4b a a ab a ⎧=+-⎪⎨⎪=+-⎩2230a a ⇒--=，1a ∴=-（舍去3a =） 此时点M 与点D 重合，QF AM =，AF QM >，AF QM ∥，则AFQM 为等腰梯形． ·················································································· 3分 （3）在射线DB 上存在一点P ，在射线CB 上存在一点H ． 使得AP PH ⊥，且AP PH =成立，证明如下：当点P 如图①所示位置时，不妨设PA PH =，过点P 作PQ BC ⊥，PM CD ⊥，（第25题图）PN AD ⊥，垂足分别为Q M N 、、．若PA PH =．由PM PN =得：AN PQ =，Rt Rt PQH APN ∴△≌△ HPQ PAN ∴∠=∠．又90PAN APN ∠+∠=°90APN HPQ ∴∠+∠=°AP PH ∴⊥． ······························································································ 2分 当点P 在如图②所示位置时，过点P 作PM BC ⊥，PN AB ⊥， 垂足分别为M N ，．同理可证Rt Rt PMH PAN △≌△． MHP NAP ∠=∠． 又MHP HPN ∠=∠，90HPA NPA HPN MHP HPM ∠=∠+∠=∠+∠=°，PH PA ∴⊥． ······························································································ 1分 当P 在如图③所示位置时，过点P 作PN BH ⊥，垂足为N ，PM AB ⊥延长线，垂足为M ．同理可证Rt Rt PHM PMA △≌△．PH PA ∴⊥． ······························································································ 1分 注意：分三种情况讨论，作图正确并给出一种情况证明正确的，同理可证出其他两种情况的给予4分；若只给出一种正确证明，其他两种情况未作出说明，可给2分，若用四点共圆知识证明且证明过程正确的也没有讨论三种情况的．只给2分．44.（09年湖北荆门）25．(本题满分12分)一开口向上的抛物线与x 轴交于A (m －2，0)，B (m ＋2，0)两点，记抛物线顶点为C ，且AC ⊥BC ． (1)若m 为常数，求抛物线的解析式；(2)若m 为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？ (3)设抛物线交y 轴正半轴于D 点，问是否存在实数m ，使得△BCD 为等腰三角形？若存在，求出m 的值；若不存在，请说明理由．B A N D MC Q HP ① HNAD CB M P ③BADM C QHP ②N（09年湖北荆门25题解析）解：(1)设抛物线的解析式为：y ＝a (x －m ＋2)(x －m －2)＝a (x －m )2－4a ．…………2分∵AC ⊥BC ，由抛物线的对称性可知：△ACB 是等腰直角三角形，又AB ＝4， ∴C (m ，－2)代入得a ＝12．∴解析式为：y ＝12(x －m )2－2．…………………………5分 (亦可求C 点，设顶点式)(2)∵m 为小于零的常数，∴只需将抛物线向右平移－m 个单位，再向上平移2个单位，可以使抛物线y ＝12(x －m )2－2顶点在坐标原点．………………………………………7分 (3)由(1)得D (0，12m 2－2)，设存在实数m ，使得△BOD 为等腰三角形． ∵△BOD 为直角三角形，∴只能OD ＝OB ．……………………………………………9分 ∴12m 2－2＝|m ＋2|，当m ＋2＞0时，解得m ＝4或m ＝－2(舍)． 当m ＋2＜0时，解得m ＝0(舍)或m ＝－2(舍)；当m ＋2＝0时，即m ＝－2时，B 、O 、D 三点重合(不合题意，舍)综上所述：存在实数m ＝4，使得△BOD 为等腰三角形．……………………………12分 45.（09年湖北十堰）25．（12分）如图①， 已知抛物线32++=bx ax y （a ≠0）与x 轴交于点A (1，0)和点B (－3，0)，与y 轴交于点C ． (1) 求抛物线的解析式；(2) 设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．(3)如图②，若点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE第25题图BDACO xy面积的最大值，并求此时E 点的坐标．（09年湖北十堰25题解析）解:(1)由题知:⎩⎨⎧=+-=++033903b a b a ……………………………………1 分 解得: ⎩⎨⎧-=-=21b a ……………………………………………………………2分∴所求抛物线解析式为: 322+=x －－x y ……………………………3分(2)存在符合条件的点P, 其坐标为P (－1, 10)或P(－1,－10)或P (－1, 6) 或P (－1, 35)………………………………………………………7分 (3)解法①：过点E 作EF ⊥x 轴于点F , 设E ( a ,-2a -2a ＋3 )( －3< a < 0 )∴EF =-2a -2a ＋3，BF =a ＋3，OF =－a ………………………………………………8分∴S 四边形BOCE =21BF ·EF + 21(OC +EF )·OF =21( a ＋3 )·(－2a －2a ＋3) + 21(－2a －2a ＋6)·（－a ）……………………………9分 =2929232+--a a ………………………………………………………………………10分=－232)23(+a +863∴当a =－23时，S 四边形BOCE 最大, 且最大值为863．……………………………11 分此时，点E 坐标为 (－23，415)……………………………………………………12分 解法②：过点E 作EF ⊥x 轴于点F ，设E ( x , y )( －3< x < 0 ) …………………………8分则S 四边形BOCE =21(3 + y )·(－x ) + 21( 3 + x )·y ………………………………………9分 = 23( y －x )= 23(332+x －－x ) …………………………………10 分= －232)23(+x + 863∴当x =－23时，S 四边形BOCE 最大，且最大值为863． …………………………11分此时，点E 坐标为 (－23，415)……………………………………………………12分说明:（1）抛物线解析式用其它形式表示，只要正确不扣分.（2）直接应用公式法求抛物线顶点坐标或最大值不扣分． （3）其它解法请参照评分说明给分. 46.（09年湖北武汉）25．（本题满分12分）如图，抛物线24y ax bx a =+-经过(10)A -，、(04)C ，两点，与x 轴交于另一点B ． （1）求抛物线的解析式；（2）已知点(1)D m m +，在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标； （3）在（2）的条件下，连接BD ，点P 为抛物线上一点，且45DBP ∠=°，求点P 的坐标．37.（09年黑龙江牡丹江）28．（本小题满分8分）如图，ABCD Y在平面直角坐标系中，6AD =，若OA 、OB 的长是关于x 的一元二次方程27120x x -+=的两个根，且OA OB >． （1）求sin ABC ∠的值．（2）若E 为x 轴上的点，且163AOE S =△，求经过D 、E 两点的直线的解析式，并判断AOE △与DAO △是否相似？（3）若点M 在平面直角坐标系内，则在直线AB 上是否存在点F ，使以A 、C 、F 、M为顶点的四边形为菱形？若存在，请直接写出F 点的坐标；若不存在，请说明理由．（09年黑龙江牡丹江28题解析）解：（1）解27120x x -+=得1243x x ==，OA OB >Q43OA OB ∴==， ·············································································· 1分 在Rt AOB △中，由勾股定理有5AB =4sin 5OA ABC AB ∴∠== ········································································ 1分 （2）∵点E 在x 轴上，163AOE S =△11623AO OE ∴⨯= 83OE ∴=880033E E ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭，或， ········································································ 1分由已知可知D （6，4）设DE y kx b =+，当803E ⎛⎫ ⎪⎝⎭，时有 46803k b k b =+⎧⎪⎨=+⎪⎩解得65165k b ⎧=⎪⎪⎨⎪=-⎪⎩ ∴61655DE y x =- ················································································ 1分 同理803E ⎛⎫- ⎪⎝⎭，时，6161313DE y x =+ ······················································· 1分28题图在AOE △中，89043AOE OA OE ∠===°，， 在AOD △中，9046OAD OA OD ∠===°，， OE OAOA OD=Q AOE DAO ∴△∽△ ············································································ 1分 （3）满足条件的点有四个123475224244(38)(30)1472525F F F F ⎛⎫⎛⎫----- ⎪ ⎪⎝⎭⎝⎭，；，；，；， ····························· 4分说明：本卷中所有题目，若由其它方法得出正确结论，可参照本评分标准酌情给分. 38.（09年黑龙江齐齐哈尔）28．（本小题满分10分） 直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．（1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式； （3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．（09年黑龙江齐齐哈尔28题解析）（1）A （8，0）B （0，6） ································· 1分 （2）86OA OB ==Q ， 10AB ∴=Q 点Q 由O 到A 的时间是881=（秒）∴点P 的速度是61028+=（单位/秒） · 1分当P 在线段OB 上运动（或03t ≤≤）时，2OQ t OP t ==，2S t = ·········································································································· 1分当P 在线段BA 上运动（或38t <≤）时，6102162OQ t AP t t ==+-=-，,如图，作PD OA ⊥于点D ，由PD AP BO AB =，得4865tPD -=， ······························ 1分 21324255S OQ PD t t ∴=⨯=-+ ······································································· 1分 （自变量取值范围写对给1分，否则不给分．）（3）82455P ⎛⎫ ⎪⎝⎭， ···························································································· 1分12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，，， ···················································· 3分注：本卷中各题，若有其它正确的解法，可酌情给分．（09年湖北武汉25题解析）解：（1）Q 抛物线24y ax bx a =+-经过(10)A -，，(04)C ，两点，404 4.a b a a --=⎧∴⎨-=⎩，解得13.a b =-⎧⎨=⎩，∴抛物线的解析式为234y x x =-++．（2）Q 点(1)D m m +，在抛物线上，2134m m m ∴+=-++，即2230m m --=，1m ∴=-或3m =．Q 点D 在第一象限，∴点D 的坐标为(34)，．由（1）知45OA OB CBA =∴∠=，°． 设点D 关于直线BC 的对称点为点E ．(04)C Q ，，CD AB ∴∥，且3CD =，45ECB DCB ∴∠=∠=°，E ∴点在y 轴上，且3CE CD ==．1OE ∴=，(01)E ∴，． 即点D 关于直线BC 对称的点的坐标为（0，1）．（3）方法一：作PF AB ⊥于F ，DE BC ⊥于E ． 由（1）有：445OB OC OBC ==∴∠=，°， 45DBP CBD PBA ∠=∴∠=∠Q °，．(04)(34)C D Q ，，，，CD OB ∴∥且3CD =．45DCE CBO ∴∠=∠=°，2DE CE ∴==． 4OB OC ==Q，BC ∴=2BE BC CE ∴=-=， 3tan tan 5DE PBF CBD BE ∴∠=∠==． 设3PF t =，则5BF t =，54OF t ∴=-，(543)P t t ∴-+，．P Q 点在抛物线上，∴23(54)3(54)4t t t =--++-++，0t ∴=（舍去）或2225t =，266525P ⎛⎫∴- ⎪⎝⎭，． 方法二：过点D 作BD 的垂线交直线PB 于点Q ，过点D 作DH x ⊥轴于H ．过Q 点作QG DH ⊥于G ．45PBD QD DB ∠=∴=Q °，． QDG BDH ∴∠+∠90=°，又90DQG QDG ∠+∠=°，DQG BDH ∴∠=∠．QDG DBH ∴△≌△，4QG DH ∴==，1DG BH ==．由（2）知(34)D ，，(13)Q ∴-，．(40)B Q ，，∴直线BP 的解析式为31255y x =-+．解方程组23431255y x x y x ⎧=-++⎪⎨=-+⎪⎩，，得1140x y =⎧⎨=⎩，；222566.25x y ⎧=-⎪⎪⎨⎪=⎪⎩， ∴点P 的坐标为266525⎛⎫- ⎪⎝⎭，．47.（09年湖北襄樊）26．（本小题满分13分）如图13，在梯形ABCD 中，24AD BC AD BC ==∥，，，点M 是AD 的中点，MBC △是等边三角形．（1）求证：梯形ABCD 是等腰梯形；（2）动点P 、Q 分别在线段BC 和MC 上运动，且60MPQ =︒∠保持不变．设PC x MQ y ==，，求y 与x 的函数关系式； （3）在（2）中：①当动点P 、Q 运动到何处时，以点P 、M 和点A 、B 、C 、D 中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数； ②当y 取最小值时，判断PQC △的形状，并说明理由．（09年湖北襄樊26题解析）（1）证明：∵MBC △是等边三角形∴60MB MC MBC MCB ===︒，∠∠ ········ 1分 ∵M 是AD 中点 ∴AM MD = ∵AD BC ∥∴60AMB MBC ==︒∠∠， 60DMC MCB ==︒∠∠ ∴AMB DMC △≌△ ······················ 2分 ∴AB DC =∴梯形ABCD 是等腰梯形． ························································ 3分（2）解：在等边MBC △中，4MB MC BC ===，60MBC MCB ==︒∠∠，60MPQ =︒∠∴120BMP BPM BPM QPC +=+=︒∠∠∠∠∴BMP QPC =∠∠ ··········································································· 4分 ∴BMP CQP △∽△∴PC CQBM BP= ······················································· 5分 ∵PC x MQ y ==，∴44BP x QC y =-=-， ······································ 6分A DC B PM Q60°图13∴444x y x -=-∴2144y x x =-+ ···························································· 7分 （3）解：①当1BP =时，则有BP AM BP MD∥∥， 则四边形ABPM 和四边形MBPD 均为平行四边形 ∴211333444MQ y ==⨯-+= ··················································· 8分 当3BP =时，则有PC AM PC MD∥∥， 则四边形MPCD 和四边形APCM 均为平行四边形∴11311444MQ y ==⨯-+= ····················································· 9分 ∴当1314BP MQ ==，或1334BP MQ ==，时，以P 、M 和A 、B 、C 、 D中的两个点为顶点的四边形是平行四边形．此时平行四边形有4个． ·························································· 10分 ②PQC △为直角三角形 ··························································· 11分 ∵()21234y x =-+ ∴当y 取最小值时，2x PC == ················································ 12分 ∴P 是BC 的中点，MP BC ⊥，而60MPQ =︒∠，∴30CPQ =︒∠，∴90PQC =︒∠ ·············································· 13分48.（09年湖北孝感）25．（本题满分12分）如图，点P 是双曲线11(00)k y k x x=<<，上一动点，过点P 作x 轴、y 轴的垂线，分别交x 轴、y 轴于A 、B 两点，交双曲线y =xk 2（0＜k 2＜|k 1|）于E 、F 两点． （1）图1中，四边形PEOF 的面积S 1=▲(用含k 1、k 2的式子表示)；（3分） （2）图2中，设P 点坐标为（－4，3）．①判断EF 与AB 的位置关系，并证明你的结论；（4分）②记2PEF OEF S S S ∆∆=-，S 2是否有最小值？若有，求出其最小值；若没有，请说明理由．（5分）（09年湖北孝感25题解析）解：（1）21k k -；… ………………………3分（2）①EF ∥AB ． ……………………………………4分 证明：如图，由题意可得A （–4，0），B （0，3），2(4,)4k E --，2(,3)3k F ．∴P A=3，PE =234k +，PB =4，PF =243k+． ∴223121234PA k PEk ==++，224121243PB k PFk ==++∴PA PBPE PF=．………………………… 6分 又∵∠APB =∠EPF ．∴△APB ∽△EPF ，∴∠P AB =∠PEF ．∴EF ∥AB ．…………………………… 7分 ②S 2没有最小值，理由如下：过E 作EM ⊥y 轴于点M ，过F 作FN ⊥x 轴于点N ，两线交于点Q ． 由上知M （0，24k -），N （23k ，0），Q （23k ，24k -）．………………8分而S △EFQ = S △PEF ，∴S 2＝S △PEF －S △OEF ＝S △EFQ －S △OEF ＝S △EOM ＋S △FON ＋S 矩形OMQN＝4321212222kk k k ⋅++ ＝222112k k +=221(6)312k +-． …………………………10分当26k >-时，S 2的值随k 2的增大而增大，而0＜k 2＜12．……………11分 ∴0＜S 2＜24，s 2没有最小值． ……………………………12分说明：1．证明AB ∥EF 时，还可利用以下三种方法．方法一：分别求出经过A 、B 两点和经过E 、F 两点的直线解析式，利用这两个解析式中x 的系数相等来证明AB ∥EF ；方法二：利用tan PAB ∠＝tan PEF ∠来证明AB ∥EF ；方法三：连接AF 、BE ，利用S △AE F ＝S △BFE 得到点A 、点B 到直线EF 的距离相等，再由A 、B 两点在直线EF 同侧可得到AB ∥EF ．2．求S 2的值时，还可进行如下变形：S 2＝ S △PEF －S △OEF ＝S △PEF －（S 四边形PEOF －S △PEF ）＝2S △PEF －S 四边形PEOF ，再利用第（1）题中的结论．注意：1．按照评分标准分步评分，不得随意变更给分点；2．第19题至第25题的其它解法，只要思路清晰，解法正确，都应按步骤给予相应分数．。