最优化方法大作业-算法源程序-0.618法、抛物线法、共轭梯度法
最优化方法

随机梯度下降每次迭代只使用一个样本,迭代 一次计算量为n 2 ,当样本个数m很大的时候, 随机梯度下降迭代一次的速度要远高于批量梯 度下降方法。 两者的关系可以这样理解:随机 梯度下降方法以损失很小的一部分精确度和增 加一定数量的迭代次数为代价,换取了总体的 优化效率的提升。增加的迭代次数远远小于样 本的数量。
2. 牛顿法和拟牛顿法(Newton's method & Quasi-Newton Methods)
牛顿法(Newton's method) 牛顿法是一种在实数域和复数域上近似求解方程 的方法。方法使用函数 f ( x ) 的泰勒级数的前 面几项来寻找方程 f ( x ) = 0 的根。牛顿法最大 的特点就在于它的收敛速度很快。
具体步骤:
首先,选择一个接近函数 f ( x ) 零点的 x 0 , 计算相应的 f ( x 0 ) 和切线斜率 f ' (x 0 ) (这 里 f ' 表示函数 f 的导数)。然后我们计算穿 过点 (x 0 , f (x 0 )) 并且斜率为 f '(x 0 ) 的直线 和 x 轴的交点的 x 坐标,也就是求如下方程的 解:
批量梯度下降法(Batch Gradient Descent,BGD)
(1)将J(theta)对theta求偏导,得到每个theta对应 的的梯度:
(2)由于是要最小化风险函数,所以按每个参数 theta的梯度负方向,来更新每个theta:
(3)从上面公式可以注意到,它得到的是一个全 局最优解,但是每迭代一步,都要用到训练集 所有的数据,如果m很大,那么可想而知这种 方法的迭代速度会相当的慢。所以,这就引入 了另外一种方法——随机梯度下降。 对于批量梯度下降法,样本个数m,x为n维向 量,一次迭代需要把m个样本全部带入计算, 迭代一次计算量为m*n 2 。
最优化理论与方法

最优化理论与方法综述李超雄最优化方法是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
最优化方法的主要研究对象是各种管理问题及其生产经营活动。
最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。
这就是我理解的整个课程的流程。
在这整个学习的过程当中,当然也会遇到很多的问题,不论是从理论上的还是从实际将算法编写出程序来解决一些问题。
下面给出学习该课程的必要性及结合老师讲解以及在作业过程中遇到的问题来阐述自己对该课程的理解。
20世纪40年代以来,由于生产和科学研究突飞猛进地发展,特别是电子计算机日益广泛应用,使最优化问题的研究不仅成为一种迫切需要,而且有了求解的有力工具。
因此最优化理论和算法迅速发展起来,形成一个新的学科。
至今已出现线性规划、整数规划、非线性规划、几何规划、动态规划、随机规划、网络流等许多分文。
最优化理论与算法包括线性规划单纯形方法、对偶理论、灵敏度分析、运输问题、内点算法、非线性规划K-T条件、无约束最优化方法、约束最优化方法、参数线性规划、运输问题、线性规划路径跟踪法、信赖域方法、二次规划路径跟踪法、整数规划和动态规划等内容。
最优化理论所研究的问题是讨论在众多的方案中什么样的方案最优以及怎样找出最优方案。
这类问题普遍存在。
例如,工程设计中怎样选择设计参数,使得设计方案满足设计要求,又能降低成本;资源分配中,怎样分配有限资源,使得分配方案既能满足各方面的基本要求,又能获得好的经济效益;生产评价安排中,选择怎样的计划方案才能提高产值和利润;原料配比问题中,怎样确定各种成分的比例,才能提高质量,降低成本;城建规划中,怎样安排基本单位的合理布局,才能方便群众,有利于城市各行各业的发展;农田规划中,怎样安排各种农作物的合理布局,才能保持高产稳产,发挥地区优势;军事指挥中,怎样确定最佳作战方案,才能有效地消灭敌人,保存自己,有利于战争的全局;在人类活动的各个领域中,诸如此类,不胜枚举。
最优化算法实验2-0.618法与斐波那契法

0.618法(斐波那契法)的Matlab 实现实验目的:1、通过本次实验了解线性搜索,加深对试探法的理解2、根据0.618法(斐波那契法)的算法步骤编写相应的Matlab 程序,并利用matlab 程序计算求解实验要求:1、学习MATLAB 利用0.618法(斐波那契法)解决最优化问题的程序设计方法。
2、对问题进行编程和解决问题。
3、按照格式规范,撰写计算机实践报告。
实验内容:1. 0.618法的基本思想:通过取代试探点和进行函数值的比较,使包含极小点的搜索区间不断缩短,当区间长度缩短到一定程度时,区间上各点的函数值均接近极小值点的近似。
使用前提:要求所考虑区间上的目标函数是单峰函数,即在这个区间上只有一个局部极小点的函数。
2.算法步骤:步 1.选取初始数据。
确定初始搜索区间[]11,b a 和精确要求t>0,设置初始试探点11,μλ,)(618.0)(382.011111111a b a a b a -+=-+=μλ计算。
,令和1)()(11=k μϕλϕ 步 2.比较目标函数值。
若)(1λϕ>)(1μϕ,转步3;否则转步4。
步 3.若t b k k ≤-λ,则停止计算,输出k μ;否则,令:)(618.0:),(:)(,:,:,:111111k k k k k k k k k k k k a b a b b a -+=====++++++μμϕλϕμλλ计算)(11+k μϕ,转步2。
步4.若t a k k ≤-μ,则停止计算,输出k λ;否则,令)(382.0:),(:)(,:,:,:111111k k k k k k k k k k k k a b a b a a -+=====++++++λλϕμϕλμμ计算)(11+k λϕ,转步2。
3.编写0.618法Matlab 程序求解最优化问题y=cos3x 在区间[1,2]上的最优值.4.参照0.618法算法为例编写菲波那切法Matlab 程序.。
常见的优化算法

常见的优化算法
摘要:
1.优化算法的定义和分类
2.最大化和最小化问题
3.梯度下降法
4.牛顿法
5.拟牛顿法
6.共轭梯度法
7.遗传算法
8.模拟退火算法
9.人工神经网络
正文:
优化算法是数学和计算机科学的一个分支,主要研究如何找到一个函数的最小值或最大值。
在实际应用中,优化问题可以分为最大化和最小化两种类型。
为了求解这类问题,人们研究了许多优化算法,下面我们来介绍一些常见的优化算法。
首先,我们来了解一些基本的优化算法。
梯度下降法是一种非常常见的优化算法,它通过计算目标函数的梯度来不断更新参数,从而使函数值逐渐下降。
牛顿法和拟牛顿法则是基于牛顿- 莱布尼茨公式来求解优化问题的方法,它们具有比梯度下降法更快的收敛速度。
共轭梯度法则是一种高效的线性规划算法,它可以在保证解全局收敛的同时,大幅提高求解速度。
除了这些传统的优化算法,还有一些新兴的优化算法。
遗传算法是一种模
拟自然界生物进化过程的优化方法,它通过基因的遗传、变异和选择来逐步改进解的质量。
模拟退火算法则是一种模拟金属冶炼过程的优化算法,它通过模拟金属冶炼过程中的退火过程来寻找全局最优解。
人工神经网络是一种模拟人脑神经网络进行信息处理的优化算法,它通过调整神经网络中的权重和阈值来逼近目标函数。
总之,优化算法是解决实际问题的重要工具,不同的优化算法适用于不同的问题。
了解这些算法的原理和特点,可以帮助我们更好地选择合适的方法来求解实际问题。
最优化问题的算法迭代格式

最优化问题的算法迭代格式最优化问题的算法迭代格式最优化问题是指在一定的条件下,寻找使某个目标函数取得极值(最大值或最小值)的变量取值。
解决最优化问题的方法有很多种,其中较为常见的是迭代法。
本文将介绍几种常用的最优化问题迭代算法及其格式。
一、梯度下降法梯度下降法是一种基于负梯度方向进行搜索的迭代算法,它通过不断地沿着目标函数的负梯度方向进行搜索,逐步接近极值点。
该方法具有收敛速度快、易于实现等优点,在许多应用领域中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和学习率 $\alpha$,梯度下降算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 更新当前点 $x_k$ 为 $x_{k+1}=x_k-\alpha\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则返回第 1 步。
2. 算法特点- 沿着负梯度方向进行搜索,能够快速收敛;- 学习率的选择对算法效果有重要影响;- 可能会陷入局部极小值。
二、共轭梯度法共轭梯度法是一种基于线性方程组求解的迭代算法,它通过不断地搜索与当前搜索方向共轭的新搜索方向,并在该方向上进行一维搜索,逐步接近极值点。
该方法具有收敛速度快、内存占用少等优点,在大规模问题中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和初始搜索方向 $d_0$,共轭梯度算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则进行下一步;- 计算当前搜索方向 $d_k$;- 在当前搜索方向上进行一维搜索,得到最优步长 $\alpha_k$;- 更新当前点为 $x_{k+1}=x_k+\alpha_k d_k$;- 计算新的搜索方向 $d_{k+1}$;- 返回第 2 步。
2. 算法特点- 搜索方向与前面所有搜索方向都正交,能够快速收敛;- 需要存储和计算大量中间变量,内存占用较大;- 可以用于非线性问题的求解。
(完整版)机械优化设计习题参考答案孙靖民第四版机械优化设计

2.黄金分割法(0.618法)
原理:提高搜索效率:1)每次只插一个值,利用一个前次的插值;2)每次的缩短率λ相同。左右对称。
程序:p52
(四)插值方法
1.抛物线法
原理:任意插3点:
算得: ; ;
要求:
设函数 用经过3点的抛物线 代替,有
解线代数方程
解得:
程序框图p57
网格法 ,缩小区间,继续搜索。
Monte Carlo方法 , ,随机数。
比较各次得到的 得解
遗传算法(专题)
(二)区间消去法(凸函数)
1.搜索区间的确定:高—低--高( )则区间内有极值。
2.区间消去法原理:在区间[a, b]内插两个点a1, b1保留有极值点区间,消去多余区间。
缩短率:
(三)0.618法
可行方向—约束允许的、函数减小的方向。(图)约束边界的切线与函数等高线的切线方向形成的区域。
数学模型
用内点法或混合法,取 ,
直接方法
(一)随机方向法
1.在可行域产生一个初始点 ,因 (约束),则
--(0,1)的随机数。
2.找k个随机方向,每个方向有n个方向余弦,要产生kn个随机数 , , ,随机方向的单位向量为
3.取一试验步长 ,计算每个方向的最优点
4.找出可行域中的最好点 得搜索方向 。以 为起点, 为搜索方向得 。最优点必须在可行域内或边界上,为此要逐步增加步长。
得
穷举下去得递推公式
3.算例
p73
4.框图p72
5.特点
作业:1. 2.
(六)变尺度法
1.引言
坐标变换
二次函数
令 为尺度变换矩阵
最优控制的计算方法

可得
3、将 代入协态方程,且由边界条件 从t=1倒向积分可得 这里选步长因子 。如此继续下去,直至指标函数随迭代变化很小为止。 由 ,得
图b 最优状态的求解
图a 用梯度法寻找最优控制 右图表示了控制和状态的初始值和第一次迭代值,可以看到第一次迭代 就几乎收敛到最优值, 与最优值还有差异,而且一般说来愈接近最优值收敛愈慢。
K=1时时,控制量为
所以,这个例子只要两步迭代即可得到最优解。一般说来,共轭梯度法比梯度法收敛快,但接近最优解后收敛性仍是较慢的。一个补救办法是重新启动,即找出几个共轭梯度方向 后,令 ,再重新迭代,寻找共轭梯度方向。
可以证明 ,即为最优控制。这只要证明
2、共轭梯度法
*
用共轭梯度法寻找最优控制时是沿着所谓共轭梯度向量的方向进行的。为了说明共轭梯度的意义,我们先从求函数极值问题的共轭梯度法开始,再推广到求泛函极值问题。
(1) 求函数极值的共轭梯度法
其中,
C为常数, Q为正定阵。
要求寻找X使F(X)取极值。
设F(X)是定义在Rn空间中的二次指标函数
直接法的特点是,在每一步迭代中,U(t)不一定要满足H 取极小的必要条件,而是逐步改善它,在迭代终了使它满足这个必要条件,而且,积分状态方程是从t0到tf ,积分协态方程是从tf到t0,这样就避免了去寻找缺少的协态初值(t0)的困难。常用的直接法有梯度法,二阶梯度法,共轭梯度法。
间接法的特点是,在每一步迭代中都要满足H取极小的必要条件,而且要同时积分状态方程和协态方程,两种方程的积分都从从t0到tf或从tf到t0 。常用的间接法有边界迭代法和拟线性化法。
最优化方法复习大纲PPT课件

2 0 2 0 0 12
问:(1)确定当前单纯型表中的基变量,基本可行解,
目标函数值。
(2)判断其是否为最优单纯型表,是则给出理由;不是, 则继续求解该问题的最优解。
10
解:
(1)基变量为 x2 , x4 , x5 ,基本可行解为 x1 (0,4,0,2,6)T 。 目标函数值为12。
(2)因为变量 x1 的检验数 1 2 0 ,所以不是最优单纯
题的最优解计算. 6. 模式搜索法:计算。
7. 最优性条件: 积极约束判断,K-T条件, K-T点 判别。
8. 惩罚函数法: 外点法惩罚函数的构造,内点法 障碍函数的构造,外点法、内点法计算。
2
9. 线性规划: 建立线性规划模型,化标准型,基 本可行解的计算,单纯型表上的单纯型算法.
3
例1. 试用梯度法解下述问题 min f ( x) x12 4 x22
min z 2 x1 x2 3 x3
x1 x2 2 x3 4
s.t .
2 x1 x3 2 2x2 x3 5
x1 , x2 0, x3无约束
解: 令 x3 x4 x5 .
max z 2 x1 x2 3 x4 3 x5
x1 x2 2 x4 2 x5 x6 4
已知初始点 x1 (1,1)T ,求迭代点x2。
解: f ( x) [ 2x1 ,8x2 ]T d1 f ( x1) [ 2, 8]T
x x1 d1 [1 2,1 8]T
记 ( ) f ( x1 d1) (1 2 )2 4(1 8 )2
令 '( ) 4(1 2 ) 64(1 8 ) 0
最优化方法复习提纲
一、概念
最优化问题,凸集,凸函数,局部极小点, 全局极小点,下降方向,最优步长,共轭方 向,可行方向,积极约束,线性规划问题, 基本解。
最优化梯度法和共轭梯度法

函数的极小点。
以下分析算法的具体步骤。
(1) 任取初始点 x (1),第一个搜索方向取为 d (1) f ( x (1) ) ;
( 2) 设已求得点 x ( k 1) , f ( x ( k 1) ) 0 , g k 1 f ( x ( k 1) ) , 若 令
局部目标函数值下降最快的方向。 最速下降法是线性收敛的算法。
三. 共轭梯度法
1. 共轭方向和共轭方向法
R 定义 设 A 是 n n 的对称正定矩阵,对于 n中的两个非零向量d 1 和 d 2,
若有 d
1T
Ad 2 0 ,则称 d 1和d 2关于A共轭。
设 d 1 , d 2 ,, d k 是 Rn 中一组非零向量,如果 它们两两关于A
以任意的 x (1) R n为初始点,依次沿 d (1) , d ( 2 ) ,, d ( k ) 进行搜索,
得到点 x ( 2) , x ( 3) ,, x ( k 1) , 则 x ( k 1) 是函数 f ( x )在 x (1) Bk 上的
极小点,其中
Bk { x | x i d ( i ) , i R }
i
d ( i ) A g i 1 d
( i )T
T
Ad
(i )
g i 1T A d ( i ) d
( i )T
Ad ( i )
g i 1T A[ ( x ( i 1) x ( i ) ) / i ] d
( i )T
A [ ( x ( i 1) x ( i ) ) / i ]
共轭,即 d i Ad j 0 , i j , i , j 1 , 2 ,, k 。
最优化方法课程设计-最优化大作业-用优化算法求解函数最值问题

最优化方法大作业---------用优化算法求解函数最值问题摘要最优化(optimization) 是应用数学的重要研究领域.它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。
最优化问题一般包括最小化问题和最大化问题,而最大化问题可以通过简单的转化使之成最最小化问题。
最小化问题分为两类,即约束最小化和无约束最小化问题。
在此报告中,前两个问题属于无约束最小化问题的求解,报告中分别使用了“牛顿法”和“共轭梯度法”。
后两个问题属于有约束最小化问题的求解,报告中分别用“外点法”和“内点法”求解。
虽然命名不一样,其实质都是构造“惩罚函数”或者“障碍函数”,通过拉格朗日乘子法将有约束问题转化为无约束问题进行求解。
再此报告中,“外点法”和“内点法”分别用了直接求导和调用“牛顿法”来求解无约束优化问题。
在此实验中,用“共轭梯度法”对“牛顿法”所解函数进行求解时出现错误,报告中另取一函数用“共轭梯度法”求解得到正确的结果。
此实验中所有的函数其理论值都是显见的,分析计算结果可知程序正确,所求结果误差处于可接受范围内。
报告中对所用到的四种方法在其使用以前都有理论说明,对“外点法”中惩罚函数和“内点法”中障碍函数的选择也有相应的说明,另外,对此次试验中的收获也在报告的三部分给出。
本报告中所用程序代码一律用MATLAB编写。
【关键字】函数最优化牛顿法共轭梯度法内点法外点法 MATLAB一,问题描述1,分别用共轭梯度发法和牛顿法来求解一下优化问题()()()()()441432243221102510min x x x x x x x x x f -+-+-++=2, 分别用外点法和内点发求解一下优化问题⎩⎨⎧≥-++01.min 212231x x t s x x二、问题求解1.1 用牛顿法求解()()()()()441432243221102510min x x x x x x x x x f -+-+-++=1.1.1问题分析:取步长为1而沿着牛顿方向迭代的方法称为牛顿法,在牛顿法中,初始点的取值随意,在以后的每次迭代中,()[]()k k k k x f x f x x ∇∇-=-+121,直到终止条件成立时停止。
最优化方法3-5共轭梯度法和共轭方向法

算法 3.5.1
设目标函数为 f (x) 1 xTGx bT x c,其中G 正定。 2
给定控制误差 。
Step1. 给定初始点 x0及初始下降方向 p0,令k 0。
Step2. 作精确一维搜索,求步长k
f
( xk
k
pk )
min
0
f
( xk
pk
)
Step3. 令 xk1 xk k pk 。
称 Fletcher-Reeves 公式,简称 FR 公式。
k 1
gkT Gpk1 pkT1Gpk 1
Gpk 1
1
k 1
(gk
g
k 1 ) ,
gkT Gpk1
1
k 1
gkT
(gk
g
k 1)
,
pkT1Gpk 1
1
k 1
(g
k1 k2
pk2 )T
(gk
g
k 1)
1
k 1
g
g T
k 1 k
1
(2)Polak-Ribiere-Polyak 公式
故
k 1
g
T k
(
gk
g
k 1)
gkT1gk 1
此式是 Polak 和 Ribiere 以及 Polyak 分别于 1969
年提出的,故称 Polak-Ribiere-Polyak 公式,简称 PRP
0,i
1,2,L
,k
(ii) xk1是二次函数在k 维超平面Hk 上的极小点。
证明 由引理 3.5.2,只需证明(i),
最优化课程练习-共轭梯度法
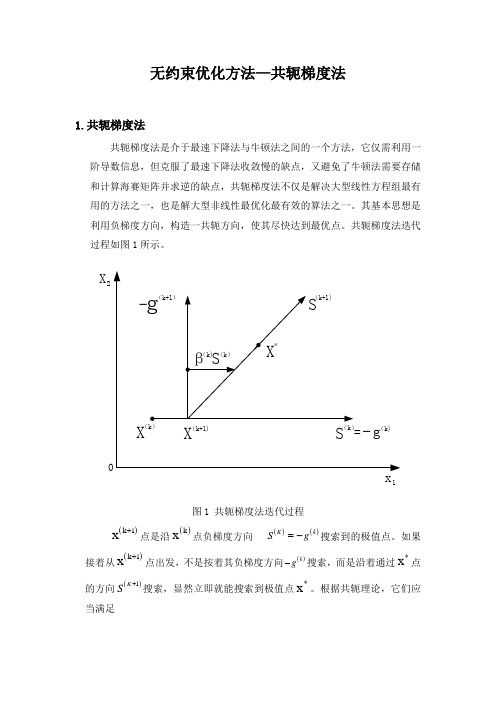
无约束优化方法—共轭梯度法1.共轭梯度法共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算海赛矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
其基本思想是利用负梯度方向,构造一共轭方向,使其尽快达到最优点。
共轭梯度法迭代过程如图1所示。
1X 2图1 共轭梯度法迭代过程()k 1x +点是沿()k x 点负梯度方向()()K k Sg =-搜索到的极值点。
如果接着从()k 1x +点出发,不是按着其负梯度方向()kg -搜索,而是沿着通过*x 点的方向()1K S +搜索,显然立即就能搜索到极值点*x 。
根据共轭理论,它们应当满足()()(1)1k Tk SAS+=即()KS 与()1K S +是互为共轭方向,新构造的共轭方向()1K S +,可由矢量合成,()(1)(1)()()2k k k k SgSβ++=-+()k β值可根据在极值点附近目标函数等值线近似为二次型函数的道理,推到出:()(1)(1)(1)2()()()()2||||3||||k T k k k k T k k gg g g g g β+++==利用两个点的梯度()k g和(1)k g+,就可以构造一个与梯度矢量为共轭的矢量()1K S +,沿着该方向搜索,即可求得极值点。
共轭梯度法程序框图如图2所示。
图2 共轭梯度法程序框图2. 共轭梯度法的应用用共轭梯度法计算22121212()52410f X x x x x x x =+---+ 的最优解,其中:初始点()0[1,1]T X =。
收敛精度ε=0.0001(1).共轭梯度法程序设计#include "stdio.h" #include "math.h"double fun1(double x1,double x2) {double y;y=x1*x1+x2*x2-5*x1*x2-2*x1-4*x2+10; return y; }double fun2(double g[],double d[]) {double buchang;buchang=-(g[0]*d[0]+g[1]*d[1])/(d[0]*(2*d[0]-5*d[1])+d[1]*(-5*d[0]+2*d[1])); return buchang; }main(){ double t, beta,x1=1,x2=1,d[2],g[4], y, m,e=0.0001; int k=1;g[0]=2*x1-5*x2-2; g[1]=2*x2-5*x1-4; m=(sqrt(g[0]*g[0]+g[1]*g[1]));while(m>e&&k<=200) { if (k==1) {d[0]=-g[0]; d[1]=-g[1];beta=0; } else {beta=(g[0]*g[0]+g[1]*g[1])/(g[2]*g[2]+g[3]*g[3]); d[0]=-g[0]+beta*d[0]; d[1]=-g[1]+beta*d[1]; }t=fun2(g,d); x1=x1+d[0]*t; x2=x2+d[1]*t; g[2]=g[0]; g[3]=g[1];g[0]= 2*x1-5*x2-2;g[1]= 2*x2-5*x1-4;m=sqrt(g[0]*g[0]+g[1]*g[1]); k++; }y=fun1(x1,x2);printf("迭代次数为k=%d\n",k);printf("分别输出x1=%f,x2=%f\n",x1,x2); printf("极小值y=%f",y); }(2).程序运行结果(3).结 论用共轭梯度法计算22121212()52410f X x x x x x x =+---+的最优解为*( 1.142857,0.857143)X =-- ,*()12.857143F X = 。
数学优化问题的求解方法

数学优化问题的求解方法数学优化问题是数学中的一个重要分支,它在各个领域都有广泛的应用。
解决数学优化问题的方法多种多样,下面将介绍几种常见的求解方法。
一、暴力搜索法暴力搜索法也称为穷举法,是最简单直接的求解数学优化问题的方法之一。
它通过枚举问题的所有可能解,并计算得出每个解对应的目标函数值,最后找到最优解。
但此方法在问题规模较大时无法满足实际需求,因为其时间复杂度过高。
二、单纯形法单纯形法是一种经典的线性规划求解算法,主要用于求解线性优化问题。
它通过在顶点集合内移动,不断寻找更优解的方法。
单纯形法具有高效性和可靠性,并且可以处理大规模的线性规划问题,成为了一种常用的求解方法。
三、梯度下降法梯度下降法是一种常见的非线性优化求解算法,主要用于求解无约束的最优化问题。
它通过迭代的方式逐步接近最优解,通过计算目标函数的梯度方向来确定搜索方向。
梯度下降法易于理解和实现,但在复杂的非凸问题中可能会陷入局部最优解。
四、遗传算法遗传算法是一种基于自然选择和遗传机制的优化算法,主要应用于复杂的非线性优化问题。
它通过模拟进化过程,利用选择、交叉和变异等操作,生成新的解,并根据适应度评估函数筛选出最优解。
遗传算法适用于多模态和多目标优化问题,但其计算量较大。
五、模拟退火算法模拟退火算法是一种随机搜索算法,主要应用于组合优化和全局优化问题。
它通过模拟固体物质退火过程中的晶格结构演化,寻找出合适的解。
模拟退火算法能够跳出局部最优解,找到全局最优解,但其收敛速度较慢。
六、动态规划法动态规划法适用于具有最优子结构的问题,通过将原问题划分为多个子问题,利用子问题的最优解推导出原问题的最优解。
动态规划法通常需要建立状态转移方程和选择最优策略,通过填表法来计算最优解。
动态规划法的时间复杂度通常较低,适用于一些具有递推性质的优化问题。
总结而言,数学优化问题的求解方法有很多种,每种方法都有其适用范围和特点。
选择合适的求解方法需要根据问题的具体情况来决定,包括约束条件、问题规模、目标函数形式等。
最优化理论与算法(第四章)

第四章 共轭梯度法§ 共轭方向法共轭方向法是无约束最优化问题的一类重要算法。
它一方面克服了最速下降法中,迭代点列呈锯齿形前进,收敛慢的缺点,同时又不像牛顿法中计算牛顿方向花费大量的工作量,尤其是共轭方向法具有所谓二次收敛性质,即当将其用于二次函数时,具有有限终止性质。
一、共轭方向概念 设G 是n n ⨯对称正定矩阵,1d ,2d 是n 维非零向量,假设120T d Gd = ()那么称1d ,2d 是G -共轭的。
类似地,设1,,m d d 是n R 中一组非零向量。
假设0T i j d Gd =()i j ≠ ()那么称向量组1,,m d d 是G -共轭的。
注:(1) 当G I =时,共轭性就变成正交性,故共轭是正交概念的推行。
(2) 若1,,m d d G -共轭,那么它们必线性无关。
二、共轭方向法共轭方向法确实是依照一组彼此共轭方向依次搜索。
模式算法:1)给出初始点0x ,计算00()g g x =,计算0d ,使000Td g <,:0k = (初始共轭方向); 2)计算k α和1k x +,使得0()min ()k k k k k f x d f x d ααα≥+=+,令1k k k k x x d α+=+;3)计算1k d +,使10Tk j d Gd +=,0,1,,j k =,令:1k k =+,转2)。
三、共轭方向法的大体定理共轭方向法最重要的性质确实是:当算法用于正定二次函数时,能够在有限多次迭代后终止,取得最优解(固然要执行精准一维搜索)。
定理 关于正定二次函数,共轭方向法最多通过n 步精准搜索终止;且对每一个1i x +,都是()f x 在线性流形00,i j j j j x x x d αα=⎧⎫⎪⎪=+∀⎨⎬⎪⎪⎩⎭∑中的极小点。
证明:首先证明对所有的1i n ≤-,都有10T i j g d +=,0,1,,j i =(即每一个迭代点处的梯度与以前的搜索方向均正交)事实上,由于目标函数是二次函数,因此有()11k k k k k k g g G x x Gd α++-=-=1)当j i <时, ()1111iTTT i j j j k k j k j g d gd g g d +++=+=+-∑110iT T j j kkj k j gd dGd α+=+=+=∑2)当j i =时,由精准搜索性质知:10T i j g d +=综上所述,有 10T i j g d += (0,1,,)j i =。
最优化各算法介绍

最速下降法:算法简单,每次迭代计算量小,占用内存量小,即使从一个不好的初始点出发,往往也能收敛到局部极小点。
沿负梯度方向函数值下降很快的特点,容易使认为这一定是最理想的搜索方向,然而事实证明,梯度法的收敛速度并不快.特别是对于等值线(面)具有狭长深谷形状的函数,收敛速度更慢。
其原因是由于每次迭代后下一次搜索方向总是与前一次搜索方向相互垂直,如此继续下去就产生所谓的锯齿现象。
从直观上看,在远离极小点的地方每次迭代可能使目标函数有较大的下降,但是在接近极小点的地方,由于锯齿现象,从而导致每次迭代行进距离缩短,因而收敛速度不快.牛顿法:基本思想:利用目标函数的一个二次函数去近似一个目标函数,然后精确的求出这个二次函数的极小点,从而该极小点近似为原目标函数的一个局部极小点。
优点 1. 当目标函数是正定二次函数时,Newton 法具有二次终止性。
2. 当目标函数的梯度和Hesse 矩阵易求时,并且能对初始点给出较好估计时,建议使用牛顿法为宜。
缺点:1. Hesse 矩阵可能为奇异矩阵,处理办法有:改为梯度方向搜索。
共轭梯度法:优点:收敛速度优于最速下降法,存贮量小,计算简单.适合于优化变量数目较多的中等规模优化问题.缺点:变度量法:较好的收敛速度,不计算Hesse 矩阵1.对称秩1 修正公式的缺点(1)要求( ) ( ) ( ) ( ) ( ) 0 k k k T k y B s s − ≠0(2)不能保证B ( k ) 正定性的传递2.BFGS 算法与DFP 算法的对比对正定二次函数效果相同,对一般可微函数效果可能不同。
1) BFGS 算法的收敛性、数值计算效率优于DFP 算法;(2) BFGS 算法要解线性方程组,而DFP 算法不需要。
基本性质:有效集法:算法思想:依据凸二次规划问题的性质2,通过求解等式约束的凸二次规划问题,可能得到原凸二次规划问题的最优解。
有效集法就是通过求解一系列等式约束凸二次规划问题,获取一般凸二次规划问题解的方法。
最优化 马昌凤 第二章作业

最优化方法及其Matlab程序设计习题作业暨实验报告学院:数学与信息科学学院班级:12级信计一班姓名:李明学号:1201214049第二章 线搜索技术一、上机问题与求解过程 1、用0.618法求解 .1)(min 2--=x x x f 初始区间]1,1[-,区间精度为50.=0δ. 解:当初始时不限制近似迭代函数值得大小,编写程序运行结果为:从结果可以看出迭代次数为9次,极小点为5016.0,极小点的函数值为2500.1-。
根据人工手算,极小值点应该为500.0,所以在设计程序的时候添加函数值误差范围,并取范围为10101-⨯。
编写的设计函数程序并调试改正如下:function [s,fs,k,G,FX,E]=gold(f,a,b,H,F) %输入:% f:目标函数,a :搜索区间左侧端点;b:搜索区间右侧端点; % H :搜索区间允许范围;F :搜索区间函数值允许范围; %输出:% s:近似极小值点:fa :近似极小点数值;k:迭代次数:% FX :近似迭代函数值;E=[h,fh],h 为近似区间误差,fh 为函数值误差 t=(sqrt(5)-1)/2;h=b-a; p=a+(1-t)*h;q=a+t*h;fa=feval(f,a);fb=feval(f,b); fp=feval(f,p);fq=feval(f,q); k=1;G(k,:)=[a,p,q,b];%初始时错误语句:G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到后面需要开辟k 行空间 FX(k,:)=[fa,fp,fq,fb];while (abs(fa-fb)>F) ((b-a)>H) if (fp<fq)b=q;fb=fq;q=p;fq=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始时错误语句:b=q;fb=fq;h=b-a;q=a+t*h;fq=feval(f,q); %初始调试的时候对0.618方法没有充分理解所以出现错误 elsea=p;fa=fp;p=q;fp=fq;h=b-a;q=a+t*h;fq=feval(f,q);%初始时错误语句:a=p;fa=fp;h=b-a;p=a+(1-t)*h;fp=feval(f,p); %初始调试的时候对0.618方法没有充分理解所以出现错误 end极小点(s) 迭代次数搜索区间误差 函数值误差 0.501690.04260.0006k=k+1;G(k,:)=[a,p,q,b];%初始时错误语句:G(1,:)=[a,p,q,b]; %初始调试的时候没有注意到前面已经开辟k 行空间 FX(k,:)=[fa,fp,fq,fb]; end if (fp<fq) s=p;fs=fp; elses=q;fs=fq; endh=b-a;fh=abs(fb-fa);%选取试探点最小的数值为近似点,并且计算出以上为搜索区间的的最后误差以及函数值误差 E=[h,fh];在命令窗口内输入如下命令:[s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) 回车之后得到如下数据结果:附:在窗口中输出的结果如下>> [s,fs,k,G,FX,E]=gold(inline('s^2-s-1'),-1,1,0.05,1e-10) s = 0.5000 fs = -1.2500 k = 24 G =-1.0000 -0.2361 0.2361 1.0000 -0.2361 0.2361 0.5279 1.0000 0.2361 0.5279 0.7082 1.0000极小点 极小点数值 迭代次数 搜索区间误差 函数值误差 0.500-1.250024410321.0-⨯0000.00.2361 0.4164 0.5279 0.70820.4164 0.5279 0.5967 0.70820.4164 0.4853 0.5279 0.59670.4164 0.4590 0.4853 0.52790.4590 0.4853 0.5016 0.52790.4853 0.5016 0.5116 0.52790.4853 0.4953 0.5016 0.51160.4953 0.5016 0.5054 0.51160.4953 0.4992 0.5016 0.50540.4953 0.4977 0.4992 0.50160.4977 0.4992 0.5001 0.50160.4992 0.5001 0.5006 0.50160.4992 0.4997 0.5001 0.50060.4997 0.5001 0.5003 0.50060.4997 0.5000 0.5001 0.50030.4997 0.4999 0.5000 0.50010.4999 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50010.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.50000.5000 0.5000 0.5000 0.5000 FX =1.0000 -0.7082 -1.1803 -1.0000 -0.7082 -1.1803 -1.2492 -1.0000 -1.1803 -1.2492 -1.2067 -1.0000 -1.1803 -1.2430 -1.2492 -1.2067 -1.2430 -1.2492 -1.2406 -1.2067 -1.2430 -1.2498 -1.2492 -1.2406 -1.2430 -1.2483 -1.2498 -1.2492 -1.2483 -1.2498 -1.2500 -1.2492 -1.2498 -1.2500 -1.2499 -1.2492 -1.2498 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2499 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.2500 -1.25001.0e-04*0.3121 0.00002、用0.618法求解.12)(min 3+-=x x x f的近似最优解,初始搜索区间为]3,0[,区间精度为50.=1δ. 解:当初始时不限制近似迭代函数值得大小,编写程序运行结果为:从结果可以看出迭代次数为8次,极小点为8115.0,极小点的函数值为0886.0-。
最优化方法代码

牛顿法:函数fun,初值x0,误差e,结果x例子:fun=x^4-4*x^3-6*x^2-16*x+4function [x]=newton(fun,x0,e)f1=diff(fun);f2=diff(fun,2);x=x0-subs(f1,x0)/subs(f2,x0);while (abs(x-x0)>=e)x0=x;x=x0-subs(f1,x0)/subs(f2,x0);end平分法:函数fun,初始区间(a,b),误差e,结果x 例子:fun=3*x^4-16*x^3+30*x^2-24*x+8function [x]=pingfen(fun,a,b,e)x=(a+b)/2;f1=diff(fun);while (abs(a-b)>=e)if(subs(f1,x)>0)b=x;x=(a+b)/2;elseif (subs(f1,x)<0)a=x;x=(a+b)/2;elseif(subs(f1,x)==0)break;endend成功失败法:函数fun,初值x0,步长h,误差e例子:fun=x^5+2*x^4-4*x^3+x^2+x+2function [x]=suc_fail(fun,x0,h,e) x=x0;y0=subs(fun,x);while(1)y=subs(fun,(x+h))if(y<y0)y0=y;x=x+h;h=2*helseif(y>=y0)if(abs(h)<e)break;elseh=-h*(1/4);endendend0.618法:例子:fun=x^2+2*xfunction [x]=f0618(fun,a0,b0,e) n=0.618;a=a0;b=b0;r=a+(1-n)*(b-a);u=a+n*(b-a);yr=subs(fun,r);yu=subs(fun,u);while(abs(b-a)>=e)if(yr>yu)a=r;r=u;u=a+n*(b-a);yr=subs(fun,r);yu=subs(fun,u);elseb=u;u=r;r=a+(1-n)*(b-a);yu=subs(fun,u);yr=subs(fun,r);endendx=0.5*(a+b);确定初始区间和初始值:function [a,b,x0]=f(fun)t0=0;h=1;y0=subs(fun,t0);t2=t0+h;y2=subs(fun,t2);if(y2<=y0)t1=t0+h;y1=subs(fun,t1);elseh=-h;t1=t0+h;y1=subs(fun,t1);endwhile(y1<=y0)h=2*h;t2=t0;t0=t1;if(y2<=y0)t1=t0+h;y1=subs(fun,t1);elseh=-h;t1=t0+h;y1=subs(fun,t1);endenda=min(t1,t2);b=max(t1,t2);x0=(a+b)/2;海塞矩阵:[n,m]=size(x);syms x1 x2 x3 x4 x5;xk=[x1;x2;x3;x4;x5];for k=1:ny(k)=xk(k);endfor i=1:ng(i)=diff(fun,xk(i));h=g(i);for k=1:ny(i)=subs(h,xk(k),x(k));h=y(i);endendg=double(y);end海塞矩阵二阶偏导:function [g]=hassion2(fun,x)[n,m]=size(x);syms x1 x2 x3 x4 x5;xk=[x1;x2;x3;x4;x5];for k=1:ny(k)=xk(k);endfor i=1:ng1(i)=diff(fun,xk(i));for j=1:ng2(i,j)=diff(g1(i),xk(j));h=g2(i,j);for p=1:ny(i,j)=subs(h,xk(p),x(p));h=y(i,j);endendendg=double(y);一维精确搜索:[n,m]=size(x);syms x1 x2 x3 x4 x5 r;xk=[x1;x2;x3;x4;x5];xx=x+r*s;for i=1:nf=subs(fun,xk(i),xx(i));fun=f;endrr=solve(diff(f,r));r=double(rr);求函数值:function [f]=fx(fun,x0)[n,m]=size(x0);syms x1 x2 x3 x4 x5;x=[x1;x2;x3;x4;x5];for k=1:nf=subs(fun,x(k),x0(k));fun=f;endf=double(f);不精确的一维搜索方法:步长r,函数fun,初值x0,方向s0 例子:fun=100*(x2-x1^2)^2+(1-x1)^2;function [r]=ods(fun,x0,s0)[n,m]=size(x0);syms x1 x2 x3 x4 x5;x=[x1;x2;x3;x4;x5];for k=1:ny(k)=x(k);y0(k)=x(k);endc1=0.1;c2=0.5;a=0;b=+inf;r=1;j=0;s=s0;x1=x0+r*s;h0=fun;h=fun;for k=1:nf=subs(h,x(k),x1(k));h=f;f0=subs(h0,x(k),x0(k));h0=f0;endy0=hassion(fun,x0);y=hassion(fun,x1);while(double(f0-f) < double((-1)*c1*r*y0*s) || double(y*s) < double(c2*y0*s))j=j+1;if(double(f0-f) < double((-1)*c1*r*y0*s))b=r;r=(r+a)/2;elsea=r;r=min(2*r,(r+b)/2);endx1=x0+r*s;h0=fun;h=fun;for k=1:nf=subs(h,x(k),x1(k));h=f;endy=hassion(fun,x1);end最速下降法:函数fun,初值x0,误差e 例子:fun=3*x1^2+2*x2^2-4*x1-6*x2function [x]=fast(fun,x0,e)x=x0;s=hassion(fun,x);while(norm(s)>=e)x0=x;r=ods(fun,x0,-s');x=x0-r*s';s=hassion(fun,x);end牛顿法(N维):结果x,函数fun,初值x0,精度e 例子:fun=x1^2+25*x2^2function [x]=newton2(fun,x0,e)x=x0;s1=hassion(fun,x)s2=hassion2(fun,x)while(norm(s1)>=e)x0=xx=x0-inv(s2)*s1';s1=hassion(fun,x);s2=hassion2(fun,x);end阻尼牛顿法:结果x,函数fun,初值x0,精度e例子:fun=x1^2+2*x2^2-4*x1-2*x1*x2function [x]=znnewton(fun,x0,e)x=x0;y1=hassion(fun,x0);y2=hassion2(fun,x0);while(norm(y1)>=e)s0=-inv(y2)*y1';r=search(fun,x0,s0);x0=x;x=x0+r*s0;y1=hassion(fun,x);y2=hassion2(fun,x);end共轭梯度法:结果x,函数fun,初值x0,精度e 例子:fun=x1^2+2*x2^2-4*x1-2*x1*x2function [x]=gongertidu(fun,x0,e)[n,m]=size(x0);k=0;flag=0;while(k==0 & flag==0)x=x0;g0=hassion(fun,x);s0=-g0;r=search(fun,x,s0');x=x0+r*s0';g1=hassion(fun,x);flag=flag+1;while(norm(g1)>=e)if(k==n-1)x0=x;k=0;flag=0;break;endu=norm(g1)^2/norm(g0)^2;s1=-g1+u*s0;r=search(fun,x,s1');x=x+r*s1';g1=hassion(fun,x);k=k+1;s0=s1;endendDPF算法:结果x,函数fun,初值x0,精度e例子:fun=x1^2+2*x2^2-4*x1-2*x1*x2function [x]=dfp(fun,x0,e)[n,m]=size(x0);h0=eye(n);k=0;flag=0;while(k==0 & flag==0)h=h0;x=x0;g0=hassion(fun,x);s0=-h0*g0';r=search(fun,x0,s0);x=x0+r*s0;g1=hassion(fun,x);flag=flag+1;while(norm(g1)>=e)if(k==n-1)x0=x;k=0;flag=0;break;endh=h0+((x-x0)*(x-x0)')/((x-x0)'*(g1-g0)')-(h0*(g1-g0)'*(h0*(g1-g0)')')/((g1-g0)*h0*(g1-g0)');s1=-h*g1';r=search(fun,x,s1);x=x+r*s1;g1=hassion(fun,x);h0=h;x0=x;k=k+1;endendBFGS算法:例子:fun=x1^2+x1*x2+x2^2;function [x]=wg(fun,x0,e)[n,m]=size(x0);k=0;flag=0;while(k==0 & flag==0)h0=eye(n);h=h0;x=x0;g0=hassion(fun,x0);g=g0;flag=flag+1;while(norm(g)>=e)if(k==n)k=0;flag=0;x0=x;break;ends=-h'*g';r=search(fun,x,s);x=x+r*s;g=hassion(fun,x);u=1+((g-g0)*h0*(g-g0)')/((x-x0)'*(g-g0)');h=h0+(u*(x-x0)*(x-x0)'-h0*(g-g0)'*(x-x0)'-(x-x0)*(g-g0)*h0)/((x-x0)'*(g-g0)')x0=x;g0=g;h0=h;k=k+1;endendpowell算法:例子:fun=x1^2+2*x2^2-4*x1-2*x1*x2function [x]=powell(fun,x0,e)[n,m]=size(x0);e=eye(n);flag=0;for j=1:ns(:,j)=e(:,j);endwhile(k==0 & flag==0)xx=x0;while(k<n)r=search(fun,xx,s(:,k+1));x(:,k+1)=xx+r*s(:,k+1);xx=x(:,k+1);k=k+1;endflag=flag+1;while(norm(x(:,n)-x0)>=e)d=fx(fun,x0)-fx(fun,x(:,1));for i=1:n-1f=fx(fun,x(:,i+1));f0=fx(fun,x(:,i));if((f0-f)>d)d=f0-f;endendf1=fx(fun,x0);f2=fx(fun,x(:,n));f3=fx(fun,(2*x(:,n)-x0));if((2*d) >= (f1-2*f2+f3))ss=x(:,n)-x0;for i=1:n-1s(:,i)=s(:,i+1);ends(:,n)=ss;elsex0=x(:,n);k=0;flag=0;break;endr=search(fun,x(:,n),ss);x0=x(:,n)+r*ss;k=0;flag=0;break;endx=x(:,n);惩罚函数(外点法)乘法因子:function [p]=chengfayinzi(g,h,x) syms x1 x2 x3 x4 x5;xk=[x1;x2;x3;x4;x5];s=length(x);m=length(g);n=length(h);k=n+m;p=x1-x1;for i=1:kif i<=ngj(i)=h(i).^2;elseq=g(i-n);for j=1:sy(j)=subs(q,xk(j),x(j));q=y(j);enda=double(q);if a<=0gj(i)=x1-x1;elsegj(i)=g(i-n).^2;endendp=p+gj(i);end惩罚函数:function [x]=chengfahanshu(f,g,h,x0,e) n=length(x0);syms x1 x2 x3 x4 x5;xk=[x1;x2;x3;x4;x5];M=1;c=10;p=chengfayinzi(g,h,x0);fun=f+M*p;x=dfp1(fun,x0,0.001);p=chengfayinzi(g,h,x);y=fx(M*p,x);while y>=ex0=x;M=c*M;p=chengfayinzi(g,h,x0);fun=f+M*p;x=dfp1(fun,x0,0.001);p=chengfayinzi(g,h,x);y=fx(M*p,x);end碰壁函数(内点法):碰壁因子:function [b]=pengbiyinzi(g)syms x1[a,n]=size(g);b=x1-x1;for i=1:ngi(i)=-log(-g(i));b=b+gi(i);end碰壁函数:function [x]=pengbihanshu(f,g,n)m=length(g);syms x1 x2 x3 x4 x5 r;xk=[x1;x2;x3;x4;x5];b=pengbiyinzi(g)fun=f+r*bflag=0;b=0;for i=1:nfi(i)=diff(fun,xk(i));endif n==1[xx1]=solve(fi(1),'x1')l1=limit(xx1,r,0);for i=1:n %验证所求出来的结果中,哪个合法for j=1:mif fx(g(j),[l1(i);l2(i)])<=0b=1;elseb=0;endendif b==1breakendendx=[double(l1(i))];elseif n==2[xx1,xx2]=solve(fi(1),fi(2),'x1','x2');l1=limit(xx1,r,0);l2=limit(xx2,r,0);for i=1:nfor j=1:mif fx(g(j),[l1(i);l2(i)])<=0b=1;elseb=0;endendif b==1breakendendx=[double(l1(i));double(l2(i))];elseif n==3[xx1,xx2,xx3]=solve(fi(1),fi(2),fi(3),'x1','x2','x3') l1=limit(x1,r,0);l2=limit(x2,r,0);l3=limit(x3,r,0);for i=1:nfor j=1:mif fx(g(j),[l1(i);l2(i)])<=0b=1;elseb=0;endendif b==1breakendendx=[double(l1(i));double(l2(i));double(l3(i))]; end。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优化方法程序作业专业:油气储运工程班级:姓名:学号:一、开发工具该应用程序采用的开发工具是Visual studio 2005,编程语言使用的是C#。
二、程序代码(1)0.618法和抛物线法求ψ(t)=sint,初始点t0=1①主程序:using System;using System.Data;using System.Configuration;using System.Web;using System.Web.Security;using System.Web.UI;using System.Web.UI.WebControls;using System.Web.UI.WebControls.WebParts;using System.Web.UI.HtmlControls;using System.Collections;public partial class_Default : System.Web.UI.Page{JiSuan JS = new JiSuan();protected void Button1_Click(object sender, EventArgs e){double xx0 = 0.01;//步长double tt0 = 1, pp = 2, qq = 0.5;ArrayList list1 = new ArrayList();list1 = (ArrayList)JS.SuoJian(xx0, tt0, pp, qq);//调用倍增半减函数double aa = double.Parse(list1[0].ToString());double bb = double.Parse(list1[1].ToString());txtShangxian.Text = bb.ToString();//在页面上显示极小区间txtXiaxian.Text = aa.ToString();ArrayList list2 = new ArrayList();list2 = (ArrayList)JS.JiXiao1(aa, bb);//调用0.618法函数double jixiao1 = double.Parse(list2[0].ToString());double fjixiao1 = double.Parse(list2[1].ToString());txtJixiao1.Text = jixiao1.ToString();//在页面上显示极小点txtFjixiao1.Text = fjixiao1.ToString();//在页面上显示极小点处的函数值ArrayList list3 = new ArrayList();list3 = (ArrayList)JS.JiXiao2(aa, bb);//调用抛物线法函数double jixiao2 = double.Parse(list3[0].ToString());double fjixiao2 = double.Parse(list3[1].ToString());txtJixiao2.Text = jixiao2.ToString();//在页面上显示极小点txtFjixiao2.Text = fjixiao2.ToString();//在页面上显示极小点处的函数值 }}②各个子函数的程序:using System;using System.Data;using System.Configuration;using System.Web;using System.Web.Security;using System.Web.UI;using System.Web.UI.WebControls;using System.Web.UI.WebControls.WebParts;using System.Web.UI.HtmlControls;using System.Collections;///<summary>/// JiSuan 的摘要说明///</summary>public class JiSuan{public JiSuan(){//// TODO: 在此处添加构造函数逻辑//}//目标函数public double f(double z){double zz = Math.Sin(z);return zz;}//倍增半减函数public ArrayList SuoJian(double x0, double t0, double p, double q){double t1;double f0, f1;double x1, t2;double f2;double a = 0, b = 0, c = 0;double fa, fc, fb;double t3, f3;bool biaozhi1 = true;//设置是否循环的标志bool biaozhi2 = true;t1 = t0 + x0;f0 = f(t0);//调用目标函数f1 = f(t1);if (f0 > f1){while (biaozhi1){x1 = p * x0;t2 = t1 + x1;f2 = f(t2);//调用目标函数if (f1 > f2){t0 = t1;t1 = t2;f0 = f1;f1 = f2;continue;}else{a = t0;c = t1;b = t2;fa = f0;fc = f1;fb = f2;break;}}}else{t3 = t1;f3 = f1;t1 = t0;f1 = f0;t0 = t3;f0 = f3;while (biaozhi2){x1 = q * x0;t2 = t1 - x1;f2 = f(t2);//调用目标函数if (f1 > f2){t0 = t1;t1 = t2;f0 = f1;f1 = f2;continue;}else{a = t2;c = t1;b = t0;fa = f2;fc = f1;fb = f0;break;}}}ArrayList list = new ArrayList();list.Add(a);list.Add(b);return list;}//0.618法函数public ArrayList JiXiao1(double a, double b) {double jd = 0.0001;//精度double p = 0.618;double t1, t2;double f1, f2;double jixiao=0;//极小点bool biaozhi1 = true;//设置是否循环标志bool biaozhi2 = true;while (biaozhi1){t1 = a + (1 - p)*(b - a);t2 = a + p * (b - a);f1 = f(t1);//调用目标函数f2 = f(t2);while (biaozhi2){if (f1 < f2){b = t2;t2 = t1;f2 = f1;t1 = a + (1 - p)*(b - a); f1 = f(t1);//调用目标函数if (Math.Abs(b - a) > jd) {continue;}else{biaozhi1 = false;break;}}else if (f1 == f2){a = t1;b = t2;if (Math.Abs(b - a) > jd) {break;}else{biaozhi1 = false;break;}}else if (f1 > f2){a = t1;t1 = t2;f1 = f2;t2 = a + p * (b - a);f2 = f(t2);//调用目标函数if (Math.Abs(b - a) > jd){continue;}else{biaozhi1 = false;break;}}}}jixiao = (a + b) / 2;double fjixiao = f(jixiao);//调用目标函数ArrayList list = new ArrayList();list.Add(jixiao);list.Add(fjixiao);return list;}//抛物线法函数public ArrayList JiXiao2(double a, double b){double jd = 0.0001;//精度double c = a + (b - a) / 2;//将c的值设为a、b点的中点double fa, fb, fc, c1, c2;double jixiao = 0;//极小点double ta, fta;double fac;bool biaozhi1 = true;//设置是否循环标志while (biaozhi1){fa = f(a);//调用目标函数fb = f(b);fc = f(c);c1 = (fb - fa) / (b - a);c2 = ((fc - fa) / (c - a) - c1) / (c - b);if (c2 == 0){jixiao = c;break;}else{ta = 0.5 * (a + b - (c1 / c2));fta = f(ta);//调用目标函数if (Math.Abs(b - a) <= jd){jixiao = ta;break;}else{if (fc > fta){if (c > ta){b = c;fb = fc;c = ta;fc = fta;continue;}else{a = c;fa = fc;c = ta;fc = fta;continue;}}else if (fc == fta){if (c > ta){a = ta;b = c;c = (c + ta) / 2;fa = fta;fb = fc;fc = f(c);//调用目标函数continue;}else if (c == ta){fac = f((a + c) / 2);//调用目标函数if (fac < fc){c = (a + c) / 2;fc = f(c);//调用目标函数b = ta;fb = fta;continue;}else{a = (a + c) / 2;fa = f(a);//调用目标函数continue;}}else if (c < ta){a = c;c = (c + ta) / 2;b = ta;fa = fc;fb = fta;fc = f(c);//调用目标函数continue;}}else if (fc < fta){if (c > ta){a = ta;fa = fta;continue;}else{b = ta;fb = fta;continue;}}}}}double fjixiao = f(jixiao);//调用目标函数ArrayList list = new ArrayList();list.Add(jixiao);list.Add(fjixiao);return list;}}(2)共轭梯度法求函数极小点:f(x)=1.5x12+0.5x22-x1x2-2x1;初始点为(-2,4)①主程序:using System;using System.Data;using System.Configuration;using System.Web;using System.Web.Security;using System.Web.UI;using System.Web.UI.WebControls;using System.Web.UI.WebControls.WebParts;using System.Web.UI.HtmlControls;using System.Collections;public partial class_Default : System.Web.UI.Page{JiSuan JS = new JiSuan();protected void Button1_Click(object sender, EventArgs e){//共轭梯度法求极小值double[] x0 = new double[2];//定义二维数组double[] x = new double[2];x0[0] = -2;x0[1] = 4;double x00 = -2;double x01 = 4;double jd = 0.0001;//精度bool biaozhi1 = true;//设置是否循环的标志bool biaozhi2 = true;double y;//定义关于x的函数值double[] g = new double[2];//定义函数在点x处的梯度值double[] p = new double[2];double ggm, ggo=0;double jixiao;double x1=0, x2=0, fy=0;int i;for (int j = 0; j < 2; j++){x[j] = x0[j];}while (biaozhi1){i = 0;while (biaozhi2){y = JS.f(x[0], x[1]);//调用目标函数g[0] = JS.g0(x[0], x[1]);//调用梯度函数,求在点x处的梯度值 g[1] = JS.g1(x[0], x[1]);ggm = g[0] * g[0] + g[1] * g[1];if (ggm <= jd){x1 = x[0];x2 = x[1];fy = y;biaozhi1 = false;break;}else{if (i == 0){p[0] = -g[0];p[1] = -g[1];}else{p[0] = -g[0] + (ggm / ggo) * p[0];p[1] = -g[1] + (ggm / ggo) * p[1];}//调用0.618法子函数,找出极小点jixiao = JS.JiXiao1(x[0], x[1], p[0], p[1], x00, x01); x[0] = x[0] + jixiao * p[0];x[1] = x[1] + jixiao * p[1];ggo = ggm;i++;if (i >= 2){break;}else{continue;}}}}txtx1.Text = x1.ToString();txtx2.Text = x2.ToString();txty.Text = fy.ToString();}}②子函数程序:using System;using System.Data;using System.Configuration;using System.Web;using System.Web.Security;using System.Web.UI;using System.Web.UI.WebControls;using System.Web.UI.WebControls.WebParts;using System.Web.UI.HtmlControls;using System.Collections;///<summary>/// JiSuan 的摘要说明///</summary>public class JiSuan{public JiSuan(){//// TODO: 在此处添加构造函数逻辑//}//目标函数public double f(double z1,double z2){double zz = 1.5 * z1 * z1 + 0.5 * z2 * z2 - z1 * z2 - 2 * z1;return zz;}//求梯度值函数public double g0(double z1, double z2){double zz = 3 * z1 - z2 - 2;return zz;}public double g1(double z1, double z2){double zz = z2 - z1;return zz;}//倍增半减函数public ArrayList SuoJian(double x0, double t0, double p, double q, double xx0, double xx1, double p0, double p1,double x00,double x01){double t1;double f0, f1;double x1, t2;double f2;double a = 0, b = 0, c = 0;double fa, fc, fb;double t3, f3;bool biaozhi1 = true;//设置是否循环的标志bool biaozhi2 = true;double x_0t1, x_1t1, x_0t2, x_1t2;x_0t1 = xx0 + t1 * p0;x_1t1 = xx1 + t1 * p1;f0 = f(x00, x01);//调用目标函数f1 = f(x_0t1, x_1t1);if (f0 > f1){while (biaozhi1){x1 = p * x0;t2 = t1 + x1;x_0t2 = x_0t1 + t2 * p0;x_1t2 = x_1t1 + t2 * p1;f2 = f(x_0t2, x_1t2);//调用目标函数if (f1 > f2){t0 = t1;t1 = t2;f0 = f1;f1 = f2;continue;}else{a = t0;c = t1;b = t2;fa = f0;fc = f1;fb = f2;break;}}}else{t3 = t1;f3 = f1;t1 = t0;f1 = f0;t0 = t3;while (biaozhi2){x1 = q * x0;t2 = t1 - x1;x_0t2 = x_0t1 + t2 * p0;x_1t2 = x_1t1 + t2 * p1;f2 = f(x_0t2, x_1t2);//调用目标函数if (f1 > f2){t0 = t1;t1 = t2;f0 = f1;f1 = f2;continue;}else{a = t2;c = t1;b = t0;fa = f2;fc = f1;fb = f0;break;}}}ArrayList list = new ArrayList();list.Add(a);list.Add(b);return list;}//0.618法函数public double JiXiao1(double x0, double x1, double p0, double p1,double x00,double x01){double jd = 0.0001;//精度double p = 0.618;double t1, t2;double jixiao = 0;//极小点bool biaozhi1 = true;//设置是否循环标志bool biaozhi2 = true;double xx0 = 0.01;//步长double tt0 = 0, pp = 2, qq = 0.5;double x_0t1, x_1t1, x_0t2, x_1t2;ArrayList list1 = new ArrayList();//调用倍增半减函数获取极小区间list1 = (ArrayList)SuoJian(xx0, tt0, pp, qq, x0, x1, p0, p1, x00, x01);double a = double.Parse(list1[0].ToString());double b = double.Parse(list1[1].ToString());while (biaozhi1){t1 = a + (1 - p) * (b - a);t2 = a + p * (b - a);x_0t1 = x00 + t1 * p0;x_1t1 = x01 + t1 * p1;x_0t2 = x_0t1 + t2 * p0;x_1t2 = x_1t1 + t2 * p1;f1 = f(x_0t1, x_1t1);//调用目标函数f2 = f(x_0t2, x_1t2);while (biaozhi2){if (f1 < f2){b = t2;t2 = t1;f2 = f1;t1 = a + (1 - p) * (b - a);x_0t1 = x00 + t1 * p0;x_1t1 = x01 + t1 * p1;f1 = f(x_0t1, x_1t1);//调用目标函数if (Math.Abs(b - a) > jd){continue;}else{biaozhi1 = false;break;}}else if (f1 == f2){a = t1;b = t2;if (Math.Abs(b - a) > jd){break;}else{biaozhi1 = false;break;}}else if (f1 > f2){a = t1;t1 = t2;f1 = f2;t2 = a + p * (b - a);x_0t2 = x_0t1 + t2 * p0;x_1t2 = x_1t1 + t2 * p1;f2 = f(x_0t2, x_1t2);//调用目标函数if (Math.Abs(b - a) > jd){continue;}else{biaozhi1 = false;break;}}}}jixiao = (a + b) / 2;return jixiao;}}三、程序运行界面及结果(1)0.618法和抛物线法求ψ(t)=sint,初始点t0=1(2)共轭梯度法求函数极小点:f(x)=1.5x12+0.5x22-x1x2-2x1;初始点为(-2,4)。
