傅里叶变换的性质及常用函数的傅里叶变换

常用傅立叶变换表完整版

常用傅立叶变换表
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
18
δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换
19 变换23的频域对应
20 由变换3和24得到.
21
由变换1和25得到，应用了:
时域信号
弧频率表示的傅里叶变换
注释
1线性
2 时域平移
3 频域平移, 变换2的频域对应
4
如果
值较大，则
会收缩到
原点附近，而会扩散并变得扁平. 当 | a | 趋向无穷时，成为 Delta 函数。

5 傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示和的卷积 — 这就是 9
和归一化的 10 变换10的频域对应。

矩形函数是理想的低通滤波器，是这类滤波器对冲击的响应。

11
tri 是 12 变换12的频域对应 13 exp( αt 2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时，这是可积的。

14
15
16 a>0
17
变换本身就是一个公式。

傅里叶变换及其性质

αt
1
单边指数函数e-αt; (b) e-αt
的幅度谱
o
(b)
F(j) f(t)ejtdt etejtdt
01 02 e(j)t (j)
01j
1
ja rcta n
ea
a22
其振幅频谱及相位频谱分
解
别为
F ( ) 1
2 2
( ) arctan
例 2.4-3 求图 2.43(a)所示双边指数函数的频谱函数。
02 或
2
B
2(rad/s)
1
Bf
(Hz)
周期信号的能量是无限的，而其平均功率是有界的，因而周期信号是功率信号。为了方便，往往将周期信号在1Ω电阻上消耗的平均功率定义为周期信号的功率。显然，对于周期信号f(t)，无论它是电压信号还是电
流信号，其平均功率均为 T
12 2
P f (t)dt 2.3.3 周期信号的功率T T2
( )
02
－
4
－
2
o
门函数； (b) 门函数的频谱；－ 4(c)－幅2 度谱； (d) 相位谱
o 2 4
2 4
－
(c)
(d )
f
(t)
e at
0
f (t)
例 2.4-2 求指数函数f(t)
的1频谱函数。 e－t (＞0)
o
t
(a)
t 0 ( 0)
t 0
图 2.4-2 单边指F(数)函数e-
性。
2.2 周期信号的连续时间傅里叶级数
f (t) Fnejnt
2.2.1 指数形式的傅里叶级数 n
满足Dirichlet条件的周期函数可以展成复指数形式的傅里叶级数:

常用傅里叶逆变换公式

常用傅里叶逆变换公式傅里叶变换和逆变换是信号处理领域中非常基础的数学工具。

在现代数字信号处理领域中，它们被广泛应用于信号滤波、数据压缩和频谱分析等方面。

作为傅里叶变换的逆运算，傅里叶逆变换起着重要的作用。

在这篇文章中，我们将详细介绍一些常用的傅里叶逆变换公式，并说明它们在实际应用中的作用。

傅里叶逆变换的定义在深入讨论傅里叶逆变换公式之前，我们需要先了解一下傅里叶逆变换的定义。

傅里叶逆变换是指将复频域信号转换成复时域信号的过程。

与傅里叶变换不同的是，逆变换是不可逆的。

即使我们进行完傅里叶逆变换之后，再进行傅里叶变换，也不能恢复原来的复频域信号。

傅里叶逆变换的数学表达式如下：$$x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(j\omega)e^{j\omega t}d\omega$$其中，$x(t)$是时域信号，$X(j\omega)$是傅里叶变换后的频域信号，$j$是虚数单位，$\omega$是频率，$t$是时间。

这个公式的意思是，我们可以通过对傅里叶变换后的复频域信号做积分，得到复时域信号$x(t)$。

傅里叶逆变换的性质在实际应用中，我们常常需要使用傅里叶逆变换公式对信号进行处理。

为了更好地利用傅里叶逆变换公式，我们需要了解一些它的性质。

下面是一些常见的性质：1. 线性性质：傅里叶逆变换具有线性性，即如果$x_1(t)$的傅里叶变换是$X_1(j\omega)$，$x_2(t)$的傅里叶变换是$X_2(j\omega)$，那么$ax_1(t)+bx_2(t)$的傅里叶逆变换就是$aX_1(j\omega)+bX_2(j\omega)$。

2. 时移性质：如果$x(t)$的傅里叶变换为$X(j\omega)$，那么$x(t-t_0)$的傅里叶逆变换就是$e^{-j\omega t_0}X(j\omega)$，其中$t_0$是一个常数。

3. 频移性质：如果$x(t)$的傅里叶变换为$X(j\omega)$，那么$x(t)e^{j\omega_0t}$的傅里叶逆变换就是$X(j(\omega-\omega_0))$，其中$\omega_0$是一个常数。

常用的连续傅里叶变换对及连续傅里叶变换性质

ωτ
2
)
ωc
π
Sa(ωc t )
⎧ 1, ω < ωc ⎪ ⎪0, ω ≥ ωc ⎩
√
√
三角 f (t ) = ⎨
⎧1 − t τ , t < τ ⎪ t ≥τ ⎪0, ⎩
τ Sa 2 (
ωτ
2
)
ωc
2π
Sa 2 ( 1
ωc t
2
)
⎧1 − ω ωc , ω < ωc ⎪ F (ω ) = ⎨ ω ≥ ωc ⎪0, ⎩
√ √ √ √
F (t ) ↔ 2πf (−ω )
f (t )e jω0 t (− jt ) f (t ) πf (0)δ (t ) + f (t ) p(t ) f (t ) − jt F (ω − ω 0 ) F '(ω )
f (t − t 0 )
f '(t )
F (ω )e − jωt0 jω F (ω ) πF (0)δ (ω ) + F (ω ) jω
T1
T T ⎤ ⎡ f 0 (t ) = f ( t ) ⎢ u (t + 1 ) − u ( t − 1 ) ⎥ ↔ F0 (ω ) 2 2 ⎦ ⎣
连续傅里叶变换性质及其对偶关系
f (t ) = 1 +∞ F (ω )e jωt dω 2π ∫3;∞
−∞
f (t )e − jωt dt
⎣ 2 2 ⎦
(ω + ω0 )τ (ω − ω0 )τ ⎤ + Sa ⎥ 2 2 ⎦
+∞
f (t ) =
n =−∞
∑ F (nω )e
1
+∞
jnω1t

信息光学基础1-6傅里叶变换性质

2
f
b 2

e
j
2
f
b 2
]
Hale Waihona Puke j2 f b e j2 fa sin( bf ) bf
b e j2 fa sin c(bf )
解法二：比例和位移性质
F sin(2
f0 x)

1 2j
[d (
fx

f0 )
d
(
fx

f0 )]
F cos(2
f0 x)
b
解法一：根据傅里叶变换的定义
F 1{rect( x a )} rect( x a ) e j2 fx dx
b

b
b 2

a
e j2 fxdx

b 2
a
j 2 fx
b 2

a
[e ]
b 2

a
j2 f
e j2 fa

[e
j
d(x)
x

d (x a)g(x)dx g(a)
d(x)函数的筛选性质

1 ei2 fxdf d (u)

2）rect 函数的傅里叶变换
f
(x,
y)

rect(x,
y)

1
0
x

1 2
,
y

1 2
其它
解：F{rect(x)}

rect(x)exp(i2 fx)dx

1 2
(ei 2
f0x

ei 2
) f0 x
1 F{ei2 f0x} 1 F{ei2 } f0x

傅里叶变换的性质以及光学中一些函数的F.T.变换式

广义Fourier 变换：函数不严格满足存在条件，但是函数可定义另一函数所组成的序列的极限，序列中的函数有Ｆ.Ｔ.；对组成序列的每一个函数进行变换，就产生一个相应的变换序列，该新序列的极限即为原函数的广义Ｆ.Ｔ.g ( x, y ) = lim f N ( x, y ) ℑ{ f N ( x, y )} = FN ( f x , f y )N →∞ N →∞lim FN ( f x , f y ) = ℑ{ g ( x, y )} = G ( f x , f y )ℑ{δ ( x, y )}lim ℑ{ N exp(−N π (x + y ))} = limexp(−2 2 2 2 N→∞π ( f x2 + f y 2 )2N→∞N fy ⎫ ⎧ 1 fx 1 2 lim ℑ{ N rect(Nx)rect(Ny)} = lim ⎨N ⋅ sin c( )N ⋅ sin c( )⎬ =1 N→∞ N→∞ N N N ⎭ ⎩ N fy ⎫ ⎧ 1 fx 1 lim ℑ{ N sin c(Nx)sin c(Ny)} = lim ⎨N ⋅ rect( )N ⋅ rect( )⎬ =1 N→∞ N→∞ N N N ⎭ ⎩ N2) =1δ−function Properties 1．筛选性(定义性质)∞ −∞∫ g ( x)δ ( x − x ) dx = g ( x )0 0δ ( x − x0 ) = 0, x ≠ x02．尺度缩放性质δ (ax) =3．偶函数x 1 1 δ ( x), δ (ax − x0 ) = δ ( x − 0 ) a a aδ ( x ) = δ ( − x ) , δ ( − x + x 0 ) = δ ( x − x0 )3．乘积性质g ( x)δ ( x − x0 ) = g ( x0 )δ ( x − x0 ); xδ ( x − x0 ) = x0δ ( x − x0 )４．积分性质∞−∞∫ Aδ ( x − x ) dx = A0∞−∞∫ δ ( x − x ) dx = 10５．卷积性质g ( x) ∗ δ ( x − x0 ) = g ( x − x0 )卷积定义∞f ( x) ∗ h( x) =−∞∫ f (a)h(x − a)da反转,平移,相乘,积分卷积在光学中的应用卷积表示一输出，在光学上就表示成像系统的像分布；对于线性空间不变光学系统，其输出的信息可表示为输入信息g与系统脉冲响应函数h（系统对点源的响应）的卷积的响应x0处点源：I 0 Δξ 对应的像强度分布P( xi − x0 )输出像：I i ( xi ) = I 0 Δξ P ( xi ) + I 0 Δξ P( xi − ξ 1 ) +KΔξ → 0：I i ( xi ) = ∫ I 0 (ξ ) P( xi − ξ )d ξ二维：g(x, y)表示物（输入信息）； h(x,y)表示系统对点源的响应（点扩散函数、脉冲响应函数）输出=g( x, y ) ∗ h(x,y)卷积的性质１．符合交换律g ( x,y ) ∗ h( x, y ) = h( x, y ) ∗ g ( x,y )２．函数平移不变性f ( x, y ) ∗ h ( x, y ) = g ( x, y ) ↔ f ( x − x0 , y − y0 ) ∗ h( x, y ) = g ( x − x0 , y − y0 )３．线性运算(af + bh) ∗ g = af ∗ g + bh ∗ g4．δ函数的卷积f ( x, y )* δ ( x, y ) = f ( x, y )δ 函数与任何函数卷积仅重新产生该函数严格再生 5．光滑作用脉冲响应函数h是对光学系统性能的定量评价。

常见的傅里叶变换+定理+各种变换的规律(推荐)

= exp[- πu2]
= Gaus(u)
结论：
Gaus（x） F.T. Gaus（u）
7
五、余弦函数的傅里叶变换
F [cos（2πu0x） ] 其中 u0 = 1 / Τ Τ 为周期 ∞
= ∫ [cos2πu0 x ]• exp[− j2πux]dx
−∞
∫ =
∞ −∞
1 2
[exp(
j
2πu0
x)
x a

= a sin(πau) πau
= a sinc(au)
证明：根据相似性定理
6
四、高斯函数的傅里叶变换
Gaus(x) = exp[- πx2]
推导一维情况
F [Gaus(x) ]= F { exp[- πx2]}
∞
= ∫ exp[-πx2 ]• exp[− j2πux]dx −∞
−∞ 1/ 2
= ∫ exp(− j2πux)dx
rect
x a

=
1, 0,
−1/ 2
=1
1/2
exp(− j2πux)
− j2πu

-1/2
= sin(πu) πu
结论：
x ≤a 2
其它
= sinc(u) rect（x） F.T. sinc（u）
5
普遍型
F
rect
˄অ㕍㹽ሴˈ㕍ゴ㹽ሴਈᇭ˅
˄˅ս〫ᇊ⨶˖ྲ᷌ F^g x ` G fx
ࡉᴹ F^g x a ` G fx exp j2Sfxa
࠭ᮠ൘オฏѝⲴᒣ〫ˈᑖᶕ仁ฏѝⲴ⴨〫
਼ᰦ F^g x exp j2Sfax ` G fx fa ࠭ᮠ൘オฏѝⲴ⴨〫ˈᑖᶕ仁ฏѝⲴᒣ〫

付立叶变换及其性质

傅里叶变换的性质这里主要介绍二维离散傅里叶变换（DFT ，discrete FT ）中的几个常用性质（可分离线、周期性和共轭对称性、平移性、旋转性质、卷积与相关定理）：可分离性二维离散傅立叶变换DFT 可分离性的基本思想是二维DFT 可分离为两次一维DFT 。

因此可以用通过计算两次一维的FFT 来得到二维快速傅立叶变换FFT 算法。

根据快速傅里叶变换的计算要求，需要图像的行列数均满足2的n 次，如果不满足，在计算FFT 之前先要对图像补零以满足2的n 次。

一个M 行N 列的二维图像f(x,y)，先按行对列变量y 做一次长度为N 的一维离散傅里叶变换，再将计算结果按列向对变量x 做一次长度为M 傅里叶变换就可以得到该图像的傅里叶变换结果，如下式所示：()()()()∑∑-=-=-⎥⎥⎦⎤⎢⎢⎣⎡-=10102exp 2exp ,1,M x N y M ux j N vy j y x f MN v u F ππ 将上式分解开来就是如下两部分，首先得到F(x,v)再由F(x,v)得到F(u,v)：∑-=-=-=101...10]/2exp[),(1),(N y N v N vy j y x f N v x F ，，，π∑-=-=-=101,...,1,0,]/2exp[),(1),(N x M v u M ux j v x F M v u F πu=0,1,2,…M-1；v=0,1,2,...N-1计算过程如下图所示：每一行有N 个点，对每一行的一维N 点序列进行离散傅里叶变换得到F(x,u)，再对得到F(x,u)按列向对每一列做M 点的离散傅里叶变换，就可以得到二维图像f(x,y)的离散傅里叶变换F(u,v)同样，做傅里叶逆变换时，先对列向做一维傅里叶逆变换，再对行做一维逆傅里叶变换，如下式所示：()()()()∑∑-=-=⎥⎦⎤⎢⎣⎡=10102exp 2exp ,,M u N v M ux j N vy j v u F y x f ππ x=0,1,2,…M-1；y=0,1,2,...N-1周期性和共轭对称性由傅里叶变换的基本性质可以知道，离散信号的频谱具有周期性。

第8章傅立叶变换

å
-
¥
cneinw0t
cn = F (nw) fT (t )的离散频谱； cn arg cn fT (t )的离散振幅频谱； fT (t )的离散相位频谱； n 蝂 .
若以fT (t )描述某种信号，则cn可以刻画 fT (t )的频率特征。
§8.1.2 付氏积分与付氏变换
1.傅里叶积分公式
对任何一个非周期函数f(t)都可以看成是由某个周期函数fT(t)当T时转化而来的. 作周期为T的函数fT(t), 使其在[-T/2,T/2]之内等于 f(t), 在[-T/2,T/2]之外按周期T延拓到整个数轴上, 则T越大, fT(t)与f(t)相等的范围也越大, 这就说明当 T时, 周期函数fT(t)便可转化为f(t), 即有
+?
sin x dx= x
F (w)
w = kpw
ì1 ï 例求函数 f (t ) = ï í ï0 ï î
t<c t> c
jw t
(c > 0) 的傅氏变换
解 F (w) =
ò
+c - c
+
f (t )e-
dt
+c
-
=
蝌
e
- j wt
dt = 2
0
e-
j wt
dt
积分表达式。
F ( w) =
蝌
- ?
+
f (t )e
- iwt
d
dt =
d
e
- iwt
e dt = - iw - d
- iwt d
1 - iwd 2d sin dw iwd =(e - e ) = dw iw
1 +? 1 iwt f (t ) = 蝌 F (w)e d w = p 2p 1 + ? 2sin w 2 = 蝌 cos wtd w = p 0 w p 0 F (w)cos wtd w

傅里叶变换的基本性质与常用函数的傅里叶变换

1FoFo
2
f (t)sinot
j FoFo
时域微分
df(t) dt
j F
dnf(t) dtn
n
j F
频域微分
jtf (t)
dF
d
n
jt f(t)
dnF
dn
时域积分
t
f( )d
1
—FF o
j
时域卷积
fi(t)f2(t)
F1F2
乘积与卷积
频域卷积
fl(t) f2(t)
—F1F2
2
t
2t
时域抽样
ftt nTo
精选文档
傅里叶变换的基本性质
性质
时域
频域
时频域对应关系
线性
n
aifi(t)
i1
n
aF()
i 1
线性叠加
对称性
F(t)
2 f()
对称
尺度变换
f(at)
1
口F（一）囘a
压缩与扩展
f( t)
F()
反褶
时移
f (tto)
F( )ej to
时移与相移
频移
f (t)ej ot
F(o)
调制与频移
f (t)cosot
n
12 n
F
To nT)
抽样与重复
频域抽样
1上2 n
—f t——
0 n0
Fn0
n
相关
R12
R21
FiF2
FiF2
自相关
R
|F|2
常用信号的傅里叶变换表
信号名称
时间函数
频谱函数
单边指数脉冲
eatu t a 0

傅里叶变换经济学

傅里叶变换经济学一、引言傅里叶变换是一种在数学、物理和工程领域广泛应用的工具，它可以将复杂的周期性信号分解为一系列正弦波的线性组合。

近年来，随着计算机技术的发展，傅里叶变换在经济学中的应用也逐渐增多。

本文将介绍傅里叶变换在经济学中的一些应用。

二、傅里叶变换的基本原理傅里叶变换的基本原理是将一个函数分解为一系列正弦波的线性组合。

对于一个实数函数f(t)，其傅里叶变换可以表示为：F(ω) = ∫f(t)e^(-iωt) dt其中，ω是角频率，i是虚数单位。

傅里叶变换的逆变换是将F(ω)还原为f(t)。

三、傅里叶变换在经济学中的应用1. 时间序列分析时间序列分析是研究时间序列数据的统计性质和规律的方法。

在经济学中，时间序列数据通常用来分析经济现象的时间趋势和周期性变化。

傅里叶变换可以将时间序列数据分解为一系列正弦波的线性组合，从而揭示其周期性成分和趋势。

通过分析傅里叶变换的结果，可以了解经济现象的周期性特征和未来趋势。

2. 金融市场波动性分析金融市场的波动性是指市场价格的波动程度。

傅里叶变换可以用于分析金融市场的波动性。

通过计算市场价格的傅里叶变换，可以得到市场价格的频谱分布。

频谱分布可以反映市场价格的波动性特征，从而帮助投资者了解市场的风险和机会。

3. 金融风险管理金融风险管理是金融机构控制风险、防止不良贷款发生的重要一环。

傅里叶变换可以用于金融风险管理中的信用风险评估。

通过分析借款人的历史信用数据，可以得到其信用风险的傅里叶变换结果。

通过比较不同借款人的傅里叶变换结果，可以发现潜在的高风险借款人，从而采取相应的风险管理措施。

4. 货币政策制定货币政策是中央银行通过调整货币供应量和利率等手段来影响经济活动的一种政策。

傅里叶变换可以用于货币政策制定中的经济周期分析。

通过分析经济数据的傅里叶变换结果，可以了解经济周期的波动特征和未来趋势，从而为货币政策制定提供科学依据。

四、结论傅里叶变换作为一种强大的数学工具，在经济学中有着广泛的应用。

§3-5 傅里叶变换的性质

FT x(t ) ←⎯→ X ( jΩ )
FT x ( t ) e jΩ 0 t ← ⎯→ X [ j ( Ω − Ω 0 )]
ℱ x ( t ) e jΩ 0 t
{
} = ∫ x (t ) e
−∞
∞
∞
jΩ 0 t
e − j Ω t dt =
−∞
∫
x ( t ) e − j ( Ω − Ω 0 ) t dt
19
设
X ( jΩ) = X ( jΩ) e jϕ( Ω ) = X R (Ω) + jX I (Ω)
X * ( jΩ) = X ( jΩ) e − jϕ( Ω ) = X R (Ω) − jX I (Ω)
于是
X * (− jΩ) = X (− jΩ) e − jϕ( − Ω ) = X R (−Ω) − jX I (−Ω)
jtx ( t ) e
− jΩ t
dt
dX ( j Ω ) tx ( t ) ← ⎯→ j dΩ
FT
例如： du ( t )
dt
= δ (t )
对应的傅里叶变换
jΩ 1 = j 0 ⋅ πδ ( Ω ) + =1 δ(t ) ←⎯→ jΩ[πδ(Ω) + ] jΩ jΩ
FT
再例如：
1 d [πδ ( Ω ) + ] 1 jΩ FT ′ = jπ δ ( Ω ) − 2 tu ( t ) ← ⎯→ j Ω dΩ
x(t )
1
τ −2 τ 2
τ
X ( jΩ )
t
2π τ
Ω
τ
X ( jt )
x (Ω )
2π
若x(t)是偶对称的，则
FT X ( jt ) ←⎯→ 2πx(Ω)

常用的傅里叶变换+定理+各种变换的规律(推荐)

a + jω (a + jω ) 2 + ω 02
e − at sin ω 0tu (t ), Re{a} > 0
te − at u (t ), Re{a} > 0 t k −1e − at u (t ), Re{a} > 0 (k − 1)!
ω0 (a + jω ) 2 + ω 02
1 ( a + jω ) 2 1 ( a + jω ) k 1 ,τ > 0 (τ − jt ) 2 2πωe −τω u (ω )
重要
名称
连续傅里叶变换对傅里叶变换 F (ω ) 连续时间函数 f (t )
W
√
⎧ ⎪ 1, t < τ f (t ) = ⎨ ⎪ ⎩0, t > τ ⎧ ⎪1 − t τ , t < τ f (t ) = ⎨ 0, t > τ ⎪ ⎩
τSa (
ωτ
2
)
π
Sa (Wt )
⎧ ⎪ 1, ω < W F (ω ) = ⎨ ⎪ ⎩0, ω > W ⎧ ⎪1 − ω W , ω < W F (ω ) = ⎨ 0, ω > W ⎪ ⎩
㵍㬒⫇䊻㰖⳦巛㠞䄧㬒⭥䊬㰄Ⳟⳉ
㠞䄧巛㰖⳦㉚㬨ⰵ䓵⢅㑠 [ 巛 P 㡑䔘䇤᱄ 㪉
[ f ( x)] F (P ) 䋓
x0 ½ a ® f [ ( x r )]¾ a ¿ ¯ b
ax r x0 [f( )] b
x0 b b exp(r j 2S P ) F ( P ) a a a
= sinc( u)
−1 / 2
∫ exp(− j 2πux )dx
a x ≤ 2 其它

三角函数傅里叶变换常用公式大全

一、三角函数基本公式1. 正弦函数（sin）的定义：在单位圆上，角θ的终边与x轴的交点横坐标为sinθ。

1）反正弦函数（arcsin）：y = arcsin(x) ⇔ sin(y) = x，定义域为[-1, 1]，值域为[-π/2, π/2]。

2）余弦函数（cos）的定义：在单位圆上，角θ的终边与x轴的交点纵坐标为cosθ。

1）反余弦函数（arccos）：y = arccos(x) ⇔ cos(y) = x，定义域为[-1, 1]，值域为[0, π]。

3）正切函数（tan）的定义：在单位圆上，角θ的终边与x轴的交点横坐标与纵坐标的比值为tanθ。

1）反正切函数（arctan）：y = arctan(x) ⇔ tan(y) = x，定义域为(-∞, +∞)，值域为(-π/2, π/2)。

二、傅里叶级数与傅里叶变换1. 傅里叶级数公式：任意周期为2π的函数f(x)可展开为正弦和余弦函数的和。

f(x) = a0 + Σ(an*cos(nx) + bn*sin(nx))，式中，a0为直流分量，an 和bn为交流分量。

1）a0 = (1/2π) * ∫[0, 2π] f(x) dx，an = (1/π) * ∫[0, 2π] f(x) *cos(nx) dx，bn = (1/π) * ∫[0, 2π] f(x) * sin(nx) dx。

2. 傅里叶变换公式：非周期信号f(t)经过连续傅里叶变换得到频谱F(ω)。

F(ω) = ∫[-∞, +∞] f(t) * e^(-iωt) dt。

1）逆傅里叶变换：F(ω)经过逆变换得到原信号f(t)。

f(t) = (1/2π) * ∫[-∞, +∞] F(ω) * e^(iωt) dω。

三、常用傅里叶变换公式1. 矩形脉冲信号：f(t) = rect(t/T)。

1）F(ω) = T * sin(ωT) / (ωT)，其中，sinc(u) = sin(u) / u。

2. 三角形脉冲信号：f(t) = tri(t/T)。

傅里叶变换的性质及常用函数的傅里叶变换

表常用的连续傅里叶变换对及其对偶关系
连续傅里叶变换对
相对偶的连续傅里叶变换对
重要
连续时间函数
傅里叶变换
连续时间函数
傅里叶变换
重要
√
1
1
√
√
√
√
√
√
√
√
√
√
√
√
√
√
连续傅里叶变换性质及其对偶关系
连续傅里叶变换对
相对偶的连续傅里叶变换对
重要
名称
连续时间函数
傅里叶变换
名称
连续时间函数
傅里叶变换
重要
√
线性
√
尺度比例变换
对偶性
√
√
时移
频移
√
时域微分性质
频域微分性质
√
时域积分性质
频域积分性质
√
时域卷积性质
频域卷积性质
√
√
对
√
时域抽样
频域抽样
√
帕什瓦尔公式
取反----------取反
共轭----共轭取反
共轭取反---

常用傅里叶变换+定理+各种变换规律(推荐)

物理意义
= exp(−i 2πux0 )
δ ( x − x0 )
一个位于 x0 点的光脉冲
F.T.
经傅氏变换
exp(−i 2πux0 ) 一束空间频率为 u 的
单位振幅平面波
3
二、梳状函数的傅里叶变换
F [comb( x)] = comb(u)
普遍型
F
comb
x a
=
a comb(au)
二维情况
2
2
2
comb(P)
rect(x)
sinc(P)
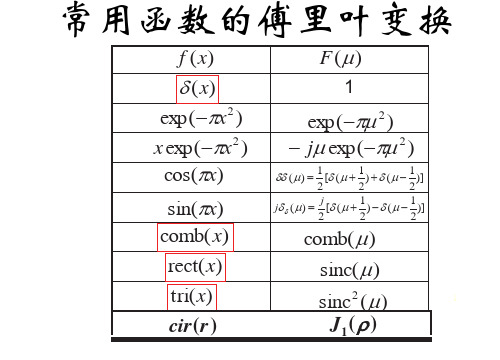
tri(x) cir (r )
sinc2 (P)
1
J1 (U )
一、δ 函数的傅里叶变换：
设： [δ ( x)] = ∆(u) ， [g( x)] = G(u)
由卷积定理知： g( x) ∗ δ ( x) = g( x)
等号两边作傅里叶变换：
F.T.
㵍㬒⫇䊻㰖⳦巛㠞䄧㬒⭥䊬㰄Ⳟⳉ 㠞䄧巛㰖⳦㉚㬨ⰵ䓵⢅㑠 [ 巛 P 㡑䔘䇤᱄
㪉 [ f (x)] F(P) 䋓
[ f (ax r x0 )] b
®f[Fra biblioteka(x
r
x0
)]½¾

¯ b a¿
b exp(r j2S x0 P) F(b P)
a
a
a
᷊᷉㘇〞ⰵ䇇⹹㻖
㪉 [ f (x)] F(P) 䋓䇱
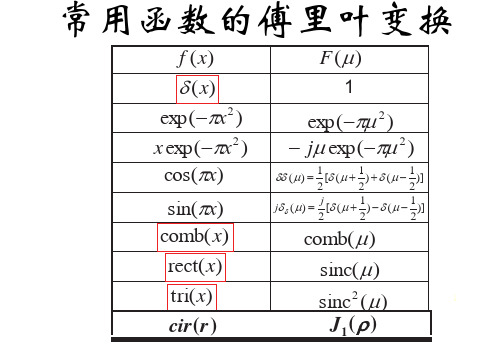
常用函数的傅里叶变换
f (x)
F(P)
G (x)
1
exp(Sx2 ) x exp(Sx2 )
exp(SP 2 ) jP exp(SP 2 )
cos(Sx)
sin(Sx)
comb( x)

傅里叶变换方法

傅里叶变换方法1. 傅里叶变换的概念傅里叶变换是一种数学工具，用于将一个函数或信号表示为一系列振幅和相位的复指数函数的和。

它可以将时域中的信号转换为频域中的信号，从而揭示出信号包含的频率成分和它们之间的关系。

傅里叶变换方法是由法国数学家约瑟夫·傅里叶在19世纪初提出的，他认为任何周期性函数都可以用一组正弦和余弦函数来表示。

这个思想被广泛应用于物理、工程、计算机科学等领域，成为了现代科学研究中不可或缺的工具。

2. 傅里叶级数与傅里叶变换傅里叶级数是指将一个周期函数表示为正弦和余弦函数的无穷级数。

它在周期性信号处理中得到广泛应用。

对于一个周期为T、连续可积的函数f(t)，其傅里叶级数定义如下：f(t)=a02+∑(a n cos(2πnTt)+b n sin(2πnTt))∞n=1其中，a0、a n和b n是系数，可以通过函数f(t)的积分计算得到。

而傅里叶变换则是将非周期函数表示为连续频谱的积分形式。

对于一个连续可积的函数f(t)，其傅里叶变换定义如下：F(ω)=∫f∞−∞(t)e−jωt dt其中，ω是频率，F(ω)表示函数f(t)在频率域中的表示。

3. 傅里叶变换的性质傅里叶变换具有许多重要的性质，这些性质使得它成为一种强大而灵活的工具。

以下是一些常见的傅里叶变换性质：•线性性质：傅里叶变换具有线性性质，即对于任意常数a和b以及两个函数f(t)和g(t)，有F(af(t)+bg(t))=aF(f(t))+bF(g(t))。

•平移性质：如果将函数在时域上平移，则其在频域上也会相应平移。

具体而言，如果f(t)经过时移得到ℎ(t)=f(t−t0)，那么它们的傅里叶变换满足H(ω)=F(ω)e−jωt0。

•尺度性质：如果将函数在时域上进行尺度变换，则其在频域上也会相应进行尺度变换。

具体而言，如果f(t)经过尺度变换得到ℎ(t)=f(at)，那么它们的傅里叶变换满足H(ω)=1|a|F(ωa)。

23傅里叶变换性质及定理(精)

e

f x e jx dx
F je jt0
时延（移位）性说明波形在时间轴上时延，不改变信号
振幅频谱，仅使信号增加一 t0 线性相位。
例2.3-1 求如图2-15所示信号 f1 t 的频谱函数 F1 ，
并作频谱图。
解
f1 t 与门函数的关系为
0

f t e j0t e jt dt

f t e j 0 t dt F 0
j0t 相乘， e 频移(调制)特性表明信号在时域中与复因子
则在频域中将使整个频谱搬移 0 。通信技术中的调制是将频谱在 0 附近的低频信号乘以e j0t ，使其频谱

f u t e jt dt d
f
1 j e d j
j

f e
d

1 j f e d j
利用积分特性可以简化由折线组成的信号频谱的求解。
例2-6 求如图2-21(a)所示 f t 的频谱函数 F 。
f t
E
/ 2
0
/2
t
（a）
解：
2 E 1 t f t 0
t t

2 2
2E / f1 t f t 2 E /
f1 t Ef t
f1 t

2
E
由上节门函数的变换
f t F Sa
0

t

2

2
再由线性与时移性，得到

常用函数的fourier变换

常用函数的fourier变换傅里叶变换是以傅里叶级数为基础的，是一种对函数进行频域处理的技术。

它将函数在时域中的表示转换为在复平面上的表示，使得函数能够被分解成一些简单的正弦和余弦波。

在数学、物理学、工程学等领域，傅里叶变换被广泛应用于信号分析、图像处理、通信等方面。

常用函数是大量傅里叶变换的基础，下面将带领你分布说明常用函数的fourier变换。

1. 对于所有实数t，f(t)=1的傅里叶变换为F(ω)=2πδ(ω)其中，δ(ω)为狄拉克函数的傅里叶变换。

δ(ω)在原点处为1，在其它位置为0，在频域中作为单位冲击项。

2. 对于所有实数t，f(t)=2πδ(t)的傅里叶变换为F(ω)=1单位冲击项在时域中作为常数项，在频域中作为单位冲击项。

3. 对于所有实数t，f(t)=cos(ω0t)的傅里叶变换为F(ω)=π[δ(ω-ω0)+δ(ω+ω0)]cos(ω0t)在时域中作为周期为2π/ω0的函数，在频域中分解成两个单位冲击项，频率分别为±ω0。

4. 对于所有实数t，f(t)=sin(ω0t)的傅里叶变换为F(ω)=jπ[δ(ω-ω0)-δ(ω+ω0)]sin(ω0t)在时域中作为周期为2π/ω0的函数，在频域中分解成两个单位冲击项，频率分别为±ω0，其中一个带有负号。

5. 对于所有实数t，f(t)=e^jω0t的傅里叶变换为F(ω)=2πδ(ω-ω0)e^jω0t在时域中作为旋转相位的函数，在频域中作为单位冲击项。

6. 对于所有实数t，f(t)=u(t-a)的傅里叶变换为F(ω)=1/jωe^-jωau(t-a)在时域中作为比a大时为1，否则为0的函数，在频域中作为1/jωe^-jωa函数。

以上就是常见函数的fourier变换，通过这些例子，我们可以更好地理解傅里叶变换，以及在信号处理和图像处理等方面的应用。

傅里叶变换的性质及常用函数的傅里叶变换

常用傅立叶变换表完整版

傅里叶变换及其性质

常用傅里叶逆变换公式

常用的连续傅里叶变换对及连续傅里叶变换性质

信息光学基础1-6傅里叶变换性质

傅里叶变换的性质以及光学中一些函数的F.T.变换式

常见的傅里叶变换+定理+各种变换的规律(推荐)

付立叶变换及其性质

第8章 傅立叶变换

傅里叶变换的基本性质与常用函数的傅里叶变换

傅里叶变换经济学

§3-5 傅里叶变换的性质

常用的傅里叶变换+定理+各种变换的规律(推荐)

三角函数傅里叶变换常用公式大全

傅里叶变换的性质及常用函数的傅里叶变换

常用傅里叶变换+定理+各种变换规律(推荐)

傅里叶变换方法

23傅里叶变换性质及定理(精)

常用函数的fourier变换

第8章傅立叶变换