矩形的折叠问题(专题)

合集下载

矩形折叠问题知识点总结

矩形折叠问题知识点总结1. 问题概述矩形折叠问题的基本情境是，给定一个长方形纸张，要求将其折叠成一个给定形状，通常是通过将纸张折叠后在两个边缘进行切割。

这个问题最早可以追溯到19世纪，由著名的数学家亨利·杜迪尼（Henri Dudeney）提出。

在这个问题中，关键点在于如何找到最优的折叠方法，使得得到的形状与目标形状最接近。

2. 解决方法矩形折叠问题涉及到了几何学、数学分析、最优化等多个学科知识，因此解决这个问题需要综合运用多种方法。

下面我将介绍一些常见的解决方法。

（1）分割法分割法是解决矩形折叠问题的一种常见方法。

首先将目标形状细分成若干个小矩形，然后将原始的长方形纸张按照这些小矩形进行折叠，最后再将边缘上多余的部分切掉，就可以得到最终的形状。

这种方法的关键在于如何将目标形状进行合理的分割，找到合适的折叠点和切割线。

（2）几何分析法几何分析法是另一种解决矩形折叠问题的常见方法。

通过对目标形状的几何特征进行分析，可以找到最优的折叠方法。

这种方法通常需要借助于数学工具，例如微积分、线性代数等，对目标形状进行数学建模，然后通过求解最优化问题，得到最佳的折叠方案。

（3）仿射变换法仿射变换法是一种比较高级的解决方法，它利用了几何变换的性质，将目标形状通过仿射变换映射成一个简单的形状，然后再将纸张按照这个简单的形状进行折叠，最后再通过逆变换将折叠后的纸张映射回原来的形状。

这种方法需要较强的数学功底和熟练的计算能力，但是可以得到非常优美的折叠结果。

3. 相关知识点解决矩形折叠问题需要涉及到很多相关的数学知识点，下面我将逐一介绍这些知识点。

（1）几何形状矩形折叠问题本质上是一个关于几何形状的问题，因此需要熟悉各种几何形状的性质，包括面积、周长、对称性等方面的知识。

在解决矩形折叠问题时，需要对目标形状进行合理的分割和组合，这就需要对几何形状的特征有深入的了解。

（2）数学分析数学分析是解决矩形折叠问题的重要数学工具，通过对目标形状进行数学建模，并利用微积分、线性代数等数学工具，可以求解最优的折叠方案。

中考数学折叠问题专项突破2—矩形的折叠问题(距离问题)

中考数学折叠问题专项突破2—矩形的折叠问题（距离问题）专题二矩形的折叠中的距离或线段长度问题【典例】在矩形纸片ABCD中，AB=3，AD=5. 如图例1-1所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动. 若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为.图例1-1 图例1-2 图例1-3【解析】此题根据题目要求准确判断出点A'的最左端和最右端位置.当点Q与点D重合时，A'的位置处于最左端，当点P与点B重合时，点A'的位置处于最右端. 根据分析结果，作出图形，利用折叠性质分别求出两种情况下的BA'或CA'的长度，二者之差即为所求.①当点Q与点D重合时，A'的位置处于最左端，如图例1-2所示.确定点A'的位置方法：因为在折叠过程中，A'Q=AQ，所以以点Q为圆心，以AQ长为半径画弧，与BC的交点即为点A'. 再作出∠A'QA的角平分线，与AB的交点即为点P.由折叠性质可知，AD= A'D=5，在Rt△A'CD中，由勾股定理得，A C==='4②当点P与点B重合时，点A'的位置处于最右端，如图例1-3所示.确定点A'的位置方法：因为在折叠过程中，A'P=AP，所以以点P为圆心，以AP长为半径画弧，与BC的交点即为点A'. 再作出∠A'P A的角平分线，与AD的交点即为点Q. 由折叠性质可知，AB= A'B=3，所以四边形AB A'Q为正方形. 所以A'C=BC－A'B=5－3=2.综上所述，点A移动的最大距离为4－2=2.故答案为：2.【小结】此类问题难度较大，主要考察学生的分析能力，作图能力。

作图的依据是折叠前后线段长度不变，据此先找到点A 的落点A '，再根据对称轴（折痕）是对应点连线的垂直平分线，确定出折痕PQ 的位置. 利用勾股定理、正方形的判定定理及其性质求得相应的线段长度.1、如图，在矩形ABCD 中，AB =2，BC =4，P 为边AD 上一动点，连接BP ，把△ABP 沿BP 折叠，使A 落在A ′处，当△A ′DC 为等腰三角形时，AP 的长为（）A ．2B ．3C ．2或3D ．2 【分析】根据△A ′DC 为等腰三角形，分三种情况进行讨论：①A 'D =A 'C ，②A 'D =DC ，③CA '=CD ，分别求得AP 的长，并判断是否符合题意．【解析】①如图，当A ′D =A ′C 时，过A ′作EF ⊥AD ，交DC 于E ，交AB 于F ，则EF 垂直平分CD ，EF 垂直平分AB∴A 'A =A 'B ，由折叠得，AB =A 'B ，∠ABP =∠A 'BP ，∴△ABA '是等边三角形，∴∠ABP =30°，∴AP =2 3333==； ②如图，当A 'D =DC 时，A 'D =2由折叠得，A 'B =AB =2，∴A 'B +A 'D =2+2=4连接BD ，则R t △ABD 中，BD =2222 2425AB AD +=+= ，∴A 'B +A 'D ＜BD （不合题意）故这种情况不存在；③如图，当CD =CA '时，CA '=2由折叠得，A 'B =AB =2，∴A 'B +A 'C =2+2=4，∴点A '落在BC 上的中点处此时，∠ABP =12∠ABA '=45°，∴AP =AB =2．综上所述，当△A′DC为等腰三角形时，AP的长为或2．故选C.【小结】本题以折叠问题为背景，主要考查了等腰三角形的性质，解决问题的关键是画出图形进行分类讨论，分类时注意不能重复，不能遗漏．2、．矩形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE的长为( )A．3 B．32C．2或3 D．3或32【分析】当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如图1所示．连结AC，先利用勾股定理计算出AC=5，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=3，可计算出CB′=2，设BE=x，则EB′=x，CE=4-x，然后在R t△CEB′中运用勾股定理可计算出x．②当点B′落在AD边上时，如图2所示．此时ABEB′为正方形．【解析】当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如图1所示．连结AC，在R t△ABC中，AB=3，BC=4，∴AC=5，∵∠B沿AE折叠，使点B落在点B′处，∴∠AB′E=∠B=90°，当△CEB′为直角三角形时，只能得到∠EB′C=90°，∴点A、B′、C共线，即∠B沿AE折叠，使点B落在AC上的点B′处，∴EB=EB′，AB=AB′=3，∴CB′=5-3=2，设BE=x，则EB′=x，CE=4-x，在R t△CEB′中，∵EB′2+CB′2=CE2，∴x2+22=（4-x）2，解得x=32，∴BE=32；②当点B′落在AD边上时，如图2所示．此时ABEB′为正方形，∴BE=AB=3．综上所述，BE的长为32或3．故选D．【小结】本题考查了折叠问题：折叠前后两图形全等，即对应线段相等；对应角相等．也考查了矩形的性质以及勾股定理．注意本题有两种情况，需要分类讨论，避免漏解．3、如图，在矩形ABCD中，AB＝√3，BC＝3，将△ABC沿对角线AC折叠，点B恰好落在点P处，CP 与AD交于点F，连接BP交AC于点G，交AD于点E，下列结论不正确的是( )A．PGCG =13B．△PBC是等边三角形C．AC＝2AP D．S△B G C＝3S△A G P【分析】如图，首先运用勾股定理求出AC的长度，进而求出∠ACB＝30°，此为解决该题的关键性结论；运用翻折变换的性质证明△BCP为等边三角形；运用射影定理求出线段C G、A G之间的数量关系，进而证明选项A、B、C成立，选项A不成立.【解析】如图，∵四边形ABCD为矩形，AC，∴∠ABC＝90°；由勾股定理得：AC2＝AB2+BC2，而AB＝√3，BC＝3，∴AC＝2√3，AB＝12∴∠ACB＝30°；由翻折变换的性质得：BP⊥AC，∠ACB＝∠ACP＝30°，BC＝PC，AB＝AP，B G＝P G，∴G C＝√3B G＝√3P G，∠BCP＝60°，AC＝2AP，∴△BCP为等边三角形，故选项B、C成立，选项A不成立；B G，C G＝3A G，∴S△BC G＝3S△AB G；由射影定理得：B G2＝C G•A G，∴A G＝√33由题意得：S△AB G＝S△A G P，∴S△B G C＝3S△A G P，故选项D正确；故选：A．【小结】考查了翻折变换的性质、矩形的性质、射影定理、三角形的面积公式等几何知识点及其应用问题；解题的关键是灵活运用矩形的性质、射影定理等几何知识点来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．4、如图，矩形纸片ABCD ，5AB =，3BC =，点P 在BC 边上，将CDP ∆沿DP 折叠，点C 落在点E 处，PE ，DE 分别交AB 于点O ，F ，且OP OF =，则AF 的值为_____________．【分析】由矩形的性质和已知条件OP OF =，可判定OEF OBP ∆≅∆,设EF x =，根据全等三角形的性质及矩形的性质可用含x 的式子表示出DF 和AF 的长，在Rt ADF ∆根据勾股定理可求出x 的值，即可确定AF 的值. 【解析】四边形ABCD 是矩形, ∴ 5CD AB ==,3AD BC ==,90B C A ︒∠=∠=∠= DEP ∆是由CDP ∆沿DP 折叠而来的，∴5DE CD ==,EP CP = ,90E C ︒∠=∠=B E ∴∠=∠，又,FOE POB OP OF ∠=∠= ，∴OEF OBP ∆≅∆（AA S ）,EF BP OE OB ∴==，BF BO OF EO OP EP CP ∴=+=+==设=EF BP x =,则5,3DF x BF CP x =-==- ，5(3)2AF AB BF x x ∴=-=--=+在Rt ADF ∆中，根据勾股定理得：222AD AF DF += ,即2223(2)(5)x x ++=- 解得67x = 620277AF ∴=+= 故答案为：207【小结】本题考查了求多边形中的线段长，主要涉及的知识点有矩形的性质，全等三角形的判定与性质，勾股定理，数学的方程思想，用同一个字母表示出直角三角形中的三边长是解题的关键.5、如图，在矩形ABCD中，AB=3，BC=2，点E为线段AB上的动点，将△CBE沿CE折叠，使点B落在矩形内点F处，则AF的最小值为__．【分析】通过观察可以发现，当∠AFE=90°时，AF最小；然后设BE=x，则：EF=x，AE=3-x，然后多次使用勾股定理即可解答；【解析】设BE=x，则：EF=x，AE=3-x在R t△ABC中，由勾股定理得：AC在R t△EBC中，由勾股定理得:EC由折叠可知CF=CB=2，所以：AF=AC-CF-2.【小结】本题考查几何图形中的最值问题，其中找到出现最值的位置和运用勾股定理解题是关键.6、如图，在矩形ABCD 中，AB ＝6，AD ＝，E 是AB 边上一点，AE ＝2，F 是直线CD 上一动点，将△AEF 沿直线EF 折叠，点A 的对应点为点A ′，当点E ，A ′，C 三点在一条直线上时，DF 的长为_____．【分析】利用勾股定理求出CE ，再证明CF =CE 即可解决问题．（注意有两种情形）【解析】如图，由翻折可知，∠FEA ＝∠FEA ′，∵CD ∥AB ，∴∠CFE ＝∠AEF ，∴∠CFE ＝∠CEF ，∴CE ＝CF ，在R t △BCE 中，EC，∴CF ＝CE＝，∵AB ＝CD ＝6，∴DF＝CD ﹣CF ＝6﹣，当点F在DC 的延长线上时，易知EF ⊥EF′，CF ＝CF ′＝，∴DF ＝CD +CF ′＝，故答案为6﹣或．【小结】本题考查翻折变换、矩形的性质、勾股定理等知识，本题的突破点是证明△CFE 的等腰三角形，属于中考常考题型．==7、如图，矩形OABC中，OA=4，AB=3，点D在边BC上，且CD=3DB，点E是边OA上一点，连接DE，将四边形ABDE沿DE折叠，若点A的对称点A′恰好落在边OC上，则OE的长为_________.【解析】连接A′D，AD，∵四边形OABC是矩形，∴BC=OA=4，OC=AB=3，∠C=∠B=∠O=90°，∵CD=3DB，∴CD=3，BD=1，∴CD=AB，∵将四边形ABDE沿DE折叠，若点A的对称点A′恰好落在边OC上，∴A′D=AD，A′E=AE，在R t△A′CD与R t△DBA中，，∴R t△A′CD≌R t△DBA（HL），∴A′C=BD=1，∴A′O=2，∵A′O2+OE2=A′E2，∴22+OE2=（4﹣OE）2，∴OE=，【小结】本题关键词：“对应点的连线段被折痕垂直平分”，“全等相似”，“十字架”，“勾股定理解方程”8、如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为．【解析】连接BF，∵BC=6，点E为BC的中点，∴BE=3，又∵AB=4，∴AE==5，∴BH=，则BF=，∵FE=BE=EC，∴∠BFC=90°，根据勾股定理得，CF===．故答案为：．9、如图，已知E为长方形纸片ABCD的边CD上一点，将纸片沿AE对折，点D的对应点D′恰好在线段BE上．若AD=3，DE=1，则AB=5．【解析】∵折叠，∴△ADE≌△AD'E，∴AD=AD'=3，DE=D'E=1，∠DEA=∠D'EA，∵四边形ABCD是矩形，∴AB∥CD，∴∠DEA=∠EAB，∴∠EAB=∠AEB，∴AB=BE，∴D'B=BE﹣D'E=AB﹣1，在R t△ABD'中，AB2=D'A2+D'B2，∴AB2=9+（AB﹣1）2，∴AB=5，故答案为：510、如图，矩形ABCD中，AB=8，BC=10，点N为边BC的中点，点M为AB边上任意一点，连接MN，把△BMN沿MN折叠，使点B落在点E处，若点E恰在矩形ABCD的对称轴上，则BM的长为5或．【解析】①当E在矩形的对称轴直线PN上时，如图1此时∠MEN=∠B=90°，∠ENB=90°，∴四边形BMEN是矩形．又∵ME=MB，∴四边形BMEN是正方形．∴BM=BN=5．②当E在矩形的对称轴直线FG上时，如图2，过N点作NH⊥FG于H点，则NH=4．根据折叠的对称性可知EN=BN=5，∴在R t△ENH中，利用勾股定理求得EH=3．∴FE=5﹣3=2．设BM=x，则EM=x，FM=4﹣x，在R t△FEM中，ME2=FE2+FM2，即x2=4+（4﹣x）2，解得x=，即BM=．故答案为5或．11、如图，矩形ABCD中，AD=4，O是BC边上的点，以OC为半径作⊙O交AB于点E，BE=AE，把四边形AECD沿着CE所在的直线对折（线段AD对应A′D′），当⊙O与A′D′相切时，线段AB的长是．【解析】设⊙O与A′D′相切于点F，连接OF，OE，则OF⊥A′D′，∵OC=OE，∴∠OCE=∠OEC，∵四边形ABCD是矩形，∴∠A=∠B=A′=90°，由折叠的性质得：∠AEC=∠A′EC，∴∠B+∠BCE=∠A′EO+∠OEC，∴∠OEA′=∠B=90°，∵OE=OF，∴四边形A′FOE是正方形，∴A′E=AE=OE=OC，∵BE=AE，设BE=3x，AE=5x，∴OE=OC=5x，∵BC=AD=4，∴OB=4﹣5x，在R t BOE中，OE2=BE2+OB2，∴（5x）2=（3x）2+（4﹣5x）2，解得：x=，x=4（舍去），∴AB=8x=．故答案为：．12、如图，矩形ABCD中，AB=2BC，E是AB上一点，O是CD上一点，以OC为半径作⊙O，将△ADE折叠至△A′DE，点A′在⊙O上，延长EA′交BC延长线于F，且恰好过点O，过点D作⊙O的切线交BC延长线于点G．若FG=1，则AD=2，⊙O半径=．【解析】作OH⊥DG于H，如图，设DA=x，则AB=2x，∵△ADE折叠至△A′DE，∴DA′=DA=x，∠DA′E=∠A=90°，∴DA′与⊙O相切，在△ODA′和△OCF中，∴△DOA′≌△FOC．∴DA′=CF=x，∵DG是⊙O的切线，OH⊥DG，∴H点为切点，∴DH=DA′=x，GH=GC=CF+GF=x+1，在R t△DCG中，∵DC2+CG2=DG2，∴（2x）2+（x+1）2=（x+x+1）2，解得x1=0（舍去），x2=2，∴AD=2，设⊙O的半径为r，则OC=OA′=r，OD=2x﹣r=4﹣r，在R t△DOA′中，∵DA′2+OA′2=DO2，∴22+r2=（4﹣r）2，解得r=，即⊙O的半径为．故答案为2，．13、在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D落在点F处．（1）如图1，若点F落在对角线AC上，且∠BAC=54°，则∠DAE的度数为18°．（2）如图2，若点F落在边BC上，且AB=6，AD=10，求CE的长．（3）如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB=6，AD=10，求CG的长．【解析】（1）∵四边形ABCD是矩形，∴∠BAD=90°，∵∠BAC=54°，∴∠DAC=90°﹣54°=36°，由折叠的性质得：∠DAE=∠F AE，∴∠DAE=∠DAC=18°；故答案为：18；（2）∵四边形ABCD是矩形，∴∠B=∠C=90°，BC=AD=10，CD=AB=6，由折叠性质：AF=AD=10，EF=ED，∴BF===8，∴CF=BC﹣BF=10﹣8=2，设CE=x，则EF=ED=6﹣x，在R t△CEF中，由勾股定理得：22+x2=（6﹣x）2，解得：x=，即CE的长为；（3）连接EG，如图3所示：∵点E是CD的中点，∴DE=CE，由折叠的性质得：AF=AD=10，∠AFE=∠D=90°，FE=DE，∴∠EFG=90°=∠C，在R t△CEG和△FEG中，，∴R t△CEG≌△FEG（HL），∴CG=FG，设CG=FG=y，则AG=AF+FG=10+y，BG=BC﹣CG=10﹣y，在R t△ABG中，由勾股定理得：62+（10﹣y）2=（10+y）2，解得：y=，即CG的长为．。

八年级折叠问题

矩形中的折叠问题专题演练
01 角度的计算
例1、如图1，把矩形ABCD沿EF对折，若 ∠1=500，求∠AEF的度数。
边长的计算
02 边长的计算
例2、如图2，沿折痕AE折叠矩形ABCD的一边，使点D落在BC边上一点F处。若 AB=8，且⊿ABF的面积为24，求EC的长。
3、如图3，是一矩形的纸片，其中AD=2.5，
例2、把图2的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处如图），已知∠MPN=90°，PM=3，PN=4，那么矩形纸片ABCD的面积为_________．
例3 如图3，矩形纸片ABCD中，AB=3cm， BC=4cm，现将A、C重合，使纸片折叠压平，设折痕为EF，则重叠部分△AFE的面积是_________．
Байду номын сангаас
AB=1.5。按下列步骤折叠：将其对折，使AB
落在AD上，折痕为AE，再将⊿ABE以BE为折
痕向右折叠，AE与DC交于点F，则CF的长是( )
A.0.5 B.0.75
C.1
D.1.25
03 折痕的计算
例4、有一矩形纸片，其中宽AB=6cm，长 BC=8cm。现按如图4所示的方法作折纸游戏，将它折叠使B点与D点重合，求折痕EF 的长。
06 矩形的折叠与阴影部分的面积
矩形的折叠问题，一般是关于面积等方面的计算问题，其在考查同学们的逻辑思维能力和空间想象能力．解决与矩形折叠有关的面积问题，关键是将轴对称特征、勾股定理以及矩形的有关性质结合起来．请看几例．
例1、如图1，将矩形ABCD沿直线AE折叠，顶点 D恰好落在BC边上F点处．已知CE=3cm，AB=8cm，则图中阴影部分的面积为_________．

七年级数学下册平行线【折叠问题】专项练习题+答案

七年级数学下册平行线【折叠问题】专项练习题+答案1、把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF．若∠CDF=38°，则∠EFD的度数是（ B ）A.72°B.64°C.48°D.52°ABCD沿AE向上折叠，使点B落在DC边上的点F处.若△AFD的周长为18，△ECF的周长为6，四边形纸片ABCD的周长为（ B ）A.20B.24C.32D.48解：由折叠的（电子版关注微信公众号：初一数学语文英语）性质知，AF=AB，EF=BE. 所以四边形纸片ABCD的周长等于△AFD和△ECF的周长和为18+6=24. 故四边形纸片ABCD的周长为24.3.将正方形纸片ABCD折叠，使得点A落在CD边上的点E处，折痕为MN．则下列说法错误的是（ D ）A.AE⊥MNB.AM=EMC.∠BNO=∠FNOD.∠OEF=90°解：在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴垂直平分，对应线段相等，对应角相等．∠BAM和∠FEM是对应角，所以∠BNO=∠FNO，∠BAM=∠FEM=90°，4.如图，先将正方形ABCD对折，折痕为EF，将这个正方形展平后，再分别将A，B 折叠到折痕EF，使点A，B都与折痕EF上的点G重合，则下列说法错误的是（ B ）A.∠MGD=90°B.∠DGF=∠MGEC.DG=CGD.∠BCN=∠GCN解：将A，B折叠到折痕EF，使点A，B都与折痕EF上的点G重合，则直线MD，NC 分别是对称轴，根据轴对称图形中，（电子版关注微信公众号：初一数学语文英语）对应线段相等，对应角相等，5.图1的长方形ABCD中，点E在AD边上，AD∥BC，∠A=∠D=90°，∠BEA=60°．（电子版关注微信公众号：初一数学语文英语）现分别以BE，CE为折线，将A，D向BC的方向折过去，图2为对折后A，B，C，D，E五点在同一平面上的位置图．若，则∠BCE的度数为（ D ）A.30°B.32.5°C.35°D.37.5°解：分别以BE，CE为折线，将A，D向BC的方向翻折，则直线BE，CE分别是对称轴，6.如图，△ABC的周长为30cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC于D，交AC于E，连接AD，若AE=4cm，则△ABD的周长是多少cm．（ D ）A.26B.16C.18D.22由轴对称图形的性质，（电子版关注微信公众号：初一数学语文英语）得AD=CD，AE=CE．7.如图，在△ABC中，AB=AC=20cm，将△ABC对折，使A与B重合，折痕为DE，（电子版关注微信公众号：初一数学语文英语）若△BCD的周长为27cm，则BC的长为多少cm．（ C ）A.10B.9C.7D.138.在Rt△ABC中，CD=3cm，现将直角边BC沿直线BD折叠，使它落在斜边AB上，且与BE重合，△ABD的面积是12cm²，则AB的长是多少cm（ A ）A.8B.4C.9D.3。

浙教版八年级数学下册第5章专题十矩形的折叠问题

专题
由勾股定理可得 BD＝ AB2＋AD2＝ 42＋32＝5. 设 AG＝x，则 BG＝4－x，A′G＝x. BA′＝BD－A′D＝BD－AD＝5－3＝2. 在 Rt△ BA′G 中，x2＋22＝(4－x)2，解得 x＝32，∴AG ＝32.由勾股定理得 DG＝ AD2＋AG2＝ 32＋322＝32 5.
形沿AC折叠，使点D落在点E处，CE与AB交于点F，
则S△ACF为(
)
A．12
B．15
C．6D．10源自题由折叠可知∠DCA＝∠ACE. ∵DC∥AB，∴∠DCA＝∠CAB， ∴∠ACE＝∠CAB，∴AF＝FC. 设 AF＝FC＝x，则 FB＝8－x，由勾股定理得 x2＝(8－x)2＋42，解得 x＝5，∴S△ACF＝12×5×4＝10. 【答案】D
专题
设 AF＝x，则 DF＝10－x. 在 Rt△ BAF 中，BF2＝x2＋42. 在 Rt△ B′DF 中，B′F2＝(10－x)2＋12， ∴x2＋42＝(10－x)2＋12，解得 x＝147.∴AF＝147.
专题
变式3如图，在矩形ABCD中，AB＝4，BC＝6，E为 BC的中点，将△ABE沿AE折叠，使点B落在矩形内的点F处，连结CF.求CF的长．
浙教版八年级下
第5章特殊平行四边形
专题十矩形的折叠问题
专题
1 母题【教材第5.1节作业题】已知：如图，将矩形纸 ABCD的四个角向内折起，恰好拼成一个无缝隙、无重叠的四边形EFGH.
专题
【方法点拨】在折叠问题中，折叠前后的图形是全等图形，折
叠前后的对应点的连线被折痕所在直线垂直平分，由此可得线段相等、角相等，结合勾股定理等知识可求线段长．
专题
变式2如图，在矩形ABCD中，BC＝10，AB＝4，点E， F分别是BC，AD上的动点，将四边形CDFE沿EF折叠，点C，D的对应点分别为C′，D′，当线段C′D′恰好过点 B，且BC′＝3BD′时，求AF的长．

专题36 矩形与折叠问题(解析版)

专题36 矩形与折叠问题一、单选题1．如图，矩形纸片ABCD 中，AB ＝6cm ，BC ＝8cm ．现将其沿AE 对折，使得点B 落在边AD 上的点B 1处，折痕与边BC 交于点E ，则CB 1的长为（）A ．cmB ．C ．8cmD ．10cm【答案】B【分析】根据翻折变换的性质可以证明四边形ABEB 1为正方形，得到BE ＝AB ，根据EC ＝BC ﹣BE 计算得到EC ，再根据勾股定理可求答案．【详解】解：∵∵AB 1E ＝∵B ＝90°，∵BAB 1＝90°，∵四边形ABEB 1为矩形，又∵AB ＝AB 1，∵四边形ABEB 1为正方形，∵BE ＝AB ＝6cm ，∵EC ＝BC ﹣BE ＝2cm ，∵CB 1cm ．故选B ．【点睛】本题考查的是翻折变换、矩形和正方形的判定和性质，掌握翻折变换的性质及矩形、正方形的判定定理和性质定理是解题的关键．2．如图，矩形ABCD 中，3AB =，9AD =，将此矩形折叠，使点B 与点D 重合，折痕为EF ，则ABE ∆的面积为（）A．12B．10C．8D．6【答案】D【分析】根据折叠的条件可得：BE＝DE，在直角∵ABE中，利用勾股定理就可以求解．【详解】将此长方形折叠，使点B与点D重合，∵BE＝ED．∵AD＝AE＋DE＝AE＋BE＝9．∵BE＝9−AE，根据勾股定理可知AB2∵AE2∵ BE2，32∵AE2∵∵9-AE∵2∵解得AE＝4．∵∵ABE的面积为3×4÷2＝6．故选：D．【点睛】本题考查了利用勾股定理解直角三角形的能力，即：直角三角形两直角边的平方和等于斜边的平方．3．如图，在矩形ABCD中，E是BC边的中点，将∵ABE沿AE所在的直线折叠得到∵AFE，延长AF交CD 于点G，已知CG＝2，DG＝1，则BC的长是（）A．B．C．D．【答案】B【分析】连接EG ，由折叠的性质可得BE ＝EF 又由E 是BC 边的中点，可得EF ＝EC ，然后证得Rt∵EGF ∵Rt∵EGC （HL ），得出FG ＝CG ＝2，继而求得线段AG 的长，再利用勾股定理求解，即可求得答案．【详解】解：连接EG ，∵E 是BC 的中点，∵BE ＝EC ，∵∵ABE 沿AE 折叠后得到∵AFE ，∵BE ＝EF ，∵EF ＝EC ，∵在矩形ABCD 中，∵∵C ＝90°，∵∵EFG ＝∵B ＝90°，∵在Rt∵EGF 和Rt∵EGC 中，EF EC EG EG=⎧⎨=⎩， ∵Rt∵EGF ∵Rt∵EGC （HL ），∵FG ＝CG ＝2，∵在矩形ABCD 中，AB ＝CD ＝CG +DG ＝2+1＝3，∵AF ＝AB ＝3，∵AG ＝AF +FG ＝3+2＝5，∵BC ＝AD ＝．故选：B ．【点睛】此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用．熟练掌握折叠的性质是关键．4．在矩形纸片ABCD 中，AB =6，AD =10．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ．当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为（）A ．8cmB ．6cmC ．4cmD ．2cm【答案】C【分析】根据翻折的性质，可得BA ′与AP 的关系，根据线段的和差，可得A ′C ，根据勾股定理，可得A ′C ，根据线段的和差，可得答案．【详解】解：∵当P 与B 重合时，BA ′=BA =6，CA ′=BC ﹣BA ′=10﹣6=4cm ，∵当Q 与D 重合时，由勾股定理，得CA cm ，CA ′最远是8，CA ′最近是4，点A ′在BC 边上可移动的最大距离为8﹣4=4cm ，故选：C ．【点睛】本题考查了翻折变换，利用了翻折的性质，勾股定理，分类讨论是解题关键．5．如图，把矩形纸片ABCD 沿EF 折叠后得到1∠，再把纸片铺平，若150∠=︒，则AEF ∠的度数为（）A ．105°B ．120°C ．130°D ．115°【答案】D【分析】点B 折叠后的点为G ，根据折叠的性质，可得∵GFE=∵BFE ，结合∵1的度数即可求出∵EFB 的度数，利用矩形的性质AD∵BC 即可求出结果．【详解】点B 折叠后的点为G ，根据折叠的性质，可得∵GFE=∵BFE ，∵∵1=50°，∵∵BFE=（180°-50°）÷2=65°，∵ABCD 是矩形，∵AD∵BC ，∵∵DEF=∵BFE=65°，∵∵AEF=180°-65°=115°，故选：D ．【点睛】本题考查了折叠的性质，矩形的性质，平行的性质，掌握折叠的性质是解题的关键．6．如图所示，在矩形ABCD 中，4AB =，8AD =，将矩形沿BD 折叠，点A 落在点E 处，DE 与BC 交于点F ，则重叠部分BDF ∆的面积是( )A ．20B ．16C ．12D ．10【答案】D【分析】根据折叠的性质可得∵ADB=∵EDB,由平行可得∵ADB=∵CBD,推出∵CBD=∵EDB,设BF 为x ,在Rt∵DCF 中根据勾股定理列出方程求出x ,再根据面积公式求出∵BDF 的面积即可．【详解】∵AD∵BC,∵∵ADB=∵CBD,∵∵BDE 是∵BDA 折叠后的图形,∵∵ADB=∵EDB,∵∵CBD=∵EDB,设BF 为x ,则DF 为x ,CF 为8－x ,在Rt∵DCF 中,()22284x x -+=解得:x =5．∵S ∵BDF =154102⨯⨯=．故选D ．【点睛】本题考查折叠中矩形的性质,关键在于利用勾股定理列出方程求解．7．如图，把一张长方形的纸沿对角线BD 折叠，使点C 落到点C '的位置，若BC '平分ABD ∠，则DBC ∠的度数是( )A ．15°B ．30°C ．45°D ．60°【答案】B【分析】根据折叠的性质，得到DBC DBC'∠=∠，再根据角平分线的性质得到''ABC DBC ∠=∠ ,得到∵ABC 被平均分成了3份，求出解决即可.【详解】解：∵把一张长方形纸片ABCD 沿BD 折叠∵DBC DBC'∠=∠∵BC '平分ABD ∠∵''ABC DBC ∠=∠∵DBC ∠=13∵ABC=30° 故选B.【点睛】本题考查了折叠的性质以及角平分线的性质，解决本题的关键是熟练掌握折叠与角平分线的性质，找到相等的角.8．将长方形ABCD 纸片沿AE 折叠，得到如图所示的图形，已知∵CED'=70°，则∵EAB 的大小是( )A ．60°B ．50°C ．75°D ．55°【答案】D【分析】首先根据折叠的性质得出∵DEA=∵D′EA=55°，然后由余角的性质得出∵DEA=∵EAD′=35°，进而得出∵D′AB=20°，最后即可得出∵EAB.【详解】根据折叠的性质，∵CED'=70°，得 ∵DEA=∵D′EA=18070552︒-︒=︒ ∵∵ADE=∵AD′E=90°∵∵DAE=∵EAD′=90°-55°=35°∵∵D′AB=90°-∵DAE -∵EAD′=90°-35°-35°=20°∵∵EAB=∵EAD′+∵D′AB=35°+20°=55°故答案为D.【点睛】此题主要考查折叠的性质以及余角的性质，熟练掌握，即可解题.9．如图，有一张长方形纸片ABCD ，其中15AB cm =，10AD cm =.将纸片沿EF 折叠，//EF AD ，若9AE cm =，折叠后重叠部分的面积为（）A ．230cmB ．260cmC ．250cmD ．290cm【答案】B【解析】【分析】根据折叠的性质，可知折叠后重叠部分的面积等于长方形ABCD 的面积减去长方形AEFD 的面积，即可得解.【详解】根据题意，得折叠后重叠部分的面积等于长方形ABCD 的面积减去长方形AEFD 的面积，∵10AD cm =，9AE cm =，//EF AD∵2=151091060ABCD AEFD S S S AB AD AE AD cm -=-=⨯-⨯=阴影长方形长方形故答案为B.【点睛】此题主要考查折叠的性质和长方形的面积求解，熟练掌握，即可解题.10．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A．B C D．6【答案】A【分析】先根据图形翻折变换的性质求出AC的长，再由勾股定理及等腰三角形的判定定理即可得出结论．【详解】解：∵∵CEO是∵CEB翻折而成，∵BC=OC，BE=OE，∵B=∵COE=90°，∵EO∵AC，∵O是矩形ABCD的中心，∵OE是AC的垂直平分线，AC=2BC=2×3=6，∵AE=CE，在Rt∵ABC中，AC2=AB2+BC2，即62=AB2+32，解得AB=33，在Rt∵AOE中，设OE=x，则AE=33-x，AE2=AO2+OE2，即（33-x）2=32+x2，解得x=3，∵AE=EC=33-3=23．故选：A．【点睛】本题考查翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解题的关键．11．如图，在矩形ABCD 中，点E 在边CD 上，将该矩形沿AE 折叠，恰好使的D 落在边BC 上的点F 处，如果∵BAF =60°，则∵DAE 的大小为（）A ．10°B ．15 °C ．20 °D ．25°【答案】B【分析】由题意可知90BAD ∠=︒，12FAE DAE DAF ∠=∠=∠．再由DAF BAD BAF ∠=∠-∠，即可求出DAE ∠的大小．【详解】∵四边形ABCD 为矩形，∵90BAD ∠=︒，∵FAE 是由DAE △沿AE 折叠而来，且F 点恰好落在BC 上， ∵12FAE DAE DAF ∠=∠=∠， ∵906030DAF BAD BAF ∠=∠-∠=︒-︒=︒， ∵130152DAE ∠=⨯︒=︒．故选：B ．【点睛】本题考查矩形的折叠问题，根据折叠的性质推出12FAE DAE DAF ∠=∠=∠是解答本题的关键． 12．如图，长方形ABCD 中，点O 是AC 的中点，E 是AB 边上的点，把∵BCE 沿CE 折叠后，点B 恰好与点O 重合，则图中全等的三角形有（）对．A ．1B ．2C ．3D ．4【答案】D【分析】由长方形的性质利用“SSS ”即可证明ADC CBA ≅，再由折叠的性质可知∵BCE ∵∵OCE ，即可得出结论90EOC EBC ∠=∠=︒，从而推出90EOA EOC ∠=∠=︒，最后由O 点为AC 中点，利用“ASA ”即可证明OCE OAE ≅，最后又可推出∵OAE ∵∵BCE ，即可选择．【详解】∵四边形ABCD 为长方形，∵在ADC 和CBA △中AD CB CD AB AC CA =⎧⎪=⎨⎪=⎩，∵()ADC CBA SSS ≅；∵∵BCE 沿CE 折叠后，点B 恰好与点O 重合，∵∵BCE ∵∵OCE ；∵O 点为AC 中点，∵AO =CO ．∵∵BCE ∵∵OCE ，∵90EOC EBC ∠=∠=︒，∵在∵OCE 和∵OAE 中，90AO CO EOA EOC OE OE =⎧⎪∠=∠=︒⎨⎪=⎩，∵()OCE OAE ASA ≅；∵∵BCE ∵∵OCE ，OCE OAE ≅，∵∵OAE ∵∵BCE综上，图中全等三角形有4对．故选：D ．【点睛】本题考查矩形的性质以及全等三角形的判定和性质．掌握全等三角形的判定条件是解答本题的关键． 13．如图，矩形纸片ABCD 中，6AB =，10AD =，折叠纸片，使点A 落在BC 边上的点A 处，折痕为PQ ，当点1A 在BC 边上移动时，折痕的端点P 、Q 分别在AB 、AD 边上移动，则当1A B 最小时其值为（）A ．2B ．3C ．4D ．5【答案】A【分析】根据翻折的性质，可得当Q 与D 重合时，A 1B 最小，根据勾股定理，可得A 1C ，从而可得答案．【详解】解：由折叠可知：当Q 与D 重合时，A 1B 最小，A 1D=AD=10，由勾股定理，得：A 1，∵A 1B=10-8=2，故选A ．【点睛】本题考查了翻折变换，利用了翻折的性质得到当Q 与D 重合时，A 1B 最小是解题的关键．14．如图，将长方形ABCD 沿对角线BD 折叠，使点C 落在点C ′处，BC ′交AD 于E ，AD ＝8，AB ＝4，则重叠部分（即BDE ）的面积为（）A ．6B ．7.5C ．10D ．20【答案】C【分析】由折叠结合矩形的性质先证明,BE DE =设,BE DE x == 则8,AE x =- 再利用勾股定理求解,x 从而可得BDE 的面积．【详解】解：长方形ABCD ，8,4,AD AB ==//,AD BC ∴,ADB CBD ∴∠=∠由对折可得：,CBD C BD '∠=∠,ADB C BD '∴∠=∠,BE DE ∴=设,BE DE x == 则8,AE x =-由222,BE AB AE =+ ()22248,x x ∴=+-1680,x ∴=5,x ∴= 5,DE BE ∴==115410.22BDE S DE AB ∴==⨯⨯= 故选：.C【点睛】本题考查的是矩形与折叠问题，勾股定理的应用，矩形的性质，掌握以上知识是解题的关键．15．如图，把一张长方形纸片沿对角线折叠，若∵EDF 是等腰三角形，则∵BDC （）A ．45ºB ．60ºC ．67.5ºD ．75º【答案】C【分析】由翻折可知：∵BDF∵∵BCD ，所以∵EBD=∵CBD ，∵E=∵C=90°，由于∵EDF 是等腰三角形，易证∵ABF=45°，所以∵CBD=12∵CBE=22.5°，从而可求出∵BDC=67.5°．【详解】解：由翻折的性质得，∵DBC=∵EBD ，∵矩形的对边AD∵BC ，∵E=∵C=90°，∵∵DBC=∵ADB ，∵∵EBD=∵ADB ，∵∵EDF 是等腰三角形，∵E=90°，∵∵EDF 是等腰直角三角形，∵∵DFE=45°，∵∵EBD+∵ADB=∵DFE ， ∵∵DBF=12∵DFE=22.5°， ∵∵CBD =22.5°，∵∵BDC=67.5°，故选：C ．【点睛】本题考查等腰三角形，涉及矩形的性质，全等三角形的判定与性质等知识，需要学生灵活运用所学知识． 16．如图，矩形纸片ABCD 中，4AB =，3AD =，折叠纸片使AD 边与对角线BD 重合，则折痕为DG 的长为（）A B C．2D【答案】D【分析】首先设AG＝x，由矩形纸片ABCD中，AB＝4，AD＝3，可求得BD的长，又由折叠的性质，可求得A′B 的长，然后由勾股定理可得方程：x2+22＝（4-x）2，解此方程即可求得AG的长，继而求得答案．【详解】解：设AG＝x，∵四边形ABCD是矩形，∵∵A＝90°，∵AB＝4，AD＝3，∵BD5，由折叠的性质可得：A′D＝AD＝3，A′G＝AG＝x，∵DA′G＝∵A＝90°，∵∵BA′G＝90°，BG＝AB-AG＝4-x，A′B＝BD-A′D＝5-3＝2，∵在Rt∵A′BG中，A′G2+A′B2＝BG2，∵x2+22＝（4-x）2，解得：x＝32，∵AG＝32，∵在Rt∵ADG中，DG=故选：D．【点睛】此题考查了折叠的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想与方程思想的应用．17．如图，在矩形纸片ABCD中，BC a=，将矩形纸片翻折，使点C恰好落在对角线交点O处，折痕为BE，点E 在边CD 上，则CE 的长为（）A ．12aB ．25aC ．2aD ．3a 【答案】D【分析】首先证明∵OBC 是等边三角形，在Rt∵EBC 中求出CE 即可解决问题；【详解】解：∵四边形ABCD 是矩形，∵OB=OC ，∵BCD=90°，由翻折不变性可知：BC=BO ，∵BC=OB=OC ，∵∵OBC 是等边三角形，∵∵OBC=60°，∵∵EBC=∵EBO=30°，∵BE=2CE根据勾股定理得：EC=3a ，故选：D ．【点睛】本题考查翻折变换，等边三角形的判定和性质等知识，解题的关键是证明∵OBC 是等边三角形． 18．如图，将矩形纸片ABCD 沿EF 折叠，点C 落在边AB 上的点H 处，点D 落在点G 处，若111GEF ∠=︒，则AHG ∠的度数为（）．A ．42°B ．69°C ．44°D ．32°【答案】A【分析】根据翻折的性质，及矩形的性质，求出AEG ∠，再利用“8”字模型求解即可．【详解】由图形翻折的性质可知，111GEF DEF ∠=∠=︒，180111AEF ∴∠=︒-︒=69︒，1116942AEG GEF AEF ∠=∠-∠=︒-︒=︒，90A G ∠=∠=︒，利用“8”字模型，42AHG AEG ∴∠=∠=︒，故选：A ．【点睛】本题考查了矩形翻折问题，能够根据图形翻折的性质推理出AEG ∠是解决问题的关键，熟练运用“8”字模型是求最终结果的关键．19．如图，已知长方形ABCD ，将∵DBC 沿BD 折叠得到∵DBC′，BC′与AD 交于点E ，若长方形的周长为20cm ，则∵ABE 的周长是（）A ．5cmB ．10cmC ．15cmD ．20cm【答案】B【分析】根据现有条件推出∵EDB=∵EBD ，得出BE=DE ，可知∵ABE 的周长=AB+AD ，是长方形的周长的一半，即可得出答案．【详解】由折叠可知：∵CBD=∵C′BD，∵四边形ABCD为平行四边形，∵AD∵BC，∵∵ADB=∵CBD，∵∵ADB=∵C′BD，∵∵EDB=∵EBD，∵BE=DE，∵∵ABE的周长=AB+AD，∵长方形的周长为20cm，∵2（AB+AD）=20cm,∵AB+AD=10cm,∵∵ABE的周长为10cm，故选：B．【点睛】本题考查了等腰三角形的性质，折叠的性质，推出BE=DE是解题关键．20．如图，将一块长方形纸片ABCD沿BD翻折后，点C与E重合，若∵ADE = 30°，EH = 2，则BC的长度为（）A．8B．7C．6.5D．6【答案】D【分析】由折叠的性质可得∵E＝∵C＝∵A=90°，再证明∵ABH∵∵EDH，得到AB的长，再求出∵DBC=30°，在Rt∵BCD 中即可求解．【详解】∵四边形ABCD是矩形，∵AD∵BC，∵C＝90°，∵将一块长方形纸片ABCD 沿BD 翻折后，∵∵E ＝∵C ＝∵A=90°，又∵AHB=∵EHD ，AB=ED∵∵ABH∵∵EDH∵∵ABH=∵ADE = 30°，AH=EH = 2∵BH=2AH=4∵CD=AB= =∵∵ABH= 30°，∵∵HBC=60°∵翻折，∵∵DBC=30°6=故选：D ．【点睛】本题考查了翻折变换，矩形的性质，含30°的直角三角形的性质，求出AB 的长是本题的关键． 21．在数学拓展课《折叠矩形纸片》上，小林发现折叠矩形纸片ABCD 可以进行如下操作：∵把ABF 翻折，点B 落在C 边上的点E 处，折痕为AF ，点F 在BC 边上；∵把ADH 翻折，点D 落在AE 边上的点G 处，折痕为AH ，点H 在CD 边上，若610AD CD ==，，则EH EF=（）A ．32B ．53C ．43D ．54【答案】A【分析】利用翻折不变性可得10AE AB ==，推出8DE =，2EC =，设BF EF x ==，在Rt EFC △中，2222(6)x x =+-，可得103x =，设DH GH y ==，在Rt EGH △中，2224(8)y y +=-，可得3y =，由此即可解决问题．【详解】解：四边形ABCD 是矩形，90C D ∴∠=∠=︒，10AB CD ==，6AD BC ==，由翻折不变性可知：10AB AE ==，6AD AG ==，BF EF =，DH HG =，4EG ∴=，在Rt ADE △中，8DE ==，1082EC ∴=-=，设BF EF x ==，在Rt EFC △中有：2222(6)x x =+-，103x ∴=，设DH GH y ==，在Rt EGH △中，2224(8)y y +=-，3y ∴=，5EH ∴=， ∴531023EH EF ==，故选：A ．【点睛】本题考查矩形的性质，翻折变换，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．22．如图，将一张矩形纸片ABCD 沿EF 折叠后，点D ，C 分别落在D ′，C ′地位置，ED ′的延长线与BC 相交于点G ，若∵EFG =68°，则∵1的度数是（）A ．112°B ．136°C ．144°D ．158°【答案】B【分析】由AD//BC，∵EFG=68°，根据两直线平行，内错角相等，可求得∵DEF的度数，然后由折叠的性质，求得∵DEG 的度数，继而求得答案．【详解】解：∵AD//BC，∵EFG=68°，∵∵DEF=∵EFG=68°，由折叠的性质可得：∵FEG=∵DEF=68°，∵∵DEG=∵DEF+∵FEG=136°，∵AD//BC，∵∵1=∵DEG=136°．故选：B．【点睛】此题考查了平行线的性质以及折叠的性质．注意掌握折叠前后图形的对应关系是解此题的关键．23．如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC边上的点F处．若AB＝3，BC＝5，则DE的长为（）A．12B．53C．25D．13【答案】B【分析】先根据矩形的性质得AD＝BC＝5，AB＝CD＝3，再根据折叠的性质得AF＝AD＝5，EF＝DE，在Rt∵ABF 中，利用勾股定理计算出BF＝4，则CF＝BC﹣BF＝1，设CE＝x，则DE＝EF＝3﹣x，然后在Rt∵ECF中根据勾股定理得到x2+12＝（3﹣x）2，解方程即可得到DE的长．【详解】解：∵四边形ABCD为矩形，∵AD＝BC＝5，AB＝CD＝3，∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，∵AF＝AD＝5，EF＝DE，在Rt∵ABF中，BF4，∵CF＝BC﹣BF＝5﹣4＝1，设CE＝x，则DE＝EF＝3﹣x，在Rt∵ECF中，CE2+FC2＝EF2，∵x2+12＝（3﹣x）2，解得x＝43，∵DE＝3﹣x＝53，故选：B．【点睛】本题考查了翻折变换、矩形的性质、勾股定理等知识，属于常考题型，灵活运用这些性质进行推理与计算是解题的关键．24．如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平，再一次折叠，使点D落到EF上的点G处，并使折痕经过点A，已知2BC=，则线段EG的长度为（）A．1B C D．2【答案】B【分析】由折叠的性质可得AE=12AD=12BC=1，AG=AD=2，由勾股定理得出EG即可．【详解】解：如图所示：∵四边形ABCD 是矩形，对折矩形纸片ABCD ，使AB 与DC 重合得到折痕EF ， ∵AE=12AD=12BC=1，EF∵AD ， ∵∵AEF=90°，∵再一次折叠，使点D 落到EF 上点G 处∵AG=AD=2，=，故选：B ．【点睛】此题主要考查了翻折变换的性质以及矩形的性质，熟练掌握折叠的性质是解题关键．25．如图，将长方形纸片ABCD 沿EF 折叠后，点C ，D 分别落在点C '，D 处，若68AFE ∠=︒，则'∠C EB 等于（）A ．68︒B ．80︒C ．44︒D ．55︒【答案】C【分析】根据矩形的性质可得AD//BC ，根据平行线的性质可得∵CEF =∵AFE ，根据折叠的性质可得∵CEF =∵C′EF ，根据平角的定义即可得答案．【详解】解：∵ABCD 是长方形，∵68AFE ∠=︒，∵∵CEF =∵AFE=68°，∵将长方形纸片ABCD 沿EF 折叠后，点C ，D 分别落在点C '，D 处，∵∵CEF =∵C′EF =68°，∵'∠C EB =180°-∵CEF -∵C′EF=44°，故选：C ．【点睛】本题考查了矩形的性质、平行线的性质，翻折变换的性质，熟记折叠的性质是解题的关键．26．如图，把长方形纸片ABCD 沿对角线折叠，设重叠部分为EBD △．下列说法错误的是（）A ．AE CE =B ．12AE BE =C ．EBD EDB ∠=∠ D ．∵ABE∵∵CDE【答案】B【分析】由折叠的性质和平行线的性质可得∵ADB=∵CBD ，可得BE=DE ，可证AE=CE ，由“SAS”可证∵ABE∵∵CDE ，即可求解．【详解】解：如图，∵把矩形纸片ABC'D 沿对角线折叠，∵∵CBD=∵DBC'，CD=C'D=AB ，AD=BC=BC'，∵∵EDB=∵DBC'，∵∵EDB=∵EBD ，故选项C 正确；∵BE=DE ，∵AD=BC ，∵AE=CE ，故选项A 正确；在∵ABE 和∵CDE 中，AB CD A C AE CE =⎧⎪∠=∠⎨⎪=⎩，∵∵ABE∵∵CDE （SAS ），故选项D 正确；没有条件能够证明12AE BE =，故选：B ．【点睛】本题考查了翻折变换，全等三角形的判定和性质，矩形的性质，掌握折叠的性质是本题的关键． 27．如图，将长方形纸片沿对角线折叠，重叠部分为BDE ，则图中全等三角形共有（）A ．0对B ．1对C ．2对D ．3对【答案】C【分析】因为图形对折，所以首先∵CDB∵∵ABD ，由于四边形是长方形，进而可得∵ABE∵∵CDE ，如此答案可得．【详解】解：∵∵BDC 是将长方形纸片ABCD 沿BD 折叠得到的，∵CD=AB ，AD=BC ，∵BD=BD ，∵∵CDB∵∵ABD （SSS ），∵∵CBD=∵ADB∵EB=ED∵CE=AE又AB=CD∵∵ABE∵∵CDE ，∵图中全等三角形共有2对故选：C【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、SSA 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．做题时要由易到难，循序渐进．28．如图，在矩形ABCD 中，点E 是AD 的中点，EBC ∠的平分线交CD 于点F ，将DEF 沿EF 折叠，点D 恰好落在BE 上M 点处，延长BC 、EF 交于点N ．有下列四个结论：∵ DF CF =；∵BF EN ⊥；∵BEN 是等边三角形；∵3BEF DEF S S =△△．其中，将正确结论的序号全部选对的是（）A ．∵∵∵B ．∵∵∵C ．∵∵∵D ．∵∵∵∵【答案】B【分析】由折叠的性质、矩形的性质与角平分线的性质，可证得CF ＝FM ＝DF ，即可判断∵；易求得∵BFE ＝∵BFN ，则可得BF∵EN ，即可判断∵；易证得∵BEN 是等腰三角形，但无法判定是等边三角形，即可判断∵；易求得BM ＝2EM ＝2DE ，即可得EB ＝3EM ，根据等高三角形的面积比等于对应底的比，即可判断∵．【详解】∵四边形ABCD 是矩形，∵∵D ＝∵BCD ＝90°，DF ＝MF ，由折叠的性质可得：∵EMF ＝∵D ＝90°，即FM∵BE ，CF∵BC ，∵BF 平分∵EBC ，∵CF ＝MF ，∵DF ＝CF ；故∵正确；∵∵BFM ＝90°−∵EBF ，∵BFC ＝90°−∵CBF ，∵∵BFM ＝∵BFC ，∵∵MFE ＝∵DFE ＝∵CFN ，∵∵BFE ＝∵BFN ，∵∵BFE ＋∵BFN ＝180°，∵∵BFE ＝90°，即BF∵EN ，故∵正确；∵在∵DEF 和∵CNF 中，90D FCN DF CFDFE CFN ∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝ ∵∵DEF∵∵CNF （ASA ），∵EF ＝FN ，∵BF 垂直平分EN ，∵BE ＝BN ，假设∵BEN 是等边三角形，则∵EBN ＝60°，∵EBA ＝30°，则AE ＝12BE ，又∵AE ＝12AD ，则AD ＝BC ＝BE ，而明显BE ＝BN ＞BC ，∵∵BEN 不是等边三角形；故∵错误；∵∵BFM ＝∵BFC ，BM∵FM ，BC∵CF ，∵BM ＝BC ＝AD ＝2DE ＝2EM ，∵BE ＝3EM ，∵S ∵BEF ＝3S ∵EMF ＝3S ∵DEF ；故∵正确．故选：B ．【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．29．如图，将长方形纸片ABCD 沿AE 折叠，使点D 恰好落在BC 边上点F 处．若6AB =，10AD =，则EC 的长为（）A ．2B ．83C ．3D ．103【答案】B【分析】由翻折可知：AD=AF=10．DE=EF ，设EC=x ，则DE=EF=6-x ．在Rt∵ECF 中，利用勾股定理构建方程即可解决问题．【详解】解：∵四边形ABCD 是矩形，∵AD=BC=10，AB=CD=6，∵∵B=∵BCD=90°，由翻折可知：AD=AF=10，DE=EF ，设EC=x ，则DE=EF=6-x ．在Rt∵ABF 中，8BF ===，∵CF=BC -BF=10-8=2，在Rt∵EFC 中，EF 2=CE 2+CF 2，∵（6-x ）2=x 2+22， ∵x=83， ∵EC=83．故选：B ．【点睛】本题考查了折叠的性质，矩形的性质，勾股定理，熟练掌握方程的思想方法是解题的关键．30．如图，已知长方形ABCD 中6cm AB =，10cm BC =，在边CD 上取一点E ，将ADE 折叠使点D 恰好落在BC 边上的点F ，CE 的长是（）A ．3B ．2.5C ．83D ．2【答案】C【分析】要求CE 的长，应先设CE 的长为x ，由将∵ADE 折叠使点D 恰好落在BC 边上的点F 可得Rt∵ADE∵Rt∵AFE ，所以AF=10cm ，EF=DE=6-x ；在Rt∵ABF 中由勾股定理得：AB 2+BF 2=AF 2，已知AB 、AF 的长可求出BF 的长，又CF=BC -BF=10-BF ，在Rt∵ECF 中由勾股定理可得：EF 2=CE 2+CF 2，即：（6-x ）2=x 2+（10-BF ）2，将求出的BF 的值代入该方程求出x 的值，即求出了CE 的长．【详解】∵四边形ABCD 是矩形，∵AD=BC=10cm ，CD=AB=6cm ，根据题意得：Rt∵ADE∵Rt∵AFE ，∵∵AFE=90°，AF=10cm ，EF=DE ，设CE=x cm ，则DE=EF=CD -CE=（6-x ）cm ，在Rt∵ABF 中由勾股定理得：AB 2+BF 2=AF 2，即62+BF 2=102，∵BF=8cm ，∵CF=BC -BF=10-8=2（cm ），在Rt∵ECF 中，由勾股定理可得：EF 2=CE 2+CF 2，即（6-x ）2=x 2+22，∵36-12x +x 2=x 2+4，∵x =83，即CE=83cm ．故选：C ．【点睛】本题主要考查了图形的翻折变换以及勾股定理、全等三角形、方程思想等知识，关键是熟练掌握勾股定理，找准对应边．31．如图，将长方形ABCD 沿AC 折叠，使点B 落在点B '处，B C '交AD 于点E ，若125∠=︒，则2∠等于（）A ．25︒B ．30C ．50︒D ．60︒【答案】C【分析】根据折叠的性质得到∵ACB '=125∠=︒，由长方形的性质得到AD∵BC ，即可得到∵2=∵BCB '=2∵1=50︒.【详解】由折叠可知：∵ACB '=125∠=︒，∵四边形ABCD 是长方形，∵AD∵BC ，∵∵2=∵BCB '=2∵1=50︒，故选：C.【点睛】此题考查折叠的性质，长方形的对边平行的性质，平行线的性质：两直线平行内错角相等.32．如图，将长方形纸片ABCD 沿对角线BD 折叠，点C 的对应点为E.若CBD 35∠=︒，则ADE ∠的度数为（）．A ．15︒B ．20︒C ．25︒D ．30【答案】B【分析】根据折叠的性质和平行线的性质，可以得到ADB ∠和EDB ∠的度数，然后即可得到ADE ∠的度数．【详解】解：由折叠的性质可得，CDB EDB ∠∠=，AD //BC ，CBD 35∠=︒，CBD ADB 35∠∠∴==︒，C 90︒∠=，CDB 55∠∴=︒，EDB 55∠∴=︒，ADE EDB ADB 553520∠∠∠∴=-=︒-︒=︒．故选：B ．【点睛】本题考查平行线的性质，解答本题的关键是明确题意，利用数形结合的思想解答．33．如图，折叠长方形纸片ABCD 的一边AD ，使点D 落在BC 边上的点F 处，已知8AB cm =，10AD cm =，则折痕EF 的长为（）．A．2cm B．3cm C．4cm D．5cm【答案】D【分析】根据折叠可得，AD=AF，然后根据勾股定理求出BF，易得CF，再由勾股定理即可求得．【详解】根据折叠可得，AD=AF=10，DE=EF在Rt∵ABF中，根据勾股定理得，BF=6∵CF=4在Rt∵CEF中，EF2=CE2+CF2即EF2=（8－EF）2+42解得EF=5cm故选D【点睛】本题考查勾股定理，掌握折叠的性质是解题关键．34．如图所示，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C'处，折痕为EF，若EFC'∠=︒，那么ABE122∠的度数为（）A．24︒B．32︒C．30D．26︒【答案】D【分析】由折叠的性质知：∵EBC′、∵BC′F都是直角，∵BEF=∵DEF，因此BE∵C′F，那么∵EFC′和∵BEF互补，这样可得出∵BEF 的度数，进而可求得∵AEB 的度数，则∵ABE 可在Rt∵ABE 中求得．【详解】解：由折叠的性质知，∵BEF=∵DEF ，∵EBC′、∵BC′F 都是直角，∵BE∵C′F ，∵∵EFC′+∵BEF=180°，又∵∵EFC′=122°，∵∵BEF=∵DEF=58°，∵∵AEB=180°-∵BEF -∵DEF=64°，在Rt∵ABE 中，∵ABE=90°-∵AEB=26°．故选D ．【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．35．如图，将矩形纸片ABCD 沿BD 折叠，得到','BC D C D ∆与AB 交于点E ，若140∠=︒，则2∠的度数为（）A ．25︒B ．20︒C ．15︒D ．10︒【答案】D【分析】根据矩形的性质，可得∵ABD=40°，∵DBC=50°，根据折叠可得∵DBC'=∵DBC=50°，最后根据∵2=∵DBC'-∵DBA 进行计算即可．【详解】解：140,//CD AB ∠=︒，40,50ABD DBC ∴∠=︒∠=︒，由折叠可知'50DBC DBC ∠=∠=︒，2504010DBC ABD '∴∠=∠-∠=︒-︒=︒．故选：D ．【点睛】本题考查了长方形性质，平行线性质，折叠性质，角的有关计算的应用，关键是求出∵DBC′和∵DBA 的度数．36．如图，在长方形ABCD 中，将∵ABC 沿AC 对折至∵AEC 位置，CE 与AD 交于点F ，如果AB ＝2，BC ＝4，则AF 的长是（）．A ．2B ．2.5C ．2.8D ．3【答案】B【分析】根据题意，根据轴对称的性质，得AB=AE=CD=2，BC=AD=4；通过证明AEF CDF △≌△得=EF FD ，再通过直角AEF 中勾股定理，计算得AF 的长．【详解】根据题意得：AB=AE=CD=2，BC=AD=4设AF=x ，则FD=AD -AF=4-x∵90AEC D AFE DFC AE CD ⎧∠=∠=⎪∠=∠⎨⎪=⎩∵AEF CDF △≌△∵=EF FD∵4EF FD x ==-∵222AE EF AF +=∵()22224x x +-=∵ 2.5x =∵AF 的长是2.5故选：B ．【点睛】本题考查了全等三角形、矩形、勾股定理、一元一次方程、轴对称的知识；解题的关键是熟练掌握全等三角形、矩形、勾股定理、轴对称的性质，从而完成求解．37．如图，矩形ABCD 沿着对角线BD 进行折叠，使点C 落在C '处，BC '交AD 于点E ，16AD =，8AB =，则DE 的长（）．A ．10B ．6C ．8D ．【答案】A【分析】先根据翻折变换的性质得出CD=C′D ，∵C=∵C′=90°，再设DE=x ，则AE=16-x ，由全等三角形的判定定理得出Rt∵ABE∵Rt∵C′DE ，可得出BE=DE=x ，在Rt∵ABE 中利用勾股定理即可求出x 的值，进而得出DE 的长．【详解】解：∵Rt DC B '△由Rt DCB △翻折而成，∵8CD C D AB '===，90C C '∠=∠=︒，设DE x =，则16AE x =-，∵90A C '∠=∠=︒，AEB DEC '∠=∠，∵ABE C DE '∠=∠，在Rt ABE △与Rt C DE '△中，90A C '∠=∠=︒，AB C D '=，ABE C DE '∠=∠∵Rt Rt ABE C DE '≌△△，∵BE DE x ==，在Rt ABE △中，222AB AE BE +=，即()222816x x +-=，解得10x =，即10DE =，故选A ．【点睛】本题考查的是翻折变换的性质及勾股定理，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．38．如图，长方形ABCD 中，AD BC 6==，10AB CD ==，点E 为射线DC 上的一个动点，ADE 与AD E '关于直线AE 对称，当'AD B 为直角三角形时，DE 的长为() A ．2或8B ．83或18C ．83或2D ．2或18【答案】D【分析】分两种情况：当E 点在线段DC 上时，当E 点在线段DC 的延长线上时，利用全等三角形的判定和性质得出答案即可．【详解】解：分两种情况讨论：∵当E 点在线段DC 上时，AD E '△∵ADE ，90AD E D '∴∠=∠=︒，90AD B '∠=︒，180AD B AD E ''∴∠+∠=︒，B ∴、D 、E 三点共线，1122ABE S BE AD AB AD AD AD ''=⋅=⋅=，， BE AB 10∴==，8BD '===，1082DE D E '∴==-=；∵当E 点在线段DC 的延长线上时，如下图，90ABD CBE ABD BAD ''''''∠+∠=∠+∠=︒，CBE BAD ''∴∠=∠，在ABD ''△和BEC △中，D BCE AD BCBAD CBE '''''∠=∠⎧⎪=⎨⎪∠=∠'⎩， ABD ''∴△∵BEC ，BE AB 10∴==，8BD ''==，81018DE D E BD BE ''''∴==+=+=，综上所知，DE 2=或18，故选：D ．【点睛】本题考查翻折的性质、三角形全等的判定与性质、勾股定理、掌握翻折的性质、分类探讨的思想方法是解决问题的关键．39．如图，四边形ABCD 是矩形纸片，AB ＝2．对折矩形纸片ABCD ，使AD 与BC 重合，折痕为EF ；展平后再过点B 折叠矩形纸片，使点A 落在EF 上的点N ，折痕BM 与EF 相交于点Q ；再次展平，连接BN ，MN，延长MN交BC于点G．有如下结论：∵∵ABN＝60°；∵AM＝1；∵AB∵CG；∵BMG是等边三角形；∵点P为线段BM上一动点，点H是BN的中点，则PN＋PH．其中正确结论有（）A．5个B．4个C．3个D．2个【答案】B【分析】∵根据折叠的性质得出AE=BE，AB=BN，∵NEB=90°，再根据含30度的直角三角形判定定理即可得出∵ENB ＝30°，即可得出∵ABN＝60°；∵根据折叠的性质得出∵ABM＝∵NBM＝30°，设AM=x，根据勾股定理即可求出AM的值；∵直接根据矩形的性质即可得出；∵根据∵ABM＝30°，得出∵MBG＝∵BMA＝60°，再根据折叠的性质和等量代换即可得出∵BGM是等边三角形；∵根据点H是BN的中点即矩形的性质得出BH＝BE，结合题意得出PE＝PH，再根据三点共线时值最小及勾股定理即可判断．【详解】解：由折叠可知，AE=BE，AB=BN，∵NEB=90°，在Rt∵BEN中，∵BN＝AB＝2BE，∵∵ENB＝30°，∵∵ABN＝60°，故∵正确；由折叠可知，∵ABM＝∵NBM＝30°，设AM=x，则BM=2x，x2+22=(2 x)2，∵x＞0，解得：x，即AM =∵错误； ∵∵ABG ＝90°，∵AB ∵CG ，故∵正确；∵∵ABM ＝30°，∵∵MBG ＝∵BMA ＝60°，由折叠可知，∵BMG ＝∵BMA ＝60°，∵∵MBG ＝∵BMG ＝∵MGB ＝60°,∵∵BGM 是等边三角形，故∵正确，连接PE ．∵点H 是BN 的中点，∵BH ＝BE ＝1，∵∵MBH ＝∵MBE ，∵E 、H 关于BM 对称，∵PE ＝PH ，∵PH +PN ＝PE +PN ，∵E 、P 、N 共线时，PH +PN 的值最小，EN ∵正确，故选为B ．【点睛】本题考查翻折变换、等边三角形的判定和性质、直角三角形中30度角的判断、轴对称最短问题等知识，解题的关键是灵活运用所学知识解决问题，属于中考填空题中的压轴题．40．如图，矩形纸片,,ABCD AB a BC b ==，满足12b a b <<，将此矩形纸片按下面顺序折叠，则图4中MN 的长为（用含,a b 的代数式表示）（）A ．2b a -B ．22b a -C ．32b a +D ．12b a + 【答案】B【分析】如图3中，由折叠的性质可得PQ ＝BC ＝b ，A 1F ＝a ﹣12b ，∵PEQ 是等腰直角三角形，进而可得∵MNE 是等腰直角三角形，然后根据等腰直角三角形的性质可得EG =12MN ，而12EG EF A F =-，进一步即可求得答案．【详解】解：如图3中，由折叠的性质可得PQ ＝BC ＝b ，A 1F ＝a ﹣12b ，∵EPQ =11904522APQ ∠=⨯︒=︒，∵EQP =11904522DQP ∠=⨯︒=︒， ∵∵PEQ =90°，∵∵PEQ 是等腰直角三角形，如图4，∵MN ∵PQ ，∵∵MNE 是等腰直角三角形，∵EG ∵MN ，∵EG=MG=NG =12MN ， ∵12EG EF A F =-=a ﹣2（a ﹣12b ）＝b ﹣a ， ∵MN =2EG =22b a -．故选：B∵【点睛】本题考查了矩形的性质、折叠的性质以及等腰直角三角形的判定与性质，正确理解题意、熟练掌握等腰直角三角形的判定和性质是解题的关键．41．将矩形纸片 ABCD 按如图所示的方式折叠，得到菱形 AECF ．若 AB ＝3，则 BC 的长为（）AB ．2C ．1.5 D【答案】D【分析】设BC x =，先根据矩形的性质可得90,B AD BC ∠=︒=，再根据折叠的性质可得,,90OA AD x OC BC x COE B ====∠=∠=︒，从而可得OA OC =，又根据菱形的性质可得AE CE =，然后根据三角形全等的判定定理与性质可得90AOE COE ∠=∠=︒，从而可得点,,A O C 共线，由此可得2AC x =，最后在Rt ABC 中，利用勾股定理即可得．【详解】设BC x =，四边形ABCD 是矩形，90,B AD BC x ∴∠=︒==，由折叠的性质得：,,90OA AD x OC BC x COE B ====∠=∠=︒，OA OC x ∴==，四边形AECF 是菱形，AE CE ∴=，。

矩形中的折叠问题

矩形中的折叠问题山东省枣庄市峄城区第二十八中学潘歌邮编：277300折叠问题（对称问题）是近几年来中考出现频率较高的一类题型，学生往往由于对折叠的实质理解不够透彻，导致对这类中档问题失分严重。

对于折叠问题（翻折变换）实质上就是轴对称变换．对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析，从中抽象出基本图形的基本规律，找到解决这类问题的常规方法。

一、求角度例1 如图把一张矩形纸片ABCD 沿EF 折叠后，点C D ，分别落在C D ''，的位置上，EC '交AD 于点G ．已知58EFG ∠=°，那么BEG ∠= °．【解析】在矩形折叠问题中，折叠前后的对应角相等来解决。

解：根据矩形的性质AD ∥BC ，有∠EFG =∠FEC =58°，再由折叠可知，∠FEC =∠C ′EF =58°，由此得∠BEG =64°例2 将一张长方形纸片按如图的方式折叠，其中BC ，BD 为折痕，折叠后BG 和BH 在同一条直线上，∠CBD = 度．【解析】折叠前后的对应角相等．解：BC 、BD 是折痕，所以有∠ABC = ∠GBC ，∠EBD = ∠HBD 则∠CBD = 90°．例4 如图四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若CD ＝6，则AF 等于（）（A ）34 （B ）33 （C ）24 （D ）8【解析】在矩形折叠问题中，求折痕等线段长度时，往往利用轴对称性转化相等的线段，再借助勾股定理构造方程来解决．解：由折叠可知，AE =AB =DC =6，在Rt △ADE 中AD =6，DE =3由勾股定理，得AD =33，设EF =x ，则FC =x -33，在Rt △EFC 中由勾股定理求得x =32,则EF =32，在Rt △AEF 中，由勾股定理得AF =A ．A B CDEFA B E C D F G C 'D 'C三、求图形面积例5如图3-1所示，将长为20cm ，宽为2cm 的长方形白纸条，折成图3-2所示的图形并在其一面着色，则着色部分的面积为（）A ．234cmB ．236cmC ．238cmD ．240cm解析：折叠后重合部分为直角三角形．解：重合部分其面积为22122=⨯⨯，因此着色部分的面积=长方形纸条面积－两个重合部分三角形的面积，即20×2－2×2＝36（2cm ）．故选B ．∴62 + (8 - x )2 = x2解得x = 254所以，阴影部分的面积S △FBD = 12 FD ×AB = 12 ×254 ×6 = 754 cm2四、数量及位置关系例7 如图将矩形纸片ABCD 沿对角线BD 折叠，点C 落在点E处，BE 交AD 于点F ，连结AE ．证明：（1）BF DF =．（2）AE BD ∥ 【解析】（1）欲证明BF =DF ，只需证∠FBD =∠FDB ；（2）欲证明AE BD ∥，则需证AEB DBE ∠=∠。

矩形折叠中的相关问题

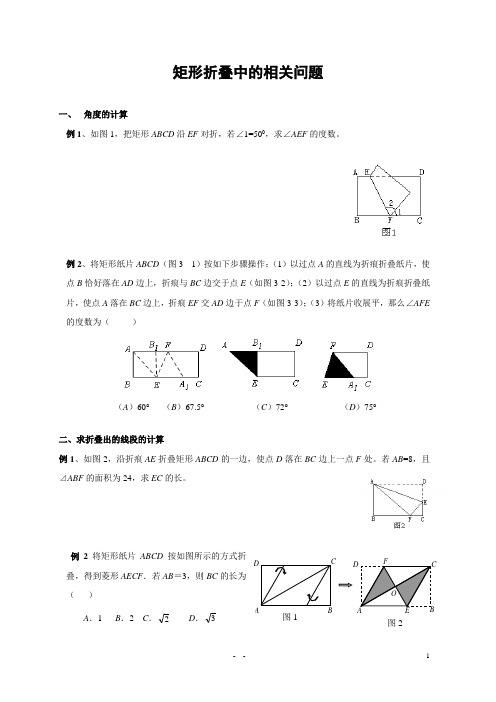
矩形折叠中的相关问题一、角度的计算例1、如图1，把矩形ABCD沿EF对折，若∠1=500，求∠AEF的度数。

例2、将矩形纸片ABCD（图3 -1）按如下步骤操作：（1）以过点A的直线为折痕折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E（如图3-2）；（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F（如图3-3）；（3）将纸片收展平，那么∠AFE 的度数为（）（A）60°（B）67.5°（C）72°（D）75°二、求折叠出的线段的计算例1、如图2，沿折痕AE折叠矩形ABCD的一边，使点D落在BC边上一点F处。

若AB=8，且⊿ABF的面积为24，求EC的长。

例2将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝3，则BC的长为（）A．1 B．2 C．2D．3BD FOD图2图1例3、如图3，是一矩形的纸片，其中AD =2.5，AB =1.5。

按下列步骤折叠：将其对折，使AB 落在AD 上，折痕为AE ，再将⊿ABE 以BE 为折痕向右折叠，AE 与DC 交于点F ，则CF 的长是( ) A .0.5 B .0.75 C .1 D .1.25三、折痕的计算例1、有一矩形纸片，其中宽AB =6cm ，长BC =8cm 。

现按如图4所示的方法作折纸游戏，将它折叠使B 点与D 点重合，求折痕EF 的长。

例2、将矩形纸片ABCD 折叠，使点C 与点A 重合，折痕为GF. AB=6，BC=8，求GF 的长四、面积的计算例1、如图5，将矩形ABCD 沿着对角线BD 折叠，使点C 落在点'C 处，'BC 交AD 于E 。

已知AD =8，AB =4，求⊿BDE 的面积。

AEFDBC G例2、如图1，是一矩形纸片ABCD中，AD=4cm，AB=10cm，现作折纸游戏，使点B与点D重合，折痕为EF，求DE的长。

沪科版2019-2020年八年级数学下册思想方法专题：矩形中的折叠问题(含答案解析)

思想方法专题：矩形中的折叠问题——体会矩形折叠中的方程思想及数形结合思想◆类型一矩形折叠问题中求角的度数1．如图，将矩形ABCD 沿AE 折叠，使点D 落在点D′处．若∠CED′＝60°，则∠BAD′的大小是( ) A ．30° B ．45° C ．50° D ．60°第1题图第2题图2．如图，将矩形纸片ABCD 折叠，使顶点B 落在边AD 上的点E 处，折痕FG 交AB 于点F ，交BC 于点G ，连接BE.若∠AEF ＝20°，则∠FGB 的度数为( )A ．25°B ．30°C ．35°D ．40° ◆类型二矩形折叠问题中求长度 3．(2017·安顺中考)如图，在矩形纸片ABCD 中，AD ＝4cm ，把纸片沿AC 折叠，点B 落在点E 处，AE 交DC 于点O.若AO ＝5cm ，则AB 的长为( )A ．6cmB ．7cmC ．8cmD ．9cm第3题图第4题图4．(2017·芜湖市期中)将矩形纸片ABCD 按如图折叠，得到菱形AECF.若AB ＝3，则BC 的长为( ) A ．2 B ．1 C . 3 D . 5 5．(2017·宜宾中考)如图，在矩形ABCD 中，BC ＝8，CD ＝6，将△ABE 沿BE 折叠，使点A 恰好落在对角线BD 上的点F 处，则DE 的长是【方法18①】( )A ．3B .245C ．5D .8916第5题图第6题图6．(2017·芜湖繁昌县期中)将矩形纸片ABCD 按如图折叠，AE 、EF 为折痕，∠BAE ＝30°，BE ＝1.折叠后，点C 落在AD 边上的C 1处，并且点B 落在EC 1边上的B 1处．则EC 的长为( )A . 3B ．2C ．3D ．2 3 7．★(2017·安庆潜山县期末)如图，在矩形ABCD 中，AB ＝4，BC ＝6，点E 为BC 的中点，将△ABE 沿AE 折叠，使点B 落在矩形内的点F 处，连接CF ，则CF 的长为________．第7题图第8题图◆类型三矩形折叠问题中求面积8．(2017·阜阳市期末)如图，在矩形纸片ABCD中，AB＝4，BC＝8，将纸片沿EF折叠，使点C与点A 重合，则△AEF的面积是()A．8 B．10 C．12 D．149．(2017·鄂州中考)如图，将矩形ABCD沿对角线AC翻折，点B落在点F处，FC交AD于点E.(1)求证：△AFE≌△CDE；(2)若AB＝4，BC＝8，求图中阴影部分的面积．参考答案与解析1．A 2.C 3.C4．C解析：∵四边形AECF为菱形，∴AE＝CE，∠FCO＝∠ECO.由折叠可得∠ECO＝∠ECB.又∵∠FCO＋∠ECO＋∠ECB＝90°，∴∠FCO＝∠ECO＝∠ECB＝30°.∵四边形ABCD是矩形，∴∠B＝90°，∴CE＝2BE，∴AE＝2BE.∵AB＝AE＋BE＝3，∴BE＝1，CE＝AE＝2，∴BC＝CE2－BE2＝ 3.故选C.5．C解析：四边形ABCD是矩形，∴∠A＝90°，AB＝CD＝6，AD＝BC＝8，∴BD＝BC2＋CD2＝10.由折叠可得BF ＝AB ＝6，EF ＝AE ，∠BFE ＝∠A ＝90°，∴∠DFE ＝90°.设DE ＝x ，则EF ＝AE ＝8－x .在Rt △DEF 中，DE 2＝EF 2＋DF 2，即x 2＝(8－x )2＋(10－6)2，解得x ＝5.即DE ＝5.故选C.6．B 解析：∵四边形ABCD 是矩形，∴∠B ＝∠BAD ＝90°.∵∠BAE ＝30°，BE ＝1，∴AE ＝2BE ＝2×1＝2，∠AEB ＝90°－∠BAE ＝90°－30°＝60°，∠EAC 1＝∠BAD －∠BAE ＝90°－30°＝60°.由折叠可得∠AEB 1＝∠AEB ＝60°.∴∠AC 1E ＝180°－∠EAC 1－∠AEB 1＝60°，∴△AEC 1是等边三角形，∴EC 1＝AE ＝2.由折叠可得EC ＝EC 1＝2.故选B.7.185 解析：如图，连接BF 交AE 于点H .∵BC ＝6，点E 为BC 的中点，∴BE ＝CE ＝12BC ＝3.由折叠可得BF ⊥AE ，BH ＝12BF .∴在Rt △ABE 中，由勾股定理得AE ＝AB 2＋BE 2＝5.∵S △ABE ＝12AB ·BE ＝12AE ·BH ，∴BH＝125，∴BF ＝2BH ＝245.由折叠可得FE ＝BE ，∴FE ＝BE ＝CE ，∴∠EBF ＝∠BFE ，∠ECF ＝∠EFC .又∵∠EBF ＋∠BFE ＋∠EFC ＋∠ECF ＝180°，∴∠BFE ＋∠EFC ＝90°，即∠BFC ＝90°.在Rt △BFC 中，由勾股定理得CF ＝BC 2－BF 2＝62－⎝⎛⎭⎫2452＝185.8．B 解析：∵四边形ABCD 是矩形，∴∠D ＝90°，AD ＝BC ＝8，CD ＝AB ＝4.由折叠可得AG ＝CD ＝4，∠G ＝∠D ＝90°，DF ＝GF .设AF ＝x ，则GF ＝DF ＝8－x .在Rt △AGF 中，AF 2－GF 2＝AG 2，即x 2－(8－x )2＝42，解得x ＝5，即AF ＝5.∴S △AEF ＝12AF ·AB ＝12×5×4＝10.故选B.9．(1)证明：∵四边形ABCD 是矩形，∴AB ＝CD ，∠B ＝∠D ＝90°.由折叠可得∠F ＝∠B ，AF ＝AB ，∴AF ＝CD ，∠F ＝∠D .在△AFE 和△CDE 中，∵⎩⎪⎨⎪⎧∠F ＝∠D ，∠AEF ＝∠CED ，AF ＝CD ，∴△AFE ≌△CDE .(2)解：∵四边形ABCD 是矩形，∴∠D ＝90°，CD ＝AB ＝4，AD ＝BC ＝8.由折叠可得CF ＝BC ＝8.由(1)可知△AFE ≌△CDE ，∴EF ＝DE .设EF ＝DE ＝x ，则CE ＝8－x .在Rt △CED 中，由勾股定理得DE 2＋CD 2＝CE 2，即x 2＋42＝(8－x )2，解得x ＝3，∴DE ＝3，∴AE ＝AD －DE ＝5，∴S 阴影＝12AE ·CD ＝12×5×4＝10.。

初中数学中的折叠问题

初中数学中的折叠问题一、矩形中的折叠折叠后BG 和BH 在再过点A ′折叠使边与对角线BD 重形中根据勾股定合，然后再沿着则∠DFB 等于的位置，已知重合部分是以折痕为底边的等腰三角形理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD 的边长为8，将其沿EF 折叠，则图中①②③④四个三角形的周长之和为折叠前后对应边相等9．如图，将边长为4的正方形ABCD 沿着折痕EF 折叠，使点B落在边AD 的中点G 处，求四边形BCFE 的面积注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等 10．如图，将一个边长为1的正方形纸片ABCD 折叠，使点B 落在边AD 上不与A 、D 重合．MN 为折痕，折叠后B ’C ’与DN 交于P ．(1)连接BB ’，那么BB ’与MN 的长度相等吗？为什么？(2)设BM =y ，AB ’=x ，求y 与x 的函数关系式；(3)猜想当B 点落在什么位置上时，折叠起来的梯形MNC ’B ’面积最小？并验证你的猜想．二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）C题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm的长方形纸条成如图所示的形状，那么折痕PQ的长是注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ 14．如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（）本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b∠GFC=140°，图c中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm的长方形纸片ABCD，沿对称轴EF折叠成如图的形状，若折叠后，AB与CD间的距离为60cm，则原纸片的宽AB是（）16．一根30cm、宽3cm的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P的长度相等，则最初折叠时，求MA的长三、三角形中的折叠实践与运用：(1)将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图③）；再沿过点E的直线折叠，使点D落在BE上的点D’处，折痕为EG（如图④）；再展平纸片（如图⑤）．求图⑤中∠α的大小．由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

中考总复习专题--折叠问题

轴 ∴△BQC≌△BQP
M
A
D
∴PB=BC=1
N是AD、BC 上的中点，BN=
∴PN= 3
2
∴MP=1-
3 2
∵M、1 2ຫໍສະໝຸດ PQ∴∠BP(2N)由=3（0°1）∴得∠PBBNN==12 6B0P°,
B
N
C
又∵BQ平分∠PBC，BQ=2QC=
23 3
∴PQ=
1 2
BQ=
3 3
. ∴PQ²=
1 3
即以PQ为边长的正方形面积等于
△ABD≌△C’DB BC’=∠C’DE,∠C’DB=∠CD
③相等的线段:
B=∠ABD
AE=C’E,BC’=BC=AD, AB=CD=C’D,BE=ED
返回目录
第二类相对顶点重合
这类折叠问题的基本图形：
A
ED
O
BF
C
引例：已知：如图，平行四边形ABCD
的对角线AC的垂直平分线与边AD、BC
分别交于E、F，求证：四边形AFCE是
返回
4．已知：将矩形ABCD沿着
E C'
直线BD折叠，使C落在C’处， BC’交AD于E ,AD=8,AB=4.
A
D
求△BED面积。（2000，山
西）
B
解二：作EF⊥BD于F
F
C
在矩形ABCD中 AD ∥ BC ∴EF:AB=DF:AD
∴∠DBC=∠EDB 当矩形ABCD沿着直线BD折
BD=4 5 ，DF=2 5
（2）常常利用矩形的对边平行且相等
和矩形折叠形成的直角三角形来综合解题
（3）前三道题的结论可以推广到平行四边形上
（4）这类折叠问题的常用图形： C'

人教版八年级数学下册-思想方法专题：矩形中的折叠问题

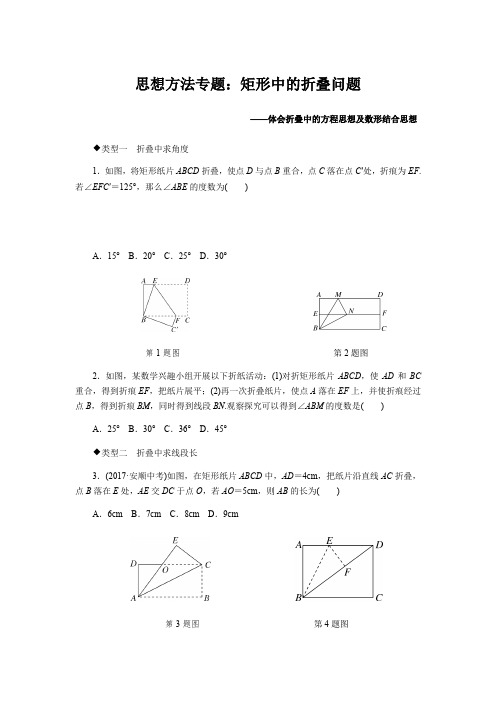
思想方法专题：矩形中的折叠问题——体会折叠中的方程思想及数形结合思想◆类型一折叠中求角度1．如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF.若∠EFC′＝125°，那么∠ABE的度数为()A．15° B．20° C．25° D．30°第1题图第2题图2．如图，某数学兴趣小组开展以下折纸活动：(1)对折矩形纸片ABCD，使AD和BC 重合，得到折痕EF，把纸片展平；(2)再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN.观察探究可以得到∠ABM的度数是()A．25° B．30° C．36° D．45°◆类型二折叠中求线段长3．(2017·安顺中考)如图，在矩形纸片ABCD中，AD＝4cm，把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若AO＝5cm，则AB的长为()A．6cm B．7cm C．8cm D．9cm第3题图第4题图4．(2017·宜宾中考)如图，在矩形ABCD 中，BC ＝8，CD ＝6，将△ABE 沿BE 折叠，使点A 恰好落在对角线BD 上的F 处，则DE 的长是( )A ．3 B.245 C ．5 D.89165．★(2016·威海中考)如图，在矩形ABCD 中，AB ＝4，BC ＝6，点E 为BC 的中点，将△ABE 沿AE 折叠，使点B 落在矩形内的点F 处，连接CF ，则CF 的长为________．◆类型三折叠中求面积6．(2017·鄂州中考)如图，将矩形ABCD 沿对角线AC 翻折，点B 落在点F 处，FC 交AD 于E .(1)求证：△AFE ≌△CDE ；(2)若AB ＝4，BC ＝8，求图中阴影部分的面积．7．★(2016·福州中考)如图，矩形ABCD中，AB＝4，AD＝3，M是边CD上的一点，将△ADM沿直线AM对折，得到△ANM.(1)当AN平分∠MAB时，求DM的长；(2)连接BN，当DM＝1时，求△ABN的面积．参考答案与解析1．B解析：由折叠可知∠EFC＝∠EFC′＝125°.∵在矩形ABCD中，AD∥BC，∴∠DEF ＝180°－125°＝55°.根据折叠可知∠BEF＝∠DEF＝55°，∴∠BED＝110°.∵四边形ABCD为矩形，∠A＝90°，∴∠ABE＝110°－90°＝20°.故选B.2．B 3.C 4.C5. 185解析：如图，连接BF 交AE 于H ，由折叠的性质可知BE ＝FE ，AB ＝AF ，∠BAE ＝∠F AE ，∴AH ⊥BF ，BH ＝FH .∵BC ＝6，点E 为BC 的中点，∴BE ＝12BC ＝3.又∵AB ＝4，∴在Rt △ABE 中，由勾股定理得AE ＝AB 2＋BE 2＝5.∵S △ABE ＝12AB ·BE ＝12AE ·BH ，∴BH ＝125，则BF ＝2BH ＝245.∵E 是BC 的中点，∴FE ＝BE ＝EC ，∴∠BFC ＝90°.在Rt △BFC 中，由勾股定理得CF ＝BC 2－BF 2＝62－⎝⎛⎭⎫2452＝185.6．(1)证明：∵四边形ABCD 是矩形，∴AB ＝CD ，∠B ＝∠D ＝90°.∵将矩形ABCD 沿对角线AC 翻折，点B 落在点F 处，∴∠F ＝∠B ，AB ＝AF ，∴AF ＝CD ，∠F ＝∠D .在△AFE与△CDE 中，⎩⎪⎨⎪⎧∠F ＝∠D ，∠AEF ＝∠CED ，AF ＝CD ，∴△AFE ≌△CDE .(2)解：∵AB ＝4，BC ＝8，∴CF ＝AD ＝8，AF ＝CD ＝AB ＝4.∵△AFE ≌△CDE ，∴EF ＝DE .在Rt △CED 中，由勾股定理得DE 2＋CD 2＝CE 2，即DE 2＋42＝(8－DE )2，∴DE ＝3，∴AE ＝8－3＝5，∴S 阴影＝12×4×5＝10. 7．解：(1)由折叠性质得△ANM ≌△ADM ，∴∠MAN ＝∠DAM .∵AN 平分∠MAB ，∴∠MAN ＝∠NAB ，∴∠DAM ＝∠MAN ＝∠NAB .∵四边形ABCD 是矩形，∴∠DAB ＝90°，∴∠DAM ＝30°，∴AM ＝2DM .在Rt △ADM 中，∵AD ＝3，∴由勾股定理得AM 2－DM 2＝AD 2，即(2DM )2－DM 2＝32，解得DM ＝ 3.(2)延长MN 交AB 的延长线于点Q ，如图所示．∵四边形ABCD 是矩形，∴AB ∥DC ，∴∠DMA ＝∠MAQ ，由折叠性质得△ANM ≌△ADM ，∴∠ANM ＝∠D ＝90°，∠DMA ＝∠AMQ ，AN ＝AD ＝3，MN ＝MD ＝1，∴∠MAQ ＝∠AMQ ，∴MQ ＝AQ .设NQ ＝x ，则AQ ＝MQ ＝MN ＋NQ ＝1＋x .∵∠ANM ＝90°，∴∠ANQ ＝90°.在Rt △ANQ 中，由勾股定理得AQ 2＝AN2＋NQ2，即(x＋1)2＝32＋x2，解得x＝4，∴NQ＝4，AQ＝5.∵△NAB和△NAQ在AB边上的高相等，AB＝4，AQ＝5，∴S△NAB＝45S△NAQ＝45×12×AN·NQ＝45×12×3×4＝245.19.2.3 一次函数与方程、不等式一．选择题（共8小题）1．一次函数y=kx+b的图象如图所示，则方程kx+b=0的解为（）A．x=2B．y=2C．x=﹣1D．y=﹣12．一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x 的方程kx+b=0的解为（）A．x=﹣1B．x=2C．x=0D．x=33．一元一次方程ax﹣b=0的解x=3，函数y=ax﹣b的图象与x轴的交点坐标为（）A．（3，0）B．（﹣3，0）C．（a，0）D．（﹣b，0）4．已知方程kx+b=0的解是x=3，则函数y=kx+b的图象可能是（）A．B．C．D．5．若方程x﹣3=0的解也是直线y=（4k+1）x﹣15与x轴的交点的横坐标，则k的值为（）A．﹣1B．0C．1D．±16．如图，直线y1=x+b与y2=kx﹣1相交于点P，点P的横坐标为﹣1，则关于x的不等式x+b＞kx﹣1的解集在数轴上表示正确的是（）A．B．C．D．7．如图，直线y=﹣x+m与y=nx+4n（n≠0）的交点的横坐标为﹣2，则关于x的不等式﹣x+m ＞nx+4n＞0的整数解为（）A．﹣1B．﹣5 C．﹣4D．﹣38．如图，一次函数y=kx+b的图象经过A、B两点，则不等式kx+b＜0的解集是（）A．x＜0B．0＜x＜1C．x＜1 D．x＞1二．填空题（共10小题）9．若直线y=2x+b与x轴交于点（﹣3，0），则方程2x+b=0的解是_________．10．如图是一次函数y=kx+b的图象，则方程kx+b=0的解为_________．11．一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为_________．12．如图，已知直线y=ax﹣b，则关于x的方程ax﹣1=b的解x=_________．13．如图，直线y=kx+b分别交x轴和y轴于点A、B，则关于x的方程kx+b=0的解为_________．14．如图，已知函数y=2x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），根据图象可得方程2x+b=ax﹣3的解是_________．15．如图，已知函数y=2x+b与函数y=kx﹣3的图象交于点P，则不等式kx﹣3＞2x+b的解集是_________．16．如图，直线y=kx+b过A（﹣1，2）、B（﹣2，0）两点，则0≤kx+b≤﹣2x的解集为_________．17．一次函数y1=kx+b与y2=x+a的图象如图，则kx+b＞x+a的解集是_________．18．如图，函数y=kx和的图象相交于A （a，2），则不等式的解集为_________．三．解答题（共4小题）19．如图，根据函数y=kx+b（k，b是常数，且k≠0）的图象，求：（1）方程kx+b=0的解；（2）式子k+b的值；（3）方程kx+b=﹣3的解．20．如图，直线l1：y=2x与直线l2：y=kx+3在同一平面直角坐标系内交于点P．（1）写出不等式2x＞kx+3的解集：_________；（2）设直线l2与x轴交于点A，求△OAP的面积．21．在平面直角坐标系x0y中，直线y=kx+b（k≠0）过（1，3）和（3，1）两点，且与x轴、y轴分别交于A、B两点，求不等式kx+b≤0的解．22．在直角坐标系xOy中，直线y=kx+b（k≠0）经过（﹣2，1）和（2，3）两点，且与x 轴、y轴分别交于A、B两点，求不等式kx+b≥0的解集．19.2.3 一次函数与方程、不等式一．选择题（共8小题）1．一次函数y=kx+b的图象如图所示，则方程kx+b=0的解为（）A．x=2B．y=2C．x=﹣1D．y=﹣12．一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x 的方程kx+b=0的解为（）A．x=﹣1B．x=2C．x=0D．x=33．一元一次方程ax﹣b=0的解x=3，函数y=ax﹣b的图象与x轴的交点坐标为（）A．（3，0）B．（﹣3，0）C．（a，0）D．（﹣b，0）4．已知方程kx+b=0的解是x=3，则函数y=kx+b的图象可能是（）A．B．C．D．5．若方程x﹣3=0的解也是直线y=（4k+1）x﹣15与x轴的交点的横坐标，则k的值为（）A．﹣1B．0C．1D．±16．如图，直线y1=x+b与y2=kx﹣1相交于点P，点P的横坐标为﹣1，则关于x的不等式x+b＞kx﹣1的解集在数轴上表示正确的是（）A．B．C．D．7．如图，直线y=﹣x+m与y=nx+4n（n≠0）的交点的横坐标为﹣2，则关于x的不等式﹣x+m ＞nx+4n＞0的整数解为（）A．﹣1B．﹣5 C．﹣4D．﹣38．如图，一次函数y=kx+b的图象经过A、B两点，则不等式kx+b＜0的解集是（）A．x＜0B．0＜x＜1C．x＜1 D．x＞1二．填空题（共10小题）9．若直线y=2x+b与x轴交于点（﹣3，0），则方程2x+b=0的解是_________．10．如图是一次函数y=kx+b的图象，则方程kx+b=0的解为_________．11．一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为_________．12．如图，已知直线y=ax﹣b，则关于x的方程ax﹣1=b的解x=_________．13．如图，直线y=kx+b分别交x轴和y轴于点A、B，则关于x的方程kx+b=0的解为_________．14．如图，已知函数y=2x+b和y=ax﹣3的图象交于点P（﹣2，﹣5），根据图象可得方程2x+b=ax﹣3的解是_________．15．如图，已知函数y=2x+b与函数y=kx﹣3的图象交于点P，则不等式kx﹣3＞2x+b的解集是_________．16．如图，直线y=kx+b过A（﹣1，2）、B（﹣2，0）两点，则0≤kx+b≤﹣2x的解集为_________．17．一次函数y1=kx+b与y2=x+a的图象如图，则kx+b＞x+a的解集是_________．18．如图，函数y=kx和的图象相交于A （a，2），则不等式的解集为_________．三．解答题（共4小题）19．如图，根据函数y=kx+b（k，b是常数，且k≠0）的图象，求：（1）方程kx+b=0的解；（2）式子k+b的值；（3）方程kx+b=﹣3的解．20．如图，直线l1：y=2x与直线l2：y=kx+3在同一平面直角坐标系内交于点P．（1）写出不等式2x＞kx+3的解集：_________；（2）设直线l2与x轴交于点A，求△OAP的面积．21．在平面直角坐标系x0y中，直线y=kx+b（k≠0）过（1，3）和（3，1）两点，且与x轴、y轴分别交于A、B两点，求不等式kx+b≤0的解．22．在直角坐标系xOy中，直线y=kx+b（k≠0）经过（﹣2，1）和（2，3）两点，且与x 轴、y轴分别交于A、B两点，求不等式kx+b≥0的解集．。

初中数学解题技巧专题---矩形中的折叠问题

第2页共4页
参考答案与解析．1 B 解析：由折叠可知∠EFC＝∠EFC′＝125°.∵在矩形 ABCD 中，AD∥BC，∴∠DEF
＝矩形180，°－∠1A2＝5°9＝0°5，5°∴.根∠据A折BE叠＝可11知0°∠－B9E0F°＝＝2∠0°D.故EF选＝B5.5°，∴∠BED＝110°.∵四边形 ABCD 为．2 B 3.C 4.C
点 A 恰好落在对角线 BD 上的 F 处，则 DE 的长是( )
．． 24
89
A 3 B. 5 C 5 D.16
5．★(2016·威海中考)如图，在矩形 ABCD 中，AB＝4，BC＝6，点 E 为 BC 的中点，将
△ABE 沿 AE 折叠，使点 B 落在矩形内的点 F 处，连接 CF，则 CF 的长为． ________
2．如图，某数第学1兴题趣图小组开展以下折纸活动：(1)对折矩形纸片第AB2C题D图，使 AD 和 BC
重合，得到折痕点 B，得到折痕
BEMF，，把同纸时片得展到平线；段(B2)N再.观一察次探折究叠可纸以片得，到使∠点AABM落的在度E数F 上是，( 并使) 折痕经过
A◆．类2型5°二
．． B 30° C 36° 折叠中求线段长
与△CDE 中，∠∠FA＝EF∠＝D∠，CED，∴△AFE≌△CDE. ＝， AF CD
(2)解：∵AB＝4，BC＝8，∴CF＝AD＝8，AF＝CD＝AB＝4.∵△AFE≌△CDE，∴EF ＝DE.在 △Rt CED 中，由勾股定理得＋＝，即 DE2 CD2 CE2 ＋＝－，∴ ＝， DE2 42 (8 DE)2 DE 3
．D 45°
3．(2017·安顺中考)如图，在矩形纸片 ABCD 中，AD＝4cm，把纸片沿直线 AC 折叠，

折叠几何综合专题---16道题目(含答案)

折叠几何综合专题---16道题目(含答案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN01如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E 处，过点E作EG∥CD交AF于点G，连接DG.(1)求证：四边形EFDG是菱形；(2)探究线段EG，GF，AF之间的数量关系，并说明理由；(3)若AG＝6，EG＝25，求BE的长．(1)证明：由折叠性质可得，EF ＝FD ，∠AEF ＝∠ADF ＝90°，∠EFA ＝∠DFA ，EG ＝GD ，∵EG ∥DC ，∴∠DFA ＝∠EGF ， ∴∠EFA ＝∠EGF ，∴EF ＝EG ＝FD ＝GD ，∴四边形EFDG 是菱形；(2)解：EG 2＝12GF ·AF .理由如下：如解图，连接ED ，交AF 于点H ，∵四边形EFDG 是菱形，∴DE ⊥AF ，FH ＝GH ＝12GF ，EH ＝DH ＝12DE ， ∵∠FEH ＝90°－∠EFA ＝∠FAE ，∠FHE ＝∠AEF ＝90°， ∴Rt △FEH ∽Rt △FAE ，∴EFAF ＝FHEF ，即EF 2＝FH ·AF ，又∵FH ＝12GF ，EG ＝EF ，∴EG 2＝12GF ·AF ；(3)解：∵AG ＝6，EG ＝25，EG 2＝12AF ·GF ，∴(25)2＝12(6＋GF )·GF ，解得GF ＝4或GF ＝－10(舍)，∴GF ＝4，∴AF ＝10.∵DF ＝EG ＝25，∴AD ＝BC ＝AF 2－DF 2＝45，DE ＝2EH ＝2EG 2－（12GF ）2＝8，∵∠CDE ＋∠DFA ＝90°，∠DAF ＋∠DFA ＝90°，∴∠CDE ＝∠DAF ，∵∠DCE ＝∠ADF ＝90°，∴Rt △DCE ∽Rt △ADF ，∴EC DF ＝DE AF ，即EC 25＝810，∴EC ＝855，∴BE ＝BC －EC ＝1255.02如图，将矩形ABCD 沿对角线BD 对折，点C 落在E 处，BE 与AD 相交于点F ，若DE ＝4，BD ＝8.(1)求证：AF ＝EF ；(2)求证：BF 平分∠ABD .证明：(1)在矩形ABCD 中，AB ＝CD ，∠A ＝∠C ＝90°， ∵△BED 是△BCD 对折得到的，∴ED ＝CD ，∠E ＝∠C ，∴ED ＝AB ，∠E ＝∠A ，(2分)又∵∠AFB ＝∠EFD ，∴△ABF ≌△EDF (AAS)，∴AF ＝EF ；(4分)(2)在Rt △BCD 中，∵DC ＝DE ＝4，BD ＝8，∴sin ∠CBD ＝DC BD ＝12， ∴∠CBD ＝30°，(5分)∴∠EBD ＝∠CBD ＝30°，∴∠ABF＝90°－30°×2＝30°，(7分)∴∠ABF＝∠EBD，∴BF平分∠ABD.(8分)03把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F 重合（E、F两点均在BD上），折痕分别为BH、DG。

专题2.3(1)矩形的折叠问题-中考数学二轮复习必会几何模型剖析(全国通用)

情况一：如图2，
C
由题意可得：DC´=DC=5,DM=4, ∴MC´=3,C´N=2.B N ´ E
对于△ENC´,设CE=x,则C´E=x,EN=4-x.
(4-x)2+22=x2, 解得:x=2.5, CE=2.5.
由勾股定理可得：
情况二：如图3，
易证C´F=CD=5, ∴NF=3,MF=2.
易证
知识梳理
矩形折叠
强化训练
提升能力
1.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG＞
60º.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与
3
∠BEG相等的角的个数为____.
2.如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D´、C´的位置,
50
一点，将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF=______.
E
D
【分析】有特殊位置关系必然有隐藏结论.
A
∴∠CEF=90º,
连接CE,易证
△CED≌△CEG(HL).
CE
=
易证△CDE∽△EAF, 可得：CD
F
EA EF
由CD=3 6,ED=EA=6. ∴CE=3 10 .
B
4 1C
∴∠KFH=75º,∠KFE=30º,
A
∵∠2=75º
3
10
5
,过点K作KP⊥BC交BC于P点，设KP=x,则
FP= 3 x,
B
EP=x.
∴x+ 3 x= 3＋1. 解得x=1.
K
H
G
∴BE=KE= 2 CF=KF=2
A
D
, 2+ 3+3

矩形的翻折问题课件

创新思考
鼓励学生发挥想象力，探索翻折问题的创新应用，培养他们的创新思维和实践能力。
THANKS
感谢观看
02
矩形翻折问题的基本解法
翻折线段的长度计算
总结词
翻折线段的长度计算是解决矩形翻折问题的关键步骤之一，需要利用几何知识来求解。
详细描述
在矩形翻折问题中，我们需要计算翻折后的线段长度。这通常涉及到利用勾股定理、相似三角形等几何知识来求解。具体计算方法包括通过已知的边长和角度，或者通过设定的变量来表示未知的边长，然后建立方程求解。
，理解空间关系和几何变换。
探索几何性质
矩形翻折问题涉及到几何图形的性质和特点，如对称性、角度、边长等，通过解决这类问题可以深入了解几何学的基本概念和性
质。
应用实际生活
矩形翻折问题在日常生活中有广泛的应用，如包装、折纸艺术、建筑设计等领域，通过解决这类问题可以帮助学生理解数学与实
际生活的联系。
在包装设计中的应用
包装设计中的矩形翻折问题主要涉及包装盒的结构设计和折叠工艺。
通过解决矩形翻折问题，包装设计师可以设计出结构稳定、易于生产和折叠的包装盒，同时保证其美观性和保护性。
例如，在食品包装设计中，包装设计师可能会遇到需要将矩形纸板翻折成特定形状的问题，以实现包装盒的结构稳定性和生产效率。
03
矩形翻折问题的实际应用
在建筑设计中的应用
建筑设计中的矩形翻折问题主要涉及建筑结构的稳定性、美观性和功能性。
例如，在建筑设计过程中，建筑师可能会遇到需要将矩形板材翻折成特定形状的问题，以实现建筑外观的独特性和功能性。
通过解决矩形翻折问题，建筑师可以设计出具有独特造型和优雅线条的建筑结构，同时保证其稳定性和安全性。