课后习题答案 (1)
大学化学课后习题参考答案

第1章 化学热力学参考答案:(一)选择题1.A 2.A 3.C 4.B 5.D 6.C 7.C 8.C 9. A 10. C 11. A 12.C (二)填空题1.40;2.等温、等容、不做非体积功,等温、等压,不做非体积功; 3.>,<,=,> 4.增大、不变 5.不变 6.3.990 kJ·mol -1(三)判断题1. ×2. ×3. ×4. ×5. √6. ×7. ×8. ×9. × 10. × (四)计算题1.解:(g)O N (l)H 2N 4242+O(l)4H (g)3N 22+(l)H N 42摩尔燃烧热为2.解:)mol ·(kJ 28.254166.963.502)84.285(401f B r --=-⨯--⨯+=∆=∆∑HH ν)mol ·(kJ 14.627211r-Θ-=∆=H Q pK1077.3109.9824.37333mr r ⨯=⨯--=∆∆=-S T 转)mol ·(kJ 78.34357.86)15.137(36.3941f B r --=---=∆=∆∑G ν)K ·mol ·(J 9.9865.21056.1975.191216.21311B r ---=--⨯+==∆∑νNO(g )CO(g )+(g)N 21(g)CO 22+)mol ·(kJ 24.37325.90)52.110(5.3931f B r --=----=∆=∆∑H ν此反应的 是较大的负值,且)(,)(-∆-∆S H 型反应,从热力学上看,在 T 转的温度以内反应都可自发进行。
3.解:外压kPa 50e =p ,11p nRT V =,22p nRTV =,2e p p = 系统所做功:定温变化,0=∆U0=+=∆W Q U ,所以Q =1 247.1(J ) 定温过程pV =常数 ∆(pV )=0 所以 0)(=∆+∆=∆pV U H 4.解:查表知CaO(s) + SO 3(g) = CaSO 4(s)求得同理求得 因为 所以根据经验推断可知,反应可以自发进行。
高等数学(上)李忠&周建莹 课后习题答案 一习题1.1

1习题1.1222222222222222222.,,.3,3.3,,313 2.961,9124,31.3,93,3,3.,,.,,,,p p p q p q p q qp p k p k p k k p k k p p k k q q k q p q p a a a b p a pb b b====+=+=++=++======为互素自然数除尽必除尽否则或除将余故类似得除尽与互素矛盾.设是正的素数为互素自然数,则素证 2.证 1.2222222,,.,..,:(1)|||1| 3.\;(2)|3| 2.0,13,22,1,(1,0);01,13,13,(0,1);1,13,3/2,(1,3/2).(1,0)(0,1)p a p a a pk p k pb pk b p b a b x x x x x x x x x x x x x x x X ===+-<-<<-+-<>->--<<+-<<>+-<<=-⋃数除尽故除尽类似得除尽此与为互素自然数矛盾.解下列不等式若则若则若则3.解(1)222(1,3/2).(2)232,15,1||5,1||(1).,(1)||||||;(2)||1,|||| 1.(1)|||()|||||||||,||||||.(2)|||()||||||x x x x x a b a b a b a b a b a a b b a b b a b b a b a b a b a b b a b b ⋃-<-<<<<<<<=⋃-+≥--<<+=++-≤++-=+++≥-=+-≤+-<设为任意实数证明设证明证4.,| 1.(1)|6|0.1;(2)||.60.160.1. 5.9 6.1.(, 6.1)( 5.9,).(2)0,(,)(,);0,;0,(,).11,01,.1, 1.11x x a l x x x x X l X a l a l l x a l X a a n na b a ++>->+>+<->-<-=-∞-⋃-+∞>=++∞⋃-∞-=≠<=-∞+∞-><-<>=>-=-=解下列不等式或或若若若若证明其中为自然数若解(1)证5.:6.1200001)(1)1).(,),(,).1/10.{|}.(,),,{|},10{|}./10,(1)/10,/10(1)/101/10n n n n n n n n n n n b b n a b a b n b a m A A m A a b A B C B A x x b C A x x a B m m C b a m m ---+++>-<-=∈⋂=∅=⋃=⋂≥=⋂≤-∈-≤-Z L 设为任意一个开区间证明中必有有理数取自然数 满足考虑有理数集合= 若则中有最小数-=证7.(,),(,).1/10.|}.10n n n n a b a b m n b a A m <-=+∈Z ,此与的选取矛盾.设为任意一个开区间证明中必有无理数取自然数 满足考虑无理数集合 以下仿8题.8.证。
第一章课后习题答案

第一章课后习题答案1、5个女生,7个男生进行排列,(a) 若女生在一起有多少种不同的排列?(b) 女生两两不相邻有多少种不同的排列?(c) 两男生A和B之间正好有3个女生的排列是多少?解:(a) 若女生在一起,可将5个女生看作一个整体参与排列,有8!种方式,然后5个女生再进行排列,有5!种方式,根据乘法法则,共有8!5!种方式。
(b) 若女生两两不相邻,可将7个男生进行排列,有7!种方式,考虑到两个男生之间的6个位置和两头的2个位置,每个位置安排一个女生均符合题意,故从中选出5个位置,然后5个女生再进行排列,按顺序安排到这5个位置,有C(8, 5)5!种方式,根据乘法法则,共有7!C(8, 5)5!=7!P(8, 5)种方式。
(c) 若两男生A和B之间正好有3个女生,可以按照顺序操作如下:首先将女生分为两组,一组3人,一组2人,有C(5, 3)种方式;将男生A和B看作一个整体,加上其他5个男生,2人一组的女生进行排列,有8!种方式;将3人一组的女生安排到男生A和B之间进行排列,有3!种方式;男生A和B进行排列,有2!种方式。
根据乘法法则,所求的排列方式为8!C(5, 3)3!2!=8!P(5, 3)2!2、求3000到8000之间的奇整数的数目,而且没有相同的数字。
解:设介于3000到8000之间的奇整数表示为abcd,则a∈{3, 4, 5, 6, 7}, d∈{1, 3, 5, 7, 9},对a进行分类如下:(1) 若a∈{3, 5, 7},则d有4种选取方式,bc有P(8, 2)种方式,根据乘法法则,此类数字有3⨯4⨯P(8, 2)=672个(2) 若a∈{4, 6},则d有5种选取方式,bc仍有P(8, 2)种方式,根据乘法法则,此类数字有2⨯5⨯P(8, 2)=560个根据加法法则,3000到8000之间数字不同的奇整数的数目为672+560=1232个3、证明nC(n-1, r)=(r+1)C(n, r+1),并给出组合解释。
(完整版)高一年级物理必修一课后习题答案

高一年级物理必修一课后习题答案第一章运动的描述1 问题与练习1.解答子弹长约几厘米,枪口到靶心的距离大于几十米,两者相差千倍以上.研究子弹从枪口击中靶心的时间一般都可忽略子弹的长度,把子弹看做质点,这样带来的时间误差不到10-4 s.子弹穿过一张薄纸的时间是从子弹头与纸接触算起到子弹尾离开纸的一段时间.若把子弹看做质点,则子弹穿过一张薄纸就不需要时间,所以,研究子弹穿过一张薄纸的时间,不能把子弹看做质点.说明能否把物体看做质点是由问题的性质决定的,而不是由物体的大小决定.选用本题是为了说明一颗小子弹,在前一种情况可看成质点,而在后一种情况就不能看成质点.2.解答“一江春水向东流”是水相对地面(岸)的运动,“地球的公转”是说地球相对太阳的运动,“钟表时、分、秒针都在运动”是说时、分、秒针相对钟表表面的运动,“太阳东升西落”是太阳相对地面的运动.说明要求学生联系一些常见的运动指认参考系,可加深学生对参考系的理解.这类问题有时也需要仔细、深入地思考才能得出正确的答案.如我们说通信卫星是静止卫星、说静止卫星相对地球静止是模糊的.说静止卫星相对地面(某点)静止是正确的,静止卫星相对地球中心是运动的.3.解答诗中描写船的运动,前两句诗写景,诗人在船上,卧看云动是以船为参考系.云与我俱东是说以两岸为参考系,云与船均向东运动,可认为云相对船不动.说明古诗文和现代文学中,我们会发现一些内容与自然科学有关,表明人文科学与自然科学是相关的.教材选用本诗是为了凸现教材的人文因素.4.解答xA=-0.44 m,xB=0.36 m2 问题与练习1.解答A.8点42分指时刻,8分钟指一段时间.B.“早”指时刻,“等了很久”指一段时间.C.“前3秒钟”、“最后3秒钟”、“第3秒钟”指一段时间,“3秒末”指时刻.2.解答公里指的是路程,汽车的行驶路线一般不是直线.3.解答(1)路程是100 m,位移大小是100 m.(2)路程是800 m,对起跑点和终点相同的运动员,位移大小为0;其他运动员起跑点各不相同而终点相同,他们的位移大小、方向也不同.4.解答3 m8 m5 m-8 m-3 m5 m-3 m5 m-8 m-3 m3 问题与练习1.解答(1)1光年=365×24×3600×3.0×108 m=9.5×1015 m.(2)需要时间为=4.2年2.解答(1)前1 s平均速度v1=9 m/s ;前2 s平均速度v2=8 m/s;前3 s平均速度v3=7 m/s 前4 s平均速度v4=6 m/s;全程的平均速度v5=5 m/sv1最接近汽车关闭油门时的瞬时速度, v1小于关闭油门时的瞬时速度.(2)1 m/s,0说明本题要求学生理解平均速度与所选取的一段时间有关,还要求学生联系实际区别平均速度和(瞬时)速度.3.解答(1)24.9 m/s,(2)36.6 m/s,(3)0说明本题说的是平均速度是路程与时间的比,这不是教材说的平均速度,实际是平均速率.应该让学生明确教材说的平均速度是矢量,是位移与时间的比,平均速率是标量,日常用语中把平均速率说成平均速度.4 问题与练习1.解答电磁打点记时器引起的误差较大.因为电磁打点记时器打点瞬时要阻碍纸带的运动. 2.解答(1)纸带左端与重物相连.(2)A点和右方邻近一点的距离Δx=7.0×10-3 m,时间Δt=0.02 s,Δt很小,可以认为A点速度v==0.35 m/s3.解答(1)甲物体有一定的初速度,乙物体初速度为0.(2)甲物体速度大小不变,乙物体先匀加速、匀速、最后匀减速运动.(3)甲、乙物体运动方向都不改变.4.解答纸带速度越大,相邻两点的距离也越大.纸带速度与相邻两点时间无关.5.解答由题意知音叉振动周期为1300s,测量纸上相邻两波峰的距离(或一个完整波形沿纸运动方向的距离)Δx,纸带运动这段距离的时间Δt=1300s,可以认为该处纸与音叉沿纸带方向的相对速度.5 问题与练习1.解答100 km/h=27.8 m/s2.解答A.汽车做匀速直线运动时.B.列车启动慢慢到达速度50 m/s,速度变化量较大,但加速时间较长,如经过2 min,则加速度为0.42 m/s2,比汽车启动时的加速度小.C、汽车向西行驶,汽车减速时加速度方向向东.D.汽车启动加速到达速度的过程中,后一阶段加速度比前一阶段小,但速度却比前一阶段大. 3.解答A的斜率,加速度.aA=0.63 m/s2,aB=0.083 m/s2,aC=-0.25 m/s2aA、aB与速度方向相同,aC与速度方向相反.4.解答滑块通过第一个光电门的速度滑块通过第二个光电门的速度滑块加速度第二章匀变速直线运动的研究1 问题与练习1.解答(1)15,16,18,19,21,23,24;图2-8(2)如图2-8所示;(3)可认为是一条直线.2.解答A做匀速直线运动,速度为15 m/s;B做初速度为零,加速度为1.9 m/s2的匀加速直线运动;C做初速度为4 m/s,加速度为0.67 m/s2的匀减速直线运动,6 s时速度为0.图2-93.(1)图2-9,(2)剪下的纸条长度表示0.1 s时间内位移大小,可近似认为速度.v∝Δx,纸条长度可认为表示速度.4.略.2 问题与练习1.解答初速度v0=36 km/h=10 m/s,加速度a=0.2 m/s2,末速度v=54 km/h根据v=v0+at得2.初速度v0=72 km/h=20 m/s,加速度a=-0.1 m/s2,时间t=2 min=120 s根据v=v0+at得v=20 m/s-0.1×120 m/s=8 m/s3.(1)4 s末速度为2 m/s,,7 s末速度为1 m/s,最小.(2)这三个时刻的速度均为正值,速度方向相同.(3)4 s末加速度为零,最小,7 s末加速度为1m/s2、.(4)1 s加速度为正值,7 s末加速度为负值,加速度方向相反.说明速度、加速度都是矢量,比较矢量的大小是按矢量的绝对值判定.图2-104.图2-103 问题与练习1.初速度v0=36 km/h=10 m/s,加速度a=0.2 m/s2,时间t=30 s根据得x=10×30 m+×0.2×302 m=390 m根据v=v0+at得v=10 m/s+0.2×30 m/s=16 m/s2.初速度v0=18 m/s,时间t=3 s,位移x=36 m根据得3.初速度v0=0, 速度v=430 km/h=119 m/s, 时间t=210 s根据v=v0+at列车加速度a=(v-0)/t=119/210 m/s2=0.567 m/s24.初速度v0=10 m/s,末速度v=0, 位移x=1.2 m根据v2-v20=2ax得5.若飞机靠自身发动机起飞,飞机初速度为0,加速度a=5 m/s2,位移x=100 m,末速度vx由v2x=2ax得,所以不行.弹射装置使飞机初速度为v0,末速度为v=50 m/s根据v2-v20=2ax得v20=v2-2ax4 问题与练习1.文具橡皮下落得快.纸片揉成很紧的小纸团后,小纸团下落变快.这是因为空气阻力的作用,纸片受的空气阻力大,小纸团受的空气阻力小.2.根据x=gt2得x= ×10×3.02 m=45 m由于空气阻力,下落加速度小于g,计算结果应小于45 m.3.设井口到水面的距离为x,石块下落做自由落体运动,设石块落到水面的时间为t,则有x=gt2=×10×2.52 m=31 m由于声音传播需要一定的时间,所以石块自由下落到水面的时间t<2.5 s,我们估算的x偏大. 4.由频闪照片知小球各个位置的速度为时间t/s速度v/(m·s-1)0.790.041.160.081.560.121.99画出v-t图象,如图2-11所示.第三章相互作用第四章牛顿运动定律1 问题与练习图4-101.(1)不能炸中目标.如图4-10所示,因为,炸弹被投下后,由于惯性,仍有与飞机相同的水平速度,如果目标是静止的,炸弹就会落到目标的前方.(2)因为,当你跳起时,由于惯性,你仍有与地球相同的速度,所以还回到原处,而不落在原地的西边.2.如果不系安全带,当紧急刹车时,车虽然停下了,但人因惯性而仍然向前运动,会发生危险.系上安全带后,人虽然因惯性向前运动,但受安全带的约束,不致发生危险.3.物体以一定速度向上抛出,在空中向上运动,是由于物体具有惯性,而继续向上运动,不是因为受到了向上的力的作用.4.如果选择了相对于静止的大树做加速运动的汽车为参考系,人在车上观察大树,大树做远离汽车的加速运动.大树的运动状态改变不是因为受到了力的作用,而是因为惯性定律在选择的参考系中不成立.2 问题与练习1.答:没有矛盾.牛顿第二定律公式F=ma中的F指的是物体所受的合力,而不是其中的某一个力.我们用力提一个放在地面上的很重的物体时,物体受到的力共有三个:手对物体向上的作用力F1,竖直向下的重力G,以及向上的支持力F2.如果F1F阻.而FAB与FBA是一对相互作用力,根据牛顿第三定律,它们总是大小相等方向相反.由牛顿第二定律:AB-F阻=maFAB=ma+F阻=4.0×103×0.3 N+2.0×103 N=3.2×103 N由牛顿第三定律:FAB与FBA是一对相互作用力,它们总是大小相等方向相反.即FAB=FBA=3.2×103 N5.小强没有注意到,相互平衡的两个力是作用在同一物体上的,而作用力和反作用力是分别作用在发生相互作用的两个物体上的,它们不可能是相互平衡的力.5 问题与练习图4-141.如图4-14所示,用作图法求出物体所受的合力F=87 Nv=at=43.5×3 m/s=131 m/sx=at2= ×43.5×32 m=196 m2.电车的加速度为:电车所受阻力为:F=ma=-6.0×103 N,负号表示与初速度方向相反3.人在气囊上下滑的加速度为:滑至底端时的速度为:4.卡车急刹车时的加速度大小为:根据运动学公式:所以:该车超速.6 问题与练习图4-151.取足球作为研究对象,由共点力的平衡条件可知,F1和G的合力F与F2大小相等、方向相反.从图4-15中力的平行四边形定则可求得:2.物体在五个力作用下保持平衡,它们的合力为零.其中任意四个力的合力一定与第五个力大小相等、方向相反.依题意,除F1以外的四个力的合力与力F1大小相等、方向相反.撤去F1,其余四个力不变,它们的合力大小等于F1,方向与F1相反.3.答:当饮料瓶自由下落时,小孔没有水喷出.因为,瓶和水均处于完全失重状态,瓶中各处的水(包括水孔处的水)的压强都是大气压强,故水不能从瓶中流出.图4-164.(1)如图4-16甲所示,由牛顿第二定律:F-mg=maF=ma+mg=7mg=70 N 绳子受到的拉力大约为70 N.(2)如图4-16乙所示,由牛顿第二定律:F+mg=ma F=ma-mg=5mg=50 N 绳子受到的拉力大约为50 N.图4-175.当坐舱离地面50 m的位置时,升降机在做自由落体运动(图4-17),人和人手中的铅球均完全失重,所以,球对手无作用力,人没有受到压力的感觉.坐舱做匀减速运动时的加速度为:方向竖直向上所以,人手对铅球的作用力为F:F-mg=ma F=ma+mg=2.7mg=135 N。
工程力学课后习题答案

图2-13
1作为力图,BC杆受一对力偶作用。
2.对于AB杆系的平衡方程
所以:
1.以BC为研究对象,列出平衡方程。
1.以AB为研究对象,列出平衡方程。
2-18如图所示,三扭拱由两个半拱和三个铰A、B、c组成,已知每个半拱的重量为P=300kN,l=32m,h=10m。求支座A和b的约束反力。
图2-15
以整体为研究对象,从对称性认识:
以BC半拱为研究对象。
2-19在图示的框架中,物体重1200N,用一根细绳横过滑轮e水平系在墙上,尺寸如图,不考虑杆和滑轮的重量。求支座A和B处的约束反力和BC杆的内力FBC。
图2-19
以整体为研究对象。
解决方案:
以CDE杆和滑轮为研究对象。
解决方案:
2-20在图示的框架中,每根杆单位长度的重量为300N/m,载荷P=10kN,固定端在A处,铰链在B、C、d处,求固定端A和铰链处B、C的约束反力。
2-24平面桁架的支撑和荷载如图所示。求杆1,2,3的内力。(提示:先截掉AD、3、2杆,用切片法分析;然后取C节点)
2-25两个相同的匀质杆AB和BC在端点B用光滑铰链连接,A端和C端放在一个不光滑的水平面上,如图所示。当ABC处于等边三角形时,系统在垂直面内处于平衡状态。求杆端和水平面之间的摩擦系数。
工程学
练习册
1-1画出下图中物体A、分量AB、BC或ABC的受力图,不考虑无重力情况下物体的重量,所有接触点都是光滑的。
(一)
(二)
(三)
(
(五)
(六)
(g)
1-2试画出图中所示各题中AC杆(带销)和BC杆的受力图。
(a) (b) (c)
(一)
1-3画出图中指定物体的受力示意图。所有的摩擦力都不算,除了图中已经画出来的以外,所有东西的自重都不算。
计算机组成原理课后习题答案(一到九章)

计算机组成原理课后习题答案(一到九章) 作业解答第一章作业解答1.1 基本的软件系统包括哪些内容?答:基本的软件系统包括系统软件与应用软件两大类。
系统软件是一组保证计算机系统高效、正确运行的基础软件,通常作为系统资源提供给用户使用。
包括:操作系统、语言处理程序、数据库管理系统、分布式软件系统、网络软件系统、各种服务程序等。
1.2 计算机硬件系统由哪些基本部件组成?它们的主要功能是什么?答:计算机的硬件系统通常由输入设备、输出设备、运算器、存储器和控制器等五大部件组成。
输入设备的主要功能是将程序和数据以机器所能识别和接受的信息形式输入到计算机内。
输出设备的主要功能是将计算机处理的结果以人们所能接受的信息形式或其它系统所要求的信息形式输出。
存储器的主要功能是存储信息,用于存放程序和数据。
运算器的主要功能是对数据进行加工处理,完成算术运算和逻辑运算。
控制器的主要功能是按事先安排好的解题步骤,控制计算机各个部件有条不紊地自动工作。
1.3 冯・诺依曼计算机的基本思想是什么?什么叫存储程序方式?答:冯・诺依曼计算机的基本思想包含三个方面:1) 计算机由输入设备、输出设备、运算器、存储器和控制器五大部件组成。
2) 采用二进制形式表示数据和指令。
3) 采用存储程序方式。
存储程序是指在用计算机解题之前,事先编制好程序,并连同所需的数据预先存入主存储器中。
在解题过程(运行程序)中,由控制器按照事先编好并存入存储器中的程序自动地、连续地从存储器中依次取出指令并执行,直到获得所要求的结果为止。
1.4 早期计算机组织结构有什么特点?现代计算机结构为什么以存储器为中心?答:早期计算机组织结构的特点是:以运算器为中心的,其它部件都通过运算器完成信息的传递。
随着微电子技术的进步,人们将运算器和控制器两个主要功能部件合二为一,集成到一个芯片里构成了微处理器。
同时随着半导体存储器代替磁芯存储器,存储容量成倍地扩大,加上需要计算机处理、加工的信息量与日俱增,以运算器为中心的结构已不能满足计算机发展的需求,甚至会影响计算机的性能。
《普通化学》课后习题答案

普通化学第一章习题答案1. 答案1-2-34- 2. 答案1c2d3a4d5abd6ad7d8d 3. 答案1燃烧前后系统的温度2水的质量和比热3弹式量热计热容4..答案根据已知条件列式KCgKgJgmolgmolJb35.29659.298120918.45.0122100032261111 Cb849J.mol-1 5.答案获得的肌肉活动的能量kJmolkJmolgg8.173028201808.311 6. 答案设计一个循环3×232sFesOFe×3 243sOFe3sFeO×2 -58.6238.16pq3-27.6 17.1661.3826.586.273molkJqp 7.答案由已知可知ΔH39.2 kJ.mol-1 ΔHΔUΔPVΔUPΔV w‘-PΔV -1×R×T -8.314×351J -2.9kJ ΔUΔH-PΔV39.2-2.936.3kJ 8.下列以应或过程的qp与qv有区别吗简单说明。
12.00mol NH4HS的分解NH4HSs NH3gH2Sg 2生成1.00mol的HCl H2gCl2g 2HClg 35.00 mol CO2s干冰的升华CO2s CO2g 4沉淀出2.00mol AgCls AgNO3aqNaClaq AgClsNaNO3aq 9.答案ΔU-ΔH -ΔPV-ΔngRT Δng为反应发生变化时气体物质的量的变化1ΔU-ΔH-2×2-0×8.314×298.15/1000 - 9.9kJ 2ΔU-ΔH-2×2-2×R×T 03ΔU-ΔH-5×1-0×8.314×273.15-78/1000 -8.11kJ 4ΔU-ΔH-2×0-0×R×T 010.14NH3g3O2g 2N2g 6H2Ol 答案-1530.5kJ.mol-1 2C2H2g H2g C2H4g 答案-174.47kJ.mol-1 3NH3g 稀盐酸答案-86.32kJ.mol-1 写出离子反应式。
电气控制与PLC应用技术课后习题答案(第一章)

习题与思考题1.电磁式电器主要由哪几部分组成?各部分的作用是什么?答:电磁式电器主要电磁机构和触点系统组成,其次还有灭弧系统和其他缓冲机构。
电磁机构由电磁线圈、铁心和衔铁三部分组成。
电磁线圈的作用是将电能转换为磁能,即产生磁通,衔铁在电磁吸力作用下产生机械位移使铁心与之吸合。
触点是一切有触点电器的执行部件,它在衔铁的带动下起接通和分断电路的作用。
2.何谓电磁式电器的吸力特性和反力特性?吸力特性与反力特性应如何配合?答:吸力特性是指电磁吸力F at随衔铁与铁心间气隙δ变化的关系曲线,不同的电磁机构,有不同的吸力特性。
反力特性是指反作用力Fr与气隙δ的关系曲线。
为了使电磁机构正常工作,保证衔铁能牢牢吸合,其吸力特性与反力特性必须配合得当。
在衔铁整个吸合过程中,其吸力都必须大于反力,即吸力特性必须始终位于反力特性上方,但不能过大或过小。
吸力过大时,动、静触点接触及衔铁与铁心接触时的冲击力很大,会使触点和衔铁发生弹跳,从而导致触点熔焊或烧毁,影响电磁机构的机械寿命;吸力过小时,又不能保证可靠吸合,难以满足高频率操作的要求。
在衔铁释放时,反力必须大于吸力(此时的吸力是由剩磁产生的),即吸力特性必须位于反力特性下方。
3.如何区分直流电磁机构和交流电磁机构?如何区分电压线圈和电流线圈?答:直流电磁机构其铁心与衔铁由软钢或工程纯铁制成,线圈为高而薄的瘦高形,不设线圈骨架;交流电磁机构其铁心由硅钢片叠铆而成,线圈为短而厚的矮胖形,设有线圈骨架。
电流线圈串联在电路中,线圈导线粗且匝数少;电压线圈并联在电路中,线圈导线细且匝数多。
4.单相交流电磁机构中的短路环的作用是什么?三相交流电磁机构是否也要装短路环?为什么?答:单相交流电磁机构中短路环的作用是消除振动和噪声,三相交流电磁机构不需要加短路环,因为三相磁通不会同时过零,产生的合成电磁吸力始终大于反力。
5.交流电磁线圈通电后,衔铁长时间卡住不能吸合,会产生什么后果?答:交流电磁线圈通电后,如果衔铁长时间卡住不能吸合,铁心和衔铁之间的空隙大,电抗小,通过线圈的激磁电流很大,往往大于工作电流的十几倍,因而引起线圈产生过热现象,严重时会将线圈烧毁。
计算机网络第五版课后习题答案(第一章)

计算机网络第五版课后习题答案(第一章)(2009-12-14 18:04:43)转载▼标签:课程-计算机教育第一章概述1-01计算机网络向用户可以提供那些服务?答:连通性和共享1-02简述分组交换的要点。
答:(1)报文分组,加首部(2)经路由器储存转发(3)在目的地合并1-03试从多个方面比较电路交换、报文交换和分组交换的主要优缺点。
答:(1)电路交换:端对端通信质量因约定了通信资源获得可靠保障,对连续传送大量数据效率高。
(2)报文交换:无须预约传输带宽,动态逐段利用传输带宽对突发式数据通信效率高,通信迅速。
(3)分组交换:具有报文交换之高效、迅速的要点,且各分组小,路由灵活,网络生存性能好。
1-04为什么说因特网是自印刷术以来人类通信方面最大的变革?答:融合其他通信网络,在信息化过程中起核心作用,提供最好的连通性和信息共享,第一次提供了各种媒体形式的实时交互能力。
1-05因特网的发展大致分为哪几个阶段?请指出这几个阶段的主要特点。
答:从单个网络APPANET向互联网发展;TCP/IP协议的初步成型建成三级结构的Internet;分为主干网、地区网和校园网;形成多层次ISP结构的Internet;ISP首次出现。
1-06简述因特网标准制定的几个阶段?答:(1)因特网草案(Internet Draft) ——在这个阶段还不是RFC 文档。
(2)建议标准(Proposed Standard) ——从这个阶段开始就成为RFC 文档。
(3)草案标准(Draft Standard)(4)因特网标准(Internet Standard)1-07小写和大写开头的英文名字 internet 和Internet在意思上有何重要区别?答:(1)internet(互联网或互连网):通用名词,它泛指由多个计算机网络互连而成的网络。
;协议无特指(2)Internet(因特网):专用名词,特指采用TCP/IP 协议的互联网络区别:后者实际上是前者的双向应用1-08计算机网络都有哪些类别?各种类别的网络都有哪些特点?答:按范围:(1)广域网WAN:远程、高速、是Internet的核心网。
部编人教版四年级语文上册课本课后习题(参考答案)

部编⼈教版四年级语⽂上册课本课后习题(参考答案)部编版四年级语⽂上册课本课后习题参考答案第⼀课《观潮》⼀、说说课⽂是按照什么顺序描写钱塘江⼤潮的,你的头脑中浮现出怎样的画⾯,选择印象最深和同学交流。
答:课⽂按潮来前,潮来时,潮过后的顺序观察描写钱塘江⼤潮。
“潮来前”的景象:江⾯上很平静,观潮⼈的⼼情急切。
闷雷滚动、⼀条⽩线“潮来时”的景象:潮的声⼤,潮头有数丈之⾼,声如“⼭崩地裂”,形如“⽩⾊城墙”、“⽩⾊战马”,横贯江⾯。
给⼈的印象就是如巨雷般的⼤潮像千军万马席地⽽卷,在呐喊、嘶鸣中奔来。
狂潮拍⽯,如同⼏⾥岸边同时⾦钟齐鸣。
“潮头过后”的景象:潮头汹涌,漫天卷地,余威犹在,恢复平静,⽔位上涨。
我印象最深的是“潮来时”的景象:那条⽩线很快地向我们移来,逐渐拉长,变粗,横贯江⾯。
再近些,只见⽩浪翻滚,形成⼀堵两丈多⾼的⽔墙。
浪潮越来越近,犹如千万匹⽩⾊战马齐头并进,浩浩荡荡地飞奔⽽来;那声⾳如同⼭崩地裂,好像⼤地都被震得颤动起来。
霎时,潮头奔腾西去,可是余波还在漫天卷地般涌来,江⾯上依旧风号浪吼。
⼆、读下⾯这⾸诗,从课⽂中找出与诗的内容相关的句⼦。
浪淘沙唐·刘禹锡⼋⽉涛声吼地来,头⾼数丈触⼭回。
须臾却⼊海门去,卷起沙堆似雪堆。
与诗的内容相关的句⼦:那条⽩线很快地向我们移来,逐渐拉长,变粗,横贯江⾯。
再近些,只见⽩浪翻滚,形成⼀堵两丈多⾼的⽔墙。
浪潮越来越近,犹如千万匹⽩⾊战马齐头并进,浩浩荡荡地飞奔⽽来;那声⾳如同⼭崩地裂,好像⼤地都被震得颤动起来。
第⼆课《⾛⽉亮》⼀、阿妈牵着我“我”⾛过“⽉光闪闪的溪岸”,“细细的溪⽔,流着⼭草和野花的⾹味,流着⽉光……”你的头脑中浮出了怎样的画⾯?课⽂中还有哪些画⾯给你留下了深刻的印象?和同学交流。
提⽰:⼭草、野花、⽉光倒映在溪⽔⾥,随着溪⽔流动着,就像是“流着⼭草、野花的⾹味,流着⽉光”。
这⾥⽤了暗喻的⼿法,把阿妈⽐作美丽的⽉亮,牵着那些闪闪烁烁的⼩星星,也就是“我”在天上⾛着。
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

m ax Z 3 x1 2 x 2 2 x1 x 2 2 ( 2) st . 3 x1 4 x 2 12 x , x 0 1 2 该问题无可行解
2
( 3)
m axZ x1 x 2 6 x1 10x 2 120 st . 5 x1 10 5 x2 8
1
(3)
max Z x1 x2 6 x1 10x2 120 st . 5 x1 10 5 x 8 2
(4)
m i nZ 2 x1 3 x 2 4 x1 6 x 2 6 (1) st . 3 x1 2 x 2 4 x ,x 0 1 2 无穷多最优解 (蓝 色 线 段 上 的 点 都 是 优 最解 ) x1 6 1 , x2 , 是 其 中 一 个 最 优 解 5 5
唯一最优解, x1 10, x 2 6 Z 16
(4)
max Z 5 x1 6 x2 2 x1 x2 2 st. 2 x1 3x2 2 x ,x 0 1 2
3
该问题有无界解
1.2
将下述线性规划问题化成标准形式。
min Z 3x1 4 x2 2 x3 5 x4 4 x1 x2 2 x3 x4 2 x x x 2 x 14 2 3 4 st 1 . 2 x1 3x2 x3 x4 2 x1 , x2 , x3 0, x4无约束
解:令 w Z , x4 x41 x42, 其 中 x41,x42 0, 同时引入松弛变量 x5, 剩 余 变 量 x6, 则 标 准 形 式 为 : m axw 3 x1 4 x 2 2 x 3 5 x41 5 x42 4 x1 x 2 2 x 3 x41 x42 x x x 2x 2x x 1 2 3 41 42 5 st 2 x1 3 x 2 x 3 x41 x42 x6 x1 , x 2 , x 3 , x41 , x42 , x6 2 14 2 3x2 6 x3 3x4 9 8 x x 4 x 2 x 10 1 2 3 5 st 3x1 x6 0 ( , j 1, ,6) x j 0
概率论课后习题答案第一章

2008年4月第一章1.1 解⑴记9件合格品分别为正1正2�6�7正9记不合格品为次则Ω正1正2正1正3正1正4�6�7正1正9正1次正2正3正2正4�6�7正2正9正2次正3正4�6�7正3正9正3次�6�7 正8正9正8次正9次A正1次正2次正3次�6�7正9次⑵记2个白球分别为w1w23个黑球分别为b1b2b34个红球分别为r1r2r3r4。
则Ωw1w2b1b2b3r1r2r3r4 ⅰA w1w2。
ⅱB r1r2r3r4。
1.2 解⑴事件ABC表示该生是三年级男生但不是运动员。
⑵ABCC等价于CAB表示全系运动员都是三年级的男生。
⑶当全系运动员都是三年级学生时。
⑷当全系女生都在三年级并且三年级学生都是女生时。
1.3 解⑴1niiA⑵22221222211nCDniCDiCDCDnCDACDCD ⑶11nnijijjiAA⑷原事件即“至少有两个零件是合格品”可表为1nijijijAA。
1.4 解1—4显然5和6的证法分别类似于课文第10—12页1.5式和1.6式的证法。
1.5 解样本点总数为28A8×7。
所得分数为既约分数必须分子分母或为71113中的两个或246812中的一个和71113中的一个组合所以事件A“所得分数为既约分数”包含28A218A×15A3×22×3×52×3×6个样本点。
于是PA23698714。
1.6 解样本点总数为5310。
所取三条线段能构成一个三角形这三条线段必须是3、5、7或5、7、9。
所以事件A“所取三条线段能构成一个三角形”包含3个样本点于是PA310。
17解显然样本点总数为13事件A“恰好组成MATHEMATICIAN”包含3222个样本点。
所以3222481313PA 18解任意固定红“车”的位置黑“车”可处在9×10-189个不同位置当它处于和红“车”同行或同列的9817个位置之一时正好互相“吃掉”。
数学物理方法课后答案 (1)

16x2 + 25 y2 = (20)2 ,点集为椭圆: ( x )2 + ( y )2 = 1 54
(4)
z −1 = z +1
(x −1)2 + y2 (x +1)2 + y2
≤1
x2 − 2x +1+ y2 ≤ x2 + 2x +1+ y2
②
将①式与②式相除,易见 c 3 = 1,即 c = 1,由此得证。
8.试利用 Re z = x ≤ x2 + y2 = z 证明 z1 + z2 ≥ z1 + z2 , z1 − z2 ≥ z1 − z2
证 将第一个不等式两边平方,则不等式右边的式子为
z1 + z 2 2 = ( z1 + z 2 )( z1 + z 2 )∗ = z1 z1∗ + z 2 z 2∗ + z1 z 2∗ + z1∗ z 2
= 2sinα 2
iπ −α
e2
= 2sin α 2
⎡π ⎢⎣cos
−α 2
+
i
sin
⎛ ⎜⎝
π
−α 2
⎞⎤ ⎟⎠⎥⎦
(6) (
3 + i)−3 = (
( 3 − i)3
=
−1i
=
1
e
−i
π 2
=
− 1 i sin π
3 + i)3( 3 − i)3 8 8
82
(7)
2i −1 +
i
新概念英语第二册课后练习答案(1-20)

新概念英语第二册课后练习答案(1~20课)Lesson 11.关键句型练习A I (1) got (2) very angry (3) .I (1) could not hear (2) the actors (3) .I (1) turned round (2) .I (1) looked at (2) the man and the woman (3) angrily (4) . They (1) did not pay (2) any attention (3) .In the end (6), I (1) could not bear (2) it (3).I (1) turned round (2) again (6) .zI (1) can't hear (2) a word (3)! {I (1) said (2) angrily (4) .zIt (1) is (2) none of your business (3) , {the young man (1) said (2) rudely (4) .zThis (1) is (2) a private conversation (3)!{B 1 I enjoyed the film yesterday.2 I listened to the news carefully.3 The man played the piano well.4 The children played games quietly in their room yesterday.5 He opened the door quietly.6 He left immediately.7 He planted a tree in the corner of the garden.8 He read the letter quickly in his office before lunch.9 I borrowed a book from the library this morning.10 The cook spoilt the soup.11 We stay at home on Sundays.12 There are a lot of people at the bus stop.13 The little boy ate greedily an apple in the kitchen this morning.14 She draws beautifully.15 I like music very much.16 They built a new school in our village last year.17 The match ended at four o'clock.18 She received a letter from her brother last week. 2.多项选择题答案1 b2 c3 b4 d5 c6 a7 d 8 b 9 a 10 c 11 c 12 cLesson 22.难点练习答案1 What a wonderful garden(this is) !2 What a surprise( this is) !3 What a lot of trouble he is causing!4 What wonderful actors (they are) !5 What a hard-workingwoman (she is) !6 What a tall building (it is) !7 What a terrible film (it is) !8 What a clever boy you are!9 What a pretty girl (she is) !10 What a strange guy (he is) !3.多项选择题答案1 c2 d3 c4 c5 a6 b7 b 8 a 9 d 10 c 11d 12 bLesson 31.关键句型练习题A went (1.1)Õvisited (1.2) Õsat(1.2) Õtaught(1.2)ÕlentÕread(1.3) Õdid notunderstandÕthought (1.4)Õpassed (1.5) Õdid not send(1.5) ÕmadeÕgo up (1.6) Õbought (1.7) Õspent(1.7) Õdid not write(1.8)C ...Roy died last year…left me…spent a lotof money…bought one or two…never went to the cinema…stayed at home…listened tomusic…often lent CDs…they kept them…lost many CDs… 2.难点练习题1 He paid some money to the shopkeeper.2 He handed the prize to me.3 The waiter brought the man a bottle of beer.4 He sold me all his books.5 The shop assistant found me some curtain material.6 He did a big favour for me.7 She showed her new hat to her husband.8 She promised the finder a reward.9 He gave some advice to his son.10 His uncle left some money to/ for him.11 He is teaching us English.12 I bought you this bunch of flowers.13 Bring me that book please.14 He offered a cigarette to me.15 Read the first paragraph to me.16 I've ordered you some soup.17 I owe a lot of money to him.18 Pass your father the mustard.3.多项选择1c 2a 3c 4a 5d 6b7c 8c 9b 10a 11b 12bLesson 121.关键句型练习答案A will sail (1.1); shall meet (1.2); will be (1.3); will set out (11.4-5); shall have(1.5); shallsee (1.5); shall say (1.6);will be (1.6); will take part (1.7) C I shall go to the theatre Reg and I shall see the first performance the producer will give a short speech. He will speak to The play will bevery people will enjoy it very much.2.难点练习答案1 He is not back yet. He will be back in ten minutes.2 A new play is on at the Globe Theatre.3 When the concert was over, We went home.4 They will set out/ off very early tomorrow morning. (Here be off is also possible.)5 You can't take the exam yet. You are not up to it.6 He will be away from home for two months.7 She swam across the English Channel and set up a new world record.3.多项选择题答案1 c2 c3 a4 d5 d6 a7 d 8 a 9 c 10 d 11 a 12 aLesson 131.关键句型练习答案A will be arriving (1.2); will be coming (1.3); will be meeting(1.4); will be singing (1.5);will be staying (1.6); will be trying (1.8)C 1 I'll be ironing the clothes.2 The train will be arriving in a few minutes.3 We'll be seeing you in the morning.4 We'll be watching the match.5 He'll be correcting exercise books.2.难点练习答案1 It's George's.2 It's Jean's.3 It's that woman's.4 I like Keats' poetry best.5 They're the children's.6 They're the soldiers'.7 I'll leave in six hours time. 8 There was a hundred pounds' worth of damage.3多线选择答案1 b2 d3 b4 c5 a6 bLesson 141.关键句型练习答案A 1 I drove on to the next town after I had left a small village.2 I said good morning to him in French as soon as he had got into the car.3 I had nearly reached the town, when the young man said: BDo you speak English?C 1 After she had written the letter, she went to the post office.2 After he had had dinner, he went to the cinema.3 When I had fastened my seat belt, the plane took off.4 We did not disturb him until he had finished work.5 As soon as he had left the room, I turned on the radio.6 He had been very ill before he died.D 1 regretted 2 had begun/ began 3 arrived2.难点练习答案1 Except for2 both of3 Apart from4 askedlask for5 neither oflasked3.多项选择答案1 b2 c3 a4 c5 d6 bLesson 151. 关键句型练习答案A 1a The secretary told me that Mr. Harmsworth would see me. bcMr. Harmsworth will see you. d2 a Mr. Harmsworth said that business was very bad.b cBusiness is very bad.d3 a Mr. Harmsworth told me that the firm could not afford to pay such large salaries.b cThe firm cannot afford to pay such large salaries. dB 1 told would come/would be coming2 said (had) cut3 told had never played4 did he say had done/would do5 did he tell (had) bought/would buy6 said could not7 said (had) worked8 told wrote/writes/had never written9 did you say were/had been10 said would wait2.难点练习答案1 study2 office3 nervous4 afford5 irritable3.多线选择答案1d 2b 3c 4b 5c 6d7a 8d 9c 10c 11c 12bLesson 201关键句型练习答案A Fishing(1.1); catching(11.1-2); catching(1. 3); having spent(1.5); fishing(1.6);fishingˆ sitting(1.8); doing (1.9) C 1 he went out of the restaurant without paying the bill.2 She bought a pair of boots instead of getting a pair of shoes.3 She was afraid of spending the night alone.4 After hearing/having heard the news, she fainted.5 Think carefully before answering my question.6 On seeing the plane coming towards me, I dashed for cover. 2难点练习答案1realized 2It'sˆunderstandˆits 3exciting 4interesting 5exciting 6interested3多项选择答案1b 2c 3b 4b 5c 6b新概念英语第二册课后习题答案详解Lesson 21练习答案Key to written exercises 1.关键句型练习答案A …passing planes can be heard(1.2); The airport was built (1.2); it co uld not be used then(1. 3); a hundred people must have been driven away(11.4-5); this house will be knocked down by a passing plane(11 .6-7); I have been offered a large sum of money(1.7)C 1 A message will be sent immediately. 2 All these goods must be sold.3 I told you the parcel would be received in time.4 The letter h as to be delivered by hand.5 Your letter must have been lost In the post. 2.难点练习答案 A (sample answers)The dog drove the sheep out of the field. The police drove the cro wds back. I drove my car into the garage. B1 home 2 houses 3 house 4 home 3.多项选择题答案1. c根据课文第3-4行Last year, however, it came into use, 只有c. came into use recently 比较接近课文的实际容,而其他3个选择都不符课文容。
(完整版)电路原理课后习题答案
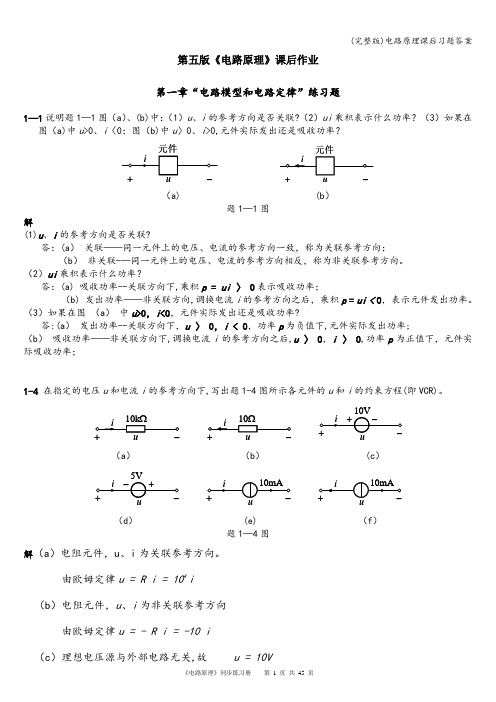
因此, 时,电路的初始条件为
t〉0后,电路的方程为
设 的解为
式中 为方程的特解,满足
根据特征方程的根
可知,电路处于衰减震荡过程,,因此,对应齐次方程的通解为
式中 。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电,所加 的波形如题7—29图所示,其中 , 。求电容电压 ,并把 :(1)用分段形式写出;(2)用一个表达式写出。
题4-17图
解:首先求出 以左部分的等效电路.断开 ,设 如题解4-17图(a)所示,并把受控电流源等效为受控电压源。由KVL可得
故开路电压
把端口短路,如题解图(b)所示应用网孔电流法求短路电流 ,网孔方程为
解得
故一端口电路的等效电阻
画出戴维宁等效电路,接上待求支路 ,如题解图(c)所示,由最大功率传输定理知 时其上获得最大功率。 获得的最大功率为
(a)(b)
题3—1图
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数 ,支路数
图(b1)中节点数 ,支路数
(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
电容电流
t=2 ms时
电容的储能为
7—20题7—20图所示电路,开关合在位置1时已达稳定状态,t=0时开关由位置1合向位置2,求t0时的电压 .
题7-20图
解:
用加压求流法求等效电阻
7-26题7—26图所示电路在开关S动作前已达稳态;t=0时S由1接至2,求t0时的 .
题7-26图
解:由图可知,t>0时
《语言学概论》课后习题参考答案

《语言学概论》练习(一)参考答案一、填空1、中国、印度、希腊—罗马具有悠久的历史文化传统,是语言学的三大发源地。
2、历史比较语言学是在19世纪逐渐发展和完善的,它是语言学走上独立发展道路的标志。
3、人的大脑分左右两半球,大脑的左半球控制语言活动,右半球掌管不需要语言的感性直观思维。
4、一个符号,如果没有意义,就失去了存在的必要,如果没有形式,我们就无法感知,符号也就失去了存在的物质基础。
5、用什么样的语音形式代表什么样的意义,完全是由使用这种语言的社会成员约定俗成。
6、语言符号具有任意性和线条性特点。
7、语言的底层是一套音位,上层是符号和符号的序列,可以分为若干级,第一级是语素,第二级是词,第三级是句子。
8、语言系统中的所有符号,既可以同别的符号组合,又可以被别的符号替换,符号之间的这种关系是组合关系和聚合关系。
9、组合关系是指符号与符号相互之间在功能上的联系,聚合关系是指符号在性质上的归类。
二、判断正误1、文字是人类最重要的交际工具。
(错)2、地主阶级和农民阶级之间没有共同语言,这说明语言是有阶级性的。
(错)3、在现代社会,文字比语言更加重要。
(错)4、现代社会,沟通的方式很多,语言的重要性日渐削弱。
(错)5、语言是思维的工具,没有语言,人类就无法思维。
(对)6、语言和思维互相依存,共同发展。
(对)7、任何一种符号,都是由内容和意义两个方面构成的。
(错)8、从本质上看,语言其实是一种符号系统。
(对)9、人类选择语音而不是色彩、手势作为语言符号的形式,是因为语音比较好听。
(错)10、语言符号的约定俗成是指语音形式和意义内容的结合是社会成员共同约定认同的。
(对)三、问答题:1、语言的作用是什么,举例说明。
为什么说语言是最重要的交际工具?答:它是人类社会的交际工具。
每个社会,无论它是经济发达的社会,还是经济十分落后的社会,都必须有属于自己的语言,都离不开语言这个交际工具,语言是组成社会必不可少的一个因素,是人类与动物区别的重要特征之一。
C语言程序设计课后习题1-8参考答案

C语言程序设计课后习题1-8参考答案习题1参考答案一、简答题1、冯诺依曼计算机模型有哪几个基本组成部分各部分的主要功能是什么?答:冯诺依曼计算机模型是由运算器、控制器、存储器、输入设备、输出设备五大功能部件组成的。
运算器又称算术逻辑部件,简称ALU,是计算机用来进行数据运算的部件。
数据运算包括算术运算和逻辑运算。
控制器是计算机的指挥系统,计算机就是在控制器的控制下有条不紊地协调工作的。
存储器是计算机中具有记忆能力的部件,用来存放程序和数据。
输入设备是用来输入程序和数据的部件。
输出设备正好与输入设备相反,是用来输出结果的部件。
2、简述计算机的工作原理。
答:计算机的工作原理可简单地概括为:各种各样的信息,通过输入设备,进入计算机的存储器,然后送到运算器,运算完毕把结果送到存储器存储,最后通过输出设备显示出来。
整个过程由控制器进行控制。
3、计算机软件系统分为哪几类答:软件内容丰富,种类繁多,通常根据软件用途将其分为两大类:系统软件和应用软件。
系统软件是指管理、监控、维护计算机正常工作和供用户操作使用计算机的软件。
这类软件一般与具体应用无关,是在系统一级上提供的服务。
系统软件主要包括以下两类:一类是面向计算机本身的软件,如操作系统、诊断程序等。
另一类是面向用户的软件,如各种语言处理程序(像BC、VC等)、实用程序、字处理程序等。
应用程序是指某特定领域中的某种具体应用,供最终用户使用的软件,它必须在操作系统的基础上运行。
4、什么叫软件说明软件与硬件之间的相互关系。
答:软件是指计算机程序及有关程序的技术文档资料。
两者中更为重要的是程序,它是计算机进行数据处理的指令集,也是计算机正常工作最重要的因素。
在不太严格的情况下,认为程序就是软件。
硬件与软件是相互依存的,软件依赖于硬件的物质条件,而硬件则需在软件支配下才能有效地工作。
在现代,软件技术变得越来越重要,有了软件,用户面对的将不再是物理计算机,而是一台抽象的逻辑计算机,人们可以不必了解计算机本身,可以采用更加方便、更加有效地手段使用计算机。
信息技术 课后习题答案 第一章习题参考答案

第一章习题参考答案1.选择题(1) A (2) B (3) A (4) B (5) C (6) D (7) A (8) B (9) B (10) B (11) A (12)A (13)B (14) D (15)C (16) ABCD (17) A (18) C (19) B (20) A2.判断题1.×2.√3. √4. √5. ×6. √7. ×8. ×9. ×10. √11. ×12. √13. ×14. √ 15. √ 16. √17. √18. X3.简答题(1)如何限制其他人对文档进行编辑?文件一保护文档一限制编辑。
(2)检查文档兼容性的目的是什么?检查是否有早期版本的Word不支持的功能。
(3)为什么要将文档导出为PDF格式?安全性高,可跨平台使用,将文字、字型、格式、颜色及独立于设备和分辨率的图形图像等封装在了一个文件中。
(4)文档的“保存”和“另存为”的区别是什么?略(5)在Word编辑过程中,如何切换“改写”与“插入”状态?这两种状态有何区别?略(6)如何选定不连续的文本?略(7)如何把一段文字的格式恢复到默认状态?开始一字体一清除所有格式。
(8)分页符的作用是什么?如何使用分页符?标记一页的结束与下一页的开始。
布局一页面设置f分隔符一分页符。
(9)什么是样式?不使用样式和使用样式的差别是什么?略(10)在WOrd的表格中,如何对内外框线设置不同的样式?表格工具设计一边框和底纹。
(H)在WOrd的表格中,如何对数据进行排序?略(12)如何将Word的表格转换成文本?略(13)在Word中,如何将文本转换成表格?略(14)文字分隔符的作用是什么?表格转换成文本时,用于分隔不同表格中的文字。
(15)在WOrd中,如何调整图形的叠放次序?略(16)简述在Word中制作特定公式的方法。
略(17)图文编排的主要目的是什么?略(18)对长文档生成目录,需要有哪些准备工作?需要对文档中的标题等应用样式或设置格式,插入页码。
模拟电子技术(第2版)课后习题答案第一章

第一章 半导体器件1.1 电路如图P1.1所示,设二极管为理想的,试判断下列情况下,电路中的二极管是导通还是截止,并求出AO 两端的电压AO U 。
(1)V V DD 61=,V V DD 122=;(2)V V DD 61=、V V DD 122-=;(3)V V DD 61-=、V V DD 122-=。
解:1、当V V DD 61=、V V DD 122=时,假设二极管是截止的,则V V B 6=、V V A 12=二极管承受反偏电压,所以二极管截止假设成立。
V V U DD AO 122==。
2、当V V DD 61=、V V DD 122-=时,假设二极管是截止的则V V B 6=、V V A 12-=二极管承受正偏电压,所以二极管截止假设不成立,二极管导通。
V V U DD AO 61==。
3、当V V DD 61-=、V V DD 122-=时,假设二极管是截止的,则V V B 6-=、V V A 12-= 二极管承受正偏电压,所以二极管截止假设不成立,二极管导通。
V V U U DD BO AO 61-===。
1.2 二极管电路如图P1.2所示,二极管的导通电压VU D 7.0)on (=,试分别求出Ω=k R 1、Ω=k R 4时,电路中的电流O I I I 、、21和输出电压O U 。
解:1、当Ω=k R 1时,假设二极管是截止的,则mA I I O 5.41192=+=-= V R I U V L O O B 5.415.4-=⨯-===V V A 3-= (V V V B A 5.1=-)由上分析可知,二极管承受正偏电压导通(假设不成立)故可得其等效电路如图P1.2b 所示:根据KCL 、 KVL :⎪⎩⎪⎨⎧+-=-+=+=RI R I R I I I I LO O222197.039 解之:mA I mAI mA I 3.56.17.3210==-=V R I U L O O 7.317.3-=⨯-==2、当Ω=k R 4时,假设二极管是截止的,则mA I I O 8.11492=+=-=VR I U V L O O B 8.118.1-=⨯-===V V A 3-= V U U B A 2.1-=-由上分析可知,二极管承受反偏电压截止(假设成立)01=I mA I I 8.102=-=V R I U L O O 8.118.1-=⨯-==3.3 设二极管为理想的,试判断P1.3所示电路中各二极管是导通还是截止,并求出AO两端的电压AO U解:(a )假设21V V 、均截止,则V V A 10=、V V B 6-=、V V O 0=, 21V V 、均承受正偏电压,但2V 管的正向偏值电压更大,故它首先导通。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
某大学为了了解学生每天上网的时间,在全校7500名学生中采取重复抽样方法随机抽取36
人,调查他们每天上网的时间,得到下面的数据:
已知:36=n ,当α为、、时,相应的645.11.0=z 、96.105.0=z 58.2201.0=z 。
根据样本数据计算得:32.3=x ,61.1=s 。
由于36=n 为大样本,所以平均上网时间的90%的置信区间为:
44.032.336
61.1645.132.32
±=⨯
±=±n
s z x α,即(,)。
平均上网时间的95%的置信区间为:
53.032.336
61.196.132.3±=⨯
±=±n
s z x α,即(,)。
平均上网时间的99%的置信区间为:
69.032.336
61.158.232.3±=⨯
±=±n
s z x α,即(,)。
一位银行的管理人员想估计每位顾客在该银行的月平均存款额。
他假设所有顾客月存款额的标准差为1000元,要求的估计误差在200元以内,置信水平为99%。
应选取多大的样本?
解:已知:σ=1000,估计误差E =200,α=,Z α/2= 应抽取的样本量为:167200100058.22
2
22
2
22≈⨯==
E z n σ
α
计算下列条件下所需的样本量。
(1)E =,π=,置信水平为96% (2)E =,π未知,置信水平为95% (3)E =,π=,置信水平为90% 解:(1)已知:E =,π=,α=,Z α/2= 应抽取的样本量为:(
)()252202.04.014.005.212
22
22≈-⨯=-=
E z n ππα
(2)已知:E =,π未知,α=,Z α/2=
由于π未知,可以使用(因为对于服从二项分布的随机变量,当π取时,其方差达到最大值。
因此,在无法得到总体比例的值时,可以用代替计算。
这样得出的必要样本容量虽然可能比实际需要的容量大一些,但可以充分保证有足够高的置信水平和尽可能小的置信区间),故应抽取的样本量为:(
)()60104
.05.015.096.112
22
2
2≈-⨯=-=
E z n ππα (3)已知:E =,π=,α=,Z α/2= 应抽取的样本量为:(
)()26805
.055.0155.0645.112
22
22≈-⨯=-=
E z n ππα 、已知两个正态总体的方差21σ和22σ未知但相等,即21σ=22σ。
从两个正态总体中分别抽取两个独立的随机样本,它们的均值和标准差如下表:
(1)求μ1-μ290%的置信区间; (2)求μ1-μ295%的置信区间。
(3)求μ1-μ299%的置信区间。
解:(1)由于两个样本均为独立小样本,当21σ和22σ未知但相等时,需要用两个样本
的方差21s 和2
2s 来估计。
总体方差的合并估计量2p
s 为: 当α=时,t α/2(19)=
μ1-μ2置信度为90%的置信区间为()()2
1
21221112n n s n n t x x p +-+±-α
=()94.78.97114
144.98729.14.432.53±=⎪⎭
⎫ ⎝⎛+⨯⨯±-,即(,)
(2)当α=时,t α/2(19)=
μ1-μ2置信度为95%的置信区间为()()2
1
21221112n n s n n t x x p +-+±-α
=()61.98.97114
144.98093.24.432.53±=⎪⎭
⎫ ⎝⎛+⨯⨯±-,即(,)
(3)当α=时,t α/2(19)=
μ1-μ2置信度为99%的置信区间为()()2
1
21221112n n s n n t x x p +-+±-α
=()14.138.97114
144.98861.24.432.53±=⎪⎭
⎫ ⎝⎛+⨯⨯±-,即(,)
、生产工序的方差是工序质量的一个重要度量。
当方差较大时,需要对序进行改进以减小方差。
下面是两部机器生产的袋茶重量(单位:g )的数据:
要求:构造两个总体方差比21σ/22σ的95%的置信区间。
解:统计量:
2
1212
2
2
2s s σσ()121,1F n n --
置信区间:22
112222
2121212,1,11,1s s s s F n n F n n αα-⎛⎫ ⎪ ⎪---- ⎪ ⎪⎝⎭
21s =,2
2s =,n 1=n 2=21
1α-=,()2121,1F n n α--=()0.02520,20F =,
()12121,1F n n α---=
()
2211
1,1F n n α--
()12121,1F n n α---=()0.97520,20F =
()
0.0251
20,20F =
()()22
112222
2121212,1,11,1s s s s F n n F n n αα-⎛⎫ ⎪ ⎪---- ⎪ ⎪⎝⎭
=(,)
8.2??一种元件,要求其使用寿命不得低于700小时。
现从一批这种元件中随机抽取36件,
测得其平均寿命为680小时。
已知该元件寿命服从正态分布,?=60小时,试在显着性水平0.05下确定这批元件是否合格。
?解:H0:μ≥700;H1:μ<700?
已知:x =680????=60?
由于n=36>30,大样本,因此检验统计量:。
