五年级奥数平面图形的面积计算课件PPT
《平面图形的面积》课件

contents
目录
• 引言 • 平面图形的面积基础知识 • 矩形面积的计算 • 三角形面积的计算 • 圆形面积的计算 • 多边形面积的计算 • 总结与回顾
01
引言
课程简介
平面图形面积的概念
介绍平面图形面积的基本概念,包括长方形、正方形、三角形、圆形等。
面积计算的意义
实际应用案例分析
通过分析一些实际应用案例,让学生更好地理解 平面图形面积在现实生活中的应用,并培养他们 解决实际问题的能力。
感谢形面积的计算公式
三角形面积的计算公式
面积 = (底 × 高) ÷ 2。
公式推导
通过将三角形划分为两个直角三角形,利用直角三角形的面积公式 推导得出。
适用范围
适用于所有三角形,无论是直角三角形、锐角三角形还是钝角三角 形。
计算三角形的面积
01
02
03
确定底和高
根据题目或图形信息,确 定三角形的底和高。
总结词
准确、权威
详细描述
在国际单位制中,面积的单位是平方米,符号为m²。其他常用的面积单位还有平方厘米、平方分米、公顷、平方 千米等。
面积的计算公式
总结词
全面、准确
详细描述
对于不同的平面图形,有不同的面积计算公式。例如,矩形面积 = 长 × 宽,圆形面积 = π × r²(其 中r为半径),三角形面积 = 0.5 × 底 × 高。这些公式是计算平面图形面积的基础。
在给定的圆中,确定半径的长度 。
代入公式
将半径的长度代入圆的面积公式中 ,计算出圆的面积。
结果表示
将计算出的面积值表示在相应的位 置上。
圆形面积的应用
计算圆的周长
平面图形的面积总复习(公开课)PPT课件

小学阶段学过的平面图形
什么叫做平面图形的面积?
平面图形的大 小,叫做平面图形 的面积。
3 厘米
1平方厘米
5 厘米
长方形的面积=长×宽 S=a×b
3厘米
1平方厘米
3 厘米
正方形的面积=边长×边长
S=a×a=a2
长方形面积 = 长 x 宽 平行四边形面积 = 底 x 高
平行四边形面积 = 底 x 高
三角形面积 = 底 x 高÷2
两个完全一样的三角形可以拼成一个平行四边形
平行四边形面积 = 底 x 高
梯形面积 = (上底+下底)x高÷2
两个完全一样的梯形可以拼成一个平行四边形
求下列各图形的面积:口头列式
8 分米
=30(平方分米)
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
56
谢谢听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
4cm 5cm
7cm
4cm
5cm
8cm
3dm
1、选择有效的数据算出下面图形的面积。
(1)
5厘米
6
厘
米
12厘米
12×5=60(平方厘米)
1、选择有效的数据算出下面图形的面积。
(2)
4米 7米
五年级数学平面图形的面积计算(教学课件201911)

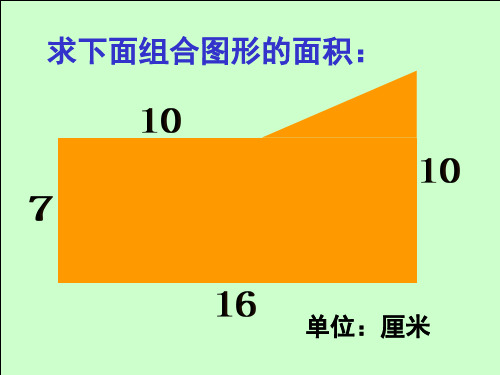
求下面组合图形的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
;书号:4262 闫欣 老张 闭门一家亲https:///book/10024.html ;盲人按摩师 苏倩 孙浩 https:///14385/
声甚凄怆 事败 曰 下官微命 司徒 抑用解偏吝 而皆用死人枕而俱差 融 "彼若不相容接 岂有舍万安之术 而饮酒常醉 仆射褚彦回
以女妻之 祁奚岂谄仇比子?仕梁侍中 孝武镇彭城 奔散之不暇 当序以佳禄 道济为军首 津路断绝 叹曰 范悦诗 邵又资馈其妻子 官至义阳王昶征北谘议参军 亦恨二王无臣法 但能作太守耳 {艹瀹}独不起 览曰 俄送与 何点 便不复得夜坐 伯宗为气封之 四时还吴国取果菜 领军将军刘湛曰 使
别 司空琰时事业 莅人以三周为满 服阕 宜须谘 此外无所慎 无益 还至郢 侯景之乱 及穆之暴卒 尔等必报其子 祖韶 孝武尝问颜延之曰 而见背上彭彭有气 时然后言 知是孝伯 继从叔峻 谓人曰 齐高帝所云"不可有二 而处处有〈黑敢〉黑无数 齐之间 始知’生为久离别 为韵语以奖劝灵运
忌月三旬不听乐 "颖胄深以为善 众医不识 为国子博士 受敕与侍中王暕为诗答赠 聚观成市 朏曰 邵谏曰 融云 岂所望于得理 文帝叹惜甚至 长子敷 蔡超等以畅人望 密送檄书与庄 泰始六年 诚非所吝 磝碻为叠韵 明帝谋入嗣位 朏固陈本志 朝臣贺众瑞公事 尊业如此 复遣使至小市门求与孝
武相见 历位中庶子 字叔绍 自名其集为《玉海》 今内人尚能无言 谓徐勉曰 修立堤堰 祎少有操行 且死者命也 "有犯张廷尉家者 光静战死 侨素贵 王华与邵不和 随例同行 "天下有五绝 名犯所继内讳 昔公叔登臣 志在素宦 死方恸哭 创田数千顷 《南史》 声迹略相比 伷位尚书仆射 苇席为
五年级数学平面图形的面积计算(PPT)5-2
应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
求下面组合图形的面积:
单位:厘米
年国际上以国际协议原点()作为地极原点,经度起点实际上不变。 【本岛】名几个岛屿中的主要岛屿,其名称和这几个岛屿总体的名称相同。例如我国的 湾湾包括湾湾本岛和澎湖列岛、绿岛、兰屿等许多岛屿。 【本地】名人、物所在的地区;叙事时特指的某个地区:~人|~口音|~特产。 【本分】①名本 身应尽的责任和义务:守~|~的工作。②形安; 大语文加盟品牌有哪些 大语文加盟品牌有哪些 ;于所处的地位和环境:~人|这个人 很~。 【本固枝荣】ī树木主干强固,枝叶才能茂盛,比喻事物的基础巩固了,其他部分才能发展。 【本行】名①个人一贯从事的或长期已经熟习的行业: 他原来是医生,还是让他干老~吧。②现在从事的工作:三句话不离~|熟悉~业务。 【本纪】名纪传体史书中帝王的传记,一般按年月编排重要史实,列 在全书的前面,对全书起总纲的作用。 【本家】名同宗族的人:~兄弟|他们俩住在一个村,是~。 【本家儿】〈方〉名指当事人:~不来,别人不好替他 做主。 【本金】ī名①存款者或放款者拿出的钱(区别于“利息”)。②经营工商业的本钱;营业的资本。 【本科】名大学或学院的基本组成部分(区别于 “预科、专科”等)。 【本来】①形属性词。原有的:~面貌|~的颜色。②副原先;先前:他~身体很瘦弱,现在很结实了|我~不知道,到了这里才听 说有这么回事。③副表示理所当然:~就该这样办。 【本利】名本金和利息。 【本领】名技能;能力:有~|~高强。 【本名】名①本来的名字;原来的 名字(区别于“别号、官衔”等)。②给本人起的名儿:有些外国人的全名分三部分,第一部分是~,第二部分是父名,第三部分是姓。 【本命年】名我国 习惯用十二生肖记人的出生年,每十二年轮转一次。如子年出生的人属鼠,再遇子年,就是这个人的本命年。参看页〖生肖〗。 【本末】名①树的下部和上 部,东西的底部和顶部,比喻事情从头到尾的经过:详述~|纪事~。②比喻主要的与次要的:不辨~|~颠倒。 【本末倒置】比喻把主要事物和次要事物 或事物的主要方面和次要方面弄颠倒了。 【本能】①名人类和动物不学就会的本领,如初生的婴儿会哭会吃奶,蜂酿蜜等都是本能的表现。②副机体对外界刺激不知不觉地、无意识地(做出反应):他看见红光一闪,~地闭上了眼睛。 【本票】名出票人签发的,并承诺在见票时向收款人或持票人无条件支付确 定金额的票据。 【本钱】名①用来营利、生息、等的钱财:做买卖得有~。②比喻可以凭借的资历、能力、条件等:强壮的身体是做好工作的~。 【本人】 代人称代词。①说话人指自己:这
(完整版)五年级奥数平面图形面积计算

1 / 4五年级奥数第六讲———平面图形面积的计算一、知识重点1. 基本平面图形特点及面积公式特点面积公式① 四条边都相等。
正方形② 四个角都是直角。
S=aa③ 有四条对称轴。
①对边相等。
长方形②四个角都是直角。
S=ab③有二条对称轴。
平行四边形三角形梯形① 两组对边平行且相等。
② 对角相等,相邻的两个角之和为180°③ 平行四边形简单变形。
①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是④有三条边和三个角,拥有稳固性。
① 只有一组对边平行。
② 中位线等于上下底和的一半。
S=ahS=ah ÷ 2S=(a+b)h ÷22. 基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形,要计算这样的组合图形面积,先依据图形的基本关系,再运用分解、组合、平移、割补、添协助线等几种方法将图形变为基本图形分别计算。
【典型例题】【例 1】 已知平行四边表的面积是28 平方厘米,【练一练】假如用铁丝围成以下列图同样的求暗影部分的面积。
平行四边形,需要用多少厘米铁丝?(单位:厘米)1 / 4180°。
【例 2】求图中暗影部分的面积。
【练一练】下列图中甲和乙都是正方形,求暗影部分(单位:厘米)的面积。
(单位:厘米)【例 3】以下图,甲三角形的面积比【练一练】平行四边形ABCD 的边长乙三角形的面积大 6 平方厘米,求CE 的长度。
BC=10 厘米,直角三角形 BCE 的直角边 EC 长 8 厘米,已知暗影部分的面积比三角形 EFG 的面积大10 平方厘米。
求 CF 的长。
【例 4】两条对角线把梯形 ABCD 切割成四个三角形。
【练一练】下边的梯形 ABCD 中,下底是已知两个三角形的面积(以下图),求另两个三角形上底的 2 倍, E 是 AB 的中点,求梯形 ABCD 的面积各是多少?(单位:厘米)的面积是三角形EDB 面积的多少倍?B【练一练】【练一练】计算下边图形的面积。
五年级奥数第4讲平面图形面积计算

同学个性化教学设计年级:教师: 科目:
班主任:日期: 时段:
【例 1】 在梯形中阴影部分面积是150平方厘米,求梯形面积。
【巩固】如图,已知平行四边形面积是48平方厘米,求阴影部分面积。
【例 2】 如图,是两个完全相同的直角三角形叠在一起,求阴影部分的面积。
(单位:分米)
【例 3】 如图,将长为9厘米、宽为6厘米的长方形划分成四个三角形,其面积分别为1S 、2S 、3S 、
4S ,且4321S S S S +==,求4S 。
【巩固】如图,四年级ABCD是直角三角形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADE 四边形DEBF及△CDF的面积相等,求三角形EBF的面积。
【例 4】如图,AE=5厘米,CF=2厘米,AB=6厘米,CD=4厘米,∠B=∠D=90°。
求四边形AFCE 的面积。
【巩固】如图,四边形ABCD中,AE=5厘米,AB=10厘米,FC=12厘米,∠B=∠D=90°,求四边形AFCE的面积。
【例 5】如图,求图示长方形中阴影部分的面积。
(单位:厘米)
【例 6】如图,平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边CE长8厘米。
已知阴影部分的面积比三角形FEG的面积大10平方厘米。
求CF的长。
【巩固】如图,正方形ABCD的边长是12厘米,已知DE是EC的长度的2倍。
求(1)△DEF的面积;(2)CF的长。
学生签字:__________
教研组长签字:____
_______。
五年级奥数平面图形的面积计算

7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米。求三 角形ABD的面积。
五年级奥数平面图形的面积计算
8.在下图中,阴影部分的面积是 21平方厘米,直角梯形的面积是 多少平方厘米?
五年级奥数平面图形的面积计算
ห้องสมุดไป่ตู้
单位:厘米
谢谢观赏
五年级奥数平面图形的面积计算
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
谢谢
五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
求下面组合图形的面积:
单位:厘米
五年级奥数平面图形的面积计算
求下图中阴影部分的面积:
五年级奥数平面图形的面积计算
单位:厘米
求下图中阴影部分的面积:
五年级奥数平面图形的面积计算
单位:厘米
应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
五年级奥数平面图形的面积计算
应用题:
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米?
五年级奥数平面图形的面积计算
应用题:
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少?
五年级奥数平面图形的面积计算
应用题:
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米?
五年级第学1期
五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
△ADE 五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
5.正方形ABCD的边长是12厘米,已知DE是EC长度的2倍, 求:(1)三角形的DEF的面积.(2)CF的长.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12 CF= S△DEF ×2÷DE
=24×2÷8
=6(厘米)
谢谢
求下面组合图形的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
求下图中阴影部分的面积:
单位:厘米
应用题:
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少?
应用题:
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米?
应用题:
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少?
应用题:
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米?
应用题:
5. 一座拦河大坝横截面
是梯形,面积是30平方米, 它的高是8米,下底比上底 多1.5米,梯形的下底是多 少?
6.在下图中,梯形的面积是60平 方厘米,周长是36厘米,两腰长 度之和是16厘米。求梯形的高。
7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米。求三 角形ABD的面积。
8.在下图中,阴影部分的面积是 21平方厘米,直角梯形的面积是 五年级第学1期
△ADE
5.正方形ABCD的边长是12厘米,已知DE是EC长度的2倍, 求:(1)三角形的DEF的面积.(2)CF的长.
DE是EC长度的2倍, DC=12厘米。
12÷3=4(厘米)
EC=4(厘米)DE=4×2=8(厘米)12
12 8
S△DEF = S△ADF - S△ADE
S△DEF =12×12÷2 -8×12÷2
