puma250机器人运动学分析
多运动模式轮腿移动机器人的运动学分析与

THANKS
感谢观看
02 考虑不确定性的控制策略
考虑到实际应用中存在的不确定性因素,如环境 变化、负载变化等,设计鲁棒性强的控制器和算 法。
03 实时优化的控制策略
根据实时获取的机器人状态信息,对控制策略进 行优化,以提高机器人的运动性能。
不同运动模式下轮腿移动机器人的控制策略
轮式运动模式
在平坦路面或短草地等环境下,机器人主要依靠 轮子进行移动,此时需要保证轮子的转速和方向 控制精确。
多运动模式轮腿移动
机器人的运动学分析
与汇报人:
日期:
目录
• 引言 • 多运动模式轮腿移动机器人的机
构设计 • 多运动模式轮腿移动机器人的运
动学模型建立 • 多运动模式轮腿移动机器人的运
动学特性分析
目录
• 多运动模式轮腿移动机器人的控 制策略研究
• 多运动模式轮腿移动机器人的实 验研究与性能评估
• 结论与展望 • 参考文献
机构设计的基本原则和要求
基本原则
多运动模式轮腿移动机器人的机构设计应遵循结构简单、紧凑、易于制造和维修的原则,同时 要保证机器人的稳定性和可靠性。
要求
在机构设计过程中,需要考虑机器人的运动性能、负载能力、灵活性、耐用性等方面的要求, 并针对不同的应用场景和任务需求进行优化和改进。
典型多运动模式轮腿移动机器人的机构组成
确定运动学参数
通过实验或计算的方 法,确定机器人的运 动学参数,如轮子和 腿的长度、角度以及 机器人的质量等。
验证模型
基于前置坐标系的PUMA机器人运动学方程的研究

—
1 置 坐标 系 建 立 的 3 原 则 。 . 前 条
一 C
di 1i + sn
di 1 OS I 十C 【
() 沿着第 i 关节方向。 1Z轴 个 ( ) 沿 着 公 垂线 方 向 , 南 z轴指 向 Z 2 置轴 并 l + 轴 () 3 轴按 右手 原 则 建立 。 2 置 坐 标 系 ( 1。 . 前 图 )
。
.
。
l
二 、 U 50 器 人 操作 臂 运 动 方 程 的建 立 P MA 6 机
P MA 6 机 器人是 由 U i a o 公司生 产的 6自由度串联 U 50 nm t n i
机 构 机 器 人 , 由 6 转 动 关 节 构 成 。假 设 机 器 人 各 关 节 角 为 它 个
工 业 技 术
● ■ 一 ■ ■ ■ ● ● ■ 一 一■ 一一 ■ ■ ■ 一 ● 一 一 麓 譬 曩 ■
I NDUS TRY TECHNOL OGY ■ 瓣 鬟
东北 大学机 械学 院 张长 江
机 器人 运 动学 研 究 的主 要 内 容 是机 器 人各 连 杆 间 的位 移 关
+. =
( , )R( , )R( , ) T Z , ・ - Z, ・ ( i +)
O
—
系 、 度 关 系 和 加 速 度 关 系 。 由 机 器 人 关 节 坐 标 系推 导 其 末 端 速 位 姿 的 过 程 称 为 机 器 人 的 正 向 运 动 学 ; 知 机 器 人 的末 端 位 姿 已 求 其 各 关 节 坐 标 系 之 间 的关 系 , 为机 器 人 的 逆 向运 动 学 。 本 称 文 中 , 者 只讨 论 正 向运 动 学 。 为 了进 行 机 器 人 的 位 姿 分 析 , 笔 D nvt H r neg 出 了 一 种 建 立 连 杆 坐 标 系 的 方 法 ( — eai和 at br 提 e DH
7 PUMA机器人运动学

如果末端连杆的位姿已经给定,求关节变量的值称为运动学反解。 Paul等人建议用未知的连杆逆变换左乘方程两边,把关节变量分 离出来,从而求解,具体步骤如下。
上海电机学院 机械学院
1.首先解出θ1,
0 1 0 1 0 1 2 3 4 5 T 1 (1 )0 T T ( ) T ( ) T ( ) T ( ) T ( ) T ( ) 6 1 1 1 1 2 2 3 3 4 4 5 5 6T (6 )
上海电机学院 机械学院
通常,把反解存在的区域称为该机器人的工作空间。 严格地讲,工作空间分成两种: (1)灵活空间,系指机器人手爪能以任意方位到达的目标点 的几何; (2)可达空间,系指机器人手爪至少能以一个方位到达的目 标点的集合。 灵活空间是可达空间的子集,在灵活空间的各点上,抓手的指向 可以任意规定。 在三维空间中,当操作臂的自由度小于6时,其灵活空间的体积为 零,不能在三维空间内获得一般的目标位姿。
(2)解的多重性。
(3)求解方法的多样性。
上海电机学院 机械学院
一、解的存在性和工作空间 如图所示的2R机械手,两连杆长度分别为l1、l2,两旋转关节 平行,其运动方程为:
反解关心的问题是:对于给定的位置矢 量(x,y),由运动学方程求出相应的 关节矢量。 求解之前最关心的问题是,对于给定的 值(x,y),相应的关节矢量是否存在。
求2在矩阵方程??????65654543432321210106ttttttt?两端左乘逆变换103?tt66t55t44t66t33543010??上海电机学院机械学院方程两边的元素14和34分别对应相等得上海电机学院机械学院s23和c23表达式的分母相等且为正于是根据解1和3的四种可能组合可以得到相应的3四种可能值于是可得到的四种可能解???3232??式中2取和3对应的值
没有对手跑不快?Puma 做了一个赛跑机器人

没有对手跑不快?Puma 做了一个赛跑机器人
每一个跑步运动员都想破纪录,世界纪录,或者自己的记录。
但在跑步时你是看不
见“记录”的,又要如何超越它?
你知道,训练跑步运动员有一个古老的办法:找个比 Ta 跑得更快的人。
或许是受这个启发,Puma 最近做了一个合格的“陪练”——可以跟人赛跑的机器人BeatBot。
它的好处在于可以恒定地维持纪录速度(考虑到即便是纪录保持者也不是每次跑都可以保持水平不变)。
开始前,输入任何一个时间记录,可以是跑者自己的最好记录、对手的记录(比如说博尔特)。
机器人内置了 9 个红外线传感器,全程追踪跑道上的线作为运动轨迹。
轮子可以监测速度和距离,然后实时处理数据,每秒钟会进行 100 次演练,以确保整个跑步过程并在精确的时间撞线。
机器人身上装了 LED 灯,方便运动员在跑步时也能用余光看到它。
前方和后方都装了 GoPro,赛跑结束后还能回顾自己跑得怎么样。
这个机器人由来自 MIT 工程系的团队开发,在下面这个视频里你可以看到它的演示,出镜的那位就是大名鼎鼎的博尔特。
在赛场上,对手是敌人;但在训练时,“对手”也可以是不错的陪练。
可惜的是,这个机器人造价昂贵,目前 Puma 只把它提供给跑步运动员和专业团体,不对大众发售。
喜欢这篇文章?去 App 商店搜 好奇心日报 ,每天看点不一样的。
好奇心日报 , 每个时代都有最好的媒体。
基于MATLAB的Puma250机器人运动仿真与分析

基于MATLAB的Puma250机器人运动仿真与分析
李瑾
【期刊名称】《现代制造技术与装备》
【年(卷),期】2018(0)11
【摘要】针对Puma250机器人,分析其结构及连杆参数.利用MATLAB工具,按照D-H参数法建立了Puma250机器人连杆结构模型.对机器人的运动学特性进行仿真实验,并验证了机器人逆运动的多解性,给出Puma250机器人连杆末端直线运动轨迹仿真方法,并提出其仿真运动过程中直线插补点精确值的求解方法.
【总页数】3页(P66-68)
【作者】李瑾
【作者单位】山西工程技术学院,阳泉 045000
【正文语种】中文
【相关文献】
1.基于MATLAB Robotic Toolbox的关节型机器人运动仿真研究 [J], 陆佳皓;平雪良;李朝阳
2.基于MATLAB与V-REP的机器人加工轨迹生成与运动仿真 [J], 刘宇;张世超;龚集响
3.基于MATLAB Robotics Toolbox的可重构模块化\r机器人运动仿真分析 [J], 卢佳佳;毛芳芳;李梅;李雅琼
4.基于MATLAB六轴喷涂机器人运动仿真研究 [J], 高方俊; 郑磊; 徐强; 檀晓宏
5.基于Coppeliasim与MATLAB的机器人建模与运动仿真 [J], 李杨;张华良;王军
因版权原因,仅展示原文概要,查看原文内容请购买。
PUMA型机器人机械结构课程设计

一总体设计
基本技术参数的选择
(1)额定负载及额定速度 手臂本体重量 13.2KG,小臂提升手腕重量不超过 1KG,最大线速度 V=1.23m/s。 (2)工作空间的确定 初定空间如图 1_1 所示:
图 1_1 工作空间示意图 由设计任务书主要技术参数所规定的操作范围 0.47m 为半径的空间球体, 初 定小臂有效长度 L2=200MM, 大臂有效长度 L1=300MM, 底座支柱有效长度 L3=500MM。 (3)驱动方式的选择 PUMA 机器人是采用直流伺服电机驱动,齿轮传动,刚性大,控制性能好, 体积小,精度高。
P T
式中: T 15.2 , 6.15 得P T 15.2 6.15 9.48W (2)电动机所需要的功率 P d :
P d P / a
式中
a ——传动装置的总效率。
a 1. 23..........
i ——每个传动副(齿轮、蜗杆、链及带) ,每对轴承,每个联轴器及卷筒的
效率 如对本设计:取偏心套 1 0.96 ,齿轮传动效率 2 0.97 ,滚动轴承效率
3 0.988 ,弹性联轴器效率为: 4 0.993 。
a 1 2 2 33 4 0.96 0.97 2 0.9883 0.98 0.854
; ;
P W 1 2 3 148.95 0.99 0.97 143.04
3 轴 P3 P2 2 3 143.04 0.99 0.97 137.36W ; 各轴输出功率为相应输入功率乘以 0.99 3)各轴的输入转矩: 电动机轴 Td 0.5N m ; 1 轴 T1 Td i0 01 0.96 1 0.993 0.95N m ; 2 轴 T2 T1 i1 12 0.95 3 0.98 0.97 2.71N m ; 3 轴 T3 T2 i2 23 2.71 4.25 0.98 0.97 10.95N m ; 各轴输出转矩为相应输入功率乘以 0.98 4)将将求得的数据列入下表: 轴名 功率(w) 转矩(N·m) 转速 (r/mi 输入 输出 输入 输出 n) 电机轴 150 0.96 1500 1轴 148.95 147.46 0.95 0.931 1500 2轴 143.04 141.61 2.71 2.656 500 3轴 137.36 135.99 10.95 10.731 117.6 传动零件的设计 减速器外传动零件的设计 1. 选择联轴器 类型选择
基于MATLAB的PUMA机器人运动仿真研究

5
4
6
1 PM 50 器人参数 设计 U A6机
11 - . D H变换 为描 述 相 邻 杆 件 间平 移 和转 动 的 关 系 ,
高新技术
SC TNG2 N0圆 CE EOY0 . &CL 1O1 N HO. .l 。{ 3 。 1
基于 MA L B的 P MA机器人运动仿真研究① T A U
邢 广成 张洛 花 ( 河南 城建 学院 电气与 电子 工程 系 河 南平顶 山 4 3 ) 6 0 6 7 摘 要 : 器人 运 动学是机 器人 学的一个 重要分 支 , 实现机 器人 运 动控 制的基 础 。 机 是 论文 VD H 4 — 坐标 系理论 为基础对P M 5 0 器人 进 u A 6机 行 了参数设 计 , 用MA L B机器人 工 具箱 , 利 TA 对机 器人 的正运 动学 , 运 动学 , 逆 轨迹 规 划进 行 了仿真 。 alb M ta 仿真结 果说 明 了所设 计的参
为 连 杆 的 扭 转 角 。 于 转 动 关 节 是 关 对 节变 量 , 其余 为 关节 参数 ( 保持 不 变)对于 移 : 动关 节 , 是 关 节 变量 , 其余 为 关 节参 数 。 1 2P MA 6 机器人 的关 节结构及其 参数设 . U 5 0 计 ( 1 图 ) P UMA5 O 器人 由6 6机 自由 度旋 转 关 节 组 成 , 构 成 如 图 1 示 。 器 人 的 回转 机 其 所 机 体 实 现 机 器 人 机 体 绕 z 轴 的 回转 ( 0 ) 。 角 , 它 由 固 定 底 座 和 回转 工 作 台 组 成 。 臂 臂 大 体 的 下 端 安 有 直 流 伺 服 电 机 , 控 制 大 臂 可 上 下摆 动 ( 0 ) 小 臂 支 承 于 大 臂 臂 体 的 角 ,。 上 关 节 处 , 驱 动 电 机 可 带 动 小 臂 做 上 下 其 俯仰( 角 )以 及 小 臂 的 回转 ( 。 器 人 , 0 )机
PUMA机器人运动学

逆向运动学的求解方法
解析法
迭代法
通过建立机器人关节变量与末端执行器位 姿之间的数学关系,求解逆向运动学方程 。
通过迭代算法逐步逼近逆向运动学解,常 用的有雅可比伪逆法和牛顿-拉夫逊法。
神经网络法
遗传算法
利用神经网络学习逆向运动学解,适用于 非线性机器人系统。
基于自然进化原理,通过不断优化关节变 量来寻找逆向运动学解。
运动学的基本概念
01
02
03
运动学
研究物体运动规律的学科, 包括位置、速度和加速度 等参数。
运动学方程
描述机器人关节角度与末 端执行器位置和姿态之间 关系的数学模型。
正运动学
根据给定的关节角度,求 解机器人末端执行器的位 置和姿态。
运动学方程的建立
基于几何学原理
利用机器人关节连杆的几 何关系,建立运动学方程。
正向运动学的优缺点分析
优点
计算速度快,精度高;适用于各种类型的机器人;可通过解析法得到封闭解, 避免数值误差积累。
缺点
对于某些复杂机器人或特殊作业任务,可能难以建立准确的数学模型;数值法 求解时需要较高的计算资源和时间成本;对于非线性或柔性机器人,正向运动 学求解可能存在较大误差。
04 Puma机器人逆向运动学
案。
逆运动学
03
已知末端执行器的位置和姿态,反推求解关节角度,是正运动
学的逆过程。
03 Puma机器人正向运动学
正向运动学的求解方法
解析法
通过建立机器人关节变量与末端 执行器位姿之间的数学关系,直 接求解出末端执行器的位置和姿
态。
数值法
通过迭代或搜索的方法,逐步逼近 目标位姿,最终得到满足精度要求 的解。
机器人技术大作业

机器人技术大作业:PUMA机器人作业要求:1.建立坐标系;2.给出D-H参数表;3.推导正运动学,逆运动学;4.编程得出工作空间;1.建立坐标系由坐标系的建立规则:Oi:设在Li与Ai+1轴线的交点上;Zi轴:与Ai+1关节轴重合,指向任意;Xi轴:与公法线Li重合,指向沿Li由Ai轴线指向Ai+1轴线;Yi轴:按右手定则确定;可以建立PUMA机器人各关节坐标系如下:图1 PUMA机器人各关机坐标系2.给出D-H参数表由各参数的确定规则:杆件长度Li:沿xi 轴,zi-1 轴与xi 轴交点到0i 的距离;杆件扭转角αi:绕xi 轴,由zi-1 转向zi;杆件偏移量di:沿zi-1 轴,zi-1 轴和xi 交点至∑0i –1 坐标系原点的距离;杆件回转角θi:绕zi-1 轴,由xi-1转向xi;可以得到PUMA机器人的D-H参数表:表1 PUMA 机器人D-H 参数表3. 推导正运动学,逆运动学解3.1正运动学以下以c 代表cos 函数,s 代表sin 函数 由D-H 参数表易得:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=100001000001111110d c s s c T θθθθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10001000022222222221d s a c s c a s c T θθθθθθ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=10000010003333333332θθθθθθs a c s c a s c T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=100001000004444443d c s s c T θθθθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=1000100000555554θθθθc s s c T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10010000006666665d c s s c T θθθθ将以上六个矩阵依次右乘,即可得到末端机械手的齐次变换矩阵:65544332211060T T T T T T T =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1060z z z z y y y yx x x x p a o n p a o n p a o n T 利用MATLAB 程序可以求出此变换矩阵各参数: syms a2 d2 a3 d4 d6syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 T01=[c1 0 -s1 0;s1 0 c1 0;0 -1 0 d1;0 0 0 1]; T12=[c2 -s2 0 a2*c2;s2 c2 0 a2*s2;0 0 1 d2;0 0 0 1]; T23=[c3 0 -s3 a3*c3;s3 0 c3 a3*s3;0 -1 0 0;0 0 0 1]; T34=[c4 0 -s4 0;s4 0 c4 0;0 -1 0 d4;0 0 0 1]; T45=[c5 0 -s5 0;s5 0 c5 0;0 -1 0 0;0 0 0 1]; T56=[c6 -s6 0 0;s6 c6 0 0;0 0 1 d6;0 0 0 1]; T06=T01*T12*T23*T34*T45*T56 得到:nx=c6(s5c1s23 + c5(s1s4+c4c1c23)) - s6(c4s1 - s4c1c23) ny=c6(s5s1s23 - c5(c1s4-c4s1c23)) + s6(c1c4 + s4s1c23) nz=c6s5c23-c4c5s23-s4s6s23ox=-s6(s5c1c23+c5(s1s4 + c4c1c23)) - c6(c4s1-s4c1c23) oy=c6(c1c4+s4s1c23)-s6s5s1s23-c5(c1s4-c4s1c23) oz=-s6(s5c23 - c4c5s23- c6s4s23) ax=c5(c1s23- s5(s1s4 + c4c1c23)) ay=c5(s1s23+ s5(c1s4 - c4s1c23)) az=c5(c23 + c4s5s23)px=d6(c5c1s23-s5(s1s4+c4c1c23))-d2s1-d4c1s23+ a2c1c2 - a3c1s2s3 + a3c1c2c3 py=d6(c5s1s23+s5(c1s4-c4s1c23))+d2c1-d4s1c23+ a2c2s1- a3s1s2s3 + a3c2c3s1 pz=d1- a2s2 -d4c23+ d6(c5c23+ c4s5s23) - a3c2s3 - a3c3s2 其中:c23=cos(θ2+θ3),s23=sin(θ2+θ3). 带入:c1=0; s1=1; c2=1; s2=0; c3=0; s3=-1; c4=-1; s4=0; c5=-1; s5=0; c6=-1; s6=0;得到:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-++--=100013001642100201060d a d d a d T与图中实际位置相符,故正解正确。
PUMA机器人正逆运动学推导及运动空间解算-机器人技术大作业全

PUMA机器人正逆运动学推导及运动空间解算求解:①建立坐标系;②给出D-H参数表;③推导正、逆运动学;④编程得工作空间1.建立坐标系根据PUMA机器人运动自由度,在各关节处建立坐标系如图2所示。
图1 PUMA560机器人坐标系图2.D-H参数表D-H 参数表可根据坐标系设定而得出,见表1。
(1)i θ为绕1i Z -轴从1i X -到i X 的角度; (2)1i α-为绕i X 轴从1i Z -到i Z 的角度;(3)1i a -为沿i X 轴从1i Z -与i X 交点到i O 的距离; (4)i d 为沿1i Z -轴从1i Z -与i X 交点到1i O -的距离。
表1 PUMA 机器人的杆件参数表3. 正运动学推导由坐标系图及各杆件参数可得个连杆变换矩阵。
111101000001100001c s s c T θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦ 22222222122000010001c s c a s c s a T d θθθθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3333333323000100001c s c a s c s a T θθθθθθ-⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦ 444434400000100001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦5555450000010001c s s c T θθθθ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦ 66665660000001001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据各连杆变换矩阵相乘,可以得到PUMA560的机械手变换矩阵,其矩阵为关节变量的函数。
()()()()()()00123456112233445566T T T T T T T θθθθθθ=将上述变换矩阵逐个依次相乘可以得到06T 。
601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦()()()()()()()()6514142315236411234651442311523614231446236235452365141423152364112346514423115236x y z x y n c c s s c c c c s s s c s c c s n c c c s c c s s s s s c c c s s n s s s c c s c c s o s c s s c c c c s s c c s c c s o s c c s c c s s s s c =--+-+⎡⎤⎣⎦=+-+-⎡⎤⎣⎦=-+=-+-+⎡⎤⎣⎦=-+-+⎡⎤⎣⎦()()()()()()()()142314623545236423152351414235123514423152345231223232165141423152314231223231265144231z x y z x y c c c s s o s c s c c s c s s a c c s s s s c c c a c s s s c s c c s a a c c s s p c a c a c d s d s s s c c c c c s c d s p s a c a c c d d s c s c c s c -=++=--=++=-=-----+⎡⎤⎣⎦=-++++()512341232342232365234523z s s d s s p c d a s a s d c c c s s ⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪+⎡⎤⎣⎦⎪=-++-⎪⎭上式中()()23232323cos ,sin c s θθθθ=+=+。
机器人在体育赛事中的角色与运动表现分析

机器人在体育赛事中的角色与运动表现分析随着科技的不断进步和机器人技术的快速发展,机器人在各个领域中发挥着越来越重要的角色,体育赛事也不例外。
本文将探讨机器人在体育赛事中所扮演的角色,并分析其在运动表现方面的优势和局限性。
一、机器人在体育赛事中的角色1. 教练员与裁判员机器人可以充当体育赛事中的教练员和裁判员,传授运动技巧和规则知识,监管比赛进行情况。
机器人具备高度的智能和计算能力,能够根据运动数据和规则判断比赛结果,确保比赛的公正性。
2. 陪练伴侣机器人还可以作为运动员的陪练伴侣,提供专业、标准的训练服务。
机器人可以根据运动员的需求,灵活调整训练强度和方式,帮助运动员提高技术水平和竞技能力。
3. 比赛助威者机器人可以被设计成具有表情、音效和动作等功能,作为观众互动的助威者。
机器人可以根据比赛情况呈现不同的表现,增加赛场氛围,提升观赛体验。
二、机器人在运动表现方面的优势1. 精准度高机器人在运动表现方面的一个明显优势是精准度高。
机器人可以根据事先设定的编程指令准确地完成各种动作,无论是投球、踢球还是击球等,都能保持高度的准确性。
2. 强大的计算和反应能力机器人搭载了强大的计算和反应能力,可以在短时间内做出精确的决策。
这使得机器人在速度类项目中具备优势,例如汽车比赛中的无人驾驶车辆、田径赛中的机器人短跑选手等。
3. 可拓展性强机器人的运动表现可以经过不断的优化和改进来提升其性能。
通过引入新的材料、算法和控制系统,机器人的速度、力量和灵活性等方面可以得到进一步的提升,提高在体育赛事中的竞技水平。
三、机器人在运动表现方面的局限性1. 灵活性限制虽然机器人在执行程序时可以做到准确无误,但其灵活性仍存在一定的限制。
机器人运动的方式通常是基于事先设定好的编程指令,难以适应比赛中的实时变化和判断。
2. 感知能力局限机器人的感知能力相对有限,无法像人类一样通过视觉、听觉等感官进行全面感知和判断。
这对于某些依赖感知能力进行的运动项目,如羽毛球、乒乓球等,机器人的表现可能会受到一定的限制。
PUMA机器人运动学逆解新算法

摘
要:6 R串联机器人的逆解求解复杂, 使用传统的 D- H 算法求解该问题计算量 大且无法避免奇异点. 将P U MA
: ( S h e n y a n g I n s t i t u t e o f C o m p u t i n g T e c h n o l o g y , C h i n e s e A c a d e m y o f S c i e n c e s , S h e n y a n g l 1 0 1 6 8 , C h i n a )
t r a d i io t na l D— H ne e d a mo u n t o f c o mp u t a t i o n s a n d e x i s t s s ng i u l a r s o l u i t o n. I n ve r s e ki n e ma ic t s o fp u ma r o bo t d e c o mpo s e s
Ke y wo r ds : 6 一 R r o b o t ; u ni t q u a t e mi o n; D・ H me t h o d ; i n v e r s e k i n e ma t i c s ; P UM A r o b o t
关键词:六关节机器人; 逆运动学; D . H 方法; 单位 四元数: P U MA机器人
Ap p l i c a i t o n o f Do u b l e Qu a t e r n i o n i n t h e I n v e r s e Ki n e ma t i c s o f 6 R S e r i a l Ro b o t s
织网机自动换梭盘机器人运动仿真

DOI :10.19333/j.mfkj.20200104005织网机自动换梭盘机器人运动仿真罗银杰,孟㊀婥,郝志昌,明灿坤,孙志军(东华大学机械工程学院,上海㊀201620)㊀㊀摘㊀要:为提高织网企业的生产效率和改善其产品质量,研发了先进的织网机㊂自动换梭盘系统是织网机的重要组成部分,该系统由自动换梭盘机器人和机器人末端执行机构组成㊂在织网机自动换梭盘系统的基础上,以织网机自动换梭盘机器人为对象,在MatLab 中建立机器人仿真模型,调用Robotics Toolbox 中的功能函数对该机器人的逆运动学进行仿真计算与轨迹规划仿真㊂结果表明:仿真结果符合织网机自动换梭盘机器人运动性能要求,为实现织网机自动换梭盘机器人的精确定位提供理论基础和重要数据㊂关键词:织网机;自动换梭盘机器人;运动仿真;轨迹规划中图分类号:TP 242㊀㊀㊀㊀文献标志码:AMotion simulation of automatic replacement of the yarncoil robot for netting machineLUO Yinjie,MENG Zhuo,HAO Zhichang,MING Cankun,SUN Zhijun(College of Mechanical Engineering,Donghua University,Shanghai 201620,China)Abstract :In order to improve the production efficiency and improve the quality of the products,theadvanced webbing machine has been developed.In this paper,based on the automatic replacement of theyarn coil system,the automatic replacement of the yarn coil robot;is taken as the object,the robot simulation model is established in MatLab,the inverse kinematics of the robot are simulated by using thefunctional function of MatLab Robotics Toolbox.Finally,the trajectory planning of the robot is carriedout,which provides the theoretical basis and important data to realize the precise positioning of robot and optimizes the trajectory of the robot in the actual operating environment.Keywords :netting machine;automatic replacement of the yarn coil robot;motion simulation;trajectory planning收稿日期:2020-01-22第一作者:罗银杰,硕士生,主要研究方向为织网装备设计与控制㊂通信作者:孟婥,教授,主要研究方向为纺织装备技术与系统,E-mail:mz@㊂㊀㊀随着科学技术的飞速发展,现代织网机也在近些年有了大幅度的改进,织网机正朝着机器高速化㊁控制现代化㊁操作便利化等方面发展㊂其中,投放使用工业机器人可实现织网机梭盘的自动取放,节省人工和提高生产效率㊂机器人的运动学分析是机器人机构分析的前提和基础,为后续织网机自动换梭盘机器人的运动与控制提供了理论依据㊂近年来,由于计算机技术与仿真技术的飞速发展,国内外不少学者对机器人仿真技术进行了研究,Dollarhide 等[1]应用DELMIA /IGRIP 软件对机器人进行建模并完成仿真,实现对机器人的实时监控㊂康嘉瑞等[2]运用Simulink 仿真技术对空间机器人逆运动学进行了研究㊂王成军等[3]采用笛卡尔空间变量法对铸件机器人工作过程中的运动轨迹进行规划㊂王玉宝等[4]采用粒子群算法对工业机器人进行空间轨迹时间优化㊂廖解能等[5]基于Solidworks-Workbench 平台建立桁架机器人仿真模型,通过静力学分析与模态分析,提取出桁架机器人的固有频率,大大提高了桁架机器人的使用寿命㊂李瑾[6]利用MatLab 工具箱,针对Puma 250机器人,对其运动特性进行研究分析,并给出了机器人运动轨迹仿真方法㊂李振雨等[7]以Puma560机器人为研究对象,建立其运动学方程并进行仿真研究,实现了工业机器人的精确作业㊂涂鹏飞等[8]采用离线编程技术来规划喷涂轨迹,大大提高了工件的喷涂效率㊂王林军等[9]基于MatLab对ABB IRB1660机器人进行了运动学仿真研究㊂上述研究中普遍对于经典机器人进行了仿真研究,较少定位于实际现场环境㊂本文以织网机换梭盘工作过程为载体,设计机器人末端执行机构,基于MatLab Robotics Toolbox模块中的功能函数,建立织网机自动换梭盘机器人仿真模型,并对其进行运动学仿真和空间运行轨迹仿真,为在实际操作环境中机器人精确定位提供理论依据,对实现企业中织网机梭盘更换自动化具有一定的研究意义㊂1㊀织网机及其换梭盘流程织网机是生产网具用品的机械装备,目前企业中较多沿用或仿制20世纪的老式织网机,织网机更换梭盘主要由人工手动完成㊂随着先进织网机的研发,设计了配套的机器人换梭盘系统㊂织网机自动换梭盘系统见图1,该系统主要由换梭盘机器人和机器人末端执行机构组成,其中末端执行机构一端与机器人末端固联,另一端插入梭盘,通过末端执行机构上的锥齿与梭盘内圈配合,末端执行机构插入与抬起梭盘时的状态见图2,随着换梭盘机器人的运动带动末端执行机构,将织网机上空梭盘取出并将装满线的梭盘放入梭箱㊂图1㊀织网机自动换梭盘系统图2㊀末端执行机构插入与抬起梭盘时的状态依据负载㊁成本等因素选择ABB IRB6700-200/2.60空间六自由度机器人作为换梭盘机器人,机器人各关节主要运动参数见表1㊂自动换梭盘机器人工作流程见图3㊂表1㊀机器人各关节运动最大速度与范围关节序号关节最大转速/(rad㊃s-1)关节运动范围rad111π/18ʃ17π/18211π/18-13π/36~17π/36311π/18-π~7π/18419π/18ʃπ/3515π/18ʃ13π/1867π/6ʃ2π图3㊀自动换梭盘机器人工作流程图在机器人换梭盘流程中,机器人将一段梭盘从织网机上抬起,定义此时机器人的空间位姿为T1,并水平旋转180ʎ,使机器人末端朝相反方向,目的是将空梭盘依次放入梭箱中,定义此时机器人的空间位姿为T2,这2个空间位姿是完成梭盘取放的关键㊂在实际操作中,为保证换梭盘效率,通过控制换梭盘机器人的转角速度,使其能够在足够短的时间内由位姿T1平滑过渡到T2㊂2㊀机器人运动学仿真2.1㊀仿真模型建立用虚拟样机对机器人进行运动仿真,首选需要对机器人的仿真模型进行构建㊂本文通过MatLab中的Robotics Toolbox模块建立了机器人驱动器仿真模型并命名为自动换梭盘机器人,此时换梭盘机器人处于从织网机上抬起梭盘时的位姿,即位姿T1,机器人各关节转角为q0=[0㊀0㊀0㊀0㊀0㊀0],机器人抬起梭盘时位姿仿真模型见图4㊂图4㊀三维平面内机器人抬起梭盘时位姿仿真模型2.2㊀逆运动学仿真机器人运动学包括了正向运动学和逆向运动学㊂在此对换梭盘机器人的逆向运动学进行仿真分析,逆向运动学是已知机器人末端执行器的位姿求其各关节角度㊂当换梭盘机器人从织网机上抬起一段梭盘在空间上旋转180ʎ后,即到达位姿T2时,此时机器6个关节转角为q1=[0㊀π/4-π/4㊀π㊀π/4㊀π/2],通过MatLab编程得出机器人在此关节转角下的末端执行器位姿矩阵为G,且G=-0.5000-0.85360.1464-0.1191-0.50000.1464-0.8536㊀1.4966㊀0.7071-0.50000.6177㊀0.65410001éëêêêêêùûúúúúú㊀㊀通过换梭盘机器人末端执行器的位姿矩阵G,使用ikine功能函数编程得出了T2位姿下机器人的有一组关节角度为q2=[0.5384㊀0.5384㊀-1.2660㊀-1.04271.2753㊀1.2429]由上发现,q1与q2这2组关节角度完全不同,经过仿真发现不同的2组关节角度可以得到换梭盘机器人相同的位姿T2㊂这是机器人逆运动学的一个特点,证明了某时刻空间机器人任意位姿可以由多组不同关节角度构成㊂q1与q2这2组关节角度分别对应的位姿模型见图5㊂3㊀机器人轨迹规划及仿真3.1㊀机器人运动轨迹规划机器人学中最常见的要求之一是把机器人末端执行器由位姿1平滑过渡移到位姿2㊂所谓轨迹规划,是指机器人在工作要求下对其运动过图5㊀关节角q1和q2对应机器人呈现相同的位姿程中的位移㊁速度㊁加速度等运动参数进行规划[10]㊂本文采用机器人关节空间中轨迹规划的方法,完成机器人各关节角速度㊁角加速度㊁角加加速度的约束与求解㊂为了验证机器人能达到换梭盘的工作要求,即换梭盘机器人理论上能够足够快地由T1位姿平滑地过渡到T2位姿,采用7次多项式插值,通过MatLab规划关节空间轨迹㊂实际运行中换梭盘机器人的2个关键位姿T1和T2分别对应的转角为q0=0㊀0㊀0㊀0㊀0㊀0[]和q1=0㊀π/4㊀-π/4㊀π㊀π/4㊀π/2[];表1给出了换梭盘机器人由位姿T1运动到T2时各关节转角变化,通过换梭盘机器人各关节最大转速和关节转角变化这2个参数可求出机器人在2个位姿之间过渡的时间,这个时间就是换梭盘机器人从位姿T1运动到T2理论上的最短时间,也是换梭盘机器人轨迹仿真时的终止时间,计算得出各关节的最短时间见表2㊂表2㊀机器人各关节在位姿T1和T2之间运动最短时间关节序号关节转角变化/rad最短时间/s1002π/49/223-π/49/224π18/195π/43/106π/23/73.2㊀机器人运动仿真由表2可知,换梭盘机器人从位姿T1运动到位姿T2理论上的最短时间为1819s,在这段时间内,设置时间采样周期为50ms,对换梭盘机器人进行仿真,采样周期越小,得到的仿真结果越贴合实际,但在周期缩短的同时会增加计算负担,本文在1819s内设置采样周期为50ms,意味着在这段时间内约有20个采样点㊂通过1819s内经过采样点连成的运动曲线验证换梭盘机器人的性能㊂仿真得到织网机自动换梭盘机器人各关节角速度曲线见图6,各关节的角加速度和角加加速度曲线见图7㊁8㊂图6㊀机器人各关节角速度仿真曲线图7㊀机器人各关节角加速度仿真曲线由图6~8可知,仿真结果表明自动换梭盘机器人各关节角速度㊁角加速度和角加加速度曲线连续平稳,无间断和跳跃等现象㊂在确定关节坐标平滑的同时,可以确定末端执行器在笛卡尔空间中的移动轨迹㊂末端执行器位置向量的各坐标分量随时间变化的曲线见图9㊂末端执行器在x-y平面内的轨迹见图10,在研究机器人末端执行器点到点的运动时,指定了其2个端点的坐标,当机器人运动过程中旋转其腰部关节,机器人末端执行器的运动轨迹自然形成圆弧㊂图8㊀机器人各关节角加加速度仿真曲线图9㊀机器人末端执行器各坐标分量随时间变化仿真曲线在实际工作中,应该注意不与附近物体干涉㊂图10㊀机器人末端执行器在x-y平面轨迹仿真曲线4㊀结㊀论本文在织网机自动换梭盘系统的基础上,以织网机自动换梭盘机器人为对象,通过MatLab建立了机器人仿真模型,对其逆运动学和关节空间轨迹规划进行了仿真,得出了以下结论:①每组关节转角都可以得出机器人末端执行器的位姿;在逆运动学仿真中,相同末端执行器的位姿可以由几组不同的关节转角实现㊂②在关节空间使用7次多项式插值对织网机自动换梭盘机器人2个关键位姿之间进行轨迹规划,仿真过程中其运动性能曲线连续平稳,无间断和跳跃等现象,证明了各关节运动性能良好,达到实际操作环境中换梭盘的要求㊂参考文献:[1]㊀DOLLARHIDE R L,AGAH A.Simulation and contral ofdistributed robot search team[J].Computer&ElectricalEngineering,2003,29(5):625-642.[2]㊀康嘉瑞,樊留群,ROMAN L.基于MatLab的机器人逆运动学研究[J].佳木斯大学学报(自然科学版),2010,28(6):824-826.[3]㊀王军成,于瑞.铸件多功能作业机器人多臂协调轨迹规划于仿真[J].液压与机床,2019,23:47-51. [4]㊀王玉宝,王诗宇,李备备,等.一种改进粒子群的工业机器人时间最优轨迹规划算法[J].软件导刊,2018(8):1878-1881.[5]㊀廖解能,马平,李健洪,等.上下桁架机器人仿真研究[J].机床与液压,2019,21:9-14,33. [6]㊀李瑾.基于Mtalab的Puma250机器人运动仿真与分析[J].现代制造技术与装备,2018(11):66-68. [7]㊀李振雨,王好臣,王泽政.工业机器人运动学分析和轨迹拟合研究[J].机床与液压,2018(5):25-28. [8]㊀涂鹏飞,颜昌亚,刘磊,等.机器人喷涂轨迹计算与仿真[J].制造技术与机床,2019(6):107-112. [9]㊀王林军,邓煜,罗彬,等.基于MatLab Robotics Toolbox的ABB IRB1660机器人运动仿真研究[J].中国农机化学报,2017,38(1):102-106.[10]㊀孙亚光,岳剑锋,钟蒲.基于MatLab的焊接机器人工作空间及轨迹规划仿真[J].机电信息,2016,19(27):81-83.。
机器人在体育领域的发展趋势与运动训练效果分析

机器人在体育领域的发展趋势与运动训练效果分析随着科技的不断进步和人工智能的快速发展,机器人已经开始在各个领域发挥重要作用,包括体育领域。
本文将对机器人在体育领域的发展趋势进行探讨,并分析其在运动训练中的效果。
一、机器人在体育领域的发展趋势随着机器人技术的不断创新和应用,机器人在体育领域的应用也日益广泛。
以下是机器人在体育领域发展的几个趋势:1. 辅助训练:机器人可以模拟人体动作,辅助运动员进行训练。
例如,一些机器人可以模拟击球动作,帮助网球选手提高发球技术。
这种辅助训练能够通过矫正动作和提供实时反馈来帮助运动员改善技术水平。
2. 智能裁判:机器人可以通过计算机视觉和人工智能技术来判断比赛中的规则违例。
例如,在足球比赛中,机器人可以通过识别越位和犯规的动作来辅助裁判做出正确的判罚。
这种智能裁判系统可以提高比赛的公正性和准确性。
3. 运动辅助器具的研发:机器人可以为运动员提供各种辅助器具,帮助他们提高训练和比赛的效果。
例如,一些机器人可以配备专业的运动传感器,用于检测运动员的动作和力量,从而帮助他们改进技术和提高表现。
二、机器人在运动训练中的效果分析1. 提供精准的数据和反馈:机器人可以通过内置的传感器和算法,提供运动员训练过程中的精准数据和反馈。
这些数据可以帮助运动员了解自己的训练进展和技术问题,并针对性地进行调整和改进。
这种精准的数据和反馈对于运动员的训练和提高非常有帮助。
2. 模拟比赛环境:机器人可以模拟比赛场景,提供更真实的训练体验。
对于一些竞技性强的体育项目,比赛环境的模拟对于运动员的训练是至关重要的。
机器人可以模拟对手的动作和战术,让运动员在真实的环境中进行训练,提高他们的竞技水平。
3. 个性化训练方案:机器人可以根据运动员的特点和需求,提供个性化的训练方案。
不同的运动员在技术、力量和耐力等方面存在差异,机器人可以根据运动员的特点进行针对性的训练,帮助他们最大限度地发挥自己的潜力。
结论机器人在体育领域的应用呈现出不断创新和发展的趋势。
puma250机器人运动学分析

焊接机器人运动分析摘 要:针对puma250焊接机器人,分析了它的正运动学、逆运动学的问题。
采用D-H坐标系对机器人puma250 建立6个关节的坐标系并获取 D-H 参数,并对其运动建立数学模型用MATLAB编程,同时仿真正运动学、逆运动学求解和轨迹规划利用pro-e对puma250建模三维模型。
关键词:puma250焊接机器人;正逆解;pro-e;Matlab;仿真1、 建立机器手三维图Puma250机器人,具有6各自由度,即6个关节,其构成示意图如图 1。
各连杆包括腰部、两个臀部、腕部和手抓。
设腰部为1连杆,两个臀部分别为2、3连杆,腰部为4连杆,手抓为5、6连杆,基座不包含在连杆范围之内,但看作0连杆 ,其中关节2、3、4使机械手工作空间可达空间成为灵活空间。
1关节连接1连杆与基座0,2关节连接2连杆与1连杆,3关节连接3连杆与2连按,4关节连接4连杆与3连杆,5关节连接5连杆与4连杆。
各连杆坐标系如图 2 所示。
图1 puma250 机器人2、 建立连杆直角坐标系。
3、 根据坐标系确定D-H表。
D-H 参数表连杆iθi di aiɑi190°0002000-90°304804-90°08-90°5-90°00-90°6020-90°4、 利用MATLAB 编程求机械手仿真图。
>>L1=Link([pi/2 0 0 0 0],'standard');L2=Link([0 0 0 -pi/2 0],'standard');L3=Link([0 -4 8 0 0],'standard');L4=Link([-pi/2 0 8 0 0],'standard');L5=Link([-pi/2 0 0 -pi/2 0],'standard');L6=Link([0 2 0 -pi/2 0],'standard');bot=SerialLink([L1 L2 L3 L4 L5 L6],'name','ROBOT');bot.plot([0 0 0 0 0 0])t=[0:0.01:1];q1=[0 0 0 0 0 0];q2=[-pi/4 0 pi/4 0 -pi/4 0];[q,qd,qdd]=jtraj(q1,q2,t);plot(bot,q)%机器人由q1状态旋转到q2状态>>subplot(2,2,1);plot(t,q(:,2));subplot(2,2,2);plot(t,qd(:,2));subplot(2,2,3);plot(t,qdd(:,2)) %q1到q2状态位移、速度、加速度5、 求正逆向运动学。
哈工大PUMA机器人大作业

2017 年秋季学期研究生课程考核(读书报告、研究报告)考核科目:机器人技术:机电学院学生所在院(系)学生所在学科:机械电子学生姓名:王学号:17S学生类别:学硕考察结果:阅卷人:PUMA 机器人正逆运动学推导及运动空间解算图1 PUMA 机器人模型任务:1.建立坐标系;2.给出D-H参数表;3.推导正、逆运动学;4.编程得工作空间。
一、 建立坐标系根据PUMA 机器人运动自由度,在各关节处建立坐标系如图2所示。
图2 PUMA 机器人坐标系建立图其中0O ∑与1O ∑原点交于一点, 4O ∑与5O ∑原点交于一点。
二、 D-H 参数表D-H 参数表可根据坐标系设定而得出,见表1。
1) i θ为绕1i Z -轴,从1i X -到i X 的角度; 2) i a 为绕i X 轴,从1i Z -到i Z 的角度; 3) i l 为沿i X 轴,从1i Z -与i X 交点到i O 的距离; 4) i d 为沿1i Z -轴,从1i Z -与i X 到1i O -的距离。
表1 PUMA 机器人杆件参数表三、 正运动学推导由坐标系及各杆件参数可得到6个连杆变换矩阵。
111101cos 0sin 0sin 0cos 001000001T θθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦ 22222222122cos sin 0cos sin cos 0sin 0010001a a T d θθθθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3333333323cos 0sin cos sin 0cos sin 01000001a a T θθθθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦ 4444344cos 0sin 0sin 0cos 00100001T d θθθθ-⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦555545cos 0sin 0sin 0cos 001000001T θθθθ⎡⎤⎢⎥-⎢⎥=-⎢⎥⎢⎥⎣⎦ 6666566cos sin 00sin cos 000010001T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据各连杆变换矩阵相乘,可以得到PUMA 机械手变换矩阵,其矩阵为关节变量的函数。
波士顿动力机器人技术细节分析

波士顿动力机器人技术细节分析波士顿动力机器人技术细节分析波士顿动力这家公司的创始人叫做MarcRaibert。
这个名字可能到现在知道的人也不算多,但是在未来,或许会是对世界影响最大的人之一。
马克·雷波特并不年轻,1949年出生,身为麻省理工的教授,雷波特一手创办了波士顿动力这家公司。
由于其在麻省理工的名望,又源源不断的吸收着最顶尖的人才加入这家机器人公司。
与比尔·盖茨、扎克·伯格等一些同样出身名校,却因为发现商业机会提前离开学校的科技先锋不同,雷波特从大学毕业起就一直呆在象牙塔里,是个典型的学术派创业者。
1977年马克·雷波特获得了麻省理工博士学位1980年在卡内基·梅隆大学创立了CMUleg实验室并担任副教授,主要从事研究与机器人相关的控制、机器视觉放方面的技术。
到了1986年,马克·雷波特回到麻省理工并任电子工程与计算机科学系的教授,他将实验室搬到了麻省理工学院,继续他的机器人事业。
1992年,雷波特与他人一同创办了波士顿动力,起初是为美国陆军提供机器人研究制造的企业,服务过包括美国国防高级研究计划局(DARPA)在内的很多军方机构,甚至还获得过国防部几千美元万的投资。
正如肯德基创始人哈兰·山德士上校一样,如今已是68岁高龄的雷波特依然是一个充满热情的创业者。
并且他已经将大半辈子的时光都投入了机器人事业,来完成他那个普通人看起来疯狂的梦想——将双足或四足机器人发展成为一种超自然状态,变成自然界的一种新生物。
尽管过于超前的技术,和短期内难以实现商业化的尴尬现状,使得波士顿动力这家排名世界第一的机器人公司在大企业间辗转来回,频频碰壁。
但是波士顿动力发布过的机器人,已经深深印刻在了我们的脑海中。
创始人对机器人技术极致的追求,也敦促着波士顿动力机器人不停地更新迭代。
从最早爆红的军用机器人大狗开始,波士顿动力每出一款机器人都及其引人注目,甚至会掀起一阵阵机器人要逆天的伦理性大讨论。
基于遗传粒子群的PUMA机器人逆运动求解

基于遗传粒子群的PUMA机器人逆运动求解吴振宇;姚明江;冯林;金博【期刊名称】《计算机仿真》【年(卷),期】2011(28)10【摘要】在优化机器人动态特性的中研究,由于机器人逆运动问题.随着运动关节的增多,逆运动求解问题越来越复杂,要建立通用的解析算法相当困难.针对目前运用的粒子群算法求解时收敛精度不高、易陷入局部最优的情况,提出利用遗传粒子群优化算法求解机器人逆运动问题.运用D-H表示法建立机器人数学模型,然后从正向运动方程出发建立优化算法的目标函数,在粒子群算法中引入遗传操作求解问题.对PUMA机器人的仿真结果表明,改进方法提高了机器人位置和姿态方面的求解精度,达到了有效计算及控制机器人参数的效果.%The research is about robot's inverse kinematics. As the kinetic joints increase, the problem of inverse kinematics is becoming more complicated, and it is very difficult to establish the general analyzing algorithm for it. Since using particle swarm algorithm in the problem has low convergence accuracy, and it is limited by local optimum, in this paper, genetic particle swarm optimization algorithm was adopted to solve the problem of robot's inversekinematics. In the proposed algorithm, robot's mathematical model was built by using D-H representation at first. Then the objective function for optimization was established based on the equations of forward kinematics. Finally, the genetic operation was adopted into the particle swarm algorithm to solve the problem. The experimental results of simulation on PUMA robot showthat, the proposed algorithm raises the accuracy in computing for the locations and postures, achieves the effective effects in computing and controlling the robot's parameters.【总页数】4页(P173-176)【作者】吴振宇;姚明江;冯林;金博【作者单位】大连理工大学创新实验学院,辽宁大连116023;大连理工大学创新实验学院,辽宁大连116023;大连理工大学创新实验学院,辽宁大连116023;大连理工大学创新实验学院,辽宁大连116023【正文语种】中文【中图分类】TP183【相关文献】1.PUMA机器人逆运动模拟退火粒子群求解方法 [J], 芮挺;朱经纬;蒋新胜;廖明2.差分粒子群算法在PUMA机器人逆运动学求解中的应用 [J], 汪院林; 袁锐波; 袁安华3.基于改进遗传算法的工业机器人逆运动学求解 [J], 杨忠瑞;杨昌明;刘渝4.基于多目标粒子群算法的机器人逆运动学求解方法 [J], 刘洋5.基于多种群遗传算法的一般机器人逆运动学求解 [J], 林阳;赵欢;丁汉因版权原因,仅展示原文概要,查看原文内容请购买。
机器人技术大作业(puma机器人的关节坐标建立、dh参数表给出、正逆运动学推导、matlab工作空间
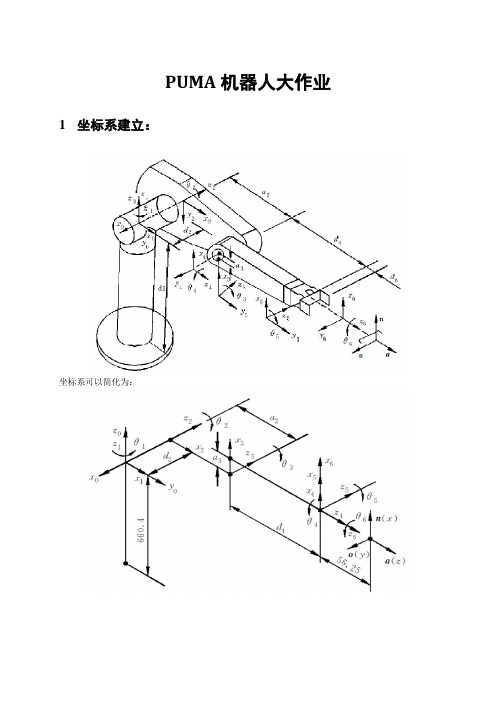
PUMA机器人大作业1坐标系建立:坐标系可以简化为:2 D-H 参数表:PUMA 机器人的杆件参数:1d 0.6604m =,2d 0.14909m =,4d 0.43307m =,6d 0.05625m =,2a 0.4318m =,3a 0.02032m =3 正运动学推导由式111111111100001ii i i i i i i i i i i i i i i i i i c s a s c c c s d s T s s c s c d c θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦可得: 111101000000100001c s s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,222122200001000001c s d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦,332332300000100001c s a s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦44343444000100001c s a d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦,554555000010000001c s T s c -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦,665666000010000001c s T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦0123456123456T T T T T T T =机械手变换矩阵601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦23654164123651654164123654164123651654164123654642365()()()x y z n c c c c c s s c s c s c c c s s s c s n c c c c s s s s s c s s c c s c s c c n s c c c s s c c s =--++=----=--- 23654164123651654164123654164123651645164123654642365()()()x y z o c s c c c c s c s s s c s c s s c c s o c s c c s c s s s s s s s s c c c c c o s s c c s s c c s =-++-+=-+++-=++ 2354123515412354123515412352354x y z a c s c c s c c s s s a c s c s s c s s s c a c c s s c =---=--+=-+ 3231221423121323122142312142332322x y z p a c c a c c d s c d s p a c s a c s d s s d c p d c a s a s =+--=+-+=---4 逆运动学推导1.求1θ用逆变换011T -左乘方程00123456123456T T T T T T T =两边: 010123451623456T T T T T T T -=11111600000010000101xx x x yy y y zz z z c s n o a p s c n o a p T n o a p ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦得112x y s p c p d -+=三角代换 cos x p ρφ=,sin y p ρφ=式中,ρ=tan 2(,)x y a p p φ=得到1θ的解12a tan 2(,)a tan 2(,y x p p d θ=-2.求3θ矩阵方程两端的元素(1,4)和(2,4)分别对应相等113232242342332322x y z c p s p a c a c d s p d c a s a s +=+-⎧⎨-=++⎩平方和为:4333d s a c k +=其中 2222222242322x y z p p p d d a a k a ++----=解得:334a tan 2(,)a tan 2(,a d k θ=- 3.求2θ在矩阵方程00123456123456T T T T T T T =两边左乘逆变换013T -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
焊接机器人运动分析
摘要:针对puma250焊接机器人,分析了它的正运动学、逆运动学的问题。
采用D-H坐标系对机器人puma250 建立6个关节的坐标系并获取D-H 参数,并对其运动建立数学模型用MATLAB编程,同时仿真正运动学、逆运动学求解和轨迹规划利用pro-e对puma250建模三维模型。
关键词:puma250焊接机器人;正逆解;pro-e;Matlab;仿真
一、建立机器手三维图
Puma250机器人,具有6各自由度,即6个关节,其构成示意图如图1。
各连杆包括腰部、两个臀部、腕部和手抓。
设腰部为1连杆,两个臀部分别为2、3连杆,腰部为4连杆,手抓为5、6连杆,基座不包含在连杆范围之内,但看作0连杆,其中关节2、3、4使机械手工作空间可达空间成为灵活空间。
1关节连接1连杆与基座0,2关节连接2连杆与1连杆,3关节连接3连杆与2连按,4关节连接4连杆与3连杆,5关节连接5连杆与4连杆。
各连杆坐标系如图 2 所示。
图1 puma250 机器人二、建立连杆直角坐标系。
三、根据坐标系确定D-H表。
四、利用MATLAB 编程求机械手仿真图。
>>L1=Link([pi/2 0 0 0 0],'standard');
L2=Link([0 0 0 -pi/2 0],'standard');
L3=Link([0 -4 8 0 0],'standard');
L4=Link([-pi/2 0 8 0 0],'standard');
L5=Link([-pi/2 0 0 -pi/2 0],'standard');
L6=Link([0 2 0 -pi/2 0],'standard');
bot=SerialLink([L1 L2 L3 L4 L5 L6],'name','ROBOT'); ([0 0 0 0 0 0])
t=[0::1];
q1=[0 0 0 0 0 0];
q2=[-pi/4 0 pi/4 0 -pi/4 0];
[q,qd,qdd]=jtraj(q1,q2,t);
plot(bot,q)%机器人由q1状态旋转到q2状态
>>subplot(2,2,1);plot(t,q(:,2));
subplot(2,2,2);plot(t,qd(:,2));
subplot(2,2,3);plot(t,qdd(:,2)) %q1到q2状态位移、速度、加速度
五、求正逆向运动学。
1、所谓运动学正问题,就是对于机器人,给定杆件的几何参数和关节的位移,求解末端连杆坐标系相对于基坐标系的位姿。
为求解运动学方程式,用齐次变换矩阵i-1A i来描述第i坐标系相对于(i-1)坐标系的位置和方位,第i坐标系相对于机座坐标系位姿的齐次变换矩阵0T i,表示为:0T i=0A11A2…i-1A i
>>T=(q2)%正向运动学方程(变换矩阵)
T =
0 0 0
2、若末端连杆的位姿已经给定,即n,o,a和p为已知,则求关节变量1,2, ,6的值称为运动反解
>>q0=(T)%逆向运动学(关节变量)
q0 =
六、求q2状态的雅克比矩阵
>>J=(q2)
J =
0 0 0 0
七、Simulink函数(利用框图设计环境实现机器手轨迹动态仿真)>>sl_rrmc2。
