培优专题：整式的乘法公式

合集下载

整式的乘除知识点

整式的乘除知识点整式的乘法运算是指对两个或多个整式进行相乘的运算。

整式的除法运算是指对一个整式除以另一个整式的运算。

整式的乘除运算是代数学中的基本运算，它在代数方程的解法、因式分解等应用中起着重要作用。

一、整式的乘法运算整式的乘法是指对两个或多个整式进行相乘的运算，其规则如下：1.单项式相乘：两个单项式相乘时，按照数字相乘，字母相乘，再将相同字母的指数相加的原则进行运算。

例如：(3x^2)(-2xy)=-6x^3y2.整式相乘：将一个整式中的每一项与另一个整式中的每一项进行相乘，然后将所得的结果相加。

例如：(x+5)(x-3)=x^2-x(3)+5(x)-15=x^2-3x+5x-15=x^2+2x-153.公式相乘：根据一些常见公式和特殊公式，可以通过整式的乘法运算简化计算。

例如：(a+b)(a-b)=a^2-(b)^2=a^2-b^2二、整式的除法运算整式的除法是指对一个整式除以另一个整式的运算，其规则如下：1.简单整式的除法：当被除式是单项式，除式也是单项式，并且除式不为零时，可以进行简单整式的除法运算。

例如：12x^3/4x=x^32.整式长除法：当被除式是一个整式，除式也是一个整式，并且除式不为零时，可以进行整式长除法运算。

例如：(3x^3-2x^2+4x-6)/(x+2)=3x^2-8x+20余-463.分式的除法：分式的除法可以利用倒数的概念进行处理，将除法问题转化为乘法问题。

例如：(a/b)÷(c/d)=(a/b)×(d/c)=(ad)/(bc)三、整式乘除运算的性质和应用1.乘法交换律：整式的乘法满足交换律，即a×b=b×a。

这个性质可以简化计算，使得整式的乘法更加灵活。

2.乘法结合律：整式的乘法满足结合律，即(a×b)×c=a×(b×c)。

这个性质可以改变运算次序，简化计算过程。

3.乘法分配律：整式的乘法满足分配律，即a×(b+c)=a×b+a×c。

整式的乘除知识点

整式的乘除知识点整式的乘除是代数运算中的重要内容，它为解决各种数学问题提供了基础工具。

下面咱们就来详细说一说整式乘除的相关知识点。

首先，咱们聊聊整式的乘法。

单项式乘以单项式，就把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

比如说，3x²乘以 2x³，系数 3 和 2 相乘得 6，相同字母 x 分别相乘，指数2 和3 相加得 5，所以结果就是 6x^5 。

单项式乘以多项式，用单项式去乘多项式的每一项，再把所得的积相加。

例如，2x(3x² 4x ＋ 5)，那就是 2x 乘以 3x²得 6x³，2x 乘以－4x 得－8x²，2x 乘以 5 得 10x ，最后相加就是 6x³ 8x²＋ 10x 。

多项式乘以多项式，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

举个例子，（x ＋ 2)（x 3)，就是 x 乘以 x得 x²，x 乘以－3 得－3x ，2 乘以 x 得 2x ，2 乘以－3 得－6 ，然后相加，结果就是 x² x 6 。

接下来，咱们再看看整式的除法。

单项式除以单项式，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。

比如说，12x³y² ÷ 3x²y ，系数 12 除以 3 得 4，同底数幂 x³除以 x²得 x ，y²除以 y 得 y ，所以结果就是 4xy 。

多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加。

例如，（6x³ 9x²＋ 3x) ÷ 3x ，6x³除以 3x 得 2x²，－9x²除以 3x 得－3x ，3x 除以 3x 得 1 ，所以结果就是 2x² 3x ＋ 1 。

第一节整式乘法及应用-学而思培优

第一节整式乘法及应用-学而思培优第一节整式乘法及应用一、课标导航二、核心纲要1.幂的运算性质1) 同底数幂的乘法同底数的幂相乘，底数不变，指数相加。

即：$a^m \cdota^n = a^{m+n}$。

（其中$m,n$都是正整数）特别地，$a^m \cdot a^{-n} = \dfrac{a^m}{a^n}$。

注：①此性质可推广到三个或三个以上同底数幂相乘，如：$a\cdot a\cdot a = a^3$。

②此性质可以逆用，即$a^{m+n} = a^m \cdot a^n$。

③当幂的指数为1时，可省略不写，但是不能认为没有，如：$a\cdot a = a^2$。

2) 幂的乘方幂的乘方，底数不变，指数相乘。

即：$(a^m)^n =a^{mn}$。

注：此性质可以逆用，即：$a^{mn} = (a^m)^n$。

3) 积的乘方积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘。

即：$(ab)^n = a^n b^n$。

（$n$是正整数）注：①此性质可推广到多个因数的积的乘方，即：$(abc)^n = a^n b^n c^n$。

②此性质可以逆用：$abc = (abc)^1 = a^1 b^1 c^1$。

2.整式乘法法则1) 单项式与单项式相乘系数、同底数幂分别相乘作为积的因式，只有一个单项式里含有的字母，则连同它的指数作为积的一个因式。

如$2abc\cdot3ab = 6a^2 b^2 c$。

注：①此法则适合多个单项式相乘；②用法则解题时，可分三步计算：第一步：将系数相乘；第二步：将相同字母相乘；第三步：将单独的单项式写在积中。

2) 单项式与多项式相乘单项式分别与多项式中的每一项相乘，然后把所得的积相加，即：$m(a+b+c) = ma+mb+mc$，其中$m$为单项式，$a+b+c$为多项式。

3) 多项式与多项式相乘将一个多项式中的每一个单项式分别与另一个多项式中的每一个单项式相乘，然后把积相加，即：a+b)(c+d) = ac+ad+bc+bd$。

整式乘法公式

整式乘法公式
整式乘法公式：是指一个整数乘以另一个整数，结果等于乘数之积。

它是数学计算中最常用的一种乘法运算方法，它可以帮助我们更快更准确的解决数学问题，其乘数之积也是最简单的乘法公式。

整式乘法公式可以简化计算过程，节省时间，提高效率，在学校里面也是数学学习的重要知识点。

它可以帮助孩子们更好的理解数学的乘法运算，掌握数学的计算技能，为他们的学习打下良好的基础。

孩子们在学习整式乘法公式时，可以通过实际例子来加深理解，例如：有一个十位数的乘数和一个个位数的乘数，可以先将十位数乘以个位数，然后再将十位数乘以十位数，最后将两个结果相加，就得到乘数之积。

此外，整式乘法公式还可以应用到生活中，比如做菜时，购物时，等等，用整式乘法公式可以更快更准确的计算出来所需要的数值，从而更好的满足我们的需求。

总之，整式乘法公式是一种非常重要的数学运算方法，它可以帮助我们更好的解决数学问题，应用到日常生活中，更加方便快捷。

人教版八上数学整式的乘法及因式分解单元培优

第1讲整式的乘法知识点梳理：复习回顾：整式的加减：同类项，合并同类项新课要点：（1）同底数幂的乘法：底数不变，指数相加。

nm n m a a a +=⋅(m 、n 都是正整数) 注意公式逆用。

（2）幂的乘方：底数不变，指数相乘。

mnnm a a =)(（m 、n 都是正整数) 注意公式逆用。

（3）积的乘方：nnnb a ab =)(（n 是正整数）注意公式逆用。

（4）整式的乘法：①单项式和单项式相乘：把它们的系数、相同的字母分别相乘，对于只在一个单项式出现的字母，则连同它的指数一起作为积的一个因式。

例如：)3(2322bc a ab -⋅=3336c b a -②单项式与多项式相乘，先用单项式去乘多项式的每一项，再把所得的积相加。

即mb ma b a m +=+)(③多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积再相加。

即nb na mb ma b a n m +++=++))((经典例题例1．（1）-x 3·x 5 （2）x m ·x 3m+1 （3）2×24×23（4）31++••m m ma a a （5）n m m m m a a a a 321⋅⋅例2．计算： ①()()()()2452232222x x x x -⋅-⋅ ②()()()32212mn m a a a a -⋅-⋅例3.计算：⑴()33x - ⑵()25ab - ⑶()22xy ⑷()4322xy z-（5）()()4234242a a a a a ⋅⋅++- （6）()()()2323337235xx xx x ⋅-+⋅例4.计算：⑴()()2353a b a -⋅- ⑵()()3225x x y ⋅-（3）()()152n a b a +-- （4）()()()232236ab a cab c --⋅（5）()()24231x x x -⋅+- （6）221232ab ab ab ⎛⎫-⋅ ⎪⎝⎭（7）()22221252a ab b a a b ab ⎛⎫-⋅+-- ⎪⎝⎭（8）()()32x y x y +-（9）()()22m n m n +- （10）2)2(b a +例5．若20x y +=，则代数式3342()x xy x y y +++的值为。

整式的乘除及因式分解知识点归纳

整式的乘除及因式分解知识点归纳整式是指由字母和常数经过加、减、乘、除运算得到的代数式。

乘除整式的运算及因式分解是代数学中非常基础和重要的知识点，下面将对乘除整式及因式分解的相关知识进行归纳。

一、乘法运算乘法运算是整式运算中最基本的运算。

在乘法运算中，有以下几个重要的法则：1.乘法交换律：a*b=b*a2.乘法结合律：(a*b)*c=a*(b*c)3.分配律：a*(b+c)=a*b+a*c4.单项式相乘法则：单项式相乘时，将各个单项式的系数相乘，同类项的指数相加。

例子：(2x^2)(3x^3)=2*3*x^2*x^3=6x^(2+3)=6x^5二、除法运算除法运算是整式运算中的一种重要运算。

除法运算可分为两种情况：1.恒等除法：当被除式为0时，整式除以0是没有意义的。

即0除以0没有定义。

2.非恒等除法：非零整式除以非零整式时，被除式乘以除数的倒数。

例子：(4x^4)/(2x^2)=4/2*x^4/x^2=2x^(4-2)=2x^2三、因式分解因式分解是指将一个整式表示为几个其它整式相乘的结果，称这些整式为原式的因式。

1.提取公因式：将一个整式的公因式提取出来，得到一个公因式和一个把原式除以公因式的商。

例子：8x^3+12x^2=4x^2(2x+3)2.根据乘法结合律和分配律，将每一个单项式的因式分别提出来。

例子：3xy + 9x + 6y + 18 = 3(x + 3) + 6(y + 3) = 3(x + 3 +2(y + 3)) = 3(x + 2y + 9)3.因式分解中，根据不同的整式形式，可以采用不同的方法进行因式分解。

常见的因式分解方法有：(1)一元二次整式的因式分解：对形如ax^2 + bx + c的一元二次整式，可以使用因式分解公式 (ax + m)(cx + n)进行分解，其中m、n分别是满足m*n=ac的两个数。

例子：x^2-5x+6=(x-2)(x-3)(2)立方差公式：对形如a^3 - b^3的整式，可以使用立方差公式 (a - b)(a^2 + ab + b^2)进行分解。

二元一次方程组、整式的乘法、因式分解培优

二元一次方程组培优1．已知关于x，y的方程组的解是，求关于x，y的方程组的解．2．南山植物园以其优美独特的自然植物景观，现已成为重庆市民春游踏青、赏四季花卉、观山城夜景的重要旅游景区．若该植物园中现有A、B两个园区，已知A园区为矩形，长为（x+y）米，宽为（x﹣y）米；B园区为正方形，边长为（x+3y）米．（1）请用代数式表示A、B两园区的面积之和并化简；（2）现根据实际需要对A园区进行整改，长增加（11x﹣y）米，宽减少（x﹣2y）米，整改后A区的长比宽多350米，且整改后两园区的周长之和为980米．若A园区全部种植C 种花，B园区全部种植D种花，且C、D两种花投入的费用与吸引游客的收益如下表：求整改后A、B两园区旅游的净收益之和．（净收益=收益﹣投入）3．阅读下列解方程组的方法，然后回答问题．解方程组解：由①﹣②得2x+2y=2即x+y=1③③×16得16x+16y=16④②﹣④得x=﹣1，从而可得y=2∴方程组的解是．（1）请你仿上面的解法解方程组．（2）猜测关于x、y的方程组的解是什么，并利用方程组的解加以验证．4．江海化工厂计划生产甲、乙两种季节性产品，在春季中，甲种产品售价50千元/件，乙种产品售价30千元/件，生产这两种产品需要A、B两种原料，生产甲产品需要A种原料4吨/件，B种原料2吨/件，生产乙产品需要A种原料3吨/件，B种原料1吨/件，每个季节该厂能获得A种原料120吨，B种原料50吨．（1）如何安排生产，才能恰好使两种原料全部用完？此时总产值是多少万元？（2）在夏季中甲种产品售价上涨10%，而乙种产品下降10%，并且要求甲种产品比乙种产品多生产25件，问如何安排甲、乙两种产品，使总产值是1375千元，A，B两种原料还剩下多少吨？整式的乘法培优【知识点归纳】1.同底数幂相乘，不变，相加。

a n.a m=(m,n 是正整数) 2.幂的乘方，不变，相乘。

(a n )m=(m,n 是正整数) 3.积的乘方，等于把，再把所得的幂。

整式乘法运算法则公式

整式乘法运算法则公式在代数中，整式乘法是一种常见的运算，它可以帮助我们简化复杂的代数表达式。

整式乘法运算法则公式是指在乘法运算中使用的规则和公式，通过这些规则和公式，我们可以将复杂的代数表达式化简为简单的形式。

本文将介绍整式乘法运算法则公式的基本概念和具体应用。

一、整式乘法的基本概念在代数中，整式是由数字、变量和运算符（如加法、减法、乘法、除法）组成的表达式。

整式乘法是指两个或多个整式相乘的运算。

例如，给定两个整式x+2和3x-4，它们的乘积可以通过整式乘法运算法则公式进行计算。

二、整式乘法运算法则公式整式乘法运算法则公式包括以下几个基本规则：1. 分配律：对于任意的整式a、b和c，有a*(b+c) = a*b + a*c。

2. 乘法交换律：对于任意的整式a和b，有a*b = b*a。

3. 乘法结合律：对于任意的整式a、b和c，有(a*b)*c =a*(b*c)。

这些基本规则可以帮助我们在整式乘法中进行化简和计算，从而得到最终的乘积结果。

三、整式乘法的具体应用整式乘法运算法则公式在代数中有着广泛的应用，特别是在多项式的乘法中。

多项式是由多个整式相加或相减而成的代数表达式，它们在代数中有着重要的地位。

通过整式乘法运算法则公式，我们可以将复杂的多项式乘法化简为简单的形式，从而更方便地进行计算和分析。

例如，考虑两个多项式(x+2)(3x-4)，我们可以利用整式乘法运算法则公式来计算它们的乘积。

首先，我们可以使用分配律将乘法展开：(x+2)(3x-4) = x*(3x-4) + 2*(3x-4)。

然后，我们再利用分配律将每一项再次展开：x*(3x-4) = 3x^2 - 4x，2*(3x-4) = 6x - 8。

最后，将这些展开后的结果相加，得到最终的乘积：(x+2)(3x-4)= 3x^2 - 4x + 6x - 8 = 3x^2 + 2x - 8。

通过以上的计算过程，我们可以看到整式乘法运算法则公式的应用非常简单直观，它可以帮助我们快速地计算多项式的乘积，从而简化代数表达式的计算。

初一-第03讲-整式的乘法与平方差公式(培优)-教案

学科教师辅导讲义学员编号：年级：七年级课时数：3学员姓名：辅导科目：数学学科教师：授课主题第03讲---整式的乘法与平方差公式授课类型T同步课堂P实战演练S归纳总结教学目标①掌握整式的乘法法则，能够准确计算整式乘法的计算题；②理解平方差公式，了解平方差公式的几何背景，会灵活运用平方差公式进行计算。

授课日期及时段T（Textbook-Based）——同步课堂一、知识框架二、知识概念（一）整式的乘法1、单项式与单项式相乘法则：把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数保持不变，作为积的因式。

2、单项式与多项式相乘法则：根据分配律用单项式乘以多项式的每一项，再把所得的积相加。

公式如下：()(,,,m a b c ma mb mc m a b c++=++都是单项式）3、多项式与多项式相乘法则：先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。

公式如下：()()(,,,m n a b ma mb na nb m n a b++=+++都是单项式）（二）平方差公式体系搭建1、平方差公式：22()()a b a b a b-+=-，即两个数的和与这两个数的差的积，等于这两个数的平方差。

公式的推导：2222()()a b a b a ab ab b a b+-=-+-=-。

平方差公式的逆用即22()()a b a b a b-=-+平方差公式的特点：（1）左边是两个二项式的积，，在这两个二项式中，有一项（a）完全相同，另一项（b和-b）互为相反数。

（2）右边是乘式中两项的平方差（相同项的平方减去符号相反项的平方）（3）公式中的a和b可以是具体数，也可以是单项式和多项式。

2、平方差公式的几何意义如图两幅图中，阴影部分的面积相等，第一个图的阴影部分的面积是：a2﹣b2，第二个图形阴影部分的面积是：（a+b）（a﹣b），则a2﹣b2=（a+b）（a﹣b）平方差公式的几何意义还有很多，有兴趣的同学可以钻研一下。

整式的乘法乘法公式

确定运算顺序
先算乘方，再算乘除，最后算加减；
运用分配律
将括号内的代数式展开，并运用分配律进行计算；
合并同类项
将同类项进行合并，得到最简结果。
整式乘法公式的计算技巧
熟记公式
熟练掌握整式乘法公式，如平方差公式、完全平方公式等；
化简代数式
在计算过程中，尽量化简代数式，减少计算量；
灵活运用运算法则
整式乘法公式是一种简化的运算方法，适用于任何两个整式的乘法运算。
整式乘法公式的特点
1
整式乘法公式具有普遍适用性，适用于任何两个整式的乘法运算。
2
整式乘法公式可以简化复杂的计算过程，提高运算效率。
3
整式乘法公式有助于培养学生的数学思维能力和符号意识。
整式乘法公式的历史与发展
01
整式乘法公式是数学运算中的基本工具，有着悠久的历史和广泛的应用。
2023
《整式的乘法乘法公式》
contents
目录
• 整式乘法公式概述 • 整式乘法公式的形式与证明 • 整式乘法公式的计算方法与技巧 • 整式乘法公式的应用实例
01
整式乘法公式概述
整式乘法公式的定义
整式乘法公式定义：整式乘法公式是单项式与单项式相乘，把他们的系数，相同字母的幂分别相乘，其余字母连同他的指数不变，作为积的因式的运算。
交换律公式
$(a+b)(c+d)=(a+b)(c+d)$
整式乘法公式的证明方法
分配律公式的证明
根据乘法分配律，可以得出$(a+b)(c+d)=ac+ad+bc+bd$。
结合律公式的证明
根据乘法结合律，可以得出$(a+b)(a+b)=a^2+2ab+b^2$。

初中数学整式乘除培优讲义(含解析)

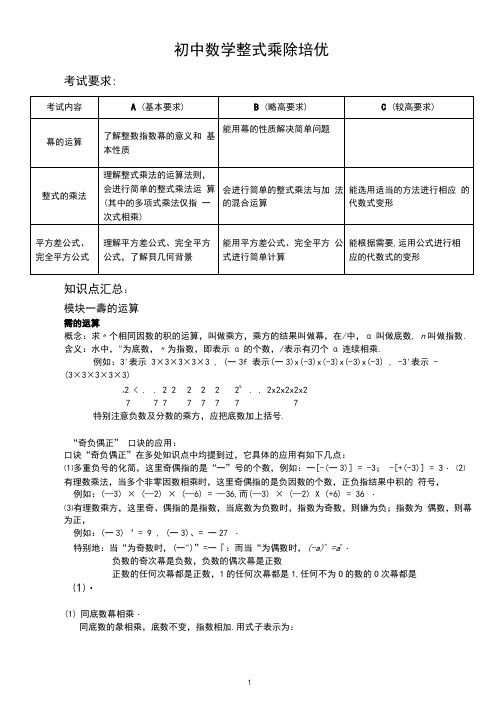
初中数学整式乘除培优考试要求:知识点汇总：模块一壽的运算需的运算概念：求〃个相同因数的积的运算，叫做乘方，乘方的结果叫做幕，在/中，α叫做底数, n叫做指数. 含义：水中，"为底数，〃为指数，即表示α的个数，/表示有刃个α连续相乘.例如：3'表示3×3×3×3×3 , (一3f 表示(一3)x(-3)x(-3)x(-3)x(-3) , -3'表示 -(3×3×3×3×3)5. . 2x2x2x2x2z2 < . . 2 2 2 2 2 27 7 7 7 7 7 7 7特别注意负数及分数的乘方，应把底数加上括号.“奇负偶正” 口诀的应用：口诀“奇负偶正”在多处知识点中均提到过，它具体的应用有如下几点：⑴多重负号的化简，这里奇偶指的是“一”号的个数，例如：一[-(一3)] = -3； -[+(-3)] = 3・⑵有理数乘法，当多个非零因数相乘时，这里奇偶指的是负因数的个数，正负指结果中积的符号，例如：(—3) × (—2) × (—6) = —36,而(—3) × (—2) X (+6) = 36 ・⑶有理数乘方，这里奇、偶指的是指数，当底数为负数时，指数为奇数，则嫌为负；指数为偶数，则幕为正，例如：(一3)‘ = 9 , (一3)、= 一27 ・特别地：当“为奇数时，(一")”=一『：而当“为偶数时，(-a)n =a n・负数的奇次幕是负数，负数的偶次幕是正数正数的任何次幕都是正数，1的任何次幕都是1,任何不为O的数的O次幕都是⑴・(1)同底数幕相乘・同底数的彖相乘，底数不变，指数相加.用式子表示为：(m√ι都是正整数)・(2) 策的乘方.幕的乘方的运算性质：幕的乘方.底数不变，指数相乘.用式子麦示为: (町=旷(m 9n 都是正整数)・ ⑶积的乘方.积的乘方的运算性质：积的乘方，等于把积的每一个因式分别乘方，再把所得的無相乘•用式子表示为： (ab)n ≈a fl h fl(“是正整数)・ (4)同底数彖相除・同底数的幕相除，底数不变，指数相减.用式子表示为:模块二整式的乘法⑴单项式与单项式相乘：系数、同底数幕分别相乘作为积的因式，只有一个单项式里含有的字母，则连同它的指数作为积的一个因式・以下举例说明单项式与单项式相乘的规则如下：Ub • 3a 2b y c 2= 3a^c 2,两个单项式的系数分别为1和3,乘积的系数是3,两个单项式中关于字母α的幕分别是α和/,乘积中d 的幕是才,同理，乘积中b 的幕是戻，另外，单项式“b 中不含C 的幕，而3i l 2b i c 2中含¢2,故乘积中含疋・ ⑵单项式与多项式相乘：单项式分别与多项式中的每一项相乘，然后把所得的积相加，公式为：m(a + b + c) = ma + mb + me ,其中加为单项式，a+b + c为多项式.⑶多项式与多项式相乘:将一个多项式中的每一个单项式分别与另一个多项式中的每一个单项式相乘，然后把积相加，公式为：(∕π + n)(a + b) = ma + mb + Ha + Hh模块三整式的除法(1) 单项式除以单项式^系数、同底数的幕分别相除作为商的因式，对于只在被除式中含有的字母，則连同它的指数作为商的一个因式•如：3a 2b 3c 2*ab = 3ab 2c 2,被除式为3a 2b 3c 2, 除式为肪，系数分别为3和1,故商中的系数为3, α的彖分别为/和α,故商中α的幕为∕τ=α,同理，〃的幕为，，另外，被除式中含Y,而除式中不含关于c ・的策，故商中e 的幕为c'・(2) 多项式除以单项式：多项式中的每一项分别除以单项式，然后把所得的商相加，公式为：(" + b + c ∙)÷∙m = "*"2 + b*m + c*"?,其中加为单项式，a + h + c 为多项式.(3) 多项式除以多项式后有专题介绍.模块四平方差公式(a+ h){a-b) = a 2 -h 2平方差公式的特点：即两数和与它们差的积等于这两数的平方差。

整式的乘法与因式分解培优

第二章整式的乘法【知识点归纳】1. 同底数幂相乘，不变，相加。

a n. a m =(m,n 是正整数 )2. 幂的乘方，不变，相乘。

(a n ) m =(m,n是正整数 )3. 积的乘方，等于把，再把所得的幂。

(ab) n =(n 是正整数 )4. 单项式与单项式相乘，把它们的、分别相乘。

5. 单项式与多项式相乘，先用单项式，再把所得的积，a （ m+n ）=6. 多项式与多项式相乘，先用一个多项式的每一项分别乘，再把所得的积，（ a+b ）（ m+n ）=。

7. 平方差公式，即两个数的与这两个数的的积等于这两个数的平方差（ a+b ）（a-b ） =8. 完全平方公式，即两数和（或差）的平方，等于它们的，加（或减）它们的积的。

（a+b ） 2=,（a-b ） 2=。

9. 公式的灵活变形：（ a+b ） 2+（a-b ）2 = ，（a+b ） 2- （a-b ）2 =，a 2+b 2=（a+b ） 2- ，a 2+b 2=（a-b ） 2+ ，（a+b ） 2=（a-b ）2 +，（ a-b ） 2=（a+b ）2 -。

【例 1】若代数式 (2 x 2 ax y 6) (2bx 2 3x 5 y 1) 的值与字母 x 的取值无关，求代数式3a 2 2b 2( 1a 2 3b 2 ) 的值 4 4【例 2】已知两个多项式 A 和 B ，A nx n 4x 3 nx 3 x 3, B 3x n 4x 4 x 3 nx 2 2x 1,试判断是否存在整数 n ，使 A B 是五次六项式？【例 3】已知 x, y, z为自然数，且 x y ，当x y 1999, z x 2000时，求 x y z 的所有值中最大的一个是多少？【例4】如果代数式ax5bx3cx 5 当x 2 时的值为7 , 那么当 x 2 时 , 该式的值是.【例 5】已知a为实数 , 且使a33a23a 2 0 ,求 ( a 1)1996( a 1)1997(a1)1998的值.【例 6】（1）已知 2x+2=a，用含 a 的代数式表示 2x；（2）已知 x=3m+2，y=9m+3m，试用含 x 的代数式表示 y．【例7】我们知道多项式的乘法可以利用图形的面积进行解释，如（2a+b）（ a+b）=2a2 +3ab+b2就能用图 1 或图2 等图形的面积表示：（ 1）请你写出图 3 所表示的一个等式：．（ 2）试画出一个图形，使它的面积能表示：（a+b）（a+3b）=a2+4ab+3b2．【例 8】归纳与猜想：（ 1）计算：①（ x﹣1）（ x+1）=；②（ x ﹣1）（ x2+x+1） =；③（ x ﹣1）（ x3+x2+x+1） =；（ 2）根据以上结果，写出下列各式的结果．①（ x﹣ 1）（x6+x5+x4+x3+x2+x+1）=；②（ x﹣ 1）（x9+x8+x7+x6+x5+x4+x3+x2+x+1）=；（ 3）（x﹣1）（ x n﹣1 +x n﹣2+x n﹣3+ +x2+x+1） =（ n 为整数）；15（ 4）若（ x﹣1）?m=x ﹣1，则 m=；（ 5）根据猜想的规律，计算：226+225++2+1．【例 9】认真阅读材料，然后回答问题：我们初中学习了多项式的运算法则，相应的，我们可以计算出多项式的展开式，如：（a+b）1=a+b，（a+b）2=a2 +2ab+b2，323223（ a+b）=（a+b）（a+b）=a +3a b+3ab +b，下面我们依次对（ a+b）n展开式的各项系数进一步研究发现，n取正整数时可以单独列成表中的形式：上面的多项式展开系数表称为“杨辉三角形” ；仔细观察“杨辉三角形” ，用你发现的规律回答下列问题：（ 1）多项式（ a+b）n的展开式是一个几次几项式？并预测第三项的系数；（ 2）推断出多项式（ a+b）n（n 取正整数）的展开式的各项系数之和为 S，（结果用含字母 n 的代数式表示）．课后作业：1、若2x 5 y30 ，求 4x32 y的值。

培优专题：整式的乘法公式

整式的乘法（二）乘法公式一.公式补充。

计算：(x +1)(Λ∙2- X + 1) = __________________练习：(X -1)( A√ + X +1) = _______________(2x +3)(4X2-6X +9)= _________________2 4 2(—a -b)(-a2 + —ab + b2) =39 3 ---------------计算：4≤-13^ + 46iχi3932.2二.例：已知"+b = 3, ab = 2 9求a2 +b29 (a -b)2 , a y +b^的值。

练习：L 已知“+" = 5, ab = 6,求a2+b2, (a-b)2 , a3+b3的值。

2.己知a2+⅛2=13, ab=β9求(a+⅛2, (a-∕>)2的值。

3.已知(a¼⅛2=7, (a-2>)2=4,求d+2Λ 胡的值。

4.己知x +j = l, X2 + J2 =3 ,求X3 +j3的值。

5.已知兀_丄=3,求X4+A的值。

三、例1：B⅛lx2-6x + y2 +10J = -34,求X』的值。

练习：L +j2+4x-12j+ 40 = 0,求x + 2y 的值。

2.已^x2 +2xy + y2 -6x-6j + 9 = 0,求x + y 的值。

3∙ BftJ</2+ b2 + l=ab+a + b f求&/一物的值。

4•已知",方,c 满足/+2Z> = 7, b1 -2c =-1 , C l -6ιι =-17,求“+b + c 的值。

例2.计算：(a +1)(«2 +1)(«4 +1)(“ — 1)练习：L 计算：6×(7 + l)×(72+l)×(74+l)×(78+l) + l2.计算:(2+1) (22+1) (24+1) (28+1)平方差公式专项练习题A卷: 基础丿一、选择题L平方差公式(a+b) (a-b) =a2-b2中字母a, b表示()A.只能是数B.只能是单项式C.只能是多项式D.以上都可以2.下列多项式的乘法中，可以用平方差公式计算的是()A. (a+b) (b+a) B・(―a+b) (a—b)C. (Ia+b) (b-1a) D・(a?—b) (b2+a)3 33.下列计算中，错误的有()①(3a+4) (3a—4) =9a2~4：②(2a2-b) (2a2+b) =4a2-b2：③ (3—X)(x+3) =x2-9：④ (—x+y)・(x+y) =— (x—y) (x+y) =—x2-y2.A・1个B. 2个C・3个D・4个4.若X2—y2=3O,且x-y=-5,贝∣] x+y 的值是()A・5 B・6 C・—6 D・—5二、填空题5・(―2x+y) ( —2x—y) = ______ ・6.( — 3x2+2y2) ( _____ ) =9x4-4y4・7.(a+b-l) (a-b+l) = ( __________ ) 2- ( ______ ) 2.8.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的而积减去较小的正方形的而积，差是_____ .三、计算题2 19.利用平方差公式计算：20-×21丄.3 310.计算：(a+2) (a2+4) (a4+16) (a-2).B卷:一、七彩题1.(多题一思路题)汁算：(1)(2+1) (22+l) (24+l ) ... (22n+l) +1 (n 是正整数)；^4()16(2)(3+1) (32+l) (34+l) ... (32008+l) 一一・22.(一题多变题)利用平方差公式计算：2009×2007-20082.二、知识交叉题3・(科内交叉题)解方程:X (x+2) + (2x+l) (2χ-l) =5 (x2+3).三、实际应用题4.广场内有一块边长为2a米的正方形草坪，经统一规划后，南北方向要缩短3米，东西方向要加长3米，则改造后的长方形草坪的面积是多少？四.经典中考题5.（2007,泰安，3分）下列运算正确的是（）A. a3+a3=3a6B. (—a) 3∙ (—a) 5=-a8C. ( — 2Qb) ・4a=—24a6t√ D・(一4b) ( — a—4b) =16b2- — a23 3 96 (2008,海南，3 分)计算：(a+l) (a-l) = ____________ ・文档从网络中收集，已重新整理排版.word版本可编借•欢迎下载支持.C卷:课标新型题1.(规律探究题)己知x≠l,计算(l+x) (1—X)=l-χ2, (1 —X)(l+x+x2) =1—X3,(1 —X)(∙ l+x+x2+x3) =I-X4・(1)观察以上各式并猜想：(I-X) (l+x+x2+...+x n) = _________ . (n为正整数)(2)根据你的猜想汁算：①(1-2) (l+2+22+23+24÷25) = ________ ・②2+22+23+...+2n= ____ (n 为正整数).③(X-I) (x w+x98+x97+...+x2+x+l) = __________ ・(3)通过以上规律请你进行下而的探索：①(a—b) (a+b) = ________ ・②(a—b) (a2+ab+b2) = ______ ・③(a—b) (a3+a2b+ab2+b3) = _______ ・2.(结论开放题)请写出一个平方差公式，使其中含有字母m, n和数字4.4、已知πΓ+rf-6m+10n+34=0,求m+n 的值文档从网络中收集，已重新整理排版.word 版本可编辑•欢迎下载支持.整式的乘法.平方差公式.完全平方公式.整式的除法(B 卷)综合运用题姓名：一、请准确填空1. 若 /+/-2M2H2二0,则『“+产5二 ________ ・2. 一个长方形的长为(2a+3b),宽为(2a-36),则长方形的面积为 ____________ •3. 5— (a —6):的最大值是 ________ ,当5— (a —6):取最大值时,a 与b 的关系是 _____4. 要使式子0・36√+i 長成为一个完全平方式，贝IJ 应加上 ______ ・45. (4a“ —6孑)j r2a *- ________ ・6. 29×31×(30s +D= ________ ・7. 己知 Y-5Λ÷1=0,则 f+A= _________ ・Jr8. 已知(2005 — Q (2003—a)=1000,请你猜想(2005 — a)'+(2003 — a)土 _____ ・二、相信你的选择9. 若 Y --Y-Zrf=(X —in) C 计 1)且-v≠0,则加等于A. — 1B. 0C. 1D. 210. (Mg)与(AH-I)的积不含X 的一次项，猜测g 间是5A. 5B. £C. — ξD. —511. 下列四个算式:①4f∕m 丄羽Qw;(D162九m8∕42a 话C ；③9<y÷3f 尸3玄兀4④ (12zπ+8∕zf -4zσ) ÷ (―2zσ)=-6/+4硏2,其中一正确的有 A.0个 B.1个 C.2个 D.3个 12. 设(√ I y rt ) ∙ (X a y S )-Xy t 则z/的值为A. 1B. -1C. 3D. -3 13•计算［&一刃(才+刃］:等于A. a ~2^b ,^b'B. a°+2aWFC. a ~2aD. a —2a 6,+∆w14. 已知(a÷∆)2=ll, aZ>=2,则(a~b)z 的值是 A. 11 B. 315. 若是一个完全平方式，那么"是A 7 SD 49 2A. — yB. —「2" 216•若為y 互为不等于0的相反数，力为正整数,你认为正确的是c. √∖芦一泄是互为相反数D ..Y 2Λ-∖ -Z-I -定相等・1・文档来源为:从网络收集整理.word 版本可编辑.C. 5D. 19D. 49/A. ΛΛ b —定是互为相反数B. (i)∖ (丄尸一定是互为相反数X y文档从网络中收集，已重新整理排版.word版本可编辑•欢迎下载支持.三S考査你的基本功17.计算(1) (a—2M∙3c)~-(a+2Z>—3c)(2)「ab(3 — b) —2a(b —丄Zf)] (―3a£);2(3)-2loo×0. 5ιcc× (-l)sooδ÷ (-1)(4)[ (∆÷2y) (-γ-2y)+4(A r—y)2—6.γ] ÷6x18.(6分)解方程*(9*一5) 一(3-Y-I) (3对1)二5・四.生活中的数学19.（6分）如果运载人造星球的火箭的速度超过11. 2 kπ√s（俗称第二宇宙速度），则人造星球将会挣脱地球的朿缚，成为绕太阳运行的恒星.一架喷气式飞机的速度为1.8×IO6m∕h,请你推算一下第二宇宙速度是飞机速度的多少倍？文档从网络中收集，已重新整理排版.word版本可编辑.欢迎下载支持.五、探究拓展与应用20.计算.(2+1) (2*1) (2s+l)= (2-1) (2+1) (2:+1) (2,+l) = (23-l) (25+l) (2*+l)= (2i-l) (2,+1) = (28-1).根据上式的计算方法，请计算(3+1) (33+l) (3t+l)…(352+l) 一—的值•2文档从网络中收集，已重新整理排版word 版本可编辑•欢迎下载支持.完全平方公式习题精选・.选择题1・下列各式中，能够成立的等式是()・ Z 9 s2 yl 2 ω ,2 (-Λ -⅛)2 = -a 2 +ab +hAe (2「刃 =4x -2D+y B. 24C. (X÷7)2=^2÷/D .(Nf)2=0p)22. 下列式了•：①(3"1)(3L 1) = (N-1)2 ②(X -37)2 =X 2-3^÷9j;2 ③A.①B.①②C.①②③D.④ 3.（）A X 2÷2ZJ ; + /B -√-2zj;-/ c.兀2_2芋 + 丿2 D x 2 + 2z ιy-/ 4. 若（"刃2 一M=（LyF ,则M 为（）.A. 2&B. ± 2卩C. 4& d . ±5. •个正方形的边长为αcm ,若边长增加6cm ,则新正方形的面积人增加了（）.A. 36cm 2 B- 12<scm 2 c . G&+ 12N ）Cnl? D 以上都不对 6. 如果X+αx + l 是-个完全平方公式，那么a 的值是（）. A ・ 2 B ・-2 C ・ ± 2 D. ±17. 若•个多项式的平方的结果为4/+12αB+滋2 ,则酬I=（）A . 9沪 B. 3⅛2 C. -9戸 D. 3⅛&下列多项式不是完全平方式的是（）.1 2一十购十购π ααA. /—4兀一4 B e 4c. 2 +6ab +⅛2 D e 4/2 +12/+9X + — = 29.已知 X ,则下列等式成立的是（〉(i-2^)2=ι-4Xy ④ STf 十2十土中正确的是（）文档从网络中收集，已重新整理排版.word版本可编辑•欢迎下载支持.Λ2÷4-=2^4÷Λ = 2护+4 = 2 "丄=C)①X ②X ③X④ 兀A.①B.①②C.①②③D.①Φ③④二、填空题1.(*b)2=_3.(2X-1)2+(2X +1)2= _____ 5. @ +疔-0-b)2 = ___________(4戲+ ”2 = [6型2 十 ________三、解答题1.运用完全平方公式计算:2. (3S)2=—4.(沪疔+S 7)2= _6.(-3X +47)2=()2 =aλ+⅛2 = {a+Λ)2 + ________(1) (卩爭(2)(-4X-I i y)2.运用乘法公式计算:(I) SZ ・P)?；⑵(x÷ l)2(x-l)2 Z ⑶◎*!) 文档从网络中收集，已重新整理排版.word 版本可编辑•欢迎下载支持.("刃2("刃：⑷(2"%+C)(C-2α + %)3. 计算:⑵(x+4)(x-4)-(x-4)2(l2m -3⅝)2(2Λ>2 + 3«)2(J)(3α -b+c)(3α ÷⅛ -C)参考答案:∙. 1・D 2・D 3・A 4・C 5・C 6. C 7・D 8・A 9・D•IΛ2÷4Λ⅛+4Λ29 9a2 - 6ab +⅛23 8^2 ÷ 2 42Λ2+2⅛25澎1. 3x-4ιy,9x2-24Λ^+16√: I朋十彳：8- -2ab .6-m1 - + -n216x2 + 4∑y -I- —ιy2三、1.⑴ 4 3 9 ；（2）4丿：■—十3&B _9护_ 2 （3） 4 :⑷ 39204 （提示：低一（2°°■ 2））.、、、.I} Am十？2 + P + Amn-AmP - 2wp2.3-√+Λ⅛-73J⑷ /一4护+12血一9护・（S） X3. ⑴Λ4-2CJ⅛2+δ4 : （2）8x-32.（3）16朋4 -72眈?泌十81刃4（4）9/- 炭 + 必匕 - / ；（5）⅛2-⅛2 -β⅛-9.（6）4诂-定+2碑-才（7） ' ■ 2今-2xz + / + 2yz +∑2（S） 400(3)-K 计算下列各式：(1) (x + 2Xx-2) (2) (l + 3dXl-3α) (3) (χ + 5yXx -5y)2^ 猜一猜：(α + bXα-Z?) = _____ - ____二、巩固练习：1、下列各式中哪些可以运用平方差公式计算 ________________ (1) (G + Z?Xd-C) (2) (X + yX-y + x) (3) (CIb -3x)(-3x-ab) (4) (-∕π-/7X777 +/?) (5) (2a+b)(2b-cι)(6) (-2χ-y)(-2x+y)2、判断：(3x- y ∖-3x+ y) = 9x 2 - y 2 ()4) (- 2x - yX~ 2x + y) = 4x 2 - y 2 ()5)(U + 2∖a -3)=Cr -6 () 6) (X + 3∖y -3)= Xy t -9 () 3、计算下列各式：(1) (4a-7b ∖4a + 7b)(2) (一 Im- n X2〃? 一 ")1 \ rι 1 、—a + —b 一 G ——b2丿 13 2丿平方差公式11) (2a + b ∖2J}-a) = 4a 2 ^b 2)3)4.填空:(1)(2x + 3y)(2x-3y)= ______________(2)(46/-1)( )=166∕2-1 (3) --- "心卜存讥9(4) (2x+ * -3y)= 4X2-9y2三、提髙练习：1、U + >'X-r-yXx2 + y2)2、X4-(2X2+1)(2X2-1)2、若疋一/=12 ,x+y = 6,求X, y的值。

培优专题整式的乘法

整式的乘法培优训练教师寄语：任何的限制，都是从自己的内心开始的。

忘掉失败，不过要牢记失败中的教训。

【知识精要】1、幂的运算性质（m、n为正整数）（m为正整数）（m、n为正整数）（m、n为正整数，且a≠0，m＞n）（a≠0）（a≠0，p为正整数）2、整式的乘法公式：3、科学记数法其中（1≤|a|＜10）4、单项式的乘法法则：单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

5、单项式乘以多项式：就是用单项式去乘多项式的每一项，再把所得的积相加。

6、多项式与多项式相乘：先用多项式的每一项乘以另一个多项式的每一项，再把所的的积相加。

7、单项式的除法法则：单项式相除，把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

8多项式除以单项式：先把这个多项式的每一项除以这个单项式，在把所的的商相加。

例1．已知1582=+xx，求2)12()1(4)2)(2(++---+xxxxx的值.练习：1．若0422=--aa, 求代数式2]3)2()1)(1[(2÷--+-+aaa的值. 2．已知012=--xx，求)5()3()2)(2(2---+-+xxxxx的值．3. 已知)1()3)(3(1,09322---+++=-+xxxxxxx）求（的值.4．已知222x x-=，求代数式2(1)(3)(3)(3)(1)x x x x x-++-+--的值．5. 已知132=-xx，求)1)(4()2()2(22--+-+-+xxxxx）（的值.例2：已知012=-+x x ，求代数式3223++x x 的值。

练习：1. 已知0332=-+x x ，求代数式103523-++x x x 的值。

2. 已知012=-+a a ，求代数式3432234+--+a a a a 的值。

3. 已知0132=+-x x ，求代数式200973223+--x x x 的值。

整式的乘除因式分解定义公式总结

整式的乘除因式分解定义公式总结.doc整式的乘除与因式分解定义公式总结一、引言整式是代数学中的基础概念，它包括多项式和单项式。

整式的乘除和因式分解是代数学中的重要操作，对于解决代数问题具有重要意义。

本文档旨在总结整式乘除的基本规则和因式分解的常用方法。

二、整式的定义单项式：由系数和变量的乘积组成的代数表达式，例如 (3x^2)。

多项式：由若干个单项式的和组成的代数表达式，例如 (3x^2 + 2x -5)。

三、整式的乘法单项式乘单项式：系数相乘，变量的指数相加，例如 (2x \cdot 3y = 6xy)。

多项式乘多项式：使用分配律逐项相乘，然后合并同类项，例如 ((x + 2)(x - 3) = x^2 - 3x + 2x - 6 = x^2 - x - 6)。

四、整式的除法多项式除以单项式：将多项式的每一项分别除以单项式，然后合并结果，例如((3x^2 + 6x + 9) ÷ 3 = x^2 + 2x + 3)。

多项式除以多项式：使用多项式长除法或合成除法，例如 ((x^2 - 4) ÷ (x - 2) = x + 2)。

五、因式分解的定义因式分解是将一个多项式表达为几个多项式的乘积的过程。

六、因式分解的基本方法提取公因式：找出所有项共有的因子并提取出来，例如 (6x^2 + 9x = 3x(2x + 3))。

公式法：利用已知的代数公式进行因式分解，例如平方差公式 (a^2 - b^2 = (a + b)(a - b))。

配方法：通过添加和减去相同的数，将多项式转化为完全平方的形式，例如 (x^2 + 4x + 4 = (x + 2)^2)。

分组法：将多项式分成几组，每组内部可以提取公因式或应用其他因式分解方法，例如 (x^3 + x^2 + x + 1 = (x^2 + 1)(x + 1))。

七、特殊多项式的因式分解完全平方三项式：形如 (a^2 - 2ab + b^2 = (a - b)^2) 的多项式。

整式的乘法与因式分解知识点总结

整式的乘法与因式分解知识点总结整式是由整数、变量和运算符号相结合，通过加、减、乘、除等运算符号连接而成的代数式。

整式的乘法是指对两个或多个整式进行相乘的操作。

一、整式的乘法1.乘法运算的简便性：相同指数的变量相乘，可以将指数相加。

例如，a^2*a^3=a^(2+3)=a^52.简单常数的乘法：整数与整式相乘，只需将整数与整式中的每一项依次相乘。

3.分配律的运用：对于多项式的乘法，可以采用分配律以简化计算过程。

例如：(x+2)(x+3)=x*x+x*3+2*x+2*3=x^2+3x+2x+6=x^2+5x+64.合并同类项：在整式的乘法中，应合并同类项，即将指数相同的项进行合并。

例如，2x*3x=6x^25.乘法的交换律：整式在乘法中满足交换律。

例如，a*b=b*a。

二、因式分解因式分解是将一个整式拆分成多个因式的乘积的过程。

因式分解的目的是将复杂的整式转化为简单的乘法形式，方便计算与研究。

1.提公因式法：通过提取公因式的方法进行因式分解。

提公因式法的步骤如下：(1)将各项中的公因式提取出来；(2)原式中的每一项除以公因式，得到一个新的因式分解。

例如：6x^2+12x=6x(x+2)2.公式法：根据一些特定的公式进行因式分解。

例如：a^2-b^2=(a-b)(a+b)x^2 + 2xy + y^2 = (x+y)(x+y) = (x+y)^23.分组分解法：根据整式中存在的属于同一类别的项的相似性，将其进行分组并提取公因式。

例如：ab + ac + bd + bc = a(b+c) + b(d+c) = (b+c)(a+d)4.公因式分解法：在整式中找出各项的公因式，并将其提取出来，得到一个新的因式分解。

例如：2a^2b^2 + 4ab^3 = 2ab^2(a + 2b)5.平方差公式：根据平方差公式进行因式分解。

例如：a^2-b^2=(a-b)(a+b)6.根据特定条件进行因式分解：对于特定形式的整式，可以根据一些特定的条件进行因式分解。

整式乘法及因式分解知识点总结

整式的乘除与因式分解一、整式的乘除1、整式的乘法：同底数幂的乘法：同底数幂相乘，底数不变，指数相加。

),(都是正整数n m a a a n m n m +=•幂的乘方：幂的乘方，底数不变，指数相乘。

),(都是正整数）（n m a a m n n m =积的乘方：积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘。

)()(都是正整数n b a ab n n n =单项式乘以单项式：把它们的系数、同底数幂分别相乘，对于只在一个单项式里出现的字母，则连同它的指数作为积的一个因式。

单项式与多项式相乘：就是用单项式去乘多项式的每一项，再把所得的积相加。

多项式与多项式相乘：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

平方差公式：22))((b a b a b a -=-+完全平方公式：2222)(b ab a b a ++=+2222)(b ab a b a +-=-2、整式的除法：同底数幂的除法：同底数幂相除，底数不变，指数相减。

)0,,(≠=÷-a n m a a a n m n m 都是正整数单项式相除：把系数、同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

多项式除以单项式：先把这个多项式的每一项除以这个单项式，再把所得的上相加。

注意：（1）单项式乘单项式的结果仍然是单项式。

（2）单项式与多项式相乘，结果是一个多项式，其项数与因式中多项式的项数相同。

（3）计算时要注意符号问题，多项式的每一项都包括它前面的符号，同时还要注意单项式的符号。

（4）多项式与多项式相乘的展开式中，有同类项的要合并同类项（5）公式中的字母可以表示数，也可以表示单项式或多项式。

（6）),0(1);0(10为正整数p a a a a a pp ≠=≠=- （7）多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加，单项式除以多项式是不能这么计算的。

八年级数学整式的乘法及因式分解培优专题：运用公式法进行因式分解(含答案)

运用公式法进行因式分解【知识精读】把乘法公式反过来，就可以得到因式分解的公式。

主要有：平方差公式a b a b a b 22-=+-()() 完全平方公式 a ab b a b 2222±+=±()立方和、立方差公式 a b a b a ab b 3322±=±⋅+()()补充：欧拉公式：a b c abc a b c a b c ab bc ca 3332223++-=++++---()()=++-+-+-12222()[()()()]a b c a b b c c a 特别地：（1）当a b c ++=0时，有a b c abc 3333++=（2）当c =0时，欧拉公式变为两数立方和公式。

运用公式法分解因式的关键是要弄清各个公式的形式和特点，熟练地掌握公式。

但有时需要经过适当的组合、变形后，方可使用公式。

用公式法因式分解在求代数式的值，解方程、几何综合题中也有广泛的应用。

因此，正确掌握公式法因式分解，熟练灵活地运用它，对今后的学习很有帮助。

下面我们就来学习用公式法进行因式分解【分类解析】1. 把a a b b 2222+--分解因式的结果是（）A. ()()()a b a b -++22B. ()()a b a b -++2C. ()()a b a b -++2D. ()()a b b a 2222-- 分析：a a b b a a b b a b 22222222212111+--=++---=+-+()()。

再利用平方差公式进行分解，最后得到()()a b a b -++2，故选择B 。

说明：解这类题目时，一般先观察现有项的特征，通过添加项凑成符合公式的形式。

同时要注意分解一定要彻底。

2. 在简便计算、求代数式的值、解方程、判断多项式的整除等方面的应用例：已知多项式232x x m -+有一个因式是21x +，求m 的值。

分析：由整式的乘法与因式分解互为逆运算，可假设另一个因式，再用待定系数法即可求出m 的值。

培优专题：整式的乘法公式

整式的乘除知识点

整式的乘除知识点

第一节 整式乘法及应用-学而思培优

整式乘法公式

人教版八上数学整式的乘法及因式分解单元培优

整式的乘除及因式分解知识点归纳

二元一次方程组、整式的乘法、因式分解培优

整式乘法运算法则公式

初一-第03讲-整式的乘法与平方差公式(培优)-教案

整式的乘法乘法公式

初中数学整式乘除培优讲义(含解析)

整式的乘法与因式分解培优

培优专题：整式的乘法公式

培优专题整式的乘法

整式的乘除因式分解定义公式总结

整式的乘法与因式分解知识点总结

整式乘法及因式分解知识点总结

八年级数学整式的乘法及因式分解培优专题：运用公式法进行因式分解(含答案)

第一节整式乘法及应用-学而思培优