简单正弦交流电路的计算
正弦交流电路的分析计算

2. 相位相同
3. 有效值关系:U IR
4. 相量关系:设 U U 0
则 I U 0 或 R
I U
U I R
(3-43)
电阻电路中的功率
1. 瞬时功率 p:瞬时电压与瞬时电流的乘积
i
u
R
i 2 I sin ( t) u 2U sin ( t)
p u i Ri 2 u 2 / R
则: I2 100 5 j5 10 2 45 A
I1 1090 j10 A I I1 I2 100 A A读数为 10安
R uR 若 i 2Isin t
u L uL 则 u 2IRsin t
C
uC
2I (L) sin(t 90 ) 2I ( 1 ) sin(t 90 )
C
(3-69)
相量模型
I
R U R
U
L U L
C U C
相量方程式:
U U R U L UC
设 I I0(参考相量)
则 U R IR
电感电路中复数形式的 欧姆定律
U I j X L
U U 领先!
其中含有幅度和相位信息
I
u、i 相位不一致 !
u iL ?
(3-51)
关于感抗的讨论
感抗(XL =ωL )是频率的函数, 表示电感电路中电
压、电流有效值之间的关系,且只对正弦波有效。
XL
+R
_e L
UL I XL
ω
ω=0时
XL = 0
P UI cos Q UI sin
S UI
S
Q
P
(有助记忆)
(3-82)
R、L、C 串联电路中的功率关系
3.3单一参数的正弦交流电路

Um Im sin2 ω t (2) 平均2功率 P
UI
sin 2 ω t
P 1
T
p dt
T0
1
T
UI sin (2ω t)dt 0
T0
C是非耗 能元件
瞬时功率 :p i u UI sin2ωt
u,i i u
o
i
+
u
ii
u+
u
-i u
- -++
p
+ p <0 + p <0
i 5 2sin(314t 30)A的电流
求(1)感抗XL;(2)线圈两端的电压u; (3)有功功率和无功功率。
3.3.3 电容元件的交流电路
1.电流与电压的关系
基本关系式: i C du
设:u
dt
2 U sin ω t
i
+
u
C
_
则:i C du 2 UC ω cos ω t 电流与电压
时值表达式不变,电路中的电流的
有效值及无功功率又如何?
解:(1) XL L 3140.1 31.4()
QL UI 2207 1540(var)
I UL 220 7(A) X L 31.4
(2)
i C du dt
U jXC I
相量图
I U
U
I I
U
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (参考方向) 关系
阻抗
电压、电流关系
功率
瞬时值
有效值 相量图 相量式 有功功率 无功功率
i
+
任务二 正弦交流电路中的电压、电流及功率【 正弦交流电路的基本概念和基本定律】
u i
o
ωt
平均功率P
P 1
T
p dt
To
p + p <0 + p <0
1
T
UI sin (2ω t)dt 0
o p >0
To
p >0
ωt
充电 放电 充电 放电
18
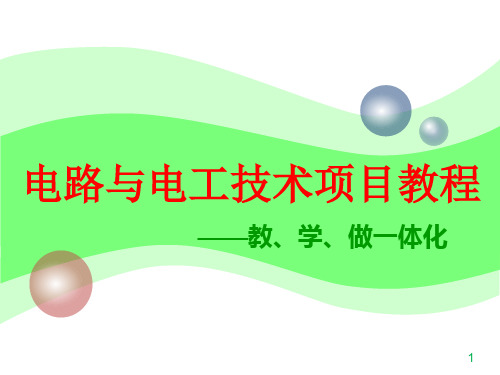
瞬时功率 p: p UI sin2 ω t
平均功率P: P 0
无功功率 Q QC U I I 2 XC U 2 XC
u
C uC
-
-
+
.
U
.
+
U
-
R
+
.
UL
-
j 1 C
-
+.
UC
-
由KVL:
. U
. UR
[R
. UL
j(L
. UC
1
C
. RI
)]I
jL
[R
. I j
1
C
j(XL
. I
X
C
)]I 28
.
IR
j L
i
+
.
U
.
+
U
-
R
+
.
U
L
-
j 1 C
-
+.
UC
-
+ u _
Z
由KVL:
. U
...
.
UR UL UC R I
R
Imsin ω t 2 I sin ω t_Biblioteka 频率: 相同相位差 :
正弦交流电路的相量表示法
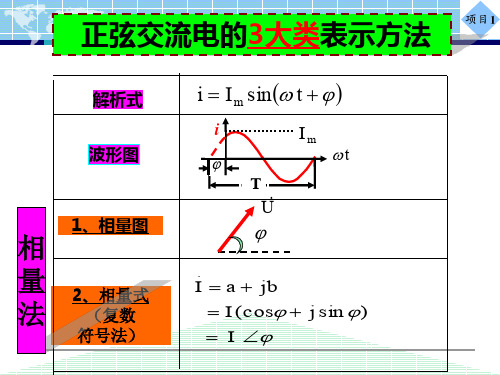
220
23
3
220 [cos( ) j sin( )] (110 j 190 .5)V
3
3
I
100 / 6
/3
220
U
u 正弦量
对应
相量图 U
t
例4
已知: u1(t) 100sin(314t 48)V ,
u2 (t) 50sin(314t 45)V
相量图: 把相量表示在复平面的图形
可不画坐标轴
2、相量式的书写方式:
模用最大值表示 ,则用符号:Um 、Im、E. m 模用有效值表示,则用符号: U 、I、E.
3注.3 意正弦:量在的实相量际表应示用法 中,模更多采用有效值表示
U I
注 意:
1) 相量只是表示正弦量,而不等于正弦量。
为了与一般的复数相区别,我们把表示正弦量的
复数称为相量,并在大写字母上打“.”表示。
设正弦量 u Umsin(ωt ψ)
相量表示:
U Uejψ Uψ 相量的模=正弦量的有效值
相量辐角=正弦量的初相角
或
Um Umejψ Umψ
相量的模=正弦量的最大值 相量辐角=正弦量的初相角
U• 220 45?
4 2 sin (ω t 30 ) ?
2
有效值
j45
瞬时值
4.已知:
U m 220 ? e45
U 100 15V
2.已知:I 1060A
i 10 sin ( ω t 60)?A
最大值
U 100V ?负号 ? U 100 ej15 V
+j
b
A
《电工》教案第十讲正弦交流电路的分析计算

第十讲正弦交流电路的分析计算正弦交流电路中的功率功率因数的提高及最大功率的计算时间:2学时重点和难点:正弦交流电路向量法求解;有功功率与无功功率的计算目的:让学生用向量图分析求解正弦交流电路的主要依据,掌握参考向量的选择方法,掌握用向量图分析电路的方法,能熟练应用向量法求解各类实际电路问题;让学生掌握瞬时功率、平均功率的意义和计算方法,掌握功率因数的概念、意义、计算方法,掌握引起无功功率的原因,掌握无功功率、复功率、视在功率、容量的计算方法。
教学方法:多媒体演示、课堂讲授主要教学内容:一、正弦交流电路的分析计算对于任意正弦交流电路,只要用相量表示正弦交流电路中的电压、电流,用阻抗或导纳对应直流电路的电阻或电导,所有的运算采用复数运算规则进行,计算电阻电路时的一些公式和方法,就可以完全用到正弦交流电路中来。
这就是说,运用相量并引用阻抗及导纳,正弦交流电路的计算方法可以仿照电阻电路的处理方法来进行。
正弦交流电路的分析,一种是依靠相量图来解决实际问题,这种方法称为相量图法,而把依靠列出相量方程来解决实际问题的方法称为相量解析法。
两者均属相量法的范畴,它们的依据是共同的。
1、正弦交流电路的相量图法分析计算:1)对于简单的正弦交流电路常借助于相量图进行辅助分析,这样可以直观表现出各电量之间的大小和相位关系。
画相量图时,应遵循以下几点:a、选择参考相量;b、画在同一相量图上的各电量一定是同频率的;c、依据欧姆定律及KCL、KVL的相量形式;d、单一参数R、L、C各元件电压与电流的相量关系;2)参考相量的选取原则:a、串联电路宜选用电流为参考相量,并联电路宜选用电压为参考相量;b 、对于较复杂的混联电路,应根据已知条件综合考虑。
可以选电路内部某并联部分电压为参考相量,也可以选其中某部分的电流为参考相量;或选用端电压或电流为参考相量。
例1 并联电路如图(a )所示,用相量图定性表明各电流相量的关系。
解:并联电路宜从两端电压入手,选电压相量S U 为参考相量。
实验6简单正弦交流电路的研究【精选】

实验原理(二)
三压法测φ原理 任意阻抗Z和R串联,如图a所示,则其相量如图b、
利用余弦定律可以计算串联后总阻抗角为φ
实验内容
1. 研究串联电路中,电压、电流大小与相位的关系, 阻抗随频率变化的关系。 按图接线,元件参数如下、C上
的电压,并进行计算,其中I=UR/R。注意,当改
测量流过各元件的电流(采用取样电阻法)数据 记录在下表中,改变元件时重调US=IV。
元件参数C=0.2μF,L=200mH,R=1KΩ,R0=10Ω (取样电阻) 信号源F=800Hz,Us=1V
思考题
当XL=XC=R 时 ①流过 R、L 、C 元件的电流相同吗? ②仅是R 、L 并联时其电流大小是否小于R 、 L 、 C 并连时的电流? ③ LC并联时的电流一定大于仅接 C时的电流吗? 以上三点根据测量数据画出向量加以说明。
电感元件:UL=jXLI ,式中XL=WL=2ΠfL 称为感抗 。 当 L为常数时, XL与频率 f成正比, f越大,XL 越 大,f 越小,。XL越小。理想电感的特征是电流I 滞 后于电压 90
电容元件:UC=-jXCI ,式中XC=1/WC=1/2ΠfC 称 为容抗。当 C为常数时,XC 与 f成反比, f越大, XC越小。. 电容元件的特点是电流I 的相位超前于电 压 90 。
实验报告要求
实验目的。 原理简述。 实验内容:实验步骤、实验电路、表格、数据等。 整理并计算实验数据,检查数据是否与理论值相
符,并加以解释分析。 画出电阻、电感、电容,RC 串联,RL 串联电流
电压的向量图。(共5个) 当频率升高时,阻抗lZ l 的变化趋势,cosφ 的变
化趋势,画出向量图加以说明。
交流电路的计算公式

交流电路的计算公式交流电路是由交流电源、电感元件、电容元件和电阻元件等组成的电路。
在交流电路中,电流和电压是随时间变化的。
为了方便计算,我们需要使用一些计算公式来描述交流电路的行为。
1.交流电流和电压的关系交流电路中,电流和电压之间存在着相位差,可以用复数形式表示。
复数形式下,电压和电流可以分别表示为:V = Vm * cos(ωt + φv)I = Im * cos(ωt + φi)其中,Vm和Im分别表示电压和电流的峰值(振幅),ω表示角频率,t表示时间,φv和φi分别表示电压和电流的相位差。
2.电流和电压的有效值在交流电路中,我们常常关注的是电流和电压的有效值,即RMS (Root Mean Square)值。
电压和电流的RMS值可以通过峰值除以√2来计算:Vrms = Vm / √2Irms = Im / √23.交流电路中的电阻在交流电路中,电阻元件对交流电流和电压没有影响,因此计算交流电路中的电阻非常简单,只需要使用欧姆定律即可:V=I*R其中,V表示电压,I表示电流,R表示电阻值。
4.交流电路中的电感电感是交流电路中常见的元件之一、电感元件对交流电流和电压有一定的阻抗,其计算公式为:XL=2πfL其中,XL表示电感的阻抗,f表示频率,L表示电感值。
当交流电路中只有电感元件时,电压和电流之间的相位差为90度。
5.交流电路中的电容电容也是交流电路中常见的元件之一、电容元件对交流电流和电压也有一定的阻抗,其计算公式为:XC=1/(2πfC)其中,XC表示电容的阻抗,f表示频率,C表示电容值。
当交流电路中只有电容元件时,电压和电流之间的相位差为-90度。
6.交流电路中的阻抗在交流电路中,电感和电容对交流电流和电压的影响是不同的。
可以使用复阻抗(Z)来描述交流电路的总阻抗,其计算公式为:Z=R+j(XL-XC)其中,R表示电阻的阻抗,XL和XC分别表示电感和电容的阻抗。
复阻抗可以分解为实部和虚部。
正弦交流电的计算公式

正弦交流电的计算公式正弦交流电路中的计算公式 设如图所示的无源二端网络,电流和电压分别为: 1、瞬时功率 则电路的瞬时功率为: 2、视在功率S 定义:电路中总电压与总电流有效值的乘积。
单位:伏安kVAS 又称为容量,表征的是电源能够提供的最大有功功率,但电源实际输出的有功功率的大小取决于负载,也就是功率因数 根据P、Q、S的计算公式,我们可以得到: P、Q、S构成了一直角三角形,称功率三角形。
3、无功功率Q 从瞬时功率的表达式中可以看出:p1≥0,它反映了电阻所消耗的瞬时功率。
p2是一个正弦量,它的频率是电源频率的两倍,在一个周期中有正有负,而且正负面积相等,它反映了电感、电容这些储能元件与电源进行能量交换的瞬时功率。
无功功率Q定义为p2的幅值。
即 无功功率Q反映的是储能元件L、C 与电源进行能量交换的规模。
当电路只含一个电阻元件时, 当电路只含一个电感元件时, 当电路只含一个电容元件时, 当电路中有若干电感、电容元件时,求总的无功功率,方法有二:(1)直接运用公式;(2)可将各部分无功功率相加获得。
可根据电路无功功率的正负,判断电路的性质。
Q》0,感性电路;Q 《0,容性电路;Q=0,阻性电路。
无功功率的单位为乏或千乏。
4、有功功率P(平均功率) 有功功率,又称为平均功率,是电路一个周期内消耗电能的平均速率。
从有功功率的表达式可以看出,电路消耗的功率不仅与电压、电流的有效值有关,还与有关。
是电压和电流的相位差,即阻抗角,由电路的参数决定。
正弦交流电路计算例题 【实例】已知:R1=5Ω,Xc1=5Ω,Xc2=10Ω,XL2=20Ω,XL3=10Ω。
求:电路的总阻抗Zab,并说明电路的性质。
【解】根据阻抗的串、并联计算公式: 电路表现为电阻.。
实验六 简单正弦交流电路的研究

实验六简单正弦交流电路的研究实验目的:1、理解正弦交流电路基本概念和相关计算方法;2、学习正弦交流电路的基本组成和特点;3、通过实验了解正弦交流电路的工作原理和基本参数。
实验仪器:正弦交流信号发生器、多用示波器、交流电压表、电阻箱、万用表等。
实验原理:正弦交流电路是指交流电流或电压大小、正负周期和相位都随时间按正弦规律周期性变化的电路。
正弦电压与正弦电流的关系可以用欧姆定律解释:U = I × R (式一)其中,U为电势差或电压,I为电流,R为电阻。
欧姆定律可以用于所有电路中,在交流电路中也同样可以适用。
因此,在深入研究正弦交流电路之前,我们先了解交流电压的基本性质:(1) 交流电压的特点u(t)= Vm sin(ωt+φ) (式二)其中,Vm为交流电压的幅值,ω为角频率,φ为相位角,t为时间,sin为正弦函数。
(2) 交流电阻理论交流电路中的电阻也称交流电阻,是指电阻对于交流电流的阻力。
交流电路中,电阻对交流电流的阻抗与电阻对直流电流的电阻是不同的,最常用的是交流电阻,即所谓的“阻抗”。
阻抗的计算式为:其中,R为电阻,L为电感,ω为角频率,j为单位虚数。
交流电路中的电感和电容都是随着时间周期性变化的被动元件。
在电路中,它们对于交流电流的阻抗值分别是:Xl = ωL (式四)Xc = 1/(ωC) (式五)交流电阻的大小取决于电阻、电容、电感等电路元件,同时也与电流的频率有关。
一个简单的正弦交流电路由以下几个基本部分组成:(1) 信号源正弦交流电路的信号源一般为交流电源,它会产生正弦波形的交流电。
(2) 负载负载是在正弦交流电路中转换电能并将其用于加热、照明等工作的部分。
负载可以是灯泡、电磁铁、电动机等。
(3) 阻抗实验步骤:1、测量交流电压源的电压并记录下来;2、接通电路并且打开示波器观测交流电压源和负载的电压大小,能够观测到依次变化的电压大小及相位差;3、根据示波器上的波形,测量出交流电压源和负载的电压幅值、频率和相位差;4、更改电压源的电压频率,重新测量交流电路的各种参数,记录下来并计算出传输功率,观察波形对应的变化,分析实验结果。
电路原理 正弦稳态电路的计算

j10Ω I
A
A
I1
I2 C1
B
5Ω j5Ω V
分析:已知电容支路的电流、电压和部分参数
求总电流和电压 解题方法有两种: (1) 用相量(复数)计算
(2) 利用相量图分析求解
15
j10Ω I
A
I1
A I2 C1
B
5Ω j5Ω V
已知:I1= 10A、 UAB =100V,
求:A、V 的读数
解法1: 用相量计算
•
US 1
+
•
U s1 -
j
X
L
I2
I3
R
•
US
2
- I1 I2 I3 0
- j2I1 5I3 100
j5I2 5I3 j100
R
•
I3
②
3.6.2图(b)
•
I2 +
•
U s2 -
8
(2)回路电流法
•
I
1
jX C
jX L
+
•
•
U s1
Ia
-
•
Ib
R
•
I3
R - j X C
Ia
RIb
IC2 UC1
IR2 UR1 1
U2C 2 I1 C 1
U2 R2
I1 R1
•
I1
R1
C1
•
IC2
U + +
•
U1
•
-
3
R2
C2
•
+ •
U2
-
I R2
-
3.6.4例5图(a)
•
正弦交流电路公式总结

正弦交流电路公式总结
正弦交流电路中的主要公式和概念包括:
1. 周期和频率:
周期(T):交变电流完成一次周期性变化(线圈转一周)所需的时间,
单位是秒(s),公式为T=2π/ω。
频率(f):交变电流在1s内完成周期性变化的次数,单位是赫兹(Hz)。
周期和频率的关系:T=1/f。
2. 正弦式交变电流的函数表达式(线圈在中性面位置开始计时):
电动势e随时间变化的规律:e=Emsinωt。
负载两端的电压u随时间变化的规律:u=Umsinωt。
电流i随时间变化的规律:i=Imsinωt。
其中ω等于线圈转动的角速度,Em=nBSω。
3. 在纯电阻性电路中,当电路与电源之间不再有能量的交换时,电路呈电阻性。
以上内容仅供参考,如需更具体全面的信息,建议查阅电路学相关书籍。
正弦交流电路_单一参数的正弦交流电路

iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(2)大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值: U m L I m 有效值: U ω L I
定义: X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 (1)瞬时功率
p ui
U m I m s in t s in t 90
(能量的吞吐)。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较,设电流 i I m s in t
u
i
为参考量,则: u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率(有功功率) P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能, 也称有功功率。
电工技术:正弦交流电路的功率

知识点小结
单相正弦交流电路的功率计算 (1)有功功率: (2)无功功率: (3)视在功率:
P UI cos Q UI sin
S Q φ
功率三角形
S UI
P
S φ Q
QN S N 2 PN 2 141.42 1002 100kVar
(2) I N
100 PN 372 A 380 0.707 U N cos
P
PN 100 1000 2 372 372 0.72 IN
R
Z
U N 380 2 1.02 X L Z R2 1.022 0.722 0.72 I N 372 XL 0.72 L 2.3mH 2 f 2 3.14 50
P I R
U2 P R
Q UI sin 0
二、几种特例电路的功率计算
2.单一纯电感元件的交流电路
i
+ u
电压超前电流900,阻抗
L
Z 有功功率: P UI cos 0
jX.阻抗角
L
900
3.单一纯电容元件的交流电路
无功功率: QL
i
2 U 2 利用电压电流有效值关系,又得: QL I X L = XL
i
R L C
uR
X L XC Z R j( X L X C ) arc tan R (1)有功功率: P UI cos
因为电路中只有电阻元件是耗能元件,因此有功功率又可以用公式:
u
uL
P I R
2
uC
(2)无功功率:
Q UI sin
U R2 P R
因为电路中只有电感元件和电容元件有无功功率,因此无功功率又可以用公式:
一般正弦交流电路的计算
& I1
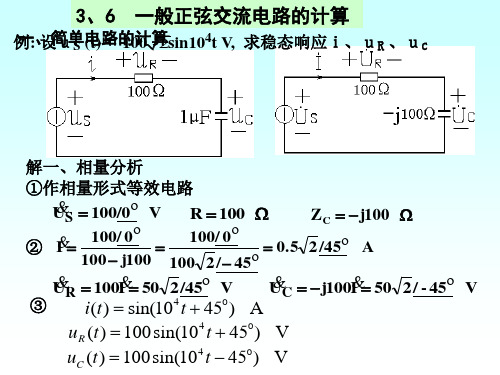
& & & I 1 = 10∠90° A, I 2 = 10∠ 30° A, I = 10∠ 30° A
& U 100∠ 0° 故X C = 10 = jX C = = j10, & 10∠ 90° I1 & U 100∠ 0° = R + jX L = = 10∠ 30° = 8.66 + j 5 & 10∠ 30° I
X C = 2R2
R2 2 + R L 2
=
1 2 R2
Z ab =
U 200 = R1 + Z ab = 5 + 2 R2 = = 20 I 10
R 2 = 7.5
X L = R2 = 7.5 , X C = 2 R2 = 15
在图示电路中,U 例: 在图示电路中 1=220V,Z1=(10+j50) ,Z2=(400+j1000) , 如要求i 的相位差为90,试求实数β的值 并求I 的值, 。如要求 2和u1的相位差为 ,试求实数 的值,并求 1和I2。 解:由KCL可得: 由KVL可得:
Z = ( jX C ) ( jX L + R ) =
(R + jX L )( jX C )
R + j X L XC
(
)
U 100 = = = 10 I 10
& I
& U & I1 I&2
U 100 U 100 2 XC = = = 10 R + jX L = R2 + X L = = = 10 I1 10 I2 10
uC = 15 2 sin(1000t 120° )V
正弦交流电电流有效值公式

正弦交流电电流有效值公式正弦交流电电流有效值公式:在一个完整的周期内,正弦交流电的电流的有效值可以根据以下公式计算:I_{RMS} = \frac{I_{max}}{\sqrt{2}}其中 I_{RMS} 表示电流的有效值,I_{max} 表示电流的最大值。
原理解释:交流电流是由于电子在导体内上下振荡而产生的。
由于电流不是恒定的,它的值随时间变化而变化。
在一个周期内,电流的值经过一系列的变化,这些变化可以用一个曲线表示,这就是正弦曲线。
正弦曲线上的任何一个瞬间,电流的值都可以通过测量从零到这个点的电流值的平均值来得到。
为了计算出电流的有效值,我们需要计算在一个完整的周期内电流的平均值。
在一个完整的周期内的电流平均值等于电流的RMS值,也就是有效值。
实际应用场景:正弦交流电电流有效值公式的应用非常广泛,它是计算交流电的电能的基础。
有效值是计算电阻、电容和电感器件导电性能的重要指标。
以下是一些应用场景的例子:1. 家庭电力消耗:在家庭中,电流的有效值经常被用于计算电器的电力消耗。
通过电表可以测量出房屋电力的总耗电量,然后通过测量电流的有效值和电压的实际值,可以计算出每个电器的功率消耗。
2. 电子设备:许多电子设备需要判断电流的有效值。
在音频放大器中,在接收输入信号之前,需要将信号转换为电流并计算其有效值,以确保信号不会过载或损坏放大器。
3. 电路设计:在电路设计中,电流的有效值可以用来计算电路元件的功率耗散。
这些元件可能包括电阻、电容和电感。
通过计算电流的有效值和电压的实际值,可以计算出电路中每个元件的实际功率。
4. 电力系统工程:在电力系统工程中,电流的有效值用于计算负载电功率。
在发电站中,为了计算出发电量和负载电流倍率,必须计算出负载电流的有效值。
有效值也是电网稳态分析的一个基本参数。
正弦交流电电流有效值公式是计算交流电能和其它电学实际应用中不可或缺的重要工具。
正弦交流电路的功率

问题与讨论 功率因数补偿到什么程度?理论上可以补偿
成以下三种情况: 成以下三种情况
& IC
ϕ <0
& U
I&
& IC
ϕ =0
& U
& IC
ϕ
ϕ >0
I& U&
I& RL
呈电容性。 呈电容性。
I&
& IRL
呈电感性
I& RL
呈电阻性
cosϕ <1
cosϕ =1
cosϕ < 1
一般情况下很难做到完全补偿 (即: cos 功率因数补偿成感性好,还是容性好? 功率因数补偿成感性好,还是容性好? & & I 'C IC
P = U N I N cos ϕ = 600kW
而需提供的无功功率为: 而需提供的无功功率为
Q = U N I N sinϕ = 800kvar
∴ 提高 cosϕ 可使发电设备的容量得以充分利用
2. 增加线路和发电机绕组的功率损耗 设输电线和发电机绕组的电阻为 r : 要求: 要求 P = U I cosϕ (P、U定值 时 定值)时
* 复功率守恒 , 不等于视在功率守恒
& I
+
.
& U
_
& + U _
1
+
& U2
_
&& & & & S = U I * = (U 1 + U 2 ) I * & & & & = U 1 I * +U 2 I * = S 1 + S 2
正弦交流电路中的功率计算

正弦交流电路中的功率计算1.瞬时功率设如图所示的无源二端网络,电流和电压分别为,,则电路的瞬时功率为:2. 有功功率P(平均功率)有功功率,又称为平均功率,是电路一个周期内消耗电能的平均速率。
单位:W或kW从有功功率的表达式可以看出,电路消耗的功率不仅与电压、电流的有效值有关,还与有关。
是电压和电流的相位差,即阻抗角,由电路的参数决定。
对于只含一个电阻的电路,=0,则对于只含一个电感或电容的电路,=±90°,则P=0由上分析,说明电路中只有电阻元件消耗有功功率,电感和电容是储能元件,不消耗有功功率。
电路中若有若干个电阻,求有功功率时可采用两种方法:(1)运用公式直接求;(2)可将各个电阻的有功功率求出,相加求得,即。
定义:——功率因数功率因数是交流电路的重要技术数据之一。
功率因数的高低,对于电气设备的利用率和分析、研究电能消耗等问题都有十分重要的意义。
功率因数的大小,取决于电路中负载的性质。
对于电阻性负载,其电压与电流的相位差为0,因此,电路的功率因数最大();在纯电感电路中,电压与电流的相位差为π/2,电压超前电流;在纯电容电路中,电压与电流的相位差则为-(π/2),即电流超前电压。
在后两种电路中,功率因数都为0。
对于一般性负载的电路,功率因数就介于0与1之间。
3.无功功率Q从瞬时功率的表达式中可以看出:p1≥0,它反映了电阻所消耗的瞬时功率。
p2是一个正弦量,它的频率是电源频率的两倍,在一个周期中有正有负,而且正负面积相等,它反映了电感、电容这些储能元件与电源进行能量交换的瞬时功率。
无功功率Q定义为p2的幅值。
即无功功率Q反映的是储能元件L、C 与电源进行能量交换的规模。
当电路只含一个电阻元件时,=0,=0,Q=0当电路只含一个电感元件时,=90º,=1,Q =UI=I2XL=U2/XL当电路只含一个电容元件时,=-90º,=-1,Q=-UI=-I2XC=-U2/XC当(感性电路)时,Q>0当(容性电路)时,Q<0当电路中有若干电感、电容元件时,求总的无功功率,方法有二:(1)直接运用公式;(2)可将各部分无功功率相加获得。
单一参数正弦交流电路的分析计算小结剖析
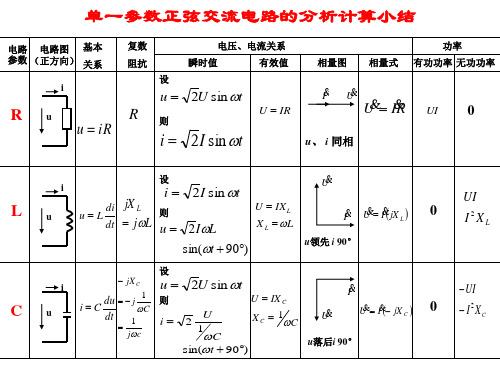
p(t ) u(t )i(t )
p(t ) 2U cos(t u ) 2I cos(t i )
UI cos(u i ) UI cos(2t u i )
UI cos UI cos(2t u i )
注: 在交流电源激励的情况下,要用相量法来求解。
“三要素”的计算
三、时间常数 原则:
的计算:
要由换路后的电路结构和参数计算。 (同一电路中各物理量的 是一样的)
RC ; 步骤: (1) 对于只含一个R和C的简单电路, 对于较复杂的一阶RC电路,将C以外的电 路,视为有源二端网络,然后求其除源网 络的等效内阻 R‘(与戴维宁定理求等效内 阻的方法相同)。则:
u 5 2 sin( t 126 9 )
I
阻抗三角形
电压三角形 功率三角形
U
Q S
R
U R
U
L C
U L
U C
Z
X L XC
R
U U L C
U R
P
(二)一般正弦交流电路的解题步骤
1、据原电路图画出相量模型图(电路结构不变)
R R 、 L jX L、 C jX C 、 i I、 e E u U
2
三相交流电路的小结(1)--三相电源
三相四线制 (Y形联接)
eC
eA
eB
A
N B C
三相电源 一般都是 对称的, 称三相对 称电源
三相三线制(Y形联接) A
eC
eA
三相三线制(Δ形联接) A
eC
eB
eA
B C
正弦交流电路的功率

p = ui
=UIcos - UIcos (2t – )
i
+
u
Z
–
瞬时功率的组成:恒定分量 UI cos, 变化分量 UI cos(2t )
u、i 同号,p > 0,网络吸收电功率 u、i 异号,p < 0,网络释放电功率
接在电压U=220V的电源上,电源频率f=50Hz。
(1)如果将功率因数提高到 cos 0.95, 试求与负载并联的电容器
的电容值和电容器并联前后的线路电流。(2)如要将功率因数从 0.95再提高到1,试问并联电容器的电容值还需增加多少? 解:计算并联电容器的电容值,可从相量图导出一个公式。
IC
I1 sin 1
4.4(23) A
Z 5053
uip
p
u
i
P t
一个周期内,p 0的面积大于p 0的面积。表明平均 功率不为0。网络内部有电阻(耗能)元件。
∫ 1 T
有功功率: P = T
uidt = UIcos
0
无功功率: Q = UIsin
功率因数:cos
视在功率: S =UI
电路的平均功率为
P UI cos 220 4.4cos53 583W
I
=
P Ucos
u
C
L
IC = IRLsin 1 –Isin
–
IC =
Psin 1 Ucos 1
– Psin
Ucos
=
P U
(tg1– tg)
IC=
U XC
= U C
C=
P
U2 (tg1– tg )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R1
R2
a
i
us(t) C1 4i
解:左图为时域电路 画出相量电路模型
b
R1
R2
a
i
i
C1
i
I
US
4I
b
R1
① R2
i
C1
i
US
4I
当ab端口短路时
a
相量电路模型---频域电路
i
当ab端口开路时
I b
i
Id
=
Uab0 = 10∠15
US
R1
−
j1
ωC1
⋅(− j2) =
⋅ 5
−j 2∠
1
ωC1
IC = β IL − IL
US R
IS
IR
IR = IS + IC
Uβ = IL ( jX L ) + US
IL
jω L +
R
−
j1
ωC
−
β IL
R
−
j1
ωC
−
IS R
=
0
IL =
R + jω L − j
IS R
1 − β R + jβ
1
ωC
ωC
例3 已知:uS (t ) = 0 i (t ) = 3sin ωt
欧姆定律
元件参数关系 KCL KVL
直流电路 U =RI I =GU R= 1
G
∑I =0 ∑U = 0
R−Z
G −Y
正弦交流电路 U=Z I I =Y U Z=1 Y
∑I =0 ∑U = 0
i
U −U
i
I−I
因此,根据基尔霍夫定律和欧姆定理所推导出的关于直流电路 的所有计算方法和定理,都可以推广应用到正弦交流电路。直 流电路中解题方法均可在交流电路中套用(无互感时)。
−Ed 2 ⋅ R ⋅ 2 ( X d + X )
( Rd
+
R)2
+ (Xd
+
X
)2
2
=0
{ } ∂P = Ed2
( Rd
+
R)2
+
(Xd
+
X
)2
−
R ⋅ 2 ( Rd
+
R)
∂R
( Rd
+
R)2
+ (Xd
+
X
)2
2
X = −Xd R = Rd
=
Ed 2
⋅ ( Rd + R) ( Rd − R) + ( X d + X )2
2.相量电路模型.
i
i
IS
a I3 C3 b R5
i
i
i
i
I5
I1
I2
I4
i
I1
+ I2 I3 +
+ I5
I3 =
= I4
IS
R1
L2
L4
US
( ) Ua +
R1
Ua +
jω L2
Ua −Ub
⋅ jωC3 = IS
( ) Ua − Ub
⋅
jωC3
+ US −Ub R5
=
Ub
jω L4
i
a I3 C3 b R5
t
−
ϕ
)]
dt
= UI cosϕ
有功功率.无功功率和视在功率
1.有功功率:即平均功率
①定义式
∫ P = 1
T
p (t) dt
= UI cosϕ
T0
② cosϕ ϕ
功率因数 阻抗角也称功率因数角
¾u, i参考方向一致时
ϕ ≤π
2
P ≥0
p(t) = UI cosϕ − UI cos(2ωt − ϕ ) = UI cosϕ − UI cos(2ωt − 2ϕ + ϕ ) = UI cosϕ − UI cos(2ωt − 2ϕ ) cosϕ + UI sin(2ωt − 2ϕ ) sinϕ = UI cosϕ[1 − cos(2ωt − 2ϕ )] + UI sinϕ sin(2ωt − 2ϕ )
dt
ub
)
=
iS
(t)
∫ c3
d
(ua −
dt
ub
)
+
uS
(t ) − ub
R5
(t)
=
1 L4
t −∞
ub
dξ
c3
d2
(ua − ub )
dt 2
+
1 R1
dua dt
+
1 L2
ua
= iS′ (t )
c3
d2
(ua −
dt 2
ub )
+
uS′
(t ) − ub′
R5
(t)
=
1 L4
ub
求解微分方程的特解
Z2 Z1 + Z2
电桥平衡,a,b为自然等位点
Z3
a,b断开:
i
i
I1
=
U Z1 +
Z3
i
i
I2
=
U Z2 +
Z4
Z4
a,b短路:
i
i
I=
U
Z1Z2 + Z3Z4
Z1 + Z2 Z3 + Z4
i
I2
=
i
I×
Z1 Z1 + Z2
Z1 × Z4 = Z2 × Z3
Z1 × Z4 = Z2 × Z3 (R1 + jX1 )(R4 + jX 4 ) = (R2 + jX 2 )(R3 + jX 3 )
3-10 简单正弦交流电路的计算
1.已知电路结构参数,求各支路电流、电压。
例1: 如图电路,已知: U=380V,XL=22Ω,ZP 为感性负载,其阻抗
角为300,且UP=UL 。 求:I、UP 的有效值
I
XL
解:
ZP
= UP I
= UP I
∠ϕ
UL
i
U
UP ZP
= U L ∠ϕ
I
= X L∠ϕ
= 22∠30
ϕ
2
i
UR
cosϕ
=U2
− U12
−
U
2 2
= 0.275
2U1U 2
i
I
ϕ = 82.26
UR = U2 cosϕ = 50cos82.26 = 13.75 UL = U2 sinϕ = 50sin 82.26 = 48.07
I = U1 = 30 = 15A R1 2
f = 50Hz
R = UR I = 0.917Ω X L = UL I = 3.205Ω
R1 R1
R4 X4
− +
X1 R4
X4 X1
= =
R2 R3 − X 2 X 3 R2 X 3 + R3 X 2
一个复数方程
两个实数方程
例1.已知:R1 ,L2 ,C3 ,L4 ,R5 ,iS(t) , us(t)
求:i1 ,i2 ,i3 ,i4 ,i5 ?
a i3 C3 b R5
is(t)
R
②
·
· UR 2U
R
·
-2U
① C
R/2
A
2C R
②
C ·
2U
·
UC
·
·UR 2U
R
① C
R/2
A
2C R
②
2C ·
2U
·
U/2
·
· U/2 2U
R/2
① C
R/2
A
2C R
②
i
i
i
UA
=
2U(jωC)-2U/ R
jωC+
2
R/2-j/2ωC
+
1 R
=
2i jU
3
§3–12 正弦交流电路的功率
uS (t) = 3sin (ωt + 30 ) i (t) = 3 2 sin (ωt + 45 ) 求: uS (t) = 4 sin (ωt + 30 ) ⇒ i (t) = ?
解: I = GUS + I0
us(t)
含源 线性 网络
i(t)
3∠45
3 2
=
I0
⇒
I0 =
3 2
=G⋅
3 2
设 u = 2U sinωt
i = 2I sin (ωt −ϕ )
1)瞬时功率
p(t) = 2UI sinωt sin(ωt −ϕ ) = UI cosϕ −UI cos(2ωt −ϕ)
波形图:
p ui
2)平均功率
∫ P = 1
T
p (t) dt
T0
=
1 T
T
∫0
[UI
cosϕ
−
UI
cos
(2ω
i4
i5
us(t)
R1
L2
L4
1
ua
R1
+
1
jω L2
+
jωC3
−
ub
⋅
jωC3
= iS (t )
ub
jωC3
+
1
jω L4
