最新电气与电子测量技术(罗利文)课后习题答案
电子测量课后答案

: 14.8V,40.8% 2.5
2.6 1.15V,0.99V;23%,19.8% 2.7 5%,0.42dB 2.8 200k,266.7k,25% 2.9 200k,199.973k,0.014% 2.10 微差法、替代法、零示法
2.11 2.5级 2.12 1000.82125, 0.047 2.13 0.9926 ±0.0008
第8章调制域测量
8.1 P270 8.2 P272 8.3 P272 8.4 P274 8.5 P275 8.6 P276 8.7 P277
第9章 非电量测量
9.1 P279 9.2 P280 9.3 P281 9.4 P282 9.5 P282 9.6 P285 9.7 P286 9.8 P287 9.9 P291
4.14 P144 4.15 0.05%, 20% 4.16 0.056% 4.17 100kHz, 40μs, 10 4.18 9.4ns 4.19 用外触发方式 4.20 滞后电源电压 45° 超前 45°
第5章 时域测量
5.1,5.2 参阅本间相关内容 5.3 李沙育图形,是圆形。 5.4 李沙育图形(1)椭圆形(2)“8”字形 5.5 被测信号频率与扫描信号频率不成整数倍,图形向左“跑动”。 5.6 被测信号频率与扫描信号频率不成整数倍,波形紊乱。 5.7 前沿有上冲,前沿弯曲。 5.8 最小周期T=0.2μs×10×10=20μs, 频率50k 5.9 最高工作频率是20MHz 5.10 最低工作频率是0.4Hz 5.11 0.02μs/cm 5.12 40ms,3ms,29ms 5.13 (1)聚焦不良(2)回扫消隐失效 5.14 引入50Hz交流电源的干扰 5.15 参阅本章相关内容
第4章 数字测量方法
电子测量与仪器课后习题解答

参考答案第一章习题解答1.1 解:测量是人类认识和改造世界的一种重要手段。
测量是通过实验方法对客观事物取得定量数据的过程。
其实测量和我们每个人都有着密切的联系,人们或多或少都对它有一定的了解。
关于测量的科学定义,可以从狭义和广义两个方面进行阐述。
狭义而言,测量是为了确定被测对象的量值而进行的实验过程。
在测量过程中,人们借助专门的设备,把被测对象直接或间接地与同类已知单位进行比较,取得用数值和单位共同表示的测量结果。
广义而言,测量不仅对被测的物理量进行定量的测量,而且包括对更广泛的被测对象进行定性、定位的测量。
例如,故障诊断、无损探伤、遥感遥测、矿藏勘探、地震源测定、卫星定位等。
电子测量是泛指以电子技术为基本手段的一种测量技术。
它是测量学和电子学互相结合的产物;也是在科学研究、生产和控制中,人们为了对被测对象所包含的信息进行定性分析、定量掌握所采取的一系列电子技术措施;是分析事物,做出有关判断和决策的依据。
在电子测量过程中,以电子技术理论为依据,以电子测量仪器为手段,对各种电量、电信号、电路特性和元器件参数进行测量,还可以通过传感器对各种非电量进行测量。
严格地讲,电子测量是指利用电子技术对电子学中有关物理量所进行的测量。
1.2 解:电子测量的范围十分广泛,从狭义上来看,对电子学中电的量值的测量是最基本、最直接的电子测量,其内容有以下几个方面:(1)电能量的测量,如测量电流、电压、功率等。
(2)电子元件和电路参数的测量,如测量电阻、电容、电感、品质因数及电子器件的其他参数等。
(3)电信号的特性和质量的测量,如测量信号的波形、频谱、调制度、失真度、信噪比等。
(4)基本电子电路特性的测量,如测量滤波器的截止频率和衰减特性等。
(5)特性曲线的测量,如测量放大器幅频特性曲线与相频特性曲线等。
1.3 解:精密度(δ)说明仪表指示值的分散性,表示在同一测量条件下对同一被测量进行多次测量时,得到的测量结果的分散程度。
电子测量技术基础课后习题答案(第二版)

电子测量技术基础课后习题答案(第二版)电子测量技术基础习题一1.1表述名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2描述轻易测量、间接测量、女团测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用轻易测量的量与被测量之间的函数关系,间接获得被测量量值的测量方法。
例如:用伏安法测量电阻消耗的直流功率p,可以通过轻易测量电压u,电流i,而后根据函数关系p=ui,经过排序,间接赢得电阻消耗的功耗p;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3表述偏差式、零位式和微差式测量法的含义,并列出测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器命令被测量与标准量成正比(均衡),从而赢得被测量从而赢得被测量。
例如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4描述电子测量的主要内容。
请问:电子测量内容包含:(1)电能量的测量例如:电压,电流电功率等;(2)电信号的特性的测量例如:信号的波形和失真度,频率,增益,阳入制度等;(3)元件和电路参数的测量例如:电阻,电容,电感,电阻,品质因数,电子器件的参数等:(4)电子电路性能的测量例如:压缩倍数,膨胀量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电气与电子测量技术(罗利文)课后习题答案

由此可见,等效阻抗与电阻率、磁导率以及几何形状有关,还与线圈的几何数、线圈中激磁电流频率f有关,同时还与线圈与导体间的距离x有关。
由此可知
M与距离x相关,可用于测量位移、振幅,厚度等。
R1、R2与传感线圈、金属导体的电导率有关,且电导率是温度函数,可用于测量表面温度、材质判别等。
设输入交流电压 为正半周,即A点为正,B点为负,则二极管 、 导通, 、 截止。在A→E→C→B支路中,C点电位由于 的增大而比平衡时低;在A→F→D→B支路中,D点电位由于 的减小而比平衡时高,即D点电位高于C点电位,此时直流电压表正向偏转。
设输入交流电压 为负半周,即A点为负,B点为正,则二极管 、 导通, 、 截止。在B→C→F→A支路中,C点电位由于 的减小而比平衡时低。在B→D→E→A支路中,D点电位由于 的增加而比平衡时的电位高。所以仍然是D点电位高于C点电位,直流电压表正向偏转。因此只要衔铁上移,不论输入电压是正半周还是负半周,电压表总是正向偏转,即输出电压 总为下正上负。
解:
图3-7变压器式交流电桥
图3-7的交流电桥图中,当衔铁向上移动和向下移动相同距离时,其输出大小相等,方向பைடு நூலகம்反。由于电源电压是交流,所以尽管式中有正负号,还是无法加以分辨。可采用带有相敏整流的交流电路,如图3-8所示。
图3-8相敏整流交流电路
当衔铁处于中间位置时,Z1=Z2=Z0,电桥处于平衡状态,输出电压 ;当衔铁上移,使上线圈阻抗增大,Z1=Z0+Z,而下线圈阻抗减少,Z2=Z0Z。
图3.1压电传感器的等效电路
由于外力作用而在压电材料上产生的电荷只有在无泄漏的情况下才能保存,即需要测量回路具有无限大的输入阻抗,这实际上是不可能的,因此压电式传感器不能用于静态测量。压电材料在交变力的作用下,电荷可以不断补充,以供给测量回路一定的电流,故适用于动态测量。
电子测量技术基础课后习题答案 (第二版)

电子测量技术基础习题一1.1 解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4 叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电工与电子技术(课后答案)

电工与电子技术(课后答案) 习题 1—5 习题 1…………………………….P 2/55 习题 2…………………………….P 18/55 习题 3…………………………….P 34/55 习题 4…………………………….P 41/55 习题 5…………………………….P 52/55
E1 4V
R2
5
取顺 定律可列方程
5
题1-4图(a)
时针为循行方向, 则由基尔霍夫电压
I ( R1 R2 ) U1 E1
代入数值可得
I
U 1 E1 10 4 1A R1 R2 24
对于右边的开口电路,由于 I 0 ,故 R3 上的压降为零,则还是取顺时针为循行方向,由基尔霍夫电压定律
故 2A 电流源两端的电压为
故是发出功率,是电源元件。
E=10V I=-2A (a) U=10V I=-2A (b) 题1-2 图
I=-1A 元件 U=-1V (c)
I=-1A 元件 U=1V (d)
;②计算图 b 中 I 、 US 、 1-3 题 1-3 为某些电路的一部分,①计算图 a 中的 I x 、 I x 、 I x 及R 。
I1 I 3 I 5 I I I 2 5 4 I1R1 I 3 R3 E1 I R I R I R 0 4 4 5 5 3 3 I 2 R2 I 4 R4 E2
代入数值:
I 1 I 3 I 5 I I I 2 5 4 5 I1 20 I 3 45 20 I 42 I 2 I 0 3 4 5 3I 2 42 I 4 48
/fuyi_fly
4 / 55
/fuyi_fly
电工与电子技术课后答案2

不出来的。
习题22-1 在图2-1所示的正弦交流电路中,电压表的读数为V 220U =,电流表的读数为A 10I =,频率Hz 50=f ,相位上u 超前i 为︒=30ϕ。
试写出u 与i 的三角函数式、相量式,并画出相量图及波形图。
解:设U 为参考正弦量,即其初相角︒=0u ψ,则电流的初相角︒-=30i ψ,角频率s rad f /3145014.322=⨯⨯==πω,电压的最大值为V 22202==U U m ,电流的最大值为A 2102==I I m ,则电压u 与电流i 的三角函数式为V 314s i n 2220)s i n (t t U u u m =+=ψω A )30314sin(210)sin(︒-=+=t t I i i m ψω相量式为 V 0220︒∠=UA 3010︒-∠=I其相量图和波形图如题2-1图(a )和题2-1图(b )所示。
2-2 已知电流A )3j 4(1+=I ,A )8j 6(2-=I ,V )100j 100(+=U 。
求:① 213I I I += ;214I I I -= ;31I U Z = ;② 电流1I 、2I 、3I 、4I 及电压U的有效值;③ 电压与各电流的相位差1ϕ 、2ϕ 、3ϕ 、4ϕ ;④ 画出电流1I 、2I 、3I 、4I 及电压U 的相量图;⑤题2-1图题2-1图(a)不出来的。
瞬时值1i 、2i 、3i 、4i 及u 。
解:①A 6.2618.115j 108j 63j 4213︒-∠=-=-++=+=I I I A 3.10018.1111j 2)8j 6(3j 4214︒∠=+-=--+=-=I I I Ω︒∠=︒-∠︒∠=︒-∠+==6.7165.126.2618.11454.1416.2618.11100j 10031I U Z②A 51=I ;A 102=I ;A 18.113=I ;A 18.114=I ;V 4.141=U ③︒==-3743tg11ψ;︒-=-=-5368tg 12ψ;︒-=6.263ψ;︒=3.1004ψ;︒=45u ψ,故电压与各电流的相位差为︒=︒-︒=-=8374511ψψϕu ︒=︒--︒=-=98)53(4522ψψϕu ︒=︒--︒=-=6.71)6.26(4533ψψϕu ︒-=︒-︒=-=3.553.1004544ψψϕu④电流1I 、2I 、3I 、4I 及电压U 的相量图如题2-2图所示。
电子测量技术基础习题解答

电子测量技术基础习题解答习题一 (1)习题二 (6)习题三 (16)习题四 (24)习题五 (30)习题六 (35)习题七 (37)习题八 (46)习题一1.1 说明名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在那个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都能够说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直截了当测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直截了当测量:它是指直截了当从测量外表的读数猎取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直截了当测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,能够通过直截了当测量电压U,电流I,而后依照函数关系P=UI,通过运算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,依照测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 说明偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器外表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平稳),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳固度。
1.4 叙述电子测量的要紧内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电子测量课后答案

4-2 已知某电压表采用正弦波有效值刻度,如何用 实验的方法确定其检波方式?列两种方法,并对 其中一种进行分析。 解:根据电压表的刻度特性,可以确定其检波方式, 举例如下 (1)用方波作为测试信号,已知方波的 Vp V V V0 用被检电压表测量这个电压。 ① 若读数 V0
2
,则该表为峰值表。 0.707V0
u1和u2经过触发电路生成门控信号u3,宽度与两个 信号的相位差对应。U3脉宽期间打开计数门,计数 器对时标信号进行计数,设为N,分频系数为k,则 t NTs fx 360 N 360 t NTs Tx fs Tx 360 Tx :被测信号周期 f s :时标信号频率,
可见,选用15V、1.5级电压表测量更合适
2-8 用电压表和电流表测量电阻值可用下图电路
(a)
(b)
设电压表内阻为Rv,电流表内阻为RA,求 被测电阻R的绝对误差和相对误差?这两 种电路分别适用于测量什么范围的内阻?
解:设被测电阻真值为 Rxo 对于图(a) 给出值:
V V Rx V V I Rxo RV
0.230 KHz
M vmax 0.045 判定有累进性误差
根据阿卑-赫梅特判据
vi vi 1
i 1
n
n 1 2 ( x)
判定有变值误差
2-16 对某电阻8次测量值如下: 10.32,10.28, 10.21,10.41,10.25,10.31,10.32,100.4 试用莱特准则和格拉布斯准则(99%置信率)判 别异常数据。
f x fi 110.060KHz
i 1
2 2 f 10 f i x i 1 10
( fx )
电工电子学课后习题答案

电工电子学课后习题答案目录电工电子学课后习题答案 (1)第一章电路的基本概念、定律与分析方法 (2)练习与思考 (2)习题 (4)第二章正弦交流电 (14)课后习题 (14)第三章电路的暂态分析 (29)第四章常用半导体器件 (41)第五章基本放大电路 (43)第六章集成运算放大器及其应用 (46)第七章数字集成电路及其应用 (54)第八章Multisim简介及其应用 (65)第九章波形的产生与变换 (65)第十章数据采集系统 (67)第十一章直流稳压电源 (69)第十二章变压器与电动机 (71)第十三章电气控制技术 (77)第十四章电力电子技术 (80)第一章电路的基本概念、定律与分析方法练习与思考1.4.2(b)a1.4.2(c)ab 1.4.3(a)b552155ababUVR=+⨯==Ω1.4.3 (b)ab666426ababU VR=+⨯==Ω1.4.3 (c)abR106510405ababU U VR=+=⨯+==Ω1.4.3 (d)ab124s su uI= I=912:23036absababKVL uuu VRI+- I==-6⨯=+1=3Ω3+61.4.4 (2)R242434311515155b bb bV V R R V V R R --I =I =-+I = I =12341243:b b b b b KCL V V V V R R R R V I =I +I +I +515-6- 5- = + +求方程中2121+9+9==50k 100k 9:=150k 100kb b b b b b b V V V V R R V V KCL V V 6-6-I =I = 6-+=b :650KI+100KI 9=01100KI=15 I=A10k 1=650k =1V10k KVL V -+--⨯习题1.1 (a ) 5427x A I =+-= (b ) 10.40.70.3x A I =-=- 20.30.20.20.1x A I =-++= (C) 40.230x ⨯I ==0.1A 6030.20.10.3x AI =+=2x 10⨯0.3+0.2⨯30I ==0.6A 1.510.30.60.9x A I =+=1.230.010.30.31A I =+=49.610.319.3A I =-=60.39.39.6AI =+=1.3114228P =-⨯=-ω发出功率211010P =⨯=ω 吸收功率 3428P =⨯=ω 吸收功率 4(110)10P =--⨯=ω 吸收功率=28=28P P ωω发吸=P P 吸发1.6612050606()12460120R R R mvV b V=== =⨯=+Ω(a) u u1.7(a )144s u V =⨯=(b) 252209s s s I A u u V = -+-⨯= = 1.812221014102110s s u V I A=⨯+==-=-121428P =-⨯=-ω 210110P =-⨯(-)=ω1.91230.450.30.450.30.15I A I A I A= = =-=1233 6.341680.1510 6.34 6.3174.40.45x y u R I R ⨯===-⨯-==ΩΩ1.10(a): 2116u u V ==(b): 2516 1.6455u V =⨯=+ (c): 251.60.16455u V =⨯=+(d): 250.160.016455u V=⨯=+1.112211128.41p pR R u u VR R R +==++222112 5.64p R u u VR R R ==++1.12B A 630.563=0.51990.5199.5CD D D R R R ⨯==+=+=ΩΩΩ12342311055235 4.23.60.650.83.6I mA I mA I mA I mA I I =⨯= = =⨯==⨯==- 10199.5 1.995=15=510 1.9950.01995AD BD s u mV u mVP =⨯=⨯=-⨯=-ω1.13 (a)RAB(b)AB1.153Ω1.5Ω1.5611.53I A -==-+1.162Ω3Ω3I311302451010110532110202121621633311633s I A I I I I A I A I A I A+==+++=-=-==--=-=-+==⨯=+=⨯=+1.17Ω821222I A-==++1.181231113333222:00I I I KVL u I R I R I R I R u += -++= --+=12316622757575I I I ==0.213 ==0.08 ==0.2931.191321232123218:14020606041012n I I I KVL I I I I I A I A I A=+=+ -++= 5-== = =1122208066014045606018108u I Vu I VP P ==== =-⨯=-ω =-⨯=-ω 电压源发出功率电流源发出功率1.201212221232+10:0.81201160.400.4116408.759.37528.125n I I IKVL I I I I I A I A I A=+= -+-= -+== = =22120:1209.3751125116:120160.75101510:10428.1251175:28.12543078.125L V P V P A P R P I R =-⨯=-ω=-⨯=-ω =-⨯⨯=-ω ==⨯=-ω1.21122212220.523133427I I V V I V I V +=----====1.22suR R212460.14020s u I AR R ===++R sI 2422240.10.10.2200.30.14020s I A R I I AR R =+==⨯=⨯=++1.2331110.250.50.5111I A=⨯=+++sI3231120.50.50.5120.250.50.75I AI A =⨯⨯=++=+=1.24 (a)1231223123:01:2130120202:21204015,10,25KCL I I I KVL I I KVL I I I A I A I A++= -+-= --== = =-(b)开关合在b 点时,求出20V 电压源单独作用时的各支路电流:2Ω''1'2'3204422442206224202222442I AI AI A=-⨯=-+//+==+//=-⨯=-+//+所以开关在b 点时,各支路电流为:123154111061625227I A I A I A=-==+==--=-1.25(b )等效变换3AAAB(3 2.5)211ab U V=+⨯=(c )等效变换abb4A(42) 1.59ab U V=+⨯=1.26 戴维宁:1220110225122110255015a ab L u V R I A=⨯===⨯=+Ω诺顿:22022505252225225255015ab ab L I A R I A ====⨯=+Ω1.28(1) 求二端网络的开路电压:10410242ab U I V ⨯=-=-=10410242ab U I V ⨯=-=-=(2)求二端网络的等效内阻(电压源短路、电流源开路)24ab R R Ω==(3)得到戴维南等效电路+1R abU abR1120.15413ab ab U I A A R R ∴==≈+1.32 (a )1231235050105205050105201007A A AA A AA I I I V V VI I I V V V V V=+-+===-+=+=- 2.3.2(a) 取电源为参考向量2()tan 6031=232R=3c C cC C U I R U I jX IR RIX X X X fc fc ••••==-====π∴π又 (b )2()tan 603=23R=32c R CL L U I jX U I RIRIX X X fL fL••••0==∴==∴= π∴π又第二章 正弦交流电课后习题 2.3.2(a) 取电源为参考向量60ο2U •RU •U •I•2()tan 6031=232R=3c C cC C U I R U I jX IR R IX X X X fc fc ••••==-====π∴π又(b )RU •2U •1U •I •60ο2()tan 603=23R=32c R CL L U I jX U I RIRIX X X fL fL••••0==∴==∴= π∴π又习题2.2111122334455,10sin(100045)45554510sin(100045)5513510sin(1000135)5513510sin(1000135)I j I i t A I AI j Ai t A I j A i t A I j A i t A•00•00•00•00=+ =∴=+==-=-=-=-+==+=--=-=-2.3(1)1••12126306308arctan =536=+=10)U V U V U U U V u t V••00•••00=∠ =∠ϕ= ∠83=ω+83(2)1210301060arctan1=45(4530)7520sin(75)I A I A I A i t A••00•0000=∠- =∠ ϕ= ∴=-+=-=ω-2.4(a) 以电流I•为参考向量•RU •10arctan =451014.145U V U V•0ϕ= ===(b )以电流I•为参考向量CRU ••22280C RC U U U U V=+∴==1122sin()sin(90)sin(45)u t i t A i t A 00=ω=ω+=ω-(c) 以电流I•为参考方向•C(200100)9010090100U V U V•00=-∠=∠=(d )以电压U•为参考方向I••RI•LI •3L I I A =∴==(e ) 以电压U•为参考方向•RI I •7.07I A ===(f )以电压U•为参考方向•I •18L CL C I I I I I I A =-∴=+=2.5 (1)3)70,2314/31.470314100219.80309.9sin()310C L L L C L I t AI A f rad s X L U I j L V Vu t V•0••0-000=ω=∠ ω=π==ω=Ω=ω=∠⨯⨯⨯10∠90=∠9=ω+90(2)3309.9sin()3101274314100L L L Lu t V U I AL X 0-=ω+90===ω⨯⨯102.6 (1)6220022011796.22 3.1402200.28796.20.280.39sin()c c C c C c C c U V U VX C U I AX I i t A•0-•0=∠ ====Ωω⨯⨯5⨯4⨯10 ====∠90=ω+90(2)0.10796.279.6c U V•000=∠-6⨯∠-90⨯=∠-1502.9 (1))22002314/)100u t V U Vf rad s i t A I A0•00•0=ω+30=∠3ω=π==ω-30=∠-3(2)22002201110060.7250L UZ I X L mH•00•0∠3===∠6=+Ω∠-3∴===ωπ⨯(3)00220102200cos 22010cos601100sin 2200sin 601905varS UI V AP UI W ==⨯=•=ϕ=⨯⨯=ϕ=ϕ=⨯=2.10(1)2u电容两端f=HZ |Z |=2000Ω 1000以1I•为参考向量=-601cos 212sin 217072110.1c c cR k K X k X c uF c X ϕ=|Z |ϕ=⨯=Ω=-|Z |ϕ=-⨯(-=Ω=∴==ωω(2)电阻两端1U •U 2R U U ••=1I•c =-30cos =2k 1X =sin =-2K =210.16R c uFc ϕ=|Z |ϕΩ|Z |ϕΩ==ω—(—)10002.12CLCZ=R+(X )10VL C R X j U -=Ω=∣Z∣I =10⨯1=102.1300000006V 1002020)3000.47sin(100020)10000.4400100200.25400900.35sin(100070)11500C 100021010020R L L L L C c C U U Vu t i R t X L U I A jX i t A X U I jX •••-••=∣Z∣I =10⨯1=10=∠+===+=ω=⨯=Ω∠===∠-70∠=-===Ωω⨯⨯∠==-0000.20500900.28sin(1000110)c A i t A =∠11∠-=+000001111111()300400500.0030.00050.003991000.33300L cZ R jX jX j j j U I AZ ••=++- =+-+ =-=∠-∴Z =300∠∠20∴===∠11∠92.14U •以为参考向量I •LI •13022101010101045C L C LC L R RR C C C R C X X I I I I I I I UI A U RVRU RI I AX X I I I A I ••••••••=∴=∴=++=== ======+=∠∴=2.15(1)601301000251030405053CZ R jX j j -=- =-⨯⨯⨯ =-Ω=∠-Ω(2)000000000001000t-30V 1030()103040304090400120120)103050535008383)R S s C s C C s u i R I AU I jX Vu t VU I Z Vu t V •••••===∠-=-=∠-⨯∠-⨯∠- =∠-=-==∠-⨯∠-=∠-=-()(3)00300103000400104000500105000cos -53=3009sin -53=-3993VarR S C C S S P U I WQ Q U I Var S UI V A P S W Q S ==⨯===-=-⨯=-==⨯=•==()()2.18U •U •222824123430.3108(12)(12)10681.5111=X 0.067=0.022C 10 1.510 4.5R L R L C C C C CC C U R I U L I L HU U U U U jU U V VU X I C F F ••••===Ωω===Ω===++ =+-∴8+-=∴= == 4.5Ω ==ω⨯⨯或1或或2.19 (a) (1)(2)10361823691243537j j Z j j j jj j j j ⨯-===Ω+Z =4-4-+ =-=∠-Ω0000010002000300040041000420100237537237483723749085323719025323729041274127 1.3337339041270.67376690U I A Z U V U V U V U V U I A j U I Aj ••••••••••∠===∠∠-=∠⨯=∠=∠⨯∠-=∠-=∠⨯∠-=∠-=∠⨯∠=∠∠===∠∠∠===∠∠(3)0cos 102cos(37)16P UI W =ϕ=⨯⨯-=(b) (1)10(4)(6)242.436102 2.443537j j Z j j j j j j j j ---===-Ω---Z =3.4+4+- =+=∠Ω(2)0000001002000300040041000420100237537237490237237483723790453237 2.490 4.81274.8127 1.2374904.81270.8376690U I A Z U V U V U V U V U I A j U I A j ••••••••••∠===∠-∠=∠-⨯3.∠=∠-=∠-⨯=∠-=∠-⨯2∠=∠=∠-⨯∠-=∠-∠-===∠--4∠-∠-===∠--∠-(3)0cos 102cos(37)16P UI W=ϕ=⨯⨯=2.2001221201115545(55)105-5)10100==10AZ 10A 10AZ=10+1045Z 141.4Z j j j Z j j U I j U I V V=-=-Ω-⨯10==Ω+∴=||∴=Ω∴=||==(读数为读数为2.23426014411111010101()11451()1222101011 1.50.5C L X C j j Z jj j X L Z j Z j-===Ωω⨯⨯⨯--===-=-+--=ω=⨯=Ω=++=-2.240000000100.5229010110.5110.5 1.1(10.5)22+2(10.5)2211+2212123 3.61c c c c R c R R L R L c U I A j U I AR I I I j A A U I R j j VU I j j j j j VU U U U j j j V P UI •••••••••••••••∠===∠90-∠-∠===∠0=+=∠90+∠0=+ =∠26.6==+⨯= ==+=-=- =++=+-++=+=∠56.3 =00os 3.61 1.1cos(W ϕ=⨯⨯56.3 -26.6)=3.452.29110012122 1.21cos cos =0.5112206024.5(tan -tan 1.21(1.7320.456)=10222 3.14502201 4.54220380 4.541727.3sin 177.3-=-VarR P KP UI UI PC U K uFP K I A U S UI V A S =ϕϕ==⨯∴ϕ=ϕ==ϕϕω- =⨯⨯⨯=====⨯=•ϕ=ϕ=⨯0.821408 ,,)()2.30161212.5617.3712.671131.58250100102206.9131.85=25.15220==8.75A25.15cos=220cosRLRLCccRL CRL CRL cZ R j L jUIZZ jj cUI AZZ ZZ ZZ ZUIZP UI-=+ω=+=∠46.3Ω===Ω∣∣==-⨯=-Ωω⨯π⨯⨯⨯===∣∣//Z==∠14.4Ω+==ϕ⨯8.75⨯14.4总总=1864.5wcos=220sin=478.73wS=UI=220.75=1925V Acos0.9686Q UI=ϕ⨯8.75⨯14.4⨯8•ϕ=2.312202.22201002.2arccos0.837100378060PP LPPU VI I AUIZ j====|Z|===Ωϕ===∠=+ Ω2.32(1)861037220220221022PPPL PZ jU VUI AI I A=+=∠ Ω======|Z|==(2)220220220221038L P L P P L P U V U U V U I A I A= =====|Z |==(3)380380380381066L P L P P L P U V U U V U I A I A= =====|Z |==(4)220,380,Y 220N L L U V U V U V == =∆ 行,形2.33C0000000000038022022002200220022002201022002201002200220100220220220L P A B C A A B B C C N A B B U V U V U V U V U V U I AR U I AR U I A R I I I I •••••••••••••= =∣Z∣=10Ω=∠ =∠-12 =∠12 ∠===∠∠-12===∠-3∠-9∠12===∠3∠9=++=∠+∠-3+∠3设002260.1022104840A A P I R W=∠==⨯=2.34000312238380,2202205.838cos cos35.63054sin sin35.6=2290Var 3817cos 0.8L P P L P L L L L L L Z j U V U V U I I A Z P I W I S I V A =+=∠35.6======∣∣∴=ϕ==ϕ=ϕ==•ϕ=2.35380,1122L A B C U V R R R ==Ω==Ω,(1)00000000022222222002200220022002201122001002222010010010022111088A B C A A A B B B N A B B A A A B C C U V U V U V U I AR U I AR I I I I A P I R I R I R •••••••••••=∠ =∠-12 =∠12 ∠∴===∠∠12 ===∠12=++=∠+∠-12+∠12=∠=++=⨯+⨯22+10⨯22=设00W(2)0000000000017.3022017.3022017.30017.3017.30300AB AB B CA CAC B AB C CA A AB CA U I A R U I A R I I A I I AI I I A•••••••••••∠3===∠3∠15===∠15=-=-=∠-15===-=∠3-∠15=∠(3)0000008.6022228.60N A BC B C B C C I I U I I AR R I A••••••==⨯∠-9=-===∠-9++=∠9,2.3605.57760cos ==1018.3 5.59700320.7320.737256.6192.4L L L L I A P W U VS I V A Z = = ϕ0.8==⨯=•∣Z∣===Ω=∠=+ Ω2.3732.919380380L P P P L P I AI AU I V U U V=====|Z |====2.380000000000380=2200220022010100000220039.3039.3L A A A AB ABA A A A U V U V U I A R U I A R I A I I I AI A••'•'•'•''''•'''•••=∠∠∴===∠===∠3=⨯∠-3=∴=+=∠+=∠∴=设第三章电路的暂态分析3.1 (1)Uc22212111120(0)1000(0)(0)100(0)100100100(0) 1.0199(0)(0)1001000(0)0(0) 1.01c c c R R R R c t u U V t u u U V u V i A R u U u V u i A R i i i A--+-+++++++= == = === =====-=-=∴===-=-(2)+-Uci cu12121112222100()()1199()()1()()99()0()()99R R c c R U i i AR R u i R V u i R V i Au u V∞=∞===++∞=∞=∞=∞=∞=∞=∞=3.2 (1)换路前:0t-=434342341234123442123(0) 1.52(0) 1.51 1.5L c L R R R K R K R R R K i uA Ku i R uA K V --=+=Ω=Ω=+=Ω====⨯= (2)换路后0t +=(0)(0) 1.5(0)(0) 1.5L L c c i i mA u u V+-+-====412146 1.5(0) 2.2511(0)0(0)(0)(0) 2.25 1.50.75(0) 1.5 1.5 1.510c L L L i mAK Ki A i i i mA mA mA u i R mA K V++++++-==+==-=-==-=-⨯Ω=(2)t =∝R 4121236232c L L c L u Vi mAKi i mA i i u V(∝)=6⨯=(∝)==(∝)=(∝)=(∝)=0A (∝)=0A (∝)=03.3(1)求()c u +0 0(0)00(0)(0)0c c c t u V t u u V --+-+= ,= = ==(2)求()c u ∞()20c t u U V =∞,∞==(3)求τ2121212121661:112)22060.12R R K C C Z Z j cZ Z Z j c j c C C C C uF RC K s-==Ω//==ω=//==ωω(2∴=//==∴τ==Ω⨯20⨯10=(4)8.330.12()20(020)2020t t c u t ee V --=+-=-s/3.4t -=13K ΩR 60V(0)10660(0)(0)60c c c u m k V u u V-+-=⨯===0t +=13K ΩR c u36=5366060(0)125C K K R K K Ki mAR K +⨯=Ω+--===-Ω总总t =∝10mAR()0()0C Ci u ∝=∝=1R 3K ΩR[]20622100105521010()()(0)()060060()tc c c c t t R K RC K s u t u u u e ee V ----+--=Ωτ==Ω⨯⨯=⎡⎤∴=∝+-∝⎣⎦ =+-=[]210010()012012()t t c i t mA ee mA ---=+--=-60cu V/t s/t s/ci mA/-123.5(1)求(0),()c ci u++3131210(0)1005020(0)(0)505010050(0) 6.2544cc ccRt u U VR Rt u u VUi AR R--+-++= ,=⨯=⨯=+= ==--===++(2)求()()c ci u∞,∞,()0,()100c ct i A u U V=∞∞=∞==(3)求τ565612651021051021088210()0(6.250) 6.25()100(50100)10050t t c t t c R R R RC s i t ee A u t ee V -----⨯⨯--⨯⨯=+=Ωτ==⨯0.25=⨯∴=+-==+-=-3.60t -=+-2R 31i 2i c u +-1U11124(0)10544c R u u VR R -=⨯=⨯=++0t +=(0)(0)5c c u u V +-==+-2R 3R 1R cuci 2i U2212232250cc i i i U iR i R i R i R =+=++-= (0)0.625(0)0.3125c i mA i mA ++∴= =t =∝R 2R120312602244100100.4R R R R K K K R R R C K s-=+=Ω+Ω=Ω+τ==Ω⨯⨯=22122120.40.50.52.5 2.51()5 2.52()05()0.62544() 2.5(5 2.5)2.5 2.5()0(0.6250)()0.625(0.31250.625)c c t c t t c t t R u U VR R i U i mAR R K K u t e e Vi t e V e mAi t e -----∝=⨯=⨯=+∝=∝===+Ω+Ω∴=+- =+ =+-- =-0.625=+- 2.50.6250.3125t e mA- =-3.7650.250.10(0)0()2050100.2()20(020)2020(0.1)0.1(0.1)20207.870.1(0.1)7.87c c tt c c c t u t u U V RC K s u t ee V t s t u e V t u V++----⨯--++= = =∝ ∝==τ==Ω⨯4⨯=∴=+-=- ≤= =-== =U(0.1)(0.1)207.8712.13R c u U u V ++=-=-=()0R t u =∝ ∝=0600.11010.11010.10.1()0252254100.1()0(12.130)12.13(0.1)()20()()12.13(0.1)()20(7.8720)R t t R c t R c t c t u RR K R C K su t e e V t t u t U Vu t U u t e V t u t eV----+-+-=∝ ∝===Ωτ==Ω⨯⨯==+-= ≥=∝ ===-= ≥=+-3.836000.2100(0.2)0.0100.2,11010100.01(0.2)(0.2)100.2,(0.2)(0.2)10(0.2)(0.2)(0.2)01010,()0()0(100)10,0.20,(0)(0)0c i c i i c t t c i t RC s u u V t u u Vu u u V t u V u t ee V t t u u V ----++-+++-------=τ==⨯⨯⨯======∴=-=-=-=∞∞=∴=+--=-≥===001000.0100,(0)(0)0(0)(0)10,()0()0(100)10,00.2c i i t t t u u V u u V t u V u t ee V t +++++-======∞∞=∴=+-=≤≤u V/t s/3.9求(0)c u + ,(0),(0)BA V V ++0(6)0,(0)515250,(0)(0)1:10(0)125(0)660(0)0.31(0)6100.31 2.9(0)(0)1 1.9c c c B A B t u Vt u u VKVL i i i mA V V V V V-+++-++++++--==⨯=+===⨯++⨯--= =∴=-⨯= =-=求(),(),()cB A u V V ∞∞∞ 67127 2.3104.375106(6)()50.35 1.510525()6100.33()()()3 1.5 1.55(1025) 4.3754.37510010 4.37510() 1.5(1 1.5) 1.50.5() 1.5(1.9 1.5c B A B c t t c A u VV V V V u V R K RC s u t ee VV t -----⨯⨯--∞=⨯=⨯=++∞=-⨯=∞=∞-∞=-==//+=Ωτ==⨯⨯=⨯∴=+-=- =+-66662.310 2.3102.310 2.310) 1.50.4()3(2.93)30.1t t t t B e e V V t e e V-⨯-⨯-⨯-⨯=+ =+-=-3.10U L求(0)L i +31312331210.531040,(0)0.25150,(0)(0)0.24()0.3257.5()0.16215 3.7518.75100.5218.75()0.16(0.20.16)0.160.04L L L L t L U t i AR R t i i A U t i AR R R ii A R R R R L ms R i t ee ---++---⨯====++====∞,∞===+//+ ∞===+//=+=Ωτ===∴ =+-=+875t A3.11 (1)121212121212121212121)0.010.020.03(0),(0)0,(0)00,(0)(0)0(0)=(0)=0(),()6,()()2210.033,0.013()2(0L L L Z Z Z j L j L j L L L L L H i i t i A t i i A L i i A i i U t i i AR R L R R R sR i t ++--++-++=+=ω+ω=ω(+∴=+=+======∞∞=∞∞=∞===++=+=Ωτ===∴=+求断开:求1000.0110012)22()22t t t ee Ai t e A----=- =-(2)1010011112000.00512202020222500.022:()2()()26()320.010.0052()3(23)3:()2()()2()00.020.021()0(20)2tt tt L i t A i t i t A U i A R L s R i t e e AL i t A i t i t Ai A L s R i t ee A-+----+---= ==∞===τ====+-=- = ==∞=τ====+-=3.12100.1220(0),(0)101201(0)(0)10220(),()110110.20.111()110(10110)110100()30,0.02L c L L t t U i i AR R R i i A U i t i A R R L s R R i t e e Ai t A t s+-+---===++++==∞=∞,∞===++τ===++∴=+-=- ==求求3.131(40')400'1000,(0) 2.5400,(0)(0) 2.5(0) 2.5'(0),'80,()0,()0140'40'5%:()0(2.50) 2.5ln 0.05'40600.0360't R tR t i A t i i A u R V u V R t i A u VL sR R t i t ee R R --++-++--++=======- ⎢⎢≤200≤Ω=∞∞=∞=τ==++=+-=≥--=Ω∴Ω≤≤80Ω求对应+00,(0)0,0(0)06()1225014.425014.40,0.057625014.4250,0.0288500L L L L t t i A t i A t i mAL R R R s R s--+==>===∞∞==τ==+=τ===Ωτ==设时,开关闭合时,时,0.05760.05760.02880.02880,() 2.4(0 2.4) 2.4 2.4250,()2(012)12126()6,0.0288ln 0.0212:02500.02t t L t t L L R i t e e R i t e ei t mA t ms R ms----==+-=-==+-=-==-=∴~Ω~延时:0.0166第四章常用半导体器件4.2 (1)∴⨯∴去掉得优先导通则V 截止,,10,0,9109,19A B DA DB A F B D D U V U V D V D ====+ (2)∴⨯∴∴ ∴∴ 去掉得优先导通则V 导通,,6, 5.8,96 5.4,191196 5.81195.596 5.59 5.8 5.590.410.21110.62A B DA DB A F B A F B F FF F FF A B A B D D U V U V D V D V V V V V V V VV VI mA I mAI I I mA ====+--+=--+==--=====+= (3)∴ ∴∴∴ 去掉得 优先导通,,5,5,551194.735 4.730.270.2710.54A B DA DB A B FFFF A B A B D D U V U V D D V V V V VI mA I mAI I I mA==--+==-====+=4.4LR->反向击穿241228,LZ RL ZLZ R U U U VR R U V ====+ RL-IU∴>80.08100:0.160.080.0880I ZR L Z R R L Z ZmU U I AR KCL I I I A mA I I -====-=-== 4.5LR -IU > ∴>2反向击穿=2100L IZ IL Z I R U U U R R U V U V=+L R-IU ∴∴∴⨯≤≤⨯∴⨯≤≤⨯∴≤≤3333:1010050050020500510301020510301050022.535R Z R L I Z ZZ LI Z I Z Z I I KCL I I I U U U I R R U I U I I U V U V----=+-=+-=+-=-4.6 (1)∆β∆∆β∆11122220500.80.410500.80.6C B C B I I I I ===-===-(2)ββ12184.50.43847.50.8--====第五章 基本放大电路5.2输出端等效电路-2U 0Ω∴∞ ∴Ω0'000'00'001,11111.1100L L LL R K U V R U U r R U r R U Vr ===+=+=== 5.4 (1)β125024026CCB BC B CE CC C C V I uAR I I mA U V I R V ?====-= (2)∴ ∴β012432640CCC CE C BV mAR I mA U V I I ======(3)1206C BE C CE U U U U V=?==5.6R-•+••(1)•••••ββββ⨯⨯011(1)(1)10020.98(1.41012)b cc u be Ei b be b E U I R R A r R U I r I R --===++++-==-+(2)()()•••••ββββ⨯⨯02211(1)(1)10120.9(1.41012)bEEu be Ei b be b E IR RU A r R U I r I R ++===++++==+(3)•••••∠0⨯∠0∠180 ω⨯∠0∠0ω 000011001000220210.9810.981.39sin(180)0.9910.991.4sin i u i u i U U A U u t mVU A U u t mV===-==+==== 5.7ΩΩβ⨯Ωβ⨯∴Ωβ∴⨯01200,20lg 20046512100,20lg10040510.0520122400052626200(1)200(120)74611007463.7320121 3.738.2u Li m C B CC B B be E Cu beu be C CE CC C C A dBmA U R K A dBI uA I I mAB V R K I mAr I RA r A r R K U V I R ==========?==++=++==-=-=-==-=-=7V 5.8分压偏置共射极放大电路(1)⨯⨯β212201236020301.52()12 1.5(32) 4.51.52560B B CC B B B BE C E E CE CC C C E CB R U V VR R V V I I mAR U V I R R V I I uA ===++--?===-+=-+==== (2)βΩ//⨯ΩΩ'026300(160) 1.361.5366088.21.361.363Lu bebe u i be R A r r K A r r K r R C K =-=++==-=-====5.9 (1)β⨯β⨯⨯⨯1295.2(1)755115095.2 4.7612(150)95.217.14CCB B EC B CE CC E E V I uAR R I I mA U V I R V===+++=====-+= (2)β⨯//⨯//ββΩ//β//⨯//1Ω//Ωβ''''0(1)51(11)0.98472.8451(11)(1)(1) 4.8626200(150)472.844.86(1)75472.84(150)(1)19.3472.84757510.741150Lu be LE B be i B be L be S R A r R I I mA r r R r R K r R r +===+++=+==++=轾=++犏臌轾=++=犏臌++===++第六章 集成运算放大器及其应用6.2(1)∴ ∴ ∴0000:i f f if L i LL ii i u u u u u u u u u u KCL R Ru u R R u R A uf u R+--++-==========(2)∴ ∴∴∴∴A 11''1'10''00100:(1)(1)i ii i f E E Ef F F I E EF E i EFc cc EE F EEc EFc F i Ei i u u u u u u i R R KCL i i u R i i R R u R i R R R R u i R u i R i i i i i R u R i R u R Ruf Au R R +-+-+=====-==-===-==-=-»=+=-+==+(3)00001i ii ii i u u u u u u u u u u u A uf u +-++---=========(4)∴∴∴∴11''033'''003013031000:i i i f f i fi ii i u u u u u u u i R R u u u i R R u u u u u i R KCL i i u u R R u R A uf u R +-++----+=====-==-==-====-==-==- 6.3(1)∴±±⨯±55520lg 100101313100.1310opp dm u A u A u U u V mVA -======(2)±⨯±5max 13100.0652dm idu I mA r -===6.4∴0201222102212222122112211111f ix A x A F A A x A F A A A x A A F A A F A F A F =++===++++6.5∴∴∴~Ω Ω∴~0101110066:6(1):01010:612FFFF i i u Vu u V u u u KCL R R R R u u u R R R K R K u V+-+-+----=====-==+=+=6.6(a) ∴改变对无影响00,0i iR iL u u u u u u u i i R R ui RR i +--+--======= (b) 改变对无影响00,0i iR L u u u i u i i RR i -+-=====6.7改变对无影响00000L i R L i R iiL u i R u u u i i u i R u i RRu i R R i +-+-=+==-===6.8作用时12,i i u u'0u 4u i u∴∴⨯'12012'12012000123()1()222i i F i i F i i u u u u u R R R u u u R VR R +-+-====++==-+=-+=-作用时34,i i u u''04R||∴∴∴34343434343434''012''0''034'''0000:()2:234737 5.52i i i i i i Fi i i i u u u u KCL R R R R u u u u u R R R R u u u KCL R R R u u u u u u u V u u u V +-+++---+-==--+=+=+=+-====+=+==+=-+=6.9。
电子测量技术基础课后习题答案 (第二版)

电子测量技术基础习题一1.1 解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4 叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电子测量课后习题答案ppt课件

扫描扩展为“10”,荧光屏x方向的可用长度为10 div,
如果要观察一个周期的波形,试计算该示波器能观察
到的正弦波的上限频率。
时基因数: 20 ns/div~0.5 s/div
10div
扫描扩展为“10”,实际的时基因数2 ns/div~0.05 s/div
t Dt x 2 ns/div ~ 0.05 s/div10 div 20 ns ~ 0.5 s
U (R) 29
由于题意未说明,故按正态分布来确定包含 因子,即查表1.4确定。
k99=2.576
电阻器的标准不确定度为:
u(x) U (x) 29 12
k p 2.576 属于B类标准不确定度的评定。
1.7 测量某电路的电流I=22.5mA,电压U=12.6V, I和U的标准不确定度分别为u(I)=0.5 mA, u(U)=0.3V,求所耗功率及其合成标准不确定度。 ( I和U互不相关) 解: 功率测量的数学模型为:
20
U x U0 1020 0.775 1020 7.75V
Px
U
2 x
Rx
7.752 500
0.12W
第四章作业评讲
在所示电路中,当直流单电桥平衡时,已知R2=100 ,其 相对标准不确定度urel(R2)=0.5%; R3=1000 ,其相对标 准不确定度urel(R3)=0.5% ; R4=4781 ,其相对标准不确 定度urel(R4)=0.5% ;问Rx的数值及其相对合成标准不确定 度ucrel(Rx)?
1.5 对某量重复测量8次,测得数据分别为: 802.40,802.50,802.38,802.48, 802.42,802.46,802.45,802.43
试分别用贝塞尔法和极差法确定测量的A类标 准不确定度。
(整理)电工与电子技术课后习题答案
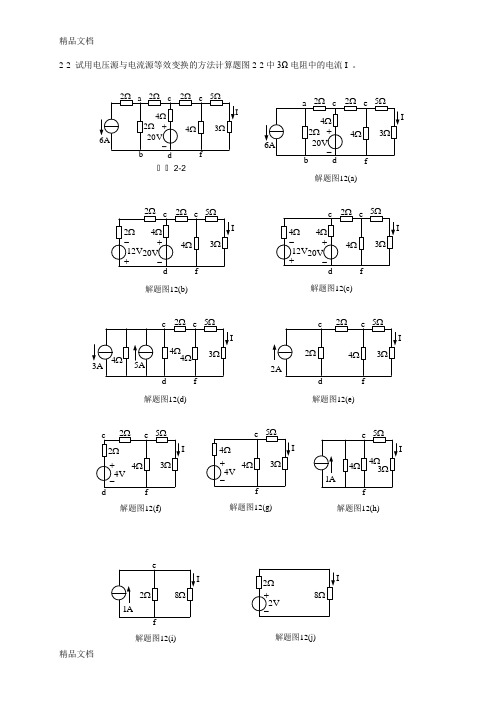
(3)根据电路的结构,应按照a-b、c-d、e-f的顺序化简,比较合理。
2-3计算题图2-3中1Ω电阻上的电压Uab。
解:该题采用两种电源的等效变换法解题比较简便。按照解题图13的顺序化简,将题图2-3所示的电路最后化简为解题图13(e)所示的电路,根据电阻串联电路分压公式计算电压Uab为
解: 已知 ,由有功功率知:
题图3-19
3-20有一日光灯电路如题图3-20报示,已知灯管功率为30W,工作时呈电阻特性;镇流器功率为4W,与灯管串接于电源电压为220V,频率f=50Hz的电路中,测得灯管电压为110V。试求:
(1)灯管的等效电阻RL、镇流器的电阻R和电感L;
(2)电路的总功率因素;
解:
为感性支路
相位超前 设
总功率因素:
3-26已知一RC高通滤波电路中, ,C=1000 pF,试求电路的下限截止频率fL及f=2fL时,传递函数的幅值 和相位角 。
解: , ,由 高通滤波电路的特征频率有:下限截止频率为:
当 时
3-27已知一RC低通滤波电路中, , ,试求其通频带的宽度 。
解: 低通滤波的通带宽度为
于是
2-15在题图2-15中,已知I =1 A,应用戴维宁定理求电阻R。
解:应用戴维宁定理,题图2-15所示的电路可化为解题图24(c)所示的等效电路。因此
根据题目的要求,可将上式改写成
依据解题图24(a)所示的电路,可求得等效电源的电动势E为
依据解题图24(b)所示的电路,可求得等效电源的内阻R0为
于是
2-10应用叠加定理计算题图2-10所示电路中的电流I。
解:根据叠加定理知
依据解题图19(a),应用分流公式可得
电子测量技术课后习题答案1-8章

《电子测量技术》------课后习题第一章1.1解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等;(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电子测量 技术 习题答案

习题1 测量与计量两者的区别联系测量与计量是缺一不可的。
计量是测量的一种特殊形式,是测量工作开展的客观需要,而测量是计量联系生产实际的重要途径,没有测量就没有计量,没有计量就会使测量数据的准确性、可靠性得不到保证,测量就会失去价值。
因此,测量与计量是相辅相成的。
2 电子测量技术的优点〔1〕测量频率范围宽〔2〕测试动态范围广〔3〕测量的准确度高〔4〕测量速度快〔5〕易于实现遥测和长期不间断的测量〔6〕易于实现测量过程的自动化和测量仪器的智能化3 有一个100V 的被测电压,假设用0.5级、量程为0-300V 和1.0级、量程为0-100V 的两只电压表测量,问哪只电压表测得更准些?为什么?要判断哪块电压表测得更准确,即判断哪块表的测量准确度更高。
〔1〕对量程为0-300V 、±0.5级电压表,根据公式有%100%%1001⨯•≤⨯∆=xs x x xm x γ %5.1%1001005.0300=⨯⨯=〔2〕对量程为0-100V 、±1.0级电压表,同样根据公式有%100%%1002⨯•≤⨯∆=xs x x xm x γ %0.1%100100.1100=⨯⨯=从计算结果可以看出,用量程为0-100V 、±1.0级电压表测量所产生的示值相对误差小,所以选用量程为0-100V 、±1.0级电压表测量更准确。
4 准确度为0.5级、量程为0-100V 的电压表,其最大允许的绝对误差为多少?V s x x m 5.0%5.0100%=⨯=•≤∆5 测量上限为500V 的电压表,在示值450V 处的实际值为445V ,求该示值的: (1) 绝对误差〔2〕相对误差〔3〕引用误差〔4〕修正值〔1〕绝对误差V V V A x x 5450445-=-=-=∆ 〔2〕相对误差%12.1%1004455%100-=⨯-=⨯∆=x x x γ 〔3〕引用误差%00.1%1005005%100-=⨯-=⨯∆=m m x x γ 〔4〕修正值V x c 5=∆-=6 对某电阻进行等精度测量10次,数据如下〔单位k Ω〕:0.992、0.993、 0.992、 0.991、 0.993、 0.994、 0.997、 0.994、 0.991 、0.998。
电子测量技术基础课后习题答案

习题一1.1 解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4 叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
电子测量技术基础课后习题答案

习题一1.1 解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2 叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3 解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
如利用惠斯登电桥测量电阻。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4 叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等:(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:由 ,
当原边电流在0-30A变化时,副边电流变化范围为0-30mA,
故
3-7影响电涡流传感器等效阻抗的因数有哪些?根据这些影响因数,推测电涡流传感器能测量哪些物理量?
L1、L2与金属导体的磁导率有关,可用于测量应力、硬度。
3-8压电传感器的等效电路是什么?为什么用压电传感器不能测量静态力?
解:压电元器件电极表面聚集电荷时,它又相当于一个以压电材料为电介质的电容器,其电容量为
式中,A——压电片的面积;
——压电材料相对介电常数;
——真空介电常数;
h——压电元器件厚度;
(2)Pt热电阻;测温范围符合要求,并且对响应速度要求不高
(3)用热电偶;测温范围符合要求,并且响应时间适应温度波动周期为100ms到200ms的情况
3-3热电偶测温为什么一定做冷端温度补偿?冷端补偿的方法有哪几种?
解:热电偶输出的电动势是两结点温度差的函数。T为被测端温度, 为参考端温度,热电偶特性分度表中只给出了 为0℃时热电偶的静态特性,但在实际中做到这一点很困难,于是产生了热电偶冷端补偿问题。目前常用的冷端温度补偿法包括:
解:
,放大倍数应为15倍。
可分辨的最小温度为
3-5霍尔电流传感器有直测式和磁平衡式两种,为什么说后者的测量精度更高?
解:霍尔直测式电流传感器按照安培环路定理,只要有电流IC流过导线,导线周围会产生磁场,磁场的大小与流过的电流IC成正比,由电流IC产生的磁场可以通过软磁材料来聚磁产生磁通=BS,那么加有激励电流的霍尔片会产生霍尔电压UH。通过放大检测获得UH,已知kH、H=B/、磁芯面积S、磁路长度L以及匝数N,由 ,可获得磁场B的大小,由安培环路定律H·L=N·IC,可直接计算出被测电流IC。不过由于kH与温度有关,难以实现高精度的测量;而磁平衡式传感器利用磁平衡原理,NPIP=ISNS,因此只要测得IS便可计算出被测电流IP,没有依赖性,精度更高。
第3章常用传感器及其调理电路
3-1从使用材料、测温范围、线性度、响应时间几个方面比较,Pt100、K型热电偶、热敏电阻有什么不同?
解:
Pt100
K型热电偶
热敏电阻
使用材料
铂
镍铬镍硅(镍铝)
半导体材料
测温范围
200℃~+850℃
-200℃~+1300℃
-100~+300℃
线性度
线性度较好
线性度好
非线性大
——压电片的介电常数;
——压电元器件的等效电容。
当压电元器件受外力作用时,两表面产生等量的正、负电荷Q,压电元器件的开路电压(认为其负载电阻为无穷大)Ua为
这样,可以把压电元器件等效为一个电压源U和一个电容器Ca串联的等效电路。当压电传感器接入测量仪器或测量电路后,必须考虑连接电缆的寄生等效电容 ,后续测量电路的输入电容Ci以及后续电路(如放大器)的输入电阻 。所以,实际压电传感器在测量系统中的等效电路如下图3.1所示。
3-10使用电场测量探头应注意什么?为什么?
解:当进行电场强度测量时,检测者必须离探头足够远,以避免使探头处的电场有明显的畸变。探头的尺寸应使得引入探头进行测量时,产生电场的边界面(带电或接地表面)上的电荷分布没有明显的畸变。
3-11磁阻传感器的基本原理是什么?
解:置于磁场中的载流金属导体或半导体材料,其电阻值随磁场变化的现象,称为磁致电阻变化效应,简称为磁阻效应。利用磁阻效应制成的元器件称为磁敏电阻,在磁场中,电流的流动路径会因磁场的作用而加长,使得材料的电阻率增加。
响应时间
10s~180s级别
20ms~400ms级别
ms级别
3-2在下列几种测温场合,应该选用哪种温度传感器?为什么?
(1)电气设备的过载保护或热保护电路;
(2)温度范围为100~800℃,温度变化缓慢;
(3)温度范围为100~800℃,温度波动周期在范围满足电力设备过载时温度范围,并且热敏电阻对温度变化响应快,适合电气设备过载保护,以减少经济措施
解:传感器线圈受电涡流影响时的等效阻抗 的函数关系式为
由此可见,等效阻抗与电阻率、磁导率以及几何形状有关,还与线圈的几何数、线圈中激磁电流频率f有关,同时还与线圈与导体间的距离x有关。
由此可知
M与距离x相关,可用于测量位移、振幅,厚度等。
R1、R2与传感线圈、金属导体的电导率有关,且电导率是温度函数,可用于测量表面温度、材质判别等。
图3.1压电传感器的等效电路
由于外力作用而在压电材料上产生的电荷只有在无泄漏的情况下才能保存,即需要测量回路具有无限大的输入阻抗,这实际上是不可能的,因此压电式传感器不能用于静态测量。压电材料在交变力的作用下,电荷可以不断补充,以供给测量回路一定的电流,故适用于动态测量。
3-9分析为什么压电传感器的调理电路不能用一般的电压放大器,而要用电荷放大器?
0℃恒温法;
冷端温度实时测量计算修正法;
补偿导线法;
自动补偿法。
3-4采用Pt100的测温调理电路如图3-5所示,设Pt100的静态特性为:Rt=R0(1+At),A=0.0039/℃,三运放构成的仪表放大电路输出送0~3V的10位ADC,恒流源电流I0= 1mA,如测温电路的测温范围为0~512℃,放大电路的放大倍数应为多少?可分辨的最小温度是多少度?
解:由于压电材料等效电路中Ca的存在,压电传感器的内阻抗很高且输出的信号非常微弱,因此对调理电路的要求是前级输入端要防止电荷迅速泄漏,减小测量误差。前置放大器的作用是将压电式传感器的高输出阻抗经放大器变换为低阻抗输出,并将微弱的信号进行放大。
由图3.1压电传感器的等效电路,电压放大器输出电压与电容C= Ca + Ci +Cc密切相关,虽然Ca和Ci都很小,但Cc会随连接电缆的长度与形状而变化,因此放大器的输出电压与连接传感器与前置放大器的电缆长度有关。从而使所配接的压电式传感器的灵敏度将随电缆分布电容及传感器自身电容的变化而变化,而且电缆的更换将引起重新标定的麻烦,所以很少使用,基本都采用便于远距离测量的电荷放大器。
