管理运筹学(第四版)第十一章习题答案
《管理运筹学》第四版课后习题答案

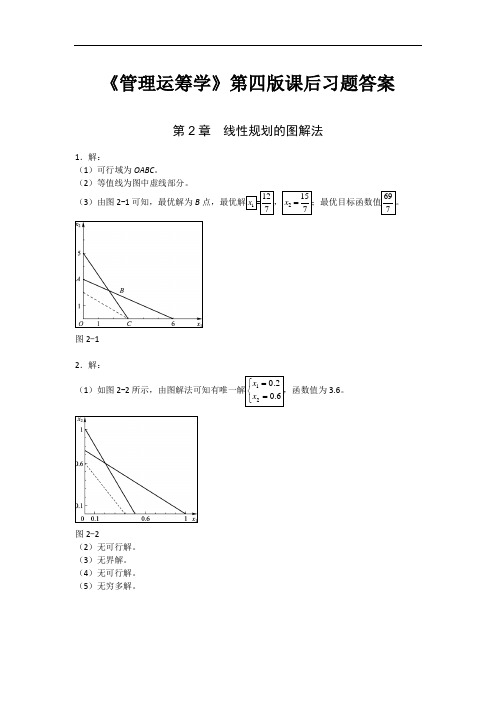
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
? (3)由图2-1可知,最优解为B 点,最优解 x =12 , x ??15 7 2 7 图2-1;最优目标函数值 69 。
72.解:(1)如图2-2所示,由图解法可知有唯一解?x 1 ??0.2 ,函数值为3.6。
?x 2 图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
? (5)无穷多解。
?x ? (6)有唯一解 ??1 ? 203 ,函数值为 92 。
8 3x ? ??2 3 3.解:(1)标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??303x 1 ??2x 2 ??s 2 ??132x 1 ??2x 2 ??s 3 ??9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2??10 7x 1 ??6x 2??4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??702x 1????5x 2????5x 2??????503x 1????2x 2????2x 2??????s 2 ??30x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4.解:标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1??95x 1 ??2x 2 ??s 2 ??8x 1, x 2 , s 1, s 2 ≥ 0≤ 松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》第四版课后习题
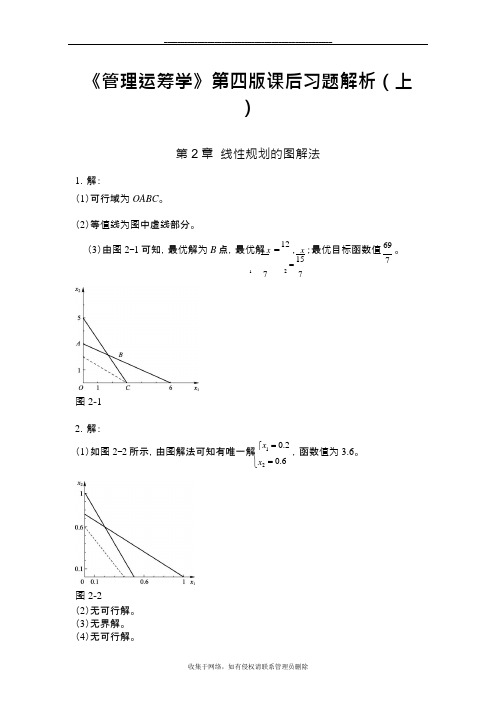
《管理运筹学》第四版课后习题答案第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解1x=127,2157x=;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6xx=⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解3.解:(1)标准形式(2)标准形式(3)标准形式4.解: 标准形式松弛变量(0,0) 最优解为 ,x 2=3/2。
5.解:标准形式剩余变量(0, 0, 13) 最优解为 x 1=1,x2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
(2(3 (4(5)最优解为 x 1=8,x 2(61,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:即作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 272082404200=⨯+⨯=最大z答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2. +2y , 线性约束条件: ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≥+≥+≥+0027315212y x y x y x y x 作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E.但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
答:应截第一种钢板4张,第二种钢板8张,能得所需三种规格的钢板,且使所用钢板的面积最小.9.解:设用甲种规格原料x 张,乙种规格原料y 张,所用原料的总面积是zm 2,目标函数z=3x +2y ⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+003222y x y x y x 作出可行域.作一组平等直线3x +2y=t . 解⎩⎨⎧=+=+3222y x y x 得)3/1,3/4(CC 不是整点,C 不是最优解.在可行域内的整点中,点B(1,1)使z 取得最小值. z 最小=3×1+2×1=5,答:用甲种规格的原料1张,乙种原料的原料1张,可使所用原料的总面积最小为5m 2.10.解:设租用大卡车x 辆,农用车y 辆,最低运费为z 元.目标函数为z=960x +360y .线性约束条件是⎪⎩⎪⎨⎧≥+≤≤≤≤1005.28200100y x y x 作出可行域,并作直线960x +360y=0. 即8x +3y=0,向上平移由⎩⎨⎧=+=1005.2810y x x 得最佳点为()10,8作直线960x +360y=0. 即8x +3y=0,向上平移至过点B(10,8)时,z=960x +360y 取到最小值.z 最小=960×10+360×8=12480答:大卡车租10辆,农用车租8辆时运费最低,最低运费为12480元.11.解:设圆桌和衣柜的生产件数分别为x 、y ,所获利润为z ,则z=6x +10y .⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+005628.008.07209.018.0y x y x y x 即⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+001400728002y x y x y x 作出可行域.平移6x +10y=0 ,如图⎩⎨⎧=+=+1400728002y x y x 得⎩⎨⎧==100350y x 即C(350,100).当直线6x +10y=0即3x +5y=0平移到经过点C(350,100)时,z=6x +10y 最大12.解:模型12max 500400z x x =+ 1211121223003540224401.2 1.5300,0x x x x x x x x ++≤≤≤≤≥(1)1150x =,270x =,即目标函数最优值是103 000。
管理运筹学第四课后习题答案

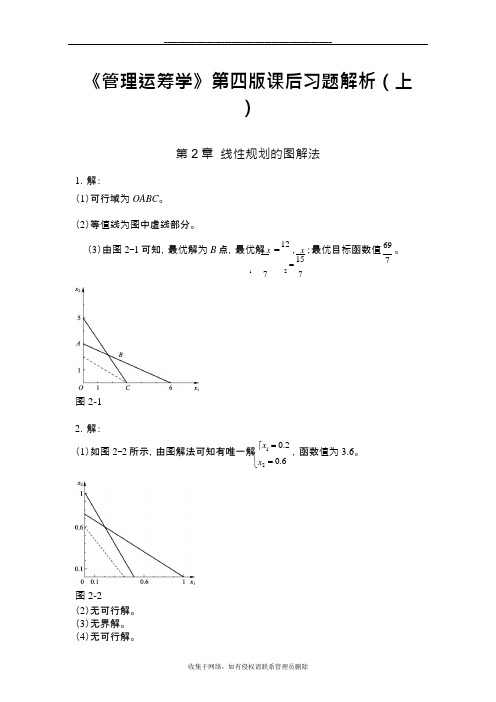
《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x = 12 , x 15 1 7 2 7图2-1;最优目标函数值 69 。
72.解:(1)如图2-2所示,由图解法可知有唯一解 x 1 ,函数值为。
x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
x (6)有唯一解 1203 ,函数值为 92 。
83 x 2 33.解:(1)标准形式max f 3x 1 2x 2 0s 10s 2 0s 3 9x 1 2x 2 s 1 30 3x 1 2x 2 s 2 132x 1 2x 2 s 3 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f 4x 1 6x 2 0s 10s 2 3x 1 x 2s 1 6x 1 2x 2s 2 107x 1 6x 2 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f x 12x 22x 20s10s 23x 15x 25x2s1 702x 15x 25x2503x 12x 22x 2s 2 30 x 1, x 2, x 2, s 1, s 2 ≥ 04.解:标准形式max z 10x 1 5x 2 0s 10s 23x1 4x2s915x1 2x2 s2 8 x, x2 , s1, s2 ≥01≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
5.解:标准形式min f 11x 1 8x 2 0s 1 0s 2 0s 310x 12x 2 s 1 20 3x 13x 2 s 2 18 4x 1 9x 2 s 3 36x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
最新《运筹学》第四版课后习题答案
作出可行域.
x2y20
2xy16
得Q(4,8)
z最大200424082720
答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.
8.解:
设需截第一种钢板x张,第二种钢板y张,所用钢板面积zm2. 目标函数z=x+2y,线性约束条件:
xy12
2xy15
x3y27
x0
y0
x3y27
(4)x16。
x24。
(5)最优解为x1=8,x2=0。
(6)不变化。因为当斜率1≤c1
c2
1,最优解不变,变化后斜率为1,所以最优解3
不变。
7.解:
设x,y分别为甲、乙两种柜的日产量, 目标函数z=200x+240y,线性约束条件:
6x12y120
8x4y64
即
x0
y0
x2y20
2xy16
x0
y0
x350
得ቤተ መጻሕፍቲ ባይዱ
y100
即C(350,100).当直线6x+10y=0即3x+5y=0平移到
经过点C(350,100)时,z=6x+10y最大
12.解:
模型maxz500x1400x2
2x1≤300
3x2≤540
2x12x1≤440
1.2x11.5x2≤300
x1,x2≥0
(1)x1150,x270,即目标函数最优值是103000。
《管理运筹学》第四版课后习题解析(上
)
第
1.解:
(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解x=12,x15
最新《运筹学》第四版课后习题答案
收集于网络,如有侵权请联系管理员删除⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x = 15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 203 ,函数值为 92 。
8 3 x = ⎪⎩ 2 33.解: (1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》第四版课后习题答案

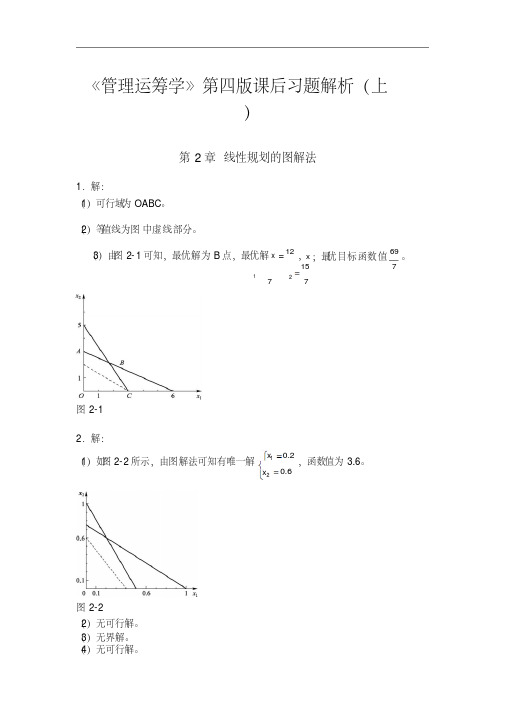
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
? (3)由图2-1可知,最优解为B 点,最优解 x =12, x ??15 727图2-1 ;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解?x 1 ??0.2,函数值为3.6。
?x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
? (5)无穷多解。
?x ? (6)有唯一解 ??1? 203,函数值为 92 。
8 3x ? ??2 33.解: (1)标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??30 3x 1 ??2x 2 ??s 2 ??13 2x 1 ??2x 2 ??s 3 ??9 x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2 ??10 7x 1 ??6x 2 ??4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??70 2x 1????5x 2????5x 2??????50 3x 1????2x 2????2x 2??????s 2 ??30 x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4.解: 标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1 ??95x 1 ??2x 2 ??s 2 ??8x1, x2 , s1, s2 ≥0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
管理运筹学第四版课后习题解析上定稿版

管理运筹学第四版课后习题解析上精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-1 2.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式(2)标准形式(3)标准形式4.解:标准形式松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
(2)113c <<。
(3)226c <<。
(4)1264x x ==。
(5)最优解为 x 1=8,x 2=0。
(6)不变化。
因为当斜率12113c c ---≤≤,最优解不变,变化后斜率为1,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+006448120126y x y x y x 即 ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+0162202y x y x y x 作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2.目标函数z=x +2y , 线性约束条件:作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E .但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
运筹学课后习题答案第四版

运筹学课后习题答案第四版
《运筹学课后习题答案第四版》
运筹学是一门研究如何最优化决策的学科,它涉及到数学、统计学和计算机科
学等多个领域。
《运筹学课后习题答案第四版》是一本备受学生和专业人士欢迎的参考书,它为读者提供了丰富的习题和答案,帮助他们更好地理解和掌握运
筹学的知识。
这本书包含了大量的习题和案例分析,涵盖了线性规划、整数规划、网络流、
动态规划等多个方面的内容。
通过练习这些习题,读者可以加深对运筹学理论
的理解,提高解决实际问题的能力。
除了习题和答案,这本书还提供了大量的案例分析,帮助读者将理论知识与实
际问题相结合。
通过分析这些案例,读者可以了解到运筹学在各个领域的应用,从而更好地理解运筹学的重要性和实用性。
《运筹学课后习题答案第四版》的出版对于推动运筹学的教学和研究具有重要
意义。
它为学生提供了一个系统的学习工具,帮助他们更好地掌握运筹学的知
识和方法。
同时,它也为专业人士提供了一个实用的参考书,帮助他们解决实
际工作中的问题。
总的来说,《运筹学课后习题答案第四版》是一本非常有价值的参考书,它不仅可以帮助读者提高运筹学的理论水平,还可以帮助他们更好地应用运筹学的方
法解决实际问题。
希望更多的人能够通过这本书,深入了解和研究运筹学,为
推动运筹学的发展做出贡献。
《管理运筹学》第四版课后习题答案
2x 7 y 1400 y 100 到
经过 点 C(350,100) 时 ,z=6x+10y 最大
12.解:
模型 max z 500 x1 400 x2
2 x1 ≤ 300 3x2 ≤ 540 2 x1 2 x1 ≤ 440 1.2x1 1.5x2 ≤ 300 x1, x2 ≥ 0
(1)x1 150 ,x2 70 ,即目 标 函数最 优值 是 103 000。
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
9 x1 2 x2 s1 30 3x1 2 x2 s2 13 2 x1 2 x2 s3 9 x1, x2 ,s1, s2, s3 ≥ 0
3x+2y,线性 约束条件
x 2y 2x y
x0 y0
2 3 作出可行域.作一 组平等直 线 3x+ 2y=t . 解
x 2y 2 得 C (4 / 3,1/ 3)
2x y 3
C不是整点,C不是最 优 解.在可行域内的整点中,点 B(1,1) 使 z 取得最小 值. z 最小 =3×1+2×1=5,
50 xA 100xB ≤ 1 200 000 5 xA 4 xB ≥ 60 000 100xB ≥ 300 000 xA , xB ≥ 0
基金 A,B 分别为 4 000 元,10 000 元,回报额为 62000 元。
(2)模型变为 max z 5xA 4 xB
50 xA 100xB ≤ 1 200 000 100xB ≥ 300 000 xA ,xB ≥ 0
《管理运筹学》第四版课后习题解析
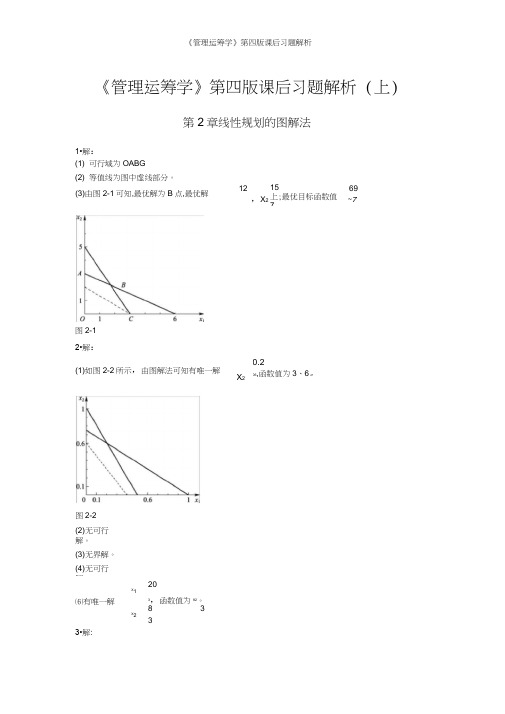
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1•解:(1) 可行域为OABG(2) 等值线为图中虚线部分。
图2-1 2•解:3•解:12,X215上;最优目标函数值769~7X20.206,函数值为3、6。
X1⑹有唯一解X2 203,函数值为92。
8 3 3(3)由图2-1可知,最优解为B点,最优解图2-2(2) 无可行解。
(3) 无界解。
(4) 无可行解。
(1)如图2-2所示,由图解法可知有唯一解(1) 标准形式max 3x1 2x2 0s1 0s2 0s39x1 2x2 s1 303x1 2x2 s2 132x1 2x2 s3 9X i,X2,®,S2,S3 > 0(2) 标准形式min f 4X1 6X2 0S1 0S23X1 X2 S1 6X1 2X2 S2 107X1 6X2 4X1, X2,S1, S2》(3) 标准形式min f X1 2X2 2X2 0S1 0S23X1 5X2 5X2 S1 702X1 5X2 5X2 503X1 2X2 2X2 S2 30X i,X2,X2,q,S2 > 0 4.解: 标准形式maX z 10X1 5X2 0S1 0S23X1 4X2 S1 95X1 2X2 S2 8X1, X2,s1,s2> 0松弛变量(0,0)最优解为X1=1,X2=3/2。
5.解: 标准形式min f 11X1 8X2 0S1 0S2 0S310X1 2X2 S1 203X1 3X2 S2 184X1 9X2 S3 36X i,X2,S i,S2,S3 > 0剩余变量(0, 0, 13)最优解为X i=1,X2=5。
6•解:(1) 最优解为X I=3,X2=7。
(2) 1 q 3。
⑶ 2 C2 6。
Xi 6。
⑷4X 4。
⑸最优解为X1=8,X2=0。
(6)不变化。
因为当斜率1 < 9 < 1,最优解不变,变化后斜率为1,所以最优解不变。
《管理运筹学》第四版课后习题答案解析
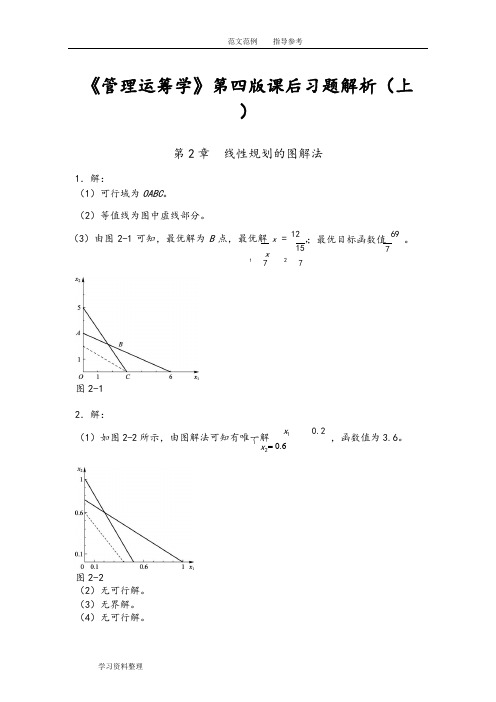
学习资料整理⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 x 10.2,函数值为3.6。
x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
x(6)有唯一解 120 3,函数值为 92 。
8 3x2 33.解:(1)标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f4x 16x 20s 10s 23x 1x 2 s 16 x 12x 2s 210 7x 16x2 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min fx 12x 22x 20s 1 0s 23x1 5x 25x 2s 1702x 15x 25x 250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04.解: 标准形式max z10x 15x 20s 10s 2范文范例 指导参考学习资料整理3x 14x 2s 19 5x 12x 2s 28x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
5.解: 标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
《管理运筹学》第四版课后习题
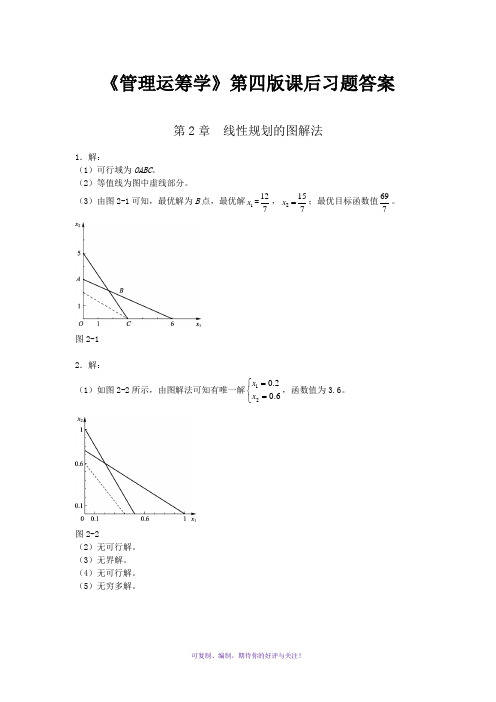
《管理运筹学》第四版课后习题答案第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解:标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
管理运筹学(第四版)第十一章习题答案

11.1解:4=λ人/小时,10660==μ人/小时,4.0104===μλρ,属于M/M/1排队模型。
(1)仓库管理员空闲的概率,即为6.04.0110=-=-=ρP(2)仓库内有4个工人的概率即为()()01536.04.04.011444=⨯-=-=ρρP(3)至少有2个工人的概率为16.024.06.01110=--=--P P(4)领工具的工人平均数人6667.0644104==-=-=λμλs L (5)排队等待领工具工人的平均数人2667.066.141044.0==-⨯=-=λμρλq L (6)平均排队时间分钟小时40667.064.04104.0===-=-=λμρq W (7)待定11.2解: 32060==λ人/小时,41560==μ人/小时,75.043===μλρ,属于M/M/1排队模型。
(1)不必等待概率,即为25.075.0110=-=-=ρP(2)不少于3个顾客排队等待的概率,即系统中有大于等于4个(或大于3个)顾客的概率,为3164.01055.01406.01875.025.0113210=----=----P P P P(3)顾客平均数人313343==-=-=λμλs L (4)平均逗留时间小时13411=-=-=λμs W (5)λλμ-=-=<4115.1s W 小时,即小时人/333.3>λ。
平均到达率超过3.333人时,店主才会考虑增加设备或理发员。
11.3解:4=λ人/小时,10660==μ人/小时,4.0104===μλρ,属于M/M/1/3排队模型。
(1)仓库内没有人领工具的概率,即为6158.04.014.0111410=--=--=+N P ρρ (2)工人到达必须排队等待的概率,即为仓库内有1个、2个和3个工人的概率和 ()()3842.04.014.014.04.04.011432132321=--⨯++=--++=+++N P P P ρρρρρ (3)新到工人离去的概率为0394.04.014.014.01143133=--⨯=--=+N P ρρρ (4)领工具的工人平均数()=-⨯--=-+--=++44114.014.044.014.0111N N s N L ρρρρ(5)排队等待领工具工人的平均数人2667.066.141044.0==-⨯=-=λμρλq L (6)平均排队时间分钟小时40667.064.04104.0===-=-=λμρq W。
《管理运筹学》第四版课后习题答案
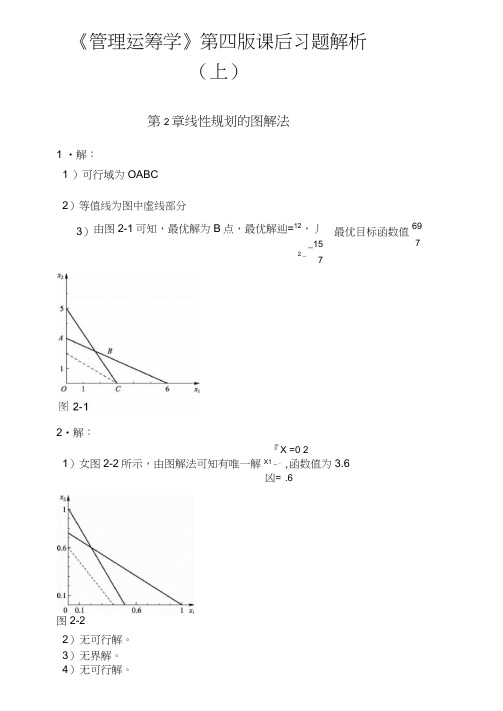
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1 •解:1 )可行域为OABC2)等值线为图中虚线部分2•解:『X =0 21)女图2-2所示,由图解法可知有唯一解X1 _ . ,函数值为3.6凶=°.6图2-22) 无可行解。
3) 无界解。
4) 无可行解。
3)由图2-1可知,最优解为B 点,最优解辿=12,丿 最优目标函数值 _152 _ 76975)无穷多解3•解:1)标准形式max f =3x i 2x 2 0s i - 0s 2 - 0s 39xi 2x 2 si =303x 1 亠2X 2 亠s =132x i 亠2x 2 亠S 3 =9x i , x 2 ,S 1, S 2, S 3》02) 标准形式min f =4x 1 亠6x 2 亠0$ 亠0s 23x i - X 2 - Si — 6x 1 2x 2 S 2 =i07x i -6x 2 =4x i , x , S i , S 2 A 03) 标准形式min f =xi —2X 2 亠2X 2 亠0s 1 亠0S 2-3x i 5x 2 -5x 2 S i =702x i -5x 2 5X 2: =503x i 2x 2 —2x 2 -S 2 =30x i , xl X 2: Si, S 2 A 0 4•解:标准形式max z =10x i ' 5x 2 ' 0s i 0S 23x 1 4x 2 Si =95xi 2x 2 S 2 =8x i , x , S i , S 2 A 06)有唯一解■: X 2=20 3,函数值为 83 92 3松弛变量0,0) 最优解为x i =1, X 2=3/2。
5•解:标准形式min f =11x i 8x 2 - 0s i - 0s 2 - 0S 310X 1 2X 2 -s 1 =203X I 亠 3X2 -S 2 =184X1 9X2 —S3 =36X 1, X 2 , S 1, S 2 , S3》0剩余变量0, 0, 13)最优解为X 1=1 , X 2=5。
运筹学第四版课后习题答案

运筹学第四版课后习题答案
《运筹学第四版课后习题答案》
运筹学是一门研究在有限资源下进行有效决策的学科,它涉及到数学、经济学、管理学等多个领域。
《运筹学第四版》是一本经典的教材,它系统地介绍了运筹学的基本理论和方法,为学习者提供了丰富的案例和习题,以帮助他们更好地
理解和掌握运筹学的知识。
在学习运筹学的过程中,习题是非常重要的一部分。
通过做习题,学习者可以
巩固所学的知识,提高解决实际问题的能力。
因此,《运筹学第四版》的课后习题答案对于学习者来说是非常重要的。
它们不仅可以帮助学习者检验自己的学
习成果,还可以指导他们在解题过程中遇到困难时进行思考和解决问题。
这本教材的习题涵盖了线性规划、整数规划、动态规划、网络流、排队论、库
存管理等多个方面的内容,涉及到了不同的应用场景和解题方法。
通过做这些
习题,学习者可以逐步掌握运筹学的基本理论和方法,培养自己的分析和解决
问题的能力。
除了对学习者有益外,课后习题答案也对教师有着重要的意义。
教师可以通过
查看习题答案来了解学生的学习情况,及时发现学生存在的问题并进行针对性
的指导。
同时,习题答案也可以帮助教师更好地备课,为学生提供更好的教学
服务。
总之,《运筹学第四版课后习题答案》是一本非常有价值的参考书,它对于学习者和教师来说都是非常重要的。
通过认真学习和应用这本书,我们相信学习者
一定能够在运筹学领域取得更好的成绩,为实际问题的解决提供更好的方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.1解:
4=λ人/小时,10660==μ人/小时,4.010
4===μλρ,属于M/M/1排队模型。
(1)仓库管理员空闲的概率,即为6.04.0110=-=-=ρP
(2)仓库内有4个工人的概率即为()()01536.04.04.011444=⨯-=-=ρρP
(3)至少有2个工人的概率为16.024.06.01110=--=--P P
(4)领工具的工人平均数人6667.06
44104==-=-=λμλ
s L (5)排队等待领工具工人的平均数人2667.06
6.141044.0==-⨯=-=λμρλq L (6)平均排队时间分钟小时4066
7.06
4.04104.0===-=-=
λμρq W (7)待定
11.2解: 32060==λ人/小时,41560==μ人/小时,75.04
3===μλρ,属于M/M/1排队模型。
(1)不必等待概率,即为25.075.0110=-=-=ρP
(2)不少于3个顾客排队等待的概率,即系统中有大于等于4个(或大于3个)顾客的概率,为
3164.01055.01406.01875.025.0113210=----=----P P P P
(3)顾客平均数人31
3343==-=-=λμλ
s L (4)平均逗留时间小时13
411=-=-=λμs W (5)λ
λμ-=-=<4115.1s W 小时,即小时人/333.3>λ。
平均到达率超过3.333人时,店主才会考虑增加设备或理发员。
11.3解:
4=λ人/小时,10660==μ人/小时,4.010
4===μλρ,属于M/M/1/3排队模型。
(1)仓库内没有人领工具的概率,即为6158.04
.014.0111410=--=--=+N P ρρ (2)工人到达必须排队等待的概率,即为仓库内有1个、2个和3个工人的概率和 ()()
3842.04.014.014.04.04.011432132321=--⨯++=--++=+++N P P P ρρρρρ (3)新到工人离去的概率为0394.04
.014.014.01143133=--⨯=--=+N P ρρρ (4)领工具的工人平均数()=-⨯--=-+--=++44114
.014.044.014.0111N N s N L ρρρρ
(5)排队等待领工具工人的平均数人2667.06
6.141044.0==-⨯=-=λμρλq L (6)平均排队时间分钟小时4066
7.064.04104.0===-=-=
λμρq W。
