北师大版七年级下册-全等三角形-章节测试

合集下载

北师大版七年级下数学《全等三角形》单元测试(含答案)

全等三角形章节测试一、心一（每小 3 分，共36 分）1. 以下法正确的选项是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A.周相等的两个三角形全等B. 面相等的两个三角形全等C. 三个角相等的两个三角形全等D.三条相等的两个三角形全等2. 以下各段能成三角形的是⋯⋯⋯⋯⋯⋯⋯⋯( )A.3cm ， 3cm， 6cmB.7cm,4cm,5cmC.3cm,4cm,8cmD.4.2cm,2.8cm,7cm3. 以下形中，与已知形全等的是⋯⋯⋯⋯⋯⋯⋯⋯( )第3题图(A) (B) (C) (D)4. 如，已知△ ABC≌△ CDE,此中 AB=CD,那么以下中， A不正确的选项是⋯⋯⋯⋯⋯⋯⋯⋯⋯( )EA.AC=CEB. ∠ BAC=∠ CDEC. ∠ ACB=∠ ECDD. ∠B=∠ D BC D第 4 题5. 以下条件中，不可以判断三角形全等的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. 三条相等B. 两和一角相等C. 两角和此中一角的相等D. 两角和它的相等6. 如，把形沿BC折，点 A 和点 D 重合，那么中共有全等三角形⋯⋯⋯⋯⋯⋯⋯( )A.1B.2 AC.3D.4B EC7.在△ ABC 和△ A′ B′C′中，已知 AB= A′ B′，∠ B=∠ B′要保△ ABC≌△ A′B′ C′，可充的条D件是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. ∠ B+∠A=900B.AC= A ′ C′C.BC=B ′ C′D.∠ A+∠ A′ =9008.已知在△ ABC和△ A′ B′ C′中，AB= A′ B′，∠ B=∠ B′，充下边一个条件，不可以明△ ABC≌△ A′B′ C′的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. BC=B ′ C′B. AC= A ′ C′C.∠ C=∠ C′D. ∠A=∠ A′9. 如，已知 AE=CF,BE=DF要.△ ABE≌△ CDF,需增添的一个条件是⋯⋯⋯( )A. ∠ BAC=∠ ACDB. ∠ ABE=∠ CDFC. ∠ DAC=∠ BCAD. ∠ AEB=∠ CFDD C A ADEA OAFA B A B C第 9 题 A 第 11题第 10题10. 如图 AD是△ ABC的角均分线， DE是△ ABD的高， EF 是△ ACD的高，则 ( )A. ∠ B=∠CB. ∠ EDB=∠ FDCC. ∠ ADE=∠ ADFD. ∠ ADB=∠ADC11. 如图 AC与 BD订交于点 O，已知 AB=CD,AD=BC,则图中全等三角形有 ( )A.1 对B.2 对C.3 对D.4 对12. 如图 ,D 、 E 分别是 AB,AC 上一点，若∠ B=∠ C，则在以下条件中， B没法判断△ ABE≌△ ACD是( ) DA.AD=AEB.AB=ACC.BE=CDD. ∠ AEB=∠ ADC A E C第 12 题二、专心填一填：（每题 3 分，共 24 分）C F13.如图，△ ABC≌△ DEF,点 B 和点 E, 点 A 和点 D 是对应极点，则 AB=，CB=,∠C=,∠ CAB=.14.若已知两个三角形有两条边对应，则要视这两个三角形全等，还需增添的条件能够是或. A DB E15. 如图已知 AC与 BD订交于点 O， AO=CO,BO=DO,则 AB=CD请说明原因 .第 13题A B解：在△ AOB和△ COD中AO CO(已知）（对顶角相等OBO DO(已知）D C∴△ AOB≌△ COD（）第 15题A ∴ AB=DC（）16. 如图，已知 AO=OB,OC=OD,AD和 BC订交于点 E， C则图中全等三角形有对 .EO BD第 16题17. 在△ ABC和△ DEF中 ,AB=4, ∠ A=350, ∠ B=700,DE=4, ∠ D= , ∠ E=700, 依据判断△ ABC≌△ DEF. A DAB=DC(已知）18.如图，在△ ABC和△ DEF中BC=DA(已知）（） B 第 18 题 C ∴△ ABC≌△ DEF( ) A D19. 如图∠ B=∠ DEF,AB=DE,要证明△ ABC≌△ DEF，(1) 若以“ ASA”为依照，需增添的条件是;B EC C第 19题(2) 若以“ SAS ”为依照，需增添的条件是 .A20. 如图，△ ABC 中， AB=AC=13cm ， AB 的垂直均分线交 A B 于 D,交 AC 于 E, 若△ EBC 的周长为 21cm,则 BC= cm.DEBC6 小题，共 40第 20 题三、耐心答一答：（此题有分）21.( 此题 4 分 ) 已知∠α、∠β和线段a, 如图，用直尺和圆规作△ABC ，使∠ A=∠α ,∠ B=∠β ,BC=a.22.( 此题 6 分 ) 已知 AD 均分∠ CAB,且 DC ⊥ AC, DB ⊥ AB ，那么 AB 和 AC 相等吗？请说明原因 .CDA23.( 此题 6 分 ) 如图，已知 BD=CD ，∠ 1=∠ 2.说出△ ABD ≌△ ACD 的原因 .AB1 2BD C24.( 此题 8 分) 如图，已知 AB=DC ， AD=BC,说出以下判断建立的原因： (1)△ ABC ≌△ CDA (2)∠ B=∠DADBC25.( 此题 8 分 ) 如图，把大小为4× 4 的正方形方格图形分别切割成两个全等图形，比如图①，请在以下图中，沿着须先画出四种不一样的分法，把4× 4 的正方形切割成两个全等图形图①26.( 此题画法1画法28 分 ) 如图，△ ABC中， AD垂直均分 BC,H是画法AD上一点，3 画法 4连结 BH,CH.(1)AD 均分∠ BAC吗？为何？(2)你能找出几堆相等的角？请把他么写出来（不需写原因）AH一、仔细选一选：（每题 3 分，共 36 分）题号 1 2 3 4 5 6 7 8 9 10B11 12 CD答案 D B B C D C C B D C D D二、专心填一填（每题 3 分，共 24 分）13.DE,FE, ∠ F, ∠ FED. 14.3 第三边相等，这两边的夹角相等15. ∠ AOB=∠ COD,SAS,全等三角形的对应边相等16.4 17.35 0, AAS 18.AC,CA, 公共边， SSS19. ∠ A=∠ D 20.8三、耐心答一答（此题有六小题，共40 分）21. 图略 22.AB=AC 23. 略24. 略25.画法 1 画法 2 画法 3 画法 426.(1) 由△ ADB≌△ ADC(SAS)得∠ BAD=∠ CAD (4)4 对，∠ BHD=∠ CHD, ∠ ABD=∠ ACD,∠HBD=∠ HCD, ∠ BDA=∠CDA。

(完整版)北师大版七年级下册_全等三角形证明经典题

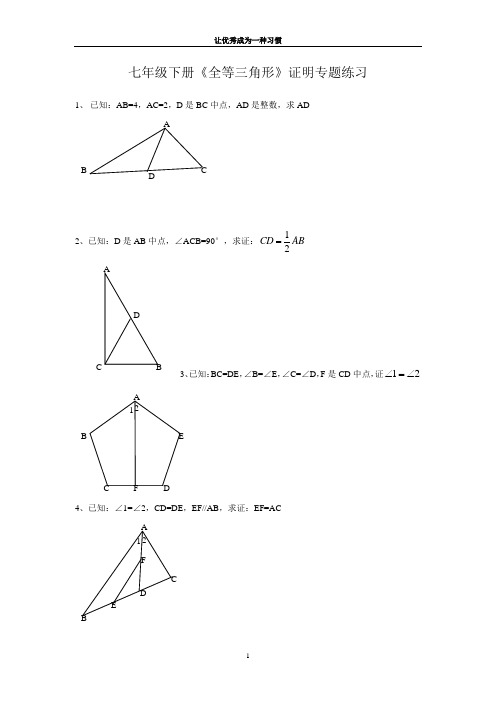
七年级下册《全等三角形》证明专题练习1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2、已知：D 是AB 中点，∠ACB=90°，求证：12CD AB =3、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，证21∠=∠4、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACADBCBA CDF2 1 E5、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C6、已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7、已知：AB=6，AC=2，D 是BC 中线，求AD 的取值范围。

8. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

9、已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠CADBCCDB DCBA FEA10、已知：AB=CD ，∠A=∠D ，求证：∠B=∠C11、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE12．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．13．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA14．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP于D ．求证：AD +BC =AB ．15．如图，△ABC 中，AD 是∠CAB 的平分线，且∠C =2∠B,求证:AB=AC+CDAB C DPEDCB A D CBA16．如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．17．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：18．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．19、如图：DF=CE ，AD=BC ，∠D=∠C 。

北师大七年级下册数学全等三角形习题精选

FED CB A 第五章全等三角形 A一、选择题1．下列三角形不一定全等的是（） A ．有两个角和一条边对应相等的三角形 B ．有两条边和一个角对应相等的三角形C ．斜边和一个锐角对应相等的两个直角三角形D ．三条边对应相等的两个三角形 2．下列说法：①所有的等边三角形都全等 ②斜边相等的直角三角形全等③顶角和腰长对应相等的等腰三角形全等 ④有两个锐角相等的直角三角形全等其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个3.如图，AB 平分∠CAD ，E 为AB 上一点，若AC=AD ，则下列结论错误的是（）=BD =DE 平分∠CBD D.图中有两对全等三角形是△ABC 的角平分线，自D 向AB 、AC 两边作垂线，垂足为E 、F ，那么下列结论中错误的是 ( )=DF =AF =CD D.∠ADE=∠ADF5.在△ABC 中，∠B=∠C ，与△ABC 全等的三角形有一个角是130°，那么△ABC 中与这个角对应的角是（）．A ．∠AB ．∠BC ．∠CD ．∠B 或∠C6.如图所示，BE ⊥AC 于点D ，且AD=CD ，BD=ED ，若∠ABC=54°，则∠E=（）．A ．25°B ．27°C ．30°D ．45° 7.如右图，△ABC 中，∠C＝90°，AC ＝BC ，AD 平分∠CAB 交BC 于点D ，DE⊥AB，且AB ＝10 cm ，则△BED 的周长为 ( ) A ．5 cm B ．10 cm; C ．15 cm D ．20 cm8．如图，AB=AC ，BE ⊥AC 于E ，CF ⊥AB 于F ，则①△ABE ≌△ACF ；②△BOF ≌△COE ；③点O 在∠BAC 的角平分线上，其中正确的结论有（）A ．3个B ．2个C ．1个D ．0个9.如图，在△ABC 中，AD 平分∠BAC ，过B 作BE ⊥AD 于E ，过E作EF ∥AC 交AB 于F ，则( ) A 、AF=2BF; B 、AF=BF; C 、AF>BF; D 、AF<BF E DCBAD A CE B CBAEF O二、填空题1.如果△ABC≌△A’B’C’，若AB ＝A’B’，∠B＝50°，∠C＝70°，则∠A’＝ °2.如图，若BD ⊥AE 于B ，DC ⊥AF 于C ，且DC=DC ，∠BAC=40°，∠ADG=130°，则∠DGF=________。

知识点详解北师大版七年级数学下册第四章三角形章节测评试题(含解析)

北师大版七年级数学下册第四章三角形章节测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知线段AB ＝9cm ，AC ＝5cm ，下面有四个说法：①线段BC 长可能为4cm ；②线段BC 长可能为14cm ；③线段BC 长不可能为3cm ；④线段BC 长可能为9cm ．所有正确说法的序号是（）A ．①②B ．③④C ．①②④D ．①②③④2、根据下列已知条件，不能画出唯一ABC 的是（）A ．60A ∠=︒，45B ∠=︒，4AB =B ．30A ∠=︒，5AB =，3BC = C ．60B ∠=︒，6AB =，10BC =D ．90C ∠=︒，5AB =，3BC =3、如图，ABC ≌DEF ，点B 、E 、C 、F 在同一直线上，若BC ＝7，EC ＝4，则CF 的长是（）A ．2B ．3C ．4D ．74、如图，ABC 和DEF 全等，且A D ∠=∠，AC 对应DE ．若6AC =，5BC =，4AB =，则DF 的长为（）A．4 B．5 C．6 D．无法确定5、将一副三角板按如图所示的方式放置，使两个直角重合，则∠AFD的度数是（）A．10°B．15°C．20°D．25°6、以下列各组长度的线段为边，能构成三角形的是（）A．1cm，1cm，8cm B．3cm，3cm，6cmC．3cm，4cm，5cm D．3cm，2cm，1cm7、如图，在ABC中，AD、AE分别是边BC上的中线与高，4AE ，CD的长为5，则ABC的面积为（）A．8 B．10 C．20 D．408、以下列各组线段为边，能组成三角形的是（）A．2cm、10cm、13cm B．3cm、7cm、4cmC．4cm、4cm、4cm D．5cm、14cm、6cm9、已知三角形的两边长分别为4cm和10cm，则下列长度的四条线段中能作为第三边的是（）A．15cm B．6cm C．7cm D．5cm10、如图，点C在∠AOB的OB边上，用尺规作出了∠NCE=∠AOD，作图痕迹中，弧FG是( )A．以点C为圆心，OD为半径的弧B．以点C为圆心，DM为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DM为半径的弧第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，某同学把一块三角形的玻璃打碎成了三片，现在他要到玻璃店去配一块完全一样形状的玻璃，那么最省事的办法是带____（填序号）去配，这样做的科学依据是_______．2、如图，在ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且ABC的面积等于24cm2，则阴影部分图形面积等于_____cm23、如图，△PBC的面积为5cm2，BP平分∠ABC，AP⊥BP于点P，则△ABC的面积为_____cm2．4、如图，∠ABD＝80°，∠C＝38°，则∠D＝___度．5、如图，要测量水池的宽度AB，可从点A出发在地面上画一条线段AC，使AC AB⊥，再从点C观测，在BA的延长线上测得一点D，使ACD ACB∠=∠，这时量得160mAD=，则水池宽AB的长度是______m．三、解答题（5小题，每小题10分，共计50分）1、如图1，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/s的速度沿BC向点C运动，设点P的运动时间为t s，且t≤5（1）PC ＝ cm （用含t 的代数式表示）（2）如图2，当点P 从点B 开始运动时，点Q 从点C 出发，以v cm/s 的速度沿CD 向点D 运动，是否存在这样的v 值，使得以A ﹑B ﹑P 为顶点的三角形与以P ﹑Q ﹑C 为顶点的三角形全等？若存在，请求出v 的值；若不存在，请说明理由．2、在边长为10厘米的等边三角形△ABC 中，如果点M ，N 都以3厘米/秒的速度匀速同时出发．（1）若点M 在线段AC 上由A 向C 运动，点N 在线段BC 上由C 向B 运动．①如图①，当BD ＝6，且点M ，N 在线段上移动了2s ，此时△AMD 和△BND 是否全等，请说明理由． ②求两点从开始运动经过几秒后，△CMN 是直角三角形．（2）若点M 在线段AC 上由A 向点C 方向运动，点N 在线段CB 上由C 向点B 方向运动，运动的过程中，连接直线AN ，BM ，交点为E ，探究所成夹角∠BEN 的变化情况，结合计算加以说明．3、如图，四边形ABCD 中，90BCD BAD ∠=∠=︒，AB AD =，AG CD ⊥于点G ．（1）如图1，求证：AG CG =；（2）如图2，延长AB 交DC 的延长线于点F ，点E 在DG 上，连接AE ，且2AEF F ∠=∠，求证：FG AE EG =+；（3）如图3，在（2）的条件下，点H 在CB 的延长线上，连接EH ，EH 交AG 于点N ，连接CN ，且=CN AE ，当5BH =，9EF =时，求NG 的长．4、如图，在长方形ABCD 中，AB =4，BC =5，延长BC 到点E ，使得CE =12CD ，连结DE ．若动点P 从点B 出发，以每秒2个单位的速度沿着BC-CD-DA 向终点A 运动，设点P 的运动时间为t 秒．（1）CE = ；当点P 在BC 上时，BP = （用含有t 的代数式表示）；（2）在整个运动过程中，点P 运动了秒；（3）当t = 秒时，△ABP 和△DCE 全等；（4）在整个运动过程中，求△ABP 的面积．5、探究与发现：如图①，在△ABC 中，∠B ＝∠C ＝45°，点D 在BC 边上，点E 在AC 边上，且∠ADE ＝∠AED ，连接DE ．（1）当∠BAD ＝60°时，求∠CDE 的度数；（2）当点D 在BC （点B 、C 除外）边上运动时，试猜想∠BAD 与∠CDE 的数量关系，并说明理由．（3）深入探究：如图②，若∠B ＝∠C ，但∠C ≠45°，其他条件不变，试探究∠BAD 与∠CDE 的数量关系．-参考答案-一、单选题1、D【分析】分三种情况：C在线段AB上，C在线段BA的延长线上以及C不在直线AB上结合线段的和差以及三角形三边的关系分别求解即可．【详解】解：∵线段AB＝9cm，AC＝5cm，∴如图1，A，B，C在一条直线上，∴BC＝AB−AC＝9−5＝4（cm），故①正确；如图2，当A，B，C在一条直线上，∴BC＝AB＋AC＝9＋5＝14（cm），故②正确；如图3，当A ，B ，C 不在一条直线上，9−5=4cm ＜BC ＜9＋5=14cm ，故线段BC 可能为9cm ，不可能为3cm ，故③，④正确．故选D ．【点睛】此题主要考查了三角形三边关系，线段之间的关系，正确分类讨论是解题关键．2、B【分析】根据三角形存在的条件去判断．【详解】∵60A ∠=︒，45B ∠=︒，4AB =，满足ASA 的要求，∴可以画出唯一的三角形，A 不符合题意；∵30A ∠=︒，5AB =，3BC =，∠A 不是AB ，BC 的夹角，∴可以画出多个三角形，B 符合题意；∵60B ∠=︒，6AB =，10BC =，满足SAS 的要求，∴可以画出唯一的三角形，C 不符合题意；∵90C ∠=︒，5AB =，3BC =，AB 最大，∴可以画出唯一的三角形，D 不符合题意；故选B ．【点睛】本题考查了三角形的存在性，熟练掌握三角形全等的判定方法是解题的关键．3、B【分析】根据全等三角形的性质可得BC EF=-即可求得答案．=，根据CF EF EC【详解】解：ABC≌DEF，∴BC EF=点B、E、C、F在同一直线上，BC＝7，EC＝4，∴CF EF ECBC EC-=-==-743故选B【点睛】本题考查了全等三角形的性质，掌握全等三角形的性质是解题的关键．4、A【分析】全等三角形对应边相等，对应角相等，根据题中信息得出对应关系即可．【详解】∵ABC和DEF全等，A D∠=∠，AC对应DE∴ABC DFE≅∴AB=DF=4故选：A．【点睛】本题考查了全等三角形的概念及性质，应注意①对应边、对应角是对两个三角形而言的，指两条边、两个角的关系，而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等，对应角的平分线相等，对应边上的中线相等，周长及面积相等③全等三角形有传递性．5、B【分析】根据三角板各角度数和三角形的外角性质可求得∠BFE，再根据对顶角相等求解即可．【详解】解：由题意，∠ABC=60°，∠E=45°，∵∠ABC=∠E+∠BFE，∴∠BFE=∠ABC－∠E=60°－45°=15°，∴∠AFD=∠BFE=15°，故选：B．【点睛】本题考查三角板各角的度数、三角形的外角性质、对顶角相等，熟知三角板各角的度数，掌握三角形的外角性质是解答的关键．6、C【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．【详解】解：A、1+1＝2＜8，不能组成三角形，故此选项不合题意；B、3+3＝6，不能组成三角形，故此选项不符合题意；C、3+4＝7＞5，能组成三角形，故此选项符合题意；D、1+2＝3，不能组成三角形，故此选项不合题意；故选：C．【点睛】本题考查了构成三角形的条件，掌握“任意两边之和大于第三边，任意两边之差小于第三边”是解题的关键．7、C【分析】根据三角形中线的性质得出CB的长为10，再用三角形面积公式计算即可．【详解】解：∵AD是边BC上的中线，CD的长为5，∴CB=2CD=10，ABC的面积为1110420 22BC AE⨯=⨯⨯=，故选：C．【点睛】本题考查了三角形中线的性质和面积公式，解题关键是明确中线的性质求出底边长．8、C【分析】由题意根据“三角形任意两边之和大于第三边，任意两边之差小于第三边”对各选项进行逐一分析即可．【详解】解：根据三角形的三边关系，A、2+10＜13，不能组成三角形，不符合题意；B、3+4＝7，不能够组成三角形，不符合题意；C 、4+4＞4，能组成三角形，符合题意；D 、5+6＜14，不能组成三角形，不符合题意．故选：C ．【点睛】本题主要考查三角形三边关系，注意掌握判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．9、C【分析】根据三角形的三边关系可得104104x -<<+，再解不等式可得答案．【详解】解：设三角形的第三边为xcm ，由题意可得：104104x -<<+，即614x <<，故选：C ．【点睛】本题主要考查了三角形的三边关系，解题的关键是掌握三角形两边之和大于第三边；三角形的两边差小于第三边．10、D【分析】根据作一个角等于已知角的步骤即可得．【详解】解：作图痕迹中，弧FG 是以点E 为圆心，DM 为半径的弧，故选：D ．【点睛】本题主要考查作图-尺规作图，解题的关键是熟练掌握作一个角等于已知角的尺规作图步骤．二、填空题1、③ ASA【分析】由题意已知三角形破损部分的边角，得到原来三角形的边角，根据三角形全等的判定方法进行分析即可．【详解】解：第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．故答案为：③；ASA．【点睛】本题主要考查全等三角形的判定方法的实际应用，要求学生将所学的知识运用于实际生活中，要认真观察图形，根据已知选择方法．2、6【分析】因为点F是CE的中点，所以△BEF的底是△BEC的底的一半，△BEF高等于△BEC的高；同理，D、E、分别是BC、AD的中点，可得△EBC的面积是△ABC面积的一半；利用三角形的等积变换可解答．【详解】解：如图，点F是CE的中点，EC，而高相等，∴△BEF的底是EF，△BEC的底是EC，即EF=12∴S△BEF=12S△BEC，∵E是AD的中点，∴S△BDE=12S△ABD，S△CDE=12S△ACD，∴S△EBC=12S△ABC，∴S△BEF=14S△ABC，且S△ABC=24cm2，∴S△BEF=6cm2，即阴影部分的面积为6cm2．故答案为6．【点睛】本题考查了三角形面积的等积变换：若两个三角形的高（或底）相等，面积之比等于底边（高）之比．3、10【分析】根据已知条件证得△ABP≌△EBP，根据全等三角形的性质得到AP=PE，得出S△ABP=S△EBP，S△ACP=S△ECP，推出S△ABC=2S△PBC，代入求出即可．【详解】解：延长AP交BC于E，∵BP 平分∠ABC ，∴∠ABP =∠EBP ，∵AP ⊥BP ，∴∠APB =∠EPB =90°，在△ABP 和△EBP 中，ABP EBP BP BPAPB EPB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABP ≌△EBP （ASA ），∴AP =PE ，∴S △ABP =S △EBP ，S △ACP =S △ECP ，∴S △ABC =2S 阴影=10（cm 2），故答案为：10．【点睛】本题考查了全等三角形的性质和判定，三角形的面积的应用，注意：等底等高的三角形的面积相等． 4、42【分析】由三角形的外角的性质可得,DABD C 代入数据即可得到答案. 【详解】解：,80,38,ABD D C ABD C 803842,D ABD C 故答案为：42【点睛】本题考查的是三角形的外角的性质，掌握“三角形的外角等于与它不相邻的两个内角之和”是解本题的关键.5、160【分析】利用全等三角形的性质解决问题即可．【详解】解：AC BD ，90CAD CAB ∴∠=∠=︒，在ACD △与ACB △中，DAC BACAC ACACD ACB∠=∠⎧⎪=⎨⎪∠=∠⎩， ACD ∴≌()ACB ASA ，160AB AD m ∴==，故答案为：160．【点睛】本题考查全等三角形的应用，解题关键是理解题意，正确寻找全等三角形解决问题．三、解答题1、（1）(10﹣2t )；（2）当v =1或v =2.4时，△ABP 和△PCQ 全等．（1）根据题意求出BP ，然后根据PC =BC -BP 计算即可；（2）分△ABP ≌△QCP 和△ABP ≌△PCQ 两种情况，根据全等三角形的性质解答即可．【详解】解：（1）∵点P 的速度是2cm /s ，∴t s 后BP =2t cm ，∴PC=BC −BP =(10−2t )cm ，故答案为：(10﹣2t )；（2）由题意得：cm CQ vt ，∠B=∠C =90°，∴只存在△ABP ≌△QCP 和△ABP ≌△PCQ 两种情况，当△ABP ≌△PCQ 时，∴AB=PC ，BP=CQ ，∴10−2t =6，2t=vt ，解得，t =2，v =2，当△ABP ≌△QCP 时，∴AB=QC ，BP=CP ，∴2t =10-2t ， vt =6，解得，t =2.5，v =2.4，∴综上所述，当v =1或v =2.4时，△ABP 和△PCQ 全等．【点睛】本题考查了全等三角形的性质，解题的关键在于能够利用分类讨论的思想求解．2、（1）①证明见解析；②经过109或209秒后，△CMN 是直角三角形；（2）∠BEN ＝60°，证明见解析（1）①根据题意得出AM ＝BD ，AD ＝BN ，根据等边三角形的性质得到∠A ＝∠B ＝∠C ＝60°，利用SAS 定理证明△AMD ≌△BDN ；②分∠CNM ＝90°、∠CMN ＝90°两种情况，根据直角三角形的性质列式计算即可；（2）证明△ABM ≌△CAN ，根据全等三角形的性质得到∠ABM ＝∠CAN ，根据三角形的外角性质计算，得到答案．【详解】（1）①∵△ABC 为等边三角形，∴∠A ＝∠B ＝∠C ＝60°，当点M ，N 在线段上移动了2s 时，AM ＝6厘米，CN ＝6厘米，∴BN ＝BC ﹣CN ＝4厘米，∵AB ＝10厘米，BD ＝6厘米，∴AD ＝4厘米，∴AM ＝BD ，AD ＝BN ，在△AMD 和△BDN 中，AM BD A B AD BN =⎧⎪∠=∠⎨⎪=⎩， ∴△AMD ≌△BDN （SAS ）；②设经过t 秒后，△CMN 是直角三角形，由题意得：CM ＝（10﹣3t ）厘米，CN ＝3t 厘米，当∠CNM ＝90°时，∵∠C ＝60°，∴∠CMN ＝30°，∴CM ＝2CN ，即10﹣3t ＝2×3t ，解得：t ＝109，当∠CMN ＝90°时，CN ＝2CM ，即2（10﹣3t ）＝3t ，解得：t ＝209，综上所述：经过109或209秒后，△CMN 是直角三角形；（2）如图所示，由题意得：AM ＝CN ，在△ABM 和△CAN 中，AM CN BAM ACN AB CA =⎧⎪∠=∠⎨⎪=⎩， ∴△ABM ≌△CAN （SAS ），∴∠ABM ＝∠CAN ，∴∠BEN ＝∠ABE +∠BAE ＝∠CAN +∠BAE ＝60°．【点睛】本题考查了全等三角形的判断以及列一元一次方程动点相关问题，两边和它们的夹角对应相等的两个三角形全等；一元一次方程与几何图形的相结合的题，多数会涉及到动点的问题，需要对动点的位置进行讨论，讨论时要注意讨论全面，做到不重不漏，通常会按照从左到右或从上到下的方位进行考虑．3、（1）见解析；（2）见解析；（3）2【分析】（1）过点B 作BQ AG ⊥于点Q ，根据AAS 证明△ABQ DAG ≅∆得AG BQ =，再证明四边形BCGQ 是矩形得BQ =CG ，从而得出结论；(2) 在GF 上截取GH =GE ，连接AH ，证明AH =FH ，GE =GH 即可；(3) 过点A 作AP HC ⊥于点P ，在FC 上截取MG GE =，连接,,AM AC AH ，证明()Rt AGE Rt CGN HL ∆≅∆得GN GE MG ==，可证明AC 是EH 的垂直平分线，再证明()Rt APH Rt AGM HL ∆≅∆和△()ABH ADM SAS ≅∆得5BH MD ==可求出4ME =，从而可得结论．【详解】解：（1）证明：过点B 作BQ AG ⊥于点Q ，如图1∵AG CD ⊥90AQB BAD ︒∴∠==∠ABQ BAQ DAG BAQ ∴∠+∠=∠+∠ABQ DAG ∴∠=∠又AB AD =，90AQB AGD ︒∠=∠=∴△()ABQ DAG AAS ≅∆B AG Q ∴=,,BC CD AG CD BQ AG ⊥⊥⊥∴四边形BCGQ 是矩形BQ CG ∴=CG AG ∴=；（2）在GF 上截取GH =GE ，连接AH ，如图2，,HG GE AG GF =⊥AH AE ∴=AEH AHE ∴∠=∠2AEF F ∠=∠2AHE F ∴∠=∠又AHE F FAH ∠=∠+∠F FAH ∴∠=∠FH AH ∴=AE FH ∴=FG FH HG AE EG ∴=+=+（3）过点A 作AP HC ⊥于点P ，在FC 上截取MG GE =，连接,,AM AC AH ，如图3，由（1）、（2）知，AP CG AG ==，,AM AE FM F FAM ==∠=∠∵EF FG GE FM ME =+=+∴9AM ME =+∵,CN AE AG CG ==∴()Rt AGE Rt CGN HL ∆≅∆∴GN GE MG ==∴∠45GNE GEN ︒=∠=∵BC FD ⊥∴∠45CHE CEH ︒=∠=∴CH CE =∵AG CG =∴∠45ACG CAG ︒=∠=∴45ACG ACH ∠=∠=︒∴AC 是EH 的垂直平分线，∴AH AE =∴AH AM =又∵AG AP =∴()Rt APH Rt AGM HL ∆≅∆∴∠HAP MAG =∠∴∠90HAM PAG ︒=∠=∵∠F FAM =∠，90,90FAM MAD F D ∠+∠=︒∠+∠=︒∴∠MAD D =∠∴AM MD =∵,,AP CH HC FD AG FD ⊥⊥⊥∴90PAG ∠=︒∴90MAG PAM ∠+∠=︒∵∠HAP MAG =∠∴90PAH MAP ∠+∠=︒，即90HAM ∠=︒∴90HAB BAM ∠+∠=︒∵90BAD ∠=︒，即90BAM MAD ∠+∠=︒∴HAB MAD ∠=∠在ABH ∆和ADM ∆中，{AA =AA∠AAA =∠AAA AA =AA∴△()ABH ADM SAS ≅∆∴5BH MD ==∴5AM FM ==∴4ME =∴2GN GE MG===【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．4、（1）2，2t；（2）7；（3）1或6；（4）△ABP的面积为54(0)25910()229284(7)2t ttt t⎧<≤⎪⎪⎪<<⎨⎪⎪-≤<⎪⎩．【分析】（1）根据CE=12CD可求得CE的长，利用速度⨯时间即可求得BP的长；（2）先计算出总路程，再利用路程÷速度即可计算出用时；（3）分两种情况，利用全等三角形的性质即可求解；（4）分三种情况，利用三角形的面积公式求解即可．【详解】解：（1）∵CE=12CD，AB=CD=4，∴CE=2，∵点P从点B出发，以每秒2个单位的速度运动，∴BP=2t；故答案为：2，2t；（2）点P运动的总路程为BC+CD+DA=5+4+5=14，∴在整个运动过程中，点P运动了1472=(秒)；故答案为：7；（3）当点P在BC上时，△ABP≌△DCE，∴BP=CE=2，∴2t=2，解得：t=1；当点P在AD上时，△BAP≌△DCE，∴AP=CE=2，点P运动的总路程为BC+CD+DA-AP=5+4+5-2=12，∴2t=12，解得：t=6；综上，当t=1或6秒时，△ABP和△DCE全等；故答案为：1或6；（4）当点P在BC上，即0<t52≤时，AB=4，BP=2t，∴△ABP的面积为12AB⨯BP=4t；当点P在CD上，即52<t92<时，AB=4，BC=5，∴△ABP的面积为12AB⨯BC=10；当点P在BC上，即92t≤<7时，AB=4，AP=14-2t，∴△ABP的面积为12AB⨯BP=28-4t；综上，△ABP的面积为54(0)25910()229284(7)2t ttt t⎧<≤⎪⎪⎪<<⎨⎪⎪-≤<⎪⎩．【点睛】本题考查了全等三角形的性质等知识，解题的关键是学会用分类讨论的思想思考问题．5、（1）30°；（2）∠BAD＝2∠CDE，理由见解析；（3）∠BAD＝2∠CDE．【分析】（1）根据三角形的外角的性质求出∠ADC，结合图形计算即可；（2）设∠BAD＝x，根据三角形的外角的性质求出∠ADC，结合图形计算即可；（3）设∠BAD＝x，仿照（2）的解法计算．【详解】解：（1）∵∠ADC是△ABD的外角，∴∠ADC＝∠BAD+∠B＝105°，∠DAE＝∠BAC﹣∠BAD＝30°，∴∠ADE＝∠AED＝75°，∴∠CDE＝105°﹣75°＝30°；（2）∠BAD＝2∠CDE，理由如下：设∠BAD＝x，∴∠ADC＝∠BAD+∠B＝45°+x，∠DAE＝∠BAC﹣∠BAD＝90°﹣x，∴∠ADE＝∠AED＝902x︒+，∴∠CDE＝45°+x﹣902x︒+＝12x，∴∠BAD＝2∠CDE；（3）设∠BAD＝x，∴∠ADC＝∠BAD+∠B＝∠B+x，∠DAE＝∠BAC﹣∠BAD＝180°﹣2∠C﹣x，∴∠ADE＝∠AED＝∠C+12x，∴∠CDE＝∠B+x﹣（∠C+12x）＝12x，∴∠BAD＝2∠CDE．【点睛】本题考查了三角形内角和和外角的性质，解题关键是熟练掌握三角形内角和和外角性质，通过设参数计算，发现角之间的关系。

北师大版七年级下册三角形全等的证明练习题以及答案

最新北师大版七年级下册三角形全等的证明练习题以及答案最新七年级下册三角形全等的证明1、已知：如图，四边形ABCD中，AC平分角BAD，CE垂直AB 于E，且角B+角D=180度，求证：AE=AD+BEA B DCE 122、已知，如图，AB=CD，DF⊥AC于F，BE⊥AC于E，DF=BE。

求证：AF=CE。

F EA CDB3、已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。

求证：BE ＝CD 。

AEDCB4、如图，DE⊥AB，DF⊥AC，垂足分别为E、F，请你从下面三个条件中任选出两个作为已知条件，另一个为结论，推出一个正确的命题。

① AB=AC ② BD=CD ③ BE=CF5、如图，△ABC中，AB=AC，过A作GE∥BC，角平分线BD、CF交于点H，它们的延长线分别交GE于E、G，试在图中找出三对全等三角形，并对其中一对给出证明。

E6、如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。

（１）请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。

你添加的条件是：________ ___（2）根据你添加的条件，再写出图中的一对全等三角形：______________（不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）7、已知：如图，AB⊥BC，AD⊥DC，AB=AD，若E是AC上一点。

求证：EB=ED。

DA E CB8、已知：如图，AB、CD交于O点，CE//DF，CE=DF，AE=BF。

求证：∠ACE=∠BDF。

AB CDEFO9、已知：如图，△ABC中，AD⊥BC于D，E是AD上一点，BE的延长线交AC于F，若BD=AD，DE=DC。

求证：BF⊥AC。

AE FDB C10、. 已知：如图，△ABC 和△A ＇B ＇C ＇中，∠BAC=∠B ＇A ＇C ＇，∠B=∠B ＇，AD 、A ＇D ＇分别是∠BAC 、∠B ＇A ＇C ＇的平分线，且AD=A ＇D ＇。

北师大版数学七年级下册第4章《三角形》单元测试试题附答案解析

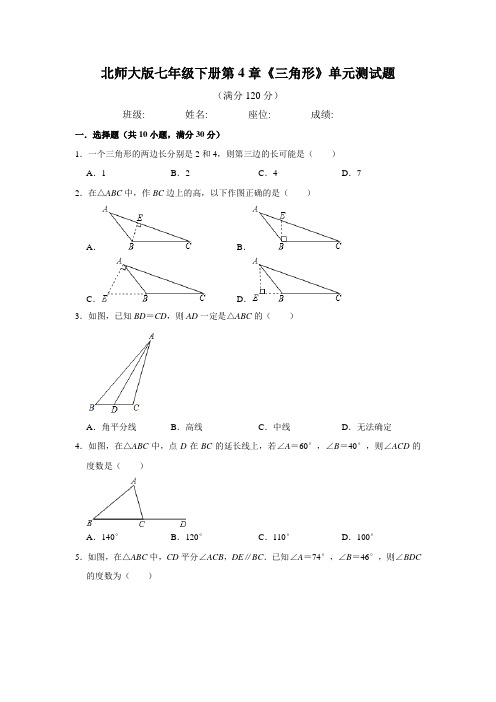
北师大版七年级下册第4章《三角形》单元测试题（满分120分）班级:________姓名:________座位:________成绩:________一．选择题（共10小题，满分30分）1．一个三角形的两边长分别是2和4，则第三边的长可能是（）A．1B．2C．4D．72．在△ABC中，作BC边上的高，以下作图正确的是（）A．B．C．D．3．如图，已知BD＝CD，则AD一定是△ABC的（）A．角平分线B．高线C．中线D．无法确定4．如图，在△ABC中，点D在BC的延长线上，若∠A＝60°，∠B＝40°，则∠ACD的度数是（）A．140°B．120°C．110°D．100°5．如图，在△ABC中，CD平分∠ACB，DE∥BC．已知∠A＝74°，∠B＝46°，则∠BDC 的度数为（）A．104°B．106°C．134°D．136°6．如图，AB＝AC，若要使△ABE≌△ACD．则添加的一个条件不能是（）A．∠B＝∠C B．∠ADC＝∠AEB C．BD＝CE D．BE＝CD7．如图，A、B两点分别位于一个池塘的两端，小明想用绳子测量A、B间的距离，如图所示的这种方法，是利用了三角形全等中的（）A．SSS B．ASA C．AAS D．SAS8．小明学习了全等三角形后总结了以下结论：①全等三角形的形状相同、大小相等；②全等三角形的对应边相等、对应角相等；③面积相等的两个三角形是全等图形；④全等三角形的周长相等．其中正确的结论个数是（）A．1B．2C．3D．49．如图，AD是△ABC的高，BE是△ABC的角平分线，BE，AD相交于点F，已知∠BAD ＝42°，则∠BFD＝（）A．45°B．54°C．56°D．66°10．如图，△ABC的三边长均为整数，且周长为22，AM是边BC上的中线，△ABM的周长比△ACM的周长大2，则BC长的可能值有（）个．A．4B．5C．6D．7二．填空题（共6小题，满分24分）11．下列4个图形中，属于全等的2个图形是．（填序号）12．如图，某人将一块三角形玻璃打碎成两块，带块（填序号）能到玻璃店配一块完全一样的玻璃，用到的数学道理是．13．如图，Rt△ABC中，∠C＝90°，∠B＝25°，分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于M、N两点，作直线MN，交BC于点D，连接AD，则∠CAD 的度数是．14．如图，在△ABC中，AC＝BC，过点A，B分别作过点C的直线的垂线AE，BF．若AE ＝CF＝3，BF＝4.5，则EF＝．15．边长为整数、周长为20的三角形的个数为．16．如图，Rt△ABC中，∠BAC＝90°，AB＝6，AC＝3，G是△ABC重心，则S△AGC＝．三．解答题（共8小题，满分66分）17．如图，在一个三角形的一条边上取四个点，把这些点与这条边所对的顶点连接起来．问图中共有多少个三角形．请你通过与数线段或数角的问题进行类比来思考．18．如图，AB＝DE，AC＝DF，BE＝CF，求证：△ABC≌△DEF．19．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合．（1）求证：△ADC≌△CEB；（2）求两堵木墙之间的距离．20．如图，已知B，D在线段AC上，且AD＝CB，BF＝DE，∠AED＝∠CFB＝90°求证：（1）△AED≌△CFB；（2）BE∥DF．21．如图，已知锐角△ABC，AB＞BC．（1）尺规作图：求作△ABC的角平分线BD；（保留作图痕迹，不写作法）（2）点E在AB边上，当BE满足什么条件时？∠BED＝∠C．并说明理由．22．如图，△ABC中，∠ACB＝90°，D为AB上一点，过D点作AB垂线，交AC于E，交BC的延长线于F．（1）∠1与∠B有什么关系？说明理由．（2）若BC＝BD，请你探索AB与FB的数量关系，并且说明理由．23．如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO 和∠ABO的角平分线，BC延长线交OM于点G．（1）若∠MON＝60°，则∠ACG＝°；若∠MON＝90°，则∠ACG＝°；（2）若∠MON＝n°．请求出∠ACG的度数；（用含n的代数式表示）（3）如图2，若∠MON＝n°，过C作直线与AB交F．若CF∥OA时，求∠BGO﹣∠ACF的度数．（用含n的代数式表示）24．如图1所示，在Rt△ABC中，∠C＝90°，点D是线段CA延长线上一点，且AD＝AB，点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt△DFE，连接EA，EA满足条件EA⊥AB．（1）若∠AEF＝20°，∠ADE＝50°，BC＝2，求AB的长度；（2）求证：AE＝AF+BC；（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明你的结论．参考答案一．选择题（共10小题）1．【解答】解：设第三边的长为x，由题意得：4﹣2＜x＜4+2，2＜x＜6，故选：C．2．【解答】解：BC边上的高应从点A向BC引垂线，只有选项D符合条件，故选：D．3．【解答】解：由于BD＝CD，则点D是边BC的中点，所以AD一定是△ABC的一条中线．故选：C．4．【解答】解：∠ACD是△ABC的一个外角，∴∠ACD＝∠A+∠B＝100°，故选：D．5．【解答】解：∵∠A＝74°，∠B＝46°，∴∠ACB＝60°，CD平分∠ACB，∴∠BCD＝∠ACD＝∠ACB＝×60°＝30°，∴∠BDC＝180°﹣∠B﹣∠BCD＝104°，故选：A．6．【解答】解：A、添加∠B＝∠C可利用ASA定理判定△ABE≌△ACD，故此选项不合题意；B、添加∠ADC＝∠AEB可利用AAS定理判定△ABE≌△ACD，故此选项不合题意；C、添加BD＝CE可得AD＝AE，可利用利用SAS定理判定△ABE≌△ACD，故此选项不合题意；D、添加BE＝CD不能判定△ABE≌△ACD，故此选项符合题意；故选：D．7．【解答】解：观察图形发现：AC＝DC，BC＝BC，∠ACB＝∠DCB，所以利用了三角形全等中的SAS，故选：D．8．【解答】解：①全等三角形的形状相同、大小相等，正确；②全等三角形的对应边相等、对应角相等，正确；③面积相等的两个三角形是全等图形，错误；④全等三角形的周长相等，正确．故选：C．9．【解答】解：∵AD是△ABC的高，∴∠ADB＝90°，∵∠BAD＝42°，∴∠ABD＝180°﹣∠ADB﹣∠BAD＝48°，∵BE是△ABC的角平分线，∴∠ABF＝∠ABD＝24°，∴∠BFD＝∠BAD+∠ABF＝42°+24°＝66°，故选：D．10．【解答】解：∵△ABC的周长为22，△ABM的周长比△ACM的周长大2，∴2＜BC＜22﹣BC，解得2＜BC＜11，又∵△ABC的三边长均为整数，△ABM的周长比△ACM的周长大2，∴AC＝为整数，∴BC边长为偶数，∴BC＝4，6，8，10，故选：A．二．填空题（共6小题）11．【解答】解：根据全等三角形的判定（SAS）可知属于全等的2个图形是①③，故答案为：①③．12．【解答】解：第①块只保留了原三角形的一个角和部分边，根据这两块中的任一块不能配一块与原来完全一样的；第②块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．应带②去．故答案为：②，ASA．13．【解答】解：∵Rt△ABC中，∠C＝90°，∠B＝25°，∴∠CAB＝90°﹣∠B＝90°﹣25°＝65°，由作图过程可知：MN是AB的垂直平分线，∴DA＝DB，∴∠DAB＝∠B＝25°，∴∠CAD＝∠CAB﹣∠DAB＝65°﹣25°＝40°．答：∠CAD的度数是40°．故答案为：40°．14．【解答】解：∵过点A，B分别作过点C的直线的垂线AE，BF，∴∠AEC＝∠CFB＝90°，在Rt△AEC和Rt△CFB中，，∴Rt△AEC≌Rt△CFB（HL），∴EC＝BF＝4.5，∴EF＝EC+CF＝4.5+3＝7.5，故答案为：7.5．15．【解答】解：边长为整数、周长为20的三角形分别是：（9，9，2）（8，8，4）（7，7，6）（6，6，8）（9，6，5）（9，7，4）（9，8，3）（8，7，5），共8个．故答案为：8．16．【解答】解：延长AG交BC于E．∵∠BAC＝90°，AB＝6，AC＝3，∴S△ABC＝•AB•AC＝9，∵G是△ABC的重心，∴AG＝2GE，BE＝EC，∴S△AEC＝×9＝4.5，∴S△AGC＝×S△AEC＝3，故答案为3三．解答题（共8小题）17．【解答】解：如图所示，图中三角形的个数有△ABC，△ACD，△ADE，△AEF，△AFG，△ABD，△ABE，△ABF，△ABG，△ACE，△ACF，△ACG，△ADF，△ADG，△AEG．18．【解答】解：∵BE＝CF，∴BE+EC＝CF+EC，即BC＝EF，在△ABC和△DEF中，∵，∴△ABC≌△DEF（SSS）．19．【解答】（1）证明：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，∴∠ADC＝∠CEB＝90°，∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，∴∠BCE＝∠DAC在△ADC和△CEB中，∴△ADC≌△CEB（AAS）；（2）解：由题意得：AD＝2×3＝6cm，BE＝7×2＝14cm，∵△ADC≌△CEB，∴EC＝AD＝6cm，DC＝BE＝14cm，∴DE＝DC+CE＝20（cm），答：两堵木墙之间的距离为20cm．20．【解答】证明（1）∵∠AED＝∠CFB＝90°，在Rt△AED和Rt△CFB中，∴Rt△AED≌Rt△CFB（HL）．（2）∵△AED≌△CFB，∴∠BDE＝∠DBF，在△DBE和△BDF中，∴△DBE≌△BDF（SAS），∴∠DBE＝∠BDF，∴BE∥DF．21．【解答】解：（1）如图，线段BD即为所求．（2）结论：BE＝BC．理由：∵BD平分∠ABC，∵BE＝BC，BD＝BD，∴△BDE≌△BDC（SAS），∴∠BED＝∠C．22．【解答】解：（1））∠1与∠B相等，理由：∵，△ABC中，∠ACB＝90°，∴∠1+∠F＝90°，∵FD⊥AB，∴∠B+∠F＝90°，∴∠1＝∠B；（2）若BC＝BD，AB与FB相等，理由：∵△ABC中，∠ACB＝90°，DF⊥AB，∴∠ACB＝∠FDB＝90°，在△ACB和△FDB中，，∴△ACB≌△FDB（AAS），∴AB＝FB．23．【解答】解：（1）∵∠MON＝60°，∴∠OBA+∠OAB＝120°，∵∠OBA、∠OAB的平分线交于点C，∴∠ABC+∠BAC＝×120°＝60°，∴∠ACB＝180°﹣60°＝120°，∴∠ACG＝60°；∵∠MON＝90°，∴∠OBA+∠OAB＝90°，∵∠OBA、∠OAB的平分线交于点C，∴∠ABC+∠BAC＝×90°＝45°，∴∠ACB＝180°﹣45°＝135°；故答案为：60，45；（2）在△AOB中，∠OBA+∠OAB＝180°﹣∠AOB＝180°﹣n°，∵∠OBA、∠OAB的平分线交于点C，∴∠ABC+∠BAC＝（∠OBA+∠OAB）＝（180°﹣n°），即∠ABC+∠BAC＝90°﹣n°，∴∠ACB＝180°﹣（∠ABC+∠BAC）＝180°﹣（90°﹣n°）＝90°+n°，∴∠ACG＝180°﹣（90°+n°）＝90°﹣n°；（3）∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠ABC＝ABO，∠BAC＝∠OAC＝，∵CF∥AO，∴∠ACF＝∠CAG，∵∠BGO＝∠BAG+∠ABG，∴∠BGO﹣∠ACF＝∠BAG+∠ABG﹣∠ACF＝2∠BAC+∠ABG﹣∠BAC＝∠ABG+∠BAC＝90°﹣n°．24．【解答】解：（1）在等腰直角三角形DEF中，∠DEF＝90°，∵∠1＝20°，∴∠2＝∠DEF﹣∠1＝70°，∵∠EDA+∠2+∠3＝180°，∴∠3＝60°，∵EA⊥AB，∴∠EAB＝90°，∵∠3+∠EAB+∠A＝180°，∴∠4＝30°，∵∠C＝90°，∴AB＝2BC＝4；（2）如图1，过D作DM⊥AE于M，在△DEM中，∠2+∠5＝90°，∵∠2+∠1＝90°，∵DE＝FE，在△DEM与△EF A中，，∴△DEM≌△EF A，∴AF＝EM，∵∠4+∠B＝90°，∵∠3+∠EAB+∠4＝180°，∴∠3+∠4＝90°，∴∠3＝∠B，在△DAM与△ABC中，，∴△DAM≌△ABC，∴BC＝AM，∴AE＝EM+AM＝AF+BC；（3）如图2，过D作DM⊥AE交AE的延长线于M，∵∠C＝90°，∴∠1+∠B＝90°，∵∠2+∠MAB+∠1＝180°，∠MAB＝90°，∴∠2+∠1＝90°，∠2＝∠B，在△ADM与△BAC中，，∴△ADM≌△BAC，∵EF＝DE，∠DEF＝90°，∵∠3+∠DEF+∠4＝180°，∴∠3+∠4＝90°，∵∠3+∠5＝90°，∴∠4＝∠5，在△MED与△AFE中，，∴△MED≌△AFE，∴ME＝AF，∴AE+AF＝AE+ME＝AM＝BC，即AE+AF＝BC．。

北师大数学七年级下册第一章到第七章单元测试题_含答案(第五章三角形全等为三套_共10套)

D. a 2 2ab b2
4。 3a 2 5a 1与 2a 2 3a 4 的和为
(）
A. 5a 2 2a 3 B。 a 2 8a 3 C。 a 2 3a 5
D. a 2 8a 5
5。下列结果正确的是
A。 1 2 1
3
9
B。 9 50 0
C. 53.70 1
2. 2x 3y 52x 3y 5
五、化简再求值： xx 2 y x 12 2x ，其中 x 1 ， y 25 . （7 分）
25
六、若 x m 4 ， x n 8 ，求 x3mn 的值。（6 分）
七、（应用题）在长为 3a 2 ，宽为 2b 1 的长方形铁片上，挖去长为 2a 4 ,宽为 b 的小长方形铁片，求剩余部分面积。（6 分）
一。选择题（本大题共 10 小题，每小题 3 分，共 30 分）
1．4。13×10－4 用小数表示为（
）
A．－41300 B．0。0413
C．0。00413 D．0.000413
2．生活在海洋中的蓝鲸，又叫长须鲸或剃刀鲸,它的体重达到 150 多吨,它体重的百万分之一
第 - 11 - 页共 61 页
三、解答题：
17、按要求作图(不写作法，但要保留作图痕迹)（3 分）
已知点 P、Q 分别在∠AOB 的边 OA，OB 上（如图）.
①作直线 PQ，
②过点 P 作 OB 的垂线，
③过点 Q 作 OA 的平行线。
18、已知线段 AB,延长 AB 到 C,使 BC∶AB=1∶3，D 为 AC 中点，若 DC = 2cm,求 AB 的长. (7 分)
. .
第 - 2 - 页共 61 页
北师大数学七年级下册第一章到第七章单元测试题_含答案(第五章三角形全等为三套_共 10 套)(word 版可编辑修改)

北师大版七年级(下)全等三角形、对称轴综合测试卷

北师大版七年级（下）轴对称数学综合测试卷一、选择题1．对于下列命题：(1)关于某一直线成轴对称的两个三角形全等；(2)等腰三角形的对称轴是顶角的平分线；(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点； (4)如果两个三角形全等，那么它们关于某直线成轴对称．其中真命题的个数为 A．0 B．1 C．2 D．3 ） ( )2．如图，△ABC 和△A′B′C′关于直线 L 对称，下列结论中正确的有（（1）△ABC≌△A′B′C′ （2）∠BAC=∠B′A′C′ （3）直线 L 垂直平分 CC′ （4）直线 BC 和 B′C′的交点不一定在直线 L 上． A．4 个 B．3 个 C．2 个 D．1 个第2题第5题第7题 3．一个角的对称轴是（） A．这个角的其中的一条边 B．这个角的其中的一条边的垂线 C．这个角的平分线 D．这个角的平分线所在的直线 4．下列四个判断：①成轴对称的两个三角形是全等三角形；②两个全等三角形一定成轴对称；③轴对称的两个圆的半径相等；④半径相等的两个圆成轴对称，其中正确的有（） A．4 个 B．3 个 C．2 个 D．1 个 5．如图，在平面内，把矩形 ABCD 沿 EF 对折，若∠1=50°，则∠AEF 等于（） A．115° B．130° C．120° D．65° 6．下图是我国几家银行的标志，其中是中心对称图形的有（）A．1 个 B．2 个 C．3 个 D．4 个 7.如图，∠1=∠2，PD⊥AB，PE⊥BC，垂足分别为 D、E，则下列结论中错误的是（） A．PD=PE B．BD=BE C．∠BPD=∠BPE D．BP=BE 8.如图，∠AOB 和一条定长线段 a，在∠AOB 内找一点 P，使 P 到 OA，OB 的距离都等于 a，作法如下：（1）作 OB 的垂线段 NH，使 NH=a，H 为垂足．（2）过 N 作 NM∥OB．（3）作∠AOB 的平分线 OP，与 NM 交于 P．（4）点 P 即为所求．其中（3）的依据是（） A．平行线之间的距离处处相等 B．到角的两边距离相等的点在角的平分线上 C．角的平分线上的点到角的两边的距离相等 D．到线段的两个端点距离相等的点在线段的垂直平分线上第8题第 10 题第 11 题 9.下列四个图形中，如果将左边的图形作轴对称变换，能变成右边的图形的是（）A．B．C．D．10．如图，在桌面上坚直放置两块镜面相对的平面镜，在两镜之间放一个小凳，那么在两镜中共可得到小凳的象（） A．2 个 B．4 个 C．16 个 D．无数个 11.如图，直线 l1、l2、l3 表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（） A．1 处 B．2 处 C．3 处 D．4 处二、填空题 11．已知等腰三角形的腰长是底边长的 ________.4 ，一边长为 11cm，则它的周长为 3第 12 题第 13 题第 14 题第 17 题12．如图，在△ABC 中， AB=AC， E 分别是 AC，上的点， BC=BD， D， AB 且 AD=DE=EB，则∠A=（）度． 13.如图，如果直线 m 是多边形 ABCDE 的对称轴，其中∠A=130°，∠B=110°．那么∠ BCD 的度数等于______________ 度． 14.如图，等边△ABC 中，D、E 分别在 AB、AC 上，且 AD=CE，BE、CD 交于点 P，若∠ ABE：∠CBE=1：2，则∠BDP= （）度．15. 等腰三角形的“三线合一”是指（）（），，（）互相重合． 16. 在直线、角、线段、等边三角形四个图形中，对称轴最多的是（），它有（）条对称轴；最少的是（），它有（）条对称轴． 17. 如图，DE 是 AB 的垂直平分线，交 AC 于点 D，若 AC=6 cm，BC=4 cm，则△BDC 的周长是（）． 18. 一天小刚照镜子时，在镜子中看见挂在身后墙上的时钟，如图，猜想实际的时间应是（）．第 18 题第 19 题第 20 题第 21 题 19.如图，在△ABC 中，∠C=90°，AD 平分∠BAC，BC=30，BD：CD=3：2，则点 D 到 AB 的距离为（） cm． 20.如图，D、E 为 AB、AC 的中点，将△ABC 沿线段 DE 折叠，使点 A 落在点 F 处，若∠ B=50°，则∠BDF=（）度． 21. 如图，直角△ABC 中，∠C=90°，∠BAC=2∠B，AD 平分∠BAC，CD：BD=1：2， BC=2.7 厘米，则点 D 到 AB 的距离 DE= 厘米，AD= （）厘米．三、解答题1．已知：如图 7—110，△ABC 中，AB＝AC，BE∥AC，∠BDE＝100°，∠BAD＝70°，则∠E 度数？2．如图 7—111，在 Rt△ABC 中，B 为直角，DE 是 AC 的垂直平分线，E 在 BC 上，∠BAE：∠ BAC＝1：5，则∠C 的度数？3．如图 7—112，∠BAC＝30°，AM 是∠BAC 的平分线，过 M 作 ME∥BA 交 AC 于 E，作 MD⊥ BA，垂足为 D，ME＝10cm，则 MD 的长度？4．如图 7—119，点 G 在 CA 的延长线上，AF＝AG，∠ADC＝∠GEC．求证：AD 平分∠BAC．5．已知：如图 7—120，等腰直角三角形 ABC 中，∠A＝90°，D 为 BC 中点，E、F 分别为 AB、 AC 上的点，且满足 EA＝CF．求证：DE＝DF．6.已知，如图Δ ABC 中，AB＝AC,D 点在 BC 上，且 BD＝AD，DC＝AC.将图中的等腰三角形全都写出来.并求∠B 的度数.ABDC7.如图，已知 P 点是∠AOB 平分线上一点，PC⊥OA，PD⊥OB，垂足为 C、D，（1）∠PCD=∠PDC 吗？为什么？（2）是 CD 的垂直平分线吗？为什么？ OPA CPODB8. 已知，△ABC 中，∠ABC 为锐角，且∠ABC=2∠ACB，AD 为 BC 边上的高，延长 AB 到 E，使 BE=BD，连接 ED 并延长交 AC 于 F．求证：AF=CF=DF．答案三、1.∠ABC=∠BDE - ∠BAD=100° =30° -70° ∠ACB = ∠ABC =30 ∠DAC = 180-100 - 30 =50 因为 BE//AC ∠E = ∠DAC=50°2∵DE 是 AC 的垂直平分线∴AE=CE ∴∠C=∠CAE ∵∠BAE∶∠BAC=1∶5 ∴∠BAE=1/5∠BAC ∴∠CAE=4/5∠BAC ∴∠C=4/5∠BAC 即∠BAC=5/4∠C ∵∠B=90° ∴∠BAC+∠C=90° ∴5/4∠C+∠C=90° ∠C=40°3 解：过 E 点作 AB 的垂线交 AB 于 F因为 ME‖AB，且 AM 是∠BAC 的平分线所以∠EMA=∠MAB=1/2 乘以 30°=15° 所以三角形 AEM 为等腰三角形所以 AE=EM=10cm 又，在直角三角形 AEF 中 ∠BAC=30° 所以 EF=1/2AE=5cm 又 EFDM 为长方形，所以 MD=EF=5cm4 证明：∵AF=AG， ∴∠G=∠GFA． ∵∠ADC=∠GEC， ∴AD∥GE． ∴∠BAD=∠GFA，∠DAC=∠G． ∴∠BAD=∠DAC，即 AD 平分∠BAC．5.证明：连 AD，如图，∵△ABC 为等腰直角三角形，D 为 BC 中点， ∴AD=DC，AD 平分∠BAC，∠C=45°， ∴∠EAD=∠C=45°，在△ADE 和△CDF 中∴△ADE≌△CDF， ∴DE=DF．6. 解析因为 AB=AC，BD=AD，DC=AC，由等腰三角形的概念得△ABC，△ADB，△ADC 是等腰三角形，再根据角之间的关系求得∠B 的度数．解答图中等腰三角形有△ABC，△ADB，△ADC ∵AB=AC ∴△ABC 是等腰三角形； ∵BD=AD，DC=AC ∴△ADB 和△ADC 是等腰三角形； ∵AB=AC ∴∠B=∠C ∵BD=AD，DC=AC ∴∠B=∠BAD，∠ADC=∠DAC ∴5∠B=180° ∴∠B=36° ．7.解：（1）∠PCD=∠PDC。

北师大版数学七年级下册《全等三角形》单元测试题含答案

全等三角形单元测试2含答案（满分100分，时间120分钟）一、选择题（每小题3分，共30分）1、在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100°，那么在△ABC 中与这100°角对应相等的角是（A ）A.∠AB.∠BC.∠CD.∠B 或∠C2、如图1，在CD 上求一点P ，使它到OA ，OB 的距离相等，则P 点是（ D ） A.线段CD 的中点 B.OA 与OB 的中垂线的交点 C.OA 与CD 的中垂线的交点 D.CD 与∠AOB 的平分线的交点图1 图2 图3 3、如图2所示，△ABD ≌△CDB ，下面四个结论中，不正确的是（） A.△ABD 和△CDB 的面积相等 B.△ABD 和△CDB 的周长相等 C.∠A +∠ABD ＝∠C +∠CBD D.AD ∥BC ，且AD ＝BC4、如图3，已知AB ＝DC ，AD ＝BC ，E ，F 在DB 上两点且BF ＝DE ，若∠AEB ＝120°，∠ADB ＝30°，则∠BCF ＝（）A.150°B.40°C.80°D.90°5、如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的ADA CB O D CBAABCEF ABCDFEOA.25°B.27°C.30°D.45°8、如图6，在△ABC 中，AD 平分∠BAC ，过B 作BE ⊥AD 于E ，过E 作EF ∥AC 交AB 于F ，则（）A.AF ＝2BFB.AF ＝BFC.AF ＞BFD.AF ＜BF9、如图7所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（） A.SSS B.SAS C.AAS D.ASA图7图8 图910、将一张长方形纸片按如图8所示的方式折叠，BC BD ，为折痕，则CBD ∠的度数为（）11、（2011河南）如图9，在△ABC 中，AB =AC ，CD 平分∠ACB ，∠A =36°，则∠BDC 的度数为 .． 12、如图10，在△ABC 中，AB ＝AC ，BE 、CF 是中线，则由可得△AFC ≌△AEB .图10 图11 图1213、如图11，AB ＝CD ，AD ＝BC ，O 为BD 中点，过O 点作直线与DA 、BC 延长线交于E 、F ，若∠ADB ＝60°，EO ＝10，则∠DBC ＝，FO ＝ .AB 边的距离为＿＿＿.15、已知：△ABC ≌△A ′B ′C ′，∠A=∠A ′，∠B=∠B ′，∠C=70°，AB=15cm ，则∠C ′=_________，A ′B ′=__________。

新北师大版数学七下第四章三角形单元测试

第四章三角形一、选择题(每小题3分,共30分)1.下面是2014年仁川亚运会的会徽和吉祥物,其中是全等图形的一组是()答案 B 选项A和D中的两个图形的形状相同,大小不同,选项C中的两个图形的形状、大小都不相同,只有选项B中的两个图形的形状、大小都相同,故选B.2.如果一个三角形的两边长分别是2和4,则第三边的长可能是()A.2B.4C.6D.8答案 B 设第三边的长为x,则4-2<x<2+4,即2<x<6,故选B.3.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A.等边三角形B.锐角三角形C.直角三角形D.钝角三角形答案 D ∵∠A=20°,∠B=60°,∴∠C=180°-∠A-∠B=180°-20°-60°=100°,∴△ABC是钝角三角形.故选D.4.如图4-6-1,D,E分别为△ABC的边AC,BC的中点,则下列说法不正确的是()图4-6-1A.DE是△BDC的中线B.BD是△ABC的中线C.AD=DC,BE=ECD.∠C的对边是DE答案 D 在△DEC中,∠C的对边是DE.5.如图4-6-2,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()图4-6-2A.30°B.35°C.40°D.45°答案 C ∵AB∥CD,∴∠FEB=∠C=70°,又∵∠AEF+∠BEF=180°,∴∠AEF=180°-70°=110°,在△AEF 中,∠A+∠F+∠AEF=180°,∴∠A=180°-∠AEF-∠F=40°.6.如图4-6-3,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()图4-6-3A.∠A=∠CB.∠D=∠BC.AD∥BCD.DF∥BE答案 B 当∠D=∠B时,在△ADF和△CBE中,∵{AD =BC,∠D =∠B,DF =BE, ∴△ADF ≌△CBE(SAS), 故选B.7.已知三角形的三边长分别为4,x,7,且x 为奇数,则满足条件的三角形的个数为( ) A.3 B.4 C.5 D.6答案 A 由已知得3<x<11,又∵x 为奇数,则x 可取5、7、9.故满足条件的三角形有3个.8.如图4-6-4,在△ABC 中,∠ABC 、∠ACB 的平分线BE 、CD 相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )图4-6-4A.118°B.119°C.120°D.121°答案 C 在△ABC 中,∠ACB=180°-∠A-∠ABC=180°-60°-42°=78°.∵BE 、CD 分别平分∠ABC 、∠ACB,∴∠FBC=12∠ABC=21°,∠FCB=12∠ACB=39°,∴∠BFC=180°-∠FBC-∠FCB=180°-21°-39°=120°.故选C. 9.图4-6-5如图4-6-5,已知AB=AC,AE=AF,BE 与CF 交于点D,则以下结论:①△ABE ≌△ACF;②△BDF ≌△CDE;③D 在∠BAC 的平分线上,其中正确的是( )A.①B.②C.①②D.①②③ 答案 D ∵AB=AC,∠A=∠A,AE=AF, ∴△ABE ≌△ACF(SAS).∴∠AEB=∠AFC,∠B=∠C,∴∠CED=∠BFD, ∵AB=AC,AF=AE,∴BF=CE. ∴△BDF ≌△CDE.∴CD=BD. 连接AD,∵AB=AC,BD=CD,AD=AD, ∴△ABD ≌△ACD(SSS),∴∠CAD=∠BAD,∴D 在∠BAC 的平分线上,故①②③都正确.图4-6-610.如图4-6-6,△ABC 的底边边长BC=a,当顶点A 沿BC 边上的高AD 由A 向D 移动到达E 点时,若DE=12AE,则△ABC 的面积将变为原来的( )A.12 B.13 C.14 D.19答案 B ∵DE=12AE=13AD, ∴S △BCE =12BC ·DE=12BC ·13AD=13S △ABC . 故选B.二、填空题(每小题4分,共24分)11.如图4-6-7,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是利用了.图4-6-7答案三角形的稳定性12.在△ABC中,BC=10,AB=6,那么AC的取值范围是.答案4<AC<16解析由三角形三边关系得10-6<AC<10+6,即4<AC<16.13.如图4-6-8,已知∠B=78°,∠C=40°,AD平分∠BAC,则∠ADB=.图4-6-8答案71°解析∵∠B=78°,∠C=40°,∴∠BAC=180°-∠B-∠C=62°,∵AD平分∠BAC=31°,∴∠ADB=180°-∠B-∠BAD=71°.∠BAC,∴∠BAD=1214. 如图4-6-9,△ABC中,AD为中线,DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE=.图4-6-9答案 2解析 ∵AD 是△ABC 的中线,∴S △ABD =S △ACD .又S △ACD =12AC ·DF=12×4×1.5=3,∴S △ABD =12AB ·DE=3,∴DE=2.15.)如图4-6-10,在△ABC 中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .图4-6-10答案 3解析 ∵∠A=∠A,∠1=∠2,BE=CD,∴△ABE ≌△ACD,∴AD=AE=2,AB=AC=5,∴CE=AC -AE=5-2=3.16.如图4-6-11所示:要说明△ABC ≌△BAD.(1)已知∠1=∠2,若要以SAS 为依据,则可添加的一个条件是 ;(2)已知∠1=∠2,若要以AAS 为依据,则可添加的一个条件是 ;(3)已知∠1=∠2,若要以ASA 为依据,则可添加的一个条件是 .图4-6-11答案 (1)BC=AD (2)∠C=∠D (3)∠BAC=∠ABD三、解答题(共46分)17.(10分)如图4-6-12,点C,E,F,B 在同一直线上,点A,D 在BC 异侧,AB ∥CD,AE=DF,∠A=∠D.求证:AB=CD.图4-6-12证明 ∵AB∥CD,∴∠B=∠C,在△ABE 和△DCF 中,{∠B =∠C,∠A =∠D,AE =DF,∴△ABE ≌△DCF,∴AB=CD.18.(12分)如图4-6-13所示,A,B 两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B 出发沿河岸画一条射线BF,在BF 上截取BC=CD,过D 作DE ∥AB,使E,C,A 在同一条直线上,则DE 的长就是A,B 之间的距离.请你说明理由.图4-6-13解析因为AB ∥DE,所以∠ABC=∠EDC, 在△ABC 和△EDC 中,{∠ABC =∠EDC,BC =DC,∠ACB =∠ECD,所以△ABC ≌△EDC,所以AB=DE.即DE 的长就是A,B 之间的距离.19.(10分)图4-6-14如图4-6-14所示,某块三角形模具ABC的阴影部分已经破损.(1)只要从残留的模具片中度量出哪些边、角,就可以不带残留的模具片到店铺加工一块与原来的三角形模具ABC的形状和大小完全相同的三角形模具A'B'C'?请简要说明理由;(2)作出三角形模具A'B'C'(要求:尺规作图,保留作图痕迹,不写作法和理由).解析(1)只要度量残留的三角形模具片的∠B,∠C的度数和边BC的长即可.理由如下:两角及其夹边对应相等的两个三角形全等.(2)如图所示.20.(14分)如图4-6-15,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.点Q在线段CA上从点C向终点A运动.(1)若点P在线段BC上以3厘米/秒的速度从点B向终点C运动,同时．．①若点Q的速度与点P的速度相等,经过1秒后,请说明△BPD≌△CQP;②若点Q的速度与点P的速度不等,当点Q的速度为多少时,能使△BPD≌△CPQ?(2)若点P 以3厘米/秒的速度从点B 向点C 运动,同时．．点Q 以5厘米/秒的速度从点C 向点A 运动,它们都依次沿△ABC 三边运动,则经过多长时间,点Q 第一次在△ABC 的哪条边上追上点P?图4-6-15解析 (1)①证明:∵BP=3×1=3厘米,CQ=3×1=3厘米,∴BP=CQ.∵D 为AB 的中点,∴BD=AD=5厘米.∵CP=BC -BP=8-3=5厘米, ∴BD=CP.又∵∠B=∠C,∴△BPD ≌△CQP(SAS).②设点Q 的运动时间为t 秒,运动速度为v 厘米/秒. ∵△BPD ≌△CPQ,∴BP=CP=4厘米,CQ=BD=5厘米,∴t=BP 3=43秒,∴v=CQ t =543=154 厘米/秒.∴当点Q 的运动速度为154 厘米/秒时,能使△BPD ≌△CPQ. (2)设经过x 秒点Q 第一次追上点P.由题意,得5x-3x=2×10,解得x=10.∴点P运动的路程为3×10=30(厘米),∵30=28+2,∴此时点P在BC边上,∴经过10秒点Q第一次在边BC上追上点P.。

第四章三角形章节测试同步练习2022-2023学年北师大版七年级数学下册

北师大版七下三角形章节测试一、选择题（共11小题）1. 下列各图中a，b，c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是( )A. 甲和乙B. 乙和丙C. 甲和丙D. 只有丙2. 如果过三角形重心的一条直线将该三角形分成两个直角三角形，则该三角形一定是( )A. 锐角三角形B. 钝角三角形C. 等腰三角形D. 等边三角形3. 已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为( )A. 2B. 3C. 5D. 134. 用直尺和圆规作已知角的平分线的示意图如图所示，则说明∠CAD=∠DAB的依据是( )A. SSSB. SASC. ASAD. AAS5. 一块三角形玻璃，被摔成如图所示的四块，小敏想去店里买一块形状、大小与原来一样的玻璃，借助“全等三角形”的相关知识，小敏只带了一块去，则这块玻璃的编号是( )A. ①B. ②C. ③D. ④6. 根据下列条件，能唯一画出△ABC的是( )A. AB=3，BC=4，AC=8B. AB=4，BC=3，∠A=30∘C. ∠A=60∘，∠B=45∘，AB=4D. ∠C=90∘，AB=67. 根据下列已知条件，能作出唯一△ABC的是( )A. AB=3，BC=4，CA=8B. AB=4，BC=3，∠A=60∘C. ∠A=60∘，∠B=45∘，AB=4D. ∠C=90∘，∠B=30∘，∠A=60∘8. 下列长度的三条线段，不能组成三角形的是( )A. 3，8，4B. 4，9，6C. 15，20，8D. 9，15，89. 下列说法中错误的是( )A. 三角形的三个内角中，最多有一个钝角B. 三角形三个内角中，至少有两个锐角C. 直角三角形中有两个锐角互余D. 三角形中两个内角和必大于90∘10. 两个边长分别为a，b，c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形，用两种不同的计算方法计算这个图形的面积，则可得等式为( )A. (a+b)2=c2B. (a−b)2=c2C. a2+b2=c2D. a2−b2=c211. 如图，点B，C分别在AE，AD上，BD与CE相交于点O，如果AB=AC，AD=AE，那么图中的全等三角形共有( )A. 2对B. 3对C. 4对D. 5对二、填空题（共8小题）12. 已知△ABC的两条中线AD，BE相交于点F．如果AF=10，那么AD的长为．13. 请完善本课的知识结构图：14. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出个．15. 如图，在5×5的正方形网格中，每个小正方形的边长都为1，以AB为一边画一个等腰三角形ABC，使点C在格点上，点C的个数．16. 在△ABC中，如果∠A−∠B=90∘，则△ABC是三角形．17. 若直角三角形的一个锐角为15∘，则另一个锐角等于．18. 如图，一块三角形玻璃碎成了Ⅰ、Ⅱ两块，现需购买同样大小的一块三角形玻璃，为方便起见，只需带上第块玻璃碎片．19. 如图所示，图中有个三角形，其中以AB为边的三角形为，含∠OCB的三角形为．在△BOC中，OC的对角是，∠OCB的对边是．三、解答题（共5小题）20. 如图所示的每个图形中各有多少个三角形?21. 如图，已知 A ，D ，C ，F 在同一条直线上，AC =FD ，AB =FE ，∠A =∠F ，请说明 △ABC 与△FED 全等的理由．22. 一个三角形的三个内角度数之比为 1:1:2．求这个三角形三个内角的度数，并说明该三角形的形状．23. 如图，AB 与 CD 相交于点 O ，如果 ∠A =∠C ，OA =OC ，那么 △AOD 与 △COB 全等吗?为什么?解：在 △AOD 和 △COB 中，{ ( ), ( ),∠AOD =∠COB ( ), 所以 △AOD ≌△COB ( )．24. 如图①，在 Rt △ABC 中，∠C =90∘，BC =9 cm ，AC =12 cm ，AB =15 cm ，现有一动点 P ，从点 A 出发，沿着三角形的边 AC →CB →BA 运动，回到点 A 停止，速度为 3 cm/s ，设运动时间为 t s ．（1）如图①，当t=时，△APC的面积等于△ABC面积的一半；（2）如图②，在△DEF中，∠E=90∘，DE=4cm，DF=5cm，∠D=∠A．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好使△APQ≌△DEF，求点Q的运动速度．答案1. B2. C【解析】∵三角形重心是三角形三边中线的交点，过这一点的直线恰好分三角形为两个直角三角形，则这条线在三角形内部的线段是高，利用三角形“三线合一”的性质，即可推断这是等腰三角形．3. B4. A【解析】从角平分线的作法得出，△AFD与△AED的三边对应相等，则△AFD≌△AED(SSS)，所以∠CAD=∠DAB．5. C【解析】因为第③块中有完整的两个角以及他们的夹边，利用ASA易证三角形全等，故应带第3块．故选：C．6. C7. C【解析】A. ∵AB=3，BC=4，CA=8，AB+BC<CA，∴不能画出三角形，故本选项不合题意；B. AB=4，BC=3，∠A=60∘，不能画出唯一三角形，故本选项不合题意；C.当∠A=60∘，∠B=45∘，AB=4时，根据“ASA”可判断△ABC的唯一性；D.已知三个角，不能画出唯一三角形，故本选项不符合题意．8. A9. D【解析】A、三角形的三个内角中，最多有一个钝角，正确．B 、三角形三个内角中，至少有两个锐角，正确．C、直角三角形中有两个锐角互余，正确，D、三角形中两个内角和必大于90∘，错误，比如钝角三角形的两个锐角的和小于90∘．10. C【解析】根据题意得：S=12(a+b)(a+b)，S=12ab+12ab+12c2，∴12(a+b)(a+b)=12ab+12ab+12c2，即(a+b)(a+b)=ab+ab+c2，整理得：a2+b2=c2．11. C12. 1513. 不在同一直线上，首尾顺次联结，三角形任意两边的和大于第三边，三角形任意两边的差小于第三边，AD，AD，BC，ADB，ADC，AE，BE，CE，BC，BC，BE，CE，AF，∠BAF，∠CAF，∠BAC，∠BAC，∠BAF，∠CAF14. 415. 7【解析】16. 钝角【解析】因为 ∠A −∠B =90∘，所以 ∠A =90∘+∠B ，所以 ∠A 是钝角，所以 △ABC 是钝角三角形．17. 75∘【解析】∵ 直角三角形的一个锐角为 15∘，∴ 另一个锐角 =90∘−15∘=75∘．18. Ⅰ19. 8，△ABO ；△ABC ；△ABD ，△BOC ；△ABC ，△OBC ，OB【解析】题图中有 8 个三角形，分别是 △ABO ，△ABD ，△ABC ，△BOC ，△ODC ，△BDC ，△ADO ，△ADC ，其中以 AB 为边的三角形为 △ABO ，△ABC ，△ABD ；含 ∠OCB 的三角形为 △BOC ，△ABC ．在 △BOC 中，OC 的对角是 ∠OBC ，∠OCB 的对边是 OB ．20. 如图所示，（1）中有 8 个三角形；（2）中有 5 个三角形；（3）中有 6 个三角形．21. 在 △ABC 和 △FED 中，{AC =DF(已知),∠A =∠F(已知),AB =FE(已知),所以 △ABC ≌△FED (SAS )．22. 45∘，45∘，90∘．等腰直角三角形．23. ∠A =∠C ；已知；OA =OC ；已知；对顶角相等；ASA24. （1） 112 或 192【解析】①当点 P 在 BC 上时，如图 1，若△APC的面积等于△ABC面积的一半，则12AC⋅CP=12⋅12AC⋅CB，∴CP=12BC=92cm，此时，点P移动的距离为AC+CP=12+92=332cm，∴移动的时间为332÷3=112s．②当点P在BA上时，过点C作CD⊥AB，交AB于D，如图2，若△APC的面积等于△ABC面积的一半，则12AP⋅CD=12⋅12AB⋅CD，∴AP=12AB，即点P为BA的中点，此时，点P移动的距离为AC+CB+BP=12+9+152=572cm，∴移动的时间为572÷3=192s．故答案为112或192．（2）∵△APQ≌△DEF，∴对应顶点为A与D，P与E，Q与F．①当点P在AC上时，如图3所示：此时，AP=4cm，AQ=5cm，∴点Q移动的速度为5÷(4÷3)=154cm/s．②当点P在AB上时，如图4所示：此时AP=4cm，AQ=5cm，即点P移动的距离为AC+CB+BP=9+12+15−4=32cm，点Q移动的距离为AB+BC+CQ=15+9+12−5=31cm，∴点Q移动的速度为31÷(32÷3)=9332cm/s，综上所述，点Q的运动速度为154cm/s或9332cm/s．第11页（共11 页）。

北师大数学七年级下《第四章三角形》章节检测题含答案

北师大版数学七年级下册第四章三角形章节检测题一、选择题1．在下列长度的四根木棒中，能与长为4 cm，9 cm的两根木棒钉成一个三角形的是( )A．4 cm B．5 cm C．9 cm D．13 cm2．在△ABC中，∠A＝20°，∠B＝60°，则△ABC的形状是( )A．等边三角形 B．锐角三角形 C．直角三角形 D．钝角三角形3．下列说法中正确的是( )A．面积相等的两个图形是全等图形B．周长相等的两个图形是全等图形C．所有正方形都是全等图形D．能够完全重合的两个图形是全等图形4．如图，AB∥FC，DE＝EF，AB＝15，CF＝8，则BD等于( )A．8 B．7 C．6 D．55．如图，为测量B点到河对面的目标A之间的距离，他们在B点同侧选择了一点C，测得∠ABC＝70°，∠ACB＝40°，然后在M处立了标杆，使∠CBM＝70°，∠BCM＝40°，那么需要测量________才能测得A，B之间的距离( )A．AB B．AC C．BM D．CM6．如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )A．α B．90°－12α C．90°－α D．180°－2α7．一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF＝100°，那么∠BMD为( )A．95° B．85° C．90° D．100°二、填空题8．如图，直线l1∥l2，若∠1＝130°，∠2＝60°，则∠3＝_______．9．如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连接AD，CD.若∠B＝65°，则∠ADC的大小为________．10．如图是一副三角板叠放的示意图，则∠α＝________.11．如图，在△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B＝40°，∠C＝78°，则∠EAD＝____°.12．一角为80°的三角形中，另两角的角平分线相交所成的锐角是________．13．如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为____．三、解答题14．如图，点C，F在线段BE上，BF＝EC，∠1＝∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．(不再添加辅助线和字母)15．(·河北)如图，点B，F，C，E在直线l上(F，C之间不能直接测量)，点A，D在l异侧，测得AB ＝DE，AC＝DF，BF＝EC.(1)求证：△ABC≌△DEF；(2)指出图中所有平行的线段，并说明理由．16．如图，在△ABC中，BE，CF分别是AC，AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连接AD，AG.求证：AG＝AD.17．某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A；②沿河岸直走20步有一棵树C，继续前行20步到达D处；③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长就是河宽AB.请你证明他们做法的正确性．18．如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AD平分∠CAB.(2)延长AC 至点E ，使CE ＝AC ，求证：DA ＝DE.答案：一、1---7 CDDBC BB二、8. 70°9. 65°10. 75°11. 19 °12. 50°13. 8三、14. 解：答案不唯一，如添加AC ＝DF ，证明：∵BF ＝EC ，∴BF －CF ＝EC －CF ，即BC ＝EF ，在△ABC 和△DEF 中，⎩⎪⎨⎪⎧AC ＝DF ，∠1＝∠2，BC ＝EF ，∴△ABC ≌△DEF15. 解：(1)∵BF ＝CE ，∴BF ＋CF ＝CE ＋CF ，即BC ＝EF ，又∵AB ＝DE ，AC ＝DF ，∴△ABC ≌△DEF(SSS) (2)AB ∥DE ，AC ∥DF.理由：∵△ABC ≌△DEF ，∴∠ABC ＝∠DEF ，∠ACF ＝∠DFE ，∴AB ∥DE ，AC16. 解：∵BE ，CF 分别是AC ，AB 两条边上的高，∴∠ABD ＋∠BAC ＝90°，∠GCA ＋∠BAC ＝90°，∴∠GCA ＝∠ABD ，在△GCA 和△ABD 中，∵GC ＝AB ，∠GCA ＝∠ABD ，CA ＝BD ，∴△GCA ≌△ABD ，∴AG ＝AD17. 解：做法正确．证明：在△ABC 和△EDC 中，∴△ABC ≌△EDC(ASA)，∴AB ＝DE18. 解：(1)∵在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，∴∠CAB ＝60°.又∵AD 平分∠CAB ，∴∠CAD ＝12∠CAB ＝30° (2)∵∠ACD ＋∠ECD ＝180°，且∠ACD ＝90°，∴∠ECD ＝90°，∴∠ACD ＝∠ECD.在△ACD 与△ECD 中，⎩⎪⎨⎪⎧AC ＝EC ，∠ACD ＝∠ECD ，CD ＝CD ，∴△ACD ≌△ECD(SAS)，∴DA ＝DE。

新北师大版七年级数学下册第三章全等三角形练习题

推理过程出现逻辑错误：在证明全等三角形的过程中，逻辑推理不严密，导致结论错误。图形绘制不准确：在绘制全等三角形时，图形绘制不准确，导致证明过程出现错误。
题目类型：选择题、填空题、证明题等解题思路：根据全等三角形的性质和判定定理，分析题目中的条件，选择合适的解题方法。易错点分析：学生在解题过程中容易出现哪些错误，如概念混淆、定理应用不当等。练习题解析：针对具体的练习题目，进行详细的解析，包括解题思路、步骤和答案。
XX,a click to unlimited possibilities
01 全等三角形的性质和判定方法 02 全等三角形的应用 03 全等三角形的综合应用 04 全等三角形的易错点分析
全等三角形对应角相等全等三角形对应边相等全等三角形的对应高、中线、角平分线相等全等三角形的周长和面积相等
添加标题
添加标题
题目：已知三角形ABC中，AB=AC，D 是BC上一点，E是线段AD上一点，且 ∠BED=2∠BAC=90°，BD=1，CD=2，求DE的长。
添加标题
题目：在三角形ABC中，AB=AC，D是 BC的中点，E是线段AD上一点，且 ∠BED=2∠BAC=90°，求证：BE⊥AD。
条件：SAS、ASA、SSS、AAS 应用：证明线段相等、角相等、证明两三角形全等证明方法：根据条件选择合适的方法进行证明注意事项：避免使用不正确的证明方法
题目：已知三角形ABC全等于三角形DEF，且三角形ABC的周长为12，若M为AB的中点，且MC=3，求DF的长。
题目：在三角形ABC中，角A=90度，AB=AC，D为BC上任意一点，求证：BD^2 + CD^2 = 2AD^2。

第4章三角形全等三角形判定(基础版) -北师大版数学七年级下册(含答案)

全等三角形判定(基础版) (北师版数学）一．选择题（共24小题）1．下列命题中正确的是（）A．有两条边相等的两个等腰三角形全等B．两腰对应相等的两个等腰三角形全等C．两角对应相等的两个等腰三角形全等D．一边对应相等的两个等边三角形全等2．如图，已知∠1＝∠2，要说明△ABD≌△ACD，还需从下列条件中选一个，错误的选法是（）A．∠ADB＝∠ADC B．∠B＝∠C C．DB＝DC D．AB＝AC3．利用尺规进行作图，根据下列条件作三角形，画出的三角形不唯一的是（）A．已知三条边B．已知三个角C．已知两角和夹边D．已知两边和夹角4．如图，已知MB＝ND，∠MBA＝∠NDC，下列哪个条件不能判定△ABM≌△CDN（）A．AM＝CN B．AB＝CD C．AM∥CN D．∠M＝∠N5．如图，∠C＝∠B，能用ASA来判断△ABD≌△ACE，需要添加的条件是（）A．AE＝AD B．AB＝AC C．CE＝BD D．∠ADB＝∠ABC 6．如图，已知∠A＝∠D，∠1＝∠2，那么要得到△ABC≌△DEF，还应给出的条件是（）A．∠B＝∠E B．CD＝AF C．AB＝EF D．BC＝ED7．如图，已知AB＝DC，需添加下列（）条件后，就一定能判定△ABC≌△DCB．A．AO＝BO B．∠ACB＝∠DBC C．AC＝DB D．BO＝CO8．用直尺和圆规作一个角等于已知角的作图痕迹如图所示，则作图的依据是（）A．SSS B．SAS C．ASA D．AAS9．下列说法正确的是（）A．垂直于同一条直线的两条直线互相平行B．如果△ABC的三个内角满足∠A：∠B：∠C＝1：2：3，则这个三角形是锐角三角形C．有两角与一边相等的两个等腰三角形全等D．角平分线上的点到这个角的两边的距离相等10．如图，E是线段AB的中点，∠AEC＝∠DEB，再添加一个条件，使得△AED≌△BEC，所添加的条件不正确的是（）A．AD＝BC B．DE＝CE C．∠A＝∠B D．∠C＝∠D 11．下列说法中正确的个数是（）①两个角和其中一角的对边对应相等的两个三角形全等；②两条边和其中一边的对角对应相等的两个三角形全等；③有一边对应相等的两个等边三角形全等．A．0B．1C．2D．312．如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ＝PQ，PR＝PS，下面三个结论：①AS＝AR②QP∥AR③△BRP≌△QSP．其中正确的是（）A．①③B．②③C．①②D．①②③13．下列判断正确的是（）A．有两角和一边对应相等的两个三角形全等B．有一角和一条边相等的两个直角三角形全等C．有两边对应相等，且有一角为30°的两个等腰三角形全等D．有两边和其中一边的对角对应相等的两个三角形全等14．下列说法错误的是（）A．同旁内角互补，两条直线平行B．相等的角不一定是对顶角C．有两个角和一条边对应相等的三角形一定全等D．两条直线被第三条直线所截，同位角相等15．不能判定两个三角形全等的条件是（）A．三条边对应相等B．两角及一边对应相等C．两边及夹角对应相等D．两边及一边的对角相等16．一定能确定△ABC≌△DEF的条件是（）A．∠A＝∠D，∠B＝∠E，∠C＝∠F B．∠A＝∠E，AB＝EF，∠B＝∠DC．∠A＝∠D，AB＝DE，∠B＝∠E D．AB＝DE，BC＝EF，∠A＝∠D17．具备下列条件的两个三角形中，不一定全等的是（）A．能够完全重合B．三边对应相等C．两角及一边对应相等D．两边及一角对应相等18．如图，已知∠A＝∠D，AF＝CD，那么要得到△ABC≌△DEF，还应该给出的条件是（）A．AB＝EF B．∠E＝∠B C．CD＝AF D．ED＝BC19．下列语句中不正确的是（）A．斜边和一锐角对应相等的两个直角三角形全等B．有两边对应相等的两个直角三角形全等C．有一条边相等，有一个内角相等的两个等腰三角形全等D．在△ABC中，边AB、BC、AC的垂直平分线相交于点P，则P A＝PB＝PC20．如图，如果平行四边形ABCD的对角线AC和BD相交于点O，那么图中的全等三角形共有（）A．1对B．2对C．3对D．4对21．如图，等腰△ABC中，点D，E分别在腰AB，AC上，添加下列条件，不能判定△ABE ≌△ACD的是（）A．AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC 22．如图，在直线AC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD交于点H，AE与DB交于点G，BE与CD交于点F，下列结论：（1）△ABE≌△DBC；（2）∠AHD＝60°；（3）△AGB≌△DFB；（4）BH平分∠GBF；（5）GF∥AC；（6）点H是线段DC的中点．正确的有（）A．6个B．5个C．4个D．3个23．如图，AB＝DB，∠ABD＝∠CBE，①BE＝BC，②∠D＝∠A，③∠C＝∠E，④AC＝DE，能使△ABC≌△DBE的条件有（）个．A．1B．2C．3D．424．如图，在△ABC中，BF平分∠ABC，点D在BC的延长线上，作∠ACD的平分线交BF延长线于E点，过点E作EG∥BD分别交AB、AC于G、H点．连接AE，有以下结论，①BG＝EG；②∠BEC＝∠BAC；③△HEF≌△CBF；④∠AEB+∠ACE＝90°；⑤BG﹣CH＝GH．其中正确的结论的个数是（）A．2B．3C．4D．5全等三角形判定(基础版) - 2021年暑假初一升初二(北师版数学）参考答案与试题解析一．选择题（共24小题）1．D2．C3．B4．A5．B6．B7．C8．A9．D10．A11．C12．C13．A14．D15．D16．C17．D18．B19．C20．D21．B22．C23．C24．B。

北师大版七年级数学下册第3章《三角形》单元测试试卷及答案(3)

，北师大版七年级数学下册第 3 章《三角形》单元测试试卷及答案（3）一、填空题（共 10 小题）1．一个等腰三角形的两边长分别是 3cm 和 7cm ，则它的周长是_________ cm ．△2．若∠A=∠B=2∠C ，则 ABC 是 _________ 三角形．（填“钝角”、“锐角”或“直角”）△3．如图， ABC≌△DEF ，△ABC 的周长为 25cm AB=6cm ，CA=8cm ，则 DE= _________ ， DF= _________ ，EF= _________ ．4．如图，AB=AD ，BC=DC ，要证∠B=∠D ，则需要连接 _________ ，从而可证 _________和 _________ 全等．5．如图，AD ，AE 分别是△ABC 的角平分线和高线，且∠B=50°，∠C=70°，则∠EAD= _________ ．△6．如图，CA⊥BE ，且 ABC≌△ADE ，则 BC 与 DE 的关系是 _________ ．7．如图，有一块边长为 4 的正方形塑料模板 ABCD ，将一块足够大的直角三角板的直角顶点落在 A 点，两条直角边分别与 CD 交于点 F ，与 CB 延长线交于点 E ．则四边形 AECF 的面积是 _________ ．8．如图，BA∥CD，∠A=90°，AB=CE，BC=ED，则△CED≌_________，根据是_________．△9．如图，ABC中，AB=AC，BC=8，BD是AC边上的中线，△ABD与△BDC的周长的差是2，则AB=_________．10．如图，对面积为1的△ABC逐次进行以下操作：第一次操作，分别延长AB，BC，CA，得到A B C，至点A，B，C，使得A B=2AB，B C=2BC，C A=2CA，顺次连接A，B，C△1 11111111111记其面积为S；第二次操作，分别延长A B，B C，C A至点A，B，C，使得A B=2A B，11111112222111，得到A B C，记其面积为S；…；按B C=2B C，C A=2C A，顺次连接A，B，C△221112111222222B C，则其面积S=_________．此规律继续下去，可得到A△5555二、选择题（共8小题）11．在下列四组线段中，能组成三角形的是（）A．2，2，5B．3，7，10C．3，5，9D．4，5，7△12．（2011•宿迁）如图，已知∠1=∠2，则不一定能使ABD≌△ACD的条件是（）A．AB=AC B．BD=CD C．∠B=∠C D．∠BDA=∠CDA 13．如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（）A．图中有三个直角三角形B．∠1=∠2C．∠1和∠B都是∠A的余角D．∠2=∠A14．如图，AC⊥BC，CD⊥AB，DE⊥BC，分别交B C，AB，BC于点C，D，E，则下列说法中不正确的是（）A．AC是△ABC和△ABE的高B．DE，DC都是△BCD的高C．DE是△DBE和△ABE的高D．AD，CD都是△ACD的高15．角α和β互补，α＞β，则β的余角为（）A．α﹣βB．180°﹣α﹣βC．D．△16．根据下列已知条件，能唯一画出ABC的是（）A．AB=3，BC=4，AC=8B．AB=4，BC=3，∠A=30°C．∠A=60°，∠B=45°，AB=4D．∠C=90°，AB=6△17．下列各组条件中，能判定ABC≌△DEF的是（）A．AB=DE，BC=EF，∠A=∠DB．∠A=∠D，∠C=∠F，AC=EFC．AB=DE，BC=EF，△ABC的周长=△DEF的周长D．∠A=∠D，∠B=∠E，∠C=∠F△18．如图，DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN．其中，正确结论的个数是（）A．3个B．2个C．1个D．0个三、解答题（共7小题）19．如图，在小河的同侧有A，B，C，D四个村庄，图中线段表示道路．邮递员从A村送信到B村，总是走经过C村的道路，不走经过D村的道路，这是为什么呢？请你用所学的数学知识说明其中的道理．20．如图，AB=AD，BC=DC，AC与BD相交于点E，由这些条件你能推出哪些结论？（不再添加辅助线，不再标注其它字母．不写推理过程，只要求写出四个你认为正确的结论即可）21．如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD 沿着角的两边放正，沿AC画一条射线AE，AE就是角平分线，请说明它的道理．22．如图，A、B两个建筑物分别位于河的两岸，为了测量它们之间的距离，可以沿河岸作射线BF，且使BF⊥AB，在BF上截取BC=CD，过D点作DE⊥BF，使E、C、A在一条直线上，则DE的长就是A、B之间的距离，请说明理由．．23．如图，公园有一条“Z”字形道路 ABCD ，其中 AB∥CD ，在 E 、M 、F 处各有一个小石凳，且 BE=CF ，M 为 BC 的中点，请问三个小石凳是否在一条直线上？说出你推断的理由．△24．如图， ABC 中，AB=BC=CA ，∠A=∠ABC=∠ACB ，在△ABC 的顶点 A ，C 处各有一只小蚂蚁，它们同时出发，分别以相同速度由 A 向 B 和由 C 向 A 爬行，经过 t （s ）后，它们分别爬行到了 D ，E 处，设 DC 与 BE 的交点为 F ．（△1）证明 ACD≌△CBE ；（2）小蚂蚁在爬行过程中，DC 与 BE 所成的∠BFC 的大小有无变化？请说明理由．25．我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？（1）阅读与证明：对于这两个三角形均为直角三角形，显然它们全等．对于这两个三角形均为钝角三角形，可证它们全等（证明略）对于这两个三角形均为锐角三角形，它们也全等，可证明如下：已知： ABC 、 A △1B C 均为锐角三角形，AB=A B ，BC=B C ，∠C=∠C ．1 1 1 1 1 l l求证：ABC≌ A △1B C ．1 1（请你将下列证明过程补充完整．）证明：分别过点 B ，B 作 BD⊥CA 于 D ， 1B D ⊥C A 于D ．1 11 11 则∠BDC=∠B D C =90°， 1 1 1∵BC=B C ，∠C=∠C ， 1 11∴ BCD≌ B △1C D ，1 1∴BD=B D ．1 1（2）归纳与叙述：由（1）可得到一个正确结论，请你写出这个结论．参考答案与试题解析一、填空题（共10小题）1．一个等腰三角形的两边长分别是3cm和7cm，则它的周长是17cm．考点：等腰三角形的性质；三角形三边关系．专题：分类讨论．分析：等腰三角形两边的长为3cm和7cm，具体哪条是底边，哪条是腰没有明确说明，因此要分两种情况讨论．解答：解：①当腰是3cm，底边是7cm时：不满足三角形的三边关系，因此舍去．②当底边是3cm，腰长是7cm时，能构成三角形，则其周长=3+7+7=17cm．故答案为：17．点评：本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．△2．若∠A=∠B=2∠C，则ABC是锐角三角形．（填“钝角”、“锐角”或“直角”）考点：三角形内角和定理．专题：计算题．分析：根据三角形的内角和为180°和已知条件设未知数，列方程求解，再判断形状．解答：解：设三角分别是∠A=a°，∵∠A=2∠B=3∠C，∴∠B=a°，∠B=a°，则a+a+a=180°，解a≈98°．所以三角形是钝角三角形．故答案为钝角．点评：此题主要考查了三角形的内角和定理：三角形的内角和为180°．正确的设出一个角并表示出其他角是解决此题的关键．△3．如图，ABC≌△DEF，△ABC的周长为25cm，AB=6cm，CA=8cm，则DE=6cm，DF=8cm，EF=11cm．考点：全等三角形的性质．分析：根据△ABC的周长求出BC，然后根据全等三角形对应边相等解答即可．解答：解：∵△ABC的周长为25cm，AB=6cm，CA=8cm，∴BC=25﹣6﹣8=11cm，∵△ABC≌△DEF，∴DE=AB=6cm，DF=AC=8cm，EF=BC=11cm．故答案为：6cm；8cm；11cm．点评：本题考查了全等三角形对应边相等的性质，熟记性质并准确找出对应边是解题的关键．4．如图，AB=AD，BC=DC，要证∠B=∠D，则需要连接AC，从而可证△ABC和△ADC全等．考点：全等三角形的判定与性质．分析：连接AC，根据AB=AD，BC=DC，AC=AC即可证明△ABC≌△ADC，于是得到∠B=∠D．解答：解：连接AC，在△ABC和△ADC中，∵，∴△ABC≌△ADC（SSS），∴∠B=∠D．故答案为△AC，ABC，△ADC．点评：本题主要考查全等三角形的判定与性质的知识点，解答本题的关键是熟练掌握其判定定理，此题基础题，比较简单．5．如图，AD，AE分别是△ABC的角平分线和高线，且∠B=50°，∠C=70°，则∠EAD= 10°．考点：三角形内角和定理．分析：根据三角形的内角和等于180°求出∠BAC，再根据角平分线的定义求出∠BAD，根据直角三角形两锐角互余求出∠B AE，然后根据∠EAD=∠BAE﹣∠BAD代入数据进行计算即可得解．解答：解：∵∠B=50°，∠C=70°，∴∠BAC=180°﹣∠B﹣∠C=180°﹣50°﹣70°=60°，∵AD是△ABC的角平分线，∴∠BAD=∠BAC=×60°=30°，∵AE是△ABC的高线，∴∠BAE=90°﹣∠B=90°﹣50°=40°，∴∠EAD=∠BAE﹣∠BAD=40°﹣30°=10°．故答案为：10°．点评：本题考查了三角形的内角和定理，三角形的角平分线、高线的定义，是基础题，准确识图找出各角度之间的关系是解题的关键．△6．如图，CA⊥BE，且ABC≌△ADE，则BC与DE的关系是相等且垂直．考点：全等三角形的性质．分析：根据全等三角形对应边相等可得BC=DE，全等三角形对应角相等可得∠C=∠E，根据垂直的定义求出∠BAC=90°，然后求出∠B+∠E=90°，从而得到∠BFE=90°，即BC⊥DE．解答：解：∵△ABC≌△ADE，∴BC=DE，∠C=∠E，∵CA⊥BE，∴∠BAC=90°，∵∠B+∠C=180°﹣∠BAC=180°﹣90°=90°，∴∠B+∠E=90°，∴∠BFE=180°﹣（∠B+∠E）=180°﹣90°=90°，∴BC⊥DE，故BC与DE的关系是相等且垂直．故答案为：相等且垂直．点评：本题考查了全等三角形的性质，主要利用了全等三角形对应边相等，全等三角形对应角相等，垂直的定义，熟记性质是解题的关键．7．如图，有一块边长为4的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角边分别与CD交于点F，与CB延长线交于点E．则四边形AECF的面积是16．△S AEB =S△=S△ ，考点：正方形的性质；全等三角形的判定与性质．分析：由四边形 ABCD 为正方形可以得到∠D=∠B=90°，AD=AB ，又∠ABE=∠D=90°，而∠EAF=90°由此可以推出∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，进一步得到∠DAF=∠BAE ，所以可以证明△AEB≌△AFD ，所以 AFD ，那么它们都加上四边形 ABCF 的面积，即可四边形 AECF 的面积=正方形的面积，从而求出其面积．解答：解：∵四边形 ABCD 为正方形，∴∠D=∠ABC=90°，AD=AB ， ∴∠ABE=∠D=90°， ∵∠EAF=90°，∴∠DAF+∠BAF=90°，∠BAE+∠BAF=90°， ∴∠DAF=∠BAE ， ∴△AEB≌△AFD ，△∴S AEB AFD∴它们都加上四边形 ABCF 的面积，可得到四边形 AECF 的面积=正方形的面积=16．故答案为：16．点评：本题需注意：在旋转过程中一定会出现全等三角形，应根据所给条件找到．8．如图，BA∥CD ，∠A=90°，AB=CE ，BC=ED ，则△CED≌ △ABC ，根据是HL ．考点：全等三角形的判定．分析：根据两直线平行，同旁内角互补求出∠DCE=90°，然后利用“HL”证明△CED 和△ABC 全等．解答：解：∵BA∥CD ，∠A=90°，∴∠DCE=180°﹣∠A=180°﹣90°=90°， ∵在 Rt△CED 和 Rt△ABC 中，，∴ CED≌ ABC （△HL ）．故答案为： ABC ，△HL ．点评：本题考查了全等三角形的判定，平行线的性质，求出∠DCE=90°是解题的关键．△9．如图， ABC 中，AB=AC ，BC=8，BD 是 AC 边上的中线，△ABD 与△BDC 的周长的差是 2，则 AB= 10 ．考点：等腰三角形的性质．分析：根据三角形中线的定义可得 AD=CD ，然后求出△ABD 与△BDC 的周长的差=AB﹣BC ，再代入数据进行计算即可得解．解答：解：∵BD 是 AC 边上的中线，∴AD=CD ，∴△ABD 与△BDC 的周长的差=（AB+AD+BD ）﹣（BC+CD+BD ）=AB ﹣BC ， ∵△ABD 与△BDC 的周长的差是 2，BC=8， ∴AB ﹣8=2， ∴AB=10．故答案为：10．点评：本题考查了等腰三角形腰上的中线的定义，求出△ABD 与△BDC 的周长的差=AB﹣BC 是解题的关键，也是本题的难点．10．如图，对面积为 1 的△ABC 逐次进行以下操作：第一次操作，分别延长 AB ，BC ，CA 至点 A ，B ，C ，使得 A B=2AB ，B C=2BC ，C A=2CA ，顺次连接 A ，B ，C △1，得到 A B C ，111111111 1 1记其面积为 S ；第二次操作，分别延长 A B ，B C ，C A 至点 A ，B ，C ，使得 A B =2A B ， 11 11 11 12222 1 1 1B C =2B C ，C A =2C A ，顺次连接 A ，B ，C △2，得到 A B C ，记其面积为 S ；…；按 2 11 12 11 1222 2 22此规律继续下去，可得到A △5BC ，则其面积 S = 195 ．5 5 5考点：三角形的面积．专题：压轴题；操作型．分析：根据高的比等于面积比推理出A △1BC 的面积是 A △1BC 面积的 2 倍，则 A △1B B 的11面积是A △1BC 面积的 3 倍…，以此类推，得出 A △2BC 的面积．2 2解答：解：连接 A C ，根据 A B=2AB ，得到：AB ：A A=1：3，111因而若过点 B ，A 作△ABC 与 AA △1C 的 AC 边上的高，则高线的比是 1：3， 1因而面积的比是 1：△3，则 A BC 的面积是△ABC 的面积的 2 倍，1设△ABC 的面积是 △a ，则 A BC 的面积是 2a ， 1同理可以得到A △1BC 的面积是 A △1BC 面积的 2 倍，是 4a ，1则 A △1B B 的面积是 6a ，1同理B △1C C 和 A △1C A 的面积都是 6a ，11△A B C 的面积是 19a ，1 1 1即 A △1B C 的面积是△ABC 的面积的 19 倍， 1 1同理A △2BC 的面积是 A △1B C 的面积的 19 倍，2 21 1即 A △1B C 的面积是 △19， A B C 的面积 192，1 12 2 2依此类推，AB C的面积是S=195=2476099．△5555点评：正确判断相邻的两个三角形面积之间的关系是解决本题的关键，本题的难度较大．二、选择题（共8小题）11．在下列四组线段中，能组成三角形的是（）A．2，2，5B．3，7，10C．3，5，9D．4，5，7考点：三角形三边关系．分析：根据三角形的任意两边之和大于第三边对各选项分析判断后利用排除法求解．解答：解：A、∵2+2=4＜5，∴2，2，5不能组成三角形，故本选项错误；B、∵3+7=10，∴3，7，10不能组成三角形，故本选项错误；C、∵3+5=8＜9，∴3，5，9不能组成三角形，故本选项错误；D、4，5，7能组成三角形，故本选项正确．故选D．点评：本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边是解题的关键．△12．（2011•宿迁）如图，已知∠1=∠2，则不一定能使ABD≌△ACD的条件是（）A．AB=AC B．BD=CD C．∠B=∠C D．∠BDA=∠CDA 考点：全等三角形的判定．专题：压轴题．分析：利用全等三角形判定定理ASA，SAS，AAS对各个选项逐一分析即可得出答案．解答：解：A、∵∠1=∠2，AD为公共边，若AB=AC，则△ABD≌△ACD（SAS）；故本选项正确，不合题意．B、∵∠1=∠2，AD为公共边，若BD=CD，不符合全等三角形判定定理，不能判定△ABD≌△ACD；故本选项错误，符合题意．C、∵∠1=∠2，AD为公共边，若∠B=∠C，则△ABD≌△ACD（AAS）；故本选项正确，不合题意．D、∵∠1=∠2，AD为公共边，若∠BDA=∠CDA，则△ABD≌△ACD（ASA）；故本选项正确，不合题意．故选B．点评：此题主要考查学生对全等三角形判定定理的理解和掌握，此题难度不大，属于基础题．13．如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（）A．图中有三个直角三角形C．∠1和∠B都是∠A的余角B．∠1=∠2 D．∠2=∠A考点：直角三角形的性质．专题：证明题．分析：在△ABC中，∠ACB=90°，CD⊥AB，因而△ACD∽△CBD∽△ABC，根据相似三角形的对应角相等，就可以证明各个选项．解答：解：∵∠ACB=90°，CD⊥AB，垂足为D，∴△ACD∽△CBD∽△ABC．A、∴图中有三个直角三角形Rt△ACD、Rt△CBD、Rt△ABC；故本选项正确；B、应为∠1=∠B、∠2=∠A；故本选项错误；C、∴∠1=∠B、∠2=∠A，而∠B是∠A的余角，∴∠1和∠B都是∠A的余角；故本选项正确；D、∴∠2=∠A；故本选项正确．故选B．点评：本题主要考查了直角三角形的性质，直角三角形斜边上的高，把这个三角形分成的两个三角形与原三角形相似．14．如图，AC⊥BC，CD⊥AB，DE⊥BC，分别交B C，AB，BC于点C，D，E，则下列说法中不正确的是（）A．AC是△ABC和△ABE的高C．DE是△DBE和△ABE的高B．DE，DC都是△BCD的高D．AD，CD都是△ACD的高考点：三角形的角平分线、中线和高．分析：三角形的高即从三角形的一个顶点向对边引垂线，顶点和垂足间的线段．根据概念可知．解答：解：A、AC是△ABC和△ABE的高，正确；B、DE，DC都是△BCD的高，正确；C、DE不是△ABE的高，错误；D、AD，CD都是△ACD的高，正确．故选C．点评：考查了三角形的高的概念．15．角α和β互补，α＞β，则β的余角为（）A．α﹣βB．180°﹣α﹣βC．D．考点：余角和补角．分析：根据互为补角的两个角的和等于180°表示出α+β，再根据互为余角的两个角的和等于90°列式整理即可得解．解答：解：∵角α和β互补，∴α+β=180°，∴β的余角为：90°﹣β=（α+β）﹣β=（α﹣β）．故选C．点评：本题考查了余角和补角，利用90°和180°的倍数关系消掉常数是解题的关键．△16．根据下列已知条件，能唯一画出ABC的是（）A．AB=3，BC=4，AC=8C．∠A=60°，∠B=45°，AB=4B．AB=4，BC=3，∠A=30°D．∠C=90°，AB=6考点：全等三角形的判定．专题：作图题；压轴题．分析：要满足唯一画出△ABC，就要求选项给出的条件符合三角形全等的判定方法，不符合判定方法的画出的图形不一样，也就是三角形不唯一，而各选项中只有C选项符合ASA，是满足题目要求的，于是答案可得．解答：解：A、因为AB+BC＜AC，所以这三边不能构成三角形；B、因为∠A不是已知两边的夹角，无法确定其他角的度数与边的长度；C、已知两角可得到第三个角的度数，已知一边，则可以根据ASA来画一个三角形；D、只有一个角和一个边无法根据此作出一个三角形．故选C．点评：此题主要考查了全等三角形的判定及三角形的作图方法等知识点；能画出唯一三角形的条件一定要满足三角形全等的判定方法，不符合判定方法的画出的三角形不确定，当然不唯一．△17．下列各组条件中，能判定ABC≌△DEF的是（）A．AB=DE，BC=EF，∠A=∠DB．∠A=∠D，∠C=∠F，AC=EFC．AB=DE，BC=EF，△ABC的周长=△DEF的周长D．∠A=∠D，∠B=∠E，∠C=∠F考点：全等三角形的判定．分析：根据全等三角形的判定（三组对应边分别相等的两个三角形全等（简称SSS））可得当AB=DE，BC=EF，AC=DF可判定△ABC≌△DEF，做题时要对选项逐个验证．解答：解：A、满足SSA，不能判定全等；B、AC=EF不是对应边，不能判定全等；C、符合SSS，能判定全等；D、满足AAA，不能判定全等．故选C．点评：本题考查了全等三角形的判定方法，在应用判定方法做题时找准对应关系，对选项逐一验证，而AAA，SSA不能作为全等的判定方法．△18．如图，DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN．其中，正确结论的个数是（）A．3个B．2个C．1个D．0个考点：全等三角形的判定与性质；等边三角形的性质．分析：根据等边三角形性质得出AC=CD，BC=CE，∠ACD=∠BCE=60°，求出∠ACE=∠BCD，根据SAS证△ACE≌△BCD，推出∠NDC=∠CAM，求出∠DCE=∠ACD，证△ACM≌△DCN，推出CM=CN，AM=DN，即可判断各个结论．解答：解：∵△DAC和△EBC均是等边三角形，∴AC=CD，BC=CE，∠ACD=∠BCE=60°，∴∠ACD+∠DCE=∠BCE+∠DCE，∴∠ACE=∠BCD，在△ACE和△BCD中∴△ACE≌△BCD（SAS）；∴①正确；∵∠ACD=∠BCE=60°，∴∠DCE=180°﹣60°﹣60°=60°=∠ACD，∵△ACE≌△BCD，∴∠NDC=∠CAM，在△ACM和△DCN中∴△ACM≌△DCN（ASA），∴CM=CN，AM=DN，∴②正确；∵△ADC是等边三角形，∴AC=AD，∠ADC=∠ACD，∵∠AMC＞∠ADC，∴∠AMC＞∠ACD，∴AC＞AM，即AC＞DN，∴③错误；故选B．点评：本题考查了等边三角形的性质和全等三角形的性质和判定的应用，主要考查学生的推理能力和辨析能力．三、解答题（共7小题）19．如图，在小河的同侧有A，B，C，D四个村庄，图中线段表示道路．邮递员从A村送信到B村，总是走经过C村的道路，不走经过D村的道路，这是为什么呢？请你用所学的数学知识说明其中的道理．考点：三角形三边关系．分析：延长AC交BD于E，根据三角形的任意两边之和大于第三边可得AD+DE＞AC+CE，CE+BE＞BC，然后整理得到AD+BD＞AC+BC，从而得解．解答：解：如图，延长AC交BD于E，在△ADE中，AD+DE＞AC+CE，在△CBE中，CE+BE＞BC，∴AD+DE+CE+BE＞AC+CE+BC，∴AD+BD＞AC+BC，因此，邮递员由A村到B村送信，经过C村路程近些，所以，他总是走经过C村的道路，不走经过D村的道路．点评：本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边是解题的关键．20．如图，AB=AD，BC=DC，AC与BD相交于点E，由这些条件你能推出哪些结论？（不再添加辅助线，不再标注其它字母．不写推理过程，只要求写出四个你认为正确的结论即可）考点：全等三角形的判定与性质．专题：开放型．分析：由AB=AD，BC=DC知，AC是BD的中垂线，∴DE⊥AC，可由SSS证得△ABC≌△ADC及AC平分∠BAD等．解答：解：由已知得，AC垂直平分BD，即直线AC为四边形ABCD的对称轴，由对称性可知：DE=BE，DE⊥AC于△E，ABC≌ADC，△AC平分∠BAD等．点评：本题考查了三角形全等的判定和性质．做题时要从已知开始思考，结合全等的判定方法进行取舍．21．如图是一个平分角的仪器，其中AB=AD，BC=DC，将点A放在角的顶点，AB和AD 沿着角的两边放正，沿AC画一条射线AE，AE就是角平分线，请说明它的道理．考点：全等三角形的应用．专题：证明题．分析：AC为公共边，其中AB=AD，BC=DC，利用SSS判断两个三角形全等，根据全等三角形的性质解题．解答：证明：△ABC与△ADC中，∵AB=AD，BC=DC，AC=AC，∴△ABC≌△ADC（SSS），∴∠BAC=∠DAC．即AE平分∠BAD．不论∠DAB是大还是小，始终有AE平分∠BAD．点评：本题考查了全等三角形的应用；这种设计，用SSS判断全等，再运用性质，是全等三角形判定及性质的综合运用，做题时要认真读题，充分理解题意．22．如图，A、B两个建筑物分别位于河的两岸，为了测量它们之间的距离，可以沿河岸作射线BF，且使BF⊥AB，在BF上截取BC=CD，过D点作DE⊥BF，使E、C、A在一条直线上，则DE的长就是A、B之间的距离，请说明理由．考点：全等三角形的应用．分析：可以沿河岸作射线BF，且使BF⊥AB，在BF上截取BC=CD，过D点作DE⊥BF，使E、C、A在一条直线上，证明出这两个三角形全等，从而可得到结论．解答：解：∵∠ACB=∠DCE，BC=CD，∠B=∠EDC=90°，∴△ACB≌△ECD，∴AB=DE．点评：本题考查全等三角形的应用，关键是证明三角形全等，从而得到线段相等，得到结论．23．如图，公园有一条“Z”字形道路ABCD，其中AB∥CD，在E、M、F处各有一个小石凳，且BE=CF，M为BC的中点，请问三个小石凳是否在一条直线上？说出你推断的理由．考点：全等三角形的应用．分析：首先连接EM、△MF，再证明BEM≌△CFM可得∠BME=∠FMC，再根据∠BME+∠EMC=180°，可得∠FMC+∠EMC=180，进而得到三个小石凳在一条直线上．解答：解：连接EM、MF，∵AB∥CD，∴∠B=∠C，又∵M为BC中点，∴BM=MC．，∴在△BEM和△CFM中∴△BEM≌△CFM（SAS），∴∠BME=∠FMC，∵∠BME+∠EMC=180°，∴∠FMC+∠EMC=180°，∴三个小石凳在一条直线上．点评：此题主要考查了全等三角形的应用，证明△BEM≌△CFM，证明出∠FMC+∠EMC=180°是解决问题的关键．△24．如图，ABC中，AB=BC=CA，∠A=∠ABC=∠ACB，在△ABC的顶点A，C处各有一只小蚂蚁，它们同时出发，分别以相同速度由A向B和由C向A爬行，经过t（s）后，它们分别爬行到了D，E处，设DC与BE的交点为F．（△1）证明ACD≌△CBE；（2）小蚂蚁在爬行过程中，DC与BE所成的∠BFC的大小有无变化？请说明理由．考点：全等三角形的应用．分析：（1）根据小蚂蚁的速度相同求出AD=CE，再利用“边角边”证明△ACD和△CBE 全等即可；（2）根据全等三角形对应角相等可得∠EBC=∠ACD，然后表示出∠BFC，再根据等边三角形的性质求出∠ACB，从而得到∠BFC．解答：（1）证明：∵小蚂蚁同时从A、C出发，速度相同，∴t（s）后两只小蚂蚁爬行的路程AD=CE，∵在△ACD和△CBE中，，∴△ACD≌△CBE（SAS）；（△2）解：∵ACD≌△CBE，∴∠EBC=∠ACD，∵∠BFC=180°﹣∠EBC﹣∠BCD，∴∠BFC=180°﹣∠ACD﹣∠BCD，=180°﹣∠ACB，∵∠A=∠ABC=∠ACB，∴∠ACB=60°，∴∠BFC=180°﹣60°=120°，∴∠BFC无变化．点评：本题考查了全等三角形的应用，主要利用了全等三角形对应角相等的性质，等边三角形的性质，根据小蚂蚁的速度相同求出AD=CE是证明三角形全等的关键．25．（2006•绍兴）我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？．△1B △1（1）阅读与证明：对于这两个三角形均为直角三角形，显然它们全等．对于这两个三角形均为钝角三角形，可证它们全等（证明略）对于这两个三角形均为锐角三角形，它们也全等，可证明如下：已知： ABC 、 A △1B C 均为锐角三角形，AB=A B ，BC=B C ，∠C=∠C ．1 1 1 1 1 l l 求证：ABC≌ A △1B C ． 1 1 （请你将下列证明过程补充完整．）证明：分别过点 B ，B 作 BD⊥CA 于 D ，1 B D ⊥C A 于 D ． 1 1 1 1 1则∠BDC=∠B D C =90°，1 1 1 ∵BC=B C ，∠C=∠C ，1 1 1 ∴ BCD≌ B △1C D ，1 1 ∴BD=B D ． 1 1 （2）归纳与叙述：由（1）可得到一个正确结论，请你写出这个结论．考点：全等三角形的判定．专题：压轴题；阅读型．分析：本题考查的是全等三角形的判定，首先易证得 ADB≌ A △1B C 然后易证出 1 1 ABC≌ A C ．1 1解答：证明：（1）证明：分别过点 B ，B 作 BD⊥CA 于 D ，1 B D ⊥C A 于 D ． 1 1 1 1 1 则∠BDC=∠B D C =90°，1 1 1∵BC=B C ，∠C=∠C ，1 1 1 ∴ BCD≌ B △1C D ，1 1 ∴BD=B D ． 1 1 补充：∵AB=A B ，∠ADB=∠A D B =90°．1 1 1 1 1 ∴ ADB≌ A △1D B （HL ），1 1 ∴∠A=∠A ， 1又∵∠C=∠C ，BC=B C ，1 1 1 在△ABC 与 A △1B C 中，1 1∵，∴ ABC≌ A △1B C （AAS ）；1 1（△2）解：若两三角形（ ABC 、 AB C ）均为锐角三角形或均为直角三角形或均 1 1为钝角三角形，则它们全等（AB=A B，BC=B C，∠C=∠C△1，则ABC≌A△1B C）．111111点评：命题立意：考查三角形全等的判定，阅读理解能力及分析归纳能力．做题时要认真读题，明白题意，然后按要求答题．。

北师大版七年级下册全等三角形专项练习

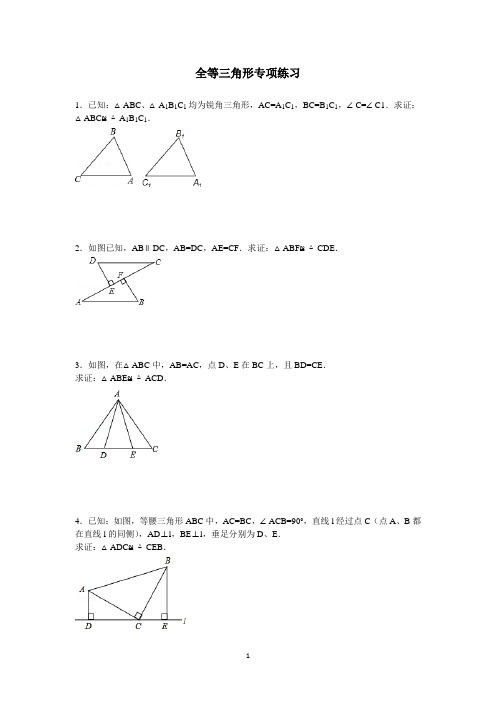
全等三角形专项练习1．已知：△ABC、△A1B1C1均为锐角三角形，AC=A1C1，BC=B1C1，∠C=∠C1．求证：△ABC≌△A1B1C1．2．如图已知，AB∥DC，AB=DC，AE=CF．求证：△ABF≌△CDE．3．如图，在△ABC中，AB=AC，点D、E在BC上，且BD=CE．求证：△ABE≌△ACD．4．已知：如图，等腰三角形ABC中，AC=BC，∠ACB=90°，直线l经过点C（点A、B都在直线l的同侧），AD⊥l，BE⊥l，垂足分别为D、E．求证：△ADC≌△CEB．5．已知：如图AC，BD相交于点O，∠A=∠D，AB=CD，求证：△AOB≌△DOC．6．如图，在直角三角形ABC中，∠ABC=90°，点D在BC的延长线上，且BD=AB，过B 作BE⊥AC，与BD的垂线DE交于点E．求证：△ABC≌△BDE．7．如图，已知两条直线AB，CD相交于点O，且CO=DO，AC∥BD，求证：△AOC≌△BOD．8．如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C．求证：△ABE≌△ACD．9．已知：如图，AB=CD，AD=CB．求证：△ABC≌△CDA．10．如图，AC⊥BC，AD⊥BD，垂足分别为C、D，AC=BD，Rt△ABC与Rt△BAD全等吗？为什么？11．已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC．求证：BC=DE．12．如图所示，△ABC和△AEF为等边三角形，点E在△ABC内部，且E到点A，B，C 的距离分别为3，4，5，求∠AEB的度数．13．已知矩形ABCD中，AF为∠DAC的角平分线，CP⊥AF于点F，且交AD的延长线于P．连接BF交对角线AC于点O．（1）若BC=4，tan∠ACB=，求S△DCP的值；（2）求证：∠AOB=3∠PAF．14．如图，AB=AC，AD=AE．求证：∠B=∠C．15．如图，在△ABC与△ABD中，BC=BD，∠ABC=∠ABD．点E为BC中点，点F为BD中点，连接AE，AF．求证：AE=AF．16．如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从下列四个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明．供选择的四个条件（请从其中选择一个）：①AB=ED；②∠A=∠D=90°；③∠ACB=∠DFE；④∠A=∠D．17．我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD，请你写出与筝形ABCD的角或者对角线有关的一个结论，并证明你的结论．18．在△ABC中，AB=AC，点D是BC的中点，点E是AD上任意一点．（1）如图1，连接BE、CE，问：BE=CE成立吗？并说明理由；（2）如图2，若∠BAC=45°，BE的延长线与AC垂直相交于点F时，问：EF=CF成立吗？并说明理由．19．如图，AC与BD交于点E，且AC=DB，AB=DC．求证：∠A=∠D．20．如图，AB=DF，AC=DE，BE=FC，求证：∠B=∠F．。

北师大版七年级数学下册第三章《全等三角形》测试卷含答案3套

全等三角形一.填空题（每题3分,共30分）1。

如图，△ABC ≌△DBC,且∠A 和∠D,∠ABC 和∠DBC 是对应角,其对应边：_______、2。

如图,△ABD ≌△ACE ，且∠BAD 和∠CAE ，∠ABD 和∠ACE,∠ADB 和∠AEC 是对应角，则对应边_________.3、已知:如图，△ABC ≌△FED ，且BC=DE 、则∠A=__________，A D=_______.4、如图,△ABD ≌△ACE,则AB 的对应边是_________，∠BAD 的对应角是______。

5、已知：如图,△ABE ≌△ACD ，∠B=∠C,则∠AEB=_______，AE=________。

6.已知:如图 , AC ⊥BC 于 C ， DE ⊥AC 于 E ， AD ⊥AB 于 A , BC=AE 。

若AB=5 , 则AD=___________.7。

已知：△ABC ≌△A ’B ’C', △A'B ’C ’的周长为12cm ，则△ABC 的周长为、 8.如图, 已知:∠1=∠2 ， ∠3=∠4 , 要证BD=CD , 需先证△AEB ≌△A EC ，根据是_________再证△BDE ≌△______ , 根据是__________。

4321E D BA9。

如图，∠1=∠2，由AAS 判定△ABD ≌△ACD,则需添加的条件是____________、10。

如图，在平面上将△ABC 绕B 点旋转到△A ’BC ’的位置时，AA ’∥BC ，∠ABC=70°,则∠CBC'为________度、二.选择题（每题3分,共30分）11、下列条件中，不能判定三角形全等的是 ( )A 、三条边对应相等B 、两边和一角对应相等C 、两角的其中一角的对边对应相等D 、两角和它们的夹边对应相等12、如果两个三角形全等,则不正确的是 ( )A B CD 12AA'BC C'A、它们的最小角相等B、它们的对应外角相等C、它们是直角三角形D、它们的最长边相等13、如图,已知：△ABE≌△ACD,∠1=∠2，∠B=∠C,不正确的等式是（）A、AB=ACB、∠BAE=∠CADC、BE=DCD、AD=DE14、图中全等的三角形是（ )A、Ⅰ和ⅡB、Ⅱ和ⅣC、Ⅱ和ⅢD、Ⅰ和Ⅲ15、下列说法中不正确的是（ )A、全等三角形的对应高相等B、全等三角形的面积相等C、全等三角形的周长相等D、周长相等的两个三角形全等16、 AD=AE ， AB=AC ， BE、CD交于F ，则图中相等的角共有(除去∠DFE=∠BFC） ( )A、5对B、4对C、3对D、2对CEDBOA17.如图,OA=OB，OC=OD, ∠O=60°, ∠C=25°则∠BED的度数是（ )A、70°B、 85°C、 65°D、以上都不对18、已知:如图，△ABC≌△DEF,AC∥DF,BC∥EF、则不正确的等式是 ( )A、AC=DF B 、AD=BE C、DF=EF D、BC=EF19。

北师大版七年级数学下册第四章三角形章节测试(含答案)

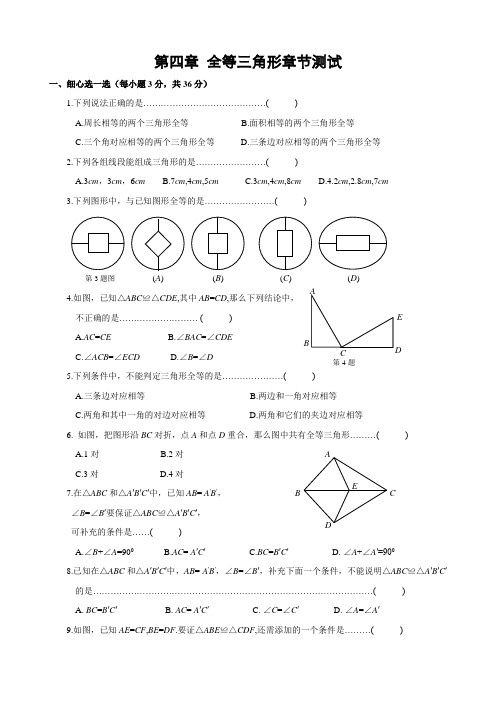
第四章全等三角形章节测试一、细心选一选（每小题3分，共36分）1.下列说法正确的是……………………………………( )A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等 2.下列各组线段能组成三角形的是……………………( )A.3cm ，3cm ，6cmB.7cm ,4cm ,5cmC.3cm ,4cm ,8cmD.4.2cm ,2.8cm ,7cm 3.下列图形中，与已知图形全等的是……………………( )4.如图，已知△ABC ≌△CDE,其中AB =CD ,那么下列结论中，不正确的是……………………… ( ) A.AC =CEB.∠BAC =∠CDEC.∠ACB =∠ECDD.∠B =∠D5.下列条件中，不能判定三角形全等的是…………………( ) A.三条边对应相等 B.两边和一角对应相等 C.两角和其中一角的对边对应相等 D.两角和它们的夹边对应相等6. 如图，把图形沿BC 对折，点A 和点D 重合，那么图中共有全等三角形………( ) A.1对 B.2对 C.3对 D.4对7.在△ABC 和△A ′B ′C ′中，已知AB = A ′B ′， ∠B =∠B ′要保证△ABC ≌△A ′B ′C ′，可补充的条件是……( )A.∠B +∠A =900B.AC = A ′C ′C.BC =B ′C ′D. ∠A +∠A ′=9008.已知在△ABC 和△A ′B ′C ′中，AB = A ′B ′，∠B =∠B ′，补充下面一个条件，不能说明△ABC ≌△A ′B ′C ′的是……………………………………………………………………………………( ) A. BC =B ′C ′ B. AC = A ′C ′ C. ∠C =∠C ′ D. ∠A =∠A ′ 9.如图，已知AE =CF ,BE =DF .要证△ABE ≌△CDF ,还需添加的一个条件是………( )(A ) (B ) (C )(D )第3题图B DE第4题ABDCEA.∠BAC =∠ACDB.∠ABE =∠CDFC.∠DAC =∠BCAD.∠AEB =∠CFD10.如图AD 是△ABC 的角平分线，DE 是△ABD 的高，EF 是△ACD 的高，则…( ) A.∠B =∠C B.∠EDB =∠FDC C.∠ADE =∠ADF D. ∠ADB =∠ADC 11.如图AC 与BD 相交于点O ，已知AB =CD ,AD =BC ,则图中全等三角形有………( ) A.1对 B.2对 C.3对 D.4对 12.如图,D 、E 分别是AB ,AC 上一点，若∠B =∠C ，则在下列条件中，无法判定△ABE ≌△ACD 是………………………………( ) A.AD =AE B.AB =ACC.BE =CDD.∠AEB =∠ADC 二、专心填一填：（每小题3分，共24分）13.如图，△ABC ≌△DEF ,点B 和点E , 点A 和点D 是对应顶点，则AB = ，CB = , ∠C = ,∠CAB = . 14.若已知两个三角形有两条边对应，则要视这两个三角形全等，还需增加的条件可以是或 .15.如图已知AC 与BD 相交于点O ，AO =CO ,BO =DO ,则AB =CD 请说明理由. 解：在△AOB 和△COD 中(BO DO(AO CO ==⎧⎪⎨⎪⎩已知）（对顶角相等已知） ∴△AOB ≌△COD （）∴AB =DC （）16.如图，已知AO =OB ,OC =OD ,AD 和BC 相交于点E ，则图中全等三角形有对.17.在△ABC 和△DEF 中,AB =4, ∠A =350, ∠B =700,DE =4, ∠D = , ∠E 根据判定△ABC ≌△DEF .ABC D F E 第9题AA AAA 第10题A BCDO第11题ABCE第12题D第13题ABC DEFABD CO第15题OABD第16题CE第18题A D18.如图，在△ABC和△DEF中AB=DC( BC=DA(=⎧⎪⎨⎪⎩已知）已知）（）∴△ABC≌△DEF( )19.如图∠B=∠DEF,AB=DE,要证明△ABC≌△DEF，(1)若以“ASA”为依据，需添加的条件是;(2)若以“SAS”为依据，需添加的条件是.20.如图，△ABC中，AB=AC=13cm，AB的垂直平分线交AB于D,交AC于E,若△EBC的周长为21cm,则BC= cm.三、耐心答一答：（本题有6小题，共40分）21.(本题4分)已知∠α、∠β和线段a, 如图，用直尺和圆规作△ABC，使∠A=∠α,∠B=∠β,BC=a.22.(本题6分)已知AD平分∠CAB,且DC⊥AC, DB⊥AB，那么AB和AC相等吗？请说明理由.第19题B CAE CDAB CED第20题DCAB23.(本题6分)如图，已知BD =CD ，∠1=∠2. 说出△ABD ≌△ACD 的理由.24.(本题8分)如图，已知AB =DC ，AD =BC ,说出下列判断成立的理由： (1) △ABC ≌△CDA (2) ∠B =∠D25.(本题8分) 如图，把大小为4×4的正方形方格图形分别分割成两个全等图形，例如图①，请在下图中，沿着须先画出四种不同的分法，把4×4的正方形分割成两个全等图形ABC12DB D图①画法1画法2画法3画法426.(本题8分)如图，△ABC 中，AD 垂直平分BC ,H 是AD 上一点，连接BH ,CH .(1)AD 平分∠BAC 吗？为什么？(2)你能找出几堆相等的角？请把他么写出来（不需写理由）ACBH D参考答案一、细心选一选：（每小题3分，共36分）题号 1 2 3 4 5 6 7 8 9 10 11 12答案D B B C D C C B D C D D二、专心填一填（每小题3分，共24分）13.DE,FE,∠F, ∠FE D. 14.3第三边相等，这两边的夹角相等15. ∠AOB=∠COD,SAS,全等三角形的对应边相等16.4 17.350, AAS18.AC,CA,公共边，SSS19.∠A=∠D20.8三、耐心答一答（本题有六小题，共40分）21.图略22.AB=AC23.略24.略25.画法1 画法2 画法3 画法426.(1)由△ADB≌△ADC(SAS)得∠BAD=∠CAD(4)4对，∠BHD=∠CHD, ∠ABD=∠ACD,∠HBD=∠HCD, ∠BDA=∠CDA。

北师大版七年级下册-全等三角形-章节测试

北师大版七年级下数学《全等三角形》单元测试(含答案)

(完整版)北师大版七年级下册_全等三角形证明经典题

北师大七年级下册数学全等三角形习题精选

知识点详解北师大版七年级数学下册第四章三角形章节测评试题(含解析)

北师大版七年级下册三角形全等的证明练习题以及答案

北师大版数学七年级下册第4章《三角形》单元测试试题附答案解析

北师大数学七年级下册第一章到第七章单元测试题_含答案(第五章三角形全等为三套_共10套)

北师大版七年级(下)全等三角形、对称轴综合测试卷

北师大版数学七年级下册《全等三角形》单元测试题含答案

最新北师大版七年级下册三角形全等(AAS或ASA)的证明试题以及答案 (共50道)

最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

新北师大版数学七下第四章三角形单元测试

第四章三角形章节测试同步练习2022-2023学年北师大版七年级数学下册

北师大数学七年级下《第四章三角形》章节检测题含答案

新北师大版七年级数学下册第三章全等三角形练习题

第4章三角形全等三角形判定(基础版) -北师大版数学七年级下册(含答案)

北师大版七年级数学下册第3章《三角形》单元测试试卷及答案(3)

北师大版七年级下册全等三角形专项练习

北师大版七年级数学下册第三章《全等三角形》测试卷含答案3套

北师大版七年级数学下册第四章三角形章节测试(含答案)

北师大版七年级下册-全等三角形-章节测试

北师大版七年级下数学《全等三角形》单元测试(含答案)

(完整版)北师大版七年级下册_全等三角形证明经典题

北师大七年级下册数学全等三角形习题精选

知识点详解北师大版七年级数学下册第四章三角形章节测评试题(含解析)

北师大版七年级下册三角形全等的证明练习题以及答案

北师大版数学七年级下册第4章《三角形》单元测试试题 附答案解析

北师大数学七年级下册第一章到第七章单元测试题_含答案(第五章三角形全等为三套_共10套)

北师大版七年级(下)全等三角形、对称轴综合测试卷

北师大版数学七年级下册《全等三角形》单元测试题含答案

最新北师大版七年级下册三角形全等(AAS或ASA)的证明试题以及答案 (共50道)

最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

新北师大版数学七下 第四章 三角形单元测试

第四章三角形 章节测试同步练习2022-2023学年北师大版七年级数学下册

北师大数学七年级下《第四章三角形》章节检测题含答案

新北师大版七年级数学下册第三章全等三角形练习题

第4章 三角形 全等三角形判定(基础版) -北师大版数学七年级下册(含答案)

北师大版七年级数学下册第3章《三角形》单元测试试卷及答案(3)

北师大版七年级下册全等三角形专项练习

北师大版七年级数学下册第三章《全等三角形》测试卷含答案3套

北师大版七年级数学下册第四章 三角形 章节测试(含答案)

北师大版数学七年级下册第4章《三角形》单元测试试题附答案解析

新北师大版数学七下第四章三角形单元测试

第四章三角形章节测试同步练习2022-2023学年北师大版七年级数学下册

第4章三角形全等三角形判定(基础版) -北师大版数学七年级下册(含答案)

北师大版七年级数学下册第四章三角形章节测试(含答案)