坐标正反算excel表格
坐标反算excel公式

坐标反算excel公式
坐标反算是指根据已知的点的经纬度坐标和大地水准面的参数,计算出该点的投影坐标或者平面坐标。
在Excel中进行坐标反算可
以通过一系列复杂的数学公式来实现。
首先,需要明确采用的坐标
系和大地水准面参数,例如WGS 84坐标系和椭球体参数。
然后,可
以使用以下公式进行坐标反算:
1. 经纬度转换为弧度:
经度弧度 = 经度(π/180)。
纬度弧度 = 纬度(π/180)。
2. 计算子午线曲率半径:
N = a / sqrt(1 e^2 sin^2(纬度弧度))。
3. 计算卯酉圈曲率半径:
M = a (1 e^2) / (1 e^2 sin^2(纬度弧度)^(3/2))。
4. 计算目标点的投影坐标:
X = N cos(纬度弧度) cos(经度弧度)。
Y = N cos(纬度弧度) sin(经度弧度)。
这些公式涉及到很多数学运算和常数,需要在Excel中逐步计算,并且需要确保输入的经纬度和参数的准确性。
另外,也可以考虑使用专业的地理信息系统(GIS)软件来进行坐标反算,这些软件通常提供了更为便捷和准确的工具和方法来进行坐标反算。
excel坐标正算的计算公式

excel坐标正算的计算公式摘要:1.Excel坐标正算简介2.Excel坐标正算公式3.如何使用Excel进行坐标正算4.坐标正算在实际应用中的案例正文:Excel坐标正算是一种通过已知的两个点坐标,计算出它们之间的距离、方位角等地理信息的方法。
在工程测量、地理信息系统等领域具有广泛的应用。
下面我们将详细介绍Excel坐标正算的计算公式、操作步骤以及实际应用案例。
一、Excel坐标正算简介Excel坐标正算主要基于平面直角坐标系中的距离公式和三角函数关系。
通过已知的两个点坐标,计算出它们之间的距离和方位角。
二、Excel坐标正算公式1.距离公式:距离= sqrt((x2-x1)^2 + (y2-y1)^2)其中,(x1, y1)和(x2, y2)分别为两个点的坐标。
2.方位角公式:方位角= atan((y2-y1)/(x2-x1))其中,(x1, y1)和(x2, y2)分别为两个点的坐标。
三、如何使用Excel进行坐标正算1.打开Excel,新建一个工作表。
2.在A1、B1单元格分别输入第一个点的横纵坐标,例如(x1, y1)。
3.在A2、B2单元格分别输入第二个点的横纵坐标,例如(x2, y2)。
4.在C1单元格输入距离公式:=SQRT((A2-A1)^2 + (B2-B1)^2)5.在C2单元格输入方位角公式:=ATAN((B2-B1)/(A2-A1))四、坐标正算在实际应用中的案例1.工程测量:在土地测量、建筑施工等领域,通过坐标正算计算两点间的距离和方位角,以指导实际工作。
2.地理信息系统:在GIS数据处理中,坐标正算常用于计算地图上的两点距离和方向,以便进行路径规划、地理分析等。
3.数据分析:在数据分析领域,坐标正算可以帮助我们更好地理解数据的空间分布,从而为决策提供依据。
总之,Excel坐标正算作为一种实用的计算方法,在各种场景中都有广泛的应用。
坐标正算、反算计算方法及在Excel中的VBA编程

坐标正算、反算计算方法及在Excel 中的VBA 编程测量中经常需要将某点相对坐标系坐标转换成线路的里程、偏距,或根据线路某一里程偏距计算出对应的相对坐标系坐标,为寻求一种快速简单高效的计算方法,本文对线路正算反算的原理进行了阐述,并结合Excel VBA 编程,将编程和Excel 的拖拽的功能相结合,编制出实用计算表,特别适用于需要大量计算边桩、围护桩的情况。
关键词:坐标方位角坐标正算坐标反算 V AB 编程循环迭代直接算法一、坐标方位角的反算1.坐标方位角反算如图1所示,已知点A 、B 的坐标,求直线AB坐标方位角α。
图1坐标方位角反算直线AB 之间的坐标增量:AB B AAB B Ax x x y y y ∆=−∆=−当0,0AB AB x y ∆>∆>时,角α位于第一象限角:arctan ABABy x α∆=∆当0,0AB AB x y ∆<∆>时,角α位于第二象限角:arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆<∆<时,角α位于第三象限角:arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆>∆<时,角α位于第二象限角:arctan360AB AB y x α∆=+°∆2.坐标方位角反算的VBA 编程可用VBA 将上述过程定义为一个名为angel()的函数,代码如下:Function angel(x0As Double, y0 As Double, x1 As Double, y1 As Double) As Double dx = x1- x0dy = y1- y0If dx > 0 And dy > 0 Thenangel = Atn(dy / dx)End IfIf dx < 0 And dy > 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx < 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx > 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979 * 2End IfEnd Function二、直线段坐标正算与反算1.直线段正算图2直线段计算已知HZ 点坐标(x1,y1)、里程N HZ ,ZH 点坐标(x2,y2),正算时已知P 点对应的中桩里程Np 和偏距e (规定沿着线路前进方向,左边偏距为负,右边偏距为正),Np>N HZ ,求P 点对应的坐标。
[应用文书]利用EXCEL进行高斯投影正反算
![[应用文书]利用EXCEL进行高斯投影正反算](https://img.taocdn.com/s3/m/eef675707f21af45b307e87101f69e314332fa98.png)
利用EXCEL 进行高斯投影正反算在工作中常需要将大量经纬度转换成高斯平面坐标、将高斯平面坐标转换成经纬度、将6度带坐标转换成3度带坐标等坐标转换问题。
面对这些问题,我们希望能找个坐标转换软件进行批量转换从而降低劳动强度、提高工作效率。
然而我们通常用的软件对批量转换往往有一定的限制而且对转换数据的格式要求比较严格不容易掌握和使用。
实际上我们通常用的办公软件EXCEL 就可以完成这项工作。
EXCEL 办公软件操作简单方便、易于掌握。
想要用EXCEL 实现正反算,我们必须知道高斯投影正反算数学公式。
(高斯投影正算实际就是把大地坐标通过高斯投影数学模型转换为平面坐标,反之则为高斯投影反算)下面就是高斯投影公式:正算公式:"2322"4""4sin cos sin cos (59)22N N x X B Bl B B t l ηρρ=++-+ "322"3524"5""3"5cos cos (1)cos (118)6120NN N y X Bl B t l B t t l ηρρρ=++-++-+ 反算公式:23222424635(539)(619045)224720f f f f f f f f f f ff f f ft t N B B y t t y t t y M N M N M N ηη=-+-+---+ 22324535111(12)(52824)cos 6cos 120cos f f f f f f f f f fl y t y t t y N B N B N B η=-+++++ 我们只需要把上述两个公式用EXCEL 函数写于EXCEL 表格中就可以进行计算了。
其实,我们用的其他软件中高斯正反算基本全都是用这两个公式实现的,然而由于各种程序语言以及软件计算数据时精度不同所以最后结果也会有很小的误差。
利用EXCEL计算转换坐标

利用EXCEL计算转换坐标在Excel中,可以使用一些内置的函数和公式来计算转换坐标。
以下是一种可能的方法:1. 打开Excel,并在第一列输入原始坐标的横坐标值。
假设这些值位于A列,从第2行开始。
如下所示:A------X1X2X3...2.在第二列输入原始坐标的纵坐标值,假设这些值位于B列,从第2行开始。
如下所示:AB------X1Y1X2Y2X3Y3...3.在第三列输入转换后的坐标的横坐标值,假设这些值位于C列,从第2行开始。
如下所示:ABC------------X1Y1X1'X2Y2X2'X3Y3X3'...4.在第四列输入转换后的坐标的纵坐标值,假设这些值位于D列,从第2行开始。
如下所示:ABCD----------------X1Y1X1'Y1'X2Y2X2'Y2'X3Y3X3'Y3'...5.在C2单元格中输入以下公式来计算转换后的横坐标值:`=A2*缩放比例+平移值`缩放比例和平移值可以根据具体的坐标转换规则来确定。
例如,假设原始坐标的单位为英尺,我们想将其转换为米,则缩放比例应为0.3048(1英尺=0.3048米),平移值为0(因为不需要进行平移)。
6.在D2单元格中输入以下公式来计算转换后的纵坐标值:`=B2*缩放比例+平移值`同样,缩放比例和平移值根据具体的坐标转换规则来确定。
7.复制C2和D2单元格的公式,并将其粘贴到剩余的单元格中,以计算所有的转换后的坐标。
通过这种方法,您可以在Excel中轻松地计算坐标的转换。
请注意,缩放比例和平移值应根据您的具体需求进行调整。
利用EXCEL实现空间直角坐标与大地坐标间的转换
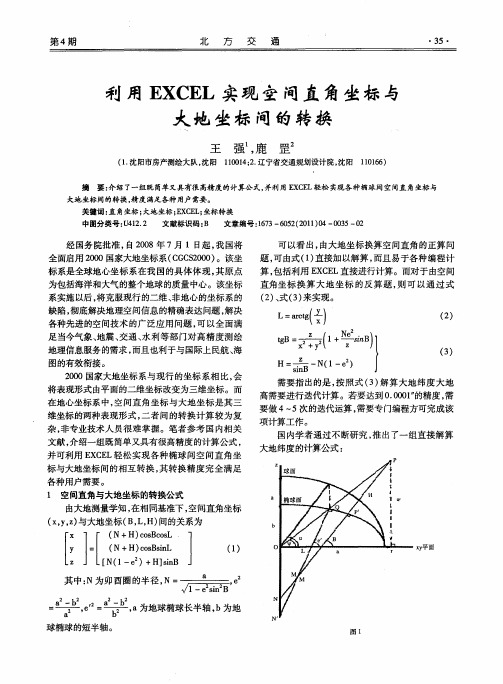
大地纬度 B 转换度分秒方法与 L 同, 相 在此不 做累述。表 1 为空间直角坐标与大地坐标的正反算 ( 反算) 有关参数 , 2为某两点的具体计算示例。 表
表 1 空间直角坐标 与大地坐标 的正反算 ( 反算 ) 有关参数
点名 x
已知数 据空 间直角坐标 Y z 经度 L ” ( )
u与 B 的转换 关 系 , 得到 Байду номын сангаас. 为 的更
需要指 出的是 , 出的 L和 B均为 度 的十进 求 制, 通常使用度分秒形式来表示经纬度 , 以需要将 所 十进制度的形式转换 为度分秒形式 , L为例 , 以 其 转换 过程 为 : 利用 E C L中的 T U C函数 , XE RN 首先将度 的整 数部分求 出: 在相应的单元格 内用 T U C L 算 0 R N ( 计 ,) 表示 即可 完成 。 然后 将 不 足整 数 的十进 制 度 化 为分 的形 式 , 同 样在 相应 的单元 格 内用 【 计 L 算一T U C( 计 0 ]X R N L 算,) 6 将计算结果对应 的单元格记为 L 。 O, 进一步将不足分 的部分化为秒 , 在相应 的单元 格内用【 T U C L ,) × 0 , L 一 R N ( 】 6” 0 将计算结果对应 的单 元格 记为 L, , 。 最终将三部分合并起来 , 即在相应 的单 元格 内
rM = e2acos3U
P ,
M= 一e b i P 2 sn U ,
rM
= e =e
2acos3u
() 7
Q
即可求 出大 地经度 L 并 保证 其为正 值 。利 用式 , (O , 1 ) 可首先计算出辅助角 , 然后利用式 ( ) 8 或式( ) 9 即可求出大地纬度 B 通过 B进而求出大地高 H。 , 大地高除可利用式 ( ) 3 求得 以外 , 可通过严 还 密公式 ( 1 求得 。 1)
用EXCEL完成GPS坐标转换的简易方法

一、用EXCEL进行高斯投影换算从经纬度BL换算到高斯平面直角坐标XY(高斯投影正算),或从XY换算成BL(高斯投影反算),一般需要专用计算机软件完成,在目前流行的换算软件中,存在一个共同的不足之处,就是灵活性较差,大都需要一个点一个点地进行,不能成批量地完成,给实际工作带来许多不便。
笔者发现,用EXCEL可以很直观、方便地完成坐标换算工作,不需要编制任何软件,只需要在EXCEL的相应单元格中输入相应的公式即可。
下面以54系为例,介绍具体的计算方法。
完成经纬度BL到平面直角坐标XY的换算,在EXCEL中大约需要占用21列,当然读者可以通过简化计算公式或考虑直观性,适当增加或减少所占列数。
在EXCEL中,输入公式的起始单元格不同,则反映出来的公式不同,以公式从第2行第1列(A2格)为起始单元格为例,各单元格的公式如下:单元格单元格内容说明A2输入中央子午线,以度.分秒形式输入,如115度30分则输入115.30 起算数据L0B2=INT(A2)+(INT(A2*100)-INT(A2)*100)/60+(A2*10000-INT(A2*100)*100)/3600把L0化成度C2以度小数形式输入纬度值,如38°14′20″则输入38.1420起算数据BD2以度小数形式输入经度值起算数据LE2=INT(C2)+(INT(C2*100)-INT(C2)*100)/60+(C2*10000-INT(C2*100) *100)/3600把B化成度F2=INT(D2)+(INT(D2*100)-INT(D2)*100)/60+(D2*10000-INT(D2*100 )*100)/3600把L化成度G2=F2-B2L-L0H2=G2/57.2957795130823 化作弧度I2=TAN(RADIANS(E2)) Tan(B)J2=COS(RADIANS(E2)) COS(B)K2=0.006738525415*J2*J2L2=I2*I2M2=1+K2N2=6399698.9018/SQRT(M2)O2=H2*H2*J2*J2P2=I2*J2Q2=P2*P2R2=(32005.78006+Q2*(133.92133+Q2*0.7031))S2=6367558.49686*E2/57.29577951308-P2*J2*R2+((((L2-58)*L2+61) *O2/30+(4*K2+5)*M2-L2)*O2/12+1)*N2*I2*O2/2计算结果XT2=((((L2-18)*L2-(58*L2-14)*K2+5)*O2/20+M2-L2)*O2/6+1)*N2*(H2 *J2)计算结果Y表中公式的来源及EXCEL软件的操作方法,请参阅有关资料,这里不再赘述。
利用EXCEL行高斯投影正反算

利用EXCEL行高斯投影正反算————————————————————————————————作者:————————————————————————————————日期:利用EXCEL 进行高斯投影正反算在工作中常需要将大量经纬度转换成高斯平面坐标、将高斯平面坐标转换成经纬度、将6度带坐标转换成3度带坐标等坐标转换问题。
面对这些问题,我们希望能找个坐标转换软件进行批量转换从而降低劳动强度、提高工作效率。
然而我们通常用的软件对批量转换往往有一定的限制而且对转换数据的格式要求比较严格不容易掌握和使用。
实际上我们通常用的办公软件EXCEL 就可以完成这项工作。
EXCEL 办公软件操作简单方便、易于掌握。
想要用EXCEL 实现正反算,我们必须知道高斯投影正反算数学公式。
(高斯投影正算实际就是把大地坐标通过高斯投影数学模型转换为平面坐标,反之则为高斯投影反算)下面就是高斯投影公式:正算公式:"2322"4""4sin cos sin cos (59)22N N x X B Bl B B t l ηρρ=++-+ "322"3524"5""3"5cos cos (1)cos (118)6120NN N y X Bl B t l B t t l ηρρρ=++-++-+反算公式:23222424635(539)(619045)224720f f f f f f f f f f ff f f ft t N B B y t t y t t y M N M N M N ηη=-+-+---+ 22324535111(12)(52824)cos 6cos 120cos f f f f f f f f f fl y t y t t y N B N B N B η=-+++++ 我们只需要把上述两个公式用EXCEL 函数写于EXCEL 表格中就可以进行计算了。
利用EXCEL进行高斯投影正反算

利用EXCEL 进行高斯投影正反算在工作中常需要将大量经纬度转换成高斯平面坐标、将高斯平面坐标转换成经纬度、将6度带坐标转换成3度带坐标等坐标转换问题。
面对这些问题,我们希望能找个坐标转换软件进行批量转换从而降低劳动强度、提高工作效率。
然而我们通常用的软件对批量转换往往有一定的限制而且对转换数据的格式要求比较严格不容易掌握和使用。
实际上我们通常用的办公软件EXCEL 就可以完成这项工作。
EXCEL 办公软件操作简单方便、易于掌握。
想要用EXCEL 实现正反算,我们必须知道高斯投影正反算数学公式。
(高斯投影正算实际就是把大地坐标通过高斯投影数学模型转换为平面坐标,反之则为高斯投影反算)下面就是高斯投影公式:正算公式:"2322"4""4sin cos sin cos (59)22N N x X B Bl B B t l ηρρ=++-+ "322"3524"5""3"5cos cos (1)cos (118)6120NN N y X Bl B t l B t t l ηρρρ=++-++-+ 反算公式:23222424635(539)(619045)224720f f f f f f f f f f ff f f ft t N B B y t t y t t y M N M N M N ηη=-+-+---+ 22324535111(12)(52824)cos 6cos 120cos f f f f f f f f f fl y t y t t y N B N B N B η=-+++++ 我们只需要把上述两个公式用EXCEL 函数写于EXCEL 表格中就可以进行计算了。
其实,我们用的其他软件中高斯正反算基本全都是用这两个公式实现的,然而由于各种程序语言以及软件计算数据时精度不同所以最后结果也会有很小的误差。
excel坐标反算方位角公式

excel坐标反算方位角公式Excel坐标反算方位角公式是一种计算两个坐标点之间方位角的数学公式。
方位角是指从一个点到另一个点的方向角度,通常以北向为参考方向。
在Excel中,可以使用以下公式来计算方位角:1. 首先,确定两个坐标点的纬度和经度值。
假设第一个点的纬度为lat1,经度为lon1;第二个点的纬度为lat2,经度为lon2。
2. 将经纬度转换为弧度制。
Excel中的弧度函数是RADIANS()。
可以使用以下公式进行转换:lat1_rad = RADIANS(lat1)lat2_rad = RADIANS(lat2)lon1_rad = RADIANS(lon1)lon2_rad = RADIANS(lon2)3. 计算方位角。
使用以下公式计算方位角:x = COS(lat2_rad) * SIN(lon2_rad - lon1_rad)y = COS(lat1_rad) * SIN(lat2_rad) - SIN(lat1_rad) * COS(lat2_rad) *COS(lon2_rad - lon1_rad)angle_rad = ATAN2(x, y)4. 将弧度制的方位角转换为度数。
Excel中的度数函数是DEGREES()。
可以使用以下公式进行转换:angle_deg = DEGREES(angle_rad)最终,angle_deg即为两个坐标点之间的方位角,以度数表示。
请注意,计算结果的范围一般为[-180, 180],其中0度表示正北,正负数表示相对于正北的偏转角度。
以上是使用Excel进行坐标反算方位角的公式。
您可以在Excel中按照上述步骤进行计算,以获得具体的方位角数值。
坐标转换快捷法:用Excel 计算高斯投影正算

坐标转换快捷法:用Excel 计算高斯投影正算1、概述GPS测量作为现代高新技术手段,能方便快捷的测定点位坐标,在操作上比全站仪等其他常规测量设备有明显的优越性。
随着我国各地GPS连续运行参考站(CORS)的不断建设,使得单机作业模式得到大范围推广,在CORS的支持下定位的精度大大提高,已经达到了亚米级、厘米级精度,能够满足国土资源调查、土地利用更新、道路工程测量、遥感监测等工作的应用。
一般情况,我们使用的是北京54坐标系统或西安80坐标系统,而GPS测定的坐标是WGS-84坐标系坐标,需要进行坐标系转换。
对于非测量专业的工作人员来说,虽然GPS定位操作非常容易,但坐标转换则难以掌握,EXCEL 是比较普及的电子表格软件,能够处理较复杂的数学运算,用它来进行GPS 坐标转换会非常轻松自如。
要进行坐标系转换,离不开高斯投影换算,下面介绍用EXCEL进行换算的方法将GPS坐标转换为平面坐标格式。
2、坐标转换从经纬度BL换算到高斯平面直角坐标XY(高斯投影正算),或从XY换算成BL(高斯投影反算),一般需要专用计算机软件完成,在目前流行的换算软件中,存在一个共同的不足之处,就是灵活性较差,大都需要一个点一个点地进行,不能成批量地完成,而具有批量转换功能的软件大多是收费的,价格不菲,这样给实际的工作带来许多不便。
2.1 用EXCEL表格进行坐标转换EXCEL可以处理复杂的数学运算,可以很直观、方便地完成坐标换算工作,不需要写代码,不需要编制任何软件,只需要在EXCEL的相应单元格中输入相应的公式即可。
下面以北京54坐标系统为例,介绍具体的计算方法。
本方法完成经纬度坐标BL到平面直角坐标XY的换算,在EXCEL表格中大约需要占用21列,也可以通过简化计算公式或考虑直观性,适当减少或增加所占列数。
在EXCEL中,输入公式的起始单元格不同,则反映出来的公式不同,以公式从第2行第1列(A2格)为起始单元格为例,各单元格的公式如下:按上面表格中的公式输入到相应单元格后,就可方便地由经纬度求得平面直角坐标。
EXCEL自定义函数(反算、正算、角度化弧度)

在Excel中建立自定义函数一、建立自定义函数㈠、录制宏:①、打开一个新的Excel工作薄②、选择“工具”菜单中的“宏”子菜单,从它的下级菜单中选择“录制新宏”③、在“录制新宏”对话框的“宏名”中输入要建立的函数名,例:Rad④、在“保存在”列表中选择“个人宏工作薄”⑤、左击“确定”⑥、在“停止录”对话框中左击蓝色的小方框㈡、写程序代码①、选择“工具”菜单中的“宏”子菜单,从它的下级菜单中选择“Visual Basic 编辑器”,双击模块*②、将sub Rad()改写成Public Function Rad(y)③、将下列程序代码写入(或拷贝)到坐标反算代码Public Function fsa(x1, y1, x2, y2)Dim aa, a, b, b1, b2, b3, a1, x, y, a0Const pi = 3.14159265358979x = x2 - x1: y = y2 - y1a = Atn(y / x)If (x < 0 And y > 0) Or (x < 0 And y < 0) Thena = a + piEnd IfIf x > 0 And y < 0 Thena = a + 2 * piEnd Ifab = aaa = Sgn(ab): If aa < 0 Then ab = Abs(ab)a0 = ab / pi * 180: b1 = Int(a0): a1 = (a0 - b1) * 60: b2 = Int(a1) / 100b3 = (a1 - b2 * 100) * 60 / 10000b = b1 + b2 + b3fsa = b * aa'计算的角度为:°′″(12.3645---12°36′45″)End Function将60进制角度化成弧度――2Public Function rad(a)Dim a1, a2, a3, a4, a5, aaaa = Sgn(a)If aa < 0 Thena = Abs(a)End Ifa1 = Int(a)a2 = Int((a - a1) * 100)a3 = ((a - a1) * 100 - a2) * 100a4 = (a1 + a2 / 60 + a3 / 3600) / 180 * 3.1415926535 rad = a4 * aaEnd Function化弧度为角度―――2Public Function deg(a)Dim a1, a2, a3, a4, a5, aaaa = Sgn(a)If aa < 0 Thena = Abs(a)End Ifa1 = a / 3.1415926535 * 180a2 = Int(a1)a3 = Int((a1 - a2) * 60)a4 = ((a1 - a2) * 60 - a3) * 60a5 = (a2 + a3 / 100 + a4 / 10000) * aadeg = a5End Function。
