箱梁有效分布宽度 - 360文档中心

空间连续组合桁梁桥有效分布宽度分析

桥面板宽度，ｍ
图３荷载形式的影响
图４桥面板宽度的影响（）一
桥面板用Ｓｅｌ１ｈｌ８单元模拟，ｌ上弦用Ｓｅ６ｈｌ３单元模拟，梁、ｌ横
腹杆及下弦采用Ｂａ８ｅｍ１８单元模拟。模型中不含预应力，且不考
３３桥面板厚度的影响．
间距为，面为等腰直角三角形，截内设有加劲，高度为３０ｍ５ｍ，
上弦节点间设有横梁，腹杆钢管外径为２０ｎｎ板厚６ｍｍ，弦５－，ｌｌ下
效分布宽度系数变化最小，减小了４８；．％而在中支点节点（Ｃ）
简支组合桁架的有效分布宽度开展了参数化分析，庆普探讨朱与均布荷载相比，中荷载作用下有效分布宽度系数普遍较集但在集中荷载附近的有效分布系数较小，明荷载形式对有效说了空问简支组合桁架有效分布宽度的影响因素，而对于空间连续大，分布宽度的影响比较大，因而以下有效分布宽度影响因素分析均基组合桁架梁桥有效分布宽度研究相对较少。
２有限元模型
选取跨径为４８ｍ的两跨连续空间桁架梁桥作为研究对象，
如图１所示，建立有限元模型，横截面尺寸如图２所示，面板厚桥度为＾，面板全宽为Ｂ。桁架采用三角形桁架形式，桥节点横桥向
于均布荷载。
３２宽跨比的影响．
中图分类号：４２５Ｕ４．文献标识码：Ａ
１概述
组合结构因为其合理地发挥了钢受拉性能强和混凝土受压

30米箱梁预制方案

30m箱梁预制施工方案目录1. 编制依据及范围 (1)1.1编制依据 (1)1.2编制范围 (1)2.工程概况及环境资源条件 (1)2.1.工程概述 (1)2.1.1.预制箱梁概述 (1)2.1.2.主要材料及工程量统计 (2)2.2 环境资源条件 (2)2.2.1 气象条件 (3)2.2.2 交通条件 (3)3 施工总体方案及工艺流程 (3)3.1 总体施工方案 (3)3.1.1 场地布置 (3)3.1.2 总体施工方案 (3)3.2 施工工艺流程 (4)4.主要施工方法 (4)4.1 箱梁预制施工 (4)4.1.1原材料的检验、规定和管理 (4)4.1.2钢筋加工 (5)4.1.3梁钢筋绑扎及预埋件安装 (5)4.1.4波纹管安装 (8)4.1.5模板加工及安装 (8)4.1.6混凝土施工 (11)4.1.7混凝土养生 (12)4.1.8预应力钢绞线施工 (13)4.1.9预应力张拉 (14)4.1.10孔道压浆 (19)4.1.11封锚 (21)4.1.12存梁 (22)5.资源需求计划及工期安排 (22)5.1资源需求计划 (22)5. 1.1劳动力配置情况 (22)5.1.2材料统计情况 (22)5.1.3机械设备配置 (22)5.2施工进度计划 (23)6质量保证保证措施 (23)6.1 质量保证措施 (23)6.1.1试验工作的质量保证措施 (23)6.1.2钢筋加工及安装质量保证措施 (24)6.1.3模板质量保证措施 (24)6.1.4混凝土施工质量保证措施 (25)6.1.5预应力施工质量保证措施 (25)7.安全保证措施 (26)7.1现场保证措施 (26)7.2施工安全措施 (27)7.3吊装工程安全防护设施 (28)7.3.1一般要求 (28)7.3.2安全防护设施 (28)7.3.3安全管理要点： (29)8. 附件：梁场平面图.......................................... 错误!未定义书签。

箱梁计算书

桥梁设计计算书课程名称道桥工程设计姓名杨鑫龙学号年级与专业 2016交通工程指导教师提交日期目录一、设计资料 (4)1.1设计资料 (4)二、主梁构造布置及尺寸 (4)2.1横截面布置 (4)2.2主梁尺寸 (5)2.3横隔梁布置 (5)2.4主梁截面特性简易计算表 (5)三、主梁内力计算 (5)3.1恒载内力计算 (6)3.2活载内力计算 (8)3.3内力组合 (14)3.4弯矩剪力包络图 (15)四、预应力钢筋截面面积估算及布置 (15)4.1预应力钢筋截面面积估算 (15)4.2非预应力钢筋截面面积估算 (17)4.3预应力钢束的布置 (17)五、换算截面几何特性 (20)5.1换算截面图示 (20)5.2换算截面几何特性计算 (20)六、钢束预应力损失计算 (21)6.1预应力钢筋与管道壁之间的摩擦引起的预应力损失 (21)6.2锚具变形、钢筋回缩和接缝压缩引起的预应力损失 (22)6.3混凝土弹性压缩引起的预应力损失 (22)6.4预应力钢筋应力松弛引起的预应力损失 (23)6.5混凝土收缩和徐变引起的预应力损失 (24)6.6预应力钢筋张拉控制应力与各阶段预应力损失组合及有效预应力值25七、持久状况承载能力极限状态计算 (26)7.1正截面强度验算 (26)7.2斜截面抗剪强度验算 (26)7.3箍筋或弯起钢筋设计 (26)八、正常使用极限状态验算 (28)8.1正截面抗裂性验算 (28)8.2斜截面抗裂性验算 (28)8.3变形验算 (30)8.3.1使用阶段挠度计算 (30)8.3.2预加力引起的反拱计算及预拱度的设置 (31)九、主梁持久状况应力验算 (31)9.1跨中截面砼法向压应力验算 (31)9.2受拉区预应力筋最大拉应力验算 (32)9.3斜截面主应力验算 (32)十、主梁短暂状态应力验算 (33)10.1主梁短暂状态应力验算 (33)十一、主梁行车道板的内力计算及配筋 (34)11.1恒载作用 (34)11.2活载作用 (35)11.3主梁肋间内力计算 (35)11.4行车道板配筋计算 (37)11.5行车道板截面复核 (38)十二、横隔梁内力计算及配筋 (39)12.1横隔梁内力计算 (39)12.2横隔梁配筋计算 (42)12.3横隔梁截面复核 (43)十三、主梁端部局部承压验算 (43)13.1端部承压区截面尺寸验算 (43)13.2端部承压区承载力验算 (44)十四、结语 (45)十五、参考文献 (45)十六、附录 (46)附录A：主梁截面尺寸图 (46)附录B:横隔梁配筋图 (46)一、设计资料1.1设计资料(1)设计跨径：标准跨径35.82m（墩中心距离），简支梁计算跨径(相邻支座中心距离)35.22m，主梁全长35.78m。

现浇连续箱梁内横梁计算方法研究

后计算查看结果。
集力Ｉ岩订一ｏｋ中Ｐ－３１１Ｎ
Ｐ２Ｐ１１１３３２ｋ一 × ． — １Ｎ
活载加载方法同杆系模型一。
３模型结果对比
空间实体模型的结果最接近实际，因此以实体模型的结果为基准，评价平面杆系模型的优劣。把４个模型中横梁Ａ－Ａ断面处负弯矩和剪力见表２列。所
图２中横梁支反力传递范围
本例中横梁悬臂长而支点间距小，以支点处所Ａ＿截面的负弯矩和剪力最为不利，该截面作为Ａ取对比截面。在实体模型中Ａ— 截面沿纵桥向有９Ａ０ｒｎ长，根中横梁前后范围的内力沿纵桥向分布规律，一如图３所示。弯矩峰值为５１６ｋ・ｍ／跨中下７Ｎｍ，降至约４０ｋ・ｍ／剪力峰值为２７０ｋｍ，０Ｎｍ；６Ｎ／跨
适、于养护等诸多优点＿，便１不仅在城市桥梁中占据主］流地位，且在高速公路建设中也应用得越来越多。而
零，实体模型中得到１４ｎ７３ｍ、５ｒ、７ｍ处是零剪力面。１３ｒ４ｎ和５ｒｎ两个零剪力面之间３箱梁的荷载传２ｍ递给中横梁，中横梁支反力传递范围如图２所示。
因为连续箱梁内横梁与箱梁是一个整体，以不同于所Ｔ梁、空心板等预制拼装结构的墩台盖梁＿，２其有两个ｊ
显著特点：梁荷载作用方式不明确［；梁计算截面横３横不明确。本文结合某高架桥标准跨３０ｍ的一联箱 ×３梁，内横梁计算方法作一些浅略的研究。对

箱涵宽度大小规范

箱涵宽度大小规范一、主要技术标准1、采用设计速度为80Km/h的双向四车道高速公路标准，整体式路基宽度为24.5m，桥梁标准断面详见下图：2、主线桥涵设计荷载等级：公路-I级；被交路（高速公路及一级公路：公路-I级，二级公路以及三、四级公路：公路-II级；四级以下：公路-II级乘以0.6～0.8系数采用）。

3、地震作用：地震动峰值加速度为0.05g。

4、设计洪水频率：特大桥1/300，大、中、小桥及涵洞1/100。

5、考虑远景可能实施维修罩面和部分特种超高车辆的通行安全，同时考虑施工净空的要求，上跨县道（含县道）以上等级路的桥梁净空高度尽可能提高到5.5m，标注为5.5 m；水泥路及乡道标注为5.0m，其它标注为4.5m。

二、设计深度1、主线桥梁上部构造通用图（含数量表、标准横断面、一般构造图、钢束布置图）20m预应力混凝土小箱梁（整体式路基0°、15°、30°）25m预应力混凝土小箱梁（整体式路基0°、15°、30°）30m预应力混凝土小箱梁（整体式路基0°、15°、30°）40m预应力混凝土小箱梁（整体式路基0°）具体图纸参见各跨径的上部构造通用图2、主线桥梁下部构造通用图（与主线桥梁上部构造通用图对应）预应力混凝土分体小箱梁（含20、25、30m、40m跨径桥台一般构造图、桥墩一般构造图）3、涵洞通用图ф1.5m钢筋混凝土圆管涵（0°～45°、5°一级）2.0、4.0、6.0m钢筋混凝土盖板涵（0°～45°、5°一级）2.0、4.0、6.0m钢筋混凝土箱涵（0°～45°、5°一级）4、普通大桥、匝道桥设计内容包括（按图纸出版顺序排列）：A全桥工程数量表B桥位平面图C桥位工程地质纵断面图（地勘单位统一设计，地质情况特殊或复杂的特大桥还需提供工程地质平面图）D桥梁方案比较表（一般桥梁无，有比较方案的桥梁需增加，具体样式如下图）E桥型布置图（中桥及中桥以上桥梁均绘制平纵数据表）F上部构造横断面图（主要针对装配式结构变宽主线桥和互通匝道桥的断面，标准宽度桥梁中不再出版）G施工工序图（针对大跨变截面箱梁等特殊结构）H特殊结构一般构造图I特殊结构钢束布置图J桥台一般构造图（主要是互通匝道桥台、主线变宽桥台或U台；U 台要求有各部分构造的混凝土数量及填挖数量）K桥墩一般构造图（主要是过渡墩、互通匝道桥墩、特殊结构的桥墩；预制结构的非特殊桥墩由下构通用图统一出版，具体桥中不再出版）5、比较方案（特殊结构大桥及特大桥均应绘制比较方案），应同时包括上述除《桥梁方案比较表》外所有图纸；6、涵洞、通道只出数量表；小桥、天桥只出典型样式图和数量表。

钢箱梁截面有效分布宽度的计算分析

钢箱梁截面有效分布宽度的计算分析摘要：超大截面钢箱梁的桥位制造过程中，以基准控制、公差控制等措施，减小了钢箱梁的误差，确保了精度的控制，从而减少了实际装配中的失误。

节段预拼装的操作，有效确保了整体线型及端口匹配平顺，减少了后续的调整，大幅度提高了制造效率。

而提梁站与步履式顶推方式的选择，能有效进行施工控制，减小钢箱梁损伤及主体结构的整体受力，减少现场施工的工期流程与额外的运输等消耗，为以后相似类型的超大截面钢箱梁桥位的流水线设计提供了宝贵的经验。

本文主要分析钢箱梁截面有效分布宽度的计算。

关键词：钢箱梁;有效宽度;单箱宽度引言进行钢箱梁桥设计时首先要确定桥梁截面布置型式。

钢箱梁的截面设计要充分考虑翼缘有效分布宽度，尽可能使截面翼缘受力时全宽有效，减小剪力滞效应对翼缘板应力计算结果的影响。

钢箱梁截面单箱宽跨比不宜过大，否则截面不经济，容易造成钢材浪费。

以跨径30m～50m的多跨连续钢箱梁桥为例，对钢箱梁截面有效分布宽度进行分析研究。

1、设计主要过程（1）考虑地形、地质及道路总体要求，结合工程区域近远期规划等要素，合理确定连续梁的平面和跨径布置。

（2）根据桥梁周边场地、交通运输条件等合理拟定桥梁的施工工艺。

（3）根据该布置情况及相应受荷计算要求确定跨中及支点截面梁高，及梁底曲线，初步确定梁体构造。

（4）建立桥梁模型，对桥梁结构进行计算，根据计算结果调整梁截面尺寸、钢板厚度、连接方式、加劲肋等的布置位置、大小及方式，进一步确定梁体构造。

（5）对全桥结构进行核算，并满足各项构造措施要求。

2、钢箱梁桥位现场节段拼装现场组装钢箱梁节段，由多个且不同的板单元进行装配，最终在胎架上组成梁段。

胎架应使用专用胎架，提交设计要求并进行计算，之后通过马板对板单元进行固定。

为避免暴力拆卸对母材造成损伤，产生咬边及弧坑，现场人员应对马板相关的拆除进行监督，严禁以锤击的方式拆除马板，应在距母材表面1~3mm处用气割切除，并在切割完成后，对该位置进行打磨。

钢-混凝土组合结构连续梁有效宽度

定，不考虑剪切变形对纵向位移的影响。因此，它
行《钢结构设计规范》Ｇ０１－０）公路（Ｂ５０７２３和《０钢筋混凝土及预应力混凝土桥涵设计规范》Ｇ（
Ｄ２２０）６－０４中有相关规定，此列出以作参考。在《结构设计规范》Ｇ０１－０）１．钢（Ｂ５０７２３第１０
１２有效宽度的计算．
的深入研究，本文拟对组合梁板体系采用非线性有限元方法，分析全过程中翼缘有效宽度的变化。
１剪力滞效应及有效宽度
１１概述．
对于组合结构连续梁桥，于翼缘有效宽度关
的计算我国尚无相关规范，但类似问题在我国现梁弯曲初等理论的基本假定是变形的平面假
２～
３混凝土板有效宽度计算
３・１
武汉二七长江大… 非通航孔深水采用６桥区… 一 … …
×
：；州
如下荷载．
’
・
５２・
土
木
工
程
与
管
理
学
报
２１年０１
（）２二期恒载；
最大法向应力。由于桥面板的横截面形状并不规
ｂ＝ｂ＋ｂ＋ｂ０ｌ２（）１
逐渐减小。所以，剪切变形沿翼板的分布是不均匀的，弯曲时远离肋板的翼板的纵向位移滞后于
近肋板的翼板的纵向位移，因此弯曲应力的横向
式中，为托板顶部的宽度（ｂ。当托板倾角仅＜５４。时，按：５计算托板顶部的宽度；应４。当无托板

对截面有效宽度的理解

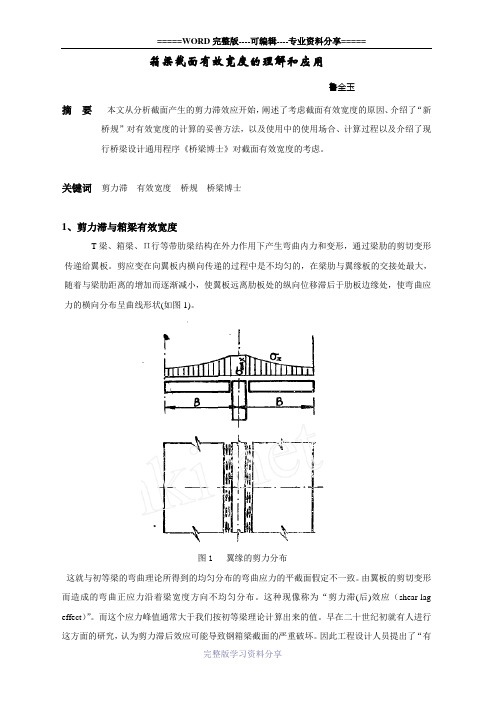
箱梁截面有效宽度的理解和应用鲁金玉摘要本文从分析截面产生的剪力滞效应开始，阐述了考虑截面有效宽度的原因、介绍了“新桥规”对有效宽度的计算的妥善方法，以及使用中的使用场合、计算过程以及介绍了现行桥梁设计通用程序《桥梁博士》对截面有效宽度的考虑。

关键词剪力滞有效宽度桥规桥梁博士1、剪力滞与箱梁有效宽度T梁、箱梁、Π行等带肋梁结构在外力作用下产生弯曲内力和变形，通过梁肋的剪切变形传递给翼板。

剪应变在向翼板内横向传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，使翼板远离肋板处的纵向位移滞后于肋板边缘处，使弯曲应力的横向分布呈曲线形状(如图1)。

图1 翼缘的剪力分布这就与初等梁的弯曲理论所得到的均匀分布的弯曲应力的平截面假定不一致。

由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布。

这种现像称为“剪力滞(后)效应（shear-lag effect）”。

而这个应力峰值通常大于我们按初等梁理论计算出来的值。

早在二十世纪初就有人进行这方面的研究，认为剪力滞后效应可能导致钢箱梁截面的严重破坏。

因此工程设计人员提出了“有效宽度”的概念，即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度，使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近，以确保结构的安全。

2、有效宽度的几何计算方法有效分布宽度问题, 实质上是以剪力滞理论为基础。

用精确的理论来分析翼缘应力的不均匀分布规律是比较复杂的, 尤其不便于工程中的应用。

为了既能利用简单的初等梁理论公式, 又能得到接近于翼缘实际应力的最大值, 便提出“翼缘有效宽度”的概念,并且由T.V.卡曼首先解决, 一直沿用至今。

翼缘有效宽度的简单定义是按初等梁理论的公式也能算得与真实应力峰值接近相等的那个翼缘折算宽度。

它的几何解释是：如图二中的真实应力峰值σmax为高度的阴影矩形面积等于真实的应力曲线所包围的面积，即阴影线矩形面积的边长，便是翼缘的有效宽度，数学表达式为：式中：be为每侧翼缘的有效宽度，b为每侧翼缘的净宽度，t为翼缘的厚度，σmax为腹板与翼板连接处的应力峰值，x为沿跨长方向的坐标，y为沿横截面宽度方向的坐标。

桥面板有效分布宽度

总结词
桥面板的有效分布宽度与跨度有关，不同跨度下需要采用不同的计算方法。
VS
详细描述
在计算桥面板的有效分布宽度时，需要考虑跨度的影响。对于不同跨度的桥梁，需要采用不同的计算方法和公式来计算有效分布宽度。此外，跨度的大小也会影响载荷的分布和桥面板的应力分布等因素。因此，在计算桥面板的有效分布宽度时，需要综合考虑跨度和载荷的特性。
对未来研究的展望
跨领域合作
桥面板有效分布宽度的研究需要结合多个学科领域的知识，如结构工程、材料科学和数值计算等，未来研究应加强跨领域合作。
新材料、新工艺的应用
随着新材料和新技术的发展，未来研究可探索将这些新材料、新工艺应用于桥面板设计中，以提高桥面板的有效分布宽度。
考虑环境因素
在未来的研究中，应更加关注环境因素对桥面板有效分布宽度的影响，如温度、湿度和荷载等。
分析。
桥面板的材料和结构
桥面板的材料类型和强度对其有效分布宽度有重要影响。
桥面板的结构形式也会影响其有效分布宽度，如连续梁和简支梁的结构形式对载荷的分布有不同的影响。
例如，高强度钢材能够承受更大的载荷，因此可以适当减小有效分布宽度。
在设计桥面板时，应充分考虑其材料和结构特点，以确保安全性和经济性。
04
桥面板有效分布宽度的应用
桥梁设计
桥面板有效分布宽度是桥梁设计的重要参数，它影响着桥梁的承载能力和稳定性。在桥梁设计中，需要考虑桥面板的有效分布宽度，以确保桥梁的结构安全和稳定性。
在设计过程中，需要根据桥面板的有效分布宽度来选择合适的材料和结构形式，以满足桥梁的承载能力和耐久性要求。
桥梁安全评估
复杂载荷作用下的有效分布宽度
总结词

对截面有效宽度的理解

箱梁截面有效宽度的理解和应用鲁金玉摘要本文从分析截面产生的剪力滞效应开始，阐述了考虑截面有效宽度的原因、介绍了“新桥规”对有效宽度的计算的妥善方法，以及使用中的使用场合、计算过程以及介绍了现行桥梁设计通用程序《桥梁博士》对截面有效宽度的考虑。

关键词剪力滞有效宽度桥规桥梁博士1、剪力滞与箱梁有效宽度T梁、箱梁、Π行等带肋梁结构在外力作用下产生弯曲内力和变形，通过梁肋的剪切变形传递给翼板。

剪应变在向翼板内横向传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，使翼板远离肋板处的纵向位移滞后于肋板边缘处，使弯曲应力的横向分布呈曲线形状(如图1)。

图1 翼缘的剪力分布这就与初等梁的弯曲理论所得到的均匀分布的弯曲应力的平截面假定不一致。

由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布。

这种现像称为“剪力滞(后)效应（shear-lag effect）”。

而这个应力峰值通常大于我们按初等梁理论计算出来的值。

早在二十世纪初就有人进行这方面的研究，认为剪力滞后效应可能导致钢箱梁截面的严重破坏。

因此工程设计人员提出了“有效宽度”的概念，即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度，使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近，以确保结构的安全。

2、有效宽度的几何计算方法有效分布宽度问题, 实质上是以剪力滞理论为基础。

用精确的理论来分析翼缘应力的不均匀分布规律是比较复杂的, 尤其不便于工程中的应用。

为了既能利用简单的初等梁理论公式, 又能得到接近于翼缘实际应力的最大值, 便提出“翼缘有效宽度”的概念,并且由T.V.卡曼首先解决, 一直沿用至今。

翼缘有效宽度的简单定义是按初等梁理论的公式也能算得与真实应力峰值接近相等的那个翼缘折算宽度。

它的几何解释是：如图二中的真实应力峰值σmax为高度的阴影矩形面积等于真实的应力曲线所包围的面积，即阴影线矩形面积的边长，便是翼缘的有效宽度，数学表达式为：式中：be为每侧翼缘的有效宽度，b为每侧翼缘的净宽度，t为翼缘的厚度，σmax为腹板与翼板连接处的应力峰值，x为沿跨长方向的坐标，y为沿横截面宽度方向的坐标。

35 35 45 35 35m钢箱梁计算书.

钢箱梁计算书（2）1.结构特点上部结构采用5孔一联钢箱梁结构，桥跨布置为(35+35+45+35+35)=185m，桥面宽度为25m，单箱多室截面，道路中心线处梁高2000mm，箱宽25m。

横隔梁的布置间距为2.0m。

钢材材质为Q345C。

钢箱梁顶面设1.5%双向横坡。

桥面铺装采用4cm细粒式沥青混凝土面层和4cm中粒式沥青混凝土底层，桥面铺装层总厚度为8cm。

另设8cm钢筋砼层。

采用混凝土防撞护栏。

2.设计荷载汽车荷载：城-A级。

3.箱梁顶板板厚的确定钢箱梁的顶板板厚对全桥的经济指标影响较大，根据目前钢箱梁的设计经验和实际汽车荷载超重的影响，箱梁顶板板厚宜取14mm。

4.箱梁标准段截面5.纵肋设计横肋布置间距a=2000mm顶板纵肋布置间距b=300mm城-A车辆前轮着地宽度2g=0.25m，分布宽度：0.25+0.08*2=0.41 m城-A车辆后轮着地宽度2g=0.6m，分布宽度：0.6+0.08*2=0.76 m5.1纵肋截面几何特性1）桥面板有效宽度的确定关于桥面板的有效计算宽度，参考日本道路桥示方书的规定进行计算。

纵肋等效跨度L=0.6a=1200mm, b/2L=0.125λ=(1.06-3.2(b/2L)+4.5(b/2L)2)*b=219.1mm, 取有效宽度为210mm。

2）截面几何特性计算纵肋板件组成：1-210x14（桥面板），1-90x10（下翼缘），1-156x8（腹板）A=50.88 cm2I= 2399.5 cm4Yc=12.2 cm （距下翼缘）Wt=413.7 cm3；Wb=196.7 cm35.2纵肋内力计算1)作用于纵肋上的恒载a)纵肋自重q1=21.48*1e-4*7.85e3*1.1=18.5 kg/mb)钢桥面板自重q2=0.014*b*7.85e3=38.5 kg/mc)桥面铺装（厚8cm）q3=0.08*b*2.4e3=67.2 kg/md)砼桥面板（厚8cm）q4=0.08*b*2.6e3=72.8 kg/me)恒载合计∑q=197.0 kg/m2)汽车冲击系数(1+μ)=1+0.4=1.43)作用于纵肋上的活载纵肋反力计算图式（尺寸单位：mm）采用Midas/Civil程序计算纵肋荷载横向分配值，后轮：在0.76m宽度内布1.0 t/m的均布力时，计算得到纵肋的最大反力为0.367 t。

箱梁有效宽度计算(高速铁路规范)

ห้องสมุดไป่ตู้
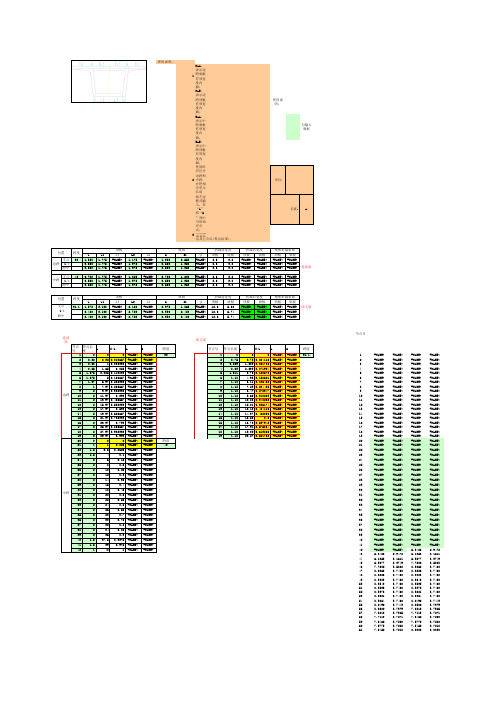
连续梁
40
中跨
位置支点 1/4 跨中
跨度 31.1
b 1.072 0.480 0.480
b1 3.100 3.100 3.100
顶板 l1 #NAME? #NAME? #NAME?
b2 2.128 2.720 2.720
l2 #NAME? #NAME? #NAME?
a 0.975 0.390 0.390
底版 a1 1.865 2.480 2.480
g1 #NAME? #NAME? #NAME?
折减前宽度顶板底板 12.6 5.68 12.6 5.74 12.6 5.74
折减后宽度顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
整体折减系数顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
a 1.350 0.550 0.550 0.700 0.550 0.550
g1 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
整体折减系数顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
简支梁
节点号连续梁节点号单元长度 x 1 0 2 0.32 3 0.68 4 0.65 5 1.675 6 1.675 7 1.97 8 1 9 2 边跨 10 2 11 2 12 2 13 2 14 2 15 2 16 2 17 2 18 2 19 2 20 0 21 1 22 1.5 23 1.5 24 2 25 2 26 2 27 2 28 2 29 2 30

小箱梁桥设计指南

但是随着小箱梁斜交角度的增大，小箱梁扭矩也随之增大，对斜交角＞30°的情况，
须单独进行计算后，谨慎使用。
构造尺寸：
跨径
梁高
腹板厚度 (跨中)
腹板厚度 (梁端)
顶板厚度
底板厚度(cm)
底板宽
(m) (cm)
(cm)
(cm)
(cm)
跨中支点
(cm)
2012018源自251818
25
100
25
140
18
25
18
18
25
100
30
160
18
25
18
18
25
100
35
180
18
25
18
18
25
100
吊装重量(简支正交)：
跨径
20m 25m 30m 35m
吊装重量 (t)
中梁
边梁
54.5
57.9
72.9
77.2
91.5
96.8
117.1
123.0
二、设计输入： 2.1 技术标准与设计规范：
2
[1]《公路工程技术标准》（JTG B01－2003）； [2]《公路桥涵设计通用规范》（JTG D60－2004）； [3]《公路钢筋混凝土及预应力混凝土设计规范》（JTG D62－2004）； [4]《公路桥涵施工技术规范》（JTJ 041－2000）； [5]《公路交通安全设施技术规范》（JTG D81－2006）； [6]《预应力混凝土用钢绞线》（GB/T5224－2003）； [7]《钢筋混凝土用热扎光圆钢筋》（GB 13013－1991）； [8]《钢筋混凝土用热扎带肋钢筋》（GB 13014－1998） 2.2 资源准备 2.2.1 资料： [1] 前阶段的研究成果和资料； [2] 设计规范和标准的掌握和理解； [3] 院小箱梁设计参考图纸（试用版）； [4] 具体项目的咨询、审查意见及施工反馈； 2.2.2 计算软件： [1] Midas Civil 2006 [2] 桥梁博士V3.1 [3] 公路桥梁结构设计系统GQJS9.7 [4] 横向分布计算、配筋设计以及验算等附属小程序。 2.2.3 主要参考文献： [1] 易建国《混凝土简支梁（板）桥（第三版）》人民交通出版社2006.9 [2] 胡兆同等《桥梁通用构造及简支梁桥》人民交通出版社2001.3 [3] 邵旭东等《桥梁设计与计算》人民交通出版社2007.2 [4] 贺栓海等《公路桥梁荷载计算方法》人民交通出版社1996.9 [5] 黄平明《混凝土斜梁桥》人民交通出版社1999 [6] 胡肇滋《桥跨结构简化分析－荷载横向分布》人民交通出版社1990 三、设计过程： 3.1 尺寸拟定与构造处理：

小箱梁设计指南

半幅全宽
(cm) 1225 1225 1600 1600 1300 1300 1675 1675 2050 2050 1400 1375 1725 1700 2100 2075
桥面净宽
L (cm) 1088.5 1125.0 1463.5 1500.0 1163.5 1200.0 1538.5 1575.0 1913.5 1950.0 1238.5 1275.0 1563.5 1600.0 1938.5 1975.0
18
18
25
100
30
160
18
25
18
18
25
100
35
180
18
25
18
18
25
100
吊装重量(简支正交)：
跨径
20m 25m 30m 35m
吊装重量 (t)
中梁
边梁
54.5
57.9
72.9
77.2
91.5
96.8
117.1
123.0
二、设计输入： 2.1 技术标准与设计规范：
2
[1]《公路工程技术标准》（JTG B01－2003）； [2]《公路桥涵设计通用规范》（JTG D60－2004）； [3]《公路钢筋混凝土及预应力混凝土设计规范》（JTG D62－2004）； [4]《公路桥涵施工技术规范》（JTJ 041－2000）； [5]《公路交通安全设施技术规范》（JTG D81－2006）； [6]《预应力混凝土用钢绞线》（GB/T5224－2003）； [7]《钢筋混凝土用热扎光圆钢筋》（GB 13013－1991）； [8]《钢筋混凝土用热扎带肋钢筋》（GB 13014－1998） 2.2 资源准备 2.2.1 资料： [1] 前阶段的研究成果和资料； [2] 设计规范和标准的掌握和理解； [3] 院小箱梁设计参考图纸（试用版）； [4] 具体项目的咨询、审查意见及施工反馈； 2.2.2 计算软件： [1] Midas Civil 2006 [2] 桥梁博士V3.1 [3] 公路桥梁结构设计系统GQJS9.7 [4] 横向分布计算、配筋设计以及验算等附属小程序。 2.2.3 主要参考文献： [1] 易建国《混凝土简支梁（板）桥（第三版）》人民交通出版社2006.9 [2] 胡兆同等《桥梁通用构造及简支梁桥》人民交通出版社2001.3 [3] 邵旭东等《桥梁设计与计算》人民交通出版社2007.2 [4] 贺栓海等《公路桥梁荷载计算方法》人民交通出版社1996.9 [5] 黄平明《混凝土斜梁桥》人民交通出版社1999 [6] 胡肇滋《桥跨结构简化分析－荷载横向分布》人民交通出版社1990 三、设计过程： 3.1 尺寸拟定与构造处理：

30m小箱梁计算书

目录目录 0一、项目概况 (1)1.1 设计计算采用的标准、规范、规程 (1)1.2 技术标准 (1)1.3 设计要点 (1)二、结构计算 (2)2.1 结构模型 (2)2.2 计算参数 (2)2.3 施工步骤 (3)2.4 荷载组合 (3)2.5 计算结果 (3)一、项目概况1.1 设计计算采用的标准、规范、规程1、《公路工程技术标准》（JTG B01-2003）；2、《公路桥涵设计通用规范》（JTG D60-2004）；3、《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）；4、《公路桥涵地基与基础设计规范》（JTG D63-2007）；5、《公路圬工桥涵设计规范》（JTG D61-2005）；6、《公路工程抗震设计细则》（JTG/T B02-01-2008）；1.2 技术标准1、采用荷载等级：公路－I级。

2、桥面宽度：0.5（护栏）+11.75（行车道）+0.5（护栏）＝12.75m3、道路等级：高速公路4、设计环境类别：I类5、地震基本烈度：Ⅵ度1.3 设计要点1、5孔30米一联预应力砼连续小箱梁，斜交角0度，先简支后连续结构；横向4片箱梁。

2、采用桥梁博士进行受力分析，预制部分为全预应力构件，现浇连接段为A类现浇构件验算，按持久状况承载能力极限状态进行强度计算，并根据荷载短期效应及长期效应组合进行应力计算。

二、结构计算2.1 结构模型采用桥梁博士3.0进行结构计算，将桥梁按照空间实用理论简化为平面杆系，永久杆件共分为123个单元，124个节点。

成桥状态计算模型见下图：计算图示2.2 计算参数1、结构安全等级一级。

2、混凝土材料：采用C50混凝土，设计强度f cd=22.4MPa，f td=1.83MPa；混凝土容重γ=26KN/m3；弹性模量E c=3.45×104MPa。

3、预应力钢束采用ΦS15.2规格，面积A y=139mm2，钢绞线标准强度f pk=1860MPa，设计强度f pd=1260MPa，弹性模量E y=1.95×105MPa，张拉控制应力σcon=1395MPa，松弛率2.5%，波纹管孔道摩擦系数μ=0.17，管道偏差影响系数k=0.0015，一端锚具变形及回缩值均为6mm。

单箱多室宽箱梁的翼缘有效宽度取值研究

单箱多室宽箱梁的翼缘有效宽度取值研究王富平;蔺鹏臻【摘要】Taking the approach bridge of Nanning bridge as an example,the effective flange widths of typical section under the dead weight and the moving load were researched by using the China highway bridge specification, American AASHTO specification and finite element model.The results showed that under the dead weight and the moving load,for the middle section of side and middle span,the distribution of effective flange width was relatively uniform along the transverse direction.The effective flange width obtained by Chinese specification was close to the result of finite element,error was less than 11%,while the error was in 10%~27% by American specification.For the fulcrum section, the effective flange width obtained by Chinese specification was too conservative, the maximum error came to 40%,while the result by American specification was partial to unsafe,the error came to -38%.Under the eccentric load,the effective flange width was varied greatly along the transverse direction,and the value obtained by Chinese specification was larger than the actual at the middle section of side and middle span,while the value by American specification was relatively conservative.%以南宁大桥引桥为例,分别采用中国公路桥梁规范、美国AASHTO规范和有限元分析方法对比研究了桥梁在自重和移动荷载作用下典型截面的翼缘有效宽度.计算结果表明:在自重和对称移动荷载作用下,对于连续梁边跨和中跨跨中截面,翼缘有效宽度沿横桥向分布比较均匀,按中国规范得到的翼缘有效宽度相对误差在11%以内,而按美国规范计算的相对误差在10%~27%;对连续梁支点截面,按中国规范得到的翼缘有效宽度取值偏于保守,最大相对误差达40%,而按美国规范所得结果偏于不安全,相对误差达-38%;在偏载作用下,翼缘有效宽度沿横桥向变化较大,按中国规范得到的翼缘有效宽度在边跨和中跨跨中截面比实际要大,而美国规范相对保守.【期刊名称】《铁道建筑》【年(卷),期】2017(057)010【总页数】6页(P6-11)【关键词】公路桥梁;有效翼缘宽度;有限元分析;宽箱梁;剪力滞效应【作者】王富平;蔺鹏臻【作者单位】兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州730070;兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州 730070【正文语种】中文【中图分类】U448.21+3预应力混凝土连续箱梁桥因其结构刚度大、变形小、动力性能好等优点在工程领域得到广泛应用。

波形钢腹板箱梁有效分布宽度分析

波形钢腹板箱梁有效分布宽度分析摘要：为了研究超大断面波形钢腹板箱形截面梁这种钢混组合结构梁的整体承载能力，基于ansys有限元平台建立32m的等截面波形钢腹板箱梁，对其钢混组合结构梁在不同几何参数及加载方式下进行模型计算和对比，得到了各个不同参数下纵桥向的坐标-应力分布曲线，进而计算得到了各个敏感参数对有效分布宽度变化的重要系数，对于这种钢混组合结构箱梁的有效分布宽度计算与规范所给的公式进行了对比分析；基于对该结构有效分布宽度的计算，简化了桥跨节段模型试验的加载方式，使得加载数值与实桥加车状态相拟合。

关键词：波形钢腹板有效分布宽度敏感参数1.1有效分布宽度的意义根据某桥跨截面桥面板在车轮荷载作用下，在桥面板的计算中，板在局部分布荷载P的作用下，不仅直接承压部分的板带参加工作，与其相邻的部分板带也会分担一部分荷载共同参与工作，需要确定所谓板的有效工作宽度a。

1）对板而言，以宽度为a的板条承受总弯矩，既满足总弯矩的要求。

2）对荷载而言，荷载只在a范围内有效且均匀分布，则荷载集度q=p/2ab1.ansys有限元模型分析2.1有限元模型的建立在建立有限元模型过程中，混凝土板采用8节点钢筋混凝土实体单元solid65，每个节点有三个自由度，即x，y，z三个方向的线位移，波纹钢腹板采用4节点弹性壳单元shell63，每个单元有6个自由度，即x，y，z三个方向的平动自由度和绕x，y，z的转动自由度，图4为整体模型；由于混凝土和钢腹板之间是通过连接键进行连接的，假定连接件是固结，在建模过程中，将混凝土和波纹钢腹板的接触面进行共节点的耦合，从而解决了因混凝土单元和壳单元因自由度不同不能限制转动自由度的问题，如图5所示。

对于钢腹板和混凝土材料均采用弹性分析，波纹钢腹板弹性模量取2.06e11Pa，泊松比0.3，混凝土弹性模量取3.45e10Pa。

为了使节段试验模型桥面板加载效果接近实桥状态的受力状况，根据单向板要求建立梁段模型l=32m使其长宽比l/b>2.5，总共有10个波纹段，根据《公路桥涵及通用规范JTG D60-2004》施加超20级后轴单个车轮重P=70KN，考虑车轮与地面接触面积0.6×0.2m2。

箱梁有效宽度研究

箱梁有效宽度研究箱梁有效宽度研究谢宝来孙东利(天津市市政工程设计研究院，天津300051)【摘要】箱形截面梁受弯时，在横桥向由于剪滞效应，贴近腹板的翼缘法向应力与腹板的法向应力相同，离腹板愈远则愈小。

这种分布对于大箱眼的单箱单室箱梁非常明显，规范也做了相关的规定，但是，在单箱多室及单箱单室的小箱眼箱梁中，因受腹板分布及支撑位置的影响，其应力分布十分复杂，应在设计中和构造上给予足够的重视。

【关键词】箱梁有效宽度剪滞效应矮塔斜拉桥一、研究模型的建立方法模型采用空间20节点的块单元，按桥梁的实际情况进行模拟。

箱梁的横隔梁起着连接各条腹板的作用，在一定情况下减弱了剪滞效应，因此在研究模型上要充分考虑，使其更加和实际情况相符。

本文不考虑活载及体内预应力影响，当考虑时，活载可以按效应进行扩大，体内预应力也可以按叠加原理加上去，毕竟每条腹板的体内预应力配置均相同。

对于矮塔斜拉桥建模，按一次成桥考虑，拉索拉力按外载荷进行加载。

(一)．单箱多室箱梁桥梁宽度16.5m，梁高2m，悬臂2m，跨径为等跨40m预应力钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距8.5m，最大箱眼净矩3.4m。

(二)．单箱单室箱梁桥梁宽度8m，梁高1.4m，悬臂2m，跨径为等跨25m普通钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距3m，最大箱眼净矩3m。

(三)．单箱单室大箱眼箱梁桥梁宽度16.5m，梁高3m，跨径为等跨55m预应力钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距3m，最大箱眼净矩7m。

(四)．矮塔斜拉桥桥梁宽度33.5m，梁高5.25～3m，跨径为90.5+150+90.5m预应力钢筋混凝土箱梁，按实际情况模拟，支座间距4m，最大箱眼净矩5.55m。

斜拉索为单索面布置，每个桥塔处为12对，每对横桥向1.2m间距布置2根OVM250AT-61钢铰线拉索，每对拉索张拉力为12000kN。

07 桥面板有效分布宽度

卡曼（T.V.Kármán）理论
如图所示，设沿梁长度方向为 2l 跨径的连续梁，翼缘板宽度为无限宽,则对于承受余弦荷载及结构均对称于 x 轴，取应力函数为[1]
(1)
应力函数选取
边界条件有
f n ( y ) = An e
nπ x φ = ∑ f n ( y ) cos l n =1 此函数应满足双调和方程
[
]
f
的压力
的弯矩
假定整个截面承受的全部弯矩 M = M f + M g ，在对称情况可写为下列 ∞ 2πx nπx πx 级数 M = M 0 + M 1 cos + M 2 cos ⋯ = ∑ M n cos l l l n =0
支承处的超静定弯矩与加载条件有关的系数
由平衡条件
N + 2t ∫ σ x dy = 0
0
2c
或
sin k n x 2k n c + sh 2k n c 1 λ = σ max k n ch 2k n c + 1 2σ max sin k n x c 1 极端情况：当 = ∞, n = 1, λ = = 0.159l 2π l
2 nπc 2 nπc sh l + l 1 λ=∑ 2nπc 2 nπ ch +1 l
0
∞
N = −2t ∫ σ x dy = −2t ∫
0
∞
∞
0
∂φ ∂y
= 0;
y =∞
∂φ ∂y
∞
y =0
nπ nπx = ∑− An cos l l n =1
∞
∂ 2φ ∂φ dy = 2t 2 ∂y ∂y