箱梁有效分布宽度计算

箱梁计算

梁配筋计算梁截面、材料信息梁宽度b= 250 mm梁高度h= 600 mmas= 60 mm a's= 35 mmh0= 540 mm梁自重 3.75 kN/m混凝土选用 C 30fc= 14.3 N/㎜2 a1= 1ft= 1.43 N/㎜2 b1= 0.8钢筋选用 2 其中，1; HPB235级钢2; HRB335级钢3; HRB400级钢fy=f'y= 300 N/㎜2 ξb= 0.550A）单筋矩形截面在纵向受拉钢筋达到充分发挥作用或不出现超筋破坏所能承受的最大弯矩设计值Mu,max= 415.68 kNmB）单筋矩形截面已知弯矩求配筋M实际= 128 kNm845.69 ㎜2取钢筋直径￠＝ 18 实取 4 根实配钢筋面积AS= 1017.88 mm2 OK!Asmin= 322.5 < AsAsmax= 3539.7 > AsC）双筋矩形截面已知弯矩求配筋M实际= 243 kNm < Mu,max受压区砼和相应的一部分受力钢筋As1的拉力所承担的受弯承载力Mu1 Mu1=Mu,max= 415.68 kNm= 3539.25 ㎜2由受压钢筋及相应的受拉钢筋承受的弯矩设计值为Mu2=M-Mu1= -172.68 kNm因此所需的受压钢筋为-1139.83 ㎜2与其对应的那部分受拉钢筋截面面积为As2=A's= -1139.83 ㎜2纵向受拉钢筋总截面面积As＝As1＋As2= 2399.42 ㎜2受拉钢筋取钢筋直径￠＝ 20 实取 9 根实配钢筋面积AS= 2827.43 mm2 OK!受压钢筋取钢筋直径￠＝ 12 实取 2 根实配钢筋面积AS= 226.19 mm2 OK!验算受压区高度x＝fyAs1/(α1fcb)= 297.00 mm2α's＝ 70.00 mm ≤ x OK!D）双筋矩形截面已知弯矩和受压钢筋求受拉配筋M实际= 80 kNm > Mu,max已知： A's＝ 942.48 3 ￠ 20为充分发挥受压钢筋A's的作用，取As2=A's= 942.48 mm2Mu2=f'yA's(h0-a's)= 142.79 kNm由弯矩Mu1按单筋矩形截面求As1Mu1=M-Mu2= -62.79 kNm因此所需的受压钢筋为-376.55 ㎜2纵向受拉钢筋总截面面积As＝As1＋As2= 565.93 ㎜2受拉钢筋取钢筋直径￠＝ 20 实取 8 根实配钢筋面积AS= 2513.27 mm2 OK!验算受压区高度x＝fyAs1/(α1fcb)= -31.60 mm 2α's＝ 70 mm ＞ x NO。

对截面有效宽度的理解

箱梁截面有效宽度的理解和应用鲁金玉摘要本文从分析截面产生的剪力滞效应开始，阐述了考虑截面有效宽度的原因、介绍了“新桥规”对有效宽度的计算的妥善方法，以及使用中的使用场合、计算过程以及介绍了现行桥梁设计通用程序《桥梁博士》对截面有效宽度的考虑。

关键词剪力滞有效宽度桥规桥梁博士1、剪力滞与箱梁有效宽度T梁、箱梁、Π行等带肋梁结构在外力作用下产生弯曲内力和变形，通过梁肋的剪切变形传递给翼板。

剪应变在向翼板内横向传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，使翼板远离肋板处的纵向位移滞后于肋板边缘处，使弯曲应力的横向分布呈曲线形状(如图1)。

图1 翼缘的剪力分布这就与初等梁的弯曲理论所得到的均匀分布的弯曲应力的平截面假定不一致。

由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布。

这种现像称为“剪力滞(后)效应（shear-lag effect）”。

而这个应力峰值通常大于我们按初等梁理论计算出来的值。

早在二十世纪初就有人进行这方面的研究，认为剪力滞后效应可能导致钢箱梁截面的严重破坏。

因此工程设计人员提出了“有效宽度”的概念，即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度，使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近，以确保结构的安全。

2、有效宽度的几何计算方法有效分布宽度问题, 实质上是以剪力滞理论为基础。

用精确的理论来分析翼缘应力的不均匀分布规律是比较复杂的, 尤其不便于工程中的应用。

为了既能利用简单的初等梁理论公式, 又能得到接近于翼缘实际应力的最大值, 便提出“翼缘有效宽度”的概念,并且由T.V.卡曼首先解决, 一直沿用至今。

翼缘有效宽度的简单定义是按初等梁理论的公式也能算得与真实应力峰值接近相等的那个翼缘折算宽度。

它的几何解释是：如图二中的真实应力峰值σmax为高度的阴影矩形面积等于真实的应力曲线所包围的面积，即阴影线矩形面积的边长，便是翼缘的有效宽度，数学表达式为：式中：be为每侧翼缘的有效宽度，b为每侧翼缘的净宽度，t为翼缘的厚度，σmax为腹板与翼板连接处的应力峰值，x为沿跨长方向的坐标，y为沿横截面宽度方向的坐标。

单箱多室宽箱梁的翼缘有效宽度取值研究

单箱多室宽箱梁的翼缘有效宽度取值研究王富平;蔺鹏臻【摘要】Taking the approach bridge of Nanning bridge as an example,the effective flange widths of typical section under the dead weight and the moving load were researched by using the China highway bridge specification, American AASHTO specification and finite element model.The results showed that under the dead weight and the moving load,for the middle section of side and middle span,the distribution of effective flange width was relatively uniform along the transverse direction.The effective flange width obtained by Chinese specification was close to the result of finite element,error was less than 11%,while the error was in 10%~27% by American specification.For the fulcrum section, the effective flange width obtained by Chinese specification was too conservative, the maximum error came to 40%,while the result by American specification was partial to unsafe,the error came to -38%.Under the eccentric load,the effective flange width was varied greatly along the transverse direction,and the value obtained by Chinese specification was larger than the actual at the middle section of side and middle span,while the value by American specification was relatively conservative.%以南宁大桥引桥为例,分别采用中国公路桥梁规范、美国AASHTO规范和有限元分析方法对比研究了桥梁在自重和移动荷载作用下典型截面的翼缘有效宽度.计算结果表明:在自重和对称移动荷载作用下,对于连续梁边跨和中跨跨中截面,翼缘有效宽度沿横桥向分布比较均匀,按中国规范得到的翼缘有效宽度相对误差在11%以内,而按美国规范计算的相对误差在10%~27%;对连续梁支点截面,按中国规范得到的翼缘有效宽度取值偏于保守,最大相对误差达40%,而按美国规范所得结果偏于不安全,相对误差达-38%;在偏载作用下,翼缘有效宽度沿横桥向变化较大,按中国规范得到的翼缘有效宽度在边跨和中跨跨中截面比实际要大,而美国规范相对保守.【期刊名称】《铁道建筑》【年(卷),期】2017(057)010【总页数】6页(P6-11)【关键词】公路桥梁;有效翼缘宽度;有限元分析;宽箱梁;剪力滞效应【作者】王富平;蔺鹏臻【作者单位】兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州730070;兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州 730070【正文语种】中文【中图分类】U448.21+3预应力混凝土连续箱梁桥因其结构刚度大、变形小、动力性能好等优点在工程领域得到广泛应用。

MIDAS钢箱梁计算书

MIDAS钢箱梁计算书1.1B07～F03 D07～H03 50.5+65+50.5m(桥宽10m)钢箱梁1.1.1计算参数及参考规范（1）标准设计荷载：城-A级；桥梁安全等级为一级，结构重要性系数1.1；（2）主要材料钢箱梁采用Q345D 钢材，桥面板采用C40混凝土。

（3）参考规范《公路钢结构桥梁设计规范》报批稿，《公路钢筋混凝土及预应力混凝土桥涵设计规范》。

1.1.2主要计算内容结构纵向整体应力，即主梁体系，采用三维有限元建模分析，采用梁格模型，计算主梁顶、底板最不利应力。

1.1.3纵向整体计算1.1.3.1.1计算模型纵向整体计算采用三维有限元建模分析，采用梁格法模型进行模拟。

参照《公路钢结构桥梁设计规范》报批稿进行钢梁有效分布宽度的计算。

根据桥面布置，汽车按最不利情况进行影响线加载。

温度考虑整体升降温20度和梯度温度。

永久支承按简支支承条件进行约束。

全桥共划分为241个单元，162个节点。

结构计算几何模型如下图：计算几何模型1.1.3.1.2计算荷载（1）一期恒载主梁顶、底和腹板采用实际板厚，钢材重力密度78.5kN/m 3，单元重力密度考虑各种加劲肋和焊缝实际重量提高1.24倍；混凝土桥面板重力密度25kN/m 3。

沥青混凝土重力密度24kN/m 3。

（2）二期恒载1.1.3.1.3计算参数（1）钢材材料特性如下表：结构钢材性能表应用结构钢箱加劲梁材质Q345D 力学性能弹性模量E(MPa) 210000 剪切模量G(MPa)81000 泊松比γ0.3 轴向容许应力[σ] (MPa)200 弯曲容许应力[σw] (MPa)210 容许剪应力[τ] (MPa) 120 屈服应力[σs] (MPa) 345 热膨胀系数(℃)0.000012（2）梯度温差：参照混凝土规范规定：升温取T1=14°C，T2=5.5°C，负温度效应按照一半考虑。

（3）基础变位：主墩沉降2cm，边墩沉降1cm。

钢箱梁—40 60 40钢箱梁计算书

1 设计要点1.1 总体设计达连坝大桥主桥为钢箱连续梁桥，跨径组合为（40+60+40）m，全长140m。

1.2 主桥上部结构设计概况（1）结构布置主桥为（40+60+40）m三跨钢箱连续梁桥，全长140m。

边中跨比为0.667。

桥梁横断面布置为：（0.5m防撞墙）+（14.75m车行道）+（0.5m防撞墙）=单幅桥总宽15.75m （2）钢箱梁主梁方案主梁采用等截面钢箱梁，单箱五室断面，桥面宽15.75m，箱宽12.0m，悬臂长1.925m。

主梁中心高度2.4m，高跨比1/25。

1.3 主桥下部结构设计概况见施工图纸。

1.4 主要材料（1）混凝土C15：承台基础垫层C30：过渡墩承台、防撞栏、桩基、主墩墩身、过渡墩墩身及盖梁C40：支座垫石（2）钢材主体结构采用Q345qD；附属结构采用Q235B；（3）支座主墩：LQZ3000GD、LQZ3000DX、LQZ3000SX；过渡墩：LQZ1500DX、LQZ1500SX；（4）伸缩缝伸缩缝：D160型伸缩缝。

2 计算依据2.1设计规范及参考资料（1）执行规范：《公路桥涵钢结构及木结构设计规范》（JTJ 025-86）《铁路桥梁钢结构设计规范》（TB 10002.2-2005）《钢结构设计规范》（GB 50017-2003）《公路桥涵设计通用规范》（JTG D60-2004）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）《公路桥梁抗风设计规范》（JTG/T D60-01-2004）（2）参考规范及文献资料：《日本道路桥示方书·同解说》《钢桥、混凝土桥及结合桥》BS5400 （1978~1982）《公路钢结构桥梁设计规范—征求意见稿》《现代钢桥》（上册）（吴冲主编 2006年4月）《公路钢结构桥梁设计规范》( 征求意见稿)《公路钢箱梁桥面铺装设计与施工技术指南》2.2技术标准（1）公路等级：双向6车道，一级公路。

20M简支箱梁计算（详细）

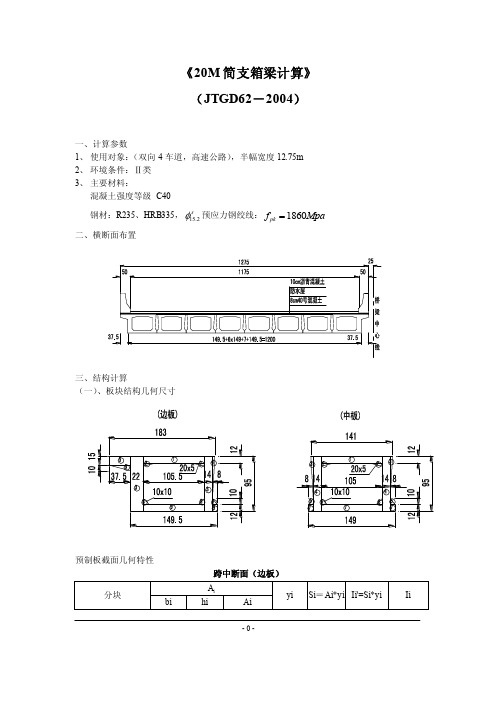
- 0 -《20M 简支箱梁计算》（JTGD62－2004）一、计算参数1、使用对象：（双向4车道，高速公路），半幅宽度12.75m2、环境条件：Ⅱ类3、主要材料：混凝土强度等级 C40钢材：R235、HRB335，15.2sφ预应力钢绞线：1860pk f Mpa =二、横断面布置三、结构计算（一）、板块结构几何尺寸预制板截面几何特性跨中断面（边板）- 1 -毛截面：314992.8943.857184isiS y cm A ===∑"4314992.8943.8513812438.23i i i I S y m ==⨯=∑'"402659390.3319638963.0413812438.238485915.14i i i I I I I m =+-=+-=∑∑∑换算截面：331440.2345.007364.74is iSy cm A ===∑234T s A I b td tα=+⎰ 221(145.5149.5)959595145.5149.522014+1812=+⨯++⨯+340.2237.520222677086600022333708cm +⨯⨯+＝＝（式中α高等学校教材“表2－4－3）跨中截面（中板）- 2 -毛截面：28595048.115944is iSy cm A ===∑'40i 2120672.7818882276.8628595048.117245895.14i i s I I I S y m =+-=+-⨯=∑∑∑换算截面：301123.3449.286110.74is iSy cm A ===∑'42120672.7820263050.9301123.3449.287544365.49i i i s I I I S y cm =+-=+-⨯=∑∑∑换22212121241()2T s A I S S h d S S S t t t t ==+++⎰221(141149)95951411492(1418)/21212=+⨯⨯+++4184100902521058834cm 11.87524.167⨯⨯+＝＝（二）荷载效应标准值 1、结构重力 1）板自重一期（预制板）326/r KN m =260.5915.45/q A K N ⨯ 中中＝r ＝＝- 3 -260.718418.68/m q A KN ⨯ 边边＝r ＝＝；二期（现浇铰缝、铺装层、护栏）铰缝混凝土 325/r K N m =[]250.950.730.08250.038 1.31/mq K N ⨯⨯⨯⨯⨯边＝(0.085)-(0.04)/2-(0.12+0.22)＝＝2 1.31 2.62/q K N m ⨯中＝＝铺装24(0.080.1) 1.5 6.48/q KN m ⨯+⨯中＝＝24(0.08 1.7850.11.375) 6.73/q KN m ⨯⨯+⨯边＝＝护栏按两侧刚性护栏对称布置，混凝土0.353/m m2(250.35)/8 2.19/q KN m ⨯⨯=栏＝1.31 6.7310.23/q KN m +∑边＝＝2.62 6.48 2.1911.29/q KN m ++∑中＝＝2）内力影响线- 4 -2、汽车荷载效应 1）公路Ⅰ级荷载均布荷载 10.5/k q K N m= 集中荷载 19.55180(1)238505k P K N -=⨯+=-当计算剪力时： 1.2238285.6k P KN =⨯= 2）冲击系数结果基频 1f =（桥JTGD62－2004条文说明4－3条） 322/ 1.57710/c m G g NS m ==⨯1 5.05f Hz ==当11.514Hz f Hz ≤≤：0.1767ln 0.0157f μ=- （桥规JTGD60－2004，4.3.2式）所以 0.270μ= 1 1.270μ+= 3）汽车荷载横向分配系数3(~)44c l lk 修正的刚性横梁法 2ii ii ii iI a I R e Ia I β=±∑∑- 5 -221112ii iGl T E a I β=+∑∑ （式中G/E=0.4 ）20.0848660.072330.604iI=⨯+⨯=∑；20.0033460.21059 1.71iT =⨯+⨯=∑222222 5.250.084862(3.75 2.250.75)0.07246 4.6779 2.85317.531i ia I=⨯⨯+++⨯=+=∑边板 1 5.25a m = 11 5.250.084860.446I a =⨯=∴210.2579119.5 1.7110.4127.531β==<⨯+⨯ 符合规定 10.084860.08486 5.250.25790.14050.0153i i R e e ⨯=±⨯=±二列车影响线布载得：(0.22250.19500.17440.1470)/c k =+++= 0.5k 支＝沿桥纵向布置：- 6 -(三)持久状态承载能力极限状态计算1、正截面抗弯承载能力按《规范》5.2.2-1式计算00()2d cd x M f bx h γ≤-顶板：0b=183cm,t=12cm,h =91cm混凝土抗力：618.41830120 4.0410cd f bt N =⨯⨯=⨯由于顶板混凝土抗力大于钢筋抗力，混凝土受压区高度x 在顶板内，'112602800280791111.418.41830Pd P sd S cd f A f A x mm f b +⨯+⨯===⨯根据JTG D60－2004 基本组合表达式（4.1.6－1）取用分项系数0γ――结构重要性系数，0γ=1.1；G γ――结构自重分项系数， G γ＝1.21Q γ――汽车荷载（含冲击力）的分项系数，取1Q γ＝1.4- 7 -001112()m nd Gi Gik Q Q k c Qj Qjk i j M S S S γγγγφγ===++∑∑[]1.11.2(887.86486.23) 1.4(10.270)613.123012.94K N m =⨯++⨯+⨯=⋅ 60111.4(18.41830111.4(910)3204.531022r cd x M f bx h N mm =-=⨯⨯-=⨯⋅03204.533012.94dK N m M K N mγ=⋅>=⋅ 符合规定 2、斜截面抗剪承载能力按《桥规》5.2.7－1式计算0d cs sb pb V V V V γ≤++ （荷载效应分项系数同正截面抗弯强度）计算斜截面位置距支点/2h ，d V 是斜截面受压端上由作用效应产生的最大剪力组合设计值：[]0 1.11.2(155.5385.17) 1.4(10.270)156.20623.22d V KN γ=⨯++⨯+⨯=1）预制板截面尺寸应符合《规范》5.2.9式000.5100.51102140910821.86623.22d V b h KN KN γ--≤⨯⋅=⨯⨯⨯=>按《规范》5.2.10式检验斜截面要不要设箍筋330200.5100.510 1.25 1.652140910159.25d td V f bh KN γα--≤⨯=⨯⨯⨯⨯⨯⨯=对于板式受弯构件 1.25159.25=199.06K N <62⨯ 所以预制板截面尺寸满足《规范》要求，但斜截面得设箍筋。

箱梁有效分布宽度计算

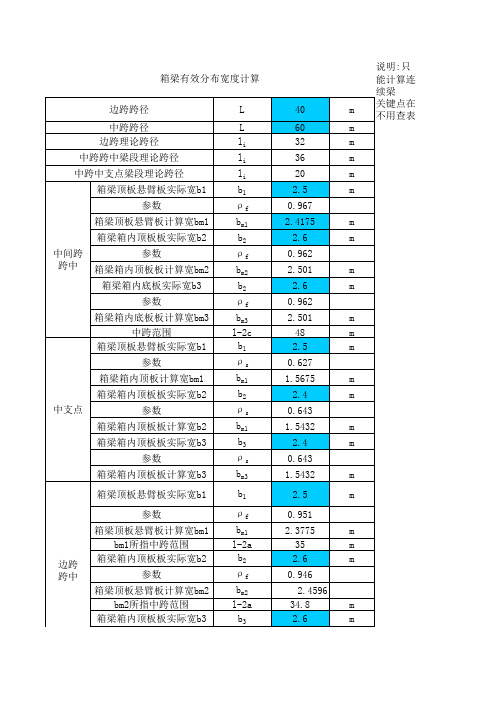
m m m m m m m m m m m m m m m m m m m
说明:只能计算连续梁关键点在不用查表
中跨跨中梁段理论跨径中跨中支点梁段理论跨径箱梁顶板悬臂板实际宽b1 参数箱梁顶板悬臂板计算宽bm1 箱梁箱内顶板板实际宽b2 中间跨跨中参数箱梁箱内顶板板计算宽bm2 箱梁箱内底板实际宽b3 参数箱梁箱内底板板计算宽bm3 中跨范围箱梁顶板悬臂板实际宽b1 参数箱梁箱内顶板计算宽bm1 箱梁箱内顶板板实际宽b2 中支点参数箱梁箱内顶板板计算宽b2 箱梁箱内顶板板实际宽b3 参数箱梁箱内顶板板计算宽b3 箱梁顶板悬臂板实际宽b1 参数箱梁顶板悬臂板计算宽bm1 bm1所指中跨范围箱梁箱内顶板板实际宽b2 参数箱梁顶板悬臂板计算宽bm2 bm2所指中跨范围箱梁箱内顶板板实际宽b3 参数箱梁箱内顶板板实际宽bm3 bm3所指中跨范围
边跨跨径中跨跨径边跨理论跨径
箱梁有效分布宽度计算 L L li li li b1 ρ
f
40 60 32 36 20 2.5 0.967 2.4175 2.6 0.962 2.501 2.6 0.962 2.501 48 2.5 0.627 1.5675 2.4 0.643 1.5432 2.4 0.643 1.5432 2.5 0.951 2.3775 35 2.6 0.946 2.4596 34.8 2.6 0.946 2.46 34.8
bm1 b2 ρ
f
bm2 b2 ρ
f
bm3 l-2c b1 ρ
s
bm1 b2 ρ
s
bm1 b3 ρ
s
bm3 b1 ρ
f
边跨跨中
bm1 l-2a b2 ρ
f

钢箱梁截面有效分布宽度的计算分析

钢箱梁截面有效分布宽度的计算分析摘要：超大截面钢箱梁的桥位制造过程中，以基准控制、公差控制等措施，减小了钢箱梁的误差，确保了精度的控制，从而减少了实际装配中的失误。

节段预拼装的操作，有效确保了整体线型及端口匹配平顺，减少了后续的调整，大幅度提高了制造效率。

而提梁站与步履式顶推方式的选择，能有效进行施工控制，减小钢箱梁损伤及主体结构的整体受力，减少现场施工的工期流程与额外的运输等消耗，为以后相似类型的超大截面钢箱梁桥位的流水线设计提供了宝贵的经验。

本文主要分析钢箱梁截面有效分布宽度的计算。

关键词：钢箱梁;有效宽度;单箱宽度引言进行钢箱梁桥设计时首先要确定桥梁截面布置型式。

钢箱梁的截面设计要充分考虑翼缘有效分布宽度，尽可能使截面翼缘受力时全宽有效，减小剪力滞效应对翼缘板应力计算结果的影响。

钢箱梁截面单箱宽跨比不宜过大，否则截面不经济，容易造成钢材浪费。

以跨径30m～50m的多跨连续钢箱梁桥为例，对钢箱梁截面有效分布宽度进行分析研究。

1、设计主要过程（1）考虑地形、地质及道路总体要求，结合工程区域近远期规划等要素，合理确定连续梁的平面和跨径布置。

（2）根据桥梁周边场地、交通运输条件等合理拟定桥梁的施工工艺。

（3）根据该布置情况及相应受荷计算要求确定跨中及支点截面梁高，及梁底曲线，初步确定梁体构造。

（4）建立桥梁模型，对桥梁结构进行计算，根据计算结果调整梁截面尺寸、钢板厚度、连接方式、加劲肋等的布置位置、大小及方式，进一步确定梁体构造。

（5）对全桥结构进行核算，并满足各项构造措施要求。

2、钢箱梁桥位现场节段拼装现场组装钢箱梁节段，由多个且不同的板单元进行装配，最终在胎架上组成梁段。

胎架应使用专用胎架，提交设计要求并进行计算，之后通过马板对板单元进行固定。

为避免暴力拆卸对母材造成损伤，产生咬边及弧坑，现场人员应对马板相关的拆除进行监督，严禁以锤击的方式拆除马板，应在距母材表面1~3mm处用气割切除，并在切割完成后，对该位置进行打磨。

35+35+45+35+35m钢箱梁计算书

钢箱梁计算书（2）1.结构特点上部结构采用5孔一联钢箱梁结构，桥跨布置为(35+35+45+35+35)=185m，桥面宽度为25m，单箱多室截面，道路中心线处梁高2000mm，箱宽25m。

横隔梁的布置间距为2.0m。

钢材材质为Q345C。

钢箱梁顶面设1.5%双向横坡。

桥面铺装采用4cm细粒式沥青混凝土面层和4cm中粒式沥青混凝土底层，桥面铺装层总厚度为8cm。

另设8cm钢筋砼层。

采用混凝土防撞护栏。

2.设计荷载汽车荷载：城-A级。

3.箱梁顶板板厚的确定钢箱梁的顶板板厚对全桥的经济指标影响较大，根据目前钢箱梁的设计经验和实际汽车荷载超重的影响，箱梁顶板板厚宜取14mm。

4.箱梁标准段截面5.纵肋设计横肋布置间距a=2000mm顶板纵肋布置间距b=300mm城-A车辆前轮着地宽度2g=0.25m，分布宽度：0.25+0.08*2=0.41 m城-A车辆后轮着地宽度2g=0.6m，分布宽度：0.6+0.08*2=0.76 m5.1纵肋截面几何特性1）桥面板有效宽度的确定关于桥面板的有效计算宽度，参考日本道路桥示方书的规定进行计算。

纵肋等效跨度L=0.6a=1200mm, b/2L=0.125λ=(1.06-3.2(b/2L)+4.5(b/2L)2)*b=219.1mm, 取有效宽度为210mm。

2）截面几何特性计算纵肋板件组成：1-210x14（桥面板），1-90x10（下翼缘），1-156x8（腹板）A=50.88 cm2I= 2399.5 cm4Yc=12.2 cm （距下翼缘）Wt=413.7 cm3；Wb=196.7 cm35.2纵肋内力计算1)作用于纵肋上的恒载a)纵肋自重q1=21.48*1e-4*7.85e3*1.1=18.5 kg/mb)钢桥面板自重q2=0.014*b*7.85e3=38.5 kg/mc)桥面铺装（厚8cm）q3=0.08*b*2.4e3=67.2 kg/md)砼桥面板（厚8cm）q4=0.08*b*2.6e3=72.8 kg/me)恒载合计∑q=197.0 kg/m2)汽车冲击系数(1+μ)=1+0.4=1.43)作用于纵肋上的活载纵肋反力计算图式（尺寸单位：mm）采用Midas/Civil程序计算纵肋荷载横向分配值，后轮：在0.76m宽度内布1.0 t/m的均布力时，计算得到纵肋的最大反力为0.367 t。

箱梁有效宽度研究

箱梁有效宽度研究箱梁有效宽度研究谢宝来孙东利(天津市市政工程设计研究院，天津300051)【摘要】箱形截面梁受弯时，在横桥向由于剪滞效应，贴近腹板的翼缘法向应力与腹板的法向应力相同，离腹板愈远则愈小。

这种分布对于大箱眼的单箱单室箱梁非常明显，规范也做了相关的规定，但是，在单箱多室及单箱单室的小箱眼箱梁中，因受腹板分布及支撑位置的影响，其应力分布十分复杂，应在设计中和构造上给予足够的重视。

【关键词】箱梁有效宽度剪滞效应矮塔斜拉桥一、研究模型的建立方法模型采用空间20节点的块单元，按桥梁的实际情况进行模拟。

箱梁的横隔梁起着连接各条腹板的作用，在一定情况下减弱了剪滞效应，因此在研究模型上要充分考虑，使其更加和实际情况相符。

本文不考虑活载及体内预应力影响，当考虑时，活载可以按效应进行扩大，体内预应力也可以按叠加原理加上去，毕竟每条腹板的体内预应力配置均相同。

对于矮塔斜拉桥建模，按一次成桥考虑，拉索拉力按外载荷进行加载。

(一)．单箱多室箱梁桥梁宽度16.5m，梁高2m，悬臂2m，跨径为等跨40m预应力钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距8.5m，最大箱眼净矩3.4m。

(二)．单箱单室箱梁桥梁宽度8m，梁高1.4m，悬臂2m，跨径为等跨25m普通钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距3m，最大箱眼净矩3m。

(三)．单箱单室大箱眼箱梁桥梁宽度16.5m，梁高3m，跨径为等跨55m预应力钢筋混凝土箱梁，分别模拟单支点、双支点和线支撑，双支点支座间距3m，最大箱眼净矩7m。

(四)．矮塔斜拉桥桥梁宽度33.5m，梁高5.25～3m，跨径为90.5+150+90.5m预应力钢筋混凝土箱梁，按实际情况模拟，支座间距4m，最大箱眼净矩5.55m。

斜拉索为单索面布置，每个桥塔处为12对，每对横桥向1.2m间距布置2根OVM250AT-61钢铰线拉索，每对拉索张拉力为12000kN。

新规范35m箱梁计算书

新规范35m箱梁计算书.一、总体概述上部箱梁构造为5×35连续小箱梁，桥宽12.25米，由4榀小箱梁联结构成，布置图如下图所示。

设计荷载公路Ⅰ级。

本计算只对边梁单榀箱梁进行分析，模的主要规范有：1．《公路桥涵设计通用规范》（JTGD60-2004）2．《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTGD62-2004）3.《公路工程技术标准》（JTGB01-2003）(一)技术指标设计荷载：公路Ⅰ级。

桥面宽度：0.5＋11.25+0.5=12.25米，单幅桥。

标准桥面横坡：2%跨径：35米斜度：0°，10°,20°,30°,40°主梁片数：4片梁。

预制梁长：34.3米。

预制梁高：1.8米。

桥面铺装：9cm沥青混凝土。

混凝土调平层: 8cm50号混凝土。

(二)相关参数相对温度 75%桥面板与其它部分的温差为±5°预应力管道成形为钢波纹管管道摩擦系数u=0.25管道偏差系数λ=0.0025l/米钢筋回缩和锚具变形为6mm(三)主要材料1．混凝土材料预制箱梁、横隔板 50号混凝土现浇连续段、封锚端、湿接缝 50号混凝土现浇桥面层50号混凝土主梁采用50号混凝土，力学性能见表1.1混凝土力学性能表表1.12预应力筋均采用符合ASTM A416-96a标准的高强低松弛270级钢绞线，公称直径φj15.24mm，公称面积为140mm2，标准强度为MPaR by1860=，，控制张拉应力为1395MPa。

弹性模量为MPaEy51095.1⨯=。

（四）预应力布置预应力构造分为两种类型：顶板索和腹板连续索。

预制小箱梁采用OVM型锚具及配套的设备。

箱梁顶板负矩钢束采用BM15型锚具及配套的设备，管道成孔采用波纹扁管，且要求钢波纹扁管的钢带厚度不小于0.35mm。

预应力张拉采用引伸量和张拉吨位双控。

并以引伸量为主。

引伸量误差不得超过-5%~10%。

对截面有效宽度的理解

箱梁截面有效宽度的理解和应用鲁金玉摘要本文从分析截面产生的剪力滞效应开始，阐述了考虑截面有效宽度的原因、介绍了“新桥规”对有效宽度的计算的妥善方法，以及使用中的使用场合、计算过程以及介绍了现行桥梁设计通用程序《桥梁博士》对截面有效宽度的考虑。

关键词剪力滞有效宽度桥规桥梁博士1、剪力滞与箱梁有效宽度T梁、箱梁、Π行等带肋梁结构在外力作用下产生弯曲内力和变形，通过梁肋的剪切变形传递给翼板。

剪应变在向翼板内横向传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，使翼板远离肋板处的纵向位移滞后于肋板边缘处，使弯曲应力的横向分布呈曲线形状(如图1)。

图1 翼缘的剪力分布这就与初等梁的弯曲理论所得到的均匀分布的弯曲应力的平截面假定不一致。

由翼板的剪切变形而造成的弯曲正应力沿着梁宽度方向不均匀分布。

这种现像称为“剪力滞(后)效应（shear-lag effect）”。

而这个应力峰值通常大于我们按初等梁理论计算出来的值。

早在二十世纪初就有人进行这方面的研究，认为剪力滞后效应可能导致钢箱梁截面的严重破坏。

因此工程设计人员提出了“有效宽度”的概念，即将翼缘实际宽度按某个系数或者某种规律折减为计算宽度，使折减后的宽度按初等梁理论算得的应力值和实际的峰值接近，以确保结构的安全。

2、有效宽度的几何计算方法有效分布宽度问题, 实质上是以剪力滞理论为基础。

用精确的理论来分析翼缘应力的不均匀分布规律是比较复杂的, 尤其不便于工程中的应用。

为了既能利用简单的初等梁理论公式, 又能得到接近于翼缘实际应力的最大值, 便提出“翼缘有效宽度”的概念,并且由T.V.卡曼首先解决, 一直沿用至今。

翼缘有效宽度的简单定义是按初等梁理论的公式也能算得与真实应力峰值接近相等的那个翼缘折算宽度。

它的几何解释是：如图二中的真实应力峰值σmax为高度的阴影矩形面积等于真实的应力曲线所包围的面积，即阴影线矩形面积的边长，便是翼缘的有效宽度，数学表达式为：式中：be为每侧翼缘的有效宽度，b为每侧翼缘的净宽度，t为翼缘的厚度，σmax为腹板与翼板连接处的应力峰值，x为沿跨长方向的坐标，y为沿横截面宽度方向的坐标。

箱梁有效宽度计算(高速铁路规范)

ห้องสมุดไป่ตู้
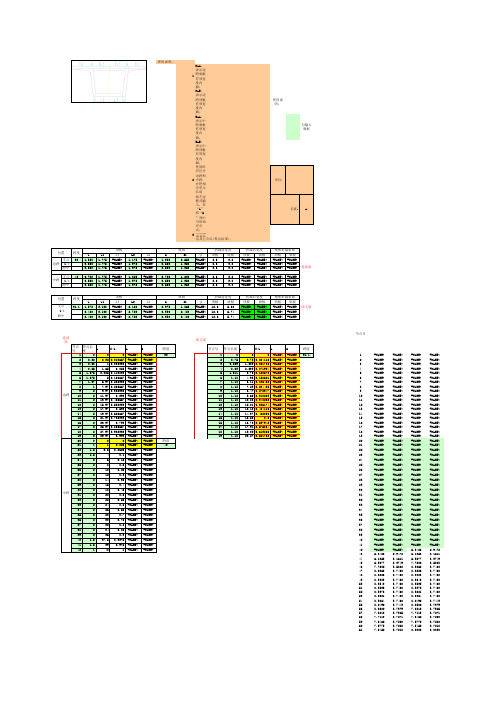
连续梁
40
中跨
位置支点 1/4 跨中
跨度 31.1
b 1.072 0.480 0.480
b1 3.100 3.100 3.100
顶板 l1 #NAME? #NAME? #NAME?
b2 2.128 2.720 2.720
l2 #NAME? #NAME? #NAME?
a 0.975 0.390 0.390
底版 a1 1.865 2.480 2.480
g1 #NAME? #NAME? #NAME?
折减前宽度顶板底板 12.6 5.68 12.6 5.74 12.6 5.74
折减后宽度顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
整体折减系数顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
a 1.350 0.550 0.550 0.700 0.550 0.550
g1 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
整体折减系数顶板底板 #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME? #NAME?
简支梁
节点号连续梁节点号单元长度 x 1 0 2 0.32 3 0.68 4 0.65 5 1.675 6 1.675 7 1.97 8 1 9 2 边跨 10 2 11 2 12 2 13 2 14 2 15 2 16 2 17 2 18 2 19 2 20 0 21 1 22 1.5 23 1.5 24 2 25 2 26 2 27 2 28 2 29 2 30

20M简支箱梁计算(详细)

- 0 -《20M 简支箱梁计算》（JTGD62－2004）一、计算参数 1、使用对象：（双向4车道，高速公路），半幅宽度12.75m 2、环境条件：Ⅱ类 3、主要材料：混凝土强度等级 C40钢材：R235、HRB335，15.2sφ预应力钢绞线：1860pk f Mpa =二、横断面布置三、结构计算（一）、板块结构几何尺寸预制板截面几何特性跨中断面（边板）- 1 -毛截面：314992.8943.857184is iSy cm A ===∑"4314992.8943.8513812438.23i i i I S y m ==⨯=∑'"402659390.3319638963.0413812438.238485915.14i i i I I I I m =+-=+-=∑∑∑换算截面：331440.2345.007364.74is iSy cm A ===∑234T s A I bt d tα=+⎰221(145.5149.5)959595145.5149.522014+1812=+⨯++⨯+340.2237.520222677086600022333708cm +⨯⨯+＝＝（式中α高等学校教材“表2－4－3）- 2 -毛截面：28595048.115944isiS y cm A ===∑'40i 2120672.7818882276.8628595048.117245895.14i i s I I I S y m =+-=+-⨯=∑∑∑换算截面：301123.3449.286110.74is iSy cm A ===∑'42120672.7820263050.9301123.3449.287544365.49i i i s I I I S y cm =+-=+-⨯=∑∑∑换22212121241()2T s A I S S hd S S S t t t t ==+++⎰221(141149)95951411492(1418)/21212=+⨯⨯+++4184100902521058834cm 11.87524.167⨯⨯+＝＝（二）荷载效应标准值 1、结构重力 1）板自重一期（预制板）326/r KN m =260.5915.45/m q A KN ⨯中中＝r ＝＝- 3 -260.718418.68/m q A KN ⨯边边＝r ＝＝；二期（现浇铰缝、铺装层、护栏）铰缝混凝土 325/r KN m =[]250.950.730.08250.038 1.31/mq KN ⨯⨯⨯⨯⨯边＝(0.085)-(0.04)/2-(0.12+0.22)＝＝2 1.31 2.62/q KN m ⨯中＝＝铺装24(0.080.1) 1.5 6.48/q KN m ⨯+⨯中＝＝24(0.08 1.7850.1 1.375) 6.73/q KN m ⨯⨯+⨯边＝＝护栏按两侧刚性护栏对称布置，混凝土0.353/m m2(250.35)/8 2.19/q KN m ⨯⨯=栏＝1.31 6.7310.23/q KN m +∑边＝＝2.62 6.48 2.1911.29/q KN m ++∑中＝＝2）内力影响线- 4 -2、汽车荷载效应 1）公路Ⅰ级荷载均布荷载 10.5/k q KN m = 集中荷载 19.55180(1)238505k P KN -=⨯+=-当计算剪力时： 1.2238285.6k P KN =⨯= 2）冲击系数结果基频 1f =（桥JTGD62－2004条文说明4－3条） 322/ 1.57710/c m G g NS m ==⨯1 5.05f Hz ==当11.514Hz f Hz ≤≤：0.1767ln 0.0157f μ=- （桥规JTGD60－2004，4.3.2式）所以 0.270μ= 1 1.270μ+= 3）汽车荷载横向分配系数3(~)44c l lk 修正的刚性横梁法 2ii ii ii iI a I R e Ia I β=±∑∑- 5 -221112ii iGl T E a I β=+∑∑ （式中G/E=0.4 ）20.0848660.072330.604iI=⨯+⨯=∑；20.0033460.21059 1.71iT =⨯+⨯=∑222222 5.250.084862(3.75 2.250.75)0.07246 4.6779 2.85317.531i ia I=⨯⨯+++⨯=+=∑边板 1 5.25a m = 11 5.250.084860.446I a =⨯=∴210.2579119.5 1.7110.4127.531β==<⨯+⨯ 符合规定 10.084860.08486 5.250.25790.14050.0153i i R e e ⨯=±⨯=±二列车影响线布载得：(0.22250.19500.17440.1470)/20.3695c k =+++= 0.5k 支＝沿桥纵向布置：- 6 -(三)持久状态承载能力极限状态计算1、正截面抗弯承载能力按《规范》5.2.2-1式计算00()2d cd x M f bx h γ≤-顶板：0b=183cm,t=12cm,h =91cm混凝土抗力：618.41830120 4.0410cd f bt N =⨯⨯=⨯由于顶板混凝土抗力大于钢筋抗力，混凝土受压区高度x 在顶板内，'112602800280791111.418.41830Pd P sd S cd f A f A x mm f b +⨯+⨯===⨯ 根据JTG D60－2004 基本组合表达式（4.1.6－1）取用分项系数0γ――结构重要性系数，0γ=1.1；G γ――结构自重分项系数， G γ＝1.21Q γ――汽车荷载（含冲击力）的分项系数，取1Q γ＝1.4- 7 -001112()m nd Gi Gik Q Q k c Qj Qjk i j M S S S γγγγφγ===++∑∑[]1.11.2(887.86486.23) 1.4(10.270)613.123012.94KN m =⨯++⨯+⨯=⋅60111.4()18.41830111.4(910)3204.531022r cd x M f bx h N mm =-=⨯⨯-=⨯⋅03204.533012.94d KN m M KN m γ=⋅>=⋅ 符合规定 2、斜截面抗剪承载能力按《桥规》5.2.7－1式计算0d cs sb pb V V V V γ≤++ （荷载效应分项系数同正截面抗弯强度）计算斜截面位置距支点/2h ，d V 是斜截面受压端上由作用效应产生的最大剪力组合设计值：[]0 1.11.2(155.5385.17) 1.4(10.270)156.20623.22d V KN γ=⨯++⨯+⨯=1）预制板截面尺寸应符合《规范》5.2.9式000.5100.51102140910821.86623.22d V b h KN KN γ--≤⨯⋅=⨯⨯⨯=>按《规范》5.2.10式检验斜截面要不要设箍筋330200.5100.510 1.25 1.652140910159.25d td V f bh KN γα--≤⨯=⨯⨯⨯⨯⨯⨯=对于板式受弯构件 1.25159.25=199.06KN<623.22KN ⨯ 所以预制板截面尺寸满足《规范》要求，但斜截面得设箍筋。

波形钢腹板箱梁有效分布宽度分析

波形钢腹板箱梁有效分布宽度分析摘要：为了研究超大断面波形钢腹板箱形截面梁这种钢混组合结构梁的整体承载能力，基于ansys有限元平台建立32m的等截面波形钢腹板箱梁，对其钢混组合结构梁在不同几何参数及加载方式下进行模型计算和对比，得到了各个不同参数下纵桥向的坐标-应力分布曲线，进而计算得到了各个敏感参数对有效分布宽度变化的重要系数，对于这种钢混组合结构箱梁的有效分布宽度计算与规范所给的公式进行了对比分析；基于对该结构有效分布宽度的计算，简化了桥跨节段模型试验的加载方式，使得加载数值与实桥加车状态相拟合。

关键词：波形钢腹板有效分布宽度敏感参数1.1有效分布宽度的意义根据某桥跨截面桥面板在车轮荷载作用下，在桥面板的计算中，板在局部分布荷载p的作用下，不仅直接承压部分的板带参加工作，与其相邻的部分板带也会分担一部分荷载共同参与工作，需要确定所谓板的有效工作宽度a。

1）对板而言，以宽度为a的板条承受总弯矩，既满足总弯矩的要求。

2）对荷载而言，荷载只在a范围内有效且均匀分布，则荷载集度q=p/2ab1.ansys有限元模型分析2.1有限元模型的建立在建立有限元模型过程中，混凝土板采用8节点钢筋混凝土实体单元solid65，每个节点有三个自由度，即x，y，z三个方向的线位移，波纹钢腹板采用4节点弹性壳单元shell63，每个单元有6个自由度，即x，y，z三个方向的平动自由度和绕x，y，z的转动自由度，图4为整体模型；由于混凝土和钢腹板之间是通过连接键进行连接的，假定连接件是固结，在建模过程中，将混凝土和波纹钢腹板的接触面进行共节点的耦合，从而解决了因混凝土单元和壳单元因自由度不同不能限制转动自由度的问题，如图5所示。

对于钢腹板和混凝土材料均采用弹性分析，波纹钢腹板弹性模量取2.06e11pa，泊松比0.3，混凝土弹性模量取3.45e10pa。

为了使节段试验模型桥面板加载效果接近实桥状态的受力状况，根据单向板要求建立梁段模型l=32m使其长宽比l/b>2.5，总共有10个波纹段，根据《公路桥涵及通用规范jtg d60-2004》施加超20级后轴单个车轮重p=70kn，考虑车轮与地面接触面积0.6×0.2m2。

钢箱梁—40+60+40 钢箱梁计算书

1 设计要点1.1 总体设计达连坝大桥主桥为钢箱连续梁桥，跨径组合为（40+60+40）m，全长140m。

1.2 主桥上部结构设计概况（1）结构布置主桥为（40+60+40）m三跨钢箱连续梁桥，全长140m。

边中跨比为0.667。

桥梁横断面布置为：（0.5m防撞墙）+（14.75m车行道）+（0.5m防撞墙）=单幅桥总宽15.75m （2）钢箱梁主梁方案主梁采用等截面钢箱梁，单箱五室断面，桥面宽15.75m，箱宽12.0m，悬臂长1.925m。

主梁中心高度2.4m，高跨比1/25。

1.3 主桥下部结构设计概况见施工图纸。

1.4 主要材料（1）混凝土C15：承台基础垫层C30：过渡墩承台、防撞栏、桩基、主墩墩身、过渡墩墩身及盖梁C40：支座垫石（2）钢材主体结构采用Q345qD；附属结构采用Q235B；（3）支座主墩：LQZ3000GD、LQZ3000DX、LQZ3000SX；过渡墩：LQZ1500DX、LQZ1500SX；（4）伸缩缝伸缩缝：D160型伸缩缝。

2 计算依据2.1设计规范及参考资料（1）执行规范：《公路桥涵钢结构及木结构设计规范》（JTJ 025-86）《铁路桥梁钢结构设计规范》（TB 10002.2-2005）《钢结构设计规范》（GB 50017-2003）《公路桥涵设计通用规范》（JTG D60-2004）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）《公路桥梁抗风设计规范》（JTG/T D60-01-2004）（2）参考规范及文献资料：《日本道路桥示方书·同解说》《钢桥、混凝土桥及结合桥》BS5400 （1978~1982）《公路钢结构桥梁设计规范—征求意见稿》《现代钢桥》（上册）（吴冲主编 2006年4月）《公路钢结构桥梁设计规范》( 征求意见稿)《公路钢箱梁桥面铺装设计与施工技术指南》2.2技术标准（1）公路等级：双向6车道，一级公路。

宽箱梁横向分布系数计算探讨

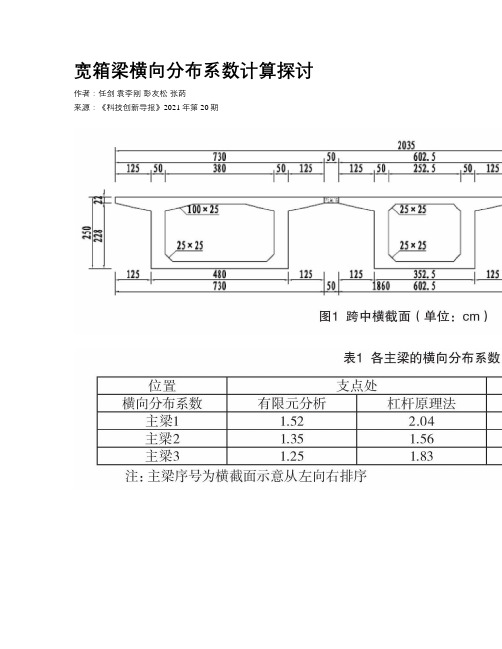
宽箱梁横向分布系数计算探讨作者：任剑袁李刚彭友松张菂来源：《科技创新导报》2021年第20期摘要：汽车、人群荷载是桥梁可变作用中的主要荷载，直接影响着桥梁结构设计。

对于多片梁桥而言，梁体之间的协同工作能力决定了荷载的横向分布。

简支梁桥常采用单梁模型考虑横向分布系数进行结构计算，因此，获得准确的横向分布系数至关重要。

对于宽箱梁而言，常规横向分布系数计算方法的准确性和适用性需要进行分析。

本文采用Ansys建立了实体分析模型，通过与常规横向分布系数的计算方法对比，结果表明：对于算例桥梁，相对于实体分析模型结果，采用常规横向分析系数计算方法得到的结果偏小约12%，采用常规算法较为危险，可为类似宽箱梁桥工程设计提供参考。

关键词：宽箱梁横向分布系数杠杆法修正偏心压力法中图分类号：K928 文献标识码：A 文章编号：1674-098X（2021）07（b）-0015-03Discussion on the Calculation of Transverse Distribution Coefficient of Wide Box GirderREN Jian YUAN Ligang PENG Yousong ZHANG Di（Sichuan Communication Surveying & Design Institute Co.， Ltd.， Chengdu， Sichuan Province， 610017 China）Abstract： Automobile and crowd loads are the main loads in the variable action of the bridge，which directly affect the bridge structure design. For multi beam bridges， the cooperative working ability between beams determines the transverse distribution of load. Single beam model is often used to calculate the structure of simply supported beam bridge considering the transverse distribution coefficient， so it is very important to obtain the accurate transverse distribution coefficient. For wide box girder， the accuracy and applicability of the conventional calculation method of transverse distribution coefficient need to be analyzed. In this paper， the solid analysis model is established by Ansys. Compared with the calculation method of conventional transverse distribution coefficient，the results show that for the example bridge， compared with the results of solid analysis model， the results obtained by conventional transverse analysis coefficient calculation method are about 12%，and it is dangerous to use conventional algorithm， which can provide reference for the engineering design of similar wide box girder bridges.Key Words： Wide box girder; Transverse distribution coefficient; Lever method; Modified eccentric pressure method1 概述簡支梁桥受力明确、施工简单，是目前应用最广的一种桥梁结构型式。

连续刚构宽箱梁剪力滞效应分析及有效分布宽度研究

连续刚构宽箱梁剪力滞效应分析及有效分布宽度研究孙志伟;刘英;邬晓光;王阳【摘要】Aiming at the shear lag effect of continuous rigid-frame box girder ,this paper presented a simplified analysis method of shear lag that based on contraflexure points combined with analogy bar method and superposi-tion principle;meanwhile,the shear lag effect was analyzed through the finite element simulation.The effective distribution width of the long span continuous rigid frame was calculated using the formula of continuous box gird-er in “highway reinf orced concrete and prestressed concrete bridge and culvert design specifications (JTG D62-2004)”.A long-span PC continuous rigid frame box girder bridge was taken as an example,of which the shear lag coefficient and effective distribution width of cross sections were calculated.Their distribution regularity of shear lag were calculated to verify if the analytical method is reasonable.The findings indicate that the design needs to focus on the side fulcrum section,side span 1/4L section,main span 1/8L section and main span cross section.This study could provide reference for the analysis and design of the shear lag effect of similar bridges.%针对连续刚构桥箱梁的剪力滞效应和有效分布宽度进行研究，提出一种基于反弯点结合比拟杆法和叠加原理的剪力滞简化分析方法，同时通过有限元仿真分析剪力滞效应，并分别按《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）建议的连续箱梁有效分布宽度公式和有限元分析结果计算连续刚构桥的有效分布宽度。

新规范35m箱梁计算书

第一章概述总体概述上部箱梁构造为5×35连续小箱梁，桥宽12.25米，由4榀小箱梁联结构成，布置图如下图所示。

设计荷载公路Ⅰ级。

本计算只对边梁单榀箱梁进行分析，模的主要规范有：1．《公路桥涵设计通用规范》（JTGD60-2004）2．《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTGD62-2004）3.《公路工程技术标准》（JTGB01-2003）(一)技术指标设计荷载：公路Ⅰ级。

桥面宽度：0.5＋11.25+0.5=12.25米，单幅桥。

标准桥面横坡：2%跨径：35米斜度：0°，10°,20°,30°,40°主梁片数：4片梁。

预制梁长：34.3米。

预制梁高：1.8米。

桥面铺装：9cm沥青混凝土。

混凝土调平层: 8cm50号混凝土。

(二)相关参数相对温度 75%桥面板与其它部分的温差为±5°预应力管道成形为钢波纹管管道摩擦系数u=0.25管道偏差系数λ=0.0025l/米钢筋回缩和锚具变形为6mm(三)主要材料1．混凝土材料预制箱梁、横隔板 50号混凝土现浇连续段、封锚端、湿接缝 50号混凝土现浇桥面层50号混凝土主梁采用50号混凝土，力学性能见表1.1混凝土力学性能表表1.12预应力筋均采用符合ASTM A416-96a标准的高强低松弛270级钢绞线，公称直径φj15.24mm，公称面积为140mm2，标准强度为MPaR by1860=，，控制张拉应力为1395MPa。

弹性模量为MPaEy51095.1⨯=。

（四）预应力布置预应力构造分为两种类型：顶板索和腹板连续索。

预制小箱梁采用OVM型锚具及配套的设备。

箱梁顶板负矩钢束采用BM15型锚具及配套的设备，管道成孔采用波纹扁管，且要求钢波纹扁管的钢带厚度不小于0.35mm。

预应力张拉采用引伸量和张拉吨位双控。

并以引伸量为主。

引伸量误差不得超过-5%~10%。

（五）施工工序⑴预制主梁，张拉预应力钢束。