计算图形的表面积和体积练习题
长方体和正方体的表面积测试题

长方体和正方体的表面积测试题篇一:长方体正方体的表面积和体积练习题精选长方体正方体的表面积和体积练习卷1. 长方体表面积的求法:长方体的表面积=a、b、h分别表示长方体的长、宽、高。
S表示它的表面积,则S= 。
长方体的体积=。
字母表示:。
2. 正方体表面积的求法:正方体的表面积=如果用字母a表示正方体的棱长,S表示正方体的表面积,则正方体的表面积计算公式是:S==母表示:。
1、一个长方体有()个面,他们一般都是()形,也有可能是()个面是正方形.2、把长方体放在桌面上,最多可以看到()个面。
3、一个长方体,长12厘米,宽和高都是8厘米,这个长方体的表面积是()。
4、一个长方体,长8厘米,宽是5厘米,高是4厘米,这个长方体的表面积是(),棱长之和是()。
5、一个正方体的棱长之和是84厘米,它的棱长是(),一个面的面积是(),表面积是()。
6、把三个棱长是1厘米的正方体拼成一个长方体,这个长方体的表面积是(),比原来3个正方体表面积之和减少了()。
7、把三个棱长是2分米的正方体拼成一个长方体,表面积是(),体积是()。
8、用棱长为1厘米的小正方体木块拼成一个较大的正方体,至少要()个这样的小木块才能拼成一个正方体。
9、一个正方体的棱长如果扩大2倍,那么表面积扩大()倍,体积扩大()倍。
10、一个无盖正方体铁桶内外进行涂漆,涂漆的是()个面.11、有一根长52厘米的铁丝,恰好可以焊接成一个长6厘米,宽4厘米,高()厘米的长方体。
12、一个长方体的长宽高分别是a ,b, h,如果高增高3米,那么表面积比原来增加()平方米,体积增加()立方米。
14、用27个体积是1立方厘米的小正方体粘合成一个大正方体,粘合后的大正方体的表面积是()15、一个长15厘米,宽6厘米,高4厘米的正方体的木块,可以截成()块棱长2厘米的正方体木块。
16、有一个长方体的木料长3厘米、宽3厘米,高2厘米。
把它切成1立方厘米的小方块,可以切成()。
表面积和体积应用题

表面积计算1、做10个棱长8厘米的正方体铁框架,至少需多长的铁丝?2、用铁皮做一个铁盒,使它的长、宽、高分别是1.8分米,1.5分米和1.2分米,做一个这样的铁盒至少要用铁皮多少平方米?3、做一个没盖的正方体玻璃鱼缸,棱长是3分米,至少需要玻璃多少平方米?4、我们学校要粉刷教室,教室长8米,宽7米,高3.5米,扣除门窗、黑板的面积13.8平方米,已知每平方米需要5元涂料费。
粉刷一个教室需要多少钱?5、一个商品盒是棱长为6厘米的正方体,在这个盒的四周贴上商标,贴商标的面积最大是多少平方厘米?6、木版做长、宽、高分别是2.8分米,1.5分米和2.2分米抽屉,做5个这样的抽屉至少要用木版多少平方米?7.有一个养鱼池长18米,宽12米,深3.5米,要在养鱼池各个面上抹一层水泥,防止渗水,如果每平方米用水泥5千克,一共需要水泥多少千克?8、加工厂要加工一批电视机机套,(没有底面)每台电视机的长60厘米,宽50厘米、高55厘米,做1000个机套至少用布多少平方米?9.做24节长方体的铁皮烟囱,每节长2米,宽4分米,高3分米,至少用多少平方米的铁皮?10、一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,修理时配上的玻璃的面积是()体积计算1、一个长方体的长是4分米,宽是2.5分米,高是3分米,求它的体积是多少立方分米?2、一个长方体沙坑,长4米,宽2米,深0.5米,如果每立方米黄沙重1.4吨,这黄沙重多少吨?3.有一种长方体钢材,长2米,横截面是边长为5厘米的正方形,每立方分米钢重7.8千克,这根方钢材重多少千克?4、一个长方体,底面积是30平方分米,高3米,它的体积是多少立方分米?5、一张写字台,长1.3m宽0.6m、高0.8m 有20张这样的写字台要占多大空间?6、一个棱长是5分米的正方体鱼缸,里面装满水,把水倒入一个底面积48平方分米,高6分米的的长方体鱼缸里,鱼缸里水有多深?7、一个棱长8分米的正方体水槽里装了490升水,把这些水倒入一个长10分米,宽7分米,高8分米的长方体水槽里,水槽里的水深是多少?8、把一块棱长8厘米的正方体钢坯,锻造成长16厘米,宽5厘米的长方体钢板,这钢板有多厚?(损耗不计)9. 一个长方体油桶,底面积是18平方分米,它可装43.2千克油,如果每升油重0.8千克,油桶内油高是多少?10、一个长方形铁皮长30cm,宽25cm,从四个角各切掉一个长为5cm的正方形,然后做成一个无盖的盒子,这个盒子用了多少铁皮?它的容积是多少?11、把一块长26dm的长方形木板,在四个角上分别剪去边长为3dm的正方形,将它制成容积为840立方分米的长方体无盖容器,这块木板原来的宽是多少?12、一个长方体游泳池长60米,宽30米,深2米,游泳池占地多少平方米?沿游泳池的内壁1.5米处用红漆划一条水位线,这条线的长度是多少?现在游泳池内的水正好到达水位线,求池内水的体积?13、一个长方体玻璃缸,从里面量长40厘米,宽25厘米,水深12厘米,把一块石头浸入水中后,水面上升到16厘米,求石块的体积?体积表面积综合练习1、80根方木,垛成一个长2米,宽2米,高1.5米的长方体,平均每根方木的体积是多少立方米?合多少立方分米?2、3个棱长都8厘米的正方体,拼成一个长方体,它的体积和表面积各是多少?3、家具厂订购500根方木,每根方木横截面面积是25平方分米,长是3.8米,这些木料的体积是多少立方米?4、把两块棱长为1.5分米的正方体木块拼成一个长方体,这个长方体的体积和表面积各是多少?5、一个长方体表面积是156平方分米,底面积是30平方分米,底面周长是32分米,长方体的体积是多少?6、把长8厘米,宽12厘米,高5厘米长方体木块锯成棱长2厘米的正方体木块,可锯多少块?7、一个底面是正方形的长方体木料,长是5米,把它截成4段,表面积增加36平方米,求长方体的体积?。
体积和表面积计算练习题

体积和表面积计算练习题在几何学中,计算物体的体积和表面积是一个常见的练。
通过这些练题,你可以巩固自己对体积和表面积的计算方法的理解。
本文将为你提供一些简单的练题,帮助你加深对这些概念的掌握。
练题1:长方体的计算1. 一个长方体的长为8厘米,宽为5厘米,高为3厘米。
请计算它的体积和表面积。
练题2:球体的计算2. 一个半径为4厘米的球体,请计算其体积和表面积。
练题3:金字塔的计算3. 一个金字塔的底边长为6厘米,高为8厘米。
请计算它的体积和表面积。
练题4:圆柱体的计算4. 一个圆柱体的底面半径为3厘米,高为10厘米。
请计算它的体积和侧面积。
练题5:立方体的计算5. 一个立方体的边长为7厘米。
请计算它的体积和表面积。
以上是一些常见的体积和表面积计算练题。
通过计算这些题目,你可以提高你的计算能力,并加深对几何体积和表面积的理解。
希望这些练题对你有所帮助!> 注意:在计算时,确保使用正确的单位。
例如,如果题目中给出的尺寸是以厘米为单位,那么计算结果也应该以厘米为单位。
参考答案:练题1:长方体的计算- 体积:长 ×宽 ×高 = 8厘米 × 5厘米 × 3厘米 = 120立方厘米- 表面积:2 × (长 ×宽 + 长 ×高 + 宽 ×高) = 2 × (8厘米 × 5厘米 + 8厘米 × 3厘米 + 5厘米 × 3厘米) = 2 × (40厘米² + 24厘米² + 15厘米²) = 2 × 79厘米² = 158厘米²练题2:球体的计算- 体积:4/3 × π × 半径³ = 4/3 × 3.14 × 4厘米³ ≈ 268.08立方厘米- 表面积:4 × π × 半径² = 4 × 3.14 × 4厘米² ≈ 200.96厘米²练题3:金字塔的计算- 体积:底边长 ×底边长 ×高 ÷ 3 = 6厘米 × 6厘米 × 8厘米 ÷ 3 = 96/3立方厘米 = 32立方厘米- 表面积:底边长 ×底边长 + 底边长 ×边长 + 边长 ×高 = 6厘米 × 6厘米 + 6厘米 × 8厘米 + 8厘米× √((6厘米/2)² + 8厘米²) ≈ 36厘米² + 48厘米² + 40.32厘米² ≈ 124.32厘米²练题4:圆柱体的计算- 体积:π × 半径² ×高 = 3.14 × 3厘米² × 10厘米≈ 94.2立方厘米- 侧面积:2 × π × 半径 ×高 = 2 × 3.14 × 3厘米 × 10厘米≈ 188.4厘米²练题5:立方体的计算- 体积:边长³ = 7厘米³ = 343立方厘米- 表面积:6 ×边长² = 6 × 7厘米² = 42厘米².以上是每个练习题的计算过程和答案。
人教版五年级数学下册长方体和正方体体积、表面积专项练习题6
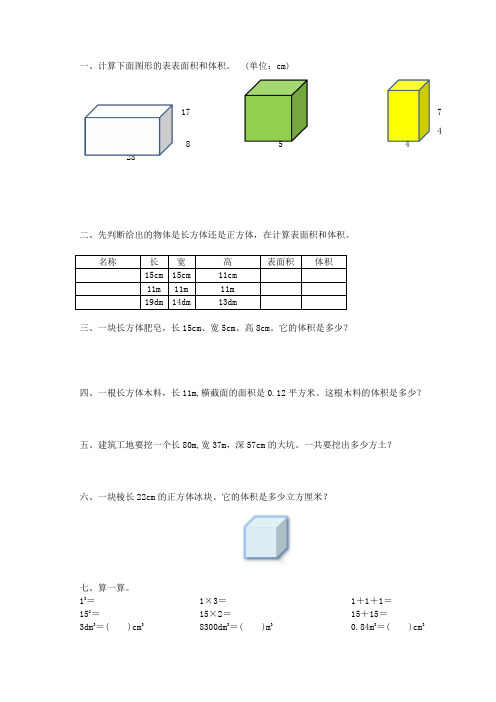
17 748 5 428二、先判断给出的物体是长方体还是正方体,在计算表面积和体积。
三、一块长方体肥皂,长15cm、宽5cm、高8cm。
它的体积是多少?四、一根长方体木料,长11m,横截面的面积是0.12平方米。
这根木料的体积是多少?五、建筑工地要挖一个长80m,宽37m,深57cm的大坑。
一共要挖出多少方土?六、一块棱长22cm的正方体冰块。
它的体积是多少立方厘米?七、算一算。
13=1×3=1+1+1=152=15×2=15+15=3dm3=( )cm38300dm3=( )m30.84m3=( )cm316 1022 9 521二、先判断给出的物体是长方体还是正方体,在计算表面积和体积。
三、一块长方体肥皂,长13cm、宽6cm、高5cm。
它的体积是多少?四、一根长方体木料,长6m,横截面的面积是0.09平方米。
这根木料的体积是多少?五、建筑工地要挖一个长60m,宽42m,深56cm的大坑。
一共要挖出多少方土?六、一块棱长50cm的正方体冰块。
它的体积是多少立方厘米?七、算一算。
43=4×3=4+4+4=122=12×2=12+12=9.1dm3=( )cm3700dm3=( )m30.14m3=( )cm312 914 10 426二、先判断给出的物体是长方体还是正方体,在计算表面积和体积。
三、一块长方体肥皂,长11cm、宽5cm、高6cm。
它的体积是多少?四、一根长方体木料,长16m,横截面的面积是0.24平方米。
这根木料的体积是多少?五、建筑工地要挖一个长90m,宽32m,深60cm的大坑。
一共要挖出多少方土?六、一块棱长39cm的正方体冰块。
它的体积是多少立方厘米?七、算一算。
13=1×3=1+1+1=142=14×2=14+14=1.1dm3=( )cm33700dm3=( )m30.98m3=( )cm311 546 6 524二、先判断给出的物体是长方体还是正方体,在计算表面积和体积。
数学题目立体几何的表面积与体积练习题

数学题目立体几何的表面积与体积练习题数学题目:立体几何的表面积与体积练习题1. 题目一:计算一个半径为3厘米的球体的表面积和体积。
解答:首先计算球的表面积。
球的表面积公式为S=4πR²,其中R 为球的半径。
代入半径为3厘米,得到表面积S=4π×3²=36π cm²。
接下来计算球的体积。
球的体积公式为V=4/3πR³,代入半径为3厘米,得到体积V=4/3π×3³=36π cm³。
2. 题目二:一个长方体的长、宽和高分别为5厘米、4厘米和6厘米。
求该长方体的表面积和体积。
解答:长方体的表面积公式为S=2(长×宽+长×高+宽×高),代入长为5厘米、宽为4厘米和高为6厘米,得到表面积S=2(5×4+5×6+4×6)=2(20+30+24)=148 cm²。
长方体的体积公式为V=长×宽×高,代入长为5厘米、宽为4厘米和高为6厘米,得到体积V=5×4×6=120 cm³。
3. 题目三:一个圆锥的底面圆半径为2.5厘米,高为7厘米。
求该圆锥的表面积和体积(保留π)。
解答:首先计算圆锥的母线,母线公式为l=√(r²+h²),其中r为底面圆半径,h为圆锥的高。
代入半径为2.5厘米和高为7厘米,得到母线l=√(2.5²+7²)≈7.416 cm。
圆锥的表面积公式为S=πr(r+l),代入底面圆半径为2.5厘米和母线长为7.416厘米,得到表面积S=π×2.5(2.5+7.416)≈82.512 cm²。
圆锥的体积公式为V=1/3πr²h,代入底面圆半径为2.5厘米和高为7厘米,得到体积V=1/3π×2.5²×7≈36.750 cm³。
长方体和正方体的表面积和体积 应用题专项训练题75题 后面带详细答案

长方体与正方体的表面积和体积应用题专项训练75题1、计算下面图形的表面积。
(单位:厘米)2、将一根长52厘米的铁丝焊接成一个长6厘米、宽4厘米的长方体框架,这个长方体框架的表面积是多少平方厘米?3、将一根长72厘米的铁丝焊接成一个长9厘米、宽3厘米的长方体框架,这个长方体框架的表面积是多少平方厘米?4、将一根长84厘米的铁丝焊接成一个正方体框架,这个正方体框架的表面积是多少平方厘米?5、小高老师要做一个长1.2米、宽45厘米、高1.5米的陈列箱,陈列箱除了正面用玻璃,其余各面都用木板。
小高老师需要准备多少平方米木板?6、舞蹈教室的长是8米,宽是6米,高是3.5米,现在要粉刷墙壁和天花板。
如果门窗和镜子的面积一共是22平方米,每平方米需要0.25千克涂料,那么粉刷这间教室一共需要多少千克涂料?7、小李老师想制作一个长1.2米、宽0.6米、高0.8米的长方体无盖玻璃缸,他至少需要准备多少平方米玻璃?120张6平方米的玻璃板最多可以做多少个这样的鱼缸?(接口处的用料忽略不计。
)8、有一个长方体,如果将它的高增加3厘米,那么它就会变成一个正方体,这时表面积会比原来增加96平方厘米。
这个长方体的表面积是多少平方厘米?9、如果把一个正方体木块一刀切成两个长方体后表面积增加了60平方厘米,那么这个木块的表面积是多少平方厘米?10、下面是一个长方体纸盒的展开图,原来这个纸盒的表面积是多少?11、一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体高是多少?表面积是多少?12、将一块棱长为8 厘米的正方体木料横切成两块完全一样的长方体木料,每块长方体木料的表面积是多少?13、一个长方体的棱长总和是72 厘米, 长是9 厘米, 宽是6 厘米。
这个长方体的表面积是多少平方厘米?14、好好的爸爸想制作一种长20 厘米、宽15 厘米、高10 厘米的长方体无盖玻璃鱼缸,165 张 2 平方分米的玻璃板最多可以做多少个这样的鱼缸?(接口处的用料忽略不计。
小升初数学试题《空间与图形》计算体积、表面积、阴影面积(含答案)

小升初数学试题《空间与图形》计算体积、表面积、阴影面积一、计算题1.求下面未知角的度数。
4.求下图阴影部分的周长2.计算下面各图形的面积. (单5.求下面立体图形的表面积和体积。
(单位: 分米)6.求阴影部分的面积7.求阴影部分的面积9.计算图中阴影部分的面积二、作图题10.分别画出每个图形底边上的高13.一个长方体的纸盒如图。
请在方格中画出这个长方体纸盒的展开图三、解答题每个12.过点 A 画直线 BC 的垂线 AD ,过点 C 画直线 AB 的14.一个长方形操场,长220 米,宽90 米。
小勇沿操场的边跑了两圈,他一共跑了多少米?15.下面的图形是由七巧板中的哪几块拼成的?你试着拼一拼.16.求下面体育场的面积.17.在一块周长是80 米的正方形花坛里,用一串红围出一个最大的圆形,这个圆形的面积是多少平方米?这个花坛还剩下多少平方米的空地?18.一间会议室长8m,宽 6.5m,用边长0.5m 的正方形瓷砖给这会议室铺上地面,大约要用瓷砖多少块?19.一个长方形的长和宽都是以厘米为单位的质数,并且周长是36 cm.这个长方形的面积最大是多少平方厘米?20.一个长方体长10 厘米、宽8 厘米、高 5 厘米.把它切成两个长方体,这两个长方体的表面积的和最大是多少平方厘米?21.如图中梯形的面积是20dm2,阴影三角形的面积是多少?22.一个圆形的铁环,直径是40 厘米,做这样一个铁环需要用多长的铁条?23.(东城区)将图中的长方形,以虚线为轴旋转一周,得到的立体形的体积是多少?24.把两个长30 厘米、宽20 厘米的长方形拼成一个大长方形,大长方形的周长比原来 2 个小长方形的周长的和少多少厘米?A画出已知直线的垂线和平行线.26.一个长方体的棱长之和是60 厘米,宽是 5 厘米,高是 2 厘米,长是多少厘米?27.到圆上各点的距离相等的点只有圆心一个点.28.画一个三角形,使它的面积与五边形(如图)面积相等.29.一块梯形的草地,上底250 米,下底150米,高是180米,它的面积是多少公顷?30.一个高30 厘米、底面半径10 厘米的无盖圆柱形铁皮水桶,要用多少平方厘米的铁皮?31.中祥小区靠墙边用46m的篱笆围了一块梯形空地(见下图)种草坪。
小升初真题-有关体积的计算(专项突破)(通用版)

小升初真题-有关体积的计算(专项突破)一、计算题1.计算圆柱的表面积和体积。
(单位:dm)2.求如图正方体挖去最大的圆锥后剩下的体积。
(单位:厘米)3.计算如图图形的体积和表面积。
(单位:分米)4.求出如图图形的表面积和体积。
5.计算下面组合图形的体积。
6.求如图中立体图形的体积。
(单位:分米)7.求如图圆柱的表面积和圆锥的体积。
(单位:厘米)8.求圆柱的表面积和体积。
9.求下列立体图形的体积。
10.计算如图图形的体积。
11.计算如图形的表面积和体积。
12.计算如图几何体的表面积和体积(缺口是棱长为2的正方体形状,单位:dm)13.计算如图所示图形的表面积和体积。
(单位:cm)14.求如图图形的表面积和体积(单位:米)。
15.图形与几何。
(1)如图是长方体纸盒侧面展开图,求它的容积。
(2)求陀螺的体积。
16.计算图形的体积。
17.计算下面图形的体积。
18.计算下面图形的体积。
19.计算下面图形的体积。
20.按要求计算。
求如图组合体的体积。
(单位:dm)21.计算出下面图形的表面积和体积。
22.求下面各图形的体积。
(单位:cm)23.求圆柱表面积及圆锥体积。
24.求出如图图形的表面积和体积。
25.计算下面图形的表面积。
参考答案一.计算题1.【分析】根据圆柱的表面积公式:S表=S侧+S底×2,体积公式:V=Sh,把数据代入公式解答。
【解答】解:3.14×8×20+3.14×(8÷2)2×2=25.12×20+3.14×16×2=502.4+100.48=602.88(平方分米)3.14×(8÷2)2×20=3.14×16×20=50.24×20=1004.8(立方分米)答:圆柱的表面积是602.88平方分米,体积是1004.8立方分米。
【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用。
立体几何计算练习题体积与表面积

立体几何计算练习题体积与表面积在几何学中,计算立体图形的体积和表面积是非常重要的。
掌握这些计算方法不仅可以帮助我们理解立体图形的特性,更能应用到实际生活和工作中。
本文将介绍几个常见的立体几何计算练习题,涵盖了体积和表面积的计算方法,希望能够对读者有所帮助。
以下是几个练习题。
练习题一:正方体的体积和表面积计算正方体是最简单的立体图形之一,它的六个面都是正方形。
我们先来计算一个边长为a的正方体的体积和表面积。
体积的计算公式为 V = a^3,其中a表示正方体的边长。
例如,如果正方体的边长为5cm,那么它的体积就是 V = 5^3 = 125 cm^3。
表面积的计算公式为 S = 6a^2,其中a表示正方体的边长。
以边长为5cm的正方体为例,它的表面积就是 S = 6(5^2) = 150 cm^2。
练习题二:圆柱体的体积和表面积计算圆柱体是常见的立体图形,它的底面是一个圆,高度为h。
我们来计算一个半径为r、高度为h的圆柱体的体积和表面积。
体积的计算公式为V = πr^2h,其中π取近似值3.14。
例如,如果圆柱体的半径为3cm,高度为8cm,那么它的体积就是V ≈ 3.14(3^2)(8) ≈ 226.08 cm^3。
表面积的计算公式为S = 2πr^2 + 2πrh,其中π取近似值3.14。
以半径为3cm、高度为8cm的圆柱体为例,它的表面积就是S ≈ 2(3.14)(3^2) + 2(3.14)(3)(8) ≈ 188.64 cm^2。
练习题三:球体的体积和表面积计算球体是没有棱和角的立体图形,它的表面都是由一个半径为r的圆所构成。
我们来计算一个半径为r的球体的体积和表面积。
体积的计算公式为 V = (4/3)πr^3,其中π取近似值3.14。
例如,如果球体的半径为6cm,那么它的体积就是V ≈ (4/3)(3.14)(6^3) ≈ 904.32 cm^3。
表面积的计算公式为S = 4πr^2,其中π取近似值3.14。
高中数学空间几何体的表面积与体积练习题及答案

空间几何体的表面积与体积专题一、选择题1.棱长为2的正四面体的表面积是( C ).A. 3 B .4 C .4 3 D .16解析 每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( B ). A .2倍 B .22倍 C.2倍 D.32倍解析 由题意知球的半径扩大到原来的2倍,则体积V =43πR 3,知体积扩大到原来的22倍.3.如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( B ). A.1423 B.2843 C.2803D.1403解析 根据三视图的知识及特点,可画出多面体 的形状,如图所示.这个多面体是由长方体截去 一个正三棱锥而得到的,所以所求多面体的体积V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843. 4.某几何体的三视图如下,则它的体积是( A) A .8-2π3 B .8-π3C .8-2πD.2π3解析 由三视图可知该几何体是一个边长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V =23-13×π×2=8-2π3.5.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( A)A .24-32π B .24-π3 C .24-π D .24-π2据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.6.某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( C )A.⎝ ⎛⎭⎪⎫95-π2 cm 2B.⎝ ⎛⎭⎪⎫94-π2 cm 2C.⎝ ⎛⎭⎪⎫94+π2 cm 2D.⎝⎛⎭⎪⎫95+π2 cm 2解析 这个空间几何体上面是一个四棱柱、中间部分是一个圆柱、下面是一个四棱柱.上面四棱柱的表面积为2×3×3+12×1-π4=30-π4;中间部分的表面积为2π×12×1=π,下面部分的表面积为2×4×4+16×2-π4=64-π4.故其表面积是94+π2.7.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S-ABC 的体积为( C).A .3 3B .2 3 C. 3 D .1解析 由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥S-ABD 和C-ABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =33x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DCB =∠DCA =60°,在△BDC 中 ,BD =3(4-x ),所以33x =3(4-x ),所以x =3,AD =BD =3,所以三角形ABD 为正三角形,所以V =13S △ABD ×4= 3.二、填空题8.三棱锥PABC 中,PA ⊥底面ABC ,PA =3,底面ABC 是边长为2的正三角形,则三棱锥PABC 的体积等于__3______.解析 依题意有,三棱锥PABC 的体积V =13S △ABC ·|PA |=13×34×22×3= 3.9.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为_ 3∶2_______.解析 设圆柱的底面半径是r ,则该圆柱的母线长是2r ,圆柱的侧面积是2πr ·2r =4πr 2,设球的半径是R ,则球的表面积是4πR 2,根据已知4πR 2=4πr 2,所以R =r .所以圆柱的体积是πr 2·2r =2πr 3,球的体积是43πr 3,所以圆柱的体积和球的体积的比是2πr 343πr 3=3∶2.10.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是___26_____.解析由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V=13×1×1×22=26.11.如图,半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是____2πR2____.解析由球的半径为R,可知球的表面积为4πR2.设内接圆柱底面半径为r,高为2h,则h2+r2=R2.而圆柱的侧面积为2πr·2h=4πrh≤4πr2+h22=2πR2(当且仅当r=h时等号成立),即内接圆柱的侧面积最大值为2πR2,此时球的表面积与内接圆柱的侧面积之差为2πR2.12.如图,已知正三棱柱ABCA1B1C1的底面边长为2 cm,高为5 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为___13_____cm. 解析根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm).三、解答题13.某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH,下半部分是长方体ABCDEFGH.图2、图3分别是该标识墩的正视图和俯视图.(1)请画出该安全标识墩的侧视图;(2)求该安全标识墩的体积.解析(1)侧视图同正视图,如图所示:(2)该安全标识墩的体积为V=VPEFGH +V ABCDEFGH=13×402×60+402×20=64 000(cm3).14 .一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V;(2)求该几何体的表面积S.解析 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为3,所以V =1×1×3= 3.(2)由三视图可知,该平行六面体中,A1D ⊥平面ABCD ,CD ⊥平面BCC1B1, 所以AA1=2,侧面ABB1A1,CDD1C1均为矩形, S =2×(1×1+1×3+1×2)=6+2 3.15.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .解析 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、 右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示. (1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2. 1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). .解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=, 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ).2.解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65, 3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是 。
人教版五年级数学下册长方体和正方体表面积和体积 解决问题专项训练2(50道含答案)
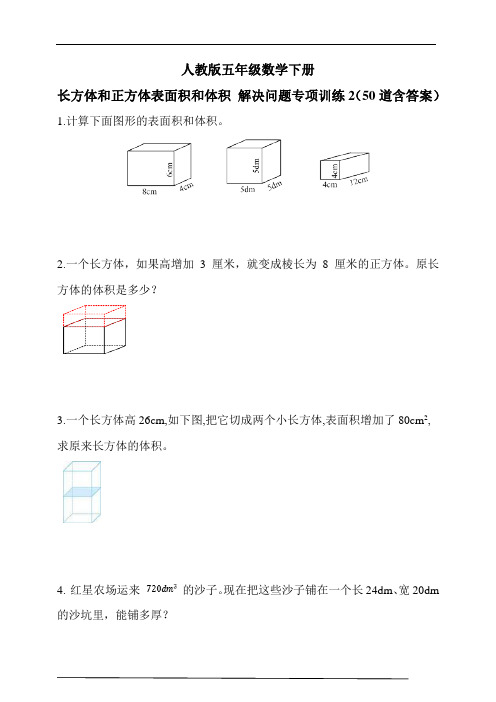
人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练2(50道含答案)1.计算下面图形的表面积和体积。
2.一个长方体,如果高增加3 厘米,就变成棱长为8 厘米的正方体。
原长方体的体积是多少?3.一个长方体高26cm,如下图,把它切成两个小长方体,表面积增加了80cm2,求原来长方体的体积。
4.红星农场运来的沙子。
现在把这些沙子铺在一个长24dm、宽20dm 的沙坑里,能铺多厚?5.在一个长为120cm、宽为60cm的长方体水箱里,浸没一块长方体的铁块后,水面就比原来上升2cm。
求铁块的体积。
6.一个游泳池长50米,宽25米,内蓄满水2500立方米。
(1)这个游泳池的高是多少米?(2)如果要把游泳池内贴上瓷砖,需下面规格的瓷砖多少块?边长是:5分米×5分米的正方形方砖(3)如果每块方砖1.4元,你会到哪个商店去购买更合算?7.有一个长方体的木料,截面是一个正方形,正方形的边长是2dm,这块木料的体积是.这块木料的长是多少分米?8.如图是一个长方体的空心管,掏空部分的长方体的长为10厘米,宽为7厘米。
求这根空心管的体积是多少?如果每立分米重7.8千克,这根管子重多少千克?(单位:厘米)9.有甲、乙两个水箱,从里面测量,甲水箱长12dm、宽8dm、高5dm,乙水箱长8dm、宽8dm、高6dm.甲水箱装满水,乙水箱空着.现将甲水箱里的一部分水抽到乙水箱中,使两箱水面高度一样.现在两个水箱的水面高多少分米?10.把下图所示的长方体木料切割成最大的正方体,正方体的体积是多少立方分米?最多能切成几个这样的正方体?11.有一个长方体的铁块,底面积是,高是4cm.把它锻造成一个截面是正方形的长方体,截面长是4cm(锻造的过程中没有损耗).求这个长方体的长是多少厘米.12.用右面的两块铁皮做一个无盖的长方体水箱。
(1)做好后里外都刷上防锈漆,刷漆的面积是多少?(2)这个水箱的容积是多少升?(忽略铁皮厚度和接头)13.一块正方体铁锭,棱长5分米.每立方分米的铁重7.8千克,这块铁锭重多少千克?14.一个长方体油箱的容积是30升.已知这个油箱底面长3分米,宽2.5分米,油箱的深是多少分米?(用方程解)15.有一个长方体,高2米,底面的周长是14米,宽3米.这个长方体的体积是多少?16.有一个正方体,底面周长是32分米,这个正方体的体积是多少?17.一个长方形水箱,长5分米,宽4分米,高3分米.装满水后倒入一个棱长是5分米的水箱内,水深多少分米?18.如图所示,在一个大长方体中挖去一个小长方体,求这个物体的表面积和体积.(单位:厘米)(按表面积、体积的顺序填写)19.一辆运土机运了36立方米的沙子,准备铺在一个长45米,宽20米的长方体沙坑里,所铺沙子的厚度是多少厘米?20.一个从里面量长和宽都是10厘米,高14厘米的长方体容器,装有8厘米深的水,现将一个铁球浸没在水中,这时量得水深是12厘米,铁球的体积是多少立方厘米?21.一个正方体容器,从里面量棱长是10厘米。
表面积和体积练习题

求表面积:1、一个长方体的铁皮水箱,长和宽都是2.5dm,深6dm。
做这样一个水箱,至少需要铁皮多少平方分米?(水箱有盖)2、一个长方体罐头盒,底面长13cm、宽7cm,高8.5cm。
如果在盒的四周贴上商标纸(上、下面不贴),这张商标纸的面积至少多少平方厘米?3、五年级同学向贫困地区捐款。
小刚把一个长50cm、宽40cm、高24cm的长方体纸箱各面都贴上了红纸作为捐款箱,除去上面捐款口的面积为350c㎡。
至少需要多少平方分米的红纸?4、一个长方体包裹,它的长、宽、高分别是4dm、3dm、2dm。
如果实际用纸是表面积的1.4倍,包装这个包裹至少要用多少平方分米的包装纸?5、一个房间长6m、宽3.5m、高3m,门窗面积是8㎡。
现在要把这个房间的四壁和顶面粉刷水泥漆。
如果每平方米需要水泥漆0.4kg,一共需要多少千克水泥漆?6、一个机器零件(如下图),要在它的前后两个面涂上红色防锈漆,其他漏出的面(底面不涂)涂上灰色防锈漆,涂红色防锈漆和灰色防锈漆的面积各是多少?7、一块正方体木料的棱长是40cm。
这块木料的表面积是多少平方厘米?求体积:1、修路队要给一段长150m、宽20m的水泥路面铺一层5cm厚的沥青,一共需要沥青多少立方米?2、一块正方体木料的棱长是40cm。
这块木料的体积是多少立方厘米?3、爸爸买回一块长方体形状的面包,面包长3dm、宽8cm、高5cm。
爸爸想把它平均分成5个长方体形状的小面包给五年人,每个人分到面包的体积是多少立方厘米?4、王大爷家要用砖砌一段长20m、宽25cm、高2.8m的院墙。
如果每立方米用砖500块,砌这段院墙一共要用多少块砖?5、某县在河道两旁修筑了亲水平台,亲水平台要安装如图所示的长方体、正方体水泥块各80块。
这些水泥块共要用水泥多少立方分米?合多少方?6、一个长方体的无盖玻璃鱼缸,长2m 、宽40cm、高80cm,(1)这个鱼缸的占地面积有多大?(2)做这个鱼缸要用多少平方米的玻璃?(3)这个鱼缸的体积是多少?7、某同学想测一块合金块的体积,他在量筒中放入了3块同等大的合金块,测量结果如图所示。
圆柱、圆锥表面积与体积练习题
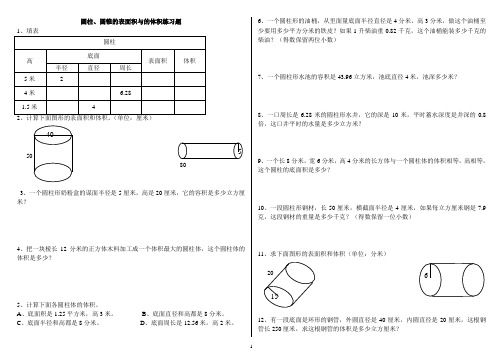
圆柱、圆锥的表面积与的体积练习题2、计算下面图形的表面积和体积。
(单位:厘米)803、一个圆柱形奶粉盒的谋面半径是5厘米,高是20厘米,它的容积是多少立方厘米?4、把一块棱长12分米的正方体木料加工成一个体积最大的圆柱体,这个圆柱体的体积是多少?5、计算下面各圆柱体的体积。
A 、底面积是1.25平方米,高3米。
B 、底面直径和高都是8分米。
6、一个圆柱形的油桶,从里面量底面半径直径是4分米,高3分米,做这个油桶至少要用多少平方分米的铁皮?如果1升柴油重0.82千克,这个油桶能装多少千克的柴油?(得数保留两位小数)7、一个圆柱形水池的容积是43.96立方米,池底直径4米,池深多少米?8、一口周长是6.28米的圆柱形水井,它的深是10米,平时蓄水深度是井深的0.8倍,这口井平时的水量是多少立方米?9、一个长8分米,宽6分米,高4分米的长方体与一个圆柱体的体积相等,高相等,这个圆柱的底面积是多少?10、一段圆柱形钢材,长50厘米,横截面半径是4厘米,如果每立方厘米钢是7.9克,这段钢材的重量是多少千克?(得数保留一位小数)11、求下面图形的表面积和体积(单位:分米)12、有一段底面是环形的钢管,外圆直径是40厘米,内圆直径是20厘米,这根钢圆柱的体积练习二1、一个圆柱的底面半径是6厘米,高是2分米,求这个圆柱的体积。
2、小刚有一个圆柱形的水杯,水杯的底面半径是5厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1升,小刚一天要喝几杯水?3、一个圆柱形水桶,底面直径和高都是40厘米,用这个水桶容积的85%装水,每升水重1千克,桶中的水大约有多少千克?4、一个底面半径是10米的圆柱形蓄水池,能蓄水2512立方米,若再挖深2米,可蓄水多少立方米?5、一个圆柱形油桶,内底面直径是40厘米,高是50厘米,它的容积是多少升?如果1升柴油重0.85千克,这具油桶可装柴油多少千克?(得数保留整千克)6、一个圆柱形玻璃杯底面半径是10厘米,里面装不水,水的高度是12厘米,把一小块铁块放进杯中,水上升到15厘米,这块铁块重多少克?(每立方厘米铁重7.8克)7、下图是一个长15厘米,宽6厘米、高15个底面半径为5厘米的圆柱形空洞,求这个零件的体积。
(五年级下册数学)计算图形的表面积和体积练习题
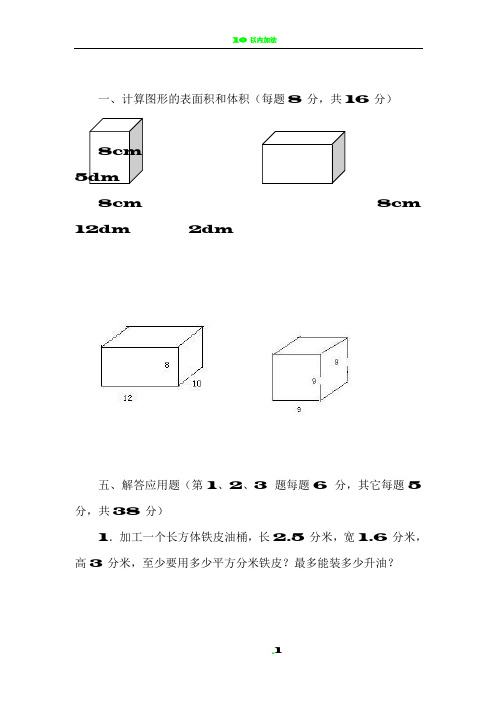
一、计算图形的表面积和体积(每题8分,共16分)
8cm
5dm
8cm 8cm 12dm 2dm
五、解答应用题(第1、2、3题每题6分,其它每题5分,共38分)
1.加工一个长方体铁皮油桶,长2.5分米,宽1.6分米,高3分米,至少要用多少平方分米铁皮?最多能装多少升油?
2.学校要挖一个长方形状沙坑,长4米,宽2米,深0.4米,它占地多少平方米?需要挖出多少立方米的黄沙?
3.做一个棱长是6分米的正方形无盖鱼缸,需要玻璃多少平方分米?它的容积是多少升?
4.把一块棱长8厘米的正方体钢坯,锻造成长3.2分米,宽1分米的长方体钢板,这钢板有多厚?(损耗不计)
5.一个长方体机油桶,长8分米,宽2分米,高6分米.如果每升机油重720克,可装机油多少千克?
6.在一个长20m,宽8m,深1.6m的长方体蓄水池的底面和四周贴瓷砖,瓷砖是边长为2dm的正方形,贴完共需瓷砖多少块?
7.一个底面长和宽都是2分米的长方体玻璃容器,里面装有5升水,将一个铁球浸没在水中,这时水深1.5分米。
这个铁球的体积是多少?。
人教版小升初数学复习专项《立体图形的表面积和体积》能力达标卷

人教版小升初数学复习专项《立体图形的表面积和体积》能力达标卷一、基础题1、把底面积是20平方厘米的两个相等的正方体拼成一个长方体,长方体的表面积是多少?2、用两个长、宽、高分别是9厘米、7厘米、4厘米的相同长方体,拼成一个大长方体,有几种拼法?拼成的长方体的表面积分别是多少?3、把19个棱长是3厘米的小正方体重叠在一起,如图所示,拼成一个立体图形,求这个立体图形的表面积?4、有一个正方体,棱长是10厘米,如果把这个正方体切成棱长是5厘米的小正方体,那么这些小正方体的表面积的和比原正方体的表面积多多少平方厘米?5、一个长是30厘米,横截面是正方形的长方体,如果它的长增加5厘米,表面积就增加80平方厘米,求原长方体的表面积?二、提高题1、从一个棱长是10厘米的正方体木块上挖去一个长10厘米,宽2厘米,高2厘米的小长方体,剩下部分的表面积是多少?2、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长是2厘米的小正方体,剩下部分的表面积是多少?3、一个长方体,如果长增加2厘米,则体积增加40立方厘米;如果宽增加3厘米,则体积增加90立方厘米;如果高增加4厘米,则体积增加96立方厘米。
求原长方体的表面积?4、一个长方体的所有棱长之和是192厘米,长、宽、高的比是7:5:4,这个长方体的体积是多少立方厘米?5、有一个正方体,如果它的高增加2厘米,就成了长方体,这个长方体的表面积比原来正方体的表面积增加96平方厘米,原来正方体的表面积和体积各是多少?6、一个长2米的长方体,沿着长截成相等的6段后,表面积增加了3.6平方米,求原来的长方体的体积?7、有一块长方形的铁皮,长是30厘米,宽是20厘米。
在这块铁皮的四个角上各剪下一个边长是4厘米的正方形后,再将剩下的部分焊接成一个无盖的长方体铁盒,求这个铁盒的表面积和体积?8、有一个长方体,它的正面和上面的面积之和是209,如果它的长、宽、高都是质数,这个长方体的体积是多少?三、竞赛题1、用3个正方体木块堆成的多面体,其中下面的正方体的棱长为10厘米,而上面的正方体下底面的4个顶点分别是其下面正方体上底面各边的中点.那么,这个多面体的表面积是多少平方厘米?2、如图所示,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积?3、一个底面是正方形的长方体木块被锯掉一部分,变成如图所示的图形,其中最长的边DH=8厘米,最短的边AB=BC=CD=DA=BF=4厘米,求这个几何体的体积是多少立方厘米?4、一个长方体的表面积是67.92平方分米,底面的面积是19平方分米,底面周长是17.6分米,这个长方体的体积是多少立方分米?(32.3)立体图形的表面积和体积能力达标卷(一)答案解析一、基础题1、答案:200平方厘米解析:把两个相同是正方体拼成一个长方体,这个长方体的表面积比原来两个正方体的表面积的和减少了两个面面的面积。
【典型习题系列】人教版小学数学五年级下册典型习题系列之期中专项练习:求不规则立体图形的表面积及体积(

五年级数学下册典型例题系列之
期中专项练习:求不规则立体图形的表面积与体积
(原卷版)
1.计算下面图形的表面积和体积。
2.求下面图形的表面积和体积。
3.分别求出下面图形的表面积和体积。
(单位:cm)
4.计算图形的表面积和体积。
(单位:cm)
5.求下列图形的表面积和体积。
(单位:cm)
6.计算下面图形的体积。
7.下图是长方体和正方体的展开图,根据图上数据,求出表面积和体积。
8.求下面组合体的体积。
(单位:cm)
9.计算下面几何体的体积。
10.如下图,求其表面积和体积。
(单位:cm)
11.算一算。
求下图的表面积和体积。
(单位:厘米)
12.下图是用棱长为2厘米的正方体堆成的立体图形,求这个立体图形的表面积
和体积。
13.一个机器零件水平放置的形状如下图所示,请计算它的占地面积和体积。
14.计算下面图形的体积。
(单位:dm)
15.计算下面图形的表面积和体积。
(单位:cm)
16.下面是小红测量土豆体积所做的实验,请你计算出该土豆的体积。
(单位:cm)
17.求下列图形的体积。
18.求下图的表面积。
(单位:dm)
19.求下面图形的体积。
(单位:厘米)
20.如图,计算这块空心砖的表面积。
(单位:厘米)。
长方体正方体体积应用题100题(带答案)
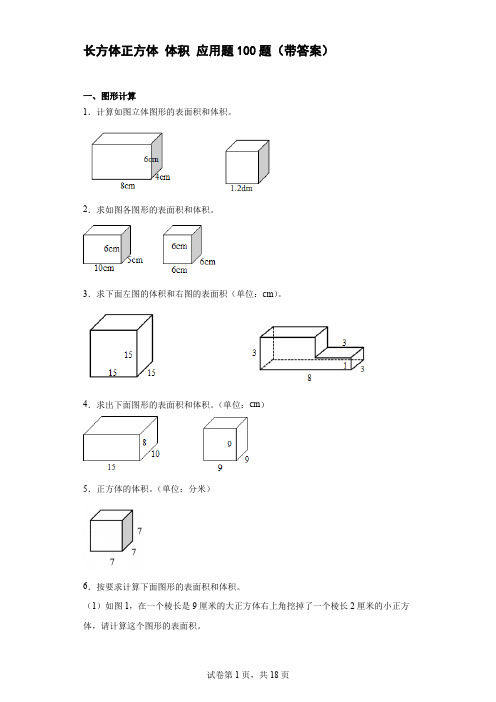
长方体正方体体积应用题100题(带答案)一、图形计算1.计算如图立体图形的表面积和体积。
2.求如图各图形的表面积和体积。
3.求下面左图的体积和右图的表面积(单位:cm)。
4.求出下面图形的表面积和体积。
(单位:cm)5.正方体的体积。
(单位:分米)6.按要求计算下面图形的表面积和体积。
(1)如图1,在一个棱长是9厘米的大正方体右上角挖掉了一个棱长2厘米的小正方体,请计算这个图形的表面积。
(2)如图2,是由若干棱长1厘米的小正方体堆成的,请计算这个图形的体积。
7.计算下面长方体的表面积和体积。
8.长方体的两个面如下。
(单位:cm)体积:表面积:9.计算下图的体积和表面积。
(单位:cm)10.求下面图形的表面积和体积。
(单位:dm)11.计算下面几何体的体积。
12.求出图形的表面积和体积。
13.计算正方体的体积。
14.求体积。
(单位:厘米)15.求图形的表面积和体积。
16.求下列图形的表面积和体积。
17.求下面各立方体的表面积和体积。
(单位:厘米)18.计算下面长方体的表面积和体积。
19.计算下面立体图形的表面积和体积。
(单位:dm)20.求长方体的体积。
21.求长方体的表面积和棱长之和;正方体的表面积和体积。
22.计算下面图形的表面积和体积。
23.计算下面图形的体积。
24.求体积。
(单位:cm)25.计算下面几何体的表面积和体积。
(单位:cm)(1)(2)26.求下面正方体和长方体的表面积和体积。
(单位:厘米)27.计算下图形的表面积和体积。
(单位:cm)28.计算下面图形的表面积和体积。
29.求下列图形的表面积和体积。
(单位:cm)表面积:体积:30.计算下列图形的表面积和体积。
(单位:厘米)31.计算下面图形的体积。
32.求正方体的表面积和体积。
(单位:cm)33.下图是长方体和正方体的展开图,根据图上数据,求出表面积和体积。
34.分别求出下面正方体的表面积和长方体的体积。
(单位:dm)35.计算下面长方体和正方体的表面积和体积。
五年级下册数学专项图形表面积和体积

五下数学专项图形表面积和体积1.计算下面长方体的表面积和体积。
(单位:厘米)解:长方体的表面积:(9×6+9×5+6×5)×2=(54+45+30)×2=129×2=258(平方厘米)长方体的体积: 9×5×6 =45×6 =270(立方厘米)2.计算下面图形的体积。
(单位:分米)3.2×12.5×3=40×3=120(立方分米)3.计算下面图形的表面积。
(单位:厘米)4×4×6=16×6=96(平方厘米)4.求下面图形的表面积和体积。
表面积=(5×5+5×3+5×3)×2+2×2×6-2×2×2=(25+15+15)×2+24-8=55×2+24-8=110+24-8=126(平方厘米)体积=5×5×3+2×2×2=75+8=83(立方厘米)。
5.求下面图形的表面积和体积。
(单位:dm)解:6×6×6=216dm26×6×6-2×3×2=204dm3答:这个图形的表面积是dm2;体积是204dm3。
6.一块长方形铁皮(如图),从四个角各切掉一个边长为3cm的正方形,然后做成盒子.这个盒子用了多少铁皮?它的容积有多少?解:①26×21﹣3×3×4=546﹣36=510(平方厘米)②(26﹣3×2)×(21﹣3×2)×3,=(26﹣6)×(21﹣6)×3,=20×15×3,=900(立方厘米)答:这个盒子用了510平方厘米铁皮;它的容积是900立方厘米.7.如图是一个长方体的表面展开图,求这个长方体的表面积和体积.(单位厘米)解:长方体的长是10厘米,宽是15厘米,高是(32-10×2)÷2=6(厘米),表面积为:10×15×2+10×6×2+15×6×2=300+120+180=600(平方厘米);体积为:10×15×6=900(立方厘米).答:表面积为600平方厘米,体积为900立方厘米.8.求下面图形的表面积和体积(单位:分米)。
长方体正方体表面积及体积练习题整理版

稍复杂的长方体和正方体的体积和表面积练习一、填空1、一个长方体的棱长总和是48cm,宽是2cm,长是宽的2倍,它的表面积是()。
2、一个长方体方木,长2m,宽和厚都是30cm,把它的长截成2段,表面积增加()。
3、长方体中最多可以有()条棱的长度相等,最少有()条棱的长度相等.4、两个完全相同的长方体,长10cm,宽7cm,高4cm,拼成一个表面积最大的长方体后,表面积是( ),比原来减少了();如果拼成一个表面积最小的长方体,表面积是( ),比原来减少了()。
5、一个正方体的棱长总和是48厘米,它的表面积是()。
二、选择1、一个棱长是1分米的正方体木块,横截成三个体积相等的小长方体后,表面积增加了()A、2平方分米B、4平方分米C、6平方分米2、大正方体棱长是小正方体棱长的3倍,大正方体的表面积是小正方体表面积的()倍。
A、3 B、6 C、93、一个正方体表面积是150平方厘米,把它平均分成两个长方体,每个长方体的表面积是()A、75平方厘米B、100平方厘米C、90平方厘米4、一个长方体有四个面的面积相等,则其余两个面是()A、长方形B、正方形C、不一定5、挖一个长8米、宽6米、深4。
5米的长方体水池,这个水池的占地面积至少是()A、48平方米B、44平方米C、36平方米D、222平方米三、计算1、一个长方体的12条棱长总和是64厘米,侧面是一个周长为24厘米的长方形,它的长是多少?2、粮店售米用的长方体木箱(上面没有盖),长1。
2米,宽0。
6米,高0.8米,制作这样一个木箱至少要用木板多少平方米?3、把一个长方体和一个正方体拼成一个新的长方体,这个新长方体的表面积比原来的长方体的表面积增加了80平方厘米,求正方体的表面积。
4、一个长方体的木块,截成两个完全相等的正方体。
两个正方体棱长之和比原来长方体棱长之和增加40厘米,求原长方体的长是多少厘米?5、用三个长3厘米,宽2厘米,高1厘米的长方体拼成一个表面积最小的大长方体,这个长方体的表面积是多少平方厘米?6、一个小食堂长10米,宽8米,高5米,要粉刷四壁和顶棚。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、计算图形的表面积和体积(每题8分,共16分)
8cm 5dm 8cm 8cm 12dm 2dm
五、解答应用题(第1、2、3题每题6分,其它每题5分,共38分)1.加工一个长方体铁皮油桶,长分米,宽分米,高3分米,至少要用多少平方分米铁皮最多能装多少升油
2.学校要挖一个长方形状沙坑,长4米,宽2米,深米,它占地多少平方米需要挖出多少立方米的黄沙
3.做一个棱长是6分米的正方形无盖鱼缸,需要玻璃多少平方分米它的容积是多少升
4.把一块棱长8厘米的正方体钢坯,锻造成长分米,宽1分米的长方体钢板,这钢板有多厚(损耗不计)
5.一个长方体机油桶,长8分米,宽2分米,高6分米.如果每升机油重720克,可装机油多少千克
6.在一个长20m,宽8m,深的长方体蓄水池的底面和四周贴瓷砖,瓷砖是边长为2dm的正方形,贴完共需瓷砖多少块
7.一个底面长和宽都是2分米的长方体玻璃容器,里面装有5升水,将一个铁球浸没在水中,这时水深分米。
这个铁球的体积是多少。
